- 1Department of Civil and Environmental Engineering, The Hong Kong Polytechnic University, Kowloon, Hong Kong SAR, China
- 2National Engineering Research Center on Rail Transit Electrification and Automation (Hong Kong Branch), Kowloon, Hong Kong SAR, China
Bayesian uncertainty quantification has a pivotal role in structural identification, yet the posterior distribution estimation of unknown parameters and system responses is still a challenging task. This study explores a novel method, named manifold-constrained Gaussian processes (GPs), for the probabilistic identification of multi-DOF structural dynamical systems, taking shear-type frames subjected to ground motion as a demonstrative paradigm. The key idea of the method is to restrict the GPs (priorly defined over system responses) on a manifold that satisfies the equation of motion of the structural system. In contrast to widely used Bayesian probabilistic model updating methods, the manifold-constrained GPs avoid the numerical integration when formulating the joint probability density function of unknown parameters and system responses, hence achieving an accurate and computationally efficient inference for the posterior distributions. An eight-storey shear-type frame is analyzed as a case study to demonstrate the effectiveness of the manifold-constrained GPs. The results indicate the posterior distributions of system responses, and unknown parameters can be successfully identified, and reliable probabilistic model updating can be achieved.
1 Introduction
The identification of structural systems, formulated as an inverse problem, refers to any systematic way of updating the model of a structure through the use of experimental data. The main purpose of structural identification is to correlate the model and the real system for the purpose of, for example, reliable estimates of performance and vulnerability of the structural system in service (Catbas et al., 2013). In the past decades, numerous structural identification techniques leveraging vibration measurements have been proposed and successfully applied to real-world civil engineering structures. These methods utilize either time-domain or frequency-domain observations (and input-output or output-only data) to inversely map the monitored data onto the corresponding structural parameters, and the parameters can be further used to predict structural response to future dynamic loads or assess the structural conditions (Sun and Betti, 2013). In time-domain identification methods, the difference in vibration responses (e.g., acceleration, velocity, displacement, and strain) between the parameterized model and the real system is directly evaluated. Some innovative methods using (incomplete) output-only time-domain data to identify structural parameters and input force have been developed by Chen and Li (2004), Lu and Law (2007), Sandesh and Shanker (2009), and Sun and Betti (2013). By contrast, the input-output–related methods executed in the time domain could be more intuitive and robust to apply, although more sensor cost would be demanded in the monitoring system. Several researchers have explored input-output–related time-domain methods, such as Behmanesh and Moaveni (2014) and Lei et al. (2019). In frequency-domain identification methods, modal properties such as natural frequencies (Hassiotis and Jeong, 1995), mode shapes (Morassi and Tonon, 2008), frequency response function (Ni et al., 2006; Zhou and Tang, 2021a), and modal strain energy (Shi et al., 2002) are extracted from measured dynamic response data of a structure of interest, and the discrepancies between the identified and model-derived modal properties are utilized for model updating and structural condition assessment. In this study, the structural responses and unknown parameters will be estimated using time-domain data.
As is often the case during the monitoring of structures, uncertainties from various sources exist in the monitored data, making the identification results unreliable or even leading to false results (Beck and Yuen, 2004). Hence, a probabilistic way of structural identification is desirable for many problems. It is well known that the Bayesian methods enable addressal of the uncertainties in structural identification, which account for various sources of uncertainties observed in the real world. Numerous research works have been conducted in pursuit of Bayes’ theorem to compute the posterior distributions of either structural responses or unknown parameters. The traditional methods, such as Bayesian Kalman filters, particle filters, and Markov chain Monte Carlo, are widely applied for the sampling-based inference of posterior distributions (Behmanesh and Moaveni, 2014; Capellari et al., 2015; Li et al., 2016). Ramancha et al. (2020) presented a sequential Monte Carlo method to update a nonlinear finite element model of a full-scale reinforced-concrete bridge subjected to seismic excitations. Parallel model evaluation is a remarkable advantage of the sequential Monte Carlo, which is ideal for updating computationally expensive models. Behmanesh et al. (2015) proposed a hierarchical Bayesian modeling technique for probabilistic finite element model updating, which predicts uncertainty in parameter estimation and captures the inherent time-variability of structural parameters as well. Sun and Betti (2015) proposed a hybrid optimization methodology to implement Bayesian inference in model updating, which could be effectively applied to determine the unknown system parameters and uncertainties over the parameters using a weighted sum of Gaussian distributions. Erazo and Nagarajaiah (2018) applied unscented Kalman filtering to estimate the parameters that define the nonlinear models of structures equipped with negative stiffness systems. Huang et al. (2017) proposed a hierarchical sparse Bayesian learning and Gibbs sampling algorithm to estimate the high-dimensional uncertain parameters which arise from sparse stiffness identification problems. Rocchetta et al. (2018) developed an efficient and robust procedure within the Bayesian model updating framework to detect crack location and size in mechanical components, where an emulator was generated as a substitution for the finite element model to reduce the computational cost and enable on-line Bayesian model updating. Kamariotis et al. (2022) developed a Bayesian model updating–based method to sequentially learn structural deterioration and estimate structural damage evolution over time. Adeagbo et al. (2021) pursued railway ballast damage identification by exploring a time-domain Markov chain Monte Carlo–based Bayesian model updating method, in which a novel stopping criterion was proposed to correctly identify the scaling factors of the system properties.
The GP-based Bayesian modeling is another attractive topic in the Bayesian community, which generally simplifies the priors to be Gaussian and thus effectively alleviates the high-computational cost faced by other Bayesian methods. A multi-task GP method was developed by Wan and Ni (2019) to reconstruct missing structural health monitoring data; specifically, the method enables the modeling of a series of tasks simultaneously. Wan and Ni (2018) presented a moving-window strategy to achieve a reduced-order GP model, which has been effectively used to forecast structural stress responses. Zhou and Tang (2018) proposed a framework based on the combination of a two-level GP emulator and Bayesian inference. The framework employed multi-fidelity data from a full-scale finite element model and a component mode synthesis reduced-order model, which has been successfully applied to update the key parameters of a structural system. Xue et al. (2020) explored the system identification of a ship dynamic model in terms of an improved GP regression algorithm. A mode shape uncertainty quantification approach was proposed by Zhou and Tang (2021b) by using a multi-response GP meta-modeling strategy, which demonstrated computation efficiency for uncertainty quantification of mode shapes at multiple locations. The aforementioned studies have demonstrated the strong capability of GPs in the framework of Bayesian inference and meanwhile, provided new thoughts on probabilistic structural identification.
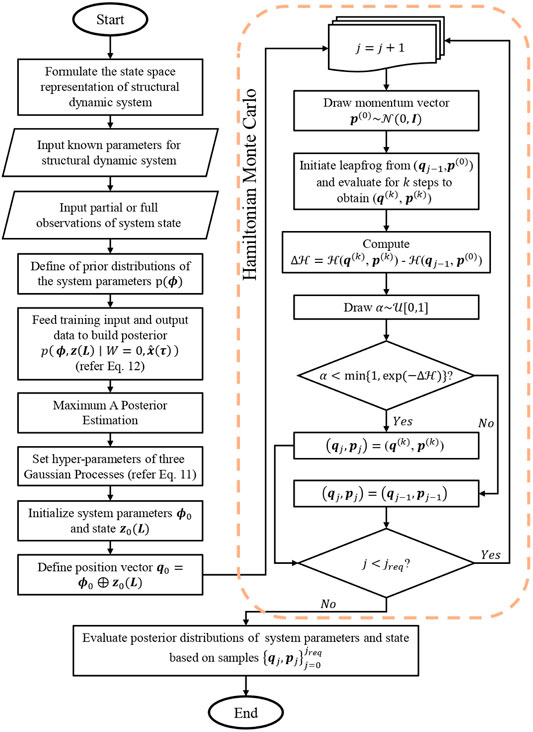
This study pursues a novel manifold-constrained GP approach (Yang et al., 2021) to estimate the joint posterior distribution of unknown structural parameters and dynamical responses. The equation of motion of a shear-type frame structure subjected to ground motion is addressed in the state space. The GP prior is pre-imposed over each system state, explicitly conditioned on a manifold constraint that the derivative of the GPs must satisfy the equation of motion of the structure. The idea behind it is that the probability density function of any multivariate Gaussian distribution has a closed-form expression (Rasmussen and Williams, 2006); whereas, for other types of joint distribution, high-dimensional integration would be inevitable in the formulation. By leveraging the manifold-constrained GPs, the joint posterior distribution of the system state and unknown parameters are decomposed as the multiplication of several multivariate Gaussian distributions and the prior of the unknown parameters, so that the Hamiltonian Monte Carlo method (Neal, 2010) can be effectively implemented to generate samples from the system state which finally makes the samples’ distribution converge to the target posterior distribution. In comparison with other Bayesian methods to conduct probabilistic identification, the advantage of the manifold-constrained GPs is completely avoiding the high-dimensional integration when formulating the posterior distribution function, thus enhancing the inference accuracy and computational efficiency.
This study is organized as follows. Section 2 elucidates the general methodology of the manifold-constrained GPs in application to multi-DOF structures subjected to ground motion. Section 3 provides a case study on an eight-storey shear-type building to explore the efficacy of the proposed method, from which the results show that the posterior distribution of the unknown structural parameters and system state can be successfully identified under different levels of noise. Conclusions are drawn in Section 4.
2 Basic Formulations
2.1 Gaussian Process
Let X be a variable set and
We assumed that a set of label pairs
where
In the implementation of GP regression, gradients of the marginal likelihood in Eq. 3 with respect to all unknown parameters
2.2 Manifold-Constrained GPs for Structural Dynamical Systems
Consider a discrete
in which the state vector
where
where
where
The goal of performing the manifold-constrained GPs for structural dynamical systems is to probabilistically identify damping and stiffness parameters
where
where for simplicity, we denote
The term on the right-hand side can be decomposed as
Here, the first term
in which the components
where
3 Results
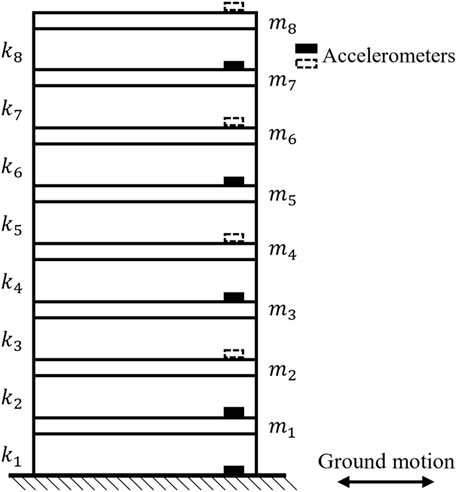
An eight-storey building simplified as a shear-type frame structure with masses lumped at each floor is shown in Figure 2. The simplified model has eight DOFs in the horizontal direction. First, it is assumed that there are nine accelerometers instrumented, eight being mounted on the structure and one on the ground. The total displacement and velocity at each DOF and at the ground are obtained by integrating the collected acceleration data series, and the relative displacement and velocity of each floor with respect to the ground could be computed according to the relationship
Figure 3 shows a fragment of the identified displacement and velocity of the third floor under different levels of noise corruption, namely, 0, 5, and 10% root mean square white noise added to the original observations. The identified results fit well with the correct displacement and velocity responses. With the noise level getting higher, the identified confidence intervals generally become wider. Figure 4 elucidates the histograms of the estimated stiffness and damping parameters using the manifold-constrained GPs. Each histogram is generated over 100 parameter sets in the simulation process of the Hamiltonian Monte Carlo, where 0, 5, and 10% root mean square white noise is, respectively, added to the original observations. For computational efficiency, the stiffness and damping parameters are normalized by default. It is seen that the results rigorously reflect the uncertainty over the parameters, for instance, the uncertainty indicated by the blue histogram is greater than that in the green and red histograms which are obtained from observations with lower noise levels. It is noted that the uncertainties on the damping constants a and b are higher than those on the stiffness parameters under the same noise corruption level. This is possibly because the damping constants are more sensitive than the stiffness parameters to noise. The input responses computed by the fourth-order Runge–Kutta method may initially pose noise to the estimation process, especially in the case of ground motion with relatively high frequencies.
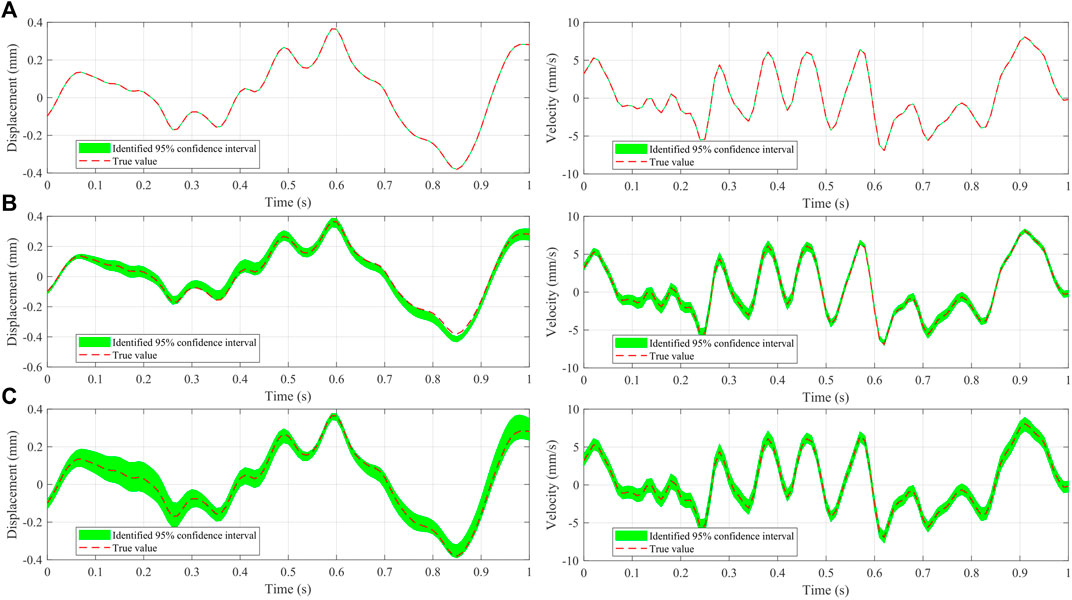
FIGURE 3. Identified displacement and velocity fragments of the third floor under three levels of noise corruption. (A) 0% noise corruption. (B) 5% noise corruption. (C) 10% noise corruption. The red dotted line denotes the true trajectory. The green area represents the identified 95% confidence interval.
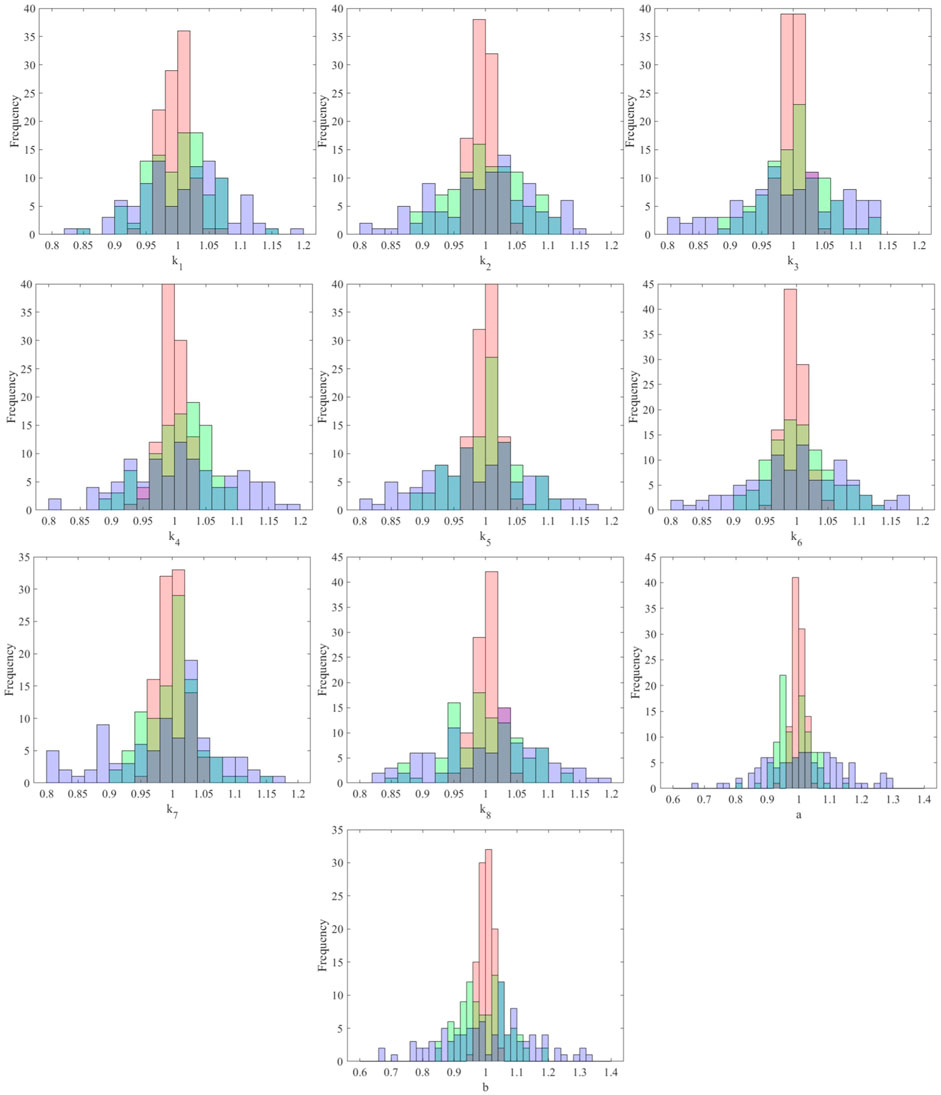
FIGURE 4. Histograms of estimated normalized stiffness and damping parameters over 100 simulated parameter sets under three levels of noise corruption. Red: 0% noise corruption. Green: 5% noise corruption. Blue: 10% noise corruption. The vertical black line is the true parameter value.
According to the basic formulation of the proposed method, the joint posterior distributions of structural parameters and responses under the condition of
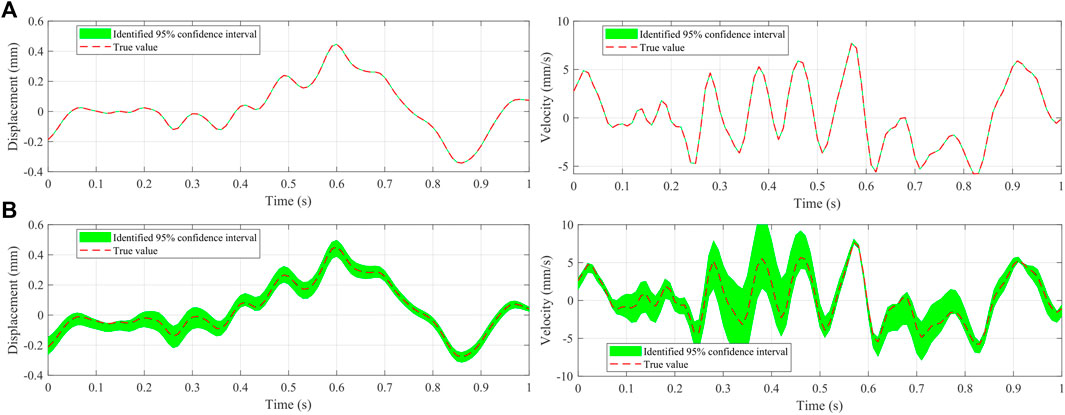
FIGURE 5. Identified displacement and velocity fragments under partial observations. (A) Displacement and velocity responses on the fifth floor. (B) Displacement and velocity responses on the sixth floor. The red dotted line denotes the true trajectory. The green area represents the identified 95% confidence interval.
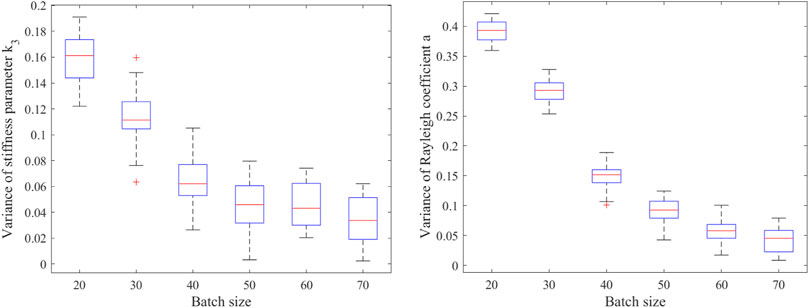
In the above implementation of the manifold-constrained GPs, all batches were set to contain 50 signal points in order to avoid the impact of batch size on the uncertainty quantification results. Our simulation studies using the manifold-constrained GPs show that the uncertainty can be further lowered when the batch size gets bigger, that is, when more signal points are contained in each batch. However, the enlargement of batch size could lead to computational inefficiency because more variables (the new signal points) are involved and their uncertainties need to be evaluated in each single Hamiltonian Monte Carlo sampling process. Therefore, for practical engineering applications using the manifold-constrained GPs, there is a trade-off between the reduction of uncertainties and the enhancement of computational efficiency. To gain an insight into how exactly the batch size affects the uncertainties of the estimated structural parameters and responses, we compare six different batch sizes containing 20, 30, 40, 50, 60, and 70 signal points, respectively. For each batch size, 20 fragments (with 5% noise corruption) are generated and evaluated by the manifold-constrained GPs. The variances of the stiffness parameter
4 Conclusion
In this study, a manifold-constrained GP approach is explored to estimate the joint posterior probability distributions of the unknown parameters and system state of multi-DOF structures subjected to ground motion. The formulation of the manifold-constrained GPs is intrinsically based on compelling the derivatives of GPs to satisfy the equation of motion of the structural dynamical system. In this approach, the posterior distribution of the unknown parameters and system state is decomposed to be the function of several multivariate Gaussian distributions and the prior distribution of the parameters, in such a way that the high-dimensional integral is avoided in computing joint posterior distributions of the unknown parameters and system state. Thus, the manifold-constrained GPs could provide accurate and computationally efficient inference for multi-DOF systems as addressed in this study. In the case study, the posterior distributions of the system state and unknown parameters are successfully identified in both full observation and partial observation scenarios, from which model updating and damage identification could be further pursued.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
SH: Conceptualization, methodology, software, validation, writing—original draft, and visualization. Y-QN: Conceptualization, supervision, funding acquisition, project administration, and writing—review and editing. S-MW: Conceptualization and supervision.
Funding
The research described in this study was supported by a grant from the Research Grants Council of the Hong Kong Special Administrative Region (SAR), China (Grant no. PolyU 152014/18E); a grant from the National Natural Science Foundation of China (Grant no. U1934209); and grants from Wuyi University’s Hong Kong and Macao Joint Research and Development Fund (Grants nos. 2019WGALH15 and 2019WGALH17). The authors would also like to appreciate the funding support by the Innovation and Technology Commission of the Hong Kong SAR Government to the Hong Kong Branch of the Chinese National Rail Transit Electrification and Automation Engineering Technology Research Center (Grant no. K-BBY1).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Adeagbo, M. O., Lam, H.-F., and Ni, Y. Q. (2021). A Bayesian Methodology for Detection of Railway Ballast Damage Using the Modified Ludwik Nonlinear Model. Eng. Struct. 236, 112047. doi:10.1016/j.engstruct.2021.112047
Beck, J. L., and Yuen, K.-V. (2004). Model Selection Using Response Measurements: Bayesian Probabilistic Approach. J. Eng. Mech. 130, 192–203. doi:10.1061/(asce)0733-9399(2004)130:2(192)
Behmanesh, I., Moaveni, B., Lombaert, G., and Papadimitriou, C. (2015). Hierarchical Bayesian Model Updating for Structural Identification. Mech. Syst. Signal Process. 64-65, 360–376. doi:10.1016/j.ymssp.2015.03.026
Behmanesh, I., and Moaveni, B. (2014). Probabilistic Identification of Simulated Damage on the Dowling Hall Footbridge through Bayesian Finite Element Model Updating. Struct. Control Health Monit. 22, 463–483. doi:10.1002/stc.1684
Capellari, G., Eftekhar Azam, S., and Mariani, S. (2015). Damage Detection in Flexible Plates through Reduced-Order Modeling and Hybrid Particle-Kalman Filtering. Sensors 16, 2. doi:10.3390/s16010002
Catbas, F. N., Kijewski-Correa, T., and Aktan, A. E. (2013). Structural Identification of Constructed Systems. Reston: ASCE Press.
Chen, J., and Li, J. (2004). Simultaneous Identification of Structural Parameters and Input Time History from Output-Only Measurements. Comput. Mech. 33, 365–374. doi:10.1007/s00466-003-0538-9
Erazo, K., and Nagarajaiah, S. (2018). Bayesian Structural Identification of a Hysteretic Negative Stiffness Earthquake Protection System Using Unscented Kalman Filtering. Struct. Control Health Monit. 25, e2203. doi:10.1002/stc.2203
Hassiotis, S., and Jeong, G. D. (1995). Identification of Stiffness Reductions Using Natural Frequencies. J. Eng. Mech. 121, 1106–1113. doi:10.1061/(asce)0733-9399(1995)121:10(1106)
Huang, Y., Beck, J. L., and Li, H. (2017). Bayesian System Identification Based on Hierarchical Sparse Bayesian Learning and Gibbs Sampling with Application to Structural Damage Assessment. Comput. Methods Appl. Mech. Eng. 318, 382–411. doi:10.1016/j.cma.2017.01.030
Kamariotis, A., Chatzi, E., and Straub, D. (2022). Value of Information from Vibration-Based Structural Health Monitoring Extracted via Bayesian Model Updating. Mech. Syst. Signal Process. 166, 108465. doi:10.1016/j.ymssp.2021.108465
Lei, Y., Xia, D., Erazo, K., and Nagarajaiah, S. (2019). A Novel Unscented Kalman Filter for Recursive State-Input-System Identification of Nonlinear Systems. Mech. Syst. Signal Process. 127, 120–135. doi:10.1016/j.ymssp.2019.03.013
Li, P. J., Xu, D. W., and Zhang, J. (2016). Probability-based Structural Health Monitoring through Markov Chain Monte Carlo Sampling. Int. J. Str. Stab. Dyn. 16, 1550039. doi:10.1142/s021945541550039x
Lu, Z. R., and Law, S. S. (2007). Identification of System Parameters and Input Force from Output Only. Mech. Syst. Signal Process. 21, 2099–2111. doi:10.1016/j.ymssp.2006.11.004
Morassi, A., and Tonon, S. (2008). Dynamic Testing for Structural Identification of a Bridge. J. Bridge Eng. 13, 573–585. doi:10.1061/(asce)1084-0702(2008)13:6(573)
Neal, R. M. (2010). “MCMC Using Hamiltonian Dynamics,” in Handbook of Markov Chain Monte Carlo. Editors S. Brooks, A. Gelman, G. Jones, and X. L. Meng (Boca Raton: CRC Press), 113–162.
Ni, Y. Q., Zhou, X. T., and Ko, J. M. (2006). Experimental Investigation of Seismic Damage Identification Using PCA-Compressed Frequency Response Functions and Neural Networks. J. Sound Vib. 290, 242–263. doi:10.1016/j.jsv.2005.03.016
Raissi, M., Perdikaris, P., and Karniadakis, G. E. (2017). Inferring Solutions of Differential Equations Using Noisy Multi-Fidelity Data. J. Comput. Phys. 335, 736–746. doi:10.1016/j.jcp.2017.01.060
Ramancha, M. K., Astroza, R., Conte, J. P., Restrepo, J. I., and Todd, M. D. (2020). Bayesian Nonlinear Finite Element Model Updating of a Full-Scale Bridge-Column Using Sequential Monte Carlo. Model. Validation Uncertain. Quantification 3, 389–397. doi:10.1007/978-3-030-47638-0_43
Rasmussen, C. E., and Williams, C. K. I. (2006). Gaussian Processes for Machine Learning. Cambridge: MIT Press.
Rocchetta, R., Broggi, M., Huchet, Q., and Patelli, E. (2018). On-line Bayesian Model Updating for Structural Health Monitoring. Mech. Syst. Signal Process. 103, 174–195. doi:10.1016/j.ymssp.2017.10.015
Sandesh, S., and Shankar, K. (2009). Time Domain Identification of Structural Parameters and Input Time History Using a Substructural Approach. Int. J. Str. Stab. Dyn. 09, 243–265. doi:10.1142/s0219455409003016
Shi, Z. Y., Law, S. S., and Zhang, L. M. (2002). Improved Damage Quantification from Elemental Modal Strain Energy Change. J. Eng. Mech. 128, 521–529. doi:10.1061/(asce)0733-9399(2002)128:5(521)
Sun, H., and Betti, R. (2015). A Hybrid Optimization Algorithm with Bayesian Inference for Probabilistic Model Updating. Computer-Aided Civ. Infrastructure Eng. 30, 602–619. doi:10.1111/mice.12142
Sun, H., and Betti, R. (2013). Simultaneous Identification of Structural Parameters and Dynamic Input with Incomplete Output-Only Measurements. Struct. Control Health Monit. 21, 868–889. doi:10.1002/stc.1619
Wan, H.-P., and Ni, Y.-Q. (2018). Bayesian Modeling Approach for Forecast of Structural Stress Response Using Structural Health Monitoring Data. J. Struct. Eng. 144, 04018130. doi:10.1061/(asce)st.1943-541x.0002085
Wan, H.-P., and Ni, Y.-Q. (2019). Bayesian Multi-Task Learning Methodology for Reconstruction of Structural Health Monitoring Data. Struct. Health Monit. 18, 1282–1309. doi:10.1177/1475921718794953
Xue, Y., Liu, Y., Ji, C., Xue, G., and Huang, S. (2020). System Identification of Ship Dynamic Model Based on Gaussian Process Regression with Input Noise. Ocean. Eng. 216, 107862. doi:10.1016/j.oceaneng.2020.107862
Yang, S., Wong, S. W. K., and Kou, S. C. (2021). Inference of Dynamic Systems from Noisy and Sparse Data via Manifold-Constrained Gaussian Processes. Proc. Natl. Acad. Sci. U.S.A. 118, e2020397118. doi:10.1073/pnas.2020397118
Zhou, K., and Tang, J. (2018). Uncertainty Quantification in Structural Dynamic Analysis Using Two-Level Gaussian Processes and Bayesian Inference. J. Sound Vib. 412, 95–115. doi:10.1016/j.jsv.2017.09.034
Zhou, K., and Tang, J. (2021a). Structural Model Updating Using Adaptive Multi-Response Gaussian Process Meta-Modeling. Mech. Syst. Signal Process. 147, 107121. doi:10.1016/j.ymssp.2020.107121
Keywords: multi-DOF structures, earthquake ground motion, time-domain system identification, manifold-constrained Gaussian processes, vibration-based structural health monitoring
Citation: Hao S, Ni Y-Q and Wang S-M (2022) Probabilistic Identification of Multi-DOF Structures Subjected to Ground Motion Using Manifold-Constrained Gaussian Processes. Front. Built Environ. 8:932765. doi: 10.3389/fbuil.2022.932765
Received: 30 April 2022; Accepted: 23 May 2022;
Published: 04 July 2022.
Edited by:
Kai Zhou, Michigan Technological University, United StatesCopyright © 2022 Hao, Ni and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yi-Qing Ni, Y2V5cW5pQHBvbHl1LmVkdS5oaw==
 Shuo Hao
Shuo Hao Yi-Qing Ni
Yi-Qing Ni Su-Mei Wang
Su-Mei Wang