- 1Department of Mechanical Engineering-Engineering Mechanics, Michigan Technological University, Houghton, MI, United States
- 2Department of Mechanical Engineering, University of Connecticut, Storrs, CT, United States
- 3College of Mechanical and Vehicle Engineering, Chongqing University, Chongqing, China
Piezoelectric impedance sensing is promising for highly accurate damage identification because of its high-frequency active interrogative nature and simplicity in data acquisition. To fully unleash the potential, effective inverse analysis is needed in order to pinpoint the damage location and identify the severity. The inverse analysis, however, may be underdetermined since there exists a very large number of unknowns (i.e., locations and severity levels) to be solved in a finite element model but only limited measurements are available in actual practice. To uncover the true damage scenario, an inverse analysis strategy built upon the multi-objective optimization, which aims at matching the multiple sets of measurements with model predictions in the damage parametric space, can be formulated to identify a small set of solutions. This solution set then allows the incorporation of empirical knowledge to facilitate final decision-making. The main disadvantage of the conventional inverse analysis strategy is that it overlooks uncertainties that exist in both baseline structural modeling and actual measurements. To address this, in this research, we formulate a probabilistic multi-objective optimization-based inverse analysis framework, which is fundamentally built upon the differential evolution Markov chain Monte Carlo (DEMC) technique. The new approach can yield the Pareto optimal set (solutions) and the respective Pareto front, which are represented in a probabilistic sense to account for uncertainties. Comprehensive case studies with experimental investigations are conducted to demonstrate the effectiveness of this new approach.
1 Introduction
Structural health monitoring (SHM) has been an important research subject, as it can provide vital information to protect engineering structures from unexpected catastrophic failure. A wide variety of investigations have utilized vibration measurement to conduct SHM tasks. The modal properties such as natural frequencies and mode shapes extracted from the vibration measurement can be used effectively to predict the structural property change due to damage (Cao et al., 2014; Capecchi et al., 2016). However, in actual practice, only lower-order modes can be realistically measured, which, however, are insensitive to small-sized damage. In order to detect and identify small-sized damage, high-frequency measurements with small characteristic wavelengths need to be acquired. One promising class of high-frequency-based detection methods is to use piezoelectric transducers which can yield the impedance or admittance information through active interrogation to facilitate fault detection and identification (Kim et al., 2015; Shuai et al., 2017; Cao et al., 2018; Kim and Wang, 2019). Impedance/admittance-based methods for damage identification rely on inherent electro-mechanical coupling. When a piezoelectric transducer is attached to a host structure, the electrical impedance of the transducer is directly coupled with the impedance of the host structure. As such, the change of the piezoelectric impedance signature can be used as the damage indicator. Owing to the self-sensing interrogative nature whereas the transducers serve as both the actuators and sensors, these methods enable highly sensitive damage detection.
Conducting damage identification generally resorts to the comparison of responses before and after damage occurrence. Leveraging upon finite element (FE) simulation to map the relation between the damage and resulting impedance/admittance response change, damage identification can then be facilitated. This approach falls into the general category of FE model updating which has become the mainstream for damage identification analysis (Zhou and Tang, 2016; Sun et al., 2017; Chen et al., 2020; Zhou and Tang, 2021b). In this approach, the damage is represented by the change of the associated structural properties, for example, mass, stiffness, and damping, and can be inversely identified in light of the measurements. Since it is critical to accurately capture the small change of impedance/admittance response due to damage, the element size should be set very small, resulting in a high-dimensional FE model. It generally leads to high computational costs in model updating. To tackle this issue, a variety of efficient approximators have been explored. Along with the recent development of machine learning technology, surrogate models have been recognized as one effective type of approximator. Once the surrogate model is trained by the credible input–output relations from FE simulations, it can be directly utilized to approximate the output given any input (Khodaparast et al., 2011; Wan and Ren, 2015; Zhou and Tang, 2021a). A noteworthy challenge of the surrogate model-based inverse analysis is its lack of ability to handle noise and uncertainty effects. Moreover, in such data-driven methods, the size and distribution of training data play an important role in dictating damage identification accuracy. The high-fidelity surrogate model may not be ensured over the entire input parametric space, which may cause prediction errors that even exceed the response changes induced by damage. The first-principle-based approximator, on the other hand, may possess higher approximation accuracy than the surrogate model. As one class of first-principle-based approximation methods, sensitivity analysis has been extensively applied (Mottershead et al., 2011; Zhou and Tang, 2015; Shuai et al., 2017; Zhu et al., 2021). The underlying idea of the sensitivity analysis is to calculate the sensitivity matrices based on the FE model using the finite difference concept, which can then be used for rapid response approximation.
Fundamentally, inverse model/damage identification can be cast into an optimization problem that aims at minimizing the difference between the measurements and model prediction in the parametric space. The aforementioned sensitivity-based approach can be viewed as a special treatment for solving such optimization problems. Oftentimes, a single objective function, that is, a holistic error function between the measurement and model prediction, is minimized. In the case of damage identification using piezoelectric impedance/admittance, such a single-objective approach becomes difficult to implement. On the one hand, to predict high-frequency impedance/admittance responses, the mesh density of the FE model has to be high, yielding a very large number of unknowns because the structural damage can occur in an arbitrary region with arbitrary severity in the model. On the other hand, the impedance/admittance measurements remain to be relatively limited. As the number of unknowns is far greater than the available measurement data points, the direct inverse analysis becomes underdetermined. Meanwhile, a single objective optimization generally leads to one single solution. As such, the solution found may not cover the actual damage scenario (Cao et al., 2018).
In comparison, multi-objective optimization can intrinsically yield multiple solutions and thus has much better possibility of capturing the actual damage scenario. Indeed, since multiple measurements are acquired in SHM practice, formulating the multi-objective optimization problem that minimizes the difference of these measurements with respect to the corresponding model prediction in the parametric space is quite intuitive. The multiple solutions obtained can then be further analyzed either through empirical experience or by deploying the additional inspection techniques. Owing to these advantages, some recent investigations have attempted multi-objective optimization in damage identification. Cao et al. (2018) proposed a multi-objective Dividing RECTangles (DIRECT) under embedded sparsity conditions to perform damage identification using the piezoelectric impedance/admittance measurement. Alexandrino et al. (2020) developed a robust framework integrating together a multi-objective genetic algorithm, neural network, and decision-making strategy to solve the damage detection problem. Magacho et al. (2021) used the multi-objective sunflower optimization algorithm to identify the damage in large-scale lattice-type structures. It is, however, worth emphasizing that the aforementioned studies were conducted on the premise that the experimental measurement and numerical FE model are both sufficiently accurate. In practical situations, both the measurement and numerical modeling are inevitably subjected to noise and uncertainties. To tackle this issue, in this research, we propose to develop a new multi-objective optimization approach that can produce solutions in the probabilistic sense to reflect the influence of noise and uncertainty. The key idea is to use statistical methodologies for characterizing sampled solutions that are uniformly scattered around the Pareto optimal set (Zhang et al., 2008). This is realized through integrating the differential evolution MCMC algorithm into the multi-objective optimization framework.
The remainder of this study is organized as follows: Section 2 outlines the new damage identification framework, including the FE-based piezoelectric impedance/admittance modeling and probabilistic multi-objective MCMC optimization. Section 3 provides the case illustrations with experimental investigation. Section 4 summarizes the concluding remarks.
2 Approach Formulation for Damage Identification
2.1 Admittance Measurement-Based Damage Identification Using Sensitivity Concept
The equation of motion of the coupled system consisting of the host structure and piezoelectric transducer with an electric circuit can be written as (Zhou et al., 2014):
where
where
where
In Eq. 5,
According to Eqs 4, 5, the admittance changes are not linearly dependent with respect to the damage index. In order to approximate the linear relationship between the admittance changes and damage index under the small damage assumption, a Taylor series expansion is applied and only the linear terms are kept:
where
The admittance changes can then be written as a linear function of the damage index
where
where
2.1.1 Multi-Objective Markov Chain Monte Carlo for Probabilistic Optimization
Let a continuous multi-objective optimization problem be defined as
where x denotes the m-dimensional decision vector and
Solving the multi-objective optimization shown in Eq. 11 yields a set of trade-off solutions referred to as the Pareto optimal set, which represents the decision vector solutions whose respective objective functions cannot be enhanced in any direction without degrading the other (Zitzler and Thiele, 1999). The Pareto optimal set usually can be determined by evaluating the dominance relations among a set of solutions. A solution
It is worth noting that most of the existing algorithms have been designed to target the Pareto optimal set deterministically. When uncertainties are involved, the probabilistic approach will need to be adopted to yield the Pareto optimal set that is represented in a probabilistic sense. The underlying idea behind such a probabilistic approach is to use statistical methodologies for characterizing sampled solutions that are uniformly scattered around the Pareto optimal set (Zhang et al., 2008). Specifically, we seek solutions in the vicinity of the Pareto optimal set such that the uncertainty effect can be characterized for every dominant solution within the Pareto optimal set. To achieve this, we construct a probability distribution using the MCMC algorithm, which is expressed as (Kirkpatrick et al., 1983):
where T is the simulated temperature.
While the aforementioned MCMC-based optimization concept has already been established, it is generally tailored for the single-objective optimization problem. To extend it into the multi-objective optimization, we specifically need to integrate differential evolution (DE) into the MCMC to form the so-called differential evolution Markov chain Monte Carlo (DEMC) that was originally proposed by Braak (2006). DEMC is a special type of population-based multi-objective Markov chain Monte Carlo (MOMCMC). DEMC involves the multiple Markov chains in parallel to generate new solutions over an entire parameter space based on the current solution. In this approach, a new solution proposal at the tth state of the kth Markov chain is formulated as the sum of its current state and the scaled difference between the current states of two randomly selected chains, given as:
where
When carrying out the DEMC-based sampling to achieve the multi-objective function optimization, special care should be taken in defining the fitness function. While it is seemingly straightforward to use the objective function as the fitness function, its resulting solutions may not be sufficiently diverse. In other words, the solutions may be clustered, and near-Pareto optimal solutions that account for the uncertainty effect will be missing. Therefore, a new fitness function of the individual solution suggested by Li (2012) is defined as:
where
The Metropolis–Hasting (MH) algorithm (Brooks et al., 2011; Zhou and Tang, 2021) is used to determine if the new solution proposed by DE is accepted which recalls Eq. 13. The acceptance probability can then be formulated as:
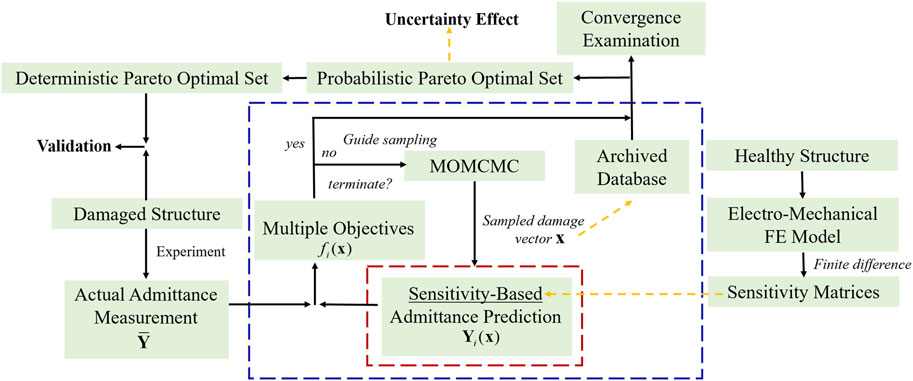
It can be clearly seen that the simulated temperature controls the acceptance rate of the MH transitions. The acceptance rate of each iteration can be calculated, which together with the desired acceptance rate specified, determines the new temperature for the next iteration. When the MOMCMC is executed, its convergence is worth examining considering the trade-off between the computational cost and accuracy. Generally, both the standard convergence indicator and the maximum iteration number defined can be used as a termination criterion. For the sake of implementation, in this research, we terminate the analysis when the maximum iteration number is reached and then use the analysis result to examine the convergence.
Combining all the above-mentioned steps, we can obtain the pseudo-code of MOMCMC for probabilistic optimization as follows:
3 Methodology Demonstration and Case Analysis
In this section, we demonstrate the new methodology through case illustrations. To fully verify the effectiveness of this new methodology, we formulate the two testing cases, both of which are validated through experimental investigations.
3.1 Problem Setup of Case Investigation
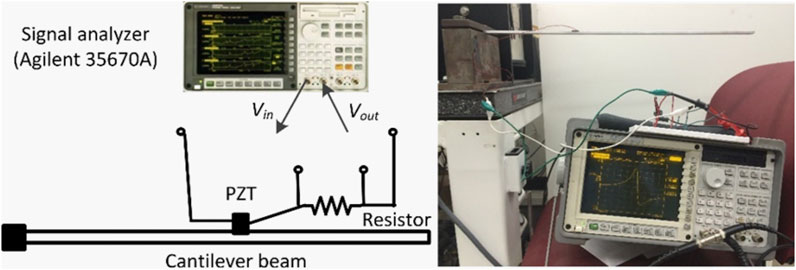
The structure to be investigated is a cantilever aluminum plate that is attached to a piezoelectric transducer. The material and geometrical properties of the plate and piezoelectric transducer are given in Table 1, and the experiment setup is shown in Figure 2. A resistor of 100
In the model updating-based damage identification, an electromechanical FE model accounting for the coupling between the plate and piezoelectric transducer is developed using the in-house MATLAB finite element code. The material and geometrical properties in Table 1 are used to build the FE model. In addition, in the FE model, the piezoelectric and impermittivity constants of the piezoelectric transducer are defined as
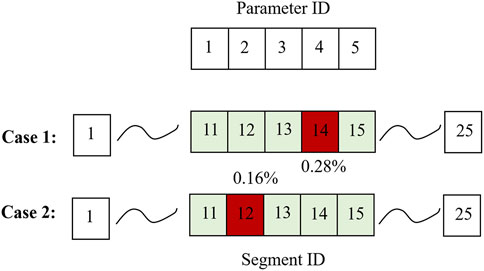
For damage identification illustration, the FE model is divided into 25 segments, which are evenly divided along the length direction of the plate. For the sake of validation, we assume that the 11–15th segments are subjected to damage (Figure 3), leading to a 5-dimensional damage parameter space. The new damage parameter ID is mapped to the segment ID for result visualization. In damage identification using admittance measurements, the admittance changes due to damage occurrence are most evident around the resonant peaks. While there are many resonances that can be used, we choose the resonant frequencies according to our prior knowledge about the damage size and FE model scale. Detecting a smaller size of damage requires a higher frequency response. However, the higher frequency response only can be accurately characterized by a larger-scale FE model with increasing mesh density, resulting in the growing computational cost. By taking such a trade-off into consideration, we eventually acquire the admittance change information around the plate’s 14th (1,893.58 Hz) and 21st (3,704.05 Hz) natural frequencies for subsequent damage identification analysis. For the damage emulations, instead of cutting the plate to reduce the local stiffness, we use the nondestructive method, that is, adding a small mass onto the plate. Mathematically, this results in the resonant frequency shift and admittance change equivalent to a local stiffness reduction. In the first experimental case, a
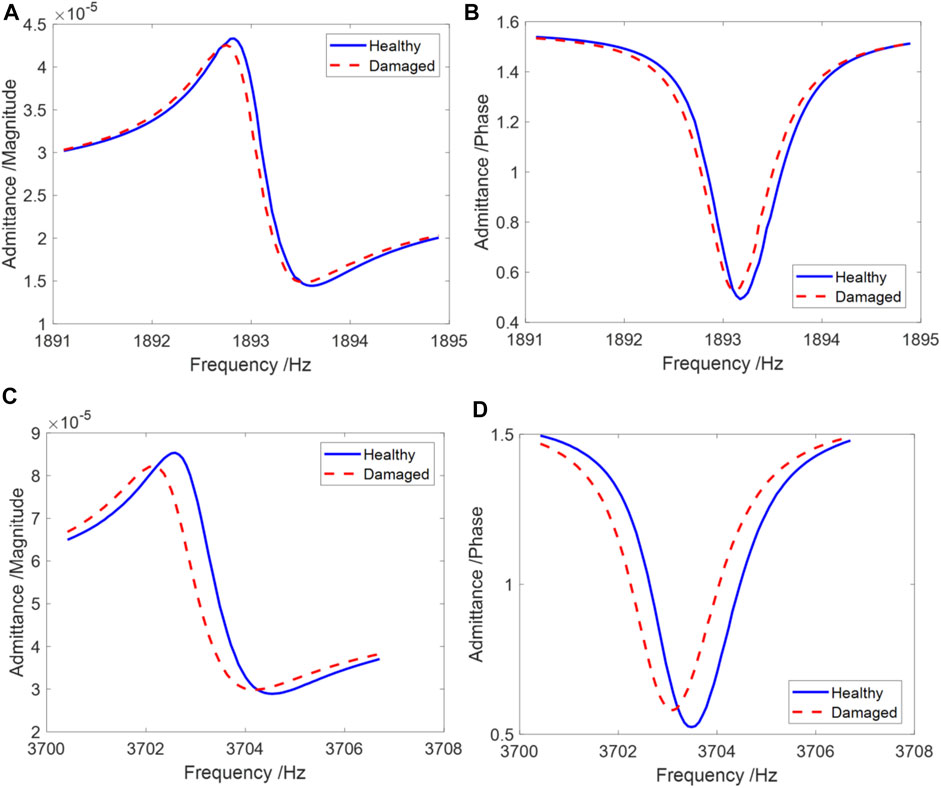
FIGURE 4. Admittance measurements over two frequency bands. (A) Magnitude (lower frequency band); (B) phase (lower frequency band); (C) magnitude (higher frequency band); and (D) phase (higher frequency band).
3.2 Damage Identification Practice on Case 1
We first examine the damage identification result of case 1 using MOMCMC. The operating parameters to execute MOMCMC are defined in Table 2. It is noted that the scaled factor is strictly calculated following the empirical formula mentioned in Section 2. The admittance measurements shown in Figure 4 are used as the evidence information to direct the inverse analysis. As can be seen clearly, the admittance indeed is sensitive to the damage, where the variations of the admittance profile and resonance are noticeable. Following the general form of the optimization problem shown in Eq. 11, we formulate the optimization problem of this inverse model updating analysis as:
where
With the required simulation setup finalized, the inverse analysis can be implemented, and the results are obtained. Figure 5 gives the probabilistic Pareto optimal set, which essentially encompasses the deterministic optimal set. There are a total of 17 solutions identified in the deterministic Pareto optimal set, which all closely agree with the “ground truth” (i.e., 0.28% damage severity of parameter 4). The closest damage severity of parameter 4 in the optimal set is found to be nearly identical to the ground truth, only with
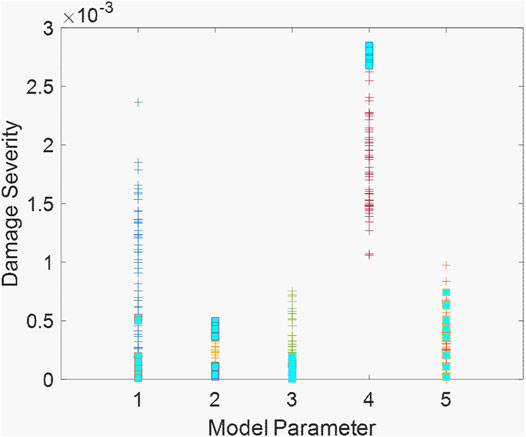
FIGURE 5. Solutions identified in the probabilistic Pareto optimal set (squared markers indicate the deterministic Pareto optimal set).
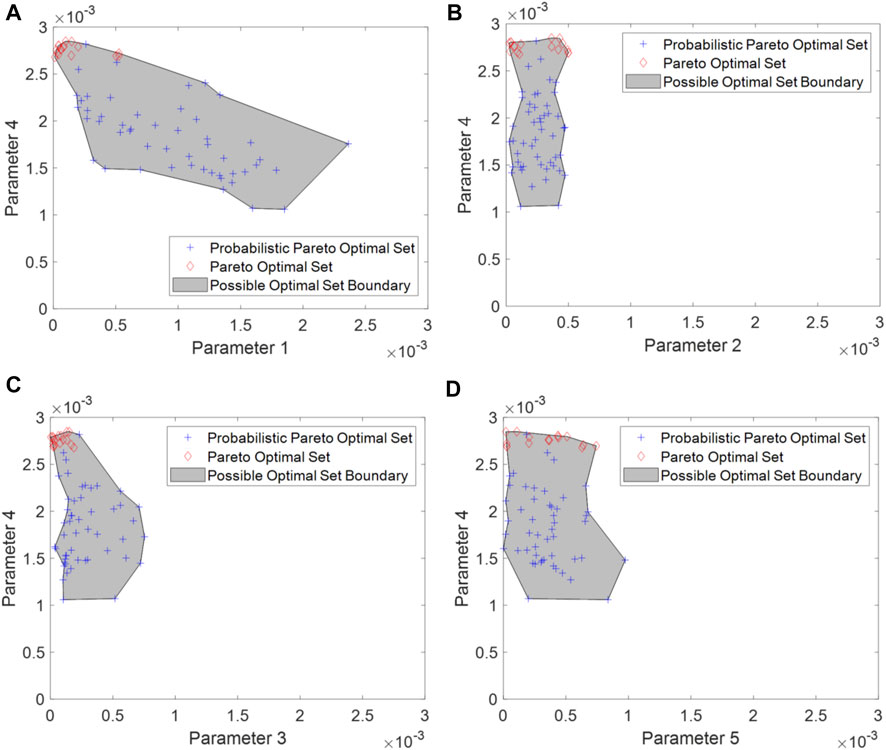
FIGURE 6. Two-dimensional illustration of the probabilistic Pareto optimal set. (A) Parameter 1 versus Parameter 4; (B) Parameter 2 versus Parameter 4; (C) Parameter 3 versus Parameter 4; and (D) Parameter 5 versus Parameter 4 (note: the Pareto optimal set boundary is roughly estimated).
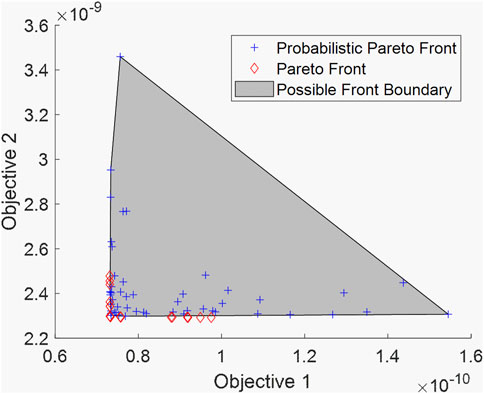
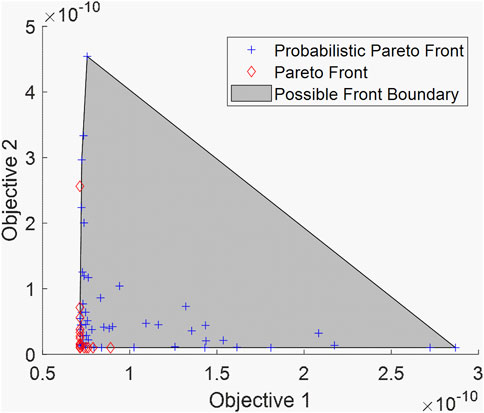
Depending on the probabilistic Pareto optimal set obtained, FE simulation can be implemented accordingly to calculate the admittance response and then identify the associated probabilistic Pareto front with the estimated boundary as shown in Figure 7. Unlike the high-dimensional probabilistic Pareto optimal set, there is no compatibility issue of boundary estimation for the two-dimensional probabilistic Pareto front. The boundary of the probabilistic Pareto front is intrinsically related to the boundary of the probabilistic Pareto optimal set.
As mentioned, the convergence of MOMCMC plays an important role in ensuring a reliable optimization result. For implementation convenience, we set a relatively large maximum iteration number which is expected to lead to the MCMC convergence. There are multiple metrics that can be used to evaluate the MCMC convergence performance (Dodds and Vicini, 2004; El Adlouni et al., 2006; Roy, 2019). Among them, the autocorrelation function (ACF) is conceptually simple, which is particularly used in this research. It is mathematically formulated as (Kumar, 2019):
where
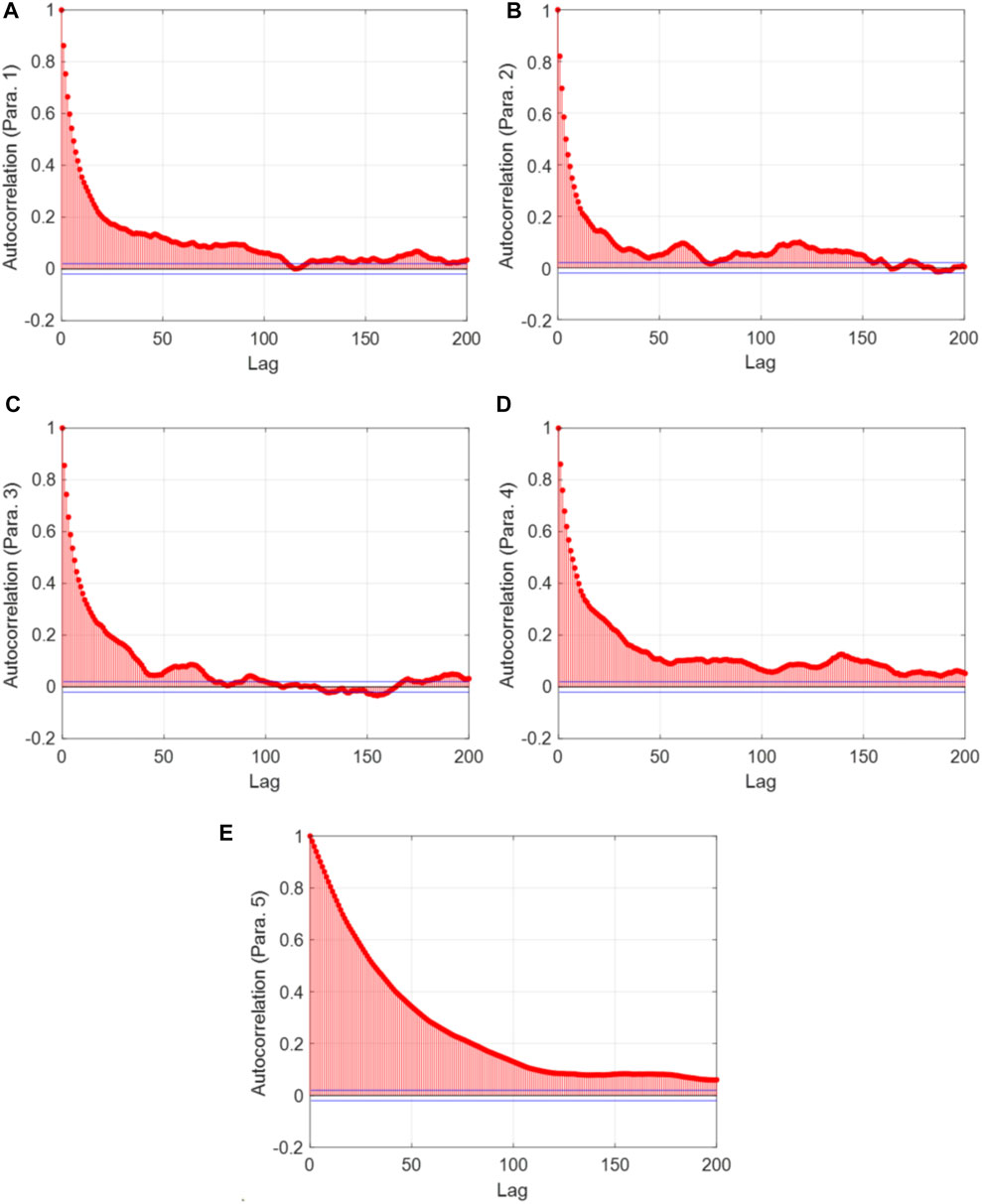
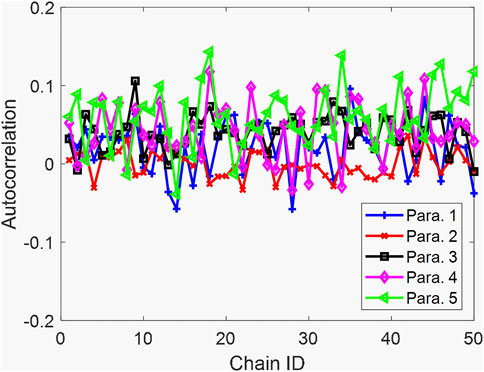
FIGURE 8. Autocorrelation of the 1st Markov chain with respect to lag. (A) Parameter 1; (B) Parameter 2; (C) Parameter 3; (D) Parameter 4; and (E) Parameter 5.
3.3 Additional Case (Case 2) Investigation–Identification of a Smaller Damage
In case 2, the location of damage (i.e., segment ID) changes, and the actual damage severity becomes smaller than that in case 1. Intuitively, the reduced damage severity in this case will pose the difficulty in pursuing the high accuracy of damage identification, since the identification result may be easily interfered with by uncertainties. We follow the same operating parameters tabulated in Table 2 and use the admittance measurement of the structure with the new damage introduction to execute the inverse model updating analysis. Following similar procedures, we first identify the probabilistic Pareto optimal set with many solutions as shown in Figure 11. The deterministic Pareto optimal set encompassed by the probabilistic Pareto optimal set includes 17 solutions, all of which well approach the actual damage scenario (i.e., 0.16% damage in parameter 2). The closest damage severity of parameter 2 in the optimal set is 0.0145%. While the discrepancy, that is, 0.015% between the best severity value and ground truth increases as compared to that of case 1, it is still very minor. The near-optimal solutions essentially are yielded as the consequence of uncertainties. The two-dimensional projections of the probabilistic Pareto optimal set are then given in Figure 12, where a similar observation is obtained. Parameter 2 is identified to be less severe when uncertainties are considered. In comparison, parameter 5 has the severer damage identified under uncertainties even though it is damage-free. The boundaries of scattered solutions are also estimated to reflect the uncertainty effect. Overall, the variation of solutions in this case appears to be smaller than that in case 1 (Figure 6), which may be because of the smaller true damage considered in this case. Based on the probabilistic Pareto optimal set, we can obtain the associated probabilistic Pareto front and estimate its boundary as given in Figure 13.
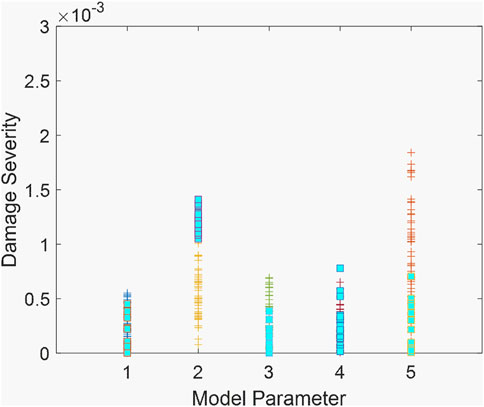
FIGURE 11. Solutions identified in the probabilistic Pareto optimal set (squared markers indicate the deterministic Pareto optimal set).
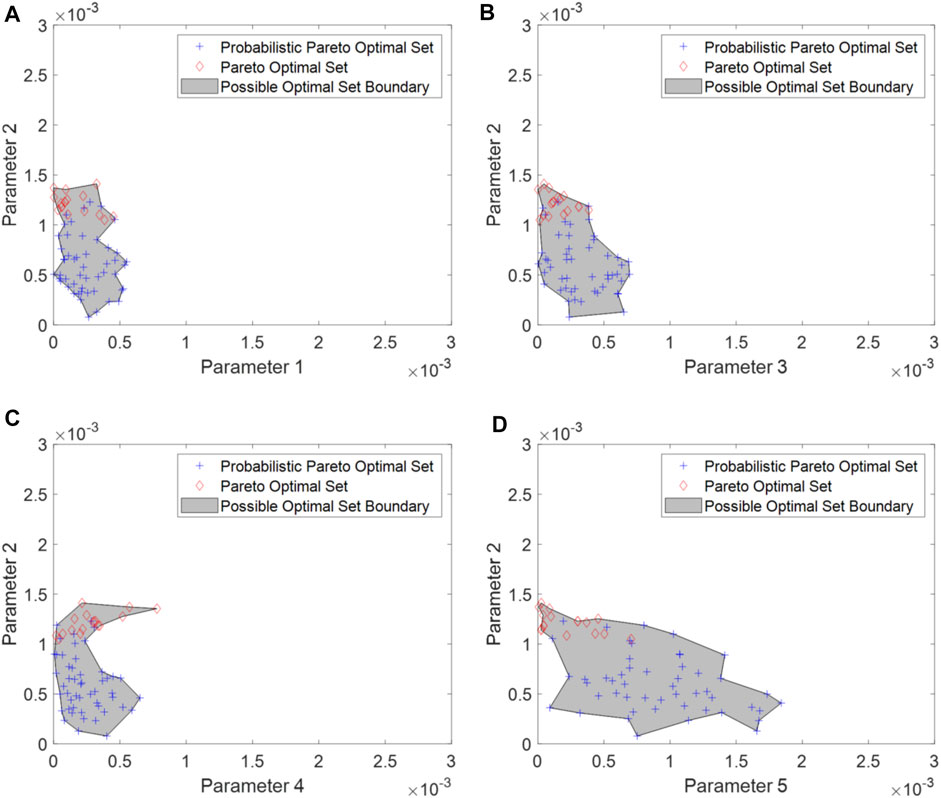
FIGURE 12. Two-dimensional illustration of the probabilistic Pareto optimal set. (A) Parameter 1 versus Parameter 4; (B) Parameter 2 versus Parameter 4; (C) Parameter 3 versus Parameter 4; and (D) Parameter 5 versus Parameter 4 (case 2).
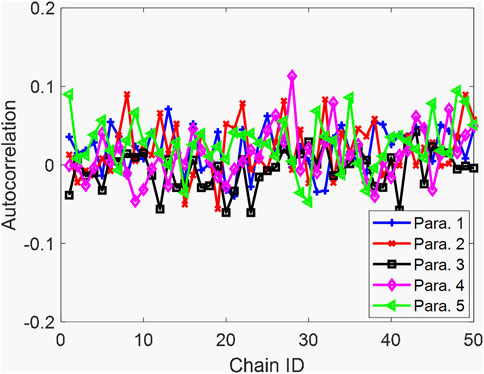
Similarly, we then implement the MCMC convergence analysis using the autocorrelation plots. The autocorrelation plots of the 1st Markov chain are shown in Figure 14. The autocorrelation of parameter 5 is higher than those of the other parameters. Specifically, the last-lag autocorrelation value of parameter 5 is around 0.1, whereas the last-lag autocorrelation values of other parameters are all close to 0. However, a quite uniform autocorrelation decreasing trend of parameter 5 implies that further increasing lags will likely continue to de-correlate two observations. Therefore, the maximum iteration number chosen in this case should also be reasonable. The last-lag autocorrelation values of all Markov chains are given in Figure 15, consistently showing a satisfactory convergence performance.
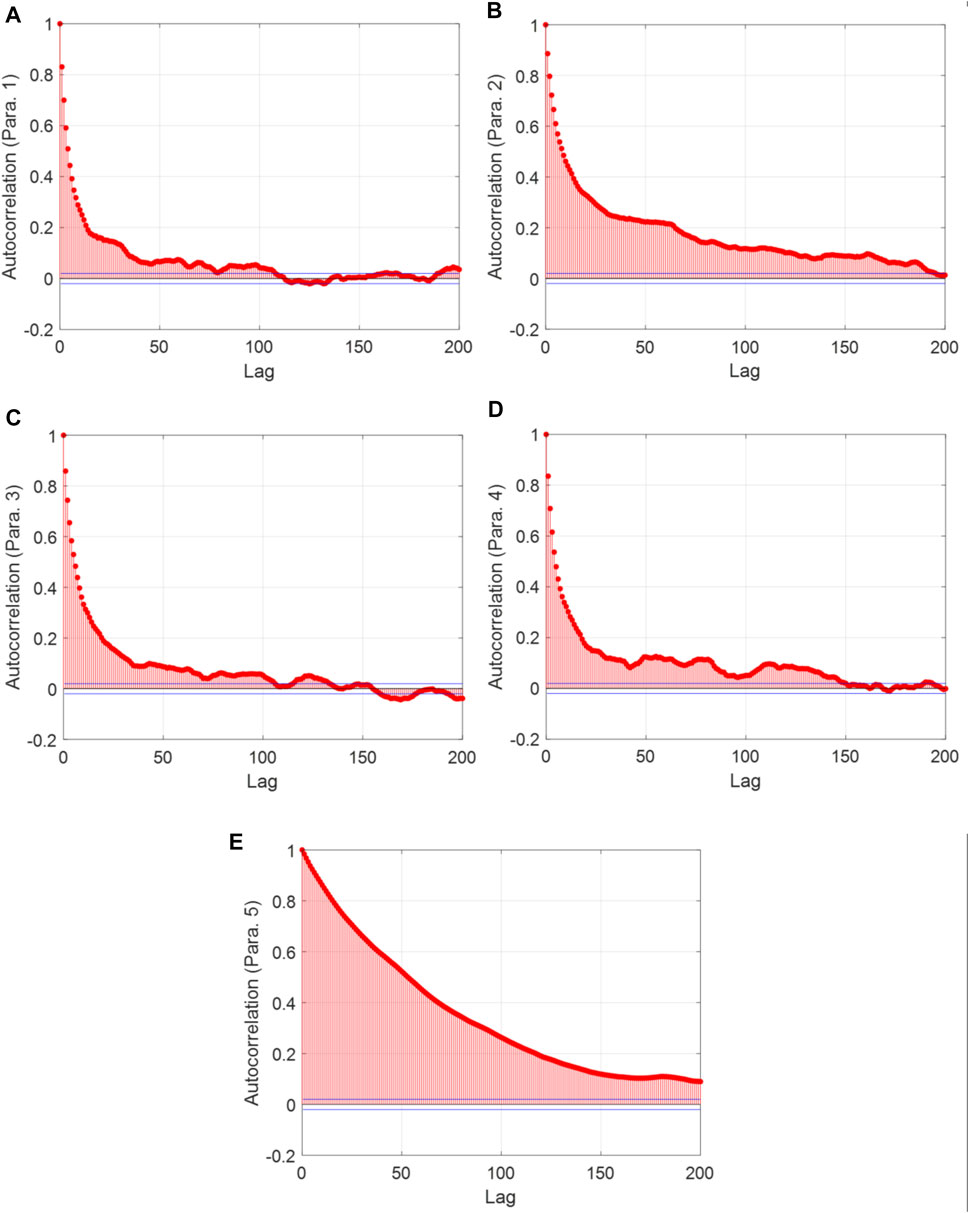
FIGURE 14. Autocorrelation of MCMC with respect to lag. (A) Parameter 1; (B) Parameter 2; (C) Parameter 3; (D) Parameter 4; and (E) Parameter 5 (case 2).
In an ideal case without the measurement uncertainties and modeling errors, the admittance response prediction of the actual damage becomes identical to the experimental admittance measurement. The deterministic Pareto optimal set, hence, is expected to embrace the “ground truth” solution, which is already captured in the results obtained through carrying out the proposed methodology. This finding indicates the effectiveness of the proposed methodology. More importantly, the unique advantage of this methodology can be fully exploited, that is, its capability in producing the solutions which can elucidate their intrinsic correlations with respect to uncertainties. This will provide in-depth insights to guide practical damage identification that is inevitably subjected to various uncertainties.
4 Conclusion
In this research, we develop a probabilistic multi-objective finite element (FE) model updating framework built on the differential evolution Markov chain Monte Carlo (DEMC) to conduct damage identification in the presence of uncertainties. Taking advantage of the high sensitivity with respect to the damage, the piezoelectric admittance measurements are particularly used to facilitate the inverse model updating analysis. This new methodology is generic since it can yield the probabilistic Pareto optimal set that already encompasses the deterministic Pareto optimal set provided through the conventional multi-objective inverse analysis. More importantly, such a probabilistic feature also is capable of accounting for the effect of uncertainties that inevitably exist either in FE modeling or measurement when performing the multi-objective inverse analysis. Systematic case studies on a cantilever plate with experimental validation clearly illustrate the effectiveness and robustness of this proposed methodology. In addition to elucidating the uncertainty effect, the proposed methodology yields the damage severity degrees which closely match the ground truth values, only with
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
KZ: conceptualization, methodology, numerical analysis and validation, and manuscript drafting and revision. YZ: numerical analysis and validation and manuscript revision. QS: experimental testing and data acquisition and manuscript revision. JT: conceptualization, methodology, manuscript revision, and supervision.
Funding
This research is supported in part by the National Science Foundation under grant CMMI—2138522 and in part by the National Science Foundation under grant CMMI—1825324.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alexandrino, P. D. S. L., Gomes, G.F., and Cunha, S. S. (2020). A Robust Optimization for Damage Detection Using Multiobjective Genetic Algorithm, Neural Network and Fuzzy Decision Making. Inverse Probl. Sci. Eng. 28 (1), 21–46. doi:10.1080/17415977.2019.1583225
Bartle, R. G. (1995). “The Elements of Integration and Lebesgue Measure,” in The Elements of Integration and Lebesgue Measure (Hoboken, NJ, USA: John Wiley & Sons). doi:10.1002/9781118164471
Braak, C. J. F. T. (2006). A Markov Chain Monte Carlo Version of the Genetic Algorithm Differential Evolution: Easy Bayesian Computing for Real Parameter Spaces. Stat. Comput. 16 (3), 239–249. doi:10.1007/s11222-006-8769-1
Brooks, S., Gelman, A., and Jones, G (2011). Handbook of Markov Chain Monte Carlo. (New York: CRC Press). Chapman \& Hall/CRC Handbooks of Modern Statistical Methods
Cao, M., Radzieński, M., Xu, W., and Ostachowicz, W. (2014). Identification of Multiple Damage in Beams Based on Robust Curvature Mode Shapes. Mech. Syst. Signal Process. 46 (2), 468–480. doi:10.1016/j.ymssp.2014.01.004
Cao, P., Qi, S., and Tang, J. (2018). Structural Damage Identification Using Piezoelectric Impedance Measurement with Sparse Inverse Analysis. Smart Mat. Struct. 27 (3), 035020. IOP Publishing. doi:10.1088/1361-665X/aaacba
Capecchi, D., Ciambella, J., Pau, A., and Vestroni, F. (2016). Damage Identification in a Parabolic Arch by Means of Natural Frequencies, Modal Shapes and Curvatures. Meccanica 51 (11), 2847–2859. doi:10.1007/s11012-016-0510-3
Chen, Z., Zhang, R., Zheng, J., and Sun, H. (2020). Sparse Bayesian Learning for Structural Damage Identification. Mech. Syst. Signal Process. 140, 106689. doi:10.1016/j.ymssp.2020.106689
Dodds, M. G., and Vicini, P. (2004). Assessing Convergence of Markov Chain Monte Carlo Simulations in Hierarchical Bayesian Models for Population Pharmacokinetics. Ann. Biomed. Eng. 32 (9), 1300–1313. doi:10.1114/B:ABME.0000039363.94089.08
El Adlouni, S., Favre, A.-C., and Bobée, B. (2006). Comparison of Methodologies to Assess the Convergence of Markov Chain Monte Carlo Methods. Comput. Statistics Data Analysis 50 (10), 2685–2701. doi:10.1016/j.csda.2005.04.018
Khodaparast, H. H., Mottershead, J. E., and Badcock, K. J. (2011). Interval Model Updating with Irreducible Uncertainty Using the Kriging Predictor. Mech. Syst. Signal Process. 25 (4), 1204–1226. doi:10.1016/j.ymssp.2010.10.009
Kim, J., Harne, R. L., and Wang, K. W. (2015). Enhancing Structural Damage Identification Robustness to Noise and Damping with Integrated Bistable and Adaptive Piezoelectric Circuitry. J. Vib. Acoust. 137 (1). 011003. doi:10.1115/1.4028308
Kim, J., and Wang, K.-W. (2019). Electromechanical Impedance-Based Damage Identification Enhancement Using Bistable and Adaptive Piezoelectric Circuitry. Struct. Health Monit. 18 (4), 1268–1281. doi:10.1177/1475921718794202
Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983). Optimization by Simulated Annealing. Science 220 (4598), 671–680. doi:10.1126/science.220.4598.671
Li, Y. (2012). MOMCMC: An Efficient Monte Carlo Method for Multi-Objective Sampling over Real Parameter Space. Comput. Math. Appl. 64 (11), 3542–3556. Elsevier Ltd. doi:10.1016/j.camwa.2012.09.003
Magacho, E. G., Jorge, A. B., and Gomes, G. F. (2021). Inverse Problem Based Multiobjective Sunflower Optimization for Structural Health Monitoring of Three-Dimensional Trusses. Evol. Intel., 1–21. doi:10.1007/s12065-021-00652-4
Mottershead, J. E., Link, M., and Friswell, M. I. (2011). The Sensitivity Method in Finite Element Model Updating: A Tutorial. Mech. Syst. Signal Process. 25 (7), 2275–2296. doi:10.1016/j.ymssp.2010.10.012
Qingfu Zhang, Q., Aimin Zhou, A., and Yaochu Jin, Y. (2008). RM-MEDA: A Regularity Model-Based Multiobjective Estimation of Distribution Algorithm. IEEE Trans. Evol. Comput. 12 (1), 41–63. doi:10.1109/TEVC.2007.894202
Roy, V. (2019). Convergence Diagnostics for Markov Chain Monte Carlo. Annu. Rev. Statistics Its Appl. 7, 387–412. doi:10.1146/annurev-statistics-031219-041300
Shuai, Q., Zhou, K., Zhou, S., and Tang, J. (2017). Fault Identification Using Piezoelectric Impedance Measurement and Model-Based Intelligent Inference with Pre-screening. Smart Mat. Struct. 26 (4), 045007. doi:10.1088/1361-665X/aa5d41
Storn, R., and Price, K. (1997). Differential Evolution - A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 11 (4), 341–359. doi:10.1023/A:1008202821328
Sun, H., Mordret, A., Prieto, G. A., Toksöz, M. N., and Büyüköztürk, O. (2017). Bayesian Characterization of Buildings Using Seismic Interferometry on Ambient Vibrations. Mech. Syst. Signal Process. 85, 468–486. doi:10.1016/j.ymssp.2016.08.038
Wan, H.-P., and Ren, W.-X. (2015). Parameter Selection in Finite-Element-Model Updating by Global Sensitivity Analysis Using Gaussian Process Metamodel. J. Struct. Eng. 141 (6), 04014164. doi:10.1061/(asce)st.1943-541x.0001108
Wang, X., and Tang, J. (2009). Damage Identification Using Piezoelectric Impedance Approach and Spectral Element Method. J. Intelligent Material Syst. Struct. 20 (8), 907–921. doi:10.1177/1045389X08099659
Xia, Y., and Hao, H. (2003). Statistical Damage Identification of Structures with Frequency Changes. J. Sound Vib. 263 (4), 853–870. doi:10.1016/S0022-460X(02)01077-5
Zhou, K., Shuai, Q., and Tang, J. (2014). “Adaptive Damage Detection Using Tunable Piezoelectric Admittance Sensor and Intelligent Inference,” in Volume 1: Development and Characterization of Multifunctional Materials; Modeling, Simulation and Control of Adaptive Systems; Structural Health Monitoring; Keynote Presentation. Newport, Rhode Island, USA, 8 September 2014, (New York, NY: American Society of Mechanical Engineers), doi:10.1115/SMASIS2014-7624
Zhou, K., and Tang, J. (2021a). Structural Model Updating Using Adaptive Multi-Response Gaussian Process Meta-Modeling. Mech. Syst. Signal Process. 147, 107121. Elsevier Ltd. doi:10.1016/j.ymssp.2020.107121
Zhou, K., and Tang, J. (2021b). Computational Inference of Vibratory System with Incomplete Modal Information Using Parallel, Interactive and Adaptive Markov Chains. J. Sound Vib. 511, 116331. doi:10.1016/j.jsv.2021.116331
Zhou, K., and Tang, J. (2016). Highly Efficient Probabilistic Finite Element Model Updating Using Intelligent Inference with Incomplete Modal Information. J. Vib. Acoust. Trans. ASME 138 (5), 1–14. doi:10.1115/1.4033965
Zhou, K., and Tang, J. (2015). Reducing Dynamic Response Variation Using Nurbs Finite Element-Based Geometry Perturbation. J. Vib. Acoust. Trans. ASME 137 (6), 1–11. doi:10.1115/1.4030902
Zhu, H., Li, J., Tian, W., Weng, S., Peng, Y., Zhang, Z., et al. (2021). An Enhanced Substructure-Based Response Sensitivity Method for Finite Element Model Updating of Large-Scale Structures. Mech. Syst. Signal Process. 154, 107359. doi:10.1016/j.ymssp.2020.107359
Keywords: damage identification, piezoelectric impedance, inverse analysis, probabilistic multi-objective optimization, differential evolution Markov chain Monte Carlo (DEMC), uncertainties
Citation: Zhou K, Zhang Y, Shuai Q and Tang J (2022) Probabilistic Multi-Objective Inverse Analysis for Damage Identification Using Piezoelectric Impedance Measurement Under Uncertainties. Front. Built Environ. 8:904690. doi: 10.3389/fbuil.2022.904690
Received: 25 March 2022; Accepted: 02 May 2022;
Published: 14 June 2022.
Edited by:
Giovanni Falsone, University of Messina, ItalyReviewed by:
Mohsen Rashki, University of Sistan and Baluchestan, IranCorrado Chisari, University of Campania Luigi Vanvitelli, Italy
Copyright © 2022 Zhou, Zhang, Shuai and Tang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kai Zhou, kzhou@mtu.edu; Jiong Tang, jiong.tang@uconn.edu
 Kai Zhou
Kai Zhou