- Institute of Hydraulic Engineering and Water Resources Management, RWTH Aachen University, Aachen, Germany
Sand-trapping fences are a frequently used nature-based solution in coastal protection for initiating and facilitating coastal dune toe growth. However, only a few researchers have evaluated the trap efficiency of sand-trapping fences based on their porosity and height. Subsequently, the design of their properties has only been based on empirical knowledge, to date. However, for restoring and maintaining coastal beach–dune systems, exact knowledge of sand-trapping fence’s optimal properties is essential. Thus, we conducted physical model tests focusing on the most crucial parameters: fence height (h = 40, 80, 120 mm) and fence porosity (ε = 22.6, 41.6, and 56.5%). These tests were conducted in an indoor subsonic, blowing-sand wind tunnel equipped with a moveable sediment bed (d50 ∼ 212 µm). The experimental mean wind velocities were u1 = 6.1 m/s, u2 = 7.4 m/s, and u3 = 9.3 m/s. We used a hot-wire anemometer to measure the flow fields, a vertical mesh sand trap to determine the sediment fluxes, and a 2D laser scanner to record the sediment accretion around the sand-trapping fences over time. The study results provide substantial theoretical and practical support for the installation and configuration of trapping fences and improving their design. The fence porosity, for example, should be chosen depending on the installation purpose. While denser fence porosities (ε1 = 22.6% and ε2 = 41.6%) can be used for initiating and facilitating the dune toe growth, fences with higher porosity (ε3 = 56.5%) are more suitable to favor the sediment accretion between foredunes and white dunes as they allow further dune growth downwind.
Introduction
Coastal dunes are present along sandy coastlines worldwide and have various functions, such as contributing to biodiversity, socioeconomic services including nature conservation, recreation, and tourism, and natural flood protection for the low-lying hinterland against storm surges (van Thiel de Vries, 2009; Hesp, 2011; de Vries, 2013; Keijsers et al., 2015). Coastal dunes also act as sediment resources in case of erosive storm events; the sediments can naturally shift and move to the beach or nearshore areas and dissipate wave energy and, thus, mitigate erosion (van Thiel de Vries, 2009). Aeolian sediment transport processes from the beach toward the coastal dunes increase coastal dune volumes, while marine processes, which predominately occur during storm surges, lead to dune erosion (Hesp, 2011). However, along with aeolian sediment transport marine processes can also contribute to foredune growth along dissipative coastlines. The highest dune growth rates are often observed during winter months, when the beach is eroding, at the highest wind velocities, and high water levels (Cohn et al., 2018; 2019). Due to the rise in the sea level caused by climate change, it is currently assumed that erosion processes will accelerate and land loss will increase as well (Harff et al., 2011; Hesp, 2011; Keijsers et al., 2015). In addition, socioeconomic pressure in coastal areas is increasing (NASA, 2020). In order to address the challenges in coastal protection and at the same time respond to people’s growing environmental awareness, there is a great need for nature-based solutions that aim to use natural processes and resources. Since sand-trapping fences are part of nature-based solutions, they are commonly installed along sandy coastlines along with barrier island systems to strengthen coastal dunes and increase the flood protection level (Li and Sherman, 2015; Itzkin et al., 2020a; Eichmanns et al., 2021). They cause a local reduction in wind velocity, leading to downwind sediment accumulation around the fences (Hotta and Horikawa, 1990; Li and Sherman, 2015; Lawlor and Jackson, 2021). The functions of sand-trapping fences in coastal areas vary and thus, range from rehabilitating eroded areas such as blowouts in coastal dunes, strengthening coastal dune toe establishment, preventing sand drifting from protectable infrastructures, limiting human access to nature, or initiating the formation of coastal dunes through selective sand deposition (O'Connel,; Adriani and Terwindt, 1974; Gerhardt, 1990; Li and Sherman, 2015; Eichmanns and Schüttrumpf, 2021). For detailed information about sand-trapping fences, refer to Eichmanns et al. (2021).
Generally, it is found that using sand-trapping fences at the seaward side of the dune leads to an increased foredune growth rate compared to no fenced areas (Jackson and Nordstrom, 2011; Eichmanns and Schüttrumpf, 2021). This additional sediment buffer can protect coastal dunes by attenuating wave energy (Ruz and Anthony, 2008; Itzkin et al., 2020b). However, the application of such sand-trapping fences can impair the sediment supply for the beaches and landward coastal dunes and create a physical boundary for the natural movement of fauna. Subsequently, a less dynamic beach–dune system affects the beach width and, therefore, the coastal protection against coastal erosion (Itzkin et al., 2020a). Wider beaches generally offer greater coastal protection against erosion than smaller beaches (Itzkin et al., 2020b). Thus, sand-trapping fences influence the natural topography of coastal dunes and present vegetation (Gallego-Fernández, 2013). For example, Itzkin et al. (2020a) found that coastal dunes are typically shorter, wider, and smaller in volume than natural foredunes in non-fenced and undeveloped areas. However, this may also be explained because fences tend to be installed close to more vulnerable coastal dunes, which are usually smaller.
Numerous studies consider the wind and turbulence field behind porous fences with variable geometry (height and length) (Mulhearn and Bradley, 1977; Ning et al., 2020), porosity (Perera, 1981; Hotta and Horikawa, 1990; Lee and Kim, 1999; Dong et al., 2007), opening size (Manohar and Bruun, 1970; Lee and Kim, 1999), incoming wind velocity, or wind turbulence (Dong et al., 2007; Yu et al., 2020). It is found that fence porosity and fence height are the predominant influencing factors on the wind field and, thus, the sand-trapping efficiency (Li and Sherman, 2015). However, recommendations on the fence height and porosity of sand-trapping fences in coastal areas are commonly based on empirical practice (Li and Sherman, 2015; Eichmanns et al., 2021). Thus, the correlation of sand-trapping efficiency as a function of, for example, fence porosity and fence height is needed.
In this study, indoor wind tunnel experiments were carried out to study the wind regime and sand-trapping efficiency of sand-trapping fences with different fence porosities and fence heights. The objective is to evaluate different fence porosities and fence heights influencing trap efficiency. Therefore, the following research goals were set:
1) Investigation of the influence of fence height and fence porosity on the wind regime.
2) Investigation of reproducibility of the sediment accretion around a single sand-trapping fence.
3) Considering the model effetcs on the sediment accretion around a single sand-trapping fence.
4) Evaluation of trap efficiency of a single sand-trapping fence over time.
5) Investigation of the influence of fence porosity on trapping sediment.
6) Giving general recommendations on fence properties.
Materials and Methods
Experimental Design
Physical model tests were conducted on sand-trapping fences with different heights and porosities in an indoor subsonic, blowing-sand wind tunnel at the Institute of Hydraulic Engineering and Water Resources Management (IWW), Rheinisch Westfälische Hochschule (RWTH) Aachen University, Germany. Fence porosity and grain size distribution of the sediment is based on in situ measurements conducted in Langeoog and Norderney, where the influence of sand-trapping fences on the dune toe growth and its relation with potential aeolian sediment transport was already investigated by the authors (see Eichmanns and Schüttrumpf, 2020, 2021).
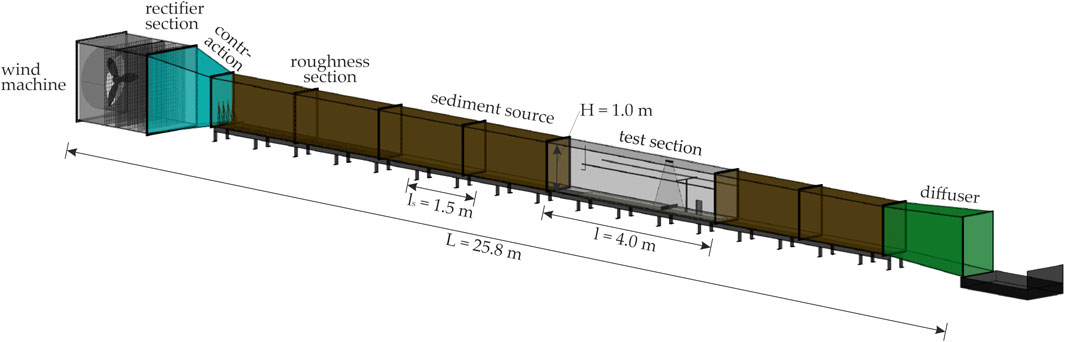
For this work, a wind tunnel was built by the IWW itself and was constructed mainly from wooden panels, except the test section was built from polymethylmethacrylate to allow visual observation of the experiments. The wind tunnel had a total length of L = 25.8 m, see Figure 1. The cross-sectional area was H = 1.0 m (height) and B = 0.58 m (width). The wind tunnel consisted of the following four parts: the power section with the wind machine, rectifier section followed by contraction section, channel with test section, and diffusion section. A sediment bed with a length of l = 4 m, a width of b = 0.4 m, and a depth of t = 0.15 m was installed in the test section. The sand-trapping fence as the focus of the investigation was installed within the sediment bed, d = 2 m from the edge of the sediment bed in the windward direction. In addition, a sediment source with a layer with a volume of V = 0.0435 m³ was placed about 1 m behind the roughness section in the main wind direction.
The Trotec TTW (Trotec) wind machine generates a continuous airflow of Q = 45.600 m³/h. The wind machine is equipped with an inverter that allowed mean wind velocities to be adjusted between umean ∼ 1–10 m/s. The wind first passes through a honeycomb, see Figure 2A, and second, through a coarser and a finer screen, see Figure 2B, to straighten the airflow. The honeycomb is designed following the findings of Barlow et al. (1999) and Mehta (1979) and was built out of ∼7.500 bounded polyvinylchloride tubes with an outer diameter of d = 16 mm and a length of l = 120 mm. In addition, the surface roughness is increased by four spires, a trip fence, and a 6-m-long artificial grass cover, see Figure 2C.

FIGURE 2. (A) Honeycomb and (B) coarser and finer screens to straighten the airflow in the main wind direction, and (C) spires, trip fence, and an artificial grass cover to increase the surface roughness.
Experimental Setup
The flow field and sediment flux measurements were conducted separately. First, a fixed sediment surface was installed to measure the wind velocities via a hot-wire anemometer. Since the hot-wire anemometer is susceptible to damages from the windblown sediment, a thin layer of sediment glued to a wooden panel was installed while measuring the wind profiles in the test section. Only wind directions perpendicular to the fences were investigated in the wind tunnel. The experimental mean wind velocities were u1 = 6.1 m/s, u2 = 7.4 m/s, and u3 = 9.3 m/s. Then a moveable sediment bed combined with a sediment source was established, where a vertical sediment trap determined the sediment flux and a 2D LiDAR sensor SICK LMS4000, the sediment accretion around the sand-trapping fence. This fixed and moveable sediment bed procedure was already carried out in comparable wind tunnel experiments such as Hotta and Horikawa (1990). A GoPro Hero 8 recorded each experiment for visual observation. In Figure 3, the instrumentation setup for the test section is shown.
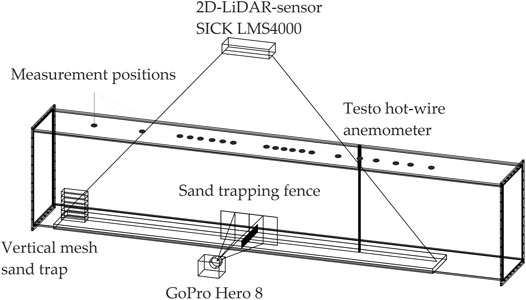
FIGURE 3. Instrumentation setup for the test section, including 2D LiDAR sensor SICK LMS4000, Testo hot-wire anemometer for the different measurement positions, vertical mesh sand trap, and GoPro Hero 8.
The sediment source is added, such as in experiments by Creyssels et al. (2009) or Ho et al. (2011, 2012), to favor the development of a steady state of saltation. Experiment’s duration is set to t = 10 min to ensure almost stationary sediment fluxes. This is in agreement with other investigations such as Chen et al. (2019, 2020), Wang et al. (2018), or Miri et al. (2019), where short measuring intervals, up to several minutes, are common. Some of these experiments were even shorter. Exceeding this experiment duration would empty the sediment source and the sediment bed. Furthermore, vertical mesh sand traps are limited to a constant sand-trapping capacity that will exceed if testing times are excessive. Moreover, we wanted to avoid the effects of supply limitations on the dune development (Swann et al., 2015) or increase the model effects at the physical boundaries (transition from wooden panels to the sediment bed).
Sediment from the study site Norderney was used for the experiments. To ensure the defined moisture content of M < 0.1%, for all investigations, the sediment was dried in a dry oven at a temperature of around T = 105°C. According to the specifications in DIN EN ISO 14688-1 (2018), a sedimentological analysis was conducted. The median grain size of the sediment was d50 ∼ 212 µm.
The investigated sand-trapping fences were modeled using locally available brushwood branches with a diameter of d ∼ 2–10 mm. In total, nine different fence configurations were investigated in the wind tunnel, varying in both fence height (h = 40, 80, 120 mm) and fence porosity (ε ∼ 20–58%). The two-dimensional porosity was determined as the open to total surface ratio. The exact porosities are shown in Figure 4 and were determined by evaluating photographs of the sand-trapping fences. Therefore, the photographs were processed with the MATLAB, 2018’s (R2018b, version 9.510.944444) Color Thresholder Application. The areas overlaid by the brushwood branches were identified and colored in black with a chosen threshold value. The contrast toward the background was increased and colored in white to indicate that there is no brushwood. For more information about the segmentation of the photographs, refer Eichmanns and Schüttrumpf (2021).

FIGURE 4. Modeling nine different sand-trapping fences with changing fence heights and fence porosities and showing the number of cases investigated (*only wind profiles were measured).
The porosity of the different sand-trapping fence configurations varies slightly over height due to the uneven nature of the branches. Thus, the modeled fences tend to become a little more porous in their upper parts. In the following, the mean porosity is determined for the three different fence heights and used for low (ε1 = 22.6%), medium (ε2 = 41.6%), and high (ε3 = 56.5%) porosity. The mean porosities generally correspond to the porosities of Langeoog and Norderney’s sand-trapping fences (Eichmanns and Schüttrumpf, 2021). However, the brushwood bundles differ in their stem characteristics, such as the stem diameter (d ∼ 2–10 mm). At present, the authors are not aware that the stem diameter significantly influences the sediment accretion around the sand-trapping fence, especially since, in a scientific research, the fence’s porosity was identified as a significant influence on trapping sediments (e.g., Arens et al., 2001; Zhang et al., 2010; Li and Sherman, 2015; Miri et al., 2019; Yu et al., 2020).
To measure the wind fields, all fence heights and porosities were investigated (27 cases); to measure the sediment accretion around the sand-trapping fence, only the highest fence height was installed (nine cases), see also Figure 4. Researching this fence height ensures that the saltation layer height does not significantly exceed the fence height, allowing the fence to capture most of the windblown sediment, see also Sediment Transport Fluxes. The influence would be more remarkable for other fence heights since the fence heights are considerably lower than the saltation layer height, and thus, the aeolian sediment would also blow over the fence.
Similarity to Nature and Compliance with Physical Model Laws
The type of aerodynamic flow in the wind tunnel can be characterized by the Mach number M (-), as follows
where c ∼ 343 m/s (temperature T = 20°C) is the speed of sound of the medium. At any point in the wind tunnel, the velocity is less than the speed of sound of the air (M < 1), and thus it is a subsonic flow (Barlow et al., 1999; Anderson, 2017). The thickness of the boundary layer in the test section was determined to be approximately
where u∞ (m/s) is the free flow velocity in front of the test section and ν ∼ 1.516·10−5 m2/s (T = 20°C) is the kinematic viscosity of air (White, 1996; Barlow et al., 1999; Cattafesta et al., 2010). The roughness Reynolds number ReR (-) is defined as follows:
where u* (m/s) is the shear velocity and z0 (mm) is the aerodynamic roughness length (Nikuradse, 1933; Vithana, 2013), see also Measurement of Wind Velocity Characteristics. The first criterion was achieved with Reflow ∼ 3 × 105, whereas the roughness Reynolds number was not achieved. The roughness Reynolds number could only be determined for experiments with the immobile sand bed, as the sensitive hot-wire probe could otherwise be destroyed by saltating sediment grains. However, we assumed that the roughness Reynolds number independence was achieved during experiments with the moveable sediment bed because the saltation process generally increases the roughness Reynolds number (Cermak, 1987; White, 1996; Barlow et al., 1999).
The minimal entrance length Lin,min ∼ 10–25·
where g = 9.81 m/s2 is the gravitational acceleration and H (m) is the wind tunnel height. The smaller the Froude number, the faster a constant shear stress velocity, and thus, a constant velocity profile is achieved during saltation (White, 1996). The Froude criterion is fulfilled for the investigated flow velocities u1–3 = 6.1–9.3 m/s with Fr << 20 (Owen and Gillette, 1985). Sidewall effects are not expected with the investigated low wind velocities and corresponding shear stress velocities in the wind tunnel. For the blockage ratio two criteria exist. The maximum blockage ratio BR1 (-) defined as
which is fulfilled for fence models with heights h1 = 40 mm and h2 = 80 mm, whereas the blockage ratio BR2 (-) can only be met for the lowest fence height h1 = 40 mm. It is defined as the ratio of the fence height h (mm) to the height of the boundary layer δ (mm):
These criteria were not always met in past studies either, such as Dong et al. (2007), Wang et al. (2018), and Yu et al. (2020), but assumed to have a minor influence as long as the fence height was at least smaller than the height of the boundary layer. Since the selected fence heights are considerably smaller than the boundary layer height, it can be assumed that no significant influence is expected by exceeding this limit value.
Measurement of Wind Velocity Characteristics
The Testo hot-wire anemometer (testo, 2021), equipped with an external data logger Testo 440 dp, was placed in the center of the wind tunnel at predefined heights (z = 3, 6, 12, 24, 40, 80, 120, 200, and 250 mm) above the surface to measure wind velocities. For this purpose, the hot-wire anemometer was inserted via a hole in the wind tunnel cover, and after measurement of the wind profile, the anemometer was moved to the next position downwind. The respective holes in the lid were sealed tightly with plugs, see Figure 3. For the flow field test, the wind velocity profiles near the sand-trapping fence were measured on the leeward side at a distance of 2, 5, 8, 10, 12, 15, and 20 h from the fence, on the windward side at distances of −2h, −5h, and −10h, and at a reference position over the wooden panel at x = −2,200 mm from the fence, where h is the height of the sand-trapping fence. We recorded a steady and uniform airflow field in the test section without a sand-trapping fence, see also Figure 7. The hot-wire anemometer has an accuracy of ±0.03 m/s and 3% of the mean wind velocity. In order to obtain reliable measurement results, the measurement duration is decisive. A measurement duration that is too short can lead to incorrect measurement results. The longer the measurement duration, the more representative the measurement results. The wind velocity was measured for 10 min at two locations and then analyzed. The 10-min measurement period is divided into ten intervals of equal time (t = 1 min), and the difference between the mean flow velocity over each 1-min interval over the whole 10-min interval is determined. The maximum difference was ±1.2%. Therefore, a measurement interval of 1 min is defined as sufficiently accurate for this investigation. Moreover, the reproducibility of the measured data for the wind profiles was ensured by repeating several measurements randomly with a maximum deviation of ±4% at one measuring point.
An appropriate analytical approach to describe the wind velocity distribution over the viscous sub boundary layer for aerodynamically rough surfaces is the law of the wall, which is valid for neutral atmospheric stability conditions, as follows (Bagnold, 1954):
where uz (m/s) is the wind velocity at height z (m) and κ (−) is the Kármán constant (here 0.41) (Nikuradse, 1933; Vithana, 2013). Figure 5 exemplifies the velocity profiles for u1 = 6.1 m/s, u2 = 7.4 m/s, and u3 = 9.3 m/s at the reference position with corresponding shear velocities u1* = 0.21 m/s, u2* = 0.25 m/s, and u3* = 0.28 m/s, and coefficient of determination R2 = 0.95–0.98 is shown. It describes the approaching airflow entering the test section.
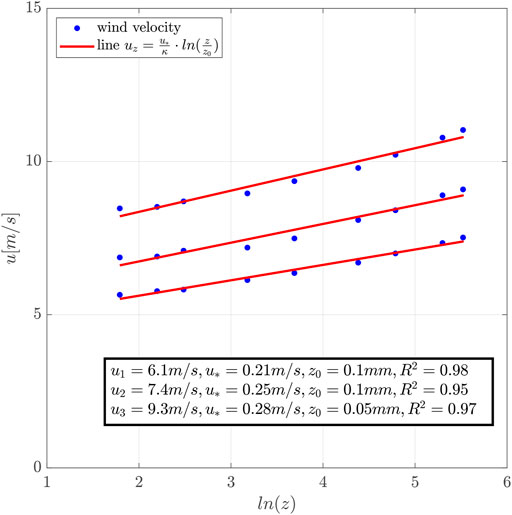
FIGURE 5. Examples of the velocity profile for u1 = 6.1 m/s, u2 = 7.4 m/s, and u3 = 9.3 m/s. The blue dots represent the measured wind velocity and the red lines indicate the regression lines, see Eq. 7.
For all measurement heights at the reference position, the corresponding standard deviations were less with σmin = 0.19 m/s, σmax = 0.61 m/s, and σmean = 0.39 m/s, respectively.
When a particular critical value of drag and lift force on the sediment grain is exceeded, sediment transport is initiated. This is the so-called critical shear stress u*t (18):
The empirical constant is given with A (-) (here 0.11), the density of air is given with ρa (kg/m³) (here 1.2 kg/m³), and the density of sediment grains with ρs (kg/m³) (here 2,650 kg/m³). The empirical constant considers the effect of cohesion; however, the influence of the protective layer of shells or moisture contents is not taken into account (Shao and Lu, 2000; Han et al., 2011; van Rijn and Strypsteen, 2019). The critical shear velocity was calculated for the wind tunnel investigations as u*t = 0.24 m/s. However, it was noted that sediment transport occurred with critical shear velocities above u*t = 0.20 m/s.
To describe the influence of different fence porosities and fence heights on the wind profile at a certain height z (mm) and distance x (mm) from the fence, the wind reduction coefficient Rc (-) is used (Cornelis and Gabriels, 2005; Wang et al., 2018; Yu et al., 2020):
The horizontal wind velocity is given with ux,z (m/s) and the horizontal wind velocity at that exact position without any fence with u0x,z (m/s). A high value indicates a high wind reduction.
Measurement of Sediment Flux
For each experimental mean wind velocity, mean sediment transport rates were measured to determine the incoming sediment flux from the sediment source. Thus, vertical mesh sand traps constructed according to Sherman et al. (2014) and already used in field experiments of Eichmanns and Schüttrumpf (2020), covering a height of z = 0.3 m above the surface, see Figure 3, were used. The vertical mesh sand trap consists of six rectangular aluminum tubes arranged one above the other. One rectangular aluminum tube has the dimensions of 0.1 m (width) × 0.05 m (height) × 0.25 m (length) and 2 mm (edges). One rectangular aluminum tube is equipped with a nylon monofilament with opening sizes of size = 50 µm. The vertical mesh sand traps were exposed to sediment flow during the defined time interval of t = 10 min, and, afterward, the collected sand was weighed per height. The empirical exponential decay function is used to describe the vertical distribution of sediment transport as follows (Ellis et al., 2009; Poortinga et al., 2014):
where qz (kg/m2/s) is the sediment transport rate at a predefined height z (m), q0 (kg/m2/s) is the extrapolated saltating sediment mass transport at the surface, and the decay rate ß (1/m) is a constant to describe the vertical concentration gradient. A regression analysis of the experimental data gives the parameters ß and q0 (Bauer and Davidson-Arnott, 2014). According to the scientific literature, the range of values for the fitting coefficient can vary significantly due to the weak correlation to physical aeolian parameters such as grain size or shear velocity (Bauer and Davidson-Arnott, 2014). Integrating Eq. 10 gives the total mass transport, as follows:
The total mass transport by saltation is given as Qs (kg/m/s) (Bauer and Davidson-Arnott, 2014). Since aeolian sediment transport is highly variable spatially and temporally, the experiments were repeated three times and the average value was used for further analysis (Baas and Sherman, 2006; Bauer and Davidson-Arnott, 2014; Strypsteen, 2019; van Rijn, 2019).
Measurement of Sand Accretion Around Sand-Trapping Fence Configurations
We deployed a 2D LiDAR scanner at the centerline of the wind tunnel, where the wind velocity profiles were also measured. We found that the centerline represents the sediment accretion around the sand-trapping fence well based on the camera recordings. The laser scanner detected the sediment surface elevations every Δt = 2 min with a systematic error of ±1.5 mm and a statistical error of ±2.5 mm (distances between 1.97–2.40 m). The measuring frequency was set to 10 Hz, and the angular resolution was 0.0833°.
In the following, the trap efficiency is used to evaluate the different sediment accretions around the configurations of the sand-trapping fence. In order to eliminate model effects on the sediment accretion caused by the fence, the sediment fluxes were distinguished based on the continuity equation. Thus, Figure 6 presents a schematic side view of the wind tunnel test section with the sediment accretion around the fence at timestep t0 = 0 min and t5 = 10 min. The yellow areas show the typical erosion areas, whereas the colored areas in orange give the accretion areas. The zero-crossing between two sediment surface elevations at different timesteps is defined as boundary condition distinguishing between the different sediment changes (sf2, sf3, and sf4), see red crosses in Figure 6.
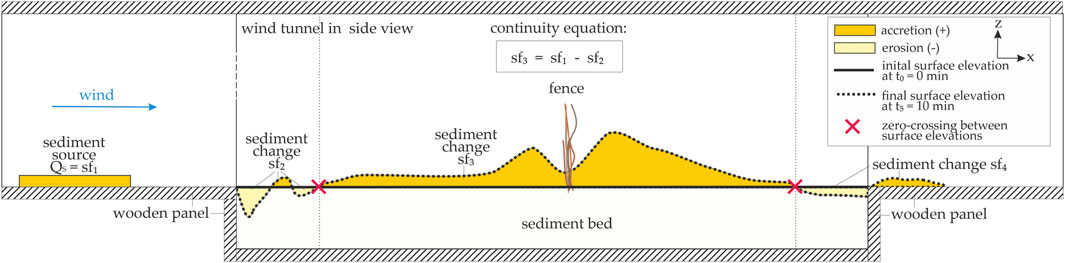
FIGURE 6. Two-dimensional side view of the wind tunnel test section showing the different sediment fluxes schematically: sf1–sf4 for determining the trapped sediment, see Eq. 13.
During the experiments, local scouring always occurred at the transition between the wooden panel and sediment bed and vice versa, see Sediment Accretion Around the Sand-Trapping Fence Configurations. These sediment changes sf2 and sf4 were caused by increasing shear stress associated with increasing surface roughness, which lead to fluctuations and turbulences, thus, initiating erosion processes (Swann et al., 2015). Since in a steady-state equilibrium, foredunes generally oscillate about a geomorphic equilibrium, accreting (recovery) and eroding (response), it is assumed that the scour sf4 at the end of the sediment bed would extend over a longer distance followed by a sediment accretion (Swann et al., 2015). Thus, this sediment change sf4 is excluded from further analysis. Excluding the sediment flux sf4 (sf4 << sf3) still provides valid results.
It is assumed that during the experimental time frame of t = 10 min, the scours have a minor effect on the accretion of sediment around the sand-trapping fence. According to experiments of Hotta and Horikawa (1990) and Ning et al. (2020), the zero-crossing between two surface elevations at different timesteps shifts insignificantly toward the fence (maximum x/h ∼ 2) such as in our experiments. Thus, it is assumed that the morphodynamics around the sand-trapping fence is modeled correctly in our experiments, see also Sediment Accretion Around the Sand-Trapping Fence Configurations. However, this can only be determined adequately with a sufficiently long wind tunnel and extensive test durations.
For evaluating the sand-trapping of different fence configurations, the trap efficiency E (-), see for example, Ning et al. (2020) or Chen et al. (2019), is defined as follows:
The trapped sediment transport Qt (kg/m/s) is estimated as the product of the bulk density of the sediment γ (kg/m³) and the cross-sectional dune area ΔA (m2) (sediment change sf3) in the time interval Δt (s), as follows:
The sediment transport for initiating the sediment accretion around the sand-trapping fence is calculated based on total mass transport Qs, see Eq. 11, from which the sediment change sf2 is subtracted. The bulk density was γ = 1,550 kg/m³ (average out of three measurements).
Since windblown sediment transport is highly variable both spatially and temporally, the experiments were repeated three to four times (Baas and Sherman, 2006; Bauer and Davidson-Arnott, 2014; van Rijn, 2019).
Results
Wind Velocity Characteristics
Figure 7A presents the flow field in the x-direction (mm) over the height z (mm) without a sand-trapping fence; Figures 7B–D depicts the flow fields in the vicinity of a sand trapping. The free mean velocity was u3 = 9.3 m/s, and the x-axis and the y-axis were normalized by the fence height. The black dots represent the measurement positions of a hot-wire anemometer with the mean wind velocity values over the 1-min measuring interval, and the brown lines indicate the fence. Generally, the airflow slows down on the upwind side of the fence. Above the fence, the airflow accelerates, and on the leeward side, the vertical eddy zone occurs, resulting from the difference of the wind velocity above and through the fence.
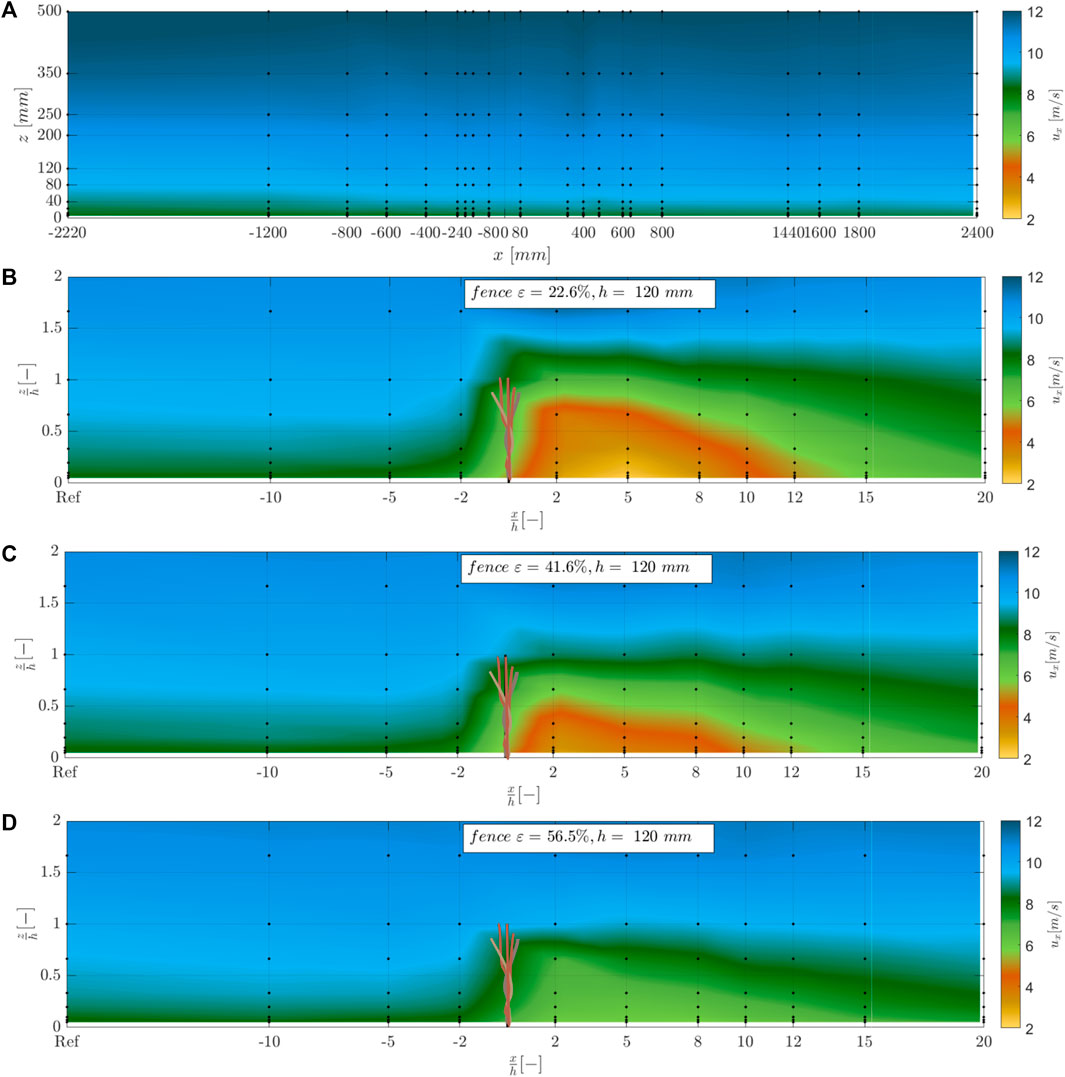
FIGURE 7. Flow fields (A) without a sand-trapping fence (B) in the vicinity of a sand-trapping fence at x/h = 0 with h3 = 120 mm and (B) a porosity of ε1 = 22.6%, (C) ε2 = 41.6%, and (D) ε3 = 56.6%. The free mean wind velocity was u3 = 9.3 m/s. The black dots show the measuring locations of the hot-wire anemometer, and the brown lines indicate the sand-trapping fence.
The complexity of the airflow fields decreased while the fence porosity increased. For the low porosity fence, the wind velocity profiles show a higher range of measured wind velocities between u = 2.3–11.3 m/s than the high porosity fence profiles showing wind velocities between u = 6.3–11.1 m/s. In addition, the wind velocities in front of and behind the fence are reduced to a greater extent. For better illustration, Figure 8 represents the mean wind velocities in the x-direction for the different fence configurations, divided into the following fence heights: (A) h1 = 40 mm (B) h2 = 80 mm, and (C) h3 = 120 mm. The mean wind velocity in the x-direction was averaged by values of wind velocities at heights of z = 3, 6, 12, 24, 40, 80, 120, 200, and 250 mm. The mean wind velocities were averaged up to a height of z = 250 mm within the boundary layer rather than the entire wind tunnel height of H = 1,000 mm.
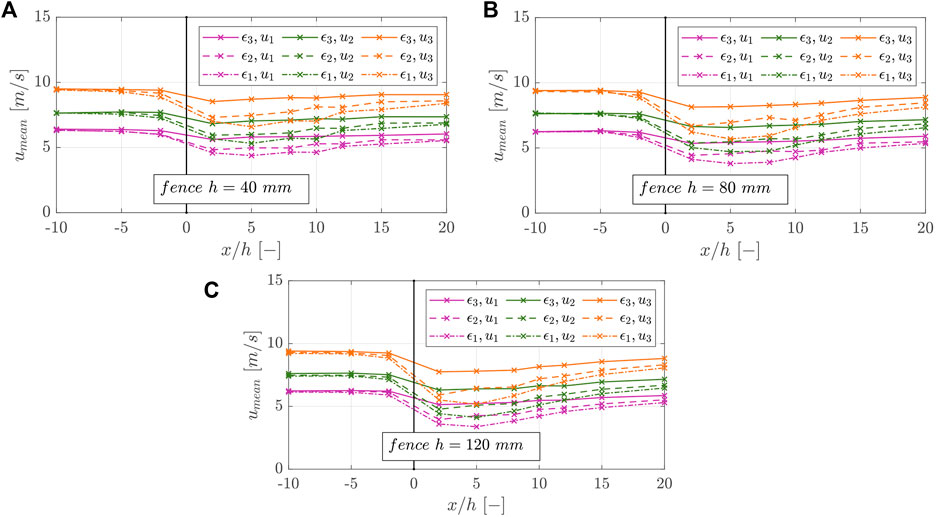
FIGURE 8. Mean wind velocity u1–u3 in the x-direction of fences with different characteristics ε1–ε3, divided into (A) the fence heights h1 = 40 mm (B) h2 = 80 mm, and (C) h3 = 120 mm.
Comparing the wind fields for the different fence heights (h1 = 40 mm, h2 = 80 mm, and h3 = 120 mm), we detected no significant differences in the mean wind velocities under constant porosity and constant free wind velocity.
For the lowest fence porosity (ε1 = 22.6%) and the highest fence height (h3 = 120 mm), the wind reduction is most significant at position x/h = 5. For the mean free wind velocity u1 = 6.1 m/s, the lowest mean wind velocity in the x-direction was umean = 3.4 m/s, whereas for the lowest fence height (h1 = 40 mm) and the lowest fence porosity (ε1 = 22.6%), the lowest mean wind velocity was umean = 4.4 m/s at position x/h = 5. In the downwind direction, the wind velocity increased, reached their minimum at position x/h = 5, and then increased again to the initial wind velocity. For all fences with the characteristics of ε2 = 41.6%, the minimum value was already reached at position x/h = 2. The higher the porosity of the fence was, the earlier the initial wind velocity of the fence was reached in the free stream.
Sediment Transport Fluxes
Figure 9 exemplifies the vertical distribution of sediment transport fluxes obtained from the vertical mesh sand traps for the wind velocity u3 = 9.3 m/s. We found that sediment was mainly caught in heights of less than z ≤ 0.05 m for all wind velocities studied. This finding is in agreement that most sediment transport in coastal areas occurs for z < 0.05 m above the surface (Strypsteen, 2019). No sediment was caught in heights over z > 0.15 m, so the saltation layer height does not significantly exceed the fence height (h3 = 120 mm), see Experimental Setup.
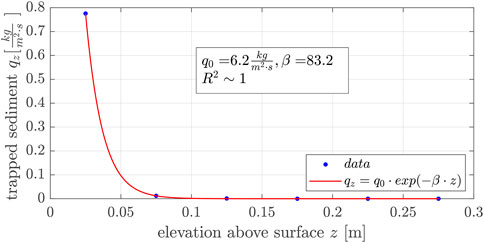
FIGURE 9. Vertical distribution of sediment transport flux obtained from the vertical mesh sand trap for wind velocity u3 = 9.3 m/s and the best fit exponential decay function for experiment No. 3.3.
Table 1 presents the results of the trapped sediment from the vertical mesh sand traps with the total mass flux Qs (kg/m/s), the decay rate ß (1/m), the extrapolated saltating sediment mass transport at the surface q0 (kg/m2/s), and the correlation coefficients R2 (-) of the regression analysis. The measuring duration was t = 10 min. The transport fluxes varied between Qs = 0.005–0.078 kg/m/s for wind velocities ranging between u1 = 6.1 m/s and u3 = 9.3 m/s. For the lowest wind velocity u1 = 6.1 m/s, the total mass fluxes show larger fluctuations than those at higher wind velocity u2 = 7.4 m/s and u3 = 9.3 m/s.
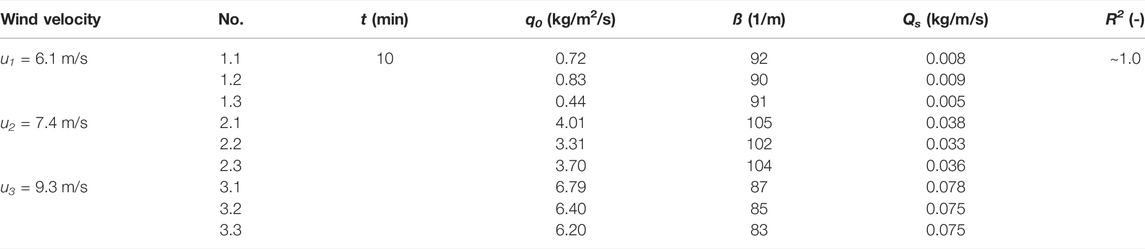
TABLE 1. Total mass flux results over the measuring duration, decay rate, extrapolated saltating sediment mass transport at the surface, and correlation coefficients of the vertical sediment profile regression analysis.
The regression parameters varied between ß = 83–105/m and q0 = 0.44–6.79 kg/m2/s, indicating that the higher the wind velocity, the higher the extrapolated saltating sediment mass transport at the surface and the amount of the total sediment transport rate. However, the decay rate and the sediment transport height did not vary significantly during the experiments for different wind velocities.
Sediment Accretion Around the Sand-Trapping Fence Configurations
Figure 10 shows sediment accretion around the investigated sand-trapping fences h3 = 120 mm over time, starting at t0 = 0 min and ending at t5 = 10 min. Both the x-axis (-) and the y-axis (-) are normalized over the fence height. The results for the investigated wind velocity u1 = 6.1 m/s are shown in Figures 10A,D,G, u2 = 7.4 m/s in Figures 10B,E,H, and u3 = 9.3 m/s in Figures 10C,F,I, respectively. The first row shows the results for ε1 = 22.6%, the second row for ε2 = 41.6%, and the third row for ε3 = 56.5%. The different colors of the lines indicate the different timesteps Δt = 2 min. The sediment changes are Δsf2 and Δsf3 is given in the legend.
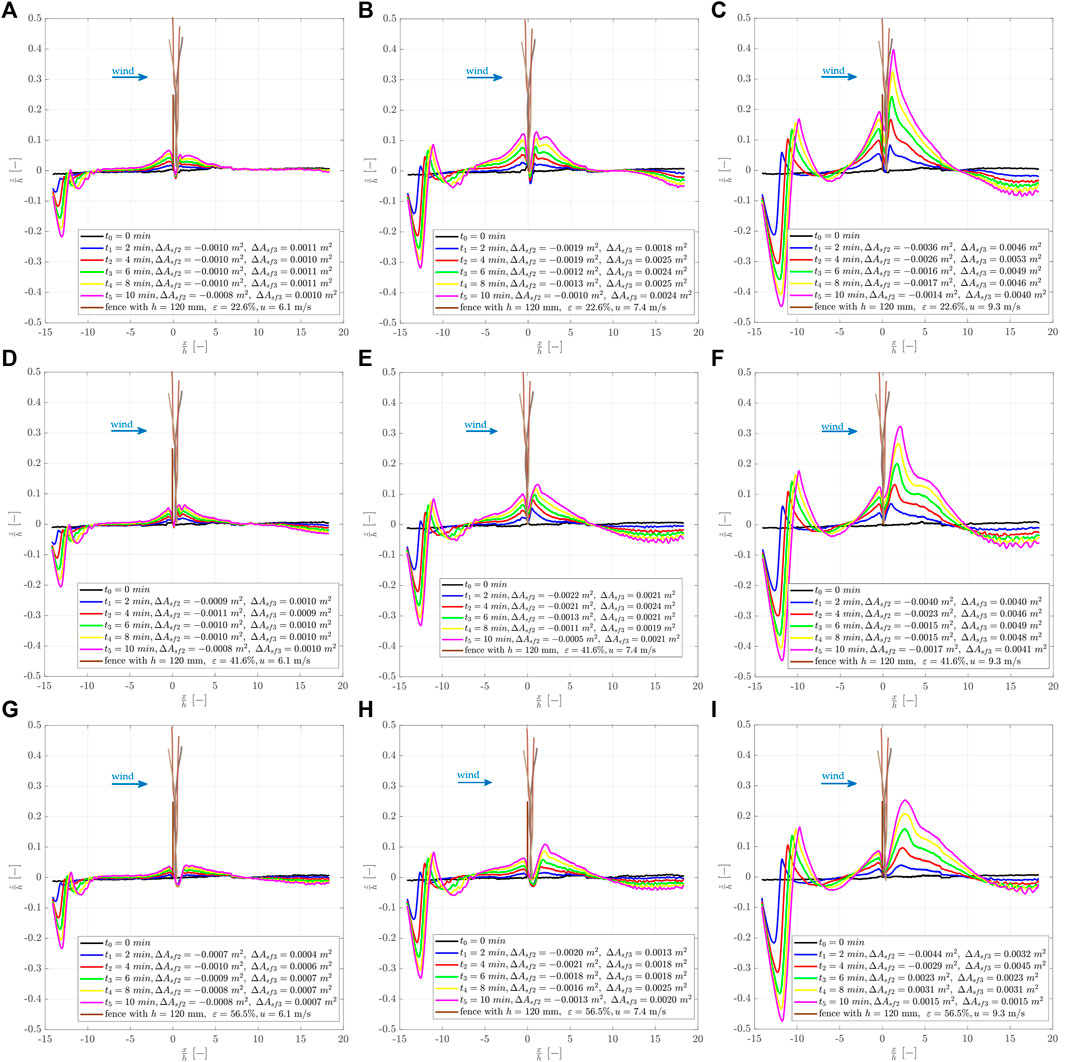
FIGURE 10. Sediment accretion around a porous fence h = 120 mm varying in fence porosity and investigated wind velocity. The first row (A-C) shows the results for ε1 = 22.6%, the second row (D-F) for ε2 = 41.6%, and the third row (G-I) for ε3 = 56.5%. The first columns show u1 = 6.1 m/s, the second column u2 = 7.4 m/s, and the third column u3 = 9.3 m/s.
The sediment accretion occurred predominantly horizontally and vertically, which corresponds to the first phase of dune growth, see for example Ning et al. (2020). Longer experiment durations would probably lead to the sediment accretion according to the second dune growth phase with almost exclusive horizontal dune growth if a sufficient sediment supply is provided. It is well seen that the higher the investigated wind velocity, the higher the total amount of deposited sediment at the sand-trapping fence at a given time, caused by a higher aeolian sediment transport rate. Furthermore, the denser the fence porosity, the higher the deposited sediment on the windward side of the sand-trapping fence at any given time. For example, for the lowest fence porosity of ε1 = 22.6%, the deposited sand reached a height of maximum z/h ∼ 0.4, whereas for the highest fence porosity of ε3 = 56.5%, the maximum height of z/h = 0.28 was reached. Generally, it can be recognized that for fences with ε2 = 41.6% and ε3 = 56.5%, scouring occurred in the main wind direction directly behind the fence at position x/h ∼ 1, whereas for ε1 = 22.6%, only little scouring was recorded at this position.
The sediment accretion on the leeward side developed simultaneously but faster than the sediment accretion on the windward side of the fence. For the lower and middle wind velocities (u1, u2), the height of the sediment accretion of the windward side is approximately the same as the height of the leeward side of the fence. For the fence with the lowest porosity, the sediment accretion on the leeward side of the fence occurred until x/h ∼ six to eight, whereas fence with the medium porosity until x/h ∼ seven to nine and for the most porous fence until x/h ∼ 8–12.
Discussion
Regarding the similarity of the physical model tests to nature, it must be taken into account that some influencing factors such as non-stationary wind conditions, attacking wind direction, moisture, salt content of the sediment, shell fragments, the presence of vegetation, or the topography cannot be modeled in the wind tunnel experiments adequately. For example, the main wind direction was modeled solely orthogonal and onshore to the fence that does not correspond to nature. In nature, the wind forces attack the fence from all wind directions. However, wind directions play a significant role in controlling the apparent fetch length, which refers to the continuous increase in sediment transport rates with increasing fetch length downwind until an equilibrium condition is reached (critical fetch length) (Jackson and Cooper, 1999; Bauer and Davidson-Arnott, 2003). When estimations of aeolian sediment transport rates from the beach toward the coastal dunes are made, they are often divided into longshore and cross-shore sediment fluxes, see for example Nickling and Davidson Arnott, (1990). Furthermore, in nature, the presence of vegetation generally increases the surface roughness, favoring sediment deposition and dune formation (Adriani and Terwindt, 1974; Hacker et al., 2012; Keijsers et al., 2015; Cohn et al., 2019; Miri et al., 2019). The presence of vegetation and the natural formation of coastal dunes also influence the sand-trapping efficiency of sand-trapping fences and may superimpose or interact with them (Houser et al., 2015). Generally, moisture content of sediment strongly affects aeolian sediment transport. With increasing moisture content the cohesion is increasing leading to lower sediment transport rates. In our investigations the sediment was dried before testing, leading to higher sediment transport rates compared to nature (Davidson-Arnott et al., 2005; van Rijn and Strypsteen, 2019). However, these influencing factors, which are usually subject to strong spatial and temporal fluctuations, have a decisive influence on the sediment accretion around sand-trapping fences in nature. The standardized wind tunnel investigations, on the other hand, offer the great possibility to observe the influence of certain fence properties under constant boundary conditions. The influence of other factors, such as the natural dune formation, can thus be eliminated, allowing us to evaluate the effeciency of sand-trapping fences in a standardized manner.
Wind Velocity Characteristics
The wind profile could be measured well and provide reproducible data in repeated experiments with the applied methodology. In Figure 11, the wind reduction factors Ru (-), according to Eq. 9, for the fence heights h = 40, 80, 120 mm are shown along the x-axis, normalized over the fence heights.
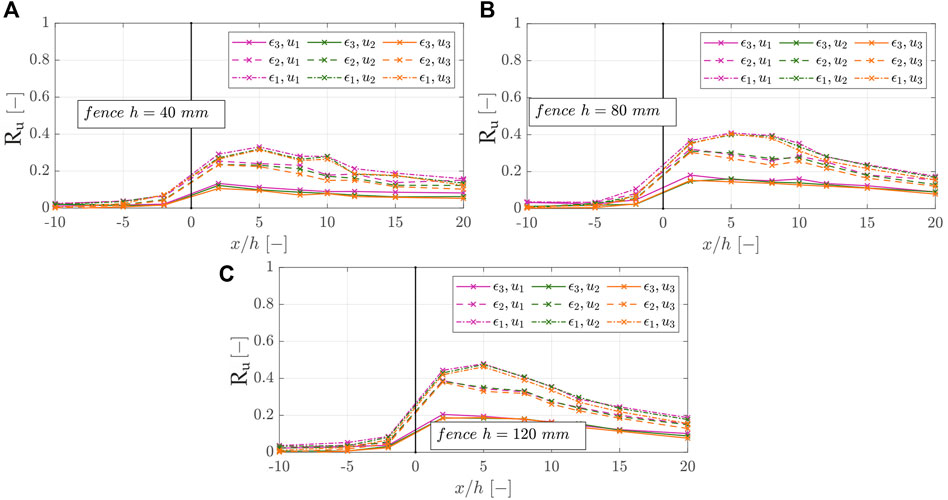
FIGURE 11. Wind reduction coefficients accordingly to Eq. 9 in the x-direction of fences with different characteristics, which are divided into (A) the fence heights h1 = 40 mm (B) h2 = 80 mm, and (C) h3 = 120 mm.
In Figure 12, the wind reduction factors Ru (-) for the fence porosities of ε = 22.6, 41.6, 56.5% are shown respectively.
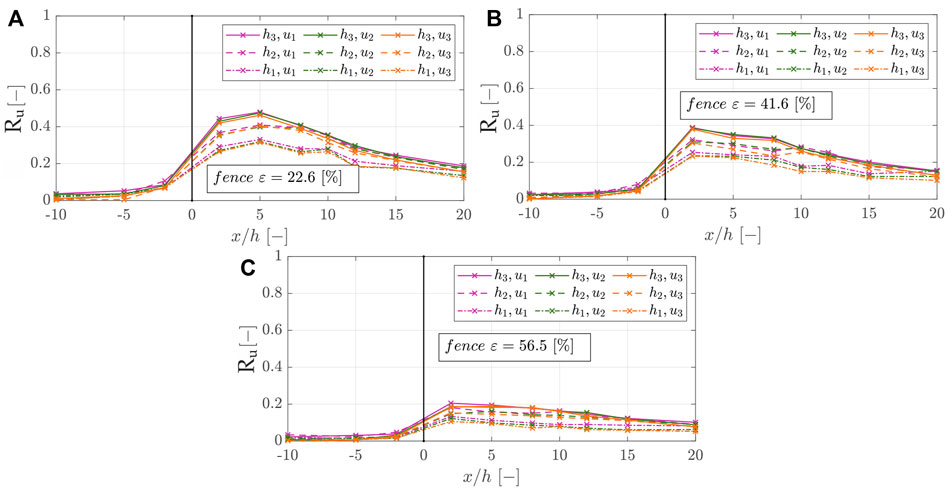
FIGURE 12. Wind reduction coefficients accordingly to Eq. 9 in the x-direction of fences with different characteristics, which are divided into (A) the fence porosities ε1 = 22.6%, (B) ε2 = 41.6%, and (C) ε3 = 56.5%.
Note that a higher wind reduction factor indicates a more substantial reduction in wind velocity and thus favors sediment deposition around the sand-trapping fence. We recognized that the wind reduction coefficients were almost the same for varying free wind velocities but varied significantly for different fence porosities and fence heights. The results show that, with increasing distance from the fence, the wind reduction coefficient increased to the maximum value and then decreased or stabilized again. The position at which Ru begins to decrease or stabilize, the protection range, generally lies between x/h = 2–5. The wind reduction coefficient was substantially greater for higher fences (Ru,max = 0.48) than lower fences (Ru,max = 0.21) and also higher for less porous fences (Ru,max = 0.48) than for more porous fences. Furthermore, it becomes clear that for the medium and high fences, the influence of the porosity is greater than for the low fences since the variety of Ru is also smaller. However, the fence height plays a minor role in the case of the most porous fence. This is in agreement with findings of Perera (1981), who found in wind tunnel experiments with vertical and horizontal slats (porosity >30–50%) or Lee and Kim (1999) who found with perforated fences (circular openings with porosity >40%), no recirculating zone occurred due to the strong bleed flow. For ε1 = 22.6% and ε2 = 41.6%, the typical airflow conditions around a single porous fence can be identified (Plate, 1971). However, for the fence of porosity ε3 = 56.5%, a strong bleed flow leads to smaller wind velocity reduction, the recirculating zone disappears, and the airflow zones become less complex (Dong et al., 2007).
Sediment Transport Fluxes and Sediment Accretion Around the Sand-Trapping Fence Configurations
We found that the two-dimensional development of the sediment accretion around the sand-trapping fences could be measured well with the 2D LiDAR scanner and is quantitatively reproducible in repeated experiments (maximum standard deviation of the sediment accretion σ ∼ 0.15). However, for low wind speeds, the ratio of the measurement error to the deposition heights is so small that the measurement error has a significant influence on the results. In addition, the aeolian sediment fluxes showed large temporal fluctuations, which were noticed especially during experiments with the wind velocity u1 = 6.1 m/s, see Table 1. As far as the authors know, the reproducibility of the sediment accretion around a sand-trapping fence is investigated for the first time with the results presented herein.
Figure 13A gives the changes of cross-sectional area and Figure 13B the trap efficiency for all configurations over time. The changes of cross-sectional areas ΔA (m2) and the trap efficiencies E (-) are shown as the average value of three up to four repeated measurements. Generally, as the sediment transport rates increase, the cross-sectional areas around the sand-trapping fence also increase; with the densest fence tending to accumulate the most sediment, then the medium-density fence, and then the porous fence. At the beginning of the experiments, the trap efficiency increases, and as time passes, the efficiency decreases or stabilizes.
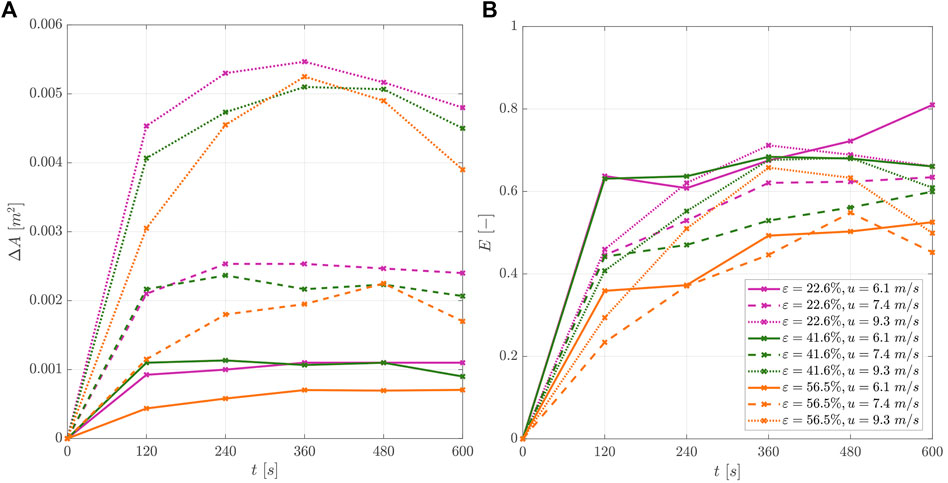
FIGURE 13. Change of (A) cross-sectional area ΔA (-) and (B) trap efficiency E (-) for different investigated fence configurations varying in fence porosities ε1 = 22.6%, ε2 = 41.6%, and ε3 = 56.5% for investigated wind velocities u1 = 6.1 m/s, u2 = 7.4 m/s, and u2 = 9.3 m/s expressed over the experiment duration t (s).
For the medium (u2 = 7.4 m/s) and high wind velocity (u3 = 9.3 m/s), the maximum trap efficiency is reached between t = 360–600 s, whereas, for the lowest wind velocity (u1 = 6.1 m/s), the maximum is reached at t = 360 s. After the trap efficiency increases to its maximum, it decreases slightly or stagnates to equilibrium during the time investigated in our experiments. This is in accordance with findings of Ning et al. (2020), where the sand-trapping is highest at the beginning of the first phase, drops significantly until the end of the first phase, and continues to drop slowly until the end of the second phase.
For the different investigated sand-trapping fence’s porosities (ε1 = 22.6%, ε2 = 41.6%, ε3 = 56.5%) and wind velocities (u1 = 6.1 m/s, u2 = 7.4 m/s, u3 = 9.3 m/s), the calculated trap efficiencies, see Eq. 12, are shown as boxplots (Figure 14). Since the efficiencies vary over time, all timesteps of the experiments are included showing the variations. The mean trap efficiencies for the dense fence (ε1 = 22.6%) Eh120,e22.6 are 0.69 (u1 = 6.1 m/s), 0.57 (u2 = 7.4 m/s), 0.63 (u3 = 9.3 m/s) and for the medium fence Eh120,e41.6 are 0.66 (u1 = 6.1 m/s), 0.52 (u2 = 7.4 m/s), 0.58 (u3 = 9.3 m/s). For the highest fence porosity (ε3 = 56.5%), the efficiencies Eh120,e56.6 are 0.45 (u1 = 6.1 m/s), 0.41 (u2 = 7.4 m/s), 0.52 (u3 = 9.3 m/s).
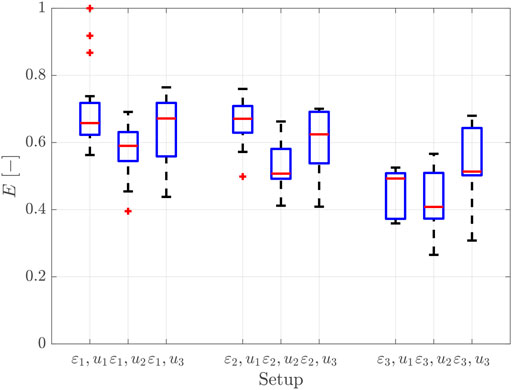
FIGURE 14. Trap efficiency E (-) calculated by Eq. 12 for different investigated fence configurations varying in fence porosity ε1 = 22.6%, ε2 = 41.6%, and ε3 = 56.5% for investigated wind velocities u1 = 6.1 m/s, u2 = 7.4 m/s, and u3 = 9.3 m/s over the whole measuring time t = 600 s.
Generally, the trap efficiency for the dense and medium fence are higher than for the lowest porosity fence. However, the shape of the resulting sediment accretion differs for the fences. Sand-trapping fences with lower porosities (ε1 = 22.6% and ε2 = 41.6%) favor localized sediment accretion directly at their brushwood lines. Fences with higher porosity (ε3 = 56.5%), allow for more sediment accretion further downwind, see also Figure 10. Thus, denser fence porosities are more suitable for constructing sand-trapping fences to initiate and facilitate the coastal dune toe growth. Fences with higher porosity could be used where the sediment accretion would occur over a longer downwind distance, for example, to allow a smoother transition between the foredunes and the white dunes.
Moreover, for the same porosity, the low wind velocity (u1 = 6.1 m/s) always gives the highest trap efficiency, followed by efficiency for the highest wind velocity (u3 = 9.3 m/s) and the medium wind velocity (u2 = 7.4 m/s). This can be explained by the fact that the critical shear stress velocity is minimally exceeded at the lowest wind velocity.
We strongly recommend extending the wind tunnel experiments over longer test sections to gain more quantitative data. This would require much larger wind tunnel dimensions with a larger sediment bed as well as a continuous sediment supply. With these proposed boundaries, it could be measured over more extended periods. Furthermore, installing numerous rows of fences in a larger wind tunnel would allow us to evaluate the optimal distance between numerous rows of fences to favor sediment accretion.
Conclusion
Physical model tests were conducted on sand-trapping fences with different fence heights (h = 40, 80, and 120 mm) and fence porosities (ε = 22.6, 41.6, and 56.5%). These tests occurred in an indoor subsonic, blowing-sand wind tunnel equipped with a moveable sediment bed (d50 ∼ 212 µm). The experimental mean wind velocities were u1 = 6.1 m/s, u2 = 7.4 m/s, and u3 = 9.3 m/s. We used a hot-wire anemometer to measure the flow fields, a vertical mesh sand trap to determine the sediment fluxes, and a 2D laser scanner to record the sediment accretion around the sand-trapping fences over time. The results of these experiments gave the following conclusions:
1) The wind profiles could be measured well with the hot-wire anemometer and provide reproducible data in repeated experiments. We recognized that the wind reduction coefficients varied significantly for different fence porosities and fence heights. It becomes clear that for the medium and high fence, the influence of the porosity is more significant than for the low fence height. However, the fence height plays a minor role for the high fence porosity. For the lower fence porosities, ε1 = 22.6% and ε2 = 41.6%, the typical airflow conditions around a single porous fence could be identified. The airflow zones around the fence of porosity ε3 = 56.5% are less complex.
2) The two-dimensional development of the sediment accretion around the sand-trapping fences could be measured well with the 2D LiDAR scanner and is quantitatively reproducible in repeated experiments. However, for the quantitative evaluation, low wind velocities and high fence porosities associated with low sediment accretion significantly influence the trapping efficiency, where the ratio of the measurement error to the deposition heights is small.
3) For the first time, the influence of model effects in wind tunnel experiments on the sediment accretion around a fence is considered. For this purpose, the different sediment fluxes are differentiated so that the sand-trapping efficiency is specified to the close range of the fence.
4) At the beginning of the experiments, the trap efficiency increases until its maximum, and as time passes, the efficiency decreases slightly or stagnates over an equilibrium during the time investigated in our experiments.
5) The porosity of the fence significantly controls the efficiency to trap sediment. More sediment deposits for fences with porosities of ε1 = 22.6% and ε2 = 41.6%, where localized sediment accretion directly at the sand-trapping fence takes place. Fences with higher porosity (ε3 = 56.5%) and an associated stronger bleed flow, allow for sediment accretion further downwind.
6) We recommend coastal managers to choose the fence porosity depending on the installation purpose. Lower fence porosities can be used to initiate and facilitate the dune toe growth, whereas fences with higher porosity would be more suitable to favor the sediment accretion between the transition of foredunes and white dunes as they have a wider range in which sediment accretes downwind.
The study results are of considerable significance for guidelines on installing sand-trapping fences and can provide theoretical support for their design.
Since experimental time, wind velocity, fence height, and the number of fence rows in wind tunnel investigations are often limited by the dimensions of the wind tunnel, long-term in situ measurements of sediment accretion around sand-trapping fences are needed containing data of changes in topography, beach slope, wet and dry beach width, tidal range, wind direction, and wind velocity.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
Conceptualization: CE; methodology: CE; formal analysis: CE; investigation: CE; data processing: CE; resources: HS; original draft preparation: CE; review and editing: HS; visualization: CE; supervision: HS; project administration: HS; and funding acquisition: CE, HS and others. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the German Federal Ministry of Education and Research (BMBF) within the project ProDune (Grant Number 03KIS125) that was initiated in the framework of the German Coastal Engineering Research Council (KFKI).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors thank the project partner Lower Saxony Water Management, Coastal Protection and Nature Conservation Agency for sharing their expertise in the project support group. The authors also thank Holger Blum for organizing sediments from the East Frisian Island of Norderney. We, furthermore, thank the technical staff and student assistants Sonja Möller, Mariana Vélez Perez, Marie Künzel, Michael Nelles, and Andrea Limberg of the IWW for their help in constructing and conducting the wind tunnel experiments.
References
Adriani, M. J., and Terwindt, J. (1974). Sand Stabilization and Dune Building. Gov. Publ. off; Government Publ. Office, GBV Gemeinsamer Bibliotheksverbund, the Hague, 68. The Hague: Rijkswaterstaat Communications.
Anderson, J. D. (2017). Fundamentals of Aerodynamics. McGraw-Hill series in aeronautical and aerospace engineering, 1130.
Arens, S. M., Baas, A. C. W., Van Boxel, J. H., and Kalkman, C. (2001). Influence of Reed Stem Density on Foredune Development. Earth Surf. Process. Landforms 26, 1161–1176. doi:10.1002/esp.257
Baas, A. C. W., and Sherman, D. J. (2006). Spatiotemporal Variability of Aeolian Sand Transport in a Coastal Dune Environment. J. Coastal Res. 225, 1198–1205. doi:10.2112/06-0002.1
Bagnold, R. A. (1971). The Physics of Blown Sand and Desert Dunes. 2nd Edition. doi:10.1007/978-94-009-5682-7
Bauer, B. O., and Davidson-Arnott, R. G. D. (2003). A General Framework for Modeling Sediment Supply to Coastal Dunes Including Wind Angle, beach Geometry, and Fetch Effects. Geomorphology 49, 89–108. doi:10.1016/S0169-555X(02)00165-4
Bauer, B. O., and Davidson-Arnott, R. G. D. (2014). Aeolian Particle Flux Profiles and Transport Unsteadiness. J. Geophys. Res. Earth Surf. 119, 1542–1563. doi:10.1002/2014JF003128
Cattafesta, L., Bahr, C., and Mathew, J. (2010). Fundamentals of Wind-Tunnel Design. Encyclopedia Aerospace Eng. 58, 467. doi:10.1002/9780470686652.eae532
Cermak, J. E. (1987). Advances in Physical Modeling for Wind Engineering. J. Eng. Mech. 113113, 7375–7756. doi:10.1061/(ASCE)0733-939910.1061/(asce)0733-9399(1987)113:5(737)
Chen, B., Cheng, J., Xin, L., and Wang, R. (2019). Effectiveness of Hole Plate-type Sand Barriers in Reducing Aeolian Sediment Flux: Evaluation of Effect of Hole Size. Aeolian Res. 38, 1–12. doi:10.1016/j.aeolia.2019.03.001
Cohn, N., Hoonhout, B., Goldstein, E., de Vries, S., Moore, L., Durán Vinent, O., et al. (2019). Exploring Marine and Aeolian Controls on Coastal Foredune Growth Using a Coupled Numerical Model. JMSE 7, 13. doi:10.3390/jmse7010013
Cohn, N., Ruggiero, P., Vries, S., and Kaminsky, G. M. (2018). New Insights on Coastal Foredune Growth: The Relative Contributions of Marine and Aeolian Processes. Geophys. Res. Lett. 45, 4965–4973. doi:10.1029/2018GL077836
Cornelis, W. M., and Gabriels, D. (2005). Optimal Windbreak Design for Wind-Erosion Control. J. Arid Environments 61, 315–332. doi:10.1016/j.jaridenv.2004.10.005
Creyssels, M., Dupont, P., El Moctar, A. O., Valance, A., Cantat, I., Jenkins, J. T., et al. (2009). Saltating Particles in a Turbulent Boundary Layer: experiment and Theory. J. Fluid Mech. 625, 47–74. doi:10.1017/S0022112008005491
Davidson-Arnott, R. G. D., MacQuarrie, K., and Aagaard, T. (2005). The Effect of Wind Gusts, Moisture Content and Fetch Length on Sand Transport on a beach. Geomorphology 68, 115–129. doi:10.1016/j.geomorph.2004.04.008
de Vries, S. (2013). Physics Of Blown Sand and Coastal Dunes. Dissertation. Delft,Netherlands: Delft University of Technology.
DIN EN ISO 14688-1 (2018). Geotechnische Erkundung und Untersuchung – Benennung, Beschreibung und Klassifizierung von Boden: Teil 1. Benennung und Beschreibung. doi:10.31030/2748424
Dong, Z., Luo, W., Qian, G., and Wang, H. (2007). A Wind Tunnel Simulation of the Mean Velocity fields behind Upright Porous Fences. Agric. For. Meteorology 146, 82–93. doi:10.1016/j.agrformet.2007.05.009
Eichmanns, C., Lechthaler, S., Zander, W., Pérez, M. V., Blum, H., Thorenz, F., et al. (2021). Sand Trapping Fences as a Nature-Based Solution for Coastal Protection: An International Review with a Focus on Installations in Germany. Environments 8, 135. doi:10.3390/environments8120135
Eichmanns, C., and Schüttrumpf, H. (2021). Influence of Sand Trapping Fences on Dune Toe Growth and its Relation with Potential Aeolian Sediment Transport. JMSE 9, 850. doi:10.3390/jmse9080850
Eichmanns, C., and Schüttrumpf, H. (2020). Investigating Changes in Aeolian Sediment Transport at Coastal Dunes and Sand Trapping Fences: A Field Study on the German Coast. JMSE 8, 1012. doi:10.3390/jmse8121012
Ellis, J. T., Li, B., Farrell, E. J., and Sherman, D. J. (2009). Protocols for Characterizing Aeolian Mass-Flux Profiles. Aeolian Res. 1, 19–26. doi:10.1016/j.aeolia.2009.02.001
Gallego-Fernández, J. B. (2013). Restoration of Coastal Dunes. Berlin, Heidelberg: Springer Berlin/Heidelberg.
Hacker, S. D., Zarnetske, P., Seabloom, E., Ruggiero, P., Mull, J., Gerrity, S., et al. (2012). Subtle Differences in Two Non-native Congeneric beach Grasses Significantly Affect Their Colonization, Spread, and Impact. Oikos 121, 138–148. doi:10.1111/j.1600-0706.2011.18887.x
Han, Q., Qu, J., Liao, K., Zhu, S., Zhang, K., Zu, R., et al. (2011). A Wind Tunnel Study of Aeolian Sand Transport on a Wetted Sand Surface Using Sands from Tropical Humid Coastal Southern China. Environ. Earth Sci. 64, 1375–1385. doi:10.1007/s12665-011-0962-7
Hesp, P. (2011). Dune Coasts. Earth Syst. Environ. Esciences, 193–221. doi:10.1016/B978-0-12-374711-2.00310-7
Ho, T. D., Dupont, P., Ould El Moctar, A., and Valance, A. (2012). Particle Velocity Distribution in Saltation Transport. Phys. Rev. E 85, 52301. doi:10.1103/PhysRevE.85.052301
Ho, T. D., Valance, A., Dupont, P., and Ould El Moctar, A. (2011). Scaling Laws in Aeolian Sand Transport. Phys. Rev. Lett. 106, 94501. doi:10.1103/PhysRevLett.106.094501
Hotta, S., and Horikawa, K. (1991). Function of Sand Fence Placed in Front of Embankment. Proc. 22nd Conf. Coastal Eng., 2754–2767. doi:10.1061/9780872627765.211
Houser, C., Wernette, P., Rentschlar, E., Jones, H., Hammond, B., and Trimble, S. (2015). Post-storm beach and Dune Recovery: Implications for Barrier Island Resilience. Geomorphology 234, 54–63. doi:10.1016/j.geomorph.2014.12.044
Itzkin, M., Moore, L. J., Ruggiero, P., Hacker, S. D., and Biel, R. G. (2020b). The Influence of Dune Aspect Ratio, Beach Width and Storm Characteristics on Dune Erosion for Managed and Unmanaged Beaches.
Itzkin, M., Moore, L. J., Ruggiero, P., and Hacker, S. D. (2020a). The Effect of Sand Fencing on the Morphology of Natural Dune Systems. Geomorphology 352, 106995. doi:10.1016/j.geomorph.2019.106995
Jackson, D. W. T., and Cooper, J. A. C. (1999). Beach Fetch Distance and Aeolian Sediment Transport. Sedimentology 46, 517–522. doi:10.1046/j.1365-3091.1999.00228.x
Jackson, N. L., and Nordstrom, K. F. (2011). Aeolian Sediment Transport and Landforms in Managed Coastal Systems: A Review. Aeolian Res. 3, 181–196. doi:10.1016/j.aeolia.2011.03.011
Keijsers, J. G. S., De Groot, A. V., and Riksen, M. J. P. M. (2015). Vegetation and Sedimentation on Coastal Foredunes. Geomorphology 228, 723–734. doi:10.1016/j.geomorph.2014.10.027
Lawlor, P., and Jackson, D. (2021). “A Nature-Based Solution for Coastal Foredune Restoration: The Case Study of Maghery, County Donegal, Ireland,” in Book: Exploring the Multiple Values of Nature: Connecting Ecosystems and People across Landscapes. 1st Edition (Springer Nature).
Lee, S.-J., and Kim, H.-B. (1999). Laboratory Measurements of Velocity and Turbulence Field behind Porous Fences. J. Wind Eng. Ind. Aerodynamics 80, 311–326. doi:10.1016/S0167-6105(98)00193-7
Li, B., and Sherman, D. J. (2015). Aerodynamics and Morphodynamics of Sand Fences: A Review. Aeolian Res. 17, 33–48. doi:10.1016/j.aeolia.2014.11.005
Manohar, M., and Bruun, P. (1970). Mechanics of Dune Growth by Sand Fences. Dock and harbour authority, 243–252.
MATLAB (2018). Natick, Massachusetts: The MathWorks Inc. Version 9.510.944444 (R2018b)Available at: https://de.mathworks.com/products/new_products/release2018b.html (Accessed March 31, 2021).
Mehta, R. D. (1979). The Aerodynamic Design of Blower Tunnels with Wide-Angle Diffusers. Prog. Aerospace Sci. 18, 59–120. doi:10.1016/0376-0421(77)90003-3
Miri, A., Dragovich, D., and Dong, Z. (2019). Wind-borne Sand Mass Flux in Vegetated Surfaces - Wind Tunnel Experiments with Live Plants. CATENA 172, 421–434. doi:10.1016/j.catena.2018.09.006
Nickling, W. G., and Davidson-Arnott, R. G. D. (1990). Aeolian Sediment Transport on Beaches and Coastal Sand Dunes. Proceedings Canadian Symposium on Costal Sand Dunes 1990. Proc. Symp. Coastal Sand Dunes, 1–36.
Ning, Q., Li, B., and Ellis, J. T. (2020). Fence Height Control on Sand Trapping. Aeolian Res. 46, 100617. doi:10.1016/j.aeolia.2020.100617
O'Connel, J. (2008). Coastal Dune Protection & Restoration: Using ‘Cape’ American Beach Grass And Fencing.
Owen, P. R., and Gillette, D. (1985). “Wind Tunnel Constraint on Saltati,” in Proceedings of the International Workshop on the Physics of Blown Sand, 253–269.
Perera, M. D. A. E. S. (1981). Shelter behind Two-Dimensional Solid and Porous Fences. J. Wind Eng. Ind. Aerodynamics 8, 93–104. doi:10.1016/0167-6105(81)90010-6
Plate, E. J. (1971). The Aerodynamics of Shelter Belts. Agric. Meteorology 8, 203–222. doi:10.1016/0002-1571(71)90109-9
Poortinga, A., Keijsers, J. G. S., Maroulis, J., and Visser, S. M. (2014). Measurement Uncertainties in Quantifying Aeolian Mass Flux: Evidence from Wind Tunnel and Field Site Data. PeerJ 2, e454. doi:10.7717/peerj.454
Ruz, M.-H., and Anthony, E. J. (2008). Sand Trapping by Brushwood Fences on a beach-foredune Contact: the Primacy of the Local Sediment Budget. zfg_suppl 52, 179–194. doi:10.1127/0372-8854/2008/0052S3-0179
Shao, Y., and Lu, H. (2000). A Simple Expression for Wind Erosion Threshold Friction Velocity. J. Geophys. Res. 105, 22437–22443. doi:10.1029/2000JD900304
Sherman, D. J., Swann, C., and Barron, J. D. (2014). A High-Efficiency, Low-Cost Aeolian Sand Trap. Aeolian Res. 13, 31–34. doi:10.1016/j.aeolia.2014.02.006
Strypsteen, G. (2019). Monitoring and Modelling Aeolian Sand Transport at the Belgian Coast. Leuven, Belgium: Dissertation. KU Leuven, Faculty of Engineering Technology, 1–226. doi:10.13140/RG.2.2.19781.88806
Swann, C., Brodie, K., and Spore, N. (2015). Coastal Foredunes: Identifying Coastal, Aeolian, and Management Interactions Driving Morphologic State Change: ERDC/CHL TR-15-17. Washington, DC 20314: U.S. Army Corps of Engineers–1000.
testo (2021). Hot-wire Anemometer and External Data Logger: Product Specifications. Testo SE & Co. KGaA.
van Rijn, L. C., and Strypsteen, G. (2020). A Fully Predictive Model for Aeolian Sand Transport. Coastal Eng. 156, 103600. doi:10.1016/j.coastaleng.2019.103600
van Thiel de Vries, J. S. M. (2009). Dune Erosion during Storm Surges. Dissertation. Netherlands. Amsterdam: Delft University of Technology, Civil Engineering and Geosciences, Hydraulic EngineeringTechnische Universität Delft.
Vithana, (2013). The Effect of Stone Protrusion on the Incipient Motion of Rock armour under the Action of Regular Waves. London: Department of Civil, Environmental & Geomatic Engineering, University College London.
Wang, T., Qu, J., Ling, Y., Liu, B., and Xiao, J. (2018). Shelter Effect Efficacy of Sand Fences: A Comparison of Systems in a Wind Tunnel. Aeolian Res. 30, 32–40. doi:10.1016/j.aeolia.2017.11.004
White, R. R. (1996). Laboratory Simulation of Aeolian Sand Transport and Physical Modeling of Flow Around Dunes. Annals of Arid Zone, 187–213.
Yu, Y.-p., Zhang, K.-c., An, Z.-s., Wang, T., and Hu, F. (2020). The Blocking Effect of the Sand Fences Quantified Using Wind Tunnel Simulations. J. Mt. Sci. 17, 2485–2496. doi:10.1007/s11629-020-6095-2
Keywords: wind tunnel experiments, nature-based solutions, sand-trapping fences, porous fences, sediment transport, coastal protection
Citation: Eichmanns C and Schüttrumpf H (2022) A Nature-Based Solution for Coastal Protection: Wind Tunnel Investigations on the Influence of Sand-Trapping Fences on Sediment Accretion. Front. Built Environ. 8:878197. doi: 10.3389/fbuil.2022.878197
Received: 17 February 2022; Accepted: 16 March 2022;
Published: 14 April 2022.
Edited by:
Jens Figlus, Texas A&M University, United StatesReviewed by:
Alec Torres-Freyermuth, Universidad Nacional Autónoma de México, MexicoEdgar Mendoza, National Autonomous University of Mexico, Mexico
Copyright © 2022 Eichmanns and Schüttrumpf. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Christiane Eichmanns, ZWljaG1hbm5zQGl3dy5yd3RoLWFhY2hlbi5kZQ==
 Christiane Eichmanns
Christiane Eichmanns Holger Schüttrumpf
Holger Schüttrumpf