Vibration Characteristics of Capped Viscous Damping Based on Frame Restoring-Force Amplitude

This study investigates the performance of several capped viscous damping models which give an upper limit to the initial-stiffness-proportional damping force. The comparing capped viscous damping models are the original and newly proposed one. The original capped damping model is expected to have a certain degree of frequency insensitiveness. However, unless the damping force reaches the capped value, the damping may be simply behaving as the initial-stiffness-proportional damping, also there is no clear physical basis for setting the capping value. Conversely, it is confirmed that the newly proposed damping model improves the original model problems faced with setting the capping value and frequency insensitiveness accuracy. In this study, the discussion is primarily focused on structural engineering using a 20-story fish bone model comprising a steel and reinforced concrete, but this argument can be applied to various engineering fields such as civil and mechanical engineering. Especially, this proposed model does not have mass term damping, it may be effective for a large nonlinear analysis such as sliding/uplifting and base-isolated structure.

1 Introduction

The main factors that influence the damping energy of a building are due to material friction and contact between non-structural elements and this damping does not greatly depend on frequency (Lazan (1968))., i.e., this damping is considered to more appropriately represent reality than viscous damping in numerical simulation (Clough and Penzien (2003)). However, in time history analysis, this hysteresis of damping must be expressed as complex damping. Hence, stiffness-proportional damping and Rayleigh damping have long been used, even if it is difficult to use if the damping should be constant over a wide frequency band. To compensate for this, constant modal damping is often used, but it lacks practicality for large-scale analysis because of to the large computing load. In recent times, performance-based building design is being increasing employed, and it is inevitable to increase the scale of analysis models via a numerical simulation technology. Therefore, there is a need to develop an ideal damping model.

Building damping is affected by various factors such as location conditions and aging, and it is difficult to evaluate it quantitatively because of the large variation. However, the selection of the damping model has considerable influence on the seismic response analysis and incorporating such physical quantities into numerical simulation is an important engineering issue. Recent papers Huang et al. (2019), Nakamura (2019), Mogi et al. (2021), and Ota et al. (2021) have attempted to solve this problem, describing a viscous damping scheme that achieves frequency independent damping over a wide frequency range. Although these damping models are excellent in overcoming the problems of the existing viscous damping models, high-level computational algorithms must be incorporated. Therefore, this study focused on the capped viscous damping for developing a damping model that easily realizes frequency independence. The capped damping model that gives an upper limit to the initial-stiffness-proportional damping force is expected to have a certain degree of frequency insensitiveness. However, unless the damping force reaches the capped value, the damping may simply behave as the initial-stiffness-proportional damping, and there is no clear physical basis for setting the capping value.

For overcoming the aforementioned problems, this study proposes a novel damping model that can clarify the concept of setting a capping force. Then, the effectiveness of the proposed model is demonstrated by comparing it with the original capped viscous damping model and other conventional models. Ultimately, we must confirm the practicality of the proposed model through 3D analysis, but first we analyzed the basic characteristics of the proposed damping model using a simple 20-story fish bone model.

2 Problems With Existing Viscous Damping Model

2.1 Rayleigh Damping

Rayleigh damping is often used owing to its ease of use. It is a classical damping model expressed by damping terms proportional to mass m and initial stiffness $k$ Eq. 1.

$c=a_0\text{m}+a_1\text{k}(1)$

Hence, if coefficients $a_0$ and $a_1$ are known, the $i$ th mode damping ratio ${\xi }_i$ can be found using the following expression.

${\xi }_i=\frac{1}{2{\omega }_i}{a}_0+\frac{{\omega }_i}{2}{a}_1(2)$

Coefficients $a_0$ and $a_1$ can be determined from the specified damping ratios ${\xi }_p$ and ${\xi }_q$ for the $p$th and $q$th modes, respectively. For these two modes in matrix form, Eq. 2 becomes.

$\frac{1}{2}\left[\begin{array}{cc}1/{\omega }_p& {\omega }_p\\ 1/{\omega }_q& {\omega }_q\end{array}\right]\left\{\begin{array}{c}{\xi }_p\\ {\xi }_q\end{array}\right\}=\left\{\begin{array}{c}{a}_0\\ a_1\end{array}\right\}(3)$

These two algebraic equations can be solved to determine coefficients $a_0$ and $a_1$.

The stiffness-proportional term $a_1\text{k}$ of Eq. 1 is a model created on the basis of an assumed initial stiffness regardless the nonlinearity of response history analysis (RHA). However, Chrisp (1980) reported that an unintended spurious damping force is generated in plastic hinges, and the mechanism of its generation was explained later by Bernal (1994). This phenomenon occurs when a stiffer nonlinear element is explicitly incorporated into the end of a beam. Additionally, Léger and Dussault (1992) and Charney (2008) pointed out nonlinearity may change the natural frequency. Therefore, to avoid all aforementioned problems, a model in which the stiffness term is proportional to the tangential stiffness $k_T$ rather than the initial stiffness $k$ used.

$c^{\ast }=a_0\text{m}+a_1{k}_T(4)$

The damping force $f_d$ is calculated as $f_d=c^{\ast }\cdot \dot{x}$ using from the tangential damping coefficient $c^{\ast }$ and velocity $\dot{x}$. Assuming the spring is completely bilinear, its behavior exhibits initial stiffness proportionality in the elastic stage and drastically the damping force suddenly becomes zero after yielding. This behavior lacks a physical basis and this discontinuity in the damping force poses problems in numerical calculations.

2.2 Wilson–Penzien Damping

Wilson and Penzien (1972) expresses the modal damping matrix $C_{WP}$ by the following equation.

${\mathit{C}}_{\mathit{WP}}=\mathit{M}\left({\displaystyle \sum }_{q=1}^n\frac{2{\xi }_q{\omega }_q}{M_q}{\mathit{\phi }}_{\mathit{q}}{\mathit{\phi }}_{\mathit{q}}^{\mathit{T}}\right)\mathit{M}(5)$

Where, $M$ is the mass matrix; and $\xi$ is the damping ratio; ${\phi }_q$ and ${\omega }_q$ are the undamped natural vibration mode vector and natural frequency of the $q$ th mode, respectively; and $M_q$ is the generalized mass ${\phi }_q^{T}M{\phi }_q$. From Eq. 5, if the rotational inertia mass is zero, no damping force is generated in the rotational degree of freedom. Therefore, the spurious damping force generated by the plasticization of the beam-end-moment is theoretically not generated. Chopra and McKenna (2016) suggested using constant modal damping as a countermeasure to the spurious damping force, but it leads to a high computational load because it uses a dense matrix. To avoid this problem, Chopra and McKenna (2016) proposed using tangential stiffness in solving simultaneous equations and treat the difference from the correct mode damping force as an unbalanced force in the equation of motion. Then, this idea was incorporated into OpenSees (McKenna, 1997). However, similar to the problem of Rayleigh damping discussed by, e.g., Hall (2006) and Ryan and Polanco (2008), Pant and Wijeyewickrema (2012), Pant et al. (2013), Hamidreza et al. (2019), if the foundation is not fixed, as in the case of an uplifting structure or base isolation system, or if there is a large peeling between elements such as the formation of cracks in concrete, the deformation will be underestimated, and the model may become nonconservative.

In addition, Luco and Lanzi (2019) reported that in modal damping, after the nonlinear element transition from the elastic state to plastic state, the degree of freedom without mass becomes an unintended velocity response because of numerical artifacts and the absence of damping terms. To avoid this problem, model damping can be improved by adding infinitesimal stiffness-proportional damping.

2.3 Original Capped Viscous Damping

The capped viscous damping model is a damping model that can be applied to a complex vibration model with large nonlinear behavior; for example, it can be applied to the sliding or uplifting of a foundation. Although tangent Rayleigh damping is effective in such an analysis, there is concern that tangent Rayleigh damping has little physical basis for reducing the damping force and that damping is overestimated owing to the influence of the mass term. Hall (2006) discusses the increase in the ratio of damping force to spring strength using a 10-story lumped mass shear model as an example. In the elastic state, the ratio of the restoring force and damping force is kept constant, but after yielding, the restoring force is limited, whereas the damping force increases in proportion to the velocity. This is unnatural and cannot be explained as a real phenomenon. In the case of initial-stiffness-proportional damping, the restoring force $f_k$ and damping force $f_d$ due to the arbitrary story stiffness k have the following relationship.

$f_k+f_d=\left(1+2\xi i\right)kx(6)$

If the spring is elastic and oscillated in the first mode, the peak values of the restoring force and damping force will maintain a ratio of $2\xi$ with a phase difference of π/2. However, the spring exceeds the yield displacement and the restoring-force peaks at yield strength $R_{max}$. Hence, the ratio to the damping force exceeds $2\xi$. Hall (2006) reports that the computed maximum value of damping force was 60% of the yield strength of the building, and this response result is nonconservative. Therefore, this problem can be avoided by setting the capped damping force as shown below [Hall (2006)].

$f_d=\pm \text{min}\left(a_{k}k\left|\dot{x}\right|\mathit{、}2\xi R_{max}\right)(7)$

Here, $R_{max}$ should be set before the analysis is executed, and there is no established idea regarding this at present. Therefore, it is necessary to set $R_{max}$ individually depending on the designer’s engineering judgment. In previous works Hall (2006), Hall (2018), and Qian et al. (2021), as examples of setting $R_{max}$, the yield strength of the story is assumed and determined by calibration.

In addition to the effect of suppressing an abnormal increase in the damping force after yielding, caped damping has the characteristic of causing a certain degree of frequency insensitiveness. The capping fraction $2\xi$ is based on the ratio of the damping and stiffness forces when a linear structure is vibrating in a mode at the resonant frequency of that mode. The single-degree-of-freedom oscillator with capped viscous damping is illustrated Figure 1. If the system is oscillating at a given displacement amplitude $(X_a$) with a random frequency below the value of $\xi$, it will behave as an initial-stiffness-proportional damping oscillator (red line). Further, if the system is oscillating at the same $X_a$ but with higher frequencies, it will be characterized with more damping than desired. However, a higher-mode damping does not increase with increasing frequencies due to a capping effect. Currently, the damping force of the oscillator has approached a frequency-insensitive state. Therefore, the capped damping force is largely dependent on the frequency-insensitive behavior. To further enhance the frequency-insensitive nature, we evaluated an adjusted capped value according to the restored force amplitude amount, which was obtained from moment to moment in some way. This approach was better than fixing the capped value in advance. Furthermore, according to previous studies, the analyzed targets have been limited to a one-way input; therefore, it is necessary to model the system so that it can be applied to a three-way simultaneous input.

FIGURE 1

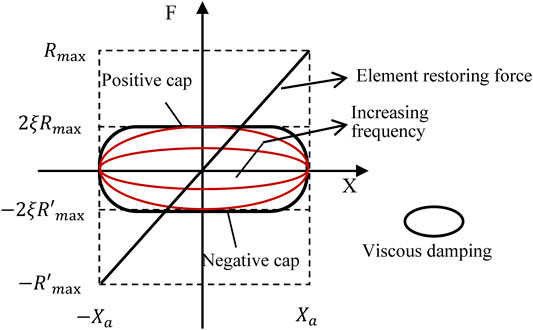
FIGURE 1. Element force and viscous damping forces vs. displacement for a single-degree-of-freedom oscillator under harmonic motion with increasing frequency at constant displacement amplitude X: R_max is maximum restoring force of spring. [presented by Hall (2018)].

2.4 Limitations of the Equivalent Viscous Damping Model

The limitations of the equivalent viscous damping model identified in previous studies are summarized as follows:

1) Generally, the viscous damping model depends on frequency (Clough and Penzien (2003)).

2) Using Rayleigh damping in inelastic RHA, a spurious damping force may be generated when stiff inelastic spring inserted at the beam-end is yielding (Chrisp (1980); Bernal (1994)).

3) The tangent Rayleigh damping concept is an ad hoc approach since there is no physical basis to such a damping mechanism (Hall (2006)).

4) Using Rayleigh or tangent Rayleigh damping in inelastic RHA, inappropriate damping forces are generated because of the changes in eigenmodes (Léger and Dussault (1992); Charney (2008)).

5) It is inappropriate to apply Rayleigh damping or constant modal damping to structures that are sliding/uplifting or to seismic base isolation structures owing to the influence of the mass term damping force (e.g., Hall (2006); Ryan and Polanco (2008); Pant and Wijeyewickrema (2012); Pant et al. (2013); Hamidreza et al. (2019)).

6) It is effective to use modal damping to avoid spurious damping force generation (Chopra and McKenna (2016)), but an unintended velocity response occurs with no mass degrees of freedom after the element transitions from elastic to inelastic (Luco and Lanzi (2019)).

7) The original capped viscous damping provides little rationale for setting the upper limit, and it is unclear how effective the capped damping force is on the frequency independence of stiffness-proportional damping. Furthermore, modeling by the story shear damping force is not enough when three-dimensional vibration is considered (Qian et al. (2021)).

In this study, we focused on the capped viscous damping proposed by Hall (2006) with the aim of exploring a well-balanced model that can avoid the aforementioned problems. The vibration characteristics were analyzed by comparing it with several damping models, and the engineering convenience/effectiveness of this damping model was considered.

3 Basic Concepts of Improved Capped Viscous Damping

The amount of capped damping force is an important factor for determining the damping characteristics. Hall (2006), Hall (2018), Qian et al. (2021) propose that the story shear damping force is capped at $2\xi F_y$ using the yield value of the restoring story force $F_y$. But unless the damping force reaches the capped damping force, the damping may be simply be initial-stiffness-proportional damping. Therefore, to realize frequency insensitiveness, it is necessary to set the capped damping force according to the real-time amplitude amount. Further, the damping mechanism should be modeled directly at the member level rather than the story level. This section proposes a mechanism to generate frequency-insensitive damping according to the amplitude of the restoring force at the member level.

3.1 Modeling Frequency-Insensitive Damping With Capped Viscous Damping

If the building undergoes simple vibration in the first mode and the displacement is the maximum amplitude $X_a$, the maximum damping force $D_{max}$ can be expressed using the story stiffness k.

$D_{max}=2\xi \cdot k\cdot X_a=2\xi \cdot R_{max}(8)$

$R_{max}$ is the maximum restoring force, which is equal to $k\cdot X_a$. And the building is oscillated in the first mode, the damping will be linear viscous damping unless the restoring force is capped by the yield strength. Next, considering the vibration system oscillates simply in the second mode, the maximum damping force can be similarly evaluated by the following equation using the maximum amplitude $X_a$.

$D_{max}=\frac{2\xi }{{\omega }_1}\cdot k\cdot {\omega }_2\cdot X_a=2\xi \cdot \frac{{\omega }_2}{{\omega }_1}\cdot R_{max}(9)$

Equation 9 shows that the damping force increases in proportion to ${\omega }_2/{\omega }_1$, Where ${\omega }_2$ is the second mode natural frequency, and this is a characteristic of the initial-stiffness-proportional damping. However, the damping force is capped at $2\xi R_{max}$, the system vibrating in the second mode has a frequency-dependent coefficient ${\omega }_2/{\omega }_1$ of 1.0. Considering that the second mode vibrates with the same amplitude, the amount of damping energy dissipated per cycle is about the same. If this principle can be incorporated into numerical analysis well, it will be possible to realize modeling that does not depend on the frequency but depends on the amplitude. Therefore, it is necessary to determine the damping force that depends on the amplitude of the current restoring force. However, a phase difference of π/2 occurs at the time of the maximum response of displacement (i.e., restoring force) and velocity. As a simple method, it is conceivable to determine the capped damping force with the maximum restoring force experienced in the past as $R_{max}$, but the frequency insensitiveness performance may be inferior after the maximum value experience. $R_{max}$ to be set during the time history analysis is an important topic. Therefore, in this study, it is assumed that the relationship of ${\dot{X}}_a\cong \omega X_a$ is approximately established between the maximum displacement $X_a$ and velocity $\dot{X_A}$ recorded near an arbitrary time, and the capped damping force $D_{max}$ can be evaluated by $D_{max}=2\xi \cdot R_{max}$ using the maximum restoring force $R_{max}$ recorded most recently. This is based on the rule of thumb that the maximum displacement $X_a$ and velocity $\dot{X_A}$ near a certain time are often governed by one primary mode with a natural frequency $\omega$. Therefore, the secondary higher-mode damping force cannot behave independently because of the capped damping force $D_{max}$. Hence, it is considered that frequency insensitiveness can be achieved to some extent. However, this concept may have weak points in that the prediction accuracy of the maximum damping force value is poor in the case where multiple modes are overlapping, e.g., in the case of simultaneous input RHA in three directions and RHA of high-rise buildings where higher modes are prominent. This point is discussed in the Discussion section.

In the next section, we explain the setting of the maximum restoring force $R_{max}$.

3.2 Update Procedure for ${\mathit{R}}_{\mathit{max}}$

This study proposes a capped damping force $2\xi R_{max}$; here, $R_{max}$ is the most recently recorded restoring-force peak. Figure 2 shows the time history of any restoring force at the nodal end of the stiffness element. The procedure for updating $R_{max}$ will be explained using this restoring-force time history as an example. $R_{max}$ stores the maximum value in each of the positive and negative directions and updates it according to the following rules.

1) If $R_{max}$ is compared with the current time restoring force and if the current time restoring force is larger, $R_{max}$ is updated by the current restoring force.

2) If the restoring-force changes from the increasing state to the decreasing state, $R_{max}$ is updated with the current restoring force.

FIGURE 2

FIGURE 2. Update procedure for the maximum amplitude of restoring force ${\mathit{R}}_{\mathit{max}}$.

The red and blue dashed lines in Figure 2 indicate the time domain in which $R_{max}$ on the positive and negative sides is updated, and circle indicates the time when $R_{max}$ was updated at the end immediately before the decrease. In the figure, “A” represents the state where the restoring force is increasing to the positive side, and at this time, the peak value ${{\displaystyle {}_{p}R}}_{max}$ on the positive side is continuously updated along the red dashed line according to Rule I. “B” represents the stage of switching to the negative side, and the restoring force increased to the negative side, and the peak value ${{\displaystyle {}_{n}R}}_{max}$ on the negative side was sequentially updated by Rule I in the area of this blue broken line. “C” represents the stage of increase on the positive side again, and ${{\displaystyle {}_{p}R}}_{max}$ is sequentially updated by Rule I in the area of the red dashed line that exceeds the most recently recorded ${{\displaystyle {}_{p}R}}_{max}$. “D” represents the stage of increase on the negative side again, and although it does not exceed the most recently recorded ${{\displaystyle {}_{n}R}}_{max}$, the value of ${{\displaystyle {}_{m}R}}_{max}$ is updated by Rule II. Even if the direction of the restoring-force changes from decreasing to increasing on the positive side as at “D’,” the ${{\displaystyle {}_{n}R}}_{max}$ is not updated.

As described earlier, by setting the peak value of the most recently recorded restoring force to $R_{max}$, a damping force that depends not on the frequency but on the amplitude near the current time is created. There is no distinction between the elastic and inelastic elements in the update of $R_{max}$, and the restoring force at that time is applied to the judgment. By updating the $R_{max}$ of each restoring-force vector of all elements according to the above rules, the general-purpose application in three-dimensional dynamic analysis will become possible.

3.3 Programmatic Implementation of Capped Damping

Figure 3 shows the program flow which is written specifically test capped viscous damping. For the total equation of motion, incremental Eq. 10 at the integral time interval $\Delta T$ is cumulatively obtained.

$\mathit{M}\ddot{\mathrm{\Delta }\mathit{x}}+\mathit{C}\mathrm{\Delta }\dot{\mathit{x}}+\mathit{K}\mathrm{\Delta }\mathit{x}=\mathrm{\Delta }\mathit{p}(10)$

FIGURE 3

FIGURE 3. Program flow.

Here, $M$ is mass, $K$ is tangent stiffness, and $C$ is the initial-stiffness-proportional damping matrix. The incremental equation forms the form of the relational expression Eq. 11 between the static load and displacement. The effective stiffness matrix $\tilde{K}$ is as shown in Eq. 12, and the effective load $\Delta \tilde{p}$ is as shown in Eq. 13.

$\tilde{\mathit{K}}\mathrm{\Delta }\mathit{x}=\mathrm{\Delta }\tilde{\mathit{p}}(11)$

$\tilde{\mathit{K}}=\mathit{K}+\frac{6}{\mathrm{\Delta }{T}^2}\mathit{M}+\frac{3}{\mathrm{\Delta }T}\mathit{C}(12)$

$\mathrm{\Delta }\tilde{\mathit{p}}=\mathrm{\Delta }\mathit{p}+\left(\frac{6}{\mathrm{\Delta }T}\mathit{x}+3\ddot{\mathit{x}}\right)\mathit{M}+\left(3\dot{\mathit{x}}+\frac{\mathrm{\Delta }T}{2}\ddot{\mathit{x}}\right)\mathit{C}(13)$

The program performs the triangular decomposition of the effective stiffness matrix $\tilde{K}$ by the modified Cholesky decomposition in 1) as shown in Figure 3. Next, the effective load shown in Eq. 13 is calculated by 2). The element stress and maximum restoring force $R_{max}$ are updated in 3). Finally, in 4), the smaller of the element damping force vector $f_d$ obtained by the element initial-stiffness-proportional damping matrix c in Eq. 14 and the element damping force vector obtained from the maximum restoring force is adopted as the element damping force $f_d^{\text{'}}$. Further, $i$ in Eq. 15 represents the degree of freedom of the local element. Here $R_{max}$ is a two-dimensional array and holds the maximum values of the positive and negative sides of the restoring force to evaluate the positive and negative directions of the $f_d$, respectively.

$f_d=c\cdot \dot{x}, c=\frac{2\xi }{{\omega }_1}\cdot k(14)$

$f_d^{\prime }\left(i\right)=\text{min}\left(f_d\left(i\right),2\xi R_{max}\left(i\right)\right)(15)$

The balance of the total equation of motion is calculated using the updated damping force vector $d^{\text{'}}$ which is the sum of each local element damping force vector $f_d^{\text{'}}$ and the unbalanced force $u$ is calculated using Eq. 16 and carried over to the next step. $p$ and $r$ are the external force and restoring-force vectors at the current time.

$\mathit{u}=\mathit{p}-\mathit{M}\ddot{\mathit{x}}-{\mathit{d}}^{\mathit{\prime }}-\mathit{r}(16)$

4 Verification by 20-Story Fish Bone Model

4.1 Analysis Model Overview

To evaluate the differences in the responses of different damping models, a comparative study was conducted using a fish bone model that simulates a high-rise building and a period for 2 s (Figure 4A). The vertical degrees of freedom of all nodes were constrained, and the horizontal displacement of the nodes at each beam level were equal to the that of the beam–column joint node by multi-point constraints. The story height was 3.5 m, and the span is assumed to be 6 m, and 3-m-long beams were set on the left and right. The beam and column sections are listed in Table 1. The beam stiffness was multiplied by Φ (=1.5) considering the slab, and the column stiffness was about 1.8–1.9 times that of the beam. A mass (59.19 t) was uniformly applied to each floor at the beam–column joint node as shown in Figure 4A so that the period was 2.0 s and the rotational inertia mass of each node was zero. To confirm the differences depending on the types of structures, two cases were considered: the case of the beam-end assuming a steel (S) structure with restoring-force characteristics is shown in Figure 4B, and the case of the beam-end assuming a reinforced concrete (RC) structure with the Takeda model is shown in Figure 4C. The initial stiffness and yield moment of the RC model are the same as those of the S model for convenience. The crack-bending strength of the Takeda model is assumed to be 0.3 times its yield strength, and the post-cracking stiffness is assumed to be 0.5 times the initial stiffness. Table 2 lists the initial stiffness (3EI/L) of the beam, post-cracking stiffness ratio, cracking moment, and yielding moment. The inelastic spring at the end of beam is generally incorporated into the element stiffness matrix implicitly or arranged explicitly with an additional node. In the arranged explicitly with an additional node case, the initial stiffness of the end hinge spring is set at a higher value so as that the linear natural vibration of the model is unaffected; however, the spurious damping force is prominent in such modeling (Chrisp (1980); Bernal (1994)). In this study, this method is used to insert an inelastic spring with stiffness 1,000 times higher than the beam (Figure 4D). Therefore, for the inelastic spring with nonlinear characteristics (Table 2), K₁ should be multiplied by 1,000, and conversely, the post-cracking stiffness ratio of K₂ and K₃ should be multiplied by 1/1,000, and K₂ gives 0.0005 and K₃ gives 1.0E-6.

FIGURE 4

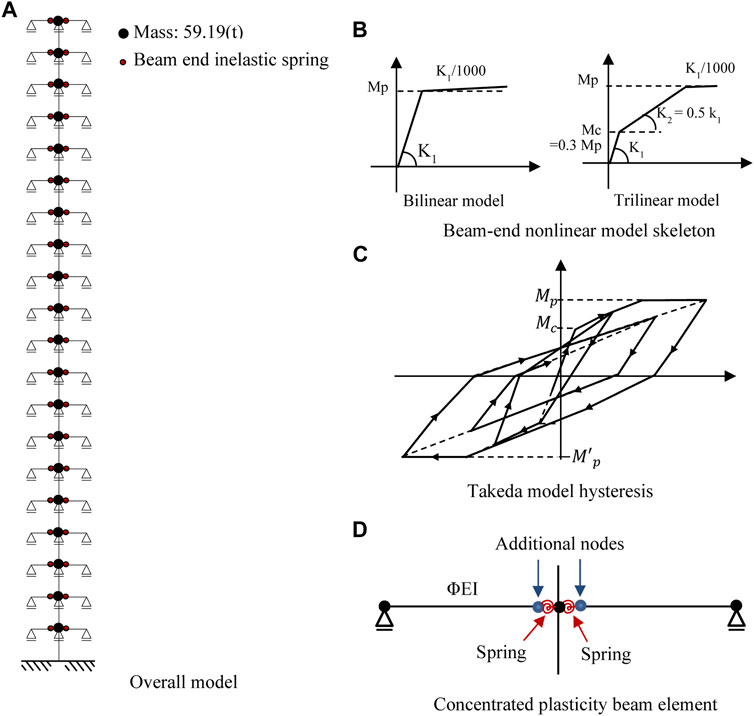
FIGURE 4. (A) Overall view of the 20-story fish bone model, (B) beam-end nonlinear model skeleton, (C) Takeda model hysteresis, and (D) concentrated plasticity beam element.

TABLE 1

TABLE 1. Element stiffness.

TABLE 2

TABLE 2. Beam-end nonlinearity.

Table 3 lists the natural period and effective mass ratio (cumulative values from lower mode).

TABLE 3

TABLE 3. Eigen value analysis results.

4.2 Ground Motion

Ground motion was created by using an acceleration response spectrum with 5% damping as the target spectrum and using the random phase characteristic (return period of 500 years). Figure 5 shows the simulated ground motion and acceleration/pseudovelocity response spectra.

FIGURE 5

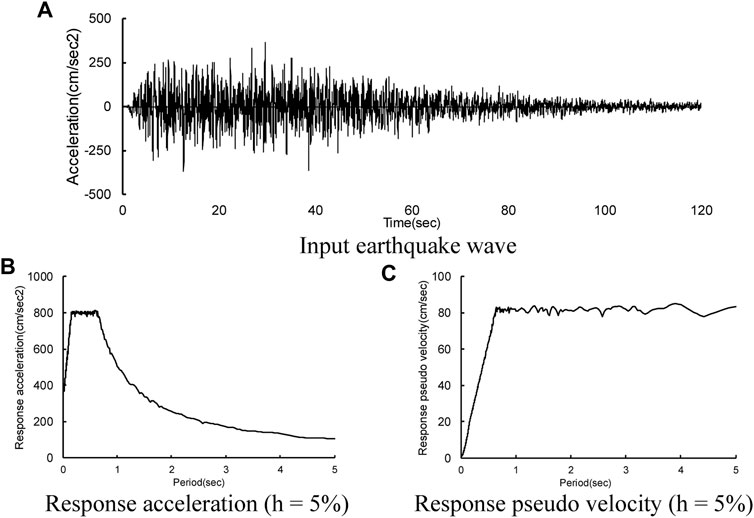
FIGURE 5. Simulated earthquake motion. (A) Input earthquake wave, (B) Response acceleration (h = 5%), (C) Response pseudo velocity (h = 5%).

4.3 Comparison of Various Capped Viscous Damping Models

The three types of capped viscous damping models, including the original capped viscous damping [CP(O)], capped viscous damping A [CP(A)], and capped viscous damping B [CP(B)] models, were compared to prove the effectiveness of the proposed modeling. The accuracy of each damping model was verified by comparison with the nonlinear constant modal damping model (WP), which creates a damping matrix by performing an eigenvalue analysis each time the structural stiffness changes.

The original or CP(O) model has been proposed as a method for giving a lateral interstory damper (Hall (2006); Hall (2018)). The same modeling was used in this study. The height-wise distribution of damper coefficients ($C_i$) was taken as proportional to the lateral interstory stiffness ($K_i$), i.e., $C_i=\alpha K_i$ (where i is a story number). With this assumption, the coefficient ($\alpha$) for the assumed first mode damping ratio (${\xi }_1$) was calculated by Eq. 17 Qian et al. (2021).

${\xi }_1=\alpha \frac{T_1{{\displaystyle \sum }}_i{K}_i{\left({\varphi }_{1,i}-{\varphi }_{1,i-1}\right)}^2}{4\pi {{\displaystyle \sum }}_i{m}_i{\varphi }_{1,i}^2}(17)$

Where, $m_i$, ${\varphi }_{1,i}$, and $T_i$ denote the mass lumped at the floor, lateral displacement vector of the first mode, and first mode period, respectively. $K_i$ was obtained by static elastic analysis with a horizontal external force (${\varphi }_{1,i}$) distribution. Based on these parameters, $\alpha =0.0127$. A story strength ($R_i$) value was estimated as the maximum story shear force responses, which resulted from a nonlinear RHA due to the assumed seismic motion with $\xi =2\%$ of the nonlinear constant modal damping. The results estimated from the measurements of elastic and inelastic RHA in RC and S structures are summarized in Table 4. The damper coefficient after the relief velocity is 1/1,000 times the initial damper coefficient.

TABLE 4

TABLE 4. Interstory capped damping force $2\xi R_i$ of CP(O) estimated from seismic RHA.

The CP(A) is a method for determining the capped damping force. This was done by setting the maximum value of the restoring force experienced in the past as $R_{max}$. This model was not the recommended model in this study; however, it was considered as the target for comparison because of its clearer mechanism. This model was also easier to implement in the program used than CP(B).

The CP(B) was considered as the main method in this study. This is a method for determining the capped damping force from the maximum value of the most recently experienced restoring force, which was set as $R_{max}$.

4.4 Elastic RHA Using Sinusoidal Waves

The oscillation characteristic of constant modal damping WP, CP(A), and CP(B) were compared using three cycles of sinusoidal wave synchronized with the building period; further, CP(O) was not compared. The input wave is shown in Figure 6A. Using this input wave, the steady vibration at the time of input and the free vibration after the input can be examined in one analysis. The maximum acceleration was 100 gal, and the response analysis time was 30 s. The integration step was 0.001 s; the damping ratio was 2%; The responses obtained by using each sinusoidal wave tuned to the first mode to the third-mode periods of the frame were compared. Figure 6 shows the maximum story drift angle and acceleration for each floor. Figure 6B is the result of the first mode periodic input. The maximum responses of CP (A) and CP (B) consistently show the same results in the first to third modes. Further, CP(A) and CP(B) have slightly larger responses than WP. This is because as suggested in the previous section, the velocity precedes the displacement, and hence, the damping force peaked at the maximum value of the past restoration force, and the damping force could not be fully exerted. Moreover, as shown Figures 6C,D, the maximum response of the CP(A) and CP(B) of the second- and third-mode periodic inputs was the same as that of the WP. Figure 7 shows the mode RHA, which is the mode response ${}_{s}y$ extracted by the expansion theorem shown in Eq. 18.

${}_{s}y=\frac{{\left\{{}_s\varphi \right\}}^T\left[M\right]\left\{x\right\}}{{\left\{{}_s\varphi \right\}}^T\left[M\right]\left\{{}_s\varphi \right\}}(18)$

$\left\{x\right\}$: Response displacement vector $\left\{{}_s\varphi \right\}$: sth mode eigenvector.

FIGURE 6

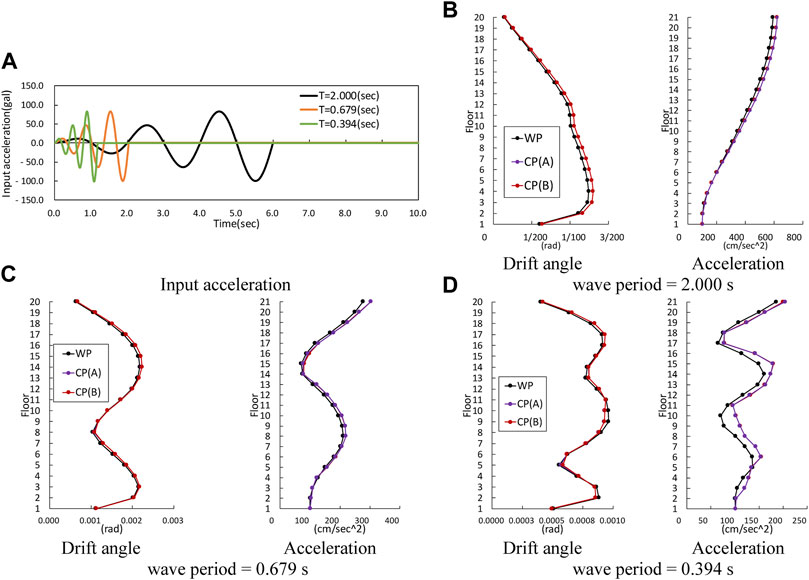
FIGURE 6. Maximum response for the sinusoidal wave. (A) Input acceleration, (B) wave period = 2.000 s, (C) wave period = 0.679 s, (D) wave period = 0.394 s.

FIGURE 7

FIGURE 7. Modal displacement.

From Figure 7, we can see that the maximum response occurs at the final peak of the sweep excitation, but CP(A) and CP(B) show a relatively frequency insensitiveness characteristics for the response of such an amplification process. However, in the free vibration after the forced-excitation phase, there is a tendency to overestimate the damping slightly compared to the estimates of WP. This overestimation is attributed to the fact that since $R_{max}$ is the previous peak value, in the case of free vibration in which the amplitude gradually decreases, the R_max is evaluated to be larger than the amplitude at the current time. CP(B) did not significantly increase the damping during free vibration compared to CP(A) because the $R_{max}$ evaluation continued to be updated even after the maximum peak.

4.5 RHA by Ground Motion

Next, Evaluate the oscillation characteristics of real-phase seismic waves as elastic and inelastic. To compare the differences in the characteristics of the steel and reinforced concrete structures, the integration time step was 0.0001 s, and the damping ratio was 2% for both S and RC structures.

4.5.1 Elastic RHA

For the elastic RHA, according to the response results of the elastic analysis shown in Figure 8, the maximum interstory drift angles of the CP(B) and WP models are similar but that of CP(O) and CP(A) are smaller. The maximum displacement of the CP(O), CP(A), and WP models are similar but that of CP(B) is slightly larger. This tendency was also seen in the examination of sinusoidal waves, but it is attributed to the slight underestimation of the attenuation of the first mode. The maximum acceleration is observed for the WP model, followed by the CP(B), CP(A), and CP(O) models. Figure 9 shows the displacement time history response of each mode decomposed by the expansion theorem of shown in Eq. 18. Although the response of the all model is almost the same in the first mode, in higher mode, the responses of CP(O) and CP(A) are smaller than CP(B) and WP and the responses of CP(B) is slightly smaller than that of WP. However, in the third mode, the responses of all capped viscous damping models were smaller than that of the WP, and the higher mode tended to reduce the frequency insensitive effect of the damping force capping. From these results, the CP(B) shows relatively more frequency-insensitive characteristics than CP(O) and CP(A) in the elastic RHA.

FIGURE 8

FIGURE 8. Maximum response of elastic response history analysis (RHA).

FIGURE 9

FIGURE 9. Time histories of the modal displacement.

4.5.2 Inelastic RHA

Figure 10 shows the maximum responses obtained by inelastic analysis. The ductility factor was evaluated by the ratio of the maximum node rotation angle of the beam–column joint to the beam yield rotation angle. The RC ductility factor diagram also shows the ratio of the crack rotation angle to the yield rotation angle.

FIGURE 10

FIGURE 10. Maximum response of inelastic RHA.

In the steel structure model, the ductility factor, CP(A), and CP(B) correspond relatively well with the WP; however, its response was larger than the WP in the lower story. CP(O) also showed a relatively good response in the upper story; however, its response in the lower story was smaller than the other damping models. As for the displacement responses, CP(B) showed a slightly larger response than the other damping models. Meanwhile, the other models provided almost the same responses. In general, there were variations in the acceleration responses, where the CP(A) showed a smaller response than the other damping models.

In the RC structure model, the ductility factor and CP(O) showed smaller responses than the other damping models. Meanwhile, the other damping models gave almost the same responses. The displacement responses were almost the same in all the damping models. In general, the acceleration responses varied; however, the CP(O), CP(A), and CP(B) showed smaller responses than the WP.

These comparisons showed that the CP(B) varied in acceleration response from the WP. However, the displacement responses and ductility factors (story drift angles) were relatively in good agreement in both steel and RC structure models. The responses of the CP(O) were not as good.

From the above comparison, it is confirmed that CP(B) shows better characteristics than CP(O) and CP(A) in the inelastic RHA.

5 Discussion

The proposed viscous damping force is estimated using the recently recorded maximum restoring force $R_{max}$, which is based on the rule of thumb that the maximum displacement and velocity near a certain time are often governed by a primary mode. Although this proposed model is expected to be applied in large-scale 3D analysis, the prediction accuracy of the maximum damping force may decrease in cases where multiple modes overlap. For example, in the case of simultaneous input in three directions, such assumptions may lead to an overestimation of vertical damping force.

This study assumes that the variable axial force due to horizontal movement does not act on the columns, but it is predicted that the large variable axial force due to the horizontal mode is applied to the corner columns or the side columns of the shear wall or brace. In this case, since the $R_{max}$ of column axial force is not the stress due to vertical mode response, the application of proposed model may lead to an overestimation of vertical mode damping compared to constant modal damping.

Currently, the damping of vertical oscillation in buildings is not as clear as horizontal motion because the vertical motion is less than the horizontal motion and the destruction of the building is primarily caused by the horizontal motion. However, in structural design practice, evaluating the axial force ratio of columns, deformation due to beam vibration, and the surface pressure of seismic isolation bearings is essential. If vertical vibration mode is critical to structural design, its mechanism should not overestimate the damping force even when considering the simultaneity of multiple vibration modes. Because the capped viscous damping depends only on the stiffness term, the damping ratio of the element deformation component predicted to be over-damped is reduced in advance.

6 Conclusion

To verify the effectiveness of capped viscous damping based on the maximum restoring force experienced in the past, original method CP(O) and simple method CP(A) based on the past maximum value and a method CP(B) based on the latest maximum value were compared and verified. Capped viscous damping is a practical damping model with low computational load and no spurious damping force excitation. It is expected to be applied in the field of structural, civil and mechanical engineering. The findings of this study are as follows:

1) The original method has a problem in the capping force setting, and the appropriate value depends on the scale of the assumed seismic motion. Conversely, the proposed method can automatically determine the capping force by the amplitude of the restoring force.

2) In the proposed method, the current maximum damping force is evaluated by the amplitude of the latest maximum restoring force of the element. Therefore, when increasing the amplitude, the damping is slightly underestimated. Conversely, when reducing the amplitude, the damping is slightly overestimated.

3) In the elastic RHA, the story drift angle of CP(B) is similar to that of nonlinear constant modal damping (WP); however, CP(O) and CP(A) are less accurate than CP(B). Further, in the inelastic RHA, CP(B) shows the closest response to WP in both steel and RC structures compared to other capped damping models. The acceleration responses of all capped viscous damping models show large variations relative to WP. Therefore, the proposed capped viscous damping CP(B) has more desirable frequency insensitiveness characteristics and practicality than the original model.

4) In contrast to the tangent Rayleigh damping, which lacks a physical basis, the proposed model provides a clear physical basis because the capping value is determined based on the concept of energy equality per cycle regardless of the frequency.

7 Future Outlook

Recently, performance-based building design is widely used, and the scale of the analytical models can be increased via numerical simulations. However, existing classical damping models do not provide enough terms, whereas Rayleigh damping and modal damping have their damping force in the mass term, so they tend to overestimate the damping force for rigid body motions such as sliding, lifting, and base isolation systems. Conversely, if tangent stiffness-proportional damping is used for such nonlinear problems, the damping force suddenly changes in time and even be discontinuous when there is a sudden change in tangent stiffness. It has been pointed out that the damping in numerical analysis has an important role in stabilizing nonlinear analysis in addition to its physical meaning [e.g., Soroushian (2018)]. On other hand, the proposed model does not have mass term damping but does have some degree of viscous damping force in the stiffness term, so it may effective for the stabilization of large nonlinear analysis.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

YM conceived of the presented idea and developed the theory and performed the computations. NN supported the conceptualization of draft, supervision, and review and editing of the draft. KN, and AO verified the analytical methods. All authors discussed the results and contributed to the final manuscript.

Conflict of Interest

YM was employed by the company Design Division, Taisei Corporation and AO was employed by the company Nuclear Facilities Division, Taisei Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank Enago (www.enago.jp) for the English language review.

References

Bernal, D. (1994). Viscous Damping in Inelastic Structural Response. J. Struct. Eng. 120 (4), 1240–1254. doi:10.1061/(asce)0733-9445(1994)120:4(1240)

CrossRef Full Text | Google Scholar

Charney, F. A. (2008). Unintended Consequences of Modeling Damping in Structures. J. Struct. Eng. 134 (4), 581–592. doi:10.1061/(asce)0733-9445(2008)134:4(581)

CrossRef Full Text | Google Scholar

Chopra, A. K., and McKenna, F. (2016). Modeling Viscous Damping in Nonlinear Response History Analysis of Buildings for Earthquake Excitation. Earthquake Engng Struct. Dyn. 45 (2), 193–211. doi:10.1002/eqe.2622

CrossRef Full Text | Google Scholar

Chrisp, D. (1980). Damping Models for Inelastic Structures. Master’s thesis. Christchurch, New Zealand: University of Canterbury.

Clough, R., and Penzien, J. (2003). Dynamics of Structures. Berkeley, California: Computer and structure, Inc.

Google Scholar

Hall, J. F. (2018). Performance of Viscous Damping in Inelastic Seismic Analysis of Moment-Frame Buildings. Earthquake Engng Struct. Dyn. 47 (14), 2756–2776. doi:10.1002/eqe.3104

CrossRef Full Text | Google Scholar

Hall, J. F. (2006). Problems Encountered from the Use (Or Misuse) of Rayleigh Damping. Earthquake Engng Struct. Dyn. 35 (5), 525–545. doi:10.1002/eqe.541

CrossRef Full Text | Google Scholar

Hamidreza, A., Ricardo, A., and Erin, S. (2019). Effects of the Improper Modeling of Viscous Damping on the First-Mode and Higher-Mode Dominated Responses of Base-Isolated Buildings. Earthq. Eng. Struct. Dyn. 49 (1), 51–73. doi:10.1002/eqe.3223

CrossRef Full Text | Google Scholar

Huang, Y., Sturt, R., and Willford, M. (2019). A Damping Model for Nonlinear Dynamic Analysis Providing Uniform Damping over a Frequency Range. Comput. Structures 212, 101–109. doi:10.1016/j.compstruc.2018.10.016

CrossRef Full Text | Google Scholar

Lazan, B. J. (1968). Damping of Materials and Members in Structural Mechanics. Oxford, UK: Pergamon.

Google Scholar

Léger, P., and Dussault, S. (1992). Seismic-Energy Dissipation in MDOF Structures. J. Struct. Eng. 118 (5), 1251–1269. doi:10.1061/(ASCE)0733-9445(1992)118:5(1251)

CrossRef Full Text | Google Scholar

Luco, J. E., and Lanzi, A. (2019). Numerical Artifacts Associated with Rayleigh and Modal Damping Models of Inelastic Structures with Massless Coordinates. Earthquake Engng Struct. Dyn. 48 (13), 1491–1507. doi:10.1002/eqe.3210

CrossRef Full Text | Google Scholar

McKenna, F. (1997). Object-Oriented Finite Element Programming: Frameworks for Analysis, Algorithms, and Parallel Computing. PhD thesis. Berkeley: Department of Civil Engineering, University of California Berkeley.

Mogi, Y., Nakamura, N., and Ota, A. (2021). Application of Extended Rayleigh Damping Model to 3D Frame Analysis -Evaluation of Damping in Elastic Response Analysis. J. Struct. Constr. Eng. Trans. AIJ 783, 738–748. doi:10.3130/aijs.86.738

CrossRef Full Text | Google Scholar

Nakamura, N. (2019). Application of Causal Hysteretic Damping Model to Nonlinear Seismic Response Analysis of Super High-Rise Building -Substitution for Viscous Damping Including Tangent Stiffness Proportional Damping. J. Struct. Constr. Eng. Trans. AIJ 759, 627–637. doi:10.3130/aijs.84.597

CrossRef Full Text | Google Scholar

Ota, A., Nakamura, N., and Mogi, Y. (2021). Examination of Applicability of Causality-Based Damping Model to Dynamic Explicit Method. J. Struct. Constr. Eng. Trans. AIJ 786, 1168–1179. doi:10.3130/aijs.86.1168

CrossRef Full Text | Google Scholar

Pant, D. R., Wijeyewickrema, A. C., and ElGawady, M. A. (2013). Appropriate Viscous Damping for Nonlinear Time-History Analysis of Base-Isolated Reinforced concrete Buildings. Earthquake Engng Struct. Dyn. 42 (15), 2321–2339. doi:10.1002/eqe.2328

CrossRef Full Text | Google Scholar

Pant, D. R., and Wijeyewickrema, A. C. (2012). Structural Performance of a Base-Isolated Reinforced concrete Building Subjected to Seismic Pounding. Earthquake Engng Struct. Dyn. 41 (12), 1709–1716. doi:10.1002/eqe.2158

CrossRef Full Text | Google Scholar

Qian, X., Chopra, A. K., and McKenna, F. (2021). Modeling Viscous Damping in Nonlinear Response History Analysis of Steel Moment‐frame Buildings: Design‐Plus Ground Motions. Earthquake Engng Struct. Dyn. 50 (3), 903–915. doi:10.1002/eqe.3358

CrossRef Full Text | Google Scholar

Ryan, K. L., and Polanco, J. (2008). Problems with Rayleigh Damping in Base-Isolated Buildings. J. Struct. Eng. 134 (11), 1780–1784. doi:10.1061/(asce)0733-9445(2008)134:11(1780)

CrossRef Full Text | Google Scholar

Soroushian, A. (2018). A General Rule for the Influence of Physical Damping on the Numerical Stability of Time Integration Analysis. J. Appl. Comput. Mech. 4 (5), 467–481. doi:10.22055/JACM.2018.25161.1235

CrossRef Full Text | Google Scholar

Wilson, E. L., and Penzien, J. (1972). Evaluation of Orthogonal Damping Matrices. Int. J. Numer. Meth. Engng. 4 (1), 5–10. doi:10.1002/nme.1620040103

CrossRef Full Text | Google Scholar