Evaluation Circular Failure of Soil Slopes Using Classification and Predictive Gene Expression Programming Schemes

This article presents an analysis of a dataset related to slope stability circular failure cases using the GeneXproTools program. Two models were developed: The first model was utilized to find a classification model that shows the stability status (S), and the second model was utilized to estimate the factor of safety and predict the mathematical model to serve as an indicator of slope stability. The proposed models include cohesion, unit weight, slope angle, coefficient of pore water pressure, internal friction angle, slope height, internal friction angle, and safety factor. The results showed that the values of accuracy and error were 93.1 and 6.9%, respectively, for classification model 1. The relationship between the actual values of the factor of safety and the output of model 2 was an R2 value of 0.96. The models developed were subjected to sensitivity analysis to determine the input variables’ impact on output for the two models. The selected slope locations with different material characterizations were introduced into geox5 software, and the results were compared to those of the two developed models. Furthermore, when the proposed models were compared to the available models in the literature, the results showed that the proposed models in this study performed better than the available models.

Introduction

Slope stability assessment is utilized to evaluate earth stability, including soil or rock slope. Analyses are commonly targeted to understand the influences that possibly activate the slope movement or the reasons for a recent slope failure. Slope failure happens when the downward material movements of shear stresses and gravity become greater than the soil shear strength. Thus, slope failure occurs when there is a decrease in soil shear strength or an increase in applied shear stresses. Cracks, swelling, pore pressure, decomposition fills of creep loads, clayey rock, strain softening, leaching, weathering, and cyclic loading can all cause a decrease in slope shear strength. In addition, shear stress might increase because of extra loads at the top of the soil slope and an increase in soil weight because of an increase in the water content, an increase in water pressure in cracks at the top of the slope, and seismic effects at the bottom of the slope. Moreover, these causes are related to slope failure, such as stress state, slope geometry, erosion, and temperature. The water impact on the slope can be measured in two locations: One is the aquifer under the groundwater or the surface that produces pore water pressure, and the second is the infiltration of rainwater that leaks through flows and the surface. It is associated with the nearby levels of rainfall, near water masses, and the geo-hydrological and topographic soil features. It is noticed that groundwater is almost present everywhere under the Earth’s surface. Groundwater fills the whole space between the grains in the soil, and it can leak into the gap existing in the rock mass, changing the air in the whole space, which leads to an increase in soil weight.

The process of avoiding the initiation movement, decelerating it through countermeasures, or it down, starting with Terzaghi’s 1950 work, landslide mechanism. Natekin and Knoll (2013) investigated the slope stability in terms of analytical, theoretical, numerical, statistical, and experimental methods that have been used throughout the world. Xu and Low (2006) used the finite element method and the limit equilibrium method. Even with these methods, certain slope failure mechanisms were too complicated for them to be effective, including internal deformation and brittle cracking, as well as creeping and liquefaction of weaker soil layers (Zhou et al., 2019). However, assessment of slope stability depends on historical performances and geotechnical characteristics of the collected slope cases by using an artificial neural network (Lu and Rosenbaum, 2003). Wang et al. (2005) also used the ANN to forecast the slope stability and precisely estimate the factor of safety for the Yodonghe landslide. The support vector machine was used to discover the non-linear relationship between its influence factors and slope stability (Zhao et al., 2012; Zhao and Li, 2021). Lollino et al. (2016) investigated two slopes in Italy: on the first slope with stiff clay, the dissipation of negative surplus pore water pressures created by earlier mine excavation at the slope toe caused a first-time collapse, and on the second slope, the stress–strain development of the old landslide reactivates mostly in rainy seasons. The benefits of using artificial intelligence and genetic algorithms in geotechnical applications have been studied in different studies (Al Bodour et al., 2022; Hanandeh et al., 2020a; Hanandeh et al., 2020b).

Additionally, for circular failure, the factors used were cohesion, unit weight, slope height, slope angle, ratio of pore water pressure, and internal friction angle. These six factors were consistent with those normally accepted for circular failure evaluation in a previous research (Sah et al., 1994). If the slope height increased, the slope stability decreased sharply, and when the angle developed like that between the normal force and the limit equilibrium state, the resultant force extended and failure happened because of shearing. Zhao (2008) worked on spherical mode failure using the incline boosting machine method and accuracy rate classification, and the coefficient of Cohen’s Kappa was used for determining the proposed model performance. The slope stability state is expressed as some classification difficulties to estimate the output either failed or stable. Ahour et al. (2020) used a numerical model that is dependent on artificial neural networks (ANN) to calculate the rock slope stability by using the comprehensive Hoek–Brown failure principle. In this research, the FOS was calculated using the finite element approach using the SSR method. Sakellariou and Ferentinou (2005) studied slope stability estimation using neural networks. This model offers forecasting abilities; therefore, it has been used for soil and rock parameter prediction and identification. In addition, substantial progress has been made in the study of slope stability difficulties. The prepared equation may be used to forecast the supplement for a given set of input variables without having to do any further work. This is regarded as among the most significant benefits of the standard soft computing methods used in today’s world. In the literature on slope stability, successful implementations of these soft computing approaches may be identified (Wang et al., 2005; Choobbasti et al., 2009; Li et al., 2009; Chakraborty and Goswami, 2017; Kumar and Basudhar, 2018; Qian et al., 2019; Ahour et al., 2020; Li et al., 2020; Ray et al., 2020; Zheng et al., 2020; Che Mamat et al., 2021; Palazzolo et al., 2021); (Das et al., 2011; Erzin and Cetin, 2012; Erzin and Cetin, 2014; Abdalla et al., 2015; Ai and Zsaki, 2017; Chakraborty and Goswami, 2018; Rukhaiyar et al., 2018; Moayedi et al., 2019; Bui et al., 2020; Chen et al., 2020; He et al., 2020; Liao and Liao, 2020; Che Mamat et al., 2020; Markovic Brankovic et al., 2021; Meng et al., 2021).

This study used GeneXproTools to propose two models: The first model was classified by including different input factors such as the cohesion (c), slope angle (), unit weight, internal friction angle, slope height, and pore water pressure coefficient, and the output was the occurrence of slope failure. The second model was a regression-based function approximation model that included various input parameters such as cohesion (c), unit weight, internal friction angle, angle of slope, coefficient of pore water pressure, slope height, and factor of safety. The output was the existence of slope failure in order to predict the failure state and function approximation to obtain a formula and a factor of safety of 2.

Methodology

The study utilized GeneXproTools, which is an enormously flexible modeling tool considered for logistic regression, linear regression, time series estimation, classification, and logic mixture. For the objective of developing an analytical or classified model for the prediction of FS on slopes with the potential for failure, a GA was used in this research. The primary goal was to establish whether variables should indeed be quantitatively converted using equations such as power, exponential, and logarithm. The quality of the regression models was improved by first converting the variables and then computing the coefficients of the regression model. In addition, it may be used to demonstrate non-linear interactions between dependent factors and independent variables. The planned GA comprised four major phases as follows: First, a collection of alternative functions was determined; next, each independent variable was assigned a transforming function; then, a combination of multiple solutions was used to identify the best one; and last, the predictive estimated values were calculated. A regression model was created to test our hypothesis. Before any more steps were taken, a group of mathematical functions was created that seem to capture the essence of the issue and have no chance of being incorrect mathematically. Each independent variable was randomly modified using one of these mathematical functions. This function has a general form independent variable and is called the conversion function. Decision was made as to what kind of modification should be applied to the variable. As a result, each of these forms was determined by a digit, and each variable was allocated to it via the use of a random technique. It was necessary to utilize this approach to generate arbitrary parameters for each of the independent variables in the system. This means that the encoded values of the numeric variables make up each possible solution. It is known as the power of the number of all feasible solutions for the problem with various transformation forms and l variable. It demonstrates that this GA was capable of creating and testing a huge number of different regression models. Following the formation of the solutions, the prediction parameters of the model for each solution were defined in order to generate a fitness value, and the regression model (a mathematical criterion such as the root-mean-square error, standard deviation, and mean square error) for every solution was calculated. Using mutation and crossover operators, the GA progressed toward the optimal solution as quickly as possible. By evaluating the best fitness function, this GA created a vast number of alternative solutions and then picks the best one from among them. Many scientific issues need the development of models to clarify the statistical connection between distinct variables, but finding the most appropriate regressing model is not always straightforward. A diagram illustrating how a genetic algorithm framework is organized is shown in Figure 1. Cramer NL was the first to create genetic programming.

FIGURE 1

FIGURE 1. Flowchart of the genetic algorithm.

Data Process

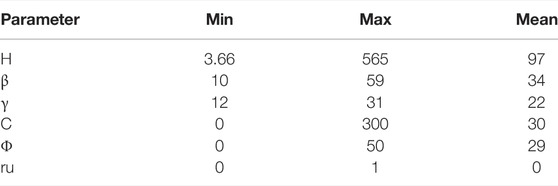
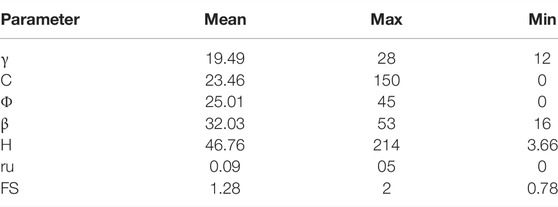
The database for model 1 contains 253 cases that were collected from real data for slope stability cases by (Sah et al., 1994), (Wang et al., 2005), (Chen and Chameau, 1983), and (Zhou et al., 2019) is shown in Table 1. The data for model 2, which includes of 220 historical cases of slope conditions and collected by Sah et al. (1994), Sakellariou and Ferentinou (2005), Samui (2008), Zhou and Chen (2009), and Li and Dong (2012), are shown in Tables 2, 3.

TABLE 1

TABLE 1. The descriptive statistical analysis of the classifcation data for model 1.

TABLE 2

TABLE 2. The descriptive statistical analysis for model 2.

TABLE 3

TABLE 3. Confusion matrix for data.

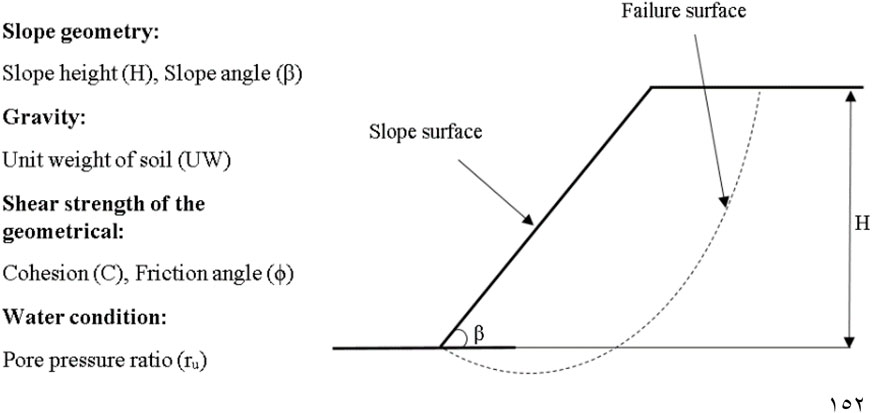
Figure 2 shows that the slope’s geometric form includes the slope angle, slope height, cohesiveness, unit weight, pore pressure ratio, and internal friction angle, which is the pore pressure-to-overburden pressure ratio.

FIGURE 2

FIGURE 2. Effective factors affecting the stability of slopes undergoing circular collapse.

Results and Analysis

Genetic Algorithm Classification Model One

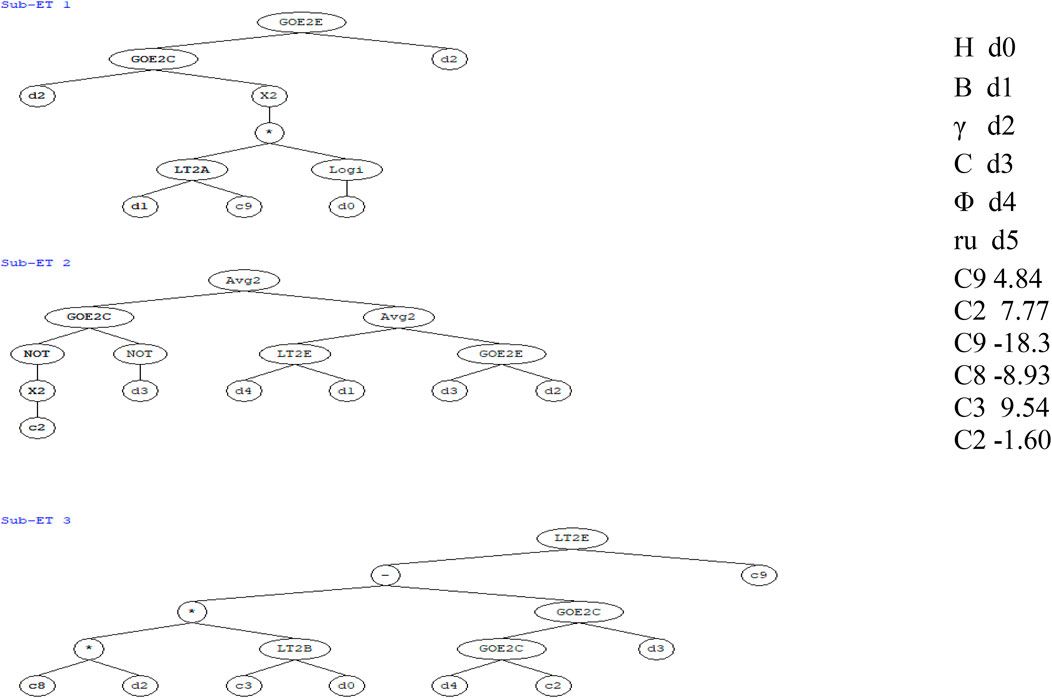
It should be noted that the binary system was used to classify the slope state, with 0 representing “failure” and 1 representing “stable.” Slope height (H), overall angle of slope (ß), unit weight (γ), cohesion (C), and the internal friction angle (φ) were used as input parameters in the program, which are in line with whatever is frequently used for the analysis of circular failure. The geometrical simple slope design factors (H), (ß), and () typically determine soil slope failure conditions and are mechanical parameters related to slope stability in geomaterials that are dependent on the Mohr–Coulomb failure standard (ru), which is the pore water pressure ratio to the overload pressure. The output was the slope state (actual) and can take two options: OK (correct match) or wrong (false match). An expression tree, as the term recommends, was terms arranged in a tree-like information configuration. It helps understand the program algorithms since it adapts to various programming languages to express the results. Another advantage of expression trees is that they can provide a formula where the same kind of inputs can be used to get an output, which in our case was stable (1) or failure (0). The number of genes in the classification stage was three genes. It means that we will have three sub-trees in Figure 3 that were produced and transformed into the numerical scheme as displayed (classification formula). The interesting part about this program is that it can deliver results with an algorithm based on the data entered. The algorithm in this program is compatible with expression trees to obtain more realistic results.

FIGURE 3

FIGURE 3. Tree Expression to classified slope stability.

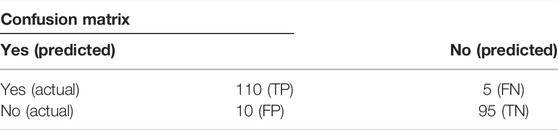
The data were organized into txt files before being loaded into the program Gene X, which contains an algorithm for generating a non-linear classification model. Then, deployment of models and ensembles to Excel was carried out. In machine learning and specifically in statistical classification difficulties, a confusion matrix is an exact table layout that permits the visualization performance of an algorithm and a classification model on a group of test data for which the true standards are identified. Every row of the matrix links to an expected class. Every column of the matrix agrees with an actual class. The program compares the results using a confusion matrix and shows them as part of the results via the match column that we discussed earlier. In Table 4, as for the 104 values that are the same in the yes predicted and the yes actual columns, take a TP symbol; as for the 19 values that are in the yes predicted and the no actual, take the FP symbol. The genetic algorithm was first evaluated on the same training data (all 220 slope instances in the database). The confusion matrix is shown in Table 4, and the variables TP (stable) and TN (failure) denote the stable and failing slopes numbers that are accurately sorted into the relevant classes. False positive (FP) stands for the number of failure slopes that are incorrectly identified as stable, whereas false negative (FN) denotes the number of stable slopes that are incorrectly classified as failed. The precision of 115 stable slopes is 95 percent (referred to as sensitivity, which is defined as TP/(TP + FN)). The accuracy (referred to as “specificity,” which equals TN divided by (TN + FP)) of the 28 failed slopes is 90.4 percent. Total accuracy (TP + TN)/(TP + TN + FP + FN) is approximately 93.1 percent, which is very good for real-world engineering.

TABLE 4

TABLE 4. Estimating function historical data.

Genetic Algorithm Prediction Model 2

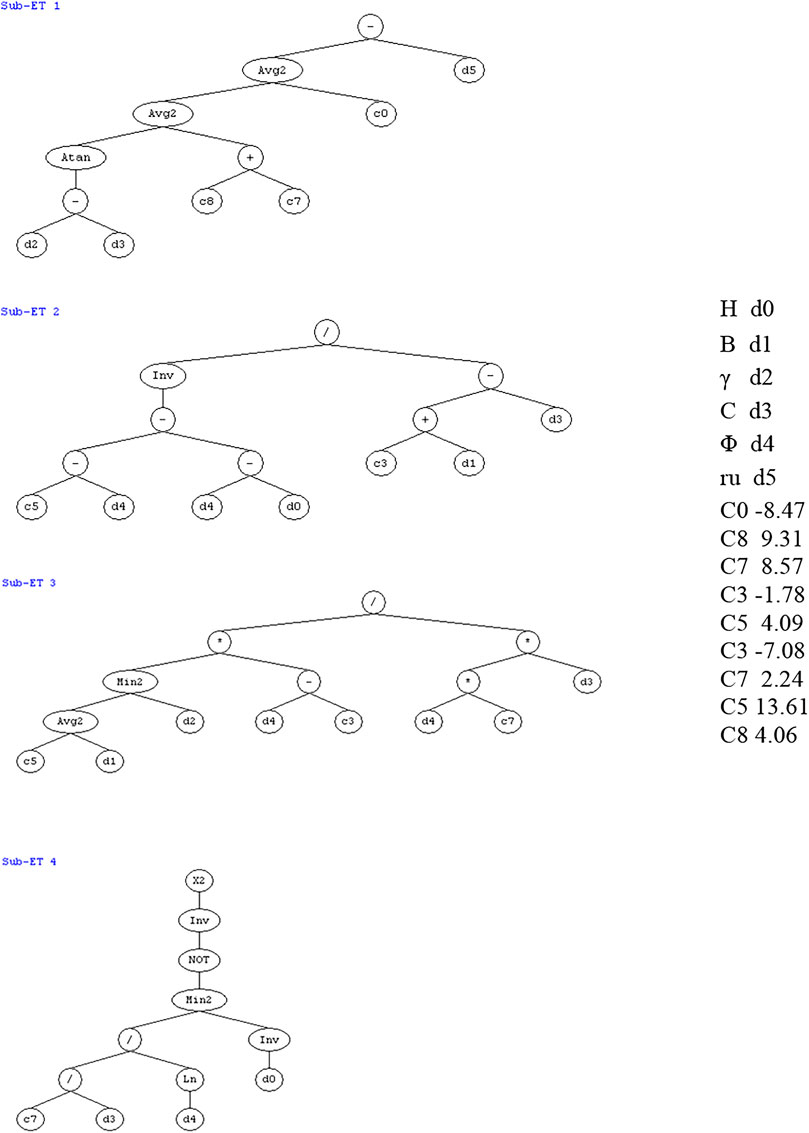
To achieve an accurate estimate of the safety factor, we need to run the data through a function approximation issue, in addition to a prediction of whether the slope state is a failure or is stable. Slope height (H), overall angle slope (ß), unit weight (γ), internal friction angle (φ), cohesion (C), and ratio of pore water (ru) were used as input parameters in the program which are in accordance with what is frequently used for circular failure analysis. The number of genes in regression stage was four genes, which means we will have four sub-trees, as shown in Figure 4.

FIGURE 4

FIGURE 4. Tree Expression to predict factor of safety.

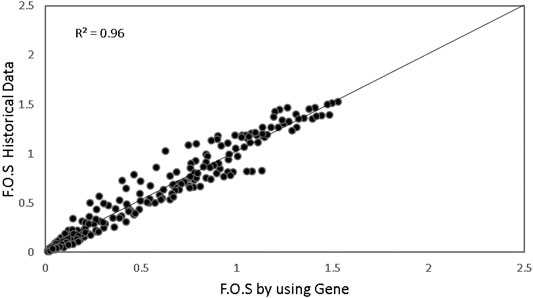
This software’s working idea is based on chromosomes, which include expression trees and genes that specify the genetic information contained in them. The Gene Expression Program (GeneXpro 5.0) saves time and effort in calculating the factor of safety. Furthermore, by establishing a link between soil types, features, and bearing capability, when the generation is 101,934, the computer tries numerous paths to get the ideal model. The trial was paused, and the best model was chosen based on certain criteria, like R² > 0.90 for all data. Figure 5 demonstrates the expected factor of safety alongside the observed safety factor. The evolutionary algorithm model also accurately predicts the destination values. However, the genetic algorithm model delivers an excellent estimate, with an R² value of 0.96.

FIGURE 5

FIGURE 5. Predicted results using gene software plot against factor of safety for measured data.

The number of genes in the regression stage was four genes. That means we will have four equations used in this generation. The estimated equations are as follows:

$F.O.S=\left[\left[\frac{ta{n}^{-1}\left(\Phi -\mathrm{\beta }\right)}{4}+0.411-ru\right]\right]+\frac{c_3+C-\beta }{\left(c5-H\right)\cdot \left(H-\gamma \right)}+\frac{min\left[\left(Av\mathrm{13.62.}C\right).\mathrm{\Phi }\ast \left(H+7.87\right)\right]}{2.24H\ast \beta }+{\left(\frac{1}{1-min\left(\frac{4.06Ln H}{\beta }.\overline{\frac{1}{\gamma }}\right)}\right)}^2.$

Sensitivity Analysis

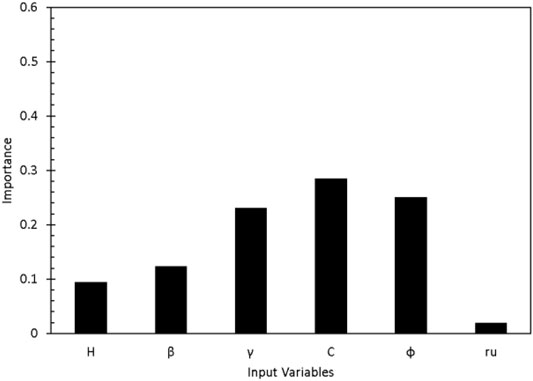
Sensitivity analysis involves adjusting an entry parameter’s amount and observing how the genetic algorithm model responds. This may reveal which variables have the most influence on genetic algorithm models and which variables affect simulation results. This assessment demonstrates how input factors affect the safety factor of slope failure. The significance of a feature is assessed by the change in the estimation of designated prediction models, and the length of the bars represents the final assignment’s feature relevance. Figure 6 shows the influence of input variables on model 1 as follows: cohesion (C), angle of internal friction (φ), unit weight (γ), overall angle slope (), slope height (H), and pore water ratio (ru). Figure 7 summarizes the features relevant to model 2. The angle of internal friction (φ), overall angle slope (ß), cohesion (C), slope height (H), pore water ratio (ru), and unit weight (γ) were the main input factors for factor safety prediction modeling.

FIGURE 6

FIGURE 6. Importance of a Feature for Classification Variable importance.

FIGURE 7

FIGURE 7. Importance of a Feature for Function estimation.

Validation by Use Slope Stability Cases in Jordan

The common landslides that happened along the routes of major roads in Jordan, and mainly along the Dead Sea-Na’our–Amman road and the Amman–Jerash–Irbid road, have considerably increased. Over the last decades, excessive hillslope disturbances have been identified during highway construction and urban development in central and northern Jordan. Most of the major engineering projects were implemented on natural, steep slopes, which were related to old landslide complexes, weak geological structures, and low shearing resistance. Thus, a wide range of landslides were reactivated, causing serious damage to highways and urban areas. Engineering activities often take place without previous appreciation of the geological and hydrological settings. The human impact of the increased probability of landslides was also ignored. The final triggering factor responsible for these slope failures was the buildup of high pore-water pressures in the materials, caused by recurrent, high-intensity rainstorms. A geotechnical stability evaluation was carried out along the Amman-Irbid highways as shown in Figure 8. It is concluded that hillslope instability problems are likely to increase with continued highway and urban development. In order to investigate the slope failure at the Amman–Irbid Highway, the site investigation and soil physical and mechanical properties were performed in the laboratory. Six boreholes were drilled in slope failure sites and the soil classification was sandstone with an unconfined compressive strength of between 3 and 45 MPa. The direct shear test was performed on the collected samples, the cohesion (C kPa) ranged between 32 and 51%, and the internal friction angle was between 7 and 49°.

FIGURE 8

FIGURE 8. Landslide area at Amman Jerash highway.

geox5 software was used to calculate the factor of safety for the slope failure in Figure 9. The soil properties with all properties were assigned to geox5. Table 4 depicts the slope stability situation at 10 slope locations in the Irbid–Jerash Highway. geox5 was used to find the factor of safety based on several material properties. Furthermore, Table 4 shows the comparison between geox5 and the 2 moles that were proposed in this study.

FIGURE 9

FIGURE 9. Geox5 for selected site at Irbid Jerash highway.

In order to verify the factor of safety models developed in this study, 10 slopes at Irbid Jerash were utilized by the Ministry of Housing. These slope cases were used to test the factor of safety models developed in this study. The factor of safety was predicted using the models created in this study first, and then geox5 was performed on the variables shown in the table.

Parametric Study by Using Gene Expression Programming

A parametric study was carried out for the established genetic expression programming model in order to investigate the impact of the input values on the anticipated factor of safety. As a result, particular input data are altered, while the other input data are left constant in order to examine the impact of each input on the anticipated factor of safety. Figures 10A, B,C show that as unit weight, cohesion (c), and internal friction angle increase, the factor of safety also increases in a direct proportion. The impact of cohesion (c) on the factor of safety is increased in a direct proportion. Figures 10D,E show that slope angle (ß) and slope height are inversely proportional to the factor of safety.

FIGURE 10

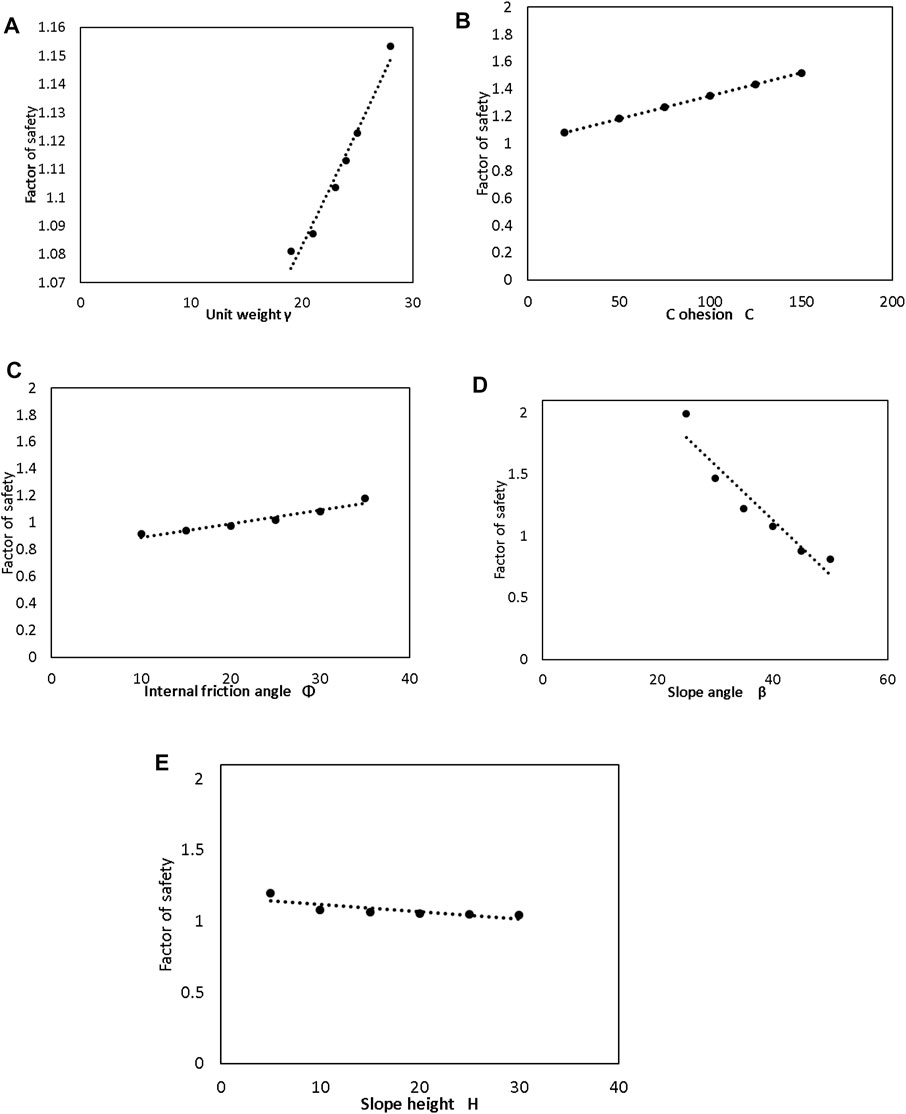
FIGURE 10. Parametric study for input variables. (A). Unit weight vs. factor of safety. (B). Cohesion vs. Factor of Safety. (C). Internal Friction Angle vs. Factor of Safety. (D). Slope Angle vs. Factor of Safety. (E). Slope height vs. Factor of safety.

Discussion and Analysis

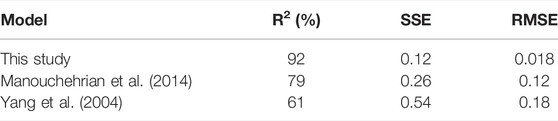
In this study, an evolutionary algorithm was used to construct a regression model for the estimation of FS for soil slopes that have the possibility of circular failure. The suggested genetic algorithm models provide a higher coefficient of determination and minimize the root-mean-square error. The sensitivity analysis shows that increasing unit weight, soil cohesion, and angle of friction increase FS, whereas increasing slope height, slope angle, and pore pressure reduce FS. In addition, the findings revealed that the most efficient FS parameters were slope angle, unit weight, and friction angle, but as unit weight increased, the model’s efficiency increased as well. The proposed genetic algorithm models were compared to the models from the literature. Compared to the model being used for validation, the offered model predicted more accurately. As a result of its simple formulation, the regression model proposed by the researchers is capable of accurately forecasting FS with a high degree of confidence, making it an effective alternative to LEM and numerical approaches in the early phases of the design process. To summarize, the suggested GA’s notable features include its easy formulation and high accuracy, which may lead to the construction of extremely helpful regression models for a wide range of issues. Table 5 summarizes the statistical assessments of the responses for model 2 compared with the other models. The results demonstrate that the genetic algorithm model proposed was more effective in assessing FS.

TABLE 5

TABLE 5. The statistical assessments of the responses for model 2 with other models.

Conclusion

The genetic algorithm technique has been effectively used to examine the slope stability situation using (252) slope conditions of verified historical cases (regression and classification). Using the GeneXproTools model, the state slope stability is expressed as a classification difficulty in which estimation outputs are either failed or stable. The study shows that the solutions from the genetic algorithms method are accurate for most cases. The results showed values of accuracy and error of 93.1 and 6.9%, respectively, where the parameter cohesion (C) was the most important aspect in the classification case. For the function estimating case, independent variables in this research involved material variables (height of slope and slope angle). Using the regression feature, an equation was established to forecast FOS of slopes. The genetic algorithm models were observed and compared to show that all approaches have a respectable agreement in forecasting the safety factor. The results of the parametric study show that increasing unit weight, cohesion, and internal friction angle increase the factor of safety, whereas increasing slope height, slope angle, and pore pressure reduce the factor of safety.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

The author has participated in conception and design; analysis and interpretation of the data; drafting the manuscript or revising it critically for important intellectual content; and approval of the final version.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdalla, J. A., Attom, M. F., and Hawileh, R. (2015). Prediction of Minimum Factor of Safety against Slope Failure in Clayey Soils Using Artificial Neural Network. Environ. Earth Sci. 73 (9), 5463–5477. doi:10.1007/s12665-014-3800-x

CrossRef Full Text | Google Scholar

Ahour, M., Hataf, N., and Azar, E. (2020). A Mathematical Model Based on Artificial Neural Networks to Predict the Stability of Rock Slopes Using the Generalized Hoek–Brown Failure Criterion. Geotech. Geol. Eng. 38, 587–604. doi:10.1007/s10706-019-01049-y

CrossRef Full Text | Google Scholar

Ai, X., and Zsaki, A. M. (2017). Stability Assessment of Homogeneous Slopes Loaded with mobile Tracked Cranes—An Artificial Neural Network Approach. Cogent Eng. 4, 1. doi:10.1080/23311916.2017.1360236

CrossRef Full Text | Google Scholar

Al Bodour, W., Hanandeh, S., Hajij, M., and Murad, Y. (2022). Development of Evaluation Framework for the Unconfined Compressive Strength of Soils Based on the Fundamental Soil Parameters Using Gene Expression Programming and Deep Learning Methods. J. Mater. Civ. Eng. 32 (2). doi:10.1061/(asce)mt.1943-5533.0004087

CrossRef Full Text | Google Scholar

Bui, X. N., Nguyen, H., Choi, Y., Nguyen-Thoi, T., Zhou, J., and Dou, J. (2020). Prediction of Slope Failure in Open-Pit Mines Using a Novel Hybrid Artificial Intelligence Model Based on Decision Tree and Evolution Algorithm. Sci. Rep. 10, 9939. doi:10.1038/s41598-020-66904-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Chakraborty, A., and Goswami, D. (2018). Prediction of Critical Safety Factor of Slopes Using Multiple Regression and Neural Network. J. Geo-engineering Sci.. [Preprint], 1–10. doi:10.3233/jgs-170047

CrossRef Full Text | Google Scholar

Chakraborty, A., and Goswami, D. (2017). Slope Stability Prediction Using Artificial Neural Network (ANN). Int. J. Eng. Comput. Sci 6 (6), 21845–21848. doi:10.18535/ijecs/v6i6.49

CrossRef Full Text | Google Scholar

Che Mamat, R., Manan Samad, A., Kasa, A., Razali, S. F. M., Ramli, A., and Omar, M. B. H. C. (2020). Slope Stability Prediction of Road Embankment on Soft Ground Treated with Prefabricated Vertical Drains Using Artificial Neural Network. Prediction embankment Stab. 9, 239–243. doi:10.11591/ijai.v9.i2.pp236-243

CrossRef Full Text | Google Scholar

Che Mamat, R., Ramli, A., Samad, A. M., Kasa, A., Razali, S. F., and Omar, M. B. (2021). Artificial Neural Networks in Slope of Road Embankment Stability Applications: A Review and Future Perspectives. Int. J. Adv. Technol. Eng. Explor. 8, 304–319. doi:10.19101/ijatee.2020.762127

CrossRef Full Text | Google Scholar

Chen, L., Zhang, W., Gao, X., Wang, L., Li, Z., Böhlke, T., et al. (2020). Design Charts for Reliability Assessment of Rock Bedding Slopes Stability against Bi-planar Sliding: SRLEM and BPNN Approaches. Georisk: Assess. Manag. Risk Engineered Syst. Geohazards, 1–16. doi:10.1080/17499518.2020.1815215

CrossRef Full Text | Google Scholar

Chen, R. H., and Chameau, J.-L. (1983). Three-dimensional Limit Equilibrium Analysis of Slopes. Géotechnique 33, 31–40. doi:10.1680/geot.1983.33.1.31

CrossRef Full Text | Google Scholar

Choobbasti, A. J., Farrokhzad, F., and Barari, A. (2009). Prediction of Slope Stability Using Artificial Neural Network (Case Study: Noabad, Mazandaran, iran). Arab. J. Geosci. 2 (4), 311–319. doi:10.1007/s12517-009-0035-3

CrossRef Full Text | Google Scholar

Das, S. K., Biswal, R. K., Sivakugan, N., and Das, B. (2011). Classification of Slopes and Prediction of Factor of Safety Using Differential Evolution Neural Networks. Environ. Earth Sci. 64, 201–210. doi:10.1007/s12665-010-0839-1

CrossRef Full Text | Google Scholar

Erzin, Y., and Cetin, T. (2014). The Prediction of the Critical Factor of Safety of Homogeneous Finite Slopes Subjected to Earthquake Forces Using Neural Networks and Multiple Regressions. Geomech. Eng. 6, 1–15. doi:10.12989/gae.2014.6.1.001

CrossRef Full Text | Google Scholar

Hanandeh, S., Alabdullah, S. F., Aldahwi, S., Obaidat, A., and Alqaseer, H. (2020a). Development of a Constitutive Model for Evaluation of Bearing Capacity From CPT and Theoretical Analysis Using ann Techniques. Int. J. Geomate. 19 (74), 229–235. doi:10.21660/2020.74.36965

CrossRef Full Text | Google Scholar

Hanandeh, S., Ardah, A., and Abu-Farsakh, M. (2020b). Using Artificial Neural Network and Genetics Algorithm to Estimate the Resilient Modulus for Stabilized Subgrade and Propose New Empirical Formula. Transp. Geotech.. doi:10.1016/j.trgeo.2020.100358

CrossRef Full Text | Google Scholar

Erzin, Y., and Cetin, T. (2012). The Use of Neural Networks for the Prediction of the Critical Factor of Safety of an Artificial Slope Subjected to Earthquake Forces. Sci. Iran. 19, 188–194. doi:10.1016/j.scient.2012.02.008

CrossRef Full Text | Google Scholar

He, X., Xu, H., Sabetamal, H., and Sheng, D. (2020). Machine Learning Aided Stochastic Reliability Analysis of Spatially Variable Slopes. Comput. Geotech 126, 103711. doi:10.1016/j.compgeo.2020.103711

CrossRef Full Text | Google Scholar

Kumar, S., and Basudhar, P. K. (2018). A Neural Network Model for Slope Stability Computations. Geotech. Lett. 8, 149–154. doi:10.1680/jgele.18.00022

CrossRef Full Text | Google Scholar

Li, A.-J., Lim, K., and Fatty, A. (2020). Stability Evaluations of Three-Layered Soil Slopes Based on Extreme Learning Neural Network. J. Chin. Inst. Eng. 43, 628–637. doi:10.1080/02533839.2020.1719899

CrossRef Full Text | Google Scholar

Li, J., and Dong, M. (2012). “Method to Predict Slope Safety Factor Using SVM,” in Earth and Space 2012-Proceedings of the 13th ASCE Aerospace Division Conference and the 5th NASA/ASCE Workshop on Granular Materials in Space Exploration (Pasadena, CA: American Society of Civil Engineers). doi:10.1061/9780784412190.095

CrossRef Full Text | Google Scholar

Li, S., Shangguan, Z., Duan, H., Liu, Y., and Luan, M. (2009). Searching for Critical Failure Surface in Slope Stability Analysis by Using Hybrid Genetic Algorithm. Geomech. Eng. 1 (1), 85–96. doi:10.12989/gae.2009.1.1.085

CrossRef Full Text | Google Scholar

Liao, Z., and Liao, Z. (2020). Slope Stability Evaluation Using Backpropagation Neural Networks and Multivariate Adaptive Regression Splines. Open Geosci. 12, 1263–1273. doi:10.1515/geo-2020-0198

CrossRef Full Text | Google Scholar

Lollino, P., Cotecchia, F., Elia, G., Mitaritonna, G., and Santaloia, F. (2016). Interpretation of Landslide Mechanisms Based on Numerical Modelling: Two Case-Histories. Eur. J. Environ. Civ. Eng. 20, 1032–1053. doi:10.1080/19648189.2014.985851

CrossRef Full Text | Google Scholar

Lu, P., and Rosenbaum, M. S. (2003). Artificial Neural Networks and Grey Systems for the Prediction of Slope Stability. Nat. Hazards 30, 383–398. doi:10.1023/b:nhaz.0000007168.00673.27

CrossRef Full Text | Google Scholar

Manouchehrian, A., Gholamnejad, J., and Sharifzadeh, M. (2014). Development of a Model for Analysis of Slope Stability for Circular Mode Failure Using Genetic Algorithm. Environ. Earth Sci. 71, 1267–1277. doi:10.1007/s12665-013-2531-8

CrossRef Full Text | Google Scholar

Markovic Brankovic, J., Markovic, M., Andrejevic Stosovic, M., Zivkovic, S., and Brankovic, B. (2021). Ann Model for Prediction of Rockfill Dam Slope Stability. Teh. Vjesn. 28, 1488–1494. doi:10.17559/TV-20200707150903

CrossRef Full Text | Google Scholar

Meng, J., Mattsson, H., and Laue, J. (2021). Three-dimensional Slope Stability Predictions Using Artificial Neural Networks. Int. J. Numer. Anal. Methods Geomech 45, 1988–2000. doi:10.1002/nag.3252

CrossRef Full Text | Google Scholar

Moayedi, H., Tien Bui, D., Gör, M., Pradhan, B., and Jaafari, A. (2019). The Feasibility of Three Prediction Techniques of the Artificial Neural Network, Adaptive Neuro-Fuzzy Inference System, and Hybrid Particle Swarm Optimization for Assessing the Safety Factor of Cohesive Slopes. ISPRS Int. J. Geo-inf. 8, 391. doi:10.3390/ijgi8090391

CrossRef Full Text | Google Scholar

Natekin, A., and Knoll, A. (2013). Gradient Boosting Machines, a Tutorial. Front. Neurorobot. 7, 21. doi:10.3389/fnbot.2013.00021

PubMed Abstract | CrossRef Full Text | Google Scholar

Palazzolo, N., Peres, D., Bordoni, M., Meisina, C., Creaco, E., and Cancelliere, A. (2021). Improving Spatial Landslide Prediction with 3D Slope Stability Analysis and Genetic Algorithm Optimization: Application to the Oltrepò Pavese. Water 13, 801. doi:10.3390/w13060801

CrossRef Full Text | Google Scholar

Qian, Z. G., Li, A. J., Chen, W. C., Lyamin, A. V., and Jiang, J. C. (2019). An Artificial Neural Network Approach to Inhomogeneous Soil Slope Stability Predictions Based on Limit Analysis Methods. Soils Found. 59, 556–569. doi:10.1016/j.sandf.2018.10.008

CrossRef Full Text | Google Scholar

Ray, A., Kumar, V., Kumar, A., Rai, R., Khandelwal, M., and Singh, T. N. (2020). Stability Prediction of Himalayan Residual Soil Slope Using Artificial Neural Network. Nat. Hazards 103, 3523–3540. doi:10.1007/s11069-020-04141-2

CrossRef Full Text | Google Scholar

Rukhaiyar, S., Alam, M. N., and Samadhiya, N. K. (2018). A PSO-ANN Hybrid Model for Predicting Factor of Safety of Slope. Int. J. Geotech. Eng. 12, 556–566. doi:10.1080/19386362.2017.1305652

CrossRef Full Text | Google Scholar

Sah, N. K., Sheorey, P. R., and Upadhyaya, L. N. (1994). Maximum Likelihood Estimation of Slope Stability. Int. J. Rock Mech. Min. Sci. 31, 47–53. doi:10.1016/0148-9062(94)92314-0

CrossRef Full Text | Google Scholar

Sakellariou, M. G., and Ferentinou, M. D. (2005). A Study of Slope Stability Prediction Using Neural Networks. Geotech. Geol. Eng. 23, 419. doi:10.1007/s10706-004-8680-5

CrossRef Full Text | Google Scholar

Samui, P. (2008). Slope Stability Analysis: A Support Vector Machine Approach. Environ. Geol. 56, 255. doi:10.1007/s00254-007-1161-4

CrossRef Full Text | Google Scholar

Wang, H. B., Xu, W. Y., and Xu, R. C. (2005). Slope Stability Evaluation Using Back Propagation Neural Networks. Eng. Geol. 80 (3), 302–315. doi:10.1016/j.enggeo.2005.06.005

CrossRef Full Text | Google Scholar

Xu, B., and Low, B. K. (2006). Probabilistic Stability Analyses of Embankments Based on Finite-Element Method. J. Geotech. Geoenvironmental Eng. 132, 1444–1454. doi:10.1061/(asce)1090-0241(2006)132:11(1444)

CrossRef Full Text | Google Scholar

Yang, C. X., Tham, L. G., Feng, X. T., Wang, Y. J., and Lee, P. K. K. (2004). Two-Stepped Evolutionary Algorithm and its Application to Stability Analysis of Slopes. J. Comput. Civ. Eng. 18, 145–153. doi:10.1061/(asce)0887-3801(2004)18:2(145)

CrossRef Full Text | Google Scholar

Zhao, H., and Li, S. (2021). Determining Geomechanical Parameters and a Deformation Uncertainty Analysis of the Longtan Hydropower Station Slope, China. Bull. Eng. Geol. Environ. 80 (8), 6429–6443. doi:10.1007/s10064-021-02339-7

CrossRef Full Text | Google Scholar

Zhao, H. (2008). Slope Reliability Analysis Using a Support Vector Machine. Comput. Geotech. 35, 459–467. doi:10.1016/j.compgeo.2007.08.002

CrossRef Full Text | Google Scholar

Zhao, H., Yin, S., and Ru, Z. (2012). Relevance Vector Machine Applied to Slope Stability Analysis. Int. J. Numer. Anal. Methods Geomech. 36, 643–652. doi:10.1002/nag.1037

CrossRef Full Text | Google Scholar

Zheng, Y., Chen, C., Meng, F., Liu, T., and Xia, K. (2020). Assessing the Stability of Rock Slopes with Respect to Flexural Toppling Failure Using a Limit Equilibrium Model and Genetic Algorithm. Comput. Geotech. 124, 103619. doi:10.1016/j.compgeo.2020.103619

CrossRef Full Text | Google Scholar

Zhou, J., Li, E., Yang, S., Wang, M., Shi, X., Yao, S., et al. (2019). Slope Stability Prediction for Circular Mode Failure Using Gradient Boosting Machine Approach Based on an Updated Database of Case Histories. Saf. Sci. 118, 505–518. doi:10.1016/j.ssci.2019.05.046

CrossRef Full Text | Google Scholar

Zhou, K. P., and Chen, Z. Q. (2009). “Stability Prediction of Tailing Dam Slope Based on Neural Network Pattern Recognition,” in 2nd International Conference on Environmental and Computer Science, ICECS 2009 (Dubai, United Arab Emirates: IEEE), 380–383. doi:10.1109/ICECS.2009.55

CrossRef Full Text | Google Scholar