Performance-Based Design of Tall Timber Buildings Under Earthquake and Wind Multi-Hazard Loads: Past, Present, and Future

Tesfamariam, S.

doi:10.3389/fbuil.2022.848698

REVIEW article

Front. Built Environ., 22 March 2022

Sec. Earthquake Engineering

Volume 8 - 2022 | https://doi.org/10.3389/fbuil.2022.848698

This article is part of the Research Topic Horizons in Built Environment View all 9 articles

Performance-Based Design of Tall Timber Buildings Under Earthquake and Wind Multi-Hazard Loads: Past, Present, and Future

S. Tesfamariam*

School of Engineering, The University of British Columbia, Kelowna, BC, Canada

The rapid growth of the urban population and associated environmental concerns are challenging city planners and developers to consider sustainable and cost-efficient building systems. Timber-based buildings, such as sustainable systems, are increasingly used. The timber buildings, however, being lighter and flexible, can be vulnerable to earthquakes and wind loads. This paper gives a state-of-the-art review on performance-based design (PBD) considerations and future direction for timber and timber-based hybrid buildings. The PBD review covered both earthquake and wind loads and multi-hazard design considerations. The review also provided 1) current practice and future direction in consideration of hazard, response, and loss assessment within the multi-hazard PBD, 2) damping and energy dissipation devices, 3) optimization under uncertainty, and 4) future of surrogate and multi-fidelity modeling in PBD.

Introduction

Evolution of Tall-Timber and Hybrid Buildings

The rapid growth of the urban population and associated environmental concerns challenged city planners to consider sustainable and cost-efficient building systems (Nygaard et al., 2019; Foster and Reynolds 2018; Smith and Frangi 2014). With the recent introduction of manufactured mass timber elements, such as cross-laminated timber (CLT), laminated veneer lumber, and glued laminated timber (glulam), sustainable tall-timber buildings have become a viable option (Tesfamariam et al., 2021a, 2019, 2015; Tesfamariam and Das 2021; van de Lindt et al., 2020; Ahmed and Arocho 2020; Ramage et al., 2017; Malo et al., 2016; Pei et al., 2015). What constitutes a “tall building” is relative to the time (Jennings 1970), and the definition of “tallness” in a mass-timber building is evolving (Foster et al., 2016). Figure 1 depicts the evolution of constructed, under construction, and proposed tall-timber buildings.

FIGURE 1

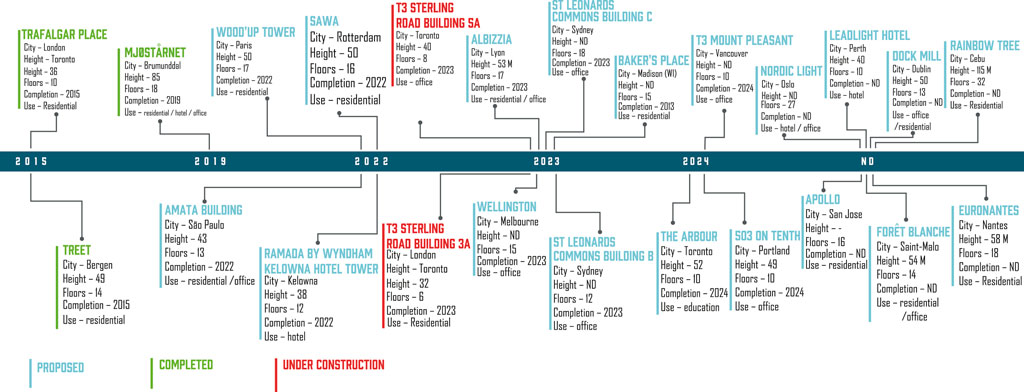
FIGURE 1. Evolution of tall-timber design and construction (compiled from the Council on Tall Buildings and Urban Habitat database on January 1, 2022).

Tall-timber buildings are lighter and more flexible (Foster and Reynolds 2018) and consequently are vulnerable to wind loads due to limited overturning moment resistance capacity and excessive vibration demand (Bezabeh et al., 2020a; Bezabeh et al., 2018a). Limited studies are published on wind performance of timber and timber-based hybrid structure substantiated with wind tunnel tests (e.g., Bezabeh et al., 2020b; Bezabeh et al., 2018a). Bezabeh et al. (2020a) carried out high-frequency pressure integration wind tunnel tests on tall-timber buildings (10, 15, 20, 30, and 40 stories). The dynamic response and serviceability-performance limits were assessed with respect to the 2015 National Building Code of Canada (NBC) (NRC 2015). With height beyond 10 stories, lateral drift and stiffness requirements can govern serviceability limit state and require stringent wind design consideration. Bezabeh et al. (2018c) experimentally and analytically assessed the performance of a 10-story mass-timber building under tornado-like laboratory simulations and atmospheric boundary layer flow at Western University, Canada. The results highlight that strong tornadoes pose significant damage to drift-sensitive nonstructural components.

Knowledge of damping in tall-timber buildings is limited and uncertain (Bezabeh et al., 2018b; Edskär and Lidelöw 2019; Reynolds et al., 2016; Kareem and Gurley 1996; Pagnini and Solari 1988). With emerging tall-timber building construction (e.g., Figure 1), the importance of damping was noted, and practical solutions were provided. “Treet” (Malo et al., 2016), for example, a 14-story timber apartment building in Norway, is using the lateral-force resisting system that is diagonal glulam beams. The CLT was used for the elevator shaft and stairways, with additional concrete topped floor to improve the wind performance. “Scotia Place” (Moore 2000) is a 12-story steel-frame apartment building located in a high seismic zone in New Zealand. Using the wood floor, the overall weight was reduced with additional cost savings in material and floor finishing. However, the lighter structure showed vulnerability to wind and the need for supplemental damping. Considering different levels of uncertain damping values, Bezabeh et al. (2018a) showed the required damping values to satisfy the NBC criteria.

Motivation

Different national and international seismic design codes, e.g., NBC (NRC 2015), International Building Code (ICC 2017), follow prescriptive (deterministic) and force-based design. The wind load design is mainly considering the first mode vibration and serviceability limit state (e.g., cladding failure, occupant comfort) (e.g., Ouyang and Spence 2021; Bezabeh et al., 2018a; Bernardini et al., 2014). The seismic design principles are for first mode deformation response and collapse prevention limit state. This is not suitable for tall-timber buildings that have higher mode contributions (Ramage et al., 2017; Willford et al., 2008; Jennings 1970). In addition, under severe earthquakes, the building can sustain irreparable damage with post-earthquake occupancy and community recovery implications (Takagi and Wada 2019). For the tall-timber and hybrid buildings that are outside of the code-oriented practice, performance-based design (PBD) is a viable approach (Golesorkhi et al., 2017; Bezabeh et al., 2015; PEER 2017; Loss et al., 2018; LATBSDC 2020; Alinejad et al., 2021; Tesfamariam et al., 2021a). In wind engineering, there is a departure from prescriptive to PBD for wind as reflected in ASCE (2019) pre-standard.

The current building design codes use combination rules (e.g., dead load and earthquake load) to achieve uniform reliability (Crosti et al., 2010; Duthinh and Simiu, 2010). In combination with other loads (dead load, live loads, snow loads, etc.), the design is governed by earthquake or wind loads (NBC 2015; ASCE 2017). The risk of exceeding a given limit state is implicitly assumed to be the same in the region where earthquake or wind is the dominant load (Kwag et al., 2021; Duthinh and Simiu 2010). In cities, such as Vancouver (high seismic zone) and Boston (low seismic zone), for example, the challenge for structural designers is an earthquake, and wind can be competing design loads (Wen and Kang 2001a; Mahmoud and Cheng 2017; Tesfamariam et al., 2019). The earthquake and wind loads multi-hazard (MH) design might not necessarily be governed by higher intensity single hazard but be dominated by the lower intensity and more frequent hazard (Wen and Kang 2001a; Wen 2001). Wen (1990) proposed a uniform reliability design rule of combination. With increasing building height, the need for MH design consideration of tall building design is apparent (e.g., Suksuwan and Spence 2018).

With increasing demand in the design and construction of tall-timber buildings, MH PBD principles beyond the current design guideline are needed. The PBD framework for wind, earthquake, and MH tall-timber design is depicted in Figure 2. From the current literature review, for PBD of tall-timber building, issues related to modeling, consideration of site-specific soil–structure interaction (SSI), energy dissipation devices, efficient optimization algorithms, and damping are apparent (Figure 2). Thus, this paper is a state-of-the-art review of the MH design consideration and discussion on the emerging modeling consideration for tall-timber design and future implementation.

FIGURE 2

FIGURE 2. Earthquake and wind MH design framework.

Objectives

In this paper, the first high-level review of the current PBD for seismic and wind loads is provided. In addition, the review is extended for the earthquake and wind MH framework. Within the PBD framework, emerging challenges for tall-timber buildings in quantifying site-specific hazard engineering demand parameters are discussed. The problem of PBD is faced with a plethora of information and computationally expensive models. This entails the use of machine learning techniques for surrogate models; emerging multi-fidelity models are discussed in more detail. The review provided in this paper is outlined below.

• Detailed review and evolution of PBD design for earthquake (e.g., FEMA 2012; PEER 2017; LATBSDC 2020) and wind (Spence and Kareem 2014; Cui and Caracoglia 2018; Bezabeh et al., 2020b; Hou and Jafari 2020; Kareem 2020) are provided in the cited literature. Thus, the review provided here is brief to set the context for the MH design consideration and emerging modeling consideration.

• With limited tall-timber buildings designed, the damping value to use for design and analysis is an ongoing challenge. This paper provides a review of the source of damping and damping values obtained from in situ measurements.

• SSI is highlighted to be important in the damping quantification and review, and future direction is provided.

• The lighter and tall-timber buildings are vulnerable to wind, and this can be mitigated using damping technologies. The different damping technologies are briefly reviewed, and current applications are highlighted. Detailed reviews on different damping technologies and applications to tall buildings are discussed in the literature (e.g., Soong and Spencer Jr 2002; Christopoulos and Filiatrault 2006; Takewaki 2011; Lago et al., 2018).

• Finally, with evolving computational tools, the different optimization techniques and surrogate models are reviewed. With the computationally intensive design and optimization, the current application of the multi-fidelity models is reviewed.

This paper is intended to give a highlight and opportunity for current state-of-the-art and future research direction.

Performance-Based Design for Earthquake Loads

In the 1990s, PBD was introduced as a new structural design procedure to meet targeted building performance subject to ground shaking (SEAOC 1995; FEMA 1997). Although the first-generation PBD methods considered actual seismic demand and nonlinear building capacity, they were deterministic in nature. The second generation of performance-based earthquake engineering (PBEE) methodology was proposed to quantify the mean annual rate of exceedance of earthquake impact λ_E(dv) by capturing the uncertainty in ground shaking, building behavior, and decision variables (Cornell and Krawinkler 2000; Porter 2003). The PBEE framework (summarized in Table 1) was put forward by the Pacific Earthquake Engineering Research Center (PEER) (Porter 2003).

TABLE 1

TABLE 1. PEER performance based design framework.

The PEER framework has been applied in the seismic design and evaluation of buildings (e.g., O'Reilly and Calvi 2019; Shome et al., 2015; Jayaram et al., 2012; Zareian and Krawinkler 2012; Liel et al., 2011; Goulet et al., 2007). The PEER's triple integral implicitly assumes that damage measure (dm) conditioned-on-engineering demand parameter (edp) is independent of intensity measure (im), and decision variable (dv) conditioned-on-dm is independent of im and edp. The seismic impact quantification is decomposed into subtasks that can be carried out by a different group of experts (Der Kiureghian 2005). This conditional independence of the PEER framework has enabled other researchers to extend it to PBD for fire (e.g., Lange et al., 2014), hurricane (Barbato et al., 2013), tsunami (Attary et al., 2017; Goda et al., 2021), and wind (e.g., Ciampoli et al., 2011; Petrini and Ciampoli, 2012).

Computing the mean annual rate of exceedance of dvs is computationally intensive, and different approximations are proposed. The triple integral in the PEER framework can be computed using computationally intensive Monte Carlo simulations (e.g., Jayaram et al., 2012; Goulet et al., 2007). Different stochastic models, such as Poisson, Markov, semi-Markov, renewal, or trigger type, have been considered for earthquake modeling (Anagnos and Kiremidjian 1984). With Poisson's occurrence of the earthquake load assumption, Der Kiureghian (2005) formulated a closed-form solution of the PEER framework. The closed-form solution of the mean annual rate is identical to the PEER framework. However, when the PEER framework is extended beyond 1 year, it gives a conservative result (Der Kiureghian 2005). Similarly, with Poisson's earthquake arrival assumption, Wen and Kang (2001a) developed a closed-form solution for earthquake load formulated under life cycle cost (LCC) (Table 2). The LCC equation shown in Table 2 is a generalized equation that can be used for earthquake, wind, and earthquake and wind MH. In addition, it accounts for the coincidence rate of earthquake and wind hazard in the calculation of the LCC. Takahashi et al. (2004) considered a renewal model of earthquake occurrences in the LCC analysis. The LCC approach has been used in buildings' seismic design applications (e.g., Wen and Kang 2001b; Liu et al., 2003; Mitropoulou et al., 2011; Castaldo et al., 2016). Mahsuli and Haukaas (2013) proposed a reliability-based approach to solving the loss assessment.

TABLE 2

TABLE 2. LCC performance based design framework.

Performance-Based Design for Wind Loads

The current wind load design follows the Davenport wind loading chain (Davenport 1967; Isyumov 2012). In the wind loading chain, the wind response of tall buildings is determined by considering local wind climatology, local wind exposure and topography, structural aerodynamic characteristics (governed by building shape), and structural dynamic properties (Kareem et al., 2019; Bezabeh et al., 2020b; Solari 2020). The framework was developed for synoptic and stationary winds. Non-stationarity of the wind load, however, has been identified as an important factor to consider (Kareem and Wu 2013; Solari et al., 2015; Hong 2016). Kareem et al. (2019) generalized the Davenport wind loading chain to account for a non-stationary wind–force–response relationship. Unlike earthquake load, for wind load, the building's aerodynamic interactions are evolving with the change in the built environment (Davenport 1983; Elshaer et al., 2017). Thus, the design for wind loads should account for the evolution of the built environment.

Bezabeh et al. (2020b) have provided a state-of-the-art review on PBD for wind loads. The PEER framework was extended for “Performance-Based Wind Engineering” (PBWE, Table 1, Ciampoli et al., 2011). Different researchers have used the PBWE framework (e.g., Augusti and Ciampoli 2008; Ciampoli et al., 2011; Ciampoli and Petrini 2012; Spence and Kareem 2014; Chuang and Spence 2017; Suksuwan and Spence 2019; Ouyang and Spence 2021). Similar to PBEE, the PBWE framework is computationally intensive and requires quantifying the probabilistic hazard to loss assessment. Wen and Kang (2001a) proposed an LCC-based closed-form solution of the probabilistic wind design framework (Table 2). The LCC framework has been applied for tall building wind load design (e.g., Le and Caracoglia 2021; Micheli et al., 2019, 2021; Cui and Caracoglia 2018, Cui and Caracoglia 2020; Ierimonti et al., 2017; Ierimonti et al., 2018). Bezabeh et al. (2018a, 2018b) extended the Davenport wind loading chain to account for uncertainties and formulated it in a reliability framework.

The wind load design was mainly undertaken for a linear response that will consequently furnish over designed system (Alinejad and Kang, 2020). The consideration of nonlinear wind design is an emerging area (e.g., Alinejad et al., 2020, 2021; Bezabeh et al., 2020b; Elezaby and El Damatty 2020; Huang and Chen 2022). To ameliorate this, the ASCE (2019) pre-standard has put forward a PBWD of buildings for wind load, where both linear elastic and nonlinear time history analysis (NLTHA) can be utilized. Chuang and Spence (2017) presented a wind PBD framework to account both for collapse and non-collapse limit states. Bezabeh et al. (2021a, 2021b) proposed a PBWD for a nonlinear wind design framework. Bezabeh et al. (2020b) proposed using self-centering systems to overcome the progressive unidirectional accumulation of plastic deformations.

Multi-Hazard Design Under Earthquake and Wind Loads

For earthquake and wind MH design framework, fragility-based (Zheng et al., 2021; Li et al., 2021; Li et al., 2020), LCC-based (Kleingesinds and Lavan 2021; Kleingesinds et al., 2021; Venanzi et al., 2018; Mahmoud and Cheng 2017; Wen and Kang 2001a; Wen and Kang 2001b), and risk-based (Crosti et al., 2010; Duthinh and Simiu 2010; Suksuwan and Spence 2018; Wang M. et al., 2021; Kwag et al., 2021; Roy et al., 2021; Zheng et al., 2021) framework have been proposed to meet different performance objectives (e.g., serviceability/comfort, life safety).

Wen and Kang (2001a) formulated a generalized LCC framework that considers both correlated and uncorrelated earthquake and wind loads (Table 2). The MH framework assumed that earthquake and wind hazards follow a Poisson model (Wen 1990). The MH PBD framework considers uncertainties in hazard, demand, capacity, and initial construction C_o and damage costs. The earthquake and wind loads vary over time; however, the co-occurrence of the maximum values for earthquake and wind loads is small, and this correlation can be ignored (Wen and Kang 2001a; Wen 2001). Suksuwan and Spence (2018) and Chulahwat and Mahmoud (2017), for example, integrated the PEER earthquake $λ_{E} (d v)$ and wind $λ_{W} (d v)$ PBD frameworks (Table 1) for earthquake and wind MH design, $λ_{M H} (D V)$ , as:

λ_{M H} (d v) = λ_{E} (d v) + λ_{W} (d v) (1)

With an increasing body of knowledge in the MH design framework, there is no reported study for tall-timber buildings. The MH framework for the tall-timber building is presented in Figure 2.

Site-Specific Hazard and Engineering Demand Parameters

In 1910, the Seismology Society of America identified three emerging areas (McGuire 2004): 1) earthquake event, 2) associated ground motions, and 3) effect on structures. The three emerging areas are still valid today for innovative building systems to reliably quantify the im and edps. In wind engineering, it has gone through similar evolution with the wind loading chain (e.g., Kareem et al., 2019; Bezabeh et al., 2020b; Solari 2020).

The edps in the PBD framework (Table 1) are structural responses, such as acceleration and inter-story drift ratio (e.g., Tesfamariam and Goda 2015; Cui and Caracoglia 2020), obtained through NLTHA. The site-specific hazard can be undertaken using probabilistic seismic hazard analysis (McGuire 2004; Atkinson and Goda 2013; Bommer and Stafford 2020) framework, considering empirical equations (Shahi and Baker 2011; Stafford 2014) or physics-based (Atkinson and Silva 2000; Yamamoto and Baker 2013) ground motion characterization. Finally, different ground motion selection algorithms are used to carry out the NLTHA (e.g., Bradley et al., 2015; Goda, 2015).

Advances in computational resources have enabled researchers to develop high-resolution coupled physics-based ground motion sources to structural simulation models (Kenawy et al., 2021; McCallen et al., 2021). This eliminates the epistemic uncertainty in quantifying free field and foundation level shaking. This model, however, requires a detailed site-specific source model and is computationally intensive. The computationally intensive PBD simulations can be ameliorated with a cloud-enabled computational platform (Deierlein et al., 2020; Kareem 2020). This might not be suitable for preliminary design iterations and verifications; however, it can be used for final design validation.

Once the im at the site is obtained through the hazard analysis, the im and edp relation is established through fragility curves (e.g., Goda and Tesfamariam 2015; De Risi et al., 2019; Cui and Caracoglia 2020; Le and Caracoglia 2021; Silva et al., 2021). Other important areas that warrant investigation for tall-timber buildings are the effect of long-duration earthquakes (Jennings 1970; Tesfamariam and Goda 2017), mainshock and aftershock earthquake sequences (Goda 2015; Tesfamariam and Goda, 2017; Tesfamariam and Goda 2015), a dependency between edps (Goda and Tesfamariam 2015; De Risi et al., 2019), and directionality of wind loads (e.g., Cui and Caracoglia 2020).

Loss Assessment

The accuracy of the loss assessment is influenced by the available data and the choices of relevant models and parameters (Hosseinpour et al., 2021; Cremen and Baker 2021; O'Reilly and Calvi 2019; Baker and Cornell 2008). In North America, the current seismic loss assessment has evolved from expert-driven (e.g., ATC 13, ATC 1985) to detailed simulation-based models (HAZUS, FEMA–NIBS 2003; FEMA P58, FEMA 2000). In a case where historical data are scarce, simulation-based methods are viable options (Yang et al., 2009; Zareian and Krawinkler 2012). HAZUS (FEMA–NIBS 2003; Kircher et al., 2006) quantifies the loss assessment using the maximum inter-story drift ratio obtained through simulation. Response of tall buildings are subject to multimodal response, and the loss assessment is better captured using a nonuniform evaluation of loss distribution over the height (Shome and Luco 2010; Shome et al., 2015). FEMA P58 (FEMA 2012; ATC 2018) developed a fragility-based loss assessment tool named performance assessment calculation tool. The performance assessment calculation tool contains a large database consisting of the mean and dispersion values of different consequence functions (repair cost, repair time, casualty, and dollar loss). Aslani and Miranda (2005) proposed a story-based loss assessment by considering the damage, downtime due to business interruption, injuries, and loss of lives. Different authors have now developed simplified story-based loss assessments (e.g., Papadopoulos et al., 2019; Shahnazaryan et al., 2021). Similar trends are followed in the loss assessment under wind load (e.g., Le and Caracoglia 2021; Micheli et al., 2019; Micheli et al., 2021; Cui and Caracoglia 2018, 2020; Ierimonti et al., 2017; Ierimonti et al., 2018).

The current state-of-the-art evaluation and design are moving from loss quantification to post-earthquake recovery, called resiliency (Cimellaro et al., 2010; Cimellaro 2013; McAllister 2016; Almufti and Willford 2021; Furley et al., 2021). A comprehensive resilience rating system, Resilience-Based Earthquake Design Initiative, was developed by Arup (Almufti and Willford 2021). Wilson et al. (2021) implemented loss assessment for CLT building using FEMA P58. Furley et al. (2021) implemented a stochastic model to quantify the resiliency of a two-story self-centering CLT building.

Soil–Structure Interaction

SSI is influenced by the site conditions, foundation embedment, flexibility, and shape on foundation impedance (Stewart et al., 1999; Sotiriadis et al., 2020). This interaction is complex, and it can have both beneficial and detrimental effects on the response (Mylonakis and Gazetas 2000). Low-fidelity spring models (e.g., Stewart et al., 1999; Sotiriadis et al., 2020) and high-fidelity finite element models (e.g., Rahmani et al., 2014; Arboleda-Monsalve et al., 2020; McCallen et al., 2021) have been used for SSI. Low-fidelity, linear, and nonlinear spring models can be used at the foundation of the building structure (e.g., Stewart et al., 1999; Sotiriadis et al., 2020). Lesgidis et al. (2018) proposed frequency- and intensity-dependent spring models for SSI.

The SSI is an important intrinsic source of damping for tall buildings (e.g., Cruz and Miranda, 2017). The SSI will consequently impact the response of tall buildings under earthquake and wind loads. However, the SSI effect is not considered in the current tall-timber building design literature. Liu et al. (2008) showed that for a wind-induced response of tall buildings incorporating tuned mass damper (TMD), neglecting the SSI overestimated the response and underestimated the effectiveness of the TMD. Zhou et al. (2018), for eddy current TMD and wind-load application on tall buildings, showed that, with consideration of SSI, the short return period acceleration response exceeded the human comfort limit states.

Damping

Damping mechanisms in tall buildings are associated with intrinsic/inherent (or structural), aerodynamic, hysteretic, and supplemental/additional (Smith et al., 2010; Lago et al., 2018). Factors that contribute to the damping are as follows (Yeh et al., 1971; Cruz and Miranda, 2016, 2017): material, friction between members and connections, structural system and joint types, foundation and soil types, interior partitions, exterior cladding, other nonstructural members, and vibration amplitude.

The damping associated with different mass timber building typologies and connections can be quantified from field measurement (e.g., Smith et al., 2010; Kijewski-Correa and Pirnia, 2007). With in situ ambient vibration measurements, Edskär and Lidelöw (2019) and Reynolds et al. (2016) reported building height and damping relationship (Figure 3). From Figure 3, it is apparent that, as expected, with the increase in building height, the damping values are decreasing. The damping–height empirical equations for steel, concrete, and steel/concrete buildings reported in Smith et al. (2010) are plotted in Figure 3. Overall, both have a similar trend, and some of the timber-building damping values are bounded between the empirical equation for steel and RC damping values. The variability in the damping values for the timber building is high, and this warrants more investigation to understand the causal relation of different explanatory factors. The current analytical studies reported on mass timber building do not consider the SSI. Thus, the response obtained through the in situ measurements and analytical studies can be different (e.g., Edskär and Lidelöw 2017, 2019). Thus, future analytical studies should incorporate the SSI in the damping calculations. The building height and frequency relationship is shown in Figure 4. One of the main explanatory factors for the reduction in damping and frequency can be intrinsic damping (e.g., Tamura and Suganuma 1996; Smith et al., 2010).

FIGURE 3

FIGURE 3. Variation of damping with height.

FIGURE 4

FIGURE 4. Variation of frequency with height.

Energy Dissipation Devices

Motions of a building, due to earthquake and wind loads, are traditionally controlled through mass and stiffness proportioning. Increasing the stiffness, however, can increase the acceleration demand. In addition, it can reduce the overall seismic energy dissipation capacity with consequent unintended failure of connections and capacity-protected elements (ASCE 2019). Using supplemental energy dissipators, the exceedance of serviceability limit state can be reduced. Figure 5 depicts the high-level category of the different supplemental energy dissipation devices.

FIGURE 5

FIGURE 5. General classification of supplemental energy dissipation devices.

The supplemental energy dissipation devices can be categorized as passive, active, semiactive, and hybrid damping systems and seismic isolation systems (Soong and Spencer Jr 2002; Takewaki 2011; Lago et al., 2018; De Domenico et al., 2019; Jafari and Alipour 2021b; Takewaki and Akehashi 2021). Traditional passive control damping, such as TMD and tuned liquid damper, are tuned to the fundamental period of the structure and are not suitable for earthquake response mitigation (Willford et al., 2008; Lago et al., 2018). Under severe earthquake loads, the structural response will undergo yielding and consequent period elongation. On the other hand, metallic damper used for earthquake loads will not be suitable for wind loads, as the serviceability wind loads will not yield metallic dampers (Willford et al., 2008). Viscoelastic dampers (Christopoulos and Montgomery 2013) are attractive damping technology that can be used both for earthquake and wind loads. Under MH design consideration, finding the right damper and location by satisfying the MH performance limit states can be cast as an optimization problem (e.g., Suksuwan and Spence 2018; Roy et al., 2021).

Different papers are published on the application of energy dissipation devices for tall buildings: earthquake (e.g., Christopoulos and Montgomery 2013; Kasagi et al., 2016; Nakamura and Hanzawa 2017; Zhou et al., 2018; Hashizume and Takewaki 2020; Uemura et al., 2021), wind (e.g., Liu et al., 2008; Giaralis and Petrini 2017), and MH (earthquake and wind) (e.g., Roy and Matsagar 2019, 2020; Wang M. et al., 2021; Li et al., 2021) loads. Use of base isolations for tall buildings under earthquake (e.g., Taniguchi et al., 2016; Makita et al., 2018), wind (e.g., Chen and Ahmadi 1992; Vulcano 1998; Cheng et al., 2002), and MH (earthquake and wind) (e.g., Roy et al., 2021) loads are also reported in the literature. Liu et al. (2008) and Zhou et al. (2018), respectively, considered the influence of SSI on TMD and eddy-current TMD on tall building response under wind loads. Façades of buildings often are considered nonstructural elements. Recent innovative connections, however, are paving the way for the potential use of the façades as distributed dampers (Jafari and Alipour 2021a,c).

The application of dampers in timber building is limited (e.g., Huang and Chang 2018; Hashemi et al., 2020). The damping for the mass timber is mostly considered with energy dissipating connectors (e.g., Pu et al., 2016; Fitzgerald et al., 2020). More studies, however, in light timber structures are reported (Bolmsvik and Brandt 2013; Jayamon et al., 2018; Ugalde et al., 2019; Tesfamariam et al., 2021b; Nakamura and Fujii 2021).

Optimization

The MH design optimization problems are subject to uncertainties both on the demand and capacity (e.g., Rosenblueth 1986; Wen 2001; Franchin 2004; Der Kiureghian and Ditlevsen 2009; Spence and Kareem 2014; Kleingesinds et al., 2021). Different optimization under uncertainty algorithms is proposed. The design optimization, under uncertainty, can be cast under reliability-based design optimization (RBDO) (Aoues and Chateauneuf 2010; Valdebenito and Schuëller 2010; Song et al., 2021) and robust design optimization (RDO) (Chatterjee et al., 2019; Chakraborty et al., 2021; Das et al., 2021) frameworks. Subsequently, the problem is solved using gradient (e.g., Franchin et al., 2018; Kleingesinds and Lavan 2021) or non-gradient (derivate-free) (e.g., Hare et al., 2013; Afshari et al., 2019; Umeura et al., 2021) optimization algorithms. In addition, the design requirements to satisfy both earthquake and wind MH loads can be conflicting, and the problem can be formulated under a multi-objective optimization framework (e.g., Afshari et al., 2019).

Reliability-Based Design Optimization

The RBDO technique has proven its utility for optimization under uncertainty (Song et al., 2021). In RBDO, although user-defined performance functions are optimized, probability failure criterion is added as a constraint. The solution for RBDO can be classified as formulated, among others, as two-level and decoupled methods (De et al., 2021). The two-level optimization, which is computationally intensive, entails the use of two nested loops, i.e., the inner loop to solve the reliability analysis and the outer loop to carry out the design optimization. The decoupled method, which is less computationally intensive, entails carrying out deterministic RBDO by replacing the inner-loop reliability analysis (Madsen and Hansen 1992). Spence et al. (2016) proposed an efficient algorithm for the RBDO of a large-scale uncertain system. Chakraborty and Roy (2011) used RBDO for the optimal design of TMD under earthquake load. Altieri et al. (2018) investigated the optimal design of a nonlinear viscous damper using RBDO under earthquake load. Das et al. (2020) showed the effectiveness of the estimation of tuning parameters of nonlinear energy sink using RBDO. Ontiveros-Perez et al. (2019) used RBDO of passive friction damper for mitigation of earthquake-induced vibration. To enhance the seismic performance of the base-isolated structure, Peng et al. (2021) proposed a reliability-based optimization technique for an adaptive sliding base isolation system. Zou et al. (2010) studied the reliability-based optimization of the base-isolated concrete building considering the drift of the superstructure as a performance criterion.

Robust Design Optimization

A system is called robust when the system is insensitive to the effects of uncertainty. The RDO method propagates uncertainty by minimizing the mean and standard deviators of the structural responses. This problem is solved as a multi-objective optimization problem. Miguel et al. (2014) showed the optimal location and parameters of friction damper using RDO. Yu et al. (2013) carried out a reliability-based RDO of TMD to mitigate the earthquake-induced vibration of building structures. The effectiveness and robustness of TMD were studied by Greco et al. (2015) to mitigate the seismic-induced vibration for buildings. Lagaros and Fragiadakis (2007) proposed an LCC-based RDO for the design of steel moment-resisting frames. The RDO, for estimating the tuning parameters of nonlinear energy sink with negative stiffness, was investigated by Chakraborty et al. (2021) and Das et al. (2021).

Topology Optimization

With advances in finite element modeling, optimizing the shape and form of the tall-timber building can be undertaken under topology optimization. The topology optimization, for a prescribed structural domain, under a set of the objective function and design constraints, provides a rational approach to obtain optimal layout (Sigmund and Maute 2013). Beghini et al. (2014) presented a review of structural topology optimization and highlighted the means of finding the balance between engineering and architecture. This can be of particular interest in tall-timber buildings, as it can integrate aesthetics and structural factors in design. Martin and Deierlein (2020) proposed modal compliance-based topology optimization for the tall building subjected to dynamic seismic excitation. Suksuwan and Spence (2018) proposed a simulation-centered performance-based MH topology optimization framework for earthquake and wind loads. Goli et al. (2021) showed the parametric topology optimization of the lateral bracing systems for tall buildings subjected to wind and gravity loads using bidirectional evolutionary structural optimization. Gomez et al. (2020, 2021) showed the topology optimization of the building subjected to seismic and wind stochastic excitations, respectively. Bobby et al. (2016, 2017) proposed a data-driven and reliability-based topology optimization of uncertain wind-excited tall buildings, respectively. Bobby et al. (2014) proposed a performance-based topology optimization framework for wind-excited tall buildings.

Multi-Fidelity Surrogate Models

High-fidelity and detailed three-dimensional building models can be used for the NLTHA of buildings (e.g., Rinaldin and Fragiacomo 2016; Lu et al., 2018; Wang and Wu 2020; Tesfamariam et al., 2021a). For computationally intensive three-dimensional models or experimental data, however, the use of a physics-informed neural network, surrogate models, and multi-fidelity models can be the future direction (Peherstorfer et al., 2018; Swischuk et al., 2019; Deierlein et al., 2020; Chakraborty 2021; Karniadakis et al., 2021).

Surrogate Models

For computationally expensive design and optimization, a surrogate model (e.g., artificial neural network, Lehký et al., 2018; response surface method, Foschi et al., 2002), constructed using few training samples, can replace the original limit state. In the surrogate model development, adaptive sampling techniques can be considered to enhance the reliability of the prediction. Such sampling techniques, for example, are Kriging (e.g., Dubourg et al., 2011; Bernardini et al., 2014; Li et al., 2016; Zhang et al., 2017), adaptive Kriging (Das and Tesfamariam 2020; Kroetz et al., 2020; Zhang et al., 2022), adaptive Bayesian support vector regression (Wang J. et al., 2021), polynomial chaos-based Kriging (Das et al., 2020), spectral representation (Zhao et al., 2021), Kriging and adaptive wavelet network (Micheli et al., 2020a), and Bayesian deep learning (Luo and Kareem 2020). In uncertainty propagation, assemble of surrogate models can be used (e.g., Wang et al., 2019; Das et al., 2021). Micheli et al. (2020b) used multiple-surrogate models for probabilistic performance assessment of wind-excited tall buildings.

Physics-Informed Neural Network

A physics-based (informed) neural network (Wu et al., 2018; Beucler et al., 2021; Haghighat and Juanes 2021) is an emerging and promising modeling technique. In a physics-based neural network, the physics of the problem (e.g., structural model output) is coupled with machine learning (e.g., neural network) to develop surrogate models. Lai et al. (2021) presented structural identification with physics-informed neural ordinary differential equations. Yucesan et al. (2021) proposed a framework using a physics-informed neural network for adjusting the outputs of torsional vibration dampers to experimental data. De (2021) applied a physics-based neural network model for base-isolated buildings and wind-excited tall structures. Wang and Wu (2020) implemented a physics-informed neural network for wind-induced nonlinear structural dynamic analysis.

Multi-Fidelity Models

A state-of-the-art review on multi-fidelity models is discussed in Peherstorfer et al. (2018). The multi-fidelity approach considers the integration of a high-fidelity (higher accuracy, higher computational cost) model with low fidelity (lower accuracy, lower computational cost). The integration in the multi-fidelity approach entails adaptation (i.e., enhancing the low-fidelity model), fusion (i.e., combining the low- and high-fidelity results), and filtering (i.e., the high-fidelity model is invoked after filter using the low-fidelity results) (Peherstorfer et al., 2018).

The multi-fidelity approach is now applied to earthquake engineering problems. Zhang et al. (2022) developed adaptive multi-fidelity Gaussian process reliability analysis to solve reliability problems. Royset et al. (2019) presented a multi-fidelity analysis for risk-adaptive statistical learning method to predict structural response. Yang and Perdikaris (2019) presented conditional deep surrogate models for probabilistic data fusion and multi-fidelity modeling of stochastic systems. Patsialis and Taflanidis (2021) used a multi-fidelity Monte Carlo simulation for seismic risk assessment. Sevieri et al. (2021) presented a multi-fidelity Bayesian framework for robust seismic fragility analysis. Chatzidaki and Vamvatsikos (2021) used a multi-fidelity model for probabilistic seismic demand models for fragility assessment. Zhou and Tang (2021) used multi-fidelity data fusion for the efficient characterization of dynamic response variation. Li and Jia (2020) used a multi-fidelity Gaussian process model integrating low- and high-fidelity data considering censoring. Xu et al. (2016) proposed a computational framework for regional seismic simulation of buildings with multiple-fidelity models. This risk assessment is suitable for regional seismic and wind hazards loss assessment. Dey et al. (2021) used a multi-fidelity approach for uncertainty quantification of buried pipeline response undergoing fault rupture displacements. Lopez-Caballero (2021) utilized a multi-fidelity approach for probabilistic seismic analysis of liquefiable embankment.

Similar multi-fidelity approaches can be considered for computing the edps under wind loads. To compute the edps in the wind loading chain, high-frequency pressure integration wind tunnel tests (Bezabeh et al., 2021a) or computational fluid dynamics (CFD) (Kareem 2020) can be considered. Moni et al. (2020) implemented an aeroelastic hybrid simulation of a base-pivoting building model in a wind tunnel. The experimental testing is not readily available for preliminary design and iteration. Reducing our reliance on physical testing was one of the grand challenges put forward by Masters (2016). Kareem (2020) and Ding and Kareem (2018) implemented a multi-fidelity CFD modeling approach, where the results of low-fidelity (e.g., Reynolds-averaged Navier–Stokes) and high-fidelity (e.g., large eddy simulation) simulations can be combined. Lamberti and Gorlé (2021) implemented a multi-fidelity machine learning framework to predict wind loads on buildings. Karem and Kwon (2017) proposed cyber-based data-enabled wind load effects on civil infrastructures. Bobby et al. (2016) proposed a data-driven simulation-based framework for the effective topology optimization of uncertain and dynamic wind-excited tall buildings. Bernardini et al. (2014) proposed an aerodynamic shape optimization of civil structures using a CFD-enabled surrogate model.

Conclusion and Future Direction

The rapid growth of the urban population and associated environmental concerns challenged city planners and developers to consider sustainable and cost-efficient building systems. Mass timbers, such as CLT panels and glulam members, have been used as viable, sustainable tall-timber buildings. The tall-timber buildings, however, are lighter and more flexible, which can make those buildings vulnerable to earthquakes and wind loads. With emerging computational tools and analytical models, carrying out PBD with high-fidelity models is apparent. With the current and future research direction in consideration, in this paper, we carried out a state-of-the-art review on PBD for earthquake, wind, and MH loads. The state-of-the-art review has highlighted the challenge and future direction for tall-timber building, which is summarized below.

• With increasing complexity in the tall-timber buildings, the need for a high-fidelity model and validation through experimental work is apparent. Subsequently, multi-fidelity modeling can be developed for design and optimization.

• Damping is a critical factor that influences the response of the building under earthquake and wind loads. As more tall-timber buildings are constructed, quantifying the damping values for tall-timber buildings is vital. This will enhance the knowledge and confidence in designing the buildings under MH. With more data collected on tall-timber buildings, data-driven models (e.g., Spence and Kareem 2013) are a viable alternative in the preliminary design phase. Frequency dependency of the intrinsic damping and different excitation levels, ameliorating the earthquake and wind MH design implementation, are challenging tasks.

• Current studies on tall-timber design and analysis do not take the SSI into consideration. The importance of the SSI was highlighted, and in this direction, future concerted efforts should be made. To reduce the computational cost, a multi-fidelity model of SSI, e.g., finite element and spring models, can be implemented.

• For the MH design framework, component-based fragility curves and loss data for tall-timber buildings should be developed and ameliorated in the FEMA P58 database.

• The design of tall-timber buildings under MH loads is complex and subject to uncertainties. This paper has provided a review on design optimization under uncertainty, with consideration of RBDO, RDO, and topology optimization.

Author Contributions

ST is the only contributor.

Funding

Funding for this research was provided by the Natural Science Engineering Research Council of Canada Discovery Grant (RGPIN-2019-05584) and the BC Forestry Innovation Investment’s (FII) Wood First Program.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Afshari, H., Hare, W., and Tesfamariam, S. (2019). Constrained Multi-Objective Optimization Algorithms: Review and Comparison with Application in Reinforced concrete Structures. Appl. Soft Comput. 83, 105631. doi:10.1016/j.asoc.2019.105631