Development of early age autogenous and thermal strains of alkali-activated slag-fly ash pastes

1 Introduction

The production of ordinary Portland cement (OPC) is the source of approximately 5–8% of the total anthropogenic greenhouse gas emissions (Damtoft et al., 2008; Benhelal et al., 2013; Olivier et al., 2015). Replacing Portland cement in concrete with industrial wastes or by-products such as fly ashes and blast-furnace slags (Ben Haha et al., 2011) has gained significant attention in the last decade. In contact with an alkaline solution, these precursors react and form a solid alkali-activated material (AAM). Different alkaline solutions have been studied: sodium hydroxide, sodium silicate, potassium hydroxide, calcium carbonate, etc. The type of solution and its dosage affect the reaction process, the microstructure, as well as the properties of the material (De Vargas et al., 2014; Lu et al., 2021). Among the different varieties of activators, sodium-based activators are widely available, affordable and cost-effective (Kua et al., 2019; Lu et al., 2021), and are thus chosen in this study. Besides the environmental benefits, these materials offer several additional advantages compared to OPC (Provis and van Deventer, 2014). They are, for instance, characterized by rapid strength development at early ages and enhanced resistance to acid and sulfate attacks (Davidovits, 2005; Shi et al., 2006; Provis and van Deventer, 2014). However, AAMs typically possess crucial shortcomings, most notably, they often exhibit large shrinkage strains which can be up to seven times larger than that of OPC (Bakharev et al., 2000). The high shrinkage may be mitigated when using biochar, superabsorbent polymers or lightweight aggregates (Ye and Radlińska, 2017; Vafaei et al., 2020; Prabahar et al., 2021). When restrained, this shrinkage causes the build-up of tensile stresses that can result in early-age cracking and thus in severely reduced mechanical and durability performance (Bendimerad et al., 2020; Serdar et al., 2020).

Early-age deformations are related to three phenomena: autogenous deformations, drying deformations, and thermal deformations. This study focuses on the development of autogenous and thermal deformations, which are therefore introduced next. Autogenous deformations are deformations which are occurring despite constant environmental conditions (particularly constant external relative humidity and constant external temperature). They are commonly related to several mechanisms, of which the most important are chemical shrinkage, self-desiccation, water absorption, and expansion pressures of precipitating reaction products. The chemical shrinkage or Le Chatelier’s contraction results from the fact that the volume of the reaction products is smaller than the volume of the reactants (Le Chatelier, 1900). Self-desiccation due to the water-consuming reaction leads to the formation of water-air menisci, and the internal relative humidity decreases, which induces a capillary depression of the pore fluid (Serdar et al., 2020). While the former two mechanisms lead to shrinkage, swelling may be caused by absorption of external water (Bjøntegaard et al., 2004; Esping, 2008; Craeye et al., 2010), absorption of internal water provided by water-releasing porous aggregates (such as light-weight or recycled aggregates; Delsaute and Staquet, 2019; Bendimerad et al., 2020; Delsaute and Staquet, 2020), or by the expansion pressure during the formation of reaction products such as ettringite (Mehta, 1973; Bentur and Ish-Shalom, 1974).

While many experimenters observe a large magnitude of autogenous shrinkage (Shen et al., 2011; Chi and Huang, 2013; Rashad, 2013; Jang et al., 2014; Marjanović et al., 2015), the micromechanical reasons for the large magnitude are less clear, but mostly linked to self-desiccation. Collins and Sanjayan (2000) track the high autogenous shrinkage of alkali-activated slags (AAS) back to the dense pore structure of the paste, which is composed of 80% of mesopores (radius between 1.25 and 25 nm). This results in high pore pressures during self-desiccation, as confirmed by Lee et al. (2014). To understand the magnitude of the expected pore pressures, internal relative humidity measurements have been performed on AAMs (Yssorche-Cubaynes and Ollivier, 1999; Hu et al., 2020), demonstrating that there is a large initial decrease in the IRH due to the high initial concentration of ions in the solution, followed by an increase in IRH due to the ion consumption, and only thereafter, the self-desiccation-related decrease in IRH can be observed. Ballekere Kumarappa et al. (2018) related shrinkage to high surface tension effects arising from the large number of ions present in the solution. Cartwright et al. (2014) highlighted the higher saturation degree and the lower elastic modulus. Another origin of the large shrinkage may be related to silica polymerization during the formation of the hydrate gel (Uppalapati and Cizer, 2018). Fang et al. (2018) stated that chemical shrinkage in the fresh state was the source of roughly 70% of the autogenous shrinkage. Li et al. (2020a) highlighted a high consumption of ions that reduces the steric-hydration force, which leads to shrinkage mainly during the acceleration period at early ages.

The main factors influencing the microstructure of AAMs, and thus the autogenous shrinkage, are the quantity and type of activators, the contents of the precursors and the water-to-binder (W/B) ratio (Lee et al., 2014). When the W/B ratio decreases, the pore size also decreases and the capillary stress increases, which results in higher autogenous shrinkage (Thomson, 1871; Lee et al., 2014). A higher dosage of activators results in a greater degree of reaction and thus more chemical shrinkage. In addition, it will decrease the porosity which influences the autogenous shrinkage by increasing the capillary stress (Lee et al., 2014; Ma and Ye, 2015; Ye and Radlińska, 2016; Ballekere Kumarappa et al., 2018). In mixes which are activated by sodium silicate and sodium hydroxide, increasing the content of hydroxide (and thus the pH) decreases the autogenous shrinkage (Cartwright et al., 2014; Hojati and Radlińska, 2017). An increase in the slag content leads to a higher degree of reaction and thus resulting in more chemical shrinkage (Lee et al., 2014), densifies the microstructure of the paste, increases capillary pressure, and amplifies the autogenous shrinkage (Lee et al., 2014; Hojati and Radlińska, 2017; Fang et al., 2018).

In addition to autogenous deformations, volume changes arise from temperature variations, triggered by environmental changes and/or the heat released during the exothermal reaction. The coefficient of thermal expansion (CTE) quantifies temperature-induced volume changes. It is herein defined as the length change of a unit length (linear CTE, µm/m/°C) upon a temperature change of one degree Celsius. Experimental results of CTE evolutions with respect to age for AAMs are absent in the literature. Only a CTE amounting to 16.6 μm/m/°C for a hardened low-calcium fly ash-based geopolymer concrete is reported (Ma and Dehn, 2017), which significantly exceeds the magnitudes between 8 and 12 μm/m/°C that are typically reported for OPC concrete (Fairbairn and Azenha, 2018). Experimental determination of CTEs during early ages is rather difficult. First, it is challenging to distinguish thermal from autogenous deformations because both evolve simultaneously (Serdar et al., 2020). Moreover, experimental monitoring of CTE during early material ages requires the application of thermal loads on the specimen. These temperature cycles significantly alter the thermo-activated maturation reactions of AAMs. Quantifying the dependence using an Arrhenius law (Joseph et al., 2018) has shown that the apparent activation energy for slag activated by sodium silicate and sodium hydroxide amounts to 53.6 kJ/mol (Huanhai et al., 1993), for slag-fly ash mixes, in turn, activated by sodium silicate and sodium hydroxide, the activation energy even amounts to 75.2 kJ/mol. Compared to the 38.0 kJ/mol of a typical Portland cement paste with a water-to-cement ratio of 0.4 (Mounanga et al., 2006), the activation energies in AAMs are significantly higher, which highlights the sensitivity of temperature changes of these pastes.

In this paper, we conduct a comprehensive experimental study to quantify the autogenous and thermal strains of sodium-silicate and sodium-hydroxide-activated slag-fly ash mixes with different solution-to-binder ratios and different silica modulus. The main objectives of this paper are twofold:

• We aim at experimental monitoring of the temporal evolution of the thermal expansion coefficients at early ages to close the knowledge gap the literature.

• Moreover, the temporal evolution of autogenous strains is quantified and linked to the heat release (as an indicator for the chemical reactions taking place during hardening) and to the internal relative humidity (as an indicator for self-desiccation). This way, insights into two critical parameters which affect the shrinkage of AAMs are targeted.

To meet the objectives, a modified AutoShrink device (Germann Instruments, 2015) is used for the quantification of both autogenous and thermal strains, which allows for applying temperature variations during the hardening. The deformation monitoring is accompanied by isothermal calorimetry conducted at three different temperatures, to monitor the reaction process (Ouyang et al., 2020; Joseph and Cizer, 2022) and to quantify the temperature activation behavior. Moreover, internal relative humidity (IRH) evolutions were measured to potentially correlate them with autogenous shrinkage results. Therefore, the paper is structured as follows. First, the materials used are described in detail, followed by the presentation of the experimental methods. Secondly, the experimental results will be discussed starting with compressive strength and heat release, which will allow for determining the apparent activation energy. After that, the results of the autogenous shrinkage and the CTE will be analyzed, followed by a discussion of IRH results. The paper is closed with conclusions.

2 Materials and methods

2.1 Materials

This study considers pastes obtained by alkali-activation of fly ash (FA) and blast-furnace slag (BFS), see Table 1 for the chemical compositions. Their particle size distribution can be found on Supplementary Figure S1 and Supplementary Figure S2. Two activators are considered: a sodium silicate solution (Na₂O + SiO₂) exhibiting a molarity of 10M with 18% (in mass) Na₂O, 28.5% SiO₂ and 53.5% H₂O, and a sodium hydroxide solution 8M (NaOH). The density of the sodium silicate solution is 1.37 g/ml. The two alkaline solutions were mixed together beforehand. The silica modulus, defined as the mass ratio between SiO₂ and Na₂O (M_s = SiO₂/Na₂O), varies between 1.04 and 1.58.

TABLE 1

TABLE 1. Chemical composition of the binders in mass percent from X-ray fluorescence spectroscopy.

2.2 Mixture proportions and sample preparation

Eight different alkali-activated slag-fly ash (AASF) pastes were prepared according to the European Standard EN 196-1:2016 (CEN, 2016). X. Dai et al. (Dai et al., 2020) reported that an increase in the fly ash content extended the setting times while an increase in the slag increases and speeds up the structural build-up. To benefit from both advantages, each composition contains 50% (in mass) slag and 50% fly ash. The solution-to-binder ratio (S/B) and silica modulus (M_s) differ, see Table 2 (where W/B is the water-to-binder ratio). The reference mix is labeled SB0.55Ms1.44, implying a solution-to-binder ratio S/B of 0.55 and a silica modulus M_s of 1.44. Firstly, four SB compositions (SB0.47, SB0.50, SB0.64, and SB0.70) with varying S/B ratios but reference M_s = 1.44 (equal to the reference composition) are studied. S/B ratios from 0.47 to 0.70 are studied because it is well-known that S/B is a crucial mix parameter that changes the mechanical properties and shrinkage of AAMs (Nedeljković et al., 2018). Secondly, three Ms compositions (Ms1.04, Ms1.24, Ms1.58) with varying M_s but reference S/B = 0.55 (equal to the reference composition) ratio are tested. All the tests are performed in sealed conditions at a curing temperature of 20°C. The results for those different compositions are compared to the ones of an ordinary Portland cement (CEM I 52.5) paste with a water-to-binder ratio (W/C) of 0.5 to have a familiar composition (Delsaute, 2016).

TABLE 2

TABLE 2. Mix proportions of the tested AASF pastes.

2.3 Experimental methods

2.3.1 Compressive strength

To determine the compressive strength of the paste, cubes of 50 mm side were cast, sealed, and then placed in a climatic chamber of constant temperature (20°C). The cubes are unmolded and tested after 2 and 7 days. The tests are performed on two different cubes (Delsaute, 2016; Saleh Mohamed and Wauters, 2016). Thanks to the excellent repeatability, additional tests are obsolete as the range between specimens is less than 5% (ASTM, 2016).

2.3.2 Autogenous and thermal deformations

The original version of the AutoShrink device (Germann Instruments, 2015) allows measuring the (linear) autogenous deformation as a function of time in an environment where the temperature remains constant. But this device was improved at the Université libre de Bruxelles (ULB) to apply controlled temperature variations to the samples (Serdar et al., 2020). These temperature changes allow determining simultaneously the CTE and the autogenous strain by imposing a variation of ± 3°C to the system, based around a central temperature of 20°C. This temperature change is produced by the thermal regulation system composed of a thermostatic bath and a convolution system as shown in Figure 1A. The device is isolated from the environment by an insulated box to improve the efficiency of the thermal regulation. The AutoShrink device contains three samples, which allows for assessing test repeatability (Delsaute, 2016; Germann Instruments, 2015). Figure 1A shows the AutoShrink device at ULB and the different elements: the thermal regulation, three corrugated tubes, the insulator, and the digital gauge.

FIGURE 1

FIGURE 1. AutoShrink device developed at ULB (A) and example of the temperature variations (B).

The paste is cast in a corrugated plastic tube with a diameter of 3 cm and a length of 40 cm. The corrugated shape of the tube allows the sample to deform freely due to the lowered longitudinal stiffness. At the end of the tube is located the digital gauge that will record the deformation during the test. Two samples are used for the monitoring of the displacement, while the third specimen is used to record the temperature inside the specimen during the whole test by using a thermocouple inserted in the middle of the specimen. Each channel has its own digital gauge that will record the displacement. In addition, the temperature inside the convolution system is monitored to consider the thermal deformation of the test rig itself (the whole test setup is thermally calibrated; Serdar et al., 2020). The data provided by the device are:

• the temperature inside the paste;

• the temperature of the air inside the isolated box;

• the temperature variations imposed by the thermostatic bath;

• the displacements recorded by the gauges.

After the removal of the thermal deformation related to the test rig, the measurement of the free strain is obtained. Those strains are a combination of the autogenous strain and the thermal strain because they occur at the same time during the reaction:

${\mathit{\epsilon }}_{\mathit{t}\mathit{o}\mathit{t}}={\mathit{\epsilon }}_{\mathit{a}\mathit{u}}+{\mathit{\alpha }}_{\mathit{c}}\bullet ∆{\mathit{T}}_{\mathit{c}}(1)$

${\epsilon }_{tot}$ is the total strain [m/m], ${\epsilon }_{au}$ is the autogenous strain [m/m], ${\alpha }_c$ is the CTE [m/m/°C] and $∆T_c$ is the temperature variation (Delsaute, 2016; Delsaute and Staquet, 2017). Temperature variations of ± 3°C are applied every 160 min, see Figure 1B. For the decoupling of total strain into autogenous and thermal strains, we followed the procedure established in Delsaute and Staquet, 2017, as shortly summarized next. We construct a fictitious strain evolution for a sample cured isothermally at 20°C by fitting (using cubic interpolation) only the measured strains at the end of the intervals when the applied temperature amounted to 20°C. These fictitious strains are then subtracted from the total measured strain evolution to isolate the thermal strains resulting from the cyclic temperature history, which allows for the determination of the CTE (Equation 2). Secondly, the autogenous strain (Equation 1) is defined. Despite the thermal variation, the value of the CTE can be considered as the same for two different temperatures because the effect of the temperature on the CTE is very small (Delsaute and Staquet, 2017).

${\mathit{\alpha }}_{\mathit{c}}=\frac{∆{\mathit{\epsilon }}_{\mathit{t}\mathit{o}\mathit{t},\mathbf{1}}-∆{\mathit{\epsilon }}_{\mathit{t}\mathit{o}\mathit{t},\mathbf{2}}}{∆{\mathit{T}}_{\mathbf{1}}-∆{\mathit{T}}_{\mathbf{2}}}(2)$

where the indexes 1 and 2 express the two different temperatures histories (Delsaute, 2016; Delsaute and Staquet, 2017).

2.3.3 Isothermal calorimetry

The heat release is determined by means of an eight-channel TAM Air micro-calorimeter device (TA Instruments, 2019). For each composition, two samples were tested for the repeatability of the results. The tests usually last 2 weeks. Thereafter, the heat flow is too low to accurately monitor it (Delsaute, 2016; TA Instruments, 2013).

By performing the calorimetry tests at three different temperatures (10°C–20°C–30°C), the temperature activation behavior is determined. Therefore, an Arrhenius law is considered to quantify the rate $K$ of the reaction, reading formally as

$\mathit{K}\left(\mathit{t}\right)=\mathit{A}\bullet \mathbf{exp}\left(\frac{-{\mathit{E}}_{\mathit{a}}}{\mathit{R}\bullet \mathit{T}}\right)(3)$

In Equation 3, $A$ is a constant of proportionality, and E_a is the sought apparent activation energy, R is the universal gas constant (8.314 J/mol/°C), and T is the absolute temperature (Joseph et al., 2018). The aim of the tests at different temperatures is to identify the activation energy E_a, for which the superposition method is used, as explained next. Therefore, the cumulative heat releases, measured at two different curing temperatures, are plotted as a function of the so-called equivalent age $t_{eq}$, reading as

${\mathit{t}}_{\mathit{e}\mathit{q}}\left(\mathit{t},\mathit{T}\right)={\int }_{\mathbf{0}}^{\mathit{t}}\mathbf{exp}\left(\frac{{\mathit{E}}_{\mathit{a}}}{\mathit{R}}\bullet \left(\frac{\mathbf{1}}{\mathbf{273}+\mathit{T}\left(\mathit{s}\right)}-\frac{\mathbf{1}}{\mathbf{273}+{\mathit{T}}_{\mathit{r}\mathit{e}\mathit{f}}}\right)\right)\bullet \mathit{d}\mathit{s}(4)$

In Equation 4, $T\left(s\right)$ is the measured temperature (in °C), and $T_{ref}$ = 20°C is the reference temperature. The activation energy is then fitted such that the error, in a least-square definition, between the two cumulative heat releases (at the two considered temperatures) is minimized. An alternative method of determination of the activation energy based on rates is explained in the Supplementary Information.

2.3.4 Internal relative humidity

The internal relative humidity (IRH) in the pastes and the relative humidity of the activator solutions themselves have been measured with HC2-AW water activity probes. The specimens are cast directly after mixing in a plastic cylinder (Ø43 mm × 12 mm), sealed, and then stored at a temperature of 20 ± 1°C. At an age between 1 and 2 days, the sensor is placed on the top of the specimen, and data are recorded at an interval of 5 min. For each composition, two samples were tested for the repeatability of the results. Similar to deformation tests and isothermal calorimetry tests, the IRH is monitored for at least 2 weeks. The probes have a nominal accuracy of ±1% RH. Before and after each measurement, all sensors are calibrated using salt solutions (e.g., KNO₃ which has an RH of 94.62% at 20°C).

3 Results and discussion

3.1 Compressive strength

Figure 2A shows the measured compressive strength of AASF pastes with different S/B respectively, after 2 and 7–days. Very remarkably, there is no clear trend of the measured strength with respect to S/B. The largest 7-day strength amounts to roughly 66 MPa and is obtained for the composition with S/B = 0.50. The evolution of the compressive strength between 2 and 7 days for the different compositions is surprisingly different. For SB0.55Ms1.44, SB0.70, and SB0.47, the compressive strength at 7 days is roughly twice as much as the value at 2 days. For SB0.64, the corresponding strength increase factor amounts to four, while for SB0.50 the factor amounts to three. The observed influence of S/B can be explained by two counteracting phenomena: the quantity of water and the quantity of activators, which both increase with increasing S/B. Increasing the amount of activators has a positive effect on the strength because they promote the formation of strength-giving C-N-A-S-H gel. Water, in turn, has a negative effect on the strength because more water will induce a larger initial volume of pores resulting in a lower strength, a well known fact from modeling and experimental studies on AAM and OPC mixes (Taplin, 1959; Feret, 1892; Königsberger et al., 2018a). If S/B is small, the positive effect of the alkali content results in an increase in strength. The positive effect of increasing the alkali content, which is a result of increasing the S/B ratio, outweighs the negative effect of the increased porosity, which is another result of increasing S/B. When the S/B ratio becomes larger than 0.50, the latter effect becomes dominant. (Wang et al., 1994).

FIGURE 2

FIGURE 2. Compressive strength of AASF pastes with different S/B (A) and with different Ms (B).

Regarding the influence of the M_s modulus, depicted in Figure 2B, the test results highlight that the compressive strength at 7 days decreases when the M_s modulus is increased, which is in accordance with results of Hojati and Radlińska (2017). The authors highlight that a higher M_s modulus implies a lower pH. This results in a rapid initial dissolution and formation of reaction products on the surface of slag and fly ash particles, hindering further reaction and preventing efficient strength development (Hojati and Radlińska, 2017).

The results are compared to an OPC paste with W/B of 0.5. At 2 days, the OPC paste outperforms all the AASF pastes. However, at 7 days, AASF compositions with S/B ≤ 0.55 already exhibit a higher compressive strength. This shows that such pastes continue to react significantly after 2 days as already observed by many authors previously (see e.g. (Feret, 1892; Cartwright et al., 2014; Lee et al., 2014; Hojati and Radlińska, 2017)).

3.2 Isothermal calorimetry

Figures 3A,B, and Figures 3C,D, present the results of heat flow and cumulative heat release as a function of the equivalent age at 20°C, respectively. Concerning the heat flow, two peaks are observed. The initial one corresponds to the early dissolution of the FA and BFS and occurs already during the mixing and is thus not recorded entirely (Fang et al., 2018; Prabahar et al., 2021; Vafaei et al., 2020). The second one corresponds to the acceleration of the formation of the C-N-A-S-H gel (Fang et al., 2018; Prabahar et al., 2021; Vafaei et al., 2020), the period in between is called “induction period” (Fang et al., 2018). Interestingly, the second peak occurs later (the induction period lasts longer) and is more pronounced for pastes with higher S/B and higher M_s. The cumulative heat release (Figure 3C,D) is, in general, relatively close for all pastes after the second heat flow peak and amounts to roughly 140 J/g after an equivalent age of 1 week (168 h).

FIGURE 3

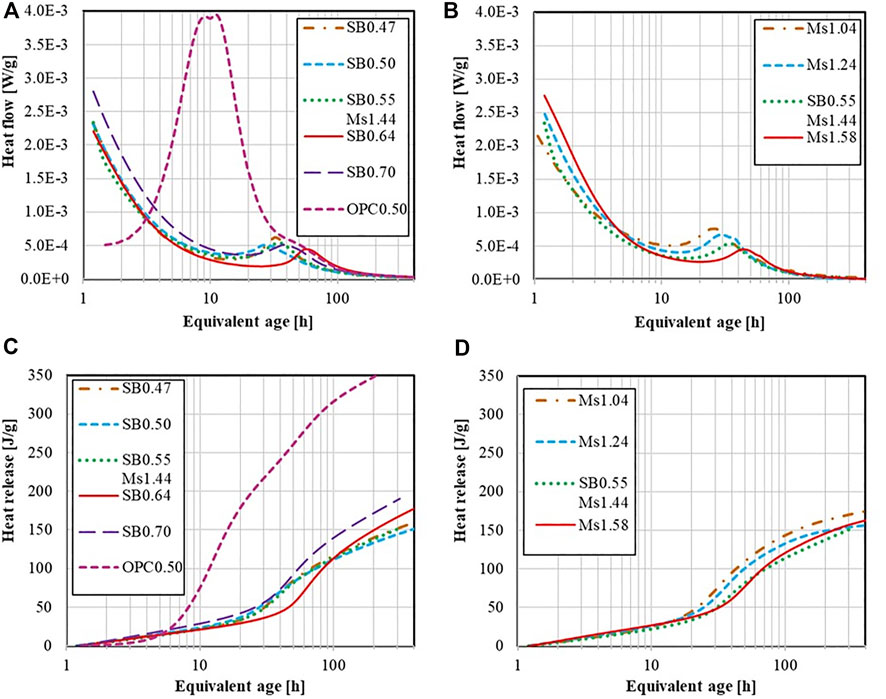
FIGURE 3. Heat flow of AASF pastes with different S/B (A), with different M_s(B); Cumulative heat release of AASF pastes with different S/B (C) and with different M_s (D).

The slightly higher cumulative heat release for the pastes with S/B ≥ 0.64 may be explained by the increase in activator solution leading to a more significant reaction. The 7-day strength, at least for the mix with S/B = 0.64, is much higher than the 2-day strength, indicating that pastes with high S/B indeed gain more strength (relative to their 2-day strength) between two and 7 days, compared to the mixes with lower S/B ratio, which is in line with the observed heat evolutions. The absolute strength values are, however, still small, given the large initial water content, as mentioned before. The observed delay of the second peak for pastes with high M_s, i.e. for pastes with more sodium hydroxide but less sodium silicate underlines that the sodium silicate leads to a faster reaction, as corroborated by earlier results (Gao et al., 2015).

The heat release of AAMs pastes is much lower than the heat release of OPC paste. This is already well known for blended cements (Moon et al., 2018; Ballim and Graham, 2009). In fact, increasing the amount of fly ash and slag reduces the heat of hydration of the paste, given that typical enthalpies of slag and fly ash in blended cement pastes are around 530 J/g and 285 J/g, respectively (Han et al., 2017), compared to the roughly 500 J/g of OPC (Bentz, 1997).

The ultimate heat release Q_∞ is estimated next, based on extrapolation of the cumulative heat release Q(t). This way, the degree of reaction α(t) can be defined as α(t) = Q(t)/Q_∞ (Joseph et al., 2018; Delsaute and Staquet, 2017). By representing the cumulative heat release as a function of the inverse of the square root of the age, a linear trend is observed after the equivalent age of around 20 h. When time tends to infinity, the inverse of the square root of the age tends to be zero. Thus, Q_∞ is defined as the intersection of the fitted straight line with the vertical axis (Medaets and Lambrette, 2014). An example of the method is illustrated in Figure 4 for the composition SB0.55Ms1.44. The resulting ultimate heats for all eight compositions are listed in Table 3. The resulting ultimate heat release increases when S/B increases while Q_∞ increases when M_s decreases (except for Ms1.24).

FIGURE 4

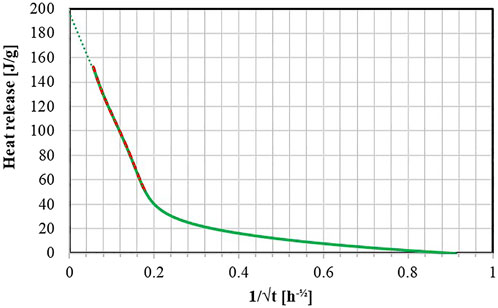
FIGURE 4. Extrapolation procedure for the ultimate heat ${\mathit{Q}}_{\mathit{\infty }}$: cumulative heat release as function of the inverse of the square root of the age for the composition SB0.55Ms1.44.

TABLE 3

TABLE 3. Extrapolated ultimate heats Q_∞ for the different compositions.

3.3 Apparent activation energy

3.3.1 Method of superposition

Next, the results of the heat release obtained at 10°C, 20°C, and 30°C, see Figure 5A for the exemplary results of the composition Ms1.58, are used to define the apparent activation energy. The apparent activation energy is calculated individually based on three combinations of measured heat releases: 10°C–20°C, 20°C–30°C, and 10°C–30°C, respectively, using first the method of superposition, as explained in Section 2.3.3 (see Equation 3). A very good superposition of the curves is observed for the three curing temperatures when expressed in function of the equivalent age, see the superimposed heat releases depicted in Figure 5B. The resulting activation energies E_a are presented in Table 4.

FIGURE 5

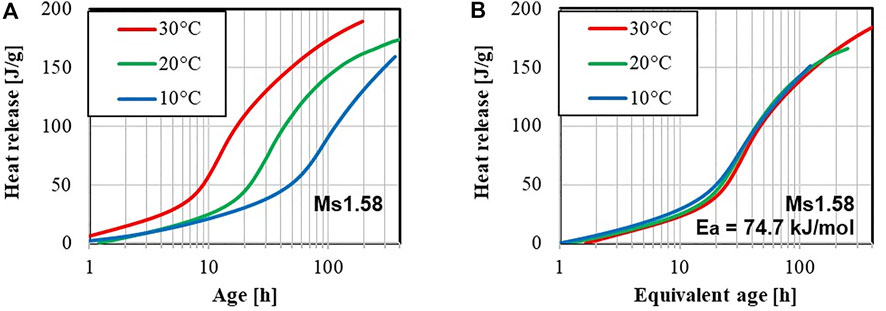
FIGURE 5. Cumulative heat of Ms1.58 (A) and results of activation energy for Ms1.58 according to the method of superposition (B).

TABLE 4

TABLE 4. Activation energies E_a expressed in kJ/mol for each composition (method of superposition).

Most remarkably, the resulting activation energies (disregarding the three outliers) are rather close to each other, ranging from 67.3 to 79.1 kJ/mol. Those results are similar to the ones of S. Joseph, S. Uppalapati & Ö. Cizer (2018; 75.2 ± 6.7 kJ/mol; Joseph et al., 2018). The average value based on temperatures 10°C–20°C is the highest, followed by the one of 10°C–30°C and finally 20°C–30°C. Thus, the apparent activation energy seems to be slightly decreasing for increasing temperature. We conclude that E_a seems related to the nature of the binder and not to the content of the activator for the range studied here.

Compared to a cement paste with an apparent activation energy of 38 kJ/mol, the apparent activation energy of the AASF is much higher (Mounanga et al., 2006). It is also interesting to compare the obtained activation energies for the tested slag-fly ash mixes to mixes with only slag or only fly ash. For alkali-activated slag, E_a was determined as 53.6 kJ/mol (Huanhai et al., 1993), for alkali-activated fly ash with a concentration of NaOH of 8M, it amounted to 83.5 kJ/mol (Nath and Kumar, 2019). Applying a simple “rule of mixture” using the aforementioned literature values for our composition with 50% slag and 50% fly ash, one would end up at an activation energy of 68.6 kJ/mol, which is reasonably close to our average.

3.3.2 Method of rates

As an alternative to the superposition method, the apparent activation energy is determined using the method of rates, as explained in Section 2.3.3 (see Equation 3), see Supplementary Figure S3A,B. In Supplementary Table S1, the mean values of the activation energies, averaged over the interval of heat releases, are listed. The obtained results based on the rate method are virtually equivalent to the results using the superposition method.

3.4 Autogenous strain

Next, AutoShrink test results are studied. Notably, autogenous strains, (excluding strains from thermal deformations, as explained in Section 2.3.2) are set to zero at the beginning of the test, around 1.5 h after the mixing of the pastes, which is the time needed to start the test. Figures 6A,B show the development of the autogenous shrinkage of AASF pastes with different values of S/B and M_s, respectively, over a period of 2 weeks as a function of the equivalent age. Most notably, shrinkage strains for all mixes are rather large, they amount to 3,800–5,000 μm/m after 2 weeks. In general, a paste with a high S/B (and thus a high W/B) exhibits a late onset as well as a reduced magnitude of autogenous shrinkage. The reason is that high W/B induces larger pores, resulting in lower capillary pressures and thus in smaller autogenous shrinkage (Lee et al., 2014). In other terms, densification due to lower W/B, implying a reduction and a refinement of the pores, leads to larger capillary pressures and thus larger shrinkage The autogenous shrinkage slightly increases when the M_s modulus decreases. A smaller M_s also means more NaOH in the composition. As for the results obtained with the compressive strength and the heat release, this higher amount of NaOH leads to a higher pH in the solution and may be at the source of the higher autogenous shrinkage. Similar results were found by Ballekere Kumarappa et al., 2018.

FIGURE 6

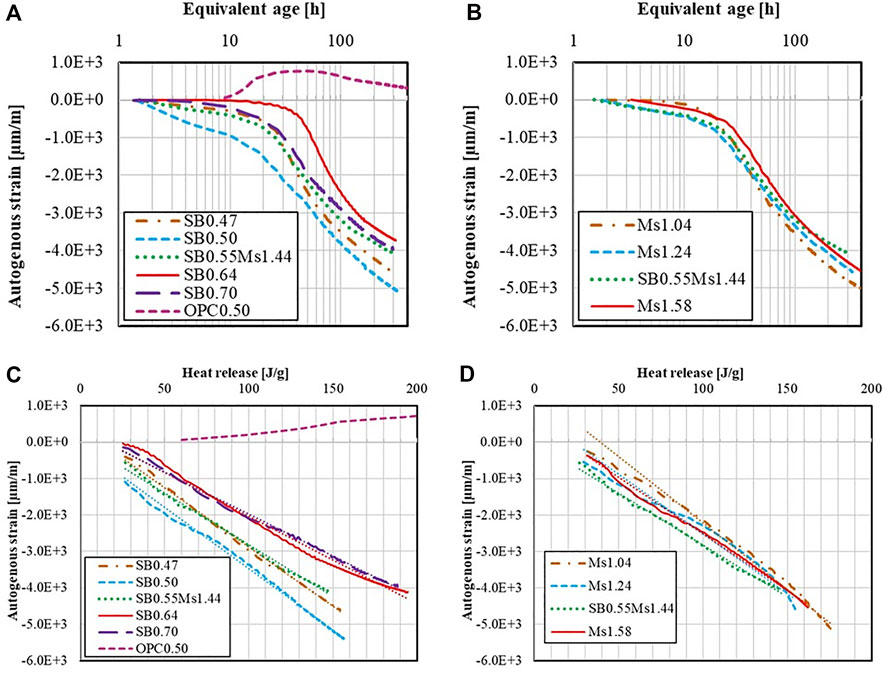
FIGURE 6. Autogenous strains of AASF pastes as a function of the equivalent age with different S/B (A) and with different M_s (B); and as a function of the cumulative heat with different S/B (C) and with different M_s (D).

The autogenous shrinkage of AASF pastes is much higher than that of OPC pastes (Jensen and Hansen, 1999). The chemical shrinkage and finer pore structure are certainly responsible for the change in magnitude (Cartwright et al., 2014; Prabahar et al., 2021; Vafaei et al., 2020). For OPC, some swelling may be observed (as is the case for our mix) just after setting, while there is no swelling for the AASF. In fact, the formation of ettringite in OPC during and after setting causes internal pressure inside the matrix and thus at the macro-scale, swelling (Carette et al., 2018). In AASF paste, no ettringite is formed which may be the reason for the absence of swelling.

As explained in the introduction section, the development of the autogenous shrinkage is associated to the reaction process (formation of finer or more refined capillary pores (Prabahar et al., 2021; Vafaei et al., 2020)) and thus the heat release. In Figures 6A,B, the development of the autogenous shrinkage is plotted according to the heat release. It is observed that the autogenous shrinkage evolved linearly with the heat release for all eight compositions. Thus, the autogenous shrinkage strains ${\epsilon }_{as}\left(t\right)$ may be readily fitted according to:

${\mathit{\epsilon }}_{\mathit{a}\mathit{s}}\left(\mathit{t}\right)=\mathit{S}\bullet \frac{\mathit{Q}\left(\mathit{t}\right)-{\mathit{Q}}_{\mathbf{0}}}{{\mathit{Q}}_{\mathit{\infty }}-{\mathit{Q}}_{\mathbf{0}}}(5)$

With $S$ as proportionality parameter, $Q_0$ is the heat release at the start of the development of autogenous shrinkage, and $Q_{\infty }$ as ultimate heat obtained from isothermal calorimetry measurements as explained in Section 3.2. The parameters $S$ and $Q_0$ are obtained by least-square fitting of the observed relations in Figures 6A,B and are listed in Table 5. The rather excellent agreement of the linear fit with the measurements (quadratic correlation coefficients above R²>96%, see Table 5) may indicate that there is one major reaction occurring that induces autogenous strains when slag and fly ash react with both NaOH and sodium silicate. Also, for the same strain, there is more heat release when the S/B is higher. And for the same heat release, there is less strain for a higher S/B ratio. For most of the compositions, the material parameter $S$ (which is proportional to the slope between the autogenous strain and the heat release) increases when the S/B ratio decreases, see Table 5. When the fitting parameter $S$ is studied as a function of M_s, a maximum emerges at M_s = 1.38. This means that the composition with a lower S/B ratio and the compositions with M_s = 1.38 may exhibit a lower cracking risk: for the same autogenous strain development, less heat is released. However, for a proper analysis of the cracking risk, stiffness, and strength developments would be required (Serdar et al., 2020).

TABLE 5

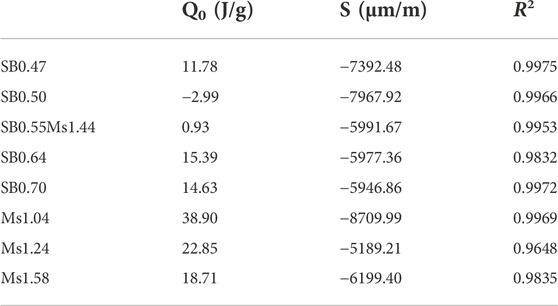
TABLE 5. Fitting parameters Q₀ and S together with the quadratic correlation coefficient R² to describe the linear relation between autogenous strain and cumulative heat release.

3.5 Coefficient of thermal expansion

This section discusses the thermal expansion coefficients (CTE), which are obtained by subtracting the autogenous strain from the measured total strains. Figures 7A,B present the results of the (linear) CTE for each composition as a function of the equivalent age. Interestingly, the CTE increases rapidly until it reaches a peak between 40 and 100 h at magnitudes of 40 μm/m/°C, followed by a moderate decline. The evolution of the CTE and the magnitude of the CTE are both sensitive with respect to S/B and M_s, as detailed next. In general, the CTE starts increasing sooner and the peak of the CTE is higher when S/B and M_s are lower. The ultimate CTE (at ages of 2 weeks and later), however, seems to increase with increasing S/B. Water has a higher CTE than the solids building up the microstructure. This means that when there is less water, the CTE decreases. This explains the fact that CTE of AAM pastes decreases as the W/B ratio decreases (Sellevold and Bjøntegaard, 2006). Also, with higher water content, the E-modulus of the paste is lower and thus the pressure applied by the water for a temperature change causes more significant volume changes. (Königsberger et al., 2018b).

FIGURE 7

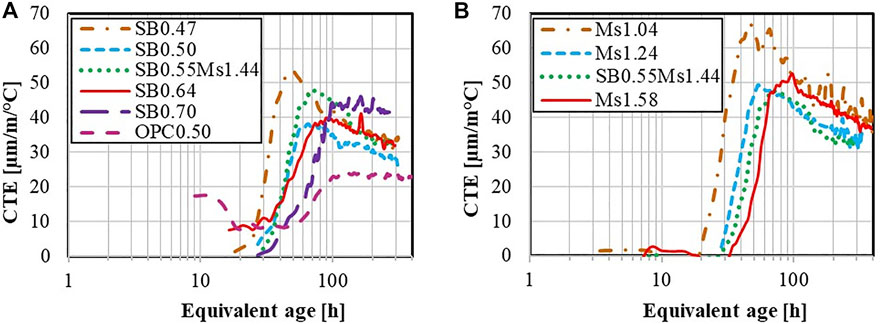
FIGURE 7. Coefficient of thermal expansion of AASF pastes as a function of the equivalent age with different S/B (A) and with different M_s (B).

Compared to an OPC paste with linear CTEs at mature ages amounting to 20–30 μm/m/°C (Königsberger et al., 2018b), the CTE for all measured compositions is significantly larger, an experimental result that raises the question whether traditional steel reinforcements may even be used with the tested AASF compositions, given the expected mismatch of thermal expansion coefficients. Moreover, the CTE evolution is slightly different, see Figure 7A. For OPC, the CTE increases and then remains almost constant, but for an AASF paste, the CTE increases and then it decreases.

3.6 Internal relative humidity

The evolution of internal relative humidity (IRH) is presented as a function of the equivalent age in Figures 8A,B for compositions with different S/B ratios and M_s moduli, respectively. For all compositions, the IRH remains rather high, namely between 94% and 100%. To further analyze the results, the measured IRH is corrected by the relative humidity (RH) above the activator solution, which is therefore measured separately, see Table 6 for the results. The RH above the activator ranges from 92% to 98% which is expected because of the ions dissolved in the water and is thus less than 100%. A slight increase from 92 to 96% is observed when M_s increases, while the dependence on S/B is less clear. We define the IRH change ΔIRH as the IRH of the composition from which the RH above the activator solution is subtracted. The resulting evolutions of ΔIRH are presented in Figures 8C,D for compositions with different S/B ratios and M_s moduli, respectively, and discussed next.

FIGURE 8

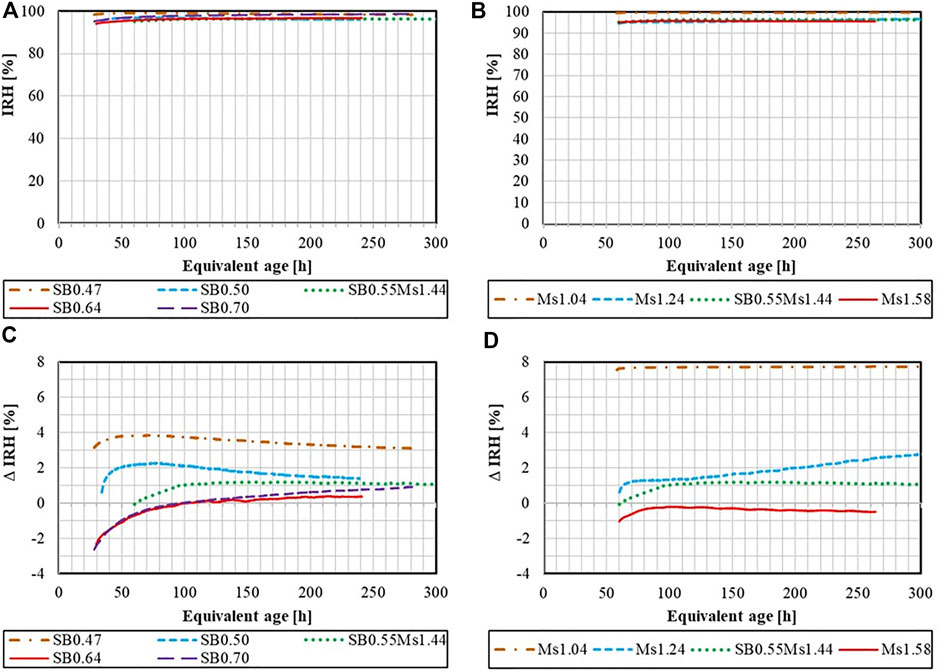
FIGURE 8. Internal relative humidity (IRH) of AASF pastes with different S/B (A) and with different M_s (B); IRH difference ΔIRH (measured RH above activator solution subtracted from the measured IRH evolution of the paste) of AASF pastes with different S/B (C) and with different M_s (D).

TABLE 6

TABLE 6. RH values of the solution of each composition.

At the beginning of the test (between 1 and 2 days), an increase in the IRH (and ΔIRH) is observed for all compositions, which is in line with literature results and is explained by the progressive reduction of the ion concentration in the pore solution during the reaction of slag (Li et al., 2020b) and fly ash (Hu et al., 2020). Thereafter, the IRH either continues to increase or decreases slightly, resulting from several phenomena (Hu et al., 2020), 1) the consumption of pore water leads to a decrease in the IRH (self-desiccation), while 2) the release of water during the polymerization of aluminum and silicate monomers leads to an increase in the IRH, 3) the continuous change of the ion composition and concentration of pore solution also affects the IRH. Our results show that the magnitude and duration of the initial increase depend on the composition. It is faster and yields a pronounced peak for pastes with S/B ≤ 0.55, for which the IRH slowly decreases after the peak, see Figure 8C. This probably is a consequence of the dominating self-desiccation mechanism. For compositions with S/B ≥ 0.64, the IRH continuously increases during the entire measurement interval of 2 weeks, which suggests that self-desiccation is less significant. The RH difference ΔIRH is significantly larger for pastes with small silica modulus M_s, as depicted in Figure 8D. It amounts to roughly 8% for the paste with Ms = 1.04 but is close to zero for the paste with Ms = 1.58.

Next, we attempt to correlate the IRH results to autogenous strain and CTE evolution, see Figures 9A,B as well as Figures 9C,D. In general, the higher ΔIRH of the paste is, the larger are the autogenous strains, see Figure 9A. This may suggest, that despite the minor changes of IRH (or ΔIRH), it can still be, at least very qualitatively, correlated to the shrinkage, suggesting that self-desiccation is an important phenomenon when explaining the high shrinkage observed in these pastes. More pronounced self-desiccation effects on IRH evolution might, in fact, be masked by the changing ion composition and concentration in the activator solution. The IRH does, however, not correlate with the measured CTE evolutions, see Figures 9C,D.

FIGURE 9

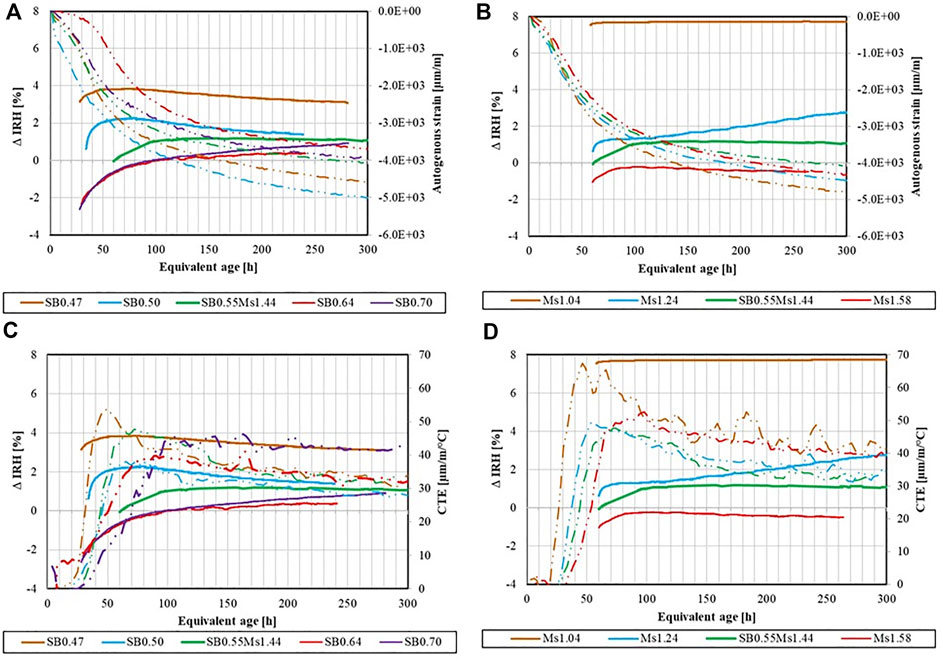
FIGURE 9. Comparison of IRH and autogenous strain with different S/B (A) and with different M_s (B); comparison of IRH and CTE with different S/B (C) and with different M_s (D).

4 Conclusions and outlook

The early-age evolutions of autogenous and thermal strains of alkali-activated slag-fly ash mixes have been experimentally quantified. These tests are accompanied by compressive strength tests, isothermal calorimetry, and internal relative humidity (IRH) tests. Based on the different experiments conducted, several conclusions can be drawn:

• Autogenous shrinkage strains are very high for all eight tested compositions, much higher than in comparable ordinary Portland cement (OPC) paste. The shrinkage is smaller for pastes with a higher solution-to-binder ratio (S/B) and a higher silica modulus (M_s). Most notably, the autogenous strains increase linearly with the cumulative heat, measured using isothermal calorimetry.

• By analogy, thermal strains in AAMs are much higher than in OPC paste. The corresponding coefficient of thermal expansion (CTE) amounts to magnitudes between 30 and 70 μm/m/°C. It is lower for pastes with smaller S/B and smaller M_s. Initially, the CTE increases rapidly for all compositions up to ages of two to 4 days, followed by a slow decrease. The generally very high expansion coefficients as well as the significant changes during the hardening underline the sensitivity of the tested AAMs upon temperature changes and may question their suitability for concrete together with steel reinforcements.

• The compressive strength of the reference AAM mix is smaller at the age of 2 days but is already larger at 7 days, compared to OPC paste with similar water content. In general, strength increases when S/B decreases. The seven-day-strength decreases slightly with increasing M_s.

• The heat flow evolutions exhibit two characteristic peaks. Interestingly, the second peak occurs later (the induction period lasts longer) and is more pronounced for pastes with higher S/B and higher M_s.

• The activation energy, determined by means of isothermal calorimetry tests performed at 10°C, 20°C and 30°C is virtually constant for all compositions, irrespective of S/B and M_s, and amounts to 73.9 kJ/mol.

• The IRH remains above 94% for all compositions up to ages of 2 weeks, despite the large autogenous strains. For pastes with S/B ≤ 0.55, the IRH increases rapidly, reaches a peak at two to 4 days, and then slowly decreases; for pastes with higher S/B, the IRH continuously increases. This may underline counteracting phenomena, self-desiccation (which decreases the IRH during maturation) and a change in ion concentration or composition in the pore solution and/or the release of water during polymerization (which lead to an IRH increase).

The striking linearity between autogenous strains and heat release motivates a deeper analysis of the origin of the shrinkage in AAMs. Therefore, ion composition and concentrations in the pore solution should be measured in parallel to the IRH, particularly during early ages. After all major phenomena are quantified individually, shrinkage predictions using micromechanics modeling can be attempted, based on the evolutions of capillary pore pressures as well as the viscoelastic behavior of the material.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

Experimental work: ML and JG; Data treatment and Discussion: ML, BD and JG; Initial version: JG and BD; Final version: ML, BD, and MK. Review: MK. Supervision: SS.

Funding

This paper is the result of research actions performed in the framework of the FNRS-FWO-EOS project 30439691 ‘INTERdisciplinary multiscale Assessment of a new generation of Concrete with alkali-activated maTerials’ (https://interact.ulb.be/). The financial support by FNRS-FWO-EOS is gratefully acknowledged. The authors acknowledge TU Wien Bibliothek for financial support through its Open Access Funding Programme.

Acknowledgments

The interact project partners from four universities (ULB, KULeuven, UGent, TU Wien) and one institution (VITO) are gratefully acknowledged. The paper has significantly benefited from the discussions during the several meetings organized during the project.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor ZL declared a past co-authorship with the authors BD, SS.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbuil.2022.1085912/full#supplementary-material

References

ASTM (2016). C109/109M-16a, ASTM International, 1–10.

Google Scholar

Bakharev, T., Sanjayan, J. G., and Cheng, Y. B. (2000). Effect of admixtures on properties of alkali-activated slag concrete. Cem. Concr. Res. 30, 1367–1374. doi:10.1016/s0008-8846(00)00349-5

CrossRef Full Text | Google Scholar

Ballekere Kumarappa, D., Peethamparan, S., and Ngami, M. (2018). Autogenous shrinkage of alkali activated slag mortars: Basic mechanisms and mitigation methods. Cem. Concr. Res. 109, 1–9. doi:10.1016/j.cemconres.2018.04.004

CrossRef Full Text | Google Scholar

Ballim, Y., and Graham, P. C. (2009). The effects of supplementary cementing materials in modifying the heat of hydration of concrete. Mat. Struct. 42, 803–811. doi:10.1617/s11527-008-9425-3

CrossRef Full Text | Google Scholar

Ben Haha, M., Le Saout, G., Winnefeld, F., and Lothenbach, B. (2011). Influence of activator type on hydration kinetics, hydrate assemblage and microstructural development of alkali activated blast-furnace slags. Cem. Concr. Res. 41, 301–310. doi:10.1016/j.cemconres.2010.11.016

CrossRef Full Text | Google Scholar

Bendimerad, A. Z., Delsaute, B., Rozière, E., Staquet, S., and Loukili, A. (2020). Advanced techniques for the study of shrinkage-induced cracking of concrete with recycled aggregates at early age. Constr. Build. Mat. 233, 117340. doi:10.1016/j.conbuildmat.2019.117340

CrossRef Full Text | Google Scholar

Benhelal, E., Zahedi, G., Shamsaei, E., and Bahadori, A. (2013). Global strategies and potentials to curb CO2 emissions in cement industry. J. Clean. Prod. 51, 142–161. doi:10.1016/j.jclepro.2012.10.049

CrossRef Full Text | Google Scholar

Bentur, A., and Ish-Shalom, M. (1974). Properties of type K expensive cement of pure components II. Proposed mechanism of ettringite formation and expansion in unrestrained paste of pure expansive component. Cem. Concr. Res. 4, 709–721. doi:10.1016/0008-8846(74)90043-x

CrossRef Full Text | Google Scholar

Bentz, D. P. (1997). Three-dimensional computer simulation of portland cement hydration and microstructure development. J. Am. Ceram. Soc. 80, 3–21. doi:10.1111/j.1151-2916.1997.tb02785.x

CrossRef Full Text | Google Scholar

Bjøntegaard, Ø., Hammer, T. A., and Sellevold, E. J. (2004). On the measurement of free deformation of early age cement paste and concrete. Cem. Concr. Compos. 26, 427–435. doi:10.1016/s0958-9465(03)00065-9

CrossRef Full Text | Google Scholar

Carette, J., Joseph, S., Cizer, Ö., and Staquet, S. (2018). Decoupling the autogenous swelling from the self-desiccation deformation in early age concrete with mineral additions: Micro-macro observations and unified modelling. Cem. Concr. Compos. 85, 122–132. doi:10.1016/j.cemconcomp.2017.10.008

CrossRef Full Text | Google Scholar

Cartwright, C., Rajabipour, F., and Radlińska, A. (2014). Shrinkage characteristics of alkali-activated slag cements. J. Mat. Civ. Eng. 27, 27. doi:10.1061/(asce)mt.1943-5533.0001058

CrossRef Full Text | Google Scholar

CEN (2016). EN 196-1:2016. European Committee for Standardization.

Google Scholar

Chi, M., and Huang, R. (2013). Binding mechanism and properties of alkali-activated fly ash/slag mortars. Constr. Build. Mat. 40, 291–298. doi:10.1016/j.conbuildmat.2012.11.003

CrossRef Full Text | Google Scholar

Collins, F., and Sanjayan, J. G. (2000). Effect of pore size distribution on drying shrinking of alkali-activated slag concrete. Cem. Concr. Res. 30, 1401–1406. doi:10.1016/s0008-8846(00)00327-6

CrossRef Full Text | Google Scholar

Craeye, B., De Schutter, G., Desmet, B., Vantomme, J., Heirman, G., Vandewalle, L., et al. (2010). Effect of mineral filler type on autogenous shrinkage of self-compacting concrete. Cem. Concr. Res. 40, 908–913. doi:10.1016/j.cemconres.2010.01.014

CrossRef Full Text | Google Scholar

Dai, X., Aydın, S., Yardımcı, M. Y., Lesage, K., and De Schutter, G. (2020). Effects of activator properties and GGBFS/FA ratio on the structural build-up and rheology of AAC. Cem. Concr. Res. 138, 106253. doi:10.1016/j.cemconres.2020.106253

CrossRef Full Text | Google Scholar

Damtoft, J. S., Lukasik, J., Herfort, D., Sorrentino, D., and Gartner, E. M. (2008). Sustainable development and climate change initiatives. Cem. Concr. Res. 38, 115–127. doi:10.1016/j.cemconres.2007.09.008

CrossRef Full Text | Google Scholar

J. Davidovits (Editor) (2005). Green chemistry and sustainable development solutions (France: Institut Géopolymère).

Google Scholar

De Vargas, A. S., Dal Molin, D. C. C., Masuero, Â. B., Vilela, A. C. F., Castro-Gomes, J., and Gutierrez, R. M. (2014). Strength development of alkali-activated fly ash produced with combined NaOH and Ca(OH)2 activators. Cem. Concr. Compos. 53, 341–349. doi:10.1016/j.cemconcomp.2014.06.012

CrossRef Full Text | Google Scholar

Delsaute, B. (2016). New approach for monitoring and modelling of the creep and shrinkage behaviour of cement pastes, mortars and concretes since setting time. Available at: https://tel.archives-ouvertes.fr/tel-01565742.

Google Scholar

Delsaute, B., and Staquet, S. (2017). Decoupling thermal and autogenous strain of concretes with different water/cement ratios during the hardening process. Adv. Civ. Eng. Mat. 6, 20160063. doi:10.1520/acem20160063

CrossRef Full Text | Google Scholar

Delsaute, B., and Staquet, S. (2019). Development of strain-induced stresses in early age concrete composed of recycled gravel or sand. J. Adv. Concr. Technol. 17, 319–334. doi:10.3151/jact.17.319

CrossRef Full Text | Google Scholar

Delsaute, B., and Staquet, S. (2020). Impact of recycled sand and gravels in concrete on volume change. Constr. Build. Mat. 232, 117279. doi:10.1016/j.conbuildmat.2019.117279

CrossRef Full Text | Google Scholar

Esping, O. (2008). Effect of limestone filler BET(H2O)-area on the fresh and hardened properties of self-compacting concrete. Cem. Concr. Res. 38, 938–944. doi:10.1016/j.cemconres.2008.03.010

CrossRef Full Text | Google Scholar

E. M. R. Fairbairn, and M. Azenha (Editors) (2018). Thermal cracking of massive concrete structures (Cham, Switzerland: Springer/RILEM). State of the Art Report of the RILEM Technical Committee 254-CMS.

Google Scholar

Fang, G., Bahrami, H., and Zhang, M. (2018). Mechanisms of autogenous shrinkage of alkali-activated fly ash-slag pastes cured at ambient temperature within 24 h. Constr. Build. Mat. 171, 377–387. doi:10.1016/j.conbuildmat.2018.03.155

CrossRef Full Text | Google Scholar

Feret, R. (1892). Sur la compacité des mortiers hydrauliques (On the compactness of hydraulic mortars). Ann. Des. Ponts Chaussées 7 (4), 5–164.

Google Scholar

Gao, X., Yu, Q. L., and Brouwers, H. J. H. (2015). Reaction kinetics, gel character and strength of ambient temperature cured alkali activated slag–fly ash blends. Constr. Build. Mat. 80, 105–115. doi:10.1016/j.conbuildmat.2015.01.065

CrossRef Full Text | Google Scholar

Germann Instruments (2015). Auto-Shrink Installation manual single system. Copenhagen: Germann Instruments.

Google Scholar

Han, F., He, X., Zhang, Z., and Liu, J. (2017). Hydration heat of slag or fly ash in the composite binder at different temperatures. Thermochim. Acta 655, 202–210. doi:10.1016/j.tca.2017.07.002

CrossRef Full Text | Google Scholar

Hojati, M., and Radlińska, A. (2017). Shrinkage and strength development of alkali-activated fly ash-slag binary cements. Constr. Build. Mat. 150, 808–816. doi:10.1016/j.conbuildmat.2017.06.040

CrossRef Full Text | Google Scholar

Hu, Z., Wyrzykowski, M., and Lura, P. (2020). Estimation of reaction kinetics of geopolymers at early ages. Cem. Concr. Res. 129, 105971. doi:10.1016/j.cemconres.2020.105971

CrossRef Full Text | Google Scholar

Huanhai, Z., Xuequan, W., Zhongzi, X., and Mingshu, T. (1993). Kinetic study on hydration of alkali-activated slag. Cem. Concr. Res. 23, 1253–1258. doi:10.1016/0008-8846(93)90062-e

CrossRef Full Text | Google Scholar

Jang, J. G., Lee, N. K., and Lee, H. K. (2014). Fresh and hardened properties of alkali-activated fly ash/slag pastes with superplasticizers. Constr. Build. Mat. 50, 169–176. doi:10.1016/j.conbuildmat.2013.09.048

CrossRef Full Text | Google Scholar

Jensen, O. M., and Hansen, P. F. (1999). Influence of temperature on autogenous deformation and relative humidity change in hardening cement paste. Cem. Concr. Res. 29 (4), 567–575. doi:10.1016/s0008-8846(99)00021-6

CrossRef Full Text | Google Scholar

Joseph, S., and Cizer, Ö. (2022). Comparative analysis of heat release, bound water content and compressive strength of alkali-activated slag-fly ash. Front. Mat. 9. doi:10.3389/fmats.2022.861283

CrossRef Full Text | Google Scholar

Joseph, S., Uppalapati, S., and Cizer, Ö. (2018). Instantaneous activation energy of alkali activated materials. RILEM Tech. Lett. 3, 121–123. doi:10.21809/rilemtechlett.2018.78

CrossRef Full Text | Google Scholar

Königsberger, M., Delsaute, B., and Staquet, S. (2018). “Thermo-poro-micromechanics of cementitious materials: Hydration-induced evolution of thermal,” in 18th Int Conf Exp Mech ICEM18., Brussels

Google Scholar

Königsberger, M., Hlobil, M., Delsaute, B., Staquet, S., Hellmich, C., and Pichler, B. (2018). Hydrate failure in ITZ governs concrete strength: A micro-to-macro validated engineering mechanics model. Cem. Concr. Res. 103, 77–94. doi:10.1016/j.cemconres.2017.10.002

CrossRef Full Text | Google Scholar

Kua, T. A., Imteaz, M. A., Arulrajah, A., and Horpibulsuk, S. (2019). Environmental and economic viability of Alkali Activated Material (AAM) comprising slag, fly ash and spent coffee ground. Int. J. Sustain. Eng. 12 (4), 223–232. doi:10.1080/19397038.2018.1492043

CrossRef Full Text | Google Scholar

Le Chatelier, H. (1900). Sur les changements de volume qui accompagnent le durcissement des ciments. Bull. la Société l’Encouragement l’Industrie Natl. 5, 54–57.

Google Scholar

Lee, N. K., Jang, J. G., and Lee, H. K. (2014). Shrinkage characteristics of alkali-activated fly ash/slag paste and mortar at early ages. Cem. Concr. Compos. 53, 239–248. doi:10.1016/j.cemconcomp.2014.07.007

CrossRef Full Text | Google Scholar

Li, Z., Lu, T., Liang, X., Dong, H., and Ye, G. (2020). Mechanisms of autogenous shrinkage of alkali-activated slag and fly ash pastes. Cem. Concr. Res. 135, 106107. doi:10.1016/j.cemconres.2020.106107

CrossRef Full Text | Google Scholar

Li, Z., Wyrzykowski, M., Dong, H., Granja, J., Azenha, M., Lura, P., et al. (2020). Internal curing by superabsorbent polymers in alkali-activated slag. Cem. Concr. Res. 135, 106123. doi:10.1016/j.cemconres.2020.106123

CrossRef Full Text | Google Scholar

Lu, C., Zhang, Z., Shi, C., Li, N., Jiao, D., and Yuan, Q. (2021). Rheology of alkali-activated materials: A review. Cem. Concr. Compos. 121, 104061. doi:10.1016/j.cemconcomp.2021.104061

CrossRef Full Text | Google Scholar

Ma, J., and Dehn, F. (2017). Investigations on the coefficient of thermal expansion of a low-calcium fly ash-based geopolymer concrete. Struct. Concr. 18, 781–791. doi:10.1002/suco.201600211

CrossRef Full Text | Google Scholar

Ma, Y., and Ye, G. (2015). The shrinkage of alkali activated fly ash. Cem. Concr. Res. 68, 75–82. doi:10.1016/j.cemconres.2014.10.024

CrossRef Full Text | Google Scholar

Marjanović, N., Komljenović, M., Baščarević, Z., Nikolić, V., and Petrović, R. (2015). Physical-mechanical and microstructural properties of alkali-activated fly ash-blast furnace slag blends. Ceram. Int. 41, 1421–1435. doi:10.1016/j.ceramint.2014.09.075

CrossRef Full Text | Google Scholar

Medaets, M., and Lambrette, N. (2014). Early behaviour of green concretes in cold and hot conditions. Brussels: Université libre de Bruxelles.

Google Scholar

Mehta, P. K. (1973). Mechanism of expansion associated with ettringite formation. Cem. Concr. Res. 3, 1–6. doi:10.1016/0008-8846(73)90056-2

CrossRef Full Text | Google Scholar

Moon, H., Ramanathan, S., Suraneni, P., Shon, C. S., Lee, C. J., and Chung, C. W. (2018). Revisiting the effect of slag in reducing heat of hydration in concrete in comparison to other supplementary cementitious materials. Mater. (Basel) 11, 1847. doi:10.3390/ma11101847

PubMed Abstract | CrossRef Full Text | Google Scholar

Mounanga, P., Baroghel-Bouny, V., Loukili, A., and Khelidj, A. (2006). Autogenous deformations of cement pastes: Part I. Temperature effects at early age and micro-macro correlations. Cem. Concr. Res. 36, 110–122. doi:10.1016/j.cemconres.2004.10.019

CrossRef Full Text | Google Scholar

Nath, S. K., and Kumar, S. (2019). Role of alkali concentration on reaction kinetics of fly ash geopolymerization. J. Non. Cryst. Solids 505, 241–251. doi:10.1016/j.jnoncrysol.2018.11.007

CrossRef Full Text | Google Scholar

Nedeljković, M., Li, Z., and Ye, G. (2018). Setting, strength, and autogenous shrinkage of alkali-activated fly ash and slag pastes: Effect of slag content. Mater. (Basel) 11 (11), 2121. doi:10.3390/ma11112121

PubMed Abstract | CrossRef Full Text | Google Scholar

Olivier, J. G. J., Janssens-Maenhout, G., Munteam, M., and Peters, J. (2015). Trends in global CO₂ emissions: 2015 report. The Hague: PBL Netherlands Environmental Assessment Agency; Ispra: European Commission.

Google Scholar

Ouyang, X., Ma, Y., Liu, Z., Liang, J., and Ye, G. (2020). Effect of the sodium silicate modulus and slag content on fresh and hardened properties of alkali-activated fly ash/slag. Minerals 10, 15. doi:10.3390/min10010015

CrossRef Full Text | Google Scholar

Prabahar, J., Vafaei, B., Baffoe, E., and Ghahremaninezhad, A. (2021). The effect of biochar on the properties of alkali-activated slag pastes. Constr. Mater. 2 (1), 1–14. doi:10.3390/constrmater2010001

CrossRef Full Text | Google Scholar

J. L. Provis, and J. S. J. van Deventer (Editors) (2014). Alkali activated materials, state-of-the-art report (Dordrecht, Netherlands: Springer/RILEM). RILEM TC 224-AAM.

Google Scholar

Rashad, A. M. (2013). Properties of alkali-activated fly ash concrete blended with slag. Iran. J. Mater Sci. Eng. 10, 57–64.

Google Scholar

Saleh Mohamed, M., and Wauters, M. (2016). Influence of the water/cement ratio and the nature of binder on the early age mechanical behaviour of cement based materials by means of multi-scale monitoring. Master’s thesis. Université libre de Bruxelles.

Google Scholar

Sellevold, E. J., and Bjøntegaard, Ø. (2006). Coefficient of thermal expansion of cement paste and concrete: Mechanisms of moisture interaction. Mat. Struct. 39, 809–815. doi:10.1617/s11527-006-9086-z

CrossRef Full Text | Google Scholar

M. Serdar, I. Gabrijel, D. Schlicke, S. Staquet, and M. Azenha (Editors) (2020). Advanced techniques for testing of cement-based materials Cham: Springer.

Google Scholar

Shen, W., Wang, Y., Zhang, T., Zhou, M., Li, J., and Cui, X. (2011). Magnesia modification of alkali-activated slag fly ash cement. J. Wuhan. Univ. Technol. -Mat. Sci. Ed. 26, 121–125. doi:10.1007/s11595-011-0182-8

CrossRef Full Text | Google Scholar

Shi, C., Roy, D., and Krivenko, P. (2006). Alkali-activated cements and concretes. London: Taylor and Francis: CRC Press. doi:10.1201/9781482266900

CrossRef Full Text | Google Scholar

TA Instruments (2013). Tam air isothermal calorimetry, New Castle: TA Instruments.

Google Scholar

TA Instruments (2019). TAM air – TA Instruments. Available at: https://www.tainstruments.com/wp-content/uploads/TAM AIR brochure.pdf.

Google Scholar

Taplin, J. H. (1959). A method for following the hydration reaction in Portland cement paste. Aust. J. Appl. Sci. 10, 329–345.

Google Scholar

Thomson, S. W. (1871). On the equilibrium of vapour at a curved surface of liquid. Lond. Edinb. Dublin Philosophical Mag. J. Sci. 42, 448–452. doi:10.1080/14786447108640606

CrossRef Full Text | Google Scholar

Uppalapati, S., and Cizer, Ö. (2018). “Understanding the autogenous shrinkage in alkali-activated slag/fly-ash blends,” in Int Conf Alkali Act Mater Geopolymers Versatile Mater Offer High Perform Low Emiss, Tomar.

Google Scholar

Vafaei, B., Farzanian, K., and Ghahremaninezhad, A. (2020). The influence of superabsorbent polymer on the properties of alkali-activated slag pastes. Constr. Build. Mat. 236, 117525. doi:10.1016/j.conbuildmat.2019.117525

CrossRef Full Text | Google Scholar

Wang, S. D., Scrivener, K. L., and Pratt, P. L. (1994). Factors affecting the strength of alkali-activated slag. Cem. Concr. Res. 24, 1033–1043. doi:10.1016/0008-8846(94)90026-4

CrossRef Full Text | Google Scholar

Ye, H., and Radlińska, A. (2016). Fly ash-slag interaction during alkaline activation: Influence of activators on phase assemblage and microstructure formation. Constr. Build. Mat. 122, 594–606. doi:10.1016/j.conbuildmat.2016.06.099

CrossRef Full Text | Google Scholar

Ye, H., and Radlińska, A. (2017). Shrinkage mitigation strategies in alkali-activated slag. Cem. Concr. Res. 101, 131–143. doi:10.1016/j.cemconres.2017.08.025

CrossRef Full Text | Google Scholar

Yssorche-Cubaynes, M. P., and Ollivier, J. P. (1999). La microfissuration d’autodessiccation et la durabilité des BHP et BTHP. Mater Struct. Constr. 32 (215), 14–21.

CrossRef Full Text | Google Scholar