Analysis and design of non-linear seismic isolation systems for building structures—An overview

Zhu, Yun-Peng; Lang, Z. Q.; Fujita, Kohei; Takewaki, Izuru

doi:10.3389/fbuil.2022.1084081

REVIEW article

Front. Built Environ., 05 January 2023

Sec. Earthquake Engineering

Volume 8 - 2022 | https://doi.org/10.3389/fbuil.2022.1084081

This article is part of the Research Topic Horizons in Built Environment 2022 View all 6 articles

Analysis and design of non-linear seismic isolation systems for building structures—An overview

Yun-Peng Zhu¹

Z. Q. Lang²*

Kohei Fujita³

Izuru Takewaki³

¹School of Engineering and Material Science, Queen Mary University of London, London, United Kingdom
²Department of Automatic Control and Systems Engineering, The University of Sheffield, Sheffield, United Kingdom
³Department of Architecture and Architectural Engineering, Kyoto University, Kyoto, Japan

In this paper, the development of non-linear building isolation systems is overviewed. The study summarizes commonly used linear building isolation systems in two categories, which are building base isolation systems and building inter-storey isolation systems. Typical isolators including Lead-Rubber Bearings Friction Pendulum Bearings inter-storey viscous damper and Tuned Mass Damper are reviewed. The analysis and design of linear building isolation systems are also reported. After that, non-linear building isolation systems are introduced from two aspects based on their dynamic characteristics. They are (i) non-linear stiffness isolators including Quasi-Zero Stiffness isolators and Non-linear Energy Sink and (ii) non-linear damping isolators including power-law viscous dampers and magnetorheological dampers. Practical implementations of these non-linear isolators are introduced. Finally, the analysis and design of non-linear building isolation systems are discussed. Traditional equivalent linearization approaches and advanced non-linear frequency design approaches are introduced. The promising applications of the non-linear frequency design approaches to building isolation systems are also demonstrated in this review paper.

1 Introduction

Severe earthquakes often result in significant damage to buildings, infrastructures, and cause casualties. For example, the 2011 Tohoku Earthquake in Japan caused over 20,000 deaths and missing, and 190,000 buildings were damaged (Okada et al., 2011; Takewaki et al., 2011). Protecting building structures under earthquakes is of great concern in earthquake-prone countries (Mazzolani, 2001; Azinovic et al., 2016; Tesfamariam, 2022; Zhang et al., 2022). To address this challenge, building isolation systems are applied to mitigate seismic hazards (Morgan, 2007; Mohammed and Mohd, 2011; Takewaki et al., 2013). The aim of applying building isolation is to reduce either the storey or inter-storey vibrations transmitted from the seismic ground motions (Hu, 2014). In practice, two types of passive building isolation systems are commonly used, which are the base isolation system (Jangid and Datta, 1995; Deb, 2004) and the super-structure isolation system, including the inter-storey isolation (De Domenico et al., 2019; Dona et al., 2022) and top floor isolation (Thakur, and Pachpor, 2012), as illustrated in Figure 1.

FIGURE 1

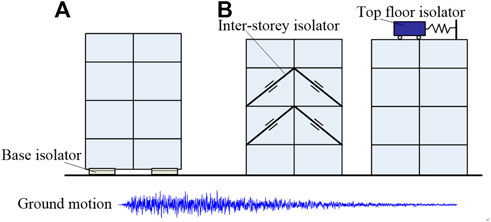
FIGURE 1. Building isolation systems (A) Base isolation system, (B) Super-structure isolation system.

In order to reduce the effects of ground motions on the whole building structure, base isolation was applied to decouple the upper structure from the ground (Akehashi et al., 2018; De Luca and Guidi, 2019). In practice, Lead-Rubber Bearings (LRB) (Jangid, 2007) and Friction Pendulum Bearings (FPB) (Chen and Jia, 2021) are commonly used to implement building base isolation systems. Both LRB and FPB produce soft stiffness to isolate earthquakes and mitigate transmitted seismic energy by friction effects (Cardone et al., 2009; Deringol and Guneyisi, 2020). Friction dampers are often applied to inter-storey isolation to mitigate the relative displacement between two storeys of the building (Lee et al., 2008; Zhang et al., 2017). In addition, the top floor isolation is often implemented by a Tuned Mass Damper (TMD) to absorb vibration energies (Chey et al., 2010; Ghaedi et al., 2017). Detailed reviews of the existing building isolation systems are as follows.

1.1 Base isolation systems

LRB is one of the most commonly used base isolators in practice. An LRB is composed of laminated rubber layers with reinforced steel plates, and a central lead core providing damping to the building structure due to the large shear deformation (Figure 2A) (Kunde and Jangid, 2003; Zordan et al., 2014). The LRB was first invented in New Zealand in 1975 and has been applied to many building structures worldwide (Komuro et al., 2005; Providakis, 2008; Komur, 2016). For example, the Shimizu Corporation Tokyo Headquarters, one of the city’s leading office buildings in Japan, applied 32 LRB and 10 NRB (Natural Rubber Bearings) to achieve a structure natural period of 5.40s (Shimazaki and Nakagawa, 2015). Christchurch Women’s Hospital in New Zealand was well protected by 41 LRB base isolators in the 2010 Darfield (Canterbury) earthquake (Gavin and Wilkinson, 2010).

FIGURE 2

FIGURE 2. Building base isolation systems (A) LRB, (B) FPB, (C) The force-displacement relation.

On the other hand, a similar type of base isolators known as the FPB was developed as shown in Figure 2B to improve the restoring capacity and durability of base isolation systems (Wang, 2002). An FPB is composed of two curved sliding surfaces providing horizontal restoring force and a hemispherical slider between the two sliding surfaces (Peng et al., 2022). The FPB base isolation systems are widely applied to solve the difficulties in isolating large displacements using LRB (Drozdov et al., 2007; Kravchuk et al., 2008; Chen and Xiong, 2022). For example, the world’s largest FPB with a 4 m diameter was installed on the Benicia Martinez Bridge in United States (Kravchuk et al., 2008). The international airport of San Francisco where 267 FPB base isolators have been in operation can bear earthquakes of up to eight Richter scale (Drozdov et al., 2007).

Both the LRB and FPB isolators have the same type of bi-linear force-displacement characteristics as illustrated in Figure 2C, where $k_{e}$ is the initial bearing elastic stiffness; $k_{d}$ is the post-yield stiffness,; $k_{eff}$ is the effective stiffness; $F_{y}$ ; $D_{y}$ are the yield strength and yield deformation of the bearing, respectively; $F_{m}$ ; $D_{m}$ are the maximum force and displacement of the bearing, respectively (Ozdemir, 2015).

In practice, the stiffness and damping of the LRB and FPB are often linearized, so that linear system theories can be applied to the analysis and design of bearing-based building base isolation systems (Syed, 2011; Ye et al., 2019; De Domenico et al., 2020). For example, linear static analysis and linear response spectrum analysis were applied to the design of multi-storey buildings in Banglades (Syed, 2011). Ye et al. (2019) proposed a direct-displacement based design procedure for the LRB base isolation systems based on the equivalent linearization of base-isolated building structures. De Domenico et al. (2020) applied tuned fluid inerters to structures with friction pendulum isolators based on system linearization approaches. Other bearing base isolation systems including High Damping Rubber Bearing (HDRB) (Dezfuli and Alam, 2016), Sliding LRB (Zheng et al., 2020) were developed based on the LRB and FPB to improve the building isolation performance under earthquakes.

1.2 Super-structure isolation systems

Reducing inter-storey displacements during earthquakes is important to prevent large deformations of buildings (Valente and Milani, 2018). This is often resolved by applying energy dissipation or vibration absorption devices to building storeys (Symans et al., 2008). A common practice is to use inter-storey isolators. For example, Ryan and Earl (2010) applied LRB to conduct inter-storey isolations as shown in Figure 3A De Domenico et al. (2019) introduced various inter-storey isolation systems based on Fluid Viscous Dampers (FVD) in Figure 3B. Palacios-Quinonero et al. (2019) applied multiple TMD to inter-storey isolation and adjacent building isolations as illustrated in Figure 3C. Viscous dampers are also applied to adjacent building isolations in Figure 3D by Kasagi et al. (2016), Fukumoto and Takewaki (2017), Hayashi et al. (2018), Makita et al. (2018), Kawai et al. (2020, 2021), Nakamura et al. (2021).

FIGURE 3

FIGURE 3. Inter-storey building isolation systems.

The design and arrangement of inter-storey dampers were studied including the optimization of the values, numbers, and position of the dampers (Singh and Moreschi, 2001; Fujita et al., 2010; Uemura et al., 2021; Akehashi and Takewaki, 2022a). The design optimization problem can be formulated as (De Domenico et al., 2019)

\min_{c_{j}} J (c_{j}) s u b j e c t t o g (c_{j}) \leq \bar{g}

where $J (c_{j})$ is the objective function depends on damping coefficients $c_{j}, j \in Z^{+}$ and $g (c_{j})$ is a constraint.

In general, there are various options to determine the objective function for system design. These may include the maximum top floor or inter-storey displacement (Constantinou and Tadjbakhsh, 1983), the total mechanical energy of the system (Gorgoze and Muller, 1992), transfer function amplitudes (Takewaki, 1997), life-cycle costs (Gidaris and Taflanidis, 2015), and damper costs (De Domenico and Hajirasouliha, 2021), etc. Evolutionary approaches and Pareto front were applied to solve the optimization problem, as well as determine the optimal placement of the inter-storey isolators based on a single bay model (Lavan and Dargush, 2009). Distribution of isolators among different bays was also investigated by researchers (Mezzi, 2010; Whittle et al., 2012; Takewaki and Akehashi, 2021). For example, Mezzi (2010) investigated seven different configurations of energy-dissipating braces for an 18-storey reinforced concrete frame, showing that random distributions of isolators in Figure 4A can offer better isolation performance than conventional regular distributions as illustrated in Figure 4B. However, the optimization of such complex decision problems is still challenging.

FIGURE 4

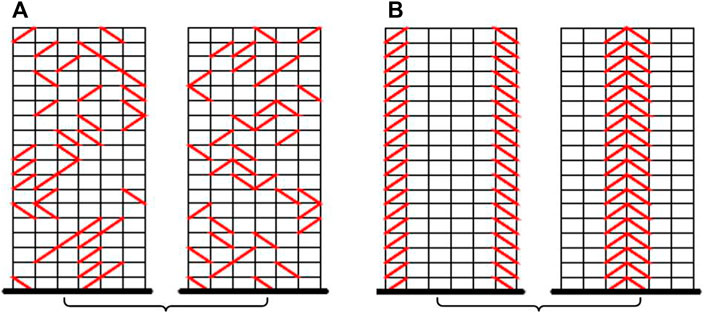
FIGURE 4. Distribution of inter-storey building isolators: (A) Random distribution, (B) Regular distribution.

Existing analysis and design of building isolation systems are often based on the linear or bi-linear characteristics of isolators, which often have limited performance in isolating near-fault earthquakes compared with far-fault long-period earthquakes (Providakis, 2009; Gur et al., 2014; Ozuygur and Noroozinejad Farsangi, 2021; Akehashi and Takewaki, 2022b). Near-fault earthquakes often contain extensive pulses and high-frequency vibrations can be amplified to the super-structures by linear base isolation systems as illustrated in Figure 5 (Ho et al., 2018). Developing non-linear base isolation systems can solve these challenges and deal with both near and far-fault earthquakes. For example, the optimal acceleration transmissibility shown in Figure 5 can be achieved by applying power-law non-linear damping based building base isolation system (Ho et al., 2018). Non-linear dampers applied to inter-storey isolation systems also have better performance in reducing inter-storey drifts than linear dampers (Fujita et al., 2014).

FIGURE 5

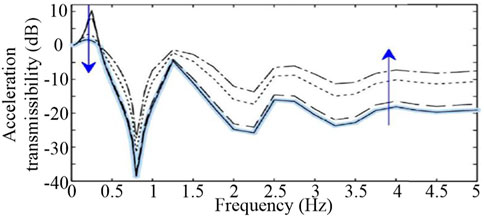
FIGURE 5. Acceleration transmissibility from ground motion to the isolation layer of the 10-storeys Sosokan building in Japan, where the linear damping $c_{1}$ (solid) < $c_{2}$ (dashed) < $c_{3}$ (dotted) < $c_{4}$ (dot-dashed). The optimal transmissibility line is notated by the thick pale blue line.

Therefore, developing non-linear building isolation systems, as well as systematic analysis and design approaches, is necessary for the development of the next-generation’s building isolation systems. Current research on the development of non-linear building isolation systems will be reviewed in the following sections.

2 Non-linear stiffness for building isolation

2.1 The quasi-zero stiffness isolator

The QZS isolator enables an isolation system to achieve low resonance in vibration while keep a high supporting capacity in static scenarios, which has demonstrated great advantages especially in solving low-frequency vibration isolation problems (Niu et al., 2013; Li et al., 2020; Yan et al., 2022). The QZS is a non-linear mount composed of a negative stiffness component and a positive stiffness component as shown in Figure 6A, where $k_{v}$ ; $k_{h}$ are the vertical and horizontal stiffness, respectively; $l_{v}$ ; $l_{h}$ are the length of the vertical and horizontal spring under the load $f$ . The force-displacement ( $F - D$ ) characteristic of a QZS is illustrated in Figure 6B, showing the high static ( $k_{v}$ ) low dynamic ( $k_{d}$ ) stiffness property.

FIGURE 6

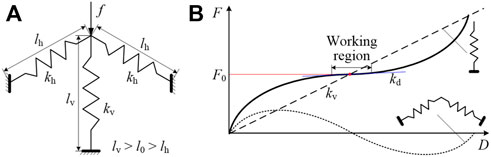
FIGURE 6. The mechanism of the QZS (A) The QZS structure; (B) The force-displacement relation of the QZS.

In practice, there are many ways to realize a QZS isolation system. For example, a QZS can be simply achieved by using a disk spring shown in Figure 7A (Zhou et al., 2022). Dai et al. (2018) and Chai et al. (2022) developed a series of bio-inspired QZS isolators as illustrated in Figure 7B, which have been applied to solve vibration isolation problems in vehicle suspensions (Feng and Jing, 2019) and hand-held jackhammers (Jing et al., 2019). A convex ball-roller mechanism was developed to enable QZS isolation for rotor systems in Figure 7C (Zhang et al., 2020). Buckled beams can naturally produce negative stiffness in Figure 7D (Liu et al., 2013), and U-shape beam structures were developed and applied to building base isolation systems as demonstrated in Figure 7E (Ene et al., 2016).

FIGURE 7

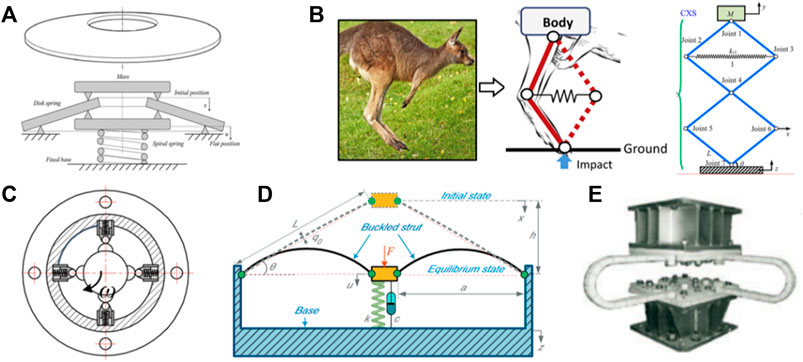
FIGURE 7. Different types of QZS isolation systems (A) The disk spring; (B) The bio-inspired QZS; (C) The torsional QZS; (D) The buckled beams; (E) The U shape QZS.

In building isolation systems, the QZS isolators are often applied to isolate vertical vibrations that are frequently observed in near-fault seismic events (Liu et al., 2018). Zhou et al. (2019) studied the base isolation of a 3-dimensional 7-storey frame concrete building by using both the disk spring with QZS and the equivalent linear spring. The results demonstrate a significant acceleration reduction of the building structure at the expense of a slight increase in displacement response compared to a fixed seismic isolation system in Figure 8.

FIGURE 8

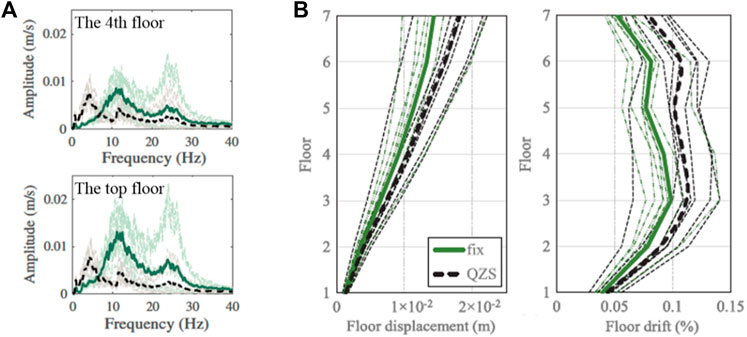
FIGURE 8. The acceleration reduction and displacement responses of a 7-storey building system (A) The accelerations of the fourth and the top floor; (B) The floor displacements and drifts.

Chen et al. (2022) developed an integrated QZS system composed of horizontal spring and LRB damper to isolate horizontal seismic input to buildings (Figure 9A). The schemes of QZS based vertical and horizontal isolation systems are shown in Figure 9B. In addition, Liu et al. (2020) developed a novel 3-dimensional seismic isolator combining the QZS system to prevent the vertical and rotational vibration of buildings. Valeev et al. (2019) reported a two-component material with the QZS property for building vibration isolation (Figure 9C).

FIGURE 9

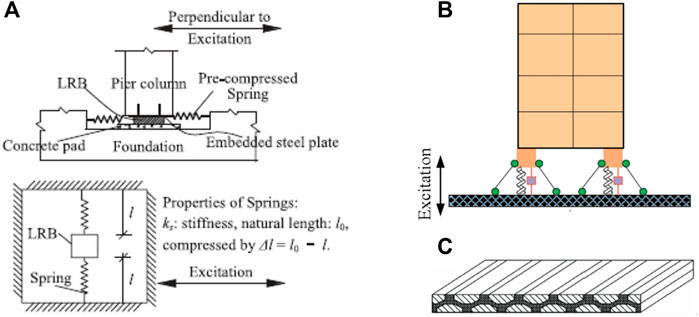
FIGURE 9. The QZS based building isolation systems (A) The horizontal QZS isolation system; (B) The vertical QZS isolation system; (C) The QZS material.

2.2 Non-linear energy sink

The TMD has been used as a vibration absorber in high-rise buildings and landscape towers such as Shanghai Tower (632 m high) (Zhou et al., 2018), Taipei 101 Tower (508 m high), New York Citicorp Center (279 m high), Boston John Hancock Tower (457 m high), and Sydney Tower (305 m high) (Chung et al., 2013). However, a TMD only works for a particular modal frequency of the building over a narrow frequency band (Saidi et al., 2006). The tuning strategy of a TMD is vitally important but usually complex due to the complexity of building structures (Ferreira et al., 2018).

To address the issues in linear TMD isolation systems, a series of non-linear TMD systems were developed (Alexander and Schilder, 2009). One of the most commonly studied non-linear TMD is the NES (Gomez et al., 2021). A typical NES is shown in Figure 10A, which integrates the TMD and QZS to achieve wider damping frequency and better robustness without increasing the resonance peak (Ding and Chen, 2020). Gourdon et al. (2007) compared the vibration isolation performance of a 2-Degree of Freedom (2DoF) system by using NES and TMD and the results indicate the NES has much better isolation performance than linear TMD as shown in Figure 10B. If the vertical damper of the NES is replaced by a linear spring, the system becomes a KDamping isolation system as shown in Figure 10C, which has been applied to energy absorption of vehicle vibrations (Papaioannou et al., 2019) and seismic isolation of bridges (Sapountzakis et al., 2016).

FIGURE 10

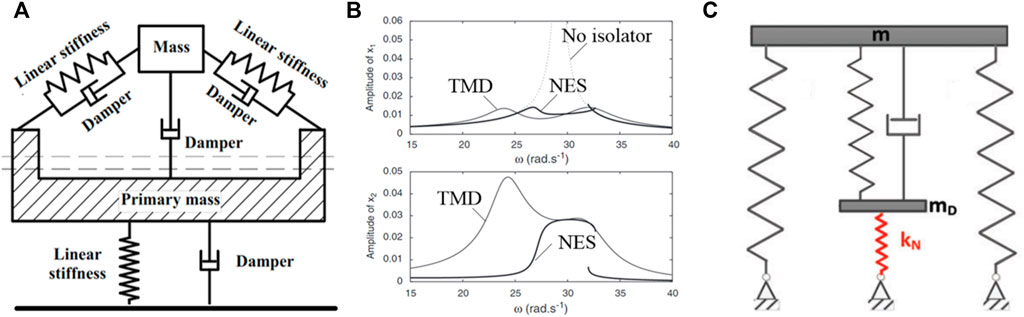
FIGURE 10. The NES isolation system and KDamper (A) The NES structure; (B) Comparison of the NES and the TMD; (C) The KDamper.

Recently, Wang et al. (2020) applied a track NES to the top of a 32-storey high-rise building, showing that a track NES is robust against changes in structural stiffness and maintains high energy absorption efficiency of building isolation systems. Luo et al. (2014) and Wierschem et al. (2014) conducted experiments on large-scale model building structures with multiple NES devices. In their studies, three historic earthquake ground motions were scaled down and implemented by a large-scale shake table, proving the efficiency of the NES based vibration mitigation in earthquakes. The design of NES isolation systems is often conducted by using non-linear dynamic analysis approaches such as the Harmonic Balance Method (HBM) (Luongo and Zulli, 2012) and the Non-linear Normal Modes (NNM) approach (Ahmadabadi and Khadem, 2012). But these approaches are often difficult to be applied to complex building isolation systems (Li et al., 2021).

3 Non-linear damping for seismic isolation

3.1 Non-linear viscous damper

In order to improve the seismic isolation performance of traditional linear building isolation systems, non-linear viscous damping has been applied to both the base and super-structure isolation of buildings. In general, the force-velocity relationship for a non-linear viscous damper can be written as (Milanchian and Hosseini, 2019).

f_{d} = c_{α} s g n (v_{d}) {|v_{d}|}^{α}

where $f_{d}$ is the damping force, $c_{α}$ is the damping coefficient, $v_{d}$ is the velocity, and $α$ is the velocity exponent.

Many studies on non-linear damping-based building isolation systems have been carried out by researchers. The non-linearly damped inter-storey isolation system is illustrated in Figure 11A (Dong et al., 2016). Martinez-Rodrigo and Romero (Martinez-Rodrigo and Romero, 2003) found that by applying non-linear inter-storey viscous dampers, the forces in the dampers can be reduced by more than 35% while having a structural performance similar to that with using linear dampers. Since large damper forces have important implications on the overall retrofitting cost, manufacturers generally strive for achieving such a non-linear behaviour in their products (De Domenico and Hajirasouliha, 2021). Kangda and Bakre (2018) studied the seismic isolation of adjacent buildings, observing that at low damping ratio, non-linear dampers perform better than linear dampers in reducing absolute accelerations. The optimal placement of non-linear dampers for building structures was investigated by Fujita et al. (2014, 2021), showing that the velocity exponent $α$ plays a key role in vibration suppression under low level seismic input. Moreover, a non-linear damper is much more effective than a linear damper under very rare earthquakes having seismic intensities larger than the design earthquakes.

FIGURE 11

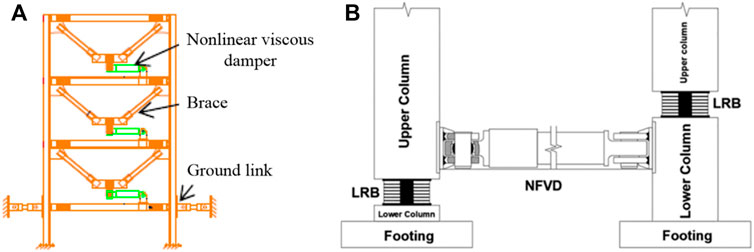
FIGURE 11. The non-linearly damped inter-storey and base isolation systems (A) The inter-storey isolation system; (B) The base isolation system.

Additional non-linear damping to building base isolation systems can bring significant benefit to seismic isolations. Deringol and Guneyisi (2021) investigated the effectiveness of non-linear fluid viscous dampers in seismic isolation with LRB shown in Figure 11B. The study found that the non-linear damper can significantly mitigate long-period seismic vibrations (T > 4s) with optimized velocity exponents $α$ and positions. Menga et al. (2021) found that non-linear damped base isolation can provide desired isolation performance over a wider range of excitation spectra than a linear damper. Lang et al. (2009) theoretically proved that a power-law non-linear damping can produce desired vibration isolation performance over both resonant and non-resonant frequency ranges. This property has been applied to the development of non-linear building isolation systems. For example, Lang et al. (2013) studied the design of power-law non-linear viscous damping for high-rise building base isolation systems under both long-period sinusoidal and random ground motions, where the energy transmissibility is applied as the objective function for non-linear damping design. The prominent advantages of non-linear damping in high-frequency seismic isolation have been proven by Ho et al. (2018), Guo et al. (2012), and Zhu et al. (2020), which can profoundly improve the building isolation performance under both far-fault and near-fault earthquakes.

3.2 Implementation of non-linear damping

In general, a desired non-linear damping characteristic cannot be achieved naturally by materials and pure mechanical design. Specific mechanical structures and materials only produce limited non-linear properties. For example, Ilbeigi et al. (2012) developed a non-linear displacement-dependent damper by introducing a varying cross-section piston guide in a damper as shown in Figure 12A. Bian and Jing (2019) applied a horizontal damper to an X shape isolator to achieve non-linear damping as shown in Figure 12B. Tang and Brennan (2013) found that a horizontal damper attached to a vibration isolator in Figure 12C can be represented by an unplugged Van der Pol equation.

FIGURE 12

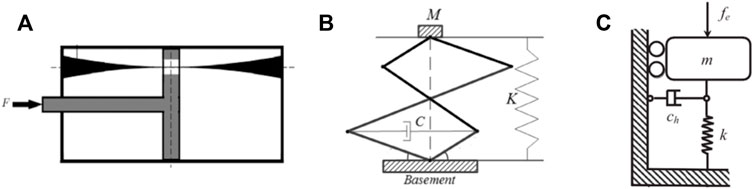
FIGURE 12. Different mechanisms of non-linear damping (A) The displacement-dependent damper; (B) The X shape isolator with additional damper; (C) The horizontal damper.

In order to achieve desired non-linear damping properties, magnetorheological (MR) damper and semi-active control approaches were employed (Yao et al., 2002). The structure of MR dampers is shown in Figure 13A, where by controlling the external magnetic field, the MR fluid can produce various damping coefficients (Li et al., 2019). A novel semi-active control of MR dampers was developed in Laalej et al. (2012) as illustrated in Figure 13B, where $f (\dot{x})$ is the desired non-linear force to be achieved; $i (t)$ ; $V (t)$ are the MR damper control current and MR damper power amplifier input voltage, respectively. The semi-active control strategy was verified by experiments in Ho et al. (2013) as shown in Figure 13C.

FIGURE 13

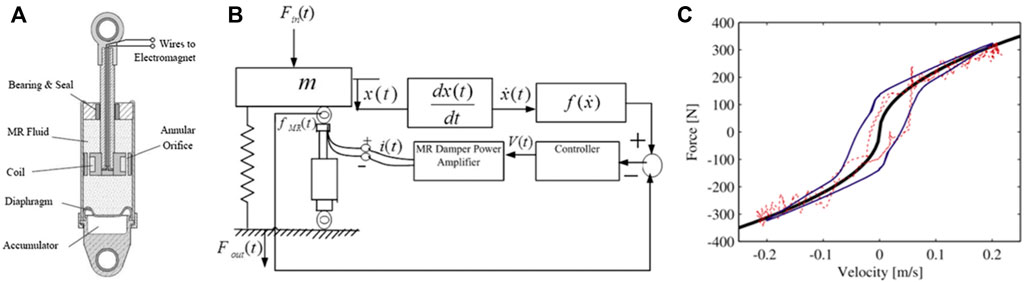
FIGURE 13. The MR damper and the semi-active control strategy (A) The MR damper; (B) The semi-active control strategy; (C) The implementation of the non-linear damping.

In addition, Ho et al. (2018) and Zhu et al. (2020) developed an open-loop semi-active control strategy based on a viscous damper with four linear damping coefficients for the base isolation of the Sosokan building (Japan) model. Ma et al. (2020) obtained desired non-linear damping force by controlling an electromagnetic shunt damping device.

4 Analysis and design of non-linear seismic isolation systems

4.1 Building isolation system analyses

In order to study the dynamic properties of building isolation systems, a building structure is often simplified as a Multiple-Degree-of-Freedom (MDoF) mass-spring-damper system (Figure 14A) (Silva-Navarro and Abundis-Fong, 2017). For example, Yamamoto et al. (2011) studied the input energy and energy input rate to a base-isolated building during an earthquake based on an MDoF N-storey shear building model. Liu et al. (2018) investigated the effectiveness of FVDs in building inter-storey isolation based on a 7DoF building model. The N-storey building model was also applied to the analysis and design of LRB base isolation systems (Kodakkal et al., 2019), TMD isolation systems (Giaralis and Taflanidis, 2018), as well as many non-linear and adjacent building isolation systems (Milanchian and Hosseini, 2019).

FIGURE 14

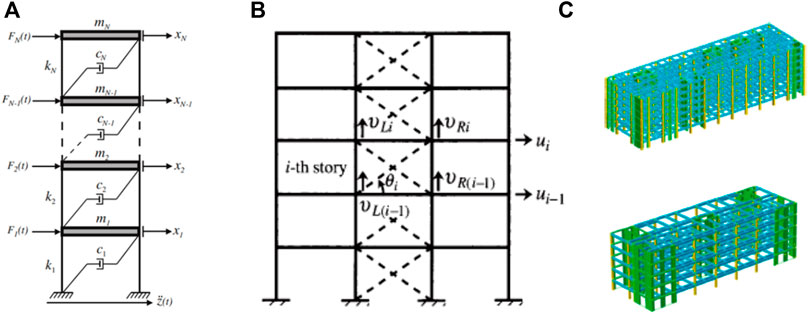
FIGURE 14. Building models for the analysis and design of isolation systems (A) The N-storey building model; (B) The frame model; (C) The FE model.

In general, an MDoF system can be easily simulated by using Runge-Kutta method (Soni et al., 2011), but it is often with low fidelity and only be used for conceptual studies of building isolation systems. To address this issue, more complex truss frame structures were considered in building isolation analyses (Figure 14B) (Takewaki, 2000), where structure mechanics approaches can be applied to compute the building responses under seismic input. For example, Eltahawy and Ryan (2020) studied the application of a 3-dimensional isolation system to the reduction of non-structural component damage caused by vertical excitations based on a frame building model. Takewaki (2000) proposed a systematic procedure by using the transfer function, in order to find the optimal damper positioning to minimize the dynamic compliance of a planar building frame. High fidelity Finite Element (FE) models are also used in the analysis of building isolation systems (Figure 14C), but they are often complex and with high computational costs in practical use (Wang et al., 2021).

4.2 Linearization approaches

In order to study the effects of non-linear building isolation systems, non-linear isolators are usually linearized as an equivalent linear isolator, so that the linear system theories can be applied for system analysis. For example, effective stiffness and damping of LRB are often evaluated for the analysis and design of LRB building isolation systems (Hwang and Chiou, 1996). In general, the linearization of the building isolation system is to find equivalent linear stiffness or damping, so that the output displacement of the linearized isolated building is equal to that of the non-linearly isolated building (Liu et al., 2014). In practice, the most commonly used linearization method was proposed by Rosenblueth and Herrera (1964) and has been adopted by many seismic codes (Eurocode eight; AASHTO; NTC). For example, Ma et al. (2013) applied the equivalent linearization method to the analysis and design of base-isolated buildings with many hysteretic devices. Zhang et al. (2020) studied the linearization of a flag-shaped isolation system, based on which the inter-storey brace isolation systems were optimized. Zordan et al. (2014) derived the equivalent damping ratio of an LRB isolated building model based on over 12 ground motions. Shinozuka et al. (2015) applied the stochastic linearization method investigate the LRB based building base isolation under random ground motions.

For the design of non-linear isolators, the equivalent linearization is often conducted based on the equivalent force or energy of the isolator. The equivalent linearization is therefore to solve the optimization problem (Zhu et al., 2022):

\min E \{{[f_{non} (t) - f_{eq} (t)]}^{2}\}

where $f_{non} (t)$ and $f_{eq} (t)$ are the non-linear and equivalent linear force of the isolator, respectively; $E \{.\}$ represents the mean value. To solve equivalent linear damping problems, Elliott et al. (2015) studied the equivalent linear damping of power-law non-linear damping under both harmonic and random excitations. Bajric and Hogsberg (2018) derived equivalent linear damping of a hysteretic system under both low and high levels of excitation amplitudes. Zhu et al. (2022) developed a novel data-driven modelling approach for building isolation systems based on the mobility analysis method, where the design of non-linear isolation damping was conducted based on the equivalent linearization method.

4.3 Non-linearity frequency design approaches

Basically, both linear and linearization approaches only work in a narrow region around the working point of the system as illustrated in Figure 15A (Zhu et al., 2021). In practice, a large class of non-linear systems can be represented by Volterra series, which enables the analysis of non-linear systems over a much wider range of operations around a working point. The Volterra series is an extension of Taylor expansion to non-linear dynamic relationships, based on which the non-linear frequency response functions, such as the Generalized Frequency Response Functions (GFRFs) (George, 1959), the Non-linear Output Frequency Response Functions (NOFRFs) (Lang and Billings, 2005), the Output Frequency Response Fucntions (OFRF) (Lang et al., 2007) and the Associated OFRF (AOFRF) (Zhu and Lang, 2018), were developed for non-linear system frequency analysis and design.

FIGURE 15

FIGURE 15. The Volterra series representation and the OFRF based design of non-linear systems.

Among these non-linear frequency response functions, the OFRF and AOFRF are one-dimensional functions, and have been applied to the design of non-linear dynamical systems. The concept of the OFRF was first developed by Lang et al. (2007), using which the system output frequency response can be written as a polynomial function of non-linear characteristic parameters:

Y (j ω) = \sum_{(j_{1}, \dots, j_{S}) \in J} λ_{(j_{1}, \dots, j_{S})} (j ω) {ξ_{1}}^{j_{1}} \dots {ξ_{S}}^{j_{S}}

where $Y (j ω)$ is the system output frequency response; $λ_{(j_{1}, \dots, j_{S})} (j ω)$ are the functions of frequency variable $ω$ and are dependent on the linear characteristic parameters of the system; $ξ_{1}, \dots, ξ_{S}$ are system non-linear design parameters; $J$ denotes integer vectors. Figure 15B shows an example of OFRF (Zhu and Lang, 2017), the spectrum of the output force of a non-linear system is represented by a polynomial function of $c_{3}$ and $k_{3}$ which are two non-linear design parameters of system non-linearity.

Based on the concept of OFRF, Peng and Lang (2008) proposed the least squares based evaluation of the OFRF representation. Guo et al. (2012) and Ho et al. (2018) conducted the OFRF based design of non-linearly damped building base isolation systems by minimizing the energy transmissibility of the buildings. Fujita et al. (2014) investigated the optimal placement of inter-storey non-linear damper using the OFRF design approach. Considering that the OFRF only considers the relationship between system output frequency responses and non-linear design parameters, recently, Zhu and Lang. (2018) developed a novel AOFRF concept to deal with the non-linear system design by determining both the system’s linear and non-linear characteristic parameters.

5 Conclusion

This paper has reviewed the development of the analysis and design of passive non-linear building isolation systems. The building isolation systems are divided into two categories, which are the base isolation systems and the super-structure isolation systems. The current analysis and design of typical LRB and FPB base isolation systems, viscous damping inter-storey isolation systems, and TMD top floor isolation systems have been overviewed. Moreover, commonly used non-linear isolators for base and super-structure isolation systems, including the QZS, NES, and non-linear viscous damper, as well as their implementations, have been summarized. It can be concluded that these non-linear isolation systems are promising solutions to both near-fault and far-fault seismic isolations.

Finally, the analysis and design approaches of non-linear building isolation systems have been introduced. These approaches include the linearization approaches and the non-linear frequency design approaches. The increasing applications of these approaches demonstrate a systematic analysis and design of non-linear building isolation systems are really needed in engineering practice. The solutions include but are not limited to the investigation of effective modelling and simulation approaches for non-linear building isolation systems, the development of systematic non-linear analysis approaches, the specification of effective design objectives in both the frequency and time domain, as well as the development of non-linear system design approaches.

Author contributions

YPZ contributes to the writing of the whole review paper; ZQL supports the review of the analysis and design of non-linear systems and helped with the proofreading; KF and IT support the review of building isolation systems.

Funding

This work was supported by the United Kingdom EPSRC: EP/R032793/1, and UK Royal Society: IE150298.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmadabadi, Z. N., and Khadem, S. E. (2012). Nonlinear vibration control of a cantilever beam by a nonlinear energy sink. Mech. Mach. Theory 50, 134–149. doi:10.1016/j.mechmachtheory.2011.11.007