Vertical response of unbonded fiber reinforced elastomeric isolators (U-FREIs) under bidirectional shear loading

Fiber Reinforced Elastomeric Isolators (FREIs) were generally studied in unbonded configuration. Due to combined axial and shear loads, the contact area between the bearing and horizontal supports reduces with the horizontal displacement. As a result, both the vertical and the horizontal stiffnesses decrease with the horizontal deformation while also the vertical deformation increases. This paper presents the results of a large set of full-scale 3D Finite Element Analyses on unbonded fiber reinforced bearings with different geometries, subjected to combined axial and multi-directional shear loads. The main vertical response parameters were studied, namely the vertical displacement, the vertical stiffness, and the effective compressive modulus, thus highlighting the influence of both geometry and horizontal loading direction on the vertical response of the FREIs. Conclusion of this study demonstrate to what extent the combined influence of geometric properties and loading conditions affects the vertical response of elastomeric bearings with flexible reinforcements.

1 Introduction

Common Steel Reinforced Elastomeric Isolators (SREIs) used in seismic isolation (Kalfas and Mitoulis, 2017; Tubaldi et al., 2018; Kalfas et al., 2020) are costly and heavy (Konstantinidis and Kelly, 2014). Fiber Reinforced Elastomeric Isolators were proposed as low-cost alternative (Kelly, 1999), replacing the embedded steel reinforcements with fiber fabrics and removing the thick steel end plates to use the devices in unbonded condition, i.e. with no bonding with the structure (Unbonded Fiber Reinforced Elastomeric Isolators, U-FREIs (Toopchi-Nezhad et al., 2008a). Different studies demonstrated the advantages in using FREIs over SREIs as (Madera Sierra et al., 2019):

• Lighter devices can be obtained using fiber fabrics as reinforcements (Kelly, 1999).

• Bearings of different size and shape can be cut from bigger pads (Moon et al., 2002).

• Hot vulcanization process require for steel reinforcement can be replaced by faster and easier cold vulcanization process used for fiber reinforcements (Moon et al., 2003).

Due to the unbonded configuration, the bearings experience the rollover deformation, i.e. the edges of the device detach from the supports following the horizontal deformation (Kelly and Konstantinidis, 2011). This deformation continues until the initial vertical faces of the bearing starting touch the support gradually becoming horizontal, resulting in the full rollover condition (Toopchi-Nezhad et al., 2008b; Losanno et al., 2019).

The reduction of the horizontal stiffness following the rollover deformation enhances the isolation system efficiency (Naeim and Kelly, 1999). However, the tangent horizontal stiffness needs to be positive in order the bearing to be stable (ASCE-7, 2010; Decree 17 January 20182018; Galano et al., 2021a; Galano et al., 2022; Russo and Pauletta, 2013; Code, 2005). Unstable U-FREIs show softening response at large lateral deformations prior to full rollover. The stable/unstable response of the U-FREIs mostly depends on the secondary shape factor (Toopchi-Nezhad et al., 2009; Pauletta et al., 20152015; Galano et al., 2021b; Calabrese et al., 2021), defined as the ratio between the base side in the direction of the horizontal load to the total rubber height (). U-FREIs with a secondary shape factor greater than 2.5 were seen to show stable response up to full rollover (de Raaf et al., 2011; Ngo et al., 2020; Galano et al., 2021; Galano, 2022; Galano, 2022), depending also on the mechanical properties, i.e. rubber compound and axial pressure.

The area reduction due to rollover increase the vertical deformation of the bearing, thus reducing the vertical stiffness (Galano, 2021). Several research works studied the vertical response of U-FREIs under pure compression or under combined axial and mono-directional shear load (Angeli et al., 2013; Osgooei et al., 2016; Osgooei et al., 2014; Al-Anany et al., 2017; Calabrese et al., 2021; Losanno et al., 2022), highlighting the influence of different geometric parameters, among all the primary shape factor, defined as the ratio between loaded and free to bulge areas.

FREIs under combined axial and multidirectional shear loading were studied considering the effect of the horizontal loading direction on the lateral response of the bearings (Osgooei et al., 2014; Ngo et al., 2017). Very little is known on the vertical response of U-FREI subjected to axial and multi-directional horizontal loading. The ratio of vertical to horizontal stiffness of these bearings needs to be large enough to support the structure and to avoid rocking motions (Kelly and Konstantinidis, 2011). Due to area reduction following the horizontal deformation, in a safety evaluation, the vertical stiffness can be computed at a generic horizontal displacement threshold.

For this purpose, this paper studies the vertical response of rectangular- and square-shaped U-FREIs through a large number of full-scale 3D Finite Element Analyses (FEAs). Different horizontal loading directions are considered for each bearing. The trends of the vertical displacements, of the vertical stiffness and of the effective compressive modulus with the main geometric parameters are given as functions of the horizontal deformation of the bearings.

2 Description of the numerical analyses

2.1 Finite element models

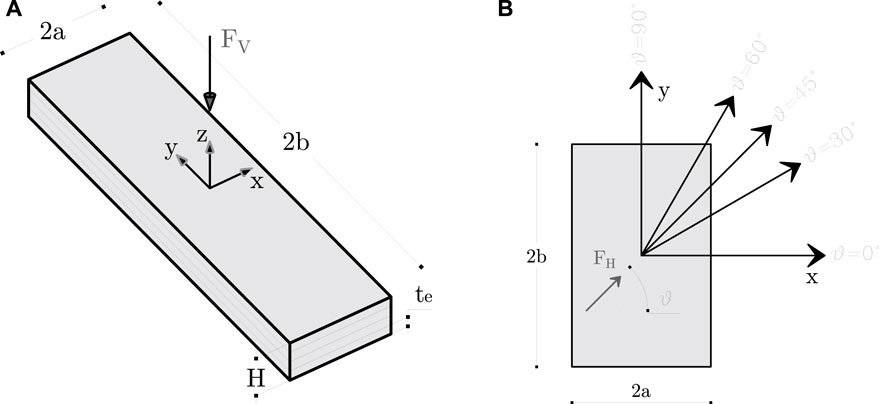
Table 1 reports the variable geometric parameters considered in the numerical analyses, while Figure 1 gives a schematic of the generic rectangular-shaped U-FREI. Four and three different values of the base side in X ($2a$) and Y ($2b$) direction are considered, respectively; also, two total heights ($H$) and thicknesses of the elastomeric layers ($t_e$) complete the variable geometric parameters. With the thickness of the elastomeric and reinforcements layers and the total heights defined in Table 1, four different values of the total number of rubber layers ($n=\left(H+t_f\right)/\left(t_e+t_f\right)$ and of the total rubber height ($t_r$) are obtained. Each bearing is loaded in five different horizontal directions, defined by the five angles ($\vartheta$) listed in Table 1 and computed counterclockwise from the X axis (Figure 1B). Combination of the variable parameters leads to a total number of 240 Finite Element Models (FEMs), as part of the set presented in (Galano et al., 2021).

TABLE 1

TABLE 1. Variable geometric parameters in the set of FEMs.

FIGURE 1

FIGURE 1. U-FREI studied: (A) geometric parameters definition, (B) horizontal loading directions.

The mechanical parameters of each bearing are kept constant in the analyses, their numerical values shown in Table 2.

TABLE 2

TABLE 2. Mechanical parameters set for the FEAs.

The primary shape factor ($S_1=ab/t_e\left(a+b\right)$), is included in the range 3.33–17.6 (Table 1). In this paper, the definitions of base side ($B\left(\vartheta \right)$) and shear strain in the horizontal loading direction (${\gamma }_H^{\vartheta }={\delta }_H^{\vartheta }/t_r=\sqrt{{\delta }_H^{X\left(\vartheta \right)}+{\delta }_H^{Y\left(\vartheta \right)}/t_r}$) given in (Galano et al., 2021) are used; accordingly, the secondary shape factors in the horizontal loading direction ($S_2^{\vartheta }=B\left(\vartheta \right)/t_r$) range from 1.02 to 12.5 (Table 1).

Each bearing was prior subjected to increasing vertical load up to a target vertical pressure (Table 2) and then displaced in the horizontal directions of Table 1 up to ${\gamma }_H^{\vartheta }=100\%$. Past this shear strain threshold, the overturning condition due to rollover deformation lead to increasing vertical and horizontal stiffnesses. Thus, no reduction of the bearing capacity of the U-FREIs would be obtained.

2.2 FEMs specifications

The numerical analyses are carried out using MSC Marc (MSC.Software Corporation, 2005), a general-purpose finite element software. The compressible Neo-Hookean hyperelastic material was used to model the elastomer. In this model, the strain energy density function is given by the following equation (MSC.Software Corporation, 2017a):

$W=C_1\left(I_1-3-2\ln J\right)+C_2{\left(J-1\right)}^2,(1)$

Where $C_1$ and $C_2$ are material constants, $I_1={\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2$ is the first invariant of the right Cauchy-Green deformation tensor and $J={\lambda }_1{\lambda }_2{\lambda }_3$ is the determinant of the deformation gradient. As for consistency with linear elasticity $C_1=G/2$ and $C_2=K/2$; thus, these constants can be set according to parameters shown in Table 2.

The fiber fabrics were modeled considering a bi-directional reinforcement mesh and using a linear elastic material model whose mechanical parameters are shown in Table 2 (last three columns).

The elastomer has been modeled using an eight node, isoparametric, arbitrary hexahedral element (element 7 in Marc (MSC.Software Corporation, 2017b), while the fiber layer has been modeled using a hollow, isoparametric 4-node membrane reinforced with rebars (element 147 in Marc (MSC.Software Corporation, 2017b). A “touch” type contact between the bearing and the upper and lower surfaces has been modeled, allowing the bearing to detach from the supports during roll-over to reproduce the unbonded condition. The supports are modeled as load-controlled rigid surfaces, while the bearings as deformable body. Based on the finite elements assigned to a contact body, the program will automatically set up the outer boundary of the deformable bodies. Also, the nonpenetration constraints are enforced using augmented Lagrangians.

Figure 2 shows a generic FEM used in the parametric FEA. Additional information on the mesh size can be found in (Galano et al., 2021).

FIGURE 2

FIGURE 2. Example of FEM used in the parametric FEA.

3 Results of the numerical analyses

In the following sections, vertical displacements, vertical stiffness and effective compressive modulus of each U-FREI of the set are studied. The influence of the main geometric parameters, namely the primary and secondary shape factors are highlighted.

3.1 Vertical displacements

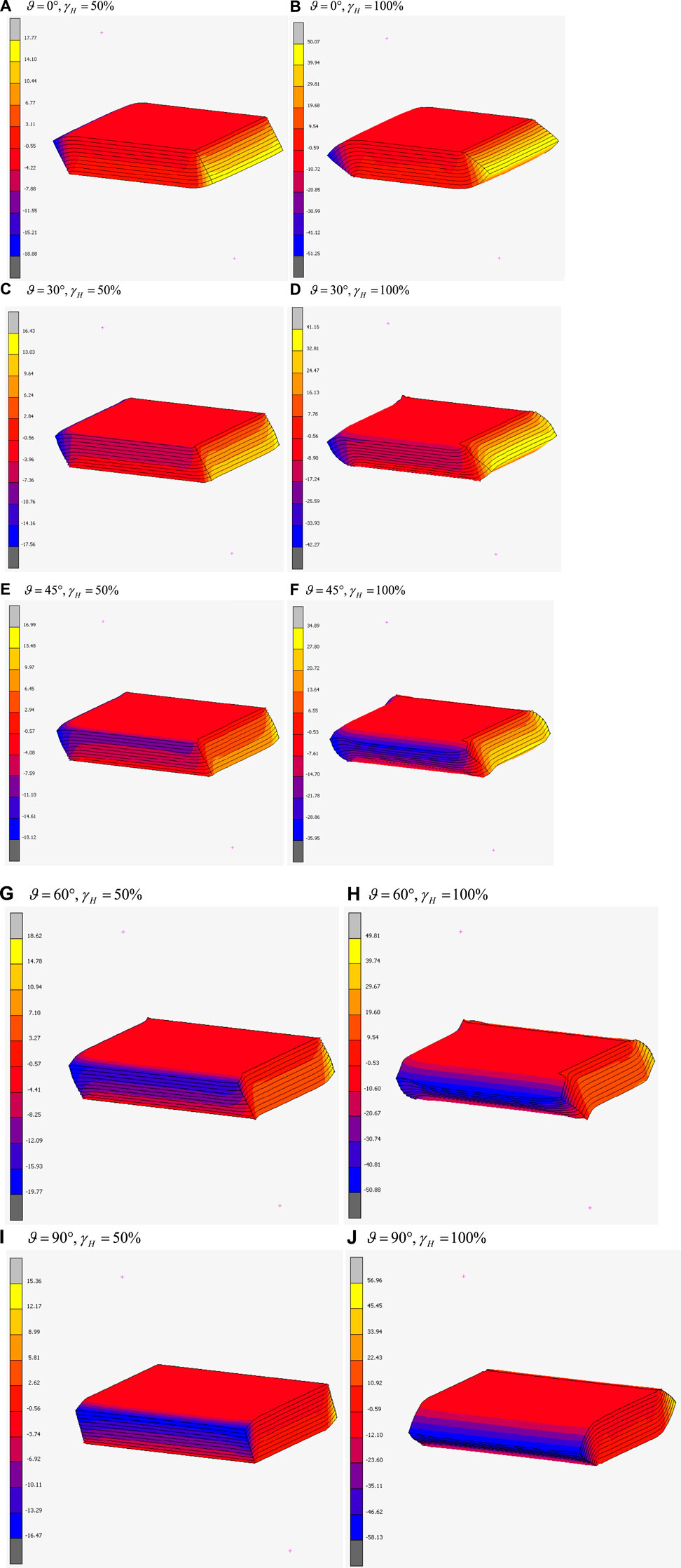
Figure 3 shows the trends of the dimensionless ratio between vertical displacements and total height of the bearing (${\delta }_v\left({\gamma }_H^{\vartheta }\right)/H$) with the primary (Figures 3A–C) and secondary shape factors (Figures 3D–F) at three significant levels of shear strain: 1) ${\gamma }_H^{\vartheta }=0\%$ (i.e. pure compression, Figures 3A,D), 2) ${\gamma }_H^{\vartheta }=50\%$ (Figures 3B,E) and 3) ${\gamma }_H^{\vartheta }=100\%$ (Figures 3C,F). In Figure 4, the deformed configurations with contour plots of the vertical displacements, of a bearing with $S_1=20$ and $S_2\left(0°,\dots ,90°\right)=\left(\mathrm{4.2,4.8,5.9,4.8,4.2}\right)$ are illustrated for the shear strain thresholds of ${\gamma }_H^{\vartheta }=50\%$ (Figures 4A,C,E,G,I) and ${\gamma }_H^{\vartheta }=100\%$ (Figures 4B,D,F,H,J).

FIGURE 3

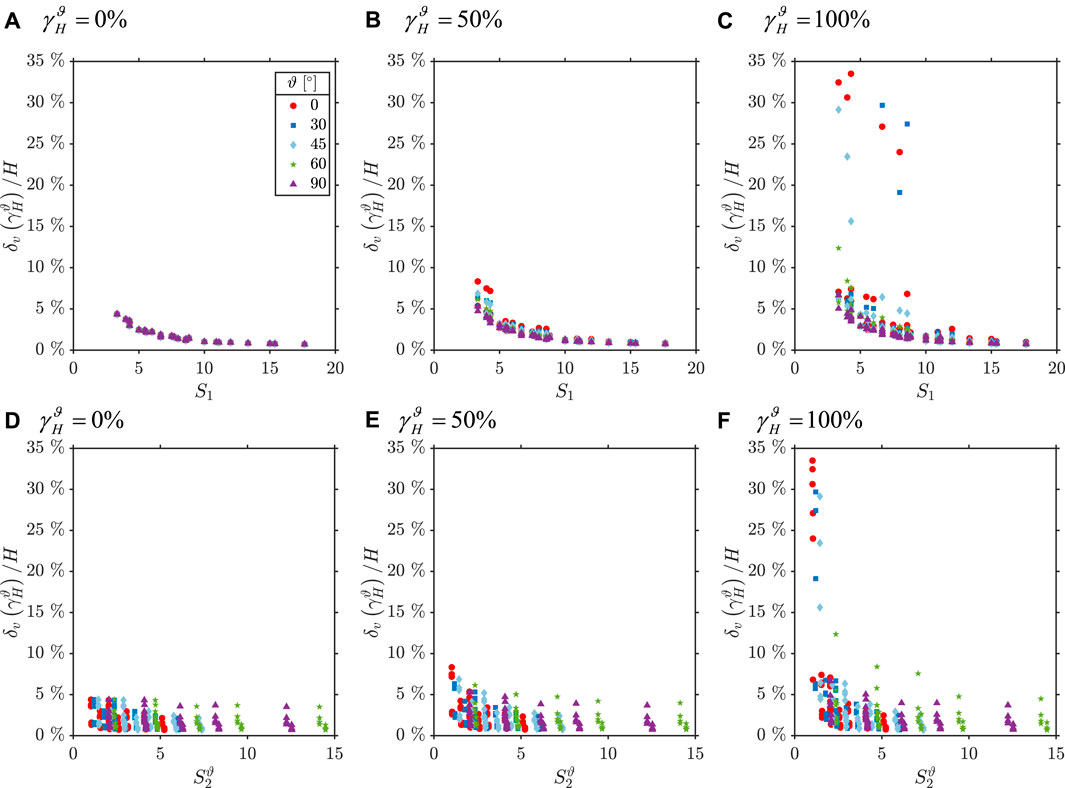
FIGURE 3. Trends of the ratio between vertical displacements and total height with the primary and secondary shape factor.

FIGURE 4

FIGURE 4. (Continued).

As expected, the vertical deformation decreases with increasing values of the primary shape factor (Figures 3A–C); an approximately exponential decreasing trends is found. The effect of the shear strain and of the horizontal loading direction can be seen comparing Figures 3A–C. The contact area between bearing and supports reduces with increasing shear strain, thus the vertical deformations increase accordingly. A higher increase is related to the smaller base side of the rectangular bearing ($\vartheta \le 45°$), i.e. smaller primary shape factor; for larger values of the primary shape factor (i.e. $S_1\ge 15$) the effect of the horizontal loading direction is negligible.

The vertical deformation appears to be slightly affected by the secondary shape factor (Figures 3D–F) when ${\gamma }_H^{\vartheta }\le 50\%$, as scattered values of vertical deformations in the range 0%–5% are obtained for the same values of $S_2^{\vartheta }$. When ${\gamma }_H^{\vartheta }>50\%$ the vertical deformation appears to decrease with an exponential trend, similar to the trend of ${\delta }_v\left({\gamma }_H^{\vartheta }\right)/H$ with $S_1$. This confirms how the secondary shape factor plays a key role on the horizontal rather than vertical deformation of the U-FREI. Larger values of $S_2^{\vartheta }$ ensue stable bearings, thus according to Figure 3F, the vertical deformation tends to increase solely when $S_2\le 2.5$. Such threshold value matches what previously found on the stability of U-FREIs both on the vertical and horizontal response (Galano et al., 2021b; Galano et al., 2021; Galano, 2022).

3.2 Vertical stiffness

The vertical stiffness as a function of the horizontal deformation of each U-FREI is defined as:

$K_v\left({\gamma }_H^{\vartheta }\right)=\frac{F_v}{{\delta }_v\left({\gamma }_H^{\vartheta }\right)}.(2)$

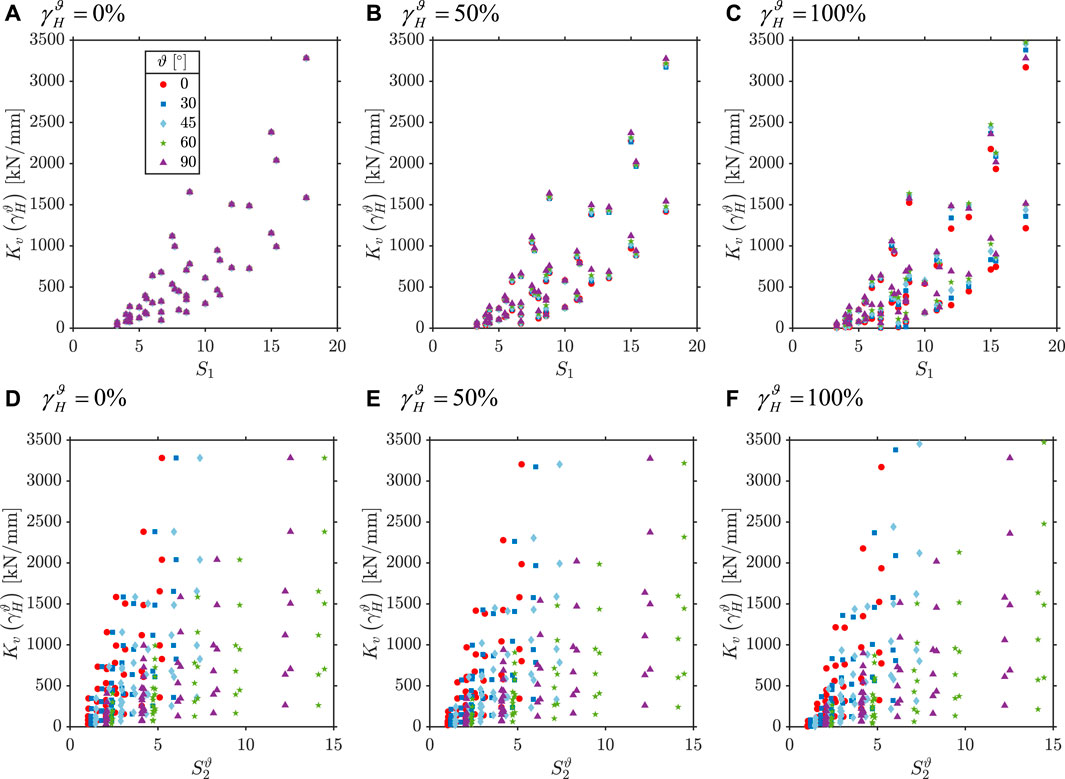
The trends of $K_v\left({\gamma }_H^{\vartheta }\right)$ with the primary and secondary shape factors are plotted in Figure 5. Similar to vertical deformations, the vertical stiffness appears to be greatly affected by the primary shape factor (Figures 5A–C), while $S_2^{\vartheta }$ plays a minor role (Figures 5D–F).

FIGURE 5

FIGURE 5. Trends of the vertical stiffness with the primary and secondary shape factor.

For increasing values of shear strain, the vertical deformation increases accordingly (see Section 3.1) and from Eq. 2 the vertical stiffness reduces. However, the coupled horizontal response of both base sides due to bidirectional shear loads may lead to a slightly increase of the vertical stiffness when $S_1\ge 15$ (Figure 5C). Marked reductions of the vertical stiffness with the shear strain are obtained from the FEMs solely when $S_1<10$ (Figures 5B,C).

3.3 Effective compressive modulus

Starting from Eq. 2, the effective compressive modulus as a function of the horizontal deformation can be obtained as:

$E_c\left({\gamma }_H^{\vartheta }\right)=\frac{K_v\left({\gamma }_H^{\vartheta }\right)\cdot t_r}{A_c}=\frac{F_v\cdot t_r}{{\delta }_v\left({\gamma }_H^{\vartheta }\right)\cdot A_c}.(3)$

Figure 6 shows the trends of $E_c\left({\gamma }_H^{\vartheta }\right)$ with $S_1$ and $S_2^{\vartheta }$. The effective compressive modulus appears to depend on the primary shape factor with an increasing linear trend (Figure 6A). With increasing values of the shear strain $E_c\left({\gamma }_H^{\vartheta }\right)$ generally reduces (see Eq. 3). The horizontal loading directions appears to affect the effective compressive modulus as greater decrease is related to U-FREI loaded along the smaller base side (i.e. $\vartheta \le 30°$, Figure 6C).

FIGURE 6

FIGURE 6. Trends of the effective compressive modulus with the primary and secondary shape factor.

Here again, the secondary shape factor plays a minor role when ${\gamma }_H^{\vartheta }\le 50\%$ (Figures 6D,E). When ${\gamma }_H^{\vartheta }>50\%$, smaller values of $S_2^{\vartheta }$ (i.e. $S_2^{\vartheta }\le 2.5$) correspond to larger reduction of $E_c\left({\gamma }_H^{\vartheta }\right)$, while increasing values of the secondary shape factor leads to stable bearings with $E_c\left({\gamma }_H^{\vartheta }\right)$ almost independent on the horizontal deformation (Figure 6F).

3.4 Combined influence of primary and secondary shape factors

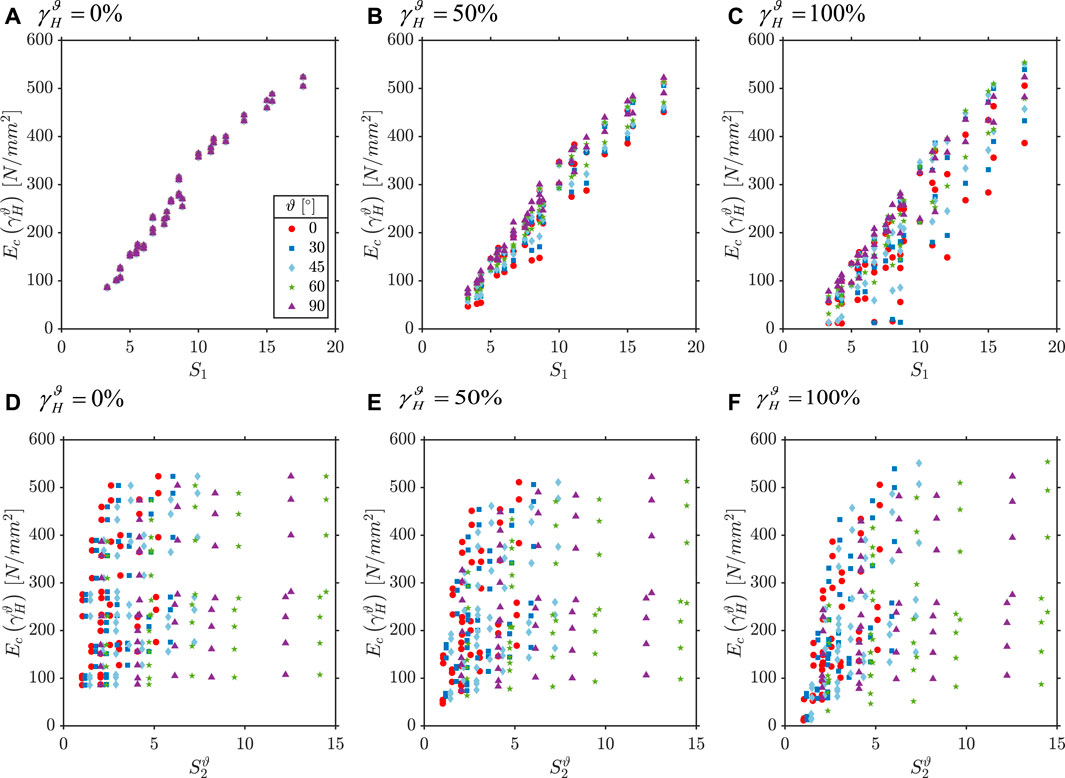
The trends of vertical deformation, vertical stiffness and effective compressive modulus with both primary and secondary shape factors are illustrated in Figure 7. This figure shows how the shape factors affect the whole vertical response of the U-FREIs under combined axial and multi-directional shear loads. In each plot of Figure 7, data fitting with regression surfaces are also proposed.

FIGURE 7

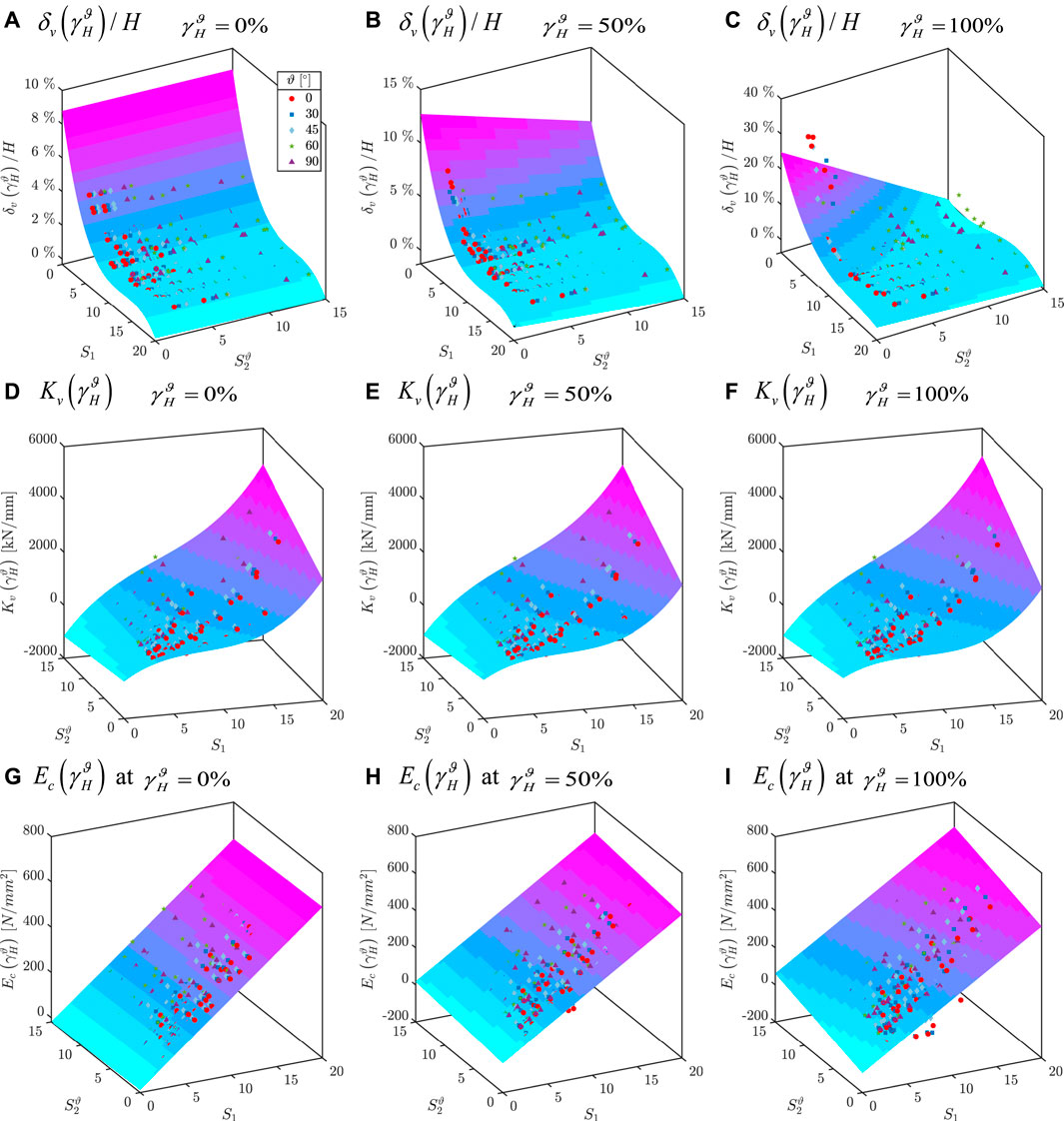
FIGURE 7. Trends of the vertical deformation, vertical stiffness and effective compressive modulus with both primary and secondary shape factors.

The surface fitting on the vertical deformation shows the influence of the shape factors with the shear strain. Under pure compression the vertical deformation slightly depends on $S_2^{\vartheta }$ and is greatly affected by $S_1$ (Figure 7A), while at larger horizontal deformation the influence of $S_2^{\vartheta }$ is greater (Figures 7B,C).

Both the vertical stiffness and the effective compressive modulus assume negative values as $S_1$ tends to zero, as expected, almost independent on the corresponding values of $S_2^{\vartheta }$ (Figures 7D,G). These two parameters largely increase when $S_1$ range from 10 to 20. The influence of $S_2^{\vartheta }$ is relevant solely when ${\gamma }_H^{\vartheta }>50\%$ (Figures 7F,I).

3.5 Percentage reduction of the vertical stiffness with the shear strain

Tables 3, 4 report the percentage reductions of the vertical stiffness with increasing shear strains, in the different horizontal loading directions. In Table 3 the influence of the primary shape factor is highlighted, considering U-FREIs with increasing values of $S_1$ and an almost constant $S_2^{\vartheta }$, while in Table 4 variable values of the secondary shape factors in the horizontal displacement directions are considered.

TABLE 3

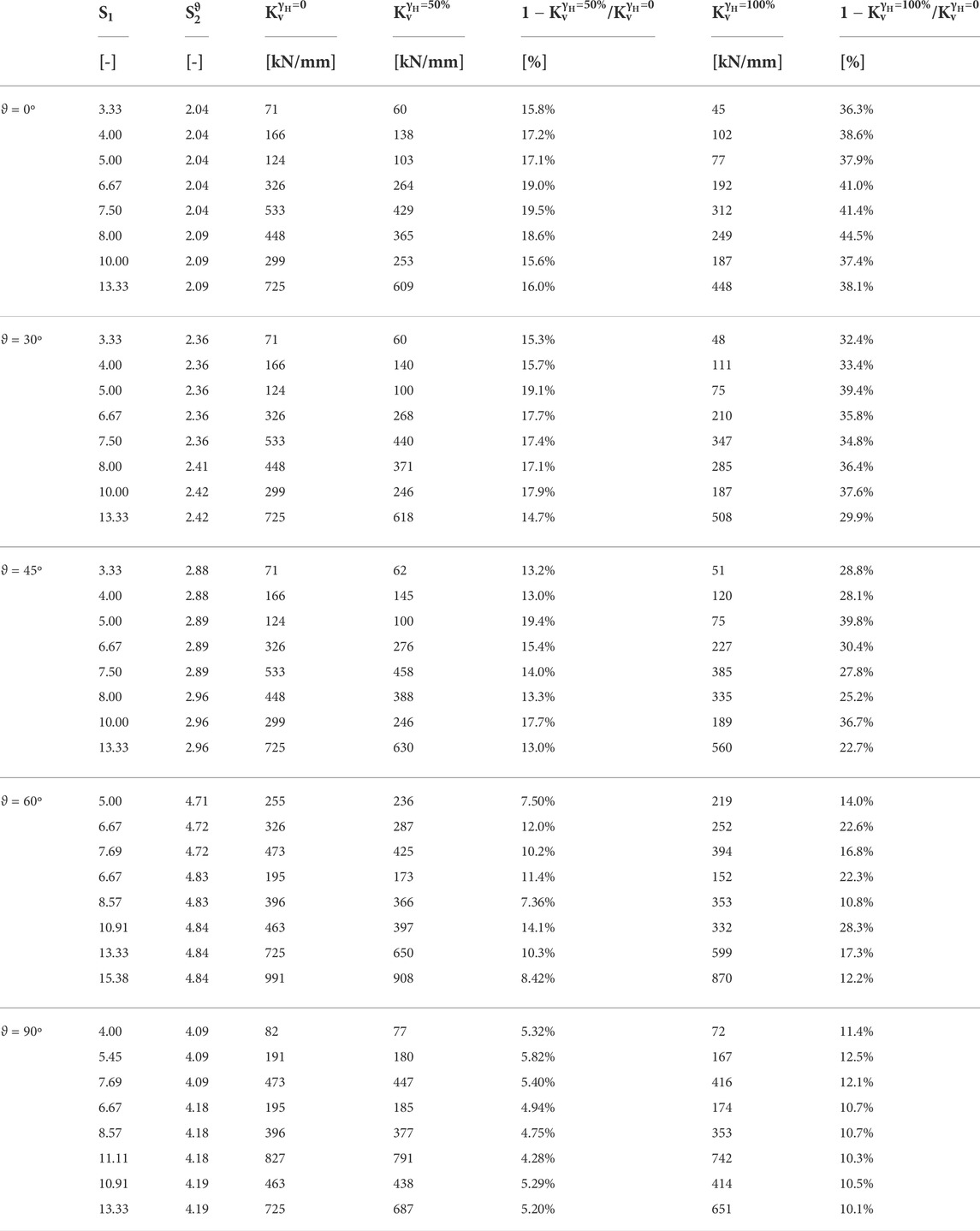
TABLE 3. Percentage reductions of the vertical stiffness with the shear strain in the different horizontal loading directions for bearings with variable primary shape factors.

TABLE 4

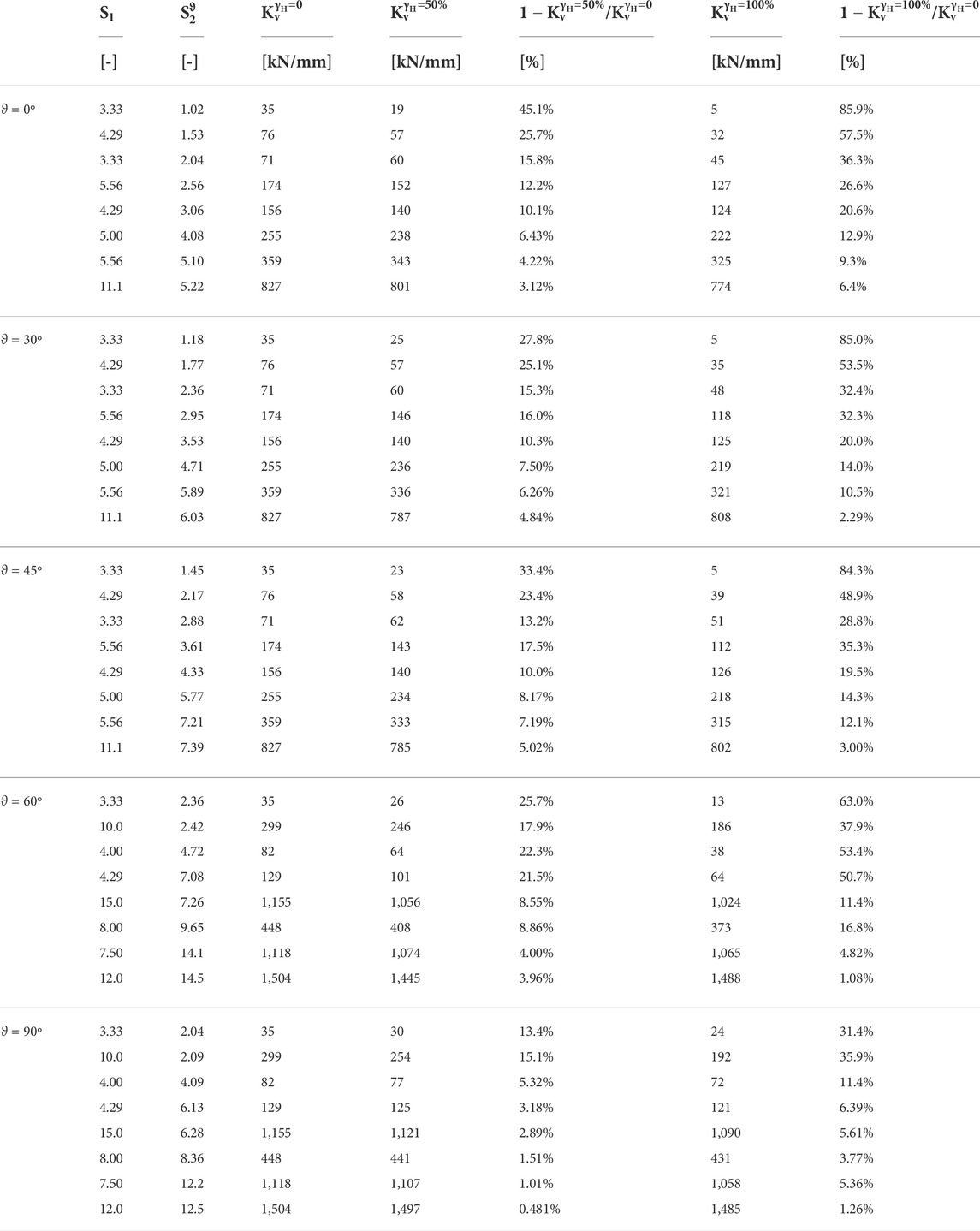
TABLE 4. Percentage reductions of the vertical stiffness with the shear strain in the different horizontal loading directions for bearings with variable secondary shape factors.

From Table 3 it can be seen how the percentage reductions of $K_v\left({\gamma }_H^{\vartheta }\right)$ in the generic horizontal loading direction are almost independent on the primary shape factor. Average reductions of the order of 17.4%, 16.9%, 14.9%, 10.2% and 5.12% for ${\gamma }_H=50\%$ and of the order of 39.4%, 35.0%, 29.9%, 18.0% and 11.0% for ${\gamma }_H=100\%$ are obtained for $\vartheta =0°$, $\vartheta =30°$, $\vartheta =45°$, $\vartheta =60°$ and $\vartheta =90°$, respectively. These values prove how greater reductions of the vertical stiffness can be expected when the U-FREI is loaded along the smaller base side, regardless of the value of $S_1$. In other words, the main influence on $K_v\left({\gamma }_H^{\vartheta }\right)$ is related to the secondary shape factor in the horizontal displacement direction. This concept is illustrated in Table 4 in numerical terms. This table shows how, when the bearing is loaded in a generic horizontal direction, the vertical stiffness always reduces with the shear strain according to the secondary shape factor in the same horizontal direction. It is worth mentioning how great percentage reductions of $K_v\left({\gamma }_H^{\vartheta }\right)$ are obtained when $S_2^{\vartheta }<2.5$, while the little reductions of the same parameter are obtained for $S_2^{\vartheta }>3$.

4 Conclusion

In this paper, the vertical response of unbonded fiber reinforced elastomeric isolators subjected to axial and multi-directional shear loading was studied through finite element analyses. A large set of bearings with different base area, total height and thickness of elastomeric layers were studied under a constant value of the vertical pressure and horizontal loading in five different directions.

The results of the finite element models were proposed in terms of vertical deformation, vertical stiffness and effective compressive modulus. The trends of these three parameters with the primary and secondary shape factors were given at different levels of shear strain and for each of the horizontal loading directions.

The vertical response of the U-FREIs was found to be greatly affected by the primary shape factor either when the bearing is subjected to pure compression or to axial and multi-directional shear loads. The secondary shape factor affects the vertical response of the bearing at large horizontal deformations, while plays a minor role at relatively small shear strain thresholds. However, when $S_2^{\vartheta }>2.5$ the bearings are stables and the vertical response is slightly dependent on the shear strain.

Finally, the combined influence of the primary and secondary shape factors on the vertical deformation, vertical stiffness and effective compressive modulus was studied using surface fitting of the results of the finite element analyses. In the range of primary and secondary shape factors of the set of numerical models, the trends at different shear strain thresholds and for the five different horizontal loading directions were proposed.

This works reports preliminary results on the vertical response of U-FREIs under vertical and multi-directional horizontal loads. Further developments include multiple values of the vertical pressure and of the shear modulus of the rubber (including reclaimed rubber compounds (Losanno et al., 2020; Cilento et al., 2022), as well as different shape of the bearings. Also, additional FEAs on elastomeric bearings needs to be carried out implementing different material models for the elastomer, including viscoelasticity, or compared with results obtained using phenomenological approaches (Vaiana et al., 2019; Vaiana and Rosati, 2023).

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

SG: Conceptualization, methodology, software, investigation, resources, Writing—Original Draft, Writing—Review Editing.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Anany, Y. M., Van Engelen, N. C., and Tait, M. J. (2017). Vertical and lateral behavior of unbonded fiber-reinforced elastomeric isolators. J. Compos. Constr. 21 (5), 4017019. doi:10.1061/(asce)cc.1943-5614.0000794

CrossRef Full Text | Google Scholar

Angeli, P., Russo, G., and Paschini, A. (2013). Carbon fiber-reinforced rectangular isolators with compressible elastomer: Analytical solution for compression and bending. Int. J. Solids Struct. 50, 3519–3527. doi:10.1016/j.ijsolstr.2013.06.016

CrossRef Full Text | Google Scholar

ASCE-7 (2010). Minimum design loads for buildings and other structures. American Society of Civil Engineers.

Google Scholar

Calabrese, A., Spizzuoco, M., Galano, S., Tran, N., Strano, S., and Terzo, S. (2021). A parametric study on the stability of fiber reinforced rubber bearings under combined axial and shear loads. Eng. Struct. 2021 (227), 111441. doi:10.1016/j.engstruct.2020.111441

CrossRef Full Text | Google Scholar

Cilento, F., Losanno, D., and Piga, L. (2022). An experimental study on a novel reclaimed rubber compound for fiber-reinforced seismic isolators. Structures 45 (11), 9–22. doi:10.1016/j.istruc.2022.09.009

CrossRef Full Text | Google Scholar

de Raaf, M. G., Tait, M. J., and Toopchi-Nezhad, H. (2011). Stability of fiber-reinforced elastomeric bearings in an unbonded application. J. Compos. Mater. 45 (18), 1873–1884. doi:10.1177/0021998310388319

CrossRef Full Text | Google Scholar

Decree January 17 (2018). Update of the "Technical standards for construction.

Google Scholar

Galano, S. (2022). Stability assessments of unbonded fiber rienforced elastomeric isolators. Naples: University of Naples Federico II.

Google Scholar

Galano, S., Calabrese, A., and Losanno, D. (2021). On the response of fiber reinforced elastomeric isolators (FREIs) under bidirectional shear loads. Structures 34, 2340–2354. doi:10.1016/j.istruc.2021.08.107

CrossRef Full Text | Google Scholar

Galano, S., Calabrese, A., Losanno, D., Serino, G., and Strano, S. (2022). Tuning the lateral response of unbonded fiber reinforced elastomeric isolators (U-FREIs) through horizontal holes: Experimental and numerical findings. Compos. Struct. 289 115454. doi:10.1016/j.compstruct.2022.115454

CrossRef Full Text | Google Scholar

Galano, S., Calabrese, A., and Losanno, D. (2021). Tuning the lateral response of unbonded fiber reinforced elastomeric isolators (U-FREIs): Experimental - numerical findings, Composite Structures, 289, 28–30. doi:10.1016/j.compstruct.2022.115454

CrossRef Full Text | Google Scholar

Galano, S., Losanno, D., and Calabrese, A. (2021). Stability analysis of unbonded fiber reinforced isolators of square shape. Eng. Struct. 245 (2021), 112846. doi:10.1016/j.engstruct.2021.112846

CrossRef Full Text | Google Scholar

Galano, S. (June 2021). “On the vertical response of fiber reinforced elastomeric isolators (FREIs) under combined vertical and lateral loading,” in Proceedings of the Compdyn 2021 - 8th ECCCOMAS thematic conference on computational methods in structural dynamics and Earthquake engineering (Athene, Greece, 28–30.

Google Scholar

Kalfas, K., and Mitoulis, S. A. (2017). Performance of steel-laminated rubber bearings subjected to combinations of axial loads and shear strains. Procedia Eng. 199, 2979–2984. doi:10.1016/j.proeng.2017.09.533

CrossRef Full Text | Google Scholar

Kalfas, K. N., Mitoulis, S. A., and Konstantinidis, D. (2020). Influence of steel reinforcement on the performance of elastomeric bearings. J. Struct. Eng. (N. Y. N. Y). 146 (10). doi:10.1061/(asce)st.1943-541x.0002710

CrossRef Full Text | Google Scholar

Kelly, J. M. (1999). Analysis of fiber-reinforced elastomeric isolators. J. Seismic Earthq. Eng. 2 (1), 19–34.

Google Scholar

Kelly, J. M., and Konstantinidis, D. A. (2011). Mechanics of rubber bearings for seismic and vibration isolation. John Wiley & Sons.

Google Scholar

Konstantinidis, D., and Kelly, J. M. (2014). “Advances in low-cost seismic isolation with rubber,” in Tenth U.S. National conference on Earthquake engineering (Alaska: Anchorage).

Google Scholar

Losanno, D., Calabrese, A., Madera-Sierra, I. E., Spizzuoco, M., Marulanda, J., Thomson, P., et al. (2020). Recycled versus natural-rubber fiber-reinforced bearings for base isolation: Review of the experimental findings. J. Earthq. Eng. 26, 1921–1940. doi:10.1080/13632469.2020.1748764

CrossRef Full Text | Google Scholar

Losanno, D., De Domenico, D., and Madera-Sierra, I. E. (2022). Experimental testing of full-scale fiber reinforced elastomeric isolators (FREIs) in unbounded configuration. Eng. Struct. 260, 114234. doi:10.1016/j.engstruct.2022.114234

CrossRef Full Text | Google Scholar

Losanno, D., Madera Sierra, I. E., Spizzuoco, M., Marulanda, J., and Thomson, P. (2019). Experimental assessment and analytical modeling of novel fiber-reinforced isolators in unbounded configuration. Compos. Struct. 212, 66–82. doi:10.1016/j.compstruct.2019.01.026

CrossRef Full Text | Google Scholar

Madera Sierra, I. E., Losanno, D., Strano, S., Marulanda, J., and Thomson, P. (2019). Development and experimental behavior of HDR seismic isolators for lowrise residential buildings. Eng. Struct. 183, 894–906. doi:10.1016/j.engstruct.2019.01.037

CrossRef Full Text | Google Scholar

Moon, B. Y., Kang, G. J., Kang, B. S., and Kelly, J. M. (2002). Design and manufacturing of fiber reinforced elastomeric isolator for seismic isolation. J. Mater. Process. Technol. 130 (131), 145–150. doi:10.1016/s0924-0136(02)00713-6

CrossRef Full Text | Google Scholar

Moon, B. Y., Kang, G. J., Kang, B. S., and Kim, H. S. (2003). Mechanical property analysis and design of shock absorber system using fiber bearing by experimental method. JSME Int. J. Ser. C 46 (1), 289–296. doi:10.1299/jsmec.46.289

CrossRef Full Text | Google Scholar

MSC.Software Corporation (2017). MAR103 experimental elastomer analysis. Santa Ana, CA, USA.

Google Scholar

MSC.Software Corporation, MSC.Marc Mentat release guide, Santa Ana, CA, USA, 2005.

Google Scholar

MSC.Software Corporation, Volume B: Element Library, Santa Ana, CA, USA, 2017.

Google Scholar

Naeim, F., and Kelly, J. M. (1999). Design of seismic isolated structures: From theory to practice. New York: John Wiley & Sons.

Google Scholar

Ngo, T. V., Deb, S. K., and Dutta, A. (2017). Effect of horizontal loading direction on performance of prototype square unbonded fibre reinforced elastomeric isolator. Struct. Control Health Monit. 25 (2112), e2112–e2118. doi:10.1002/stc.2112

CrossRef Full Text | Google Scholar

Ngo, T. V., Dutta, A., and Deb, S. K. (2020). Predicting stability of a prototype unbonded fiber-reinforced elastomeric isolator by finite element analysis. Int. J. Comput. Methods 17 (10), 2050015. doi:10.1142/s0219876220500152

CrossRef Full Text | Google Scholar

Osgooei, P. M., Konstantinidis, D., and Tait, M. J. (2016). Variation of the vertical stiffness of strip-shaped fiber-reinforced elastomeric isolators under lateral loading. Compos. Struct. 144, 177–184. doi:10.1016/j.compstruct.2016.01.089

CrossRef Full Text | Google Scholar

Osgooei, P. M., Tait, M. J., and Konstantinidis, D. (2014). Finite element analysis of unbonded square fiber-reinforced elastomeric isolators (FREIs) under lateral loading in different directions. Compos. Struct. 113, 164–173. doi:10.1016/j.compstruct.2014.02.033

CrossRef Full Text | Google Scholar

Osgooei, P. M., Tait, M. J., and Konstantinidis, D. (2014). Three-dimensional finite element analysis of circular fiber-reinforced elastomeric bearings under compression. Compos. Struct. 108, 191–204. doi:10.1016/j.compstruct.2013.09.008

CrossRef Full Text | Google Scholar

Pauletta, M., Cortesia, A., and Russo, G. (2015). Roll-out instability of small size fiber-reinforced elastomeric isolators in unbonded applications. Eng. Struct. 102, 358–368. doi:10.1016/j.engstruct.2015.08.019

CrossRef Full Text | Google Scholar

Russo, G., and Pauletta, M. (2013). Sliding instability of fiber-reinforced elastomeric isolators in unbonded applications. Eng. Struct. 48, 70–80. doi:10.1016/j.engstruct.2012.08.031

CrossRef Full Text | Google Scholar

Toopchi-Nezhad, H., Drysdale, R. G., and Tait, M. J. (2009). Parametric study on the response of stable unbonded-fiber reinforced elastomeric isolators (SU-FREIs). J. Compos. Mater. 43 (15), 1569–1587. doi:10.1177/0021998308106322

CrossRef Full Text | Google Scholar

Toopchi-Nezhad, H., Tait, M. J., and Drysdale, R. G. (2008). Lateral response evaluation of fiber-reinforced neoprene seismic isolators utilized in an unbonded application. J. Struct. Eng. (N. Y. N. Y). 134 (10), 1627–1637. doi:10.1061/(asce)0733-9445(2008)134:10(1627)

CrossRef Full Text | Google Scholar

Toopchi-Nezhad, H., Tait, M. J., and Drysdale, R. G. (2008). Testing and modeling of square carbon fiber-reinforced elastomeric seismic isolators. Struct. Control Health Monit. 15, 876–900. doi:10.1002/stc.225

CrossRef Full Text | Google Scholar

Tubaldi, E., Mitoulis, S. A., and Ahmadi, H. (2018). Comparison of different models for high damping rubber bearings in seismically isolated bridges. Soil Dyn. Earthq. Eng. 104, 329–345. doi:10.1016/j.soildyn.2017.09.017

CrossRef Full Text | Google Scholar

Code, P., (1998-1:20132). Eurocode 8 - design of structures for earthquake resistance - Part 1: General rules, seismic actions and rules for buildings, 2005,

Google Scholar

Vaiana, N., and Rosati, L. (2023). Classification and unified phenomenological modeling of complex uniaxial rate-independent hysteretic responses. Mech. Syst. Signal Process. 182, 109539. doi:10.1016/j.ymssp.2022.109539

CrossRef Full Text | Google Scholar

Vaiana, N., Sessa, S., Marmo, F., and Rosati, L. (2019). An accurate and computationally efficient uniaxial phenomenological model for steel and fiber reinforced elastomeric bearings. Compos. Struct. 211, 196–212. doi:10.1016/j.compstruct.2018.12.017

CrossRef Full Text | Google Scholar