Computational intelligence methods in simulation and modeling of structures: A state-of-the-art review using bibliometric maps

The modeling and simulation of structural systems is a task that requires high precision and reliable results to ensure the stability and safety of construction projects of all kinds. For many years now, structural engineers have relied on hard computing strategies for solving engineering problems, such as the application of the Finite Element Method (FEM) for structural analysis. However, despite the great success of FEM, as the complexity and difficulty of modern constructions increases, the numerical procedures required for their appropriated design become much harder to process using traditional methods. Therefore, other alternatives such as Computational Intelligence (CI) techniques are gaining substantial popularity among professionals and researchers in the field. In this study, a data-driven bibliometric analysis is presented with the aim to investigate the current research directions and the applications of CI-based methodologies for the simulation and modeling of structures. The presented study is centered on a self-mined database of nearly 8000 publications from 1990 to 2022 with topics related to the aforementioned field. The database is processed to create various two-dimensional bibliometric maps and analyze the relevant research metrics. From the maps, some of the trending topics and research gaps are identified based on an analysis of the keywords. Similarly, the most contributing authors and their collaborations are assessed through an analysis of the corresponding citations. Finally, based on the discovered research directions, various recent publications are selected from the literature and discussed in detail to set examples of innovative CI-based applications for the modeling and simulation of structures. The full methodology that is used to obtain the data and generate the bibliometric maps is presented in detail as a means to provide a clearer interpretation of the bibliometric analysis results.

1 Introduction

Nowadays, modern construction projects are becoming much more challenging for structural engineers in terms of the required numerical simulations and procedures to achieve sustainable, safe, and economic designs (Plevris and Tsiatas, 2018). A few examples of some of these challenges are: 1) the usage of newly developed materials (Khan et al., 2020); 2) the complex geometries that arise from the implementation of structural optimization techniques (Vantyghem et al., 2020); 3) the required high resilience under extreme loading conditions (Frangopol and Soliman, 2016); 4) quantification and modeling of uncertainties (Möller et al., 2000). Therefore, it is clear that quick, robust, and reliable simulation and modeling techniques are required to ensure the feasibility, stability, and overall safety of modern structures. For many years now, using the Finite Element Method (FEM) (Bathe, 2008; Liu et al., 2022) has become a standard procedure for most practical applications in the analysis and design of structures. Despite the enormous success of the FEM in the field of structural engineering so far, the truth is that its traditional implementation is becoming impractical for some of the previously mentioned modern challenges.

Mathematical models that are created with a precise analytical description, such as FEM, are also referred to as hard-computing models/methods. Because of their precise formulation, hard-computing models produce deterministic and exact results that rely completely on the quality of the given input parameters. Nonetheless, for certain problems and applications, the estimation of the model parameters may be a difficult task that cannot be achieved with complete certainty (Fong et al., 2006). Moreover, there are highly complex phenomena that are just too difficult to be mathematically described with high precision, e.g. modeling material composites or including complex mechanical behaviour such as cracking or yielding. In such cases, there are normally two alternatives to solve the problem: 1) create a detailed but very computationally expensive model (Lin et al., 2022); 2) define a series of rules and assumptions to drastically simplify the system (Shi et al., 2018). Either way, both approaches significantly reduce the practical applicability of the method. Thereby, it is well-known that hard-computing strategies generally lack robustness.

In contrast to hard-computing deterministic models, soft-computing (SC) methods are another category of strategies that are used to find approximate solutions to complex problems (Ibrahim, 2016). These methods are inspired by multiple biological processes that are observed in nature. For example, the process of natural evolution, the way neurons process information inside the brain, and the complexity of the human language. Inspiration from these three nature processes have given birth to the popular methods of evolutionary algorithms (EA) (Katoch et al., 2021), artificial neural networks (ANN) (Schmidhuber, 2015), and fuzzy systems (FS) (Blanco-Mesa et al., 2017), respectively. The soft-computing paradigm is also commonly referred to as computational intelligence (CI), and it is considered a sub-field of artificial intelligence (AI) (Bezdek, 1994). According to the IEEE Computational Intelligence Society (IEEE-CIS, 2021), CI is the theory, design, application, and development of biologically and linguistically motivated computational methods in which three main pillars are identified: artificial neural networks, fuzzy systems, and evolutionary algorithms. Nevertheless, CI is not limited to these areas as it is an evolving field that embraces new emerging nature-inspired computational strategies, e.g. ambient intelligence, artificial life, and social reasoning, among others.

In essence, soft-computing techniques tend to increase the robustness of the solution strategy by replacing some of the complex mathematical operators that are part of the hard-computing approach (such as differential equations), with approximations based on probabilistic and stochastic methods (such as data-driven regression models and optimization algorithms) (Ghaboussi, 2018). Naturally, a full soft-computing solution approach is not often the best strategy for a particular problem. However, it may present a potential opportunity to enhance the hard-computing model. Therefore, sometimes the most efficient alternative is to combine the best of both worlds, the accuracy contained in the mathematical description of the hard-computing approach, and the added robustness from the soft-computing strategy (Ovaska, 2004).

This paper aims to explore the current research directions regarding the application of the CI paradigm into the modeling and simulation of structures. It is evident that CI methodologies are quickly gaining popularity and acceptance in the field of structural engineering. This may be attributed to the fact that the research, technology and tools that allow the study and application of CI techniques are rapidly maturing and becoming easily accessible. Therefore, the fast-paced environment, and the potential opportunities that arise with it, serve as the main motivation for this study.

The implementation of soft-computing techniques in simulation and modeling of structures is an area of research that has opened new discussions and led to innovative research and applications. Various authors have published comprehensive review-oriented studies on similar areas in the last couple decades. For instance, a review of ANNs in the field of civil engineering was conducted by Ian Flood as early as 1994 (Flood and Kartam, 1994a,b). Similarly, Adeli (Adeli, 2001a) also reviewed the applications of ANNs in civil engineering in the decade 1990 to 2000. Ghaboussi (Ghaboussi, 2010a) provides a thorough and comprehensive panorama regarding the advantages and limitations of the soft computing techniques to the traditional hard computing approach in the context of computational mechanics, focusing but not limited to the usage of artificial neural networks. More recently, the work from Salehi et al. (Salehi and Burgueño, 2018) provides a general overview of the emerging artificial intelligence methodologies in the structural engineering domain. Falcone et al. (Falcone et al., 2020) reviews the application of soft-computing strategies in earthquake and structural engineering. Likewise, Lu et al. Lu et al. (2022) explore four main AI-driven studies also in the field of earthquake and structural engineering. Kumar and Kochmann (Kumar and Kochmann, 2022) identify promising applications of machine learning methods in computational solid mechanics. Lagaros and Plevris (Lagaros and Plevris, 2022a,b) analyzed the emerging AI powered methodologies in civil engineering, focusing in recent contributions from 2021 to 2022.

What stands-out in the investigation presented in this paper is that it is centered around a data-driven bibliometric analysis using modern science mapping techniques. The analysis is conducted on a vast database of 8107 publications relevant to the application of CI methods in the simulation and modeling of structures. The database is self-obtained using advanced search capabilities provided by the Scopus scientific web-based search engine (Elsevier, 2021a). Our main goal is to explore the available scientific literature in a broader sense, letting the data speak for itself to provide an unbiased report without human intervention. In addition to the bibliometric analysis results, a detailed description of the implemented science mapping methodology is presented, which is carried out using custom-made algorithms and visualization tools for the purposes of the study. The later is included as an attempt to provide the reader with the necessary tools for a correct interpretation of the bibliometric analysis results.

Lately, the popularity of bibliometric analysis-based studies such as the one presented in this paper, has significantly increased due to the development and accessibility of modern data analysis tools and web-based scientific databases. This has resulted in numerous studies adopting these innovative techniques. Particularly, in the field of civil engineering, such methodologies involving bibliometric maps have been used to uncover the state of the art regarding blockchain technology in Civil Engineering (Plevris et al., 2022); to map the social network interactions in the sub-field of sustainability (Zhou et al., 2020); to study the status and development trends of the Journal of Civil Engineering and Management (Yu et al., 2019); mapping the progress and advances of the industry 4.0 in construction (Zabidin et al., 2020); to investigate the usage of BIM technologies in the Structural Engineering field (Vilutien et al., 2019).

The rest of the paper is organized as follows. A brief overview of the bibliometric analysis topic is provided in Section 2, including a detailed explanation of the science mapping methodology that is developed and later used. In Section 3, the results of the results from the bibliometric analysis are presented, starting with a description of the procedure to obtain the database in Section 3.1, and followed by the analysis of various metrics in Sections 3.2–3.4. In Section 3.5, the bibliometric maps are presented and their properties are highlighted and discussed. Additionally, the authors provide their own interpretation of the maps in Section 3.6. Finally, in Section 4, several examples of recent studies of CI-powered methodologies relevant to the topic of modeling and simulation of structures are provided.

2 Introduction to bibliometric analysis and science mapping

The term “bibliometric analysis” is related to methodologies that utilize quantitative and statistical tools to process and analyse large volumes of published literature of a specific domain (Broadus, 1987). They are used for a variety of reasons such as to discover emerging trends in article and journal performance, collaborations patterns, and to explore the intellectual structure of the specific domain. There are two main distinguished categories of bibliometric analysis techniques: performance analysis and science mapping. Performance analysis attempts to measure the overall contribution of research constituents such as authors, publishers, institutions, countries, etc. (Narin and Hamilton, 1996; Kostoff, 2002). Two of the most commonly adopted performance indicators are the number of publications and the number of citations received. The number of publications is usually associated with productivity whereas the number of citations is related to the impact or influence of a research work or an individual researcher. There are other hybrid measurements such as the h-index which combines both the number of citations and the number of publications in a compact, simple, and elegant metric (Hirsch, 2005); or newer metrics such as the PageRank algorithm (Yan and Ding, 2011). On the other hand, science mapping (or bibliometric mapping) techniques focus on the analysis of the relationships between the research constituents. In essence, it allows the mapping of the cumulative scientific knowledge by making sense of large volumes of unstructured data (Donthu et al., 2021). For example, science mapping techniques can be used to process the relationship between all the different keywords on a large database of publications to discover the overall thematic. Similarly, it can be used for analysing the authorship of publications to map the collaboration between researchers or institutions. Such relationships are then presented in two-dimensional network maps that tend to form clusters of similar terms that are quite intuitive, easy to read and interpret, and may reveal interesting features that were “hidden” or difficult to track before (Cobo et al., 2011). The true potential of bibliometric analysis comes when both performance analysis and science mapping techniques are combined together. As stated by Donthu et al. (Donthu et al., 2021), bibliometric studies that are well done are able to create a strong foundation for advancing a field, enabling researchers to gain a one-stop overview, identify knowledge gaps, derive novel ideas, and position their intended contribution in the field.

2.1 Construction process of bibliometric maps

A bibliometric map provides a graphical representation of the relationships between specific fields of information that are extracted from a large database of publications. Most commonly, they are created from fields or items that can be either keywords, authors, publishers, institutions, or citations. The construction of the map requires the counting of the occurrences and the relevant co-occurrences of the chosen field or item (e.g. the keywords) among all the publications in the analyzed database. Using these quantities, a similarity measurement is defined to quantify how closely related each item is in relation to all the others (e.g. how similar is one keyword to any other). Finally, all the items are positioned inside a 2D (or less often, 3D) space, so that a big map is created where the similarities between all the items are represented by their relative euclidean distances. In other words, similar items are positioned closer together creating networks of well-defined clusters that may reveal useful information with a simple visual inspection. Finding the position of all the items is a challenging problem known as multidimensional scaling (MDS) (Borg and Groenen, 2005). Because of the dimensionality reduction and the fact that a multidimensional space needs to be properly “mapped” to a reduced 2D (or 3D) space, the exact solution to the MDS problem does not exist, instead an optimization problem is formulated to find an approximate solution that minimizes a representation error.

It is useful to provide the basic idea on the process that is used to construct the bibliometric maps, in order to reduce the chance of a miss-interpretation of the results. For that reason, the next Sections 2.1.2–2.1.4 are dedicated to providing a detailed explanation of the procedure. Moreover, the authors present a self-developed mapping technique that uses a genetic algorithm to solve the optimization task that arises from the multidimensional scaling problem. The proposed method is an improved version of a tool created in a previous study (Plevris et al., 2019), which in turn was inspired from other well-established bibliometric mapping techniques such as the VOS method and software (van Eck and Waltman, 2010; Waltman et al., 2010). In the following, the mapping process is explained in the context of a keyword analysis, however, the same concepts may be applied to other type of fields, such as authors or institutions.

2.1.1 Mapping of keywords

Creating a bibliometric map of keywords may reveal the underlying theme of a large collection of scientific publications, as well as potentially identifying the emerging trends and gaps on the field. The keywords in a publication are a reflection of the whole content of the document and provide a simple way of linking various publications together. When two or more publications have one or more keywords in common, it usually indicates that they are related, i.e. they are dealing with similar research topics. In the Scopus database, each publication may have two types of associated keywords: author keywords and index keywords. The author keywords are based on the author’s description of their own work and are chosen manually by the authors. On the other hand, the index keywords are determined by the content suppliers or publishers and are often created by applying modern linguistic analysis techniques to the abstract of the publication or the article itself (Elsevier, 2021b). One example is the Perceptron Training Rule which assigns weights to the words on sentences of abstracts and processes them with an algorithm to determine the keywords (Bhowmik, 2008).

2.1.2 Ocurrence and co-ocurrence

The quantification of the occurrence and co-occurrence of all the unique items nkey (in this case, keywords) that are used in the studied database is an essential step in the construction of bibliometric maps. The total number of publications in the database is denoted as npub. The occurrence O_i is a number that quantifies how many publications are using a specific keyword k_i (e.g. if the keyword k_i has an occurrence value of O_i = 10, it means that it appears in 10 publications of the database). The co-occurrence value C_ij indicates in how many publications a keyword k_i appears together with another keyword k_j (e.g. a co-ocurrence of C_ij = C_ji = 5 means that the keyword k_i appears together with the keyword k_j in five publication records). The occurrence and co-occurrence of the total n keywords may be expressed mathematically in matrix form as:

$\mathbf{O}={\left\{O_1,\dots ,O_n\right\}}^T(1)$

$\mathbf{C}=\left[\begin{array}{ccc}\hfill C_{11}\hfill & \hfill \cdots \hfill & \hfill C_{1n}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill C_{n1}\hfill & \hfill \cdots \hfill & \hfill C_{nn}\hfill \end{array}\right](2)$

Normally, the total number of unique keywords nkey contained in all the publications of the database is considerably large and it is a common practice to choose a lower number n to construct the map. The chosen quantity n may be based on a predefined occurrence value (i.e. choose all the keywords with a occurrence value higher than a specified threshold). Alternatively, a fixed amount of keywords may be chosen (e.g. select the first 50 keywords with the highest occurrence value).

2.1.3 Similarity and dissimilarity measures

The co-occurrence matrix C is the base for the construction of the map. However, it is argued that the co-occurrence itself does not accurately represent a real similarity measure between items (van Eck et al., 2010). Instead, a specific similarity or dissimilarity quantity must be determinated (Gower, 2005). There are two common approaches that can be used to compute the similarity between two items k_i and k_j from the co-occurrence matrix: 1) Direct methods that simply rely on a normalization of their specific co-occurrence values C_ij (Eck and Waltman, 2009); and 2) indirect methods that take into consideration the co-occurrence of the items k_i and k_j with all the other items {k₁, …, k_n}. In other words, indirect methods compare the full rows C_i: and C_j:. One example of an indirect method is using the Pearson’s correlation coefficient as a similarity measure (Ahlgren et al., 2003).

In this study, an indirect approach is implemented to determine a dissimilarity value between each item k_i and k_j. The idea is to calculate the relative error that results from comparing all the elements in the ith row with all the elements of the jth row to obtain a value D_ij that quantifies their dissimilarity. The respective operations are written as follows:

$\mathbf{D}=\left[\begin{array}{ccc}\hfill D_{11}\hfill & \hfill \cdots \hfill & \hfill D_{1n}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill D_{n1}\hfill & \hfill \cdots \hfill & \hfill D_{nn}\hfill \end{array}\right](3)$

$D_{ij}=\sum _{r=1}^n\mid \frac{C_{ir}}{T_i}-\frac{C_{jr}}{T_j}\mid (4)$

$T_i=\sum _{t=1}^n{C}_{it},T_j=\sum _{t=1}^n{C}_{jt}(5)$

A high value of D_ij indicates that the items k_i and k_j are not similar, whereas a low value indicates that they are similar. One disadvantage on the proposed dissimilarity measure is when comparing two items that do not share any co-occurrence with any other item (e.g. T_i = 0 and T_j = 0). In that case, the computed dissimilarity would be D_ij = 0, which suggests that the terms are very similar when there is no information to suggest that they actually are. In fact, terms with no co-occurrence with any item may increase the error of the mapping technique considerably as they represent isolated items that do not share any similarity with any other item. In any case, displaying isolated items on the map does not comply with the concept and goals of bibliometric mapping where the aim is to find relationships. Therefore, in the presented methodology, items with 0 co-occurrences are excluded from the map.

2.1.4 Multidimensional scaling by optimization algorithms

In a bibliometric map, each keyword is represented by a point in the 2-dimensional or 3-dimensional euclidean space. The distance between any two points k_i and k_j is dictated by their corresponding dissimilarity value D_ij. A pair of keywords k_i and k_j that are not similar should be far away from each other (high value of D_ij). On the contrary, if two keywords are very similar they should be close to one another (low value of D_ij).

In general, for realistic applications, the number of items n is much larger compared to the number of dimensions of the graphical space where the map is drawn (2D or 3D). Therefore, it is graphically impossible to position all the points to exactly match the computed dissimilarity values. In other words, a multidimensional space of at least n − 1 dimensions would be required to achieve an error of absolute 0% between the real distance and the computed dissimilarity, which is clearly unfeasible from a graphical point of view. However, using an optimization algorithm, the error can be minimized so that the result is an approximation that still provides a good-enough visual representation of the similarities in a lower 2- or 3- dimensional space that the human eye can easily read and interpret. Hence, the optimization algorithm will provide the solution to the MDS problem mentioned earlier (Borg and Groenen, 2005).

In this study, a genetic algorithm (GA) is used to solve the optimization problem that results from the MDS. Other search strategies such as the MM algorithm (which stands for maximization by minimization) are also commonly applied in the creation of bibliometric maps (Groenen and Velden, 2016). Even simple optimizations strategies such as the pure random orthogonal search (PROS) (Plevris et al., 2021) can be used to solve the MDS problem, as shown in (Koutsantonis et al., 2022). For the purpose of this study, the GA approach is selected which has shown good overall performance comparable to the MM algorithm. Additionally, it provides more flexibility and allows the implementation of constraint functions such as restricting the mapping space to a specific shape (as shown later in section 3.5.4).

The optimization problem is written as an unconstrained minimization problem where the objective function f(p) is defined as the squared error e that results from comparing the item’s euclidean distances Z with their corresponding calculated dissimilarities D. The respective operations are written as follows:

$e=f\left(\mathbf{p}\right)=\sum _{i=1}^n\sum _{j=1}^n{\left(Z_{ij}-D_{ij}\right)}^2(6)$

$\mathbf{p}=\left\{x_1,y_1,x_2,y_2,\dots ,x_n,y_n\right\}(7)$

$\mathbf{Z}=\left[\begin{array}{ccc}\hfill Z_{11}\hfill & \hfill \cdots \hfill & \hfill Z_{1n}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill Z_{n1}\hfill & \hfill \cdots \hfill & \hfill Z_{nn}\hfill \end{array}\right](8)$

$Z_{ij}=\sqrt{{\left(x_j-x_i\right)}^2+{\left(y_j-y_i\right)}^2}(9)$

The design vector p contains all the x, y coordinates of the n items of a respective configuration of the map. The optimization task is to find a vector p^opt that minimizes the error e. The matrix Z is initialized by randomizing the positions of all the items in the map and computing their euclidean distances using Eq. 9. The upper xy_max and lower xy_min bounds of the coordinates x, y are set to xy_max = 2 ⋅ max(D) and xy_min = −2 ⋅ max(D). It should be noted that the optimization problem is in fact unconstrained and therefore the defined bounds are only used to sample random uniform values at the initialization of the optimization process.

The implemented GA uses the following genetic operators: tournament selection (Coello and Mezura-Montes, 2002), SBX crossover (Deb et al., 2007) and polynomial mutation (Deb and Deb, 2014). The population size is set to s = 100 and the termination criterion is taken as a fixed number of generations maxgen which is chosen based on the number of items n. The design vector with the lowest objective value p^opt at the last generation is used to construct the final bibliometric map.

2.1.5 Clustering

After the configuration of the map has been defined (i.e. the optimization problem has been solved), the resulting map layout is processed by a clustering algorithm to provide an appealing visual feedback by classifying the items into clusters using different colors. In our study, the k-means clustering algorithm is implemented using the real euclidean distances of the obtained configuration (Omran et al., 2007). Alternatively, one can use the computed dissimilarity measure or a combination of both, such as in (Waltman et al., 2010). The main advantages of the k-means algorithm are that it is easy implement, it is computationally inexpensive and it is very flexible. Its main disadvantage lies in the fact that it requires the number of clusters as an input value and it may fail to capture clusters with highly irregular shapes. Nonetheless, the obtained results using the k-mean clustering algorithm proved to be very satisfactory for the goals of the present study.

3 Bibliometric analysis

3.1 Database of literature

The first step for the bibliometric analysis is the collection of an extensive database based on the literature. In this study, the Scopus search engine is used to that end (Elsevier, 2021a). Scopus provides a very powerful and advanced search capability that allows the user to conduct quick queries based on multiple combinations of keywords, authors, publishers, publication year, and other relevant parameters. Various queries based on two groups of keywords are conducted. The first keyword group involves terms about CI methods in general, whereas the second keyword group contains terms related to modeling and simulation of structures. Table 1 shows the two groups of keywords that were used in the study. The terms from the first column are combined with the terms on the second column using the AND operator. On the other hand, the terms that belong to the same column are combined with the OR operator (e.g. Fuzzy theory OR Neural Networks AND Structural Analysis OR Finite Element Method).

TABLE 1

TABLE 1. List of the keywords used in the Scopus query to obtain the database of literature used in the bibliometric analysis.

The search is restricted to the years 1990 to August 2022. The final keywords for the query were chosen after multiple attempts to narrow down the search to include only the topics that are directly related to the modeling and simulation of structures and CI methodologies. More general terms such as “Structure” or “Modeling” are avoided as they produce vast results from other fields of engineering that are not relevant to the present study. Additionally, some unwanted keywords were also directly included using the operator “AND NOT.” This is done to prevent retrieving topics outside our scope, e.g. the keywords: “Medical,” “Biomedical,” “Magnetic,” “Electric.” The full database is constructed using nine different queries according to Table 1. The database was created and updated multiple times during the creation of this study. The last and final update used is the one created on 12 August 2022. The following paragraph provides an example of one of the nine search queries introduced into the Scopus advanced search field.

Example of the search query used in Scopus for the keyword “Finite Element”: SUBJAREA(engi) AND (TITLE-ABS-KEY(“neural network”+“Finite Element”)) OR (TITLE-ABS-KEY(“fuzzy system”+“Finite Element”)) OR (TITLE-ABS-KEY(“genetic algorithm”+“Finite Element”)) OR (TITLE-ABS-KEY(“soft computing”+“Finite Element”)) OR (TITLE-ABS-KEY(“computational intelligence”+“Finite Element”)) AND NOT (TITLE-ABS-KEY(“Magnetic”)) AND NOT (TITLE-ABS-KEY(“Electric”)) AND NOT (TITLE-ABS-KEY(“Medical”)) AND NOT (TITLE-ABS-KEY(“Biomedical”)) AND (PUBYEAR AFT 1990).

The result from each search query is downloaded to a CSV file. Scopus lets the user select which fields of the metadata of each publication are to be downloaded. For this study, the downloaded fields are the following: title, DOI, publication year, authors names, author IDs, author keywords, index keywords, citations, publishers and affiliations. The nine CVS files (one for each search query) were then combined and merged into a single file. The duplicates were properly removed using Microsoft’s Excel tools based on the unique DOI field. The final database contains a total of 8107 publications.

3.2 Publications per year

The first metric to be analyzed is the production of publications over time. With that intention, a histogram is created that shows the number of publications per year, as shown in Figure 1. It has to be noted that 2022 is still a year in progress, so the data for this year are incomplete and the relevant number of publications for 2022 is expected to grow significantly. It can be observed that there has been a relatively steady growth in the quantity of publications until the year 2015, with a linear-like growth scheme. After 2015, the number of publications noticeably accelerates and appears to show an exponential growth. Such behaviour coincides with the current hype and development in machine learning topics observed in the global scientific community. For instance, in the AI index report 2022 created by the Institute for Human-Centered AI of the Stanford University (Zhang et al., 2020), the same accelerated growth is observed starting around 2015–2016, see Figure 2. The rapidly growing increase in research is an indicator that the acceptance and implementation of CI-powered techniques is gaining popularity among the Structural Engineering research community.

FIGURE 1

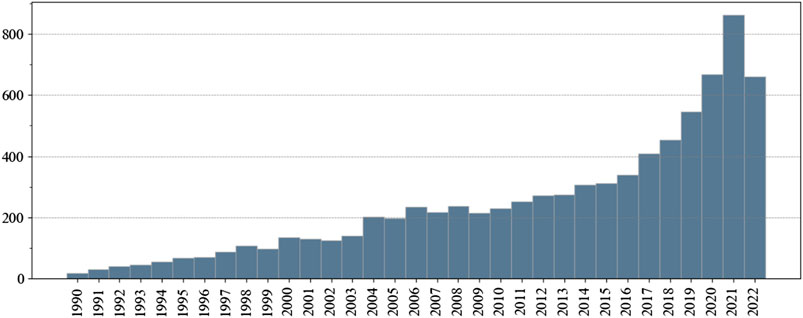
FIGURE 1. Number of publications per year regarding the application of CI methods in the structural engineering field. The year 2022 is counted only until August.

FIGURE 2

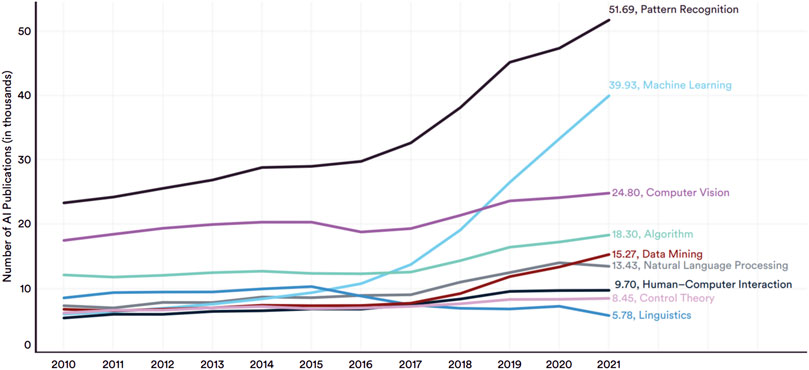
FIGURE 2. Number of AI publications by Field of Study. Source: Center for Security and Emerging Technology, 2021; Chart: 2022 Index Report (Zhang et al., 2020).

3.3 Most utilized journals

The total of 8107 publications that comprises our database is published in 548 different journals. The top 25 journals in terms of the number of published papers (considering only those in the studied database) is presented in Table 2. The Scopus CiteScore (corresponding to the year 2021), and the Source Normalized Impact per Paper (SNIP) are also included in the table. The current CiteScore measures the average citations received per document published in the year 2021 and the SNIP measures the actual citations received relative to citations expected in the same field for the year 2021. Note that the metrics related to the number of citations and number of publications that are included in the table (first two columns) only consider the publications in the studied database, but CiteScore and SNIP (last two columns) are metrics derived by Scopus based on all the publications of the Journal in the corresponding year. The table on its own provides some hints of the research directions in the application of CI methodologies. For example, looking at the Journals in the top positions 1 and 4, it can be assumed that the analysis of composite structures and structural optimization are two topics where CI methodologies are constantly applied.

TABLE 2

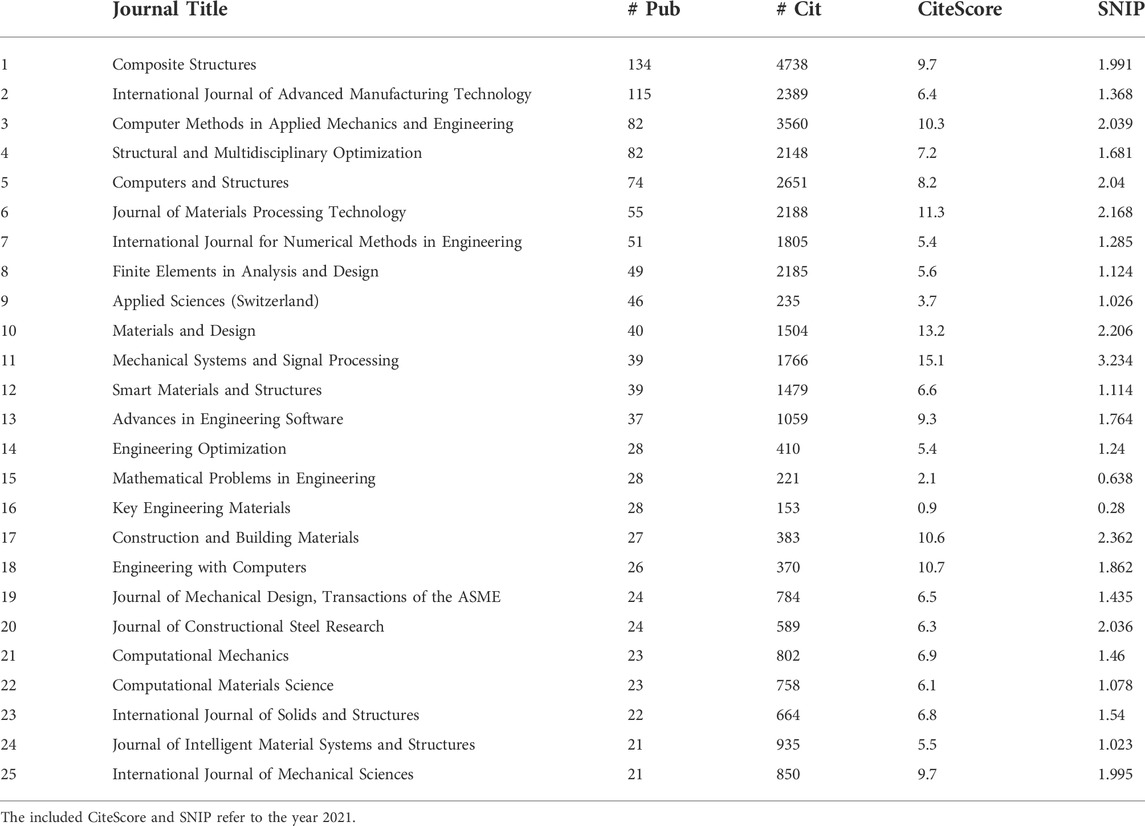
TABLE 2. Top 25 journals in terms of the number of published papers contained in the studied database.

3.4 Most cited papers

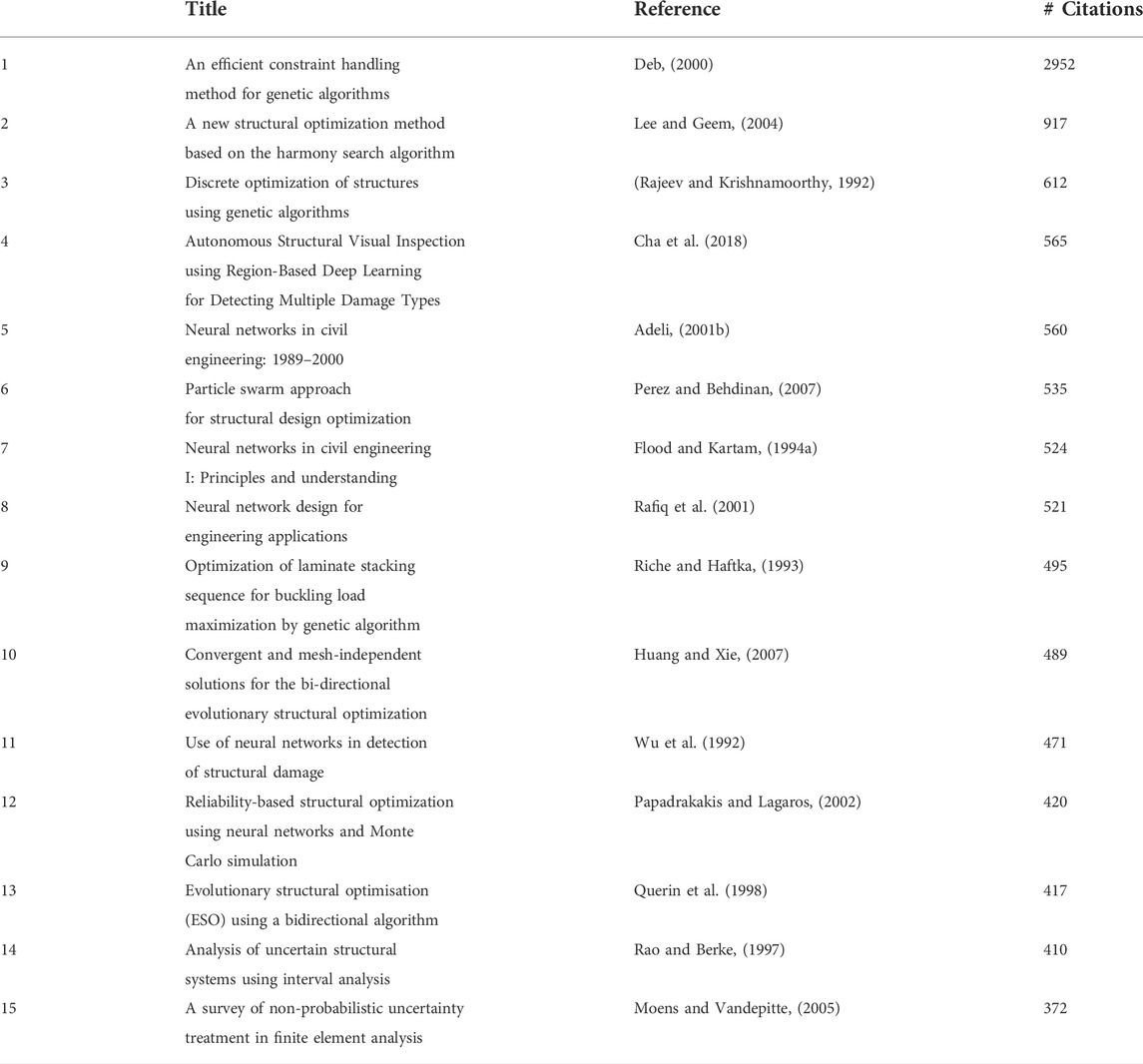
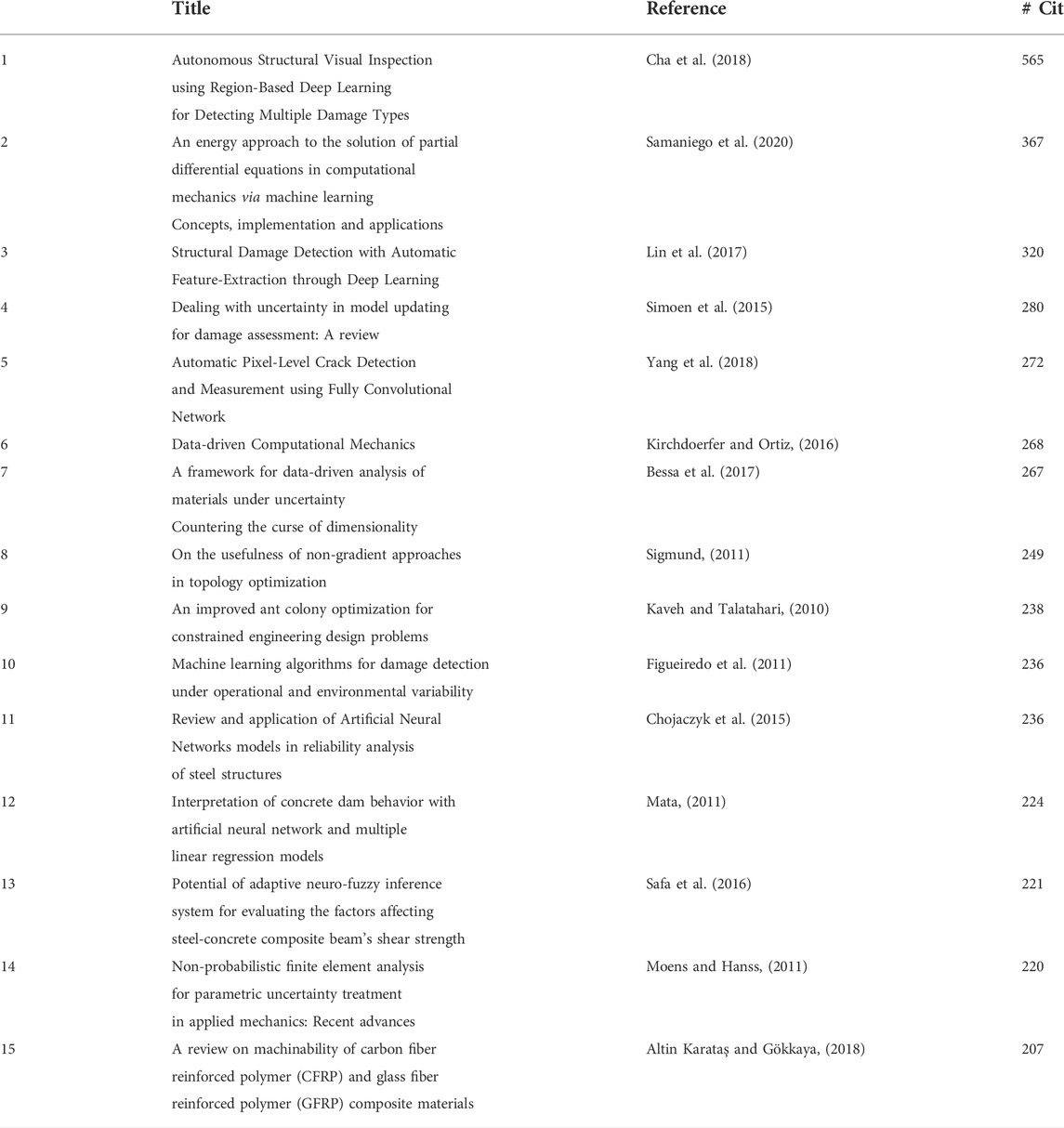
The number of citations is commonly used as a simple metric to measure the impact or influence of publications. With that in mind, two tables that show the most cited publications are constructed. Table 3 shows the top 15 most cited papers from 1990 to 2022 whereas Table 4 only considers papers published from 2010 to 2022. While the top 15 most cited papers cannot be considered a representative sample from the complete 8107 publications, it still provides a preliminary idea on some of the main research areas in the studied literature. From the first table, the top publication (with 2952 citations) is a constraint handling technique for genetic algorithms (Deb, 2000) which has become widely adopted in optimization problems using GA. In the paper, the methodology is applied to some mechanical engineering examples which is the reason why the publication made it to our database. Further inspection reveals that publications 2, 3, 6, 8, 9, 10, 12, and 13 deal with the topic of structural optimization. Publications 5, 7, and 8 are review studies about applications of neural networks, while publications 4 and 11 deal with the topic of damage detection. From the second table including publications after 2010, the top publication (with 565 citations) is a damaged-detection technique that leverages the power of deep learning (this publication also appears in the first table). Furthermore, publications 3, 4, 5, 9, 10 are also related to the damage detection and assessment in structures. Publications 2 and 13 explore methods to enhance the mathematical procedures of FEM while publications 7 and 8 treat the structural optimization topic.

TABLE 3

TABLE 3. Top 15 most cite publications in the studied database from 1990 to 2022.

TABLE 4

TABLE 4. Top 15 most cite publications in the studied database from 2010 to 2022.

3.5 Bibliometric maps

3.5.1 Graphics and visualization

The graphical representation adopted to draw the maps is as follows: each item (keyword, author, etc.) is drawn as a single point. The occurrence O_i of each item is represented by the size of the point. A larger point accounts for high occurrence values and a smaller point indicates low occurrence values. The co-occurrence C_ij between two items i, j is indicated by a line that connects them both. The line thickness indicates the strength of the co-occurrence, where a higher line thickness accounts for higher co-occurrences. However, small thickness values are used to avoid overly saturating the maps with lines. The colors of the items represent the different computed clusters, so that points with the same color belong to the same cluster. The maps are created with a limited number of items n so that they can be easily interpreted and understood given the limited space dictated by the size and format of this paper. In a virtual environment provided by a computer program, bibliometric maps can usually contain many more items as they can be properly explored with zoom, panning, and scaling capabilities provided by an interactive graphical user interface. The presented maps are created and visualized with our own tailor-made computational tools and algorithms. Python and Java are used for the backend, and the Javafx library has been used for the frontend (i.e. the graphics).

3.5.2 Bibliometric map of keywords

The total number of unique keywords in the whole database is nkey = 40, 830, considering both authors and index keywords. Prior to the construction of the map, a list of various similar keywords is manually created and fed to the algorithm so that similar keywords are merged together. This step is performed to remove redundant keywords, e.g. the keywords “neural networks” and “artificial neural network(s)” are all merged into a single keyword “neural network.” The number of keywords to be displayed in the map is chosen to be n = 150 so that the image is readable and fits the provided space in this paper. The number of computed clusters is set to five to facilitate the identification of general research trends. The resulting map is shown in Figure 3 and a zoom-in of the obtained clusters is presented in Figure 4.

FIGURE 3

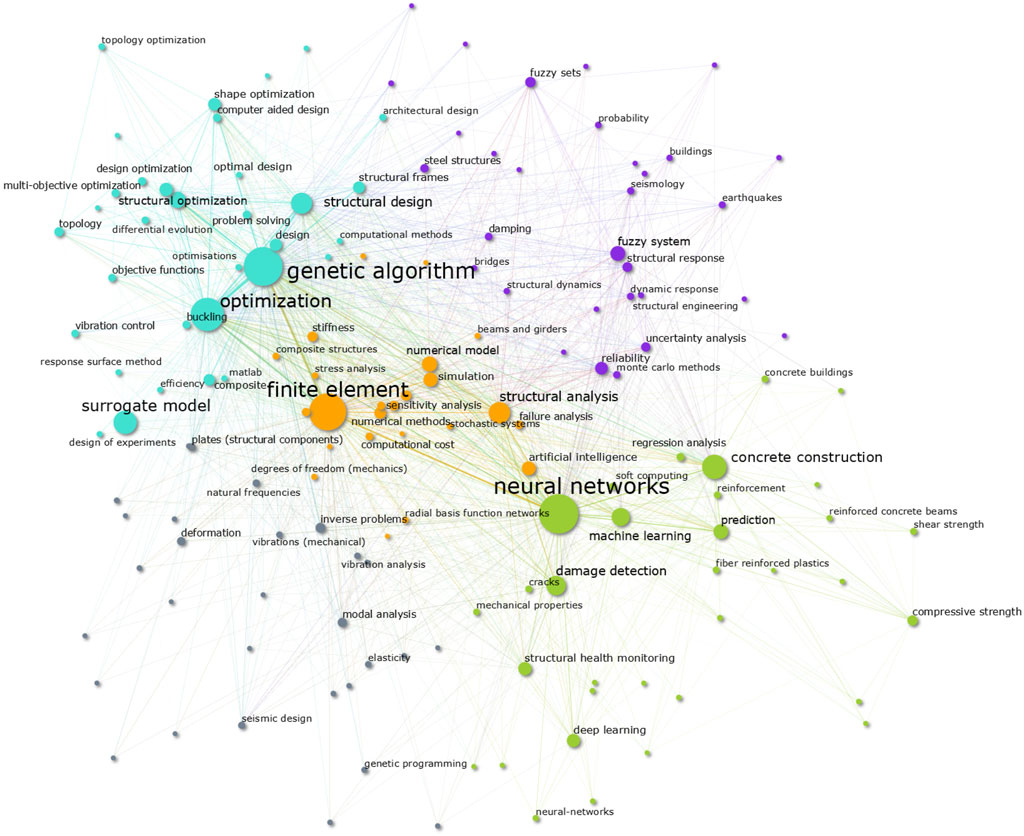
FIGURE 3. Bibliometric map of keywords. The 200 most frequent keywords are displayed in the map. The text of the items is only shown for the keywords with 200 occurrences or more. The co-occurrence connectivity line is only rendered if the value is higher than 10.

FIGURE 4

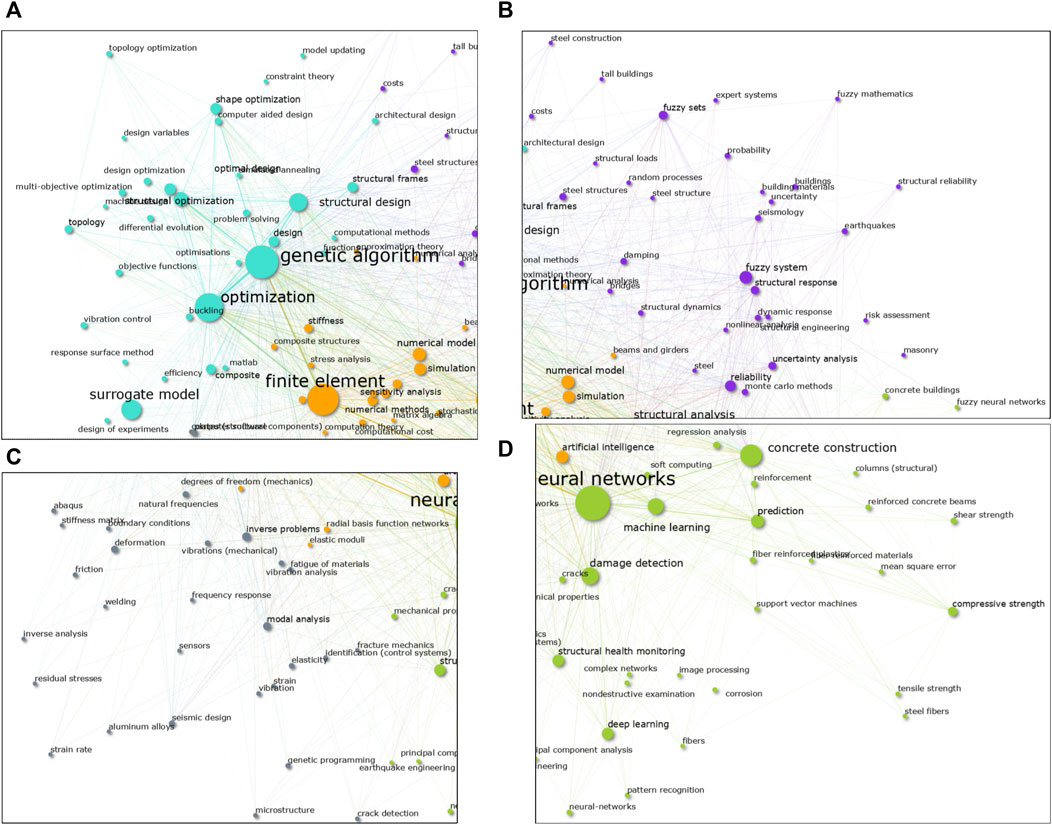
FIGURE 4. Close-up view to the bibliometric map of keywords. (A) Top-left quadrant. (B) Top-right quadrant. (C) Bottom-left quadrant. (D) Bottom-right quadrant.

3.5.3 Bibliometric map of authors

In this map, each item represents an author. The author-ID field provided by Scopus is used to avoid redundancies of two authors having similar or equal names, or the case where a single author has published papers using different names. The occurrence value of an author denotes the number of publications in which the author is participating. The co-occurrence value between two authors indicates the number of publications in which the two authors are collaborating (i.e. appearing together as authors). There is a total of nat = 19, 916 unique authors in the database making an average of nkey/nat = 2.05 authors per publication. Only the first 200 authors with the highest number of publications from the corresponding list are included in the map. Note that only the publications contained in the analyzed database are counted. The authors that appear in this study may have more publications that were not captured in the search query (see section 3.1). That being said, from the 200 top authors, some of them have a co-occurrence of 0 with all the other 199 authors. That does not necessarily means that those authors do not cooperate with others, but rather that their strongest collaborations are with authors that are not among the other top 199. Including items with 0 co-occurrence in the bibliometric map translates into isolated points that tend to increase the overall error and reduce the quality of the map considerably (see section 2.1.4). Therefore, the authors with 0 co-occurrences are removed so that the final map contains only 127 authors in which every author is connected to least one other author. The obtained map is shown in Figure 5. This time, instead of using the k-means algorithm, the clustering is made following the connectivity of the nodes so that each cluster contains a different network that is isolated from the rest.

FIGURE 5

FIGURE 5. Author collaborations map. Constructed using the 200 top authors with the highest number of publications from the studied database.

3.5.4 Brain-shaped bibliometric map of keywords 2015–2021

An alternative keyword map is presented using only the papers from 2015 to 2021. This results on a secondary list of npub = 4558 publications with nkey = 27, 337 unique keywords. For this specific case, the map-space (or the drawing area) has been restricted to resemble the silhouette of a human brain, thus, making a small visual analogy to the Computational Intelligence topic, see Figure 6. The main purpose of this map is to test our GA-based mapping methodology with the additional challenge of constraints, and to investigate potential changes in the research trend in the years 2015 to 2021 compared to the previous keyword map that includes years 1990 to 2021. The map is created by introducing an equality constraint function g(x) = 0 to the optimization algorithm described in 2.1.4. For a design vector x, the constraint function is equal to the number of points that are outside the given bounds.

FIGURE 6

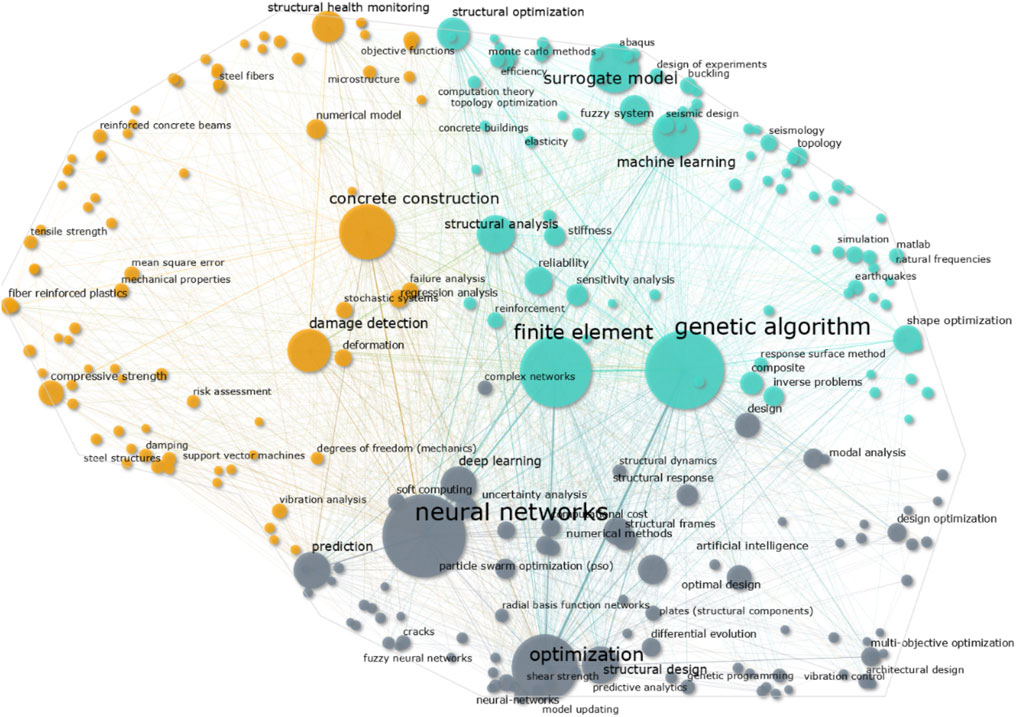
FIGURE 6. Bibliometric map of keywords using only the papers from 2015 to 2021. The 250 most frequent keywords are displayed in the map. The text is only shown for the keywords with 60 occurrences or more. The co-occurrence connectivity line is only rendered if the value is higher than 10.

3.5.5 Authors clusters and their keywords

A final diagram is constructed where the clusters obtained in the authors map are linked to the top 30 most frequent keywords. Each group of authors and the keywords are enclosed in rectangular areas. A straight line connecting the authors with the respective keywords is generated if the group of authors have published more than five papers using that particularly keyword. The connection line gets thicker as the number of publications is higher than 5. The resulting diagram is presented in Figure 7. Note that the keywords and author boxes are arranged in random order to prevent some areas of the map being overly saturated with lines.

FIGURE 7

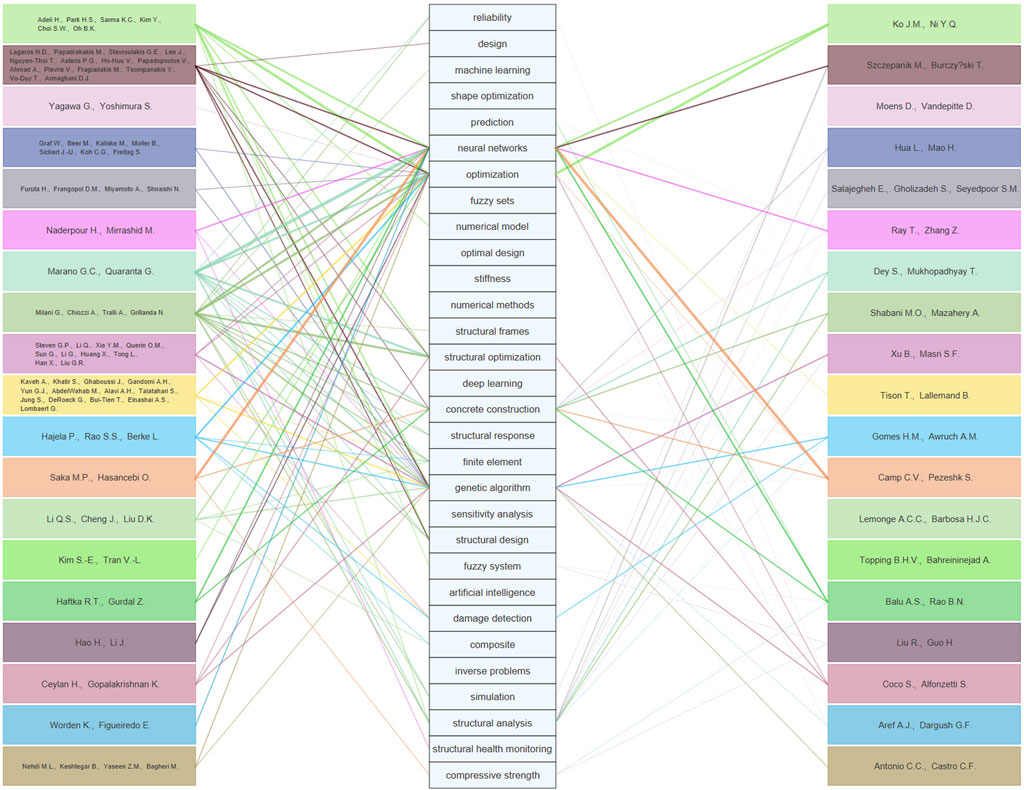
FIGURE 7. Map that links the author clusters with the top 30 most frequent keywords of the database. The connections lines are rendered only if the group of authors have five publications or more using the corresponding keyword.

3.6 Interpretation of the bibliometric maps

3.6.1 Main thematic

Looking at the first bibliometric map in Figure 3, the most frequent keywords in four of the computed clusters can be easily identified by visual inspection. To facilitate the discussion of the results, we have opted to associate each cluster to its most frequent keyword and use such keywords to refer to the clusters throughout the discussion. With that in mind, the obtained clusters are the following: 1) the orange colored “finite element” cluster in the middle-left; 2) the turquoise “optimization” cluster at the top-left (Figure 4A); 3) the green “neural network” cluster at the bottom (Figure 4D), and 4) the purple “fuzzy systems” cluster in the top-right (Figure 4B).

In the middle of the map, the concept of simulation and modeling of structures is depicted by the “finite element” cluster where we can read keywords such as “structural analysis,” “simulation,” and “numerical model.” As it lays in the center of the map, it is surrounded by the rest of the clusters that are related to CI methodologies and applications. Thus, the map is a clear visual analogy to the studied topic in this paper: Computational Intelligence methods in the simulation and modeling of structures. Such finding, which is not a surprise but rather expected, provides clear evidence that the mapping methodology has worked as intended.

3.6.2 Research trends

Some of the trending topics and research directions can be inferred by inspecting the keywords maps in Figures 3, 7. For that, we should look at the areas of the map that are densely populated with highly recurrent keywords as these may represent popular topics. However, it is important to keep in mind that keywords used directly in the search query (see Table 1) are expected to have the highest occurrence values and may not necessarily indicate research trends as they were put manually in the search. Instead, it is better to inspect and consider the whole area surrounding these keywords. On the following paragraphs, we expose the topics that we consider to be trending based on the keyword map in Figure 3. Although the interpretation of bibliometric maps is a subjective activity influenced by the own knowledge of the interpreter, we try to be as unbiased as possible and provide the reasoning of our selections.

Enhancing the FEM with CI

At the very center lays the finite element cluster containing the keywords: “simulation,” “numerical model,” “structural analysis,” “numerical methods,” “stiffness,” “matrix algebra,” “efficiency,” and “computational cost.” We believe that these keywords symbolize the core mathematical procedure of the FEM. Considering that from the center all these terms share multiple connections to all the other keywords in the entire map, we consider that using CI methodologies to increase the computational efficiency of the FEM is an implicit research direction present in the map.

Structural optimization

Perhaps, the most notable research direction is the applications of CI methodologies to the structural optimization problem. This conclusion comes after noticing that the optimization cluster (Figure 4A) looks much denser than other areas of the map, encompassing many keywords with high occurrence values such “structural design,” “structural optimization,” “shape optimization,” “topology optimization,” “optimal design,” and other similar words.

FEM surrogate models

At the middle-left side of the map, we can observe the keyword “surrogate model” with a noticeably large size that denotes a high occurrence value. Furthermore, it lays very close to the finite element and optimization clusters. We can then assume that the usage of finite element surrogate models in optimization problems is one popular research direction.

Earthquake engineering, uncertainty and reliability analysis

At the top-right side of the map, which corresponds to the fuzzy system cluster (Figure 4B), we can identify various keywords related to earthquake engineering and risk assessment, e.g. “earthquakes,” “seismology,” “dynamic response,” “structural reliability,” “Monte Carlo methods,” and “uncertainty analysis.” Therefore, pointing out the success of applying fuzzy methodologies in earthquake engineering, and for uncertainty and reliability analysis.

Structural health monitoring

At the bottom part of the map, at the neural network cluster (Figure 4D), we can observe the keywords “damage detection,” “structural health monitoring,” “cracks,” “image processing,” “patter recognition,” and “corrosion.” This highlights one more popular research direction in the usage of machine learning methodologies for structural health monitoring.

Modeling concrete material behaviour

Around the right-side of the neural network cluster (Figure 4D), we can find the keywords “concrete construction,” “columns,” “reinforced concrete beams,” “concrete building,” and other similar terms with a relatively high occurrence value. In the neighborhood around these keywords, we can also find the terms “prediction,” “neural network,” “machine learning,” “support vector machine,” “compressive strength,” “shear strength,” “tensile strength,” and “reinforcement.” Such arrangement of the items suggest that NNs and other regression models are commonly used to overcome the well-known difficulties in the numerical modeling of reinforced concrete.

Machine learning

From the second keyword map considering only the publications from 2010 to 2022 (Figure 6), we can observe more or less the same trends. Although it is difficult to assess visually, when looking at the numbers we can notice that there are subtle changes such as an increase of the usage of “machine learning,” “neural network” and “deep learning” keywords. This is consistent with the recent hype in machine learning that is happening nowadays in the research community as pointed out in section 3.2. It is then clear that an outgoing trend is in the machine learning direction.

3.6.3 Author collaborations

Bibliometric maps constructed from the authoring information contain far less connections between the items when compared to the keywords map. Consequentially, the result is a circular-shaped-map with several isolated groups, see Figure 5. These groups reveal the collaborations among the most notable researchers on the studied literature. Furthermore, we can identify some experts in specific areas by linking the authors to their most frequent keywords as it is done in Figure 7. For example, the turquoise colored cluster in the middle of the map formed by the authors: Lagaros N.D., Papadrakakis M., Plevris V., Papadopoulus V., Tsompanakis Y., Stavrtoulakis G.E., and Ahmad A. Some of the most frequent keywords of this group of authors are “neural networks,” “optimization,” “genetic algorithm,” “structural optimization” and “structural design” (see Figure 7). Therefore, the data suggest that we have identified a group of researchers working in the structural optimization topic. This information is useful as it provides a starting point to investigate the literature of a certain topic in more detail. One could directly take a look at the publications by such a group of authors, with some certainty based on the data that they are experts in the field.

3.7 Limitations of the bibliometric analysis

Although a large number of publications was used in the bilbiometric study, it has to be noted that only the Scopus database has been accessed. There are other large scientific databases such as Web of Science (WoS) which could contain more publications that may influence the results. However, as the main purpose is to obtain an overall picture, using any database that is sufficiently large (Pranckut, 2021), should lead to similar conclusions. Additionally, there are some processes that are difficult to automate and require the input of a human being, thus, influencing the outcome with one’s own knowledge. For example, the problem of dealing with similar keywords stated in Section 3.5.2, or the interpretation of the bibliometric maps 3.6. Still, the adoption of data-driven bibliometric analysis has proven to be highly valuable to study the literature of a specific domain, and most of the times, it can provide an initial perspective which is far more efficient than exploring the literature manually.

4 Applications

After obtaining a global panorama based on the results of our bibliometric analysis, now we focus our investigation in analyzing recent papers that provide clear examples of application of computational intelligence methods in modeling and simulation of structures. Note that our aim is not to provide a comprehensive systematic review of the whole domain as that could lead to an excessive amount of information. Instead, we carefully select a number of well-developed studies and applications to show the main advantages of the CI paradigm over the traditional hard-computing strategies. For each selected study we provide a brief, yet complete summary highlighting the implemented methodologies, the biggest challenges, the most interesting findings, and the main advantages it offers.

4.1 Machine learning

Machine learning powered applications are definitely one of the biggest research directions found in the studied literature. Essentially, ML models are numerical procedures that are able to process and find patterns from large structured databases without being explicitly programmed to do so (Ghaboussi, 2010b). One of the most successful ML models is artificial neural networks which has proven to be a powerful technique capable of tackling complex task such as image and speech recognition, both of which are incredibly difficult to deal with using conventional algorithms. The enormous success of ANNs is driven by their relatively simple chain-like numerical formulation that is straightforward to implement in a computer program and requires little to no adjustments to scale-up its capabilities. Typically, the same computer program and core methodology can be used to create a small model containing just a few parameters, or a larger model containing billions of parameters trained with vast volumes of data (Brown et al., 2020). The difference between small models and large models is normally emphasized by using the term “deep” for the larger ones, such as in deep learning (DL) or deep neural network (DNN) Alzubaidi et al. (2021). Naturally, the limits to the capabilities of ANNs appears to be imposed by the availability and efficiency of computational resources, which are becoming more easily accessible and powerful every day. There exist different types of ANNs, each one particularly efficient or suited to solve specific types of problems. For instance, convolutional neural networks (CNN) (Aloysius and Geetha, 2017) and physical informed neural networks (PINN) (Vadyala et al., 2022), just to mention a couple. However, the essence methodology and the scalability properties remain the same for all the different kinds. Therefore, ML-based applications, and specifically neural networks, are methodologies that are gaining an immense popularity. In the following Sections 4.2–4.6, many of the discussed CI applications related to the simulation and modeling of structures are in fact using ML-based methodologies such as regular ANN, DNN, CNN, and PINN.

4.2 Structural optimization

Structural optimization deals with the problem of finding the most optimal configuration of a structure or a structural component. In the context of structural engineering, the most optimal configuration of a structure may be defined as the final design that minimizes or maximizes a desired property, e.g. a design that minimizes the material volume or the material cost. The two most common problems in the optimization of structures are topology optimization and shape optimization (Mei and Wang, 2021). In topology optimization, the goal is to find the most optimal distribution of a limited quantity of material inside a given arbitrary design domain. On the other hand, in size optimization the shape is predefined and composed of several individual parts (e.g. a truss structure). The problem is then to find the size of each individual element that leads to the most optimal design of the whole structure. Hybrid problems that combine topology and shape optimization are also common (Christiansen et al., 2015). Evidently, finding such optimal designs is a computationally intensive operation that involves a highly iterative process of trial and error. It is then no surprise that engineers have looked after CI-powered methodologies to deal with structural optimization problems, especially the usage of nature-inspired metaheuristic search strategies which have yielded numerous successful optimization strategies (Yang et al., 2014; Lagaros et al., 2022). Next, we present a few examples of recent and innovative applications using CI-powered methodologies for structural optimization.

Ahrari and Deb (Ahrari and Deb, 2016) developed an optimization algorithm for the simultaneous topology, shape, and size optimization of truss structures based on fully-stressed design and evolutionary strategies (referred as FSD-ES-II). They test their algorithm in various truss-design problems containing a large number of variables and depicting real-life truss design conditions considering multiple load cases as well as stress limits due to buckling and yielding of the members. They estimate that a reduction of the weight up to 32% may be achieved, compared to an iterative manual design. Furthermore, the examples that they developed for their case studies may serve as benchmark problems can be used by other optimization strategies as they are realistic structural engineering design tasks.

Liu and Xia (Liu and Xia, 2022) proposed a hybrid strategy using Genetic Algorithms and Deep Neural Networks (called Hybrid Intelligent Genetic Algorithm HIGA) for the optimization of truss structures. In their approach, they enhance a GA-based optimization technique by progressively training a DNN with the data generated during the iterative GA process. This DNN is then used as a surrogate model to substitute the FEA and perform a second nested GA where a set of populations are randomly generated. The best individual from each population, plus the current overall best, are used to create a new population for the next outer GA loop iteration. Thus, greatly increasing the exploration capabilities of the search strategy. Their DNN uses two hidden layers with 200 neurons each, ReLU activation functions and Adam optimizer. Their methodology is tested for several truss optimization problems showing more stable optimization procedures and reducing the computational cost to 7.7% compared to a pure GA approach.

Kallioras et al., (Kallioras et al., 2020) developed a methodology to enhance the popular SIMP (Bendsøe and Kikuchi, 1988) method that is used in topology optimization problems by means of deep belief networks (DBN). They implement a two-stage procedure. In the first phase, a specific number of iterations of the SIMP are executed. Then, a pre-trained DNB is used to compute the optimal element density based on the density history throughout these initial SIMP iterations. In the second phase, the SIMP is used to fine-tune the results obtained with the DBN at the first phase. The procedure is tested for various 2D and 3D examples. For the 3D cases, they test three problems with a domain discretized with 72,000, 86,000, and 140,000 finite elements. They achieve optimal results comparable to those obtained with the full SIMP approach but using 81%, 62%, and 52% less iterations in each problem respectively. Furthermore, by using GPU-based acceleration, they are able to speedup the procedure up to 17× times (compared to pure SIMP-CPU) for the larger 3D example.

4.2.1 Structural design

CI techniques, and particularly Genetic Algorithms, are also widely used for the optimal design of entire structures or individual elements such as beams, columns, walls, footings, etc. These problems fall into the category of size optimization and are in fact the regular everyday task of structural engineers working on real-life construction projects. The traditional approach usually consists of iterating the design manually until the engineer is satisfied with the result. This may lead to an inefficient and expensive design process. Alternatively, one could leverage the advantages of CI-powered methodologies such as GA to fully automate the design task (Hamidavi et al., 2018). However, the practical application of such optimization strategies is still not widely adopted. We believe that this is mainly due to the exhaustive training in optimization methods that is required for their successful implementation, as well as the limited availability of ready-to-use and easy to implement optimization tools. Therefore, researchers are trying to bring down the gap between the research-oriented and real-life applications by developing accessible methodologies, algorithms, tools, and even benchmark functions and problems (Ahrari and Deb, 2016; Plevris and Solorzano, 2022). A few examples in this direction are presented next.

Solorzano and Plevris (Solorzano and Plevris, 2020) used Genetic Algorithms to find the optimal design of concrete isolated footings (both pure axially loaded and with eccentricities) according to the ACI318-19 code regulations. They use the minimization of the material cost including both the concrete and the steel reinforcement as the objective function. The compliance with the ACI318 code is enforced by a set of constraint functions based on the multiple checks that are specified in the code, e.g. the allowable bearing pressure, the punching shear and flexural strength of the slab. Their work shows that the optimal design can be obtained in a few seconds (4.8 s for their tested example), thus, greatly reducing the time spent by the engineer in the design process.

Similarly, Moayyeri et al. (Moayyeri et al., 2019) proposed a methodology for the optimum design of RC retaining walls using the Particle Swarm Optimization algorithm. In their strategy, they test three different techniques to model the soil-structure interaction to obtain the bearing capacity. They define a total of 26 constraint functions to enforce a code-complying design consistent with the ACI318-14 code. Their study shows promising results as they were able to successfully obtain optimal designs for various examples despite the large number of constraints, pointing out that the Meyerhof soil-structure modeling produced the most cost-effective designs.

Another similar approach is proposed by Chen et al. (Chen et al., 2019). They develop a methodology for the design of RC framed structures using Genetic Algorithms. The optimization problem is defined with various constraints that control the design of the beam and columns based on the ACI318-11 code. Their design variables include the cross sectional dimensions of each beam and column as well as the reinforcement ratios on three different points for the beams and two points in the columns. Optimizing multiple types of elements at once, such as beams and columns, is an interesting challenge given that the dimensions of one element may be link to another to obtain realistic designs (e.g. the column dimensions must be big enough to allow the connectivity of the beams). They solve such problem by imposing additional constraints to restrict the dimensions to realistic conditions. Their GA approach is able to find an optimal value in a single optimization run, thus, reducing considerable the design time of a full RC building. Additionally, it is noted that the obtained result is 2% higher (in terms of the material cost) than the optimal design obtained without considering realistic dimensions as a constraint.

4.3 FE surrogate models

There are certain applications in structural engineering that require numerous repetitive numerical simulations that may result in high computational cost, and consequentially, turn the application impractical for engineering purposes. A few examples which appear in our bibliometric maps are the areas of topology and shape optimization of structures, multi-scale analysis of composite materials, reliability, failure, and uncertainty analyses, among other areas. It is then a very attractive and active area of research the development of less expensive alternative numerical models. Soft computing techniques, and neural networks in particular, have proven as powerful and reliable methods to create computationally efficient data-driven surrogate models (Kudela and Matousek, 2022). These type of surrogate models are able to approximate the results of an expensive model with only a fraction of the computational cost. However, most of the times, the training procedure of the surrogate model requires a large database of reliable and accurate results that must be created using the same computationally expensive model that is being substituted. Thus, the creation of a surrogate model may seem paradoxical as it may end up being a computational expensive operation, as well. Nevertheless, usually that is not the case as the data creation and the training procedures are one-time-only processes that can be conveniently done at any given time. Furthermore, one can take advantage of advanced computational capabilities such as parallelization and GPU processing. Once the surrogate model is fully trained, it can be used indefinitely as a significantly less computational expensive alternative. Next, we present a few examples of recent developments of computationally efficient surrogate models for FEM simulations.

Hau et al. (Mai et al., 2021) developed a deep neural network surrogate model to replace the FEM analyses in a truss optimization algorithm that considers the geometrically non-linear behaviour. Their DNN model has an architecture of 4-335-335-335-335-2 and is trained with 1320 samples. Using this methodology, the authors were able to significantly reduce the computational demand of an optimization run which normally requires thousands of NLFE analyses. The time reduction goes from 8559 s using NLFE, to 0.56 s with the DNN surrogate model (almost 16,000 times faster). The training and data collection took around 3756 s showing that the total procedure including training and data collection is still 2× times faster.

Abbueidda et al. (Abueidda et al., 2020) developed a convolutional neural network (CNN) surrogate model for 2D topology optimization considering non-linear hyperelastic materials. A single optimization task using the hyperelastic material and a 32 × 32 mesh takes around 90 min to be computed on a regular Core-i5 laptop. Thus, generating a large database of optimal solutions is a computationally intensive operation. To alleviate the cost, they use high performance computing (HPC) to run 10 parallel processes, achieving a data generation rate of 3.2 min per data point. They created a database of 18,000 optimum topologies which were used to train a NN model. The NN can then infer almost instantly good quality non-linear topology optimization results.

Papadopoulos et al. (Papadopoulos et al., 2017) created a neural network surrogate beam element for the geometrically non-linear analysis of carbon nanotubes. They use about 500 results of NLFE simulations of a detailed carbon nanotube (CNT) model for the training procedure. Their NN surrogate model can be used in stochastic multi-scale optimization problems that implements realistic RVEs (representative volume elements) reinforced with embedded CNT, reducing the computational effort by remarkably two orders of magnitude.

White et al. (White et al., 2019) present a novel topology optimization strategy to optimize a large macroscale structure made of a spatially varying micro architected material. The micromaterial is characterized by 21 elastic stiffness coefficients which can be obtained by using highly detailed FEM simulations. Simulating a representative cell of the microstructure material to compute the stiffness coefficients with an error of 1% requires a mesh of 10 million elements. To reduce the computational cost, they developed a novel approach using a single layer feedforward NN trained with the Sobolev norm to create a surrogate model. The network input is the material layout of an unit cell of the micromaterial, and the output are its 21 stiffness coefficients and the effective density. By substituting the expensive model in the macroscale analaysis, they are able to perform topology optimization of multiscale materials, which otherwise is practically impossible due to the extremely high computational cost.

4.4 Enhancing the FE procedure with CI

While surrogate models substitute entirely the FE model, CI techniques also provide various ways of enhancing some of the core numerical procedures of the FE. A few examples are: alleviating the computational cost on the generation of the stiffness matrix, developing computationally efficient constitutive models, approximating the solution of partial different equations (PDEs), accurately estimating material parameters (Ahmad et al., 2020). Naturally, due to their efficiency and robustness, NNs are among the most preferred CI methodologies for these type of problems. The resulting strategy is a hybrid NN-FE methodology where only a specific part of the FE is substituted with a NN. The development of a general neural network methodology that can represent physical phenomena without problem-specific restrictions such as the geometry, loading, and boundary conditions, is still an open challenge. (Pantidis and Mobasher, 2022).

Jung et al. (Jung et al., 2020) developed an innovative approach to compute the stiffness matrix of solid 2D isoparametric finite elements with four and eight nodes using DNN (called Deep Learned Finite Elements). They implemented a geometry normalization technique to create a vast data set comprised of elements of all kind of shapes, thus, considerably reducing the required amount of data for the training procedure. Their network takes as input the Poisson’s ratio and the nodal coordinates of the element which are pre-processed and transformed to the normalized space; the output is the strain-displacement matrix which is then post-processed back to the original geometric space and the final stiffness matrix is computed. The DNN is trained with 300,000 data points and uses an architecture containing six fully connected layers with 378 neurons each. They tested their developed elements (DL4, DL8) with several FE examples that implement standard elements such as Q4, Q8, Q9 and QM6. Their DL8 formulation outperformed most of them, both in terms of computational efficiency and convergence.

The previous authors and Jun (Jung et al., 2022) developed a similar strategy called self updated four-node finite element (SUFE). Their approach aims to eliminate the shearlocking effect that affects FE models with coarse meshes, eliminating the necessity of mesh refinement. They achieve this by using a mode-base description of the isoparametric 4-node element and an internal iterative procedure to correct the stiffness matrix. Such correction requires the solution of a costly optimization problem to find the optimal bending directions of the FE. The DNN is implemented to alleviate the cost of the optimization procedure. The DNN takes as input the nodal coordinates, displacements and the Poisson’s ratio; the output is the optimal bending direction. The DNN architecture uses 10 fully connected layers with 320 neurons each and is trained with a large number of 3,000,000 samples (vast data is required in order to generalize the DNN to account for any possible FE geometry). The element shows promising results, outperforming the tested standard FEs in several examples. Furthermore, their idea can be extended to other types of finite elements.

Samaniego et al. (Samaniego et al., 2020) developed a Deep Neural Network approach to approximate the solution of PDEs in computational mechanics. Their approach consists of defining a physical informed DNN using the energy of the system as a loss function, thus, the NN is directly used to built the approximation space. In their paper, they solve various problems related to mechanical engineering. For each problem, the DNN architecture and the corresponding loss function are designed accordingly. For a hyperelasticity problem consisting of a cuboid subjected to twisting, they use a 3-30-30-30-3 DNN where the inputs are the nodal coordinates and the output are the displacements. They use a total of 64,000 points for the training phase. The loss function is the potential energy of the system which contains the information related to the boundary conditions and constitutive equations. By training the neural network with standard gradient-based methods, the potential is minimized and the corresponding solution is obtained in the form of nodal displacements.

Ortiz and Kirchdoerfer (Kirchdoerfer and Ortiz, 2016) presented a new paradigm which they refer as data-driven computational mechanics. Their methodology substitute the hard-coded material constitutive law in the FE procedure with reliable experimental data. The solver seeks to assign each material point of the model with the closest material state from a predefined material dataset by solving a constrained optimization problem during an iterative procedure. They argue that by incorporating the experimental data directly in the mathematical model, simulations outside the data range are discouraged and the errors and uncertainties are greatly reduced.

4.5 Earthquake engineering, uncertainty, and risk assessment

One of the most evident drawbacks of the hard computing techniques in the simulation and modeling of structures is their lack of mechanisms to treat uncertainties in the solution process. Uncertainties are inherent, and can be considered as an irremovable characteristic that is present in all engineering problems. They arise from simple situations such as errors or inaccuracies in the measurement of properties; or from highly complex phenomena that are nearly impossible to model accurately, e.g. the micro-structure of materials or the expected seismic loads in a building. Needless to say, uncertainties are tied with the risk assessment of structures. It is virtually impossible to accurately predict the failure probability of a structure due to the numerous uncertainties involved in their design and construction. However, it is possible to develop reliable estimations exploiting the advantages of CI-powered techniques. Similarly, predicting or modeling the response of structures to seismic events and designing appropriated control systems to reduce their impact (Lagaros et al., 2001) are other challenging endeavours in which CI-powered techniques have proven valuable. We provide a few examples of relevant studies in the following paragraphs.

Ebrahimi et al. (Ebrahimi et al., 2022) developed a methodology based on fuzzy systems to properly address the uncertainties encountered when defining the performance levels and the loading conditions in the performance based design of buildings. They perform a fuzzy structural analysis (Möller et al., 2000) using fuzzy sets to define the loading conditions and apply a Genetic Algorithm to find the minimum and maximum response of the corresponding alpha-cut. Finally, they derive a novel method for comparing the two fuzzy sets (i.e. fuzzy structural response and the corresponding loading conditions) to assess the performance level of the structure more reliably. Thus, significantly reducing the uncertainty that characterizes such decisions. Similarly, Guo et al. (Guo et al., 2022) propose a fuzzy global seismic vulnerability analysis framework to investigate the effect of stochastic and epistemic uncertainties in RC structures. The stochastic uncertainties refer to the ground motion and the structural design parameters, while the epistemic uncertainties refer to the definition of the limit states and the parameters of the probabilistic model. In their approach, each story is idealized as a random variable and the correlations between these random variables are computed using the vine copula theory. They use a FEM model of a RC building using non-linear beam and column elements with a displacement-based fiber section in OpenSees. The failure limit state is described using the maximum inter-story drift and the peak ground acceleration based on the IDA method (Wu et al., 2020). With their methodology, they obtain a fuzzy global vulnerability curve for each performance level that considers both stochastic and epistemic uncertainties; helping engineers and researchers in the decision-making process in the context of risk assesment.

Javidan et al. (Javidan et al., 2018) developed a NN-based surrogate model to estimate the collapse probability of structures under extreme actions. They apply their methodology in a case scenario of a multi-story framed structure subjected to car impact load. The reliability analysis requires 20,000 realizations using Monte Carlo sampling. A detailed NLFE simulation using LS-DYNA takes 112 h to compute, and therefore, is not a viable option to run 20,000 different cases. An alternative simplified model using adaptively shifted integration method (ASI) is implemented to reduce the cost to 20 s per analysis. To achieve a further reduction of the computational time, a NN-based surrogate model is created and trained using 10,000 samples generated with the ASI model. They compare the surrogate model with the ASI method and observe good agreement in the results (low MSE and good R²). By substituting the ASI method with the trained NN in the reliability analysis, the computational demand is reduced approximately from 20,000*(20 s) = 400,000 s per analysis, to only a few seconds.

4.6 Structural health monitoring

Sometimes the initial conditions or purposes for which a structure was initially build may change over time. Consequentially, the simulation and modeling of existing structures for retrofitting or conservation purposes is another important area in structural engineering. This fact can be clearly observed in the bilbiometric map at Figure 3. In the neural networks cluster, there are several terms related to structural health monitoring and damage detection. Therefore, the data itself points out to the usage of Machine Learning models for structural health monitoring (Azimi et al., 2020). A couple of examples are given next.

Georgioudakis and Plevris (Georgioudakis and Plevris, 2018) implemented an innovative technique for the damage identification in structures based on incomplete modal data. They create a finite element model of the structure and assign a damage index to each member. The idea is then to define a unconstrained optimization problem to find the appropriated damage index for each member. They solve such task with an implementation of the differential evolution algorithm using as objective function a combination of two different correlation criteria between the real damage (experimentally measured) and the damaged that is predicted by the finite element model. It is shown in various simulated examples that their developed technique using the combined criteria throws better results than those obtained using each criteria individually.

Wand and Cheng (Wang et al., 2021) propose a new crack detection method using deep neural networks. Their methodology, namely the reference anchor point method, employs a deep convolutional neural network that is based on the ResNet architecture. In principle, the approach discretizes the image with a 2D array of points and the NN is trained to detect whether or not each point is near a crack. Therefore, obtaining a full map of the cracks made up by closely positioned points. This is a particularly challenging problem as cracks comes in all sizes and shapes, however, they propose clever ideas such as the fixed-distance decentalization algorithm to solve the problem. Their approach is able to map the cracks on an image in just a fraction of a second (using a NVIDIA GeForce GTX 1080 GPU). Furthermore, the resolution (i.e. number of points used for crack detection) can be easily manipulated for better quality or faster results, depending on the problem specific needs.

5 Summary and conclusion

We have conducted a thorough data-driven bibliometric analysis on the topic of Computational Intelligence techniques in the simulation and modeling of structures. The results presented in this study correspond to the analysis of a database of 8107 publications in the aforementioned field. We present metrics such as the yearly growth of scientific publications, the most utilized journals, the most cited papers, and most notable authors. Furthermore, we create various bibliometric maps using the keywords and the authorship information contained in all the publications in the database. From the bibliometric maps created with the keywords, we obtain a general overview of the research directions in the field where we have successfully identified the following seven topics: 1) FEM enhanced by CI; 2) structural optimization; 3) surrogate modeling; 4) earthquake engineering, uncertainties, and risk assessment; 5) structural health monitoring; 6) modeling of complex RC behaviour; and 7) machine learning applications. Alternatively, from the bibliometric map created from the authorship information, we obtain valuable information on the most notable authors and the collaborations between them. We relate these authors to the top 30 (most recurrent) keywords to discover the most influential authors in particular topics. Based on the results and our interpretation of the bibliometric analysis, we provide several examples of recent publications implementing innovative CI-related approaches, highlighting the main methodologies and achievements of each individual study. Additionally, since the interpretation of bibliometric maps is highly subjective, we have dedicated a full section of the paper to provide a detailed description of the science mapping methodology that was implemented in the construction of the presented maps. Thus, empowering the reader with the necessary information for their own interpretation of the results.

The analyzed data and the findings obtained in this study suggest that there is a clear hype and an increasing trend regarding the implementation of CI techniques in engineering applications. Particularly, in the studied topic of simulation and modeling of structures, we can observe that many of the traditional long-lasting methodologies are being substituted or enhanced by some form of CI. Engineers no longer have to manually iterate to find the most optimal design of a structure, as they can leverage the power of innovative optimization techniques such as genetic algorithms. The risk assessment of structures has become much more efficient and reliable by modeling uncertainties using fuzzy systems and variables. Neural Networks have demonstrated an unmatched performance for the automatic damage identification in structures, greatly improving and facilitating the retrofitting process. Additionally, Neural Networks also serve as powerful non-linear mapping functions providing an ideal framework to create computational efficient surrogate models of large FE simulations. Naturally, all these applications are driven by the enormous advances and availability in computational technology and resources, as well as due to the continuous investment in research and development of Artificial Intelligence applications, both of which are likely to keep growing and accelerate in the near future. Therefore, it is conceivable that we will continue to see many innovative applications and a fast-paced growing output of research in this direction. Inevitably, these strategies are heading to become standard practices in the future, for both research and industrial applications.

Author contributions

Conceptualization, GS and VP; methodology, GS and VP; software, GS and VP; formal analysis, GS and VP; investigation, VP and GS; resources, VP and GS; data curation, GS; writing—original draft preparation, GS and VP; writing—review and editing, GS and VP; visualization, GS and VP; supervision, VP; project administration, VP; funding acquisition, GS. All authors have read and agreed to the published version of the manuscript.

Funding

The APC was funded by Oslo Metropolitan University.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abueidda, D. W., Koric, S., and Sobh, N. A. (2020). Topology optimization of 2D structures with nonlinearities using deep learning. Comput. Struct. 237, 106283. doi:10.1016/j.compstruc.2020.106283

CrossRef Full Text | Google Scholar

Adeli, H. (2001a). Neural networks in civil engineering: 1989-2000. Computer-Aided Civ. Infrastructure Eng. 16, 126–142. doi:10.1111/0885-9507.00219

CrossRef Full Text | Google Scholar

Adeli, H. (2001b). Neural networks in civil engineering: 1989–2000. Computer-Aided Civ. Infrastructure Eng. 16, 126–142. doi:10.1111/0885-9507.00219

CrossRef Full Text | Google Scholar

Ahlgren, P., Jarneving, B., and Rousseau, R. (2003). Requirements for a cocitation similarity measure, with special reference to Pearson’s correlation coefficient. J. Am. Soc. Inf. Sci. Technol. 54, 550–560. doi:10.1002/asi.10242

CrossRef Full Text | Google Scholar

Ahmad, A., Plevris, V., and Khan, Q.-u.-Z. (2020). Prediction of properties of FRP-confined concrete cylinders based on artificial neural networks. Crystals 10, 811–822. doi:10.3390/cryst10090811

CrossRef Full Text | Google Scholar

Ahrari, A., and Deb, K. (2016). An improved fully stressed design evolution strategy for layout optimization of truss structures. Comput. Struct. 164, 127–144. doi:10.1016/j.compstruc.2015.11.009

CrossRef Full Text | Google Scholar

Aloysius, N., and Geetha, M. (2017). “A review on deep convolutional neural networks,” in 2017 International Conference on Communication and Signal Processing (ICCSP), 0588–0592.

CrossRef Full Text | Google Scholar

Altin Karataş, M., and Gökkaya, H. (2018). A review on machinability of carbon fiber reinforced polymer (CFRP) and glass fiber reinforced polymer (GFRP) composite materials. Def. Technol. 14, 318–326. doi:10.1016/j.dt.2018.02.001

CrossRef Full Text | Google Scholar

Alzubaidi, L., Zhang, J., Humaidi, A. J., Al-Dujaili, A., Duan, Y., Al-Shamma, O., et al. (2021). Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 8, 53. doi:10.1186/s40537-021-00444-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Azimi, M., Eslamlou, A. D., and Pekcan, G. (2020). Data-driven structural health monitoring and damage detection through deep learning: State-of-the-Art review. Sensors 20, 2778. doi:10.3390/s20102778

PubMed Abstract | CrossRef Full Text | Google Scholar

Bathe, K.-J. (2008). “Finite element method,” in Wiley encyclopedia of computer science and engineering (American Cancer Society), 1–12. doi:10.1002/9780470050118.ecse159

CrossRef Full Text | Google Scholar

Bendsøe, M. P., and Kikuchi, N. (1988). Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 71, 197–224. doi:10.1016/0045-7825(88)90086-2

CrossRef Full Text | Google Scholar

Bessa, M. A., Bostanabad, R., Liu, Z., Hu, A., Apley, D. W., Brinson, C., et al. (2017). A framework for data-driven analysis of materials under uncertainty: Countering the curse of dimensionality. Comput. Methods Appl. Mech. Eng. 320, 633–667. doi:10.1016/j.cma.2017.03.037

CrossRef Full Text | Google Scholar

Bezdek, J. (1994). in What is computational intelligence? Computational intelligence: Imitating life. Editors J. M Zurada, R. J Marks, and C. J Robinson (IEEE Press), 1–12.

Google Scholar

Bhowmik, R. (2008). Keyword extraction from abstracts and titles. IEEE S. 2008, 610–617. doi:10.1109/SECON.2008.4494366

CrossRef Full Text | Google Scholar

Blanco-Mesa, F., Merigó, J., and Gil-Lafuente, A. (2017). Fuzzy decision making: A bibliometric-based review. J. Intelligent Fuzzy Syst. 32, 2033–2050. doi:10.3233/JIFS-161640

CrossRef Full Text | Google Scholar

Borg, I., and Groenen, P. J. F. (2005). “Modern multidimensional scaling: Theory and applications,” in Springer series in statistics (New York: Springer-Verlag). doi:10.1007/0-387-28981-X

CrossRef Full Text | Google Scholar

Broadus, R. N. (1987). Toward a definition of “bibliometrics”. Scientometrics 12, 373–379. doi:10.1007/BF02016680

CrossRef Full Text | Google Scholar

Brown, T. B., Mann, B., Ryder, N., Subbiah, M., Kaplan, J., Dhariwal, P., et al. (2020). Language models are few-shot learners. CoRR abs/2005.14165.

Google Scholar

Cha, Y.-J., Choi, W., Suh, G., Mahmoudkhani, S., and Büyüköztürk, O. (2018). Autonomous structural visual inspection using region-based deep learning for detecting multiple damage types. Computer-Aided Civ. Infrastructure Eng. 33, 731–747. doi:10.1111/mice.12334

CrossRef Full Text | Google Scholar

Chen, C., Yousif, S. T., Najem, R. M., Abavisani, A., Pham, B. T., Wakil, K., et al. (2019). Optimum cost design of frames using genetic algorithms. Steel Compos. Struct. 30, 293–304. doi:10.12989/scs.2019.30.3.293

CrossRef Full Text | Google Scholar

Chojaczyk, A. A., Teixeira, A. P., Neves, L. C., Cardoso, J. B., and Guedes Soares, C. (2015). Review and application of Artificial Neural Networks models in reliability analysis of steel structures. Struct. Saf. 52, 78–89. doi:10.1016/j.strusafe.2014.09.002

CrossRef Full Text | Google Scholar

Christiansen, A., Brentzen, J., Nobel-Jørgensen, M., Aage, N., and Sigmund, O. (2015). Combined shape and topology optimization of 3D structures. Comput. Graph. X. 46, 25–35. doi:10.1016/j.cag.2014.09.021

CrossRef Full Text | Google Scholar

Cobo, M., López-Herrera, A., Herrera-Viedma, E., and Herrera, F. (2011). An approach for detecting, quantifying, and visualizing the evolution of a research field: A practical application to the fuzzy sets theory field. J. Inf. 5, 146–166. doi:10.1016/j.joi.2010.10.002

CrossRef Full Text | Google Scholar

Coello, C., and Mezura-Montes, E. (2002). Constraint-handling in genetic algorithms through the use of dominance-based tournament selection. Adv. Eng. Inf. 16, 193–203. doi:10.1016/S1474-0346(02)00011-3

CrossRef Full Text | Google Scholar

Deb, K. (2000). An efficient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Eng. 186, 311–338. doi:10.1016/S0045-7825(99)00389-8

CrossRef Full Text | Google Scholar

Deb, K., and Deb, D. (2014). Analysing mutation schemes for real-parameter genetic algorithms. Int. J. Artif. Intell. Soft Comput. 4, 1–28. doi:10.1504/IJAISC.2014.059280

CrossRef Full Text | Google Scholar

Deb, K., Sindhya, K., and Okabe, T. (2007). “Self-adaptive simulated binary crossover for real-parameter optimization,” in Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation, New York, NY, USA (New York (NY), United States: Association for Computing Machinery), 1187–1194. doi:10.1145/1276958.1277190

CrossRef Full Text | Google Scholar

Donthu, N., Kumar, S., Mukherjee, D., Pandey, N., and Lim, W. M. (2021). How to conduct a bibliometric analysis: An overview and guidelines. J. Bus. Res. 133, 285–296. doi:10.1016/j.jbusres.2021.04.070

CrossRef Full Text | Google Scholar

Ebrahimi, E., Abdollahzadeh, G., and Jahani, E. (2022). Developing the structural analysis considering fuzzy performance levels. Appl. Soft Comput. 115, 108180. doi:10.1016/j.asoc.2021.108180

CrossRef Full Text | Google Scholar

Eck, N. J. v., and Waltman, L. (2009). How to normalize cooccurrence data? An analysis of some well-known similarity measures. J. Am. Soc. Inf. Sci. Technol. 60, 1635–1651. doi:10.1002/asi.21075

CrossRef Full Text | Google Scholar

Elsevier (2021a). About Scopus - abstract and citation database.

Google Scholar

Elsevier (2021b). About scopus - how do author and indexed keywords work?

Google Scholar

Falcone, R., Lima, C., and Martinelli, E. (2020). Soft computing techniques in structural and earthquake engineering: A literature review. Eng. Struct. 207. doi:10.1016/j.engstruct.2020.110269

CrossRef Full Text | Google Scholar

Figueiredo, E., Park, G., Farrar, C. R., Worden, K., and Figueiras, J. (2011). Machine learning algorithms for damage detection under operational and environmental variability. Struct. Health Monit. 10, 559–572. doi:10.1177/1475921710388971

CrossRef Full Text | Google Scholar

Flood, I., and Kartam, N. (1994a). Neural networks in civil engineering. i: Principles and understanding. J. Comput. Civ. Eng. 8, 131–148. doi:10.1061/(asce)0887-3801(1994)8:2(131)

CrossRef Full Text | Google Scholar

Flood, I., and Kartam, N. (1994b). Neural networks in civil engineering. ii: Systems and application. J. Comput. Civ. Eng. 8. doi:10.1061/(asce)0887-3801(1994)8:2(149)

CrossRef Full Text | Google Scholar

Fong, J., Filliben, J., Fields, R., Bernstein, B., and Marcal, P. (2006). Uncertainty in finite element modeling and failure analysis: A metrology-based approach. J. Press. Vessel Technol. 128, 140–147. doi:10.1115/1.2150843

CrossRef Full Text | Google Scholar

Frangopol, D., and Soliman, M. (2016). Life-cycle of structural systems: Recent achievements and future directions. Struct. Infrastructure Eng. 12, 1–20. doi:10.1080/15732479.2014.999794

CrossRef Full Text | Google Scholar

Georgioudakis, M., and Plevris, V. (2018). A combined modal correlation criterion for structural damage identification with noisy modal data. Adv. Civ. Eng. 2018, 1–20. doi:10.1155/2018/3183067

CrossRef Full Text | Google Scholar

Ghaboussi, J. (2010a). Advances in neural networks in computational mechanics and engineering. CISM Int. Centre Mech. Sci. Courses Lect. 512, 191–236. doi:10.1007/978-3-211-99768-0_4

CrossRef Full Text | Google Scholar

Ghaboussi, J. (2010b). “Advances in neural networks in computational mechanics and engineering,” in Advances of soft computing in engineering. Editor Z. Waszczyszyn (Vienna: SpringerCISM International Centre for Mechanical Sciences), 191–236. doi:10.1007/978-3-211-99768-0_4

CrossRef Full Text | Google Scholar

Ghaboussi, J. (2018). Soft computing in engineering. Boca Raton, Florida, United States: CRC Press.

Google Scholar

Gower, J. C. (2005). “Similarity, dissimilarity, and distance measure,” in Encyclopedia of biostatistics (American Cancer Society). doi:10.1002/0470011815.b2a10084

CrossRef Full Text | Google Scholar

Groenen, P., and Velden, M. (2016). Multidimensional scaling by majorization: A review. J. Stat. Softw. 73. doi:10.18637/jss.v073.i08

CrossRef Full Text | Google Scholar

Guo, M., Huang, H., Xue, C., and Huang, M. (2022). Assessment of fuzzy global seismic vulnerability for RC structures. J. Build. Eng. 57, 104952. doi:10.1016/j.jobe.2022.104952

CrossRef Full Text | Google Scholar

Hamidavi, T., Abrishami, S., Ponterosso, P., Begg, D., and Nanos, N. (2018). Optimisation of structural design by integrating genetic algorithms in the building information modelling environment. Int. J. Archit. Civ. Constr. Sci. 11, 149–169. doi:10.1108/ci-11-2019-0126

CrossRef Full Text | Google Scholar

Hirsch, J. E. (2005). An index to quantify an individual’s scientific research output. Proc. Natl. Acad. Sci. U. S. A. 102, 16569–16572. doi:10.1073/pnas.0507655102

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, X., and Xie, Y. M. (2007). Convergent and mesh-independent solutions for the bi-directional evolutionary structural optimization method. Finite Elem. Analysis Des. 43, 1039–1049. doi:10.1016/j.finel.2007.06.006

CrossRef Full Text | Google Scholar

Ibrahim, D. (2016). An overview of soft computing. Procedia Comput. Sci. 102, 34–38. doi:10.1016/j.procs.2016.09.366

CrossRef Full Text | Google Scholar

IEEE-CIS (2021). What is computational intelligence? IEEE Computational Intelligence Society.

Google Scholar

Javidan, M., Kang, H., Isobe, D., and Kim, J. (2018). Computationally efficient framework for probabilistic collapse analysis of structures under extreme actions. Eng. Struct. 172, 440–452. doi:10.1016/j.engstruct.2018.06.022

CrossRef Full Text | Google Scholar

Jung, J., Jun, H., and Lee, P.-S. (2022). Self-updated four-node finite element using deep learning. Comput. Mech. 69, 23–44. doi:10.1007/s00466-021-02081-7

CrossRef Full Text | Google Scholar

Jung, J., Yoon, K., and Lee, P.-S. (2020). Deep learned finite elements. Comput. Methods Appl. Mech. Eng. 372, 113401. doi:10.1016/j.cma.2020.113401

CrossRef Full Text | Google Scholar

Kallioras, N., Kazakis, G., and Lagaros, N. (2020). Accelerated topology optimization by means of deep learning. Struct. Multidiscipl. Optim. 62, 1185–1212. doi:10.1007/s00158-020-02545-z

CrossRef Full Text | Google Scholar

Katoch, S., Chauhan, S. S., and Kumar, V. (2021). A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 80, 8091–8126. doi:10.1007/s11042-020-10139-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaveh, A., and Talatahari, S. (2010). An improved ant colony optimization for constrained engineering design problems. Eng. Comput. Swans. 27, 155–182. doi:10.1108/02644401011008577

CrossRef Full Text | Google Scholar

Khan, M., Cao, M., and Ali, M. (2020). Cracking behaviour and constitutive modelling of hybrid fibre reinforced concrete. J. Build. Eng. 30, 101272. doi:10.1016/j.jobe.2020.101272

CrossRef Full Text | Google Scholar

Kirchdoerfer, T., and Ortiz, M. (2016). Data-driven computational mechanics. Comput. Methods Appl. Mech. Eng. 304, 81–101. doi:10.1016/j.cma.2016.02.001

CrossRef Full Text | Google Scholar

Kostoff, R. N. (2002). Citation analysis of research performer quality. Scientometrics 53, 49–71. doi:10.1023/A:1014831920172

CrossRef Full Text | Google Scholar

Koutsantonis, D., Koutsantonis, K., Bakas, N. P., Plevris, V., Langousis, A., and Chatzichristofis, S. A. (2022). Bibliometric literature review of adaptive learning systems. Sustainability 14. doi:10.3390/su141912684

CrossRef Full Text | Google Scholar

Kudela, J., and Matousek, R. (2022). Recent advances and applications of surrogate models for finite element method computations: A review. Soft Comput. doi:10.1007/s00500-022-07362-8

CrossRef Full Text | Google Scholar

Kumar, S., and Kochmann, D. M. (2022). “What machine learning can do for computational solid mechanics,” in Current trends and open problems in computational mechanics. Editors F. Aldakheel, B. Hudobivnik, M. Soleimani, H. Wessels, C. Weißenfels, and M. Marino (Cham: Springer International Publishing), 275–285. doi:10.1007/978-3-030-87312-7

CrossRef Full Text | Google Scholar

Lagaros, N. D., and Plevris, V. (2022a). Artificial intelligence (AI) applied in civil engineering. Appl. Sci. 12, 7595. doi:10.3390/app12157595

CrossRef Full Text | Google Scholar

Lagaros, N. D., and Plevris, V. (2022b). Artificial intelligence (AI) applied in civil engineering, 698. Basel, Switzerland: Multidisciplinary Digital Publishing Institute (MDPI). doi:10.3390/books978-3-0365-5084-8

CrossRef Full Text | Google Scholar

Lagaros, N. D., Plevris, V., and Mitropoulou, C. C. (2001). Design optimization of active and passive structural control systems (IGI global).

Google Scholar

Lagaros, N., Plevris, V., and Kallioras, N. (2022). The mosaic of metaheuristic algorithms in structural optimization. Arch. Comput. Methods Eng. doi:10.1007/s11831-022-09773-0

CrossRef Full Text | Google Scholar

Lee, K. S., and Geem, Z. W. (2004). A new structural optimization method based on the harmony search algorithm. Comput. Struct. 82, 781–798. doi:10.1016/j.compstruc.2004.01.002

CrossRef Full Text | Google Scholar

Lin, T., Wang, Z., Hu, F., and Wang, P. (2022). Finite-element analysis of high-strength steel extended end-plate connections under cyclic loading. Materials 15, 2912. doi:10.3390/ma15082912

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, Y.-z., Nie, Z.-h., and Ma, H.-w. (2017). Structural damage detection with automatic feature-extraction through deep learning. Computer-Aided Civ. Infrastructure Eng. 32, 1025–1046. doi:10.1111/mice.12313

CrossRef Full Text | Google Scholar

Liu, J., and Xia, Y. (2022). A hybrid intelligent genetic algorithm for truss optimization based on deep neutral network. Swarm Evol. Comput. 73, 101120. doi:10.1016/j.swevo.2022.101120

CrossRef Full Text | Google Scholar

Liu, W. K., Li, S., and Park, H. S. (2022). Eighty years of the finite element method: Birth, evolution, and future. Arch. Comput. Methods Eng. 29, 4431–4453. doi:10.1007/s11831-022-09740-9

CrossRef Full Text | Google Scholar

Lu, X., Plevris, V., Tsiatas, G., and De Domenico, D. (2022). Editorial: Artificial intelligence-powered methodologies and applications in earthquake and structural engineering. Front. Built Environ. 8. doi:10.3389/fbuil.2022.876077

CrossRef Full Text | Google Scholar

Mai, H. T., Kang, J., and Lee, J. (2021). A machine learning-based surrogate model for optimization of truss structures with geometrically nonlinear behavior. Finite Elem. Analysis Des. 196, 103572. doi:10.1016/j.finel.2021.103572

CrossRef Full Text | Google Scholar

Mata, J. (2011). Interpretation of concrete dam behaviour with artificial neural network and multiple linear regression models. Eng. Struct. 33, 903–910. doi:10.1016/j.engstruct.2010.12.011

CrossRef Full Text | Google Scholar

Mei, L., and Wang, Q. (2021). Structural optimization in civil engineering: A literature review. Buildings 11, 66. doi:10.3390/buildings11020066

CrossRef Full Text | Google Scholar

Moayyeri, N., Gharehbaghi, S., and Plevris, V. (2019). Cost-based optimum design of reinforced concrete retaining walls considering different methods of bearing capacity computation. Mathematics 7, 1232. doi:10.3390/math7121232

CrossRef Full Text | Google Scholar

Moens, D., and Hanss, M. (2011). Non-probabilistic finite element analysis for parametric uncertainty treatment in applied mechanics: Recent advances. Finite Elem. Analysis Des. 47, 4–16. doi:10.1016/j.finel.2010.07.010

CrossRef Full Text | Google Scholar

Moens, D., and Vandepitte, D. (2005). A survey of non-probabilistic uncertainty treatment in finite element analysis. Comput. Methods Appl. Mech. Eng. 194, 1527–1555. doi:10.1016/j.cma.2004.03.019

CrossRef Full Text | Google Scholar

Möller, B., Graf, W., and Beer, M. (2000). Fuzzy structural analysis using alpha-level optimization. Comput. Mech. 26, 547–565. doi:10.1007/s004660000204

CrossRef Full Text | Google Scholar

Narin, F., and Hamilton, K. (1996). Bibliometric performance measures. Scientometrics 36, 293–310. doi:10.1007/BF02129596

CrossRef Full Text | Google Scholar

Omran, M., Engelbrecht, A., and Salman, A. (2007). An overview of clustering methods. Intell. Data Anal. 11, 583–605. doi:10.3233/IDA-2007-11602

CrossRef Full Text | Google Scholar

S. J. Ovaska (Editor) (2004). Computationally intelligent hybrid systems: The fusion of soft computing and hard computing (IEEE Press Series on Computational Intelligence).

Google Scholar

Pantidis, P., and Mobasher, M. E. (2022). Integrated finite element neural network (i-fenn) for non-local continuum damage mechanics. doi:10.48550/ARXIV.2207.09908

CrossRef Full Text | Google Scholar

Papadopoulos, V., Soimiris, G., Giovanis, D., and Manolis, P. (2017). A neural network-based surrogate model for carbon nanotubes with geometric nonlinearities. Comput. Methods Appl. Mech. Eng. 328, 411–430. doi:10.1016/j.cma.2017.09.010

CrossRef Full Text | Google Scholar

Papadrakakis, M., and Lagaros, N. D. (2002). Reliability-based structural optimization using neural networks and Monte Carlo simulation. Comput. Methods Appl. Mech. Eng. 191, 3491–3507. doi:10.1016/S0045-7825(02)00287-6

CrossRef Full Text | Google Scholar

Perez, R. E., and Behdinan, K. (2007). Particle swarm approach for structural design optimization. Comput. Struct. 85, 1579–1588. doi:10.1016/j.compstruc.2006.10.013

CrossRef Full Text | Google Scholar

Plevris, V., Bakas, N. P., and Solorzano, G. (2021). Pure random orthogonal search (PROS): A plain and elegant parameterless algorithm for global optimization. Appl. Sci. 11, 5053. doi:10.3390/app11115053

CrossRef Full Text | Google Scholar

Plevris, V., Lagaros, N. D., and Zeytinci, A. (2022). Blockchain in civil engineering, architecture and construction industry: State of the art, evolution, challenges and opportunities. Front. Built Environ. 8. doi:10.3389/fbuil.2022.840303

CrossRef Full Text | Google Scholar

Plevris, V., and Solorzano, G. (2022). A collection of 30 multidimensional functions for global optimization benchmarking. Data 7, 46. doi:10.3390/data7040046

CrossRef Full Text | Google Scholar

Plevris, V., Solorzano, G., and Bakas, N. (2019). “Literature review of historical masonry structures with machine learning,” in Proceedings of the 7th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2019) (European Community on Computational Methods in Applied Sciences (ECCOMAS)),, 1547–1562. doi:10.7712/120119.7018.21053

CrossRef Full Text | Google Scholar

Plevris, V., Tsiatas, G. C., Goodrich, D. C., Unkrich, C., Kepner, W. G., and Burns, I. S. (2018). Computational structural engineering: Past achievements and future challenges. Front. Built Environ. 4, 21–15. doi:10.3389/fbuil.2018.00058

CrossRef Full Text | Google Scholar

Pranckut, R. (2021). Web of science (wos) and scopus: The titans of bibliographic information in today’s academic world. Publications 9. doi:10.3390/publications9010012

CrossRef Full Text | Google Scholar

Querin, O., Steven, G., and Xie, Y. (1998). Evolutionary structural optimisation (ESO) using a bidirectional algorithm. Eng. Comput. Swans. 15, 1031–1048. doi:10.1108/02644409810244129

CrossRef Full Text | Google Scholar

Rafiq, M. Y., Bugmann, G., and Easterbrook, D. J. (2001). Neural network design for engineering applications. Comput. Struct. 79, 1541–1552. doi:10.1016/S0045-7949(01)00039-6

CrossRef Full Text | Google Scholar

Rajeev, S., and Krishnamoorthy, C. S. (1992). Discrete optimization of structures using genetic algorithms. J. Struct. Eng. (N. Y. N. Y). 118, 1233–1250. doi:10.1061/(asce)0733-9445(1992)118:5(1233)

CrossRef Full Text | Google Scholar

Rao, S. S., and Berke, L. (1997). Analysis of uncertain structural systems using interval analysis. AIAA J. 35, 727–735. doi:10.2514/2.164

CrossRef Full Text | Google Scholar

Riche, R. L., and Haftka, R. T. (1993). Optimization of laminate stacking sequence for buckling load maximization by genetic algorithm. AIAA J. 31, 951–956. doi:10.2514/3.11710

CrossRef Full Text | Google Scholar

Safa, M., Shariati, M., Ibrahim, Z., Toghroli, A., Baharom, S. B., Nor, N. M., et al. (2016). Potential of adaptive neuro fuzzy inference system for evaluating the factors affecting steel-concrete composite beam∖’s shear strength. Steel compos. Struct. 21, 679–688. doi:10.12989/scs.2016.21.3.679

CrossRef Full Text | Google Scholar

Salehi, H., and Burgueño, R. (2018). Emerging artificial intelligence methods in structural engineering. Eng. Struct. 171, 170–189. doi:10.1016/j.engstruct.2018.05.084

CrossRef Full Text | Google Scholar

Samaniego, E., Anitescu, C., Goswami, S., Nguyen-Thanh, V. M., Guo, H., Hamdia, K., et al. (2020). An energy approach to the solution of partial differential equations in computational mechanics via machine learning: Concepts, implementation and applications. Comput. Methods Appl. Mech. Eng. 362, 112790. doi:10.1016/j.cma.2019.112790

CrossRef Full Text | Google Scholar

Schmidhuber, J. (2015). Deep learning in neural networks: An overview. Neural Netw. 61, 85–117. doi:10.1016/j.neunet.2014.09.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, R., Huang, S.-S., and Davison, B. (2018). A simplified steel beam-to-column connection modelling approach and influence of connection ductility on frame behaviour in fire. Int. J. High-Rise Build. 7, 343–362. doi:10.21022/IJHRB.2018.7.4.343

CrossRef Full Text | Google Scholar

Sigmund, O. (2011). On the usefulness of non-gradient approaches in topology optimization. Struct. Multidiscipl. Optim. 43, 589–596. doi:10.1007/s00158-011-0638-7

CrossRef Full Text | Google Scholar

Simoen, E., De Roeck, G., and Lombaert, G. (2015). Dealing with uncertainty in model updating for damage assessment: A review. Mech. Syst. Signal Process. 56-57, 123–149. doi:10.1016/j.ymssp.2014.11.001

CrossRef Full Text | Google Scholar

Solorzano, G., and Plevris, V. (2020). Optimum design of RC footings with genetic algorithms according to ACI 318-19. Buildings 10, 110. doi:10.3390/buildings10060110

CrossRef Full Text | Google Scholar

Vadyala, S. R., Betgeri, S. N., Matthews, J. C., and Matthews, E. (2022). A review of physics-based machine learning in civil engineering. Results Eng. 13, 100316. doi:10.1016/j.rineng.2021.100316

CrossRef Full Text | Google Scholar

van Eck, N. J., Waltman, L., Dekker, R., and van den Berg, J. (2010). A comparison of two techniques for bibliometric mapping: Multidimensional scaling and vos. J. Am. Soc. Inf. Sci. Technol. 61, 2405–2416. doi:10.1002/asi.21421

CrossRef Full Text | Google Scholar

van Eck, N. J., and Waltman, L. (2010). Software survey: VOSviewer, a computer program for bibliometric mapping. Scientometrics 84, 523–538. doi:10.1007/s11192-009-0146-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Vantyghem, G., De Corte, W., Shakour, E., and Amir, O. (2020). 3D printing of a post-tensioned concrete girder designed by topology optimization. Automation Constr. 112, 103084. doi:10.1016/j.autcon.2020.103084

CrossRef Full Text | Google Scholar

Vilutien, T., Kalibatiene, D., Hosseini, M. R., Pellicer, E., and Zavadskas, E. (2019). Building information modeling (bim) for structural engineering: A bibliometric analysis of the literature. Adv. Civ. Eng. 2019, 1–19. doi:10.1155/2019/5290690

CrossRef Full Text | Google Scholar

Waltman, L., van Eck, N. J., and Noyons, E. C. M. (2010). A unified approach to mapping and clustering of bibliometric networks. J. Inf. 4, 629–635. doi:10.1016/j.joi.2010.07.002

CrossRef Full Text | Google Scholar

Wang, D., Cheng, J., and Cai, H. (2021). Detection based on crack key point and deep convolutional neural network. Appl. Sci. 11, 11321. doi:10.3390/app112311321

CrossRef Full Text | Google Scholar

White, D. A., Arrighi, W. J., Kudo, J., and Watts, S. E. (2019). Multiscale topology optimization using neural network surrogate models. Comput. Methods Appl. Mech. Eng. 346, 1118–1135. doi:10.1016/j.cma.2018.09.007

CrossRef Full Text | Google Scholar

Wu, C., Pan, Z., Jin, C., and Meng, S. (2020). Evaluation of deformation-based seismic performance of RECC frames based on IDA method. Eng. Struct. 211, 110499. doi:10.1016/j.engstruct.2020.110499

CrossRef Full Text | Google Scholar

Wu, X., Ghaboussi, J., and Garrett, J. H. (1992). Use of neural networks in detection of structural damage. Comput. Struct. 42, 649–659. doi:10.1016/0045-7949(92)90132-J

CrossRef Full Text | Google Scholar

Yan, E., and Ding, Y. (2011). Discovering author impact: A pagerank perspective. Inf. Process. Manag. 47, 125–134. doi:10.1016/j.ipm.2010.05.002

CrossRef Full Text | Google Scholar

Yang, X.-S., Chien, S. F., and Ting, T. O. (2014). Computational intelligence and metaheuristic algorithms with applications. Sci. World J. 2014, 1–4. doi:10.1155/2014/425853

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, X., Li, H., Yu, Y., Luo, X., Huang, T., and Yang, X. (2018). Automatic pixel-level crack detection and measurement using fully convolutional network. Computer-Aided Civ. Infrastructure Eng. 33, 1090–1109. doi:10.1111/mice.12412

CrossRef Full Text | Google Scholar

Yu, D., Xu, Z., and Antucheviciene, J. (2019). Bibliometric analysis of the journal of civil engineering and management between 2008 and 2018. J. Civ. Eng. Manag. 25, 402–410. doi:10.3846/jcem.2019.9925

CrossRef Full Text | Google Scholar

Zabidin, N., Belayutham, S., and Che Ibrahim, C. K. I. (2020). A bibliometric and scientometric mapping of industry 4.0 in construction. ITcon. 25, 287–307. doi:10.36680/j.itcon.2020.017

CrossRef Full Text | Google Scholar

Zhang, D., Maslej, N., Clark, J., and Perrault, R. (2020). The AI index 2022 annual report. Tech. rep., AI Index Steering Committee. Stanford Institute for Human-Centered AI, Stanford University.

Google Scholar

Zhou, S., Zhou, M., Wang, Y., Gao, Y., Liu, Y., Shi, C., et al. (2020). Bibliometric and social network analysis of civil engineering sustainability research from 2015 to 2019. Sustainability 12. doi:10.3390/su12176842

CrossRef Full Text | Google Scholar