
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Built Environ., 04 January 2023
Sec. Earthquake Engineering
Volume 8 - 2022 | https://doi.org/10.3389/fbuil.2022.1022736
This article is part of the Research TopicHorizons in Built Environment 2022View all 6 articles
Probabilistic risk models for natural hazards, or natural catastrophe models, are indispensable tools for forecasting and quantifying the impacts of cascading and compounding earthquake-tsunami hazards. Their applications facilitate improved disaster risk mitigation and management. Uncertainties associated with forecasted multi-hazard impacts can be substantial, and practitioners and policymakers need guidance on implementing disaster risk reduction actions at all levels (local, regional, national, and international). In communicating such broad ranges of possible consequences with stakeholders, disaster scenarios need to be carefully selected and presented. This article reviews the state-of-the-art of earthquake, tsunami, and earthquake-tsunami catastrophe modelling and discusses future perspectives for earthquake-tsunami risk assessments.
Coastal communities in active subduction regions are exposed to significant risks from megathrust earthquakes and tsunamis. Such risks are low-probability, high-consequence events and often involve joint occurrences of multiple perils that are triggered by a single initiating event. Cascading chains of hazard events can consist of numerous combinations of ground surface rupture, strong ground motion, tsunami inundation, landslide, liquefaction, and aftershocks, and their combined effects can significantly worsen consequences compared to individual impacts of these hazard events (Goda et al., 2018). In the last 20 years, moment magnitude (M) 9-class megathrust earthquakes caused catastrophic disasters in the Indian Oceans, Japan, and Chile. Devastating events can strike other subduction zones globally (e.g., Cascadia, Mexico, and Makran), and their economic consequences to various sectors can be severe (de Ruiter et al., 2020). As more population migrates to coastal regions worldwide, earthquake-triggered shaking and tsunami pose more significant threats than ever before. Currently, coastal communities face urgent needs for operational decision-support tools that provide accurate performance assessments of infrastructures under multi-hazard actions (Tilloy et al., 2019). Resilience and sustainability are the fundamental requirements for modern infrastructures, and major progress has been made in disaster risk management (e.g., Bruneau and Reinhorn, 2007; Ayyub, 2014; Bozza et al., 2015; UNDRR, 2022). A key to achieving effective disaster resilience and sustainability is implementing a holistic risk management strategy that integrates all phases of a disaster cycle (i.e., mitigation, preparedness, response, and recovery) across different administrative levels.
Natural catastrophe modelling offers a versatile platform for calculating the economic loss due to natural disasters (Woo, 2011; Mitchell-Wallace et al., 2017). It has become a vital tool not only for the insurance and reinsurance industry but also for governmental agencies that are responsible for implementing disaster risk management policies at local, regional, and national levels. Key elements of quantitative risk assessments are hazard, exposure, and vulnerability, and uncertainties associated with these components are integrated into the final risk assessments (Beven et al., 2018; Foulser-Piggott et al., 2020). Standard outputs from catastrophe models are often obtained as exceedance probability (EP) curve and annual expected loss (AEL). These outputs inform disaster risk reduction policies and help take mitigation actions from socioeconomic and financial perspectives. Furthermore, these risk outputs can be used to identify critical scenarios based on quantified risk metrics and to generate a set of hazard and risk maps that correspond to the identified scenarios (Goda et al., 2021). Such integrated use of the catastrophe model outputs will enhance the current selection of critical scenarios, typically done deterministically in an ad-hoc manner.
Conventional risk assessments focus on individual hazards in isolation, and uncertainty associated with such events is not characterized and propagated comprehensively (Gill and Malamud, 2014, 2016; Beven et al., 2018b). A probabilistic multi-hazard analysis quantifies disaster risks and facilitates the evaluation of the cost-benefit effectiveness of available risk mitigation options (Scolobig et al., 2017; Akiyama et al., 2020). Several recent studies have proposed multi-risk approaches (Marzocchi et al., 2012; Selva, 2013; Mignan et al., 2014; Liu et al., 2015; Kameshwar et al., 2019) by integrating the performance-based engineering philosophy with new methodologies that enable to homogenize multiple risk components in different ways. For earthquake-related hazards, accurate urban-scale hazard and risk assessments have enhanced risk mitigation and preparedness (Liel and Deierlein, 2013; Rodrigues et al., 2018). Also, recent advances have led to the development of new multi-hazard risk assessment methods for earthquakes and tsunamis (Goda and De Risi, 2018; Park et al., 2019). For instance, Goda and De Risi (2018) proposed a multi-hazard loss model for Japanese subduction earthquakes by simulating shaking-tsunami hazard processes sequentially and applying seismic and tsunami fragility functions. Their work extended the performance-based earthquake engineering methodology (Baker et al., 2021) into the performance-based earthquake-tsunami engineering methodology for regional risk assessments. Moreover, the advanced simulation-based multi-hazard approaches, such as Dunant et al. (2021), can capture concurrent and cascading hazards and can be used to evaluate their risks to exposed populations and assets. In short, new multi-hazard catastrophe modelling frameworks have a high potential for practical applications, such as multi-hazard early warning, rapid impact assessments, and risk financing via insurance and other risk transfer approaches.
This review article summarizes the state-of-the-art of earthquake and tsunami catastrophe modelling in Section 2. Subsequently, a multi-hazard catastrophe modelling framework for strong shaking and tsunami inundation due to megathrust subduction earthquakes is presented in Section 3. The multi-hazard earthquake-tsunami catastrophe model that is described in this article incoporates time-dependent hazards by adopting renewal processes for earthquake occurrence and stochastic source modelling for earthquake ruptures that are common to all triggered perils. Therefore, the proposed method facilitates the quantification of multi-hazard earthquake-tsunami risks over an extended period. In Section 4, future perspectives of the multi-hazard approaches for earthquakes and tsunamis are discussed, together with several possible applications for improving disaster risk management and enhancing disaster preparedness and resilience. The review and discussion will be focused on physical damage and economic loss due to earthquakes and tsunamis.
A general catastrophe modelling framework involves hazard characterization, exposure database, and vulnerability assessment (i.e., risk = hazard × exposure × vulnerability) and requires the incorporation of uncertainties associated with key model components (Mitchell-Wallace et al., 2017). A standard approach for conducting such quantitative risk assessments for earthquakes and tsunamis is to generate a stochastic event set that contains various possible seismic events in a region of interest and then to carry out seismic or tsunami hazard assessments for the sites of interest where the target buildings and infrastructures are located.
The hazard simulations depend on peril types. For shaking hazards, using empirical ground motion models is a standard approach (Baker et al., 2021). When multiple sites are considered for regional seismic risk assessments, spatially correlated ground motion fields are generated statistically (Goda and Atkinson, 2010). Although computationally expensive, alternative physics-based approaches can simulate ground motion time-series at the sites of interest (Graves and Pitarka, 2010; Kurahashi and Iikura, 2013; Frankel et al., 2018). For tsunami hazards, it is common and computationally tractable to solve the governing equations of tsunami wave propagation and run-up numerically for a given initial water dislocation due to an earthquake rupture (Park et al., 2019). In this case, temporal and spatial variations of tsunami waves are simulated based on physics, unlike statistically characterized ground motion fields. The selection of suitable simulation methods depends on various situations related to the availability and applicability of existing models, validation data, and computational resources allocated to the investigations of interest. Regarding the other two elements of the risk formula, exposure is common to shaking and tsunami hazards. In contrast, vulnerability is characterized differently as the responses of buildings to seismic and tsunami perturbances are different. In the following, brief summaries of the state-of-the-art earthquake and tsunami risk assessments are presented.
Strong motions generated by earthquakes are the primary source of seismic damage and loss. Accurately assessing seismic hazards and risks is arduous because significant uncertainties are involved with earthquake rupture processes, seismic wave propagation, near-surface site effects, and seismic vulnerability of buildings and infrastructure. The performance-based earthquake engineering (PBEE) methodology can be employed to assess the seismic risk of structures and infrastructure (Cornell and Krawinkler, 2000).
Figure 1 shows a computational flow of the PBEE framework. Such a framework involves seismic hazard, structural, and damage-loss analysis. Mathematically, the mean annual rate of exceeding a seismic performance metric νE(DV) can be expressed as:
where the decision variable DV represents the consequence. λ(IM) is the mean annual rate of exceeding a given intensity measure (IM) and is computed via probabilistic seismic hazard analysis (PSHA; Gerstenberger et al., 2020; Baker et al., 2021). The structural analysis develops a probabilistic relationship between IM and engineering demand parameter (EDP), which is denoted by the complementary cumulative probability distribution function G(EDP|IM). Typical EDP parameters include structural response variables, such as the maximum inter-story drift ratio and peak floor acceleration for structural and non-structural components. The damage-loss analysis relates EDP to DV, such as repair/reconstruction costs, downtime, and fatalities. Many studies that implement the PBEE approach have been conducted in the literature (Porter et al., 2006; Goulet et al., 2007; Tesfamariam and Goda, 2015; Rodrigues et al., 2018).

FIGURE 1. Probabilistic seismic loss estimation framework (modified after Tesfamariam and Goda (2015)).
The output of Eq. 1 is typically summarized as a seismic loss EP curve, and various risk metrics, such as AEL, value at risk (VaR), and conditional value at risk (CVaR), can be calculated. These quantities are often used to develop stakeholders’ views of risk for managing financial earthquake risks and play a critical role in making various business decisions in a broader context (Mitchell-Wallace et al., 2017). The results also serve as input to the cost-benefit analysis of seismic risk mitigation measures (Liel and Deierlein, 2013) and risk financing through earthquake insurance and alternative risk transfer mechanisms (Michel-Kerjan et al., 2013; Bozza et al., 2015; Goda, 2015).
Tsunamis that are triggered by megathrust subduction earthquakes are highly destructive. A proper assessment of future tsunami hazard scenarios requires a robust treatment of uncertainties, especially those related to the earthquake rupture. On the other hand, tsunami risk assessments should consider various wave effects, such as hydrostatic, hydrodynamic, and debris impact forces, acting on the physical components of the built environment in coastal areas exposed to tsunami hazards. The analytical approaches for tsunami hazard and risk assessments parallel those of seismic hazards and risks. Recent advances in probabilistic tsunami hazard analysis (PTHA) incorporate uncertainties associated with earthquake occurrence and rupture characteristics of future megathrust events (Fukutani et al., 2015; Grezio et al., 2017; Behrens et al., 2021). Two important components that significantly affect PTHA results are earthquake occurrence modelling (time independent versus time-dependent; Goda, 2019) and earthquake rupture modelling (uniform versus heterogeneous distribution of earthquake slip; Geist, 2002; Davies et al., 2015; Melgar et al., 2019). The latter can be typically carried out by generating numerous stochastic source models with varying geometry and slip distributions (Goda et al., 2016). It is important to note that both occurrence and rupture models are common to earthquakes and tsunamis. Empirical tsunami fragility and vulnerability functions can be used to quantify the expected damage or loss due to tsunamis (Tarbotton et al., 2015; Macabuag et al., 2016). The integration of PTHA and tsunami vulnerability has led to the development of performance-based tsunami engineering (PBTE) approaches (Attary et al., 2017; Goda and De Risi, 2017).
Using stochastic source models, a computational flow of the PBTE framework is shown in Figure 2, and can be formulated as (Goda and De Risi, 2017):
where νT(L ≥ l) is the mean annual occurrence rate that the tsunami loss L for a portfolio of buildings exceeds a specific loss threshold l. The variables M, S, IM, and DS correspond to earthquake magnitude, earthquake source parameters, tsunami intensity measures, and tsunami damage states, respectively. In Eq. 2,
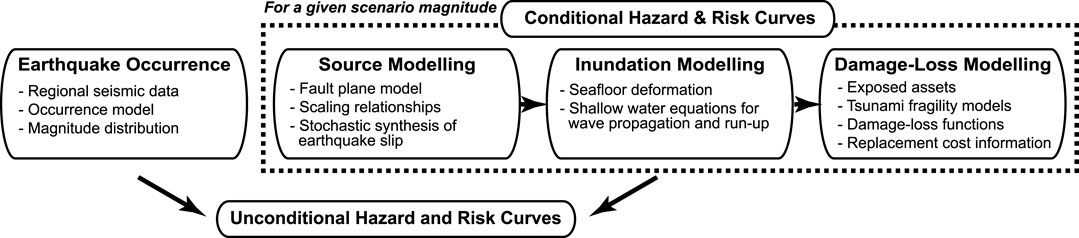
FIGURE 2. Probabilistic tsunami loss estimation framework using stochastic source models (modified after Goda and De Risi (2017)).
Outputs from tsunami hazard assessments include site-specific tsunami hazard curves, which can be used for engineering design (Chock, 2016), and tsunami inundation maps at different return period levels, which can serve as the fundamental input to developing local and regional hazard evacuation plans (Muhammad et al., 2017; Wood et al., 2019). The results are also helpful for financial tsunami risk management through tsunami insurance coverage (Song and Goda, 2019) and tsunami catastrophe bonds (Goda et al., 2019).
Shaking and tsunami hazards/risks have similar and dissimilar characteristics, as seen in Section 2. Firstly, the earthquake occurrence is concurrent in shaking and tsunami risks. The probability of a catastrophic earthquake-tsunami event over a given period can be influenced by the quasi-periodic nature of megathrust subduction earthquakes (Sykes and Menke, 2006; Williams et al., 2019; Griffin et al., 2020). When different time-dependent characteristics are considered, shaking and tsunami risks are affected simultaneously, resulting in significant variations of shaking and tsunami loss curves (Goda, 2020). Secondly, earthquake rupture is common in both perils. When a megathrust earthquake occurs, it is likely that coastal communities will experience strong shaking first and then tsunami inundation (i.e., cascading hazards). The buildings will be subjected to both types of external loads, and the cumulative effects of shaking and tsunami damage can exacerbate the consequences (Park et al., 2012; Attary et al., 2021). Generally speaking, ground motion hazards at a fixed distance from the fault rupture tend to saturate in their amplitudes with respect to earthquake magnitude (Abrahamson and Gulerce, 2020), whereas tsunami inundation extent tends to increase with earthquake magnitude. These differences typically result in bimodal distributions of earthquake-tsunami loss (Goda and De Risi, 2018; Goda et al., 2021).
To contrast the differences between shaking and tsunami risks, Figure 3 shows several major aspects that require attention in developing viable multi-hazard approaches for earthquakes and tsunamis (note: although main features are categorized into six blue hexagonal panels in Figure 3, they only serve as exemplars rather than a comprehensive list of such features):
• Megathrust events are rare and are not best described by conventional time-independent Poisson processes. Nevertheless, available data are usually limited, and fitting statistical models to historical, geological, and paleoseismic/tsunami data is not easy due to inherent uncertainty in these records (Ogata, 1999). Moreover, the rupture patterns of the subduction zone can exhibit more frequent segmented ruptures and long quiescent super-cycle ruptures (Philibosian and Meltzner, 2020). These aspects significantly affect earthquake occurrence modelling (see panels 1 and 2).
• When the earthquake rupture is characterized, past historical events are limited to relatively recent earthquakes, although a global database of earthquake source inversion models has been growing steadily (Mai and Thingbaijam, 2014). In empirical ground motion models, the source representation is rather simplistic (i.e., earthquake magnitude and corresponding fault geometry as finite-fault with uniform earthquake slip) unless more physical approaches are adopted (Frankel et al., 2018). Tsunami simulations require detailed earthquake rupture processes (i.e., heterogeneous earthquake slip distribution and kinematic evolution). Considering the computational requirements and available geophysical data, the preceding situations often result in adopting statistical models for shaking hazard simulations in contrast with solving nonlinear shallow water equations for tsunami simulations (see panels 3 and 4).
• In the propagation phase of the two hazards, tsunami waves are significantly slower than seismic waves. Nevertheless, near-tsunami waves tend to cause far more destruction along the coast than shaking when the seismic event is significant in magnitude (see panel 5), noting that the tsunami impact significantly depends on local topography. On the other hand, the shaking impact is relatively less destructive because of relatively larger distance between the causative fault rupture and buildings (Goda and Atkinson, 2014). Historical examples of such tsunami disasters include the 2004 Indian Ocean event (Murata et al., 2010) and the 2011 Tohoku, Japan event (Fraser et al., 2013). This often leads to more opportunities to improve tsunami early warning and evacuation (Muhammad et al., 2017; Wood et al., 2016), although achieving the improved evacuation often requires a holistic solution that effectively combines hard measures and soft measures at community levels (Cosson, 2020; Oregon Seismic Safety Policy Advisory Council, 2021).
• In the damage and loss generation phase of the two hazards, shaking and tsunami affect the different physical components of the built environment (e.g., buildings and infrastructure) differently (see panel 6). Generally, the tsunami fragility functions have steeper slopes, i.e., rapid damage accumulation with respect to tsunami hazard parameters (Goda and De Risi, 2018; Park et al., 2019). The shaking risks are more widespread spatially, but their effects on individual structures are more variable. From a structural design viewpoint, earthquake damage can be better controlled by enforcing adequate seismic design and construction practices. In contrast, although some structural measures for reducing tsunami risks can be implemented for individual buildings, the extent of the tsunami inundation in a given area is significantly affected by the coastal defence structures (e.g., seawalls, dikes, breakwaters, and coastal forests) that are in place. In other words, different risk management strategies are necessary for mitigating the shaking and tsunami risks effectively.
Overall, the analytical and computational framework for megathrust subduction earthquakes and tsunamis needs to consider various uncertainties in the risk assessments by accommodating the commonality and discrepancy of the shaking and tsunami perils (Section 3.1). The stochastic event-based catastrophe modelling approach, which is usually implemented for single perils, can integrate different model components flexibly and is well suited for extending single-hazard models into multi-hazard ones (Mitchell-Wallace et al., 2017). The stochastic event-based approach also facilitates the incorporation of other earthquake-triggered perils, such as aftershocks (Zhang et al., 2018) and geohazards (De Risi et al., 2018; Goda and Shoaeifar, 2022). A prototype of such a multi-hazard catastrophe model for time-dependent shaking and tsunami risks has been developed by adopting stochastic source modelling (Goda, 2020). The generic feature of this model is summarized in the following. The formulations and specific applications of the multi-hazard loss model can be found in Goda and De Risi (2018) and Goda (2020). Figure 4 depicts the computational framework of the probabilistic earthquake-tsunami loss estimation.
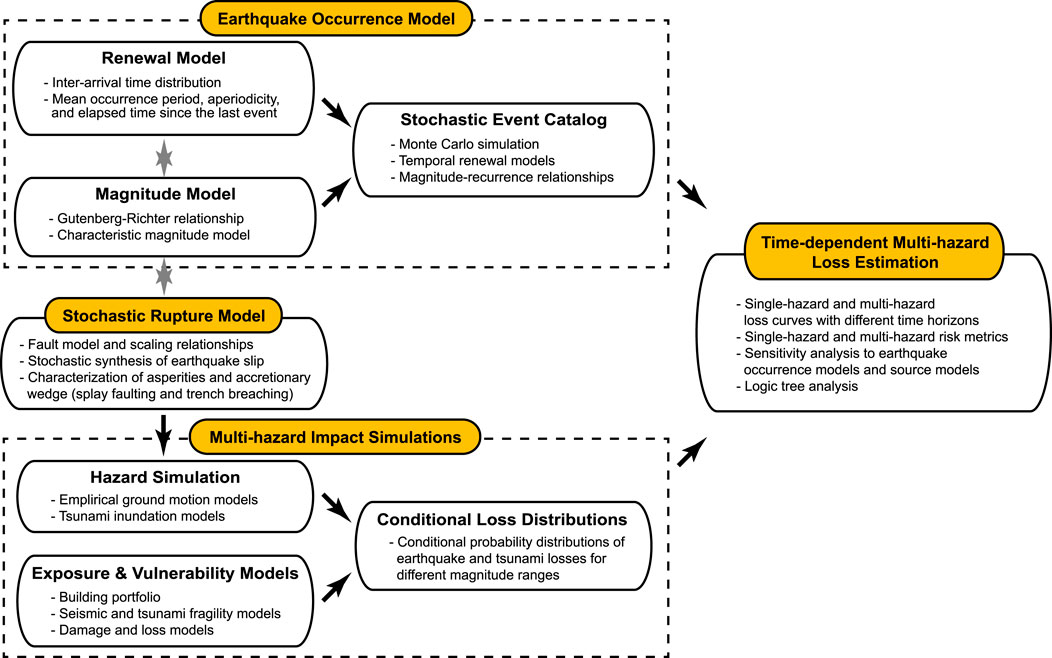
FIGURE 4. Probabilistic time-dependent earthquake-tsunami loss estimation framework using stochastic source models (modified after Goda (2020)).
Earthquake occurrence is one of the most significant elements in PSHA and PTHA and involves significant uncertainty. By observing the quasi-periodic occurrence of the past megathrust subduction events, both physics-inspired occurrence models (Shimazaki and Nakata, 1980; Kiremidjian and Anagnos, 1984) and statistical renewal models (Cornell and Winterstein, 1988) have been proposed in the literature. To implement time-dependent earthquake occurrence models in catastrophe modelling, a standard approach is to adopt renewal processes (Matthews et al., 2002). Their characteristics can be specified by the inter-arrival time distribution (e.g., Brownian Passage Time and Weibull distributions), mean and standard deviation of recurrence period, and elapsed time since the last event. The consideration of the elapsed time is essential as it adjusts the time clock for the risk assessment with respect to the recurrence interval. A recent time-space interaction model of earthquake occurrence can capture spatiotemporally interacting rupture segments of the megathrust event (Ceferino et al., 2020) and can be used for multi-hazard risk assessments.
The earthquake occurrence module shown in Figure 4 generates numerous stochastic event sets for a specified duration by considering quasi-periodic characteristics of major tsunamigenic earthquakes, represented by a renewal model. The corresponding magnitude of the simulated events can be specified by using applicable magnitude models, such as Gutenberg-Richter relationships and characteristic models. In defining the temporal and magnitude characteristics of the earthquake occurrence model, it is important to ensure that the regional seismic moment release rate is appropriately balanced with regard to long-term historical seismicity and geodetic observations. In other words, the above-mentioned two aspects are interrelated. Stochastic event sets can be generated via Monte Carlo simulations (Goda, 2019).
Earthquake rupture is a complex process influenced by pre-rupture stress and frictional conditions of the fault. The first step for earthquake rupture modelling, shown in Figure 4, is to define a fault geometry based on the seismotectonic characteristics of the region of interest. A useful source of such subduction interface geometry is the Slab2 model by Hayes et al. (2018). The spatiotemporal rupture process can be estimated by matching key features of simulated data with observations. To characterize earthquake sources of future events, empirical scaling relationships of fault geometry and earthquake slip can be utilized (Goda et al., 2016; Melgar and Hayes, 2019), and their realized values can be sampled from these equations.
To characterize the spatial distribution of earthquake slip, spectral analysis can be used to determine the wavenumber representation of earthquake slip heterogeneity (Herrero and Bernard, 1994; Mai and Beroza, 2002; Lavallée et al., 2006). The derived spectral model, such as the von Karman spectrum, can be used to synthesize stochastic earthquake slip distributions (Mai and Beroza, 2002). To quantify the uncertainties of tsunami earthquake rupture, such stochastic source models have been used in various tsunami hazard studies that account for heterogeneous earthquake slips (Davies et al., 2015; Sepúlveda et al., 2018). Generating realistic earthquake rupture scenarios via stochastic source modelling requires careful consideration of regional seismotectonic and geophysical characteristics. Defining possible areas of large earthquake slip concentrations (i.e., asperities) involves epistemic uncertainties and typically is dealt with via a logic tree (Fukutani et al., 2015). Furthermore, different rupture behavior of the outer wedge of the accretionary prism near the trench, such as splay rupturing and trench breaching (Gao et al., 2018), can also be characterized through stochastic source modelling (Momeni et al., 2022).
The third major building block of the probabilistic loss model for shaking and tsunami risks is the multi-hazard impact simulations (see Figure 4), whose results are represented by the conditional multi-hazard loss distributions. For a given earthquake magnitude, for all generated stochastic rupture models, ground motion and tsunami inundation simulations can be performed for a building portfolio of interest in a coastal community, and the results are summarized as empirical probability distributions of the selected risk metric (e.g., multi-hazard portfolio loss) or as fitted parametric probability distributions. Note that the seismic and tsunami intensity simulations are carried out for the same event and rupture case. Once shaking and inundation intensity measures at the locations of interest, seismic and tsunami fragility functions as well as relevant damage-loss functions are applied to evaluate damage severities of the exposed assets. Repeating this process facilitates the evaluation of the probability distribution functions of single-hazard and multi-hazard loss metrics to be obtained for different magnitude ranges (Goda and De Risi, 2018).
Seismic and tsunami fragility functions implemented in the multi-hazard impact simulations should capture the damage accumulation effects (Park et al., 2012; Attary et al., 2021). At present, such shaking-tsunami damage accumulation models, which need to be developed through numerical simulations of the combined seismic-tsunami effects on buildings due to unavailability of empirical damage data in such multi-hazard situations, are not available for many subduction regions. Since structural design requirements and construction practice usually differ across seismic regions, these analytical multi-hazard fragility functions will be region- and structure-specific. This is an open area of future research in advancing the multi-hazard catastrophe models for shaking and tsunami risks.
To combine the outputs from the three modules, for each event in the stochastic event catalogs from Section 3.2.1, the single-hazard and multi-hazard loss values are sampled from the conditional loss distribution that corresponds to the event’s magnitude (from Section 3.2.3). By repeating this sampling for all events in a single stochastic catalog, one sample of the multi-hazard loss can be obtained. This process of Monte Carlo sampling can be iterated for all generated stochastic event catalogs, and the results can be summarized as a multi-hazard EP loss curve. These simulated samples of the multi-hazard loss can be used to quantify several risk metrics, such as AEL and VaR, for making risk management decisions. Individual loss results for shaking and tsunami risks are retained for the post-processing, noting that single-hazard EP curves and risk metrics can also be obtained as part of the catastrophe model output. An advantage of the proposed method is the computational efficiency. Although performing several thousands of tsunami inundation simulations require a high computing capacity and resource, this usually does not become a significant obstacle because the tsunami simulation based on shallow water theory is computationally less expensive than solving the governing equations in 3D (i.e., Navier-Stokes equations) or conducting 3D seismic ground motion simulations (Graves and Pitarka, 2010; Frankel et al., 2018). The decoupled approach to earthquake occurrence and the multi-hazard impact simulation also achieves a high computational efficiency when numerous kinds of earthquake occurrence models are considered in the risk assessments.
To illustrate the above-mentioned multi-hazard risk approach, a regional seismic-tsunami loss that was obtained for the southern part of Miyagi Prefecture, Japan, is considered. Figure 5 shows an example of multi-hazard loss curves and joint multi-hazard maps for shaking and tsunami risks, which are modified from Goda and De Risi (2018). Using the multi-hazard loss curve (blue line in the central panel), the overall risk level for the considered building portfolio (i.e., 6,096 wooden houses) can be quantified. For each point on the loss curve at a selected return period level (e.g., 100 and 500 years return periods on the top and bottom rows, respectively), a corresponding earthquake rupture scenario can be referenced, and joint shaking and tsunami inundation hazard maps can be drawn. Such joint mapping of the multi-hazard intensities is useful for visualizing multi-hazard scenarios and communicating risk assessment results with stakeholders. The results can be presented for different hazard and risk quantities, such as damage states and losses of buildings (Goda et al., 2021). These scenarios can be further linked with evacuation simulation results to convey a range of multi-hazard risk results under different scenarios (Muhammad et al., 2021). The versatility and extendibility of the proposed multi-hazard catastrophe model for shaking and tsunami risks are particularly valuable.
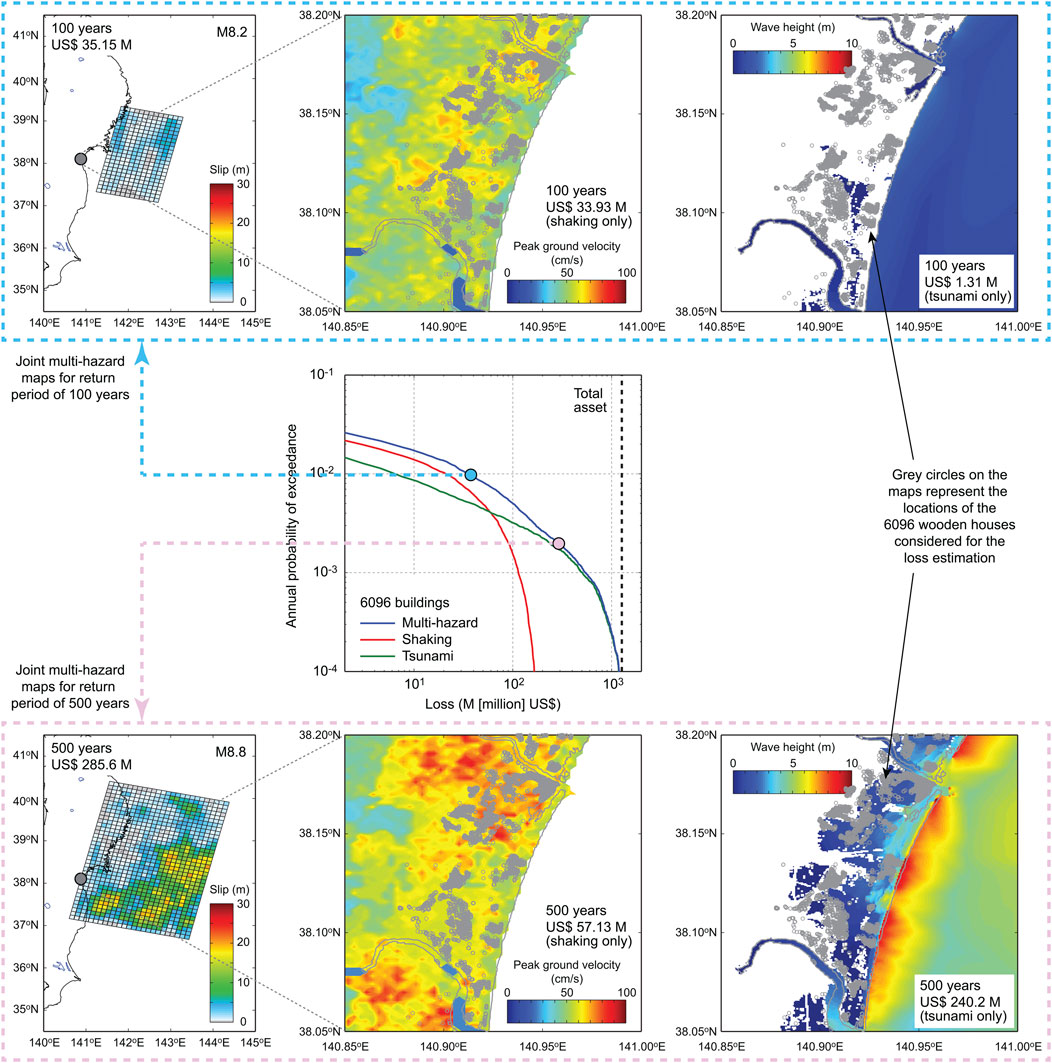
FIGURE 5. Example of multi-hazard loss curves and joint multi-hazard maps for shaking and tsunami risks (modified after Goda and De Risi (2018)). The seismic intensity is represented by peak ground velocity, whereas the tsunami intensity is represented by tsunami height.
Our society and infrastructure are subjected to multiple types of cascading hazards. Integrated hazard and risk assessment and management policies are needed to mitigate consequences due to multiple concurrent hazards (Tilloy et al., 2019). In this context, new time-dependent earthquake-tsunami risk models will serve as essential decision-support tools for reducing and managing disaster risks from future megathrust subduction earthquakes and tsunamis. Types of investigations that can be explored using the new risk quantification tools are broad, ranging from improved mapping and forecasting of cascading and compounding earthquake and tsunami risks to developing community-focused solutions, such as early warning system, evacuation planning, and land-use planning. The multi-hazard loss models are also indispensable for developing disaster risk financing tools, such as insurance rate-making and alternative risk transfer instruments. They can be used to quantify and compare the benefits and costs associated with different alternatives (Scolobig et al., 2017), thereby promoting risk-informed decision-making in managing catastrophic earthquake-tsunami risks. Moreover, the new approaches can incorporate maintenance and inspection costs, and other environmental impacts from “cradle to grave”, to further improve both resilience and sustainability of society and built environments for coastal communities and infrastructures (Akiyama et al., 2020).
In this section, future perspectives of earthquake-tsunami risk assessments are discussed by adopting a disaster management cycle, i.e., mitigation, preparedness, response, and recovery, as a guiding framework for enhancing earthquake-tsunami risk management. This is illustrated in Figure 6. Enhanced disaster management aims to reduce/avoid the potential losses from cascading hazards, assure prompt and appropriate response and support/assistance for victims, and achieve rapid and effective recovery (Bruneau and Reinhorn, 2007). By integrating these key elements of earthquake-tsunami risk mitigation measures from a holistic risk management perspective, future resilience-based approaches for earthquakes and tsunamis will emerge. Ultimately, resilient capacity building in coastal communities will empower residents, responders, organizations, communities, governments, and society to share the responsibility to prevent disasters and adapt to future perils (Ayyub, 2014; UNDRR, 2022).
The mitigation (prevention) phase of the disaster management cycle aims to minimize disaster effects (e.g., retrofitting and zoning, vulnerability analyses, and public education). Protection via physical measures is the primary approach for controlling disaster risks to built environments, and building codes have played a key role (Chock, 2016). In promoting more resilient building design and construction practices, the life-cycle cost-benefit assessments based on suitable catastrophe models are essential (Liel and Deierlein, 2013; Akiyama et al., 2020), and quantitative comparisons of the benefits and costs facilitate the more efficient use of available resources and budgets for disaster risk reduction.
Improving the accuracy of the hazard and risk assessment methods is important, which will eventually lead to enhanced actions for risk mitigation. Developing new time-dependent multi-hazard risk models for cascading and compounding earthquake perils is an exemplar (Section 3). A critical research gap in the new multi-hazard earthquake-tsunami catastrophe modelling is the multi-hazard fragility that accounts for the damage accumulation effects from multiple concurrent perils (Attary et al., 2021). Resolving this research bottleneck will require interdisciplinary collaboration between earthquake-tsunami scientists and seismic-coastal engineers. The inputs to numerical structural models must come from advanced multi-hazard simulators of strong motion and tsunami waves (Maeda et al., 2013; Goda et al., 2017) by accounting for uncertainties of the multi-hazard processes and scenarios (note: a myriad of possible multi-hazard loading scenarios exist; Dunant et al., 2021). These hazard inputs are used to conduct the multi-hazard damage assessments of the structural models via analytical approaches, such as sequential nonlinear static analyses (Petrone et al., 2017) and more computationally demanding nonlinear dynamic analyses (Park et al., 2012; Attary et al., 2021). The multi-hazard tools must be further extended to resolve these research challenges.
The preparedness phase is focused on planning how to respond to a disaster and includes preparedness planning, emergency exercises/training, and warning systems. The multi-hazard catastrophe models for earthquakes and tsunamis can contribute to this phase of the disaster management cycle in various ways. For instance, joint multi-hazard mapping in relation to an overall portfolio risk promotes the direct association of possible disaster scenarios and consequences by considering uncertainties and helps visualize these multi-hazard risk results (Figure 5). This is particularly useful for risk communications with local residents and community responders.
The developed multi-hazard catastrophe models can be used as multi-hazard scenario simulators that take into account different hazard interactions (e.g., triggering, exacerbating, catalyzing, and impeding relationships; Gill and Malamud, 2014, 2016). When the cumulative impacts from multiple damaging perils are fully developed in the models (Section 4.1), deteriorating vulnerability, which represents the diminishing capacity of society and infrastructure subjected to the cascade of multiple compounding risks, can be incorporated into the risk assessments. The changing exposure can also be integrated into the risk assessments (Mesta et al., 2022). As Gill and Malamud (2014, 2016) demonstrated, hazard interactions, which are likely to be affected by natural, anthropogenic, and technological processes, are complex. In the above context, natural hazards are not limited to geological risks (strong motion, tsunami, landslide, liquefaction, and aftershock) but include meteorological and climate risks. To visualize the complex multi-hazard interaction and its impact on the built environment, Dunant et al. (2021) utilized a graph theory combined with a probabilistic multi-hazard catastrophe model for earthquake and rainfall-triggered landslides. Their results demonstrated that the primary risk in the case study area is affected by earthquakes. In contrast, in extreme situations, landslide risks triggered by either heavy rainfalls or major earthquakes become important and increase overall risks due to hazard interaction.
The response phase of the disaster management cycle strives to minimize the hazard impacts created by a disaster and can involve search and rescue, emergency relief, early warning announcement and evacuation, and rapid risk assessment. In implementing disaster risk reduction actions for this phase, it is important to consider the impact to human fatalities (Latcharote et al., 2018), in addition to physical damage and economic loss, which has been mainly focused upon in this article. In conducting the research related to the response, key competing requirements are accuracy and time (e.g., issuing warning messages) and must consider uncertainties and errors associated with such assessments and decisions.
Although tsunamis cannot be prevented, their severe impact can be mitigated through enhanced tsunami preparedness, timely warning, and effective response, and a tsunami early warning system is an effective tool to reduce victims (Harig et al., 2019). In creating a comprehensive database for a tsunami early warning system and developing an effective algorithm for issuing accurate warning messages, it is important that the system is tested to work well for a variety of possible earthquake ruptures. However, there is no abundant historical tsunami data that can be directly used for developing such a warning system. Because it is uncertain how future tsunami events may unfold, it is sensible to use synthetic tsunami wave data to calibrate the tsunami early warning algorithm based on the conventional earthquake information (e.g., magnitude estimate and epicenter location) as well as offshore wave data (e.g., S-net in Japan; Kanazawa, 2013). For this purpose, adopting stochastic tsunami simulation models is a viable approach (Mulia and Satake, 2021; Li and Goda, 2022), which allows the consideration of realistic heterogeneous earthquake slips and is statistically and seismologically compatible with inferred earthquake slips via source inversion analyses (Section 3). Another important development for tsunami forecasting and warning is the real-time data assimilation technique using a dense array of wave recording stations and numerical tsunami simulations (Gusman et al., 2016; Wang and Satake, 2021). When the multi-hazard risk outputs are included, not only conventional hazard-based warning systems but also risk-based warning systems can be developed. Furthermore, the use of synthetically simulated hazard and risk data allows more advanced statistical and machine learning methods to be applied to the development of early warning systems (Makinoshima et al., 2021).
The use of multi-hazard simulators also presents new research avenues for carrying out earthquake-tsunami evacuation. Agent-based evacuation models can capture the dynamics of tsunami inundation, interaction with the built environment (e.g., road network capacity), and complex human interactions (Lammel et al., 2010; Wood et al., 2016). When agent-based models are implemented within a stochastic source modelling framework, the effectiveness of current and proposed evacuation systems (different routes and destinations, including vertical evacuation shelters) can be evaluated by fully accounting for uncertainties of different multi-hazard scenarios (Muhammad et al., 2017, 2021). The results from such integrated hazard-evacuation simulations are insightful as they produce the community-level performance metrics of different evacuation systems and strategies.
Rapid tsunami impact assessment methods are currently lacking. This contrasts sharply with rapid earthquake impact assessment tools implemented globally in the USGS PAGER (Prompt Assessment of Global Earthquakes for Response) system (Wald et al., 2010). Conventionally, the earthquake and tsunami impact can be assessed quickly based on earthquake magnitude and location. With the expansion of recording networks of earthquakes (K-NET and KiK-net in Japan) and tsunamis (e.g., S-net in Japan), real-time recorded shaking and wave information could be employed. Moreover, recent availability of satellite imageries and semi-automated image processing, combined with machine learning techniques, could be exploited to develop multi-hazard rapid impact assessment tools (Moya et al., 2018; Goda et al., 2019; Naito et al., 2020). The fusion of remote sensing technology and advanced data analytics is a promising research field for post-disaster hazard monitoring and risk management (Voigt et al., 2016).
The recovery phase concerns returning to normality for the affected communities as soon as possible by providing victims with temporary housing, financial aid, and medical/mental care. Insurance can be viewed as a financial means for affected households to recover from the disaster impacts and to expedite the recovery process.
Although earthquake insurance is usually available for many earthquake-prone countries and regions (OECD, 2018), tsunami insurance coverage is not widely offered for coastal areas that are exposed to potential tsunami risks. The development of tsunami insurance products requires the fair quantification of tsunami risks for their pricing. In this regard, capable tsunami catastrophe models are essential (Song and Goda, 2019). Furthermore, when multi-hazard insurance products for shaking and tsunami risks are to be offered, accurate multi-hazard catastrophe models will be needed to differentiate insurance rates for multi-hazard shaking-tsunami loss coverage by focusing on strong shaking intensity and effects of land elevation and topography.
To mitigate the economic impact of catastrophic shaking-tsunami hazards for insurers and local/central governments, financial risk transfer instruments offer alternative ways to diversify the financial risk exposures due to natural catastrophes. For instance, the insurance/reinsurance industry and governments can use parametric catastrophe bonds to transfer catastrophic risks to the financial markets (Goda, 2015; Goda, 2021). The advantages of the parametric catastrophe bonds are low moral hazard (Cummins, 2008) and swiftness/transparency of the payment (unlike conventional insurance; King et al., 2014). The disadvantage is the basis risk (i.e., the discrepancy between the payment and actual loss). The accurate catastrophe models are necessary for designing effective bond triggers and for reducing the basis risk. In this context, rapid risk assessment methods for earthquakes and tsunamis (Section 4.3) will facilitate the new development in disaster risk financing tools.
The catastrophe models are effective tools to quantify the financial impact due to natural disasters. The models are based on the modular hazard-exposure-vulnerability framework. Therefore, they can be updated/extended flexibly for different hazard types and built environment. Future research must address cascading hazards and their compounding impacts by accounting for the physical causes of the multi-hazards and evaluating the effectiveness of response and recovery measures for mitigating impacts and enhancing disaster resilience of built environments. Using a diaster cycle as a framework, several key areas of future research have been mentioned in Section 4. The catastrophe models have a vast range of applications in the private and public sectors. The tools and their applications will enable new approaches for more efficient disaster risk management over the entire disaster cycle.
The prototype multi-hazard catastrophe model introduced in Section 3 promotes time-dependent multi-hazard risk assessments for coastal communities (i.e., people and infrastructure). With the broader perspectives on future disaster risk management for coastal active subduction regions, non-geological hazards can pose significant risks. For instance, relative sea level rise will affect the baseline water level for tsunami hazard and risk assessments and is an important factor for long-term infrastructure planning (Li et al., 2018; Alhamid et al., 2022). Coastal hazards, such as storm surges, could affect the integrity of the coastal defence structures in place and impacts of geological hazards could depend on those of preceding hazards. On the other hand, if a major subduction earthquake precedes local storm surge events, coastal structures may be impaired before storms, and tectonic subsidence due to the earthquake may reduce the height capacity of the defence structures. These compounding climate-geological risks can interact and amplify their impacts, and their hazard sequences, depending on timing and severity, will become more critical for disaster risk management. To quantify the interaction of cascading and compounding climate-geological risks, the current multi-hazard catastrophe models must be extended to a dynamic multi-hazard risk framework that accommodates changing characteristics of social, demographic, and built environments.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
KG is funded by the Canada Research Chair program (950-32015) and the NSERC Discovery Grant (RGPIN-2019-05898).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abrahamson, N., and Gulerce, Z. (2020). Regionalized ground-motion models for subduction earthquakes based on the NGA-SUB database. Tech. Rept. PEER Rept. 2020/25, 1–197.
Akiyama, M., Frangopol, D. M., and Ishibashi, H. (2020). Toward life-cycle reliability-risk- and resilience-based design and assessment of bridges and bridge networks under independent and interacting hazards: Emphasis on earthquake, tsunami and corrosion. Struct. Infrastructure Eng. 16, 26–50. doi:10.1080/15732479.2019.1604770
Alhamid, A. K., Akiyama, M., Ishibashi, H., Aoki, K., Koshimura, S., and Frangopol, D. M. (2022). Framework for probabilistic tsunami hazard assessment considering the effects of sea-level rise due to climate change. Struct. Saf. 94, 102152. doi:10.1016/j.strusafe.2021.102152
Attary, N., Unnikrishnan, V. U., van De Lindt, J. W., Cox, D. T., and Barbosa, A. R. (2017). Performance-Based Tsunami Engineering methodology for risk assessment of structures. Eng. Struct. 141, 676–686. doi:10.1016/j.engstruct.2017.03.071
Attary, N., van De Lindt, J. W., Barbosa, A. R., Cox, D. T., and Unnikrishnan, V. U. (2021). Performance-based tsunami engineering for risk assessment of structures subjected to multi-hazards: Tsunami following earthquake. J. Earthq. Eng. 25, 2065–2084.
Ayyub, B. M. (2014). Systems resilience for multi-hazard environments: Definition, metrics, and valuation for decision making. Risk Anal. 34, 340–355. doi:10.1111/risa.12093
Baker, J. W., Bradley, B., and Stafford, P. (2021). Seismic hazard and risk analysis. Cambridge University Press, 600.
Behrens, J., Løvholt, F., Jalayer, F., Lorito, S., Salgado-Gálvez, M. A., Sørensen, M., et al. (2021). Probabilistic tsunami hazard and risk analysis: A review of research gaps. Front. Earth Sci. (Lausanne). 9, 628772. doi:10.3389/feart.2021.628772
Beven, K. J., Almeida, S., Aspinall, W. P., Bates, P. D., Blazkova, S., Borgomeo, E., et al. (2018). Epistemic uncertainties and natural hazard risk assessment - part 1: A review of different natural hazard areas. Nat. Hazards Earth Syst. Sci. 18, 2741–2768. doi:10.5194/nhess-18-2741-2018
Beven, K. J., Aspinall, W. P., Bates, P. D., Borgomeo, E., Goda, K., Hall, J. W., et al. (2018). Epistemic uncertainties and natural hazard risk assessment - part 2: What should constitute good practice? Nat. Hazards Earth Syst. Sci. 18, 2769–2783. doi:10.5194/nhess-18-2769-2018
Bozza, A., Asprone, D., and Manfredi, G. (2015). Developing an integrated framework to quantify resilience of urban systems against disasters. Nat. Hazards (Dordr). 78, 1729–1748. doi:10.1007/s11069-015-1798-3
Bruneau, M., and Reinhorn, A. (2007). Exploring the concept of seismic resilience for acute care facilities. Earthq. Spectra 23 (1), 41–62. doi:10.1193/1.2431396
Ceferino, L., Kiremidjian, A., and Deierlein, G. (2020). Probabilistic space- and time-interaction modeling of mainshock earthquake rupture occurrence. Bull. Seismol. Soc. Am. 105, 2498–2518. doi:10.1785/0120180220
Chock, G. Y. K. (2016). Design for tsunami loads and effects in the ASCE 7-16 standard. J. Struct. Eng. (N. Y. N. Y). 142, 04016093. doi:10.1061/(asce)st.1943-541x.0001565
Cornell, C. A., and Krawinkler, H. (2000). Progress and challenges in seismic performance assessment, 3. Berkeley, CA: Pacific Earthquake Engineering Research Center. Available at: http://peer.berkeley.edu/news/2000spring/performance.html.
Cornell, C. A., and Winterstein, S. R. (1988). Temporal and magnitude dependence in earthquake recurrence models. Bull. Seismol. Soc. Am. 78, 1522–1537.
Cosson, C. (2020). Build back better”: Between public policy and local implementation, the challenges in tohoku’s reconstruction. Archit. Urban Plan. 16, 1–4. doi:10.2478/aup-2020-0001
Cummins, D. J. (2008). CAT bonds and other risk-linked securities: State of the market and recent developments. Risk Manag. Insur. Rev. 11, 23–47. doi:10.1111/j.1540-6296.2008.00127.x
Davies, G., Horspool, N., and Miller, V. (2015). Tsunami inundation from heterogeneous earthquake slip distributions: Evaluation of synthetic source models. J. Geophys. Res. Solid Earth 120, 6431–6451. doi:10.1002/2015jb012272
De Risi, R., De Luca, F., Kwon, O. S., and Sextos, A. (2018). Scenario-based seismic risk assessment for buried transmission gas pipelines at regional scale. J. Pipeline Syst. Eng. Pract. 9, 04018018. doi:10.1061/(asce)ps.1949-1204.0000330
De Risi, R., Goda, K., Yasuda, T., and Mori, N. (2017). Is flow velocity important in tsunami empirical fragility modeling? Earth-Science Rev. 166, 64–82. doi:10.1016/j.earscirev.2016.12.015
de Ruiter, M. C., Couasnon, A., van den Homberg, M. J. C., Daniell, J. E., Gill, J. C., and Ward, P. J. (2020). Why we can no longer ignore consecutive disasters. Earth's. Future 8, e2019EF001425. doi:10.1029/2019ef001425
Dunant, A., Bebbington, M., and Davies, T. (2021). Probabilistic cascading multi-hazard risk assessment methodology using graph theory, a New Zealand trial. Int. J. Disaster Risk Reduct. 54, 102018. doi:10.1016/j.ijdrr.2020.102018
Foulser-Piggott, R., Bowman, G., and Hughes, M. (2020). A framework for understanding uncertainty in seismic risk assessment. Risk Anal. 40, 169–182. doi:10.1111/risa.12919
Frankel, A., Wirth, E., Marafi, N., Vidale, J., and Stephenson, W. (2018). Broadband synthetic seismograms for magnitude 9 earthquakes on the Cascadia megathrust based on 3D simulations and stochastic synthetics, Part 1: Methodology and overall results. Bull. Seismol. Soc. Am. 108, 2347–2369. doi:10.1785/0120180034
Fraser, S., Pomonis, A., Raby, A., Goda, K., Chian, S. C., Macabuag, J., et al. (2013). Tsunami damage to coastal defences and buildings in the March 11th 2011 Mw9.0 Great East Japan earthquake and tsunami. Bull. Earthq. Eng. 11, 205–239. doi:10.1007/s10518-012-9348-9
Fukutani, Y., Suppasri, A., and Imamura, F. (2015). Stochastic analysis and uncertainty assessment of tsunami wave height using a random source parameter model that targets a Tohoku-type earthquake fault. Stoch. Environ. Res. Risk Assess. 29, 1763–1779. doi:10.1007/s00477-014-0966-4
Gao, D., Wang, K., Insua, T. L., Sypus, M., Riedel, M., and Sun, T. (2018). Defining megathrust tsunami source scenarios for northernmost Cascadia. Nat. Hazards (Dordr). 94, 445–469. doi:10.1007/s11069-018-3397-6
Geist, E. L. (2002). Complex earthquake rupture and local tsunamis. J. Geophys. Res. 107 (-), 2086–ESE 2-15. doi:10.1029/2000jb000139
Gerstenberger, M. C., Marzocchi, W., Allen, T., Pagani, M., Adams, J., Danciu, L., et al. (2020). Probabilistic seismic hazard analysis at regional and national scales: State of the art and future challenges. Rev. Geophys. 58, e2019RG000653. doi:10.1029/2019rg000653
Gill, J. C., and Malamud, B. D. (2016). Hazard interactions and interaction networks (cascades) within multi-hazard methodologies. Earth Syst. Dyn. 7, 659–679. doi:10.5194/esd-7-659-2016
Gill, J. C., and Malamud, B. D. (2014). Reviewing and visualizing the interactions of natural hazards. Rev. Geophys. 52, 680–722. doi:10.1002/2013rg000445
Goda, K., and Atkinson, G. M. (2010). Intraevent spatial correlation of ground-motion parameters using SK-net data. Bull. Seismol. Soc. Am. 100, 3055–3067. doi:10.1785/0120100031
Goda, K., and Atkinson, G. M. (2014). Variation of source-to-site distance for megathrust subduction earthquakes: Effects on ground motion prediction equations. Earthq. Spectra 30, 845–866. doi:10.1193/080512eqs254m
Goda, K., De Risi, R., De Luca, F., Muhammad, A., Yasuda, T., and Mori, N. (2021). Multi-hazard earthquake-tsunami loss estimation of Kuroshio Town, Kochi Prefecture, Japan considering the Nankai-Tonankai megathrust rupture scenarios. Int. J. Disaster Risk Reduct. 54, 102050. doi:10.1016/j.ijdrr.2021.102050
Goda, K., and De Risi, R. (2018). Multi-hazard loss estimation for shaking and tsunami using stochastic rupture sources. Int. J. Disaster Risk Reduct. 28, 539–554. doi:10.1016/j.ijdrr.2018.01.002
Goda, K., and De Risi, R. (2017). Probabilistic tsunami loss estimation methodology: Stochastic earthquake scenario approach. Earthq. Spectra 33, 1301–1323. doi:10.1193/012617eqs019m
Goda, K., Mori, N., and Yasuda, T. (2019). Rapid tsunami loss estimation using regional inundation hazard metrics derived from stochastic tsunami simulation. Int. J. Disaster Risk Reduct. 40, 101152. doi:10.1016/j.ijdrr.2019.101152
Goda, K. (2021). Multi-hazard parametric catastrophe bond trigger design for subduction earthquakes and tsunamis. Earthq. Spectra 37, 1827–1848. doi:10.1177/8755293020981974
Goda, K. (2020). Multi-hazard portfolio loss estimation for time-dependent shaking and tsunami hazards. Front. Earth Sci. (Lausanne). 8, 592444. doi:10.3389/feart.2020.592444
Goda, K., Petrone, C., De Risi, R., and Rossetto, T. (2017). Stochastic coupled simulation of strong motion and tsunami for the 2011 Tohoku, Japan earthquake. Stoch. Environ. Res. Risk Assess. 31, 2337–2355. doi:10.1007/s00477-016-1352-1
Goda, K., Rossetto, T., Mori, N., and Tesfamariam, S. (2018). Editorial: Mega quakes: Cascading earthquake hazards and compounding risks. Front. Built Environ. 4, 8. doi:10.3389/fbuil.2018.00008
Goda, K. (2015). Seismic risk management of insurance portfolio using catastrophe bonds. Computer-Aided Civ. Infrastructure Eng. 30, 570–582. doi:10.1111/mice.12093
Goda, K., and Shoaeifar, P. (2022). Probabilistic fault displacement hazard analysis using stochastic source models: A prospective evaluation for the leach river valley fault zone. GeoHazards 3, 277–293. doi:10.3390/geohazards3020015
Goda, K. (2019). Time-dependent probabilistic tsunami hazard analysis using stochastic rupture sources. Stoch. Environ. Res. Risk Assess. 33, 341–358. doi:10.1007/s00477-018-1634-x
Goda, K., Yasuda, T., Mori, N., and Maruyama, T. (2016). New scaling relationships of earthquake source parameters for stochastic tsunami simulation. Coast. Eng. J. 58, 1650010-1–1650010-40. doi:10.1142/s0578563416500108
Goulet, C. A., Haselton, C. B., Mitrani-Reiser, J., Beck, J. L., Deierlein, G. G., Porter, K. A., et al. (2007). Evaluation of the seismic performance of a code-conforming reinforced-concrete frame building - from seismic hazard to collapse safety and economic losses. Earthq. Eng. Struct. Dyn. 36, 1973–1997. doi:10.1002/eqe.694
Graves, R. W., and Pitarka, A. (2010). Broadband ground-motion simulation using a hybrid approach. Bull. Seismol. Soc. Am. 100 (5A), 2095–2123. doi:10.1785/0120100057
Grezio, A., Babeyko, A., Baptista, M. A., Behrens, J., Costa, A., Davies, G., et al. (2017). Probabilistic tsunami hazard analysis: Multiple sources and global applications. Rev. Geophys. 55, 1158–1198. doi:10.1002/2017rg000579
Griffin, J. D., Stirling, M. W., and Wang, T. (2020). Periodicity and clustering in the long-term earthquake record. Geophys. Res. Lett. 47, e2020GL089272. doi:10.1029/2020gl089272
Gusman, A. R., Sheehan, A. F., Satake, K., Heidarzadeh, M., Mulia, I. E., and Maeda, T. (2016). Tsunami data assimilation of Cascadia seafloor pressure gauge records from the 2012 Haida Gwaii earthquake. Geophys. Res. Lett. 43, 4189–4196. doi:10.1002/2016gl068368
Harig, S., Immerz, A., WenizaGriffin, J., Weber, B., Babeyko, A., Rakowsky, N., et al. (2019). The tsunami scenario database of the Indonesia tsunami early warning system (InaTEWS): Evolution of the coverage and the involved modeling approaches. Pure Appl. Geophys. 177, 1379–1401. doi:10.1007/s00024-019-02305-1
Hayes, G. P., Moore, G. L., Portner, D. E., Hearne, M., Flamme, H., Furtney, M., et al. (2018). Slab2, a comprehensive subduction zone geometry model. Science 362, 641058–641061. doi:10.1126/science.aat4723
Herrero, A., and Bernard, P. (1994). A kinematic self-similar rupture process for earthquakes. Bull. Seismol. Soc. Am. 84, 1216–1228. doi:10.1785/bssa0840041216
Kameshwar, S., Park, H., Alam, S., Farokhnia, K., Barbosa, A. R., Cox, D. T., et al. (2019). Probabilistic decision-support framework for community resilience: Incorporating multi-hazards, infrastructure interdependencies, and resilience goals in a Bayesian network. Reliab. Eng. Syst. Saf. 191, 106568. doi:10.1016/j.ress.2019.106568
Kanazawa, T. (2013). Japan Trench earthquake and tsunami monitoring network of cable-linked 150 ocean bottom observatories and its impact to Earth disaster science. IEEE Int. Underw. Technol. Symp., 1–5.
King, A., Middleton, D., Brown, C., Johnston, D., and Johal, S. (2014). Insurance: Its role in recovery from the 2010–2011 canterbury earthquake sequence. Earthq. Spectra 30, 475–491. doi:10.1193/022813eqs058m
Kiremidjian, A. S., and Anagnos, T. (1984). Stochastic slip-predictable model for earthquake occurrences. Bull. Seismol. Soc. Am. 74, 739–755. doi:10.1785/bssa0740020739
Kurahashi, S., and Iikura, K. (2013). Short-period source model of the 2011 Mw 9.0 off the Pacific coast of Tohoku earthquake. Bull. Seismol. Soc. Am. 103, 1373–1393. doi:10.1785/0120120157
Lammel, G., Rieser, M., Nagel, K., Taubenbock, H., Strunz, G., Goseberg, N., et al. (2010). Emergency preparedness in the case of a tsunami—evacuation analysis and traffic optimization for the Indonesian city of padang. Pedestrian and evacuation dynamics 2008. Berlin: Springer, 171–182.
Latcharote, P., Leelawat, N., Suppasri, A., Thamarux, P., and Imamura, F. (2018). Estimation of fatality ratios and investigation of influential factors in the 2011 Great East Japan Tsunami. Int. J. Disaster Risk Reduct. 29, 37–54. doi:10.1016/j.ijdrr.2017.06.024
Lavallée, D., Liu, P., and Archuleta, R. J. (2006). Stochastic model of heterogeneity in earthquake slip spatial distributions. Geophys. J. Int. 165, 622–640. doi:10.1111/j.1365-246x.2006.02943.x
Li, L., Switzer, A. D., Wang, Y., Chan, C. H., Qiu, Q., and Weiss, R. (2018). A modest 0.5-m rise in sea level will double the tsunami hazard in Macau. Sci. Adv. 4, eaat1180. doi:10.1126/sciadv.aat1180
Li, Y., and Goda, K. (2022). Hazard and risk-based tsunami early warning algorithms for ocean bottom sensor S-net system in Tohoku, Japan, using sequential multiple linear regression. Geosciences 12, 350. doi:10.3390/geosciences12090350
Liel, A. B., and Deierlein, G. G. (2013). Cost-benefit evaluation of seismic risk mitigation alternatives for older concrete frame buildings. Earthq. Spectra 29, 1391–1411. doi:10.1193/030911eqs040m
Liu, Z., Nadim, F., Garcia-Aristizabal, A., Mignan, A., Fleming, K., and Luna, B. Q. (2015). A three-level framework for multi-risk assessment. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 9, 59–74. doi:10.1080/17499518.2015.1041989
Macabuag, J., Rossetto, T., Ioannou, I., Suppasri, A., Sugawara, D., Adriano, B., et al. (2016). A proposed methodology for deriving tsunami fragility functions for buildings using optimum intensity measures. Nat. Hazards (Dordr). 84, 1257–1285. doi:10.1007/s11069-016-2485-8
Maeda, T., Furumura, T., Noguchi, S., Takemura, S., Sakai, S., Shinohara, M., et al. (2013). Seismic- and tsunami-wave propagation of the 2011 off the Pacific coast of Tohoku earthquake as inferred from the tsunami-coupled finite-difference simulation. Bull. Seismol. Soc. Am. 103, 1456–1472. doi:10.1785/0120120118
Mai, P. M., and Beroza, G. C. (2002). A spatial random field model to characterize complexity in earthquake slip. J. Geophys. Res. 107, ESE 10-1. 1–ESE 10-21. doi:10.1029/2001jb000588
Mai, P. M., and Thingbaijam, K. K. S. (2014). Srcmod: An online database of finite-fault rupture models. Seismol. Res. Lett. 85, 1348–1357. doi:10.1785/0220140077
Makinoshima, F., Oishi, Y., Yamazaki, T., Furumura, T., and Imamura, F. (2021). Early forecasting of tsunami inundation from tsunami and geodetic observation data with convolutional neural networks. Nat. Commun. 12, 2253. doi:10.1038/s41467-021-22348-0
Marzocchi, W., Garcia-Aristizabal, A., Gasparini, P., Mastellone, M. L., and Di Ruocco, A. (2012). Basic principles of multi-risk assessment: A case study in Italy. Nat. Hazards (Dordr). 62, 551–573. doi:10.1007/s11069-012-0092-x
Matthews, M. V., Ellsworth, W. L., and Reasenberg, P. A. (2002). A Brownian model for recurrent earthquakes. Bull. Seismol. Soc. Am. 92, 2233–2250. doi:10.1785/0120010267
Melgar, D., and Hayes, G. P. (2019). The correlation lengths and hypocentral positions of great earthquakes. Bull. Seismol. Soc. Am. 109, 2582–2593. doi:10.1785/0120190164
Melgar, D., Williamson, A. L., and Salazar-Monroy, E. F. (2019). Differences between heterogeneous and homogenous slip in regional tsunami hazards modelling. Geophys. J. Int. 219, 553–562.
Mesta, C., Cremen, G., and Galasso, C. (2022). Urban growth modelling and social vulnerability assessment for a hazardous Kathmandu Valley. Sci. Rep. 12, 6152. doi:10.1038/s41598-022-09347-x
Michel-Kerjan, E., Hochrainer-Stigler, S., Kunreuther, H., Linnerooth-Bayer, J., Melcher, R., Muir-Wood, R., et al. (2013). Catastrophe risk models for evaluating disaster risk reduction investments in developing countries. Risk Anal. 33, 984–999. doi:10.1111/j.1539-6924.2012.01928.x
Mignan, A., Wiemer, S., and Giardini, D. (2014). The quantification of low-probability–high-consequences events: Part I. A generic multi-risk approach. Nat. Hazards (Dordr). 73, 1999–2022. doi:10.1007/s11069-014-1178-4
Mitchell-Wallace, K., Jones, M., Hillier, J., and Foote, M. (2017). Natural catastrophe risk management and modelling: A practitioner’s guide. Chichester, UK: Wiley-Blackwell, 536.
Momeni, P., Goda, K., Mokhtari, M., and Heidarzadeh, M. (2022). A new tsunami hazard assessment for eastern Makran subduction zone by considering splay faults and applying stochastic modeling. Coast. Eng. J., 1–30. doi:10.1080/21664250.2022.2117585
Moya, L., Mas, E., Adriano, B., Kshimura, S., Ymazaki, F., and Liu, W. (2018). An integrated method to extract collapsed buildings from satellite imagery, hazard distribution and fragility curves. Int. J. Disaster Risk Reduct. 31, 1374–1384. doi:10.1016/j.ijdrr.2018.03.034
Muhammad, A., De Risi, R., De Luca, F., Mori, N., Yasuda, T., and Goda, K. (2021). Are current tsunami evacuation approaches safe enough? Stoch. Environ. Res. Risk Assess. 35, 759–779. doi:10.1007/s00477-021-02000-5
Muhammad, A., Goda, K., Alexander, N. A., Kongko, W., and Muhari, A. (2017). Tsunami evacuation plans for future megathrust earthquakes in Padang, Indonesia considering stochastic earthquake scenarios. Nat. Hazards Earth Syst. Sci. 17, 2245–2270. doi:10.5194/nhess-17-2245-2017
Mulia, I. E., and Satake, K. (2021). Synthetic analysis of the efficacy of the S-net system in tsunami forecasting. Earth Planets Space 73, 36. doi:10.1186/s40623-021-01368-6
Murata, S., Katoh, K., Kawata, Y., Imamura, F., Takahashi, S., and Takayama, T. (2010). Tsunami: To survive from tsunami. World Scientific Publishing, 302.
Naito, S., Tomozawa, H., Mori, Y., Nagata, T., Monma, N., Nakamura, H., et al. (2020). Building-damage detection method based on machine learning utilizing aerial photographs of the Kumamoto earthquake. Earthq. Spectra 36, 1166–1187. doi:10.1177/8755293019901309
OECD (2018). Financial management of earthquake risk. Available at: https://www.oecd.org/finance/financial-management-of-earthquake-risk.htm.
Ogata, Y. (1999). Estimating the hazard of rupture using uncertain occurrence times of paleo earthquakes. J. Geophys. Res. 104, 17995–18014. doi:10.1029/1999jb900115
Oregon Seismic Safety Policy Advisory Council, (2021). Tsunami resilience on the Oregon coast. The State of Oregon: OSSPAC Publication, 21.
Park, H., Alam, M. S., Cox, D. T., Barbosa, A. R., and van de Lindt, J. W. (2019). Probabilistic seismic and tsunami damage analysis (PSTDA) of the Cascadia Subduction Zone applied to Seaside, Oregon. Int. J. Disaster Risk Reduct. 35, 101076. doi:10.1016/j.ijdrr.2019.101076
Park, P., van de Lindt, J. W., Cox, D. T., Gupta, R., and Aguiniga, F. (2012). Successive earthquake-tsunami analysis to develop collapse fragilities. J. Earthq. Eng. 16, 851–863. doi:10.1080/13632469.2012.685209
Petrone, C., Rossetto, T., and Goda, K. (2017). Fragility assessment of a RC structure under tsunami actions via nonlinear static and dynamic analyses. Eng. Struct. 136, 36–53. doi:10.1016/j.engstruct.2017.01.013
Philibosian, B., and Meltzner, A. J. (2020). Segmentation and supercycles: A catalog of earthquake rupture patterns from the sumatran sunda megathrust and other well-studied faults worldwide. Quat. Sci. Rev. 241, 106390. doi:10.1016/j.quascirev.2020.106390
Porter, K. A., Scawthorn, C. R., and Beck, J. L. (2006). Cost-effectiveness of stronger woodframe buildings. Earthq. Spectra 22, 239–266. doi:10.1193/1.2162567
Rodrigues, D., Crowley, H., and Silva, V. (2018). Earthquake loss assessment of precast RC industrial structures in Tuscany (Italy). Bull. Earthq. Eng. 16, 203–228. doi:10.1007/s10518-017-0195-6
Scolobig, A., Komendantova, N., and Arnaud, M. (2017). Mainstreaming multi-risk approaches into policy. Geosciences 7, 129. doi:10.3390/geosciences7040129
Selva, J. (2013). Long-term multi-risk assessment: Statistical treatment of interaction among risks. Nat. Hazards (Dordr). 67, 701–722. doi:10.1007/s11069-013-0599-9
Sepúlveda, I., Liu, P. L. F., and Grigoriu, M. D. (2018). Probabilistic tsunami hazard assessment in south China sea with consideration of uncertain earthquake characteristics. J. Geophys. Res. Solid Earth 124, 658–688. doi:10.1029/2018jb016620
Shimazaki, K., and Nakata, T. (1980). Time-predictable recurrence model for large earthquakes. Geophys. Res. Lett. 7, 279–282. doi:10.1029/gl007i004p00279
Song, J., and Goda, K. (2019). Influence of elevation data resolution on tsunami loss estimation and insurance rate-making. Front. Earth Sci. (Lausanne). 7, 246. doi:10.3389/feart.2019.00246
Sykes, L. R., and Menke, W. (2006). Repeat times of large earthquakes: Implications for earthquake mechanics and long-term prediction. Bull. Seismol. Soc. Am. 96, 1569–1596. doi:10.1785/0120050083
Tarbotton, C., Dall’Osso, F., Dominey-Howes, D., and Goff, J. (2015). The use of empirical vulnerability functions to assess the response of buildings to tsunami impact: Comparative review and summary of best practice. Earth-Science Rev. 142, 120–134. doi:10.1016/j.earscirev.2015.01.002
Tesfamariam, S., and Goda, K. (2015). Loss estimation for non-ductile reinforced concrete building in victoria, British columbia, Canada: Effects of mega-thrust mw9-class subduction earthquakes and aftershocks. Earthq. Eng. Struct. Dyn. 44, 2303–2320. doi:10.1002/eqe.2585
Tilloy, A., Malamud, M. D., Winter, H., and Joly-Laugel, A. (2019). A review of quantification methodologies for multi-hazard interrelationships. Earth-Science Rev. 196, 102881. doi:10.1016/j.earscirev.2019.102881
UNDRR (2022). Technical guidance on comprehensive risk assessment and planning in the context of climate change. Geneva, Switzerland: United Nations Office for Disaster Risk Reduction, 132. Available at:https://www.undrr.org/publication/technical-guidance-comprehensive-risk-assessment-and-planning-context-climate-change. p.
Voigt, S., Giulio-Tonolo, F., Lyons, J., Kučera, J., Jones, B., Schneiderhan, T., et al. (2016). Global trends in satellite-based emergency mapping. Science 353, 247–252. doi:10.1126/science.aad8728
Wald, D. J., Jaiswal, K. S., Marano, K. D., Bausch, D. B., and Hearne, M. G ( (2010). Pager — rapid assessment of an earthquake’s impact. U.S. Geol. Surv. Fact. Sheet 2010– 3036, 4.
Wang, Y., and Satake, K. (2021). Real-time tsunami data assimilation of S-net pressure gauge records during the 2016 Fukushima earthquake. Seismol. Res. Lett. 92, 2145–2155. doi:10.1785/0220200447
Williams, R. T., Davis, J. R., and Goodwin, L. B. (2019). Do large earthquakes occur at regular intervals through time? A perspective from the geologic record. Geophys. Res. Lett. 46, 8074–8081. doi:10.1029/2019gl083291
Wood, N., Jones, J., Schmidtlein, M., Schelling, J., and Frazier, T. (2016). Pedestrian flow-path modeling to support tsunami evacuation and disaster relief planning in the US Pacific Northwest. Int. J. Disaster Risk Reduct. 18, 41–55. doi:10.1016/j.ijdrr.2016.05.010
Keywords: earthquake, tsunami, multi-hazard, catastrophe modelling, cascading hazards, compounding risks
Citation: Goda K and De Risi R (2023) Future perspectives of earthquake-tsunami catastrophe modelling: From single-hazards to cascading and compounding multi-hazards. Front. Built Environ. 8:1022736. doi: 10.3389/fbuil.2022.1022736
Received: 18 August 2022; Accepted: 05 October 2022;
Published: 04 January 2023.
Edited by:
Izuru Takewaki, Kyoto University, JapanReviewed by:
Gaofeng Jia, Colorado State University, United StatesCopyright © 2023 Goda and De Risi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Katsuichiro Goda, a2dvZGEyQHV3by5jYQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.