The wall–frame interaction effect in CLT-steel hybrid systems

Behaviour and capacity of cross-laminated timber (CLT) infills built inside steel frames have been given increasing research attention in recent years. It is widely accepted that when the CLT wall panel is built in tight contact with the bounding steel frame to participate in the load sharing, its inherently large in-plane stiffness will attract additional forces to the frame area and change the behaviour of the hybrid system. If not designed properly, the structural integrity of both the infill and the frame will be compromised. It is thus crucial to accurately evaluate the contribution of the infill CLT wall panel to the stiffness and strength of the hybrid system. To that end, a finite element study was performed to investigate the frame-wall interaction effect on the behaviour of hybrid systems. The lateral stiffness, lateral load capacities and hysteretic characteristics of the hybrid systems with frictional and connected interfaces were investigated. The load-sharing effect between the CLT wall and the steel frame was studied. The numerical results showed that the connected models were very effective as the infill absorbed a substantial part of the lateral load, during the initial stages of loading.

1 Introduction

Traditionally, hybrid wall systems involve the use of reinforced concrete (RC) walls or composite steel-concrete (CSC) walls to provide a lateral-load resisting system for earthquake ground motions (Wallace and Wada, 2000). One example of CSC is the composite steel frame with RC walls system (SRCW) (Hajjar, 2002), classified according to the frame of Eurocode 8 as Type 1 composite structural system (European Commision, 2008). The main advantage of a code-designed SRCW system is that it has both higher flexural resistance and stiffness in comparison to a conventional RC wall of the same cross-sectional geometry (Fardis et al., 2005). These composite structures are also referred to as infilled frames and have increased lateral stiffness than structures that have bare frames. In the past six decades, extensive experimental and numerical research has been conducted to understand the combined behaviour of infilled frames, but most of these scholars investigated the behaviour and capacity of masonry infills built inside concrete or steel frames (Mehrabi et al., 1996; Chen and Liu, 2016; Margiacchi et al., 2016; Repapis and Zeris, 2019). Only a few researchers investigated the response of steel frames connected with infill RC walls (Makino et al., 1980; Saari et al., 2004; INNO-HYCO, 2015; Vogiatzis and Avdelas, 2018; Pallarés et al., 2020).

Today, as the construction must comply with the requirements of sustainable developments, timber has been gaining increased popularity in both residential and non-residential projects (Wang et al., 2015), as a renewable building material with a low carbon footprint, environmental friendliness, and easy assembly. Cross-laminated timber (CLT) is a prefabricated multi-layered engineer wood product, manufactured using at least three pieces of parallel boards by gluing their surfaces together using adhesives (FPInnovations Institute, 2013; Pečnik et al., 2021). Due to its cross-lamination technique, this type exhibits substantially better dimensional stability in comparison to solid wood, and offers high in-plane stiffness and strength when placed as a vertical wall element in mid-rise buildings (Carrero et al., 2021). CLT systems provide not only a high level of prefabrication and flexibility in planning, which reduces hence total cost of projects [FPInnovations (Institute), 2013]. Countries such as Japan have a long history of timber buildings that can effectively resist earthquakes. More recently, Canada, New Zealand, Italy and Greece have been developing structural systems for either larger buildings or semi-open sports facilities that can withstand earthquakes with minimal damage.

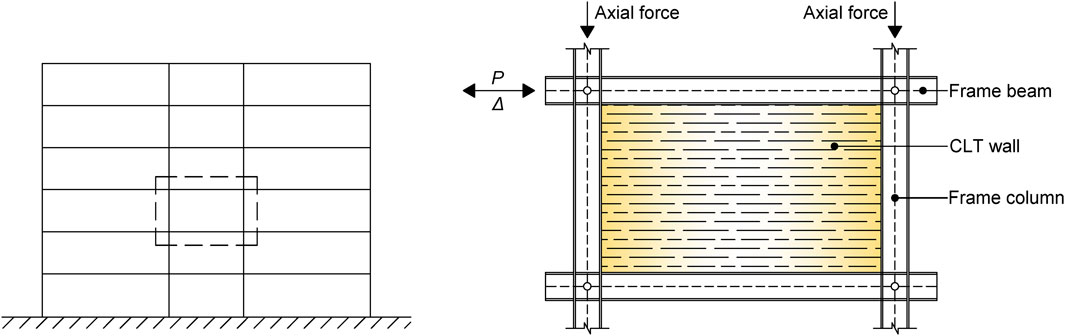
The CLT building material has opened new dimensions in steel-timber hybrid systems and allows researchers to focus on new solutions for structures with sustainable design considerations. Moreover, the benefits of CLT-Steel hybrid systems include more efficient use of materials and improved seismic resistance. Increased efficiency can be obtained because the strength, stiffness and weight of some materials can be utilised where it is most beneficial within a building. Seismic performance can similarly be enhanced by combining materials to optimise ductility, strength, and stiffness, all of which contribute to the dynamic structural behaviour of buildings (Quintana Gallo and Carradine, 2018). The most popular concepts of steel-timber hybrid systems are the steel frame with CLT shear walls (Dickof et al., 2014; Tesfamariam et al., 2014; Vogiatzis et al., 2019) and the timber frame with steel plate shear walls, (Conrad and Phillips, 2019; Igbal et al., 2020), the former concept is the focus of this work. Please note that in this as well as the following sections, unless otherwise stated, the abbreviation STSW refers to the concept of steel frame with CLT shear walls, as shown in Figure 1.

FIGURE 1

FIGURE 1. Typical elements of a steel frame with CLT shear wall hybrid system, STSW.

One of the first works on hybrid systems composed of steel frames and CLT shear walls was conducted by (Tesfamariam et al., 2014). The results of this work showed that the peak inter-story drift was less than two per cent for multistorey buildings. To overcome this challenge, a hybrid system composed of steel columns, timber beams, and oriented strand board panels with good in-plane strength and ductility was proposed by (Trutalli et al., 2017). Moreover, a hybrid wall system consisting of a light-frame wood shear wall and steel frame was tested by (He et al., 2014). The aforementioned tested hybrid system was numerically investigated by (Li et al., 2014), and further developed with a post-tensioned steel frame and light frame wood shear wall by (Cui et al., 2020). Recently, a hybrid system composed of steel frames with semi-rigid connections and CLT shear walls was designed and analyzed by the authors (Vogiatzis et al., 2019), although the post-elastic phase was not considered in that work.

2 Methodology section

2.1 Design consideration

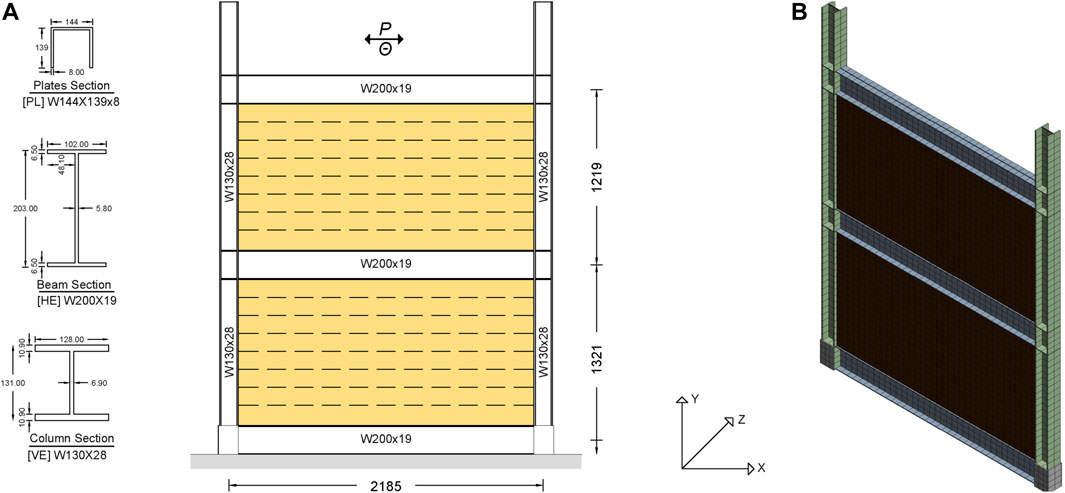
The STSW system considered for this research represents the first two stories of a multi-story mixed building designed for core-wall hybrid lateral load-resisting systems (Shahrooz et al., 1996). The specimen geometry, material, and boundary conditions reflected the physical model of the SRCW system tested by (Tong et al., 2001), as an idealized representation (one-third scale) of the bottom two stories of a six-story building, although the frame and the infill were modeled with cross-laminated timber shear walls and rigid connections, respectively. The columns consist of W130X28 wide flange steel sections and the beams consist of W200X19 wide flange steel sections. The infill was assumed to transfer 100% of the seismic story shear. The building was designed according to the NEHRP provision, using an acceleration and velocity coefficient of 0.4 and a force reduction factor R, of 5.5, (larger than the Eurocodes’ requirement for q due to overstrength) (Vogiatzis, 2019). Figure 2A shows a schematic view of the STSW system considered for this work. Table 1 summarises the FE models developed in this study, while a list of abbreviations for different parameters is also included.

FIGURE 2

FIGURE 2. STSW Hybrid System (A) Specimen configuration, (B) Finite element model.

TABLE 1

TABLE 1. Specifications of STSW models.

There is a clear lack of studies exploring the wall–frame interaction effect on the overall behaviour of STSW systems under monotonic and cyclic loading conditions. Hence, in the current, work numerous STSW models were developed as part of a parametric study, that aims to understand the influence of the wall–frame interaction effect on the response of STSW systems under different loading conditions. The parametric study was performed on a frame that had fixed-ended columns and rigid beam-to-column connections, as shown in Figure 2A. The dimensions of the STSW models are 2,184 mm (length) × 2,540 mm (height), measured from center to center of the steel sections. The beam and column dimensions are also shown in Figure 2A. The steel parameters are listed in Table 2. The STSW systems, had an infill CLT panel with length set to 2,054 mm and a height set to 1,016 mm, by using outside adhesion, between the infill CLT panels and the boundary steel frame. The material properties of the CLT shear wall under consideration are given in Table 3.

TABLE 2

TABLE 2. Mechanical properties of steel members used in the FE-models.

TABLE 3

TABLE 3. Mechanical properties of timber members used in the FE models.

2.2 Finite element analysis

2.2.1 Finite element model

To accurately simulate the behaviour of the STSW system, all the components of the specimen must be included in the simulation. These components, shown in Figure 3A, are the infill CLT panels and the boundary frame members (beams, columns). Furthermore, the interaction between components is critical. Both H-shaped steel frame and infill CLT wall are modelled in ANSYS R1 (ANSYS Inc, 2019) with the twenty-node structural brick element (SOLID186) as presented in Figure 2B. This element has been commonly used for three-dimensional finite element modelling of steel-timber hybrid structures (Rahmzadeh and Iqbal, 2021). Specifications of the analyzed models are shown in Table 1.

FIGURE 3

FIGURE 3. (A) Loading history, (B) Hysteretic curve of bare frame.

2.2.2 Steel material model

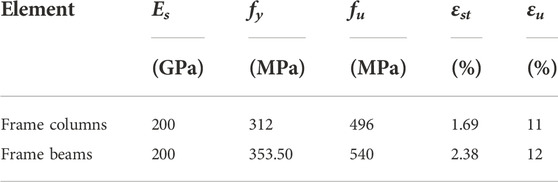
Multi-linear forms are usually used to define the steel stress-strain relationship, giving acceptable results under monotonic loading. However, Shi et al. (2011) showed that in the cases of cyclic loading, it was difficult for their results to meet the calculation accuracy. Therefore, the constitutive model suggested by Chaboche (Chaboche, 1986; Chaboche, 1989) is adopted which is parameterized in ANSYS R1 (ANSYS Inc, 2019). The material properties of each steel element were adopted from (Vogiatzis et al., 2019) and are given in Table 2.

2.2.3 Timber material model

The complexity of the mechanical response of CLT origins in the orthogonal grain direction and the overall anisotropy of wood as a material. The elastic mechanical properties have different values along the three principal axes. There is the grain (axial), the circumferential and the radial directions. The stiffness and strength in the axial direction have greater values than those in the other two directions (Furtmüller et al., 2018). Regarding the failure modes of timber, the three most common failure mechanisms are: 1) failure occurring due to compression parallel to grain (ductile failure mode), 2) failure occurring due to compression perpendicular to the grain (ductile failure mode), and 3) failure caused by shear parallel to the grain that it is accompanied by tension perpendicular to the grain (brittle failure mode) (Xu et al., 2014).

The theory of plasticity employs a set of constitutive equations to describe the complex multiaxial stress state. This is achieved by using three basic parameters: a yield criterion, a flow rule and a hardening rule. To capture the material’s non-linearity with accuracy, Hill’s yield criterion (Hill, 1948; Hill, 1998) has been selected to describe the anisotropic plastic behaviour of the cross-laminated timber. The accuracy of Hill’s model for capturing the non-linear behaviour and failure mode of timber has been previously investigated by (Xu et al., 2014; He et al., 2018; Vogiatzis et al., 2020).

The validity of Hill’s criterion, as implemented in ANSYS, has been investigated for timber structural systems under cyclic loading conditions by (Rahmzadeh and Iqbal, 2021). In that work the form of the quadratic Hill yield criterion was presented as shown in Eq. 1. Where the stresses ${\sigma }_{ij}$ are the normal yield stresses according to the principal directions of anisotropy, and the constants F, G, H, L, M and N, can be defined either experimentally or by Eqs 2–5. More information on the background of Hill’s criterion is given by (Imaoka, 2008).

$F{\left({\sigma }_{yy}-{\sigma }_{zz}\right)}^2+G{\left({\sigma }_{zz}-{\sigma }_{xx}\right)}^2+H{\left({\sigma }_{xx}-{\sigma }_{yy}\right)}^2+2L{\tau }_{yz}^2+2M{\tau }_{zx}^2+2N{\tau }_{xy}^2(1)$

$F=\frac{1}{2}+\left(\frac{1}{{\left({\sigma }_{yy}^y\right)}^2}+\frac{1}{{\left({\sigma }_{zz}^y\right)}^2}-\frac{1}{{\left({\sigma }_{xx}^y\right)}^2}\right)(2)$

$G=\frac{1}{2}+\left(\frac{1}{{\left({\sigma }_{zz}^y\right)}^2}+\frac{1}{{\left({\sigma }_{xx}^y\right)}^2}-\frac{1}{{\left({\sigma }_{yy}^y\right)}^2}\right)(3)$

$H=\frac{1}{2}+\left(\frac{1}{{\left({\sigma }_{xx}^y\right)}^2}+\frac{1}{{\left({\sigma }_{yy}^y\right)}^2}-\frac{1}{{\left({\sigma }_{zz}^y\right)}^2}\right)(4)$

$L=\frac{1}{2{\left({\tau }_{yz}^y\right)}^2}M=\frac{1}{2{\left({\tau }_{zx}^y\right)}^2}N=\frac{1}{2{\left({\tau }_{xy}^y\right)}^2}(5)$

where ${\sigma }_{ij}^y$ (i = j) are yield stresses in the principal axes of anisotropy and ${\tau }_{ij}^y$ (i $\ne$ j) are yield stresses in shear concerning the principal axis of anisotropy. Based on Hill’s criterion, in the case of an anisotropy with three mutually orthogonal planes of symmetry, yielding under a multiaxial stress state occurs when Eq. 1 is equal to one. The matrix must be positive-definite so that negative strain energy is avoided. This thermodynamic requirement can be satisfied using the following equations (Lempriere, 1968):

$\left(1-{\nu }_{yz}{v}_{zy}\right),\left(1-{\nu }_{xz}{v}_{zx}\right),\left(1-{\nu }_{xy}{v}_{yx}\right)\rangle 0(6)$

$1-{\nu }_{xy}{v}_{yx}-{\nu }_{yz}{v}_{zy}-2{\nu }_{xy}{v}_{yz}{v}_{zx}>0(7)$

The values of the wood elastic properties, for both the longitudinal and the transverse layers of the CLT have been obtained from (Stazi et al., 2019), corresponding to red spruce C24 boards. Table 3 summarises these parameters: parallel-to-grain (E_0,m) and perpendicular-to-grain (E_90,m) moduli of elasticity, shear moduli values (G_m), parallel-to-grain (f_t,0,k) and perpendicular-to-grain (f_t,90,k) tensile strength values, parallel-to-grain (f_c,0,k) and perpendicular-to-grain (f_c,90,k) compressive strength values, parallel-to-grain (f_v,090,k) and perpendicular-to-grain (f_v,9090,k) characteristic shear strength values.

2.2.4 Contact modelling

The contact elements for the STSW models were simulated with CONTA174 elements and target elements were modeled with TARGE170. It was proven by (He et al., 2018) that the CLT neighboring layers could be bonded in finite element model (He et al., 2018), which could not affect the produced results. Hence, the interaction at the interface of different layers of the CLT assembly were simulated using paired surface-to-surface contact elements (CONTA174 and TARGE170). This indicates that the relative movement between two contacting surfaces was not permitted. Those interface elements were also used for the contact along the perimeter between the steel boundary frame members and the CLT shear wall. This contact surface, along the interface of the steel sections and the CLT panel, was defined as a frictional contact for the HW1 models and bonded for the HW2 models. Coefficient of friction for all frictional contact bodies was set at 0.4.

2.2.5 Boundary conditions, loading procedure and validation

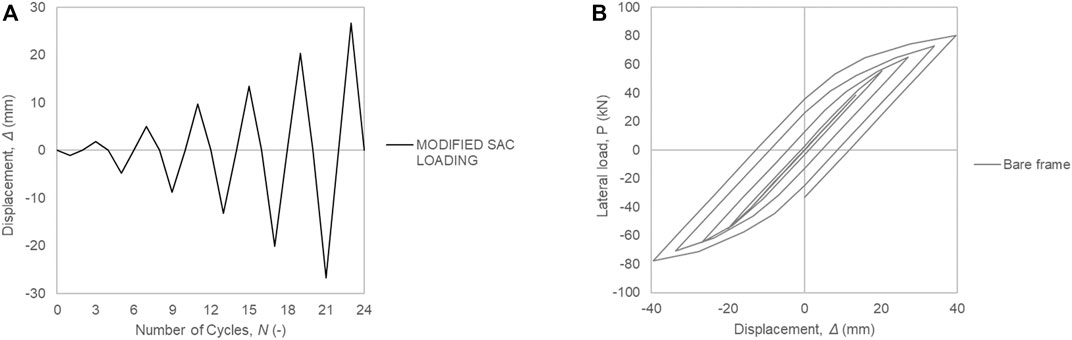
During the numerical analysis, lateral displacements are applied to the upper flange of the top beam as shown in Figure 2A. In the finite element model, the out-of-plane degrees of freedom along the height of the beam centerline were constrained to simulate the lateral support. All the degrees of freedom for the bottom of the columns and the lower flange of the ground beam were completely constrained to simulate the fixed support. Firstly, the gravity loads are applied. Secondly, the lateral displacement Δ is imposed to simulate the monotonic or cyclic loading conditions. At the first step of loading, the gravity loads were implemented and kept constant throughout the subsequent step. Next step was to apply cyclic loading, using displacement control mode, at the top flange of the systems upper beam. The imposed cyclic loading pattern is shown in Figure 3A, as it was modified according to SAC protocol for testing of steel beam-column connections and other steel elements (Tong et al., 2001).

The numerical model could not be validated against experimental results since there is lack of available experimental data of the same hybrid system in the international literature. Therefore, the authors used as a guide a numerical model of a similar hybrid system that they had built in a recent study (Vogiatzis et al., 2020) which had been validated using experimental data found in (Conrad and Phillips, 2019). Material parameters and techniques used in that model were employed in the current numerical simulation to ensure the validity and accuracy of the model. Moreover, the validation of a numerical model based on previous numerical simulations of similar systems as a technique was also used within the classification validation types conducted by (Archambeault and Connor, 2008). To sum up, the numerical model used to simulate the bare steel frame, as shown in Figure 3B, had been already validated against experimental results by (Vogiatzis, 2019). The CLT shear walls were modelled based on the methodology developed by (Vogiatzis et al., 2020) for a similar steel-timber hybrid system under monotonic loading which had been validated using experimental data. It has been shown in the literature that the Hill’s criterion, as implemented in ANSYS, once validated for monotonic loading then it has the ability to be used for the investigation of the same specimen under cyclic loading conditions without further calibration on new inputs required (Rahmzadeh and Iqbal, 2021).

3 Results

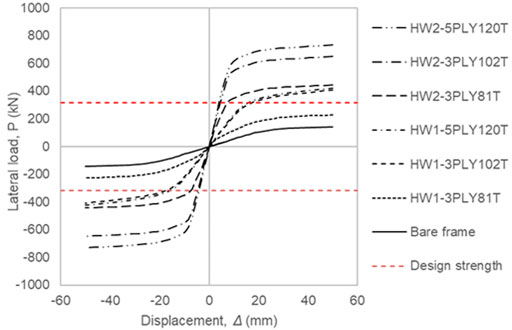
The effect of the two main wall–frame connection types, on the response of CLT-Steel hybrid wall systems under monotonic and cyclic loading conditions is explored. To this end, several finite element models with thicknesses of the infill CLT walls t_w, equal to 81, 102 and 120 mm, respectively, are evaluated. The lateral load P versus displacement Δ curves obtained from this study are shown in Figures 4A–D for the frictional STSW models and in Figures 5A–D for the connected STSW models. Where, the horizontal line marks the designed shear strength of the prototype building.

FIGURE 4

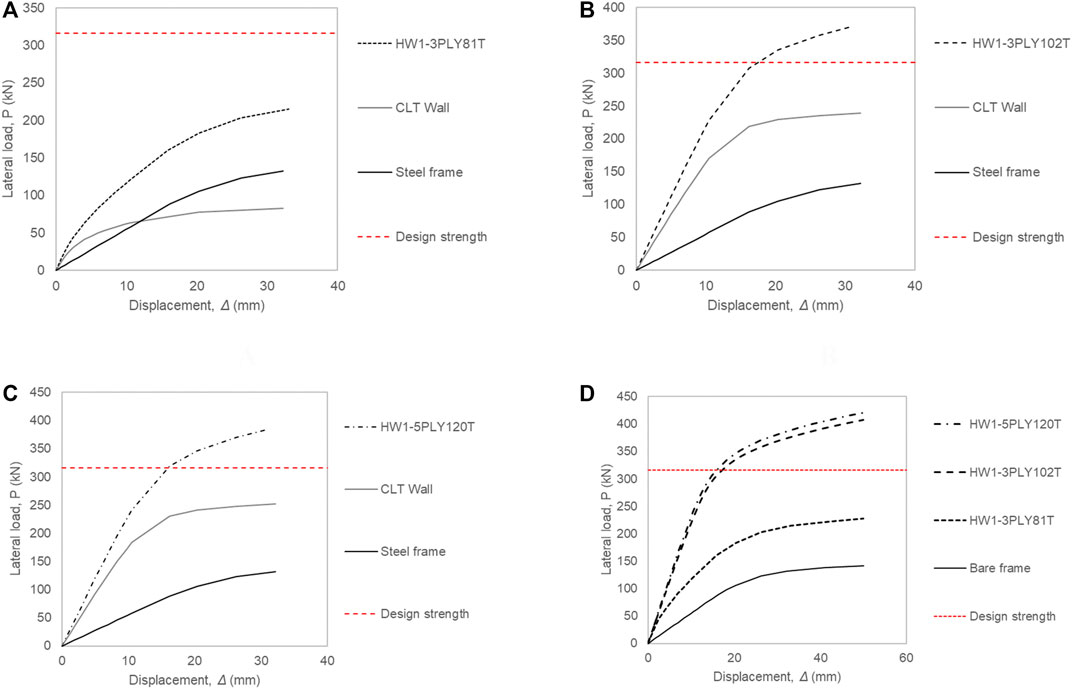
FIGURE 4. Behaviour of STSW specimens with frictional infill-frame interface (A) 3-ply (81 mm thick), (B) 3-ply (102 mm thick), (C) 5-ply (120 mm thick), (D) Comparative diagram.

FIGURE 5

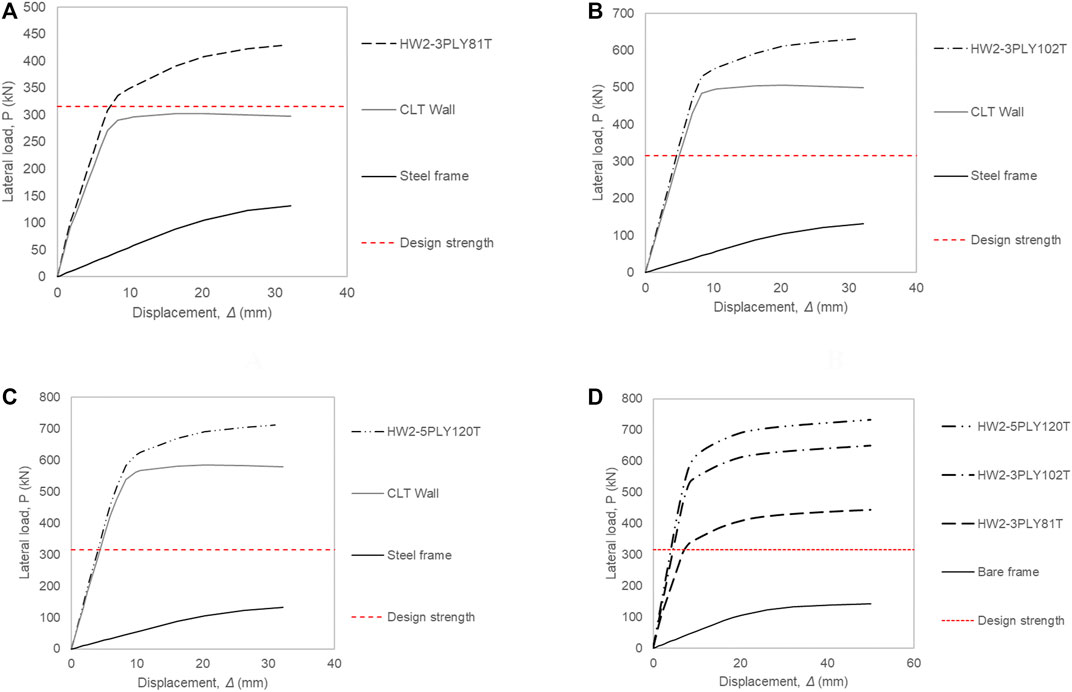
FIGURE 5. Behaviour of STSW specimens with connected infill-frame interface (A) 3-ply (81 mm thick), (B) 3-ply (102 mm thick), (C) 5-ply (120 mm thick), (D) Comparative diagram.

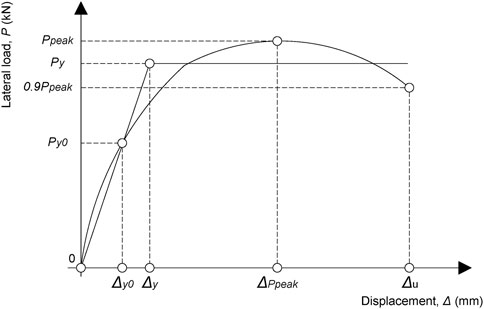
Ductility (μ) is a sign of displacement induced in plastic region without strength degradation. The ductility factor can be defined from Eq. 8. It is assumed that the P-Δ backbone curve is elastic and perfectly plastic according to the procedure explained and used by (Kennedy-Kuiper et al., 2022).

$\mu =\frac{{\mathit{\Delta }}_u}{{\mathit{\Delta }}_y}(8)$

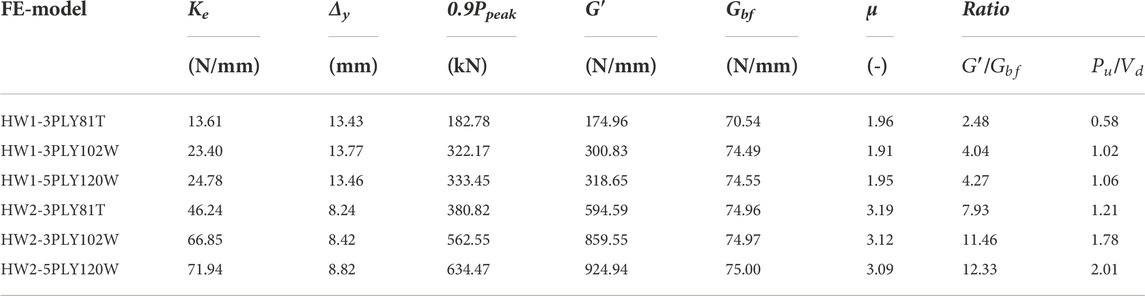
The yield displacement (Δ_yield) was measured through the concept of equal plastic energy, so that the area enclosed by the idealized elasto-plastic curve was equal to that of the actual pushover curve, as depicted in Figure 6. Figures 7A, 8A, 9 compare the backbone curves of the CLT-steel hybrid systems. The capacity parameters of the developed specimens are presented in Table 4. Where the stiffness (K_e) is computed by Eq. 9, the secant shear modulus of the CLT wall (G′) is given by Eq. 10, and the secant shear modulus of the bare steel frame (G_bf) is produced by Eq. 11.

$K_e=0.4\frac{P_{peak}}{{\mathit{\Delta }}_{0.4P_{peak}}}(9)$

$G^{\prime }=\frac{0.4P_{peak}}{{\mathit{\Delta }}_{0.4P_{peak}}}\times \frac{H}{L}(10)$

$G_{bf}=\frac{P_{bf}}{{\mathit{\Delta }}_{bf}}\times \frac{H}{L}(11)$

FIGURE 6

FIGURE 6. Actual response curve and equivalent idealized elastic-plastic curve.

FIGURE 7

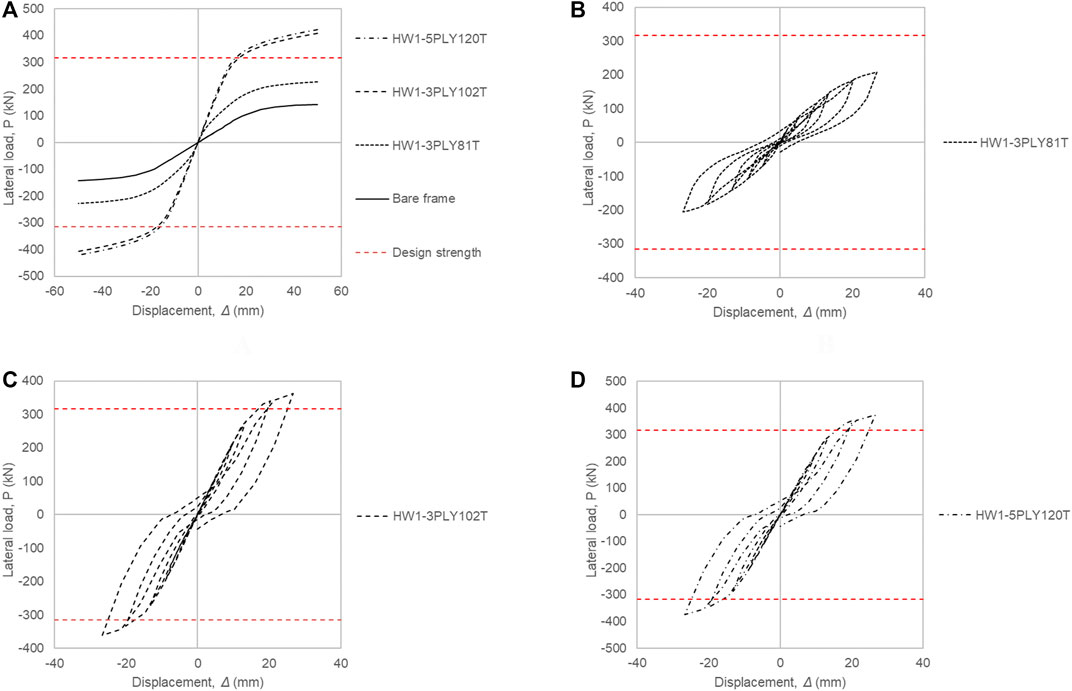
FIGURE 7. Hysteretic and backbone curves of the specimens with frictional infill-frame interface (A) Comparative diagram, (B) 3-ply (81 mm thick), (C) 3-ply (102 mm thick), (D) 5-ply (120 mm thick).

FIGURE 8

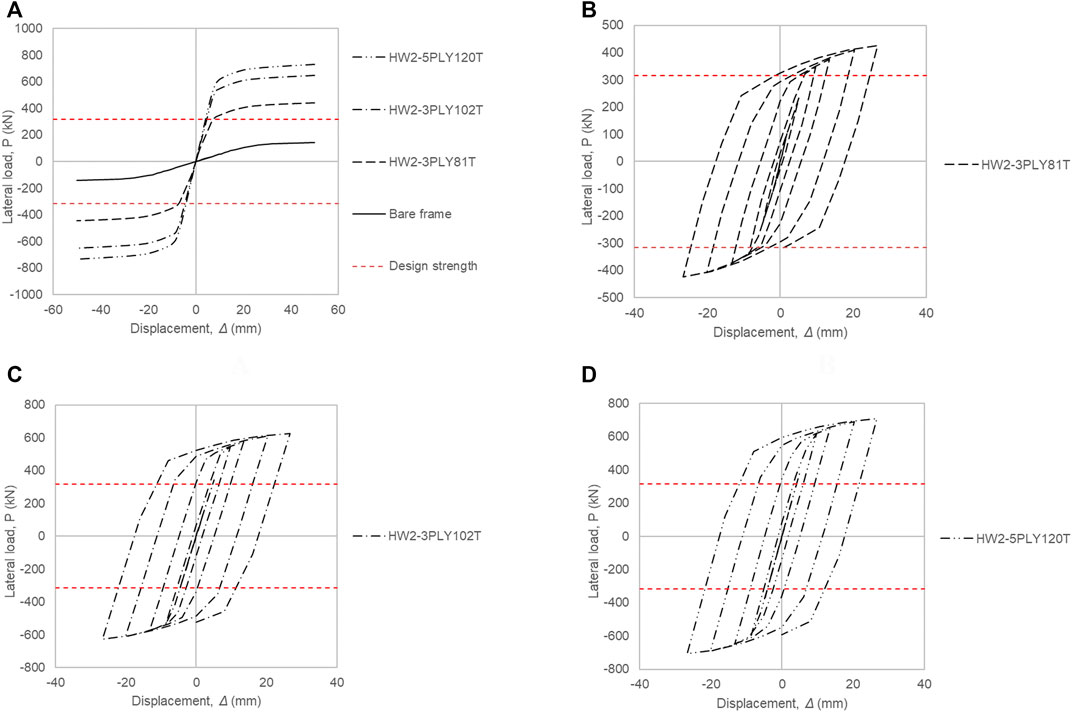
FIGURE 8. Hysteretic and backbone curves of specimens with connected infill-frame interface (A) Comparative diagram, (B) 3-ply (81 mm thick), (C) 3-ply (102 mm thick), (D) 5-ply (120 mm thick).

FIGURE 9

FIGURE 9. Backbone curves for the developed CLT-Steel hybrid systems.

TABLE 4

TABLE 4. Summary of numerical results.

The findings of this study show that an ascent on the infill plate thickness from 81 to 102 mm can increase the shear capacity up to 40% for frictional STSW models, and up to 70% for frictional STSW models. Moreover, as presented in Figures 7, 8, the frictional STSW specimens fail to reach the design strength by 40% when the thickness is 80 mm but they provide adequate strength when the thickness of the infill is either 102 or 120 mm. From the same results it is obvious that this is not the case for the connected STSW specimens as their strength ratio is ranging from 1.06 to 2.01, meaning they provide overstrength more than 70% Comparison with the bare frame results, as presented in Figures 4, 5 and Table 4, show that the incorporation of the CLT infill wall can significantly increase the initial lateral stiffness of the bare steel frame, up to 3 times for the frictional STSWs and up to 11 times for the connected STSW systems. Further, it is observed that stronger infills led to higher lateral load capacity, initial lateral stiffness, and yield load. However, the increase of the ductility was limited.

4 Conclusion

Based on the findings of this research study, the following conclusions can be drawn within the limitation of the current research:

• For the connected hybrid steel-timber wall systems the lateral stiffness is decreased with the horizontal displacement increasing, showing a strong nonlinear feature, as shown before in Figures 4, 5.

• As expected, an increase in the number of the plies of the panels positively influences the load-carrying capacity of the wall. However, the contribution of their thickness (width) is more prominent since it affects to a greater extent the structural performance of the wall systems.

• An increase in the number of the plies of the panels does not necessarily reduces the displacement of the hybrid wall. This has been concluded by comparison of 3-ply and 5-ply CLT panels. On the contrary, a reduction in the thickness of the CLT infill results in the smaller displacement of the wall system.

• Among the models of the hybrid steel-timber wall systems examined, the models with the presence of friction have showed higher values of lateral drift capacities but in smaller lateral loads. This indicates the effect of friction on these types of wall systems.

• The connected STSW models have shown higher energy dissipation capacities than the frictional STSW models of the same wall systems. The increase in the energy absorption has been more significant in the case of the 5-ply CLT infilled hybrid wall.

Overall, hybrid CLT-Steel wall systems have shown great potential and they can be regarded as reliable alternative systems to traditional shear walls. The effects of parameters, such as different geometries and mechanical properties, that can affect the structural performance of STSW systems have not been examined as they have not been within the scope of the paper. However, these studies can produce interesting findings in addition to the results from the current study.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

TV, TT, and EE contributed conception and design of the study. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

ANSYS Inc (2019). Ansys®Academic Research Release.

Google Scholar

Archambeault, B., and Connor, S. (2008). “Proper model validation is important for all EMI/EMC applications,” in IEEE International Symposium on Electromagnetic Compatibility 2008-Janua, August 18–August 22, 2008, Detroit Michigan, United States. doi:10.1109/ISEMC.2008.4652152

CrossRef Full Text | Google Scholar

Carrero, T., Montaño, J., Berwart, S., Santa María, H., and Guindos, P. (2021). Seismic behavior of innovative hybrid CLT-steel shear wall for mid-rise buildings. Bull. Earthq. Eng. 19, 5917–5951. doi:10.1007/s10518-021-01204-y

CrossRef Full Text | Google Scholar

Chaboche, J. L. (1989). Constitutive equations for cyclic plasticity and cyclic viscoplasticity. Int. J. Plast. 5, 247–302. doi:10.1016/0749-6419(89)90015-6

CrossRef Full Text | Google Scholar

Chaboche, J. L. (1986). Time-independent constitutive theories for cyclic plasticity. Int. J. Plast. 2, 149–188. doi:10.1016/0749-6419(86)90010-0

CrossRef Full Text | Google Scholar

Chen, X., and Liu, Y. (2016). A finite element study of the effect of vertical loading on the in-plane behavior of concrete masonry infills bounded by steel frames. Eng. Struct. 117, 118–129. doi:10.1016/j.engstruct.2016.03.010

CrossRef Full Text | Google Scholar

Conrad, K., and Phillips, A. R. (2019). Full scale testing and development of wood-steel composite shear walls. Structures 20, 268–278. doi:10.1016/j.istruc.2019.04.010

CrossRef Full Text | Google Scholar

Cui, Y., Chen, F., Li, Z., and Qian, X. (2020). Self-centering steel-timber hybrid shear wall: Experimental test and parametric analysis. Materials 13, 2518. doi:10.3390/ma13112518

PubMed Abstract | CrossRef Full Text | Google Scholar

Dickof, C., Stiemer, S. F., Bezabeh, M. A., and Tesfamariam, S. (2014). CLT-steel hybrid System: ductility and overstrength values based on static pushover analysis. J. Perform. Constr. Facil. 28, A4014012. doi:10.1061/(asce)cf.1943-5509.0000614

CrossRef Full Text | Google Scholar

European Commision (2008). Eurocode-8:– Design of structures for earthquake resistance – Part 1: General rules, seismic actions and rules for buildings. Brussels.

Google Scholar

Fardis, M., Carvalho, E., Elnashai, A., Faccioli, E., Pinto, P., and Plumier, A. (2005). Designers guide to EN 1998-1 and EN 1998-5, Eurocode 8: Design of structures for earthquake resistance. London, U.K: Thomas Telford Ltd.

Google Scholar

FPInnovations Institute (2013). CLT handbook: Cross-laminated timber. US edition: Quebec, Canada.

Google Scholar

Furtmüller, T., Giger, B., and Adam, C. (2018). General shell section properties and failure model for cross-laminated timber obtained by numerical homogenization. Eng. Struct. 163, 77–92. doi:10.1016/j.engstruct.2018.02.017

CrossRef Full Text | Google Scholar

Hajjar, J. F. (2002). Composite steel and concrete structural systems for seismic engineering. J. Constr. Steel Res. 58, 703–723. doi:10.1016/S0143-974X(01)00093-1

CrossRef Full Text | Google Scholar

He, M., Li, Z., Lam, F., Ma, R., and Ma, Z. (2014). Experimental investigation on lateral performance of timber-steel hybrid shear wall systems. J. Struct. Eng. (N. Y. N. Y). 140, 04014029. doi:10.1061/(asce)st.1943-541x.0000855

CrossRef Full Text | Google Scholar

He, M., Sun, X., and Li, Z. (2018). Bending and compressive properties of cross-laminated timber (CLT) panels made from Canadian hemlock. Constr. Build. Mat. 185, 175–183. doi:10.1016/j.conbuildmat.2018.07.072

CrossRef Full Text | Google Scholar

Hill, R. (1948). A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. Lond A Math. Phys. Sci. 193, 281–297. doi:10.1098/rspa.1948.0045

CrossRef Full Text | Google Scholar

Hill, R. (1998). The mathematical theory of plasticity. New York, United States: Clarendon Press.

Google Scholar

Igbal, A., Todorov, B., and Billah, A. (2020). “Combination of steel plate shear walls and timber moment frames for improved seismic performance,” in 17th world conference on earthquake engineering (Sendai, Japan), 2.

Google Scholar

Imaoka, S. (2008). Hill’s potential. ansys.net Tips and Tricks.

Google Scholar

INNO-HYCO (2015). Innovative hybrid and composite steel-concrete structural solutions for building in seismic area, Final Report. Brussels: EUR 26932 EN. doi:10.2777/85404

CrossRef Full Text | Google Scholar

Kennedy-Kuiper, R. C. S., Wakjira, T. G., and Alam, M. S. (2022). Repair and retrofit of RC bridge piers with steel-reinforced grout jackets: An experimental investigation. J. Bridge Eng. 27, 1–11. doi:10.1061/(asce)be.1943-5592.0001903

CrossRef Full Text | Google Scholar

Lempriere, B. M. (1968). Poisson’s ratio in orthotropic materials. AIAA J. 6, 2226–2227. doi:10.2514/3.4974

CrossRef Full Text | Google Scholar

Li, Z., He, M., Lam, F., Li, M., Ma, R., and Ma, Z. (2014). Finite element modeling and parametric analysis of timber-steel hybrid structures. Struct. Des. Tall Spec. Build. 23, 1045–1063. doi:10.1002/tal.1107

CrossRef Full Text | Google Scholar

Makino, M., Kawano, A., Kurobane, Y., Saisho, M., and Yoshinaga, K. (1980). “An investigation for the design of framed structures with infill walls,” in The seventh world conference on earthquake engineering (Turkey, Istanbul: Kelaynak), 369.

Google Scholar

Margiacchi, F., Salvatori, L., Orlando, M., de Stefano, M., and Spinelli, P. (2016). Seismic response of masonry-infilled steel frames via multi-scale finite-element analyses. Bull. Earthq. Eng. 14, 3529–3546. doi:10.1007/s10518-016-0012-7

CrossRef Full Text | Google Scholar

Mehrabi, A. B., Benson Shing, P., Schuller, M. P., and Noland, J. L. (1996). Experimental evaluation of masonry-infilled RC frames. J. Struct. Eng. (N. Y. N. Y). 122, 228–237. doi:10.1061/(asce)0733-9445(1996)122:3(228)

CrossRef Full Text | Google Scholar

Pallarés, L., Agüero Ramon-Llin, A., Martí-Vargas, J. R., and Pallarés, F. J. (2020). Behaviour of headed studs subjected to cyclic shear in steel frames with reinforced concrete infill walls. Constr. Build. Mat. 262, 120018. doi:10.1016/j.conbuildmat.2020.120018

CrossRef Full Text | Google Scholar

Pečnik, J. G., Gavrić, I., Sebera, V., Kržan, M., Kwiecień, A., Zając, B., et al. (2021). Mechanical performance of timber connections made of thick flexible polyurethane adhesives. Eng. Struct. 247, 113125. doi:10.1016/j.engstruct.2021.113125

CrossRef Full Text | Google Scholar

Quintana Gallo, P., and Carradine, D. (2018). State of the art of timber- based hybrid seismic- resistant structures. Porirua, New Zealand: BRANZ research report SR400.

Google Scholar

Rahmzadeh, A., and Iqbal, A. (2021). Numerical modelling and analysis of post-tensioned timber beam-column joint. Eng. Struct. 245, 112762. doi:10.1016/j.engstruct.2021.112762

CrossRef Full Text | Google Scholar

Repapis, C., and Zeris, C. A. (2019). Seismic assessment of non-conforming infilled RC buildings using IDA procedures. Front. Built Environ. 4, 88. doi:10.3389/fbuil.2018.00088

CrossRef Full Text | Google Scholar

Saari, W. K., Hajjar, J. F., Schultz, A. E., and Shield, C. K. (2004). Behavior of shear studs in steel frames with reinforced concrete infill walls. J. Constr. Steel Res. 60, 1453–1480. doi:10.1016/j.jcsr.2004.03.003

CrossRef Full Text | Google Scholar

Shahrooz, B. M., Gong, B., and Arnold, J. (1996). Seismic behavior and design of composite coupling beam: Internal Report. Cincinnati, U.S.A: University of Minnesota.

Google Scholar

Shi, Y., Wang, M., and Wang, Y. (2011). Experimental and constitutive model study of structural steel under cyclic loading. J. Constr. Steel Res. 67, 1185–1197. doi:10.1016/j.jcsr.2011.02.011

CrossRef Full Text | Google Scholar

Stazi, F., Serpilli, M., Maracchini, G., and Pavone, A. (2019). An experimental and numerical study on CLT panels used as infill shear walls for RC buildings retrofit. Constr. Build. Mat. 211, 605–616. doi:10.1016/j.conbuildmat.2019.03.196

CrossRef Full Text | Google Scholar

Tesfamariam, S., Stiemer, S. F., Dickof, C., and Bezabeh, M. A. (2014). Seismic vulnerability assessment of hybrid steel-timber structure: Steel moment-resisting frames with CLT infill. J. Earthq. Eng. 18, 929–944. doi:10.1080/13632469.2014.916240

CrossRef Full Text | Google Scholar

Tong, X., Schultz, A. E., Hajjar, J. F., and Shield, C. K. (2001). Seismic behavior of composite steel frame-reinforced concrete infill wall structural system: A report from the national science foundation U.S.-Japan cooperative research program phase 5, composite and hybrid structuresMineapolis, Minnesota 55455-0116. United States: University of Minnesota.

Google Scholar

Trutalli, D., Marchi, L., Scotta, R., Pozza, L., and Stefani, L. de (2017). Seismic response of a platform-frame system with steel columns. Buildings 7, 33. doi:10.3390/buildings7020033

CrossRef Full Text | Google Scholar

Vogiatzis, T., and Avdelas, A. (2018). Study of composite steel frame with reinforced-concrete infill. Proc. Institution Civ. Eng. - Struct. Build. 171, 178–192. doi:10.1680/jstbu.16.00192

CrossRef Full Text | Google Scholar

Vogiatzis, T. (2019). Nonlinear numerical study on the behaviour of seismic resistant composite structural systems of steel moment frames with reinforced concrete infill walls. Thessaloniki, Greece: Aristotle University of Thessaloniki. doi:10.12681/eadd/45230

CrossRef Full Text | Google Scholar

Vogiatzis, T., Tsalkatidis, T., and Avdelas, A. (2019). Steel framed structures with cross laminated timber infill shear walls and semi-rigid connections. Int. J. Eng. Technol. 8, 433. doi:10.14419/ijet.v8i4.29742

CrossRef Full Text | Google Scholar

Vogiatzis, T., Tsalkatidis, T., and Avdelas, A. (2020). Wood-steel composite shear walls with openings. Int. J. Eng. Technol. 10, 14. doi:10.14419/ijet.v10i1.31255

CrossRef Full Text | Google Scholar

Wallace, J., and Wada, A. (2000). “Hybrid wall systems: US-Japan research,” in Proceedings of 12th World Conference on Earthquake Engineering, January 30–February 04, 2000, Auckland, New Zeland.

Google Scholar

Wang, Z., Gong, M., and Chui, Y. H. (2015). Mechanical properties of laminated strand lumber and hybrid cross-laminated timber. Constr. Build. Mat. 101, 622–627. doi:10.1016/J.CONBUILDMAT.2015.10.035

CrossRef Full Text | Google Scholar

Xu, B.-H., Bouchaïr, A., and Racher, P. (2014). Appropriate wood constitutive law for simulation of nonlinear behavior of timber joints. J. Mat. Civ. Eng. 26, 04014004. doi:10.1061/(asce)mt.1943-5533.0000905

CrossRef Full Text | Google Scholar