Global Simultaneous Optimization of Oil, Hysteretic and Inertial Dampers Using Real-Valued Genetic Algorithm and Local Search

A method for global simultaneous optimization of oil, hysteretic and inertial dampers is proposed for building structures using a real-valued genetic algorithm and local search. Oil dampers has the property that they can reduce both displacement and acceleration without significant change of natural frequencies and hysteretic dampers possess the characteristic that they can absorb energy efficiently and reduce displacement effectively in compensation for the increase of acceleration. On the other hand, inertial dampers can change (prolong) the natural periods with negative stiffness and reduce the effective input and the maximum acceleration in compensation for the increase of deformation. By using the proposed simultaneous optimization method, structural designers can select the best choice of these three dampers from the viewpoints of cost and performance indices (displacement, acceleration). For attaining the global optimal solution which cannot be attained by the conventional sensitivity-based approach, a method including a real-valued genetic algorithm and local search is devised. In the first stage, a real-valued genetic algorithm is used for searching an approximate global optimal solution. Then a local search procedure is activated for enhancing the optimal character of the solutions by reducing the total quantity of three types of dampers. It is demonstrated that a better design from the viewpoint of global optimality can be obtained by the proposed method and the preference of damper selection strongly depends on the design target (displacement, acceleration). Finally, a multi-objective optimization for the minimum deformation and acceleration is investigated.

1 Introduction

Passive dampers are becoming innovative and inevitable technologies for reducing the vibration of structures and infrastructure against natural disturbances, e.g. earthquakes, strong winds. In particular, large-scale structures, e.g. high-rise buildings, cannot be designed in earthquake-prone or hurricane (typhoon)-prone countries without passive dampers. Varieties of passive dampers have been developed worldwide and respective dampers have been used in view of their advantageous features and costs. The historical sketch can be found in some monographs (Soong and Dargush 1997; Srinivasan and McFarland 2000; Hanson and Soong 2001; Christopoulos and Filiatrault 2006; Takewaki 2009) and review articles (Uetani et al., 2003; Palermo et al., 2017; Wang and Mahin 2018; De Domenico et al., 2019; Saeed et al., 2021; Takewaki and Akehashi 2021). Recent developments can be found in some papers (Cunico and Cavalheiro, 2019; Chitra and Rugmini, 2020; Elias et al., 2021; Saeed et al., 2021; Narayan and Pathak 2022).

The problem of damper optimization has been investigated extensively since the milestone research due to Zhang and Soong (1992) where a sensitivity-based approach (or sequential allocation approach) was developed by including a simple sequential algorithm of damper allocation. The approach uses a response index obtained by the response analysis and allocates the next-step damper to the most effective position. The sensitivity-based approach was advanced afterward for elastic building structures with linear oil dampers by incorporating the mathematical and mechanics-based backgrounds (Takewaki 1997; Takewaki et al., 1999). Then, Adachi et al. (2013) extended this approach to the optimal allocation of nonlinear oil dampers.

Although the optimal damper problem has been widely studied in the literature, there are still gaps in the global optimization of these different types of dampers. The hybrid use of several passive dampers is a unique and smart attempt to enhance the ability of respective dampers to the maximum level. Simultaneous use of multiple kinds of passive dampers provides robustness and redundancy for main building structures because the uncertainty levels in passive dampers are larger than those in main building structures. Another merit of the use of different types of dampers is the introduction of mechanical properties with different phase properties. For example, while the variability of mechanical properties of hysteretic dampers (buckling-restrained braces etc) are rather small, those of oil dampers and inertial dampers are large. In addition, the dependences of those dampers on frequency, temperature and amplitude are completely different. Moreover, the over use of single-type dampers sometimes increases the acceleration. The use of multiple types of dampers with different phase properties can overcome this issue. Murakami et al. (2013) tackled this hybrid use design problem and developed a new sensitivity-based approach for attaining the minimum deformation of building structures under earthquake ground motions with a constant total cost. Although the approach due to Murakami et al. (2013) is pioneering, the issues of straying into to the local minimum and unstable sensitivities encountered in hysteretic materials (sudden change of stiffness) and random earthquake inputs posed a new problem to be overcome.

Compared to the sensitivity-based approach, another possibility is a meta-heuristic approach, e.g. genetic algorithms, etc. (Singh and Moreschi 2000, Wongprasert and Symans 2004, Liu et al., 2005, Movaffaghi and Friberg 2006, Lavan and Dargush 2009, Akehashi and Takewaki 2021a, b). It is well known that most of meta-heuristic approaches are often time-consuming. By overcoming the issue of the computational cost efficiency, e.g. a partial use of those approaches during the overall optimization process, the meta-heuristic approach can substitute the sensitivity-based approach even partially and provide the global optimal solution which is not expected by the sensitivity-based approach.

In this paper, a global simultaneous optimization technique of oil, hysteretic and inertial dampers is proposed for building structures using a real-valued genetic algorithm (Eshelman and Schaffer 1993) and local search (Akehashi and Takewaki 2021a, b). While most of the previous papers dealt with the optimization of single-type passive dampers even in the recent work using a real-valued genetic algorithm and local search (Akehashi and Takewaki 2021a, b), the present paper tackles simultaneous optimization of three kinds of passive dampers. Furthermore, the minimization of absolute accelerations is investigated by taking full advantage of mechanical characteristics of respective dampers. This minimization of accelerations was not performed in the previous works (Murakami et al., 2013, Akehashi and Takewaki 2021a, b). From the viewpoint of ‘resilience’, both performances of deformation and acceleration are critically important for reducing the risk of structural damage (related to deformation) and non-structural damage (related to acceleration). Oil dampers has the property that they can reduce both displacement and acceleration without change of natural frequencies and hysteretic dampers possess the characteristic that they can absorb energy efficiently and reduce displacement effectively. On the other hand, inertial dampers can change (prolong) the natural periods with negative stiffness and reduce the effective input and the maximum acceleration. By using the proposed simultaneous optimization method, structural designers can select the best choice of these three dampers from the viewpoints of cost and performance indices (displacement, acceleration). For attaining global optimal solution, a method including a real-valued genetic algorithm and local search is devised. In the first stage, a real-valued genetic algorithm is used for searching an approximate global optimal solution. Then a local search procedure is activated for enhancing the optimal character of the solutions. A ten-story shear building model under two recorded ground motions is used to present the effectiveness of the proposed approach and reveal the best allocation properties of three types of dampers.

2 Modeling of Oil, Hysteretic and Inertial Dampers and Their Properties in Response Reduction

Consider a shear building model, as shown in Figure 1, including oil, hysteretic and inertial dampers in parallel. In practice, it is not usual to use all these three types of dampers in the same story. Since the preference of use of selected dampers is investigated in this paper, the possibility of placement of three types of dampers in the same story is provided.

FIGURE 1

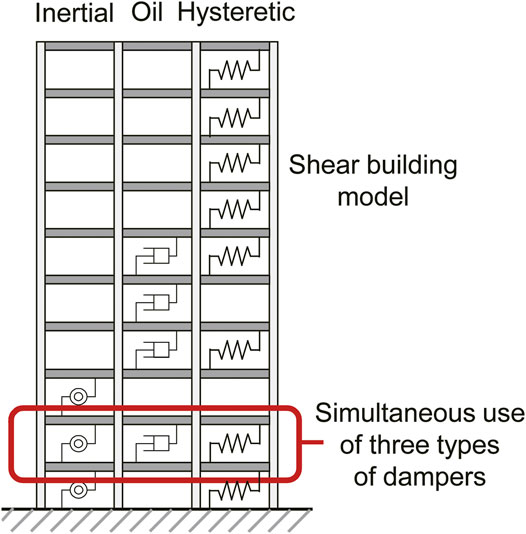
FIGURE 1. Shear building model with three types of dampers (Murakami et al., 2013).

Let $k_j$, $c_j$, ${\omega }_{ND}^{\left(1\right)}$, $h_S$ denote the jth story stiffness, the jth story structural viscous damping coefficient, the undamped fundamental natural circular frequency and the structural damping ratio of the shear building model without dampers. The jth story structural viscous damping coefficient can be expressed by

$c_j=\frac{2h_S}{{\omega }_{ND}^{\left(1\right)}}{k}_j(1)$

Let $m_j$ denote the jth floor mass and $c_{dj},R_j,k_{dj},z_j$ denote the damping coefficient of the jth story oil damper ($c_{1j},c_{2j}$ are used later for the first and second-branch coefficients), the relief force of the jth story oil damper, the elastic stiffness of the jth story hysteretic damper and the coefficient of the jth story inertial damper.

2.1 Oil Damper

Consider a nonlinear oil damper whose mechanical properties are shown in Figure 2 in comparison with a linear oil damper (Adachi et al., 2013; Noshi et al., 2013). The first and second-branch damping coefficients of the jth story oil damper are denoted by $c_{1j},c_{2j}$ and their ratio $\gamma$ is given by

$\gamma =c_{2j}/c_{1j}(2)$

FIGURE 2

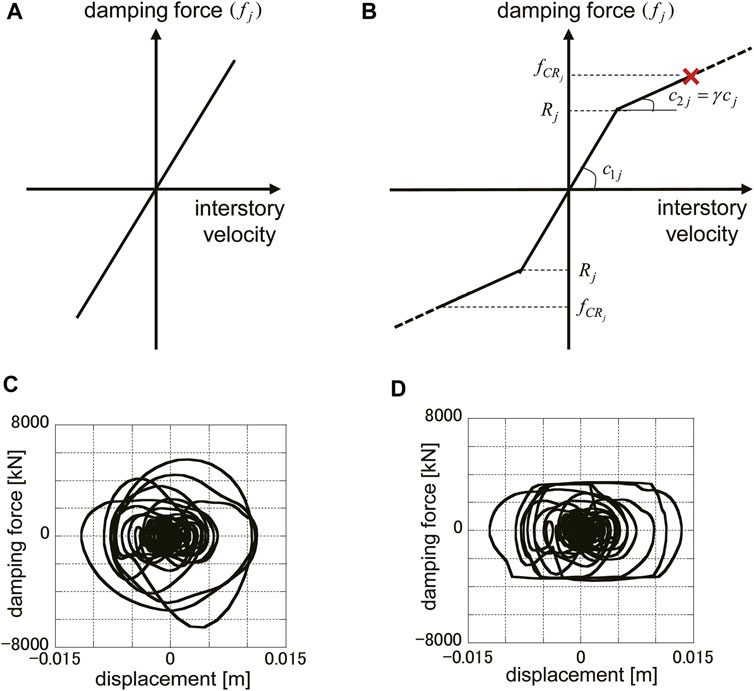
FIGURE 2. Mechanical properties of linear and nonlinear oil dampers, (A) Damping force-velocity relation (linear oil damper), (B) Damping force-velocity relation (nonlinear oil damper), (C) Damping force-deformation relation (linear oil damper), (D) Damping force-deformation relation (nonlinear oil damper).

The maximum allowable force $f_{CRj}$ of the jth story oil damper is related to the relief force with a given parameter $\overline{\alpha }$

$f_{CRj}=\overline{\alpha }{R}_j(3)$

In oil dampers, the ratio $r_{j\max }=$ (maximum damping force/ $R_j$) must be smaller than $\overline{\alpha }$, i.e. the maximum damping force must be smaller than $f_{CRj}$. The design variables for oil dampers are {$c_{1j}$} and {$R_j$}.

2.2 Hysteretic Damper

Consider a hysteretic damper which has an elastic-perfectly plastic restoring-force characteristic as shown in Figure 3. Let $u_y$ denote the specified yield deformation of the hysteretic damper. The yield story shear force $Q_{yj}$ in the jth story can be expressed by

$Q_{yj}=\left(k_j+k_{dj}\right)u_y(4)$

FIGURE 3

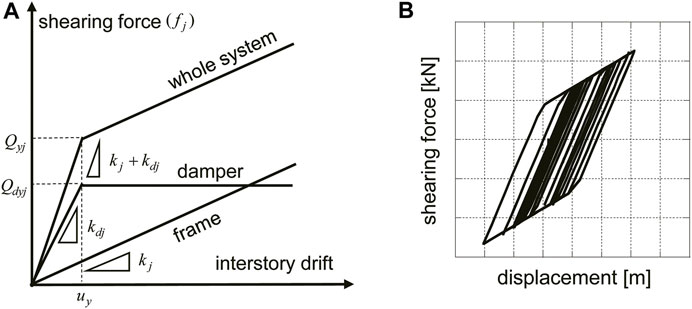
FIGURE 3. Restoring-force characteristic of frame and hysteretic damper, (A) Monotonic loading case, (B) Cyclic loading case (frame with hysteretic damper).

The design variables of hysteretic dampers are {$k_{dj}$}.

2.3 Inertial Damper

Consider an inertial damper whose mechanism is shown in Figure 4A. The force-deformation relation of the inertial damper is illustrated in Figure 4B in comparison with those of viscous (linear oil) and hysteretic dampers. Assume that the inertial dampers are installed here in a linear shear building model with linear structural viscous damping. Let ${\ddot{u}}_g$ denote the input base acceleration and let $z_j$ denote the coefficient of the inertial damper (inertial mass) in the jth story. When $z_j$ is multiplied by the corresponding relative acceleration, it gives a force related to the inertial damper. Using the mass, structural damping, stiffness, inertial damper matrices [M], [C], [K], [Z], the relative displacement {x} and the influence coefficient vector {1}, the equations of motion for the models without and with inertial dampers can be expressed respectively by

$\left[M\right]\left\{\ddot{x}\right\}+\left[C\right]\left\{\dot{x}\right\}+\left[K\right]\left\{x\right\}=-\left[M\right]\left\{1\right\}{\ddot{u}}_g(5)$

$\left(\left[M\right]+\left[Z\right]\right)\left\{\ddot{x}\right\}+\left[C\right]\left\{\dot{x}\right\}+\left[K\right]\left\{x\right\}=-\left[M\right]\left\{1\right\}{\ddot{u}}_g(6)$

where

$\left[M\right]=\left[\begin{array}{cccc}{m}_1& 0& \cdots & 0\\ 0& \ddots & \ddots & ⋮\\ ⋮& \ddots & \ddots & 0\\ 0& \cdots & 0& m_N\end{array}\right](7)$

$\left[Z\right]=\left[\begin{array}{cccccc}{z}_1+z_2& -z_2& 0& \cdots & \cdots & 0\\ -z_2& z_2+z_3& -z_3& \ddots & & ⋮\\ 0& -z_3& \ddots & \ddots & \ddots & ⋮\\ ⋮& \ddots & \ddots & \ddots & -z_{N-1}& 0\\ ⋮& & \ddots & -z_{N-1}& z_{N-1}+z_N& -z_N\\ 0& \cdots & \cdots & 0& -z_N& z_N\end{array}\right](8)$

$\left[C\right]=\left[\begin{array}{cccccc}{c}_1+c_2& -c_2& 0& \cdots & \cdots & 0\\ -c_2& c_2+c_3& -c_3& \ddots & & ⋮\\ 0& -c_3& \ddots & \ddots & \ddots & ⋮\\ ⋮& \ddots & \ddots & \ddots & -c_{N-1}& 0\\ ⋮& & \ddots & -c_{N-1}& c_{N-1}+c_N& -c_N\\ 0& \cdots & \cdots & 0& -c_N& c_N\end{array}\right](9)$

$\left[K\right]=\left[\begin{array}{cccccc}{k}_1+k_2& -k_2& 0& \cdots & \cdots & 0\\ -k_2& k_2+k_3& -k_3& \ddots & & ⋮\\ 0& -k_3& \ddots & \ddots & \ddots & ⋮\\ ⋮& \ddots & \ddots & \ddots & -k_{N-1}& 0\\ ⋮& & \ddots & -k_{N-1}& k_{N-1}+k_N& -k_N\\ 0& \cdots & \cdots & 0& -k_N& k_N\end{array}\right](10)$

$\left\{x\right\}={\left\{x_1,x_2,\cdots ,x_N\right\}}^T(11)$

FIGURE 4

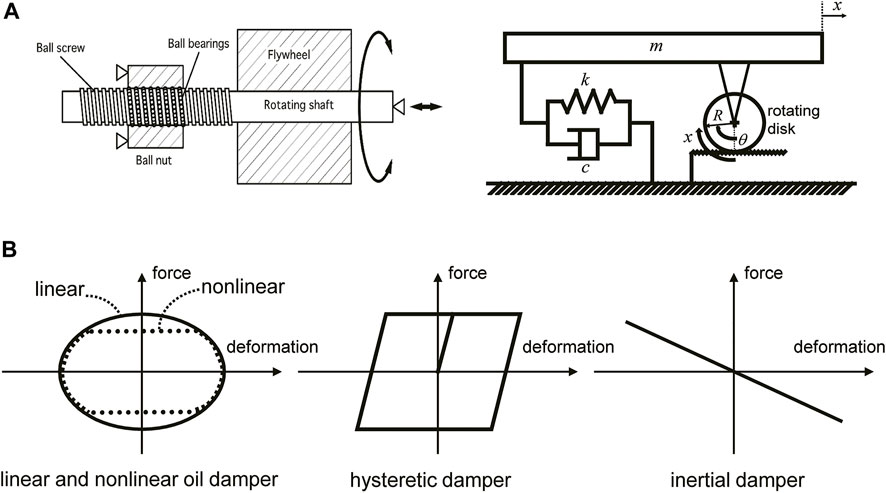
FIGURE 4. Mechanism of inertial damper and restoring-force characteristics of three dampers (oil, hysteretic and inertial), (A) Mechanism of inertial damper, (B) restoring-force characteristics of three dampers (oil, hysteretic and inertial) (Takewaki et al., 2012).

Introduce the input reduction coefficient vector $\left\{\eta \right\}$ (Takewaki et al., 2012).

$\left\{\eta \right\}={\left(\left[M\right]+\left[Z\right]\right)}^{-1}\left[M\right]\left\{1\right\}(12)$

Then, Eq. 6 can be reduced to

$\left(\left[M\right]+\left[Z\right]\right)\left\{\ddot{x}\right\}+\left[C\right]\left\{\dot{x}\right\}+\left[K\right]\left\{x\right\}=-\left(\left[M\right]+\left[Z\right]\right)\left\{\eta \right\}{\ddot{u}}_g(13)$

Equation 13 indicates that the effect of the input acceleration is reduced.

The design variables of inertial dampers are {$z_j$}.

2.4 Properties of Three Types of Dampers in Response Reduction

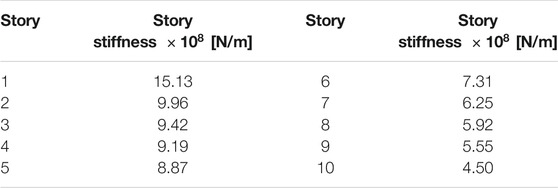
In this section, the properties of three types of dampers are investigated from the viewpoint of the response reduction. Consider a ten-story shear building model with a realistic distribution of story stiffnesses and constant floor mass $1.0\times {10}^6\left[\text{kg}\right]$ which corresponds to the 30 $\times$ 30 [m] plan building (Murakami et al., 2013). The story stiffnesses of the model are shown in Table 1. The fundamental natural period is 1.05 [s] and the structural damping ratio is $h_S=0.02$.

TABLE 1

TABLE 1. Story stiffness of building model.

In using different types of dampers, the cost of dampers is important. Murakami et al. (2013) introduced the cost ratio for different types of dampers. They considered the stiffness in [N/m] for hysteretic dampers, the limiting force in [N] for oil dampers, the unit capacity per unit mass in [kg] for inertial dampers as their reference quantities. For these reference quantities, the damper cost ratios are given by $Y_K:Y_C:Y_Z$. We assume that the used inertial damper (size) is fixed and the inertance (upper limit) is fixed. Then, multiple inertial dampers with the same size are introduced and the damper capacity is assumed to be proportional to the number of such fixed inertial dampers. In such circumstance, the cost of inertial dampers is proportional to the inertance. When only one inertial damper is used and the capacity (size) of the inertial damper is changed, another formulation (cost is proportional to the allowable force) may be possible (for example, see Nakaminami et al., 2017; Taflanidis et al., 2019; Pietrosanti et al., 2021). This treatment will be discussed in the future.

Figure 5 shows the damper forces for specifying damper costs. Let $u_y$, $Q_{dy}$, $f_{CR}$, $Q_{zy}$, $g$ denote the yield deformation and strength of hysteretic dampers, the maximum allowable force of oil dampers, the maximum burden force of inertial dampers and acceleration of gravity, respectively.

FIGURE 5

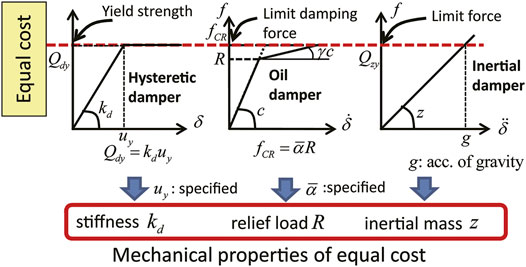
FIGURE 5. Damper forces specifying damper costs (Murakami et al., 2013).

From the cost investigation of hysteretic dampers and oil dampers, the following relation is derived.

$\frac{Q}{u_y}\cdot Y_K:\frac{Q}{\overline{\alpha }}\cdot Y_C=1:2,(14)$

where $Q$ is the common force ($Q_{dy}$ or $f_{CR}$). For another cost investigation of oil dampers and inertial dampers, the following relation is also derived.

$\frac{Q}{\overline{\alpha }}\cdot Y_C:\frac{Q}{g}\cdot Y_Z=3:4,(15)$

where $Q$ is the common force ($f_{CR}$ or $Q_{zy}$). From Eqs 14 and 15, the following cost relation is obtained.

$Y_K:Y_C:Y_Z=3u_y:6\overline{\alpha }:8g(16)$

In the present investigation, the cost parameters are set as $Y_K$ = 0.001538 [JPY $·$ m/N], $Y_C$ = 0.667 [JPY/N], $Y_Z$ = 8 [JPY/kg]. The total cost of dampers is set as $1.23\times {10}^8$ [JPY] following Murakami et al. (2013). The dampers are designed by solving the following problems where ${\overline{C}}_d$ is the total damper cost.

For hysteretic dampers,

$\begin{array}{cc}\mathrm{minimize}& f={\widehat{D}}_{\max }\left(\left\{k_{dj}\right\}\right),(\text{or }f={\widehat{A}}_{\max }\left(\left\{k_{dj}\right\}\right))\end{array}(17)$

$\begin{array}{cc}\mathrm{subject\; to}& Y_K{\displaystyle \sum _{j=1}^N{k}_{dj}={\overline{C}}_d}\end{array}(18)$

For oil dampers,

$\begin{array}{cc}\mathrm{minimize}& f={\widehat{D}}_{\max }\left(\left\{R_j\right\}\right),(\text{or }f={\widehat{A}}_{\max }\left(\left\{R_j\right\}\right))\end{array}(19)$

$\begin{array}{cc}\mathrm{subject\; to}& Y_C{\displaystyle \sum _{j=1}^N{R}_j={\overline{C}}_d}\end{array}(20)$

${\widehat{r}}_{j\max }\le \overline{\alpha }(j=\mathrm{1,2},\cdots ,N),({\widehat{r}}_{j\max }=\text{maximum damping force}/R_j)(21)$

For inertial dampers,

$\begin{array}{cc}\mathrm{minimize}& f={\widehat{D}}_{\max }\left(\left\{z_j\right\}\right),(\text{or }f={\widehat{A}}_{\max }\left(\left\{z_j\right\}\right))\end{array}(22)$

$\begin{array}{cc}\mathrm{subject\; to}& Y_Z{\displaystyle \sum _{j=1}^N{z}_j={\overline{C}}_d}\end{array}(23)$

Figure 6 shows the maximum interstory drifts and maximum absolute accelerations for each objective function optimization problem (${\widehat{D}}_{\max }$ or ${\widehat{A}}_{\max }$). Two ground motions were used as in Section 5, El Centro NS (1940) and Hachinohe NS (1968) whose PGV = 0.50 [m/s]. The envelope value of the responses to these two input ground motions is employed as the response value. The method explained in Section 4 is used for the damper optimization although a single type of dampers is used. It is noted that, while the damper optimization is conducted for varied total damper cost ${\overline{C}}_d$ in Section 4 for the comparison with the sensitivity-based approach, a single quantity is used in this section.

FIGURE 6

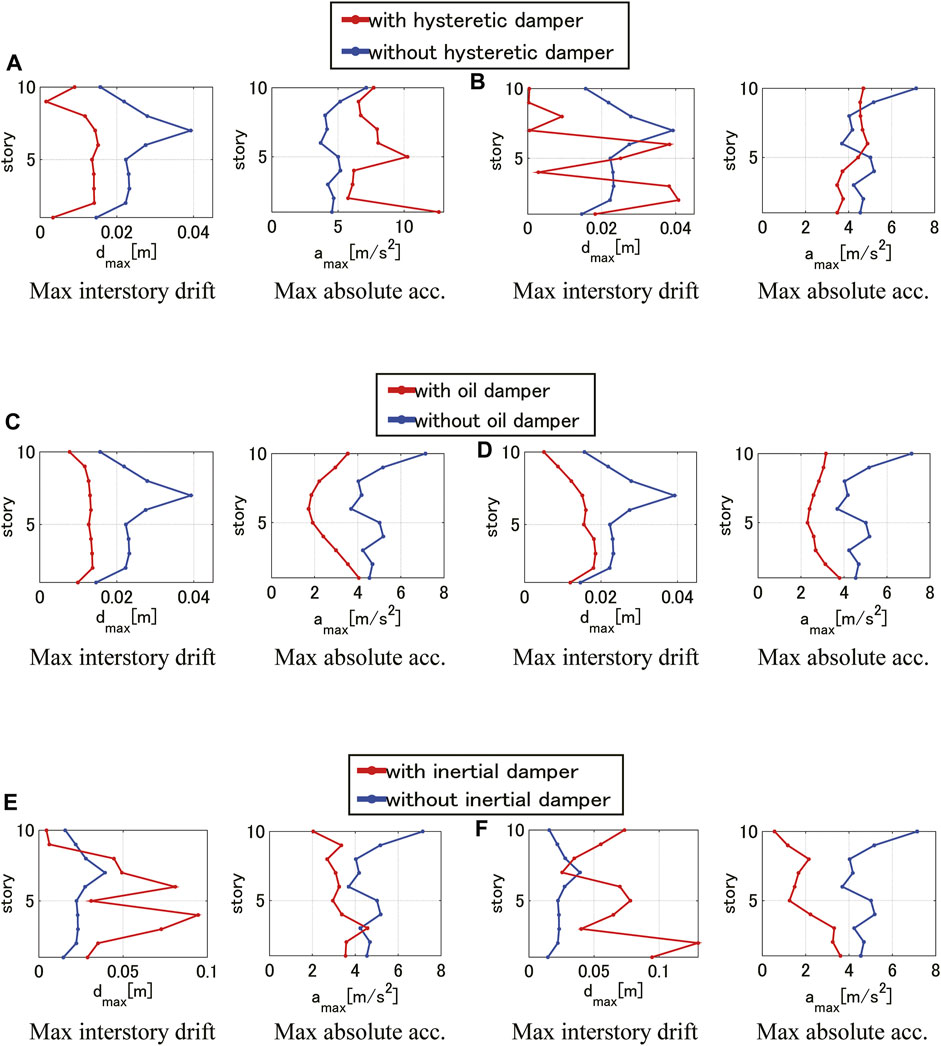
FIGURE 6. Maximum interstory drifts and maximum absolute acceleration (Total cost: $1.23\times {10}^8$ [JPY]), (A) Optimization for interstory drift (hysteretic damper), (B) Optimization for acceleration (hysteretic damper), (C) Optimization for interstory drift (oil damper), (D) Optimization for acceleration (oil damper), (E) Optimization for interstory drift (inertial damper), (F) Optimization for acceleration (inertial damper).

The following results are derived from Figure 6.

1) While the hysteretic dampers can reduce the maximum interstory drift in the minimization problem of deformation, the maximum acceleration becomes larger. For the reduction of the maximum acceleration, the parallel use of another type of dampers is desired.

2) As for hysteretic dampers, the minimization problem of the maximum acceleration does not cause the increase of the maximum acceleration. But the maximum interstory drift becomes larger.

3) Oil dampers are effective both for the reduction of the maximum interstory drift and the maximum acceleration.

4) The effectiveness of oil dampers in the reduction of the maximum interstory drift is almost equivalent to hysteretic dampers. The use of both dampers seems to depend on other design factors.

5) Although inertial dampers are effective for the reduction of the maximum acceleration, they may increase the maximum interstory drift. For the reduction of the maximum interstory drift, the parallel use of another type of dampers is desired.

3 Problem of Simultaneous Optimal Design of Oil, Hysteretic and Inertial Dampers

3.1 Optimal Design Problem

The optimal design problem of three types of dampers can be described as follows.

$\begin{array}{cc}\mathrm{minimize}& f={\widehat{D}}_{\max }(\left\{R_j\right\},\left\{c_{dj}\right\},\left\{k_{dj}\right\},\left\{z_j\right\})\end{array}(24)$

$\begin{array}{cc}\mathrm{subject\; to}& Y_C{\displaystyle \sum _{j=1}^N{R}_j}+Y_K{\displaystyle \sum _{j=1}^N{k}_{dj}+Y_Z{\displaystyle \sum _{j=1}^N{z}_j}={\overline{C}}_d}\end{array}(25)$

${\widehat{r}}_{j\max }\le \overline{\alpha }(j=\mathrm{1,2},\cdots ,N)(26)$

In Eq. 26, $r_{j\max }=$ (maximum damping force/ $R_j$) as explained before.

3.2 Design Variables of Three Dampers

As stated in Section 2, the design variables for oil dampers are {$c_{1j}$} and {$R_j$}, those for hysteretic dampers are {$k_{dj}$}, and those for inertial dampers are {$z_j$}.

It should be remarked that for oil dampers, the relief forces {$R_j$} are directly related to the cost of oil dampers because the response forces are related to the size of dampers. However, since Eq. 26 has to be satisfied for oil dampers, the damping coefficients {$c_{1j}$} are used as sub parameters. If a candidate design which does not satisfy Eq. 26 appears, the design modification is made by changing {$c_{1j}$} to keep the cost constant.

4 Optimal Design Procedure Using Real-Valued Genetic Algorithm and Local Search

In this section, the solution algorithm for the above-mentioned optimization problem is presented. The proposed method consists of the real-valued genetic algorithm (GA) and local search. Although a gene is expressed by the binary form (0 or 1) in the conventional GA, design variable vectors are directly treated to create new individuals in the real-valued GA. In the application of the proposed crossover procedure in the real-valued GA, the total costs of the added dampers are kept constant. This leads to an efficient search of the solutions. A local search is conducted for high accuracy after the search by the real-valued GA. In Section 4.1, the difference between the conventional GA and the real-valued GA is explained briefly. In Section 4.2, the solution algorithm combining the real-valued GA and local search is explained.

4.1 Real-Valued Genetic Algorithm and Conventional Genetic Algorithm

Figures 7A,B show the overview of the conventional GA and the real-valued GA. In the conventional GA, the binary expression (0 or 1) of the design variables is required. Although the conventional GA is one of the famous metaheuristics, it is not easy for inexperienced users to employ this. The success of the optimization largely depends on whether the design variables are transformed into the binary expression effectively or not. On the other hand, design variable vectors are directly treated to create new individuals in the real-valued GA. Although the binary expression is not required, a suitable crossover method for the problem should be selected for the successful search.

FIGURE 7

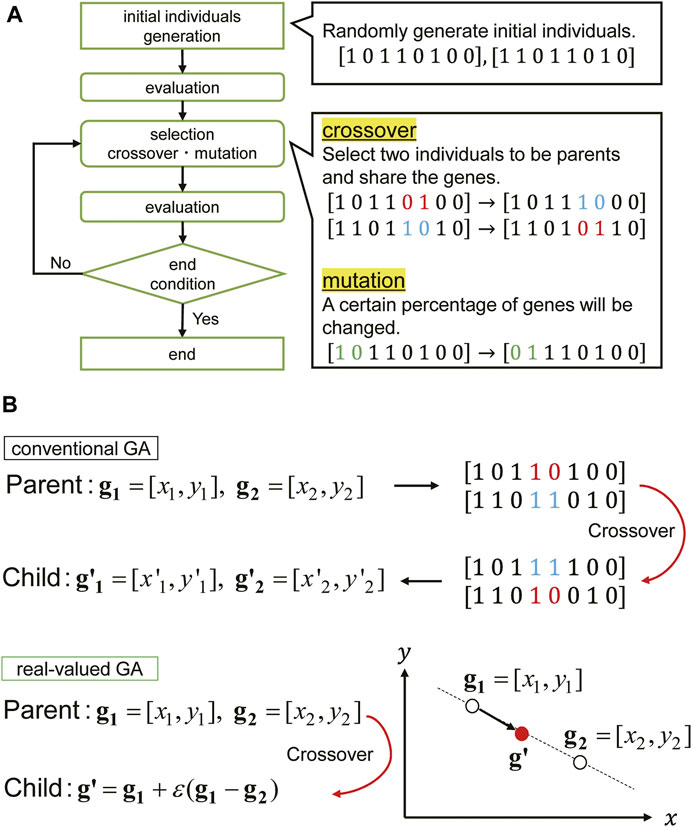
FIGURE 7. Overview of conventional GA and real-valued GA, (A) Conventional GA, (B) Comparison between conventional GA and real-valued GA (proposed method).

It is noted that the real-valued GA is adopted in this paper because the sensitivity-based approach will not work effectively for the simultaneous optimization of oil, hysteretic and inertial dampers. Although the objective function has multiple peaks due to the nonlinearity of the hysteretic dampers and the oil dampers, the real-valued GA will work effectively.

4.2 Optimal Design Procedure Using Real-Valued Genetic Algorithm and Local Search

The solution algorithm may be described as follows.

Step 1. Put $i_C\to 1,i_{cr}\to 1$. Randomly generate $M_1(\ge 3N)$ individuals with constant total costs ${\overline{C}}_{d,i_C}$ $\left(=Y_C{\displaystyle {\sum }_{j=1}^N{R}_j+}{Y}_K{\displaystyle {\sum }_{j=1}^N{k}_{dj}+}{Y}_Z{\displaystyle {\sum }_{j=1}^N{z}_j}\right)$ of the dampers (Akehashi and Takewaki (2021a, b)).

Step 2. Obtain $3n_{cr}N$ models by the crossover operator (the details of the crossover operator are explained below).

Step 3. Choose $M_2$ models among all the individuals by the elitist selection, and randomly create $M_3$ models. Then choose $(M_1-M_2-M_3)$ models among the remaining individuals by the roulette wheel selection. If $i_{cr}=I_{cr}$, go to Step 4. Otherwise, put $i_{cr}\to i_{cr}+1$ and return to Step 2.

Step 4. Apply the local search operator $(n_{ls}\to n_{ls,1})$ to the lastly chosen $M_2$ individuals (the details of the local search operator are explained below). Select the individual with the minimum value of the objective function.

Step 5. Multiply $\left(\left\{R_j\right\},\left\{c_{dj}\right\},\left\{k_{dj}\right\},\left\{z_j\right\}\right)$ of the obtained individual by $({\overline{C}}_{d,i_C+1}/{\overline{C}}_{d,i_C})$ to create the new individuals with ${\overline{C}}_{d,i_C+1}$.

Step 6. Apply the local search operator $(n_{ls}\to n_{ls,2})$ to the obtained individual. If $i_C<I_C$, put $i_C\to i_C+1$ and return to Step 5. If $i_C=I_C$, then finalize the process.[Crossover operator]Choose $3N$ individuals among the obtained ones by the roulette wheel selection. Let ${\mathbf{Y}}_i={(Y_C{R}_1,\mathrm{...},Y_C{R}_N,Y_K{k}_{d1},\mathrm{...},Y_K{k}_{dN},Y_Z{z}_1,\mathrm{...},Y_Z{z}_N)}^T$ denote the cost vector by the dampers of the ith individual (i = 1, … , 3N). Obtain $3N$ individuals from

${\mathbf{Y}}_i\prime ={\mathbf{Y}}_i+{\displaystyle {\sum }_{j=1,j\ne i}^{3N}{\epsilon }_j({\mathbf{Y}}_j-{\mathbf{Y}}_i)},(27)$

where ${\epsilon }_j$ is a uniform random number. When any value of the components in ${\mathbf{Y}}_{\mathrm{i}}\prime$ becomes negative, change the value of the corresponding component into zero, and then multiply a constant on ${\mathbf{Y}}_i\prime$ so that the constraint on the total costs of the dampers is continued to be satisfied. When $f_{\max }>f_{CR}$ ($f_{\max }$: maximum damping force of oil damper), modify the values of the added viscous damping coefficients so that $f_{\max }\le f_{CR}$ is satisfied (Noshi et al., 2013).[Local search operator]Calculate $\Delta \mathbf{Y}$ by

$\mathbf{\Delta Y}=s\left\{{\displaystyle {\sum }_{k=1}^{3N-1}\frac{x_k}{\sqrt{x_1^2+\cdots +x_{3N-1}^2}}{\mathit{i}}_{\mathit{k}}}\right\},(28)$

where ${\mathit{i}}_1,\mathrm{...},{\mathit{i}}_{3N-1}$ is an orthonormal set of the hyperplane $\Delta {\mathbf{Y}}^T\cdot \mathbf{1}=0$. $x_k$ is a standard normal random number, and $x_k,x_j$ are independent each other when $k\ne j$. $s$ is a random number whose probability distribution is given by

$f\left(s\right)=\frac{3N-1}{S^{3N-1}}{s}^{3N-2}(0\le s\le S)(29)$

When $f_{\max }>f_{CR}$, modify the values of the added viscous damping coefficients so that $f_{\max }\le f_{CR}$ is satisfied. If the design with $\mathbf{Y}+\mathbf{\Delta }\mathbf{Y}$ is superior to the design with $\mathbf{Y}$, update $\mathbf{Y}\to \mathbf{Y}+\mathbf{\Delta }\mathbf{Y}$. Repeat these procedures $n_{ls}$ times.Figure 8 shows the overview of the proposed method. Figure 8A presents the optimization algorithm of the proposed method and Figure 8B illustrates the overview of the proposed method combining the real-valued GA and the local search. The procedures in Steps 1–4 explained above correspond to the search of the optimal design with the total costs ${\overline{C}}_{d,1}$ and the procedures in Steps 6 correspond to the search of the optimal design with the total costs ${\overline{C}}_{d,2},\mathrm{...},{\overline{C}}_{d,I_C}$. The total costs are changed only by the procedures in Step 5. It is noted that the application of the crossover operator does not change the total cost since ${\mathbf{Y}}_1^{\mathbf{T}}\cdot \mathbf{1}=\mathrm{...}={\mathbf{Y}}_{3N}^T\cdot \mathbf{1}(const.)$.Figure 9A presents an example of the application of the crossover operator. In that case, only the oil dampers are treated. The limitation of the search range by the crossover operator leads to an efficient search of the optimal solution because the number of the dimensions of the search range decreases from 3N to (3N-1) and the multimodality of the objective function is greatly weakened.Figure 9B shows an example of the application of the local search operator. The crossover operator dynamically searches the optimal solution, and then the local search operator is used to search around the obtained solution for the improvement. The likelihood of $\mathrm{\Delta }\mathbf{Y}$ is uniform in the internal domain of the hypersphere with the radius $S$, whose center is located at the origin of $\Delta {\mathbf{Y}}^T\cdot \mathrm{1}=0$ (Muller 1959). It is noted that the value of $s$ can be calculated by the inverse transform sampling such as

$s=F^{1/(3N-1)}S,(30)$

where $F=\text{Unif}\left[\mathrm{0,1}\right]$. An example of ${\mathbf{i}}_1,\mathrm{...},{\mathbf{i}}_{3N-1}$ is expressed as follows.

${\mathit{i}}_1=\frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\ -1\\ 0\\ ⋮\\ 0\\ 0\end{array}\right),{\mathit{i}}_2=\frac{1}{\sqrt{6}}\left(\begin{array}{c}1\\ 1\\ -2\\ 0\\ ⋮\\ 0\end{array}\right),{\mathit{i}}_3=\frac{1}{\sqrt{12}}\left(\begin{array}{c}1\\ 1\\ 1\\ -3\\ ⋮\\ 0\end{array}\right),\cdots ,{\mathit{i}}_{3N-1}=\frac{1}{\sqrt{3N(3N-1)}}\left(\begin{array}{c}1\\ 1\\ ⋮\\ 1\\ 1\\ -(3N-1)\end{array}\right)(31)$

FIGURE 8

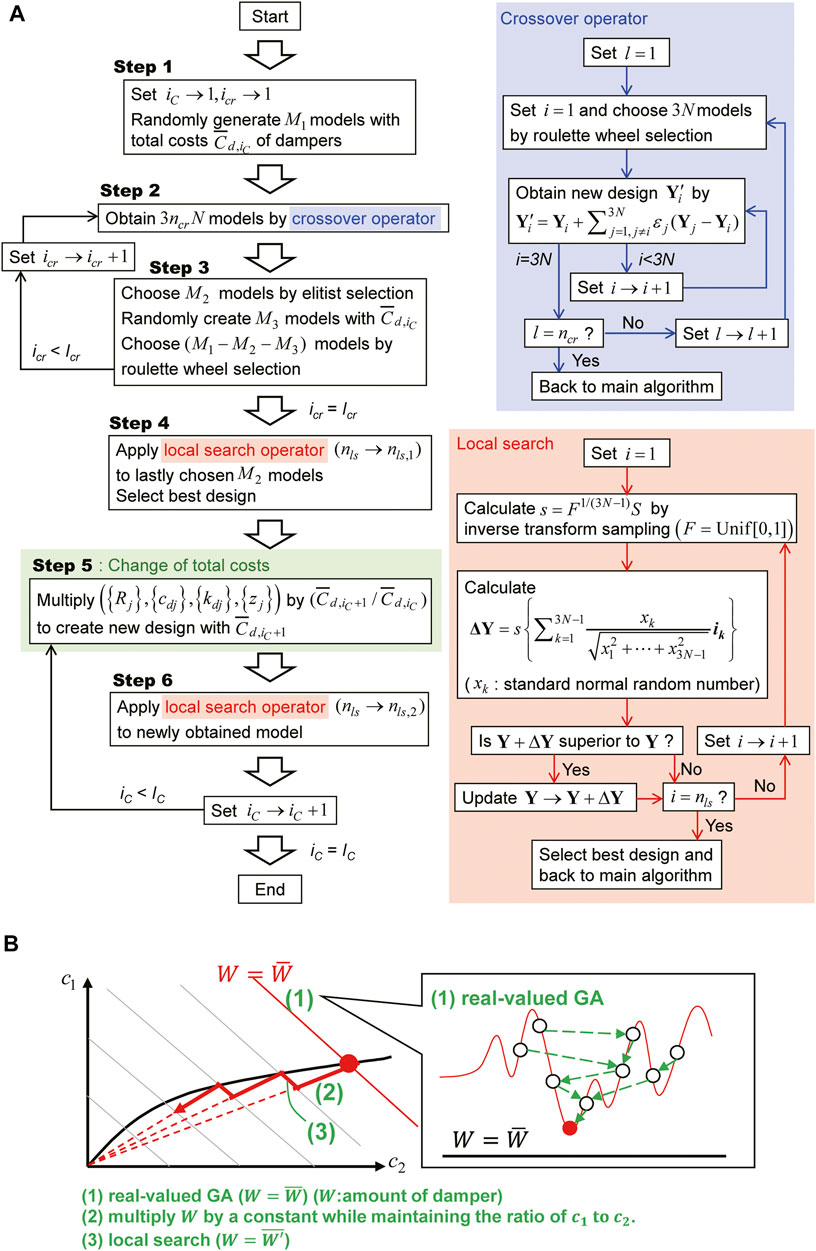
FIGURE 8. Overview of proposed method, (A) Optimization algorithm of proposed method, (B) Overview of proposed method combining real-valued GA and local search.

FIGURE 9

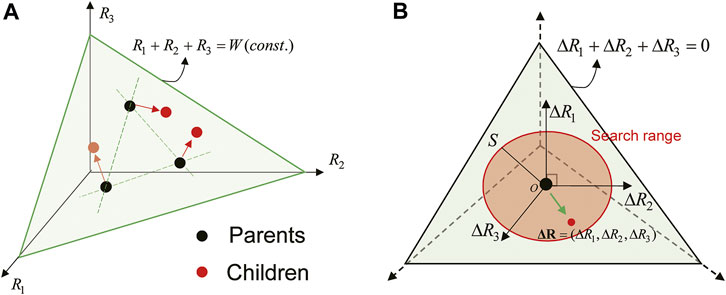
FIGURE 9. Crossover operator and search domain in local search for 3-story model, (A) Crossover operator, (B) Search domain in local search.

5 Design Examples

Consider a 10-story shear building model as used in Section 2.1. The story stiffnesses of the shear building model are shown in Table 1. The common floor mass is $1.0\times {10}^6$ [kg]. In this section, the total damper cost ${\overline{C}}_d$ is decreased from the initial value to compare with the sensitivity-based design (Murakami et al., 2013). Other parameters are: initial value of total cost, $1.23\times {10}^8$ [JPY], decrement of total cost: $2.0\times {10}^5$ [JPY] ($I_c=600$), $Y_C$: 0.667 [JPY/N], $Y_K$: 0.001538 [JPY $·$ m/N],: $Y_Z$: 8 [JPY/kg], story height: 3.5 [m], $n_{cr}$: 2, $I_{cr}$ [100, 300, 450, 600], number of application of local search operator $n_{ls,1}$: 100, $n_{ls,2}$: 40, $S$: $0.03\times {\overline{C}}_d$, initial produced number of individuals $M_1$: $65(=6N+M_3)$, elite selection number of individuals $M_2$: 1, number of mutation individuals $M_3$: $5(=N/2)$.

The input ground accelerations are El Centro NS (1940) and Hachinohe NS (1968) whose PGV = 0.50 [m/s]. The envelope value of the responses to these two input ground motions is employed as the response value for the optimization. The number of adopted ground motions may cause some issue of computational cost. The concept of ‘critical double impulse’ may be one possibility to resolve the computational cost issue (Akehashi and Takewaki 2019; Takewaki and Akehashi 2021). The critical double impulse is expected to bound the responses under multiple ground motions in a smart manner.

The optimal design using the proposed method in Section 4 is presented. The comparison with the result for the sensitivity-based approach is made.

5.1 Design Problem for Minimizing the Maximum Interstory Drift

The optimal design problem of dampers for the reduction of deformation may be stated as follows.

$\begin{array}{cc}\mathrm{minimize}& f={\widehat{D}}_{\max }(\left\{R_j\right\},\left\{c_{dj}\right\},\left\{k_{dj}\right\},\left\{z_j\right\})\end{array}(32)$

$\begin{array}{cc}\mathrm{subject\; to}& Y_C{\displaystyle \sum _{j=1}^N{R}_j}+Y_K{\displaystyle \sum _{j=1}^N{k}_{dj}+Y_Z{\displaystyle \sum _{j=1}^N{z}_j}={\overline{C}}_d}\end{array}(33)$

${\widehat{r}}_{j\max }\le \overline{\alpha }(j=\mathrm{1,2},\cdots ,N)(34)$

Figure 10 shows the comparison of the change of the maximum interstory drifts and the costs of dampers obtained by the proposed method with the sensitivity-based approach (Murakami et al., 2013). The horizontal axis indicates the advancement of computation and each step corresponds to the decrease of the damper cost by $2.0\times {10}^5$ [JPY]. Figure 11 presents the maximum interstory drift for several cost reduction steps (crossover by 100). The obtained results can be summarized as follows.

1) The proposed approach provides a smaller value of the maximum interstory drift than the sensitivity-based approach as shown in Figures 10(i)A–D. It seems that the proposed approach including the real-valued GA prevents from attaining a local minimum which is often reached by the sensitivity-based approach.

2) When the cost reduction step advances and a certain amount of dampers are removed from the initial total value, the sensitivity-based approach will work well within an allowable accuracy. On the other hand, the proposed approach can provide a better design even in the beginning stage as shown in Figures 11A–C. In addition, it can be understood from Figure 10(ii) that the proposed approach provides a small amount of inertial dampers which is thought to be ineffective for the reduction of the maximum interstory drift from the beginning stage. On the contrary, it takes a certain amount of time for inertial dampers to be removed because an arbitrary allocation of all dampers is made in the sensitivity-based approach.

3) In the case of reducing the maximum interstory drift, the effectiveness order is (i) hysteretic dampers, (ii) oil dampers, (iii) inertial dampers.

FIGURE 10

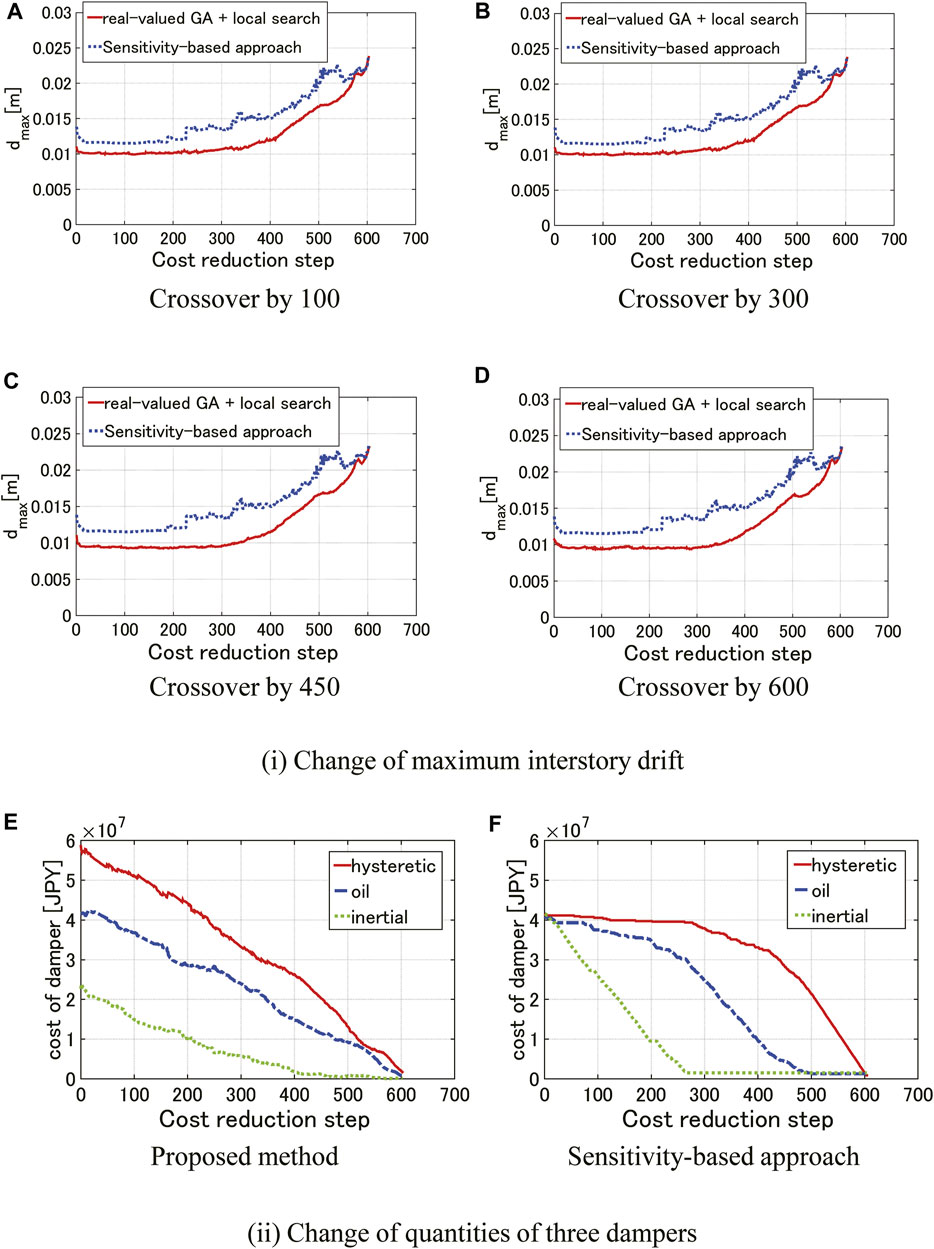
FIGURE 10. Comparison of change of maximum interstory drifts and cost of dampers with sensitivity-based approach (Murakami et al., 2013).

FIGURE 11

FIGURE 11. Maximum interstory drift for several cost reduction steps (crossover by 100).

It is noted that the required number of time-history response analyses throughout the proposed approach is approximately equal to 2 (number of input ground motions) times $\left[\left\{M_1+I_{cr}(3n_{cr}N+M_3)\right\}+M_2{n}_{ls,1}+I_C{n}_{ls,2}\right]$ $\simeq 61300$. $\left\{M_1+I_{cr}(3n_{cr}N+M_3)\right\}$ is the required number for the real-valued GA (Steps 1–3 in Section 4.2) under single ground motion, and $\left(M_2{n}_{ls,1}+I_c{n}_{ls,2}\right)$ is the required number for the local search (Steps 4–6 in Section 4.2) under single ground motion. On the other hand, the required number of time-history response analyses throughout the sensitivity-based approach is approximately equal to 2 times $3N{I}_c\simeq 36000$ Although the proposed method requires an about 1.7 times larger number of time-history response analysis compared to the sensitivity-based algorithm, the proposed method works better throughout the optimization procedure than the sensitivity-based algorithm. It is noted that another aspect can be observed in the multi-objective optimization for the maximum interstory drift and maximum floor acceleration. This will be explained in Section 6.2.

It is also pointed out that the required number of time-history response analyses for the proposed method increases linearly with the initial total cost of dampers, when the decrement of the total cost is identical. It is reminded that the real-valued GA is applied only to Cost Reduction Step 1, and the local search is applied from Cost Reduction Step 2 to Cost Reduction Step $I_C$ (final step). The required number of time-history response analyses for the sensitivity-based algorithm also increases linearly with the initial total cost of dampers.

5.2 Design Problem for Minimizing the Maximum Acceleration

The optimal design problem of dampers for the reduction of acceleration may be stated as follows.

$\begin{array}{cc}\mathrm{minimize}& f={\widehat{A}}_{\max }(\left\{k_{dj}\right\},\left\{R_j\right\},\left\{c_{dj}\right\},\left\{z_j\right\})\end{array}(35)$

$\begin{array}{cc}\mathrm{subject\; to}& Y_K{\displaystyle \sum _{j=1}^N{k}_{dj}}+Y_C{\displaystyle \sum _{j=1}^N{R}_j}+Y_Z{\displaystyle \sum _{j=1}^N{z}_j}={\overline{C}}_d\end{array}(36)$

${\widehat{r}}_{j\max }\le \overline{\alpha }(j=\mathrm{1,2},\cdots ,N)(37)$

Figure 12 shows the comparison of the change of the maximum absolute acceleration and the costs of dampers obtained by the proposed method with the sensitivity-based approach (Murakami et al., 2013). The findings can be summarized as follows.

1) The proposed approach provides a smaller value of the maximum acceleration than the sensitivity-based approach as shown in Figure 12(i). It seems that the proposed approach works well also for the reduction of the maximum acceleration.

2) As in the reduction of the maximum interstory drift (see Figure 10), when the step advances and a certain amount of dampers are removed from the initial total value based on an appropriate setting of initial designs, the sensitivity-based approach will work well within an allowable accuracy. On the other hand, the proposed approach can provide a better design even in the beginning stage.

3) In the case of reducing the maximum acceleration, the effectiveness order is (i) inertial dampers, (ii) oil dampers, (iii) hysteretic dampers. This property is a remarkable contrast to the case of reducing the maximum interstory drifts shown in Figure 10. Furthermore, it can be seen that the proposed method can judge quickly that the hysteretic dampers should be removed in the beginning stage compared to the sensitivity-based approach in the case of reducing the maximum acceleration. It is also understood that the effectiveness of inertial dampers is reflected in the proposed method in the case of reducing the maximum acceleration.

FIGURE 12

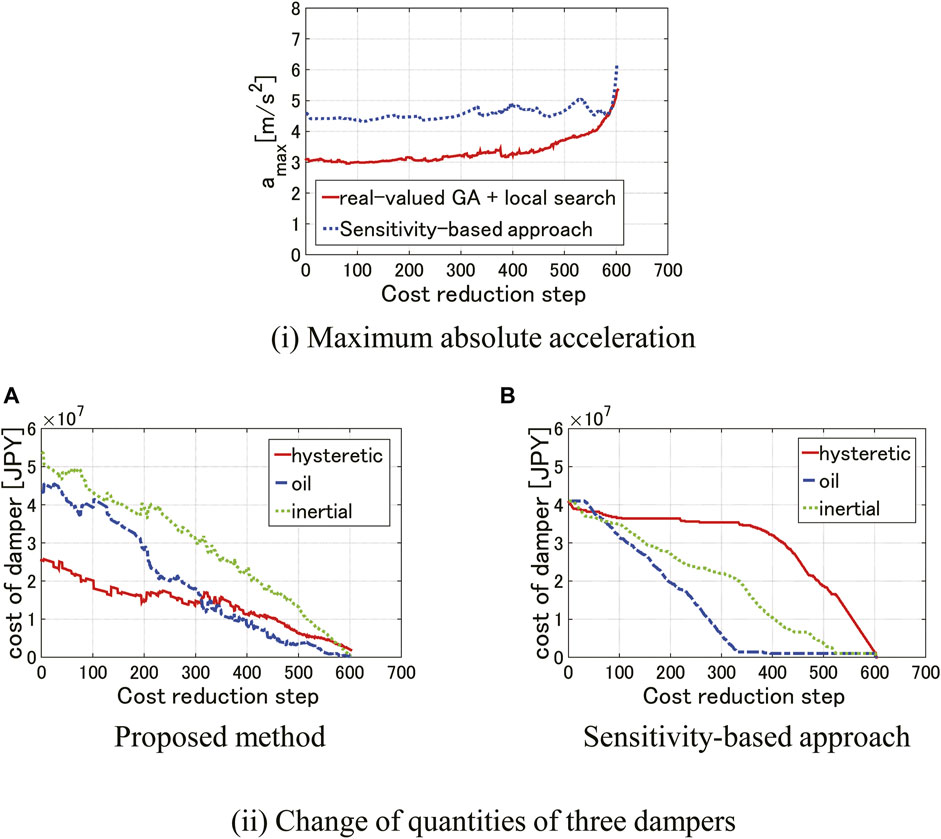
FIGURE 12. Comparison of change of maximum absolute acceleration and cost of dampers obtained by the proposed method with sensitivity-based approach by Murakami et al. (2013).

6 Multi-Objective Optimization Using Three Types of Dampers

6.1 Multi-Objective Optimization for Maximum Interstory Drift and Maximum Absolute Acceleration

The multi-objective optimization problem using three types of dampers for a N-story shear building model can be described as follows.

$\mathrm{minimize}\begin{array}{l}{f}_1={\widehat{D}}_{\max }(\left\{k_{dj}\right\},\left\{R_j\right\},\left\{c_{dj}\right\},\left\{z_j\right\})\\ f_2={\widehat{A}}_{\max }(\left\{k_{dj}\right\},\left\{R_j\right\},\left\{c_{dj}\right\},\left\{z_j\right\})\end{array}(38)$

$\begin{array}{cc}\mathrm{subject\; to}& Y_C{\displaystyle \sum _{j=1}^N{R}_j}+Y_K{\displaystyle \sum _{j=1}^N{k}_{dj}+Y_Z{\displaystyle \sum _{j=1}^N{z}_j}={\overline{C}}_d}\end{array}(39)$

${\widehat{r}}_{j\max }\le \overline{\alpha }(j=\mathrm{1,2},\cdots ,N)(40)$

The solution algorithm explained in Section 4 is extended to the multi-objective optimization.

Step 1. Put $i_C\to 1,i_{cr}\to 1$. Randomly generate $M_1(\ge 3N)$ individuals with constant total costs ${\overline{C}}_{d,i_C}$ $\left(=Y_C{\displaystyle {\sum }_{j=1}^N{R}_j+}{Y}_K{\displaystyle {\sum }_{j=1}^N{k}_{dj}+}{Y}_Z{\displaystyle {\sum }_{j=1}^N{z}_j}\right)$ of the dampers.

Step 2. Obtain $3n_{cr}N$ models by the crossover operator. The reciprocal number of the Pareto rank is applied to the fitness function in the roulette wheel selection (Fonseca and Fleming 1993).

Step 3. Randomly create $M_3$ models. Then choose $(M_1-M_3)$ models among the remaining $(M_1+3n_{cr}N)$ individuals by the roulette wheel selection. These $M_1$ models are selected as the individuals in the successive generation. Delete the data of the individuals whose Pareto ranks are more than one, and save the data of the individuals whose Pareto ranks are one. If $i_{cr}=I_{cr}$, evaluate the Pareto ranks of all the saved individuals, and delete the individuals whose Pareto ranks are more than one, then go to Step 4. Otherwise, put $i_{cr}\to i_{cr}+1$ and return to Step 2.

Step 4. Choose $M_4$ individuals by the roulette wheel selection and apply the local search operator to the $M_4$ individuals. Re-evaluate the Pareto ranks and delete the data of the individuals, whose Pareto ranks are more than one, each time when individuals are newly generated.

Step 5. Multiply $\left(\left\{R_j\right\},\left\{c_{dj}\right\},\left\{k_{dj}\right\},\left\{z_j\right\}\right)$ of the obtained individual by $({\overline{C}}_{d,i_C+1}/{\overline{C}}_{d,i_C})$ to create the new individuals with ${\overline{C}}_{d,i_C+1}$. If $i_C<I_C$, put $i_C\to i_C+1$ and return to Step 4. If $i_C=I_C$, finalize the process.

6.2 Application Example for 10-Story Shear Building Model

Consider a 10-story shear building model treated in Section 5. Other parameters are: initial value of total cost: $1.23\times {10}^8$ [JPY], decrement of total cost: $2.0\times {10}^5$ [JPY] ($I_C=600$), $Y_C$: 0.667 [JPY/N], $Y_K$: 0.001538 [JPY*m/N],: $Y_Z$: 8 [JPY/kg], story height: 3.5 [m], $n_{cr}$: 1, $I_{cr}$: 600, number of application of local search operator $n_{ls}$: 100, $S$: $0.03\times {\overline{C}}_d$, initial produced number of individuals $M_1$: $63(=6N+M_3)$, number of mutation individuals $M_3$: 3, $M_4$: $10(=N)$ .

The input ground accelerations are the same as in Section 5, i.e. El Centro NS (1940) and Hachinohe NS (1968) whose PGV = 0.50 [m/s]. The envelope value of the responses to these two input ground motions is employed as the response value for the optimization. Figure 13 shows the result of multi-objective optimization. Figure 13A presents the maximum interstory drift versus the maximum absolute acceleration at the 100^th step (total damper cost: $1.03\times {10}^8$ [JPY]) and Figure 13B illustrates the number of time-history response analyses with respect to the step number for only the real-valued GA and the proposed method. The obtained results can be summarized as follows.

FIGURE 13

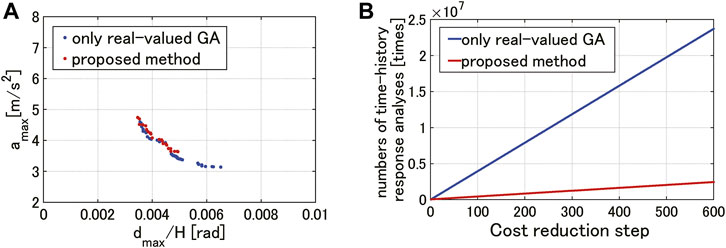
FIGURE 13. Result of multi-objective optimization, (A) Maximum interstory drift versus maximum absolute acceleration at 100^th step (total damper cost: $1.03\times {10}^8$ [JPY]), (B) Number of time-history response analyses with respect to step number for only real-valued GA and proposed method.

1) Hybrid use of three types of dampers can reduce the maximum interstory drift and the maximum absolute acceleration effectively than the case of single type use of dampers.

2) The Pareto solution by the proposed method is almost equivalent to that by only the real-valued GA. The proposed method can obtain an accurate solution with a shorter computational time by decreasing the dimension for search (without the damper cost as the design variable). In the present case, the number of time-history response analyses by the proposed method is one-tenth of that by only the real-valued GA.

It is noted that, when the sensitivity-based algorithm is applied to the weighted bi-objective optimization, the required number of time-history response analyses is $N_W$ times as many as that for the single objective optimization, where $N_W$ denotes the number of the combination of the weights. For example, when 11 combinations [0,1] [0.1, 0.9], … [1,0] are considered for the weight of the maximum interstory drift and the maximum floor acceleration, the bi-objective optimization requires the time-history response analyses 11 times as many as that for the single objective optimization. On the other hand, the required number of time-history response analyses for the multi-objective optimization by the GA-based algorithms including the proposed approach does not increase much compared with the case of the single objective optimization. Therefore, the proposed method can search the Pareto solutions for the multi-objective optimization more efficiently than the sensitivity-based algorithm, depending on $N_W$.

7 Conclusion

A method for global simultaneous optimization of oil, hysteretic and inertial dampers was proposed for building structures using a real-valued genetic algorithm and a local search. Simultaneous use of multiple kinds of passive dampers is required from the viewpoint of robustness and redundancy which play an important role under the circumstances of uncertain earthquake inputs and variabilities of damper properties. The conclusions can be summarized as follows.

1) The proposed approach consists of a real-valued GA and a local search. In the application of the proposed crossover procedure in the real-valued GA, the total costs of the added dampers are kept constant. A local search is conducted for high accuracy after the search by the real-valued GA. The proposed approach can provide a smaller maximum interstory drift than the sensitivity-based approach by Murakami et al. (2013). The proposed approach including the real-valued GA prevents from attaining a local minimum which is often reached by the sensitivity-based approach.

2) When the cost reduction step goes forward and a certain amount of dampers are removed from the initial total value, the sensitivity-based approach will work well within an allowable accuracy. On the other hand, the proposed approach including the real-valued GA can provide a better design even in the beginning stage

3) The proposed approach provides a small amount of inertial dampers from the beginning stage which are thought to be ineffective for the reduction of the maximum interstory drift, while it takes a certain amount of time for inertial dampers to be removed in the sensitivity-based approach. This indicates a clear preference of the proposed approach for the reduction of the maximum interstory drift over the sensitivity-based approach.

4) In reducing the maximum interstory drift, the effectiveness order is (i) hysteretic dampers, (ii) oil dampers, (iii) inertial dampers. The proposed approach can capture the mechanical properties of respective passive dampers in an accurate manner for the reduction of the maximum interstory drift from the beginning stage.

5) The proposed approach provides a smaller maximum acceleration than the sensitivity-based approach and works well also for the reduction of the maximum acceleration.

6) As in the reduction of the maximum interstory drift (item (2)), the proposed approach can provide a better design even in the beginning stage.

7) In reducing the maximum acceleration, the effectiveness order is (i) inertial dampers, (ii) oil dampers, (iii) hysteretic dampers. This property is a remarkable contrast to the case of reducing the maximum interstory drifts (item (4)).

8) A multi-objective optimization for deformation and acceleration was investigated. The Pareto optimal solution by the proposed method is almost equivalent to that by only the real-valued GA. The proposed method can obtain an accurate solution with a shorter computational time than the method using only the real-valued GA.

9) In the case of single objective optimization, the sensitivity-based algorithm requires a smaller number of time-history response analyses than the proposed method, although the latter reduces the objective function more effectively than the former (global optimality). In the case of multi-objective optimization, the proposed method requires a smaller number of time-history response analyses than the sensitivity-based algorithm, depending on the number of the combination of the weight coefficients of the objective functions.

In this paper, the cost ratios among three types of dampers were determined by the interview around 2012 and recently for structural engineers in Japan. A slight change of cost ratios may affect the optimization result, but the principal results on the preference of dampers will not be changed. The proposed method can be applied straightforwardly to other cost ratios once the data are available.

In the current building structural design, the concept of ‘resilience’ plays an important role. This means the preference of the structural design philosophy that the responses of buildings (especially tall buildings) under earthquake ground motions should be limited to the elastic range with the use of structural control technologies. The main objective of the present paper is to discuss the preference of different types of dampers from the viewpoints of structural performances (deformation and acceleration) and costs. However, since the investigation on the nonlinear response of building structures with inertial dampers under large-amplitude ground motions is of great interest (Patsialis et al., 2021; Talley et al., 2021), further discussion on the detailed behaviors of nonlinear building structures with inertial dampers under unexpected large-amplitude earthquake ground motions will be made in the future.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

RU formulated the problem, conducted the computation and wrote the paper. HA conducted the computation, discussed the results and wrote the paper. KF discussed the results and wrote the paper. IT supervised the research and wrote the paper.

Funding

Part of the present work is supported by the JSPS KAKENHI (No.18H01584). This support is greatly appreciated.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adachi, F., Yoshitomi, S., Tsuji, M., and Takewaki, I. (2013). Nonlinear Optimal Oil Damper Design in Seismically Controlled Multi-story Building Frame. Soil Dyn. Earthquake Eng. 44 (1), 1–13. doi:10.1016/j.soildyn.2012.08.010

CrossRef Full Text | Google Scholar

Akehashi, H., and Takewaki, I. (2021b). Global Optimization of Hysteretic Dampers for Elastic-Plastic MDOF Structures via Hybrid Approach of Real-Coded Genetic Algorithm and Local Search. J. Struct. Construction Eng. 86, 1335–1344. (in Japanese). doi:10.3130/aijs.86.1335

CrossRef Full Text | Google Scholar

Akehashi, H., and Takewaki, I. (2021a). Modeling of Resilience Based on Categorized Recovery Scenario and Improving Resilience with Viscous Damper. J. Struct. Construction Eng. 86, 577–588. (in Japanese). doi:10.3130/aijs.86.577

CrossRef Full Text | Google Scholar

Akehashi, H., and Takewaki, I. (2019). Optimal Viscous Damper Placement for Elastic-Plastic MDOF Structures under Critical Double Impulse. Front. Built Environ. 5, 20. doi:10.3389/fbuil.2019.00020

CrossRef Full Text | Google Scholar

Chitra, M. D., and Rugmini, B. K. (2020). Influence of Buckling Restrained Reinforcement on Behavior of Columns. Pract. Periodical Struct. Des. Construction 25 (4), 520. doi:10.1061/(ASCE)SC.1943-5576.0000520

CrossRef Full Text | Google Scholar

Christopoulos, C., and Filiatrault, A. (2006). Principle of Passive Supplemental Damping and Seismic Isolation. Italy: IUSS Press, University of Pavia.

Google Scholar

De Domenico, D., Ricciardi, G., and Takewaki, I. (2019). Design Strategies of Viscous Dampers for Seismic protection of Building Structures: A Review. Soil Dyn. Earthquake Eng. 118, 144–165. doi:10.1016/j.soildyn.2018.12.024

CrossRef Full Text | Google Scholar

Elias, S., Rupakhety, R., De Domenico, D., and Olafsson, S. (2021). Seismic Response Control of Bridges with Nonlinear Tuned Vibration Absorbers. Structures 34, 262–274. doi:10.1016/j.istruc.2021.07.066

CrossRef Full Text | Google Scholar

Eshelman, L. J., and Schaffer, J. D. (1993). Real-coded Genetic Algorithms and Interval-Schemata. Foundations of Genetic Algorithms Vol. 2, 187–202. doi:10.1016/b978-0-08-094832-4.50018-0

CrossRef Full Text | Google Scholar

Fonseca, C. M., and Fleming, P. J. (1993). Genetic Algorithms for Multiobjective Optimization: Formulation, Discussion and Generalization. Proc. Fifth Int. Conf. Genet. Algorithms, 416–423.

Google Scholar

Hanson, R. D., and Soong, T. T. (2001). Seismic Design with Supplemental Energy Dissipation Devices. Oakland, CA: EERI.

Google Scholar

Lavan, O., and Dargush, G. F. (2009). Multi-objective Evolutionary Seismic Design with Passive Energy Dissipation Systems. J. Earthquake Eng. 13 (6), 758–790. doi:10.1080/13632460802598545

CrossRef Full Text | Google Scholar

Liu, W., Tong, M., and Lee, G. C. (2005). Optimization Methodology for Damper Configuration Based on Building Performance Indices. J. Struct. Eng. 131 (11), 1746–1756. doi:10.1061/(asce)0733-9445(2005)131:11(1746)

CrossRef Full Text | Google Scholar

Movaffaghi, H., and Friberg, O. (2006). Optimal Placement of Dampers in Structures Using Genetic Algorithm. Eng. Computations 23 (6), 597–606. doi:10.1108/02644400610680324

CrossRef Full Text | Google Scholar

Muller, M. E. (1959). A Note on a Method for Generating Points Uniformly on N -dimensional Spheres. Commun. ACM 2 (4), 19–20. doi:10.1145/377939.377946

CrossRef Full Text | Google Scholar

Murakami, Y., Noshi, K., Fujita, K., Tsuji, M., and Takewaki, I. (2013). Simultaneous Optimal Damper Placement Using Oil, Hysteretic and Inertial Mass Dampers. Earthquakes and Structures 5 (3), 261–276. doi:10.12989/eas.2013.5.3.261

CrossRef Full Text | Google Scholar

Nakaminami, S., Kida, H., Ikago, K., and Inoue, N. (2017). Dynamic Testing of a Full-Scale Hydraulic Inerter-Damper for the Seismic protection of Civil Structures. Proc. 7^thInt. Conf. Adv. Exp. Struct. Eng. AESE, 41–54. doi:10.7414/7aese.T1.55

CrossRef Full Text | Google Scholar

Narayan , , and Pathak, K. K. (2022). Numerical Analysis of Multilevel Eccentric Chevron Braced Frame for Improved Inelastic Behavior. Pract. Periodical Struct. Des. Construction 27 (1). 647. doi:10.1061/(ASCE)SC.1943-5576.0000647

CrossRef Full Text | Google Scholar

Noshi, K. Yoshitomi, S. Tsuji, M., and Takewaki, I. (2013). Optimal Nonlinear Oil Damper Design in Seismically Controlled Multi-story Buildings for Relief Forces and Damping Coefficients, J. Struct. Eng. 59B.

Google Scholar

Palermo, M., Silvestri, S., Gasparini, G., Dib, A., and Trombetti, T. (2017). A Direct Design Procedure for Frame Structures with Added Viscous Dampers for the Mitigation of Earthquake-Induced Vibrations. Proced. Eng. 199, 1755–1760. doi:10.1016/j.proeng.2017.09.441

CrossRef Full Text | Google Scholar

Patsialis, D., Taflanidis1, A. A., and Giaralis, A. (2021). Tuned-mass-damper-inerter Optimal Design and Performance Assessment for Multi-Storey Hysteretic Buildings under Seismic Excitation. Bull. Earthq Eng. doi:10.1007/s10518-021-01236-4

CrossRef Full Text | Google Scholar

Pietrosanti, D., De Angelis, M., and Giaralis, A. (2021). Experimental Seismic Performance Assessment and Numerical Modelling of Nonlinear Inerter Vibration Absorber (IVA)‐equipped Base Isolated Structures Tested on Shaking Table. Earthquake Engng Struct. Dyn. 50, 2732–2753. doi:10.1002/eqe.3469

CrossRef Full Text | Google Scholar

Saeed, M. U., Sun, Z., and Elias, S. (2021). Research Developments in Adaptive Intelligent Vibration Control of Smart Civil Structures. J. Low Frequency Noise, Vibration Active Control., 146134842110327. doi:10.1177/14613484211032758

CrossRef Full Text | Google Scholar

Singh, M. P., and Moreschi, L. M. (2000). Optimal Placement of Dampers for Passive Response Control. Earthq. Eng. Struct. Dyn. 31, 955–976.

Google Scholar

Soong, T. T., and Dargush, G. F. (1997). Passive Energy Dissipation Systems in Structural Engineering. Chichester: John Wiley & Sons.

Google Scholar

Srinivasan, A. V., and McFarland, D. M. (2000). Smart Structures: Analysis and Design. Cambridge University Press.

Google Scholar

Taflanidis, A. A., Giaralis, A., and Patsialis, D. (2019). Multi-objective Optimal Design of Inerter-Based Vibration Absorbers for Earthquake protection of Multi-Storey Building Structures. J. Franklin Inst. 356, 7754–7784. doi:10.1016/j.jfranklin.2019.02.022

CrossRef Full Text | Google Scholar

Takewaki, I., and Akehashi, H. (2021). Comprehensive Review of Optimal and Smart Design of Nonlinear Building Structures with and without Passive Dampers Subjected to Earthquake Loading. Front. Built Environ. 7, 631114. doi:10.3389/fbuil.2021.631114

CrossRef Full Text | Google Scholar

Takewaki, I. (2009). Building Control with Passive Dampers: -Optimal Performance-Based Design for Earthquakes-. John Wiley & Sons.

Google Scholar

Takewaki, I., Murakami, S., Yoshitomi, S., and Tsuji, M. (2012). Fundamental Mechanism of Earthquake Response Reduction in Building Structures with Inertial Dampers. Struct. Control. Health Monit. 19 (6), 590–608. doi:10.1002/stc.457

CrossRef Full Text | Google Scholar

Takewaki, I. (1997). Optimal Damper Placement for Minimum Transfer Functions. Earthquake Engng. Struct. Dyn. 26 (11), 1113–1124. doi:10.1002/(sici)1096-9845(199711)26:11<1113:aid-eqe696>3.0.co;2-x

CrossRef Full Text | Google Scholar

Takewaki, I., Yoshitomi, S., Uetani, K., and Tsuji, M. (1999). Non‐monotonic Optimal Damper Placement via Steepest Direction Search. Earthquake Engng. Struct. Dyn. 28 (6), 655–670. doi:10.1002/(sici)1096-9845(199906)28:6<655:aid-eqe833>3.0.co;2-t

CrossRef Full Text | Google Scholar

Talley, P. C., Javidialesaadi, A., Wierschem, N. E., and Denavit, M. D. (2021). Evaluation of Steel Building Structures with Inerter-Based Dampers under Seismic Loading. Eng. Structures 242, 112488. doi:10.1016/j.engstruct.2021.112488

CrossRef Full Text | Google Scholar

Uetani, K., Tsuji, M., and Takewaki, I. (2003). Application of an Optimum Design Method to Practical Building Frames with Viscous Dampers and Hysteretic Dampers. Eng. Structures 25, 579–592. doi:10.1016/s0141-0296(02)00168-2

CrossRef Full Text | Google Scholar

Wang, S., and Mahin, S. A. (2018). High-performance Computer-Aided Optimization of Viscous Dampers for Improving the Seismic Performance of a Tall Building. Soil Dyn. Earthquake Eng. 113, 454–461. doi:10.1016/j.soildyn.2018.06.008

CrossRef Full Text | Google Scholar

Wesley Machado Cunico, M., and Desiree Medeiros Cavalheiro, J. (2019). Analysis and Optimization of the Effects of Frictional and Viscous Dampers on Dynamical Systems. J. Low Frequency Noise, Vibration Active Control. 38 (2), 255–269. doi:10.1177/1461348418821515

CrossRef Full Text | Google Scholar

Wongprasert, N., and Symans, M. D. (2004). Application of a Genetic Algorithm for Optimal Damper Distribution within the Nonlinear Seismic Benchmark Building. J. Eng. Mech. 130 (4), 401–406. doi:10.1061/(asce)0733-9399(2004)130:4(401)

CrossRef Full Text | Google Scholar

Zhang, R. H., and Soong, T. T. (1992). Seismic Design of Viscoelastic Dampers for Structural Applications. J. Struct. Eng. 118, 1375–1392. doi:10.1061/(asce)0733-9445(1992)118:5(1375)

CrossRef Full Text | Google Scholar