- 1Chair of Structural Analysis, Technical University of Munich, Munich, Germany
- 2Geobrugg AG, Romanshorn, Switzerland
- 3Appenzell Ausserrhoden, Department of Construction and Economics, Civil Engineering Office, Hydraulic Engineering, Herisau, Switzerland
- 4School of Civil Engineering, The University of Queensland, Brisbane, QLD, Australia
- 5International Center for Numerical Methods in Engineering, Technical University of Catalonia, Barcelona, Spain
Attenuator barriers, in contrast to conventional safety nets, tend to smoothly guide impacting rocks instead of absorbing large amounts of strain energy arresting them. It has been shown that the rock’s rotation plays an important role in the bearing capacity of these systems. Although experimental tests have to be conducted to gain a detailed insight into the behavior of both the structures and the rock itself, these tests are usually costly, time-consuming, and offer limited generalizability to other structure/environment combinations. Thus, in order to support the engineer’s design decision, reinforce test results and confidently predict barrier performance beyond experimental configurations this work describes an appropriate numerical modeling and simulation method of this coupled problem. For this purpose, the Discrete Element Method (DEM) and the Finite Element Method (FEM) are coupled in an open-source multi-physics code. In order to flexibly model rocks of any shape, sphere clusters are used which employ simple and efficient contact algorithms despite arbitrarily complicated shapes. A general summary of the FEM formulation is presented as well as detailed derivations of finite elements particularly pertinent to rockfall simulations. The presented modeling and coupling method is validated against experimental testing conducted by the company Geobrugg. Good agreement is achieved between the simulated and experimental results, demonstrating the successful practical application of the proposed method.
1 Introduction
Rock impact is an exceptional load case due to many factors. The shape, the density and the motion process itself of the impacting object can be arbitrary and difficult to predict. The additional dynamics and arbitrariness of the impact point make it impossible to determine a generally valid load assumption formula. This raises the question of how to design protective structures for such load cases. During rock impact events, protective structures are generally engineered to deform greatly, which reduces peak system decelerations and safely dissipates large amounts of energy.
In order to allow the protective structure to undergo large deformations, a wide variety of details (such as ring elements and braking elements in Figure 1B) are installed, the direct finite element modeling of which represents a demanding task.

FIGURE 1. All photos are property of Geobrugg (www.geobrugg.com). (A) Banya railway rockfall protection. (B) Monserrate walking path. (C) Kaikoura State Highway, Attenuator barrier. (D) Attenuator barrier after impact. Photo of the experiment discussed in section 3.
Rockfall protective structures may be divided into two different categories: active and passive measures. While near-surface nets (see Figure 1A) for slope stabilization represent a so called active measure and are easier to dimension, passive protective measures are installed as soon as the cause of the rockfall cannot be prevented. Passive protection structures are the focus of the present work and can in turn be divided into self-cleaning and non-self-cleaning (see Figures 1B,C). In the course of this work an experiment of an Attenuator barrier protective structure (illustrated in Figure 1D) is numerically replicated. The principle of an Attenuator is to intercept rockfall trajectories and attenuate their kinetic energy, while guiding the rockfall to a designated catchment area. These systems have been employed for several decades as described in Muhunthan et al. (2005) and were the subject of many field tests (Arndt et al., 2009; Glover and Ammann, 2016; Wyllie et al., 2016). An Attenuator barrier rockfall experiment program conducted by the company Geobrugg in 2017 is the primary experimental focus in this work.
Experiments confirm that the rotation of the impacting object has a substantial influence on the performance of Attenuator barriers. This behavior is further investigated with the help of numerical simulations in the present work. Throughout the experimental program, an accelerometer was installed in the center of the test objects and recorded data such as accelerations and angular velocities. Since the exact orientation of the rock at impact cannot be determined precisely, these data are only compared in terms of their general trends instead of exact values (see section 5.2). In order to better understand the interaction between impacting objects and highly flexible protective structures and to better answer practice-oriented questions, numerical methods are used. These allow a detailed insight into the structure, its utilization and have the potential to show optimization possibilities. By employing coupled simulations, different numerical methods, each with their individual strengths and domain of application, may be brought together to model and analyze the interaction of different physical problems.
The present work couples the Discrete Element Method (DEM) with the Finite Element Method (FEM) to simulate the interaction between impacting objects and highly flexible protective structures. The DEM is used to simulate the impacting object while the FEM is used to calculate the appropriate dynamic structural response. The advantages of this choice of simulation methods are explained in the following sections. To demonstrate the accuracy and applicability of the aforementioned coupling strategy the 2017 Geobrugg experimental program is modeled and simulated. The resulting data show good agreement with the experimental data demonstrating the efficacy of the numerical method, as well as confirming the effectiveness of the Attenuator barrier design. Two different experiments are simulated to guarantee the validity and applicability of the method presented here.
The discrete element method is a discrete particle method with unique strengths in analyzing the movement and interaction of individual particles. The method was first proposed by Cundall and Strack (1979) and has been increasingly adopted since. Matuttis and Chen (2014) describe in detail the underlying theories of DEM while many publications deal with the precise analysis of contact formulations. Special mention should be made of Shäfer et al. (1996) who has done some fundamental work in this topic. Building on this, Schwager and Pöschel (2007); Cummins et al. (2012); Thornton et al. (2012) have described improved formulations and contact models, contributing to the current state of the art. A detailed description of contact search and calculation of contact between discrete spherical particles and boundary conditions discretized by finite elements was provided by Santasusana (2016), Santasusana et al. (2016) which lay the foundation for the present work. Gao and Feng (2019) extended this idea by exchanging the FEM with the isogeometric method, however, this is not expected to confer any advantages for this paper’s scope. Irazábal et al. (2019) conducted a detailed investigation of suitable time integrators, especially with regard to the integration of the rotational motion, which is of great importance in the present case. Specifically related to the case of rockfall Chau et al. (2002) studied the appropriate coefficient of restitution for rockfall events. The use of simple spherical particle clustered together to describe arbitrarily shaped objects in DEM was formulated by Madhusudhan et al. (2009) and subsequently employed by Sautter et al. (2021) for the analysis of rotation-free rockfall events. This flexible modeling strategy, employed in this paper, allows the use of simple contact algorithms without sacrificing the approximate modeling of irregular rock geometries. As already mentioned, experiments confirm that the rotation of the impacting objects has a large influence on the overall behavior of the impact, which is why the shape of the rock has to be taken into account. Disc shaped one for example have normally much higher rotational energy compared to cube shaped blocks.
The FEM is used to numerically solve partial differential equations to analyze continuous, deformable bodies. For the interested reader, notable FEM references include Basar and Weichert (2000), Belytschko et al. (2000), Holzapfel (2010). A general FEM summary follows in subsection 2.2 that also includes a detailed derivation of the finite element formulations used in this work.
The coupling of the finite element and discrete element numerical methods builds on the work of Santasusana (2016), Santasusana et al. (2016) and was continued in Sautter et al. (2020). The implementation is in an open source multi-phyiscs code called KRATOS based on the work of Dadvand et al. (2010), Dadvand et al. (2013); Ferrándiz et al. (2020). The importance of an open source solution for the analysis and assessment of natural events such as rockfall [studied in detail by Volkwein (2004), Volkwein (2005); Zhao et al. (2020b)], strong wind [fluid-structure interaction described by Wüchner (2006)] and debris flows [discussed in detail by Wendeler (2008), von Bötticher (2012), Zhao et al. (2020a)] cannot be overemphasized. In combination with the detailed description of element formulations, contact algorithms, and coupling methods this work offers the possibility to carry out independent analyses of any rockfall events and the evaluation of suitable protective structures.
In principle, it is conceivable to employ other particle methods for the analysis and simulation of the impacting objects. In contrast to DEM, the Material Point Method (MPM) and the Particle Finite Element Method (PFEM) are continuum-based particle methods. Due to their continuum-based approach, both methods possess particular strengths compared to DEM, for example, in the modeling of debris flows or avalanches. Due to the properties of rockfall, DEM is preferable in this case [see also Lisjak and Grasselli (2010), Lisjak et al. (2010). Further information on MPM can be found in Zhang et al. (2016), Chandra et al. (2019), Larese et al. (2020), Wilson et al. (2020), while Salazar et al. (2015), Larese (2016) describe PFEM.
A comprehensive review and prospective on the subject of the simulation of rockfall protection systems is given in Volkwein (2004), Volkwein (2005) and represents the basis for the current state of the art. The work lead to Escallon et al. (2015) describing highly detailed modeling of flexible protection structures and their components. The exact modeling of the individual components often turns out to be overhead, especially when the global structural behavior is of interest. In order to reduce the complexity of the simulations while accurately analyzing protection structure components at selected local areas, a hybrid model is described in Tahmasbi et al. (2019). The idea is to use a simple element formulation in the boundary regions of the protective structure while local locations of interest are modeled with the formulations from Escallon et al. (2015). Other works by Sasiharan et al. (2006), Dhakhal et al. (2011), Mentani et al. (2018) among others, also employ the concept of representing the complex protection structure with a simpler surface description composed of shell and isotropic membrane elements (Tahmasbi et al., 2019). In the present work, we will take up the idea of membrane elements, and incorporate the anisotropic material law of Münsch and Reinhardt (1995) to represent the different behavior in the two main directions that can be observed in experiments.
From a formal point of view, the structure of the paper is as follows:
• Section 2 briefly describes the underlying coupling theory and the respective components in this multi-physics simulation. A summary and description of the finite element formulations used within this work is added in subsection 2.2.
• Section 3 discusses the 2017 Geobrugg experiment used for validation and calibration.
• Section 4 presents the modeling of the numerical simulation used to replicate the experiment. Both the modeling of the structure itself (in subsection 4.1) and the modeling of the impacting object (in subsection 4.2) are covered.
• Section 5 illustrates the numerical examples and their results across displacements (in subsection 5.1), translational velocities (in subsection 5.3), and angular velocities (in subsection 5.2).
• Section 6 finalizes this work with a conclusion and an outlook for future research.
2 DEM-FEM Coupling
To realize the coupled simulation, the DEM and the FEM are coupled in a staggered framework, summarized in subsection 2.3 [refer to Sautter et al. (2020) for full details], which allows the use of any two standalone solvers for the DEM and the FEM components. In principle, many different methods can be used to analyze the problem at hand. In order to find the combination of suitable methods, one has to think about the general characteristics of the problem at hand. Rockfall is a discrete event, so one must be able to model discrete objects. This can be solved with the FEM, as shown by Volkwein (2004), Volkwein (2005), Sasiharan et al. (2006), Dhakhal et al. (2011), Escallon et al. (2015); Mentani et al. (2018), Tahmasbi et al. (2019). The surface of the discrete objects is modeled with the help of points, lines, and surfaces. If one now wants to find the contact to a structure that is also modeled with points, lines, and surfaces, very complex contact algorithms are necessary. The contact between surface/surface, surface/line, and line/line is sometimes very demanding and computationally intensive. If, on the other hand, a particle method is used that represents/approximates the discrete objects as simple spheres, the contact check is extremely simplified, see the work by Santasusana (2016), Santasusana et al. (2016). Contact algorithms for the combination sphere/surface, sphere/line, and sphere/vertex are very effective and fast to perform. By using clusters of spherical particles, arbitrarily shaped objects can be modeled despite the efficient contact algorithms for spheres (Sautter et al., 2021) describes the successful application of these clusters already for the simulation of other types of rockfall protection systems]. To decide on the appropriate particle method, it is again helpful to look at the discrete characteristics of the rockfall event. Other particle methods such as MPM [first proposed by Sulsky et al. (1994)], PFEM (Cremonesi et al., 2020), or Smoothed-Particle Hydrodynamics(SPH) [first proposed by Gingold and Monaghan (1977), Lucy (1977)] are particularly suitable for the simulation of non-discrete natural events such as debris flows, avalanches, or shallow landslides. For this reason, DEM is chosen to model and simulate the impacting objects (in this case rocks). To model the structure the FEM is used, as it has proven to be very effective and well established. It allows to model special structural elements and to effectively assess structural stress and deformation states. With the help of the coupling environment in KRATOS [see Dadvand et al., (2010), Dadvand et al., (2013), Ferrándiz et al. (2020)], which we co-developed, these methods can be efficiently combined with each other, providing a suitable simulation environment for the problem at hand. Subsection 2.1 briefly describes the DEM and introduces key aspects to give a general overview of the topic. The FEM is briefly summarized in subsection 2.2 which includes detailed descriptions of the element formulations employed in this study. Throughout this work, bold symbols indicate tensors while italics denote scalars.
2.1 DEM
In contrast to continuum-based particle methods like the MPM (Zhang et al., 2016; Chandra et al., 2019; Larese et al. 2020; Wilson et al. 2020]) or the PFEM, the DEM is a numerical method to simulate the motion and interaction of discrete particles. Since Cundall and Strack (1979) introduced the first considerations regarding DEM, the method has been increasingly adopted for the analysis of discrete particles both in research and industry. The motion and interaction between particles and also between particles and finite element discretized boundary conditions can be simulated very effectively, see Santasusana (2016), Santasusana et al. (2016). In the present work only spherical particles are used which reduces the effort of contact search with arbitrary geometries enormously and thus leads to a very efficient simulation method. Although spherical particles are unable to model complex geometries by themselves, this work combines spherical particles together into clusters to model complex rock geometries while still using the simple contact search of the spherical particles. Madhusudhan et al. (2009) has studied these in detail and Sautter et al. (2021) has already used clusters of spheres for simple rockfall events. Chapter 4.2 describes in detail how this strategy is used in the simulation.
The search for contact with spherical particles has been studied in detail and is exhaustively discussed in Santasusana (2016), Santasusana et al. (2016). Each particle has a radius
As soon as contact is detected, contact forces are calculated. There are a number of different contact laws available, and the user has to select the most appropriate for the current case at hand. In this work a Hertz-Mindlin spring-dashpot contact model was used (abbreviated with HM + D). The corresponding rheological model is shown in Figures 2A,B. To calculate the contact force, the normal and tangential spring stiffness
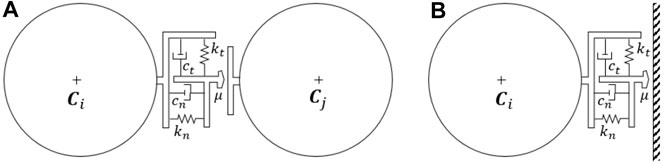
FIGURE 2. (A) DEM-DEM rheological model adapted from Santasusana (2016). (B) DEM-FEM rheological model adapted from Santasusana (2016).
Finally the equation of motion according to Newton’s second law is integrated in time and one advances to the next time step.
More detailed descriptions of the DEM can be found in Santasusana (2016), Santasusana et al. (2016). Matuttis and Chen (2014) provide an overview of the whole method and also discuss the use of non-spherical particles. A detailed discussion of appropriate time integrators may be found in Irazábal et al. (2019) while Schwager and Pöschel (2007), Cummins et al. (2012), Thornton et al. (2012), Shäfer et al. (1996) discuss the modeling of non-elastic collisions and the appropriate choice of the coefficient of restitution.
2.2 FEM
The FEM is used in this work to discretize the protective structure. As described in Belytschko et al. (2000), Holzapfel (2010), the virtual work
As depicted in Eq. 1 the second Piola-Kirchhoff stress
This equilibrium is solved numerically with a Newton’s type iterative solution technique operating on linearized virtual work components as discussed in Belytschko et al. (2000). Internal element forces
Additionally, the tangent stiffness matrix
is often needed for Newton’s type solution schemes [see also Belytschko et al. (2000), Holzapfel (2010)].
In the subsequent sections lower case symbols represent quantities in the current configuration (
In view of complex protective structures, such as Attenuator barriers, the structure must be modeled accurately with attention to detail. This work introduces the application of two unique finite element formulations to be used in the simulation of such structures: the sliding cable element and the plane-stress membrane element.
2.2.1 Sliding Cable Element
Compliant structures, such as Attenuator barriers rely on the ability of large deformations to reduce peak decelerations and withstand impacting objects. One feature which is used to realize large deformations is the “loose” connection of the net to upper ropes as illustrated in Figure 3. The net is connected orthogonal to the dark blue support rope but is allowed to slide along the rope, impeded only by friction.
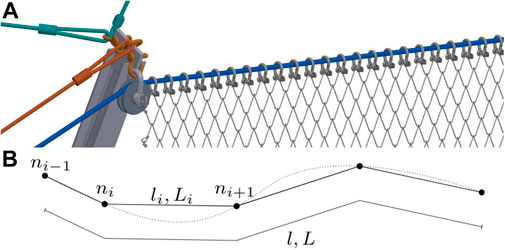
FIGURE 3. Upper support rope. (A) Installation taken from Geobrugg (2019). (B) Sliding cable element, FEM discretization.
To properly model this behavior in a FEM simulation a sliding cable element formulation [Volkwein (2004), Boulaud and Douthe (2017)] is employed, which also enables to integrate a deflection roller into the simulation (left side of Figure 3A).
Instead of single linear cable elements connecting the nodes
As described in Belytschko et al. (2000), Holzapfel (2010) these quantities are used to express the 1-dimensional Green-Lagrange strain ε, and the 1-dimensional
with the help of the Young’s Modulus E. Including the prestress
where A represents the reference cross-section of the cable element. Following the derivation in Boulaud and Douthe (2017) an explicit formulation for
Here n denotes the total number of nodes and the coordinates
Additionally, the friction is included and needs to be evaluated at each discrete node in the element by first calculating an equal and opposite force
To validate the correct implementation of the sliding cable element, a simple gravity driven impact simulation is illustrated in Figures 4A,B, demonstrating the expected large sliding deformation of the net shackles.
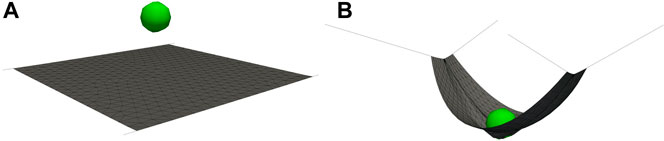
FIGURE 4. Sliding cable elements on two opposing sides applying the tension field theory, described by Nakashino and Natori (2005), to exclude compression stiffness from the plate in membrane finite elements. (A) Reference configuration, fixed on four corner nodes. (B) Sliding cable element formulation allows for a sliding of the discrete element nodes.
Alternative solutions to enable the sliding of nodes along a cable element can be achieved using the penalty method [see Bauer et al. (2018)], Lagrange multipliers [see Holzapfel (2010)], or multi point constraints (MPC) as described in Abel and Shephard (1979). While the first two methods minimize the orthogonal distance between an arbitrary node and the axis of the sliding cable, the MPC approach directly couples degrees of freedom in such a way that the node travels along the desired path. Compared to these abstracted approaches, the sliding cable formulation, which inherently represents sliding nodes in its formulation, is the most robust solution to the problem presented and adopted in this work.
2.2.2 Plate in Membrane Action
As described in Sasiharan et al. (2006), Dhakhal et al. (2011), Sautter et al. (2021) membrane finite elements are suitable to approximate the behavior and response of rock-fall cable nets. With respect to the mesh geometry illustrated in Figure 6C, an anisotropic material law defined in Eq. 11 appropriately describes the net’s direction-dependent behavior and is employed henceforth.
Derivation of the 2-dimensional plane-stress membrane element within 3-dimensional space commences by defining the general covariant base-vectors that span an arbitrary angled local coordinate system
in which the standard FEM shape functions
Belytschko et al. (2000) notes that these arbitrary base-vectors are not necessarily orthonormal and are used to calculate the Green-Lagrange strain tensor
where
In order to express the elastic stress-strain relation
The anisotropic elastic consistent linearized tangent modulus
Since the
The covariant strain coefficients
2.3 Coupling Procedure
A partitioned coupling approach is employed to couple independent discrete element and finite element methods together in this work. Felippa et al. (2001) note that partitioned solution schemes possess the notable benefits of software modularity and also application of the most appropriate discretization and solution techniques to each individual component. Although this approach allows the use of arbitrary DEM and FEM codes, the user must consider the coupling of the two. Santasusana (2016) has already discussed this in detail and Sautter et al. (2020) has continued this coupling by introducing an additional Gauss-Seidel loop on the interface
all of which are dependent on the time t. Figure 5 describes the use of additional iteration loops at each time step to achieve the convergent strong coupling as described by Sautter et al. (2020) (which also includes more details of the coupling).
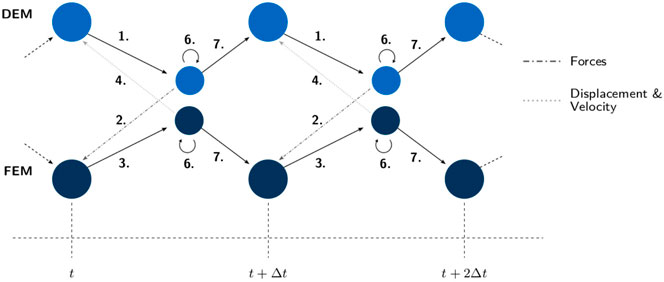
FIGURE 5. Strong coupling communication diagram from Sautter et al. (2020). With t as the current time and
The steps in Figure 5 are summarized below:
1. Solve DEM component to obtain the contact force.
2. Map the forces to the structure.
3. Solve the structure with FEM to obtain nodal displacements, velocities and accelerations.
4. Map displacements, velocities and accelerations back to the discretized boundary in the DEM solver.
5. If necessary: Calculate interface residuals as described by Küttler and Wall (2008), Winterstein et al. (2018), Sautter et al. (2020) among others.
6. If necessary: Repeat steps 1–5 until Eqs 15–17 are satisfied to a given tolerance.
7. Advance in time to next time step.
3 2017 Geobrugg Rockfall Experiments
In 2017 the Swiss company Geobrugg conducted an experimental program to confirm the effectiveness of a novel SPIDER mesh (Geobrugg, 2020). The following section is a brief summary of key test aspects relevant for numerical replication, refer to Hofmann et al. (2019) for full testing details.
3.1 Test Site
The test site was a near-vertical approximately 60 m high slope situated in a disused granite quarry in British Columbia, Canada. The Attenuator design investigated was the hanging net style with limited slope contact of the netting as per Figure 6A. The test set up consisted of three 8 m steel posts set 9 m apart and anchored to the slope with six retention ropes, two lateral support ropes, and one top rope penetrating through the post heads. The netting is attached to the top rope with shackles in each mesh opening as detailed in Figure 3A. Three principal zones of attenuation were investigated by varying the impact, transition, and collection zones of the high tensile steel wire nets. The experiments of 2017 are described in greater detail in Hofmann et al. (2019).

FIGURE 6. Experiment setup. (A) Additional weight at the bottom of the protection net to ensure a more controlled structural deformation. (B) Photo of the impacting object T092 (some damage can be observed). The visible metal cap covers the housing of the motion sensors. (C) Technical drawing of the SPIDER® S4-130, taken from Geobrugg (2020),
3.2 Site Survey and Rockfall Modeling
A terrain survey of the site was performed by Truline Survey in 2016 which was used as basis for rockfall modeling to adapt the Attenuator geometry between the testing series of 2016 and 2017. Particularly relevant to this paper, Sautter et al. (2020) demonstrates how such terrain models may be incorporated into simulations to further enhance accuracy and predictive confidence.
3.3 Impacting Object
The rocks used for testing were either granite blocks of various characteristic shapes (such as cubic, angular, and disc-like) or prefabricated concrete blocks with a special housing in the center for rock motion sensors (see Figure 6B). The blocks and rocks were then released by an excavator on top of the slope. The rocks bounced 3–4 times on the granite slope before impacting the netting.
3.4 Instrumentation
Experimental instrumentation included load-cells in all ropes, high-speed cameras filming the block’s trajectory from different angles and rock motion sensors in the concrete blocks. This work will predominantly focus on the trajectory path, translational velocity and rotational velocity experimental data collected.
3.4.1 High Speed Cameras
Analysis of the high speed camera videos with a sampling rate of 500 fps facilitated quantification of the rockfall dynamics. By tracking the position of the block through time a translational velocity could be obtained and the tracking of every
3.4.2 Rock Motion Sensors
The rock motion sensors measured the accelerations and rotations of the block about its three axes for the duration of each test. A comparison of the angular velocity obtained from the video analysis and the rock motion sensor shows good agreement and therefore provides confidence in the translational velocity data estimated by video analysis.
3.5 Tests Used for Numerical Validation
The tests used to validate the modeling and simulation used a Geobrugg SPIDER S4/130 mesh [described in Geobrugg (2020) and visualized in Figure 6C]. Additional weights in the form of steel bars were shackled to the bottom of the mesh (see Figure 6A) to increase the inertia and vertically pre-tension the system and is incorporated in the simulation with additional point masses (discussed in subsection 4.1.1). The middle post was slightly bent after sustaining two rock impacts in previous tests, but the integrity and function of the system was not compromised, accordingly testing was continued, but it was chosen to incorporate it anyway in the modeling of the structure. The blocks used during the test, were a near-cubic
Key experimental data pertinent to numerical replication including translational and rotational velocity at the time of netting impact and the rock’s path and mass are summarized in subsection 4.2.
4 Numerical Modeling
4.1 Structural Modeling
Figure 7 is adapted from Geobrugg (2019) and depicts the respective participants in the simulation, each of which are discussed below.
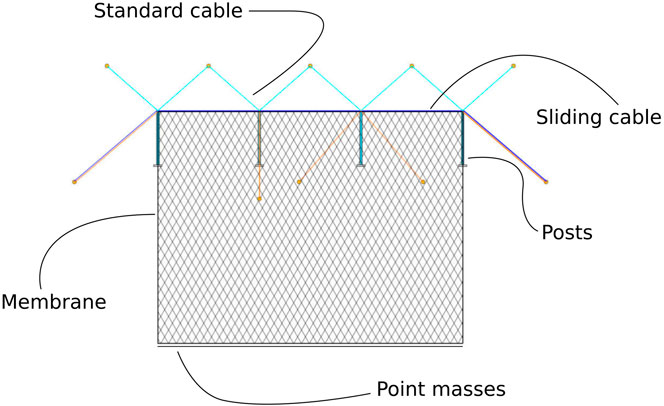
FIGURE 7. Participants in the FEM model, adapted from Geobrugg (2019).
Due to the small time steps necessary to resolve the impact, an explicit time integration scheme was selected (instead of an implicit scheme). The central-difference explicit scheme as described by Belytschko et al. (2000) was used to conduct the numerical time integration of the structural response with a time step of
4.1.1 Point Masses
The additional weights at the bottom of the protection net, depicted in Figure 6, are modeled with single point masses (summing to an additional total mass of
4.1.2 Sliding Cable Element
Modeling of the upper support rope, illustrated in Figure 3, demands a sophisticated element formulation, which is discussed in subsection 2.2.1. This formulation allows internal nodes to slide along the element, while internal forces are calculated based on the change of the total length, as discussed in Volkwein (2004); Boulaud and Douthe (2017). The following structural properties, based on construction plans in Geobrugg (2019), were applied in the simulation: Young’s Modulus
4.1.3 Standard Cable Element
Bracing cables, modeled with standard cable elements, are anchored in the rock and connected to strategically selected points on the supports of the protective structure. As presented in Belytschko et al. (2000), a 1-dimensional truss element formulation is applied and combined with an additional check for compression stresses in the element. If such stresses are detected the elemental stiffness contribution is temporarily eliminated from the global system of equations. Realistic structural properties were also obtained from construction plans provided in Geobrugg (2019) and listed in the following: Young’s Modulus
4.1.4 Posts
The posts, which predominantly carry vertical loads to support the protective structure, are simply supported in the rock. At the top they are connected to both the upper support rope as well as the bracing cables (seeFigure 3). In accordance with Belytschko et al. (2000), these posts may be suitably modeled as 1-dimensional truss elements (neglecting any initial damaged bending), with the following data: Young’s Modulus
4.1.5 Protection Net
Due to the set-up of the experiment, similar to the set-up in Sautter et al. (2021), and the complicated geometry of the SPIDER net system (see Figure 6C), the net has been idealized as a closed homogeneous surface discretized with plane-stress membrane finite elements. Publications such as Mentani et al. (2018), Tahmasbi et al. (2019) suggest shell elements to be used, although they introduce additional complexity and computational expense compared to membrane elements. In the interest of simplicity, membrane elements described in subsection 2.2.2 were employed, which, considering the good agreement achieved with experimental results in section 5, appear sufficiently accurate for the present study.
The following properties, determined from the mesh technical drawing in Figure 6C, technical data sheets (Geobrugg, 2020) and proprietary Geobrugg experimental tensile tests, were applied to membrane elements for the simulation: Thickness
Although the material behavior is in principle non-linear, the large deformations are predominantly rigid and accompanied by small strains, justifying the assumption of linear elastic material behavior.
By comparing Figures 8A,B a perfect agreement between the reference computer model and the real structure cannot be achieved as some posts in Figure 8B are already damaged. Additionally, the position and alignment of the supporting structure is unlikely to exactly match construction plans.

FIGURE 8. Deformation panel after dead-load equilibrium (before impact). (A) Simulation. (B) Experiment photographed just before impact.
4.2 Impacting Object
In contrast to preceding works, such as Volkwein (2004), Volkwein (2005), Mentani et al. (2018) this work follows Sautter et al. (2021) to flexibly model arbitrary objects with discrete spherical element clusters. The advantage compared to standard finite element discretized objects is the simplified contact detection between arbitrary boundary objects and single spheres contained in the cluster as described by Santasusana et al. (2016). Figure 9 presents the DEM cluster models used within this work, and Figure 6B shows the real impacting object. While the clusters in Figures 9A,B represent the test object T092, Figures 9C,D show the cluster approximation of the test object T089. A study on the proper refinement level of such clusters can be found in Sautter et al. (2021). Special algorithms are required to create the refined cluster file, with this work employing the algorithms described in Bradshaw and O’Sullivan (2002), Bradshaw and O’Sullivan (2004) available in an online toolkit [http://isg.cs.tcd.ie/spheretree/].

FIGURE 9. Cluster of spheres to model impacting objects. (A) Test object T092 front view. (B) Test object T092 perspective view. (C) Test object T089 front view. (D) Test object T089 perspective view.
Within this work several DEM particle properties are varied and their influence on the simulation result is studied, namely the friction, coefficient of restitution, and Young’s Modulus. Contrasting this, the following physical properties are constant throughout all simulation runs:
-T092
-Mass
-Dimension
-Impact translational velocity horizontal
-Impact translational velocity vertical (gravity direction)
-Impact rotational velocity
-T089
- Mass
-Dimension
-Impact translational velocity horizontal
-Impact translational velocity vertical (gravity direction)
- Impact rotational velocity
Comparing Figures 6B, 9A it can be observed that the testing objects have already suffered damage from previous experiments. When comparing the simulation results with the ones obtained by the experiment in section 5 this unavoidable difference should be considered.
An explicit central-difference scheme as described by Matuttis and Chen (2014) was used to conduct the numerical time integration of the translational velocity of the cluster with a time step of
5 Validation
The following section presents the simulated Geobrugg 2017 experiment results to ascertain the practical applicability and accuracy of the aforementioned numerical modeling approaches and technologies.
For clarity, key assumptions and uncertainties discussed in the preceding sections are summarized below:
- The exact impact location was estimated from video records.
- The model of the protective structure is taken from construction plans. However, it can be seen from photos and video recordings that the actual structure is partially crooked and already shows damage.
- The reference angular orientation
- Three further DEM specific parameters cannot be taken unambiguously from the test and have to be varied to study their influence. Young’s Modulus
- As visualized in Figure 6B the impacting test object already shows damage, which will be neglected in the modeling of the DEM sphere cluster.
The rock trajectory and the general trends of angular and translational velocities are used for comparison with the experiment.
5.1 Trajectories
The most reliable and functionally-important comparison is the simulated versus experimental rock trajectory. Attenuator barriers are used to protect exposed areas such as motorways from falling rocks, therefore the path of the object is of particular interest. In the following investigation the unknown model parameters were varied to check their influence on the results of the test run T092. To validate the results the test T089 was simulated subsequently with the best suitable parameters obtained from the investigation of T092. Figures 10, 11 illustrate the influence of the DEM parameters for T092 (which are not clearly defined and have to varied to study their influence).
- In Figure 10A the coefficient of restitution is varied between
- In Figure 10B the friction is varied between
- In Figure 11A the Young’s Modulus is varied between
- In Figure 11B the reference angular orientation is varied between
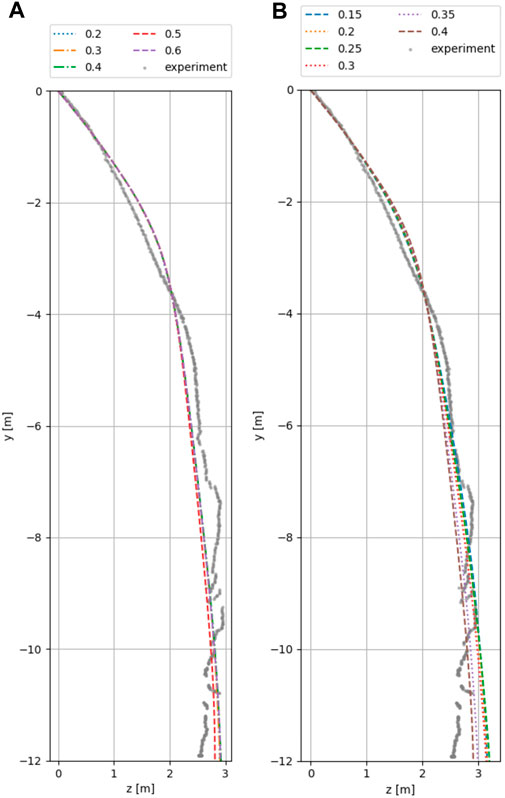
FIGURE 10. Visualization of object path for varying parameters for T092. (A) Coefficient of restitution. The result data for
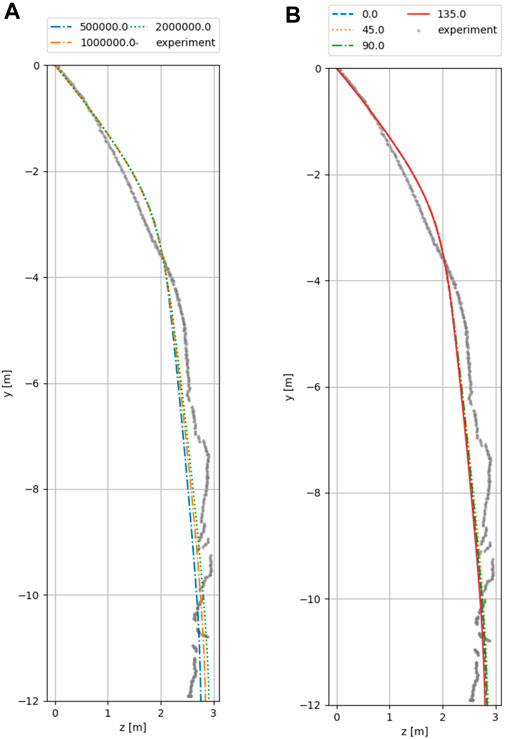
FIGURE 11. Visualization of object path for varying parameters for T092. (A) Young’s Modulus
While the deformation of the impacting object is not of interest for this study the so-called Young’s Modulus
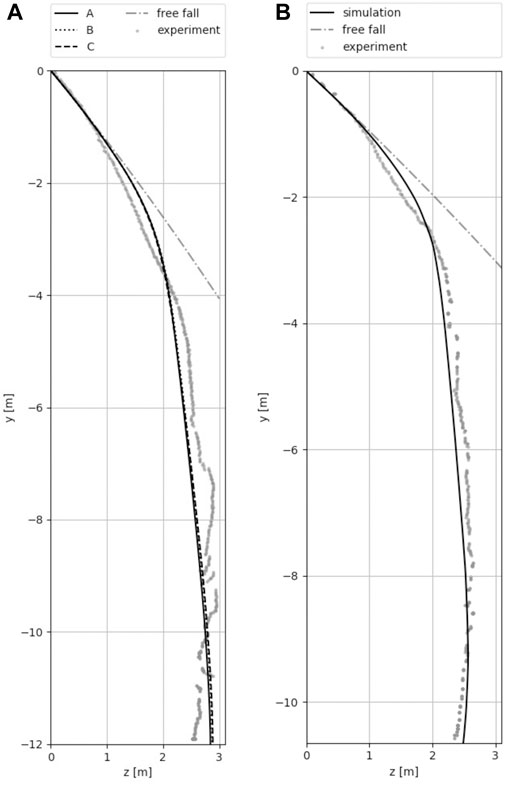
FIGURE 12. Visualization of object path. Additionally, the free fall trajectory is added to demonstrate the correctness of the object path at the beginning of the simulation and the effectiveness of the Attenuator barrier. (A) The three optimal parameter combinations for T092. The solution for parameter set B is very similar to the one for parameter set A and thus not easily distinguishable. (B) T089 with parameter set C.
An initial observation is that all variations give very good agreement with the test results for T092 and accurately predict the final position of the rock with a maximum error of +10%. While varying the reference angular orientation seems to have the least influence (see Figure 11B) the proper choice of a suitable friction value strongly influences the simulation as shown in Figure 10B. This sensitivity is expected as this experiment heavily depends on the rotation of the impacting object. The variation of the Young’s Modulus in Figure 11A as well as the variation of the coefficient of restitution in Figure 10A show little influence, likely since the Attenuator barrier primarily retards via kinetic energy instead of strain energy.
In the following, only the three best parameter variants for T092 will be discussed, as the quality of the trajectories allows direct conclusions to be drawn about the correctness of the respective velocities. The three optimal parameter combinations are presented in the following list and their trajectories are visualized in Figure 12A together with the path of a free falling object to demonstrate the efficacy of the Attenuator barrier.
- Parameter set A:
- Friction
- Coefficient of restitution
- Young’s Modulus
- Reference angular orientation
- Parameter set B:
- Friction
- Coefficient of restitution
- Young’s Modulus
- Reference angular orientation
- Parameter set C:
- Friction
- Coefficient of restitution
- Young’s Modulus
- Reference angular orientation
The data obtained from the simulations is not only in strong accordance with the experiment results but also clearly demonstrates the effectiveness of the herein presented Attenuator barrier. A rock at height of
The results, which are shown in Figure 12B relate to the simulation of T089 with the parameter set C of T092. It can be clearly seen that the experimental results are properly re-produced without any further need of parameter investigation. This ensures that this parameter set can be used to recalculate further scenarios and creates confidence in the accuracy and applicability of the study presented here.
5.2 Angular Velocity
The experimental observations presented in Figure 13A illustrate the impacting object angularly decelerating and subsequently accelerating in the opposing angular direction. Unfortunately, the experimental data do not provide any information about predominate rotation axis, the individual rotation components of each axis, or the rotational orientation of the specimen at the time of impact. Nevertheless, it is useful to compare the general rotation behavior with the simulation results, with Figure 13B illustrating the simulation exhibits the same rotational trend as the experiment in Figure 13A. Additionally, Figure 14A visualizes the angular velocity about one of the main axes of the impacting object, which clearly illustrates the time period in which the aforementioned deceleration and subsequent acceleration take place. The same behavior can be observed in Figure 14B, which depicts the general trend of the angular velocity obtained from the experiment.
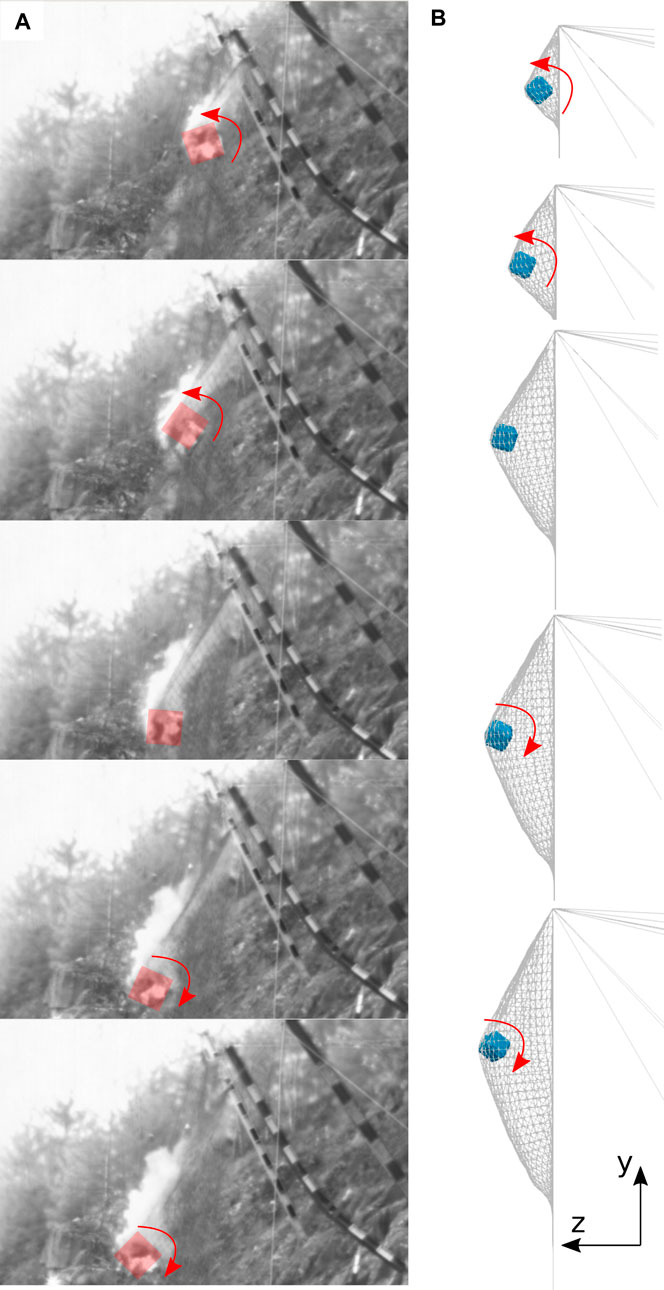
FIGURE 13. The test object impacts with a certain angular velocity, stops rotating, slides for a short time period and starts rotating in the opposite direction subsequently. (A) Photos from the experiment. (B) Simulation.
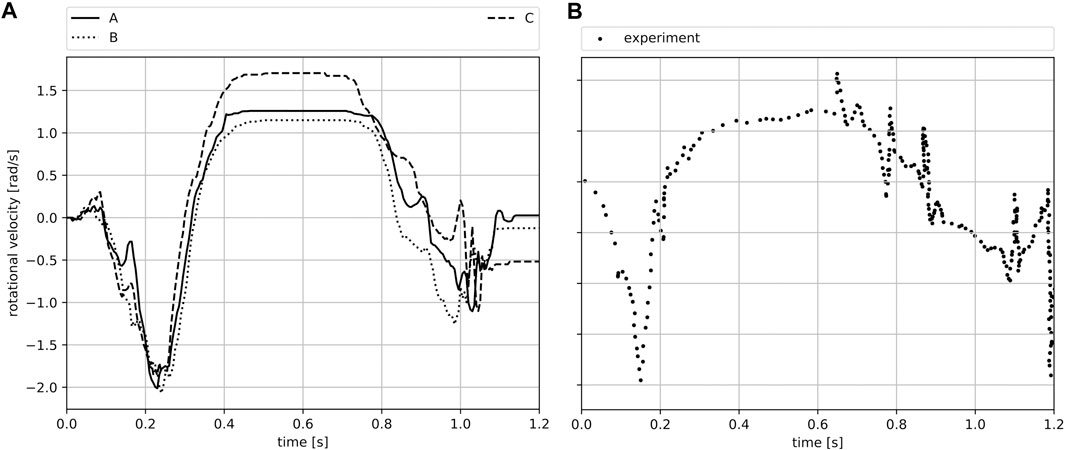
FIGURE 14. Visualization of angular velocity about one of the main axis of the impacting object T092. (A) Simulation. (B) General trend from experiment.
5.3 Translational Velocity
The translational velocity of the three optimal parameter sets (as per subsection 5.1) and the experiment are illustrated in Figure 15A. It can be seen that the deceleration of the impacting rock in the horizontal direction (perpendicular to the protection net) is accurately modeled by the simulation. This is of particular importance for the design of protection structures, since the management of horizontal momentum is the primary arresting mechanism. Although experimental results for the vertical (gravity) direction are substantially scattered, the simulation demonstrates a good agreement with the general trend of the experimental data.
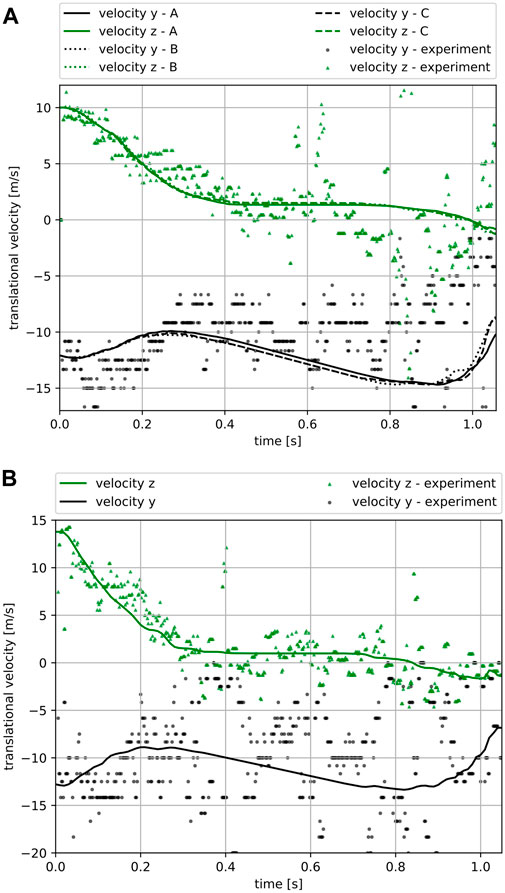
FIGURE 15. Comparison of translational velocity for both the horizontal direction, z and the vertical in gravity direction, y. (A) The three optimal parameter combinations for T092. (B) T089 with parameter set C.
Just as in subsection 5.1, the velocity components of the simulation and the experiment of T089 are also compared in the following. Figure 15B shows that these data could also be reproduced with very good agreement and thus allows suitable statements to be made about future rockfall events in Attenuator barriers.
6 Conclusion
This work has applied an advanced modeling and simulation approach to characterize the behavior of Attenuator barriers. Two independent numerical methods were coupled within an open-source multi-physics code to analyze the interaction of the impacting object and the protective structure. The impacting objects were simulated using DEM whereby arbitrarily shaped rocks were flexibly modeled as clusters of single spherical particles. This effective procedure allows the simultaneous use of simple contact algorithms and the possibility to consider the influence of arbitrary rock shapes. The structure itself was simulated using FEM employing a variety of advanced element formulations appropriate for each structural component. A homogeneous anisotropic membrane element was used to simplify the complicated protection mesh. As in Sautter et al. (2021), this simplification was found to be applicable when the global deformation behavior has to be investigated. A sophisticated yet elegant sliding cable formulation was applied to model the sliding nodes on the support ropes, allowing the boundary kinematics of the net to be fully resolved. Due to the robust implementation in the open-source code KRATOS [see Dadvand et al. (2010), Dadvand et al. (2013); Ferrándiz et al. (2020)], this work allows engineers and researchers alike to perform independent analyses of any rockfall event and the evaluation of suitable protection structures.
Another objective of this work was evaluating the performance of Attenuator barriers. It was demonstrated that this type of flexible protective structure offers dramatically increased protection against rockfalls by retarding impacts and subsequently guiding them to designated collection zones. In subsection 5.1 the simulation and experimental results agree that the Attenuator barrier considered reduced the danger zone by approximately two thirds compared to a free falling object. The fact that the Young’s modulus and the coefficient of restitution of the DEM cluster have little influence on the trajectory of the impacting object was expected, since little energy is absorbed by strains and internal forces and the rock is instead deflected. On the other hand, the correct choice of interface friction was found to be important, as the experimental data is strongly influenced by the rotation of the impacting object. To support the conclusions of this study, another test was simulated without varying the unknown parameters. The set of best parameters from the previous tests was applied directly. The results of this work clearly show that with this procedure the experimental results can be calculated with a very good agreement. Thus, future questions regarding Attenuator barriers can be answered confidently, quickly and efficiently. The CPU system settings for this study is an Intel(R) Xeon(R) CPU E5-2,623 v4 at 2.60GHz, while it takes approximately 700 s (11.667 min) to run one simulation.
Live experiments are time-consuming and very costly, especially if every new change in the design has to be investigated experimentally. The numerical analysis of these tests can support the design process and thus make the development of new protective structures more cost-effective. Considering the global change of temperature and general environmental influences, the development and realization of simulation methods in open-source multi-physics codes (such as KRATOS) is of great importance and cannot be overemphasized. A community of engineers and programmers working together on such computer programs that are freely accessible to everyone is of paramount importance.
Data Availability Statement
The data analyzed in this study is subject to the following licenses/restrictions: The comparative data in this work are the results of several experiments conducted by Geobrugg. The experiments were carried out in 2017 in Nicolum Quarry, British Columbia, Canada, with Wyllie and Norrish Rock Engineers and Geobrugg North America Ltd. The data are the property of Geobrugg and are partly published in the course of this work, the remaining data are not publicly available.
Author Contributions
KS, PB, and RW have jointly developed the basic theory of the paper. KS has worked on the modeling, development and simulation of the multi-physics simulation discussed here. HH wrote the detailed explanation of the experiments and played a leading role in the ongoing discussions. CW, RW and K-UB provided the initial ideas and advised while developing the methods. KS, HH, CW and PW were involved in preparing and finalizing the paper.
Funding
This work was supported by the Technical University of Munich (TUM).
Conflict of Interest
HH and CW were employed by Geobrugg AG.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to thank Geobrugg for their support and the test data provided.
Abbreviations
DEM, Discrete Element Method; FEM, Finite Element Method; HM + D, Hertz-Mindlin Spring-Dashpot MPM, Material Point Method; PFEM, Particle Finite Element Method; SPH, Smoothed-Particle Hydrodynamics; Bold letters indicate vectors and tensors.
References
Abel, J. F., and Shephard, M. S. (1979). An Algorithm for Multipoint Constraints in Finite Element Analysis. Int. J. Numer. Methods Eng. 14, 464–467.
Arndt, B., Ortiz, T., and Turner, K. (2009). Colorado’s Full-Scale Field Testing of Rockfall Attenuator Systems. Transportation Research Circular E-C141. Washington, DC: Transportation Research Board.
Bauer, A. M., Wüchner, R., and Bletzinger, K.-U. (2018). Innovative CAD-Integrated Isogeometric Simulation of Sliding Edge Cables in Lightweight Structures. J. Int. Assoc. Shell Spat. Structures 59, 251–258. doi:10.20898/j.iass.2018.198.039
Belytschko, T., Kam, L. W., Moran, B., and Elkhodary, K. I. (2000). Nonlinear Finite Elements for Continua and Structures. New Haven: John Wiley & Sons, Ltd).
Boulaud, R., and Douthe, C. (2017). IASS Annual Symposium. A Sliding Cable Model for Rockfall Barrier Simulations Using Dynamic Relaxation.
Bradshaw, G., and O’Sullivan, C. (2004). Adaptive Medial-Axis Approximation for Sphere-Tree Construction. ACM Trans. Graphics 23, 1–26. doi:10.1145/966131.966132
Bradshaw, G., and O’Sullivan, C. (2002). Sphere-Tree Construction Using Dynamic Medial Axis Approximation. ACM Trans. Graphics 33–40. doi:10.1145/545261.545267
Chandra, B., Larese, A., Bucher, P., and Wüchner, R. (2019). Coupled Soil-Structure Interaction Modeling and Simulation of Landslide Protective Structures (Coupled Problems).
Chau, K. T., Wong, R. H. C., and Wu, J. J. (2002). Coefficient of Restitution and Rotational Motions of rockfall Impacts. Amsterdam, The Netherlands: Elsevier.
Cremonesi, M., Franci, A., Idelsohn, S., and Oñate, E. (2020). A State of the Art Review of the Particle Finite Element Method (PFEM). Arch. Comput. Methods Eng. 27, 1709–1735.
Cummins, S. J., Thornton, C., and Cleary, P. W. (2012). Contact Force Models in Inelastic Collisions. Ninth International Conference on CFD in the Minerals and Process Industries.
Cundall, P. A., and Strack, O. D. L. (1979). A Discrete Numerical Model for Granular Assemblies. Gotechnique 29, 47–65. doi:10.1680/geot.1979.29.1.47
Dadvand, P., Rossi, R., Gil, M., Martorell, X., Cotela, J., Juanpere, E., et al. (2013). Migration of a Generic Multi-Physics Framework to HPC Environments. Comput. Fluids, 301–309.
Dadvand, P., Rossi, R., and Oñate, E. (2010). An Object-Oriented Environment for Developing Finite Element Codes for Multi-Disciplinary Applications. Arch. Comput. Methods Eng. 17, 253–297. doi:10.1007/s11831-010-9045-2
Dhakhal, S., Bhandary, N., Yatabe, R., and Kinoshita, R. (2011). Experimental, Numerical and Analytical Modelling of a Newly Developed rockfall Protective cable-net Structure. Nat. Hazards Earth Syst. Sci. 11, 3197–3212. doi:10.5194/nhess-11-3197-2011
Escallon, J. P., Boetticher, V., Wendeler, C., Chatzi, E., and Bartelt, P. (2015). Mechanics of Chain-Link Wire Nets with Loose Connections. Amsterdam, The Netherlands: Elsevier.
Felippa, C. A., Park, K.-C., and Farhat, C. (2001). Partitioned Analysis of Coupled Mechanical Systems. Comp. Methods Appl. Mech. Eng. 190, 3247–3270.
Ferrándiz, V. M., Bucher, P., Rossi, R., Cotela, J., Carbonell, J., Zorrilla, R., et al. (2020). KratosMultiphysics. (Version 8.0). Zenodo.
Gao, W., and Feng, Y. T. (2019). A Coupled 3D Discrete Elements/isogeometric Method for Particle/structure Interaction Problems. Comput. Part. Mech. 7, 869–880. doi:10.1007/s40571-019-00267-8
Geobrugg, A. G. R. (2020). SPIDER®. Available at: www.geobrugg.com.
Gingold, R. A., and Monaghan, J. J. (1977). Smoothed Particle Hydrodynamics: Theory and Application to Non-spherical Stars. Monthly Notices R. Astronomical Soc. 181, 375–389. doi:10.1093/mnras/181.3.375
Glover, J., and Ammann, W. (2016). Geobrugg Internal Testing Report No. 1-a, Rockfall Attenuator Testing Nicolum Quarry, Hope BC, Global Risk Forum Davos. Switzerland: GRF.
Hamilton, W. R. (1844). On Quaternions, or on a New System of Imaginaries in Algebra. Lond. Edinb. Dublin Phil. Mag. 10–13.
Hofmann, H., Glover, J., and Wyllie, D. (2019). Development of a Dimensioning Concept for the Flexible rockfall protection Solution Attenuator. International Congress on Rock Mechanics and Rock Engineering, Foz do Iguassu, Brazil.
Holzapfel, G. A. (2010). Nonlinear Solid Mechanics a Continuum Approach for Engineering. Chichester: Wiley.
Irazábal, J., Salazar, F., Santasusana, M., and Oñate, E. (2019). Effect of the Integration Scheme on the Rotation of Non-spherical Particles with the Discrete Element Method. Comput. Part. Mech. 6, 545–559. doi:10.1007/s40571-019-00232-5
Kiendl, J. (2011). Isogeometric Analysis and Shape Optimal Design of Shell Structures. Ph.D. thesis, TUM.
Küttler, U., and Wall, W. (2008). Computational Mechanics.Fixed-point Fluid Structure Interaction Solvers with Dynamic Relaxation.
Larese, A. (2016). A Lagrangian PFEM Approach for Non-newtonian Viscoplastic Materials. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería 33, 307–317. doi:10.1016/j.rimni.2016.07.002
Larese, A., Iaconeta, I., Chandra, B., and Singer, V. (2020). Implicit MPM and Coupled MPM-FEM in Geomechanics. In Point based numerical methods in geomechanics. 1534–1572.
Lisjak, A., and Grasselli, G. (2010). Rock Impact Modelling Using FEM/DEM. In 5th Int. Conference on Discrete Element Method.
Lisjak, A., Spadari, M., Giacomini, A., and Graselli, G. (2010). Rock Fall Numerical Modelling Using a Combined Finite-Discrete Element Approach. Symp. Rock Slope Stab.
Lucy, L. B. (1977). A Numerical Approach to the Testing of the Fission Hypothesis. Astrophysical J. 82, 1013–1024. doi:10.1086/112164
Madhusudhan, K., Rahul, B., Jennifer, C., and Carl, H. B. W. (2009). Force Model Considerations for Glued-Sphere Discrete Element Method Simulations. Chem. Eng. Sci. 64, 3466–3475. doi:10.1016/j.ces.2009.04.025
Matuttis, H.-G., and Chen, J. (2014). Understanding the Discrete Element Method: Simulation of Non-spherical Particles for Granular and Multi-Body Systems. Wiley.
Mentani, A., Govoni, L., Giacomini, A., Gottardi, G., and Buzzi, O. (2018). Rock Mechanics and Rock Engineering.An Equivalent Continuum Approach to Efficiently Model the Response of Steel Wire Meshes to Rockfall Impacts.
Muhunthan, B., Shu, S., Sasiharan, N., Hattamleh, O. A., Badger, T. C., Lowell, S. L., et al. (2005). Analysis and Design or Wire Mesh/Cable Net Slope Protection. Seattle, Washington, WA-RD: Washington State Transportation Centre, 267. 612 1.
Münsch, R., and Reinhardt, H.-W. (1995). Zur Berechnung von Membrantragwerken aus .beschichteten Geweben mit Hilfe genäherter elastischer Materialparameter. Bauingenieur 70, 271–275.
Nakashino, K., and Natori, M. C. (2005). Efficient Modification Scheme of Stress-Strain Tensor for Wrinkled Membranes. AIAA J. 43, 206–215. doi:10.2514/1.7143
Salazar, F., González, J. I., Larese, A., and Oñate, E. (2015). Numerical Modelling of Landslide-Generated Waves with the Particle Finite Element Method (PFEM) and a Non-newtonian Flow Model. Int. J. Numer. Anal. Methods Geomechanics 40, 809–826. doi:10.1002/nag.2428
Santasusana, M., Irazábal, J., Oñate, E., and Carbonell, J. M. (2016). The Double Hierarchy Method. A Parallel 3D Contact Method for the Interaction of Spherical Particles with Rigid FE Boundaries Using the DEM. Comput. Part. Mech. 3, 407–428. doi:10.1007/s40571-016-0109-4
Santasusana, M. (2016). Numerical Techniques for Non-linear Analysis of Structures Combining Discrete Element and Finite Element Methods. Ph.D. thesis, CIMNE.
Sasiharan, N., Muhunthan, B., Badger, T., Shu, S., and Carradine, D. M. (2006). Numerical Analysis of the Performance of Wire Mesh and cable Net rockfall protection Systems. Eng. Geology. 88, 121–132. doi:10.1016/j.enggeo.2006.09.005
Sautter, K. B., Hofmann, H., Wendeler, C., Wüchner, R., and Bletzinger, K.-U. (2021). Computational Particle Mechanics.Influence of DE-Cluster Refinement on Numerical Analysis of Rock-Fall Experiments.
Sautter, K. B., Teschemacher, T., Celigueta, M. A., Bucher, P., Bletzinger, K.-U., and Wüchner, R. (2020). Partitioned Strong Coupling of Discrete Elements with Large Deformation Structural Finite Elements to Model Impact on Highly Flexible Tension Structures. Adv. Civil Eng 2020, 1–28. doi:10.1155/2020/5135194
Schwager, T., and Pöschel, T. (2007). Coefficient of Restitution and Linear–Dashpot Model Revisited. Granular Matter 9, 465–469. doi:10.1007/s10035-007-0065-z
Shäfer, J., Dippel, S., and Wolf, D. (1996). Force Schemes in Simulations of Granular Materials. J. de Physique.
Sulsky, D., Chen, Z., and Schreyer, H. L. (1994). A Particle Method for History-dependent Materials. Comp. Methods Appl. Mech. Eng. 118, 179–196. doi:10.1016/0045-7825(94)90112-0
Tahmasbi, S., Giacomini, A., Wendeler, C., and Buzzi, O. (2019). On the Computational Efficiency of the Hybrid Approach in Numerical Simulation of Rockall Flexible Chain-Link Mesh. Rock Mech. Rock Eng. doi:10.1007/s00603-019-01795-8
Thornton, C., Cummins, S. J., and Cleary, P. W. (2012). An Investigation of the Comparative Behaviour of Alternative Contact Force Models during Inelastic Collisions. Powder Technology.
Tianyang, W. (2016). Development of Co-simulation Environment and Mapping Algorithms (Ph.D. thesis, TUM).
Volkwein, A. (2005). Numerical Simulation of Flexible rockfall protection Systems. Comput. Civil Eng. 2005
Volkwein, A. (2004). Numerische Simulation von flexiblen Steinschlagschutzsystemen (Ph.D. thesis, ETH).
von Bötticher, A. (2012). Flexible Hangmurenbarrieren: Eine numerische Modellierung des Tragwerks, der Hangmure und der Fluid-Struktur-Interaktion (Ph.D. thesis, TUM).
Wendeler, C. (2008). Murgangrückhalt in Wildbächen - Grundlagen zu Planung und Berechnung von flexiblen Barrieren (Ph.D. thesis, ETH).
Wilson, P., Wüchner, R., and Fernando, D. (2020). Distillation of the Material point Method Cell Crossing Error Leading to a Novel Quadrature-Based C0 Remedy. Int. J. Numer. Methods Eng. (n/a).
Winterstein, A., Lerch, C., Bletzinger, K.-U., and Wüchner, R. (2018). Partitioned Simulation Strategies for Fluid–Structure–Control Interaction Problems by Gauss–Seidel Formulations. Adv. Model. Simulation Eng. Sci.
Wüchner, R. (2006). Computational Mechanics of Formfinding and Fluid-Structure Interaction of Membrane Structures. Ph.D. Thesis, TUM.
Wyllie, D., Shevlin, T., Glover, J., and Buechi, A. (2016). Attenuators for Controlling rockfall: First Results of a State-Of-The-Art Full-Scale Testing Program. 69th Can. Geotechnical Conf.
Zhang, X., Chen, Z., and Liu, Y. (2016). The Material Point Method: A Continuum-Based Particle Method for Extreme Loading Cases. Cambridge).
Zhao, L., He, J. W., Yu, Z. X., Liu, Y. P., Zhou, Z. H., and Chan, S. L. (2020a). Coupled Numerical Simulation of a Flexible Barrier Impacted by Debris Flow with Boulders in Front. Landslides. doi:10.1007/s10346-020-01463-x
Keywords: DEM, FEM, rockfall, impact, cluster, experiment, particles, coupling
Citation: Sautter KB, Hofmann H, Wendeler C, Wilson P, Bucher P, Bletzinger K-U and Wüchner R (2021) Advanced Modeling and Simulation of Rockfall Attenuator Barriers Via Partitioned DEM-FEM Coupling. Front. Built Environ. 7:659382. doi: 10.3389/fbuil.2021.659382
Received: 27 January 2021; Accepted: 18 May 2021;
Published: 14 June 2021.
Edited by:
Stefano de Miranda, University of Bologna, ItalyReviewed by:
Alessio Mentani, University of Bologna, ItalyRossana Dimitri, University of Salento, Italy
Shuji Moriguchi, Tohoku University, Japan
Lei Zhao, Southwest Jiaotong University, China
Copyright © 2021 Sautter, Hofmann, Wendeler, Wilson, Bucher, Bletzinger and Wüchner. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Klaus Bernd Sautter, a2xhdXMuc2F1dHRlckB0dW0uZGU=
 Klaus Bernd Sautter
Klaus Bernd Sautter Helene Hofmann
Helene Hofmann Corinna Wendeler
Corinna Wendeler Peter Wilson
Peter Wilson Philipp Bucher
Philipp Bucher Kai-Uwe Bletzinger
Kai-Uwe Bletzinger Roland Wüchner
Roland Wüchner