Critical Response of High-Rise Buildings With Deformation-Concentration Seismic Control System Under Double and Multi Impulses Representing Pulse-Type and Long-Duration Ground Motions

The critical responses are investigated for a high-rise building with a deformation-concentration seismic control system under double and multi impulses representing pulse-type and long-duration ground motions, respectively. The critical responses were studied for an elastic-plastic multi-degree-of-freedom (MDOF) shear building model under a double impulse and a multi impulse in the previous papers. However, it seems difficult to derive the critical response for a realistic three-dimensional (3-D) nonlinear frame model with a deformation-concentration seismic control system under such double and multi impulses. The criteria on the criticality of the double and multi impulses for the elastic-plastic MDOF shear building model derived in the previous research are extended to this realistic controlled 3-D frame model by regarding the sum of base story shear forces of both main and sub buildings as a key quantity. In the analysis, the concepts of “Double Impulse Pushover (DIP)” and “Multi Impulse Pushover (MIP)” introduced before are used effectively for clarifying the progressive performances for the increasing input level. The analyses of total input energy, frame hysteretic energy and damper dissipation energy are conducted and the criticality of the input derived based on the above-mentioned criteria is investigated in detail.

Introduction

In the early stage of earthquake resistant design of building structures and infrastructures, near-fault ground motions were recorded extensively all over the world and used as principal design ground motions (Bertero et al., 1978; Mavroeidis et al., 2004; Kojima and Takewaki 2015a). The near-fault ground motions can be characterized by pulse-type waves. The fault-parallel component is expressed by the fling-step input (one-cycle sine wave of acceleration) and the fault normal component is represented by the forward-directivity input (one-cycle sine wave of velocity). The existence of forward-directivity pulse is the main feature of the near-fault ground motions and the forward-directivity pulse is well known to influence the building response more strongly than the fling-step input in general (Hall et al., 1995; Kalkan and Kunnath 2006; Champion and Liel 2012; Kohrangi et al., 2018; Khansefid and Bakhshi 2019; Khansefid 2020). The effects of near-fault ground motions on building responses are known to cause serious and critical deformation concentration in lower stories of flexible tall buildings.

The Mexico earthquake in 1985, the Tokachi-oki earthquake in 2003 and the Tohoku earthquake in 2011 induced long-period and long-duration ground motions and changed the common sense in the definition of design ground motions. During these earthquakes, heavy damages to building structures and infrastructure were investigated, e.g., the Mexico earthquake (Beck and Hall 1986), the Tokachi-oki earthquake in 2003 (Hatayama et al., 2004) and the Tohoku earthquake in 2011 (Takewaki et al., 2011a, Takewaki et al,. 2013). A historically famous resonant response was observed in a high-rise steel building over 250 m high in Osaka, Japan during the 2011 Tohoku earthquake (Takewaki et al., 2011a). Only non-structural elements were damaged and structural members behaved well. However, such phenomenon was not understood in the design stage and it was remarked that the careful investigation is inevitable from the viewpoint of resilience of important structures against unpredictable risks (Takewaki et al., 2013). It is believed that passive structural control is the most promising for the enhancement of resilience of building structures and infrastructures against such unpredictable risks (Takewaki et al., 2011b; Takewaki, 2013; De Domenico et al., 2019).

It should be kept in mind that the nonlinear response of building structures and infrastructures was initially taken into account for long-duration sinusoidal input (for example, Caughey, 1960a; Caughey, 1960b). It was recognized that the resonant frequency must be analyzed for a specified input level by changing the input frequency parametrically in the response to a harmonic wave (Caughey 1960a; Caughey, 1960b; Iwan, 1961; Iwan, 1965a; Iwan, 1965b). Efficient and effective tools without laborious computational iteration have been desired for initial structural design in which nonlinear responses are allowed.

An innovative approach using the double impulse was initiated by Kojima and Takewaki (2015a). The double impulse is superior in characterizing the fling-step ground motion. The magnitude was scaled to express an approximate response to the corresponding sinusoidal wave as a representative of near-fault ground motions (Akehashi et al., 2018b; Akehashi et al., 2018c). A closed-form expression was derived for the maximum elastic-plastic response of a SDOF structure under the “critical double impulse” (Kojima and Takewaki, 2015a).

A long-period and long-duration ground motion has been simulated successfully by the multi impulse (Kojima and Takewaki, 2015b; Kojima and Takewaki (2017), Akehashi et al., 2018a; Hayashi et al., 2018; Kawai and Takewaki, 2020). The multi impulse has an advantage that, since only the free vibration appears, the response analysis can be conducted without specification of input frequency. An energy balance law can then be used for obtaining the maximum elastic-plastic response without solving differential equations directly. This process is done by equating the initial (or intermediate) kinetic energy to the combined elastic strain and hysteretic energies. The critical timing of the impulses can be characterized by the timing of attaining the zero restoring force in the unloading stage. The critical resonant frequency can be found automatically for the gradually increasing input level of the multi impulse.

It is noted that the above-mentioned energy balance approach initiated by Kojima and Takewaki (2015a) can be applied only to SDOF models. Akehashi and Takewaki (2019), Akehashi and Takewaki (2020), Kawai and Takewaki (2020) generalized it to MDOF shear building models under the double impulse and the multi impulse, respectively, although the closed-form expressions are difficult for MDOF models. Criteria on the critical input timing of the second impulse in the double impulse and the subsequent impulse in the multi impulse were derived and the critical responses were computed by the time-history response analyses. To investigate the elastic-plastic performances of MDOF models under the progressive resonant double and multi impulses, the Double Impulse Pushover (DIP) and Multi Impulse Pushover (MIP) were newly exploited (Akehashi and Takewaki, 2019; Kawai and Takewaki, 2020).

In this paper, the critical response is analyzed for a high-rise building with a deformation-concentration seismic control system under double and multi impulses representing pulse-type and long-duration ground motions, respectively. The critical responses of an elastic-plastic SDOF model under a multi impulse were investigated in the previous papers (Kojima and Takewaki, 2015b; Akehashi et al., 2018a; Hayashi et al., 2018) and the critical responses of an elastic-plastic MDOF shear building model under a multi impulse were analyzed (Kawai and Takewaki, 2020). However, it is not certain whether the procedure for the MDOF shear building model is applicable to realistic three-dimensional (3-D) nonlinear frame models with deformation-concentrated vibration control systems. The criteria on the criticality of the double and multi impulses for the elastic-plastic MDOF shear building model derived in the previous research are extended to this realistic controlled 3-D frame model by regarding the sum of base story shear forces of both main and sub buildings as a key quantity. The influence of damper quantities on the responses is clarified in terms of local deformation indices and global energy responses by using the original concepts, “Double Impulse Pushover (DIP)” and “Multi Impulse Pushover (MIP)”.

Three-Dimensional (3-D) Frame Model With Deformation-Concentration Seismic Control System

Consider a reinforced concrete high-rise building (apartment house) with a deformation-concentration damper system as shown in Figure 1 (Maeda et al., 2020; Kawai et al., 2020). The passive control system consists of the main frame, the sub frame and the large-stroke viscous oil dampers. The main frame is connected to a strong-back core frame, as shown in Figure 1A. This control system is proposed to reduce the seismic response of high-rise buildings. It is assumed that the main building is used for an apartment house and the lower strong-back core frame is used for car parking. The upper strong-back core frame is used only for the stiffness element connecting the top of the main frame to the lower strong-back core frame. To enable the efficient use of passive dampers, a stiff core (strong-back core frame) is constructed and attached to the foundation. Another stiff core frame is hung from the top story stiff sub-assemblage of the main building. The height of the lower strong-back core frame is determined from the architectural user demand based on the number of parked cars. Because this lower strong-back core frame is made of a wall-type reinforced concrete structure with relatively small mass, the horizontal force demand is not significant. Since deformation, or story drift demand, is concentrated in the connecting story, a large stroke is required for viscous oil dampers. Oil dampers of large stroke typically used usually for base-isolation systems are employed in this system.

FIGURE 1

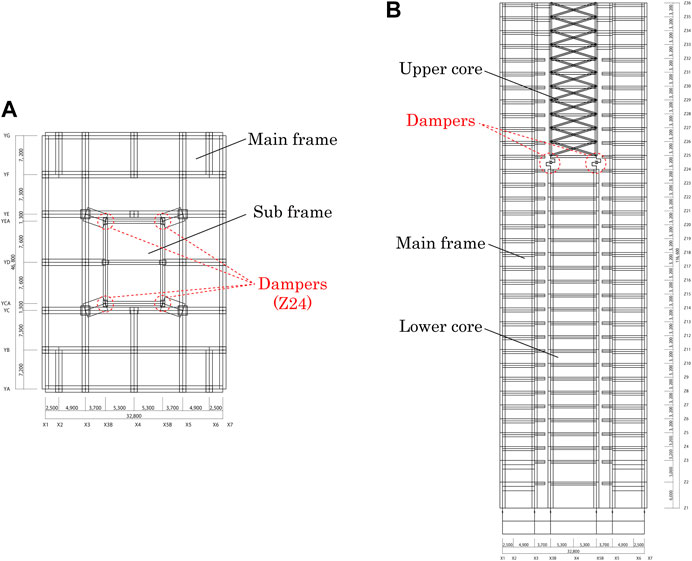
FIGURE 1. High-rise building with deformation-concentration vibration control system, (A) Plan, (B) Section.

The properties of the frame and dampers were determined from the investigation on realistic building structural design (Maeda et al., 2020). The structural damping ratio of the super-structure (instantaneous stiffness-proportional damping) is set to 0.03. Eight viscous oil dampers of damping coefficient 2,500 [kNs/m] are used in the control story and the total damping coefficient is $C_d=2.0\times {10}^4[\text{kNs}/\text{m}]$. This damper quantity is an original basic quantity and this quantity will be changed later.

The main frame is a reinforced-concrete moment-resisting frame consisting of column (1200 × 1200) and beam (850 × 850, 950 × 950, 1050 × 950, 1200 × 1200). The materials are concrete of strength Fc80, steel bar SD590 and lateral reinforcement KH785. The bending of the beam is modeled by a modified Takeda model (Takeda et al., 1970) and the shear deformation is assumed to be elastic. The axial and bending action of the column is modeled by a tri-linear MN model and the shear deformation is assumed to be elastic.

The sub frame is a reinforced-concrete shear-wall structure with shear wall (thickness t = 800 mm). The materials are concrete Fc80 and steel bar SD345, SD390. The shear action is modeled by a origin-oriented tri-linear model and the axial action is expressed by a multi-spring modified Takeda model.

The upper strong-back core frame is a brace system consisting of column (box-600 × 36, SM490), beam (H-498 × 432, SM490) and brace (H-400 × 400, SM490). Each member is assumed to be elastic.

The whole structural model was expressed by the 3-D frame analysis computer software SNAP (Kozo System Co. 2019). In this program, member and floor masses are computed automatically and allocated to each node point.

To investigate the restoring-force characteristics of the high-rise building with the proposed deformation-concentration vibration control system, static pushover analyses were conducted for the main frame and the sub frame by using a 3-D frame analysis computer software SNAP (Kozo System Co. 2019). Figure 2A shows the story shear-interstory relations of the main frame and Figure 2B presents those for the sub frame. It can be observed that the stiffness of the sub frame is slightly smaller than that of the main frame. However, since the mass of the sub frame is much smaller than that of the main frame, the fundamental natural period of the sub frame is greatly shorter than that of the main frame. This property is advantageous for the effective vibration suppression by the proposed system.

FIGURE 2

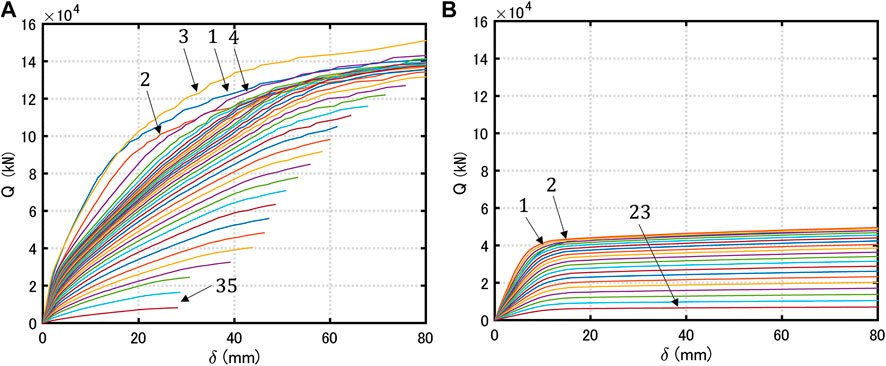
FIGURE 2. Static pushover analysis (story shear vs interstory drift), (A) Main frame, (B) Sub frame (number in figure indicates story number).

Response Characteristics of Proposed Vibration Control System Under Critical Double Impulse and Critical Multi Impulse

Double Impulse Pushover

Consider first the case where the high-rise building with the proposed control system is subjected to the critical double impulse. To investigate the overall characteristics of this case, the double impulse pushover (DIP) analysis proposed by Akehashi and Takewaki (2019) is applied.

In the DIP analysis, first of all, the range of the velocity amplitude of the double impulse is assumed. Then the response to the critical double impulse with the smallest velocity amplitude is computed. This procedure is repeated for the increasing velocity-amplitude of the double impulse. The plot of the maximum interstory drift with respect to the velocity-amplitude of the double impulse expresses the result of the DIP analysis. As a similar analysis, an incremental dynamic analysis (IDA) was proposed by Vamvatsikos and Cornell (2002). It should be noted that, while IDA is intended to obtain the relation of the story shear with the maximum interstory drift by repeating the time-history response analyses for the gradually increasing level set of selected ground motions, the DIP analysis uses only the increasing-level critical (worst) input resonant to the nonlinear structures experiencing the respective expanding responses.

Figures 3A,B show the results of the DIP analysis for the elastic-plastic 3-D frame with the proposed deformation-concentration seismic control system ($V_{DI}=0.20\sim 1.00\left[m/s\right]$ with increment $0.20\left[m/s\right]$). The time increment of the response analysis is 0.01 (s). The Newmark-beta method was used. The critical second impulse is inputted at the timing when the total story shear in the first story $F_{1,total}=F_{1,main}+F_{1,sub}$ becomes 0. This critical timing was demonstrated to be valid from the maximization of the input energy by the second impulse to the total building system (Akehashi and Takewaki, 2019). This criticality will be discussed in the following section. The overall elastic-plastic deformation properties for the increasing input level can be well expressed. It can be seen that the lower-story interstory drifts around the 5th story in the main frame become large for the increasing input level and the lowest portions of the main and sub frames exhibit a large deformation for the critical double impulse with $V_{DI}=1.00\left[m/s\right]$. These phenomena are often seen in the MDOF models under the critical double impulse.

FIGURE 3

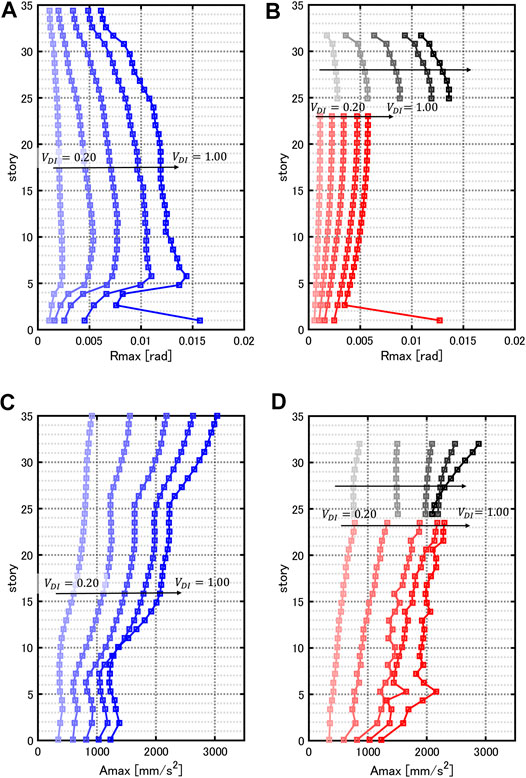
FIGURE 3. Double impulse pushover (DIP) analysis of maximum interstory drifts and one-cycle sinusoidal input analysis of maximum accelerations for elastic-plastic 3-D frame with deformation-concentration seismic control system ($V_{DI}=0.20\sim 1.00\left[m/s\right]$ with increment $0.20\left[m/s\right]$), (A) Maximum interstory drift angle of main frame, (B) Maximum interstory drift angle of sub frame, (C) Maximum acceleration of main frame, (D) Maximum acceleration of sub frame.

Figures 3C,D present the maximum accelerations of the same elastic-plastic 3-D frame with the proposed deformation-concentration seismic control system subjected to the one-cycle sinusoidal waves equivalent to the critical double impulses ($V_{DI}=0.20\sim 1.00\left[m/s\right]$ with increment $0.20\left[m/s\right]$). It is known that, while the double impulse can simulate the maximum interstory drifts properly (Hashizume and Takewaki, 2020), it cannot simulate the maximum accelerations due to its impulsive nature. For this reason, the equivalent one-cycle sinusoidal waves are used. The frequency of the sinusoidal wave is determined from the corresponding critical double impulse and the amplitude is determined from the transformation relation (Hashizume and Takewaki, 2020). The non-iterative direct determination of the resonant frequency of the equivalent one-cycle sinusoidal waves from the critical double impulse analysis is the key point in this approach of using the equivalent one-cycle sinusoidal waves for the evaluation of the maximum acceleration.

Figure 4 illustrates the time-histories of the first-story shear forces (main frame, sub frame and total) and the input timings of the two impulses ($V_{DI}=0.60[m/s]$). It can be observed that the second impulse was certainly inputted at the timing when the total story shear in the first story $F_{1,total}=F_{1,main}+F_{1,sub}$ becomes 0.

FIGURE 4

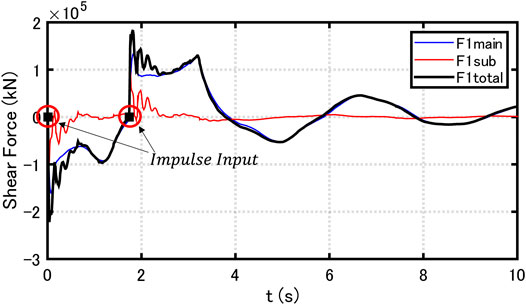
FIGURE 4. Time-histories of first-story shear forces (main frame, sub frame and total) and input timings of two impulses ($V_{DI}=0.60[m/s]$).

Multi Impulse Pushover

Consider next the case where the object controlled building is subjected to the critical multi impulse. To clarify the overall characteristics of this case, the multi impulse pushover (MIP) analysis proposed by Kawai and Takewaki (2020) is applied.

In the MIP analysis, first of all, the range of the velocity amplitude of the multi impulse is determined. Then the response to the critical multi impulse with the smallest velocity amplitude is computed. This procedure is repeated for the increasing velocity-amplitude of the multi impulse. The plot of the maximum interstory drift with respect to the velocity-amplitude of the multi impulse expresses the result of the MIP analysis.

Figures 5A,B show the results of the MIP analysis for the elastic-plastic 3-D frame with the proposed deformation-concentration seismic control system ($V_{MI}=0.10\sim 0.60\left[m/s\right]$ with increment $0.10\left[m/s\right]$). The time increment of the analysis is 0.01 (s). The Newmark-beta method was used. The critical impulse is inputted at the timing when the total story shear in the first story $F_{1,total}=F_{1,main}+F_{1,sub}$ after the input of the previous impulse becomes 0. This critical timing was validated from the viewpoint of the maximization of the input energy to the total building system (Kawai and Takewaki 2020). This criticality will be discussed in the following section. The overall elastic-plastic deformation properties for the increasing input level can be well expressed. It can be found that a proportional deformation magnification can be observed different from the case for the DIP analysis.

FIGURE 5

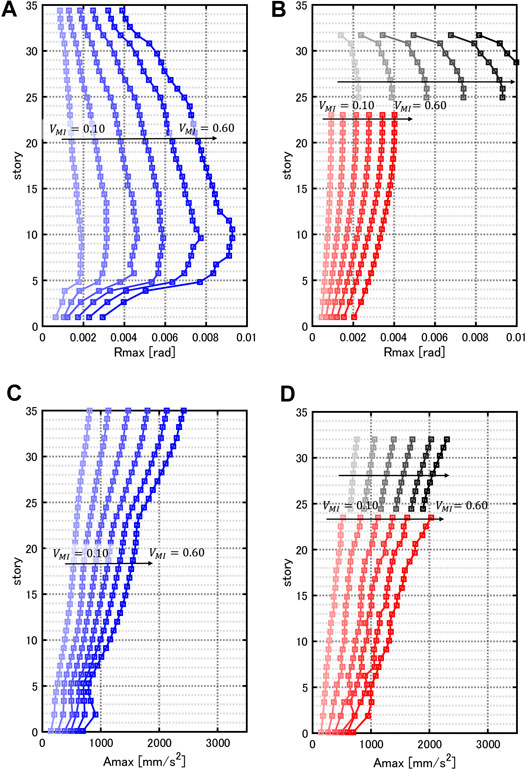
FIGURE 5. Multi impulse pushover (MIP) analysis of maximum interstory drifts and 5-cycle sinusoidal input analysis of maximum accelerations for elastic-plastic 3-D frame with deformation-concentration seismic control system ($V_{MI}=0.10\sim 0.60\left[m/s\right]$ with increment $0.10\left[m/s\right]$), (A) Maximum interstory drift angle of main frame, (B) Maximum interstory drift angle of sub frame, (C) Maximum acceleration of main frame, (D) Maximum acceleration of sub frame.

Figures 5C,D present the maximum accelerations of the same elastic-plastic 3-D frame with the proposed deformation-concentration seismic control system subjected to the 5-cycle sinusoidal waves equivalent to the critical multi impulses ($V_{MI}=0.10\sim 0.60\left[m/s\right]$ with increment $0.10\left[m/s\right]$). It is known that, while the multi impulse can simulate the maximum interstory drifts properly (Kawai and Takewaki, 2020), it cannot simulate the maximum accelerations due to its impulsive nature. For this reason, the equivalent 5-cycle sinusoidal waves are used. The frequency of the sinusoidal wave is determined from the corresponding critical multi impulse and the amplitude is determined from the transformation relation (Kawai and Takewaki, 2020). As stated in the double impulse input, the non-iterative direct determination of the resonant frequency of the equivalent 5-cycle sinusoidal waves from the critical multi impulse analysis is the key point in this approach of using the equivalent 5-cycle sinusoidal waves for the evaluation of the maximum acceleration.

Figure 6 illustrates the relation of the interval of impulses with the impulse number. Half of the damped fundamental natural period of the elastic model is also shown. It can be observed that, as the input level of the multi impulse becomes larger, the interval of impulses becomes longer. In addition, the interval of impulses for the elastic-plastic models converges to a constant value around the fifth input and this convergence rate becomes faster for the increasing input level. This may result from the effect of hysteretic damping in the large plastic deformation range. Double of this interval $T_P=2t_p$ is defined as the resonant period of the elastic-plastic model and used as the input period of the corresponding resonant sinusoidal wave.

FIGURE 6

FIGURE 6. Relation of interval of impulses with impulse number.

Verification of Critical Input Timing of Double Impulse and Multi Impulse in Energy Input

Figure 7 shows the energy responses ($E_I$: total input energy, $E_d$: damper dissipation energy, $E_c$: structural damping dissipation energy, $E_p$: frame hysteretic dissipation energy) with respect to the interval of double impulses for $V_{DI}=0.20, 0.60, 1.0[m/s]$. The time increment of the response analysis is $\Delta t=0.001\left[s\right]$ for accuracy assurance in energy computation. $t_p$ is the timing of two impulses of the critical double impulse and $t_0$ is an arbitrary timing of two impulses of the double impulse. It can be observed that the total input energy is maximized for $t_p$. This means that, although the criticality criterion was constructed on the input energy by the second impulse, it is also valid for the total input energy by the overall double impulse.

FIGURE 7

FIGURE 7. Input energy with respect to interval of double impulses ($\Delta t=0.001\left[s\right]$), (A)$V_{DI}=0.20\left[m/s\right]$, (B)$V_{DI}=0.60[m/s]$, (C). $V_{DI}=1.00[m/s]$.

As for the multi impulse, the investigation of criticality by using the equivalent sinusoidal wave ${{\ddot{u}}_g}^{MSW}\left(t\right)$ is conducted. This is because a steady state is treated for the multi impulses and it seems appropriate to deal with the sinusoidal wave directly. Let $V_{MSW}$ and $N_{MI}$ denote the velocity amplitude of the equivalent sinusoidal wave ${{\ddot{u}}_g}^{MSW}\left(t\right)$ and the number of the multi impulses.

From the equivalence of the maximum Fourier amplitudes, $V_{MSW}=(2/\pi )V_{MI}$. Furthermore, based on the overall observation on the coincidence of the maximum response, $V_{MSW}$ is amplified by 1.05. ${{\ddot{u}}_g}^{MSW}\left(t\right)$ can then be expressed by

${\ddot{u}}_g^{MSW}\left(t\right)=\{\begin{array}{l}0.5\left(\pi /t_p\right)V_{MSW}\sin \left(\pi t/t_p\right)\\ \left(\pi /t_p\right)V_{MSW}\sin \left(\pi t/t_p\right)\end{array}\begin{array}{c}\left(0\le t\le t_p\right)\\ \left(t_p\le t\le N_{MI}{t}_p\right)\end{array}(1)$

Figure 8 presents the energy responses ($E_I$: total input energy, $E_d$: damper dissipation energy, $E_c$: structural damping dissipation energy, $E_p$: frame hysteretic dissipation energy) with respect to the period of the equivalent sinusoidal wave (steady-state phase of equivalent 10-cycle sine wave) for $V_{MI}=0.20, 0.40, 0.60 [m/s]$. $T_p$ is double the timing of two consecutive impulses of the critical multi impulses, i.e. $T_p=2t_p$, and $T_l$ is an arbitrary period of the equivalent sinusoidal wave. It is found that, as the input level becomes larger, $T_p$ becomes longer. As in the double impulse, the total input energy is maximized for $T_p$. This means that, since the critical timing of the multi impulse is defined for one cycle in the steady-state phase, it is also valid for the total input energy during the 10-cycle sinusoidal wave.

FIGURE 8

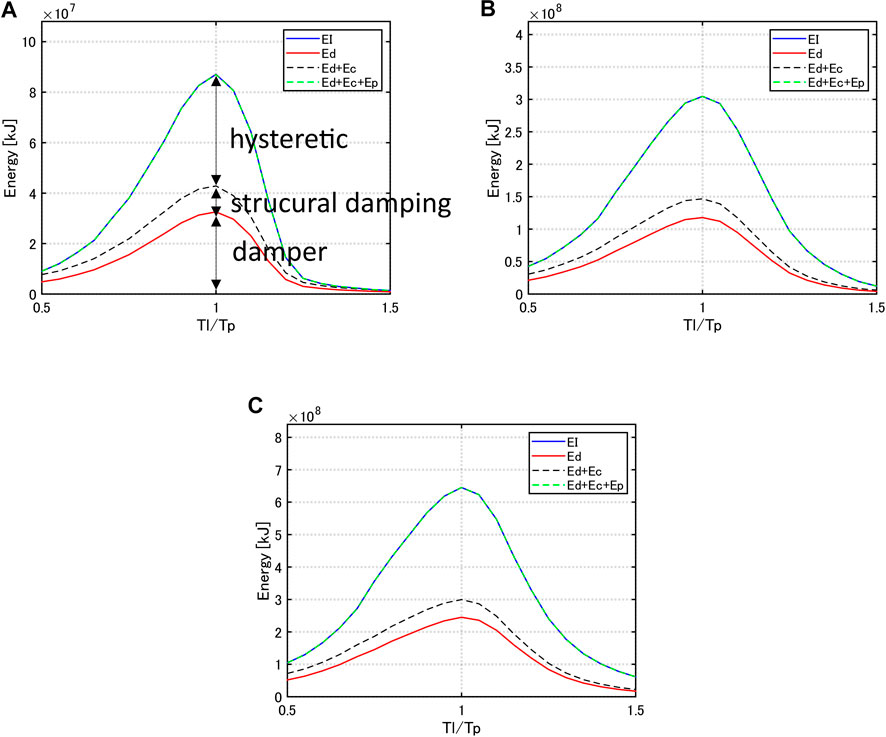
FIGURE 8. Input energy with respect to period of equivalent sinusoidal wave (steady-state phase of equivalent 10-cycle sine wave), (A)$V_{MI}=0.20[m/s]$, $T_p=3.04\left[s\right]$, (B)$V_{MI}=0.40[m/s]$, $T_p=3.32\left[s\right]$, (C)$V_{MI}=0.60[m/s]$, $T_p=3.52\left[s\right]$.

Figure 9 shows the energy responses to the resonant equivalent sine waves with various input levels. It can be observed that, as the input level becomes larger, the ratios among $E_d$ (damper dissipation energy) $E_c$ (structural damping dissipation energy) and $E_p$ (frame hysteretic dissipation energy) converge to constant values.

FIGURE 9

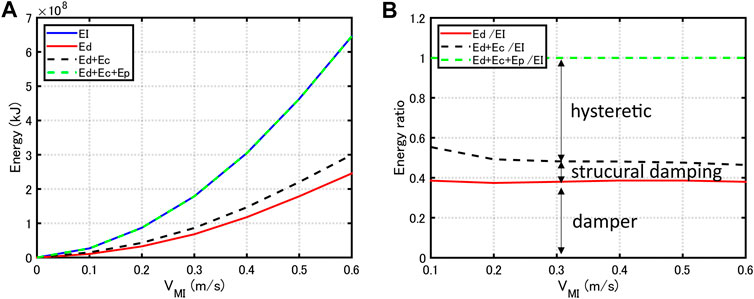
FIGURE 9. Energy responses to input level of resonant equivalent sine waves, (A) Energy response, (B) Energy ratio.

Effect of Damper Quantities on Responses Under Critical Double and Multi Impulses With Various Input Levels

Figures 10A–C present the maximum interstory drift angle of the object controlled models with various damper quantities under the critical double impulses with various input levels ($V_{DI}=0.20,0.60,1.00[m/s]$). For the original standard damper quantity $C_d=2.0\times {10}^4\left[\text{kNs}/\text{m}\right]$, various damper quantities $C_d=0.0\sim 4.0\times {10}^4\left[\text{kNs}/\text{m}\right]$ are installed with the increment $0.50\times {10}^4\left[\text{kNs}/\text{m}\right]$. It can be observed that, even if the input level becomes larger, the excessive interstory drift responses of the main and sub frames in the first story can be suppressed well by the introduction of sufficient dampers. However, it appears that the damper quantity larger than $C_d=1.5\times {10}^4\left[\text{kNs}/\text{m}\right]$ is not effective for the response reduction. In addition, the horizontal stiffness of the first story in the main frame is large compared to other stories because the foundation beam stiffness is very large. It seems that this fact affects the gradual variation of the maximum interstory drifts in the lower several stories. The large interstory drifts of the stories at and above the 24th story in the sub frame result from the fact that the large stroke oil dampers are installed in the 24th story of the sub frame and the horizontal stiffness of the upper core is not so large compared to that of the lower core.

FIGURE 10

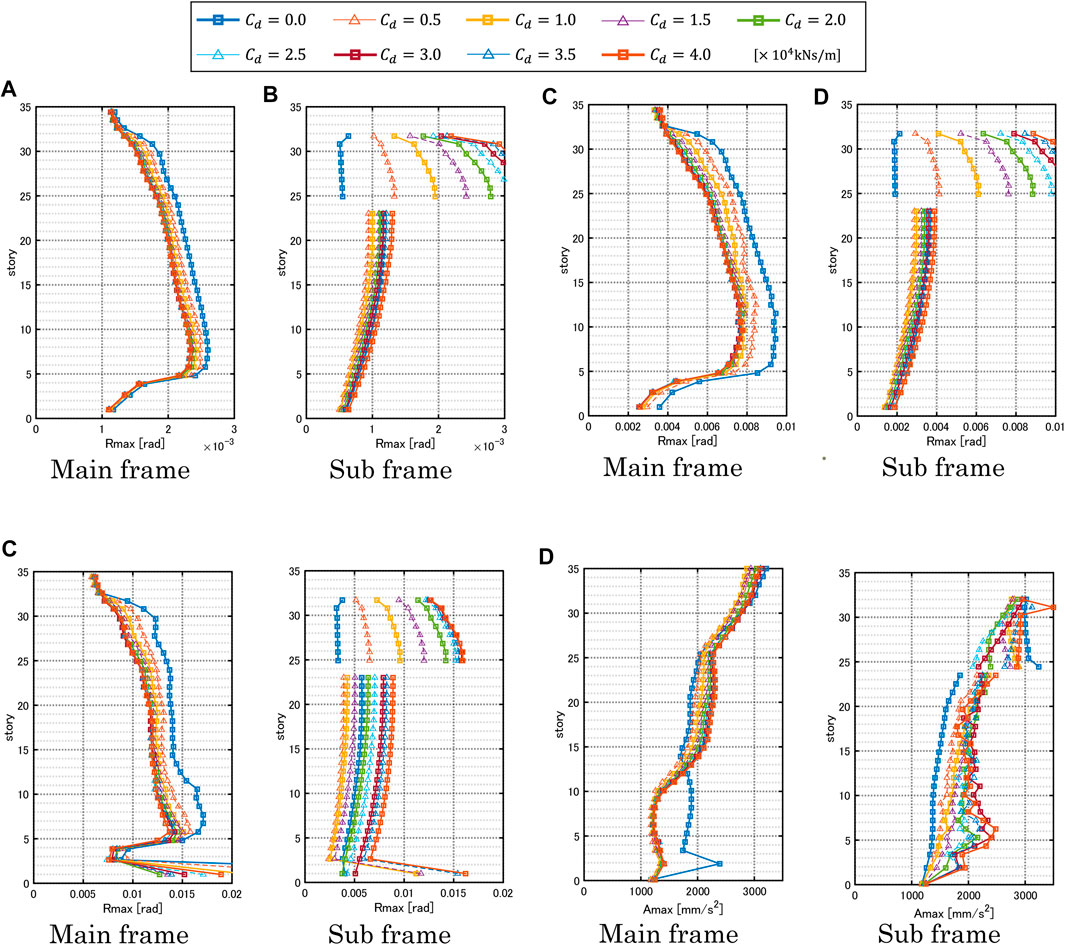
FIGURE 10. Maximum interstory drift angle under critical double impulse and maximum acceleration under equivalent one-cycle sinusoidal wave for various damper quantities, (A) Maximum interstory drift angle for $V_{DI}=0.20[m/s]$, (B) Maximum interstory drift angle for $V_{DI}=0.60[m/s]$, (C) Maximum interstory drift angle for $V_{DI}=1.00[m/s]$, (D) Maximum acceleration for one-cycle sinusoidal wave equivalent to $V_{DI}=1.00[m/s]$.

Figure 10D shows the maximum accelerations of the same model under the equivalent one-cycle sinusoidal waves. As explained in Figure 3, the equivalent sinusoidal waves corresponding to the critical double impulses were used for the evaluation of acceleration. It can be observed that, while the maximum accelerations in the main frame are decreased in lower stories for the increasing damper damping coefficient, those are increased in middle stories. On the other hand, while the maximum accelerations in the lower core of the sub frame are increased, those in the upper core of the sub frame are decreased. Since the lower core of the sub frame is used as a car parking, the increase of the maximum accelerations does not cause a serious problem. In addition, the upper core is only the stiffness element and the acceleration increase does not cause any problem.

Figure 11 illustrates the energy responses with respect to damper quantity under the critical double impulses with various input levels $V_{DI}=0.20,0.60,1.00[m/s]$. It can be observed that the total input energy and the structural damping dissipation energy do not depend on the damper quantity so much. On the other hand, the damper dissipation energy does not increase after $C_d=1.5\sim 2.0\times {10}^4\left[\text{kNs}/\text{m}\right]$. From this fact, it seems that $C_d=1.5\sim 2.0\times {10}^4\left[\text{kNs}/\text{m}\right]$ is sufficient. Furthermore, under the input of $V_{DI}=1.00[m/s]$, the decrease in the damper dissipation energy is seen after $C_d=2.5\times {10}^4\left[\text{kNs}/\text{m}\right]$. This means that the excessive damper allocation for the large input is inappropriate.

FIGURE 11

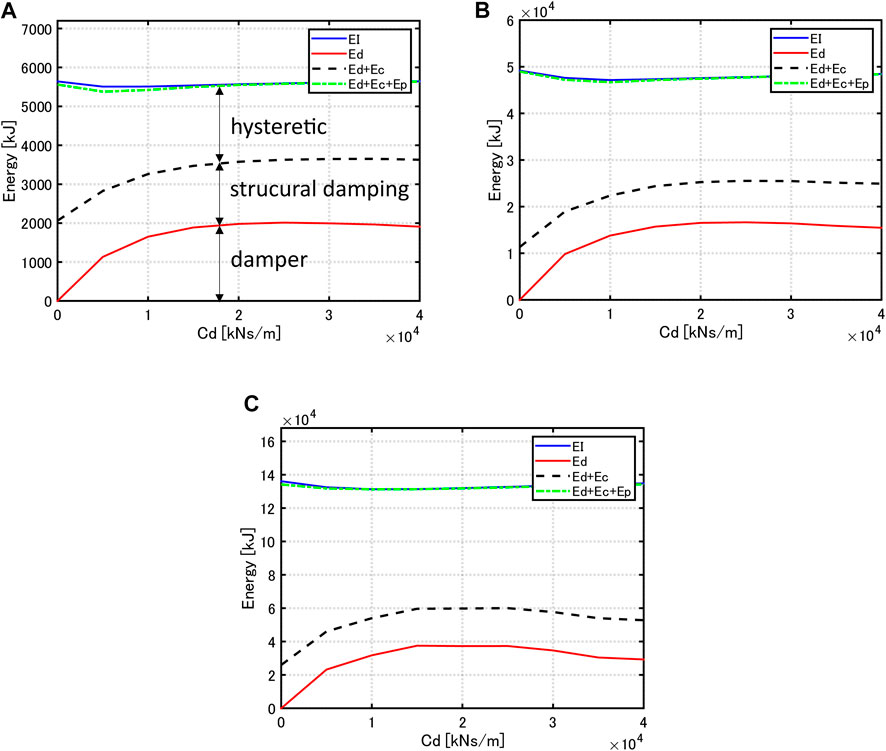
FIGURE 11. Energy response with respect to damper quantity under critical double impulse, (A)$V_{DI}=0.20[m/s]$, (B)$V_{DI}=0.40[m/s]$, (C)$V_{DI}=0.60[m/s]$.

Figures 12A–C present the maximum interstory drift angle of the object controlled models with various damper quantities under the critical multi impulses with various input levels ($V_{MI}=0.20,0.40,0.60\left[m/s\right],N_{MI}=10$). It can be observed that the excessive interstory drift responses of the main and sub frames in the first story do not appear different from in the case under the double impulses. Furthermore, it appears that the maximum responses under all the input levels attain the minimum for $C_d=2.0\times {10}^4\left[\text{kNs}/\text{m}\right]$ and those responses for $C_d=4.0\times {10}^4\left[\text{kNs}/\text{m}\right]$ exhibit larger values. This phenomenon was not observed for the response under the double impulse. As for the response reduction properties by dampers, the difference for various input levels does not appear. This means the effectiveness of the proposed vibration control system for long-period and long-duration ground motions.

FIGURE 12

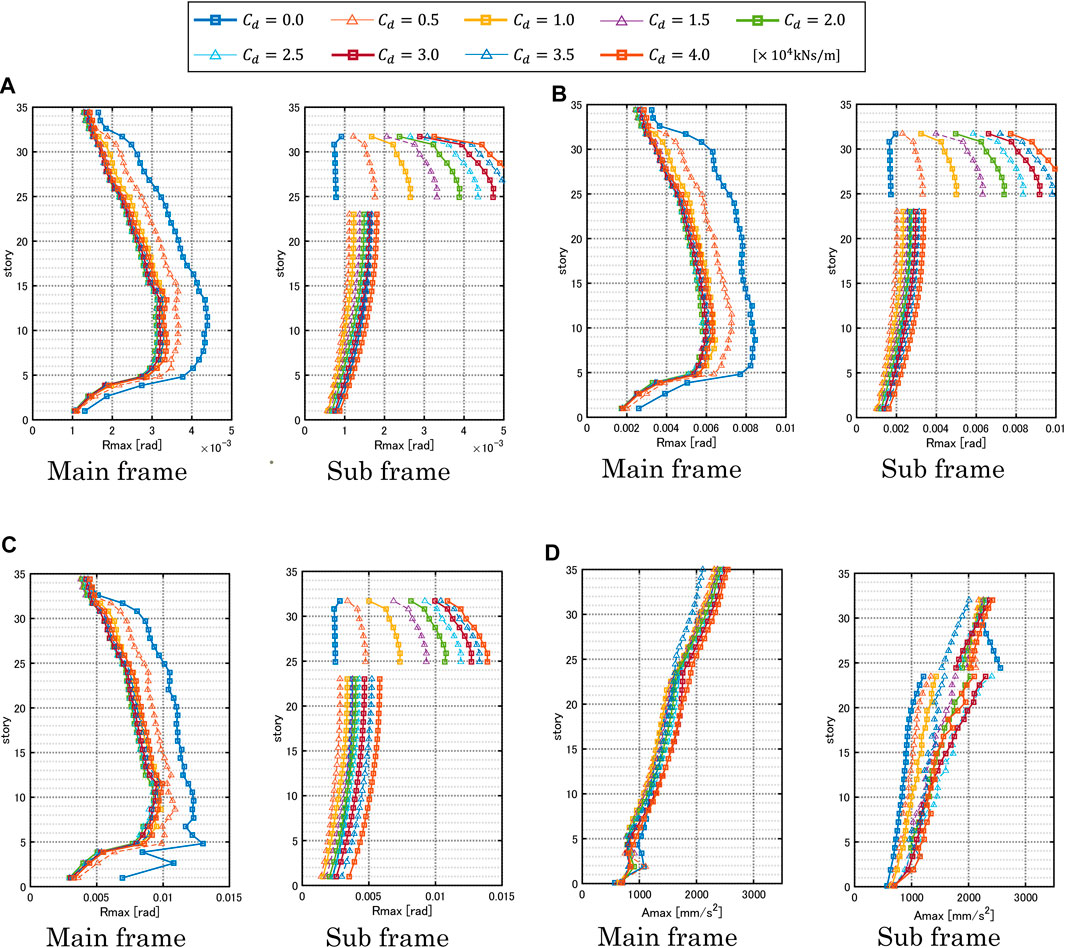
FIGURE 12. Maximum interstory drift angle under critical multi impulse and maximum acceleration under equivalent 5-cycle sinusoidal wave for various damper quantities, (A) Maximum interstory drift angle for $V_{MI}=0.20[m/s]$, (B) Maximum interstory drift angle for $V_{MI}=0.40[m/s]$, (C) Maximum interstory drift angle for $V_{MI}=0.60[m/s]$, (D) Maximum acceleration for 5-cycle sinusoidal wave equivalent to $V_{MI}=0.60[m/s]$.

Figure 12D shows the maximum accelerations of the same model under the 5-cycle sinusoidal waves equivalent to $V_{MI}=0.60[m/s]$. As explained in Figure 3, the equivalent sinusoidal waves corresponding to the critical multi impulses were used for the evaluation of acceleration. As explained in Figure 5, the equivalent sinusoidal waves corresponding to the critical multi impulses were used for the evaluation of acceleration. It can be observed that, while the maximum accelerations in the main frame do not change so much in the lower and middle stories for the increasing damper damping coefficient, those are decreased in upper stories in case of the installation of dampers with large damping coefficients. On the other hand, while the maximum accelerations in the lower core of the sub frame are increased, those in the upper core of the sub frame are decreased except for a few stories near the top.

Figure 13 illustrates the energy responses with respect to damper quantity under the critical multi impulses with various input levels $V_{DI}=0.20,0.60,1.00[m/s]$. It can be observed that the total input energy and the structural damping dissipation energy do not depend on the damper quantity so much. On the other hand, the damper dissipation energy does not increase for the model with damper quantities larger than $C_d=1.5\sim 2.0\times {10}^4\left[\text{kNs}/\text{m}\right]$. From this fact, it seems that $C_d=1.5\sim 2.0\times {10}^4\left[\text{kNs}/\text{m}\right]$ is sufficient. Furthermore, under the input of $V_{DI}=1.00[m/s]$, the decrease in the damper dissipation energy is seen in the model with damper quantities larger than $C_d=2.5\times {10}^4\left[\text{kNs}/\text{m}\right]$. This means that the excessive damper allocation for the large input is inappropriate.

FIGURE 13

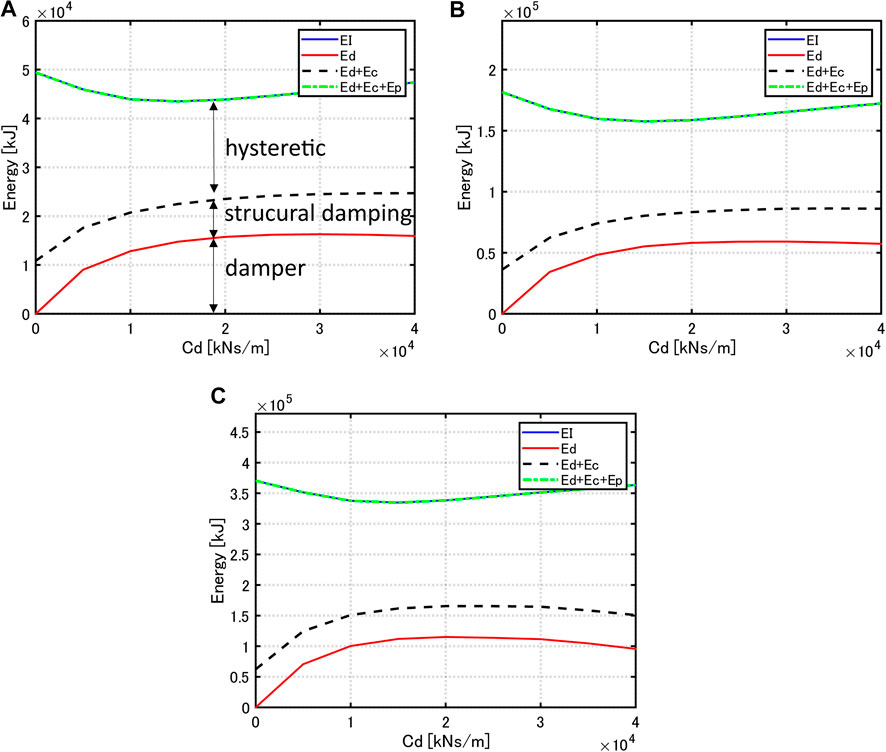
FIGURE 13. Energy response with respect to damper quantity under critical multi impulse, (A)$V_{MI}=0.20[m/s]$, (B)$V_{MI}=0.40[m/s]$, (C)$V_{MI}=0.60[m/s]$.

Figure 14 shows the resonant period of the multi impulse with respect to the damper quantity ($C_d=0.5\sim 4.0\times {10}^4\left[\text{kNs}/\text{m}\right]$) and input velocity ($V_{MI}=0.10\sim 0.60\left[m/s\right],\text{increment }0.10\left[m/s\right],N_{MI}=10$). In Figure 14, the response of the elastic model under the critical multi impulse with $V_{MI}=0.10\left[m/s\right]$ is also presented for comparison. It can be observed that, as the damper quantities become larger, the resonant elastic-plastic period becomes shorter. This effect is remarkable for $C_d=0.5\sim 2.0\times {10}^4\left[\text{kNs}/\text{m}\right]$ and the change is small for larger damper quantities. These observations correspond well to the response characteristics in Figures 12, 13. As for the influence of the input level on the resonant period $2t_p$, $t_p$ becomes longer remarkably up until $V_{MI}=0.20\left[m/s\right]$ and its speed goes down after $V_{MI}=0.20\left[m/s\right]$. This phenomenon corresponds to the behavior that the deformation of the main frame becomes larger than the first bending point in Figure 2A.

FIGURE 14

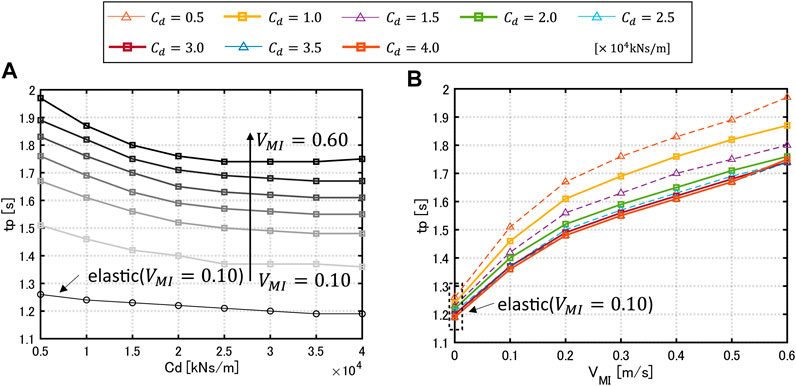
FIGURE 14. Resonant period of multi impulse with respect to damper quantity and input velocity, (A) With respect to damper quantity, (B) With respect to input velocity.

Application to Recorded Ground Motions

To investigate the response characteristics of the proposed building with the vibration control system for recorded ground motions, five recorded ground motions (El Centro NS 1940, Taft EW 1952, Hachinohe NS 1968, JMA Kobe NS 1995, and Rinaldi Station FN 1994) were used. The first three motions (El Centro NS 1940, Taft EW 1952, and Hachinohe NS 1968) are often used in Japan for structural design of tall and base-isolated buildings. The maximum ground velocities are adjusted to 0.5 (m/s) as Level-2 motions (called “very rare motion”). On the other hand, for the remaining two motions (JMA Kobe NS 1995, Rinaldi Station FN 1994), original ground motions were used. The maximum ground accelerations of these five ground motions used in this analysis are 5.11, 4.97, 3.49, 8.18, and 8.26 (m/s²). The analysis time of these ground motions except Rinaldi Station FN 1994 is 60 (s) and that of Rinaldi Station FN 1994 is 30 (s).

Figure 15 shows the maximum interstory drifts of the main frame and the sub frame for these five ground motions. Nine damping coefficients of the dampers are used in the range $C_d=0\sim 4.0\times {10}^4\left[\text{kNs}/\text{m}\right]$. It can be observed that the remarkable response reduction cannot be seen over $C_d=2.0\times {10}^4\left[\text{kNs}/\text{m}\right]$ in most cases. This phenomenon corresponds well to the results for the critical double and multi impulses. This means that the critical double and multi impulse analysis represent the response characteristics for most recorded ground motions.

FIGURE 15

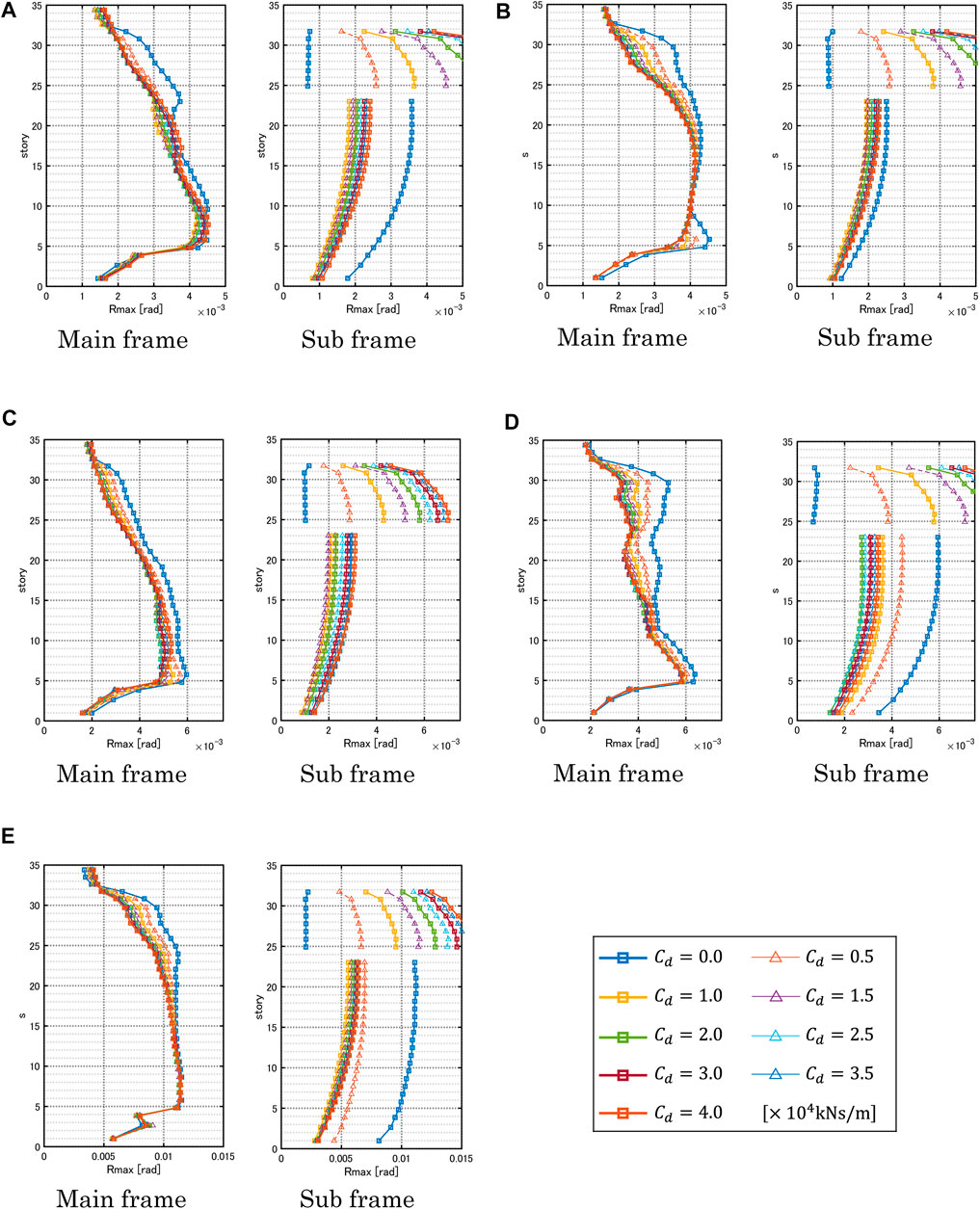
FIGURE 15. Maximum interstory drifts of buildings with nine-level dampers for five recorded ground motions, (A) El Centro NS, (B) Taft EW, (C) Hachinohe NS, (D) JMA Kobe NS, (E) Rinaldi Station FN.

It should also be remarked that, while the analysis for recorded ground motions does not necessarily represent the critical resonant case dependent on the relation between the structure and the input ground motion and on the input level, the analysis for the critical double and multi impulses discloses the intrinsic nature of the critical (resonant) and worst case. This fact can also apply for the incremental dynamic analysis (IDA, Vamvatsikos and Cornell, 2002) and the DIP analysis.

Although the acceleration responses are not shown here, for impulsive ground motions, the critical acceleration responses for the increasing input velocity levels were shown in Figures 3C,D, and for long-duration ground motions, the critical acceleration responses for the increasing input velocity levels were shown in Figures 5C,D. Furthermore, for impulsive ground motions, the critical acceleration responses for various damping coefficient levels of dampers were shown in Figure 10D, and for long-duration ground motions, the critical acceleration responses for various damping coefficient levels of dampers were shown in Figure 12D.

Summaries and Conclusion

The critical responses under a double impulse as a representative of near-fault ground motions and a multi impulse as a representative of long-period long-duration ground motions were sought for a high-rise building with the proposed deformation-concentration vibration control system which was modeled as a three-dimensional (3-D) nonlinear frame. Compared to an elastic-plastic SDOF model and an elastic-plastic single MDOF shear building model, it is complicated to derive the critical response for such complex 3-D nonlinear frames with connected sub frames. A new approach aimed for multi frames was developed based on a criterion on the criticality of input timing of the double and multi impulses for the elastic-plastic multi-frame model and the concepts of “Double Impulse Pushover (DIP)” and “Multi Impulse Pushover (MIP)” introduced in the previous paper were extended. Summaries and conclusions are as follows:

(1) The criteria on the criticality of input timing of the double and multi impulses for a connected 3-D damped nonlinear frames were constructed and the properties of the critical responses were investigated in detail. The critical input timings of the double and multi impulses are the time at which the story shear force (the sum of the story shear force of the main frame and that of the sub frame) in the first story attains zero in the unloading process.

(2) It was shown that the concept of “Double Impulse Pushover (DIP)” and “Multi Impulse Pushover (MIP)” introduced for a single frame model in the previous paper can be extended to multi-frame models. It is noted that only the nonlinear resonant responses were treated in these analyses for the increasing input level. As in the single frame model, the DIP and the MIP enable the progressive performance evaluation for the increasing input level of the double and multi impulses. The existence of the deformation concentration to lower stories for some input level can be captured by these DIP and MIP analyses.

(3) The analysis of total input energy, frame hysteretic dissipation energy and damper dissipation energy and the comparison with the response to the corresponding sinusoidal wave were made to assure the reliability and practicality of the proposed method using the double impulse as a substitute of pulse-type ground motions and the multi impulse as a substitute of long-period long-duration ground motions.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

AK formulated the problem, conducted the computation, and wrote the paper. TM conducted the computation and discussed the results. IT supervised the research and wrote the paper.

Funding

Part of the present work is supported by the Grant-in-Aid for Scientific Research (KAKENHI) of Japan Society for the Promotion of Science (No.18H01584). This support is greatly appreciated.

Conflict of Interest

TM was employed by Takenaka Corporation

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Akehashi, H., Kojima, K., Farsangi, E. N., and Takewaki, I. (2018a). Critical response evaluation of damped bilinear hysteretic SDOF model under long duration ground motion simulated by multi impulse motion. Int. J. Earthq. Impact Eng. 2 (4), 298–321. doi:10.1504/ijeie.2018.099361

CrossRef Full Text | Google Scholar

Akehashi, H., Kojima, K., Fujita, K., and Takewaki, I. (2018c). Critical response of nonlinear base-isolated building considering soil-structure interaction under double impulse as substitute for near-fault ground motion. Front. Built Environ. 4, 34. doi:10.3389/fbuil.2018.00034

CrossRef Full Text | Google Scholar

Akehashi, H., Kojima, K., and Takewaki, I. (2018b). Critical response of single-degree-of-freedom damped bilinear hysteretic system under double impulse as substitute for near-fault ground motion. Front. Built Environ. 4, 5. doi:10.3389/fbuil.2018.00005

CrossRef Full Text | Google Scholar

Akehashi, H., and Takewaki, I. (2020). Comparative investigation on optimal viscous damper placement for elastic-plastic MDOF structures: transfer function amplitude or double impulse. Soil Dyn. Earthq. Eng. 130, 105987. doi:10.1016/j.soildyn.2019.105987

CrossRef Full Text | Google Scholar

Akehashi, H., and Takewaki, I. (2019). Optimal viscous damper placement for elastic-plastic mdof structures under critical double impulse. Front. Built Environ. 5, 20. doi:10.3389/fbuil.2019.00020

CrossRef Full Text | Google Scholar

Beck, J. L., and Hall, J. F. (1986). Factors contributing to the catastrophe in Mexico City during the earthquake of September 19, 1985. Geophys. Res. Lett. 13 (6), 593–596. doi:10.1029/gl013i006p00593

CrossRef Full Text | Google Scholar

Bertero, V. V., Mahin, S. A., and Herrera, R. A. (1978). Aseismic design implications of near-fault San Fernando earthquake records. Earthq. Eng. Struct. Dyn. 6 (1), 31–42. doi:10.1002/eqe.4290060105

CrossRef Full Text | Google Scholar

Caughey, T. K. (1960b). Random excitation of a system with bilinear hysteresis. J. Appl. Mech. 27, 649–652. doi:10.1115/1.3644077

CrossRef Full Text | Google Scholar

Caughey, T. K. (1960a). Sinusoidal excitation of a system with bilinear hysteresis. J. Appl. Mech. 27, 640–643. doi:10.1115/1.3644075

CrossRef Full Text | Google Scholar

Champion, C., and Liel, A. (2012). The effect of near-fault directivity on building seismic collapse risk. Earthq. Eng. Struct. Dyn. 41 (10), 1391–1409. doi:10.1002/eqe.1188

CrossRef Full Text | Google Scholar

De Domenico, D., Ricciardi, G., and Takewaki, I. (2019). Design strategies of viscous dampers for seismic protection of building structures: a review. Soil Dyn. Earthq. Eng. 118, 144–165. doi:10.1016/j.soildyn.2018.12.024

CrossRef Full Text | Google Scholar

Hall, J. F., Heaton, T. H., Halling, M. W., and Wald, D. J. (1995). Near-source ground motion and its effects on flexible buildings. Earthq. Spectra 11 (4), 569–605. doi:10.1193/1.1585828

CrossRef Full Text | Google Scholar

Hashizume, S., and Takewaki, I. (2020). Hysteretic-viscous hybrid damper system with stopper mechanism for tall buildings under earthquake ground motions of extremely large amplitude. Front. Built Environ. 6, 583543. doi:10.3389/fbuil.2020.583543

CrossRef Full Text | Google Scholar

Hatayama, K., Zama, S., Nishi, H., Yamada, M., Hirokawa, Y., and Inoue, R. (2004). Long-period strong ground motion and damage to oil storage tanks due to the 2003 Tokachi-oki earthquake. Jishin 257 (2), 83–103. doi:10.4294/zisin1948.57.2_83

CrossRef Full Text | Google Scholar

Hayashi, K., Fujita, K., Tsuji, M., and Takewaki, I. (2018). A simple response evaluation method for base-isolation building-connection hybrid structural system under long-period and long-duration ground motion. Front. Built Environ. 4, 2. doi:10.3389/fbuil.2018.00002

CrossRef Full Text | Google Scholar

Iwan, W. D. (1961). The dynamic response of bilinear hysteretic systems. PhD thesis. Pasadena (CA): California Institute of Technology.

Google Scholar

Iwan, W. D. (1965b). “The dynamic response of the one-degree-of-freedom bilinear hysteretic system,” in Proceedings of the third world conference on earthquake engineering, Auckland, New Zealand, 2, 783–796.

Google Scholar

Iwan, W. D. (1965a). The steady-state response of a two-degree-of-freedom bilinear hysteretic system. J. Appl. Mech. 32 (1), 151–156. doi:10.1115/1.3625711

CrossRef Full Text | Google Scholar

Kalkan, E., and Kunnath, S. K. (2006). Effects of fling step and forward directivity on seismic response of buildings. Earthq. Spectra 22 (2), 367–390. doi:10.1193/1.2192560

CrossRef Full Text | Google Scholar

Kawai, A., Maeda, T., and Takewaki, I. (2020). Smart seismic control system for high-rise buildings using large-stroke viscous dampers through connection to strong-back core frame. Front. Built Environ. 6, 29. doi:10.3389/fbuil.2020.00029

CrossRef Full Text | Google Scholar

Kawai, A., and Takewaki, I. (2020). Critical response of multi-story damped bilinear hysteretic shear building under multi impulse as representative of long-period long-duration earthquake ground motions. Front. Built Environ. 6, 588980. doi:10.3389/fbuil.2020.588980

CrossRef Full Text | Google Scholar

Khansefid, A., and Bakhshi, A. (2019). Development of declustered processed earthquake accelerogram database for the Iranian Plateau: including near-field record categorization. J. Seismol. 23, 869–888. doi:10.1007/s10950-019-09839-w

CrossRef Full Text | Google Scholar

Khansefid, A. (2020). Pulse-like ground motions: statistical characteristics, and GMPE development for the Iranian Plateau. Soil Dyn. Earthq. Eng. 134, 106164. doi:10.1016/j.soildyn.2020.106164

CrossRef Full Text | Google Scholar

Kohrangi, M., Vamvatsikos, D., and Bazzurro, P. (2018). Pulse‐like versus non‐pulse‐like ground motion records: spectral shape comparisons and record selection strategies. Earthq. Eng. Struct. Dyn. 48 (1), 46–64. doi:10.1002/eqe.3122

CrossRef Full Text | Google Scholar

Kojima, K., and Takewaki, I. (2015a). Critical earthquake response of elastic-plastic structures under near-fault ground motions (Part 1: fling-step input). Front. Built Environ. 1, 12. doi:10.3389/fbuil.2015.00012

CrossRef Full Text | Google Scholar

Kojima, K., and Takewaki, I. (2015b). Critical input and response of elastic-plastic structures under long-duration earthquake ground motions. Front. Built Environ. 1, 15. doi:10.3389/fbuil.2015.00015

CrossRef Full Text | Google Scholar

Kojima, K., and Takewaki, I. (2017). Critical steady-state response of single-degree-of-freedom bilinear hysteretic system under multi impulse as substitute of long-duration ground motion. Front. Built Environ. 3, 41. doi:10.3389/fbuil.2017.00041

CrossRef Full Text | Google Scholar

Kozo System Co (2019). SNAP: software for elastic-plastic analysis of three-dimensional frames of arbitrary shapes. Version 7. http://step.esa.int/main/new-release-of-snap-7-0-public-beta-is-available/.

Google Scholar

Maeda, T., Sone, T., Uozumi, N., Saburi, K., Yanagisawa, N., Zhang, Z., et al. (2020). Structural control system enhancing damping efficiency of dampers by utilizing displacement and velocity gap of double columns. J. Struct. Eng. 66B, 375–385. [in Japanese, with English summary].

Google Scholar

Mavroeidis, G. P., Dong, G., and Papageorgiou, A. S. (2004). Near-fault ground motions, and the response of elastic and inelastic single-degree-freedom (SDOF) systems. Earthq. Eng. Struct. Dyn. 33, 1023–1049. doi:10.1002/eqe.391

CrossRef Full Text | Google Scholar

Takeda, T., Sozen, M. A., and Nielsen, N. N. (1970). Reinforced concrete response to simulated earthquakes. J. Struct. Div. 96 (12), 2557–2573. doi:10.1061/jsdeag.0002765

CrossRef Full Text | Google Scholar

Takewaki, I., Fujita, K., Yamamoto, K., and Takabatake, H. (2011b). Smart passive damper control for greater building earthquake resilience in sustainable cities. Sustain. Cities Soc. 1 (1), 3–15. doi:10.1016/j.scs.2010.08.002

CrossRef Full Text | Google Scholar

Takewaki, I., Moustafa, A., and Fujita, K. (2013). Improving the earthquake resilience of buildings: the worst case approach. London, United Kingdom: Springer-Verlag, 324.

Takewaki, I., Murakami, S., Fujita, K., Yoshitomi, S., and Tsuji, M. (2011a). The 2011 off the Pacific coast of Tohoku earthquake and response of high-rise buildings under long-period ground motions. Soil Dyn. Earthq. Eng. 31 (11), 1511–1528. doi:10.1016/j.soildyn.2011.06.001

CrossRef Full Text | Google Scholar

Takewaki, I. (2013). Toward greater building earthquake resilience using concept of critical excitation: a review. Sustain. Cities Soc. 9, 39–53. doi:10.1016/j.scs.2013.02.001

CrossRef Full Text | Google Scholar

Vamvatsikos, D., and Cornell, C. A. (2002). Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 31 (3), 491–514. doi:10.1002/eqe.141

CrossRef Full Text | Google Scholar