- Department of Architecture and Architectural Engineering, Graduate School of Engineering, Kyoto University, Kyoto, Japan
The optimal and smart design of nonlinear building structures with and without passive dampers subjected to earthquake loading is of great concern in the structural design of building structures. The research started around 1980 and many investigations have been conducted. A comprehensive review on this subject is made in this article. After the description of essential features of the optimal design problem of nonlinear building structures under earthquake ground motions, analysis types of optimization problems are explained and the significance of the dynamic pushover analysis is discussed from the viewpoint of analysis of limit states under earthquake ground motions of magnitude larger than the code-specified level. Then, the categorization by the response of frames and dampers was made. In this categorization, several subjects are discussed first: 1) Optimal design of bare nonlinear building frames under seismic loading, 2) Optimal design of nonlinear dampers for elastic building frames under seismic loading, 3) Optimal design of linear dampers for nonlinear building frames under seismic loading, 4) Optimal design of nonlinear building frames with specified nonlinear dampers under seismic loading, 5) Optimal design of nonlinear dampers for specified nonlinear building frames under seismic loading, 6) Simultaneous optimization of elastic-plastic building structures and passive dampers. Finally, the classification of researches in view of solution strategies is conducted for providing another viewpoint.
Introduction
The optimal design of nonlinear building structures and nonlinear passive dampers under earthquake ground motions is of great concern in the structural design of building structures in earthquake-prone countries. The research on the optimal design of bare nonlinear building frames under dynamic earthquake loading started in 1980s. Because the structural design of building frames under severe earthquake ground motions relied on the capacity of plastic energy dissipation in structural members in the past, the optimal design problem for nonlinear responses of bare frames was one of the main themes. As passive dampers are becoming powerful means for seismic protection and the actual recording of extremely large earthquake ground motions requests the investigation of responses of nonlinear building structures with nonlinear passive dampers at their limit states, the optimal design of linear or nonlinear building structures with dampers and the optimal design of linear or nonlinear passive dampers used for linear building frames are getting much interest from the viewpoints of theoretical, numerical and practical significances.
In this article, the optimal design of nonlinear building structures and nonlinear passive dampers is reviewed. Several subjects are discussed (see Figure 1) first: 1) Optimal design of bare nonlinear building frames under seismic loading, 2) Optimal design of nonlinear dampers for elastic building frames under seismic loading, 3) Optimal design of linear dampers for nonlinear building frames under seismic loading, 4) Optimal design of nonlinear building frames with specified nonlinear dampers under seismic loading, 5) Optimal design of nonlinear dampers for specified nonlinear building frames under seismic loading, 6) Simultaneous optimization of elastic-plastic building structures and passive dampers. The significance of the dynamic pushover analysis is discussed from the viewpoint of analysis of limit states under earthquake ground motions of magnitude larger than the code-specified level. Finally, the classification of researches in view of solution strategies is conducted for providing another viewpoint.
Although the optimal design of linear elastic building structures with and without linear dampers has been treated extensively in the field of structural optimization using mathematical programming procedures, they will not be treated here. The response evaluation methods, e.g. a time-history response analysis method, a response spectrum method, can be used efficiently and the optimization of such structures may be straightforward. Furthermore, base-isolation systems, single TMD (tuned-mass-damper) systems and other dampers for single-story frames are not treated here because elastic frame designs are their main targets or frame designs are not intended.
Dual design criteria for DBE (design base earthquake) and MCE (maximum credible earthquake) in the optimal design of linear and nonlinear building frames were introduced by the Pister’s research group in 1980s (for example Balling et al., 1983). The predominant period and its relation with structural natural period together with the type of earthquakes are examples of important factors in selecting earthquake ground motions for reliable fragility analysis. However, this reliable setting of design earthquake ground motions is a hard task because of insufficient development of theoretical analysis on occurrence probability of earthquakes and insufficient data on uncertain wave propagation. To tackle this difficult problem from another viewpoint, the critical excitation method was developed. The double impulse pushover (DIP) analysis (Akehashi and Takewaki 2019), a kind of fragility analysis, deals with only the nonlinear resonant response for the increasing input level.
Optimal Seismic Design Problem of Nonlinear Building Structures
Essential Features of Optimal Design Problem of Nonlinear Building Structures Under Earthquake Ground Motions
It may be critical in understanding the intrinsic natures of optimal design problems of nonlinear building structures under earthquake ground motions to describe the essential features of such problems. The difficulties in investigating such problems can be stated as follows:
(1) The nonlinear time-history response analysis is the only method for evaluating the accurate responses of nonlinear building structures under random earthquake ground motions. It is costly and accuracy check is mandatory for reliable processing of optimization procedures.
(2) The design modification or update (redesign) approach based on response sensitivity is useful, but does not necessarily provide the global minimum solutions.
(3) Genetic algorithm or other metaheuristic methods can lead to the global optimal solution with high possibilities, but its handling may not be easy and may sometimes be costly.
Many attempts have been conducted to tackle and resolve the above-mentioned difficulties. In the following sections, original reviews will be provided. In the former section (Section Categorization by Response of Building Frames and Dampers), the categorization by the response of frames and dampers is made. Then in the latter section (Section Classification in View of Solution Strategies), the classification by the strategies of solution procedures is provided.
Incremental Dynamic Analysis and Double Impulse Pushover Analysis
Optimal seismic design problems of nonlinear building structures for design earthquake ground motions with a given input level can be solved by mathematical programming approaches, optimality criteria approaches, the GA-based or partially GA-based approaches, metaheuristic approaches, combined approaches of the sensitivity-based procedure and the optimality criteria (or some preferences)-based procedure, etc. The categorization in view of such analysis type of optimal design problems will be presented in Section Classification in View of Solution Strategies.
Recently, many earthquake ground motions of magnitude extremely larger than the code-specified level have been reported (Northridge 1994; Hyogoken-Nanbu (Kobe) 1995; East Japan earthquake 2011; Kumamoto 2016). This fact strongly suggested the need to investigate the critical limit state of inelastic building structures with and without passive dampers. The static pushover analysis was first introduced to evaluate the elastic-plastic restoring-force characteristics of building structures under monotonic loading. The modal pushover analysis was then proposed to take into account the higher-mode effect on the restoring-force characteristics. To reflect the influence of input level and randomness of earthquake ground motions on the structural response, IDA (incremental dynamic analysis) was further proposed by Vamvatsikos and Cornell (2001). In IDA, a set of representative ground motions are selected by normalizing the input level and a series of nonlinear time-history response analysis are conducted for the increasing input level of such set of ground motions. It is well known that the selection of such representative ground motions affects much on the resulting nonlinear restoring force characteristics.
Although the IDA procedure is a good technique to reflect the input level and randomness of earthquake ground motions and clarify the limit state of elastic-plastic structures under dynamic loading in terms of force-deformation relations, it may be clear that the resonant critical case should be considered adequately to reach the true limit state. To respond to this request, the DIP (double impulse pushover) analysis was proposed by Akehashi and Takewaki (2019). The acceleration of the double impulse
Categorization by Response of Building Frames and Dampers
Optimal Design of Bare Nonlinear Building Frames Under Seismic Loading
The research group of Dr. Pister developed a general optimal design approach using the mathematical programming for elastic and elastic-plastic building frames in 1980s (Bhatti and Pister, 1981; Bhatti et al., 1981; Balling et al., 1981a; Balling et al., 1981b; Balling et al., 1983; Austin et al., 1985; Austin et al., 1987). They used the feasible direction method as one of the mathematical programming techniques. Bhatti et al. (1981) introduced the dual criteria for the response constraints under variable design earthquake ground motions. Balling et al. (1981a); Balling et al. (1981b); Balling et al. (1983) investigated the applicability of the mathematical programming approach to various response constraints under several design earthquake ground motions. Austin et al. (1985) and Austin et al. (1987) discussed a more general optimal design method for nonlinear building frames with passive dampers (friction dampers).
Nakamura and Takewaki (1989) proposed a uniform ductility design using the optimal nonlinear elastic frames for static loading. If the envelope of the maximum horizontal loads induced by the earthquake ground motions can be evaluated appropriately, this static approach may be reasonable. Insensitiveness of story shears in nonlinear building frames (softening type in most cases) with respect to design change seems to enable the development of such static load-based design method. Takewaki et al. (1991) developed a multi-objective optimal design method for elastic-plastic building frames under a set of uncertain ground motions based on the dissatisfaction description of objectives and constraints similar to the Fuzzy theory. They constrained the design space by expressing the frame member design parameters in terms of simple deformation parameters. Takewaki (1997a) introduced a new technique for bounding the maximum elastic-plastic responses of inelastic building frames under the spectrum-compatible earthquake ground motions. In this response bounding, the response spectrum method for evaluating the maximum deformation (ductility) was introduced and the property of acceleration response spectra was used, i.e., monotonically decreasing properties with respect to natural period and damping ratio.
Optimal Design of Nonlinear Dampers for Elastic Building Frames Under Seismic Loading
There are several popular dampers used in the structural design of building structures. Nonlinear fluid viscous dampers (FVD: often called oil dampers), viscous wall dampers, viscoelastic dampers (high-damping rubber dampers), buckling restrained braces (BRB), other hysteretic dampers, inertial mass dampers are examples. FVD is modeled by a bilinear force-velocity rule and hysteretic dampers are modeled by some hysteretic rules, e.g. elastic-perfectly plastic rule. Figure 2 shows the damping force-relative velocity relation of nonlinear FVD and Figure 3 indicates the damping force-deformation relations of a linear (or nonlinear) viscous damper, a viscoelastic damper, a hysteretic damper and an inertial mass damper. The research by Zhang and Soong (1992) may be the first theoretical approach using a simple optimization algorithm incorporating response sensitivity analysis of frames including viscoelastic dampers and it seems easy to apply this approach to more general optimization problems. Takewaki (2009) summarized the history of passive structural control by the year of 2008 and presented some methods for optimal design of passive dampers in linear or nonlinear building structures. Then De Domenico et al. (2019) presented a thorough review on the research using viscous dampers. It is not easy to extend the discussion on viscous dampers to hysteretic dampers because it is well known that the hysteretic dampers induce unstable design sensitivities due to the drastic change of stiffness resulting from the stiffness addition and yielding of hysteretic dampers (Murakami et al., 2013).
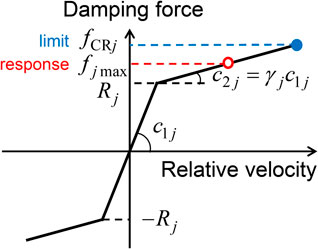
FIGURE 2. Damping force-relative velocity relation of nonlinear fluid viscous damper (FVD, often called oil damper) (Adachi et al., 2013).

FIGURE 3. Force-deformation relations of viscous damper (linear and nonlinear), viscoelastic damper, hysteretic damper and inertial mass damper.
Uetani et al. (2003) proposed a mathematical programming-based optimal design method of hysteretic dampers and viscous dampers for a fixed linear elastic building frame which was designed under many usual design constraints. They developed an optimization algorithm (Gradient-projection method) for frames with hysteretic dampers and introduced a two-step design method using an inverse-problem formulation for frames with viscous dampers. They modeled the main frame experiencing inelastic responses under severe design ground motions into an equivalent linear model. Then, they applied the proposed method to an actual high-rise building in Osaka, Japan.
Martinez-Rodrigo and Romero (2003) built a simple method which leads to an optimum retrofitting by using nonlinear fluid viscous dampers. Lee et al. (2008) developed a seismic design method of friction dampers based on the story shear force distribution of an elastic building structure. They used the optimal stiffness ratios of the brace vs. primary structure.
There are some researches using the genetic algorithm (GA). Moreschi and Singh (2003) presented a method to find the optimal design parameters of passive dampers in a building attaining a desired performance objective. For metallic dampers, the device yield level, device stiffness, and brace stiffness were chosen as design parameters. For friction dampers, the slip load level and brace stiffness were selected as parameters. To solve this, a genetic algorithm was used. Apostolakis and Dargush (2010) proposed a numerical procedure for finding the optimal design of yielding buckling restrained braces and friction dampers in steel moment-resisting frames under seismic loading. A genetic algorithm was used to solve the discrete optimum design problem. Although GA has some advantages, i.e., possibility of search of global optimal designs, facilitation of use of discrete optimal design problems, etc., researchers have to be accustomed to its use and have to learn about the aspects for what parameters should be selected as GA variables and how to reduce the computational load.
Silvestri et al. (2010) and Palermo et al. (2017) proposed a practical design method of linear and nonlinear viscous dampers for building frames. Their methods consist of five steps for complete implementation. The design philosophy is aimed at limiting the structural damages under severe earthquakes. A target damping reduction factor is chosen first to satisfy the requirement on the desired reduction in terms of the peak structural response. The damping coefficients of the equivalent linear viscous dampers for nonlinear dampers are computed by using effectively the properties of modal damping ratios as classically damped systems. Simple analytical formulas for the estimation of peak interstory velocities are then used and an energy criterion is also established to identify the non-linear mechanical characteristics of viscous dampers. Finally, the responses of structural elements are estimated from the maximum responses of two equivalent static analyses.
Adachi et al. (2013) developed an innovative optimal design method for nonlinear oil dampers (FVD) by employing relief forces of oil dampers as design variables and introducing a sensitivity-based optimization algorithm. The optimal design problem includes a constraint on the maximum ratio of the damping force to the relief force and a constraint on the total quantity of relief forces in oil dampers. They transformed the original problem of minimizing the maximum interstory drift into another problem to find the most inactive damper and to reduce the quantity of such damper sequentially. Murakami et al. (2013) investigated a problem of simultaneous optimization of hysteretic dampers, oil dampers (FVD) and inertial dampers. They pointed out a difficulty in performing the sensitivity analysis for hysteretic dampers under irregular recorded ground motions and devised a smart technique for such sensitivity analysis (taking mean sensitivity for several sensitivity analyses). They presented an algorithm of computing simultaneous sensitivities for three dampers. Lang et al. (2013) and Fujita et al. (2014) investigated an optimization problem for nonlinear viscous dampers by using an original technique, called the output frequency response function formulation, in frequency domain for nonlinear system.
Castaldo and De Iuliis (2014) presented an integrated seismic design procedure for tall buildings with viscous dampers and viscoelastic dampers. An energy dissipating brace-damper system was proposed and developed to check a seismic design performance in the framework of the displacement-based design. They took into account the dynamic behavior of structure and control systems. The integrated seismic optimal design was defined as the variables that minimizes a suitable index.
Pollini et al. (2017a) presented an effective approach for attaining the minimum-cost design for seismic retrofitting using nonlinear fluid viscous dampers. The damper damping coefficients and the stiffness of the supporting braces were designed optimally. A retrofitting cost was minimized subject to constraints on interstory drifts at the peripheries of frame structures. The cost function accounts for costs related to both the topology and the sizes of the dampers. The behavior of each damper-brace element was defined by the Maxwell model.
Parcianello et al. (2017) investigated an optimization-based approach for the design of nonlinear viscous dampers which are installed to improve the seismic behavior of frame structures. They showed the validity of the proposed method through an illustrative example in which it is demonstrated how different structural requirements (minimization of interstory drifts and/or forces transferred by the devices) can be easily taken into account.
Shiomi et al. (2018) presented a sensitivity-based hysteretic damper optimization method in which dual hysteretic dampers for short and long amplitude ranges are used and the long-amplitude range dampers include a gap mechanism. They examined the reliability of the proposed method by comparing with the result by a genetic algorithm.
De Domenico and Ricciardi (2019) investigated an optimization problem of nonlinear viscous dampers used in building frames. The nonlinear power law in the constitutive relation of the devices was introduced in the optimal design process. The proposed strategy included a performance criterion based on the energy balance equation of the system in terms of stochastic parameters. To handle the nonlinear characteristics of the fluid viscous dampers, a new equal-energy non-Gaussian stochastic linearization technique was utilized.
Optimal Design of Linear Dampers for Nonlinear Building Frames Under Seismic Loading
In this section, the optimal design of linear dampers for nonlinear building frames under seismic loading is reviewed. Since elastic-plastic responses are easy to induce higher-mode responses (Akehashi and Takewaki, 2020a), the optimal allocation of linear dampers plays an important role.
Wongprasert and Symans (2004) presented a method for finding the optimal distribution of dampers to control the response of a 20-story building under earthquake ground motions. A genetic algorithm was employed to determine the damper locations. In the optimization, H2 and H∞-norms of the transfer function were used as the objective functions. Weighting in the frequency domain was introduced so that the genetic algorithm works well in the minimization of the response in the second mode instead of the dominant first mode.
Lavan and Levy (2005) presented an optimal design method of viscous dampers for regular as well as irregular yielding shear-type building structures. They discussed the problem of minimizing the quantity of added damping under a constraint on a damage index in terms of energy for an ensemble of realistic recorded ground motions. The application of the method to irregular structures was conducted by choosing an appropriate energy-based global damage index. A gradient-based approach was developed and the design of equal damage for all stories was achieved.
Attard (2007) proposed an optimization algorithm of gradient-base to control all interstory displacements in nonlinearly degrading steel building frames with the optimal viscous dampers. The optimal damping ratios were computed in each vibration mode by minimizing the sum of the errors between the interstory displacements and the just-yielded performance objectives.
Aydin et al. (2007) extended the method of Takewaki (1997b) treating the transfer function amplitude of the top displacement of a structure into the problem of optimization of the transfer function amplitude for the base shear force at the fundamental natural frequency in the retrofitting of building frames. In the optimization process, the damper damping coefficients were treated as design variables. An active constraint was considered on the sum of the damper damping coefficients and the upper and lower bounds of damper level were taken into consideration in each damper. Although their approach is limited to elastic models, the concept of base shear force design is unique.
Cimellaro and Retamales (2007) presented three techniques for determining the optimal locations of dampers and the corresponding capacities of dampers and softened stories. Three optimal design procedures were proposed: 1) a procedure for finding the optimal story stiffnesses and damper quantities that minimize the sum of amplitudes of the transfer functions of inter-story drifts, 2) an optimal control theory-based method incorporating a gain matrix obtained from the linear quadratic regulator (LQR) algorithm, 3) a modification of the simplified sequential search algorithm (SSSA).
Lavan et al. (2008) presented a technique of weakening and damping that limits the total acceleration through the weakening, and decreases the interstory drifts by introducing damping. They investigated the optimal weakening and damping by searching for the optimal locations and quantity of structural components for weakening as well as the optimal locations and quantities of added dampers. They used a nonlinear active control procedure and found the control forces which were calculated and implemented by using equivalent passive dampers and weakening elements. A case study of an eight-story nonlinear building was conducted to show the validity of the proposed method. It was clarified that the optimal design is effective for the reduction of both peak interstory drifts and peak total accelerations.
Cimellaro et al. (2009) developed a design procedure for control of buildings experiencing inelastic deformations under seismic loading. The strategy is using weakened, and/or softened, elements to control simultaneously accelerations and deformations. They presented a two-stage design procedure: first 1) to use an algorithm of nonlinear active control for determining the new structural parameters while insuring stability, then 2) to determine the properties of equivalent structural parameters of passive systems, which can be achieved by removing or weakening some structural elements, or connections, and by adding energy dissipation systems. Passive dampers and weakened elements were designed by introducing an optimization algorithm to capture a response as close as possible to an actively controlled system.
Lavan and Levy (2010) presented an optimal seismic design of added viscous dampers in yielding plane frames. The total added damping was minimized for some local performance indices (maximum interstory drift and/or normalized hysteretic energy dissipated at plastic hinges) under the excitation of an ensemble of ground motions in both regular and irregular structures.
Lavan and Avishur (2013) examined the sensitivity of the response of optimally damped frames with respect to uncertainty level in structural and damping properties. Viscous dampers were first designed in an optimal manner for nominal properties of the retrofitted structures and a given ensemble of records for each structure. The maximum interstory drift of the retrofitted structures under the consideration of uncertainty in their member and damper properties was then evaluated using Monte Carlo simulation. It was clarified that the uncertain properties lead to larger mean interstory drifts than those without uncertainty, and that some designs are more sensitive than others. They clarified the reasons for this response.
Aguirre et al. (2013) evaluated the optimal distribution of damper in linear and nonlinear systems. A procedure of optimization was presented using control indices called a min–max algorithm. Then, this technique was compared with two simple methodologies: 1) the fully stressed design, and 2) the simplified sequential search algorithm (SSSA). It was pointed out that the SSSA is a fixed-step descent-type method. The employed examples showed that the SSSA is a discrete approximation of the min–max algorithm for linear and nonlinear structures with linear and nonlinear passive dampers.
Lavan (2015) presented a novel procedure for the design of nonlinear structures with passive viscous dampers exhibiting desired interstory drifts. The method also reduced seismic forces as well. The author used a negative stiffness device.
Elias and Matsagar (2019) and Elias et al. (2019) dealt with nonlinear frame responses using multiple TMD optimization. It is noted that, although single TMD is effective for the control of linear frames, multiple TMDs were taken full advantage.
Akehashi and Takewaki (2019) developed a new strategy for finding optimal viscous damper placement in elastic-plastic MDOF structures subjected to the critical double impulse as a representative of near-fault ground motions. The double impulse is composed of two impulses with opposite directions and the critical interval of two impulses is characterized by the clear criterion on the maximum input energy by the second impulse. The objective function and the constraint in terms of the maximum interstory drift or the sum of the maximum interstory drifts in all stories were selected and the reliability of the corresponding optimization algorithm including time-history response analysis and sensitivity analysis was examined. Another new concept of double impulse pushover (DIP) analysis explained in Section Incremental Dynamic Analysis and Double Impulse Pushover Analysis was proposed for determining the input velocity level of the critical double impulse in view of the magnitude of inelastic responses. They presented three algorithms for three problems, (Algorithm 1 for Problem 1): minimization of total damper quantity under the condition that all the maximum interstory drifts are smaller than the target values, (Algorithm 2 for Problem 2): minimization of the sum of the maximum interstory drifts under the constraint on total damper quantity, (Algorithm 3 for Problem 3): application of Algorithm 1 and Algorithm 2 in this sequence. It was demonstrated that in Algorithm 1 for Problem 1, the analysis in the elastic range is not easy because of the inability to set the total damper quantity and the maximum interstory drift distribution is unstable (not uniform) in the final model obtained by Algorithm 2 for Problem 2 depending on the model. On the contrary, it was confirmed that a stable damper allocation is possible only by Algorithm 3 for Problem 3 and the final maximum interstory drift distributions often become uniform. They clarified that the minimum performance can be obtained by Algorithm 3 by using a small amount of passive dampers and the structural response reduction can be conducted globally by using the additional amount of passive dampers. They treated three models: (Model 1): uniform distribution of story stiffnesses, (Model 2): straight-line lowest eigenmode (often called inverse triangular), (Model 3) stepped distribution of story stiffnesses in each group of several stories (upper four stories, middle four stories and lower four stories have uniform stiffness distributions with different values: the ratios among them are 1:1.5:2).
Figure 4 presents the maximum interstory drifts
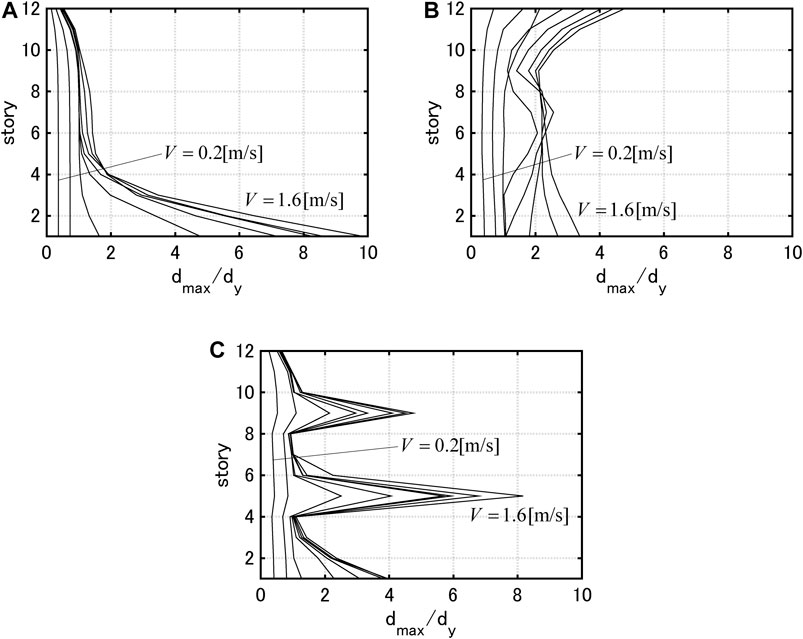
FIGURE 4. Maximum interstory drift by the DIP analysis: (A) Model 1, (B) Model 2, (C) Model 3 (Akehashi and Takewaki, 2019).
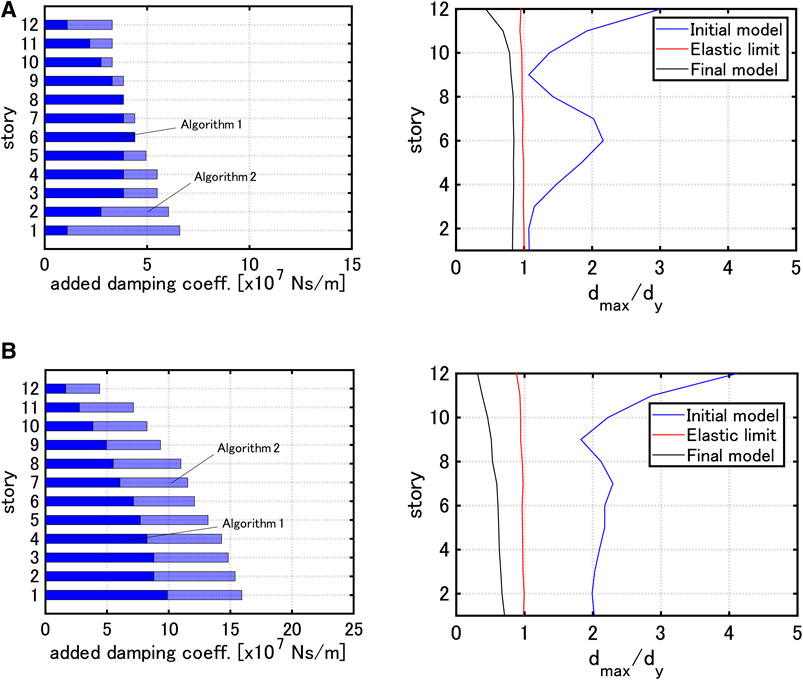
FIGURE 5. Distribution of added damping coefficients and distribution of
Akehashi and Takewaki (2020a) discussed the effectiveness of the derived optimal viscous damper placement for elastic-plastic MDOF structures under the critical double impulse by comparing with the optimal damper placement for elastic MDOF structures designed based on the criterion, proposed by Takewaki (1997b), on the transfer function amplitudes at natural frequencies. It was made clear that the optimal viscous damper placement for elastic-plastic MDOF structures under the critical double impulse is more effective for pulse-type recorded earthquake ground motions than the optimal damper placement designed with respect to transfer function amplitudes at natural frequencies. This is because several higher modes arising in the elastic-plastic response under pulse-type recorded earthquake ground motions can be well captured and controlled by the design for the double impulse.
As stated above, De Domenico et al. (2019) presented a comprehensive review on the design of building structures with passive dampers.
Optimal Design of Nonlinear Building Frames with Specified Nonlinear Dampers Under Seismic Loading
The research on the optimal design of nonlinear building frames with specified nonlinear dampers under seismic loading is very limited. This is because passive dampers are usually installed to keep main frames within the elastic limit for avoiding unnecessary damage to the main frames from the viewpoint of “resilience.” Austin and Pister (1985) presented a mathematical programming-based optimal design method (feasible direction algorithm) of nonlinear building frames with friction dampers. The compressive resistance of the friction joint was set to zero and the allowable tensile friction force was given as the product of section area times the brace yield stress. They treated three design load types, gravity loads alone, gravity loads + moderate earthquake and gravity loads + sever earthquake. Minimum volume, minimum dissipated energy and minimum sum of squared story drifts were chosen as objective functions.
Optimal Design of Nonlinear Dampers for Specified Nonlinear Building Frames Under Seismic Loading
The research on the optimal design of nonlinear dampers for specified nonlinear building frames under seismic loading is also very limited. The usual structural design objective using passive dampers stated just above may be one of the principal reasons. However, the actual recording of extremely large earthquake ground motions requests the investigation of responses of nonlinear building structures with nonlinear passive dampers at their limit states.
Pollini et al. (2017b) formulated a consistent adjoint sensitivity analysis for optimizing hysteretic dynamic systems subjected to transient excitation and including nonlinear viscous dampers.
Altieri et al. (2018) proposed a new method for the optimal design of nonlinear viscous dampers in building frames considering the effects of uncertainties in intensity, duration and frequency content. The method enables to find the optimal damper properties that minimize an objective function related to the dampers cost together with considering a constraint on the performance of the nonlinear frame.
Wang and Mahin (2017); Wang and Mahin (2018) proposed an optimization procedure of nonlinear fluid viscous dampers to improve the seismic performance of high-rise buildings. An existing 35-story steel moment-resisting frame was chosen as a case-study building to verify this procedure. The retrofit design was conducted to improve the building's seismic performance. This was aimed to avoid collapse under a Level 2 in the basic safety earthquake event. An objective function of building's total loss under such event was used and its optimal damper patterns were proposed. The efficiency of the optimization procedure was demonstrated and compared with the manual procedure.
Simultaneous Optimization of Elastic-Plastic Building Structures and Passive Dampers
The research due to Austin and Pister (1985) includes the treatment of simultaneous optimization of elastic-plastic building structures and passive dampers (friction-damped braces). Since their approach is general, the subsequent researches have not appeared at once.
Idels and Lavan (2020) proposed a mathematical programming-based approach to the simultaneous optimization of elastic-plastic steel building frame and nonlinear viscous dampers. The optimization problem was first formulated as a mixed-integer problem. Then the problem was reformulated in a continuous differentiable form and solved using an efficient gradient-based optimization approach. In the selection of discrete design variables (discrete member sections), GA was used effectively.
Akehashi and Takewaki (2020b) proposed a simple sensitivity-based method for simultaneous optimization of elastic-plastic main building structures and linear viscous dampers. They pointed out that the cycle-by-cycle alternating redesign of structural stiffness and damper damping magnitude is critical to the achievement of reasonable designs. They derived an important conclusion that the proposed simultaneous optimal design method enables the high yield-strength design with effective seismic energy absorption and the high limit-strength design effective for extremely large disturbances, as shown in Figure 6. They showed an example of the simultaneous optimal design for the total damper quantity (total damping coefficient)
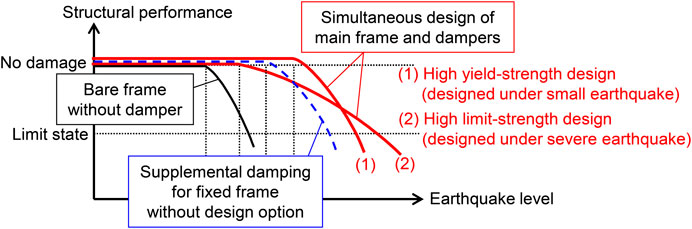
FIGURE 6. Concept of simultaneous design of main structures and dampers (Akehashi and Takewaki, 2020b).
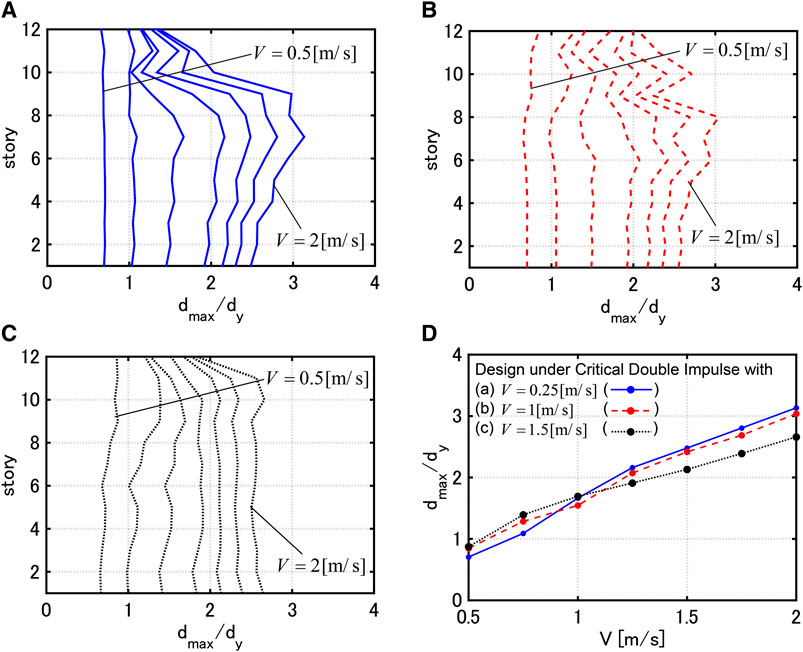
FIGURE 7. DIP analysis for three models, (A) Model designed for
To demonstrate the validity of use of the critical double impulse for design, the designed frames with dampers were subjected to two recorded near-fault ground motions. Figure 8 illustrates the maximum interstory drifts for amplified recorded ground motions (Rinaldi Station FN during Northridge 1994; Kobe Univ NS during Hyogoken-Nanbu 1995). It can be observed that the deformations in the middle and lower stories are large for the model designed for
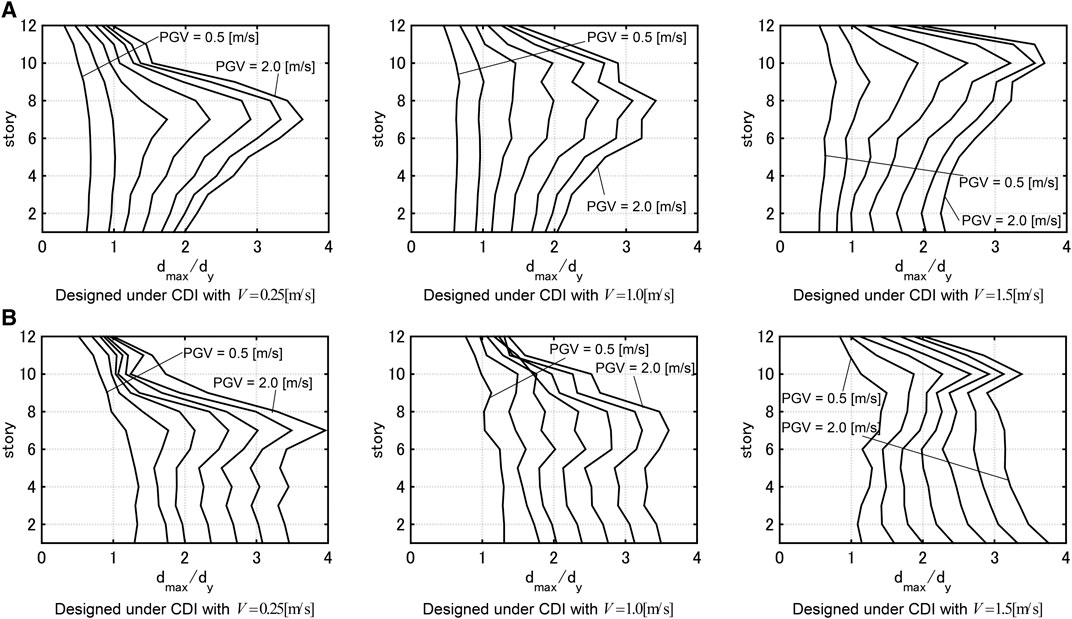
FIGURE 8. Maximum interstory drifts for amplified recorded ground motions, (A) Rinaldi station FN (Northridge, 1994), (B) Kobe Univ NS (Hyogoken-Nanbu, 1995) (Akehashi and Takewaki, 2020b).
Classification in View of Solution Strategies
In this review, papers are limited to the problems dealing with models including nonlinear frames and/or nonlinear dampers under earthquake ground motions. In Section Categorization by Response of Building Frames and Dampers, the categorization by the response of frames and dampers was made because the researches were advanced gradually by taking into account nonlinear responses and the categorization from this viewpoint is useful in its history. On the contrary, in this section, the classification by the strategies of solution procedures is provided. Although clear classification is difficult because most researches use several solution strategies and sometimes combine them, an attempt is conducted by taking the principal aspects.
The mathematical programming approach (feasible direction method, gradient projection method, etc.) is the most general solution strategy. This is a kind of response sensitivity-based approaches including objective function sensitivity. As explained before, a general optimal design approach using the mathematical programming for elastic and elastic-plastic bare building frames in 1980s (Bhatti and Pister 1981; Bhatti et al., 1981; Balling et al., 1981a; Balling et al., 1981b; Balling et al., 1983; Austin et al., 1985; Austin et al., 1987). As the computer power becomes large, many contributions have been accumulated. Examples using this approach cited in the above sections are Uetani et al. (2003); Lavan and Levy (2005); Attard (2007); Aydin et al. (2007); Lavan et al. (2008); Lavan and Levy (2010); Lavan and Avishur (2013); Lavan (2015); Pollini et al. (2017b); Altieri et al. (2018); Elias and Matsagar (2019); Elias et al. (2019). It should be remarked that, although the mathematical programming approach can solve various kinds of structural design problems, it seems difficult to derive design formulas that lead to design guidelines.
The second approach is the optimality criteria approach initiated by Dr. Prager in 1960–70s. Most of this approach were developed for elastic global performances, e.g., fundamental natural frequency etc., and local response constraints were checked as a result. Most of such researches deal with elastic response or inelastic response under static loads because the costly nonlinear time-history response analysis is the only method for evaluating the accurate responses of nonlinear building structures under random earthquake ground motions as explained in Section Essential Features of Optimal Design Problem of Nonlinear Building Structures Under Earthquake Ground Motions. Since this approach does not use the nonlinear time-history response analysis directly in the optimization process, the accuracy and reliability are somewhat lower than the methods using the nonlinear time-history response analysis. Examples in this approach cited in the above sections are Nakamura and Takewaki (1989); Takewaki et al. (1991); Nakamura et al. (1993); Takewaki (1997a).
The GA-based or partially GA-based approaches and metaheuristic approaches were successfully developed independently. In these approaches, a sophisticated strategy for reducing the number of selections of GA parameters becomes important because the costly nonlinear time-history response analysis has to be implemented in the redesign stage. Examples included in this branch and cited in the above sections are Moreschi and Singh (2003); Wongprasert and Symans (2004); Apostolakis and Dargush (2010); Shiomi et al. (2018); Idels and Lavan (2020).
The last one is a combined approach of the sensitivity-based procedure and the optimality criteria (or some preferences)-based procedure. This approach was developed for reducing the burden encountered in the costly nonlinear time-history response analysis. Examples in this approach cited in the above sections are Zhang and Soong (1992); Martinez-Rodrigo and Romero (2003); Cimellaro and Retamales (2007); Lee et al. (2008); Cimellaro et al. (2009); Silvestri et al. (2010); Aguirre et al. (2013); Adachi et al. (2013); Murakami et al. (2013); Lang et al. (2013); Fujita et al. (2014); Castaldo and De Iuliis (2014); Palermo et al. (2017); Pollini et al. (2017a); Parcianello et al. (2017); Wang and Mahin (2017); Wang and Mahin, (2018); De Domenico and Ricciardi (2019); Akehashi and Takewaki (2019); Akehashi and Takewaki (2020a); Akehashi and Takewaki (2020b).
Conclusion
A comprehensive review on the optimal and smart design of nonlinear building structures with and without passive dampers subjected to earthquake loading was conducted. After the start of the investigations around 1980, many significant investigations have been accumulated. First, the essential features of the optimal design problem of nonlinear building structures under earthquake ground motions were described. In addition, analysis types of optimization problems were explained and the significance of the dynamic pushover analysis was discussed from the viewpoint of analysis of limit states under earthquake ground motions of magnitude larger than the code-specified level. Then, the categorization by the response of frames and dampers was made. In this categorization, several subjects were discussed: 1) Optimal design of bare nonlinear building frames under seismic loading, 2) Optimal design of nonlinear dampers for elastic building frames under seismic loading, 3) Optimal design of linear dampers for nonlinear building frames under seismic loading, 4) Optimal design of nonlinear building frames with specified nonlinear dampers under seismic loading, 5) Optimal design of nonlinear dampers for specified nonlinear building frames under seismic loading, 6) Simultaneous optimization of elastic-plastic building structures and passive dampers. Finally, the classification of researches in view of solution strategies was conducted for providing another viewpoint.
Author Contributions
IT surveyed the research and wrote the paper. HA surveyed the research, wrote the paper and draw the figures.
Funding
Part of the present work is supported by the Grant-in-Aid for Scientific Research (KAKENHI) of Japan Society for the Promotion of Science (Nos. 18H01584 and JP20J20811). This support is greatly appreciated.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Adachi, F., Yoshitomi, S., Tsuji, M., and Takewaki, I. (2013). Nonlinear optimal oil damper design in seismically controlled multi-story building frame. Soil Dynam. Earthq. Eng. 44 (1), 1–13. doi:10.1016/j.soildyn.2012.08.010
Aguirre, J. J., Almazán, J. L., and Paul, C. J. (2013). Optimal control of linear and nonlinear asymmetric structures by means of passive energy dampers. Earthq. Eng. Struct. Dynam. 42 (3), 377–395. doi:10.1002/eqe.2211
Akehashi, H., and Takewaki, I. (2020a). Comparative investigation on optimal viscous damper placement for elastic-plastic MDOF structures: transfer function amplitude or double impulse. Soil Dynam. Earthq. Eng. 130, 105987. doi:10.1016/j.soildyn.2019.105987
Akehashi, H., and Takewaki, I. (2019). Optimal viscous damper placement for elastic-plastic MDOF structures under critical double impulse. Front. Built Environ. 5, 20. doi:10.3389/fbuil.2019.00020
Akehashi, H., and Takewaki, I. (2020b). Simultaneous optimization of elastic-plastic building structures and viscous dampers under critical double impulse. Front. Built Environ. 6, 623832. doi:10.3389/fbuil.2020.623832
Altieri, D., Tubaldi, E., De Angelis, M., Patelli, E., and Dall’Asta, A. (2018). Reliability-based optimal design of nonlinear viscous dampers for the seismic protection of structural systems. Bull. Earthq. Eng. 16 (2), 963–982. doi:10.1007/s10518-017-0233-4
Apostolakis, G., and Dargush, G. F. (2010). Optimal seismic design of moment-resisting steel frames with hysteretic passive devices. Earthq. Eng. Struct. Dynam. 39, 355–376. doi:10.1002/eqe.944
Attard, T. L. (2007). Controlling all interstory displacements in highly nonlinear steel buildings using optimal viscous damping. J. Struct. Eng. 133 (9), 1331–1340. doi:10.1061/(asce)0733-9445(2007)133:9(1331)
Austin, M. A., and Pister, K. S. (1985). Design of seismic-resistant friction-braced frame. J. Struct. Eng. 111 (12), 2751–2769. doi:10.1061/(asce)0733-9445(1985)111:12(2751)
Austin, M. A., Pister, K. S., and Mahin, S. A. (1985). Report No.UCB/EERC-85/13, December 1985. A methodology for the computer-aided design of seismic-resistant steel structures. Berkeley, CA: Earthquake Engineering Research Center, University of California, Berkeley.
Austin, M. A., Pister, K. S., and Mahin, S. A. (1987). Probabilistic design of moment-resistant frames under seismic loading. J. Struct. Eng. 113 (8), 1660–1677. doi:10.1061/(asce)0733-9445(1987)113:8(1660)
Aydin, E., Boduroglub, M. H., and Guney, D. (2007). Optimal damper distribution for seismic rehabilitation of planar building structures. Eng. Struct. 29, 176–185. doi:10.1016/j.engstruct.2006.04.016
Balling, R. J., Bhatti, M. A., Ciampi, V., and Pister, K. S. (1981a). “Interactive optimal design of dynamically loaded structures using the optnsr software system,” Proceedings of international symposium on optimum structural design, the 11th ONR naval structural mechanics symposium, Tucson, AZ, October 19–22, 1981 (Tucson, AZ: University of Arizona), 12.9–12.17.
Balling, R. J., Pister, K. S., and Ciampi, V. (1983). Optimal seismic-resistant design of a planar steel frame. Earthq. Eng. Struct. Dynam. 11, 541–556. doi:10.1002/eqe.4290110407
Balling, R. J., Pister, K. S., and Polak, E. (1981b). Report No. UCB/EERC-81/19, December 1981. DELIGHT.STRUCT: a computer-aided design environment for structural engineering. Berkeley, CA: Earthquake Engineering Research Center, University of California, Berkeley.
Bhatti, M. A., Ciampi, V., Pister, K. S., and Polak, E. (1981). “An interactive software system for optimal design of statically and dynamically loaded structures with nonlinear response,” Proceedings of international symposium on optimum structural design, the 11th ONR naval structural mechanics symposium, Tucson, AZ, October 19–22, 1981 (Tucson, AZ: University of Arizona), 12.1–12.8.
Bhatti, M. A., and Pister, K. S. (1981). A dual criteria approach for optimal design of earthquake-resistant structural systems. Earthq. Eng. Struct. Dynam. 9, 557–572.
Castaldo, P., and De Iuliis, M. (2014). Optimal integrated seismic design of structural and viscoelastic bracing-damper systems. Earthq. Eng. Struct. Dynam. 43 (12), 1809–1827. doi:10.1002/eqe.2425
Cimellaro, G. P., Lavan, O., and Reinhorn, A. M. (2009). Design of passive systems for control of inelastic structures. Earthq. Eng. Struct. Dynam. 38 (6), 783–804. doi:10.1002/eqe.867
Cimellaro, G. P., and Retamales, R. (2007). Optimal softening and damping design for buildings. Struct. Contr. Health Monit. 14, 831–857. doi:10.1002/stc.181
De Domenico, D., and Ricciardi, G. (2019). Earthquake protection of structures with nonlinear viscous dampers optimized through an energy-based stochastic approach. Eng. Struct. 179, 523–539. doi:10.1016/j.engstruct.2018.09.076
De Domenico, D., Ricciardi, G., and Takewaki, I. (2019). Design strategies of viscous dampers for seismic protection of building structures: a review. Soil Dynam. Earthq. Eng. 118, 144–165. doi:10.1016/j.soildyn.2018.12.024
Elias, S., Matsagar, V., and Datta, T. K. (2019). Distributed tuned mass dampers for multi-mode control of benchmark building under seismic excitations. J. Earthq. Eng. 23 (7), 1137–1172. doi:10.1080/13632469.2017.1351407
Elias, S., and Matsagar, V. (2019). Seismic vulnerability of a non-linear building with distributed multiple tuned vibration absorbers. Struct Infrastruct Eng. 15 (8), 1103–1118. doi:10.1080/15732479.2019.1602149
Elias, S., Rupakhety, R., and Ólafsson, S. (2020). Tuned mass dampers for response reduction of a reinforced concrete chimney under near-fault pulse-like ground motions. Front. Built Environ. 6, 92. doi:10.3389/fbuil.2020.00092
Fujita, K., Kasagi, M., Lang, Z.-Q., Guo, P. F., and Takewaki, I. (2014). Optimal placement and design of nonlinear dampers for building structures in the frequency domain. Earthq. Struct. 7 (6), 1025–1044. doi:10.12989/eas.2014.7.6.1025
Idels, O., and Lavan, O. (2020). Optimization based seismic design of steel moment resisting frames with nonlinear viscous dampers. Struct. Contr. Health Monit. 28 (1), e2655. doi:10.1002/stc.2655
Kojima, K., and Takewaki, I. (2015). Critical earthquake response of elastic-plastic structures under near-fault ground motions (Part 1: fling-step input). Front. Built Environ. 1, 12. doi:10.3389/fbuil.2015.00012
Lang, Z. Q., Guo, P. F., and Takewaki, I. (2013). Output frequency response function based design of additional nonlinear viscous dampers for vibration control of multi-degree-of-freedom systems. J. Sound Vib. 332 (19), 4461–4481. doi:10.1016/j.jsv.2013.04.001
Lavan, O. (2015). A methodology for the integrated seismic design of nonlinear buildings with supplemental damping. Struct. Contr. Health Monit. 22 (3), 484–499. doi:10.1002/stc.1688
Lavan, O., and Avishur, M. (2013). Seismic behavior of viscously damped yielding frames under structural and damping uncertainties. Bull. Earthq. Eng. 11 (6), 2309–2332. doi:10.1007/s10518-013-9479-7
Lavan, O., Cimellaro, G. P., and Reinhorn, A. M. (2008). Noniterative optimization procedure for seismic weakening and damping of inelastic structures. J. Struct. Eng. 134 (10), 1638–1648. doi:10.1061/(asce)0733-9445(2008)134:10(1638)
Lavan, O., and Levy, R. (2005). Optimal design of supplemental viscous dampers for irregular shear-frames in the presence of yielding. Earthq. Eng. Struct. Dynam. 34 (8), 889–907. doi:10.1002/eqe.458
Lavan, O., and Levy, R. (2010). Performance based optimal seismic retrofitting of yielding plane frames using added viscous damping. Earthq. Struct. 1 (3), 307–326. doi:10.12989/eas.2010.1.3.307
Lee, S.-H., Park, J.-H., Lee, S.-K., and Min, K.-W. (2008). Allocation and slip load of friction dampers for a seismically excited building structure based on story shear force distribution. Eng. Struct. 30 (4), 930–940. doi:10.1016/j.engstruct.2007.03.020
Martinez-Rodrigo, M., and Romero, M. L. (2003). An optimum retrofit strategy for moment resisting frames with nonlinear viscous dampers for seismic applications. Eng. Struct. 25 (7), 913–925. doi:10.1016/s0141-0296(03)00025-7
Moreschi, L. M., and Singh, M. P. (2003). Design of yielding metallic and friction dampers for optimal seismic performance. Earthq. Eng. Struct. Dynam. 32 (8), 1291–1311. doi:10.1002/eqe.275
Murakami, Y., Noshi, K., Fujita, K., Tsuji, M., and Takewaki, I. (2013). Simultaneous optimal damper placement using oil, hysteretic and inertial mass dampers. Earthq. Struct. 5 (3), 261–276. doi:10.12989/eas.2013.5.3.261
Nakamura, T., and Takewaki, I. (1989). Ductility design via optimum design of nonlinear elastic frames. J. Struct. Eng. 115 (3), 608–625. doi:10.1061/(asce)0733-9445(1989)115:3(608)
Nakamura, T., Tsuji, M., and Takewaki, I. (1993). Design of steel frames for specified seismic member ductility via inverse eigenmode formulation. Comput. Struct. 47 (6), 1017–1030. doi:10.1016/0045-7949(93)90306-x
Palermo, M., Silvestri, S., Gasparini, G., Dib, A., and Trombetti, T. (2017). A direct design procedure for frame structures with added viscous dampers for the mitigation of earthquake-induced vibrations. Procedia Eng. 199, 1755–1760. doi:10.1016/j.proeng.2017.09.441
Parcianello, E., Chisari, C., and Amadio, C. (2017). Optimal design of nonlinear viscous dampers for frame structures. Soil Dynam. Earthq. Eng. 100, 257–260. doi:10.1016/j.soildyn.2017.06.006
Pollini, N., Lavan, O., and Amir, O. (2017b). Adjoint sensitivity analysis and optimization of hysteretic dynamic systems with nonlinear viscous dampers. Struct. Multidiscip. Optim. 57 (6), 2273–2289. doi:10.1007/s00158-017-1858-2
Pollini, N., Lavan, O., and Amir, O. (2017a). Minimum-cost optimization of nonlinear fluid viscous dampers and their supporting members for seismic retrofitting. Earthq. Eng. Struct. Dynam. 46 (12), 1941–1961. doi:10.1002/eqe.2888
Shiomi, T., Fujita, K., Tsuji, M., and Takewaki, I. (2018). Dual hysteretic damper system effective for broader class of earthquake ground motions. Int. J. Earthq. Impact Eng. 2 (3), 175–202. doi:10.1504/ijeie.2018.093391
Silvestri, S., Gasparini, G., and Trombetti, T. (2010). A five-step procedure for the dimensioning of viscous dampers to be inserted in building structures. J. Earthq. Eng. 14 (3), 417–447. doi:10.1080/13632460903093891
Takewaki, I. (2009). Building control with passive dampers: optimal performance-based design for earthquakes. Singapore: John Wiley & Sons Ltd. (Asia).
Takewaki, I., Conte, J. P., Mahin, S. A., and Pister, K. S. (1991). A unified earthquake-resistant design method for steel frames using ARMA models. Earthq. Eng. Struct. Dynam. 20 (5), 483–501. doi:10.1002/eqe.4290200508
Takewaki, I. (1997a). Design-oriented ductility bound of a plane frame under seismic loading. J. Vib. Contr. 3 (4), 411–434. doi:10.1177/107754639700300404
Takewaki, I. (1997b). Optimal damper placement for minimum transfer functions. Earthq. Eng. Struct. Dynam. 26 (11), 1113–1124. doi:10.1002/(sici)1096-9845(199711)26:11<1113::aid-eqe696>3.0.co;2-x
Uetani, K., Tsuji, M., and Takewaki, I. (2003). Application of optimum design method to practical building frames with viscous dampers and hysteretic dampers. Eng. Struct. 25 (5), 579–592. doi:10.1016/s0141-0296(02)00168-2
Vamvatsikos, D., and Cornell, C. A. (2001). Incremental dynamic analysis. Earthq. Eng. Struct. Dynam. 31 (3), 491–514. doi:10.1002/eqe.141
Wang, S., and Mahin, S. A. (2018). High-performance computer-aided optimization of viscous dampers for improving the seismic performance of a tall building. Soil Dynam. Earthq. Eng. 113, 454–461. doi:10.1016/j.soildyn.2018.06.008
Wang, S., and Mahin, S. A. (2017). Seismic retrofit of a high-rise steel moment-resisting frame using fluid viscous dampers. Struct. Des. Tall Special Build. 26, e1367. doi:10.1002/tal.1367
Wongprasert, N., and Symans, M. D. (2004). Application of a genetic algorithm for optimal damper distribution within the nonlinear seismic benchmark building. J. Eng. Mech. 130 (4), 401–406. doi:10.1061/(asce)0733-9399(2004)130:4(401)
Keywords: optimal design, earthquake response, elastic-plastic response, passive damper, simultaneous optimization
Citation: Takewaki I and Akehashi H (2021) Comprehensive Review of Optimal and Smart Design of Nonlinear Building Structures With and Without Passive Dampers Subjected to Earthquake Loading. Front. Built Environ. 7:631114. doi: 10.3389/fbuil.2021.631114
Received: 19 November 2020; Accepted: 18 January 2021;
Published: 11 February 2021.
Edited by:
Dario De Domenico, University of Messina, ItalyReviewed by:
Said Elias Rahimi, University of Iceland, IcelandCorrado Chisari, University of Campania Luigi Vanvitelli, Italy
Ehsan Noroozinejad Farsangi, Graduate University of Advanced Technology, Iran
Copyright © 2021 Takewaki and Akehashi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Izuru Takewaki, dGFrZXdha2lAYXJjaGkua3lvdG8tdS5hYy5qcA==
 Izuru Takewaki
Izuru Takewaki Hiroki Akehashi
Hiroki Akehashi