- 1Department of Civil Engineering and Architecture, University of Pavia, Pavia, Italy
- 2Center of Infrastructure Performance and Reliability, University of Newcastle, Newcastle, NSW, Australia
- 3Department of Structures and Infrastructures, Eucentre Pavia, Pavia, Italy
- 4IUSS Pavia (University School for Advanced Studies Pavia), Pavia, Italy
- 5Structural Engineering at Cairepro, Reggio Emilia, Italy
The threat to human lives and the economic losses due to high seismic vulnerability of non-engineered traditional masonry infills subjected to earthquakes have been highlighted by several post-seismic surveys and experimental and numerical investigations. In the past decades, researchers have proposed different techniques to mitigate problems related to the seismic vulnerability of traditional masonry infills; however, a viable, practical, and universally accepted solution has not been achieved yet. Among the possible innovative techniques, the one using ductile (or pliable) infills have shown promising results in recent experimental tests. These infills have provided, indeed, a reduced in-plane stiffness and a very high displacement capacity. The research units of the University of Pavia/EUCENTRE (Italy) and the University of Newcastle (Australia) have proposed two different systems for ductile masonry infill based on dividing the masonry panel into a number of segments interconnected through horizontal sliding joints. The ductile masonry infill proposed by the University of Pavia subdivides the masonry panel into four horizontal subpanels using specially engineered sliding joints and presents a deformable mortar at the infill/structure interface, while the one conceived by the University of Newcastle is made of mortar-less specially shaped masonry units capable of sliding on all bed joints. The experiments conducted on the two novel systems have permitted the calibration of two numerical macromodels capable to replicate the overall in-plane seismic response of these ductile masonry infills. One approach is based on a spring model, as usually adopted for traditional masonry infill; the other calibrates the response of a semi-active damper model. The calibrated macromodel approaches have been adopted to demonstrate the enhanced behavior and the reduction of the seismic vulnerability of reinforced concrete (RC) framed structures with the employment of the ductile infills in comparison to structures with non-engineered masonry infills.
Introduction
The in-plane and the out-of-plane seismic responses of traditional masonry infill solutions, where the panels are constructed in full adherence with the reinforced concrete (RC) frame without any gap or fastening around the boundaries and subsequently the complete hardening of the RC members, have revealed some limits that are dependent also on the mechanical characteristics and the type of masonry of the infill. These issues have been continuously highlighted in both experimental campaigns and post-seismic surveys (see e.g., Braga et al., 2011; Manzini and Morandi, 2012; and Fragomeli et al., 2017), with failures and collapses/expulsions of infills and partitions in the in-plane and out-of-plane directions. Meanwhile, weak/slender infill panels are more prone to out-of-plane collapse due to the reduction of the out-of-plane resistance related to uncontrolled levels of in-plane damage (see e.g., Calvi and Bolognini, 2001; Furtado et al., 2016); for strong/thick masonry infills (e.g., Paulay and Priestley, 1992; da Porto et al., 2013; Morandi et al., 2018a), the most critical aspects are represented by the local unfavorable effects on RC elements due to the thrust of the adjacent infill and the influence on the global behavior of the structure.
In the last decade, many innovative infill solutions have been proposed to exceed the limitation of “traditional” infills, and one approach is to develop pliable/ductile masonry infills with limited interaction with the structural members.
Different ductile systems that subdivide the infill through sliding or deformable joints have been studied independently by the University of Pavia and the University of Newcastle. These solutions have provided a promising experimental seismic response, and their lateral behavior influences the global behavior of the structure in a different way with respect to traditional infills.
Within the present paper, it is shown that a classical non-linear single-strut spring macromodel can efficiently simulate the experimental results, although, in some cases, the nature of the innovative ductile infill may require a strut model with a “damping mechanism,” in this case based on an equivalent semi-active damper. Finally, the calibrated equivalent spring strut models have been adopted to study the influence of the innovative infills in RC frames through non-linear static and non-linear dynamic analyses. The results, discussed in terms of pushover capacity curves and in terms of displacement profiles and performance limit states of infills for dynamic analyses, have demonstrated a significant improvement of the overall seismic response of the structure with the employment of the two innovative infills with respect to the use of a “traditional” masonry solution.
The scientific and technological improvement of the knowledge of the arguments discussed in the present work is borne on the need of innovative infill systems to replace or upgrade the existing solutions due to the several limitations that have been observed in post-seismic surveys or past experimental/numerical researches. Although, recently, many solutions have been proposed and their experimental response has often been proved to be seismic efficient, for the real application, a series of studies (i.e., influence of the global behavior of the structure) is needed. The most common study on the seismic behavior of masonry infill is usually addressed to investigate the seismic in-plane performance of infilled structures through a macromodel non-linear analysis. Therefore, the need to pioneer the macromodel approach of new innovative infills could foster the study on these techniques and the improvement of the seismic behavior of the masonry infilled structures. Moreover, the present study highlights the difference between two apparently similar systems that belong to the same innovative infill typology (ductile masonry infill), focusing the attention on the need for properly calibrated and suitably defined macromodel elements, being the selection of the element typology, also dependent on the infill seismic response and the expected/attained deformation of the structure.
Ductile Masonry Infill Solution in Past and Recent Applications
The adoption of masonry infill still represents a valid solution for many needs, such as architectural and energetic requirements, but the considerable cost of repair, downtime losses, and the threat to human lives shown during the recent earthquakes have boosted the research toward new systems for masonry infills.
The innovative solutions aim at maintaining or improving the current thermal, acoustic, and durability performance and, simultaneously, at reducing the in-plane/out-of-plane seismic vulnerability of infills and the interaction with the structural members.
The new systems can be subdivided into three groups: the enhanced infills, the uncoupled solutions, and the ductile systems. In the enhanced infills, the in-plane/out-of-plane resistance is improved (Figure 1A) through the inclusion, for example, of vertical and/or horizontal reinforcement (steel bars or light trusses) in the masonry panel, steel wire meshes (Calvi and Bolognini, 2001), or other types of fiber sometimes coupled with cementitious materials, as “carbon fiber reinforced polymer” (CFRP) (Yuksel et al., 2010) or “fiber reinforced cementitious matrix” (FRCM) systems (Koutas et al., 2013; Furtado et al., 2019; Gkournelos et al., 2019; De Risi et al., 2020). These interventions improve the in-plane and out-of-plane resistance without reducing the possible negative interaction effects between the infill and the frame. The second category of modern solutions found in literature (e.g., FEMA E-711; Tsantilis and Triantafillou, 2013; Canbay et al., 2018; Binici et al., 2019; Butenweg et al., 2019) aims at uncoupling the infills from the structure by using deformable joints at the panel–structure interface (see examples in Figure 1B). These solutions often require the adoption of out-of-plane restraints to guarantee the out-of-plane stability of the panel. The third group of innovative systems consists of reducing the infill–frame interaction by creating a ductile (or pliable) panel. The adoption of “sliding” or “weak plane” joints allows to concentrate the in-plane deformation and damage in selected points.
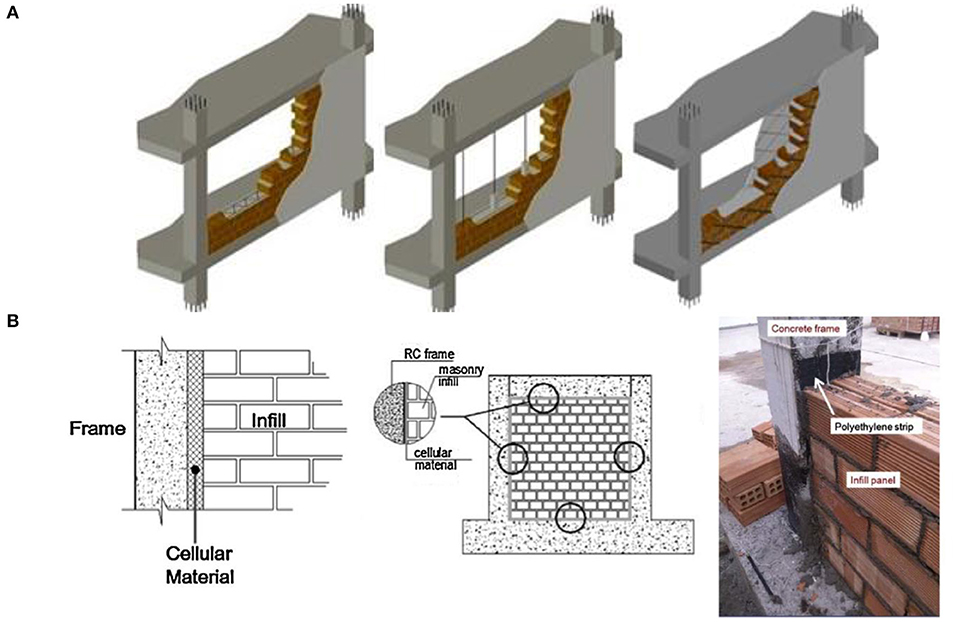
Figure 1. (A) Solutions with enhanced in-plane/out-of-plane resistance (from Morandi et al., 2018); (B) “uncoupled” solution with flexible joints (Tsantilis and Triantafillou, 2013).
With reference to the ductile infills, the masonry section research group of the University of Pavia, involved in the European FP7 “INSYSME2” project, and the University of Newcastle (Australia) have developed and implemented two different innovative ductile masonry infill systems: one mortar-less made of specially shaped masonry units capable of sliding on all bed-joints (Lin et al., 2011a,b, 2016; Totoev and Lin, 2012; Totoev and Al Harthy, 2016); another with an infill masonry panel subdivided into several horizontal subpanels using specially engineered sliding joints (Morandi et al., 2018b; Milanesi et al., 2020). Moreover, other researchers, within the “INSYSME” project (e.g., Verlato et al., 2016) or in other studies (e.g., Mohammadi et al., 2001; Preti et al., 2016, 2017; Cheng et al., 2020), have proposed and studied through experimental campaigns alternative systems that can be categorized as solutions with “weak plane” joints.
Although the best option to analyze these latter typologies of infills is with the use of micromodels (e.g., Bolis et al., 2017; Hemmat et al., 2019), able to investigate the detailed response of the system and the local interactions with the structure, simplified macromodels that assume a single strut along each diagonal, pin-ended at the RC member centerline intersections can also be adopted, as done in the past for traditional rigidly attached infills (e.g., Hak et al., 2013; Di Trapani et al., 2017). Although such models are not able to determine the local effects on RC members that may occur due to the structural members/masonry infill interaction, since the focus of the present work is on the infills, and their in-plane seismic response is essentially governed by inter-story drift and “overall” frame behavior, the single-strut model is considered to be adequate for global structural analyses of infilled buildings with innovative systems, also for its low computational burden.
Within the present work, the calibration of non-linear single-strut macroelements is presented as an efficient model technique to represent in-plane seismic response of the ductile masonry infills.
Numerical Strategies for the Simulation of Ductile Systems Through Non-Linear Macroelements
The in-plane non-linear numerical modeling of masonry infills has been addressed with many approaches, and several authors have provided an overview on the state of the art of the numerical modeling of masonry infills mainly focusing on the in-plane response (e.g., Asteris et al., 2011, 2013; Chrysostomou and Asteris, 2012; Tarque et al., 2015), whereas the out-of-plane behavior has been studied more recently (e.g., Asteris et al., 2017; Liberatore et al., 2020).
Surely, a suitable detailed micromodeling (e.g., Milanesi et al., 2019) or the meso-modeling (e.g., Mehrabi and Shing, 1997; Akhoundi et al., 2016; Milanesi et al., 2018) is able to properly simulate the response of the masonry infill and the interaction with the structural members at different levels of precision, also in ductile infills, as successfully performed by, e.g., Bolis et al. (2017). However, one of the most common approaches is still to model the infill through macroelements. The common macroelement modeling adopts single- or multi-strut elements (Crisafulli et al., 2000; El-Dakhakhni et al., 2003), representing the diagonal compressive strut typical of a traditional rigidly attached masonry infill. Alternatively, some authors have recently proposed a simplified bidimensional macromodeling approach to reduce the computational burden of detailed modeling (e.g., Caliò and Pantò, 2014; Pantò et al., 2018).
The more frequent employment of macroelements with respect to micro/meso approaches is due to a minor computational burden and request of mechanical properties to be included in the model and, therefore, to be validated through an experimental test of mechanical characterization. Although the macroelements with two single diagonal struts may not be, in principle, physically the best representation for ductile infill, they could represent a valid solution to avoid micromodeling to study the seismic response of the whole structure and to adapt past studies on traditional infills in order to have a direct comparison of the different infill typologies.
The present section discusses two different macroelement approaches: one with a classic equivalent single spring and the other with the use of an equivalent semi-active damper with the aim to improve the response for ductile masonry infills where the equivalent spring element seems not to be sufficiently accurate, as for the semi-interlocking masonry (SIM).
Equivalent Spring Approach
The RC members of the frames were defined as one-component Giberson elements (Giberson, 1967) with concentrated plasticity at their ends. Assuming that the design of the frame was properly performed, the possibility of shear failures in the structural members was not taken into account. In accordance with the recommendations of Priestley et al. (2007), the region of intersection between the beam and the columns was characterized by perfectly elastic short elements. The hysteresis rule adopted to simulate the behavior of the RC section of the columns was the Schoettler-Restrepo rule (Carr, 2007), while the non-linear behavior of the beam was defined by the Fukada rule (Fukada, 1969). Further information on the functioning of the hysteretic constitutive laws shown in Figure 2 is reported in the Ruaumoko Manuals (Carr, 2007).
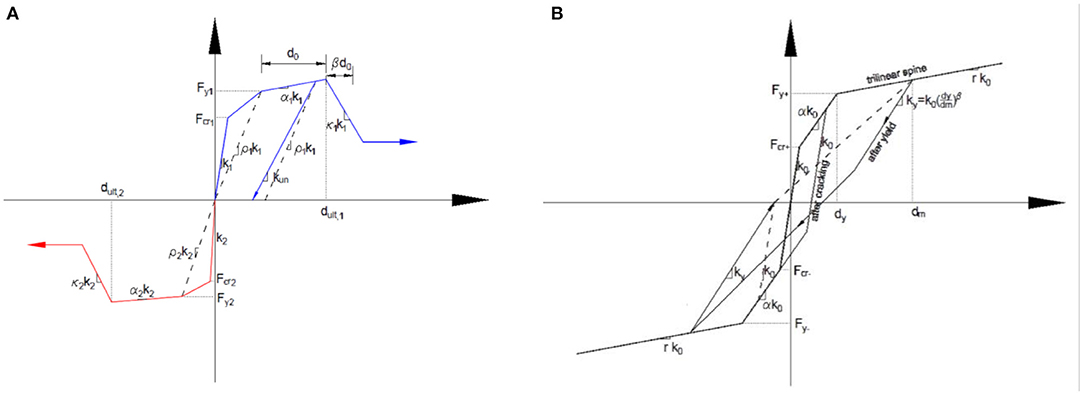
Figure 2. (A) Backbone curve of Schoettler–Restrepo rule (Carr, 2007); (B) Fukada degrading tri-linear hysteresis rule (Fukada, 1969).
Considering the infilled frame cases, two diagonal non-linear springs that represent the innovative infill system have been considered. These elements were pinned to the extreme nodes of the frame and work only in compression (“no tension” elements/struts). The hysteresis rule associated with the non-linear behavior of the two diagonal struts representing the infills was the one proposed by Crisafulli (1997), as reported in Figure 3.
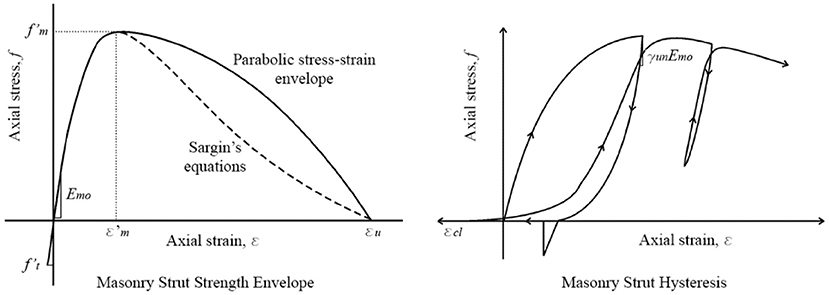
Figure 3. Masonry strut strength envelope and masonry strut hysteresis for Crisafulli rule (Crisafulli, 1997).
The spring elements, defined by the Crisafulli hysteresis rule, are defined by an elastic modulus (Emo), a compressive strength (f'm) and an initial stiffness (KD) equal to (Emo)·(AREA1)/(element length). The area of the section of the element is assumed to be dependent on the deformation, AREA1 (initial cross-sectional area) at displacement R1, and AREA2 (final cross-sectional area) at displacemet R2. The shape of the envelope of the hysteretic cycles was assumed to be parabolic. The peak of the curve was defined by the point (ε'm, f'm), and the intersection with the x-axis occurs at the value of deformation εu. The slope of the descending branch of the curve was determined by the factor γun, while the reloading factor αre defines the point at which the reloading curves attain the strength envelope. The closing strain, εcl, corresponds to the partial closing of the cracks where the compressive stresses could be developed.
Equivalent Semi-Active Damper Approach
Although the resettable semi-active damper, which is a device developed at the University of Canterbury (Chase et al., 2007; Mulligan et al., 2010; Franco-Anaya et al., 2014, 2017; Hemmat et al., 2020a), has a field of application and practical use, which is completely different from the masonry infill, its numerical behavior can be associated with some ductile infills. The hysteretic constitutive curve of the semi-active damper is suitable to a user-defined response if properly calibrated. In Figure 4A, some examples of possible constitutive laws associated with the air-cylinder semi-active damper are reported. Depending on the resisting force, different control laws cover quadrants of the force–displacement curve (1-2-3-4 or 2-4 or 1-3). However, the modified constitutive model for the specific application of semi-active damper spring to simulate masonry panels has been summarized in Figure 4B. For this application, 1-2-3-4 quadrants are covered by the loading and unloading rule. Area of the piston, free length for the movement of the piston inside the cylinder, the force capacity of the spring, and the residual friction force are determinant parameters of the semi-active damper spring in to predict the response of masonry infill panels (Hossain et al., 2017).
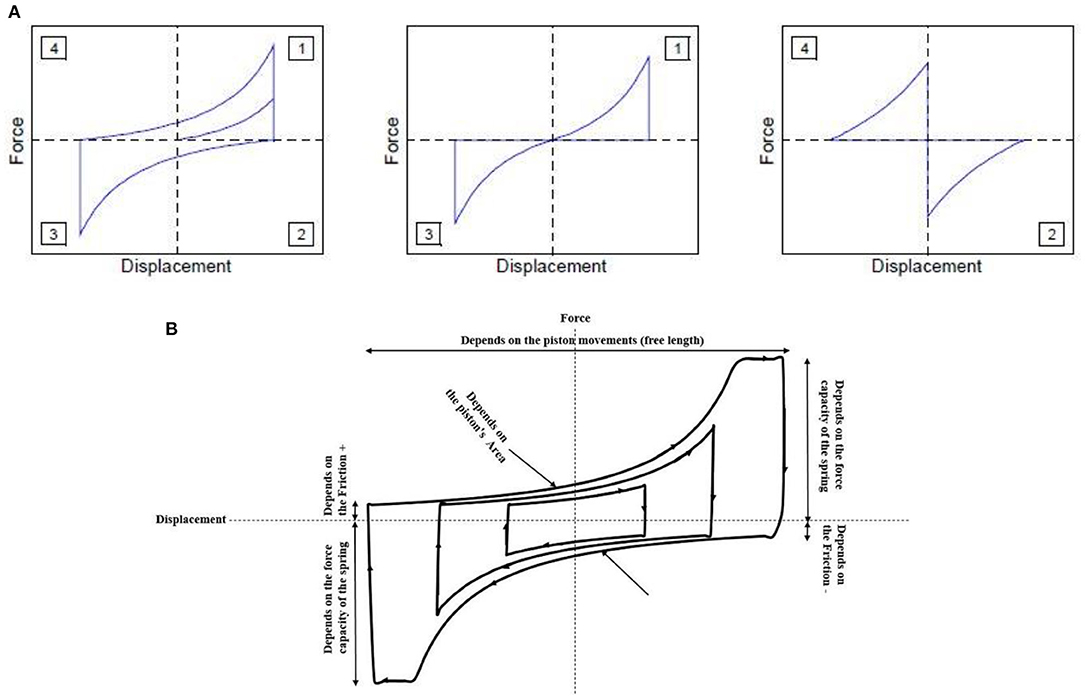
Figure 4. (A) Example of constitutive law for the air-cylinder semi-active damper (Franco-Anaya et al., 2014). (B) The modified constitutive model of semi-active damper spring for the application to represent masonry infill panels.
The non-linear model of semi-active springs is conceptually similar to the shear sliding behavior of masonry infill panels with sliding joints, as both systems increase stiffness with respect to the bare frame without the effect of reducing yield displacement capacity as occurs, for example, for traditional masonry infills. Hence, the behavior of a masonry panel with sliding joints was conservatively represented by the resettable semi-active damper springs (Hemmat et al., 2020a). The numerical model for semi-active dampers has been developed in the Ruaumoko program (Carr, 2007). Figure 4 illustrates, two diagonal shear springs with the hysteresis rule associated with the semi-active damper model were employed to represent the masonry panel. Also in this case, the behavior of the frame was modeled using the one-component Giberson frame element with two hinges at both ends of the element associated with the bilinear hysteresis behavior (Giberson, 1967) due to the different frames tested (see section Summary of the Experimental Response). The simpler bilinear hysteretic behavior for the steel frame elements with respect to the Schoettler–Restrepo rule adopted for RC members, as described in section Equivalent Spring Approach, has provided valuable results (Hemmat et al., 2020a), although the approach cannot be extended for the RC frame tested at the University of Pavia (see section Summary of the In-Plane Experimental Response). Moreover, concerning the model of the TSJ system, the contribution of the infill only, computed as the difference between the infilled specimen with respect to the RC bare frame, has been considered. Despite different experimental and numerical approaches for the structural frame have been adopted, the present study is focused on the response of the infill, and the numerical simulation of the frame has been necessary only for the calibration and validation of the numerical approaches (see sections Numerical Calibration under Masonry Infills Subdivided in Subpanels Through Sliding Joints–University of Pavia and Numerical Calibration under Infill Made of Semi-Interlocking Masonry (SIM)–University Of Newcastle); therefore, the calibration of the equivalent semi-active damper has been conducted by modeling the structural frame as a negligible structure in terms of strength and stiffness in the in-plane direction. The model of infilled frame was composed by eight nodes and six elements, including two diagonal semi-active damper springs. The frame elements were pinned in corners to reduce the contribution of the frame in the resulted cyclic responses of the infill panel.
Masonry Infills Subdivided in Subpanels Through Sliding Joints–University of Pavia
A brief description of the systems developed by the University of Pavia, a summary of the main experimental findings, and the numerical calibration according to the two aforementioned approaches are presented.
Description of the System and the Experimental Campaign
The masonry division research unit of the University of Pavia, within the European FP7 “INSYSME” project, has developed a seismic-resistant masonry infill system with sliding joints (Morandi et al., 2018b; Milanesi et al., 2020) with original details on which a vast experimental campaign has been conducted. The proposed engineered system, called “TSJ,” aims to localize the damage in specific parts of the infills and to decrease the in-plane structure/infill interaction. The infill is subdivided into four horizontal subpanels, which can mutually slide through properly conformed sliding joints (corrugated male–female plastic elements; Figure 5C). A deformable joint at the frame/infill interface reduces the stress concentration and the local effects often related to the detrimental local interactions between the structural members and the masonry panel. The unreinforced masonry used in the subpanels of the infill is realized with vertically perforated lightweight clay units (Figure 5D) and general-purpose 1-cm-thick mortar bed and head joints. The detailed description of the proposed system is discussed by Morandi et al. (2018b). Figure 5A reports the layout of the system.
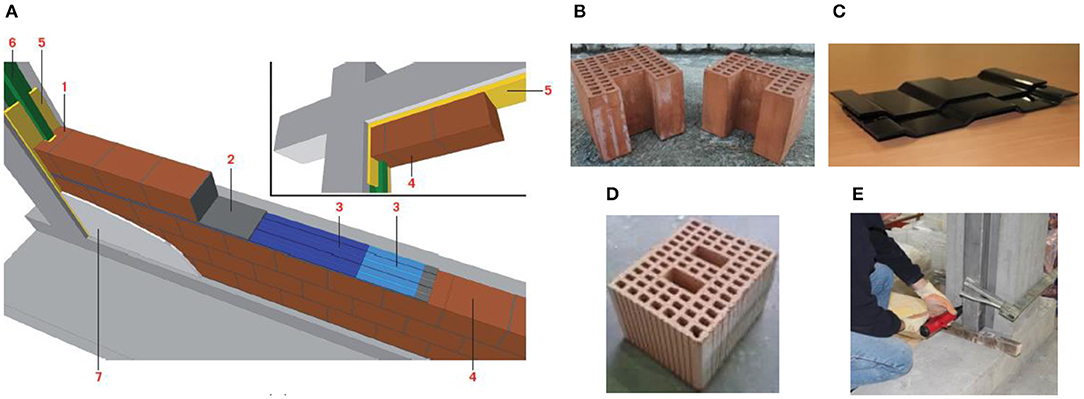
Figure 5. (A) Details of the innovative masonry infill with sliding joints. (1) C-shaped units (B). (2) Mortar bed joints. (3) Sliding joints (C). (4) Clay units (D). (5) Interface joints. (6) Shear keys (E). (7) Plaster (Morandi et al., 2018).
The seismic performance of the proposed system has been investigated through an extensive experimental campaign that included tests of characterization of the materials (i.e., clay units, mortar, masonry) on two different configurations (with and without a central opening) of full-scale one-bay one-story RC infilled frames tested cyclically in the in-plane direction (Morandi et al., 2018b) and, subsequently, in the out-of-plane direction with dynamic tests on the shaking table (Milanesi et al., 2020). A dynamic shaking table test on a 1:1 scale two-story structure was also carried out (Manzini et al., 2018). According to the results of the in-plane cyclic tests (Morandi et al., 2018b), the system has provided an excellent performance along the in-plane direction by limiting the damage in the panel and the interaction between the infill and the structure.
Moreover, the execution of dynamic tests on the shaking table on the specimens already tested in-plane cyclically has allowed to study the seismic out-of-plane experimental response. The out-of-plane behavior is related to the horizontal flexural/arching resistance of the masonry stripes, and the stability in the out-of-plane direction is ensured by “omega”-shaped steel profiles “shear keys” attached to the column by means of nails shot with a nail gun (Figure 5E). Moreover, C-shaped units with a recess to accommodate the shear keys (Figure 5B) are located at the vertical edges of the panel (adjacent to the columns and to the openings). The out-of-plane stability of the panels is furthermore increased by the mechanical interlocking of the sliding joints that have a ribbed shape and the plaster placed on both sides of the masonry.
In the present study, the following sections are only focused on the in-plane behavior of this system.
Summary of the In-Plane Experimental Response
A fully and a partially infilled (with a central opening) full-scale one-story one-bay RC frames have been tested in the in-plane direction with a pseudo-static cyclic protocol (i.e., TSJ1_IPL). The solid infill has been subjected to the same loading protocol applied at two different velocities; the “high velocity” (TSJ1_IPH) one has been performed to study the effect of dynamic action to the response of the sliding. In the present work, only the fully infilled specimen has been considered.
The one-story one-bay RC frame specimen represents a part of a realistically full-scale RC frame structure. The clear frame for the allocation of the infill has a length of 4.22 m and a height of 2.95 m. The RC frame specimen, which is widely described in Morandi et al. (2018a), was designed following the European code provisions (EC 8-Part 1, 2004 and the Italian national code Norme Tecniche per le Costruzioni, 2008). The fully infilled specimen, named TSJ1, is reported in Figure 6A.
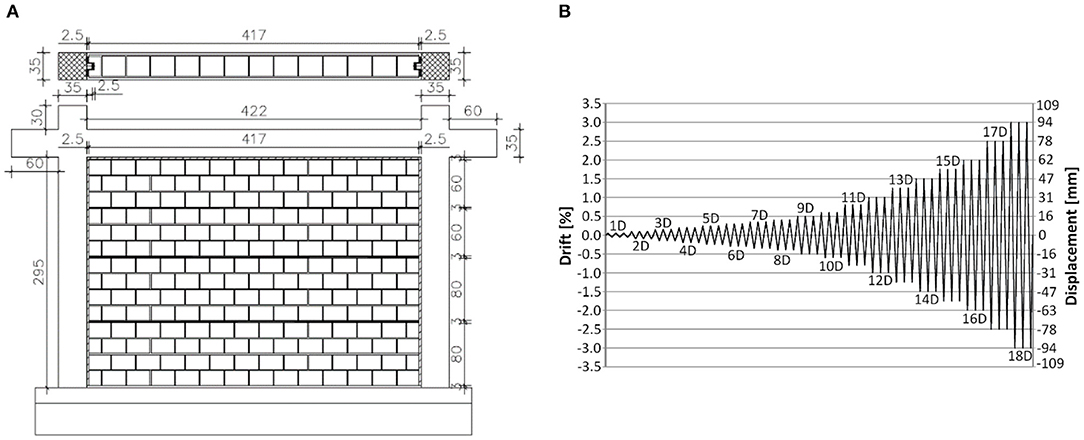
Figure 6. (A) Layout of the fully infilled reinforced concrete (RC) frame specimen (TSJ1) represented without plaster. Measures in cm. (B) In-plane testing protocol for “low-velocity” test.
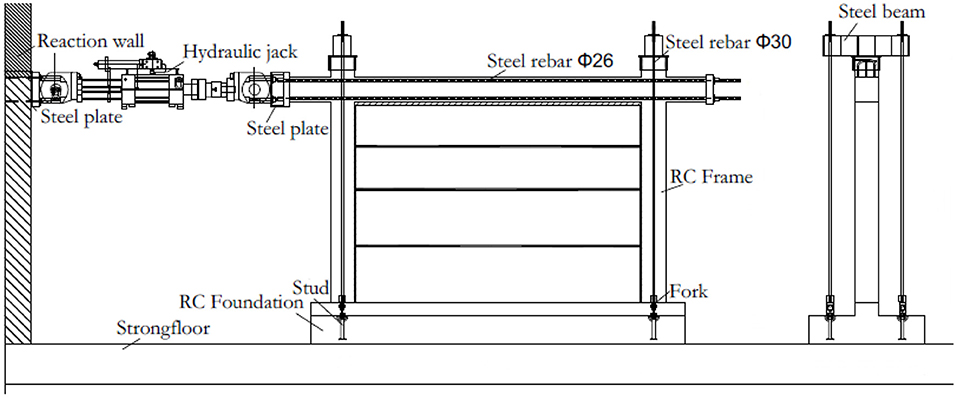
The in-plane cyclic tests have been carried out at the laboratory of EUCENTRE and of the Department of Civil Engineering and Architecture of the University of Pavia. The layout of the in-plane experimental setup is shown in Figure 7; further details on the cyclic pseudo-static in-plane testing procedures are reported by Morandi et al. (2018b). After the application of a vertical load of 400 kN per column to simulate the upper stories of the building, the frame has been subjected to the cyclic horizontal in-plane loading history (first pull, then push) that consists of displacement-controlled loading cycles at increasing levels of in-plane drift up to 3.00% drift. For each level of target displacement, three complete reverse loading cycles have been completed with a velocity of application approximately constant. Figure 6B reports the in-plane “low-velocity” testing protocol. The displacements and the deformations of the specimens have been measured through displacement transducers (45 linear potentiometers have been installed for test on TSJ1) and an optical acquisition system with markers located on the masonry infills and the RC frame.
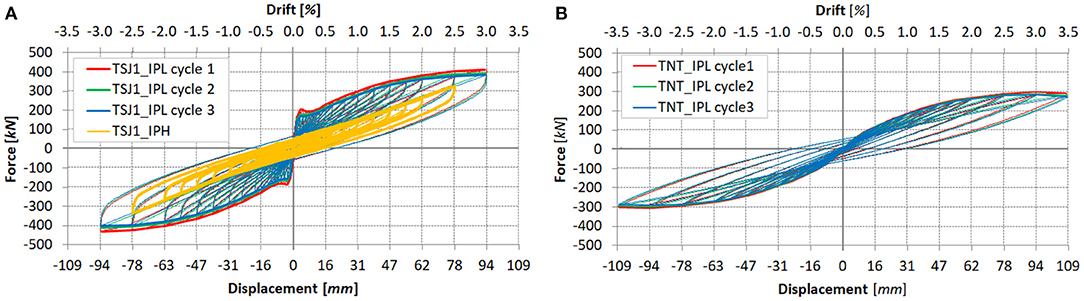
The results of the cyclic in-plane tests on the fully infilled frame TSJ1 (“low-” and “high-velocity”) are shown in Figure 8A, in terms of force–displacement hysteretic curve and corresponding envelopes for each cycle. The “high-velocity” test has been conducted on the same specimen that had been previously subjected to the “low-velocity” loading protocol; therefore, the in-plane response obtained was consistent with the third loading cycle at the last target drift (3.0%) at “low-displacement” due to cracked in-plane stiffness of the RC infilled specimen. To properly evaluate the infill contribution, a test on the RC bare frame (named TNT) that has been tested during a previous experimental campaign (Morandi et al., 2018a) has been taken as reference. Such assumption has been possible since the TNT specimen has the same characteristics (dimensions, RC sections, details/amount of reinforcement, nominal concrete and steel and steel strength values) of the RC frames of the infilled specimens. The test on the bare frame has been performed up to a drift of 3.50% with a “low-velocity” testing protocol analogous to the one adopted for TSJ1; the force–displacement curve and the envelopes for each cycle are shown in Figure 8B.
Based on the plots reported in Figures 8A,B, it has been possible to compute the infill contribution as the difference between the cycling response of the infilled specimen and the bare frame; although the procedure is not rigorous and a detailed finite element method (FEM) analysis study should have been pursued, the assumption can be considered as a valid approximation to define the force–displacement curve of the infill with sliding joints.
The sliding mechanism and its activation have been monitored by computing the relative horizontal displacement of the horizontal edges of the masonry subpanels from the processing of the data of the potentiometers. Further details are reported by Morandi et al. (2018b).
Moreover, the dissipated hysteretic energy of tested infilled frames has been evaluated through a simplified criterion consisting of the determination of the equivalent viscous damping ξeq. For each load–displacement cycle, ξeq can be computed as the ratio between the dissipated energy Wd (area enclosed by each hysteretic loop) and the elastic energy at peak displacement We (amount of elastic energy stored in the same loop), as reported in Equation (1) (where signs + and – indicate the positive and the negative elastic branches, respectively):
The equivalent viscous damping values for TNT and TSJ1 (both for “low-” and “high-velocity” tests) curves for the first cycles are shown in Figure 9. For the RC bare frame, the damping starts to increase at 1.50% drift, where it is about 3%, up to 10%. In the TSJ1 specimen, the damping decreases from approximately 12% to about 7% up to 1.50% drift; subsequently, the damping starts growing up to about 11%. The “high-velocity” test on the fully infilled specimen (TSJ1_IPH) exhibited damping values similar to those of the “low-velocity” test (TSJ1_IPL). Furthermore, the area enclosed in the hysteretic cycles of the infilled framed after the deduction of the area of the bare frame hysteretic curves has been computed in order to estimate the dissipation capacity in terms of equivalent viscous damping (Equation 1) due to the infill only. The results are reported in Figure 9 in dashed lines, together with those of the infilled frame represented in solid lines. After a drift of 0.60%, the damping does not show a clear trend, with values between 15 and 20% and an average value ξeq, av., drift_0.60−3.00% = 17.6%, considerably larger than that of the bare frame.
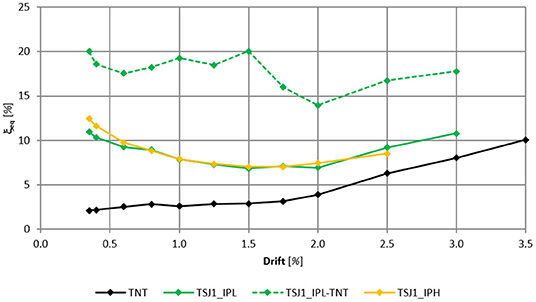
Figure 9. Equivalent viscous damping of TNT, TSJ1 (for “low-” and “high-velocity” tests), and TSJ1-TNT at the first cycles.
The infill seismic performance has finally been evaluated as specified in Morandi et al. (2018a,b) in terms of drift attained to a correspondent level of damage derived from in-plane cyclic tests on infills. An operational limit state (OLS), a damage limit state (DLS), and a life safety limit state (LSS or ULS) are defined specifically for infill performance. At OLS, the infill is considered undamaged or slightly damaged; at DLS, the infill is damaged but can be effectively and economically repaired; whereas at LSS/ULS, the infill is considered severely damaged and reparability is economically questionable, but lives are not threatened. For the case of the infill solution proposed by the University of Pavia, the following limits have been evaluated: OLS at 0.5% drift and DLS at 3.0% drift; the LSS (or ULS) has not been reached during the test, since at 3.0%, the infill panel was still far from an ultimate condition.
Numerical Calibration
The numerical-macro models presented in section Numerical Strategies for the Simulation of Ductile Systems Through Non-linear Macroelements were calibrated, taking as reference the in-plane cyclic tests previously described. The results of the experimental tests were compared to the response of the numerical macromodels in terms of force–displacement curves for the entire displacement history.
The purpose of the calibration was to reproduce numerically the in-plane experimental behavior of the frames with the ductile infill systems studied at the University of Pavia and compare the two numerical approaches.
The calibration has been pursued using Ruaumoko program (Carr, 2007), and it is referred to the experimental results summarized in section Summary of the In-Plane Experimental Response.
Equivalent Spring Approach
Figures 10A,B show the comparison, in terms of force–displacement curve, between the in-plane cyclic tests TSJ1_IPL (black line) and the numerical models (red line) on the bare frames and on the frame infilled with the innovative system. The input of the numerical-model was given by the loading history of the displacement effectively applied at the half-height of the top beam during the pseudo-static cyclic tests. The plots show that the force–displacement curves of the numerical models match very well the experimental ones during all the cycles.
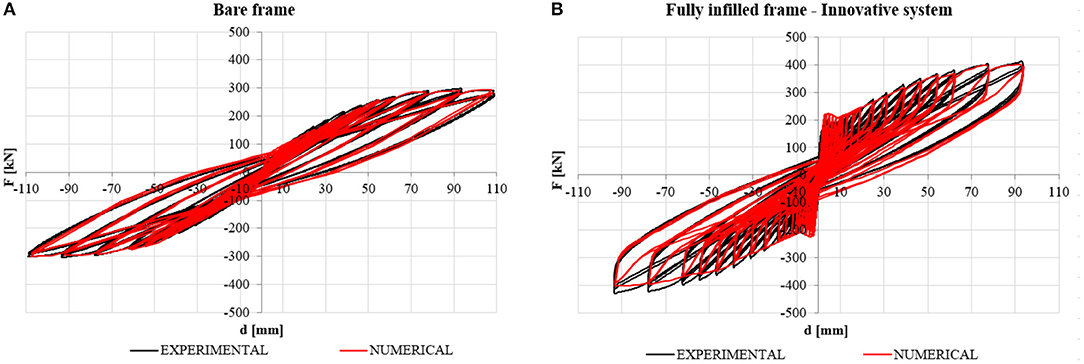
Figure 10. Comparison between the force–displacement experimental and numerical curves. (A) Bare frame. (B) Fully infilled case.
The final parameters of the calibrated diagonal macroelements representing the innovative infill system of the University of Pavia, included in the Ruaumoko program, are listed in Table 1.

Table 1. Parameters of the diagonal struts for infill with sliding joints of the University of Pavia.
Equivalent Semi-Active Damper Approach
The parameters of the semi-active damper spring were calibrated according to the results of the tests of the innovative system TSJ. In particular, the so-called TSJ1-IPL specimen was modeled in Ruaumoko program using eight nodes and six elements including two diagonal semi-active damper springs. The frame elements were pinned in corners to reduce the contribution of the frame in the resulted cyclic responses of the infill panel. The 1-2-3-4 control law that covers all quadrants of the force–displacement curves was selected for this simulation (Carr, 2007). The force capacity of springs, the area of the piston, and the range of the axial movements of the piston inside the cylinder (free length) were parameters in the macromodel that were calibrated. Table 2 shows the calibrated parameters of the resettable semi-active springs. Figure 11 compares the experimental load–displacement curve of the infill panel (“Infill contribution TSJ1-TNT cyclic experimental” for the cyclic response and “Infill contribution TSJ1-TNT backbone experimental” for the backbone curve of the cyclic behavior), computed as the difference between the infilled specimen (TSJ1_IPL reported in Figure 8A) and the bare frame (Figure 8B) response, with the resulting numerical hysteresis curve from the semi-active spring model. The residual force in reverse cycles associated with the friction force in the resettable semi-active spring model may create a different cyclic shear demand, and it is one of the reasons of the discrepancy between numerical results and the experimental ones; as a result, the semi-active spring model overestimates the values of energy dissipation of the University of Pavia's infill panel.
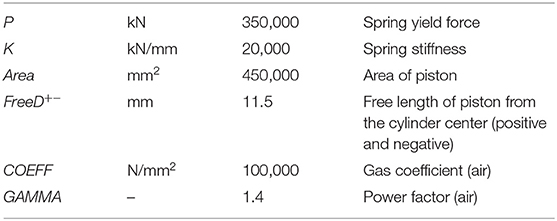
Table 2. Parameters of the semi-active spring model for infill with sliding joints of the University of Pavia.
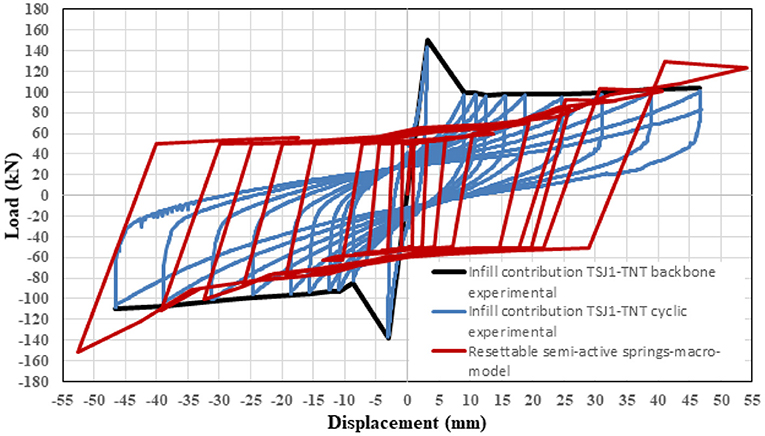
Figure 11. Comparison between the force-displacement experimental curves for infill with sliding joints of the University of Pavia and numerical curvers for semi-active spring model.
Infill Made of Semi-Interlocking Masonry–University of Newcastle
Within this section, a brief description of the system developed by the University of Newcastle and a summary of the main experimental findings and the numerical calibration following two approaches are presented.
Description of the System
SIM is an innovative masonry system (Figures 12A,C) developed at the University of Newcastle to improve the earthquake performance of framed structures with infill masonry panels. In this system, mortar-less masonry walls utilize unbounded bricks that allow relative sliding of brick courses in-plane of a wall and prevent out-of-plane relative movement of bricks. SIM makes walls deformable and provides structures with artificially added damping. The sliding of brick courses induces frictional forces on joints that lead to the occurrence of energy dissipation in a SIM wall (Totoev and Al Harthy, 2016).

Figure 12. (A) Details of the semi-interlocking masonry SIM infill, (B) SIM units: topological, (C) Window frame made of steel channel or angles perimeter out-of-plane restraint made of steel angles attached to the frame, (D) SIM units: mechanical, (E) Sliding joints with linseed oil-based putty.
The lateral load resistance of SIM walls is mainly due to frictional forces on joints. Considering a SIM infill panel, a constant part of the lateral resistance comes from the self-weight of the SIM panel. In addition, the interaction of the panel with its surrounding frame creates a clamping zone in the panel that depends on the values of deformation in the wall. This interaction produces additional frictional forces in the SIM panel that considerably contributes to the lateral load resistance of the wall (Hemmat et al., 2020b).
Two variants of semi-interlocking systems have been developed (Figures 12B,D). One is topological SIM that uses special-shaped bricks and the other is mechanical SIM, which is similar to conventionally shaped bricks but with perforations and dowels (Totoev, 2015). Complementary researches on the water penetration and the thermal insulation conducted by Forghani et al. (2016) identified two types of joint filler between SIM units; subsequently, the coefficient of friction of SIM depending on the joint fillers has been investigated by Hossain et al. (2016).
More recently, an experimental campaign has been conducted to investigate the cyclic behavior of SIM panels with mechanical and topological SIM units using quasi-static tests. SIM panel specimens were built using the putty as a joint filler (Figure 12E) between the SIM units, according to the best findings of Forghani et al. (2016) and Hossain et al. (2016). The interface between the top of the infill and the steel frames has been filled with self-expandable foam and cement grout, and their influence on the cyclic behavior of the SIM panel has been considered.
Summary of the Experimental Response
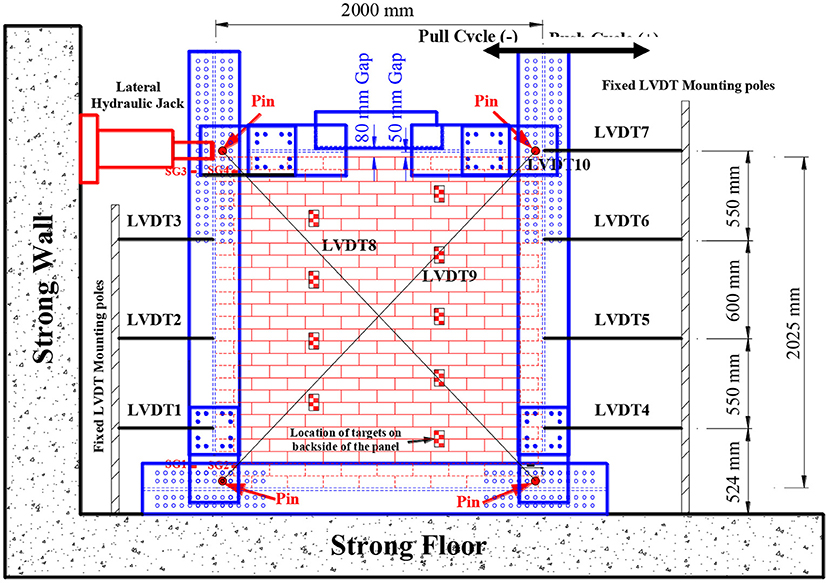
A special steel frame made of Australian standard 310UC137 sections and T-sections restrained to the strong floor (Figure 13) has been designed for the experimental campaign. The frame presented four pin connections at each node (Figure 13) to apply the force on a corner of the frame; a lateral hydraulic jack cylinder has been placed on a strong wall. The setup permits to perform in-plane pseudo-static test on the masonry panel up to an imposed top shear displacement of 120 mm.
The instrumentation for the measures related to the panel consisted of 10 linear variable differential transformers (LVDTs) and four electrical strain gauges, which were placed as reported in Figure 13. Moreover, the relative displacements of the SIM layers have been quantified through nine targets located on the backside of the panels and monitored with a secondary camera.
The SIM panel has been constructed after the assembly of the bare frame with four pin connections; the panel has been built with SIM units and bed and head joints filled with putty.
The average compressive strength of the SIM concrete unit was 31.5 MPa (with coefficient of variance of 20%, performed on 50 samples following AS/NZS4456.4:2003); the density of the units was 2,250 kg/m3 (computed using AS3700-2011 on a sample of 30 specimens). The construction process of the SIM panels planned that the gap between the top of the panel and the steel frame was about 50 mm at the edges and approximately 80 mm in the middle (Figure 14). Three different solutions have been studied: one where the gap remained open during testing (MO), one presenting a self-expanding polyurethane foam to create a soft gap filler (MF), and the latter with a hard gap filler made of cement grout (MG) (Figure 15).

Figure 14. Gap between the steel beam and top of the masonry panel, Panel MO (A) center of the panel; (B) edges of the panel.

Figure 15. (A) Top panel–Steel beam interface joint filled with self-expanding polyurethane foam (MF). (B) Top panel–Steel beam interface joint filled with grout (MG).
In the MF specimens, the top joint at the panel/beam interface has been sealed with a self-expanding polyurethane foam; meanwhile, the grout used for the MG panels was a mixture of cement and sand with a cement–sand ratio of 1:6. The average compressive strength, computed on six samples, of the grout after 28 days of curing was 13.94 MPa with a coefficient of variance of 12.70% (using ASTM International, 2016).
In Figure 16, where the bare frame specimen and an infilled one are shown, the speckle pattern to apply the digital image correlation (DIC) on the infill is reported. The results obtained from DIC analysis are not presented herein.

Figure 16. Picture of the specimens. (A) Bare Frame. (B) General vision of the steel frame infilled with a semi-interlocking masonry (SIM) panel.
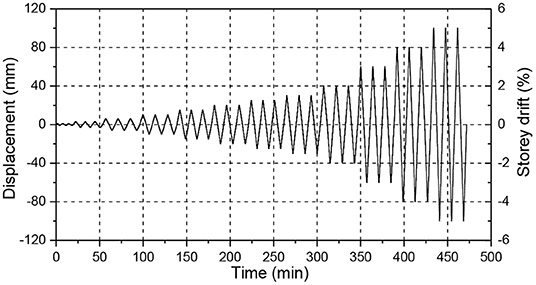
The specimens have been tested in-plane by imposing the same displacement history loading protocol in cyclic form as reported in Figure 17. Every target displacement has been attained three times in the cyclic form. During the test, the cracking has been monitored through visual inspection, with the acquisition always active.
The total applied horizontal force and imposed displacement, measured by LVDTs, were recorded, and the total duration of the test was about 450–500 min.
The experimental hysteretic force–displacement curves obtained for each specimen from the cyclic testing protocol aforementioned and the envelope curves of the first cycle at every target displacement are reported in Figure 18. The forces reached at similar displacement are not comparable, since the plots reported have indeed different vertical axis scaling. The bare frame specimen (Panel zero) has provided a hysteretic behavior almost constant for each level of displacement (Figure 18A) with no significant stiffness degradation between the three cycles, indicating the absence of any damage propagation during the test.
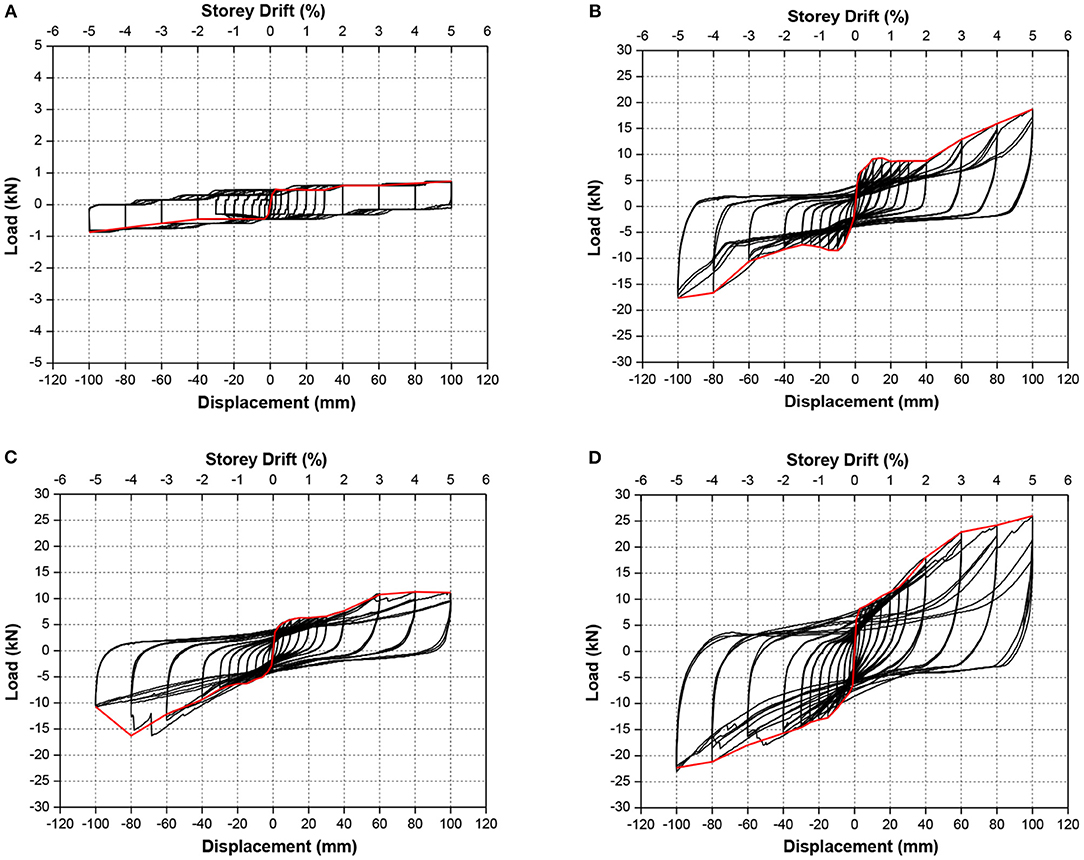
Figure 18. Force–displacement cyclic response of the specimens. (A) Bare frame (Panel zero). (B) Panel MO: semi-interlocking masonry (SIM) infill panel with an open gap at the beam/panel interface. (C) Panel MF: SIM infill panel with foam at the beam/panel interface. (D) Panel MG: SIM infill panel with grout at the beam/panel interface.
However, the different top infill/beam interface strongly influences the behavior of the frames infilled with mechanically interlocking SIM panel tests, as shown in Figures 18B–D.
Other experimental studies on SIM were focused on the out-of-plane performance of SIM infill panels (Totoev and Wang, 2013; Zarrin et al., 2019).
Numerical Calibration
The calibration has been pursued using Ruaumoko program (Carr, 2007), and it is referred to the experimental results summarized in section Summary of the Experimental Response related to SIM infill Panel MO.
Equivalent Spring Approach
Figure 19 shows the comparison, in terms of force–displacement curve, between the in-plane cyclic tests (black line) and the numerical models (red line) on the SIM infill Panel MO. The input of the numerical model was given by the loading history of the displacement effectively applied at the half-height of the top beam during the pseudo-static cyclic tests. The plot shows that the force–displacement curve of the numerical model matches quite well the overall experimental response during all the cycles that have been considered relevant for the present study (up to 2.0% of drift); meanwhile, for displacement higher than 40 mm, the equivalent spring approach has not been able to replicate the hardening behavior of the SIM Panel MO specimen. In this case, the nature of the innovative ductile infill requires an improved macromodel with some damping mechanism since the test results are not precisely captured when force inversion occurs.
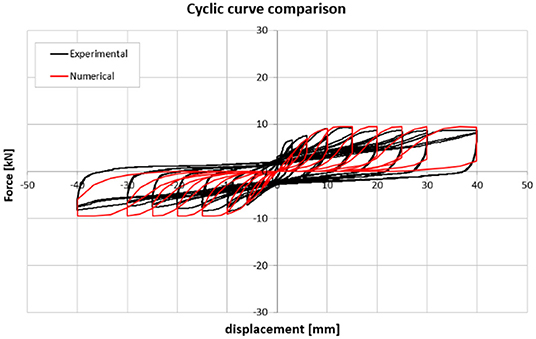
Figure 19. Comparison between the force–displacement experimental and numerical curves of the semi-interlocking masonry (SIM) infill.
The final parameters of the calibrated diagonal macroelements, representing the mechanical interlocking SIM infill panel MO tested by the University of Newcastle, are listed in Table 3. The data are referred to the 2.0 m × 2.0 m infill frame, as described previously.

Table 3. Parameters of the diagonal struts for semi-interlocking masonry (SIM) of the University of Newcastle.
Equivalent Semi-Active Damper Approach
Figure 20 presents the comparison between the in-plane load–displacement cyclic tests of Panel MO (dash line) and the numerical models using the semi-active spring (red line) for the SIM infill. Overall, an acceptable match exists between the numerical curves and experimental curves. Apart from the initial stiff behavior, the semi-active spring model could successfully obtain the performance of SIM infill panel in terms of energy dissipation, force, and displacement capacities.
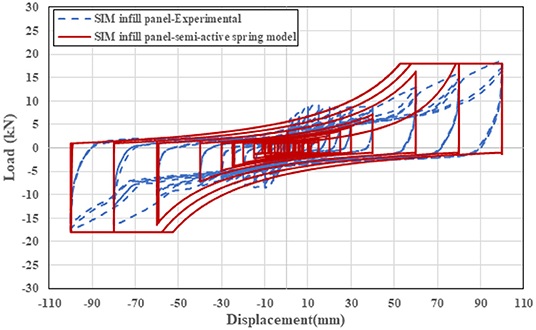
Figure 20. Comparison between the force–displacement experimental and numerical curves of the semi-interlocking masonry (SIM) infill from semi-active spring model.
In addition, it is observed that the numerical model based on the semi-active diagonal springs well-predicts the existing residual shear force in the experimental cycles. The calibrated parameters for the semi-active spring model are shown in Table 4.
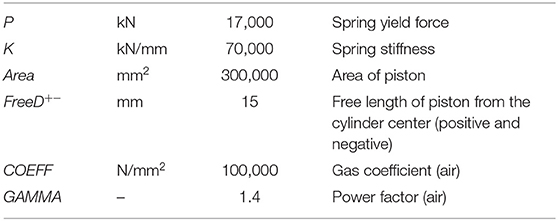
Table 4. Parameters of the semi-active spring model for semi-interlocking masonry (SIM) infill panel.
Seismic Response of Multi-Story Reinforced Concrete Structures With Ductile Infills and Comparison With Traditional Masonry Panels
The aforementioned numerical calibrations can be included in structural models of different buildings in order to study the influence of the two typologies of ductile infills in the global seismic response of RC framed structures. Within the present study, a six-story RC plane structure has been considered using, for the modeling of the infill, only the equivalent spring modeling. Although the equivalent semi-active damper has shown better results in simulating the in-plane behavior of the SIM, especially for drift higher than 2.0%, the equivalent spring model has allowed a direct comparison with “traditional” infill solutions based on previous numerical studies (e.g., Hak et al., 2018). Future studies will also include the modeling of the infilled structures adopting the semi-active damper approach for the SIM system.
The global in-plane response of the RC framed structure with ductile infills has been investigated through non-linear static (“pushover”) and dynamic time history analyses performed on the six-story case-study building shown in Figure 21A. A bare frame and a frame infilled in the two external bays have been considered. The macromodeling approach using the program Ruaumoko was adopted, as defined for the numerical calibration of the single infilled frames. The case-study frame was designed for a level of peak ground acceleration (PGA) equal to 0.35 g·S according to EC8. An infill solution constituted by a double-leaf masonry with 12-cm-thick horizontally highly perforated clay blocks (Figure 21C) has been considered as reference infill (called “T2”), as typical and common infill solution also frequently adopted in seismic-prone areas of some countries in southern Europe (“traditional masonry”). More information on the RC structure and of the traditional infill T2 and their modeling are reported in Hak et al. (2018). The infills with sliding joints have been modeled according to the calibration of the equivalent spring approach described previously, being the dimensions of the tested panel very similar to the ones of the bay of the considered building. Instead, for the mechanical interlocking SIM panel MO, the calibrated values have been properly scaled according to the bay dimension of the frame. The numerical outcomes of the infilled frames have been compared with the bare frame configuration of the same building (Figure 21B). The backbone curves of the infill contributions for the three infill typologies taken into account are reported in Figure 22.
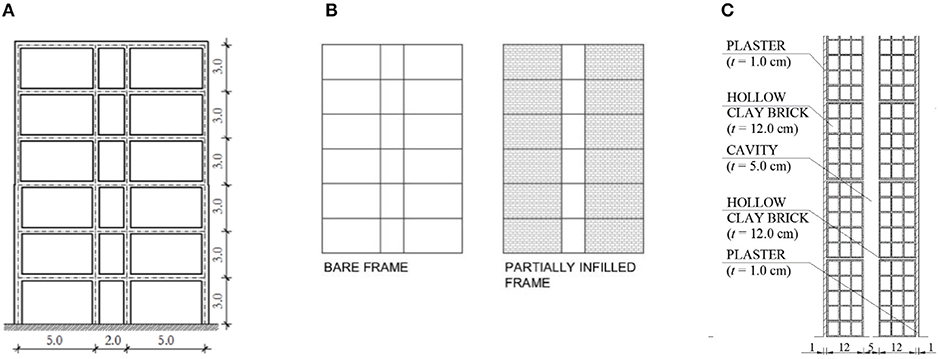
Figure 21. (A) Elevation of two-dimensional prototype structure. (B) Infilled configurations for the six-story building. (C) Details of the “traditional” masonry infill “T2”.
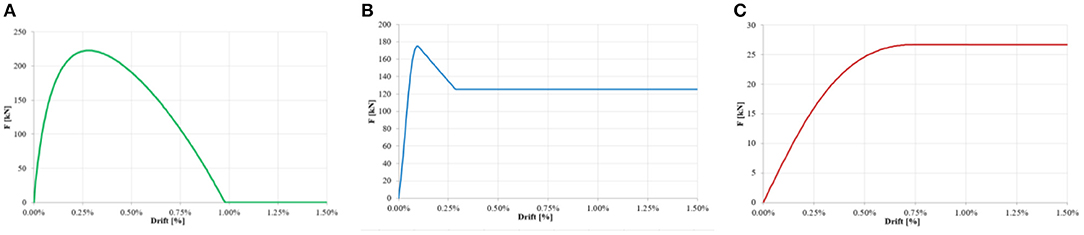
Figure 22. Backbone curves for the infill contribution: (A) Traditional masonry infill “T2”; (B) Infill with sliding joints (TSJ); (C) semi-interlocking masonry (SIM).
Non-linear Static Analyses
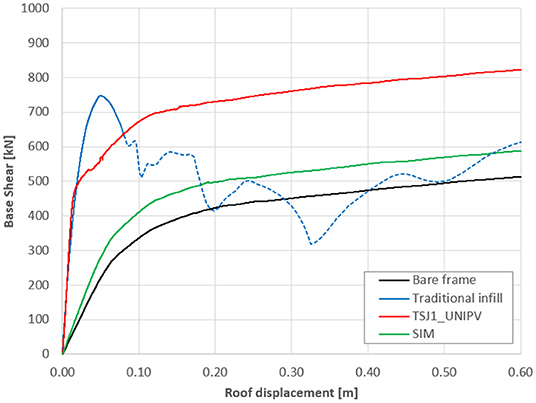
In the non-linear static analyses, the horizontal action was given by means of equivalent horizontal loads applied at each mass of the structure. The intensity of the forces has increased monotonically, while their distribution was kept constant and proportional to the first modal shape of the structure. The results of the pushover curves (base shear vs. lateral displacement of the top floor, see Figure 23) show how the innovative infills provide a response that is almost parallel to the bare frame, with the solution of the University of Pavia having an initial stiffness similar to the one of the traditional infill. The building with SIM infill provides a lateral response, which is very similar to the one of the bare frame. Both the cases with innovative infills present a better performance than the traditional infills; in fact, the traditional solution produces a strong strength and stiffness degradation after the peak, meaning a significant level of damage in the masonry panels, above all at large displacements (see the dashed blue line of Figure 23). On the other hand, the innovative infills do not show any degradation and therefore no or limited level of damage up to very large lateral displacements.
Non-linear Dynamic Analyses
In addition, non-linear time history analyses also have been conducted on the same structure with the three different infills. The selection of the earthquake records was done based on the recommendation of previous studies (Iervolino et al., 2008) on natural ground motions scaled to specified levels of seismicity. Ten earthquake input ground motions were considered per group of analyses relative to a specific frame model. The software REXEL (Iervolino et al., 2010) was adopted to select the earthquakes from the European database. The average value of the 10 records was matched with the target spectrum (±10%) in a range between 0.2·T1 and 2·T1, where T1 is the fundamental period of the structure. The selected spectrum-compatible records were scaled to the design value of PGA (agS) of the case-study frames. The records were compatible to EC8 spectrum Type 1. In accordance with the design process, a reduction factor (ν) of 0.5 has been applied to have records compatible with the spectrum of the damage limitation limit state. Only ground motions recorded on soil class B with magnitudes between 5.5 and 8.0 have been taken into account. In Figure 24, the spectra of the spectrum-compatible earthquake records at the DLS and the ULS have been reported.
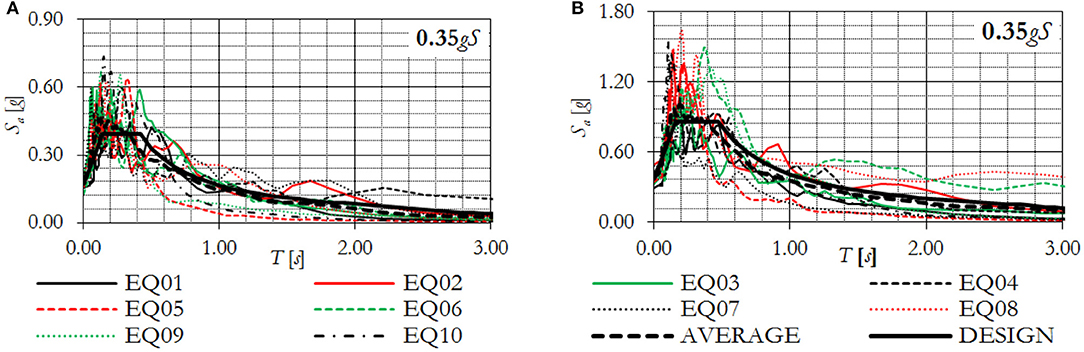
Figure 24. Design spectrum-compatible earthquake records at the (A) damage limit state (DLS) and (B) life safety limit state (LSS/ULS).
The floor displacements and inter-story drifts coming from the dynamic non-linear analyses have been evaluated. The selection of the input ground motion has a great influence in the response on the structures, also considering that different frame typologies, both infilled and bare, with different modes of vibrations, behave differently to the same earthquake. Nevertheless, considering that the sets of input ground motion adopted in the analyses were composed of 10 spectrum-compatible accelerograms, the quantities related to the response of the structure were analyzed in terms of average values. Figure 25 summarizes the displacement and drift profiles for each set of accelerograms, considering the bare frames and the infilled configurations with the three infills. Displacement profiles referred to the moment when the maximum displacement reached in any of the story has been acquired for every building configuration and for every ground motion record. The lines in the displacement plots (Figures 25A,B) represent the average values of the displacement for the specific set of accelerograms. Similarly to the displacement profiles, also the drift ones have been computed for any of the building configuration type and ground motion record considered. The drift profiles correspond to the instance of a maximum drift recorded in any of the stories.
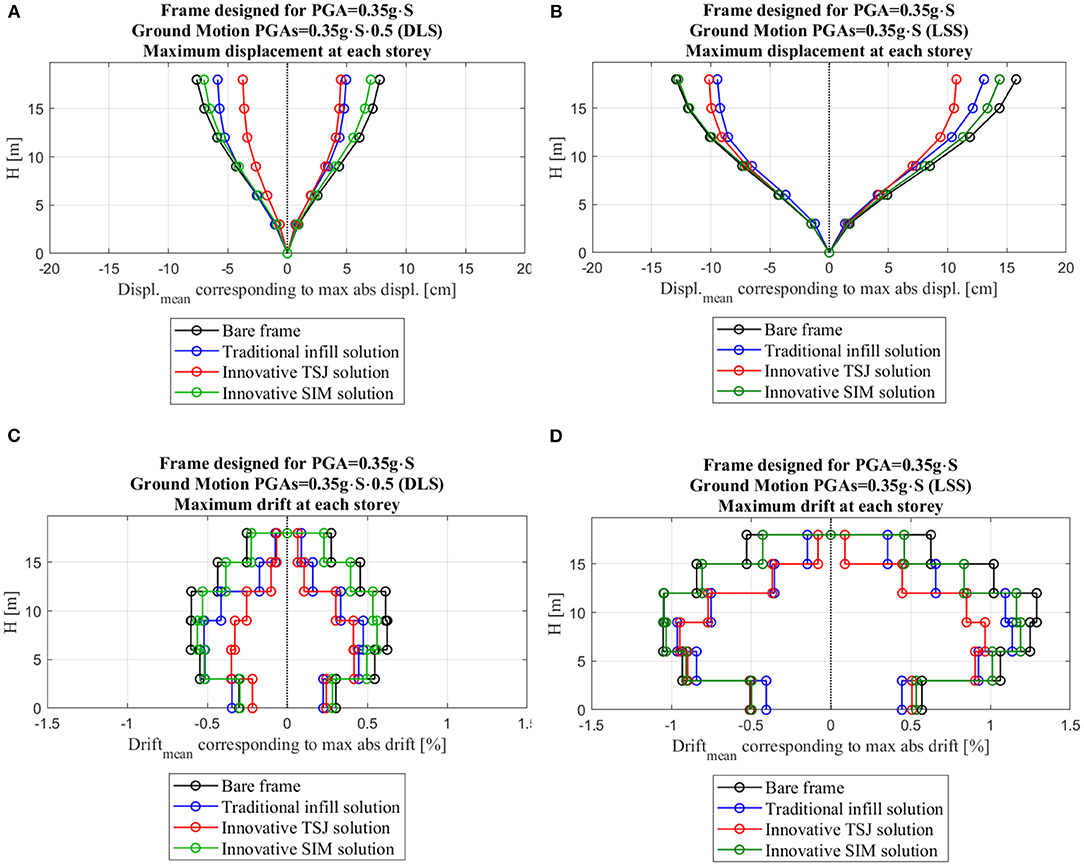
Figure 25. (A) Displacement profiles at damage limit state (DLS). (B) Displacement profiles at life safety limit state (ULS/LSS). (C) Inter-story drift profiles at DLS. (D) Inter-story drift profiles at ULS/LSS.
Looking at the results of the non-linear dynamic analyses, the two innovative infills have shown different seismic responses. While the SIM infilled structure provides an overall deformation similar to the one of the bare frame due to its small stiffness, the building infilled with the TSJ solution supplies a significant decrease of the inter-story drift demand in comparison with both the bare frame and the traditional infill; this latter aspect is of paramount importance since, at the same level of global initial stiffness of the infilled structure (see pushover curves in Figure 23), the displacement demand from time histories is strongly reduced, thanks to the large values of damping of the TSJ system.
In-Plane Performance of the Infilled Buildings: Comparison Between Traditional Infills and Innovative System TSJ
From the results of the dynamic non-linear analyses for different infill configurations at the different limit states, the attainment of the in-plane performance due to the action of selected ground motion records has been determined. The comparison only refers to the innovative infill TSJ, whereas the performance of the SIM solution will be the object of future research. The performance limit states of a single infill is assessed based on the level of in-plane drift according to the level of damage observed in cyclic in-plane tests on infilled simple frames, in agreement with the approach proposed by Morandi et al. (2018a), where three limit states were assumed (“Operational” OLS, “Damage” DLS, and “Life safety/Ultimate” LSS/ULS). Table 5 reports a resume of such drift limits for the innovative infill solution TSJ (Morandi et al., 2018b) and for the traditional solution (Hak et al., 2012). The frames are assumed to fulfill the global performance criteria, i.e., the requirement at the level of the entire structure, with the design seismic action at DLS and ULS, if the requirements defined in Table 5 are satisfied for more than 50% of the earthquake records (at least six out of 10).
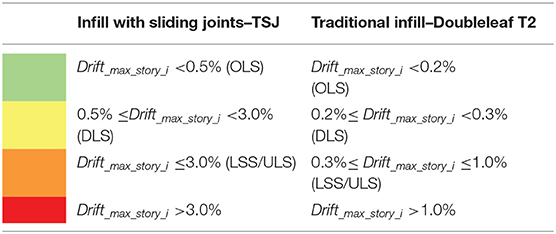
Table 5. Performance levels of the infills (from Hak et al., 2012; Morandi et al., 2018b).
Figure 26 reports the comparison of the in-plane damage distribution obtained for each record of the infilled frames designed for PGA = 0.35 g·S, subjected to the input ground motions scaled at DLS (PGA = 0.35 g·S·0.5). Figure 27 illustrates the same comparison but with the input ground motions scaled at ULS (PGA = 0.35 g·S). The colors of the infills indicate if the limit state is exceeded or not, according to what was reported in Table 5.
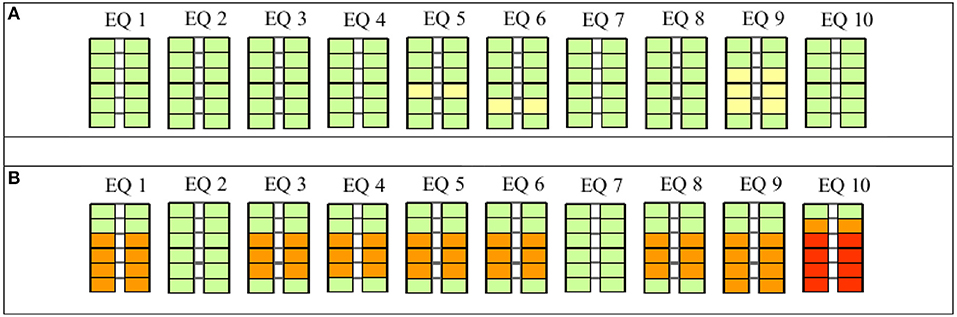
Figure 26. Damage distribution of infilled frame designed for peak ground acceleration (PGA) = 0.35 g·S and subjected to the input ground motions scaled to damage limit state (DLS): PGA = 0.35 g·S·0.5. (A) Innovative infills and (B) “traditional-T2” infills.
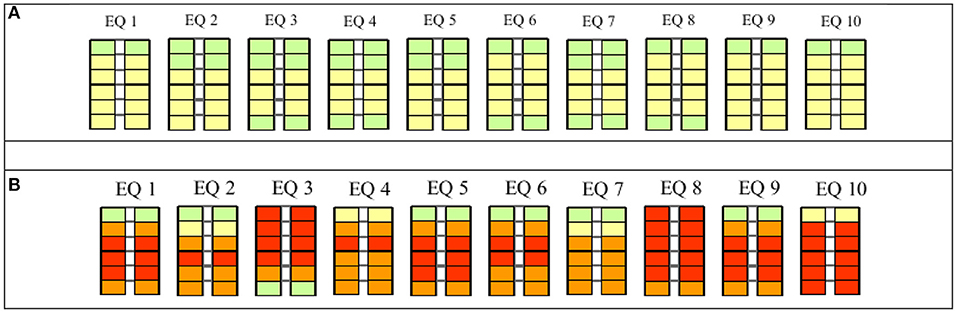
Figure 27. Damage distribution of infilled frame designed for peak ground acceleration (PGA) = 0.35 g·S and subjected to the input ground motions scaled to life safety limit state (LSS/ULS): PGA = 0.35 g·S. (A) Innovative infills and (B) “traditional-T2” infills.
With the records scaled at the design seismic action for DLS, the majority of the innovative infills TSJ of the RC structure actually result undamaged, with the exception of a few panels, which attain an “operational” damaged state. On the other side, on the same structure with traditional infills, seven records out of 10 trigger the exceedance of the DLS in many infills and, in one case, also the collapse of the infills in the bottom four stories of the building. Therefore, with the European codified design assumptions on infills at DLS, i.e., that the inter-story drift should be <0.50% on bare frames, the fulfillment of the verifications at DLS is not satisfied.
With the records scaled at the design seismic action for ULS, many of the innovative infills are not undamaged anymore, but none exceeds the DLS and, therefore, can be easily reparable at small costs. Conversely, in the case of traditional infills, for nine records out of 10, at least one panel of the building collapses for a level of design seismic force equal to the one used for the design at the building at ULS; in particular, for six cases, the panels exceed the LSS/ULS condition in three, four, and five stories of the structure. Also at ULS, the codified design requirements on traditional infills do not allow a safe design.
Conclusions
Post-seismic inspections and research studies have continuously highlighted a series of issues related to the seismic response of traditional rigidly attached masonry infills. In order to solve such well-known issues, several technological solutions have been recently proposed. Among the possible systems, one of the most promising belongs to the ductile infill category, where the infills can deform up to relevant drifts, even larger than 2.0%, with a limited interaction with the structure. The seismic response of the ductile infills has been studied through experimental campaigns at the University of Pavia and the University of Newcastle, where two different deformable infill solutions with horizontal sliding and deformable joints have been separately developed. The experiments, consisting of in-plane and out-of-plane cyclic seismic tests on solid infills, have provided a very good lateral performance, promising for the practical application of such systems.
With the aim of analyzing the in-plane response of RC structures infilled with these ductile masonry infills, the present study deals with different modeling strategies, which could be adopted in order to identify simple but effective macromodeling techniques for their calibration. The apparently complex in-plane seismic behavior has been simulated through non-linear single-strut with lumped plasticity macromodels, as usually done for traditional infills. The calibration of the two solutions has been fulfilled by replicating the overall force–displacement experimental curves obtained from the cyclic in-plane tests. In addition to the common equivalent single-strut model, an alternative approach, based on an equivalent semi-active damper, has been introduced.
The results have shown that the equivalent spring model is more appropriate for the TSJ system, whereas the equivalent semi-active damper appears more suitable for SIM systems, especially for typologies where the dissipation energy is relevant, a negative constant force is experimentally observed in the unloading branch of the cyclic test, and the hardening of the experimental force–displacement curve occurs for medium–high imposed displacements.
The calibrated equivalent spring macromodels have been used to perform a study on the seismic global behavior of infilled RC frame buildings through non-linear static and dynamic analyses. A comparison between the performance of the frame with innovative infills and the one with a traditional infill solution has shown that all these systems can modify the global behavior of the structure differently from each other. The two innovative infills have shown some mutual differences in seismic response. Meanwhile, the structure infilled with SIM system has provided an overall deformation slightly lower than the one of the bare frame due to its small stiffness, the building infilled with TSJ solution has supplied a significant decrease of the inter-story drift demand in comparison with both the bare frame and the traditional infill. Therefore, the SIM infills are able to slightly reduce the deformation demand with respect to the bare frame, also thanks to its damping contribution, which is however slightly underestimated with the adopted equivalent spring model. On the other side, the TSJ system allows to strongly reduce the displacement demand, thanks to its high values of damping, which has been demonstrated by values of drifts lower than the ones of the structure infilled with traditional masonry, although having the same levels of global initial stiffness. Moreover, such good performance of the ductile solutions is attained without any significant damage on the infills at different levels of seismic actions, i.e., at records scaled for design action at DLS and ULS, whereas the traditional infills attain large levels of in-plane damage (and sometimes collapse) already at DLS. With design seismic action at DLS, the innovative infill TSJ actually results even undamaged and, at ULS, none exceeds the DLS and, therefore, can be easily reparable at small costs.
In the case of the structure infilled with the traditional masonry solution, the comply of the DLS and the ULS is never fulfilled due to the fact that the drift limitations of the bare frame imposed by the standards at the design levels (i.e., 0.50% of seismic design action at DLS included in EC8 and NTC2018) are not safe-sided for weak/slender infills, as already pointed out by Hak et al. (2018) and Morandi et al. (2018a).
The employment of the equivalent semi-active damper approach to model the SIM system in RC structures, which is ongoing, will represent an interesting step forward in order to suitably capture the damping level attained during the tests.
This first investigation on the seismic performance of the ductile infills in RC structures and the comparison with “traditional” masonry infills need certainly to be widened on other structural configurations, infill layouts, and panels with openings, but they has provided some early interesting findings on the effectiveness of these infill systems in the reduction of the seismic vulnerability of RC structures.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
For the development of the University of Pavia system, the financial support of the European Commission within the project INSYSME INnovative SYStems of earthquake resistant Masonry Enclosures in RC buildings, Grant FP7-SME-2013-2-GA606229, 2013–2016 was acknowledged.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The present research has been conducted by the University of Pavia, EUCENTRE Foundation, and University of Newcastle. ANDIL and its associated companies, and RUREDIL spa are gratefully acknowledged as industrial partners of the project. The contribution of Capaccioli srl for the supply of the sliding joints is also acknowledged. MH acknowledged Australian Government Research Training Program Scholarship.
Footnotes
1. ^FEMA E-71. Reducing Risks of Non-structural Earthquake Damage. Washington DC: FEMA.
2. ^INSYSME INnovative SYStems for earthquake resistant Masonry Enclosures in RC building. European project, grant FP7-SME-2913-2-GA606229, 2013-2016.
References
Akhoundi, F., Lourenço, P. B., and Vasconcelos, G. (2016). Numerically based proposals for the stiffness and strength of masonry infills with openings in reinforced concrete frames. Earthquake Eng. Struct. Dyn. 45:869–891. doi: 10.1002/eqe.2688
Asteris, P. G., Antoniou, S. T., Sophianopoulos, D. S., and Chrysostomou, C. Z. (2011). Mathematical macromodeling of infilled frames: state of the art. J. Struct. Eng. 137, 1508–1517. doi: 10.1061/(ASCE)ST.1943-541X.0000384
Asteris, P. G., Cavaleri, L., Di Trapani, F., and Tasris, A. K. (2017). Numerical modelling of out-of-plane response of infilled frames: state of the art and future challenges for the equivalent strut macromodels. Eng. Struct. 132, 110–122. doi: 10.1016/j.engstruct.2016.10.012
Asteris, P. G., Cotsovos, D. M., Chrysostomou, C. Z., Mohebkhah, A., and Al-Chaar, G. K. (2013). Mathematical micromodeling of infilled frames: state of the art. Eng. Struct. 56, 1905–1921. doi: 10.1016/j.engstruct.2013.08.010
ASTM International. (2016). ASTM C109/C109M-16: Standard Test Method for Compressive Strength of Hydraulic Cement mortars.
Binici, B., Canbay, E., Aldermir, A., Demirel, I. O., Uzgan, U., Eryurtlu, Z., et al. (2019). Seismic behaviour and improvement of autoclaved aerated concrete infill walls. Eng. Struct. 193, 68–81. doi: 10.1016/j.engstruct.2019.05.032
Bolis, V., Stavridis, A., and Preti, M. (2017). Numerical investigation of the in-plane performance of masonry-infilled RC frames with sliding subpanels. J. Struct. Eng. 143:04016168. doi: 10.1061/(ASCE)ST.1943-541X.0001651
Braga, F., Manfredi, V., Masi, A., Salvatori, A., and Vona, M. (2011). Performance of non-structural elements in RC buildings during L'Aquilta 2009 earthquake. Bull. Earthquake Eng. 9, 307–324. doi: 10.1007/s10518-010-9205-7
Butenweg, C., Marinkovic, M., and Salatic, R. (2019). Experimental results of reinforced concrete frames with masonry infills under combined quasi-static in-plane and out-of-plane seismic loading. Bull. Earthquake Eng. 17, 3397–3422. doi: 10.1007/s10518-019-00602-7
Caliò, I., and Pantò, B. (2014). A macro-element modelling approach of infilled frame structures. Comput. Struct. 143, 91–107. doi: 10.1016/j.compstruc.2014.07.008
Calvi, G. M., and Bolognini, D. (2001). Seismic response of reinforced concrete frames infilled with weakly reinforced masonry panels. J. Earthquake Eng. 5, 153–185. doi: 10.1080/13632460109350390
Canbay, E., Binici, B., Demirel, I. O., Aldemir, A., Uzgan, U., Eryurtlu, Z., et al. (2018). DEGAS: an innovative earthquake-proof AAC wall system. ce/papers 2, 247–252. doi: 10.1002/cepa.816
Chase, J. G., Mulligan, K. J., Elliott, R. B., Rodgers, G. W., Mander, J. B., Carr, A. J., et al. (2007). “Re-shaping hysteresis: seismic semi-active control experiments for a 1/5th scale structure,” in Proceedings 8th Pacific Conference On Earthquake Engineering (8PCEE). Singapore.
Cheng, X., Zou, Z., Zhu, Z., Zhai, S., Yuan, S., Mo, Y., et al. (2020). A new construction technology suitable for frame partitioned infill walls with sliding nodes and large openings: test results. Construct. Build. Mater. 258:119644. doi: 10.1016/j.conbuildmat.2020.119644
Chrysostomou, C. Z., and Asteris, P. G. (2012). On the in-plane properties and capacities of infilled frames. Eng. Struct. 41, 385–402. doi: 10.1016/j.engstruct.2012.03.057
Crisafulli, F. J. (1997). Seismic behaviour of reinforced concrete structures with masonry infills (Ph.D. dissertation). Department of Civil Engineering. University of Canterbury. Canterbury. New Zealand.
Crisafulli, F. J., Carr, A. J., and Park, R. (2000). Analytical modeling of infilled frame structures - a general review. Bull. N Zeal Soc Earthquake Eng. 33, 30–47. doi: 10.5459/bnzsee.33.1.30-47
da Porto, F., Guidi, G., Dalla Benetta, M., and Verlato, N. (2013). “Combined in-plane/out-of-plane experimental behaviour of reinforced and strengthened infill masonry walls,” in Proceedings of 12th Canadian Masonry Symposium (Vancouver, BC).
De Risi, M. T., Furtado, A., Rodrigues, H., Melo, J., Verderame, G. M., Arede, A., et al. (2020). Experimental analysis of strengthening solutions for the out-of-plane collapse of masonry infills in RC structures through textile reinforced mortars. Eng. Struct. 207:110203. doi: 10.1016/j.engstruct.2020.110203
Di Trapani, F., Shing, P. B., and Cavaleri, L. (2017). Macroelement model for in-plane and out-of-plane responses of masonry infills in frame structures. J. Struct. Eng. 144:04017198. doi: 10.1061/(ASCE)ST.1943-541X.0001926
EC 8-Part 1 (2004). Eurocode 8 – Design of structures for earthquake resistance – Part 1: General Rules, Seismic Actions and Rules for Buildings. ECS, EN 1998-1, Brussels.
El-Dakhakhni, W. W., Elgaaly, M., and Hamid, A. A. (2003). Three-strut model for concrete masonry-infilled steel frames. J. Struct. Eng. 129, 177–185. doi: 10.1061/(ASCE)0733-9445(2003)129:2(177)
Forghani, R., Totoev, Y. Z., Kanjanabootra, K., and Davison, A. (2016). Experimental investigation of water penetration through semi-interlocking masonry walls. J. Arch. Eng. 23:227. doi: 10.1061/(ASCE)AE.1943-5568.0000227
Fragomeli, A., Galasco, A., Graziotti, F., Guerrini, G., Kallioras, S., Magenes, G., et al. (2017). Comportamento degli edifici in muratura nella sequenza sismica dell'Italia centrale del 2016 – Parte 1: Quadro generale (in Italian). Progettazione Sismica 8, 49–77.
Franco-Anaya, R., Carr, A., and Chase, J. (2014). “Shaking table tests of a model structure with semi-active resattable devices,” in Proceedings of 10th US National Conference of Earthquake Engineering Frontiers of Earthquake Enginnering (Anchorage, AL).
Franco-Anaya, R., Carr, A., and Chase, J. (2017). “Experimentally validated analytical model of a semi-active resettable tendon for seismic protection,” in Proceedings of 16 WCEE (Santiago de Chile).
Fukada, Y. (1969). “Study on the restoring force characteristics of reinforced concrete buildings,” in [in Japanese], Proceedings Kanto District Symposium. Architectural Institute of Japan (Tokyo), 40.
Furtado, A., Rodrigues, H., Arede, A., and Varum, H. (2016). Experimental evaluation of out-of-plane capacity of masonry infill walls. Eng. Struct. 111, 48–63. doi: 10.1016/j.engstruct.2015.12.013
Furtado, A., Rodrigues, H., Melo, J., Arede, A., and Varum, H. (2019). “Experimental assessment of strengthening strategy to improve the masonry infills out-of-plane behaviour through textile reinforced mortar,” in Proceedings 7th ECCOMAS – COMPDYN 2019 (Crete). doi: 10.7712/120119.7060.19426
Giberson, M. F. (1967). “The response of nonlinear multi-storey structures subjected to earthquake excitation,” in EERL Report California Institute of Technology (Pasadena, CA).
Gkournelos, P. D., Bournas, D. A., and Triantafillou, T. C. (2019). Combined seismic and energy upgrading of existing reinforced concrete building using TRM jacketing and thermal insulation. Earthquakes Struct. 16, 625–639. doi: 10.12989/eas.2019.16.5.625
Hak, S., Morandi, P., and Magenes, G. (2013). Evaluation of infill strut properties based on in-plane cyclic tests. Gravedinar 6, 411–422. doi: 10.14256/JCE.868.2013
Hak, S., Morandi, P., and Magenes, G. (2018). Prediction of inter-storey drifts for regular RC structures with masonry infills based on bare frame modelling. Bull. Earthquake Eng. 16, 397–425. doi: 10.1007/s10518-017-0210-y
Hak, S., Morandi, P., Magenes, G., and Sullivan, T. (2012). Damage control for clay masonry infills in the design of RC frame structures. J. Earthquake Eng. 16, 1–35. doi: 10.1080/13632469.2012.670575
Hemmat, M., Totoev, Y. Z., and Masia, M. (2019). “Finite element simulation of confined semi-interlocking masonry walls,” in Proceeding of the 13th North American Masonry Conference (Salt Lake City, UT).
Hemmat, M., Totoev, Y. Z., and Masia, M. (2020a). The assessment of confined semi-interlocking masonry buildings usign macro-modelling approach. Proceeding of 17th IBMAC (Krakow). doi: 10.1201/9781003098508-150
Hemmat, M., Totoev, Y. Z., and Masia, M. (2020b). The introduction of confined semi-interlocking masonry system for buildings to improve earthquake performance. Int. J. Masonry Res. Innovat. 5, 348–365. doi: 10.1504/IJMRI.2020.107989
Hossain, M. A., Totoev, Y. Z., Masia, M., and Friend, M. (2017). “In-plane cyclic behaviour of semi interlocking masonry panel under large drift,” in Proceeding of the 13th Canadian Masonry Symposium (Halifax Regional Municipality, NS).
Hossain, M. A., Totoev, Y. Z., and Masia, M. J. (2016). “Friction on mortar-less joints in semi interlocking masonry,” in Proceedings of 16th International Brick and Block Masonry Conference (Padova). doi: 10.1201/b21889-203
Iervolino, I., Galasso, C., and Cosenza, E. (2010). REXEL: computer aided record selection for code-based seismic structural analysis. Bull. Earthquake Eng. 8, 339–362. doi: 10.1007/s10518-009-9146-1
Iervolino, I., Maddaloni, G., and Cosenza, E. (2008). Eurocode 8 compliant real record sets for seismic analysis of structures. J. Earthquake Eng. 12, 54–90. doi: 10.1080/13632460701457173
Koutas, L., Pitytzogia, A., Triantafillou, T. C., and Bousias, S. N. (2013). Strengthening of infilled reinforced concrete frames with TRM: study on the development and testing of textile-based anchors. J. Composit. Construct. 18:316. doi: 10.1061/(ASCE)CC.1943-5614.0000316
Liberatore, L., AlShawa, O., Marson, C., Pasca, M., and Sorrentino, L. (2020). Out-of-plane capacity equations for masonry infills walls accounting for openings and boundary conditions. Eng. Struct. 207:110198. doi: 10.1016/j.engstruct.2020.110198
Lin, K., Totoev, Y. Z., and Lin, H. (2011a). “Energy dissipation during cyclic tests in framed dry stack and unreinforced masonry panels,” in Proceedings of the 9th Australian Masonry Conference (Queenstown), 15–18.
Lin, K., Totoev, Y. Z., Lin, H., and Guo, T. (2016). In-plane behaviour of a reinforcement concrete frame with a dry stack masonry panel. Materials 9:108. doi: 10.3390/ma9020108
Lin, K., Totoev, Y. Z., and Lin, H. J. (2011b). In-plane cyclic test on framed dry-stack masonry panel. Adv. Mater. Res. J. 163–167, 3899–3903. doi: 10.4028/www.scientific.net/AMR.163-167.3899
Manzini, C. F., and Morandi, P. (2012). Rapporto preliminare sulle prestazioni ed i danneggiameti agli edifici in muratura portante moderni a seguito degli eventi sismici emiliani del 2012 (in Italian), Eucentre. Available online at: www.eqclearinghouse.org/2012-05-20-italy/
Manzini, C. F., Morandi, P., Milanesi, R. R., and Magenes, G. (2018). “Shaking-table test on a two-storey RC framed structured with innovative infills with sliding joints,” in Proceedings of the 16th ECEE, 18-21 June 2018 (Thessaloniki).
Mehrabi, A., and Shing, P. B. (1997). Finite element modeling of masonry-infilled RC frames. J. Struct. Eng. 123, 604–613. doi: 10.1061/(ASCE)0733-9445(1997)123:5(604)
Milanesi, R. R., Andreotti, A., Morandi, P., and Penna, A. (2019). “FEM simulation of the in-plane seismic experimental response of r.c. frames with unreinforced and bed-joint reinforced AAC masonry infills,” in Proceedings 7th ECCOMAS – COMPDYN 2019 (Crete), 24–26. doi: 10.7712/120119.7089.18853
Milanesi, R. R., Morandi, P., and Magenes, G. (2018). Local effects on RC frames induced by AAC masonry infills through FEM simulation of in-plane tests. Bull. Earthquake Eng. 16, 4053–4080. doi: 10.1007/s10518-018-0353-5
Milanesi, R. R., Morandi, P., Manzini, C. F., Albanesi, L., and Magenes, G. (2020). Out-of-plane response of an innovative masonry infill with sliding joints from shaking table tests. J. Earthquake Eng. 1–35. doi: 10.1080/13632469.2020.1739173
Mohammadi, M., Akrami, V., and Mohammadi-Ghazi, R. (2001). Methods to improve infilled frame ductility. J. Struct. Eng. 137, 646–653. doi: 10.1061/(ASCE)ST.1943-541X.0000322
Morandi, P., Hak, S., and Magenes, G. (2018a). Performance-based interpretation of in-plane cyclic tests on RC frames with strong masonry infills. Eng. Struct. 155, 503–521. doi: 10.1016/j.engstruct.2017.11.058
Morandi, P., Milanesi, R. R., and Magenes, G. (2018b). Innovative solution for seismic-resistant masonry infills with sliding joints: in-plane experimental performance. Eng. Struct. 176, 719–733. doi: 10.1016/j.engstruct.2018.09.018
Mulligan, K. J., Chase, J. G., Mander, J. B., Rodgers, G. W., and Elliott, R. B. (2010). Nonlinear models and validation for resettable device design and enhanced force capacity. Struct. Control Health Monitor. 17, 301–316. doi: 10.1002/stc.298
Norme Tecniche per le Costruzioni (2008). D.M. 14/01/2008. Norme Tecniche per le Costruzioni (NTC08), 2008. Gazzetta Ufficiale, n.29 14/02/2008 – Supplemento ordinario n.30, Roma. Italy (in Italian).
Pantò, B., Caliò, I., and Lourencço, P. B. (2018). A 3D discrete macro-element for modelling the out-of-plane behaviour of infilled frame structures. Eng. Struct. 175, 371–385. doi: 10.1016/j.engstruct.2018.08.022
Paulay, T., and Priestley, M. J. (1992). Seismic Design of Reinforced Concrete and Masonry Building. New York, NY: John Wiley & Sons. doi: 10.1002/9780470172841
Preti, M., Bettini, N., Migliorati, L., Bolis, V., Stavridis, A., and Plizzari, G. A. (2016). Analysis of the in-plane response of earthen masonry infill panels partitioned by sliding joints. Earthquake Eng. Struct. Dyn. 45, 1209–1232. doi: 10.1002/eqe.2703
Preti, M., Bolis, V., and Stavridis, A. (2017). Seismic infill-frame interaction of masonry walls partitioned with horizontal sliding joints: analysis and simplified modeling. J. Earthquake Eng. 23, 1651–1677. doi: 10.1080/13632469.2017.1387195
Priestley, M. J. N., Calvi, G. M., and Kowalsky, M. J. (2007). Displacement-Based Seismic Design of Structures. Pavia: IUSS Press.
Tarque, N., Candido, L., Camata, G., and Spacone, E. (2015). Masonry infilled frame structures: state of the art and review of numerical modelling. Earthquake Struct. 8, 225–251. doi: 10.12989/eas.2015.8.1.225
Totoev, Y. (2015). Design procedure for semi interlocking masonry. J. Civil Eng. Arch. 9, 517–525. doi: 10.17265/1934-7359/2015.05.003
Totoev, Y., and Wang, Z. (2013). “In-plane and out-of-plane tests on steel frame with SIM infill,” in Proceedings of the 12th Canadian Masonry Symposium (Vancouver, BC).
Totoev, Y. Z., and Al Harthy, A. (2016). Semi interlocking masonry as infill wall system for earthquake resistant buildings: a review. J. Eng. Res. 13, 33–41. doi: 10.24200/tjer.vol13iss1pp33-41
Totoev, Y. Z., and Lin, K. (2012). Frictional energy dissipation and damping capacity of framed semi-interlocking masonry infill panel. Proceedings of the 15th IBMAC (Florianapolis).
Tsantilis, A. V., and Triantafillou, T. C. (2013). Innovative seismic isolation of infills using cellular materials at the interface with the surrounding RC frames. Eng. Struct. 155, 279–297. doi: 10.1016/j.engstruct.2017.11.025
Verlato, N., Guidi, G., da Porto, F., and Modena, C. (2016). “Innovative systems for masonry infill walls based on the use of deformable joints: Combined in-plane/out-of-plane tests,” in Proceedings of the 16th IBMAC (Padova), 26–30. doi: 10.1201/b21889-168
Keywords: innovative masonry infills, sliding joints, semi-interlocking masonry (SIM), in-plane seismic response, non-linear analyses, macro-modeling of infilled structures, reduced seismic vulnerability
Citation: Milanesi RR, Hemmat M, Morandi P, Totoev Y, Rossi A and Magenes G (2020) Modeling Strategies of Ductile Masonry Infills for the Reduction of the Seismic Vulnerability of RC Frames. Front. Built Environ. 6:601215. doi: 10.3389/fbuil.2020.601215
Received: 31 August 2020; Accepted: 16 November 2020;
Published: 21 December 2020.
Edited by:
André Furtado, University of Porto, PortugalReviewed by:
Bartolomeo Pantò, Imperial College London, United KingdomPanagiotis G. Asteris, School of Pedagogical & Technological Education, Greece
Liborio Cavaleri, University of Palermo, Italy
Copyright © 2020 Milanesi, Hemmat, Morandi, Totoev, Rossi and Magenes. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Riccardo R. Milanesi, cmljY2FyZG8ubWlsYW5lc2lAdW5pcHYuaXQ=
 Riccardo R. Milanesi
Riccardo R. Milanesi Mehdi Hemmat
Mehdi Hemmat Paolo Morandi3
Paolo Morandi3