Tuned Mass Dampers for Response Reduction of a Reinforced Concrete Chimney Under Near-Fault Pulse-Like Ground Motions

The article investigates response mitigation of a reinforced concrete (RC) chimney subjected to pulse-like near-fault ground motions using tuned mass damper (TMD) schemes. The total height of the chimney is 265 m with a mass of 11,109 ton. Three TMD schemes are used: single tuned mass damper (STMD), multiple TMDs having equal stiffness (w-MTMDs) and multiple TMDs having equal masses (e-MTMDs). The STMD is tuned to the fundamental frequency of the chimney while both w-MTMDs and e-MTMDs have three TMDs for controlling each of the first and second modes (total of six TMDs) of vibration. Response of the uncontrolled and controlled structures is calculated for 69 recorded ground motions containing a dominant velocity pulse. Displacement and acceleration at top node of the RC chimney are the response of interest for performance assessment. It is found that e-MTMDs are more effective and robust than other schemes. It is also found that the pulse period of ground motion plays a very important role in how effective the control schemes are. There is a large variability in the reduction of response across these ground motions, and optimization methods independent of ground motion are not robust. There is a need for more advanced optimization methods incorporating information about local seismic sources.

Introduction

Reinforced concrete (RC) chimneys are tall structures. They are very sensitive to earthquake ground motion Wilson (2003) explained that seismic response of a tall chimney is not adequately described by a single degree of freedom (SDOF) model, and that significant contribution from higher modes can be expected, especially in acceleration response. Distribution of shear force and moment demands along the height of such chimneys, is therefore, not as is implied by many design standards which typically rely on the mode shape of the fundamental normal mode.

Seismic vibration mitigation of tall structures has been an active area of research. Longarini and Zucca (2014) studied a 50 m tall masonry chimney and found that tuned mass damper (TMD) can be used to reduce its seismic response. Multiple TMDs (MTMDs) could be more beneficial to control a range of frequencies, which provides robustness against detuning caused by variations of the frequencies of the structure (Wang and Shi, 2019). Elias et al. (2016) showed that multiple TMDS tuned to different vibration modes and distributed over the structure (d-MTMDs) are superior to a single TMD tuned to the fundamental mode of vibration in controlling seismic response of tall chimneys. Application of d-MTMDs for wind response control of a chimney is presented in Elias et al. (2017, 2019a). The concept of d-MTMDs is well-established and defined for response control of different structures subjected to different loading conditions (Gill et al., 2017; Elias, 2018, 2019; Elias and Matsagar, 2019; Elias et al., 2019b; Matin et al., 2019; Nigdeli and Bekdas, 2019). Etedali et al. (2019) demonstrated that friction TMDs (FTMDs) can mitigate structural response better than TMDs. Other solutions such as inerter TMDs or particle dampers (Greco and Marano, 2013; Reggio and Angelis, 2015; De Domenico and Ricciardi, 2018a,b; De Domenico et al., 2018; Lu et al., 2018; Rezaee and Aly, 2018; Cao and Li, 2019) have also been proposed in the vibration control literature. Different optimization techniques are used by researchers to improve the performance of TMDs (Nigdeli and Bekdas, 2013, 2017; Bekdas et al., 2018; Yucel et al., 2019). Huergo and Hernández (2019a,b) presented a structural model using coupled shear and flexural beams incorporating an arbitrary number of TMDs along the height. A detailed literature survey on passive TMDs is provided by Elias and Matsagar (2017).

Ground motions close to an earthquake source are often impulsive. Forward-rupture directivity results in constructive interference of seismic waves radiated by different sections of a rupturing fault as they arrive at a station, and this is manifest as a strong, short duration velocity pulse (see, for example, Rupakhety et al., 2011). Such dominant pulses have been found to be demanding on tall and flexible structures. For example, Sigurðsson et al. (2019) have shown that near-fault pulse-like ground motions are more demanding than far-fault non-pulse-like ground motion of same peak acceleration to a utility-scale land-based wind turbine. Since the strong shaking in these pulse-like ground motions is impulsive in nature, TMD masses do not have enough time to respond to the excitation and thereby control structural response effectively. This has been generally acknowledged in the literature (see for example Chen and Wu, 2001). Matta (2013), however, showed that TMDs can be used to control response of structures to pulse-like ground motion, provided the TMD has a large enough mass. The potential effectiveness of TMDs also depends on the structure being considered. For example, effectiveness of TMDs might be better for tall and flexible structures, which are very susceptible to pulse-like ground motions, than for very stiff structures. Effectiveness of TMDs in controlling response of tall structures like chimneys when subjected to pulse-like ground motions is missing in the literature. This work investigates this important issue using numerical simulation of response of a tall reinforced concrete chimney subjected to many near-fault pulse-like ground motions recorded during past earthquakes. To quantify the effect of such ground motions, a set of 69 recorded earthquake ground motions are selected from the database given in Sigurðsson et al. (2019), and further described in Rupakhety (2010).

Three TMD schemes namely single TMD (STMD); MTMDs with equal stiffness (w-MTMDs); and MTMDs with equal masses (e-MTMDs) are considered in this study. The STMD is tuned to the fundamental frequency of the chimney, while w-MTMDs and e-MTMDs are designed to control the response around two modes.

Mathematical Modeling

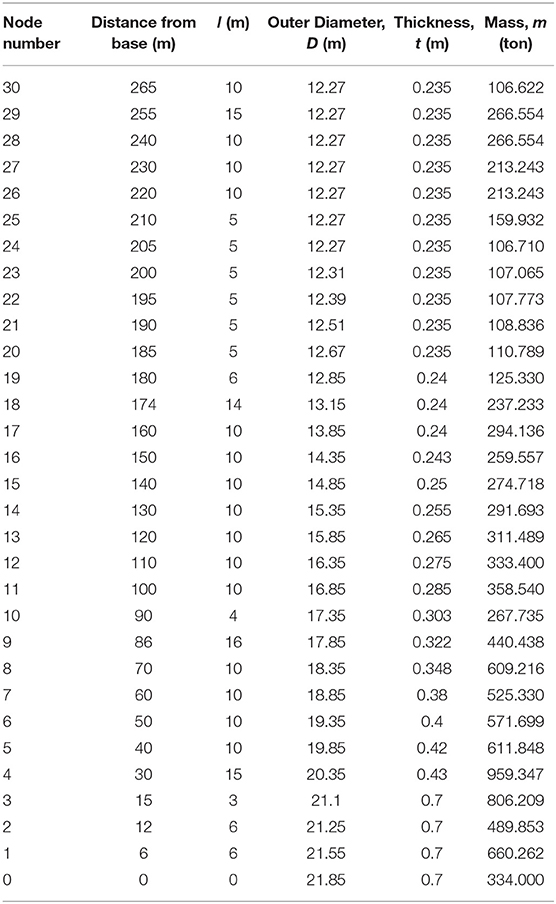
A 265 m high reinforced concrete (RC) chimney which has been studied by several investigators and originally reported by Melbourne et al. (1983) is considered as the case-study structure. Inelastic deformations and soil-structure interaction are ignored in this study. Schematic representation of the chimney with and without TMDs is presented in Figure 1. Further details about the structure can be found in Melbourne et al. (1983). Figure 1A shows the basic geometry of the structure. A typical cross section of the chimney and a schematic of a typical tuned mass damper is shown in Figure 1B. The structure is modeled with 30 2-dimensional uniform Euler-Bernoulli beam elements The geometrical details of these 30 sections are given in Table 1.

FIGURE 1

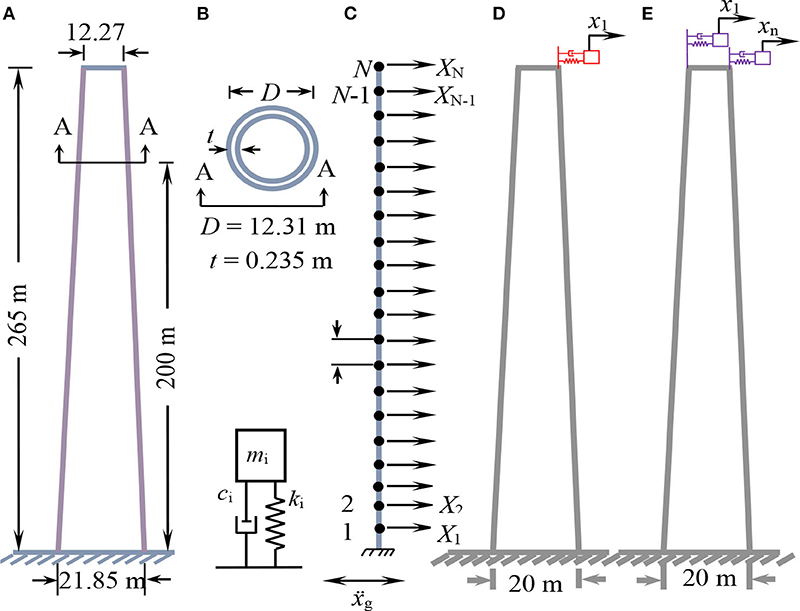
Figure 1. (A) Geometry of the chimney, (B) schematic diagram of TMD and section A-A (C) lumped mass idealization model (D) representation of a STMD, and (E) representation of MTMDs.

TABLE 1

Table 1. Geometric details of the RC chimney.

Each node has one translational and one rotational degree of freedom, which is statically condensed. The base of the chimney is assumed to be fixed. A lumped mass matrix formulation is used. The statically condensed stiffness matrix is denoted as [K_N] and the corresponding diagonal mass matrix is denoted by [M_N]. The damping matrix ([C_N]) is constructed in such a way that damping ratio in all the modes of vibration is 5% of critical damping.

Three different TMD schemes are considered. In the STMD scheme, a single TMD is placed at the top of the chimney. In the MTMD scheme, multiple TMDs are placed at the top of the chimney. The mass, stiffness, and damping coefficient of the i^th TMD are denoted by m_i, k_i, and c_i, respectively. The structural matrices with the TMDs incorporated into them are denoted by [K_s], [C_s], and [M_s], and are of order (N+n) × (N+n) where N is 30 and n represents the number of TMDs used.

The equations of motion for the coupled system, under ground motion can be stated as,

$\begin{array}{ll}\left[M_s\right]\left\{{ẍ}_s\right\}+\left[C_s\right]\left\{{ẋ}_s\right\}+\left[K_s\right]\left\{x_s\right\}=-\left[M_s\right]\left\{r\right\}{ẍ}_g& (1)\end{array}$

where the displacement, velocity, and acceleration vectors are denoted by {x_s}, $\left\{\stackrel{\bullet }{x_s}\right\}$, and $\left\{\ddot{x_s}\right\}$; ẍ_g is the ground acceleration and {r} is the influence coefficient vector populated by 1. The system of equations is solved by the Newmark's integration method.

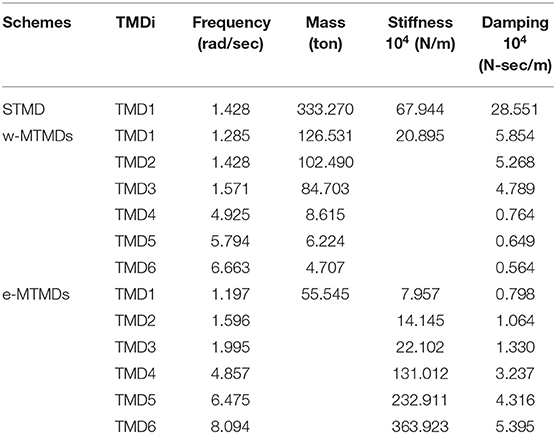
The optimum parameters (frequency tuning ratio and damping ratio) of the TMDs are based on a detailed parametric study explained in the following sections. Two different types of MTMDs are considered: e-MTMDs where all the TMDs have the same mass, and w-MTMDs where all the TMDs have the same stiffness.

The multiple TMDs are tuned to the first two modes of vibration, and their frequencies are uniformly distributed around the corresponding modal frequencies. The natural frequency of each TMD (ω_i) is expressed by (Li, 2000; Li and Qu, 2006; Han and Li, 2008),

$\begin{array}{ll}{\omega }_i={\omega }_{\text{T}}\left[1+\left(i-\frac{n+1}{2}\right)\frac{\beta }{n-1}\right]i=1\text{ to }n& (2)\end{array}$

and

$\begin{array}{ll}{\omega }_T={\displaystyle \sum _i^n}\frac{{\omega }_i}{n}& (3)\end{array}$

$\begin{array}{ll}\beta =\frac{{\omega }_n-{\omega }_1}{{\omega }_T}& (4)\end{array}$

where ω_T is the average frequency of MTMDs and β is the non-dimensional frequency bandwidth of the MTMDs systems (for more details see Li, 2000). The average frequency of the MTMDs are tuned to the first two frequencies of the structure, and are denoted as ω_T1, ω_T2 and n is equal to 6, implying that 3 TMDS are used to control each mode. For e-MTMDs, the mass of each TMD $m_{\mathrm{\text{i}}}=\frac{m_t}{n}$. where m_t, is the total mass of the TMDs. The stiffness (k_i) is then given by,

$\begin{array}{ll}{k}_i=m_i{\omega }_i^{2}i=1ton.& (5)\end{array}$

For w-TMDs, the stiffness of each TMD is given by

$\begin{array}{ll}{k}_i=\frac{m_t}{\left(\frac{1}{{\omega }_1^2}+\frac{1}{{\omega }_2^2}+\cdots \frac{1}{{\omega }_n^2}\right)}i=1to6& (6)\end{array}$

$\begin{array}{ll}{m}_i=\frac{k_i}{{\omega }_i^2}& (7)\end{array}$

The damping ratio (ζ_d = ζ₁ = ζ₂ = … = ζ_n) of the TMDs is kept the same and the damping coefficients (c_i) of the TMDs is calculated as follows:

$\begin{array}{ll}{c}_{\text{i}}=2{\zeta }_d{m}_i{\omega }_{i}i=1ton& (8)\end{array}$

The total mass of the TMDs is assumed to be 3% of the total mass of the chimney, which is 11,109 ton. The resulting design parameters of the different TMD schemes are shown in Table 2. The first three frequencies of the uncontrolled chimney are 1.6798 rad/sec (0.267 Hz), 6.816 rad/sec (1.085 Hz) and 16.090 rad/sec (2.562 Hz). The corresponding modal mass participation for the three modes are 0.321, 0.193, and 0.112, respectively. Optimal frequency tuning ratio and damping ratio for STMD are 0.85 and 0.3, respectively. In case of w-MTMDs, the optimal frequency tuning ratio is found to be the same as STMD, but the optimal damping ratio is 0.18. Also, the frequency bandwidth of the three TMDs tuned to fundamental mode is 0.2 and that of those tuned to the second mode is 0.1. Frequency tuning ratio and damping ratio of the e-MTMDs 0.95 and 0.11, respectively. In this case, the bandwidth of all the TMDs is 0.3. These parameters were obtained by a detailed parametric study discussed in the next section.

TABLE 2

Table 2. Design parameters of TMDs.

Numerical Study

Numerical simulation of response of the Chimney without and with different TMD schemes are carried using 69 near-fault pulse-like ground motions recorded during different past earthquakes. These ground motions were all affected by forward directivity effect and contain a dominant velocity pulse. Some salient features of the ground motions relevant for this study are given in Table A1.

Parameters of the TMDs were optimized through a parametric study. In the first step, tuning frequency was assumed to be equal to 1, and damping ratio of the TMD was varied from 0.01 to 0.5, with an increment of 0.01. The damping ratio corresponding to the best average response reduction across the 69 ground motions was selected as the optimal solution. Once the damping ratio is fixed, the frequency tuning ratio was varied between 0.85 and 1.15 with an increment of 0.01. The optimal solution was selected as the one that provided the best average response reduction across the 69 ground motions. Performance of TMDs

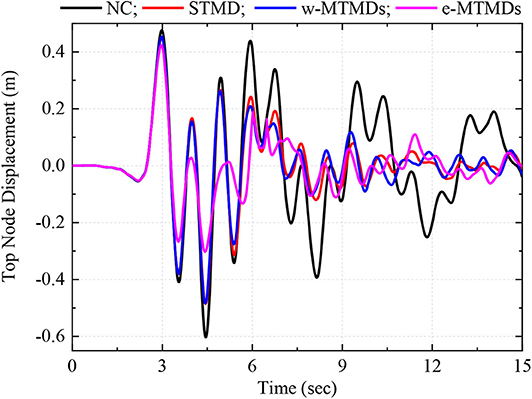
An example from one of the ground motions is presented here. The ground motion is from the 2004 Parkfield earthquake, 2004 earthquake recorded at the fault zone 12 station. The time variation of top node displacement of the uncontrolled (NC) and controlled structures is shown in Figure 2.

FIGURE 2

Figure 2. Time history of top node displacement response of chimney with and without TMD schemes.

The peak top node displacement is 0.602, 0.486, 0.484, and 0.42 m respectively for NC, STMD, w-MTMDs, and e-MTMDs. The STMD, w-MTMDs and e-MTMDs reduce the top node displacement by 19, 19.6, and 30%, respectively. The time history of top node acceleration is presented in Figure 3. Response reduction in acceleration is 11.6, 10.5, and 49.6% respectively for STMD, w-MTMDs, and e-MTMDs.

FIGURE 3

Figure 3. Time history of top node acceleration response of chimney with and without TMD schemes.

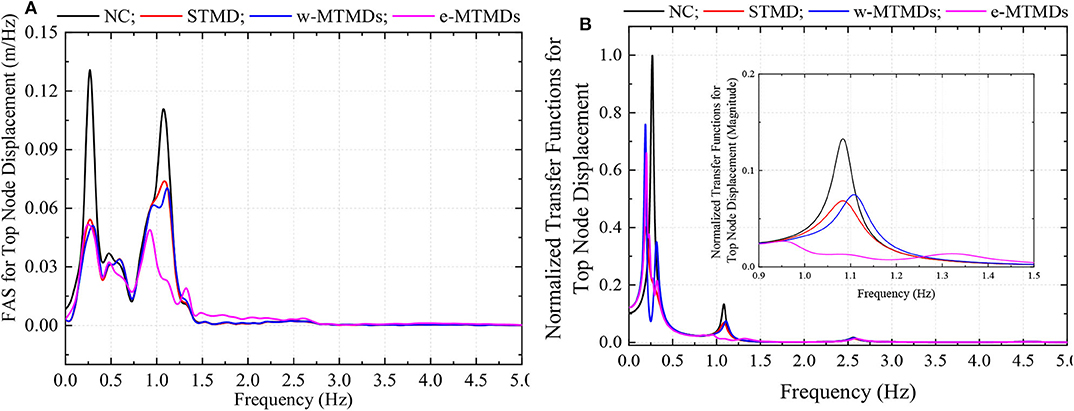
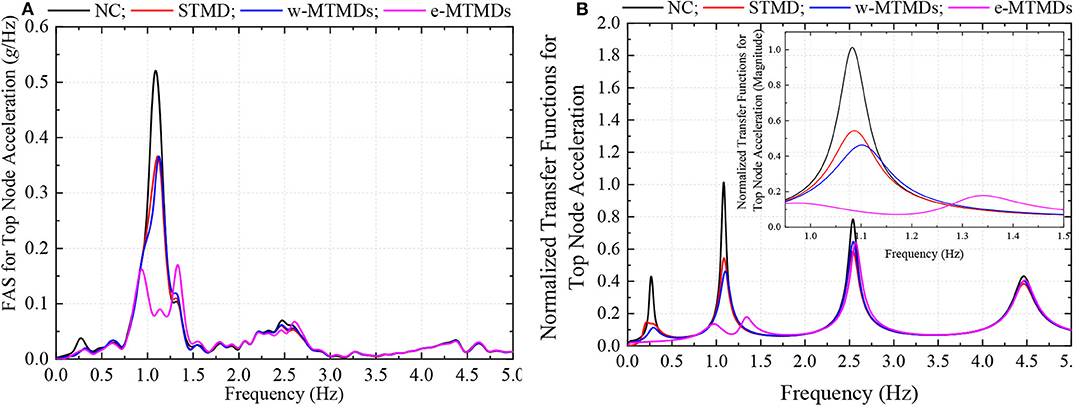
The difference in the performance of the different schemes can be understood by inspecting the response in the frequency domain. Fourier amplitude spectra (FAS) of the top node displacement and top node acceleration are plotted in Figures 4A, 5A. The corresponding transfer functions are shown in Figures 4B, 5B. These transfer functions relate ground acceleration to top node displacement and acceleration, respectively. For ease of visualization, the transfer functions are normalized by the peak of the transfer function of the uncontrolled structure.

FIGURE 4

Figure 4. FAS (A) and normalized transfer function (B) of top node displacement.

FIGURE 5

Figure 5. FAS (A) and normalized transfer function (B) of top node acceleration.

Figure 4 shows that the displacement response is mainly contributed by the first and the second modes of vibration. All the TMD schemes are equally effective in controlling the response due to the first mode. However, e-MTMDs outperform the other schemes in controlling the second mode. In this also evident from the transfer functions shown in Figure 4B. Because there is significant contribution from the second vibration mode, the e-MTMDs is more effective in controlling overall displacement response. Although the w-MTMDs are also intended to control the second mode, they are not as effective as the e-MTMDs because the TMD masses tuned to the second mode are rather low. Second mode contribution is even higher in acceleration response as shown in Figure 5A. The second mode contributes a lot more than the first in the acceleration response. The pulse period of this ground motion is about 1 Hz which resonates with the second mode of the structure. Therefore, the e-MTMDs, which control the second mode the best, are the most effective in controlling the overall response. Apart from the pulse, high frequency part of the near-fault ground motion can also have significant impact on structure response (Rupakhety and Sigbjörnsson, 2011).

Next we discuss a scenario when the pulse period of the ground motion is close to the fundamental period of vibration of the chimney. Ground motion from the 1992 Landers earthquake recorded at the LUC station has a dominant pulse frequency of about 0.25 Hz. Top node displacement and acceleration due to this ground motion are shown in Figure 6. The TMDs are effective in controlling the displacement response, but not so effective in controlling acceleration. Unlike in the previous case where the e-MTMDs were found to be the best scheme, the w-MTMDs perform the best against this ground motion. This is because the w-MTMDs control the first vibration mode the best as a lot of mass is provided to those TMDs that are tuned to this mode. From the FAS of the response presented in Figure 7, it is clear that the displacement response is dominated by the first mode of vibration while the third mode has significant contribution in the acceleration response. These results show that the pulse period of near-fault ground motion relative to the vibration frequencies of the structure plays an important role in the structural response. This effect is further investigated in the next section.

FIGURE 6

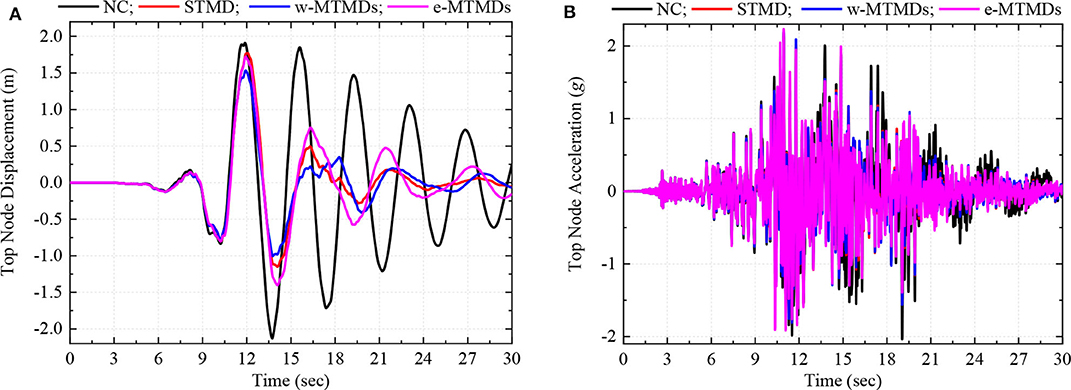
Figure 6. Time history of top node displacement (A) and acceleration (B) response of chimney with and without TMD schemes.

FIGURE 7

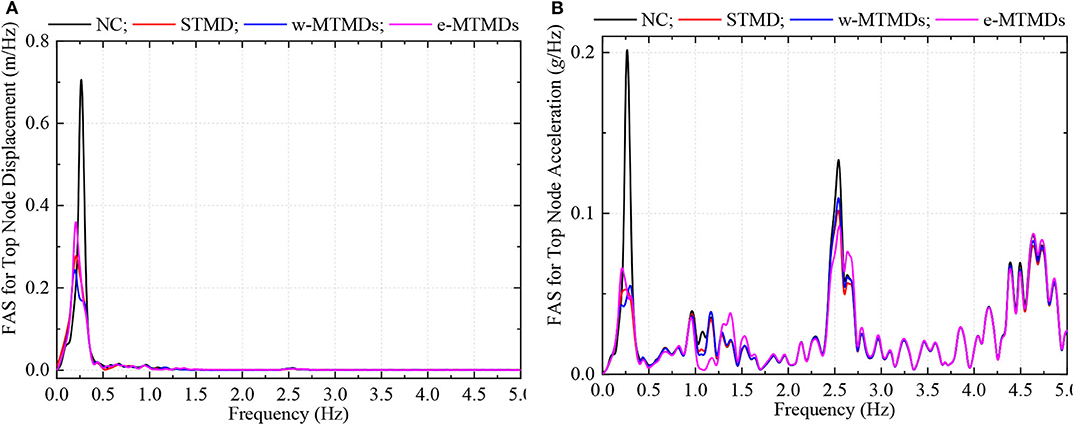
Figure 7. FAS of top node displacement (A) and acceleration (B) response of chimney with and without TMD schemes.

Effect of Frequency Content of Ground Motions

To study the effect of pulse period response reduction ratios are plotted against the first mode period of the chimney normalized by the pulse period of 69 near-fault ground motions is shown in Figure 8. In controlling the peak displacement, the TMD schemes are, in general, not very effective, except when the ground motion pulse resonates with the structure. In a narrow band around resonance with the first mode, the effectiveness is higher. In this band, there is no significant difference between the STMD and MTMDs. When the second mode period is close to the pulse period, the TMDs reduce the displacement by up to 40%, and the e-TMDs outperform the other schemes. It is noted that the structural experiences the highest displacement demand, and in such cases, response reduction is in the range of 15–30%. In general, the e-MTMD seems to be the most effective scheme. Similar observations can be made in Figure 8B which shows response reduction in acceleration. In this case, the e-MTMDs are clearly superior to the other schemes.

FIGURE 8

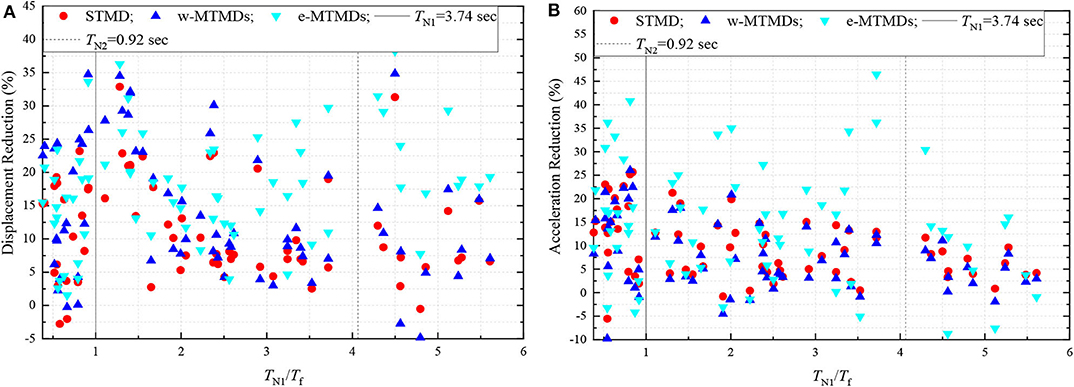
Figure 8. (A,B) Variation of displacement and acceleration reduction with the normalized period. The results correspond to 69 near-fault ground motions.

These results highlight that some degree of response reduction can be achieved in tall chimneys subjected to near-fault pulse-like ground motions by passive control schemes using TMDs. The effectiveness of the control schemes, however, differs a lot of ground motion characteristics, most importantly on its frequency content relative to the vibration frequencies of the structure. Since a structure, during its useful life, might face ground motions with different frequency contents, such control schemes are not expected to be beneficial in all cases. However, the most critical cases which require control are those when the fundamental mode of the structure resonates with the ground motion pulse. In such cases, TMDs can be effective in controlling structural displacement demand. The TMDs presented in this research are optimized by maximizing their average performance against all the ground motions. The large variability in response reduction observed from the results presented here, a more focused optimization scheme might be more beneficial. For example, the TMDs can be optimized for a sub-set of ground motions which impose the largest demands on the uncontrolled structure. This and other advanced optimization schemes need further research, and might potentially provide better control, but it is clear that optimization schemes that are independent of ground motions, for example, that of Sadek et al. (1997) are not expected to be robust enough when the structure is subjected to near-fault ground motions.

Conclusions

The results discussed above lead to the following conclusions.

1. Passive TMDs optimized by maximizing average response reduction across a set of ground motions show large variability in control performance and offer limited effectiveness against most of the ground motions.

2. In the critical cases when the fundamental mode of the structure resonates with the ground motion pulse, structural displacements can be controlled by 10–35%.

3. Multiple TMDs, especially the e-MTMDs tuned to the first two modes of vibration provide more robust control than STMDs. This is more the case in acceleration control.

4. When the pulse period is much larger than the fundamental period of the structure, the TMDs don't provide effective control.

5. Traditional methods of optimization which are independent of ground motion do not provide effective and robust vibration control against near-fault ground motions. In this regard, the optimization needs to be target to a certain type of ground motions that are the most critical for the structure. This corresponds to situations when the first and the second vibration mode of the structure resonates with the pulse period. For such situations, e-MTMDs optimized for only those ground motions that resonate with the first and the second mode of the structure, might provide better control of displacement and acceleration demand. For practical applications, this requires a good understanding of the impending hazard and the critical seismic sources near the construction site. The pulse period is dependent on earthquake magnitude (see Rupakhety et al., 2011) and can be estimated empirically. With such estimates, a more targeted optimization can be carried out so that the TMDs provide superior performance when subjected to the most critical ground motions.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

We acknowledge support from University of Iceland Research Fund.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbuil.2020.00092/full#supplementary-material

References

Bekdas, G., Nigdeli, S. M., and Yang, X. S. (2018). A novel bat algorithm based optimum tuning of mass dampers for improving the seismic safety of structures. Eng. Struct. 159, 89–98. doi: 10.1016/j.engstruct.2017.12.037

CrossRef Full Text | Google Scholar

Cao, L., and Li, C. (2019). Tuned tandem mass dampers-inerters with broadband high effectiveness for structures under white noise base excitations. Struct. Con. Health Monit. 26:e2319. doi: 10.1002/stc.2319

CrossRef Full Text | Google Scholar

Chen, G., and Wu, J. (2001). Optimal placement of multiple tune mass dampers for seismic structures. J. Struct. Eng. 127, 1054–1062. doi: 10.1061/(ASCE)0733-9445(2001)127:9(1054)

CrossRef Full Text | Google Scholar

De Domenico, D., Deastra, P., Ricciardi, G., Sims, N. D., and Wagg, D. J. (2018). Novel fluid inerter based tuned mass dampers for optimised structural control of base-isolated buildings. J. Franklin Inst. 356, 7626–7649. doi: 10.1016/j.jfranklin.2018.11.012

CrossRef Full Text | Google Scholar

De Domenico, D., and Ricciardi, G. (2018a). Optimal design and seismic performance of tuned mass damper inerter (TMDI) for structures with nonlinear base isolation systems. Earthq. Eng. Struct. Dyn. 47, 2539–2560. doi: 10.1002/eqe.3098

CrossRef Full Text | Google Scholar

De Domenico, D., and Ricciardi, G. (2018b). Earthquake-resilient design of base isolated buildings with TMD at basement: application to a case study. Soil Dyn. Earthq. Eng. 113, 503–521. doi: 10.1016/j.soildyn.2018.06.022

CrossRef Full Text | Google Scholar

Elias, S. (2018). Seismic energy assessment of buildings with tuned vibration absorbers. Shock Vibrat. 2018:2051687. doi: 10.1155/2018/2051687

CrossRef Full Text | Google Scholar

Elias, S. (2019). Effect of SSI on vibration control of structures with tuned vibration absorbers. Shock Vibrat. 2019:7463031. doi: 10.1155/2019/7463031

CrossRef Full Text | Google Scholar

Elias, S., and Matsagar, V. (2017). Research developments in vibration control of structures using passive tuned mass dampers. Annu. Rev. Control 44, 129–156. doi: 10.1016/j.arcontrol.2017.09.015

CrossRef Full Text | Google Scholar

Elias, S., and Matsagar, V. (2019). Seismic vulnerability of non-linear building with distributed multiple tuned vibration absorbers. Struct. Infrastruct. Eng. 15, 1103–1118. doi: 10.1080/15732479.2019.1602149

CrossRef Full Text | Google Scholar

Elias, S., Matsagar, V., and Datta, T. K. (2016). Effectiveness of distributed tuned mass dampers for multi-mode control of chimney under earthquakes. Eng. Struct. 124, 1–16. doi: 10.1016/j.engstruct.2016.06.006

CrossRef Full Text | Google Scholar

Elias, S., Matsagar, V., and Datta, T. K. (2017). Distributed tuned mass dampers for multi-mode control of benchmark building under seismic excitations. J. Earthq. Eng. 23, 1137–1172. doi: 10.1080/13632469.2017.1351407

CrossRef Full Text | Google Scholar

Elias, S., Matsagar, V., and Datta, T. K. (2019a). Along-wind response control of chimneys with distributed multiple tuned mass dampers. Struct. Control Health Mon. 26:e2275. doi: 10.1002/stc.2275

CrossRef Full Text | Google Scholar

Elias, S., Matsagar, V., and Datta, T. K. (2019b). Dynamic response control of a wind-excited tall building with distributed multiple tuned mass dampers. Intern. J. Struct. Stab. Dyn. 19:1950059. doi: 10.1142/S0219455419500597

CrossRef Full Text | Google Scholar

Etedali, S., Akbari, M., and Seifi, M. (2019). MOCS-based optimum design of TMD and FTMD for tall buildings under near-field earthquakes including SSI effects. Soil Dyn. Earthq. Eng. 119, 36–50. doi: 10.1016/j.soildyn.2018.12.027

CrossRef Full Text | Google Scholar

Gill, D., Elias, S., Steinbrecher, A., Schröder, C., and Matsagar, V. (2017). Robustness of multi-mode control using tuned mass dampers for seismically excited structures. Bull. Earthq. Eng. 15, 5579–5603. doi: 10.1007/s10518-017-0187-6

CrossRef Full Text | Google Scholar

Greco, R., and Marano, G. C. (2013). Optimum design of tuned mass dampers by displacement and energy perspectives. Soil Dyn. Earthq. Eng. 49, 243–253. doi: 10.1016/j.soildyn.2013.02.013

CrossRef Full Text | Google Scholar

Han, B., and Li, C. (2008). Characteristics of linearly distributed parameter-based multiple-tuned mass dampers. Struct. Control Health Mon. 5, 839–856. doi: 10.1002/stc.222

CrossRef Full Text | Google Scholar

Huergo, I. F., and Hernández, H. (2019a). Coupled shear-flexural model for dynamic analysis of fixed-base tall buildings with tuned mass dampers. Struct. Des. Tall Spec. Build. 28:e1671. doi: 10.1002/tal.1671

CrossRef Full Text | Google Scholar

Huergo, I. F., and Hernández, H. (2019b). Coupled-two-beam discrete model for dynamic analysis of tall buildings with tuned mass dampers including soil–structure interaction. Struct. Des. Tall Spec. Build. 29:e1683. doi: 10.1002/tal.1683

CrossRef Full Text | Google Scholar

Li, C. (2000). Performance of multiple tuned mass dampers for attenuating undesirable oscillations of structures under the ground acceleration. Earthq. Eng. Struct. Dynam. 29, 1405–1421. doi: 10.1002/1096-9845(200009)29:9<1405::AID-EQE976>3.0.CO;2-4

CrossRef Full Text | Google Scholar

Li, C., and Qu, W. (2006). Optimum properties of multiple tuned mass dampers for reduction of translational and torsional response of structures subject to ground acceleration. Eng. Struct. 28, 472–494. doi: 10.1016/j.engstruct.2005.09.003

CrossRef Full Text | Google Scholar

Longarini, N., and Zucca, M. (2014). A chimney's seismic assessment by a tuned mass damper. Eng. Struct. 79, 290–296. doi: 10.1016/j.engstruct.2014.05.020

CrossRef Full Text | Google Scholar

Lu, Z., Li, K., and Zhou, Y. (2018). Comparative studies on structures with a tuned mass damper and a particle damper. J. Aerosp. Eng. 31:04018090. doi: 10.1061/(ASCE)AS.1943-5525.0000878

CrossRef Full Text | Google Scholar

Matin, A., Elias, S., and Matsagar, V. (2019). Distributed multiple tuned mass dampers for seismic response control in bridges. Proc. Instit. Civil Eng. Struct. Build. 173, 217–234. doi: 10.1680/jstbu.18.00067

CrossRef Full Text | Google Scholar

Matta, E. (2013). Effectiveness of tuned mass dampers against ground motion pulses. J. Struct. Eng. 139, 188–198. doi: 10.1061/(ASCE)ST.1943-541X.0000629

CrossRef Full Text | Google Scholar

Melbourne, W. H., Cheung, J. C., and Goddard, C. R. (1983). Response to wind action of 265-m Mount Isa stack. J. Struct. Eng. 109, 2561–2577. doi: 10.1061/(ASCE)0733-9445(1983)109:11(2561)

CrossRef Full Text | Google Scholar

Nigdeli, S.M., and Bekdas, G. (2017). Optimum tuned mass damper design in frequency domain for structures. KSCE J. Civil Eng. 21, 912–922. doi: 10.1007/s12205-016-0829-2

CrossRef Full Text | Google Scholar

Nigdeli, S. M., and Bekdas, G. (2013). Optimum tuned mass damper design for preventing brittle fracture of RC buildings. Smart Struct. Syst. 12, 137–155. doi: 10.12989/sss.2013.12.2.137

CrossRef Full Text | Google Scholar

Nigdeli, S. M., and Bekdas, G. (2019). Optimum design of multiple positioned tuned mass dampers for structures constrained with axial force capacity. Struct. Design Tall Spec. Build. 28:e1593. doi: 10.1002/tal.1593

CrossRef Full Text | Google Scholar

Reggio, A., and Angelis, M. D. (2015). Optimal energy-based seismic design of non-conventional Tuned Mass Damper (TMD) implemented via inter-story isolation. Earthq. Eng. Struct. Dyn. 44, 1623–1642. doi: 10.1002/eqe.2548

CrossRef Full Text | Google Scholar

Rezaee, M., and Aly, A.M. (2018). Vibration control in wind turbines to achieve de-sired system-level performance under single and multiple hazard loadings. Struct. Control Health Mon. 25:e2261 doi: 10.1002/stc.2261

CrossRef Full Text | Google Scholar

Rupakhety, R. (2010). Contemporary issues in earthquake engineering research: processing of accelerometric data, modelling of inelastic structural response, and quantification of near-fault effects (Doctoral dissertation). University of Iceland, Reykjavik, Iceland.

Google Scholar

Rupakhety, R., and Sigbjörnsson, R. (2011). Can simple pulses adequately represent near-fault ground motions?. J. Earthq. Eng. 15, 1260–1272. doi: 10.1080/13632469.2011.565863

CrossRef Full Text | Google Scholar

Rupakhety, R., Sigurdsson, S. U., Papageorgiou, A. S., and Sigbjörnsson, R. (2011). Quantification of ground-motion parameters and response spectra in the near-fault region. Bull. Earthq. Eng. 9, 893–930. doi: 10.1007/s10518-011-9255-5

CrossRef Full Text | Google Scholar

Sadek, F., Mohraz, B., Taylor, A. W., and Chung, R. M. (1997). A method of estimating the parameters of tuned mass dampers for seismic applications. Earthquake Engineering and Structural Dynamics, 26, 617–635.

Google Scholar

Sigurðsson, G. Ö., Rupakhety, R., Rahimi, S. E., and Olafsson, S. (2019). Effect of pulse-like near-fault ground motions on utility-scale land-based wind turbines. Bull. Earthq. Eng. 18, 1–16. doi: 10.1007/s10518-019-00743-9

CrossRef Full Text | Google Scholar

Wang, C., and Shi, W. (2019). Optimal design and application of a multiple tuned mass damper system for an in-service footbridge. Sustainability 11:2801. doi: 10.3390/su11102801

CrossRef Full Text | Google Scholar

Wilson, J. L. (2003). Earthquake response of tall reinforced concrete chimneys. Eng. Struct. 25, 11–24. doi: 10.1016/S0141-0296(02)00098-6

CrossRef Full Text | Google Scholar

Yucel, M., Bekdaş, G., Nigdeli, S. M., and Sevgen, S. (2019). Estimation of optimum tuned mass damper parameters via machine learning. J. Build. Eng. 26:100847. doi: 10.1016/j.jobe.2019.100847

CrossRef Full Text | Google Scholar