Engineering-Based Tornado Damage Assessment: Numerical Tool for Assessing Tornado Vulnerability of Residential Structures

Following a series of deadly tornadoes between 2011 and 2013, this paper develops a numerical tool to help communities better predict and quantify the potential tornado damage to single-family residential structures from a tornado strike. The objective is to determine the predictive capability of an engineering-based tornado damage-assessment (ETDA) Tool using published building damage observations captured by the authors in a recent tornado. The research is motivated by the need for the public to visualize the extent of tornado vulnerabilities of residential buildings in our communities. The research developed a numerical estimation model to aggregate damage that a specified tornado would cause to the residential wood-framed structures in a community. The ETDA Tool was developed around a Monte Carlo simulation engine, using theoretical models for tornado wind velocity and pressure drop in the tornado vortex, as well as experimentally-determined probability distribution functions for the structural resistances of eight building component systems selected to describe the structure. The output of the EDTA Tool is presented as series of mean damage ratios, and other statistics quantifying tornado-damage caused, plotted against distance away from the tornado vortex centerline. The paper explains the methodology of the approach and presents results comparing hindcast damage ratios against observed values of field-observations collected after a tornado strike on residential communities in Garland/Rowlett, TX. It was found the ETDA Tool provides reasonable agreement with the field damage observations to houses. The Tool could be used by a community to model any tornado path and/or size and estimate future damage. More research to further our understanding of tornado-induced wind loads and wind-borne debris effects is needed to increase confidence in its application to any tornado and any city.

Introduction

In the United States, 2011 was an outlier tornado year in which 1,700 tornadoes occurred with 560 tornado-related deaths. This was by far the highest death toll from tornadoes since the 1950s. On average today's U.S. tornado-related fatalities are <100 per year (NWS, 2020) and the average tornado-caused annual economic losses are between $4.7B and $7.2B (Simmons et al., 2013); no more than 1–3% of the annual Gross Domestic Products of the most-affected states. These remarkably low fatality numbers are partly due to good outcomes of meteorological and engineering research, and partly to good fortune that more tornadoes had not directly affected our largest cities and residential communities. Economic losses from tornadoes are still high. There has been $130 Billion (CPI-adjusted estimate) losses due to 54 “U.S. billion-dollar disaster” events (plus many thousands of less-costly events) involving tornadoes spawned by severe storm in the United States over the past 40 years (since 1981). This figure is lower but of a comparable order of magnitude to hurricane-related losses of nearly $1 Trillion dollars ($954 Billion) over the period 1980–2019 from 45 hurricanes. These most costly tornado and hurricane events caused just 1,270 and 6,507 fatalities, respectively (NOAA National Centers for Environmental Information (NCEI), 2020).

The research to improve forecasting of major tornado activity of the National Weather Service has, since 1950, improved tornado warning lead times, reducing the numbers of tornado-related fatalities and injuries (NSSL, 2013). The life-saving activities of the Federal Emergency Management Agency and some states provided grants to construct in-home and in-school tornado shelters that protect many against loss of life and injuries in tornadoes (Herseth et al., 2017). Only recently has there been any effort to apply engineering knowhow to improve the tornado-resilience of buildings.

Thus, single-family residential buildings remain highly exposed and at risk of catastrophic damage from tornadoes. The vast majority of those buildings are light-framed wood structural systems (van de Lindt John and Dao Thang, 2009), that are prescriptively designed for 115 mph 3 s gust basic wind speeds in most tornado-prone regions of the United States. A typical house is therefore designed to withstand just 62% of the forces a strong EF-2 tornado will produce. The full implications of this choice was made apparent in 2011, when convective storm (storms producing tornadoes) damage jumped to nearly $28 billion (in 2013 dollars) in insured losses (Simmons et al., 2013).

In order to minimize future economic losses from tornado damage, communities must replace current inventories with stronger, tornado-resilient buildings. Arguably, the engineering community is aware of the appropriate structural details necessary to mitigate tornado damage (Prevatt et al., 2012b; Roueche et al., 2015; Ramseyer et al., 2016). However, such provisions are not implemented widely enough to impact the level of tornado damage caused to residential buildings, which remains disproportionately high. Stronger building systems will cost more than current structures and therefore any increase in tornado-resilient buildings will occur only when the public is convinced of the value of such mitigation.

Despite decades of tornado research and post-tornado studies (Minor et al., 1977; BPAT, 1999; Prevatt et al., 2013; Coulbourne et al., 2015), few recommendations have been adopted by building codes or implemented in the design and construction of schools, commercial buildings and residential structures. Tornado-resilient building codes were not implemented because of a misconception that tornado-resilient construction was economically unfeasible for the majority of buildings. Further the literature cited the low probability of tornado occurrences as a basis for excluding tornado-resilient provisions from building codes (ASCE, 2010; Ramseyer et al., 2016). Moore, OK is the only jurisdiction out of 89,000 in the United States that specifically adopted tornado-resilient building code provisions after suffering three deadly tornadoes within a 14 year period (Simmons et al., 2015; Ramseyer et al., 2016).

The lack of tornado-mitigation measures despite available knowledge, perhaps indicates public perception that severe tornado damage is caused by catastrophically strong winds, rather than the predictable outcome of structurally inadequate construction impacted by moderately strong winds. The public is unaware of the high vulnerability of their homes and their easy access to safer tornado-resilient designs. Prevatt et al. (2012b) and Simmons et al. (2015) show that tornado-resilient residential design is feasible today, and the details and costs are generally of the same order of magnitude as structural details for hurricane-resistant houses in South Florida. Clearly tools are needed to make tornado risks more visible to community leaders and the general public. We believe creating a numerical modeling tool is a more efficient method to illustrate potential tornado effects that could be used by many.

This paper proposes a new numerical tool to illustrate potential tornado damage scenarios and assist tornado-prone communities comprehend and quantify the potential tornado damage to their buildings. This paper proposes such scenario-driven simulations, at the individual building scale, utilizing the advanced engineering-based models for predicting damage to residential communities.

Existing Numerical Tools to Predicting Community Damage from Windstorms

Predicting building damage from wind hazards is well-accepted in hurricane-prone regions. Several models exist, such as the Florida Public Hurricane Loss Model (Pita et al., 2015) and HAZUS-MH (Vickery et al., 2009). These models estimate building damage using engineering models of the hurricane, and probabilistic data on the structural capacity of buildings within the hurricane's path. These models are essential for predicting future risks and impacts of hazard events on communities and they are used to evaluate the benefits and costs of strengthened infrastructure, and communicate this damage potential to the public, insurance providers, and other stakeholders.

Masoomi and van de Lindt (2017) demonstrated scenario-driven tornado risk modeling for a virtual community based upon a dataset of tornado paths extracted from the U.S. historical tornado record for EF0 to EF5 strength tornadoes. Their model relied upon fragility surfaces, based on assumed structural systems and component resistances and estimated tornado-induced wind loads. Because no analogy exists of a real town to compare this virtual community there are limited measures for validating its predictive capabilities. Such validations are important for tornadoes, as high uncertainties still prevail in the scientific communities' understanding of tornado-induced wind loads, tornado debris clouds, structural response to the tornado-induced wind loads, and more. It is of value then to develop a tornado-damage model that predicts damage at the individual building scale, such that outputs can be used to validate existing engineering models as well as inform the public of fine-scale potential damage scenarios.

Objective and Structure of Paper

The objective of this paper is to develop and determine the predictive capability of an engineering-based tornado damage-assessment (ETDA) Tool using published building damage observations captured by the authors in two recent tornadoes (Prevatt et al., 2013, 2016). The motivating challenge is to use engineering knowledge to illustrate the damaging effects of tornadoes for the general public. The paper presents the methodology of the approach and results comparing hindcast damage ratios against observed values.

The paper is organized as follows: Section Development of the ETDA Tool provides a more detailed background to the ETDA Tool, Section Details of the ETDA Tool describes the modules of the ETDA Tool. Section Tornado Dataset for Validation presents the field collection and analysis to develop the data set of building damage for testing, Section Validation of the EDTA Tool provides results and validation of the ETDA Tool against the empirical datasets of the field observations. Section Discussion provides a discussion of the results and recommends key topics requiring additional research, and section Conclusions summarizes our conclusions.

Development of the ETDA Tool

Peng et al. (2016) developed an engineering-based tornado damage assessment (ETDA) Tool that is capable of simulating component level damage to individual residential structures and to portfolios of single-family, light-framed wood structural residential buildings. The ETDA tool research is a culmination of many studies to formulate a scientific base for characterizing tornado damage initiated since the 2011 tornado season. The motivation for developing this tool was to provide a paradigm shift in how tornado damage studies since the Lubbock 1970 tornado (Fujita, 1971) can be used to further research. In the past, engineers and others who surveyed the damage from tornadoes were limited to presenting observations in photographs and some limited mapping, because the dearth of information available on the wind speeds and characteristics of the tornado itself. From the 2011 tornado season the second and third authors introduced new technologies that were game-changing:

• We used geo-located photographs. During the Tuscaloosa tornado photographs were taken using special cameras and a few mobile phones that imprinted a latitude/longitude location with each photograph.

• We developed methodologies for collecting damage survey by uploading data from individuals to a single online database.

• Common server and GIS platform. Using ArcGIS, the damage survey team can populate and share results with others.

• Use of Parallel Computing / Distributed Computing to improve efficiency and reduce simulation run time

This first use of this electronic data collection technology within the wind engineering world (Graettinger et al., 2012; Prevatt et al., 2012a; Roueche and Prevatt, 2013; Haan et al., 2014) enabled for more efficient data collection, analysis and dissemination of the results. Further for the first time in the context of wind hazard damage surveys, the use of these technologies turned photographs into raw data points, by associating observed structural damage to a building with a location in space, and distance of the structure from the centerline of the tornado vortex. These improvements substantially improved the data collection exercises, reducing the production time for a report from many months to weeks. Since researchers used equipment that could upload their data electronically it has been relatively easy to extract and organize information, produce electronic maps and to share the output within near real-time (within hours) at the end of each day. These changes facilitated faster dissemination of the results and encouraged greater collaboration. In total these steps resulted in a resurgence of interest in studying the interactions of tornadoes with building structures. A further benefit of these advances was now that the data can be electronically shared, much of the assumptions of the relationship between tornado strengths and structural damage could be numerically modeled and scientifically queried. Our goal has focused on characterizing the wind strength using existing models of the Enhanced Fujita scale (McDonald and Mehta, 2006; Mehta, 2013).

Ultimately the University of Florida research provided lasting benefit to wind engineering by forming a basis for development of wind design codes for tornado-resilient communities (Coulbourne and Prevatt, 2013), which has been used as the basis for wind-design provisions included in ASCE/SEI 7-16 (ASCE, 2017).

Details of the ETDA Tool

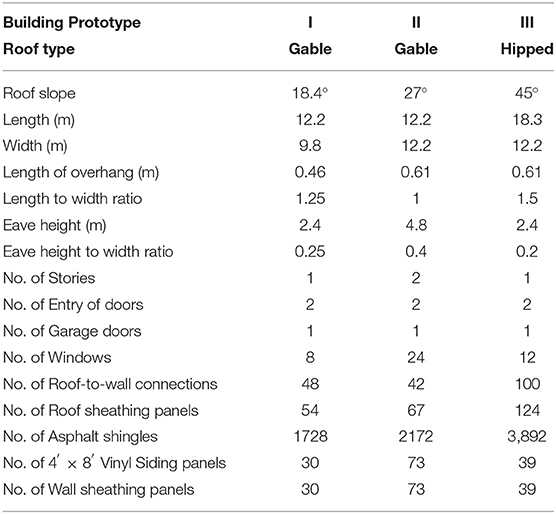
The Engineering-Based Tornado Damage Assessment (ETDA) Tool is a numerical model developed in MATLAB computing environment that estimates tornado-induced damage and economic losses to low-rise wood framed structures. The structural system for all houses is generic and simplified to three prototype house structures and just eight critical building components comprising of the following: (1) Roof covering (RC); (2) Roof sheathing (RS); (3) Roof-to-wall (R2W) connections; (4) Wall sheathing (WS); (5) Wall covering (WC); (6) Entry doors (ED); (7) Windows (W); and (8) Garage door (GD). The three prototype house structures are assigned to individual structures to represent the variability of housing within a particular community, described in Table 1 below.

TABLE 1

Table 1. Metadata on Building Components within the Prototype Houses of the ETDA Tool.

The ETDA Tool calculates the tornado load effects on individual structural components of a house using probabilistic models of the tornado wind speed, tornado wind pressure, and atmospheric pressure drop within the tornado's vortex, and models of the structural capacities of the building components. The ETDA Tool simulates a tornado vortex translation along a straight-line path for a distance of eight times the radius to maximum wind speeds, r_max of the tornado (determined by observation), in increments of ${0.2}^{*}{r}_{max}$for a total of 41 such increments. Each increment is called a time step, and the completion of 41 time-steps represents one simulation. Wind field parameters are set deterministically and held constant for all simulations. Structural resistances are sampled probabilistically to initialize each simulation. Wind speed, atmospheric pressure, and aerodynamic coefficients are sampled probabilistically at each time step. The ETDA Tool then determines the damage for each component at each time step using Equation (1).

$\begin{array}{ll}g(R,S)=R-S& (1)\end{array}$

where, R is the structural resistance of the component element (e.g., individual roof sheathing panel), and S is the tornado load acting on the component element. The component element failure occurs when, g(R, S) < 0. R, the structural resistance capacity is determined using the probability distribution functions (pdfs) for each component, that are derived and available in the literature. A detailed description is included in section Structural Response Module, below.

The ETDA Tool generates 5,000 simulations to sample the structural loads and structural resistances for each component from probabilistic distributions in order to calculate failure distributions. Failure is defined as a damage ratio, or the fraction of damaged (failed) elements within each building component divided by the total number of those elements within the component category (e.g., Four windows damaged out of eight total windows, results in damage ratio of 50%). The damage assessment is cumulative, progressing with each time step, with the final damage states defined by the cumulative damage ratios for each building component. Peng et al. (2016) conducted a sensitivity analysis to determine the effect of number simulations on the accuracy of the ETDA Tool's results. The damage results were calculated for a series of simulations ranging from 100,000 simulations down to 100 simulations. A simulation count of 5,000 was selected because the standard error of the mean damage ratio was 0.5% and was judged a reasonable balance between consistency and computation time.

The ETDA Tool is structured in four modules: (1) the tornado wind field module, (2) the wind load module, (3) the wind-borne debris module, and (4) the structural response module. Each module is briefly described below. A complete treatment of the ETDA Tool, its flowchart, progressive tornado-induced damage assessment and component level-load vs. resistance analysis model are provided in Peng et al. (2016).

Tornado Wind Field Module

The tornado wind field module simulates the instantaneous wind field of a tornado vortex, based upon the Rankine vortex model (Rankine and Miller, 1888), as it translates along a predefined path over a defined grid. At each moment in time at each grid point within the analysis domain, the tornado wind velocity is the vector sum of three velocity vectors, namely, tangential velocity, radial velocity, and vortex translation velocity as shown in Equations (2), (3), and (4). The vertical velocity component is not modeled here. There have been some recent advancements in the understanding and modeling of the vertical component (Kopp and Wu, 2017; Baker and Sterling, 2018) which could be incorporated into a future version of the ETDA tool. The tangential velocity is assumed to follow the Rankine vortex model (Rankine and Miller, 1888). The rotational velocity of tornado (u(r)) is approximated as half the tangential velocity (Hoecker, 1960). The translation speed can be estimated from radar for deterministic simulations or assigned any reasonable value. The longitudinal velocity gradient is assumed constant with height within the elevations of the buildings being modeled.

The atmospheric pressure deficit in the tornado, p_r is modeled as a function of the air density, ρ, distance to the tornado center, r, the radius to maximum wind speeds, r_max and the maximum tangential velocity, V_max after Simiu and Scanlan (1996) as shown in Equation (5).

$\begin{array}{ll}v(r)=\{\begin{array}{c}\frac{r\times V_{max}}{r_{max}},0\le r\le r_{max}\\ \frac{r_{max}\times V_{max}}{r},r_{max}\le r\le \infty \end{array}& (2)\end{array}$

$\begin{array}{ll}u(r)=\frac{v(r)}{2}& (3)\end{array}$

$\begin{array}{ll}\overrightarrow{V_{res}((r))}=\overrightarrow{v(r)}+\overrightarrow{u(r)}+\overrightarrow{V_{TS}}& (4)\end{array}$

$\begin{array}{ll}{p}_{a(r)}=\{\begin{array}{c}\rho V_{max}^2\left(2-\frac{r^2}{r_{max}^2}\right),0\le r\le r_{max}\\ \rho \left(\frac{V_{max}^2}{2}\right)\left(\frac{r_{max}^2}{r^2}\right),r_{max}\le r<\infty \end{array}& (5)\end{array}$

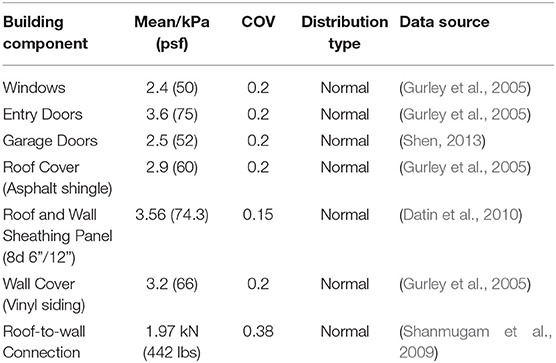
Probabilistic wind speeds and atmospheric pressures are incorporated into the analysis by first obtaining deterministic values for v(r) and p_a (r) for a given house location (in terms of r/r_max) using Equations (4) and (5). Then a random value is chosen for each variable from a normal distribution constructed about their respective mean values from Equations (4) and (5) with a COV of 0.2. The COV of 0.2 is based on engineering judgement and is selected to sample values closer to mean value as compared to a COV of 0.4 (Gurley et al., 2005).

Wind Load Module

Since at present there exists no database containing measured tornado-induced wind loads on low-rise buildings for a suitable variety of building locations and tornado characteristics, the current ETDA Tool defines the net tornado-induced surface pressures on buildings as the combination of surface pressure estimated using straight-line wind-induced pressures (from wind tunnel testing) and the atmospheric pressure deficit caused by the vortex core. The net surface pressure is thus defined as shown in Equation (6):

$\begin{array}{ll}{P}_T=\frac{1}{2}{\rho }_a{V}_h^2\times \left[G{C}_p-G{C}_{pi}\right]+p_a(r)& (6)\end{array}$

where, P_T is the net pressure acting on the component, ρ_a is the density of air, V_h is the 3 s gust wind speed at the mean roof height, obtained from the tornado wind field module, GC_p is the peak-external wind pressure coefficient obtained from straight-line wind model from the Tokyo Polytechnic University's wind tunnel database of surface pressures on low-rise buildings (Tamura, 2012), GC_pi is the internal pressure coefficient, and p_a(r) is the atmospheric pressure drop for a given radial distance, r from the tornado center associated with the rotational airflow of the vortex. The internal pressure coefficient, GCp_i, is estimated by solving the continuity equation assuming quasi-static conditions, as given in Holmes (2001), which results in:

$\begin{array}{ll}{\displaystyle \sum _1^N}{A}_i\sqrt{|p_{e,j}-p_i|}=0& (7)\end{array}$

here A_j is the area of opening j, and p_e,j is the external pressure at opening j, and p_i is the internal pressure, which is assumed to be constant throughout the interior volume (Oh et al., 2007). The approach outlined above does not directly model the inertial effects of the internal pressure changes as discussed in Baker and Sterling (2018), and thus is likely to underestimate net tornado-induced wind loads in buildings with minimal leakage through the building envelope. Previous research has shown however that most residential buildings either have sufficient background leakage, or incur damage to dominant openings, to enable rapid response of the internal pressure to external pressure changes (Roueche and Prevatt, 2013; Roueche et al., 2020).

The ETDA Tool's Wind Field Module determines the magnitude and direction of wind speed at the house based on the distance from the tornado centerline. Based on the direction of wind speed, the ETDA Tool classifies the wind angle into eight wind angles ranging from 0 to 315 degree in 45-degree increments. For each wind angle, the ETDA Tool determines the peak-external wind pressure coefficients (GC_p) for each of the eight building components using the TPU wind tunnel database. The TPU database contains pressure tap time-history data for roof and wall surfaces of 116 low-rise building configurations with gable, hipped, and flat roof shapes. To calculate the GC_p for eight house components, the following procedure is adopted:

1. The pressure coefficient readings are generated throughout the roof/wall surface by linearly interpolating the pressure taps over a fine uniform grid (grid spacing of 0.01 m).

2. For each house component surface, the interpolated points within the component polygon are taken and averaged to represent the area-averaged pressure coefficient time history.

3. The area-averaged pressure coefficient time histories for each component is divided into 10 equal segments corresponding to peak evaluation time of 1 min.

4. The peak pressure coefficients are calculated from the area-averaged pressure coefficient time history using the Lieblein BLUE method (Lieblein, 1974), assuming a 78% percentile peak value.

At each time step of each simulation, the peak GCp and the GCpi is randomly sampled from a normal distribution with COV of 0.05 about the mean value, which is taken as the deterministic GCp and GCpi calculated as described above.

Wind-borne Debris Module

The ETDA Tool uses the wind borne debris module defined by (Balderrama Garcia Mendez, 2009). This module simulates the effect of planar debris produced by the tornado wind, as it damages the roof covering of the building. The model simulates the loss of asphalt shingles (~300 mm by 900 mm (12 in. by 36 in.) sizes. The windborne debris module is designed to respond to the progressive damage occurring to the structure during passage of the tornado. For example, if an asphalt shingle fails, it becomes windborne debris in the next time-step iteration of the ETDA Tool and is included in the model with potential for creating openings in the building envelope.

In the model the windborne debris is generated from and acts upon a single house, i.e., should a roof cover fail on House A, the ETDA Tool cannot simulate a flight path of the debris to another house in the database. The limitation of the wind-borne debris module is that the missiles are not cumulative with distance and increment time steps nor is debris cumulative for all houses within the tornado path.

Structural Response Module

The structural response module assigns probabilistic capacities to each element of each building component (e.g., each individual roof sheathing panel), and at each time step, evaluates whether the capacity has been exceeded by the net surface pressures from the tornado load module. The structural capacities of building components are taken from available scientific literature. At each time-step iteration, the structural loads on each of the building components are calculated and compared to the structural capacity of the component. When the load exceeds the structural capacity, that component is assumed to have failed and the model is modified to remove that element from the prototype model (or redistribute its load to adjacent members in the case of roof-to-wall connections), in future time steps of the analysis.

Each house structure is modeled by eight (8) building components and the probabilistic structural capacity distributions for each are taken from previous studies; including Datin et al. (2010), Gurley et al. (2005), Shen (2013), and Shanmugam et al. (2009). The structural capacities in the model can be easily adjusted to better represent local construction practices if warranted. The base values shown in Table 2 were chosen to represent typical non-engineered structures in tornado-prone regions of the United States without wind-resilient building codes.

TABLE 2

Table 2. Mean value and Standard Deviations of structural capacities for the house components.

The structural resistance model also redistributes component loads and removes damaged elements within the process. The logic of the redistribution module is adopted from the Florida Public Hurricane Loss Model described in Gurley et al. (2005). The redistribution module finds the closest two intact connections on either side of the failed roof-to-wall connection and shares the load of the failed connection with four neighboring connections when possible. Specifically, one-third of the load is redistributed to each of the two closest connections, and one-sixth of the load is redistributed to the next closest intact connections on either side. When only one intact connection is available to the left or right of the failed connection, half of the load from the failed connection is redistributed. This failure check and load redistribution process occurs until no new connection failures are discovered, or until an entire side of the roof is unfastened from its supporting wall.

When a roof cover fails its weight is removed from the underlying roof sheathing and roof-to-wall connections. When roof sheathing fails, all the roof coverings attached to it also experience failure and are removed from subsequent analysis. Consequently, the wind pressures acting on the roof sheathing that are connected to roof-trusses are removed, which causes removal of wind load from the roof-to-wall connections. Conversely, roof-to-wall connection failures in the ETDA tool do not cause the roof sheathing and roof cover within its tributary area to also fail. This approach is used because if the roof-to-wall connection loads are redistributed safely to adjacent connections, generally the truss or rafter remains in place with the sheathing and roof cover still in place. Only when a large section of the roof structure fails does it tend to actually be physically removed from the structure, taking sections of sheathing and roof cover with it.

Tornado Dataset for Validation

Since 2011, the fourth author has led detailed forensic investigations following a number of catastrophic tornadoes, including the Tuscaloosa, AL and Joplin, MO tornadoes in 2011, the Moore, OK tornado in 2013, the Garland/Rowlett, TX tornado in 2015, and multiple smaller tornado events in Florida and Georgia. The investigations relied primarily upon collections of terrestrial, geotagged photographs of each building, from which damage information was culled to define the overall damage state (utilizing the Degrees of Damage from the Enhanced Fujita Scale; McDonald and Mehta, 2006). Of these investigations, only the Garland/Rowlett, TX tornado response specifically focused on collecting data suitable for estimating component-level damage ratios, which requires clear photographs from all four elevations of the building. This dataset is used for validation of the ETDA tool.

The 2015 Garland/Rowlett, TX tornado was rated an EF-4 tornado by the National Weather Service with maximum wind speeds close to 80 m/s. In the third and fourth authors' response to the tornado, a total of 5,615 photographs were taken during the assessment, documenting the damage to 712 individual homes. Maps were created (shown in Figure 1) of the survey regions identifying each parcel to be surveyed along with its year of construction and street address for ease of identification in the field. Data from the Dallas Central Appraisal District (http://www.dallascad.org/) was used to study housing demographics of the two cities. Surveying started at the point of no damage on one side of the tornado path and progressed across the width of the tornado to the point of no observable damage on the opposite side of the tornado path in five distinct regions chosen for their distributions of old and new homes.

FIGURE 1

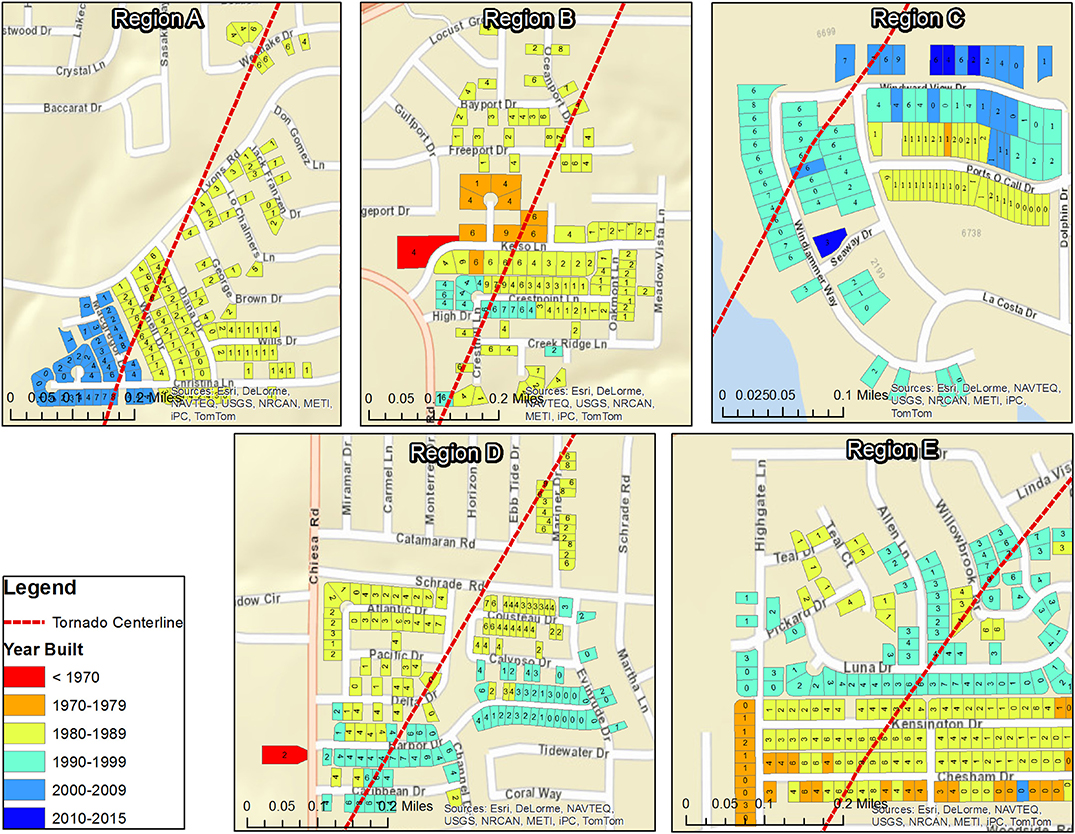
Figure 1. Locations of all surveyed homes by region. Colors depict the decade in which the home was built. Numbers inside each parcel give the assigned damage rating.

In the aforementioned dataset, damage ratios to the eight primary building components were estimated, using geotagged photographs documenting the condition of the building from all four sides. The damage ratios were independently estimated visually by two evaluators, and the average damage ratio was taken of the two estimates. Using this methodology, precise damage estimates are georeferenced with respect to the location of the tornado path and the resulting tornado wind field, providing an ideal validation dataset for engineering models and tools like the ETDA Tool. Table 3 summarizes the Garland/Rowlett, TX tornado and the database captured that was used for validation in the current study.

TABLE 3

Table 3. Characteristics of the Garland/Rowlett TX tornado.

The centerline of the path and the translation speed for the Garland/Rowlett tornado was based on the field survey and subsequent report by the National Weather Service (National Weather Service, 2016).

In order to generate tornado wind fields within the ETDA Tool, several additional parameters of the tornado were required, namely the tornado core radius, the maximum tangential velocity, and the translation speed. For the Joplin tornado, the core radius was taken as 257 m, based on the tree-fall conditioned tornado wind field model used in Lombardo et al. (2015). The translation speed was taken as 13.3 m/s from Kuligowski et al. (2014). The maximum tangential velocity was then adjusted until the maximum wind speed in the ensuing wind field model reached 88.9 m/s, matching the EF4 intensity estimated by the National Weather Service. For the Garland/Rowlett tornado, core radius was estimated by assuming the ratio of the width of damaging winds to the core diameter was the same as in the Joplin tornado (3,220/503 = 6.4). Based on the maximum width in the Garland/Rowlett tornado of 1,610 m, this gave a core diameter estimate of 160 m, or a core radius estimate of 80 m. Similar to the Joplin tornado, the maximum tangential wind speed was then adjusted until the resulting wind field produced a maximum wind speed of 73.6 m/s, equivalent to an EF3 tornado.

Validation of the EDTA Tool

The validation of ETDA Tool is performed by comparing the visually observed damage against ETDA Tool predicted damage. Two methods of comparison are employed:

Comparing Structural Components Damage for Individual Houses

Figure 2 shows post tornado damage photos and spider plot for a single-family home in the Garland/Rowlett tornado. This is a graphical method for comparing the average ETDA Tool predicted damage ratios to the actual observed damage ratios for a single house. All eight components are shown on the same plot for ease of comparison. The ETDA Tool predictions represent the average, or expected, damage ratio to each of the eight components obtained from five thousand simulations. Uncertainty in the predictions is demonstrated by plotting +/– 1 standard deviation about the mean predicted damage ratios. The damaged house is located at a perpendicular distance of 18 m (59 ft.) from tornado center line and had an assigned DOD 6 and EF-3 rating. There can be many possible damage scenarios in the simulations, illustrating the uncertainty in the wind loads, structural capacities, and more. The observed damage ratios essentially represent one possibility of the simulations; therefore, it is not unsurprising if comparisons of individual houses demonstrate differences between predicted and observed damage ratios.

FIGURE 2

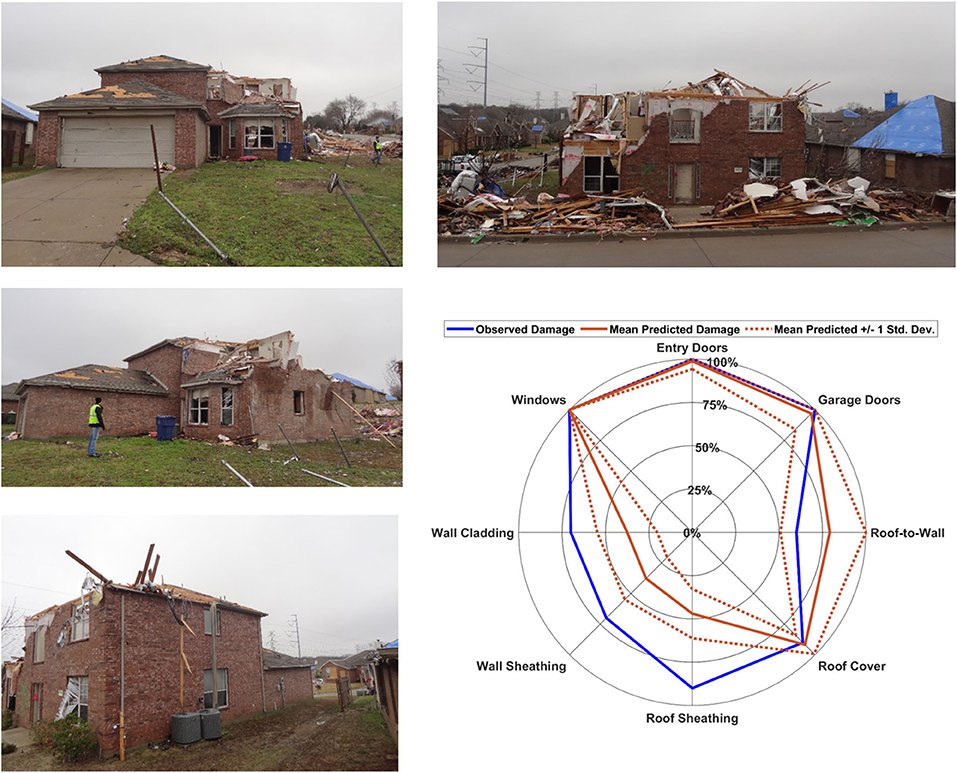
Figure 2. Spider plot and post tornado photographs of a single-family home damaged in the 2015 Garland/Rowlett, TX, tornado.

Mean Structural Component Damage Ratios—ETDA-predicted vs. Empirical Data

The observed damage ratios represent one scenario of tornado translation over the house, whereas the ETDA Tool's estimated damage ratios represent the average of 5,000 simulations of tornado translation. Thus, a direct comparison between observed damage ratios and ETDA Tool predicted damage ratios is not an equivalent comparison. To address this, the damage ratios are discretized into equal bins by distance from the tornado center. Thus, each point represents the average observed or average predicted damage ratio for a single component over a given bin. For the Garland/Rowlett tornado, 25 m bins are used. Figure 3 shows the houses in each bin for the Garland/Rowlett tornado. The number of houses in each bin varies along the distance from the tornado center, with a higher proportion of houses near the tornado center than away from it. Damage ratios for all houses within that bin are averaged to obtain a single value. Thus, for a bin centered at a distance of 12.5 m, all the houses between 0 and 25 m from the center of the tornado are selected and the average damage ratio for each component is calculated.

FIGURE 3

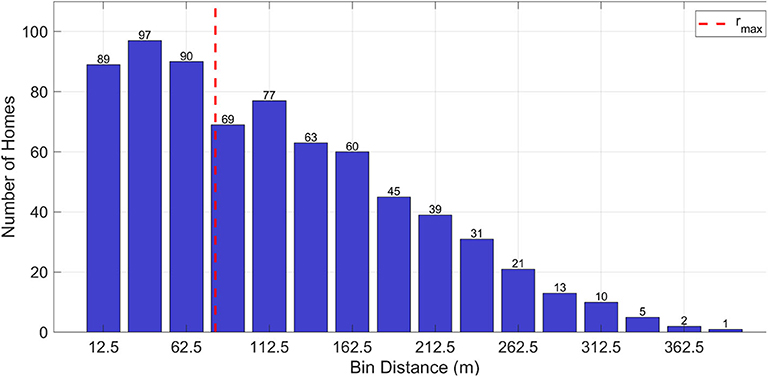
Figure 3. Distribution of 712 Garland/Rowlett houses with binned distance from tornado center. Each value above a bar represents the number of houses present in that bin. Bin size = 25 m. The red dashed line indicates the radius to maximum wind speeds (RMW).

Figure 4 shows the average binned damage progression plots for the Garland/Rowlett houses. Here, Dataset A models all structures as Prototype I homes, Dataset B as Prototype II homes, and Dataset C as Prototype III homes, with Dataset D being a blend of the three prototypes based on visually matching each house in the dataset to the best matching prototype based on aspect ratio, roof shape and number of stories.

FIGURE 4

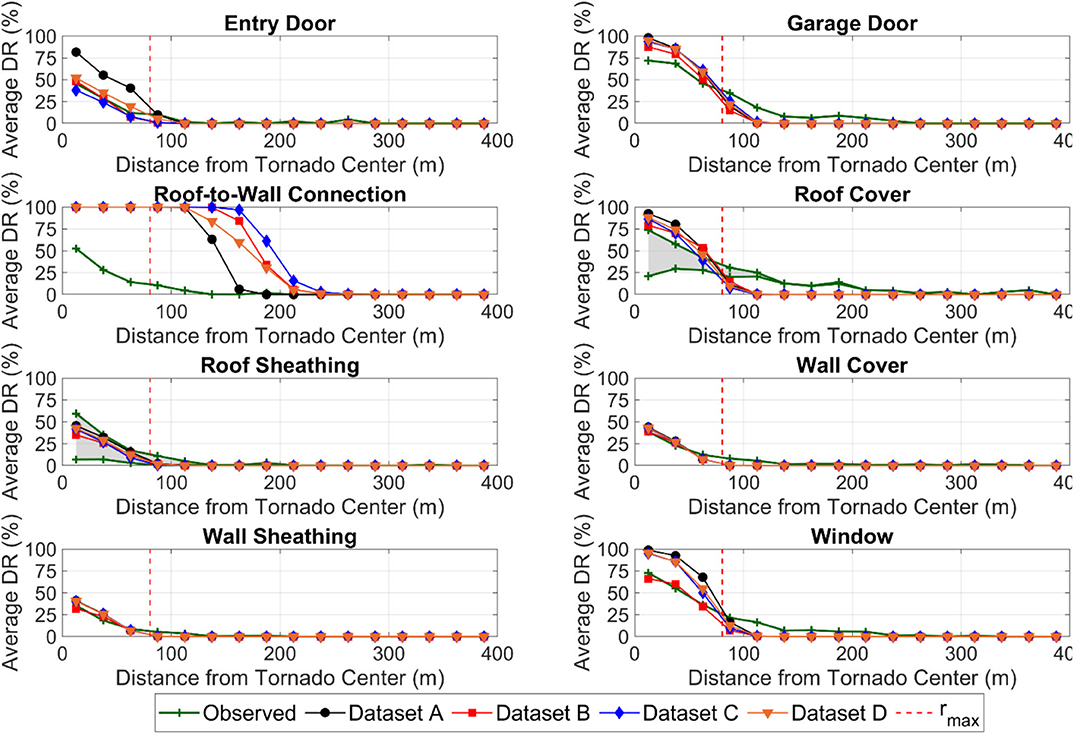
Figure 4. Average observed and ETDA Tool predicted damage ratios (DR) for the Garland/Rowlett tornado. Bin size is 25 m. The red dashed line indicates the radius to maximum wind speeds (RMW). Gray shaded regions show the lower to upper bound ranges for observed damage ratio for roof sheathing damage ratio and roof cover damage ratio.

One of the challenges in component-based validation is how to validate roof cover and roof sheathing damage ratios separately from roof structure damage ratios. When portions of the roof structure fail, it is generally not possible to estimate whether sheathing or roof cover also failed for these same portions of the roof. To address this challenge, the observed roof cover and roof sheathing damage ratios were calculated in two ways to capture the lower bound and upper bound. For roof sheathing, the lower bound is taken to be DR_rst − DR_rs, where DR_rst is the roof structure damage ratio and DR_rs is the roof sheathing damage ratio. The upper bound is taken as simply DR_rs. The lower bound assumes none of the roof sheathing was failed on the failed section of roof structure, while the upper bound assumes all the roof sheathing was failed on the failed section of roof structure. The true value would lie somewhere between these two bounds. A similar method was used for roof cover, only using the roof cover damage ratio. Both the upper bound and lower bound are presented in Figure 4.

Figure 4 shows that both the ETDA Tool estimated damage ratios and observed damage ratios follow a similar trend of damage progression, with houses close to the tornado centerline experiencing higher damage than houses away from tornado centerline as expected. For roof sheathing, the predictions lie within the upper and lower bound. However, for roof cover, the predictions are too high outside the core and too low inside the core, indicating some further improvements could be implemented. Overall, the ETDA tool estimated damage ratios match the observed damage ratios reasonably well for all components except the roof-to-wall connections, which are predicted to fail significantly sooner than observed. One hypothesis for the over-prediction was that the atmospheric pressure component was significantly enhancing the roof uplift loads, causing them to fail prematurely. This was explored but was determined to not be the source of over-prediction. The atmospheric pressure component was generally equalized early on in the time-stepping model for each home due to the debris-impact model predicting one or more breaches in the building envelope.

The binned damage progression plots present a qualitative comparison between observed and ETDA Tool estimated damage ratios. For quantitative comparison, predictive capability analysis of ETDA Tool is evaluated in the following section.

Prediction Capability Analysis of Mean Error

The prediction capability of ETDA Tool is calculated by determining the error in prediction for each house component using the binned damage ratios. The weighted mean of absolute difference between ETDA Tool predicted binned damage ratio and observed binned damage ratio is calculated. Mean error for each prototype dataset is calculated by averaging the errors of each house component. Equations (8) and (9) show the formulae to compute both component error and mean error for the four prototype datasets.

$\begin{array}{ll}{\epsilon }_C=\frac{{\displaystyle {\sum }_{i=1}^{nBins}}{w}_i\times \left[|D{R}_{ETD{A}_i}-D{R}_{Ob{s}_i}|\right]}{{\displaystyle {\sum }_{i=1}^{nBins}}{w}_i}& (8)\end{array}$

$\begin{array}{ll}{\epsilon }_P=\frac{{\displaystyle {\sum }_{j=1}^{nComponent}}\left[{\epsilon }_{C_j}\right]}{nComponent}& (9)\end{array}$

where DR_ETDAi, DR_Obsi are the binned damage ratios, w_i weight of bin i, i.e., the ratio of no. of houses in bin i over the total no. of houses, nBins are the number of bins, nComponent are the number of components, and ${\epsilon }_C$, ${\epsilon }_P$ are the weighted mean errors in component C and prototype dataset P.

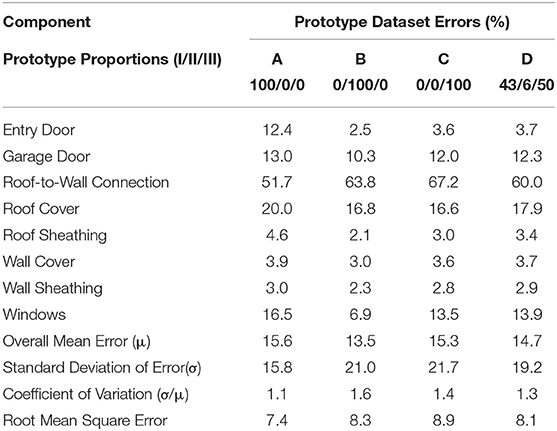
Table 4 shows the weighted mean error in damage ratios for each house component within the four prototype datasets. The overall means, standard deviations, coefficient of variation and root mean square errors are also presented.

TABLE 4

Table 4. Percent weighted mean component error for each prototype dataset.

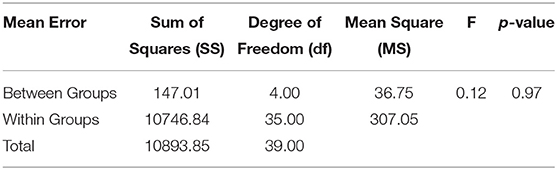
The individual component mean errors are <20% for all the prototype datasets, except for roof-to-wall connections, which ranges between 51 and 60%. Table 4 also shows that the overall mean errors for all the four datasets are <20%, but have a high standard deviation, and a coefficient of variation >1. An ANOVA (Analysis of Variance) analysis to test statistical significance of the differences in mean errors returned a p-value of 97%, indicating there is no statistically significant difference among mean errors for the prototype datasets, meaning the results could be drawn from a single population, see Table 5. Given the other uncertainties in the damage prediction process, the use of multiple prototypes does not significantly improve the predictive capabilities of the ETDA Tool.

TABLE 5

Table 5. Results of ANOVA for the mean errors between prototype datasets.

Discussion

The performance of ETDA Tool is evaluated against post-tornado damage observations published by the fourth author. The ETDA Tool results for estimating damage ratios were computed for three prototype houses, representing (1) single-story gable roof, (2) two-story gable roof, and (3) single storied hip roof. The post-tornado damaged houses are divided into four datasets with the first three datasets having assigned the single prototype house, and Prototype Dataset IV having the most representative prototype house among the three. Two methods are used for evaluating ETDA Tool's performance: (1) individual house comparison, (2) average house comparison with predictive capability analysis.

The individual house comparison graphically shows the observed damage and ETDA Tool estimated damage in one plot for each house. Caution should be exercised in reading too much into these single comparisons, as the ETDA Tool's result represent the average damage ratio to each of the eight components obtained from thousands of simulations. There can be many possible damage scenarios in the simulations, illustrating the uncertainty in the wind loads, structural capacities, and more. The observed damage ratios on the other hand essentially represent one possibility of the simulations, therefore the comparisons of individual houses infer large differences between predicted and observed damage ratios.

The spatially averaged comparison graphically shows the average observed damage ratios against average ETDA Tool predicted damage ratios for given distances from the tornado center. These plots highlight some general observations for prototype datasets: (1) the observed damages and ETDA Tool predicted damages for each component follow the same damage progression trend, (2) the observed and ETDA Tool predicted damages for all building components are maximum near the tornado centerline and reduce moving away from the tornado centerline. Apart from observing general trends, it is difficult to pinpoint the prototype dataset with best match against observed damage ratios.

The predictive capability analysis shows the quantitate comparison between observed and ETDA Tool estimated damage ratios. The overall mean errors for each prototype datasets are <16% but have a high coefficient of variations ranging from 1.1 to 1.5. The CV values >1 imply that the mean errors among the prototype components are highly dispersed from the mean values. Among the four prototype datasets, Dataset B shows the smallest mean error, and not Dataset IV, which contains best match prototype for each house. However, the overall mean errors for the prototype datasets are relatively similar, hence an ANOVA test was performed to determine whether this variation is statistically significant. The ANOVA test shows that the results among the four prototype datasets are statistically insignificant, which implies that they can be inferred singularly from any of the four datasets.

The most concerning element of the ETDA Tool is the prediction of roof structure damage, as the ETDA overpredicts the damage substantially. The list below explores some possible reasons for the observed discrepancies in the roof-to-wall connection damage model within the ETDA Tool:

1. The load-sharing model for roof structure, which transfers wind uplift load from the failed roof-to-wall connections to surrounding intact roof-to-wall connections may not be appropriate. The wind loads are obtained by integrating surface pressures within the tributary area of each of the roof-to-wall connection. While this tributary area approach is commonly used in damage assessment models, Datin and Prevatt (2013) found that in low-rise, light-framed wood structures there is more extensive load sharing beyond the “tributary area” of a single element (i.e., roof-to-wall connection). This increased load sharing acts to smooth out peak loads by distributing some of the load to the connections further away. Incorporating the Datin and Prevatt (2013) load sharing behavior would reduce the damage ratios for roof-to-wall connections and bring them closer in line to the observations but was not possible within the constraints of this study.

2. It is possible that the field investigators underestimated the actual number of failed roof-to-wall connections during the field survey (Prevatt et al., 2016). Damage ratios are assigned by visual examination of the four elevations of the house, and the exact structural status of roof-to-wall connection failures below the roof-deck are not investigated. Thus, it is possible to visually grade a failed roof-to-wall connection as intact, even when it has failed.

3. It is possible the location of failures with respect to the tornado center may not be accurate. The tornado model used for the Garland/Rowlett, TX tornado was developed in derivative manner from the validated tornado wind speed model used for the 2011 Joplin, MO tornado, in which an independent estimate of the peak wind speeds was determined from tree-fall patterns (Lombardo et al., 2015). The uncertainty associated with the tornado model may be high given the assumptions of scaling made to use the characteristics of the Joplin tornado to this smaller event. The wind field model in the ETDA Tool is based on a simplified 2-D Rankine vortex model, and the predicted wind speeds throughout the tornado path may not be well-conditioned to the actual wind speeds that occurred.

The above discussion emphasizes many uncertainties surrounding both post-tornado damage observations as well as the ETDA Tool itself. The effect of minimal change suggests that the geometry of the structure is not yet a significant factor relative to the other uncertainties in the tornado-structure interaction model. Among these uncertainties may be effects of local terrain, sheltering effects from surrounding structures, uncertainties in the tornado-induced wind load model, wind-borne debris in tornadoes, and the vertical gradient of the velocity profile. More research into these effects is needed. The modular structure of the ETDA Tool allows upgrades to be incorporated as new data becomes available. The methodology presented in this study provides a framework for predicting and validating tornado-induced damage to single-family residences.

Conclusions

The ETDA Tool is an engineering-based model capable of simulating component level tornado-induced damage to individual residential structures and to portfolios of single-family, light-framed wood structural residential buildings. In this paper, the performance of the ETDA Tool is evaluated by comparing building component-level damage ratios estimated by the ETDA Tool estimated damage ratios against observed damage ratios. Damage comparisons at the individual house level were found to contain too much uncertainty, in both the observations and estimations of damage, to hold much value as of yet. Instead, quantitative damage comparisons were made as a function of the distance from the tornado centerline, with estimations and observations binned over reasonable sample sizes (no more than 100 per bin). This approach reduced the variability sufficiently to explore more robust trends in the comparisons, while still maintaining a more granular framework than more community-scale validation approaches. The individual house comparison and average house comparisons provided qualitative evaluation, while predictive capability analysis provided a quantitative measure of performance. Using this approach, The overall mean errors absolute value of the difference between mean (i.e., averaged within each bin) ETDA estimated damage ratios and mean observed damage ratios are <16% overall, and with individual component errors are <17% for all individual components except roof-to-wall connections. The roof-to-wall connection damage ratios are highly over predicted by ETDA Tool, resulting in large errors, with an average maximum error of 67.2%. This error may be indicative of the specific challenge of both modeling and estimating observed roof-to-wall connections failures, since due to load sharing, roof-to-wall connections are not necessarily removed from the structure after their failure if the load is safely redistributed elsewhere.

Presently, the ETDA Tool models tornado-induced damage using with three prototype houses, but the three prototypes showed little difference in performance amongst themselves, suggesting differences in the load path and aerodynamics of specific buildings is not yet meaningful given the larger uncertainties present in the modeling efforts. The ETDA Tool serves as a framework for predicting tornado-induced damage, with increased accuracy expected as individual components of the tool are upgraded and refined with the latest research advancements.

The importance of robust comparisons against field data as a benchmark for tornado-induced wind damage models cannot be overstated. The errors present in the current tool, which utilized many standard assumptions and simplifications (e.g., tributary area based structural analysis, straight-line wind pressures with simple addition of the atmospheric pressure deficit, quasi-static analysis via time-stepping damage model), serve as a reminder that tornado-structure interaction remains highly uncertain at the individual building scale.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

AJ and AB participated in this research as graduate students under the supervision of DP. Each produced a thesis on their contributions. In this context, AJ and AB were responsible to develop Matlab codes and run analyses on the UF HiperGATOR supercomputer. DR was directly involved in the proposal development and mentoring of the graduate students' activities as a Ph.D. candidate and as a Post-Doctoral Fellow. DP was the Principal Investigator, main proposer, and supervisor of the work of the three students. He was responsible for quality control, data curation, and comparison of the results against previously collected empirical data. All authors contributed to the article and approved the submitted version.

Funding

This research was supported by the Risk Prediction Initiative at Bermuda Institute of Ocean Sciences (RPI-BIOS). RPI-BIOS supported two graduate students MS theses, including stipends and experimental support for high-performance computing. This work was supported by the National Science Foundation (NSF) under Grant No. 1150975, The NSF support supported 1.5 Ph.D. students effort, supporting the initial work on tornado-resilient communities. The NSF Graduate Research Fellowship, and a University of Florida Alumni Fellowship supported DR as a Ph.D. candidate and GRFP Fellow.

Conflict of Interest

AJ was employed by the company GSE Engineering & Consulting, Inc., and AB was employed by the company BCC Engineering, LLC.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors are grateful for the generous support received from the Risk Prediction Initiative of the Bermuda Institute of Ocean Sciences (RPI-BIOS) through two research project awards. This data collection and analysis of the field data was supported by the National Science Foundation (NSF) under Grant No. 1150975. The third author received part support through an NSF Graduate Research Fellowship, and the Alumni Fellowship from the University of Florida. Any opinions, findings, and conclusions are those of the authors and do not necessarily represent the views of the National Science Foundation.

References

ASCE (2010). ASCE 7-10, Minimum Design Loads for Buildings and Other Structures. Reston, VA: American Society of Civil Engineers.

ASCE (2017). Minimum Design Loads and Associated Criteria for Buildings and Other Structures (7-16). ASCE 7-16.

PubMed Abstract

Baker, C. J., and Sterling, M. (2018). A conceptual model for wind and debris impact loading of structures due to tornadoes. J. Wind Eng. Ind. Aerod. 175, 283–291. doi: 10.1016/j.jweia.2017.11.029

CrossRef Full Text | Google Scholar

Balderrama Garcia Mendez, J. A. (2009). Development of a Hurricane Loss Projection Model for Commercial Residential Buildings (added by NS). University of Florida, Gainesville, FA.

Google Scholar

BPAT, F. (1999). Midwest Tornadoes of May 3, 1999: Observations, Recommendations and Technical Guidance. REP. FEMA, Federal Emergency Management Agency.

Google Scholar

Coulbourne, W. L., Prevatt David, O., Eric Stafford, T., Ramseyer Christopher, C., and Joyce John, M. (2015). Moore, Oklahoma, Tornado of 2013: Performance of Schools and Critical Facilities. ASCE.

Coulbourne, W. L., and Prevatt, D. O. (2013). “Using hurricane wind engineering to inform designs for improved performance in tornado events,” in 12th Americas Conference on Wind Engineering 2013, ACWE 2013: Wind Effects on Structures, Communities, and Energy Generation (Seattle, WA), 243–255.

Google Scholar

Datin, P. L., and Prevatt, D. O. (2013). Using instrumented small-scale models to study structural load paths in wood-framed buildings. Eng. Struct. 54, 47–56. doi: 10.1016/j.engstruct.2013.03.039

CrossRef Full Text | Google Scholar

Datin, P. L., Prevatt, D. O., and Pang, W. (2010). Wind-uplift capacity of residential wood roof-sheathing panels retrofitted with insulating foam adhesive. J. Arch. Eng. 17, 144–154. doi: 10.1061/(ASCE)AE.1943-5568.0000034

CrossRef Full Text | Google Scholar

Fujita, T. T. (1971). “Proposed Characterization of Tornadoes and Hurricanes by Area and Intensity. Satellite and Mesometeorology Research Project Report 91. The University of Chicago.

Google Scholar

Graettinger, A. J., Grau, D., Van De Lindt, J., and Prevatt, D. O. (2012). “GIS for the geo-referenced analysis and rapid dissemination of forensic evidence collected in the aftermath of the Tuscaloosa tornado,” in Construction Research Congress 2012: Construction Challenges in a Flat World, Proceedings of the 2012 Construction Research Congress (West Lafayette, IN), 2170–2179.

Google Scholar

Gurley, K., Pinelli, J. P., Subramanian, C., Cope, A., Zhang, L., and Murphree, J. (2005). Florida Public Hurricane Loss Projection Model Engineering Team. Final Report. International Hurricane Research Center, Florida International University, Miami, FL.

Haan, F. L., Sarkar, P. P., Prevatt, D., Roueche, D., Graettinger, A., Dao, T. N., et al. (2014). “Using tornado damage surveys to improve laboratory tornado simulations,” in Structures Congress 2014 - Proceedings of the 2014 Structures Congress (Boston, MA), 1472–1483.

Google Scholar

Herseth, A., Goldsmith-Grinspoon, J., and Scott, P. (2017). Prepare to protect: operating and maintaining a tornado safe room. J. Bus. Contin. Emer. Plan. 10, 328–338.

PubMed Abstract | Google Scholar

Hoecker, W. H. (1960). Wind speed and air flow patterns in the Dallas tornado of April 2, 1957. Mon. Wea. Rev. 88, 167–180.

Google Scholar

Holmes, J. D. (2001). Wind Loading of Structures. London; New York, NY: Spon Press.

Google Scholar

Kopp, G. A., and Wu, C. H. (2017). “A framework for the aerodynamics of low-rise buildings in tornadoes: can boundary layer wind tunnels give us everything we need?,” in Americas Conference on Wind Engineering (Gainesville, FL).

Kuligowski, E. D., Lombardo, F. T., Phan, L. T., Levitan, M. L., and Jorgensen, D. P. (2014). Final Report, National Institute of Standards and Technology (NIST) Technical Investigation of the May 22, 2011, Tornado in Joplin, Missouri. NIST.

Google Scholar

Lieblein, J. (1974). Efficient Methods of Extreme-Value Methodology. Report NBSIR 74-602, National Bureau of Standards, Washington, DC.

Google Scholar

Lombardo, F. T., Roueche, D. B., and Prevatt, D. O. (2015). Comparison of two methods of near-surface wind speed estimation in the 22 May, 2011 Joplin, Missouri Tornado. J. Wind Eng. Ind. Aerodyn. 138, 87–97. doi: 10.1016/j.jweia.2014.12.007

CrossRef Full Text | Google Scholar

Masoomi, H., and van de Lindt, J. W. (2017). Tornado community-level spatial damage prediction including pressure deficit modeling. Sustain. Resilient. Infrastruct. 2, 179–193. doi: 10.1080/23789689.2017.1345254

CrossRef Full Text | Google Scholar

McDonald, J. R., and Mehta, K. C. (2006). A Recommendation for an Enhanced Fujita Scale (EF-Scale), Wind Science and Engineering Center. Lubbock, TX: Wind Science and Engineering Center, Texas Tech University.

Mehta, K. C. (2013). Development of the EF-scale for tornado intensity. J. Disaster Res. 8, 1034–1041. doi: 10.20965/jdr.2013.p1034

CrossRef Full Text | Google Scholar

Minor, J. E., McDonald, J. R., and Mehta, K. C. (1977). The Tornado: An Engineering-Oriented Perspective. NASA STI/Recon Technical Report N.

Google Scholar

National Weather Service (2016). North and Central Texas December 26, 2015 Tornado Outbreak. Available online at: https://www.weather.gov/fwd/dec26tornadoes

NOAA National Centers for Environmental Information (NCEI) (2020). Billion-Dollar Weather and Climate Disasters. Available online at: https://www.ncdc.noaa.gov/billions

Google Scholar

NSSL (2013). US Tornado Deaths/Millions People. Available online at: https://blog.nssl.noaa.gov/nsslnews/2009/03/us-annual-tornado-death-tolls-1875-present

NWS (2020). Weather Related Fatality and Injury Statistics. National Weather Service. Available online at: https://www.weather.gov/hazstat/

Oh, J. H., Kopp, G. A., and Inculet, D. R. (2007). The UWO contribution to the NIST aerodynamic database for wind loads on low buildings: part 3. internal pressures. J. Wind Eng. Ind. Aerodyn. 95, 755–779. doi: 10.1016/j.jweia.2007.01.007

CrossRef Full Text | Google Scholar

Peng, X., Roueche, D. B., Prevatt, D. O., and Gurley, K. R. (2016). “An engineering-based approach to predict tornado-induced damage,” in Multi-hazard Approaches to Civil Infrastructure Engineering, eds P. Gardoni and J. M. LaFave (Cham: Springer International Publishing), 311–335.

Google Scholar

Pita, G., Pinelli, J. P., Gurley, K., and Mitrani-Reiser, J. (2015). State of the art of hurricane vulnerability estimation methods: a review. Nat. Hazards Rev. 16:04014022. doi: 10.1061/(ASCE)NH.1527-6996.0000153

CrossRef Full Text | Google Scholar

Prevatt, D. O., Coulbourne, W., Graettinger, A. J., Shiling, P., Gupta, R., and Grau, D. (2013). Joplin Missouri Tornado of May 22, 2011. Structural Damage Survey and Case for Tornado-Resilient Building Codes. Reston, VA: American Society of Civil Engineers.

Google Scholar

Prevatt, D. O., Roueche, D. B., and Chen, A. (2016). Preliminary Analysis of Post-Tornado Damage Survey Data from the 2015 Christmas Tornado in Garland, Texas. Gainesville, FL: University of Florida.

Google Scholar

Prevatt, D. O., Roueche, D. B., Van De Lindt, J. W., Pei, S., Dao, T., Coulbourne, W., et al. (2012a). “Building damage observations and ef classifications from the tuscaloosa, al and joplin, mo tornadoes,” in Proceedings Structures Congress 2012, March 29, 2012 - March 31, 2012. (Chicagi, IL: American Society of Civil Engineers (ASCE)), 999–1010.

Prevatt, D. O., Van De Lindt, J. W., Back, E. W., Graettinger, A. J., Shiling, P., Coulbourne, W., et al. (2012b). Making the case for improved structural design: Tornado outbreaks of 2011. Leadersh. Manag. Eng. 12, 254–270. doi: 10.1061/(ASCE)LM.1943-5630.0000192

CrossRef Full Text | Google Scholar

Ramseyer, C., Holliday, L., and Floyd, R. (2016). Enhanced residential building code for tornado safety. J. Perform. Construct. Fac. 30:04015084. doi: 10.1061/(ASCE)CF.1943-5509.0000832

CrossRef Full Text | Google Scholar

Rankine, W. J. M., and Miller, W. J. (1888). A Manual of Applied Mechanics. London: William John Macquorn Rankine, C. Griffin and Co.

Google Scholar

Roueche, D. B., Haan, F. L., and Prevatt, D. O. (2020). Tornado-induced and straight-line wind loads on a low-rise building with consideration of internal pressure. Front. Built Environ. 6:18. doi: 10.3389/fbuil.2020.00018

CrossRef Full Text | Google Scholar

Roueche, D. B., and Prevatt, D. O. (2013). Residential damage patterns following the 2011 Tuscaloosa, AL and Joplin, MO Tornadoes. J. Disaster Res. 8, 1061–1067. doi: 10.20965/jdr.2013.p1061

CrossRef Full Text | Google Scholar

Roueche, D. B., Prevatt, D. O., Haan, F. L., and Datin, P. L. (2015). An estimate of tornado loads on a wood-frame building using database-assisted design methodology. J. Wind Eng. Ind. Aerodyn. 138, 27–35. doi: 10.1016/j.jweia.2014.11.011

CrossRef Full Text | Google Scholar

Shanmugam, B., Nielson, B. G., and Prevatt, D. O. (2009). Statistical and analytical models for roof components in existing light-framed wood structures. Eng. Struct. 31, 2607–2616. doi: 10.1016/j.engstruct.2009.06.009

CrossRef Full Text | Google Scholar

Shen, Y. (2013). Assessing the wind resistance of sectional door systems for facilities in hurricane-prone areas through full-and component-scale experimental methods and finite element analysis (Ph.D. dissertation). Gainesville, FL: Graduate Schoolof The University of Florida.

Google Scholar

Simiu, E., and Scanlan, R. H. (1996). Wind Effects on Structures - Fundamentals and Applications to Design. New York, NY: Wiley.

Google Scholar

Simmons, K. M., Kovacs, P., and Kopp, G. A. (2015). Tornado damage mitigation: benefit–cost analysis of enhanced building codes in Oklahoma. Weather Clim. Soc. 7, 169–178. doi: 10.1175/WCAS-D-14-00032.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Simmons, K. M., Sutter, D., and Pielke, R. (2013). Normalized tornado damage in the United States: 1950–2011. Environ. Hazards 12, 132–147. doi: 10.1080/17477891.2012.738642

CrossRef Full Text | Google Scholar

Tamura, Y. (2012). Aerodynamic Database for Low-Rise Buildings. Global Center of Excellence Program, Tokyo Polytechnic University, Tokyo. Available online at: http://www.wind.arch.t-kougei.ac.jp/info_center/windpressure/lowrise/mainpage.html (accessed December 12, 2013).

van de Lindt John, W., and Dao Thang, N. (2009). Performance-based wind engineering for wood-frame buildings. J. Struct. Eng. 135, 169–177. doi: 10.1061/(ASCE)0733-9445(2009)135:2(169)

CrossRef Full Text | Google Scholar

Vickery, P. J., Masters, F. J., Powell, M. D., and Wadhera, D. (2009). Hurricane hazard modeling: the past, present, and future. J. Wind Eng. Ind. Aerodyn. 97, 392–405. doi: 10.1016/j.jweia.2009.05.005

CrossRef Full Text | Google Scholar