Bridge Load Testing for Identifying Live Load Distribution, Load Rating, Serviceability and Dynamic Response

Introduction

Bridge load testing is commonly employed to determine issues that cannot be easily resolved by visual inspection or simple analysis. Visual inspection, load-testing, structural health monitoring (SHM), non-destructive testing (NDT) and finite element (FE)-based structural modeling are commonly utilized to address issues related to a bridge or a population of bridges. For example, AASHTO-MBE (2018) recommends load testing for structural condition rating of highway concrete deck bridges. The load test objectives may vary from case by case, and such a test may be needed on particular bridge or a population of similar bridges in question to make decisions such as bridge closure, bridge load posting, replacement, and retrofit.

A general structural identification framework that also encompasses bridge testing was presented in detail along with utilization of field experimental and analytical studies for decision making (Catbas et al., 2013). A particular bridge can be tested to understand critical issues, and sometimes a sample representative bridge can be tested to address issues related to the similar bridge population (Gokce et al., 2011). Similarly, a representative bridge population sample can be tested to be able to make decisions on the entire bridge population (Catbas et al., 2005). In order to conduct rapid experimental test on a reinforced concrete bridge population, the researchers proposed a method to determine the moment DFs for single-span-T-beam bridges (Catbas et al., 2012). They presented that the new approach could be predicted live load reasonably well when compared to standard girder analysis given in the (AASHTO, 2017) code. Based on the load and resistant factor rating (LRFR) approach, load rating factors were obtained for a fully instrumented bridge for three different methods (standard, experimental strain data, and FEM) (Sanayei et al., 2016). Standard approach resulted lower rating factors than the others. Static and dynamic testing was also carried out by Catbas et al. (2006) for a concrete T-Beam bridge taking into account before and after retrofit of the bridge through carbon fiber–reinforced polymer (CFRP) material. According to the results of experimental data for both cases, they clearly showed that the CFRP retrofit had an ability to improve structural response of the concrete bridge. In order to quantify the effect of deterioration on live-load response of an existing concrete bridge, Torres et al. (2019) performed experimental and numerical study. Based on the results from load-test as well as visual inspection, they found heavily deteriorated deck, undamaged girders and moderate connection problems at the longitudinal joints. By performing a parametric study on the calibrated the FE model of the bridge, the moment and shear girder distribution factor (DF) equations were developed in that study. Tawadrous et al. (2019) carried out live load-testing on two concrete bridges with different deck systems: (i) newly developed precast concrete deck and (ii) standard cast-in-place (CIS) deck to compare their performances on the basis of strain and deflection. The influence of foundation movements and geohydraulic hazards on load rating of a highway bridge was also investigated by Davis et al. (2018). The proposed load rating approach was obtained to give more conservative RF values than those of the standard method if foundation movements were considered. More recent load-test implementations to concrete bridge can be found in the study of Omar and Nehdi (2018). On the other hand, some researchers also recently demonstrated that more effective bridge condition assessments could be done through other technologies (computer vision, image, thermal camera, etc.) (Agdas et al., 2016; Zaurin et al., 2016; Hiasa et al., 2018; Dong and Catbas, 2019). In these studies, these technologies were determined to be an effective complementary tool. More recently, civil infrastructure technologies were grouped to be utilized for commonly seen bridge failures (Bas and Catbas, 2019).

The main objective of this paper is to present a bridge load test with particular engineering objectives regarding a multi-span bridge with several spans of the same geometry and material properties. The span under consideration is the worst condition span and acceptable performance from this span will be favorably extrapolated to the entire bridge. The specifics goals of the load test are as follows: (i) obtain impact factors (IM) under different loads and speeds, (ii) obtain dynamic responses in terms of structural frequencies and mode shapes, and (iii) obtain load distribution of the bridge and evaluation of the load carrying capacity of the bridge. During the bridge test, the strain/stress responses, displacements and accelerations under different truck loads were collected by using proper sensors and data acquisition systems. For this aim, instrumentation plan and truck load configuration for the bridge were given. From static load-test with different truck loads, distribution (DF) and load rating (RF) factors, and deflection check of the bridge were determined. Dynamic load-testing with different truck loads and speeds were carried out to calculate the IM and dynamic characteristics of the bridge. The DF results from the experimental field test and FEM were compared with the standard formulation given in AASHTO (2017).

General Features of the Bridge

As shown in Figure 1A, the bridge considered in the study is a multi-span concrete bridge with a bascule section in the middle, located in Florida, United States. The bridge was constructed in 1964 and has a total length of 912 m. Each span consists of five pre-stressed I-beam spans, two flanking spans, and a steel double leaf bascule main span, which is 39.5 m between trunnion centers. AASHTO Type II Girders are spaced at 2.4 m with an 18 cm cast in place deck and 5.1 cm wearing surface. All approach spans are 15.9 m each. The substructure is composed of two cast in place reinforced concrete end bent caps founded on 61 cm square pre-stressed concrete piles with rubble riprap slope protection retained by a seawall system, 53 intermediate reinforced concrete bent caps founded on 61 cm square pre-stressed concrete piles. The aged bridge underwent a retrofit of the deteriorated girders, including removal of all spalled and delaminated concrete, cleaning the corroded steel and rebar, installing special splice when a strand was severed or has more than 50% sectional loss, repairing hairline cracks. The load test here would explore if the load carrying capacity is adequate.

FIGURE 1

Figure 1. (A) The concrete highway bridge (B) Sensor instrumentation plan.

Instrumentation Plan

As shown in Figure 1B, three types of sensors were installed on the bridge. Totally, 15 accelerometers were installed at the 1/4 span, mid span and 3/4 span of five girders (G1–G5) to test the dynamic responses during load test.

Five displacement sensors (i.e., potentiometers) were installed at the mid span of each girder to measure the displacement. Three cameras were employed to measure the displacements at the same location. The camera-based monitoring and computer vision implementation will be presented separately in other publications. Five strain gauges were installed at the 1/4 span of each girder. One camera was employed to record the traffic footage. Details of the sensors and cameras are shown in Table 1. All the sensors were installed at the bottom of the girders as shown in Figure 2A.

TABLE 1

Table 1. Specifications of sensors and cameras.

FIGURE 2

Figure 2. (A) Sensors installed on the bottom of the girders (B) Loading trucks.

Loading Plan

The truck loading test plan consisted of static and dynamic loads with two different trucks separately. Two types of trucks, Truck 1 (T1) and Truck 2 (T2) were operated to conduct the load test. The trucks and loading plan are shown in Figures 2B, 3A,B.

FIGURE 3

Figure 3. (A) Static loading plan of Truck 1 (T1) (B) Truck 2 (T2).

In the static test, the truck (T1 or T2) was stopped and remained at four different locations of each lane (Lane 1 and Lane 2), and it took four steps for one test round. According to the types of the truck and the lanes, Table 2 summarizes the static loading cases. In this study, to point out the loading location or step, S_i (i = 1, 2, 3, 4) is added at the end of the case name. For example, the load location in Figure 3A is represented by T1L1S1.

TABLE 2

Table 2. Static loading cases.

In the dynamic test, the load configuration was similar to the static test. The difference is instead of putting the trucks statically in all four locations, the trucks moved in the lane with different speeds. According to the types of the truck, moving speeds and the lanes, Table 3 summarizes the dynamic loading cases.

TABLE 3

Table 3. Dynamic loading cases.

Static Load-Test

General

Figure 4A shows the displacement results of T2L1. This figure shows both the displacement results from cameras and potentiometers. The results from the cameras and the potentiometers are very consistent with each other and the maximum difference is within 2.5% range. Only small motions of the potentiometers installed at the two exterior girders (P6 and P10) were observed during the load test. Therefore, only results from cameras are shown in Figure 4A and only these results were used for assessment. Details of the test and use of computer vision based implementation are given by Catbas et al. (2019) and will be presented in other presentations. From Figure 4A, it can be seen that the displacement gives a flat level at each test step and when the truck was loaded on L1, the girder under the truck has the largest displacement response. For example, here P9 is the mid span of Girder 4 and it gives the largest displacement, 2.76 mm at step 3 (S3) among all the girder measurement points. The displacement of P6, P7, P8, and P10 at step 4 is 0.41, 1.48, 2.69, and 1.49 mm, respectively.

FIGURE 4

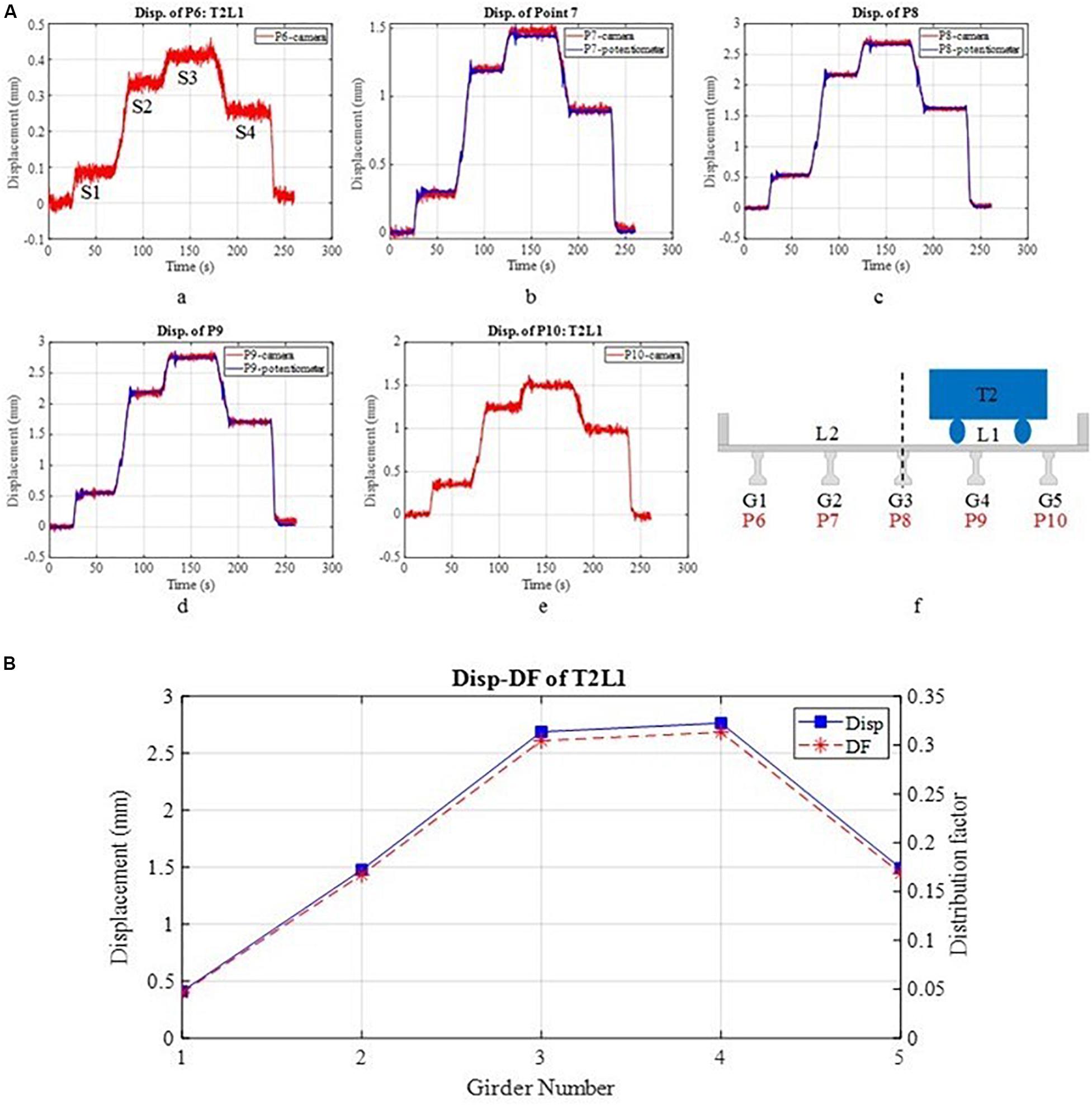
Figure 4. (A) Displacement results of static load case T2L1 (B) Distribution factor calculated from displacement results.

FE Model of the Bridge

As shown in Figure 5, FE model of the bridge was established using beam elements and shell elements for the reinforced concrete prestress girders and deck, respectively. Besides, tendon elements was utilized to consider the prestress effect in the analyses. All considerations for FE model of the bridge were obtained according to its calculation report and project drawings. For this aim, structural analysis software, SAP2000 (CSI, 2019), was utilized. The bridge was then updated as per the modal characteristics and displacement results obtained from the experimental field test. The live load DF and load-rating (RF) of the updated FE model are also taken into account for the sake of the comparison of experimental and AASHTO (AASHTO, 2017) calculation.

FIGURE 5

Figure 5. FE Model of the bridge.

Linearity Check

The linearity check of the bridge was carried out mainly for two reasons. First, it is to determine the load rating with larger load levels and secondly to be able to calculate multiple presence factors by combining separate test results. Under regular operational loads, the bridge response should not reach ultimate response levels. As such, it would be possible to observe linear behavior under given increasing load conditions. To check the linearity of the bridge, the girders with the largest responses were selected and here it is for the case the truck loaded on L1, the girder is G4. Two loading cases T1L1 and T2L1 were taken as an example to check the linearity (Figure 6). The load increase is observed to be 2.65 due ratio of the weight of T2 to T1 as shown in Figure 6. It should be noted that the axle number and total length of truck are not exactly the same. In addition, the placement of the trucks in real life are somewhat different as one truck has two and the other has three rear axles as shown in Figure 3. From Figure 6, it can be seen that the displacement and the strain increase ratios are quite consistent and gives 3.16 and 3.08, respectively. Considering the change of axle number and total length of truck, and also the similar trend between displacement and strain (both in the range of 15 ± 1% to the difference of weight increase), it is fair to say that the linearity is validated. This provides proof that the bridge behaves linearly under operational loads in the range of 26–70 kip range.

FIGURE 6

Figure 6. Trucks loaded the left lane Truck-1 and Truck-2.

Distribution Factor Using Experimental Data and FEM

Using the responses across the bridge, we can obtain bridge load distribution, which is critical for bridge response and load rating. With the displacement results of each girder, the DF can be calculated based on Eq. (1) below:

$${\text{DF}}_i=\frac{{\mathrm{\alpha }}_i}{{\sum }_{j=6}^{10}{\mathrm{\alpha }}_j}(1)$$

where i and j are the girder numbers with the range from 6 to 10 and a_i or a_j are the strain or displacement of the girder at the same section depending on the data being used. The DFs calculated from the experimental displacement results are shown in Figure 4B for T2L1 load case. It should be noted that Figure 4B has two vertical axes and the left vertical axis represents the displacement and the right one is for DF. The DF can also be calculated from the strain data. Figure 7A shows the strain result of each girder at 1/4 span. Due to the signal noise and the small strain measurements, the raw data (in red line) was filtered and the filtered data was shown in blue line. The DF results are very similar to those obtained from displacements. The strain of Girder 4 (G4) gives the largest value due to the loading also shown in Figure 7A. Figure 7B illustrates the DFs obtained from the load test with Truck 2 (loaded truck T2) on Lane 1 (L1). It is observed that the max DF is 0.4 right under the truck load. This DF of 0.4 is indicating that there is good load distribution across the bridge. This fully loaded truck DF results can be predicted due to T2 on L2, and this will allow addition of the DFs to obtain multi-load case, which is more conservative than the multi-presence factor given in AASHTO (2017). Similar calculations for DF were carried out based on the results from the FE analysis as given in Figure 7A and almost similar DF values to the experimental test were yielded.

FIGURE 7

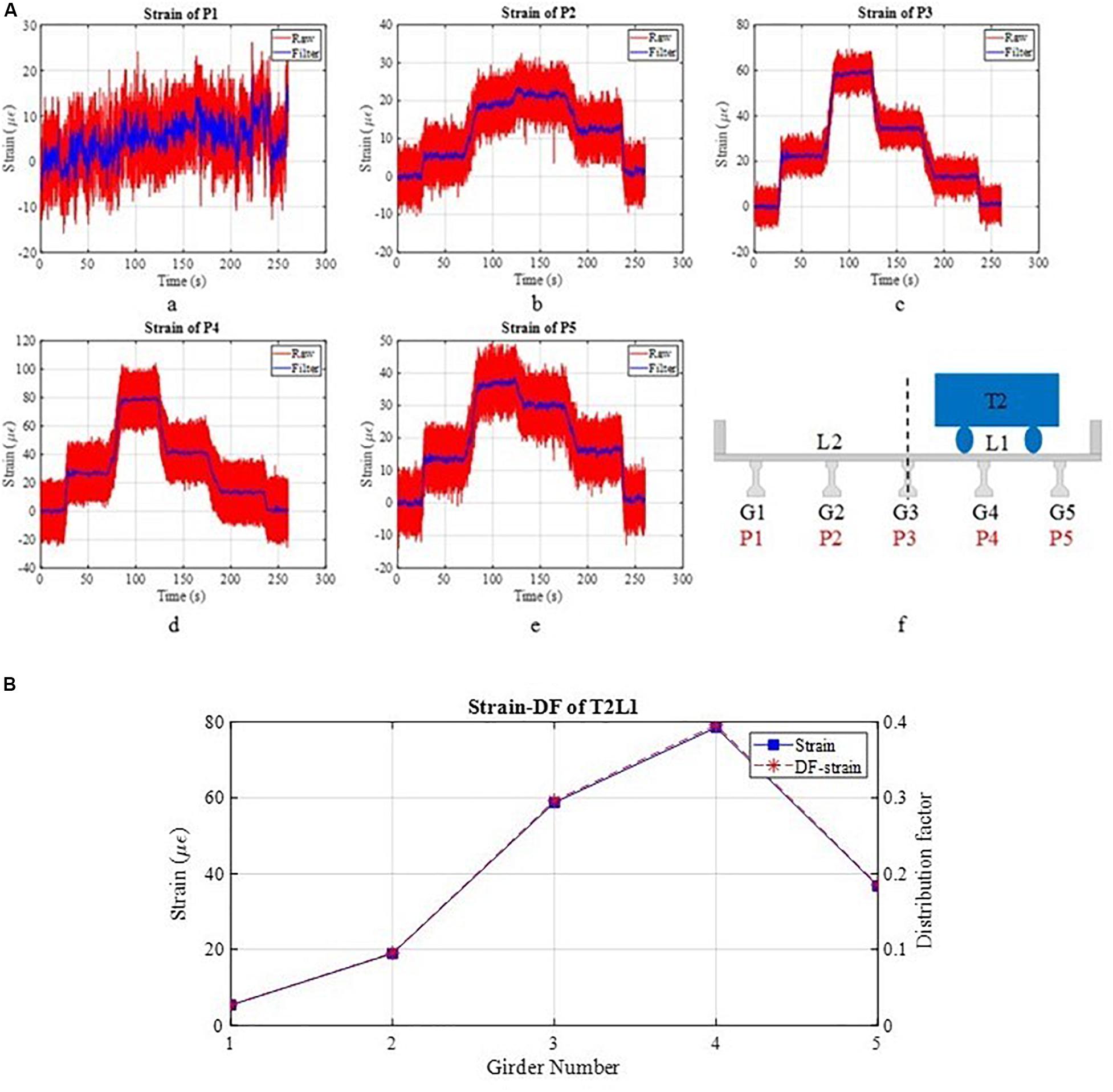
Figure 7. (A) Strain results of static load case T2L1 (B) Distribution factor calculated from strain results.

AASHTO (2017) utilizes a multi-parameter formulation for the load distribution. The DF was employed for the load rating of the bridge by means of girder line analysis. The detailed formulation for DF calculation can be seen in Table 4. It should be noted that the DF calculations by using displacement or strain only consider one single truck in one of the two lanes. In real cases, there is still a chance that multiple vehicles are present in multiple lanes at the same time. AASHTO (2017) code considers this scenario and use the larger value of DFs between the multiple design lanes loaded and single one.

TABLE 4

Table 4. Distribution factor calculation in AASHTO (2017).

In this study, due to the symmetry of this bridge, the DFs of multiple lanes (two vehicles here) were also calculated and shown in Figure 8A. The unit of displacement in the results is millimeter and the unit of strain is με. From Figure 8A, it can be seen that the DFs calculated by experimental displacement and strain at Girder 3 (G3) are very close to the ones calculated by AASHTO (2017). Similarly, this agreement was also seen for the DF results from FEM as shown in Figure 8A. It should be mentioned again that the multi girder DFs were calculated under two heavy loaded truck side by side and this would create a load case more conservative than the AASHTO (2017) based DF results. In other words, considering a combined DF of 0.6 can be regarded to be conservative. While the DFs of the other girders calculated by experimental and FEM displacement and strain are much smaller than those calculated by AASHTO (2017). It means that AASHTO (2017) gives more conservative DF, especially for the girders away from the boundary of two adjacent lanes, e.g., G1, G2, G3, and G4. For the girder close to the boundary of two adjacent lanes, e.g., G3, the DFs calculated from displacement and strain are close to those calculated by AASHTO (2017), but still smaller.

FIGURE 8

Figure 8. Comparison (A) DF (B) RF results.

Load Rating

By utilizing the results of DFs from the experimental study and FE model, a simple method yet widely used the load rating factor can be calculated using formulations given in AASHTO (2017). The rating factors (RF) calculated by using different DFs and HL 93 truck for Strength Limit I are listed as shown in Figure 8B. General formulation for load rating from AASHTO (2017) is given with Eq. (2). The load factors such as φ, φ_s, φ_c,γ_DC,γ_DW,γ_p,γ_L can be found in AASHTO (2017) standard.

$$\text{RF}=\frac{{\mathrm{\phi }}_c{\mathrm{\phi }}_s\mathrm{\phi }R-{\mathrm{\gamma }}_{DC}\text{DC}-{\mathrm{\gamma }}_{DW}\text{DW}\mp {\mathrm{\gamma }}_{p}P}{{\mathrm{\gamma }}_L\left(\text{LL}+\text{IM}\right)}(2)$$

As stated in the calculation of DF, the load rating using the DF calculated from AASHTO (2017) also indicates that AASHTO codes give the more conservative rating factors than the ones obtained by experimental and FEM method (RF-disp and RF-strain), especially for the girders away from the boundary of two adjacent lanes, e.g., G1, G2, G3, and G4. For the girder close to the boundary of two adjacent lanes, e.g., G3, the RFs from displacement and strain are close to those calculated by AASHTO (2017), but still larger. The experimental case also presents a more conservative case due to low probability of having two such heavy trucks side by side creating the most critical load case. As a result, it can be concluded that the RFs in real life can even be considered to be even higher than reported in Figure 8B.

Deflection of Limit Check

The deflection limit check is to check whether the maximum displacement of mid span is larger than the value calculated by (L/800). This limit is commonly used to evaluate the serviceability of the bridge. Here L is the length of span, which is 15,849.61 mm (52 ft). Here (L/800 = 52/800 = 0.065 ft) is 19.81 mm. As demonstrated in Figure 6, the maximum displacement of mid span of Girder 4 in loading case T2L1 under static vehicle load is 2.75 mm, which is considerably less than the serviceability deflection limit. This finding can be somewhat expected due to the number of AASHTO girders and the span length of the bridge. In conclusion, the bridge fulfills AASHTO (2017) serviceability requirement.

Dynamic Load-Test

Modal Testing

To estimate the dynamic properties of the bridge, the accelerations versus time histories collected by fifteen accelerometers installed on the bridge were processed. One of the other objective of the modal testing is to use its results to update the FE model of the bridge as developed in the previous section above. These dynamic results can be tracked over time to determine any global changes. They were employed to validate or calibrate FEM of the bridge. Here load case T2L1-55 (Truck 2 moved on Lane 1 with a speed of 55 mph = 80.7 ft/s) is considered for the dynamic analysis. It is seen based on the speed of the truck it takes about 0.64 s to cross the bridge. Figure 9A shows the acceleration time histories of each measurement point for load case T2L1-55. Figure 9B shows the FFT analysis of acceleration at P4 and possible modal frequencies were marked. Based on all the collected time histories, operational modal analysis methods, enhanced frequency-domain decomposition (EFDD) and stochastic subspace identification-unweighted principal component (SSI-UPC) as shown in Figure 9C, is employed to identify the modal frequencies, damping ratio and mode shapes (Artemis-Modal, 2015). Both methods are generally used to identify modal parameters of linear systems using output-only measurements. In the SSI method, dynamic response of a structural system is assumed to consist of state and observation parts. The philosophy of this approach is to represent dynamics of a structure is modeled as n × n state matrix (n: state space dimension). Observation matrix can be estimated from a part of the state matrix. Thus, the system response vector that includes the modal characteristics of structure considered is obtained as different version of observable part of the state matrix. More details can be found in Van Overschee and De Moor (1996). The main idea of EFDD approach is to decompose appropriately the system response into a certain number of independent single degree of freedom systems (SDOF). First, spectral density matrices are predicted from raw experimental data. Singular value decomposition of the estimated spectral density matrices is then performed. The average singular values and corresponding singular vectors present modal frequencies and mode shapes of structural system, respectively. More details can be reached to the study of Brincker et al. (2000).

FIGURE 9

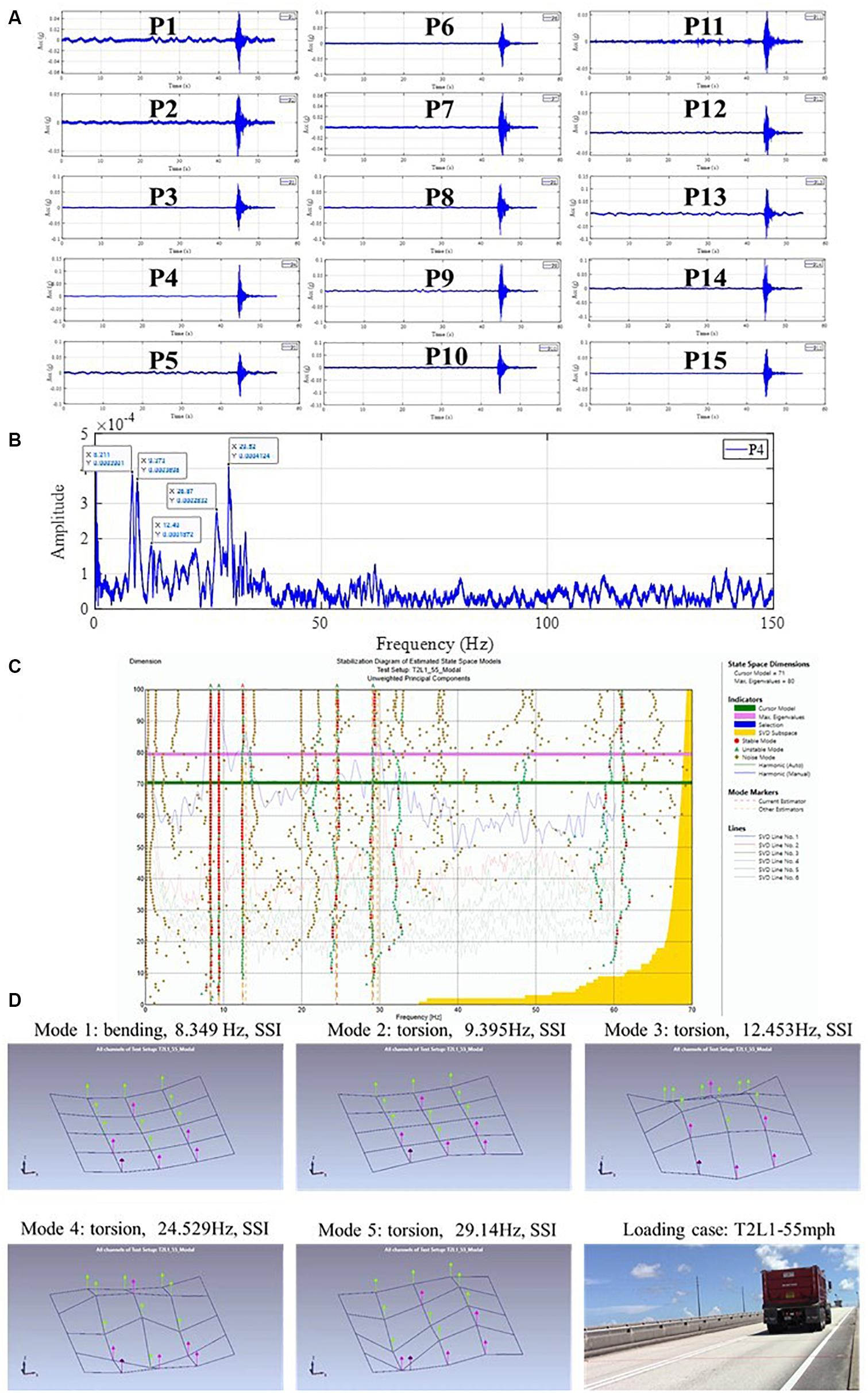
Figure 9. (A) Acceleration time-histories (B) FFT analysis of P4 acceleration (C) Stabilization diagram for SDDD (D) Estimated modal characteristics.

Figure 9D presents the estimated modal parameters and modes shapes. The frequency of the first bending mode (Mode 1) is 8.35 Hz and the frequency of the second bending mode (Mode 5) is 29.14 Hz. The others are torsion modes. The outcomes from FE analysis of the bridge were also given in Table 5 with the comparison of those from the experimental. When compared with the updated FE model of the bridge, it was observed to be difference only for the 3rd mode. However, the modal participation mass ratio of this mode (3rd mode) was obtained to be relatively lower, which means that the importance of this mode on a dynamic load can be neglected. Such data and dynamic response can be collected efficiently under operating traffic and can be evaluated to track any stiffness or boundary condition change.

TABLE 5

Table 5. Comparison of modal frequencies.

Impact Factor

Identification of the IM can be important for bridge operation to possibly reduce live load effects on the bridge. This can be achieved by improving the bridge surface, smooth expansion joints, or limiting the traffic speed. As a result, it is critical to determine the IM. In this study, the most conservative cases were selected to obtain the impact effect caused by moving loads. Table 6a shows the IM of three girders (G2, G3, and G4) calculated by the displacement data of T2L2, T2L2-35, and T2L2-55. Here, the speed of the truck increased from static cases to 35 and 55 mph. From Table 6a, it can be seen that with the increase of the speed, the IM also increases. The maximum IM obtained from all data sets is 15.94%, (Girder 3, 55 mph), which is much smaller than the value (33%) recommended by AASHTO (2017).

TABLE 6

Table 6. (a) Impact factor Truck 2 for displacement (b) Truck 1 for strain.

Table 6b shows the IM of three girders (G2, G3, and G4) calculated by the strain data of T1L1, T1L1-35, and T1L1-55. One should note that the strain data has more signal noise than displacements. In addition, the displacement data were cross-validated using computer vision data. Nevertheless, the IM from strain measurements were also obtained. The maximum IM is 22.3%, (Girder 2, 35 mph), which is also much smaller than the value (33%) recommended by AASHTO (2017). While the impact factor of IM-35 of Girder 2, 22.3%, is larger than that of IM-55, 10.5%, which is not reasonable as one would expect a higher IM under higher speed vehicle, as also shown in Table 6a with deflections. For Girder 3, the IM are almost the same and for Girder 4, they are negative. The abnormal values here might be caused by the signal noise received by the strain gauges.

Combining Table 6a and Table 6b, the author recommends that the IM using deflections can be utilized. For the truck with 35 mph velocity, the IM is 5.96% and the truck with 55 mph velocity, the IM is 15.94%.

Summary and Conclusion

In this study, static and dynamic load test were conducted for an existing in-service concrete pre-stressed girder bridge through the field test. Thus, the DF, load rating (RF), deflection limit check, modal characteristics and IM were obtained and compared with those from the conventional calculation methods and FE model. Bridge behavior characterized with these indices (e.g., DF, RF) are to be obtained as summarized in this paper to be able to make decisions about load posting, repair effectiveness, reducing traffic speed and ultimately major retrofit or replacement. A general framework for such a field study is presented along with an example on a typical highway bridge. Some of the specific findings for this bridge are summarized in the following:

• The DF of live load calculated by AASHTO standards gives more conservative results when compared with the experimental and FEM approaches. The DF for a single load case is 0.4. The conservative experimental DF with two heavy truck loads side by side gives 0.59, which is less than 0.62 of AASHTO code. This value was obtained as 0.52 from the updated FE model.

• The load-rating factor (RF) of live load calculated by AASHTO standards gives more conservative results comparing with the experimental and FEM approaches using practical DFs. Rating factors of Strength Limit I are all larger than “2.0” for HL93 trucks for single lane and RF for multilane is 1.10 which is slightly larger than AASHTO code.

• Maximum deflections in static cases and dynamic cases are within the limit calculated by (L/800) and deflections are much less than the AASHTO code based L/800.

• Impact factors among all the cases are much smaller than the one recommended by AASHTO standards (33%). We observe 16%, which was observed under fully loaded truck at 55 mph on the bridge.

• Modal testing results were obtained through the experimental data. These results were used for developing updated FE model of the bridge. The DF and RF outcomes from the updated FE model were obtained to be good agreement with those form the field test. Hence, the updated FE model can be adopted reliably for advanced analysis of the bridge.

• The study showed that bridge condition assessment could be conducted reliably fast with no need for blocking traffic/interrupting bridge’s operation. Therefore, the framework given in the study can be practically implemented to a bridge in the same bridge population. Computer vision methods and technology (camera, image, etc.) can be considerably effective for this aim.

• Based on the findings, it is shown that the bridge has sufficient load carrying capacity and the retrofitted bridge can carry large truck loads. The full truck is ∼70 kips, very comparable to 72 kips HL-93 AASHTO truck. For the load rating under multiple vehicles, the 70 kip truck was employed by means of superposition due to linearity to obtain the rating factor for the most critical condition. It is shown the AASHTO based formulations satisfy the rating factor, and even the calibrated FE based load rating is even higher. As a result, the bridge can continue to serve and no load posting is necessary based on the results given in this paper.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author COntributions

FC investigated the study. CD conducted the field studies. SB conducted the field and analytical studies. NA and MD supported field operations and document development. All authors contributed to the field studies and preparation of the manuscript.

Funding

The authors declare that this study received funding from Sanalil Construction Inc. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to acknowledge the input and field support by Mr. Manny Cabrera, PE throughout the study. Mr. Armon Rahmankhah, PE also provided field coordination for the study, which facilitated the field applications. In addition, they would like to acknowledge members of the Civil Infrastructure Technologies for Resilience and Safety (CITRS) research group at University of Central Florida for their support in creation of this work. The authors acknowledge Mr. Wesley Shattenkirk and Mr. Ivan Del Barco of CITRS for their valuable support during the field execution of the study. The second and fourth authors would like to kindly acknowledge The Scientific and Technological Research Council of Turkey (TUBITAK) through grant number 2219. The authors would also like to thank Dr. Fuat Aras for his discussions on dynamic analysis particularly related to the use of dynamic analysis software. The authors acknowledge the contributions of these individuals. The study presented here was supported by Sanalil Construction Inc. where Dr. Catbas served as the PI. The PI and his team thank Sanalil Construction for sponsoring this study.

References

AASHTO (2017). LRFD Bridge Design Specifications. Washington, DC: American Association of State Highway and Transportation Officials.

Google Scholar

AASHTO-MBE (2018). The Manual for Bridge Evaluation (MBE), 3rd Edn. Washington, DC: American Association of State Highway and Transportation Officials.

Google Scholar

Agdas, D., Rice, J. A., Martinez, J. R., and Lasa, I. R. (2016). Comparison of visual inspection and structural-health monitoring as bridge condition assessment methods. J. Perform. Const. Facil. 30:04015049. doi: 10.1061/(ASCE)CF.1943-5509.0000802

CrossRef Full Text | Google Scholar

Artemis-Modal (2015). User’s Guide, Structural Vibration Solutions. Aalborg: Artemis-Modal.

Google Scholar

Bas, S., and Catbas, F. N. (2019). “Bridge failures and mitigation using monitoring technologies,” in Developments in International Bridge Engineering, eds A. Caner, P. Gülkan, and K. Mahmoud (Cham: Springer).

Google Scholar

Brincker, R., Zhang, L., and Andersen, P. (2000). “Modal identification from ambient responses using frequency domain decomposition,” in Proceedings of the 18th International Modal Analysis Conference (IMAC), San Antonio, TX.

Google Scholar

Catbas, F. N., Ciloglu, K., and Aktan, A. E. (2005). Strategies for condition assessment of infrastructure populations: a case study on T-beam bridges. Struct. Infrastruct. Eng. J. SIE 1, 221–238. doi: 10.1080/15732470500031008

CrossRef Full Text | Google Scholar

Catbas, F. N., Dong, C., Bas, S., and Alver, N. (2019). Indian River Bridge Test, Final Project Report by UCF CITRS. Fort Lauderdale, FL: Sanalil Construction Inc.

Google Scholar

Catbas, F. N., Gokce, H. B., and Gul, M. (2012). Practical approach for estimating distribution factor for load rating: demonstration on reinforced concrete T-beam bridges. J. Bridge Eng. 17, 652–661. doi: 10.1061/(ASCE)BE.1943-5592.0000284

CrossRef Full Text | Google Scholar

Catbas, F. N., Grimmelsman, K. A., Ciloglu, S. K., Burgos-Gil, I., and Coll-Borgo, M. (2006). Static and dynamic testing of a concrete T-beam bridge before and after carbon fiber–reinforced polymer retrofit. Transport. Res. Rec. 1976, 76–87. doi: 10.1177/0361198106197600109

CrossRef Full Text | Google Scholar

Catbas, F. N., Kijewski-Correa, T., and Aktan, A. E. (2013). Structural Identification of Constructed Systems: Approaches, Methods, and Technologies for Effective Practice of St-Id. Reston: American Society of Civil Engineers.

Google Scholar

CSI (2019). SAP2000: Integrated Finite Element Analysis and Design of Structures. Berkeley, CA: Computers and Structures Inc.

Google Scholar

Davis, N. T., Hoomaan, E., Sanayei, M., Agrawal, A. K., and Jalinoos, F. (2018). Integrated superstructure-substructure load rating for bridges with foundation movements. J. Bridge Eng. 23:04018022. doi: 10.1061/(ASCE)BE.1943-5592.0001232

CrossRef Full Text | Google Scholar

Dong, C.-Z., and Catbas, F. N. (2019). A non-target structural displacement measurement method using advanced feature matching strategy. Adv. Struct. Eng. 22, 3461–3472. doi: 10.1177/1369433219856171

CrossRef Full Text | Google Scholar

Gokce, H. B., Catbas, F. N., and Dan, M. F. (2011). System reliability and load rating evaluation of a movable bridge. Transp. Res. Rec. J. Transp. Res. Board 2251, 114–122. doi: 10.3141/2251-12

CrossRef Full Text | Google Scholar

Hiasa, S., Karaaslan, E., Shattenkirk, W., Mildner, C., and Catbas, F. N. (2018). “Bridge inspection and condition assessment using image-based technologies with UAVs,” in Proceedings of the Conference on Structures Congress, (Reston: ASCE), 217–228.

Google Scholar

Omar, T., and Nehdi, M. L. (2018). Condition assessment of reinforced concrete bridges: current practice and research challenges. Infrastructures 3:36. doi: 10.3390/infrastructures3030036

CrossRef Full Text | Google Scholar

Sanayei, M., Reiff, A. J., Brenner, B. R., and Imbaro, G. R. (2016). Load rating of a fully instrumented bridge: comparison of LRFR approaches. J. Perform. Construct. Facil. 30:04015019. doi: 10.1061/(ASCE)CF.1943-5509.0000752

CrossRef Full Text | Google Scholar

Tawadrous, R., Morcous, G., and Maguire, M. (2019). Performance evaluation of a new precast concrete bridge deck system. J. Bridge Eng. 24:04019051. doi: 10.1061/(ASCE)BE.1943-5592.0001422

CrossRef Full Text | Google Scholar

Torres, V., Zolghadri, N., Maguire, M., Barr, P., and Halling, M. (2019). Experimental and analytical investigation of live-load distribution factors for double tee bridges. J. Perform. Construct. Facil. 33:04018107. doi: 10.1061/(ASCE)CF.1943-5509.0001259

CrossRef Full Text | Google Scholar

Van Overschee, P., and De Moor, B. (1996). Subspace Identification for Linear Systems: Theory - Implementation - Applications. Dordrecht: Kluwer Academic Publishers.

Google Scholar

Zaurin, R., Khuc, T., and Catbas, F. N. (2016). Hybrid sensor-camera monitoring for damage detection: case study of a real bridge. J. Bridge Eng. 21:05016002. doi: 10.1061/(ASCE)BE.1943-5592.0000811

CrossRef Full Text | Google Scholar