Long-Term Dynamic Monitoring of Medieval Masonry Towers

The aim of the paper is to present and discuss the results of an ambient vibration monitoring campaign conducted in the old town of Lucca, over the period 2015–2018. Despite the low level of the ambient vibrations in the historic center, using high-sensitivity instrumentation allowed the authors to measure and study the dynamic behavior of two medieval masonry towers: the San Frediano belfry and the Clock Tower. The main results of the dynamic identification of the towers are summarized, together with the variation over time of their dynamic properties. Some insights on the towers' response to the anthropic activities in the historic center are also presented. Finally, a finite element simulation is performed with the aim of assessing the influence of temperature variations on the towers' natural frequencies; good agreement is found between numerical and experimental results. The paper provides the scientific and technical community with a detailed report on a singular experiment in the field of architectural heritage.

Introduction

In recent decades the advantages of continuous long-term dynamic monitoring of age-old structures are become evident. This technique can supplement the results coming from the more traditional static monitoring, yielding a large amount of information on the health status of these structures and actions they are subjected to over time. Moreover, continuous monitoring provides information on the sources of vibrations and the structures' dynamic responses to environmental and anthropic actions. Moreover, through finite element (FE) model updating techniques, the experimental data can also be used to improve our knowledge of their constituent materials. Thus, continuous long-term dynamic monitoring can be regarded as a non-destructive survey of the structural health (Maeck et al., 2001; Wang et al., 2016), and recent developments in both measurement devices and computational resources have allowed extending application of this technique to historic buildings (Ramos et al., 2010; Saisi et al., 2015).

The paper presents the results of an ambient vibration monitoring campaign conducted in the old town of Lucca during the period 2015–2018. In particular, the vibrations of two historic masonry towers were measured, the San Frediano Cathedral bell tower and the Clock Tower. Similar experiments on analogous structures date back to 2010, and the authors refer to Azzara et al. (2019a) for an exhaustive report of the existing literature. The experiment presented herein possesses two-fold novelty: direct comparison of the results obtained on two similar structures in the same historic center, as well as the use, on both the towers, of two different high-sensitivity measurement devices. These devices—four tri-axial velocimeters usually employed in geophysics, and two tri-axial accelerometers developed for gravitation measurements (Iafolla et al., 2015)—used together are able to cover a wide range of frequencies, thereby enabling the measurement of a number of different vibration sources, as well as the low-frequency displacements of the tower. Together with (Azzara et al., 2018, 2019a), the paper provides the scientific and technical community with a complete, detailed report of an original experiment in the field of architectural heritage. The last part of the paper is devoted to FE modeling of the towers, with a focus on the effects of temperature on the structures' dynamic properties.

Experimental Campaigns on the Clock Tower and San Frediano Bell Tower

This section describes the dynamic monitoring conducted on two of the many towers in Lucca: the Clock Tower and the San Frediano bell tower, adjacent to the homonymous cathedral. Two kinds of instruments have been installed on the towers: four SARA SS20 seismometric stations (tri-axial velocimeters) (SARA Electronic Instruments, https://www.sara.pg.it) owned by Italy's National Institute of Geophysics and Volcanology (INGV), in the following named S.942, S.943, S.944, S.945, and two tri-axial accelerometers developed by the firm Assist in Gravitation and Instrumentation (AGI S.r.l.), in the following named S.1 and S.2. The SARA sensors were coupled with a 24-bit digitizer, and the signal was sampled at 100 Hz; the sensors were synchronized to GPS. The AGI data were acquired by a laptop at a sampling frequency of 20 Hz using a 24-bit digitizer; even if the sampling frequency corresponds to a Nyquist frequency of 10 Hz, this range is sufficient to detect the structures' main vibration modes (Pellegrini et al., 2017; Azzara et al., 2018). With regard to the main characteristics of the instruments used in the monitoring campaign, the SS20 velocity transducers have a nominal sensitivity of 200 V/(m/s), eigenfrequency of 2 Hz, and usable band from 0.1 to 100 Hz. The AGI accelerometers have an acceleration noise density of 2·10⁻⁸ g/$\sqrt{Hz}$ and usable band from 10⁻⁵ to 50 Hz. It is worth noting that together the instruments can cover a very wide band of frequencies.

In November 2017 a continuous long-term ambient vibration monitoring experiment was begun on the Clock Tower. Six instruments were fitted along the tower's height: the instrumentation was kept running on the tower up until March 2018. Figure 1 shows the layout of the sensors along the tower during the experiment: seismic station S.942 was placed at the base, collecting data from the ground, S.943 was at the height of 24 m above street level, while the remaining two stations S.943 and S.944 were placed on the bell chamber, at about 42 m above street level. The AGI stations were both installed on the upper part of the structure, S.2 at +37 m and S.1 at the bell chamber level.

FIGURE 1

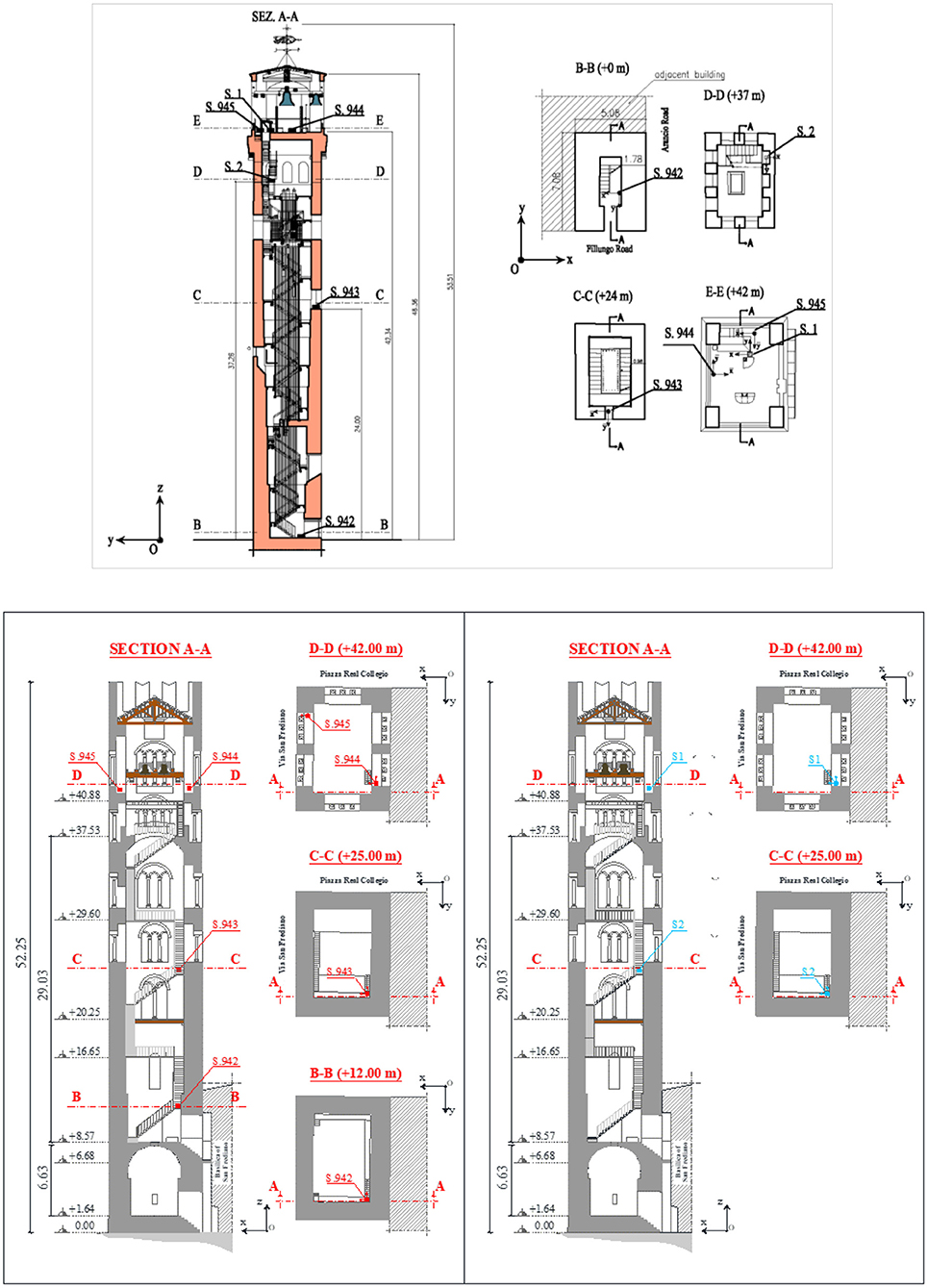
Figure 1. Sensor arrangements on the Clock Tower (top) and on the San Frediano bell tower (bottom): sensors S.942, S.943, S.944, S.945 (SARA), sensors S.1, S.2 (AGI).

The San Frediano bell tower was continuously monitored from May to June 2015 and subsequently from October 2015 to October 2016 via SARA instruments, while from March to July 2017 the tower vibrations were monitored by the two AGI devices. The instruments setup, seismic stations as well as accelerometers, is shown in Figure 1.

Dynamic Identification and Environmental Effects

A detailed description of the dynamic identification of the two towers has been published in Azzara et al. (2018) and Azzara et al. (2019a), respectively for the San Frediano bell tower and the Clock Tower. Here we limit ourselves to recalling the main findings on the dynamic behavior of the towers and their variability over the monitoring period. Table 1 highlights that the towers, both about 50 m high, have similar dynamic responses, in terms of natural frequencies and mode shapes. The frequency values change over time, with variations on the order of 5% a year, 2–3% a day. The total variations recorded on the Clock Tower are smaller than those recorded on the San Frediano bell tower, because of the different duration of the monitoring period (4 months for the Clock Tower vs. 1 year for the San Frediano bell tower). The results of the Clock Tower's highest modes exhibit wide dispersion, on account of the low level of excitation in the structure, which is located in a pedestrian area. In the case of the San Frediano bell tower the variability of the higher frequencies is in the same range as the lower ones because the structure is located in a restricted vehicular traffic area, so the excitation level is generally higher. Previous studies on the towers (Azzara et al., 2018, 2019a) highlight a correlation between natural frequencies and air temperature, with the frequencies tending to increase with temperature, a behavior confirmed by the results of numerous long-term dynamic monitoring on historic masonry towers. The daily variations of the first two natural frequencies are shown in Figure 2 for the San Frediano bell tower (from 6 to 8 June 2016) and in Figure 3 for the Clock Tower (from 6 to 8 January 2018), thus showing the towers' behavior during two different seasons (Clinton et al., 2006; Guillier et al., 2016). The curves exhibit a clear daily periodicity, with the frequencies increasing during the first half of the day (when temperatures increase) and decreasing in the latter half. As can be seen in the figures, the daily temperature variations recorded in Lucca's historical center (www.sir.toscana.it) were on the order of 10°C for summer, and 4°C for winter. Correspondingly, the frequency variations were on the order of 2% during summer, and 0.2–0.4% during winter. In both cases, the curves appear to be shifted by about 1–2 h with respect to the temperature trend, an effect of the tower's thermal inertia. This phenomenon also guarantees that the reported effects on the frequencies are not attributable to the experimental apparatus.

TABLE 1

Table 1. Mean values f_i of the natural frequencies measured by the instruments during the monitoring period and their variation Δ_i= (${\text{f}}_{\text{i}}^1$-${\text{f}}_{\text{i}}^{99}$)/${\text{f}}_{\text{i}}^1$, where ${\text{f}}_{\text{i}}^1$ and ${\text{f}}_{\text{i}}^{99}$ represent the first and 99th percentile of the dataset, respectively.

FIGURE 2

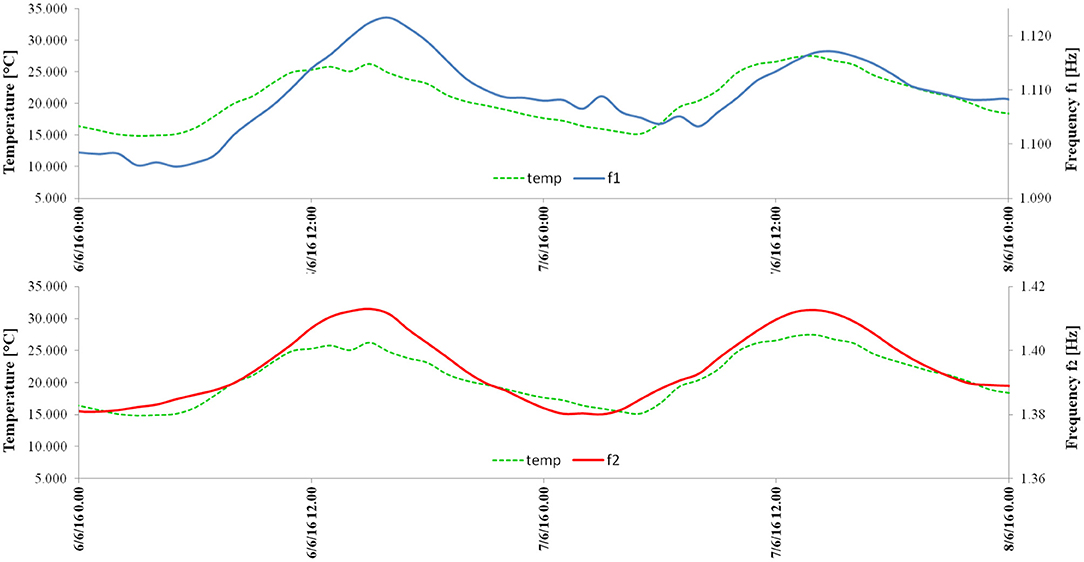
Figure 2. San Frediano bell tower: the first and second natural frequencies plotted vs. time, from 6 to 8 June 2016. The dashed green line indicates the air temperature.

FIGURE 3

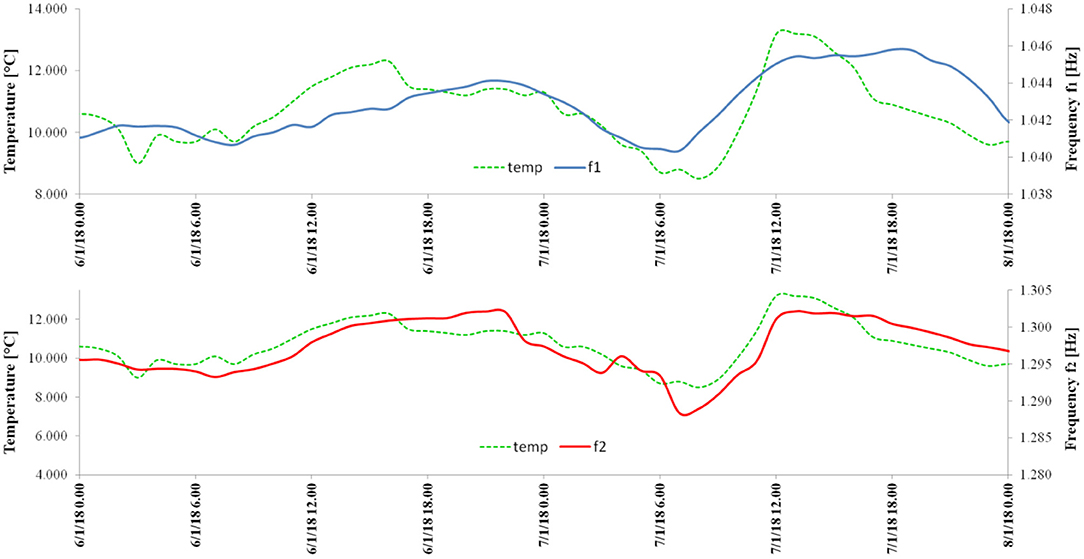
Figure 3. Clock Tower: the first and second natural frequencies plotted vs. time, from 6 to 8 January 2018. The dashed green line indicates the air temperature.

The correlation found between frequencies and temperatures for longer periods is shown in section Non-linear FE Modeling and Experimental Results, where a numerical simulation is also performed with the aim of providing a mechanical interpretation of the experimental evidence.

Information on the daily movements of the towers can be extracted from the data from the AGI instruments, after downsampling of the signal from 20 to 1 Hz. In particular, Figure 4 shows the zero-meaned low-frequency accelerations of the tower measured over 3 days, from 7 to 9 June 2017. The signals exhibit a clear daily periodicity; the figure reports the signals of both the AGI stations, which were placed at different heights along the tower. The good superposition of measurements acquired at different heights demonstrates that the recorded signals actually refer to rigid movements of the tower with respect to the vertical direction. The temperature values measured by the S.1 instrument are also reported in the figure (dashed line). As for the frequencies, also in this case the acceleration signal is shifted (by about 2–3 h) with respect to the temperature, thus demonstrating that the recorded oscillations are not caused by any direct effect of the temperature on the instrument. Figure 5 reports the daily movements of the tower recorded by S.1 in the x-y plane. This information can be easily extracted from Figure 4: in fact, for small oscillations, the modulus of the horizontal acceleration expressed in g coincides with the inclination angle of the tower in radians. The restraining effects of the adjacent Basilica (located in the -x, -y quarter, see Figure 1) are clearly visible in the diagram, whose shape differs from those obtained for isolated towers (Burland and Viggiani, 1994). Similar analysis was performed for the Clock Tower and is shown in Azzara et al. (2019a). The San Frediano bell tower seems to undergo daily movements larger than the Clock Tower, probably because surface and basement of the former are more exposed to the sun and its lateral constraints less effective. The monitoring period with the AGI instruments was too short to allow for measurement of quasi-permanent or seasonal trends in the tower's movements. In any case, these data should be confirmed by other classical devices for static measurements and, in particular, by measurements at the ground.

FIGURE 4

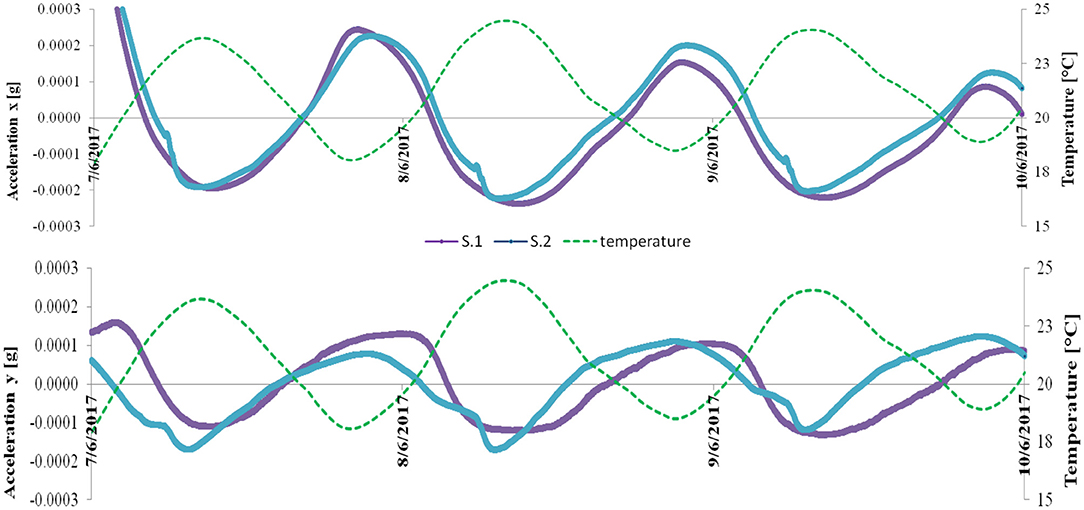
Figure 4. San Frediano bell tower: low-frequency accelerations along the x and y directions, from 7 June to 10 June 2017. The purple line indicates the signal measured by S. 1 (+42.00 m), cyan line is for the signal measured by S.2 (+25 m), and the dashed green line is for the temperature measured by the S.1 device.

FIGURE 5

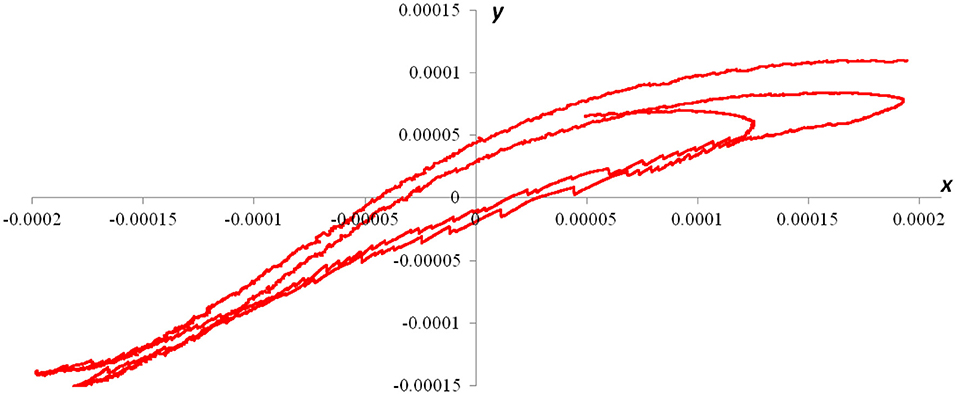
Figure 5. San Frediano bell tower: daily tilt (rad) of the tower along the x and the y directions, from 8 to 9 June 2018.

Effects of Anthropic Factors

Long-term ambient vibrations monitoring of a building can provide important information not only about its dynamic behavior (natural frequencies, mode shapes, and damping ratios) over time, but also on the main sources of vibration and the amplitude over time of the structural response. Usually this is done by processing the data collected by numerical methods known as operational modal analysis (OMA) techniques, through which it is possible to estimate a structure's dynamic properties under the hypothesis of unknown input forces, which are modeled as white noise. Another way to assess the effects of the environmental and anthropic factors on a structure is to resort to spectrograms, which allow for characterizing the dynamic behavior of a system (limited to natural frequencies) and investigating its variation over time, without requiring the use of OMA methods.

Figure 6 shows the spectrogram of the station S.945 (at an altitude of 42 m) recorded on the San Frediano bell tower from 29 October to 8 November 2015. The image is made up of three spectrograms of the recorded signal, one for each direction: x (upper), y (middle) and z (lower). In the figure, the tower's first two main frequencies (corresponding to bending mode shapes) are clearly identifiable: f ₁ = 1.10 Hz in the x direction and f ₂ = 1.39 Hz in the y direction. On 31 October and 1 November, there is an evident increase in the power spectral energy (characterized by a −60 dB peak) of the signal recorded on the tower. This is due to the crowds of people around the city during the Lucca Comics Festival, Europe's most important event in the field of comics, animation, role-playing, video games and fantasy, which takes place every year in Lucca, attracting people from all over the world (Barsocchi et al., 2018). In particular, a major concert at the bastion called Baluardo S. Donato (Figures 6, 7), about 1 km far from the tower, is the probable cause of the 7:00 pm peak in the spectrogram. Furthermore, an energy increase is exhibited throughout the entire signal frequency range, meaning that the event was able to excite even the tower's higher mode shapes. Another peak distinguishable on 1 November is presumably due to a Marching Band which convened around 1:00 pm from Piazza Real Collegio, the square behind the church. Further detailed scrutiny of the spectrograms reveals two other peaks occurring on 7 November (Saturday) at 6:00 p.m. and on 8 November at 11:00 am (Sunday), which were due to the swinging of the bells during ceremonies in the Basilica. Moreover, every day from Monday to Friday at 7:00 am a regularly occurring peak is visible in the spectrogram (see Figure 8). This phenomenon can be attributed to the garbage truck that passes by the tower every working day morning at 7:00 a.m.

FIGURE 6

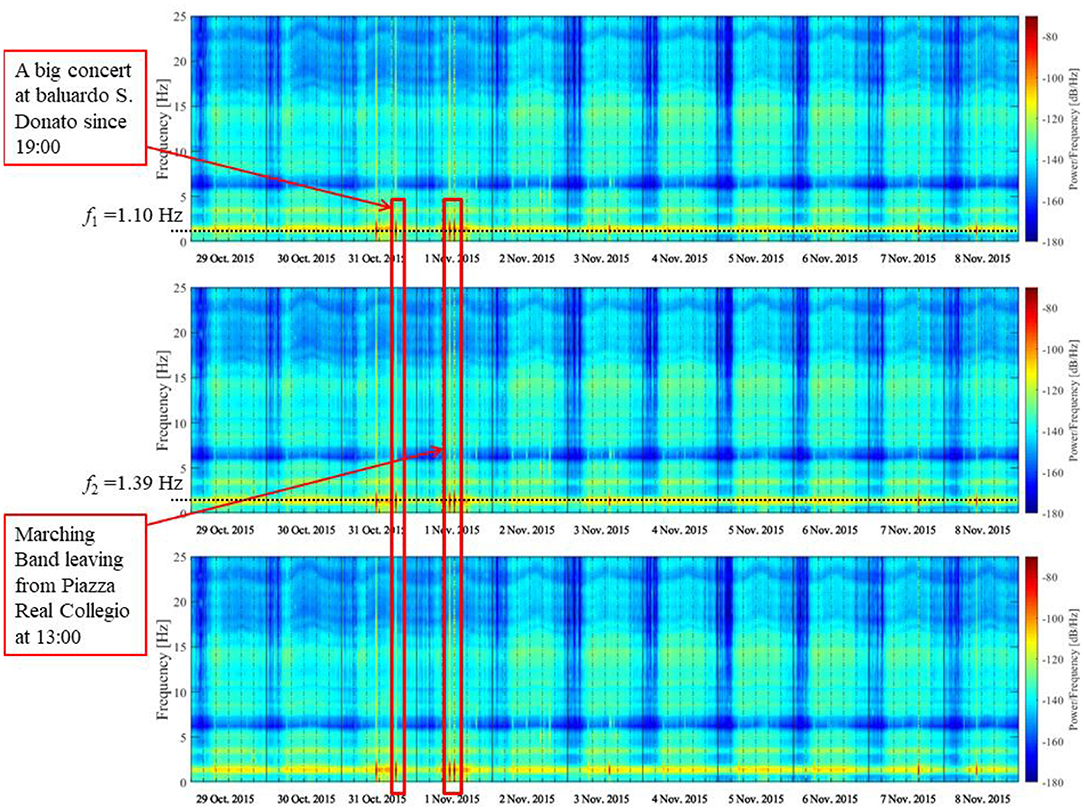
Figure 6. San Frediano bell tower: spectrogram of the signal recorded by S.945 (+42.00 m) in the x (upper), y (middle) and z (lower) directions from 29 October to 8 November 2015.

FIGURE 7

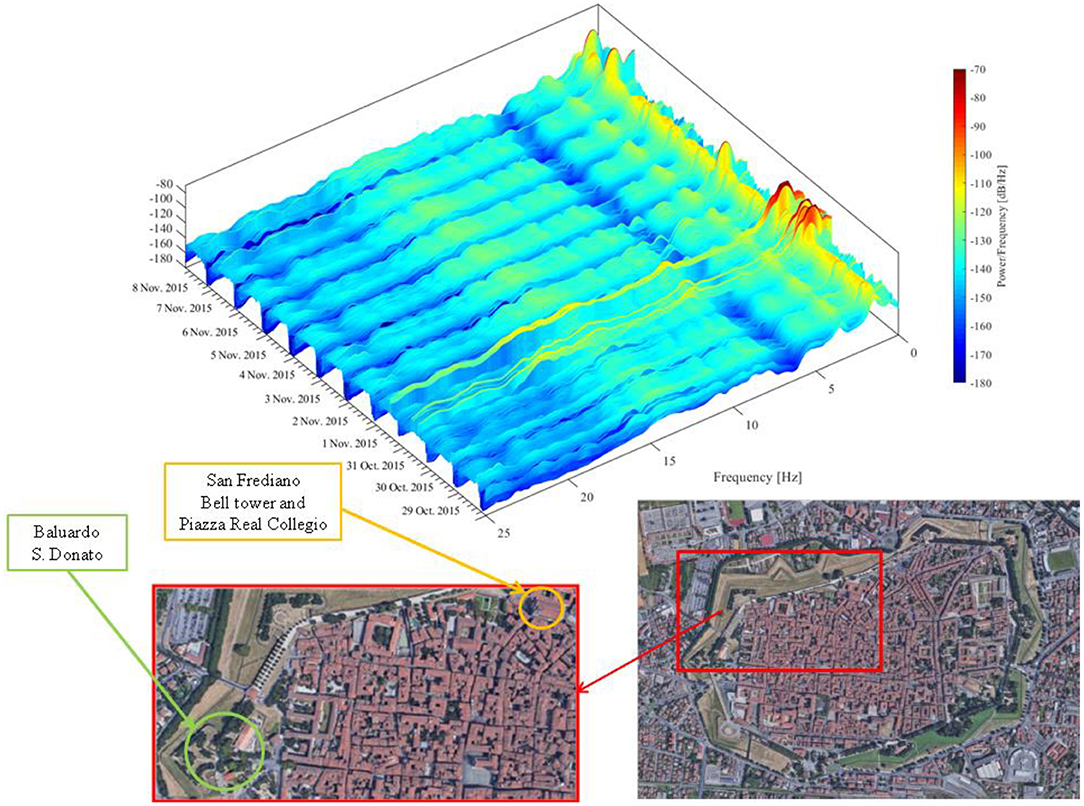
Figure 7. San Frediano bell tower: three-dimensional spectrogram of the signal recorded by S.945 (+42.00 m) in the x direction from 29 October to 8 November 2015.

FIGURE 8

Figure 8. San Frediano bell tower: magnification of the spectrogram of the signal recorded by S.945 (+42.00 m) in the x direction from 2 to 8 November 2015.

With regard to the amplitude of the tower response over time, Figure 9 shows the maximum daily velocities recorded on the top of the tower by the S.944 seismic station (+42 m), from 29 October to 31 December 2015, while Figure 10 shows the maximum daily accelerations recorded on the top of the tower by the S.1 seismic station (+42 m), from March to June 2017, after high-pass filtering of the signal (with cutoff frequency of 0.1 Hz). The most relevant values correspond to the swinging of the bells on Saturday and Sunday, with the maximum values in the direction of the bell's swinging (y in the current reference), on the order of 1–1.5 mm/s for the velocities, 0.01–0.015 m/s² for accelerations. Atypical amplification of the tower's movements was recorded in the periods 29 October to 1 November 2015 (Lucca comics), 17–18 November 2015 (celebrations of St Frediano), 24–25 December (Christmas), up to 3 mm/s, 16 April 2017 (Easter), and 4 June 2017 (Pentecost), up to 0.025 m/s². All these events (with the exception of Lucca Comics, whose effects on the tower's vibrations were due to the crowds in the square) corresponded to the full swinging motion of the San Frediano bells. The wind affected the tower to a lesser extent and the vibrations reached relevant values only for quite high wind velocities, over 50 Km/h (for example, on 21 November 2015 the maximum recorded velocity on the tower was on the order of 5 10⁻⁴ m/s, against a maximum wind velocity of 60 km/h, while on 28 June 2017 the maximum acceleration on the tower was about 0.01 m/s² corresponding to a maximum wind velocity of 56 km/h); the correlation between the maximum recorded values and the wind speed is in fact very low.

FIGURE 9

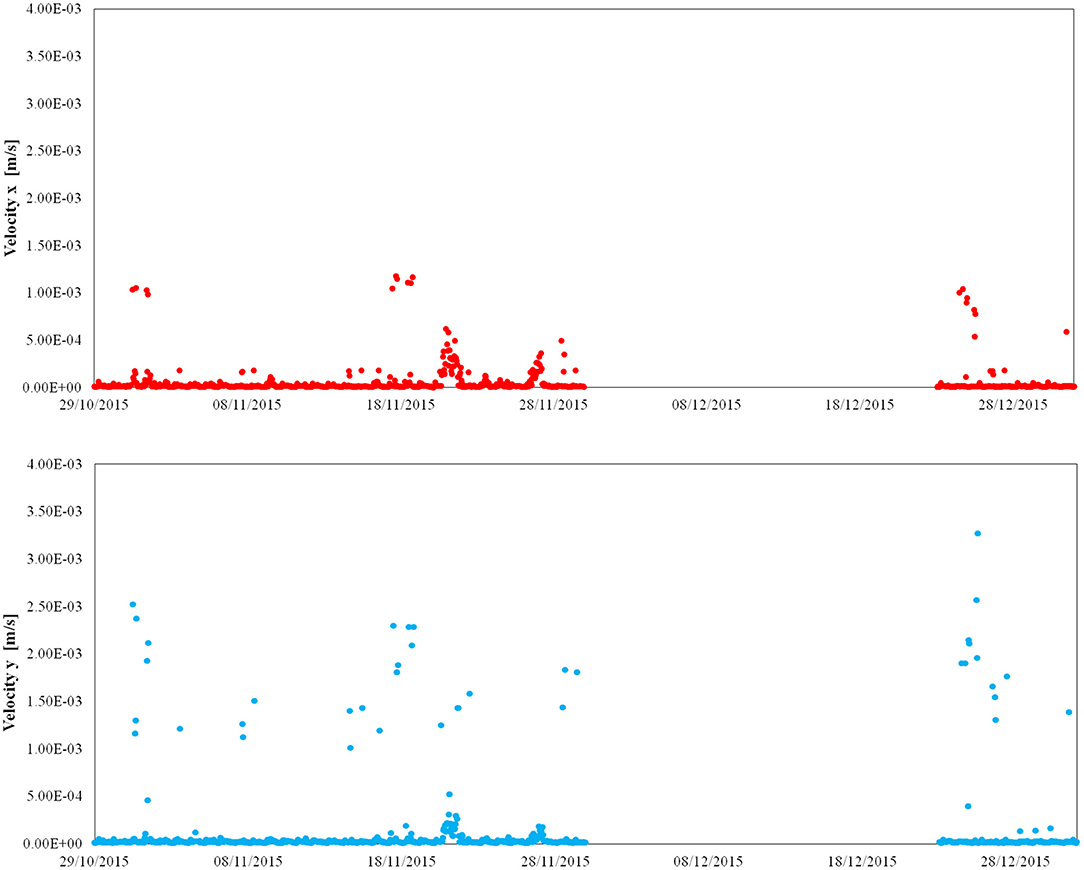
Figure 9. San Frediano bell tower: maximum absolute values per hour of the velocities recorded by the S.944 seismic station (+42 m) in the x and y directions from 29 October to 31 December 2015.

FIGURE 10

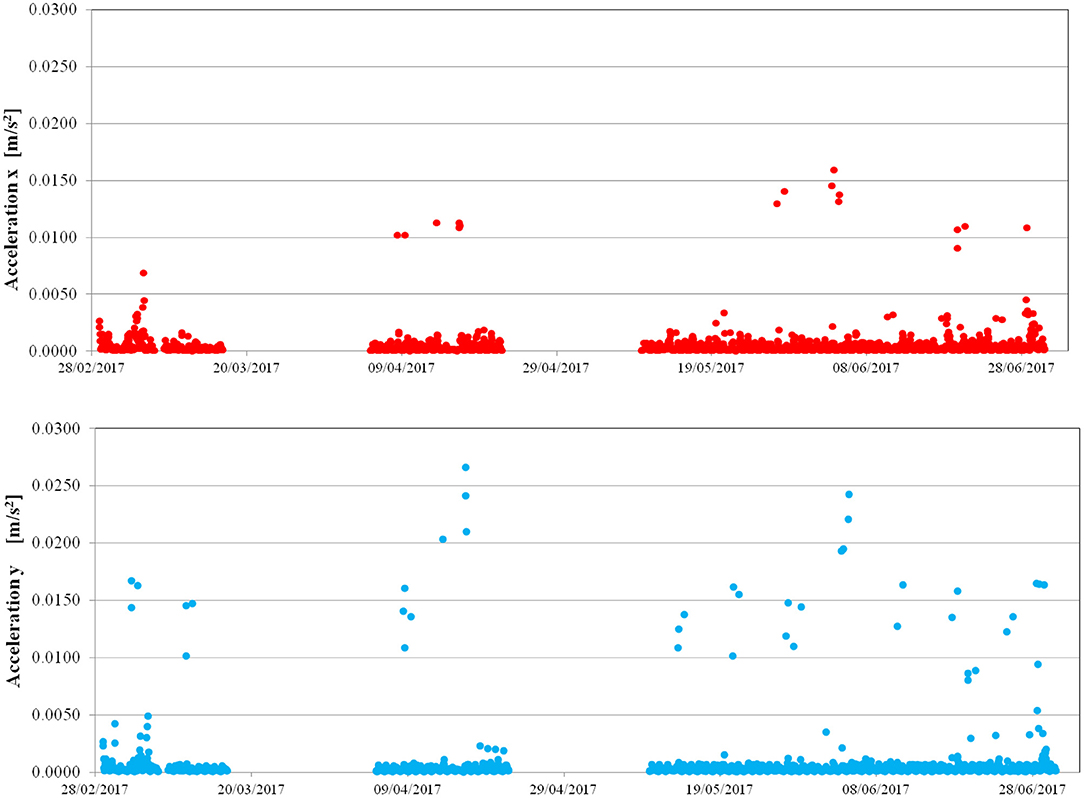
Figure 10. San Frediano bell tower: maximum absolute values per hour of the accelerations recorded by the S.1 instrument (+42 m) in the x and y directions from 28 February to 1 June 2017.

Measurements on the Clock Tower depicted a different situation, as shown in Figure 11 (Azzara et al., 2019a): the maximum acceleration values are caused by wind, while the bells, which are not swung but rang by hammers every quarter hour, induce on the tower accelerations which are about 10 times lower than those measured on the San Frediano bell tower.

FIGURE 11

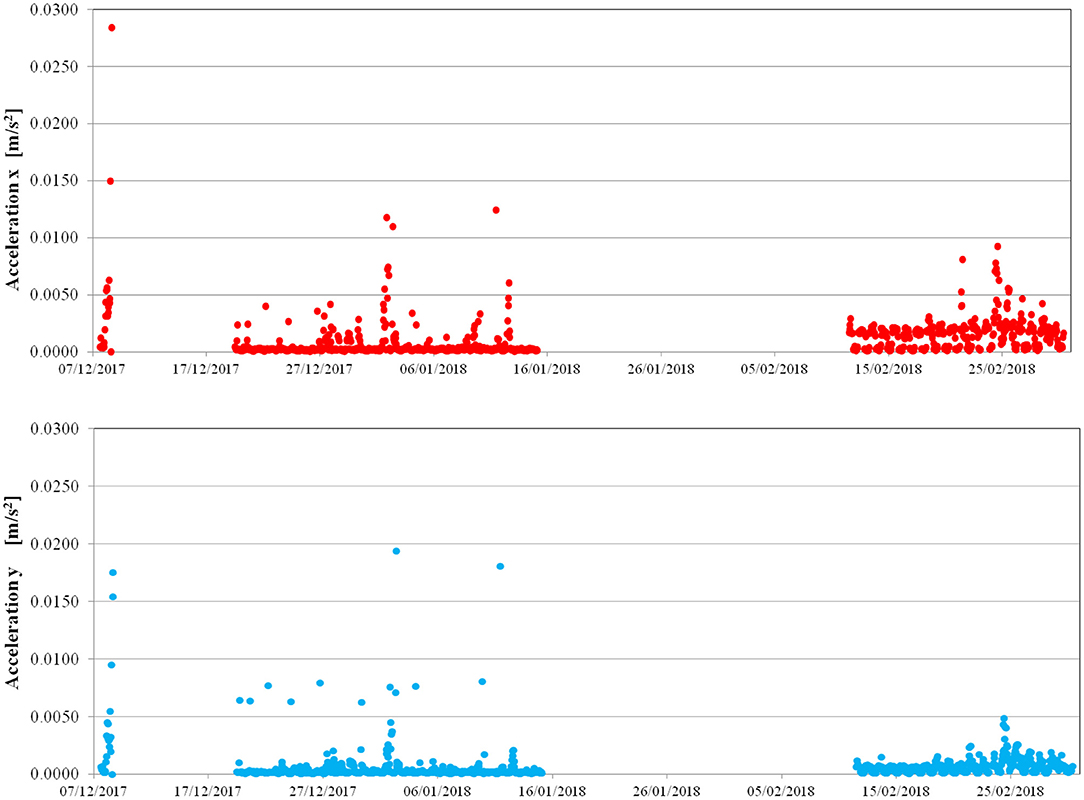
Figure 11. Clock Tower: maximum absolute values per hour of the accelerations recorded by the S.2 instrument (+37 m) in the x and y directions from 7 December 2017 to 2 March 2018.

Non-Linear Fe Modeling and Experimental Results

This section is dedicated to numerical simulation of the effects of temperature on the dynamic behavior of masonry towers. In fact, as pointed out in the previous sections, several long-term ambient vibrations campaigns have demonstrated that the natural frequencies of monumental masonry buildings are influenced by environmental factors such as temperature, humidity, etc. (Ramos et al., 2010; Saisi et al., 2015; Gentile et al., 2016, 2019; Ubertini et al., 2016, 2017; Baraccani et al., 2017; Masciotta et al., 2017; Tsogka et al., 2017; Barsocchi et al., 2019). In particular, for masonry towers the amplitudes of natural frequencies are increasing functions of temperature, and for the structures monitored in Saisi et al. (2015) and Azzara et al. (2018) their relative yearly differences are on the order of 5%. An explanation for this behavior is currently found in the closing of the micro-cracks in masonry, due to the thermal expansion.

Here we recall the procedure proposed in Girardi et al. (2019) and adopted in Girardi et al. (2017) to take into account the strain field due to thermal variations and assess its influence on the dynamic properties of masonry structures. Masonry is modeled as a non-isothermal masonry–like material, whose constitutive equation has been introduced in Lucchesi et al. (2008) and implemented in NOSA-ITACA (Girardi et al., 2015).

Masonry Solids Subjected to Thermal Loads

Masonry is modeled as an isotropic non-linear elastic material with zero tensile strength and infinite compressive strength (Del Piero, 1989). Let us denote by θ ∈ [θ₁, θ₂], with θ₁ > 0, the temperature and θ₀ ∈ [θ₁, θ₂] the reference temperature. We assume that the thermal dilatation due to the temperature variation θ − θ₀ is the spherical tensor α(θ − θ₀)I, where α is the linear coefficient of thermal expansion and I the identity tensor. It is possible to prove that for every infinitesimal strain tensor E and θ ∈ [θ₁, θ₂], there exists a unique triplet (T, E^e, E^f) of symmetric tensors such that E − α(θ − θ₀)I is the sum of the elastic strain E^e and the positive semidefinite fracture strain E^f, and that the Cauchy stress T, negative semidefinite and orthogonal to E^f, depends linearly and isotropically on E^e, through the Young's modulus E and Poisson's ratio ν (Lucchesi et al., 2008). Here, in view of the modest amplitude of the temperature range considered in the analysis, the elastic constants E and ν, which in general are functions of temperature (Padovani et al., 2000), do not depend on θ. T is the stress corresponding to strain E and temperature θ. Masonry-like materials, which can be generalized to take into account weak tensile strength and limited compressive strength, are then characterized by the stress function $\overline{\text{T}}$ given by

$\begin{array}{ll}\bar{\text{T}}(\text{E},\theta )=\text{T},\text{for }\text{E}\text{ symmetric tensor and }\theta \in \left[{\theta }_1,{\theta }_2\right],& (1)\end{array}$

whose explicit expression is reported in Lucchesi et al. (2008), along with its derivative ${\overline{\text{T}}}_{\text{E}}(\text{E},\theta )$ with respect to E.

The equilibrium problem of masonry-like solids subjected to both mechanical and thermal loads is addressed in Lucchesi et al. (2008), which describes the procedure implemented in the finite element code NOSA-ITACA with the aim of determining its numerical solution. In Girardi et al. (2017), the authors presented an algorithm implemented in NOSA-ITACA, which enables calculating the frequencies and mode shapes of masonry constructions, while taking into account the presence of cracks due to mechanical and thermal loads. More precisely, given the masonry structure, which is discretized into finite elements, and given its materials properties, together with the kinematic constraints and loads (both mechanical and thermal) acting on it, the algorithm is based on a linear perturbation about the solution to the equilibrium problem (Pellegrini et al., 2018) and consists of the following steps.

Step 1. The non-linear equilibrium problem of the structure subjected to the given loads, temperatures and boundary conditions is solved through a Newton-Raphson scheme, and its numerical solution, consisting of displacements, strain and stress fields, calculated. The tangent stiffness matrix K_T is calculated using the derivative of the stress with respect to the strain ${\overline{\text{T}}}_{\text{E}}(E,\theta )$.

Step 2. The generalized eigenvalue problem

$\begin{array}{ll}{\text{K}}_{\text{T}}\varphi ={\omega }^2\text{M}\varphi & (2)\end{array}$

with M the mass matrix, is solved and the natural frequencies f_i = ω_i/2π and mode shapes ϕ_i calculated. Thus, the natural frequencies and mode shapes turn out to be functions of temperature and can be compared with their experimental counterparts.

Comparison of Numerical and Experimental Outcomes

The procedure described in subsection Masonry Solids Subjected to Thermal Loads has been applied to the Clock and San Frediano towers, and numerical results compared with experimental data.

The Clock Tower

The finite element model of the tower consists of 11,383 brick elements (www.nosaitaca.it/software). Model updating procedures, aimed at fitting the experimental frequencies, have allowed us to determine the optimal values, E = 4.5 · 10⁹ Pa and ρ = 2100 kg/m³, for the Young's modulus and mass density of the masonry, which is modeled as a homogeneous masonry-like material with Poisson's ratio ν = 0.2 and zero tensile strength. The reference temperature is θ₀ = 5°C and the thermal expansion coefficient α = 6.0 · 10⁻⁶(°C)⁻¹. The adjacent buildings about the tower on two sides along the Fillungo and Arancio roads for a height of about 12 m and constitute asymmetric boundary conditions. The tower is subjected to its own weight and five incremental homogeneous temperature variations Δθ increasing from − 10 to 10°C. For each thermal load increment, the solution to the equilibrium problem is determined and the natural frequencies f₁ and f₂ are calculated, along with the corresponding mode shapes ϕ₁ and ϕ₂.

The influence of temperature on the tower's dynamic behavior is shown in Figure 12, which presents the correlation of the first two natural frequencies with air temperature in Lucca's historic center (https://www.sir.toscana.it/). As found in similar long-term vibration monitoring campaigns on historical towers (Cabboi et al., 2017; Ubertini et al., 2017), as well as on the San Frediano bell tower (Azzara et al., 2018), frequencies tend to increase with temperature. This behavior is confirmed from a numerical point of view by the trend of black squares in Figure 12, which represent the frequency values yielded by the non-linear FE analysis of the Clock Tower conducted by assigning incremental thermal variations. The numerical simulation supports the hypothesis that an increase in temperature induces a reduction in the fracture strains within the masonry, thus increasing the structure's global stiffness. Similar behavior is described in Guidi (1906), where the influence of temperature on masonry constructions is reported, including the opening (closing) of cracks in bridges and vaults during the winter (summer).

FIGURE 12

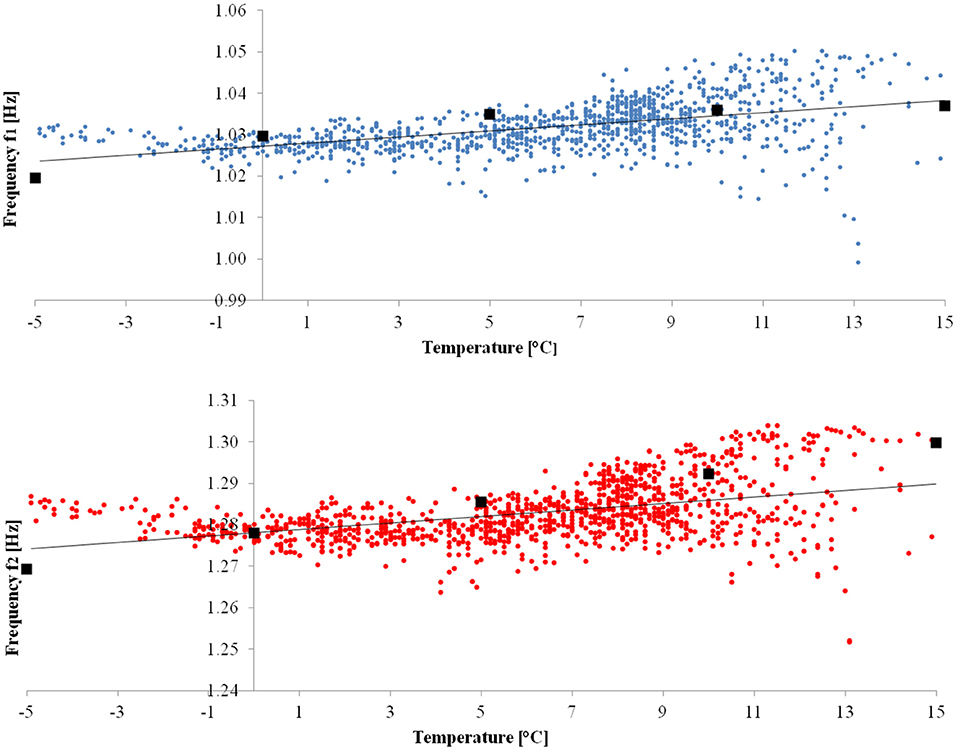
Figure 12. Clock Tower: The first (blue) and second (red) experimental frequencies [Hz] vs. temperature [°C] and their respective regression lines (black). Black squares are the values of the numerical frequencies calculated at assigned thermal variations.

With regard to negative temperature values, Figure 12 shows that experimental frequencies tend to increase when the temperature decreases. This phenomenon was mainly observed in the latter part of February 2018, when temperatures consistently dropped below zero (Azzara et al., 2019a). The behavior below freezing has also been reported for similar weather conditions in Ubertini et al. (2017) and Cabboi et al. (2017), where increasing frequencies when the temperature goes below zero have been ascribed to the fact that ice tends to close micro-cracks and hence stiffen the masonry or to site effects (Guegen et al., 2016). The constitutive equation adopted in NOSA-ITACA is able to model the opening of cracks for negative θ, as confirmed in Figure 12, but unable to take into account the stiffening effect of ice. Thus, as expected, numerical frequencies decrease as temperature decreases.

It is worth noting that thermal loads do not affect mode shapes, which do not change significantly as temperature varies; this is also confirmed by the monitoring campaigns conducted by the authors.

The San Frediano Bell Tower

Unlike the Clock Tower, which was continuously monitored for only 5 months (from November 2017 to March 2018), the San Frediano bell tower was studied for a full year (from October 2015 to October 2016). The availability of such a complete dataset has allowed us to investigate the behavior of the structure for a wide range of temperature, from around − 5°C in winter to + 35°C in summer. The San Frediano tower has been analyzed in Azzara et al. (2018) and Azzara et al. (2019b), where the results of the experimental campaign conducted from October 2015 to October 2016 are reported. The finite element model of the tower consists of 18,645 shell elements. The structures of the adjacent Basilica are taken into account in the model via constraints applied along two corners of the tower, up to about 13 m. Model updating procedures, aimed at fitting the experimental frequencies calculated via operational modal analysis techniques, have allowed us to determine the optimal values, E = 4.25 · 10⁹ Pa and ρ = 2000 kg/m³, for the Young's modulus and mass density of the masonry, which is modeled as a homogeneous masonry-like material with Poisson's ratio ν = 0.2 and tensile strength σ_t = 0.04 MPa. The reference temperature is θ₀= 15°C (equal to the average annual temperature) and the thermal expansion coefficient α = 6.0· 10⁻⁶(°C)⁻¹.

The tower is subjected to its own weight and five incremental homogeneous temperature variations θ ranging from − 20°C to 20°C. For each thermal load increment, the solution to the equilibrium problem is determined, and the natural frequencies f₁ and f₂ are calculated together with the corresponding mode shapes ϕ₁ and ϕ₂.

The influence of temperature on the dynamic behavior of the tower is highlighted in Figure 13, which shows the correlation of the first two natural frequencies with air temperature. As already pointed out in Azzara et al. (2018), frequencies tend to increase with temperature. The black squares in Figure 13 are the frequency values furnished by a non-linear FE analysis of the tower conducted by assigning incremental thermal variations. In order to obtain an effective visualization of the crack distribution in the tower, let us consider the elemental ratio

$\begin{array}{ll}{e}^f=\frac{\int tr\left({\text{E}}^f\right)dV}{V}& (3)\end{array}$

between the integral of the trace of the fracture strain on the element and the element's volume.

FIGURE 13

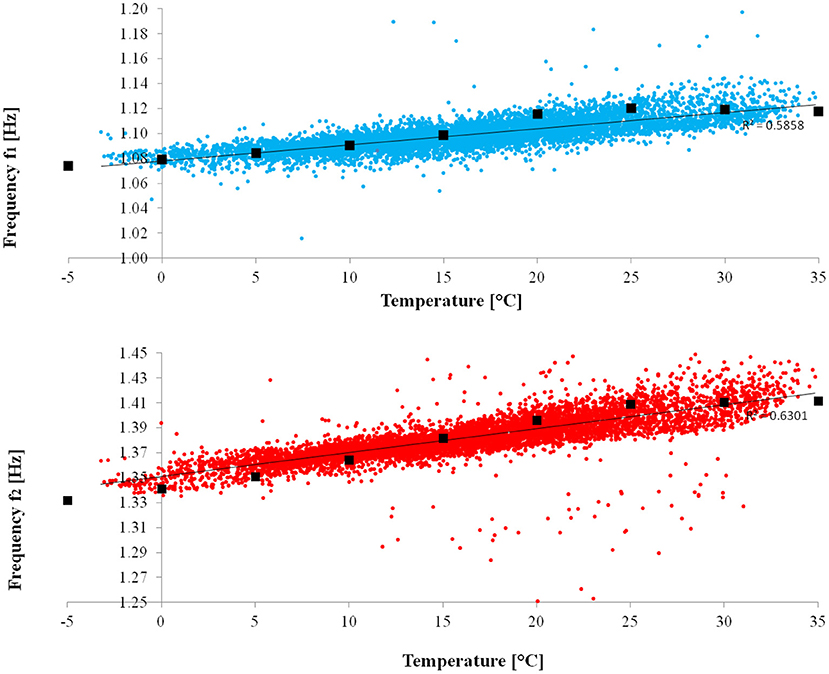
Figure 13. San Frediano bell tower: The first (blue) and second (red) experimental frequencies [Hz] vs. temperature [°C] and their respective regression lines (black). Black squares are the values of the numerical frequencies calculated at assigned thermal variations.

Figure 14 shows the quantity e^f as a function of the height h, for Δθ = − 20, 0, and 20°C (from the top). For Δθ = 0°C the distribution and low values of e^f indicate a limited level of cracking within the tower. Fracture strains are concentrated around the bifora and trifora windows, in the two vaults supporting the bell chamber (+40.00 m) and the first slab (+8.00 m), and in the regions constrained by the adjacent Basilica. When the temperature decreases (Δθ = − 20°C), e^f increases in the tower's lower region, between 0 and 13 m; on the other hand, when θ = 20°C, e^f decreases in the same region. The figure also highlights the effect of the adjacent Basilica, whose action on the tower likely depends on seasonal thermal variations, as well as the effects of temperature on the vaults, which act as diaphragms for the tower's structure. As for the Clock Tower, thermal loads do not significantly affect mode shapes, which do not change as temperature varies.

FIGURE 14

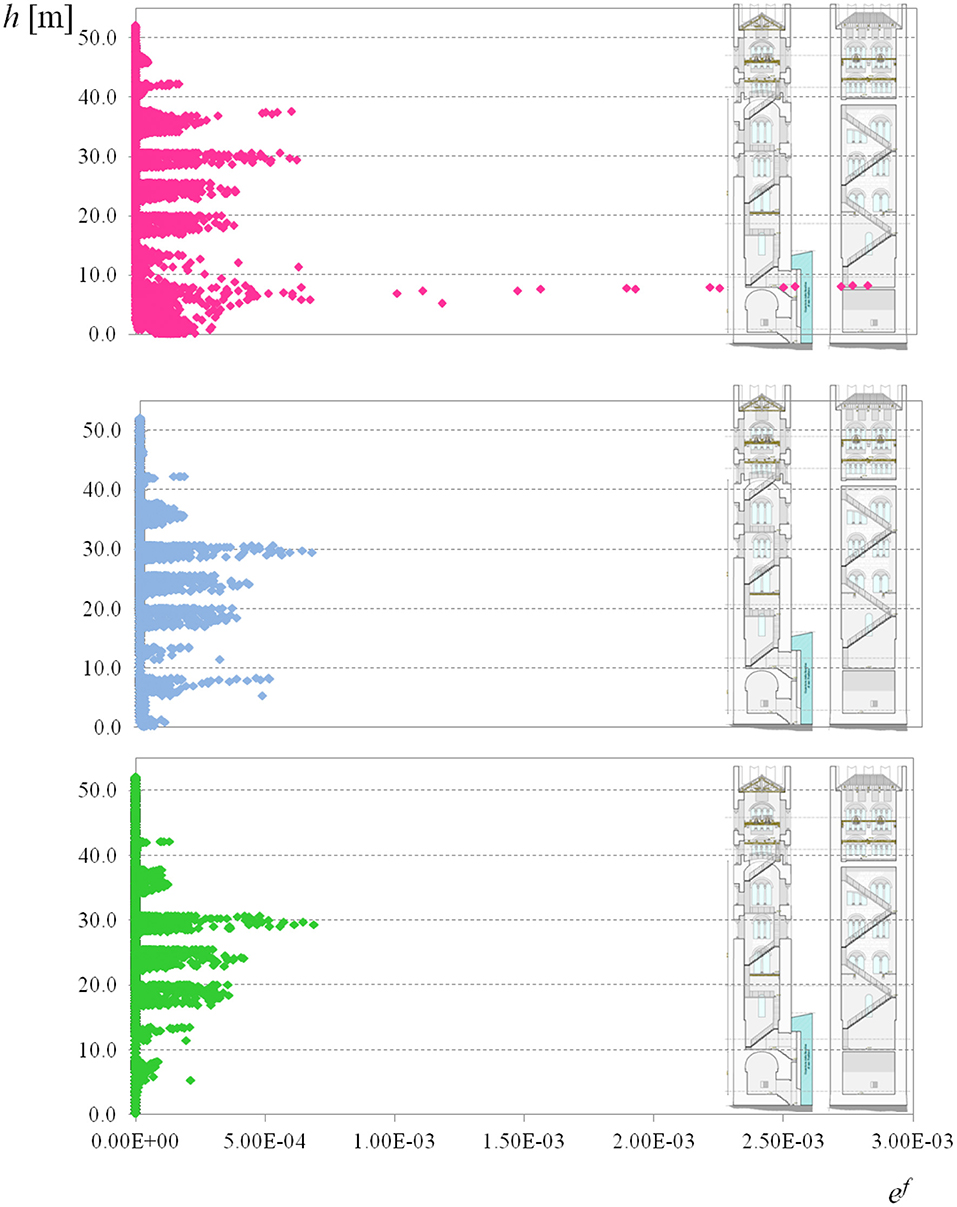
Figure 14. San Frediano bell tower: plot of e^f vs. the tower's height h, for Δθ = −20°C (pink), Δθ = 0°C (blue) and Δθ = +20°C (green). The reference temperature is θ₀ = 15°C.

Conclusions

The paper presents results from a long-term dynamic monitoring campaign of two historic masonry towers in Lucca. The effects of environmental factors and anthropic activities on the structures under consideration have been highlighted. The last part of the paper studies the effects of thermal variations on the towers' frequencies via non-linear FE modeling, and the results of the numerical models are compared with experimental data.

The following conclusions can be drawn:

- the availability of different high-sensitivity devices allows for cross-validation of the data and measurements over a broad range of frequencies;

- the main sources of vibration for the structures under consideration are the wind for the Clock Tower, the swinging of the bells for the San Frediano Cathedral belfry;

- major public events and movement of crowds in the historic center are clearly recognizable in the towers' dynamic responses;

- the towers' dynamic responses are influenced by temperature and thermal insulation, on both the daily and yearly scale, with natural frequencies generally increasing with temperature;

- both the towers exhibit daily movements, which can be recognized in their low-frequency dynamic response;

- non-linear FE modeling, which can take into account the weak tensile strength of masonry, has enabled effectively simulating the influence of thermal variations on the towers' dynamics.

Data Availability Statement

The datasets analyzed in this article are not publicly available. Requests to access the datasets should be directed to bWFyaWEuZ2lyYXJkaSYjeDAwMDQwO2lzdGkuY25yLml0.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This research has been partially supported by the Fondazione Cassa di Risparmio di Lucca (TITANIO project, 2016–2018) and the Region of Tuscany and MIUR (MOSCARDO project, FAR-FAS 2014, 2016–2018). These supports are gratefully acknowledged.

Conflict of Interest

VI was employed by the company AGI srl.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Azzara, R. M., De Roeck, G., Girardi, M., Padovani, C., Pellegrini, D., and Reynders, E. (2018). The influence of environmental parameters on the dynamic behaviour of the San Frediano bell tower in Lucca. Eng. Struct. 156, 175–187. doi: 10.1016/j.engstruct.2017.10.045

CrossRef Full Text | Google Scholar

Azzara, R. M., Girardi, M., Iafolla, V., Lucchesi, D., Padovani, C., and Pellegrini, D. (2019a). Ambient vibrations of age-old masonry towers: results of long-term dynamic monitoring in the historic centre of Lucca. Int. J. Archit. Herit. 1–17. doi: 10.1080/15583058.2019.1695155

CrossRef Full Text | Google Scholar

Azzara, R. M., Girardi, M., Padovani, C., and Pellegrini, D. (2019b). Experimental and numerical investigations on the seismic behaviour of the San Frediano bell tower in Lucca. Ann. Geophys. 62:SE342. doi: 10.4401/ag-8025

CrossRef Full Text | Google Scholar

Baraccani, S., Palermo, M., Azzara, R. M., Gasparini, G., Silvestri, S., and Trombetti, T. (2017). Structural interpretation of data from static and dynamic structural health monitoring of monumental buildings. Key Eng. Mater. 747, 431–439. doi: 10.4028/www.scientific.net/KEM.747.431

CrossRef Full Text | Google Scholar

Barsocchi, P., Bartoli, G., Betti, M., Girardi, M., Mammolito, S., Pellegrini, D., et al. (2019). Wireless sensor networks for continuous structural health monitoring of historic masonry towers. Int J Archit herit.

Google Scholar

Barsocchi, P., Cassara, P., Mavilia, F., and Pellegrini, D. (2018). Sensing a City's State of Health: structural monitoring system by internet-of-things wireless sensing devices. IEEE Consum. Electr. M. 7, 22–31. doi: 10.1109/MCE.2017.2717198

CrossRef Full Text | Google Scholar

Burland, J. B., and Viggiani, C. (1994). Osservazioni sul comportamento della Torre di Pisa. Rivista Italiana Geotecnica. 179–200.

Google Scholar

Cabboi, A., Gentile, C., and Saisi, A. (2017). From continuous vibration monitoring to FEM-based damage assessment: application on a stone-masonry tower. Constr. Build. Mater. 156, 252–265. doi: 10.1016/j.conbuildmat.2017.08.160

CrossRef Full Text | Google Scholar

Clinton, J. F., Case Bradford, S., Heaton, T. H., and Favela, J. (2006). The observed wander of the natural frequencies in a structure. Bull. Seismol. Soc. Am. 96, 237–257. doi: 10.1785/0120050052

CrossRef Full Text | Google Scholar

Del Piero, G. (1989). Constitutive equation and compatibility of the external loads for linearly-elastic masonry-like materials. Meccanica 24, 150–162. doi: 10.1007/BF01559418

CrossRef Full Text | Google Scholar

Gentile, C., Guidobaldi, M., and Saisi, A. (2016). One-year dynamic monitoring of a historic tower: damage detection under changing environment. Meccanica 51, 2873–2889. doi: 10.1007/s11012-016-0482-3

CrossRef Full Text | Google Scholar

Gentile, C., Ruccolo, A., and Canali, F. (2019). Continuous monitoring of the Milan Cathedral: dynamic characteristics and vibration-based SHM. J. Civ. Struct. Health Monit. 9, 671–688. doi: 10.1007/s13349-019-00361-8

CrossRef Full Text | Google Scholar

Girardi, M., Padovani, C., and Pellegrini, D. (2015). The NOSA-ITACA code for the safety assessment of ancient constructions: a case study in Livorno. Adv. Eng. Softw. 89, 64–76. doi: 10.1016/j.advengsoft.2015.04.002

CrossRef Full Text | Google Scholar

Girardi, M., Padovani, C., and Pellegrini, D. (2017). “Effects of the stress field on the dynamic properties of masonry bell towers,” in AIMETA 2017 - Proceedings of the 23rd Conference of the Italian Association of Theoretical and Applied Mechanics (Salerno), 216–229.

Google Scholar

Girardi, M., Padovani, C., and Pellegrini, D. (2019). Modal analysis of masonry structures. Math. Mech. Solids 24, 616–636. doi: 10.1177/1081286517751837

CrossRef Full Text | Google Scholar

Guegen, P., Langlais, M., Garambois, S., Voisin, C., and Douste-Bacqué, I. (2016). How sensitive are site effects and building response to extreme cold temperature? The case of the Grenoble's (France) City Hall building. Bull. Earthq. Eng. 15, 889–906. doi: 10.1007/s10518-016-9995-3

CrossRef Full Text | Google Scholar

Guidi, C. (1906). Influenza della temperatura sulle costruzioni murarie. Atti Reale Accademia delle Scienze di Torino. 319–330.

Google Scholar

Guillier, B., Chatelain, J.-L., Perfettini, H., Oubaiche, E. H., Voison, C., Bensalem, R., et al. (2016). Building frequency fluctuations from continuous monitoring of ambient vibrations and their relationship to temperature variations. Bull. Earthq. Eng. 14, 2213–2227. doi: 10.1007/s10518-016-9901-z

CrossRef Full Text | Google Scholar

Iafolla, L., Carmisciano, C., Fiorenza, E., Iafolla, V., Montani, L., Burlando, M., et al. (2015). “OS-IS a new method for the sea waves monitoring, MTS/IEEE OCEANS 2015,” in Discovering Sustainable Ocean Energy for a New World (Genova). doi: 10.1109/OCEANS-Genova.2015.7271432

CrossRef Full Text | Google Scholar

Lucchesi, M., Padovani, C., Pasquinelli, G., and Zani, N. (2008). “Masonry constructions: mechanical models and numerical applications,” in Lecture Notes in Applied and Computational Mechanics (Berlin; Heidelberg: Springer-Verlag).

Google Scholar

Maeck, J., Peeters, B., and De Roeck, G. (2001). Damage identification on the Z24 bridge using vibration monitoring. Smart Mater. Struct. 10, 512–517. doi: 10.1088/0964-1726/10/3/313

CrossRef Full Text | Google Scholar

Masciotta, M. G., Ramos, L. F., and Lourenço, P. B. (2017). The importance of structural monitoring as a diagnosis and control tool in the restoration process of heritage structures: a case study in Portugal. J. Cult. Herit. 27, 36–47. doi: 10.1016/j.culher.2017.04.003

CrossRef Full Text | Google Scholar

Padovani, C., Pasquinelli, G., and Zani, N. (2000). A numerical method for solving equilibrium problems of no-tension solids subjected to thermal loads. Comput. Methods Appl. Mech. Eng. 190, 55–73. doi: 10.1016/S0045-7825(99)00346-1

CrossRef Full Text | Google Scholar

Pellegrini, D., Girardi, M., Lourenço, P. B., Masciotta, M. G., Mendes, N., Padovani, C., et al. (2018). Modal analysis of historical masonry structures: linear perturbation and software benchmarking. Constr. Build. Mater. 189, 1232–1250. doi: 10.1016/j.conbuildmat.2018.09.034

CrossRef Full Text | Google Scholar

Pellegrini, D., Girardi, M., Padovani, C., and Azzara, R. M. (2017). “A new numerical procedure for assessing the dynamic behaviour of ancient masonry towers,” in COMPDYN 2017, 6th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, eds M. Papadrakakis, and M. Fragiadakis (Rhodes Island).

Google Scholar

Ramos, L. F., Marques, L., Lourenco, P. B., De Roeck, G., Campos-Costa, A., and Roque, J. (2010). Monitoring historical masonry structures with operational modal analysis: two case studies. Mech. Syst. Signal Process. 24, 1291–1305. doi: 10.1016/j.ymssp.2010.01.011

CrossRef Full Text | Google Scholar

Saisi, A., Gentile, C., and Guidobaldi, M. (2015). Post–earthquake continuous dynamic monitoring of the Gabbia Tower in Mantua, Italy. Constr. Build. Mater. 81, 101–112. doi: 10.1016/j.conbuildmat.2015.02.010

CrossRef Full Text | Google Scholar

Tsogka, C., Daskalakis, E., Comanducci, G., and Ubertini, F. (2017). The stretching method for vibration–based structural health monitoring of civil structures. Comput.-Aided Civ. Infrastruct. Eng. 32, 288–303. doi: 10.1111/mice.12255

CrossRef Full Text | Google Scholar

Ubertini, F., Comanducci, G., and Cavalagli, N. (2016). Vibration–based structural health monitoring of a historic bell–tower using output–only measurements and multivariate statistical analysis. Struct. Health Monit. 15, 438–457. doi: 10.1177/1475921716643948

CrossRef Full Text | Google Scholar

Ubertini, F., Comanducci, G., Cavalagli, N., Pisello, A. L., Materazzi, A. L., and Cotana, F. (2017). Environmental effects on natural frequencies of the San Pietro bell tower in Perugia, Italy, and their removal for structural performance assessment. Mech. Syst. Signal Process. 82, 307–322. doi: 10.1016/j.ymssp.2016.05.025

CrossRef Full Text | Google Scholar

Wang, H., Tao, T., Li, A., and Zhang, Y. (2016). Structural health monitoring system for Sutong cable-stayed bridge. Smart Struct. Syst. 18, 317–334. doi: 10.12989/sss.2016.18.2.317

CrossRef Full Text | Google Scholar