- 1Hinman Consulting Engineers, Inc., San Francisco, CA, United States
- 2Lyles School of Civil Engineering, Purdue University, West Lafayette, IN, United States
- 3Department of Computer and Information Technology, Purdue University, West Lafayette, IN, United States
Dynamic response of structures is a complex process that is not well-understood. Seismic design codes allow structural systems of buildings to behave inelastically during strong ground shaking. While hysteretic energy dissipation due to inelastic behavior is rather well-understood, there exist other energy dissipation mechanisms which are not as well-understood. Energy dissipation due to mechanisms other than material non-linearity are often modeled in the form of a single, velocity proportional damping mechanism with an equivalent viscous damping ratio. In seismic design and dynamic analysis of structures, this equivalent viscous damping ratio is generally taken to be constant (e.g., 2 or 5% of the critical) regardless the response is elastic or inelastic. Instead of making such a strong assumption about the viscous damping ratio, which may have large influence on the peak response levels, it is advisable to use an effective viscous damping estimate based on studying the actual response of real structures responding to dynamic loads. Use of such obtained viscous damping will allow extraction of restoring forces from dynamic force estimates. At low strain-rate levels, such as those observed during seismic response, restoring forces match the resistance that develops during quasi-static loading, a method to estimate effective viscous damping and restoring force empirically from dynamic response of a structure is presented. The method considers inelastic response explicitly, i.e., no linearization assumptions are made for the load-deformation behavior of the structure. The presented method is tested on several computational simulation models with various hysteretic behaviors and a preset constant viscous damping ratio to verify that the algorithm (1) estimates a damping ratio close to the value used in the simulations, and accordingly, (2) captures the hysteretic behavior accurately. The method is illustrated using data obtained from reinforced concrete test specimens subjected to design-level base excitations on an earthquake simulator.
Introduction
Modern seismic design codes are built on the principle that buildings may be designed to respond to extreme seismic loads in a controlled, inelastic manner. In seismic design, and even in dynamic analysis, energy dissipation apart from material non-linearity (hysteresis) is often considered using constant viscous damping ratios (modal damping ratios). Rather than making a constant viscous damping ratio assumption, which has its roots in linearization approaches, one should consider effective viscous damping ratios obtained empirically, and with minimal assumptions, using actual earthquake response data recorded in buildings. In this paper, a method to estimate the effective viscous damping ratio of a real structural system from its dynamic response is presented. The term “effective viscous damping” as used in here indicates the estimate of the inherent damping from real response data and independent of hysteretic damping. In other words, it represents the rate dependent energy dissipation in the structure and not energy absorption due to inelastic behavior of the structural elements. For this purpose, an algorithm is developed which accepts the measured acceleration data as the input, processes the data and outputs the effective viscous damping ratio as well as the restoring force estimates. The proposed method is applied to six computational simulation models with different hysteretic behavior, constant viscous damping ratio, and different ground motion excitations. The aim is to observe if the algorithm will return an equivalent damping ratio within ±10% of the preset constant value used in the simulation. The method is also applied to measured acceleration data from eight small-scale reinforced concrete (RC) laboratory test specimens subjected to design-level base accelerations to observe the values of the effective viscous damping ratio in actual structures (Hesam, 2016).
Background
Algan (1982), after studying data from several laboratory experiments (Otani and Sozen, 1972; Cecen, 1979; Schultz, 1986; Eberhard and Sozen, 1989), demonstrated that in reinforced concrete structures, the peak inelastic displacement the structure experiences during strong base excitation (simulating earthquake ground motion)has a strong correlation with the initial, elastic fundamental period of the structure. Different researchers proposed different approaches to estimate the maximum drift the structure may undergo. For example, Lepage (1996) suggested use of elastic period and equivalent viscous damping ratio. Others (Newmark and Hall, 1982; Miranda, 2000) used displacement modification factors. Others (Rosenblueth and Herrera, 1964; Gulkan and Sozen, 1974; Iwan, 1980; Kowalsky et al., 1994; Priestley et al., 1996) related these parameters to displacement ductility ratio, another modeling parameter.
Effective Viscous Damping Ratio Derivation
Dynamic response data obtained in a building can be used to estimate a proper value for the viscous damping ratio (“equivalent viscous damping ratio”) for the building. Here, the building is modeled as a single-degree-of-freedom system (SDOF) and damping force is considered to be proportional to drift rate, i.e., velocity of the mass relative to that of the ground. Let M be the mass of the SDOF, C be the constant viscous damping coefficient, Fs(t) be the restoring force of the structural system (if linear, equal to Kx(t) where with K is the lateral elastic stiffness of the building). If x(t) is the displacement of the mass relative to base, ẍ(t) is acceleration of the mass relative to base, ẍg(t) is the base (ground) acceleration, the equation of motion for the SDOF can be written as
Normalizing with respect to mass, the damping force can then be written as:
In Equation (2), Cm is the equivalent viscous damping coefficient (normalized w.r.t. mass) and, therefore, Cmẋ(t) is equivalent viscous damping force (normalized w.r.t. mass).ẍ(t)+ẍg(t) is the absolute acceleration of the mass, which is equivalent to inertial force normalized w.r.t. mass. Fsm(t) is the restoring force (normalized w.r.t. mass).
The objective is to estimate Cm, the damping coefficient normalized w.r.t. mass. Dowgala's method (Dowgala, 2013; Dowgala and Irfanoglu, 2016) is adopted, with modifications. The principle fundamental to the procedure is simple: a peak in restoring force occurs at an instance of peak distortion. These instances correspond to instances during which the mass of the structure moves at the same rate as the base of the structure (ground), i.e., instances of zero velocity relative to ground. At these instances, the inertial force will not have a peak if there is viscous (velocity proportional) damping in the structure. Figure 1 shows the difference in time between instances of zero relative velocity and the peak in inertial force, used in estimating the velocity-proportional damping force present in the system.
Figure 1. Damping correction procedure (Dowgala, 2013).
The principle of “local maximum restoring force happens at an instance of zero relative velocity” is enforced by adjusting the damping coefficient so that a peak in restoring force occurs at the instant of zero relative velocity closest to the local peak in absolute acceleration. This process yields a collection of damping coefficients, one for each occurrence of zero relative velocity. Then, a log-normal distribution is fitted to the extracted damping coefficient values. From the resulting distribution, a single effective damping coefficient value, which will be an average value applicable for the whole duration of the ground motion, can be obtained. The effective viscous damping ratio, in a sub-critically damped structure represented as a SDOF, can be written as
where,
β : equivalent viscous damping ratio
Cm : equivalent viscous damping coefficient (normalized w.r.t. mass)
Tn : natural period of the system (Apparent Period, see below)
In structures with multiple degrees of freedom (MDOF), often the first mode is the dominant mode of response. In those cases, a low-pass filter can be applied to eliminate the higher mode effects (Hesam, 2016). The criteria used in setting the low-pass cut-off frequency are: (1) keep it high enough to capture the highest frequency the fundamental mode appears at during the response (this would avoid loss of details particularly near the peaks of hysteretic loops; Dowgala, 2013); (2) keep it low enough to eliminate the second and higher mode effects (to avoid mixing of modes). Detailed cases are illustrated in Hesam (2016).
The proposed method is applied to six numerical models, each with a different hysteretic behavior, subjected to different ground motion excitations. The OpenSees (2016) platform has been used in the computational simulations. The method has been also applied to eight MDOF RC test specimens subjected to the design-level base accelerations.
Testing the Algorithm Using Numerical Simulation Data
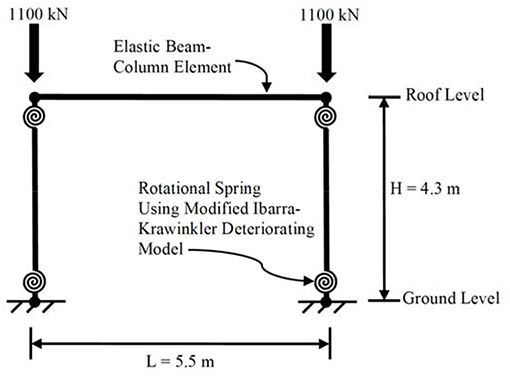
Before applying the method to data obtained from the actual structures, in which the damping ratios are unknown, the algorithm was tested against numerical simulations with assigned (known) values for the damping ratio. For this purpose, the method was applied to the results obtained from six single-story single-bay planar moment resisting frames (MRF) modeled in the OpenSees simulation platform. Figure 2 shows the geometry of the OpenSees models with non-linear rotational springs in its columns.
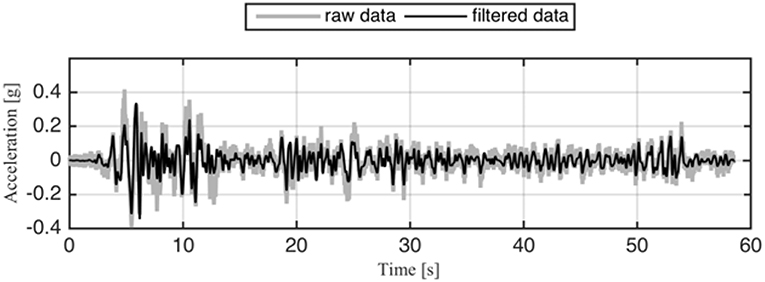
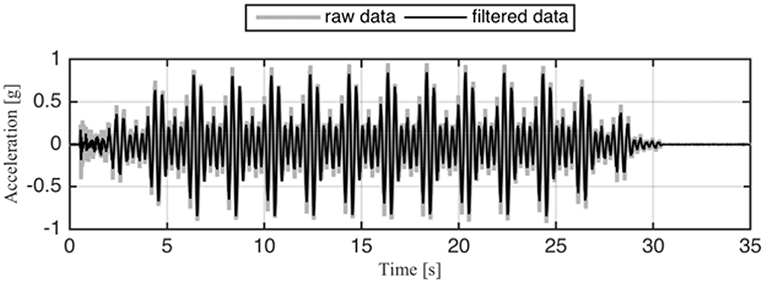
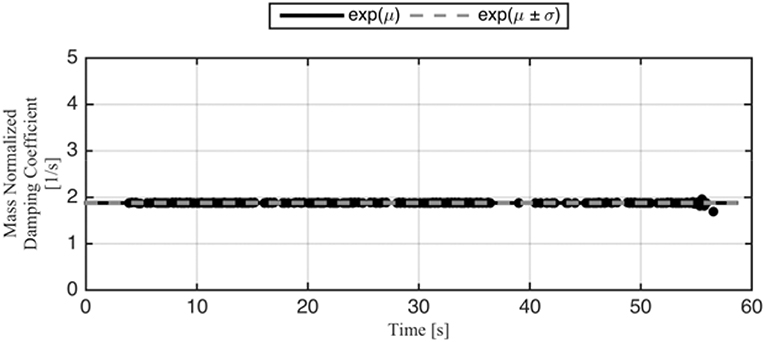
The elastic beam-column elements are assumed to be much stiffer than the rotational springs so that all of the deformations occur at the location of the rotational springs (i.e., lumped material non-linearity). Uniaxial modified Ibarra–Krawinkler deteriorating models (Ibarra, 2005) with different hysteretic behavior are assigned to the rotational springs in each simulation model so that the viscous damping ratio extraction algorithm is tested against different hysteretic behavior. The elastic period of the numerical models are 0.4 s and the viscous damping ratio is set at 5% of the critical. Six different simulation models in OpenSees were studied. Figures 3, 4 show, respectively, the 1940 El Centro earthquake and the harmonic base excitations. Figure 5 shows the Fast Fourier Transform. The Apparent Frequency (inverse of Apparent Period) is the frequency with the peak Fourier spectral amplitude (Cecen, 1979). In Figure 5, which shows both the band-pass filter and the Fourier Spectrum in normalized sense, the Apparent Frequency is the one with normalized magnitude of unity. The Apparent Frequency of the studied model is around 3 Hz. Hence the apparent period is 0.3 s, as listed in Table 1. A high-pass Butterworth filter of 1.8 Hz with the order of 4 is applied to acceleration records obtained at the base and roof levels to eliminate permanent offset before integrating the acceleration data to estimate the velocity and displacement responses. A low-pass Butterworth filter of 17 Hz with the order of 9 is also applied to either exclude the insignificant higher frequencies of the responses in SDOF structures or to eliminate the higher mode effects in case of MDOF structures. Figure 6 shows the roof absolute acceleration, roof-to-ground relative velocity and the damping coefficient estimate for the harmonically excited MRF with inelastic hysteretic behavior in which there is no degradation in stiffness or in strength.
Figure 5. Normalized Fourier spectrum (obtained via Fast Fourier Transform) and band-pass filter (dashed line).

Table 1. Results from analysis of an inelastic frame with no degradation in strength or stiffness that was subjected to harmonic base motion.
Figure 6. Roof absolute acceleration, roof-to-ground relative velocity, and mass-normalized damping coefficient responses—Inelastic with no degradation in stiffness or strength. Logarithmic Mean, exp(μ); Logarithmic Mean ± One Standard Deviation, exp(μ ± σ).
In Table 1, a summary of the simulation results for a model representing inelastic hysteretic behavior with no degradation in stiffness or in strength when subjected to harmonic base excitation. The period of the inelastic structure is taken as its Apparent Period, i.e., the period with peak Fourier spectral amplitude, as explained above and shown in Figure 5. The equivalent damping coefficient is defined as the exponential value of the logarithmic mean shown in Figure 6. As mentioned earlier, a constant 5% viscous damping ratio was used in the simulations. The effective viscous damping ratio is estimated using Equation (3). It is observed that the algorithm estimates that viscous damping at 5% of the critical damping was present in the model, i.e., it estimates the damping ratio with no error. Ground motions with different frequency contents are used in the dynamic response simulations of structures with different levels of damping. In each case the effective viscous damping ratios estimated using the algorithm matches the value set for the corresponding simulation.
The same approach was followed to test the algorithm under different material models, i.e., different hysteretic models. Figure 7 shows estimated damping coefficients extracted from the response data of a linear elastic structure subjected to the 1940 El Centro earthquake excitation at its base, shown in Figure 3.
Figure 8 shows the damping coefficient values for the case of inelastic behavior with degradation in both stiffness and strength, extracted from its response to the same 1940 El Centro earthquake base excitation.
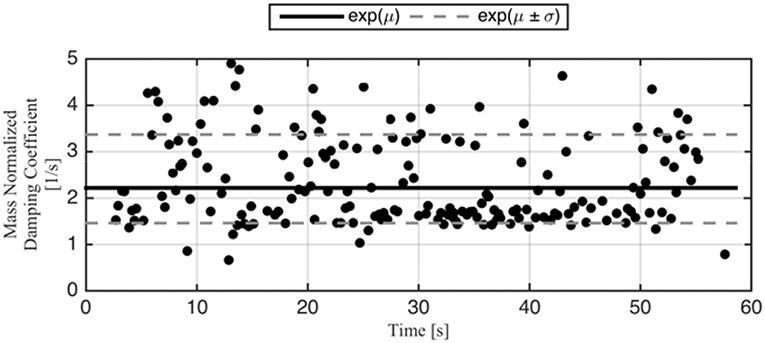
Figure 8. Mass-normalized damping coefficients—inelastic with degradation in stiffness and in strength.
The restoring force vs. story drift for different numerical models excited by different ground motion accelerations are presented in Figure 9.
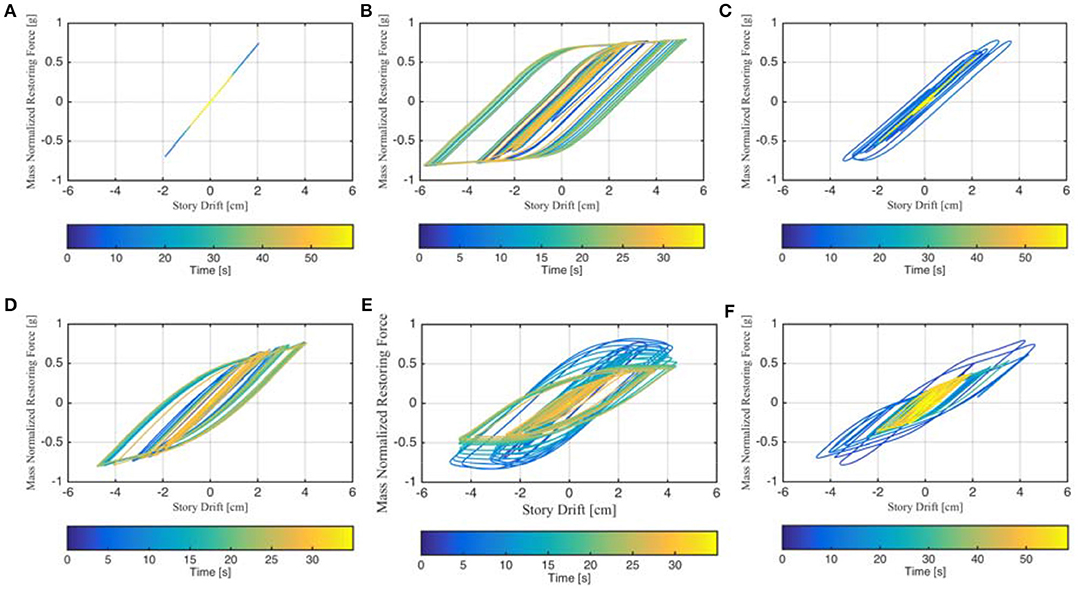
Figure 9. Mass-normalized restoring force vs. story drift. (A) Linear elastic model excited by 1940 El Centro record. (B) Inelastic model with no degradation in stiffness or in strength excited by harmonic base motion (representing non-linear behavior of structural steel). (C) Inelastic model with no degradation in stiffness or strength excited by 1940 El Centro record (representing non-linear behavior of structural steel). (D) Inelastic model representing non-linear behavior of the reinforced concrete excited by harmonic base motion. (E) Inelastic model with degradation in both stiffness and strength excited by harmonic base motion. (F) Inelastic with degradation in strength model excited by 1940 El Centro record.
It has been found that the results obtained from the algorithm match the set value (within ±10%) when it is applied to simulation results for various numerical models with different material behavior (Hesam, 2016). In Figures 9, the time from the beginning of the excitation is indicated by the color coding shown in the color-bar: from blue for earlier in the event and yellow toward the end of the event.
Summary of Observations From Laboratory Experiments
The effective viscous damping ratio extraction method has been used to study behavior of several reinforced concrete structures tested in laboratory (Hesam, 2016). As examples, two of the studied specimens will be described in detail. They are a pair of 9-story, 3-bay RC laboratory test structures studied by Eberhard and Sozen (1989). The specimens, identical in geometry but differing in strength, had a pair of parallel, full-height, two-bay RC moment-resisting frames (MRFs) and a slender wall in between the frames (Figure 10). The girders were designed to have higher plastic moment capacity than the columns. This was to account for the effect of the stiffness of the slabs in actual buildings. Girders were 38 × 57 mm and columns were 38 × 38 mm in cross-section. Walls were 38 × 114 mm. Girders had reinforcement ratio of 2.6% in floors 1–3, and 1.8% in floors 4–9. Walls had a longitudinal reinforcement ratio, ρ of 1.5%. In ES1 exterior columns had ρ = 1.8% (first story) and 1.2% (above first story). ES1 interior columns had ρ = 3.5% (first story), 2.3% (stories 2~8), and 1.2% (story 9). ES2 exterior columns had ρ = 1.2%. Interior columns in ES2 had ρ = 1.2%. The as-built structure fundamental frequency was found to be 5.5 Hz in ES1 and 6.2 Hz in ES2 from free vibration tests (Eberhard and Sozen, 1989). Both ES1 and ES2 were designed to resist 1940 El Centro earthquake base excitation scaled to give peak ground acceleration (PGA) of 0.35 g, where is the gravitational acceleration. Three acceleration records were used as base excitation: 1940 El Centro ground motion scaled to give PGAs of 0.35, 0.50, and 0.65 g. The method described above was used to analyze the response of specimens ES1 and ES2 subjected to the design-level ground excitations. Based on the analyses of the acceleration response data measured at each floor of the test specimens as well as at the base of the specimens, the first mode (fundamental mode) is the dominant mode of response in these two structures. A band-pass filter was applied to exclude the higher mode effects and to eliminate the permanent offsets from the response records. Therefore, the MDOF structural system was converted to a SDOF with fundamental mode being the sole mode studied. Table 2 shows a summary of the observations obtained from analyzing the test data under design-level base excitations. It is shown that the apparent periods of both structures were 0.4 s and the damping ratio of the two test specimens responding to the design-level ground motions are 1.5 and 1.6%.
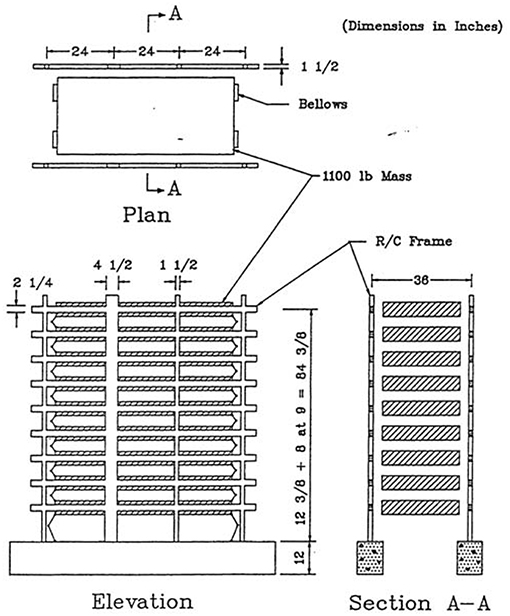
Figure 10. Dimensions of the Eberhard test specimen (Eberhard and Sozen, 1989).

Table 2. Summary of results for specimens ES1 and ES2 responses excited under design-level ground motions.
Figure 11 shows the restoring force vs. story drift for the ground story, estimated by analyzing the design-level response data for ES1. Additional analysis results, for both ES1 and ES2, are given in Hesam (2016) and Hesam et al. (2016).
The same approach was used to estimate the effective viscous damping ratios in six other small-scale test specimens subjected to the design-level ground accelerations (Hesam, 2016): a pair of 10-story 3-bay RC MRFs which had girders yielded (specimens H1 and H2; tested by Cecen, 1979), a pair of 9-story 3-bay soft-story RC MRFs which had columns yielded (specimens SS1 and SS2; tested by Schultz, 1986); a pair of 9-story 3-bay soft-story RC MRFs, which had columns yielded, with one of the specimens having a ground story shear wall acting in parallel with the MRFs (specimens FNW and FSW, tested by Moehle and Sozen, 1980). Table 3 shows the summary of observations obtained from analyzing the small-scale test specimen data under design-level base excitations.
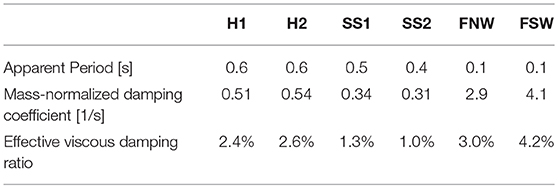
Table 3. Summary of results for small-scale test specimen responses under design-level ground excitations.
Conclusions
A method to estimate the effective viscous damping ratio in a real structural system using its dynamic response to earthquake ground excitation was presented. The proposed method is found to give accurate estimates when it is applied to simulation results for various numerical models with different material behavior including linear elastic, inelastic with no degradation in stiffness or strength, inelastic with degradation in stiffness, inelastic with degradation in strength, and inelastic with degradation in both stiffness and strength. It was found that the results obtained from the algorithm match the set value (within ±10%) when it is applied to simulation results for various numerical models with different material behavior. This results in peak restoring force estimates which differ no more than 10% from the theoretical (preset) values. The method was also applied to eight small-scale test specimens subjected to the design-level ground accelerations (Cecen, 1979; Moehle and Sozen, 1980; Schultz, 1986; Eberhard and Sozen, 1989). All of the original test data and information regarding specimen properties, drawings, test setups, and instrumentation are available at https://datacenterhub.org/resources/378 (DataCenterHub, 2015). If and when more response data recorded in buildings during earthquakes at different shaking intensity are available, it could be possible to estimate effective viscous damping ratios for different building structural configurations and for response levels. In designing a building, assuming a viscous damping ratio higher than the appropriate value would result in underestimation of the displacements. In a such-designed building, more than expected damage to the structure and its contents could be observed during strong earthquakes.
Author Contributions
The manuscript presents doctoral research that was carried out by PH, advised and supported by AI and TH.
Funding
This material is based on work supported by the U.S. National Science Foundation under Grant 0927178 and through a teaching assistantship provided by the Lyles School of Civil Engineering at Purdue University.
Conflict of Interest Statement
PH is employed by Hinman Consulting Engineers, Inc. in San Francisco, California, USA.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Algan, B. (1982). Drift and Damage Considerations in Earthquake-Resistant Design of Reinforced Concrete Buildings. Ph.D. dissertation, University of Illinois, Urbana-Champaign, IL.
Cecen, H. (1979). Response of Ten Story, Reinforced Concrete Model Frames to Simulated Earthquakes. Ph.D. dissertation, University of Illinois, Urbana-Champaign, IL.
DataCenterHub (2015). Earthquake Simulation Tests on the DataCenterHub, A Public Platform to Organize, Share, and Explore Research Data. Available online at: https://datacenterhub.org/resources/378
Dowgala, J., and Irfanoglu, A. (2016). A method for extracting building empirical capacity curves from earthquake response data. Earthq. Spectra 32, 2229–2244. doi: 10.1193/122714EQS219M
Dowgala, J. D. (2013). Detecting and Quantifying Damage in Buildings Using Earthquake Response Data and Capacity Curves. Ph.D. Dissertation, Purdue University, West Lafayette, IN.
Eberhard, M. O., and Sozen, M. A. (1989). Experiments and Analysis to Study the Seismic Response of Reinforced Concrete Frame-Wall Structures With Yielding Columns. Structural Research Series Report No. 548, University of Illinois, Urbana-Champaign, IL.
Gulkan, P., and Sozen, M. A. (1974). Inelastic response of reinforced concrete structures to earthquake motions. ACI J. 71, 604–610.
Hesam, P. (2016). Estimating Effective Viscous Damping and Restoring Force in Reinforced Concrete Structures. Ph.D. dissertation, Purdue University, West Lafayette, IN.
Hesam, P., Irfanoglu, A., and Hacker, T. J. (2016). “Estimating effective viscous damping and restoring force in reinforced concrete buildings,” in Dynamics of Civil Structures, Vol. 2, Conference Proceedings of the Society for Experimental Mechanics Series, eds S. Pakzad and C. Juan (Cham: Springer). doi: 10.1007/978-3-319-29751-4_27
Ibarra, L. M. (2005). Hysteretic models that incorporate strength and stiffness deterioration. Earthq. Eng. Struct. Dyn. 34, 1489–1511. doi: 10.1002/eqe.495
Iwan, W. D. (1980). Estimating inelastic spectra from elastic spectra. Earthq. Eng. Struct. Dyn. 8, 375–388. doi: 10.1002/eqe.4290080407
Kowalsky, M. J., Priestley, M., and MacRae, G. A. (1994). Displacement-Based Design, a Methodology for Seismic Design Applied to Single Degree of Freedom Reinforced Concrete Structures. University of California, San Diego, CA.
Lepage, A. (1996). “Seismic drift estimates for RC structures,” in 11th World Conference on Earthquake Engineering (11WCEE) (Mexico).
Miranda, E. (2000). Inelastic displacement ratios for structures on firm sites. J. Struct. Eng. 126, 1150–1159. doi: 10.1061/(ASCE)0733-9445(2000)126:10(1150)
Moehle, J. P., and Sozen, M. A. (1980). Experiments to Study Earthquake Response of RC Structures with Stiffness Interruptions. University of Illinois, Urbana-Champaign, IL.
Newmark, N. M., and Hall, W. J. (1982). Earthquake Spectra and Design. Berkeley, CA: Earthquake Engineering Research Institute.
OpenSees (2016). The Open System for Earthquake Engineering Eimulation. Computer Software. Version 2.4. Available online at: http://opensees.berkeley.edu/
Otani, S., and Sozen, M. A. (1972). Behavior of Multistory Reinforced Concrete Frames During Earthquakes. University of Illinois, Urbana-Champaign, IL.
Priestley, M., Kowalsky, M., Ranzo, G., and Benzoni, G. (1996). “Preliminary development of direct displacement-based design for multi- degree of freedom systems,” in Proceedings 65th Annual Convention (Maui, HI: Structural Engineers Association of California).
Keywords: viscous damping ratio, hysteresis, inelastic response, reinforced concrete, seismic response
Citation: Hesam P, Irfanoglu A and Hacker TJ (2019) A Method to Estimate Effective Viscous Damping Ratio and Restoring Force From the Dynamic Response Data of Structures. Front. Built Environ. 5:19. doi: 10.3389/fbuil.2019.00019
Received: 20 November 2018; Accepted: 08 February 2019;
Published: 01 March 2019.
Edited by:
Baki Ozturk, Hacettepe University, TurkeyReviewed by:
Ehsan Noroozinejad Farsangi, Graduate University of Advanced Technology, IranErsin Aydin, Niğde Ömer Halisdemir University, Turkey
Safa Bozkurt Coskun, Kocaeli University, Turkey
Kemal Edip, Institute of Earthquake Engineering and Engineering Seismology, Macedonia
Copyright © 2019 Hesam, Irfanoglu and Hacker. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ayhan Irfanoglu, YXloYW5AcHVyZHVlLmVkdQ==
 Pedram Hesam
Pedram Hesam Ayhan Irfanoglu
Ayhan Irfanoglu Thomas J. Hacker
Thomas J. Hacker