Impact of Soil Saturation Level on the Dynamic Response of Masonry Buildings

The present study investigates the impact of the soil saturation level on the performance of unreinforced masonry (URM) buildings when subjected to seismic excitations. More specifically, this paper examines the dynamic response of an ordinary stone-built URM building, firstly in its initial state and subsequently when it is slightly retrofitted with reinforced concrete beams at the perimeter in both storeys and also reinforced concrete instead of wooden lintels above the openings. The assessment of the behavior of this typical URM building, taking into account the soil-structure interaction (SSI) along with the nonlinear behavior both of the soil and the structure is examined through incremental dynamic analyses. For this purpose, a compatible in terms of soil conditions, set of 20 ground motions was selected, each scaled to several levels of seismic intensity. Subsequently, multiple nonlinear dynamic analyses of the coupled model of soil and structure were performed. In addition, these calculations were repeated for eight different saturation levels covering a wide range of soil conditions to elaborately investigate the problem at hand.

Introduction

In engineering practice, apart from following the general guidelines of the seismic norms, usually none special attention is given on soil compliance and the related soil—structure interaction when designing a low-rise ordinary building. This simplification of the seismic design process is realistic when the construction is founded on rock or on a very stiff soil layer. However, very frequently the foundation soil layer has the capability to deform, which affects the foundation compliance at the base of the structure and the dynamic response of the soil—foundation—structure system. This phenomenon depends both on the special characteristics of the seismic ground motion as well as the local site conditions, the dynamic properties of the soil and the structure.

In recent years, the so-called soil-structure interaction (SSI) phenomenon, is more often taken into account (e.g., Mylonakis and Gazetas, 2000; Paolucci et al., 2013; Millen et al., 2014; Pecker et al., 2014; Gazetas, 2015) when studying the seismic response of any type of structure and infrastructure. Consequently, contemporary seismic norms have also started to include SSI in seismic design guidelines. This is an important step toward a more realistic seismic design of structures, which, however, still needs further improvements.

To the best of authors' knowledge, existing studies investigate the SSI phenomenon without considering the saturation level of soil and its impact on the structural response. More specifically, soil is usually considered as dry or occasionally as fully saturated. For instance, two reinforced concrete moment resisting frame buildings founded on a homogenous sandy soil profile for two hydraulic conditions: dry and fully saturated, were studied by Saez (2009). However, in reality the soil saturation level is constantly changing and it is directly dependent on external factors.

So far it has not been examined to which extent the dynamic response of any type of building is affected by the change of the soil saturation level. The lack of such studies is due to the difficulty of establishing accurate and reliable models to simulate unsaturated soils dynamic behavior. Consequently, the variation of the mechanical properties of soils depending on their saturation level has not been studied very thoroughly. The present study aims to simulate the saturated soil conditions as accurately as possible based on experimental results. For this purpose, the foundation of a characteristic unreinforced masonry (URM) building, stone-built and constructed over a silty sand layer, with mechanical properties depending on the saturation level, is considered. Subsequently, the coupled model of the soil and the superstructure is examined for various dynamic loading conditions.

Overview of the Examined Problem

Description of the Masonry Building Typology

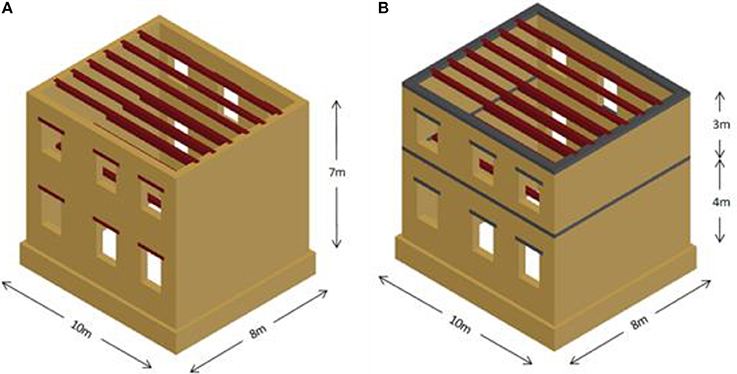
The examined structural model is a typical form of a two-storey, symmetrical URM building (the so-called “neoclassical” buildings) that were constructed in Greece from the nineteenth century and later on. Typically, they have been used as residences and their volume is closed and cubic, while a basic tripartite separation is used to ensure symmetry in the faces. On the facade of the building, this typology is formed via the axially positioned entrance and the symmetrically located openings that imply the different function of the three parts of the house. In many towns in Greece (e.g., in Chania, Crete) such buildings are still well-preserved and functioning, as shown in Figure 1.

FIGURE 1

Figure 1. Typical masonry buildings in Chania, Crete, Greece.

As aforementioned, this work investigates the change of the dynamic non-linear behavior of the silty sand foundation layer, depending on the variations in the saturation level, and its impact on a typical masonry building shown in Figure 2A. In addition, a quite simple and light reinforcement of the building for the same soil conditions is examined. Retrofitting is performed by placing proper reinforced concrete (RC) elements. As illustrated in Figure 2B, the retrofitted URM building has RC beams (freezes) at the perimeter in both storeys and additional RC lintels above the openings (i.e., reinforced concrete instead of wooden lintels). The inclusion of RC freezes is an efficient and relatively cost-effective method for reinforcing masonry structures, in order to increase their resistance to out-of-plane seismic loading, control the horizontal displacements and minimize the risk of exterior wall falling. The addition of RC freezes (referred also as ring RC beams, e.g., Senaldi et al., 2014) improves the performance of the building by increasing the floor stiffness, thus, enhancing the rigid diaphragm behavior of the building.

FIGURE 2

Figure 2. The initial (A) and the slightly retrofitted (B) masonry building.

This is a simple and economical retrofitting method and it is often applied in masonry (stone and brick) structures in Greece and other countries. Certainly, floor strengthening of the URM building could be further enhanced with more heavy interventions via concrete slabs, composite steel-concrete slabs, metal grids, and steel ties (e.g., Branco and Guerreiro, 2011). However, this light intervention scheme was deliberately chosen in order to keep unchanged the weight and the fundamental period of the examined building, since any change most probably would alter substantially the impact of soil saturation level and the related SSI on the structural system, which is the main focus of the present study.

As explained in the subsequent sections, finite element models for each degree of saturation were developed and multiple non-linear dynamic analyses were conducted following an incremental procedure utilizing a suitably selected suite of ground motions recorded in similar soil conditions. The process has high computational cost, since a total of 3,200 dynamic nonlinear analyses had to be performed (2 buildings × 8 soil saturation degrees × 20 earthquakes × 10 scaling levels). The post-processing and interpretation of the results was also demanding and time-consuming since the volume of the output data is huge.

Soil-Structure Interaction

As aforementioned, when structures are founded on soft soil layers then soil-structure interaction plays an important role in their dynamic behavior, which has been presented among other structural systems also for masonry buildings (e.g., Karatzetzou et al., 2015; Pitilakis and Karatzetzou, 2015). During an earthquake the ground deforms and this affects the foundation and the supported structure, while the presence of a structure substantially alters the ground response compared to free-field conditions. In general, there are three primary categories of SSI effects (FEMA-440, 2005):

- Flexible foundation effects to structure due to the flexibility of the soil-foundation system;

- Kinematic effects due to filtering of the transmitted ground motion to the structure;

- Foundation damping effects due to energy dissipation of soil-structure system via radiation and hysteretic soil damping.

Including SSI effects results in a more realistic evaluation of the probable structural behavior and performance compared to fixed-base or decoupled approaches. Several modern seismic norms (e.g., Eurocode 8; EC8, 2004) recognize the impact of SSI on the dynamic structural response, but usually consider it as neutral or beneficial for typical structures due to period elongation and lower spectral acceleration values, while they suggest to examine it more thoroughly for special types of structures. Nevertheless, the study of the SSI phenomenon in the case of partially saturated soils has not been investigated, mainly due to the difficulty of the simulation of the dynamic behavior for varying soil properties due to the changes of the soil saturation level. Hence, the current work aims to shed some light to soil and structural dynamic responses for such circumstances.

Partially Saturated Soils

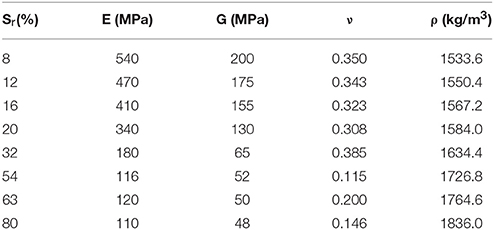
Examining the complex phenomenon of SSI for partially saturated soil layers is a challenging task (Al Rjoub, 2007). In laboratory, the behavior of unsaturated soils is usually determined via matric suction, while the degree of saturation, S_r, is assumed to be directly related to suction. In finite element numerical simulations, the characteristic material properties of the soil are Young's modulus, E, and Poisson ratio, ν; while shear modulus, G, is easily computed by: G = E/2·(1+v). Given the values of Young's and Shear's moduli, the Poisson's ratio can be easily calculated by: v = (E-2·G)/2·G. The density, ρ, of the soil is given by:

$\begin{array}{rc}\rho =G/V_s^2& (1)\end{array}$

in which, V_s, denotes shear wave velocity. Moreover, the density of the partially saturated soil is derived in terms of Sr by:

$\begin{array}{rc}\rho =f(S_r)={\rho }_d+e{S}_r{\rho }_w& (2)\end{array}$

where e is the void ratio and ρ_w = 1,000 kg/m³ the water density, while the density of the dry, silty soil was chosen equal to ρ_d = 1,500 kg/m³ (Byun et al., 2013).

A considerable research effort has been devoted lately to investigate the variation of the mechanical characteristics for unsaturated soils. However, as it is very difficult to interpret analytically soil saturation level, S_r, with respect to basic mechanical properties, the related research is mainly conducted in laboratory. For instance, in the experimental study by Byun et al. (2013), both Young's and shear moduli of fine-grained silty sand were presented in the form of suitable graphs (see Figure 3). The soil properties that have been presented in the aforementioned study have been adopted in the current investigation.

FIGURE 3

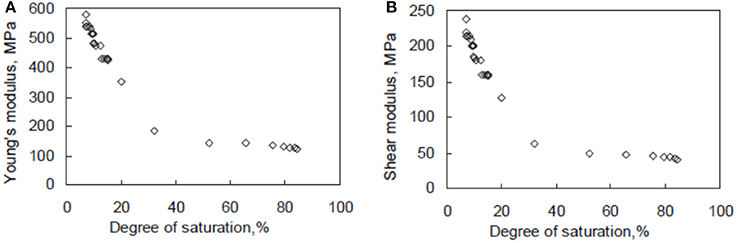
Figure 3. Impact of degree of saturation for silty sand soil on (adopted from Byun et al., 2013): (A) Young's modulus; (B) shear modulus.

Apart from determining the mechanical properties of unsaturated soils, the implementation of a suitable yield criterion is also a difficult task in soil mechanics. The most popular yield criteria such as the Von Mises and the Mohr-Coulomb refer to saturated or dry soils. An exception is the extension of the modified Cam-Clay yield criterion for unsaturated soils (Casini et al., 2008). In the international literature the use of the Cam-Clay yield criterion is recommended for the description of the non-linear behavior of clay soils. However, this criterion has been used in several studies for other soil types, either in its initial form (e.g., Fall et al., 2011) or slightly modified (McDowell and Hau, 2004). The Cam-Clay yield criterion according to the Critical State theory (Casini et al., 2008) has been used in this study.

Incremental Dynamic Analyses

Over the last years multi-step or incremental dynamic analysis (Vamvatsikos and Cornell, 2002) methodologies have been developed in order to assess more accurately the non-linear behavior of engineering structures under seismic excitations. These approaches are based on the simple principle of performing the dynamic analysis of the structure for one or preferably more seismic records, which are scaled to represent the changes of seismic intensity -through proper intensity measures (IMs)- and the related response of the structural system, described via engineering demand parameters (EDPs) and structural damage indices (DI). The main aim is to produce -usually in the form of IM–EDP plots a relation between the seismic hazard intensity level and the dynamic response of the structural system.

Certainly, the dynamic behavior of any structure strongly depends on the selected records characteristics; therefore, in order to describe the structural response more accurately, an adequate number of suitable records must be used. Consequently, selecting and scaling earthquake ground motions for performing response-history analysis has attracted the interest of many researchers (e.g., Haselton et al., 2012; Reyes and Kalkan, 2012; among others) and the development of related software [e.g., REXEL (Iervolino et al., 2009); ISASRS (Katsanos and Sextos, 2013)].

The vast number of dynamic nonlinear analyses is typically implemented in a multi-step manner, which is an extremely demanding computational task. The most applicable methods to accomplish this goal are multiple-stripe dynamic analysis (MSDA), incremental dynamic analysis (IDA), and its extension multi-component incremental dynamic analysis (MIDA). In the adopted MSDA approach, the intensity measure is the first mode spectral acceleration for damping equal to 5%, S_a(T₁,5%), while repeated non-linear dynamic analyses are performed for several predefined spectral acceleration levels (the so-called stripes). Nonetheless, alternative IMs, such as peak ground acceleration (PGA) and IMs related to velocity or displacement instead of acceleration can be used (Giovenale et al., 2004; Tothong and Cornell, 2007).

Depending on the structural system special characteristics, damages may be quantified using EDPs that represent certain limit states (e.g., nodal displacements, inter-storey drifts, accelerations). There are many relevant studies in the field of vulnerability and integrity assessment of masonry structures (Kappos et al., 2006; Rota et al., 2010; Karantoni et al., 2012; Frankie et al., 2013; Negulescu et al., 2014; Lagomarsino, 2015; EQ-Assess, 2016; among others). In the current study, the total drift at the top of the building (i.e., the difference of top and base displacements divided by its height) has been chosen, since it can be directly related to predefined performance levels (immediate occupancy, life safety, collapse prevention) for masonry buildings.

Numerical Simulations

Geometry and Modeling Details

Since the emphasis is given on the soil, the initial structural model is a rather simple two-story URM building shown in Figure 2A, which has dimensions 10 × 8 m with a ground floor height of 4 m and a first-floor height of 3 m, while masonry walls width is 0.40 m. The foundation of the structure was constructed at a 1.8 m depth with a widening of the masonry walls. Both sides in the X′X direction include 6 openings with wooden lintels, while no openings were placed on the other two sides. Between the floors and at the top of the structure there are wooden beams with dimensions 0.20 × 0.30 m, spaced in 1.5 m. Based on a detailed parametric investigation, the optimal dimensions -in terms of computational cost and efficiency- of the soil layer were set as 18 × 20 × 15 m (simulated with 10,085 tetrahedral finite elements), while the soil continuity was represented via suitable springs (Liratzakis, 2016).

The second model is the original building after a slight retrofitting, in which wooden lintels are replaced with RC lintels, and RC friezes with height of 0.20 m and width of 0.40 m, are placed at the floor levels (see Figure 2B) to improve the dynamic behavior of the structure without altering its geometry, mass and vibration period. On the other hand, these quite simple and cost-effective interventions are often implemented since they can enhance drastically the dynamic behavior of masonry buildings, as they enable them to resist horizontal seismic loads. The geometrical dimensions as well as the material properties of the structure and the soil layer are the same as in the original model, since as aforementioned in the introduction, the focus of this work is given on the impact of soil saturation level, thus, it was indented to maintain the structure's fundamental period unchanged.

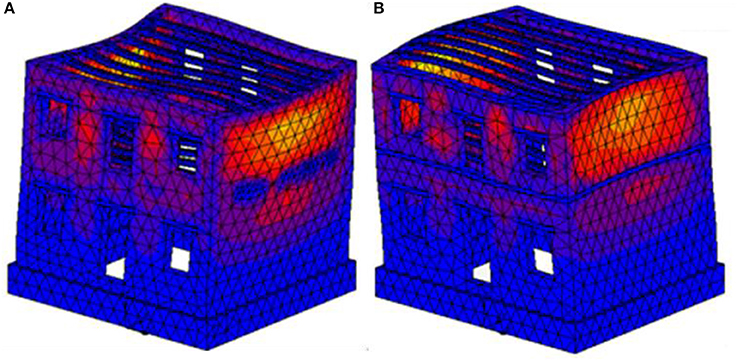
In general, with reference to the most suitable approach for simulating the dynamic behavior of a masonry building, depending on its special characteristics one can select among various methodologies (finite element-based, discrete interface models, macroelements, equivalent frame modeling) (Lagomarsino and Cattari, 2015; Caddemi et al., 2017). In the present investigation, a detailed finite element model of the examined coupled SSI problem has been developed. Numerical analyses were performed utilizing general purpose finite element software MSC Marc (2014). For the discretization of the coupled models, 3D solid tetrahedral elements have been used. More specifically, the model for the initial building (Figure 4A) has 4,982 nodes and 16,401 elements, from which 3,972 elements have been used for the simulation of wooden beams and lintels. The retrofitted building (Figure 4B) has been simulated using 5,012 nodes and 17,302 elements, 3,106 of which have been used to model the RC friezes and lintels, while the interior wooden beams have been simulated with 2,984 elements.

FIGURE 4

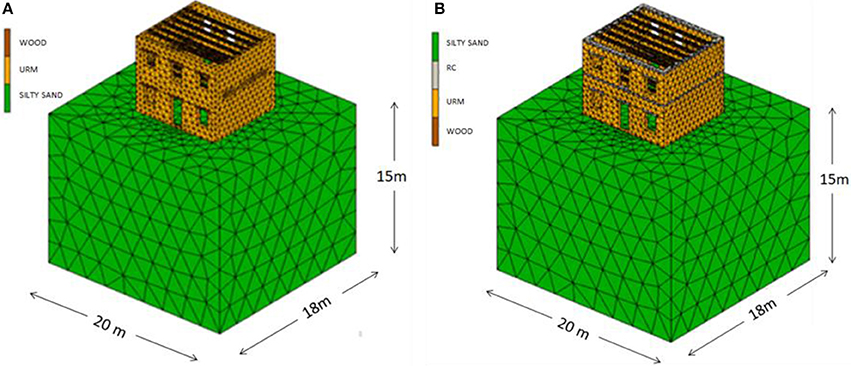
Figure 4. The finite element models for: (A) the building in its initial state and (B) the slightly retrofitted masonry building.

Finally, the soil layer has been simulated with 10,085 finite elements for both structural models after a thorough investigation and taking into account the excessive computational cost of the repeated non-linear dynamic analyses. The soil layer is considered to have quite large dimensions, thus, only an adequate surrounding part of the foundation was included, while the continuity was represented in the boundary nodes at the perimeter of the finite element grid via suitable springs with stiffness k_s = 12,000 kN/m³ (Liratzakis, 2016).

Mechanical Properties of the Masonry Buildings

One of the main issues in numerical modeling and assessment of masonry buildings is the availability of reliable mechanical parameters, especially for historic/heritage ones (due to the invasiveness of several in situ testing methods, the probable measurements errors, in homogeneity of materials, aging/deterioration). Reference values of the main mechanical parameters of masonry (elastic modulus, shear, and compressive strength) are provided in the literature for various stone and brick types, based on available data from norms (Eurocode 6) or experimental tests (KrŽan et al., 2015).

The calculation of the compressive strength, f_k, of the masonry was made for general purpose mortar according to Eurocode 6 (EC6, 2005):

$\begin{array}{ll}{f}_k=\kappa f_b^{0.7}{f}_m^{0.3}& (3)\end{array}$

where coefficient K is derived from EC6 for manufactured natural stones and standard mortar to be equal to 0.45. For the compressive strength of stones, f_b, and mortar, f_m, two rather conservative values were used: 35 and 0.5 MPa, respectively, which are suggested for existing unreinforced masonry buildings in Greece (Chronopoulos and Zygouris, 2008) and are within the typical range of values for real masonry buildings (Abdelmegeed, 2015). The compressive design strength was computed using a safety coefficient of γ_m = 2 for Greek traditional UMR structures. Based on these values, the compressive strength of the masonry was equal to 2.2 MPa. The tensile strength of the load-bearing masonry is calculated based on the compressive strength of the mortar. The tensile strength of the masonry along the joints is equal to ¼ of f_m, while with respect to the vertical direction it is equal to ½ f_m (EC6). Therefore, the tensile strength of the masonry parallel and perpendicular to the joints is f_t// = 0.125 MPa and f_t⊥ = 0.25 MPa, respectively.

Young's modulus of the load-bearing masonry is calculated analogous to the compressive strength (E = 1,000 f_k) and is equal to E = 2.2 GPa [EC6 (3.7.2.)]. For Poisson's ratio, the typical value of v = 0.3 is used (Chronopoulos and Zygouris, 2008). For the description of the non-linear behavior of the masonry the parabolic Drucker-Prager yield criterion is used. The parameters σ and β of the yield criterion are determined by the uniaxial tensile and compressive strength of the material (σ = 680 kPa, β = 2.98). Wooden members in the models were assumed (Liratzakis, 2016) to be constructed by wood material of type C24, according to Eurocode 5 guidelines (EC5, 2004). The mechanical properties of this material are as follows: the tensile strength parallel and perpendicular to the fibers is f_t// = 14 MPa and f_t⊥ = 0.5 MPa, respectively; the compressive strength parallel and perpendicular to the fibers is f_c// = 21 MPa and f_c⊥ = 2.5 MPa, respectively; Poisson ratio is v = 0.4; Young's modulus is E = 11 GPa; density is ρ = 350 kg/m³. Finally, regarding retrofitting interventions, C20/25 concrete material was used.

Simulation of Soil Mechanical Properties

To take into account in the numerical simulations the impact of soil saturation level on the mechanical properties of the soil, the experimental data related to the change of Young's modulus (E), density (ρ), and Poisson's ratio (v) were used. As aforementioned, it was considered that the masonry building is located on a silty soil layer. The mechanical properties of a soil of this type with respect to the degree of saturation are derived from the experimental study of Byun et al. (2013), as illustrated in the plots of Figure 3.

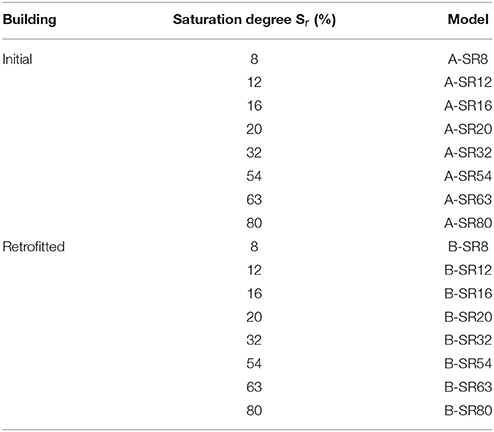
Based on the experimental data of Byun et al. (2013), eight characteristic saturation levels were examined. The corresponding mechanical properties shown in Table 1 were used in the numerical simulations. It should be noted that these values are taken as precisely as possible from the available data. Finally, as previously stated, the modified Cam-Clay yield criterion was used for the description of the non-linear behavior of the silty soil.

TABLE 1

Table 1. Basic properties of silty soil for various saturation levels.

Modal Analysis

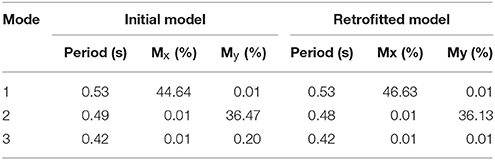
Initially, a modal analysis was performed in MSC Marc software to determine the fundamental period of the examined buildings. The calculation of the fundamental period of the decoupled structure is necessary for the non-linear incremental dynamic analyses, as the scaling of the accelerograms is based on the spectral acceleration of the fundamental period for 5% damping. As aforementioned, this study examines the impact of SSI, which affects the fundamental period that is usually shifted to the right (i.e., it is increased due to foundation compliance). Hence, the modal analysis of the decoupled buildings was performed including the impact of the presence of the soft soil foundation layer, by applying springs at the base of the structures having stiffness (characteristic for silty sand) k_s = 12,000 kN/m³. For comparison, it should be mentioned that for fixed-base conditions the fundamental period was equal to 0.22 s instead of 0.53 s when SSI is taken into account. The fundamental period of the coupled model is ~2.4 times higher than the period of the fixed-base building due to the compliance of the soft foundation layer. This increase has also been confirmed by applying the relevant formula proposed by Veletsos and Meek (1974) for flexibly-supported structures. Furthermore, as earlier explained, period values are almost identical for both buildings, due to the minor interventions that do not alter the dimensions and stiffness of the structure. Figure 5 depicts the first eigenmode, while Table 2 presents the period of the first three modes and the percentages of the activated mass along X′X and Y′Y axis for the initial and the retrofitted building, respectively.

FIGURE 5

Figure 5. First eigenmode for: (A) the model in its initial state, and (B) the retrofitted model.

TABLE 2

Table 2. Modal analysis results considering SSI effect.

Selection of Accelerograms

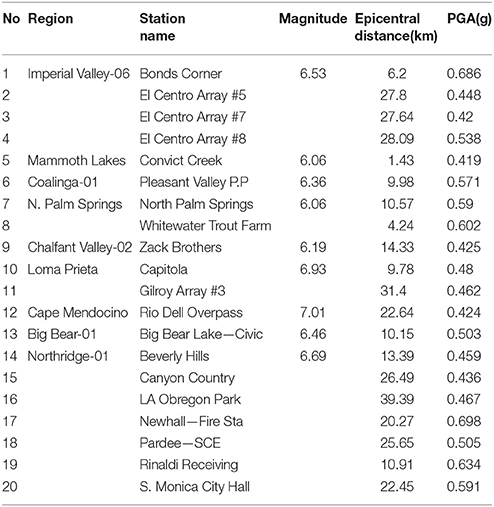
Various requirements for selecting ground motions were considered: in terms of seismic intensity, compatibility with the site conditions, modification to match with the EC8 (2004) target spectrum. Accordingly, a suite of twenty input motions was selected to obtain a reliable assessment of the dispersion of EDPs of the examined masonry buildings and soil conditions. The records were imposed (both horizontal components) at the base nodes of the numerical models shown in Figure 4. The seismic records that were used in this study were selected from PEER (2015) database based on the following criteria:

- Type 1 EC8 design spectrum;

- near and medium field earthquakes (epicentral distance below 30 km);

- earthquakes with a ground acceleration ranging from 0.4 to 0.7 g;

- earthquake magnitude ranging from 6 to 7.5;

- site Class D soil conditions.

Consequently, the twenty-ground motions listed in Table 3 were chosen which present these specific features and were repeatedly imposed at the bottom nodes of the two models shown in Figure 4.

TABLE 3

Table 3. Characteristics of the ground motions.

The spectral-matching procedure was utilized to adjust frequency content of accelerograms within predefined limits according to EC8 (2004) design spectrum. Figure 6 displays the mean spectrum together with the spectra for the twenty records, which were derived utilizing ISSARS (Katsanos and Sextos, 2013) software for 5%-damped first mode spectral acceleration, i.e., S_a(T₁, 5%). The silty soil was classified according to Eurocode 8 as category D. Using modal analysis results (Table 2), the elongated (due to SSI) fundamental period for both coupled models of the masonry building was equal to T₁ = 0.53s, since as aforementioned, it is not affected by the intentionally chosen minor interventions.

FIGURE 6

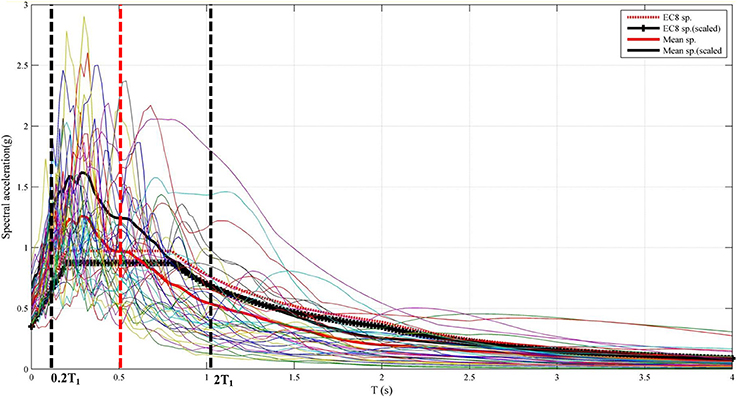
Figure 6. Acceleration spectra and mean spectrum of the selected records derived from ISSASRS (Katsanos and Sextos, 2013).

Scaling of the mean spectrum of the selected time-histories was performed, in order to match it with EC8 design spectrum. According to EC8 (2004) guidelines (Part 1, section 3.2.3.1.3) the lower bound of the design spectrum (necessary for the spectral matching procedure) imposed by EC8 is firstly calculated by ISSARS. The software adjusts the EC8 design spectrum to 90% of its values and then calculates the new values of mean spectrum so that in a certain range of periods (from 0.20 to 2.0 times the fundamental period T₁ = 0.53 s) the resulting scaled mean spectrum (marked with black continuous line in the plot) will be above the modified EC8 design spectrum (marked with black crosses in the plot). Accordingly, the scaled mean spectral acceleration S_a(T₁, 5%) was approximately equal to 1.28 g, as shown in Figure 6. Subsequently, the scaling of the records in 10 equal steps (0.1, 0.2, …, 0.9, 1.0) up to this spectral acceleration value was performed and the resulting time-histories were used for the subsequent incremental dynamic analyses.

Results and Discussion

Following the framework described in the previous sections, multi-stripe dynamic analyses of the two building models for the selected group of seismic records with a gradual escalation of their intensity in 10 steps was performed for both masonry structures. As presented in the sequence, the whole process was repeated for eight different soil saturation conditions, as shown in Table 4, and multiple IM-EDP plots were produced, in which dynamic instability occurred as a result of a sudden increase in the chosen EDP.

TABLE 4

Table 4. List of abbreviations for the examined models.

Regarding the original building, for most records, in the first part of MSDA curves almost linear elastic behavior was obtained, in which drifts were linearly proportional to seismic intensity level, irrespective to ground motion characteristics. In the second part, however, structural softening was observed which gradually evolved to dynamic instability in the third part of the dynamic analyses for several records.

Moreover, the response of the initial building has proven to be directly dependent on the degree of saturation of the soil. In particular, it was observed that the increase of soil saturation contributes to the reduction of the total drift (i.e., the difference of top and base displacements divided by its height) of the building. More specifically, when the building is founded on a relatively dry soil, with a S_r ≤ 20%, the total drift of the building is approximately doubled compared to the cases when S_r ≥ 32%.The difference is clearly shown in the plots of Figure 7, where the MSDA curves of the A-Sr8, A-Sr12, A-Sr16, A-Sr20, A-Sr32, A-Sr54, A-Sr63, and A-Sr80 models are shown. In particular, the median value of the total drift at the last scaling step was 4.1% for the A-Sr8 model, while for A-Sr32 up to A-Sr80 models remained close to 2.14%. Note that 4.1% exceeds the “Extensive Damage State” threshold values: 0.0245 and 0.04, respectively, for old (“Pre-Code”) and even new (“High-Code”) masonry buildings, according to HAZUS methodology (FEMA, 2003).

FIGURE 7

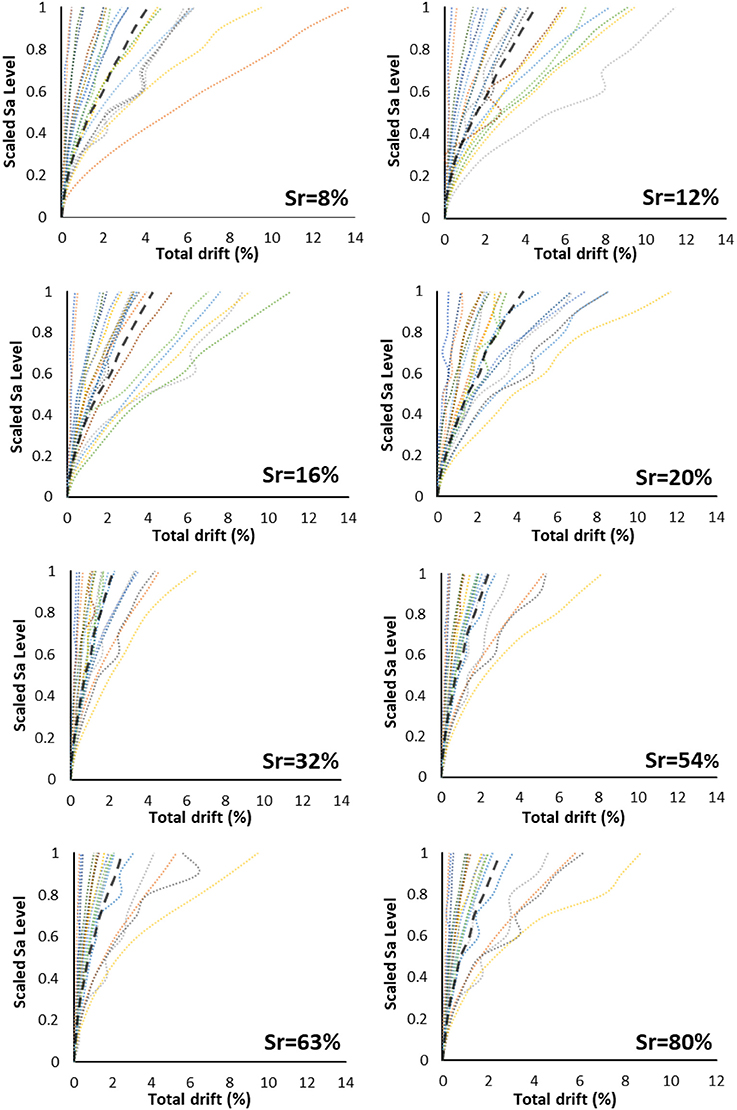
Figure 7. Total drift MSDA curves for the building in its initial state, in which dashed curves show median values.

The change of the median values of the total drift with respect to the degree of saturation of the soil, are more clearly shown in Figure 8, in which the variation of median values response of the MSDA process for the 10 scaling steps is illustrated. Evidently, bottom curve shows that soil conditions do not influence the results due to the low seismic intensity and the resulting linear response. Conversely, the dispersion of results starts from the third scaling step and gradually increases as the seismic intensity is amplified. It appears that the behavior of the A-Sr8, A-Sr12, A-Sr16, and A-Sr20 models is worse than the corresponding ones of the A-Sr32, A-Sr53, A-Sr64, and A-Sr80 models. This finding indicates that after a critical soil saturation level (i.e., Sr 20%) the decrease of the soil stiffness due to the increase of soil saturation, is beneficial for the structure.

FIGURE 8

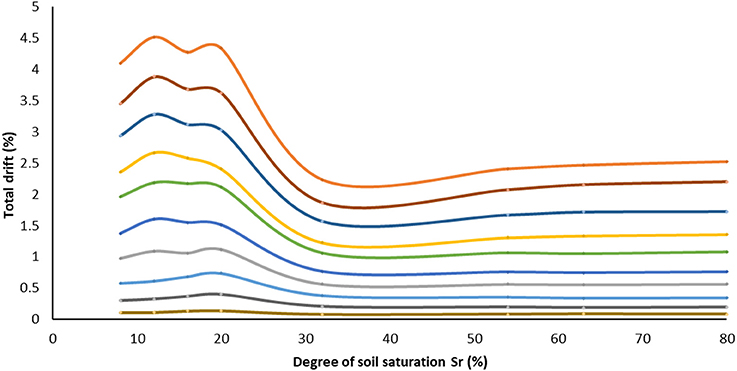
Figure 8. Building in its initial state: total drift as a function of soil saturation level for the 10 scaling steps. Curves present median values of the MSDA process.

Since the drifts of the initial building are quite high, therefore the retrofitting of the structure was deemed necessary, even with the deliberately chosen scheme of a slight intervention with reinforced concrete lintels and friezes. The application of the RC members improved significantly the dynamic response of the building, reducing the total drift below 1.43% at the final scaling step and almost three times less than the corresponding median values of the original building.

As it is presented in Figure 9, when the building is founded on soil with a Sr 20%, the median value of total drift at the last scaling step is quite low (e.g., for B-Sr8 it is 1.24%), whereas in B-Sr32, B-Sr54, B-Sr63, and B-Sr80 models the drifts are even smaller. Even after the retrofitting, the response of the structure varies depending on the degree of soil saturation; nonetheless, the variation is obviously marginal compared to the structure in its initial state. As it is depicted in Figure 9, the response of the structure is slightly better for high degrees of saturation. However, the decrease of the total drift with respect to the increase of the degree of saturation is not so intense compared to the original building, as shown in Figure 10.

FIGURE 9

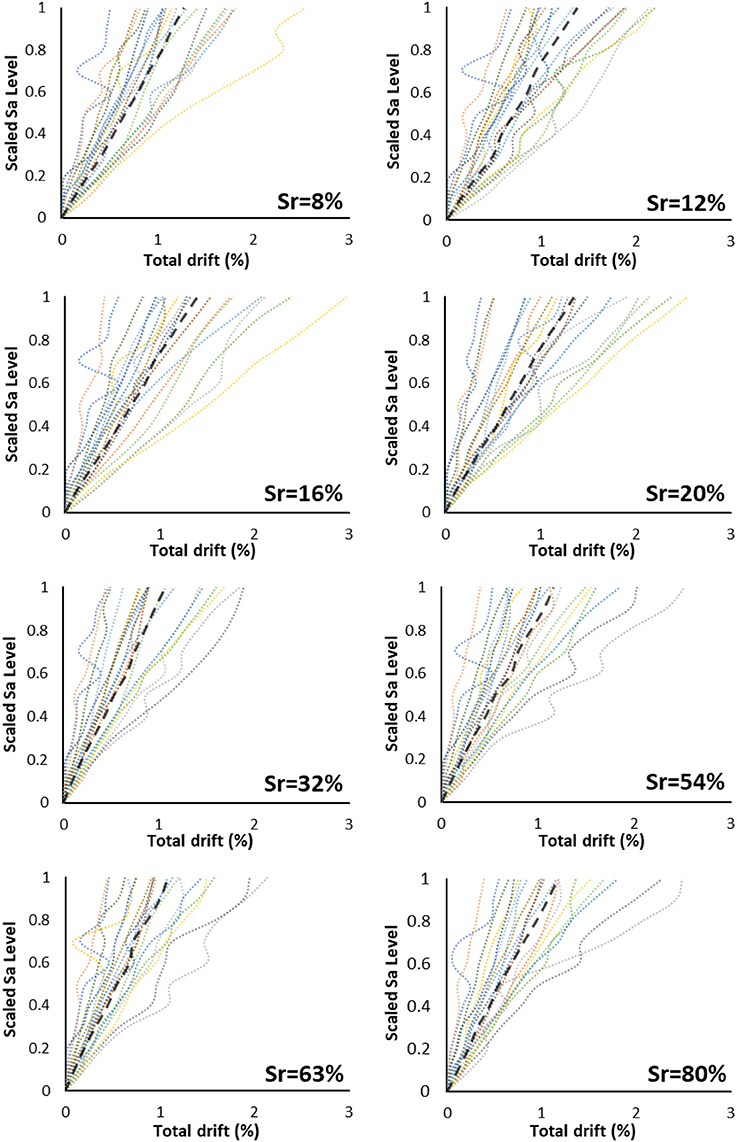
Figure 9. Total drift MSDA curves for the retrofitted building, in which dashed curves show median values.

FIGURE 10

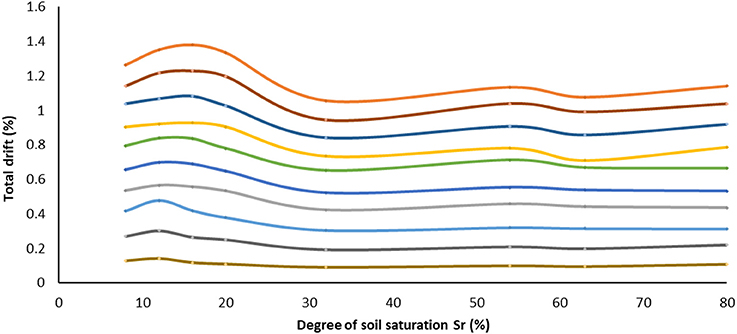
Figure 10. Retrofitted building: total drift as a function of soil saturation level for the 10 scaling steps. Curves present median values of the MSDA process.

This is further illustrated in the comparative plot of Figure 11, in which the improvement of the response by retrofitting the structure is clearly shown. Moreover, it has to be noticed that during the first scaling steps the MSDA curves of the original and the retrofitted buildings are identical. In other words, for low seismic intensity levels the soil saturation conditions do not play a crucial role. More specifically, for higher saturation levels (S_r > 32%), the response of the structure is not particularly improved in the first four steps of record scaling (up to 40% of maximum spectral acceleration). For higher scaling values, the application of this retrofitting scheme, drastically improves the response of the structure. For high degrees of saturation, the improvement of the response of the structure is even more pronounced. This improvement is not only in terms of median values, but in the dispersion of the MSDA curves as well, which is evident by comparing subplots of Figures 7, 9 for the same Sr. Moreover, the total drift of the original model is significantly higher than those of the retrofitted building. More specifically, in the last step of scaling process, the response of the structure is remarkably improved, since the total drifts (i.e., upper extreme MSDA curves) are more than four to five times lower for all saturation levels.

FIGURE 11

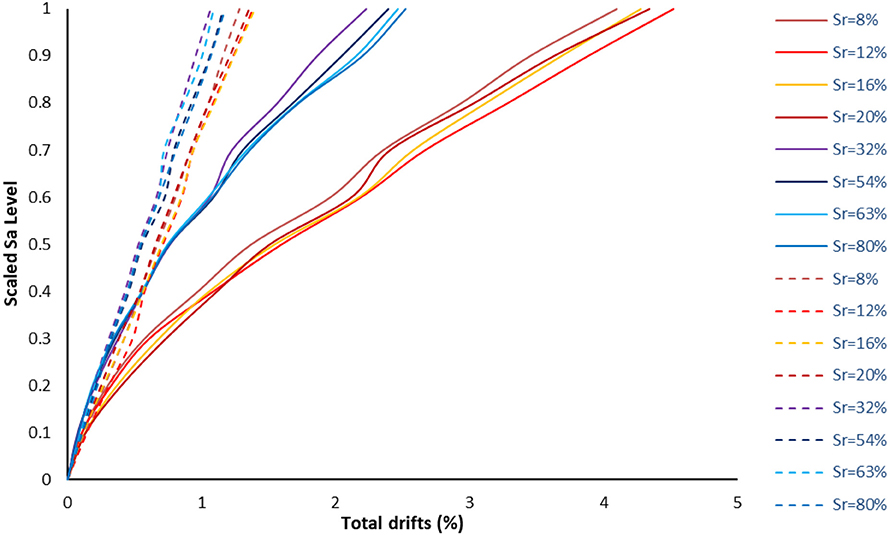
Figure 11. Total drift median MSDA curves for the building in its initial state (solid curves) and the retrofitted building (dashed curves).

In Figure 11, the results of the initial UMR building seem to be grouped, i.e., to have slight variations for low (S_r = 8–20%) and high (S_r = 32–80%) saturation levels. This is due to the variation of soil stiffness for these soil conditions, since according to the experimental data (adopted from Byun et al., 2013), the impact of saturation level for the examined soil substantially affects its basic mechanical parameters. As it can be easily observed in the plots of Figure 3, Young and shear moduli values do not change significantly for low and especially for high saturation levels and this directly affects the dynamic response of the initial masonry building. In contrast, the slight retrofitting -among the other beneficial impacts on the building's dynamic response- results in a substantial reduction of the scattering of the results and decreases substantially the impact of soil saturation conditions.

Conclusions

In this work the seismic response of a typical two-story masonry building was studied via finite element modeling utilizing an incremental non-linear dynamic process. In particular, the interaction of the building with the silty sand soil layer for various saturation levels was examined. In addition, the impact of the minor retrofitting of the building with reinforced concrete lintels and friezes was also investigated. This study confirmed that, despite the excessive computational cost and the complexity of its implementation, incremental dynamic analysis is a robust method for seismic design and/or assessment of masonry structures. Through a large range of possible problem resolutions, the application of the method can assist engineers to fully understand and correctly assess the seismic performance of a structure for a variety of different settings.

The original hypothesis that the response of the structure is influenced by the degree of soil saturation was confirmed by the results. Both the original and the retrofitted building, presented higher drifts when the structure is constructed on relatively dry soil. This is attributed to the decrease of soil stiffness for higher saturation levels. Additionally, it is worth noticing the improvement of the response of the building due to the minor retrofitting with RC lintels and friezes. These light interventions significantly reduce the total drifts as well as the scattering of the results due to varying soil saturation conditions. Certainly, alternative retrofitting schemes could be investigated in order to examine their effectiveness in similar soil conditions. Furthermore, the time-varying soil saturation level during a year (i.e., dry in summer) should also be investigated in order to implement the findings of this study into a life-cycle analysis framework.

Finally, it should be added that higher drifts at control nodes do not necessarily correspond to higher damage levels. Aspects such as yielding and ultimate displacements and ductility influence the structural response and resulting damages. A more detailed investigation regarding the vulnerability assessment of the examined masonry buildings needs to be performed as an extension of the present work.

Author Contributions

YT supervised the study and guided AL to carry out the literature review, to develop the numerical models and to perform the required runs for the repeated dynamic analyses. Both authors analyzed and interpreted the results and contributed to the completion of the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to thank Dr. A. Sextos and Dr. E. Katsanos for providing useful advice regarding the application of ISSARS software.

References

Abdelmegeed, M. M. M. (2015). Damage Assessment and Rehabilitation of Historic Traditional Structures. Ph.D. thesis, School of Civil Engineering, National Technical University of Athens, Greece.

Al Rjoub, Y. S. (2007). Soil Structure Interaction in Poroelastic Soils. Ph.D. thesis, University of Southern California, Los Angeles, CA.

Branco, M., and Guerreiro, L. M. (2011). Seismic rehabilitation of historical masonry buildings. Eng. Struct. 33, 1626–1634. doi: 10.1016/j.engstruct.2011.01.033

CrossRef Full Text | Google Scholar

Byun, Y. H., Lee, J. S., Cho, S. H., and Yoon, H. K. (2013). “Evaluation of void ratio and elastic modulus of unsaturated soil using elastic waves,” in Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering (Paris).

Caddemi, S., Caliò, I., Cannizzaro, F., and Pantò, B. (2017). New frontiers on seismic modeling of masonry structures. Front. Built Environ. Earthquake Eng. 3:39. doi: 10.3389/fbuil.2017.00039

CrossRef Full Text | Google Scholar

Casini, F., Vassallo, R., Mancuso, C., and Desideri, A. (2008). “Application to a compacted soil of a Cam Clay model extended to unsaturated conditions,” in Proceedings of the 1^st European Conference of Unsaturated Soils (E-Unsat 2008) (Durham), 609–615.

Google Scholar

Chronopoulos, M., and Zygouris, N. (2008). “Issues related to seismic design of traditional buildings, examples of retrofitting/mitigation applications,” in Seminar on Seismic Protection of Traditional Buildings (Athens).

EC5 (2004). Eurocode 5: Design of Timber Structures - Part 1-1: General - Common Rules and Rules for Buildings. Brussels: European Committee for Standardization (CEN).

EC6 (2005). Eurocode 6: Design of Masonry Structures-Part 1-1: General Rules for Reinforced and Unreinforced Masonry Structures. Brussels: European Committee for Standardization (CEN).

EC8 (2004). Eurocode 8: Design Provisions of Structures for Earthquake Resistance. Brussels: European Committee for Standardization (CEN).

EQ-Assess (2016). The Seismic Assessment of Existing Buildings. Part C8: Seismic Assessment of Unreinforced Masonry Buildings. EQ-Assess Project. Available online at: http://www.eq-assess.org.nz/wp-content/uploads/2016/05/Part-C8-Seismic-Assessment-of-Unreinforced-Masonry-Buildings.pdf

Fall, M., Samb, S. S., Ndiaye, M., Sall, O. A., and Samb, F. (2011). Cam-clay models using Castem 2000 and Plaxis for the study of the slope stability of the “CornicheOuest” of the Dakar Peninsula (Senegal, West Africa). Geomaterials 1, 51–58. doi: 10.4236/gm.2011.12009

CrossRef Full Text | Google Scholar

FEMA (2003). HAZUS-MH-Multi-Hazard Loss Estimation Methodology. Technical and user's manual. Washington, DC: Federal Emergency Management Agency.

FEMA-440 (2005). Improvement of Nonlinear Static Seismic Analysis Procedures. Washington, DC: Federal Emergency Management Agency.

Frankie, T., Gencturk, B., and Elnashai, A. (2013). Simulation-based fragility relationships for unreinforced masonry buildings. ASCE J. Struct. Eng. 139, 400–410. doi: 10.1061/(ASCE)ST.1943-541X.0000648

CrossRef Full Text | Google Scholar

Gazetas, G. (2015). 4th Ishihara lecture: soil–foundation–structure systems beyond conventional seismic failure thresholds. Soil Dyn. Earthquake Eng. 68, 23–39. doi: 10.1016/j.soildyn.2014.09.012

CrossRef Full Text | Google Scholar

Giovenale, P., Cornell, C. A., and Esteva, L. (2004). Comparing the adequacy of alternative ground motion intensity measures for the estimation of structural responses. Earthquake Eng. Struct. Dyn. 33, 951–979. doi: 10.1002/eqe.386

CrossRef Full Text | Google Scholar

Haselton, C., Whittaker, A. S., Hortacsu, A., Baker, J. W., Bray, J., and Grant, D. (2012). “Selecting and scaling earthquake ground motions for performing response-history analysis,” in Proceedings of the 15th World Conference on Earthquake Engineering, Paper 4383, (Lisbon).

Google Scholar

Iervolino, I., Galasso, C., and Cosenza, E. (2009). REXEL: Computer aided record selection for code based seismic structural analysis. Bull. Earthquake Eng. 8, 339–362. doi: 10.1007/s10518-009-9146-1

CrossRef Full Text | Google Scholar

Kappos, A. J., Panagopoulos, G., Panagiotopoulos, C., and Penelis, G. (2006). A hybrid method for the vulnerability assessment of R/C and URM buildings. Bull. Earthquake Eng. 4, 391–413. doi: 10.1007/s10518-006-9023-0

CrossRef Full Text | Google Scholar

Karantoni, F., Lyrantzaki, F., Tsionis, G., and Fardis, M. N. (2012). “Seismic fragility functions of stone masonry buildings,” in Proceedings of the 15^thWorld Conference on Earthquake Engineering, Paper 5229, (Lisbon).

Google Scholar

Karatzetzou, A., Pitilakis, D., KrŽan, M., and Bosiljkov, V. (2015). Soil–foundation–structure interaction and vulnerability assessment of the neoclassical school in Rhodes, Greece. Bull. Earthquake Eng. 13, 411–428. doi: 10.1007/S10518-014-9637-6

CrossRef Full Text | Google Scholar

Katsanos, E. I., and Sextos, A. G. (2013). ISSARS: An integrated software environment for structure-specific earthquake ground motion selection. Adv. Eng. Softw. 58, 70–85. doi: 10.1016/j.advengsoft.2013.01.003

CrossRef Full Text | Google Scholar

KrŽan, M., Gostič, S., Cattari, S., and Bosiljkov, V. (2015). Acquiring reference parameters of masonry for the structural performance analysis of historical buildings. Bull. Earthquake Eng. 13, 203–236. doi: 10.1007/s10518-014-9686-x

CrossRef Full Text | Google Scholar

Lagomarsino, S. (2015). Seismic assessment of rocking masonry structures. Bull. Earthquake Eng. 13, 97–128. doi: 10.1007/s10518-014-9609-x

CrossRef Full Text | Google Scholar

Lagomarsino, S., and Cattari, S. (2015). Perpetuate guidelines for seismic performance-based assessment of cultural heritage masonry structures. Bull. Earthquake Eng. 13, 13–47. doi: 10.1007/s10518-014-9674-1

CrossRef Full Text | Google Scholar

Liratzakis, A. (2016). Impact of Soil Saturation Level on Structural Assessment and Retrofitting of Masonry Buildings via Incremental Dynamic Non-Linear Analysis. MSc. thesis, School of Architectural Engineering, Technical University of Crete, Greece.

McDowell, G. R., and Hau, K. W. (2004). Ageneralized modified Cam clay model for clay and sand incorporating kinematic hardening and bounding surface plasticity. Granular Matter 6, 11–16. doi: 10.1007/s10035-003-0152-8

CrossRef Full Text | Google Scholar

Millen, M. D. L., Pampanin, S., Cubrinovski, M., and Carr, A. (2014). “A design framework for soil-foundation-structure interaction,” in Proceedings of 2ndEuropean Conference in Earthquake Engineering and Seismology (ECEES) (Istanbul).

MSC Marc (2014). Marc 2014.2: Software Documentation. MSC Software Corporation, Newport Beach, CA.

Mylonakis, G., and Gazetas, G. (2000). Seismic soil–structure interaction: beneficial or detrimental? J. Earthquake Eng. 4, 277–301. doi: 10.1080/13632460009350372

CrossRef Full Text | Google Scholar

Negulescu, C., Ulrich, T., Seyedi, D. M., and Baills, A. (2014). Fragility curves for masonry structures submitted to permanent ground displacements. Nat. Hazards 74, 1461–1474. doi: 10.1007/s11069-014-1253-x

CrossRef Full Text | Google Scholar

Paolucci, R., Figini, R., and Petrini, L. (2013). Introducing dynamic nonlinear soil-foundation-structure interaction effects in displacement-based seismic design. Earthquake Spectra 29, 475–496. doi: 10.1193/1.4000135

CrossRef Full Text | Google Scholar

PEER (2015). PEER NGA-West2ground Motion Database. Pacific Earthquake Engineering Research Center, University of California, Berkeley, CA. Available online at: http://ngawest2.berkeley.edu/

Pecker, A., Paolucci, R., Chatzigogos, C., Correia, A. A., and Figini, R. (2014). The role of non-linear dynamic soil–foundation interaction on the seismic response of structures. Bull. Earthquake Eng. 12, 1157–1176. doi: 10.1007/s10518-013-9457-0

CrossRef Full Text | Google Scholar

Pitilakis, D., and Karatzetzou, A. (2015). Dynamic stiffness of monumental flexible masonry foundations. Bull. Earthquake Eng. 13, 67–82. doi: 10.1007/s10518-014-9611-3

CrossRef Full Text | Google Scholar

Reyes, J. C., and Kalkan, E. (2012). How many records should be used in an ASCE/SEI-7 ground motion scaling procedure? Earthquake Spectra 28, 1223–1242. doi: 10.1193/1.4000066

CrossRef Full Text | Google Scholar

Rota, M., Penna, A., and Magenes, G. (2010). A methodology for deriving analytical fragility curves for masonry buildings based on stochastic nonlinear analyses. Eng. Struct. 32, 1312–1323. doi: 10.1016/j.engstruct.2010.01.009

CrossRef Full Text | Google Scholar

Saez, E. (2009). Dynamic Non-Linear Soil-Structure Interaction. Ph.D. thesis, Ecole Centrale, Paris.

Senaldi, I., Magenes, G., Penna, A., Galasco, A., and Rota, M. (2014). The effect of stiffened floor and roof diaphragms on the experimental seismic response of a full-scale unreinforced stone masonry building. J. Earthquake Eng. 18, 407–443. doi: 10.1080/13632469.2013.876946

CrossRef Full Text | Google Scholar

Tothong, P., and Cornell, C. A. (2007). Probabilistic Seismic Demand Analysis Using Advanced Ground Motion Intensity Measures, Attenuation Relationships, and Near-Fault Effects. PEER Report 2006/11, University of California, Berkeley, CA.

Vamvatsikos, D., and Cornell, C. A. (2002). Incremental dynamic analysis. Earthquake Eng. Struct. Dyn. 31, 491–514. doi: 10.1002/eqe.141

CrossRef Full Text | Google Scholar

Veletsos, A. S., and Meek, J. W. (1974). Dynamic behaviour of building-foundation systems. Earthquake Eng. Struct. Dyn. 3, 121–138. doi: 10.1002/eqe.4290030203

CrossRef Full Text | Google Scholar