Experimental Study on Influence of Hardening of Isolator in Multiple Isolation Building

Introduction

The multiple isolation system has been proposed recently to upgrade the performance of seismic vibration suppression of existing base-isolated buildings (Pan et al., 1995; Pan and Cui, 1998; Chey et al., 2013; Tsuji et al., 2014; Tracy and Ashkan, 2016). Although the base isolation system for building structures is well known as an effective mechanism to control the inter-story drifts and accelerations of superstructures (Naeim and Kelly, 1999; Ariga et al., 2006; Takewaki, 2008), there exists a great concern that the long-period and long-duration ground motions may cause severe damage to isolators. In order to prevent the damage to seismic isolators and the collision to retaining walls due to the large deformation of the isolators, various approaches have been studied so far, e.g., mid-story isolation system (Sueoka et al., 2004; Wang et al., 2012), inter-story isolation system (Ryan and Earl, 2010), inter-connection system (Dua and Jain, 2004; Murase et al., 2013), and so on. The multiple isolation system is one of these solutions where the deformation of the base isolators can be decreased by distributing a part of the input energy to the mid-story isolators. So far, some researchers have investigated the multiple isolation system numerically (Pan et al., 1995). However, to the best of the authors’ knowledge, the multiple isolation system has never been applied to the project of seismic upgrading of the existing base-isolated buildings or the new construction.

It is known that there exist hardening phenomena in the seismic isolators (natural rubber bearings and lead rubber bearing). The hardening property often causes the increase of the shear stiffness of isolators in a large deformation range (Kikuchi and Aiken, 1997; Kikuchi et al., 2010). Therefore, it seems important to evaluate the structural safety of the base-isolated building under the influence of such non-linearity of the isolators (Alhan and Gavin, 2004). When we take into account, the influence of the seismic isolator’s hardening property in the large deformation range caused by extremely strong far-field ground motion with long period, it should be discussed whether the response of the superstructure may also increase compared with the case without hardening. However, since the modeling of the isolator’s restoring-force characteristic, including the hardening effect, is still difficult in the strong non-linearity domain, a simplified analytical model of isolators should be investigated in more detail in the response evaluation.

This paper presents an experimental study on the multiple isolation system. It is compared with the base-isolation system, especially in terms of the influence of non-linearity (hardening) in the restoring-force characteristic of isolators. The vibration test using a shaking table is implemented for scaled structural models. The scaled base-isolated model is also used to assess the basic properties of the multiple isolation system. Furthermore, the non-linear restoring-force characteristic in the scaled model is provided through the geometrical non-linearity by placing the linear springs in the direction perpendicular to the vibration direction. By considering various isolators and combination of various springs, the influence of the hardening effect on the response is investigated experimentally for the multiple isolation model and base-isolated model. In the numerical simulation, the observations from the experimental results are investigated in detail.

Multiple Isolation Model with Hardening Effect of Seismic Isolators

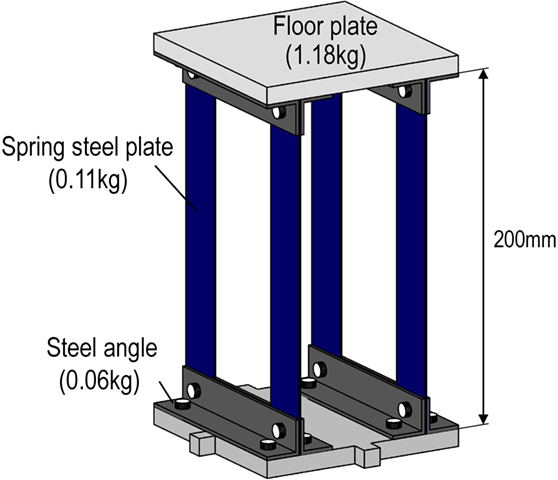
A simplified seismic analysis of conventional base-isolated buildings can be conducted by regarding both the superstructure and the base isolation story as a one-degree-of-freedom (1DOF) system. The basic seismic performance of the base-isolated building can be investigated by using such 2DOF model. Figure 1A shows the relationship between an actual base-isolated building and its simplified 2DOF structural model. In a similar way, the multiple isolation building can be reduced into a 4DOF model as a simple analytical model as shown in Figure 1B. This 4DOF model is composed of a base isolation layer, a mid-story isolation layer, a superstructure below the mid-story isolation layer, and a superstructure above the mid-story isolation layer. Two kinds of scaled structural models, i.e., the multiple isolation model and the base isolation model, are designed to investigate the multiple isolation system experimentally. Figure 2 shows the elevation of these scaled structural models. In order to compare the seismic vibration suppression performance of the multiple isolation structure with that of the base isolation structure in the experimental study, the base-isolated structural model is given by fixing the mid-story isolation layer in the multiple isolation structural model. Therefore, the structural property of this base-isolated structural model is the same as that of the multiple isolation model except the existence of the mid-story isolation layer. Figure 3 shows the overview of the scaled multiple isolation model on the shaking table.

FIGURE 1

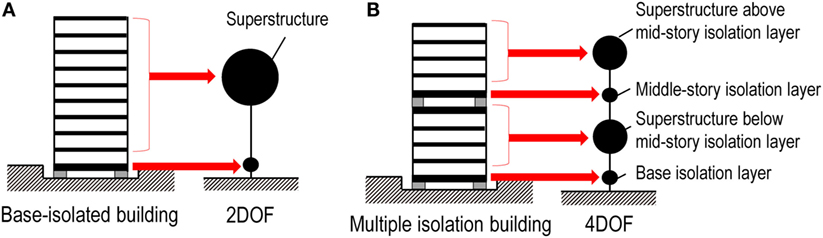
Figure 1. Simplified analytical model of isolated buildings: (A) base-isolated building and (B) multiple isolation building.

FIGURE 2

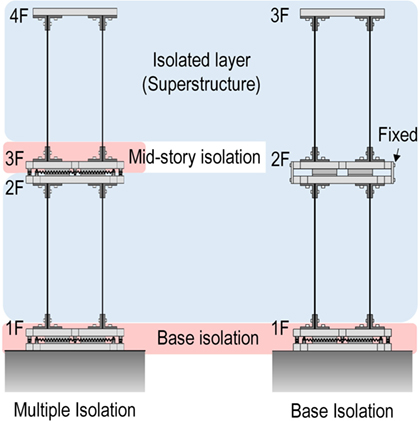
Figure 2. Elevation of scaled structural models: multiple isolation model (left) and base-isolation model (right).

FIGURE 3

Figure 3. Overview of scaled multiple isolation model.

In order to investigate the mechanism of response suppression in the multiple isolation system and the influence of the hardening of isolators in the multiple isolation building by using a scaled structural model, the mechanical demands of the isolation layer in the scaled structural model have been set. This can be summarized as follows: the relatively small horizontal stiffness compared with the superstructure, the large stroke, the resistance to the vertical loading, and the appropriate damping. Furthermore, in order to consider the hardening effect of the isolators, a mechanical system to provide the non-linear restoring-force characteristic in the isolation layer has been introduced.

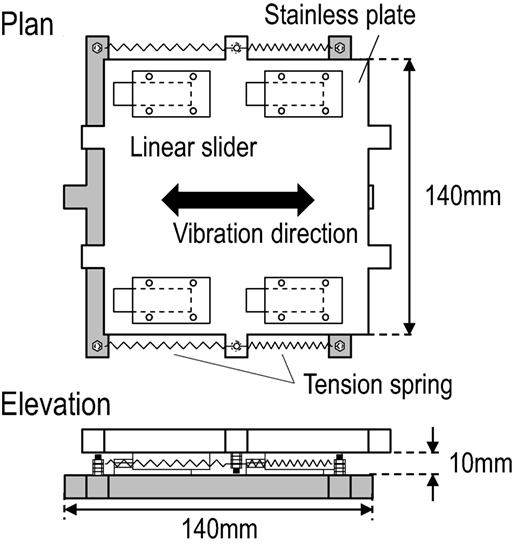
As a seismic isolator in the scaled structure model, a linear slider (BSG-H10) is used to provide a large horizontal stroke in the scaled structural model. The maximum stroke of this isolator is 11 mm in the half amplitude. The isolation layer is supported by four isolators placed in the corner on the base. This placement of the isolators can be resistant to the overturning moment caused by the large deformation of the superstructure. It is also confirmed that the friction of these isolators can provide the appropriate hysteretic damping. Figure 4 shows the photo of the linear slider.

FIGURE 4

Figure 4. Linear slider (BSG-H10).

A restoring-force characteristic in the isolation layer is given by the tension springs. Two different placements of the springs are introduced, so as to consider the influence of the hardening of the isolators. First, the tension springs are inserted in parallel with the vibration direction as shown in Figure 5. This placement of the springs provides the linear restoring-force characteristic F_l for the horizontal displacement y of the isolation layer, which can be described by

FIGURE 5

Figure 5. Placement of tension spring (linear restoring-force characteristic).

$F_{\text{l}}=4ky$ (1)

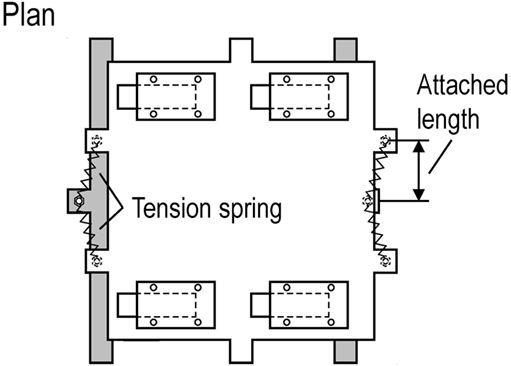
where k denotes the spring constant. In another spring placement, the tension springs are inserted perpendicular to the vibration direction as shown in Figure 6, which can provide a geometrical non-linearity. The non-linear restoring-force characteristic F_n in this isolator placement can be described by

FIGURE 6

Figure 6. Placement of tension spring (non-linear restoring-force characteristic).

$F_n=4\left\{k\left(\sqrt{L^2+y^2}-L_0\right)+f_0\right\}\frac{y}{\sqrt{L^2+y^2}}$ (2)

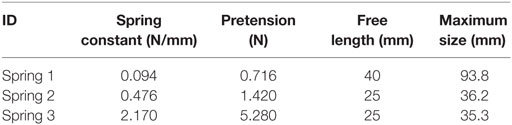
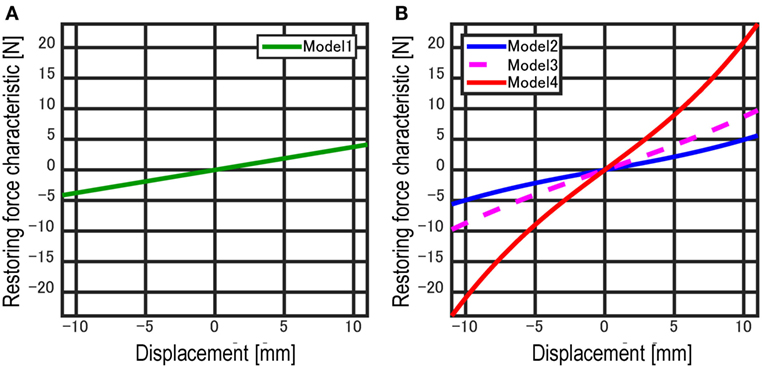
where L₀, f₀, and L are a free length, an initial force, and an attached length of the tension spring, respectively. Table 1 shows the list of the tension springs used in the scaled structural model. Figure 7 shows the comparison of restoring-force characteristics F_l and F_n evaluated by the specified spring constant shown in Table 1. The combination of the tension springs is summarized in Table 2. The non-linearity of the restoring-force can be observed from Figure 7B.

TABLE 1

Table 1. Linear spring property.

FIGURE 7

Figure 7. Restoring-force characteristic of isolation layer: (A) linear and (B) non-linear.

TABLE 2

Table 2. Isolation layer property.

The superstructure as the isolated story is composed of the spring steel plates and steel angles as shown in Figure 8. The end of the spring steel plate is fixed to the floor plates by steel angles. By neglecting the rigid part in the spring steel plates fixed by steel angles, the restoring-force of the non-isolation layer can be derived as

$F=\frac{4Eb{t}^3}{h^3}y$ (3)

where b, h, t, and E denote the width, height, thickness of the spring steel plate, and Young’s modulus, respectively.

FIGURE 8

Figure 8. Components of isolated story.

Experimental Results

Static Loading Test for Evaluation of Restoring-Force Characteristic of Isolated Layer

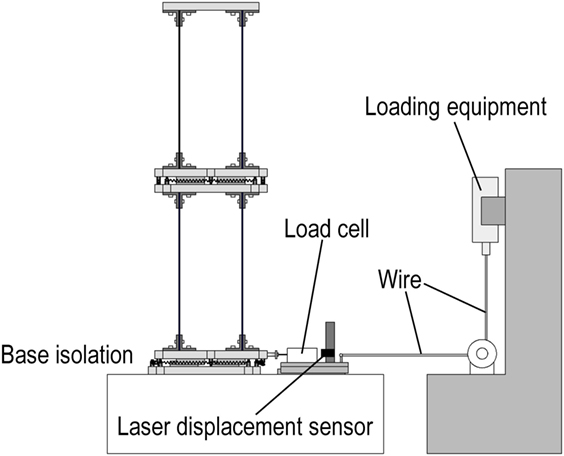
The static loading test is planned to confirm the basic characteristic of the isolation layer where the tension springs are inserted by two different ways as shown above (Figures 5 and 6). The properties of the restoring-force characteristic and the friction in the isolation layer can be evaluated in the static loading test. The setup of the static loading test is illustrated in Figure 9. In the static loading test, the mid-story isolation layer is fixed and all components are installed, which can provide the vertical loading to the isolators. The base isolation layer is pulled directly by a loading machine. The relationship between the restoring-force and the displacement in the isolation layer can be evaluated by the recorded data from a load cell attached to the load supporting equipment and a laser displacement sensor.

FIGURE 9

Figure 9. Static loading test.

Figure 10 shows the obtained non-linear restoring-force characteristic of the isolation layer where two different combinations of the tension springs (Models 2 and 4 defined in Table 2) are compared. In Figure 10, the restoring-forces simulated in Eq. 2 using the specified spring properties are also shown. In this simulation, the influence of the friction force is neglected. From this figure, the results in the static loading test are well simulated within an allowable accuracy by using the specified spring properties. Furthermore, the hardening in the restoring-force characteristic can be observed also in the experimental results. It may be concluded that the stiffness of the isolation layer can be estimated by using the specified spring stiffness as shown in Table 1. In addition, the friction force can be observed from the difference between the positive and negative loadings’ paths in Figure 10. However, the estimated friction coefficient in the isolation layer is not identical in these two different spring combinations. This may be caused by unavoidable setting error at the supporting member of tension springs and the temperature dependency of the friction by lubricant in the linear sliders. Since it is difficult to control these various uncertainties, the friction force at the isolators, i.e., a friction coefficient, cannot be determined in this static loading test. In the numerical simulation, the friction coefficient is identified parametrically.

FIGURE 10

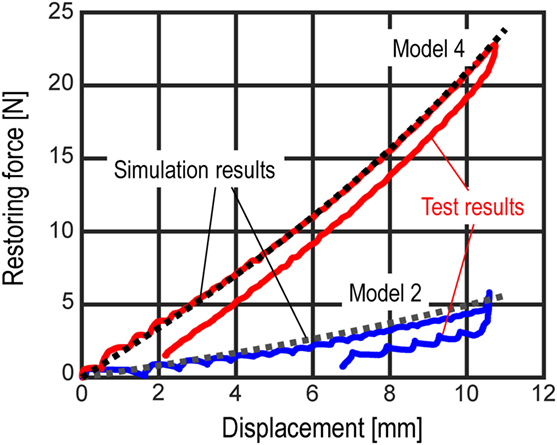
Figure 10. Comparison of restoring-force characteristic of isolation layer from static loading test with simulation.

Sweeping Test for Evaluation of Transfer Function

The sweeping test where the input frequency is gradually varied in the specified frequency range is applied to estimate the natural frequencies and the transfer function of the scaled structural models. A compact shaking table is used for the vibration tests. In the case where the amplitude of the acceleration is controlled to be constant in all frequency range, the displacement of the base input becomes small in a high frequency domain, which causes a difficulty in the measurement of the deformation at the superstructure and the displacement of the isolation layers due to the measurement limitation of the sensors. Therefore, in the sweeping test, the horizontal displacement amplitude of the shaking table is controlled to be almost constant even in the high frequency domain. The acceleration and displacement in each story, including the isolation layers and the shaking table, are measured by accelerometers (AS-2GB, Kyowa-Dengyo) and laser displacement sensors (IL-300, Keyence). The transfer function of each story to the base input is evaluated in a conventional way by using the ratio of the ensemble average of the cross spectrum between the base input and the floor response to that of the power spectrum of the base input. The inter-story drift transfer function indicates the transfer function of the inter-story drift to the base displacement. In addition, the acceleration transfer function indicates the transfer function of the floor acceleration to the base acceleration.

Figure 11 shows the comparison of the inter-story drift and acceleration transfer functions of the base-isolated model with those of the multiple isolation model. The restoring-force characteristics of the isolation layers are non-linear in both the multiple isolation model and the base-isolated model. The non-linear restoring-force characteristics are given by Model 4 defined in Table 2. From these figures, when the structural property of the mid-story isolation layer is the same as that of the base isolation layer, the fundamental natural frequency of the multiple isolation model is smaller than that of the base-isolated model. The difference of the fundamental natural frequency can also be observed from the numerical eigenvalue analysis using the initial stiffness of the isolation layer. Furthermore, the inter-story drifts of both isolation layers and non-isolation layers are decreased in the multiple isolation model. This advantage in the multiple isolation model comes from the energy consumption at the mid-story isolation layer. As for the acceleration response, the peak value of the acceleration transfer function at the isolated story below the mid-story isolation layer in the multiple isolation model becomes smaller than that of the base-isolation model. Therefore, the multiple isolation system is effective to enhance the habitability in lower stories in terms of the acceleration.

FIGURE 11

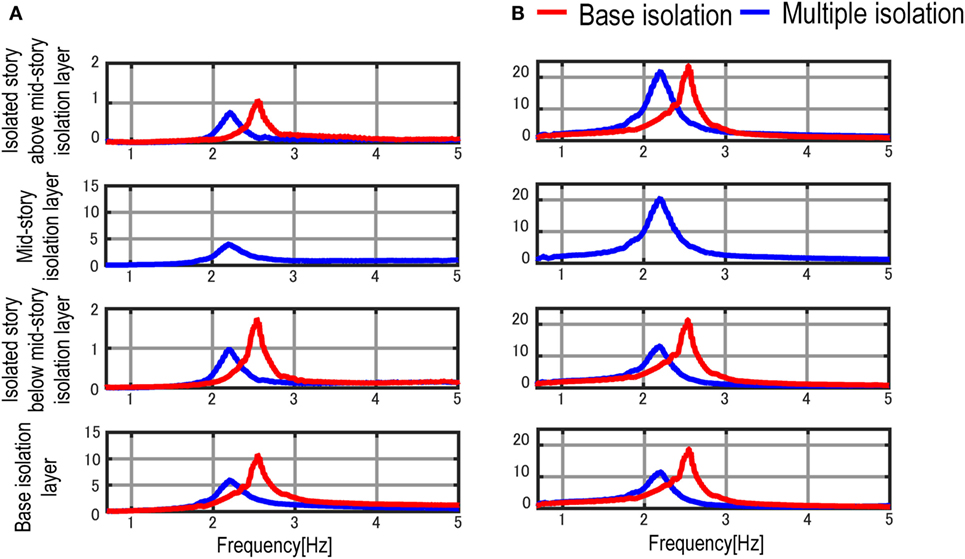
Figure 11. Comparison of multiple isolation model with base-isolated model: (A) inter-story drift transfer function and (B) acceleration transfer function.

Vibration Test Using Long-Duration Stationary Input

Although the sweeping test is useful to obtain the transfer function of the structure, the structural response measured in the sweeping test may include the transient responses due to the limited measurement duration. For evaluating the property of the frequency response in an accurate manner, a stationary sine wave input that has a single specified frequency is input to the scaled structural models. The transfer function of the isolated models, especially focused on the fundamental natural frequency, is evaluated from the ratio of the root mean square (RMS) of the recorded floor responses to that of the base input in each specified frequency.

Figure 12 shows the comparison of the transfer functions of the multiple isolation model, including the isolators of the non-linear restoring-force characteristic (Model 2), with that of the multiple isolation model, including the isolators of the linear restoring-force characteristic (Model 1). Since these multiple isolation models are designed to have almost the same initial stiffness, the frequency response of these multiple isolation models can be compared in the same frequency range. From Figure 12, it can be observed that the variation in the transfer function in the multiple isolation model with non-linear restoring-force characteristic is small in the frequency range around the fundamental natural frequency. As seen in the amplitude of transfer functions, both the inter-story drift and acceleration in the multiple isolation model with the non-linear restoring-force characteristic can be decreased compared with those of the model with the linear restoring-force characteristic. This may result from the difference of the hysteretic damping in the multiple isolation model with non-linear restoring-force characteristic due to the friction in the supporting members. However, in the sweeping test, since this difference in terms of the amplitude of the transfer function cannot be observed clearly, more investigation may be needed.

FIGURE 12

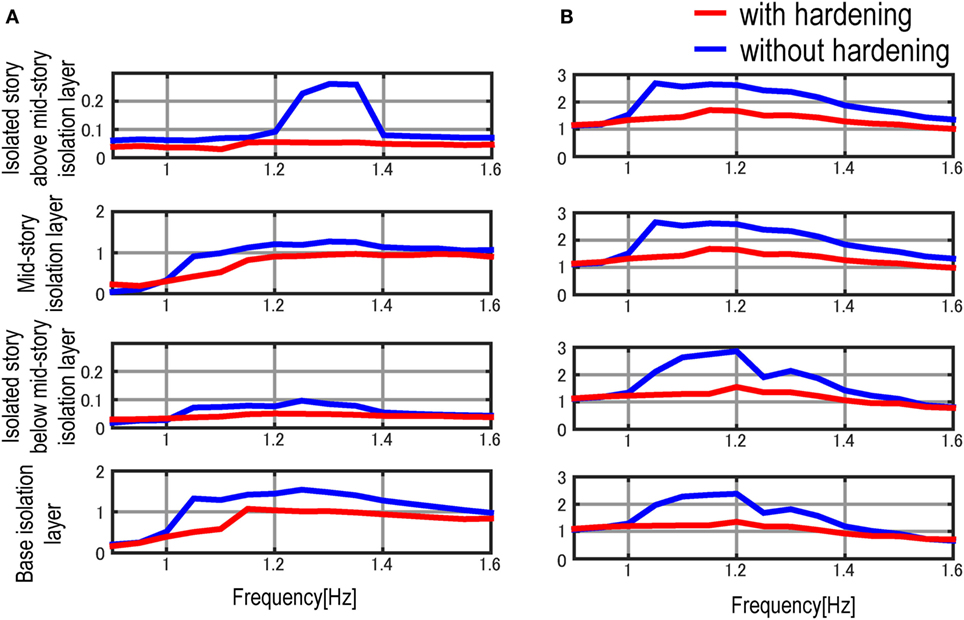
Figure 12. Comparison of linear restoring-force characteristic with non-linear restoring-force characteristic in multiple isolation: (A) inter-story drift transfer function and (B) acceleration transfer function.

Figure 13 presents the influence of the combination of the stiffnesses of the base isolation layer and mid-story isolation layer. In these figures, three different cases are investigated where the stiffnesses of the base isolation layer are the same and the stiffnesses of the mid-story isolation layer are varied. The restoring-force characteristic of the base isolation layer is given by Model 3 in Table 2. The restoring-force characteristic of the mid-story isolation layer is varied using Model 2 (Soft), Model 3 (Normal), and Model 4 (Hard). As seen in Figure 13, the inter-story drift of the base isolation layer and the superstructure’s acceleration below the mid-story isolation layer can be decreased in the case where the stiffness of the mid-story isolation layer is smaller than that of the base isolation layer. Therefore, for enhancing the seismic performance of the base-isolated building, the stiffness of the mid-story isolation layer is recommended to be small compared with the stiffness of the base isolation layer. In addition, when the stiffness of the mid-story isolation layer is the same as that of the base isolation layer, the floor responses (both inter-story drift and acceleration) at the fundamental natural frequency are increased compared with other combinations. This has also been confirmed in the sweeping test.

FIGURE 13

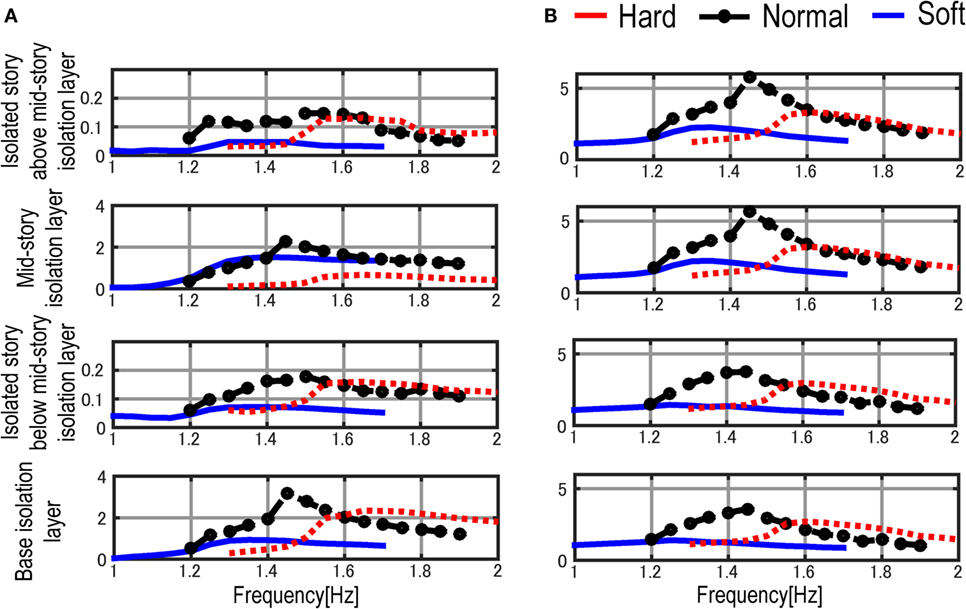
Figure 13. Comparison of various combinations of stiffness of mid-story isolation layer: (A) inter-story drift transfer function and (B) acceleration transfer function.

Numerical Verifications

For verifying the observations from the vibration test, the numerical simulation has been conducted through the time–history response analysis. The mass matrix M is constructed based on the measured mass at each floor and supporting members. Detailed values of masses are shown in Figure 8. The stiffness matrix K for the isolated model with the linear restoring-force characteristic is obtained from the story stiffnesses in Eqs 1 and 3. On the other hand, the restoring-force for the isolated model, including the non-linear restoring-force characteristic, is directly derived using Eq. 2. In addition, the damping matrix C as the structural damping is assumed to be given by the tangent stiffness proportional damping in the non-linear time–history analysis. The damping ratio at the fundamental natural frequency is given by 0.02.

The Coulomb friction at the linear slider is taken into account in the numerical simulations. Since the static friction coefficient is difficult to identify as seen in the static loading test, the static friction effect is given as linear to the inter-story velocity $\dot{y}$ in the time–history analysis when the inter-story velocity is relatively small. The friction force at the isolation layer is given by

$F(\dot{y})=\{\begin{array}{c}-\mu Mg\mathrm{sgn}(\dot{y})(|\dot{y}|\ge v_{\lim })\\ -\mu Mg\dot{y}/v_{\lim }(|\dot{y}|<v_{\lim })\end{array}$ (4)

where μ, M, g, and ν_lim denote the friction coefficient, total mass above the isolators, acceleration of gravity, and limit value ν_lim = 10⁻² m/s, respectively. Finally, in the case where the restoring-force characteristic of the isolation layer is non-linear, the following equation of motion is considered in the time–history response analysis.

$M\ddot{y}+C\dot{y}+Ky=-Mr{\ddot{u}}_g-F_n\left(y\right)-F\left(\dot{y}\right)$ (5)

where F_n(y), $F(\dot{y})$, r, and ${\ddot{u}}_{\text{g}}$ denote the restoring-force in the isolation layer evaluated from Eq. 2, the friction force in the isolation layer, an influence coefficient vector, and the base acceleration, respectively.

The transfer function of the isolated building is given by the ratio of the RMS of the time–history data of floor responses and that of the input excitation. The input excitation is provided as a long-duration stationary sine wave having only one predominant frequency where the displacement amplitude is fixed according to the allowable peak-to-peak amplitude of the objective model. By altering the input frequency, the transfer function of the isolated models, including the hardening property, can be derived. The friction coefficient was parametrically examined by providing the observed transfer function in the numerical simulation. Figure 14 shows the comparison of the acceleration transfer functions derived by using various friction coefficients from μ = 0.002 to 0.02 with that observed in the Section “Vibration Test Using Long-Duration Stationary Input.” It can be observed from Figure 14 that the peak frequency in the transfer function of the multiple isolation model with non-linear isolators moves to higher frequency as the amplitude caused by a smaller friction coefficient becomes larger. This property of the transfer function is specific to non-linear systems with hardening restoring-force characteristic. From these observations in Figure 14, the friction coefficients in the multiple isolation models can be identified and used in the following numerical simulations.

FIGURE 14

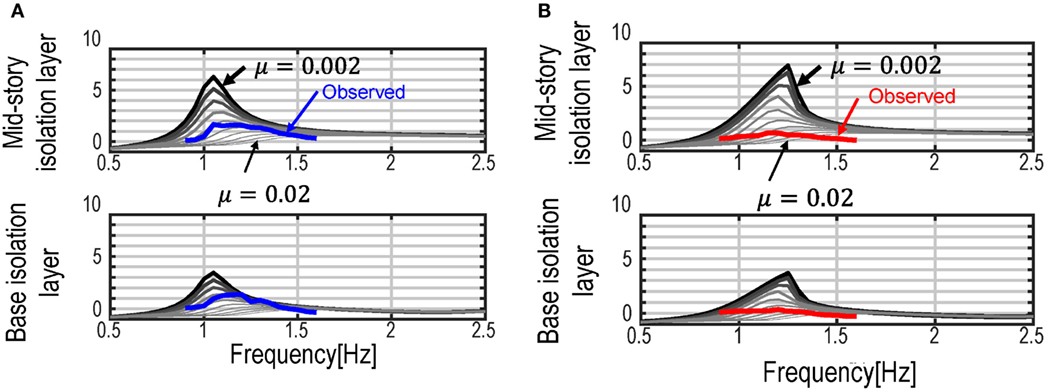
Figure 14. Comparison of simulated acceleration transfer function with observed transfer function: (A) multiple isolation model with linear restoring-force characteristic and (B) multiple isolation model with non-linear restoring-force characteristic.

Figure 15 shows the comparison of the simulated inter-story drift and acceleration transfer functions in the multiple isolation models. The friction coefficient is identified as μ = 0.01. In this figure, the linear and non-linear restoring-force characteristics are investigated in both the base isolation layer and the mid-story isolation layer. The corresponding experimentally derived transfer functions are presented in Figure 12. It can be confirmed from Figure 15 that both the inter-story drift and acceleration amplitudes of the transfer function in the multiple isolation model with the non-linear restoring-force characteristic are decreased compared with the multiple isolation model with the linear restoring-force characteristic. This difference in the transfer function was also observed experimentally in Figure 12.

FIGURE 15

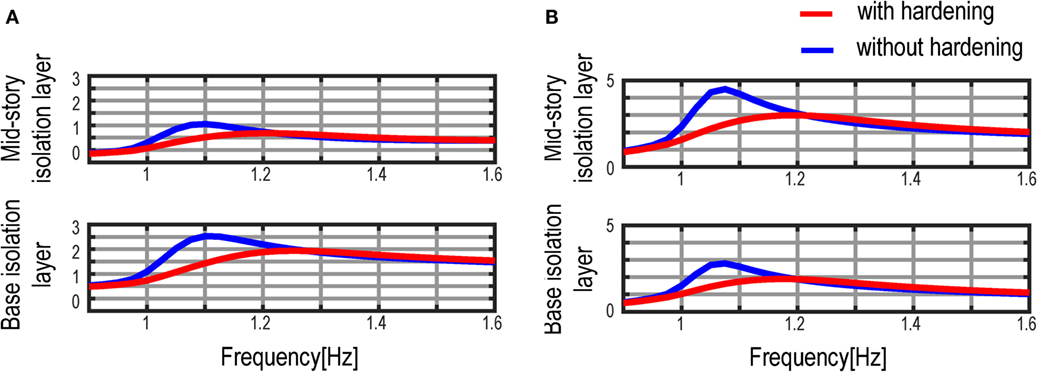
Figure 15. Verification of influence of isolator hardening on transfer functions at isolation layers: (A) inter-story drift transfer function and (B) acceleration transfer function.

Figure 16 shows the verification in terms of the influence of the stiffness combinations. The friction coefficient is fixed as μ = 0.008 in all cases. The corresponding experimental result is shown in Figure 13. From these simulations, it can be confirmed that the amplitudes of the transfer function in terms of the inter-story drift and the acceleration at the base isolation layer can be decreased in the case where the stiffness of the mid-story isolation layer is smaller than that of the base isolation layer. This investigation was also derived in experimentally in Figure 13.

FIGURE 16

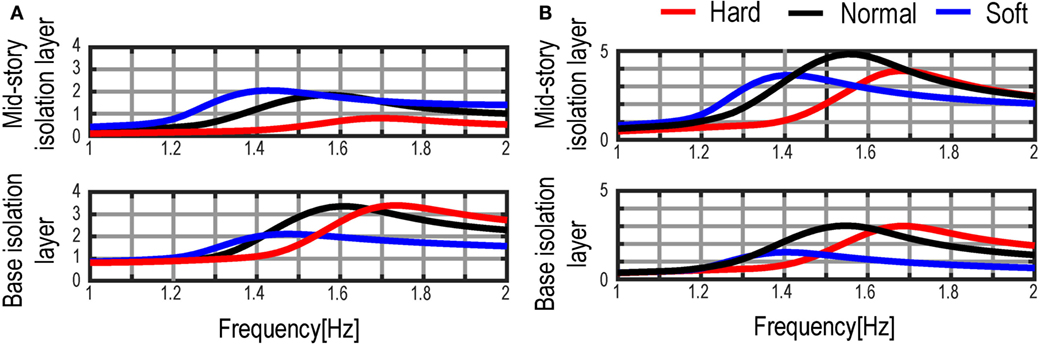
Figure 16. Verification of influence of various stiffness combinations at mid-story isolation layer: (A) inter-story drift transfer function and (B) acceleration transfer function.

Conclusion

The influence of the hardening property of seismic isolators in a multiple isolation building has been investigated by the shaking table test of a scaled structural model and the numerical simulations. Conclusions are summarized as follows.

(1) From the experimentally obtained transfer functions of the multiple isolation structure with a non-linear restoring-force characteristic, it was confirmed that the structural responses, such as inter-story drifts of isolated stories near the fundamental natural frequency, can be decreased compared with the multiple isolation structure with a linear restoring-force characteristic. Similar results were also observed in the numerical simulations. However, it was difficult to simulate numerically the time–history response of the scaled structural model due to the effect of hysteretic damping effect of the isolation layers.

(2) The seismic vibration suppression performance of the multiple isolation structure was assessed by the shaking table test from the following point of view. In the case where the stiffnesses of the base isolation layer have the same values in the multiple isolation structure and the base-isolated structure, the fundamental natural frequency of the multiple isolation structure becomes lower than that of the base-isolated structure. This shifting of the fundamental natural frequency may contribute to the effective seismic upgrading of the existing base-isolated building by reducing the risk of resonance with long-period ground motions. In addition, this shifting is also favorable for the input with a large spectral value in the short period range (approximately 0–2 s). The inter-story drift of the base isolation layer of the multiple isolation structure and the acceleration at the isolated stories below the mid-story isolation layer can be reduced for the stationary sine wave, i.e., a long-duration and long-period ground motion, compared with the base-isolated building.

(3) The influence of the stiffness of the mid-story isolation layer on the seismic vibration suppression performance was investigated by comparing various combinations of the stiffnesses in the mid-story isolation layer and the base isolation layer. For reducing the displacement of the base isolation layer and acceleration in the isolated stories, the stiffness of the mid-story isolation layer needs to be smaller than that of the base isolation layer. When the stiffness of the mid-story isolation layer is almost the same as that of the base isolation layer, the displacement of the base isolation layer and acceleration at the isolated stories are increased, especially under the ground motion such that the predominant frequency is near the fundamental natural frequency of the multiple isolation building.

Author Contributions

KF is a corresponding author and conducted the theoretical, experimental, and numerical analyses. TM conducted the experiment and the numerical simulations. MT contributed to the planning of the experimental models and formulations in the numerical simulations. IT supervised experiment and numerical analysis.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Funding

Part of the present work is supported by the Grant-in-Aid for Scientific Research (KAKENHI) of Japan Society for the Promotion of Science (No. 15H04079). This support is greatly appreciated.

References

Alhan, C., and Gavin, H. (2004). A parametric study of linear and non-linear passively damped seismic isolation systems for buildings. Eng. Struct 26, 485–497. doi: 10.1016/j.engstruct.2003.11.004

CrossRef Full Text | Google Scholar

Ariga, T., Kanno, Y., and Takewaki, I. (2006). Resonant behavior of base-isolated buildings under long-period ground motions. Struct. Des. Tall Special Build. 15, 325–338. doi:10.1002/tal.298

CrossRef Full Text | Google Scholar

Chey, M., Chase, J., Mander, J., and Carr, A. (2013). Innovative seismic retrofitting strategy of added stories isolation system. Front. Struct. Civ. Eng. 7:13–23. doi:10.1007/s11709-013-0195-9

CrossRef Full Text | Google Scholar

Dua, R., and Jain, A. K. (2004). Seismic bifurcation for response-control of tall building structures. J. Struct. Stab. Dyn 4, 197–221. doi:10.1142/S0219455404001197

CrossRef Full Text | Google Scholar

Kikuchi, M., and Aiken, I. D. (1997). An analytical hysteresis model for elastomeric seismic isolation bearings. Earthq. Eng. Struct. Dyn. 26, 215–231. doi:10.1002/(SICI)1096-9845(199702)26:2<215::AID-EQE640>3.3.CO;2-0

CrossRef Full Text | Google Scholar

Kikuchi, M., Ishii, K., and Kato, H. (2010). Prediction of high-damping rubber isolation bearing behavior under large shear deformations and severe axial loads. J. Struct. Eng 56B, 179–188; in Japanese.

Google Scholar

Murase, M., Tsuji, M., and Takewaki, I. (2013). Smart passive control of buildings with higher redundancy and robustness using base-isolation and inter-connection. Earthq. Struct. 4, 649–670. doi:10.12989/eas.2013.4.6.649

CrossRef Full Text | Google Scholar

Naeim, F., and Kelly, J. M. (1999). Design of Seismic Isolated Structure: From Theory to Practice. New York: Wiley.

Google Scholar

Pan, T. C., and Cui, W. (1998). Response of segmental buildings to random seismic motions. J. Earthq. Tech 35, 105–112.

Google Scholar

Pan, T. C., Ling, S. F., and Cui, W. (1995). Seismic response of segmental buildings. Earthq. Eng. Struct. Dyn. 24, 1039–1048. doi:10.1002/eqe.4290240708

CrossRef Full Text | Google Scholar

Ryan, K. L., and Earl, C. L. (2010). Analysis and design of inter-story isolation systems with nonlinear devices. J. Earthq. Eng. 14, 1044–1062. doi:10.1080/13632461003668020

CrossRef Full Text | Google Scholar

Sueoka, Y., Torii, S., and Tsuneki, Y. (2004). “The application of response control design using middle-story isolation system to high-rise building,” in Proceeding of 13th World Conference on Earthquake Engineering, Vancouver.

Google Scholar

Takewaki, I. (2008). Robustness of base-isolated high-rise buildings under code-specified ground motions. Struct. Des. Tall Spec. Build. 17, 257–271. doi:10.1002/tal.350

CrossRef Full Text | Google Scholar

Tracy, B., and Ashkan, E. (2016). Enhanced performance through a dual isolation seismic protection system. Struct. Des. Tall Spec. Build. 25, 72–89. doi:10.1002/tal.1229

CrossRef Full Text | Google Scholar

Tsuji, M., Tsuji, C., and Kataoka, N. (2014). Seismic characteristics of multiple isolation building with plural isolation stories. J. Struct. Constr. Eng. AIJ 79, 1613–1623; in Japanese. doi:10.3130/aijs.79.1613

CrossRef Full Text | Google Scholar

Wang, S., Chang, K., Hwang, J., Hsiao, J., Lee, B., and Hung, Y. (2012). Dynamic behavior of a building structure tested with base and mid-story isolation system. Eng. Struct. 42, 420–433. doi:10.1016/j.engstruct.2012.04.035

CrossRef Full Text | Google Scholar