Gas fees on the Ethereum blockchain: from foundations to derivative valuations

The “gas fee” paid for inclusion in the blockchain is analyzed in two parts. First, we consider how “effort” in terms of resources required to process and store a transaction turns into a “gas limit,” which, through a fee comprised of the “base” and “priority fee” in the current version of Ethereum, is converted into the cost paid by the user. We adhere closely to the Ethereum protocol to simplify the analysis and to constrain the design choices when considering “multidimensional gas.” Second, we assume that the “gas” price is given deus ex machina by a fractional Ornstein–Uhlenbeck process and evaluate various derivatives. These contracts can, for example, mitigate gas cost volatility. The ability to price and trade “forwards” in addition to the existing “spot” inclusion into the blockchain could enable users to hedge against future cost fluctuations. Overall, this article offers a comprehensive analysis of gas fee dynamics on the Ethereum blockchain, integrating supply-side constraints with demand-side modelling to enhance the predictability and stability of transaction costs.

1 Introduction

The supply and demand of blockchain real estate, divided into blocks and incrementally released, are entangled but analyzed separately in this article. In the first part of the article, we consider what can be roughly termed the supply side, whereas in the second part, we consider the demand side.

Gas is central to our discussion. It is paid for by blockchain users and plays an integral part in blockchain construction. Who receives the payment is blockchain-dependent. It can fund the maintenance of a blockchain and often helps block builders prioritize transactions in the mempool, that is, the pool of pending transactions¹.

In the case of Ethereum², the blockchain, through the Ethereum virtual machine (EVM), sustains the state and carries out instructions that update it. This could be a simple transfer of ether, the chain’s native token, or a more complicated execution of a smart contract. Note that a transfer in isolation does not constitute a contract because a contract under English common law requires consideration.

The next two sections on blockchain supply convert the multidimensional resource requirements into an updated gas cost formula. Afterward, in three sections on blockchain demand, the gas price is modeled as a fractional Ornstein–Uhlenbeck process following earlier work on weather derivatives, where this process turned out to be a sound choice.

The article is rounded off with some general remarks.

2 Gas: the supply side

The choice of gas price function largely determines what is included in the blockchain. From this, it derives its importance. The amount of gas fee users offer above the minimum allows a ranking based on the profitability of proposed transactions, mostly submitted to the generally observable mempool. Block builders create blocks with the largest economic benefit for them from the transactions, which means maximizing the “priority fees” while staying within the constraint governing block size. This ignores MEVs or other possible side deals. What maximizes block builders’ economic benefit is not self-evidently best for current and potential users and the wider set of nodes maintaining the network.

Each group might be further subdivided. Users might have a variety of different latency requirements and cost sensitivities. Operational nodes have different storage and computational costs associated with transactions because some transactions are computationally more expensive, whereas others are dominated by storage or bandwidth requirements. The question of how to quantify and capture these different requirements naturally arises.

A fully multidimensional cost would be a natural response because each resource has its own cost and limitations. This is always possible, but one less ambitious option is to retain simplicity for the multitude of users and shift as much additional complexity as possible to the smaller number of block builders. The toy model below will show how this can be done.

In the article “Prices vs. Quantities” (Weitzman, 1974), Weitzman discussed the trade-off between implementing constraints on price and quantity. A detailed application to tokens, which we will not repeat, can be found in Buterin (2018), while a more recent discussion is in Ndiaye (2024).

We remark that both price and quantity can be employed to constrain usage. Network failure due to breaches of hardware-induced constraints on bandwidth, storage space, or computational capacity of nodes seems, from heuristic grounds, harder to reverse than mispricing, which might see businesses migrate to other blockchains but could be reversible through fine-tuning. The ultimate restraint on functionality is state growth³, as it slows down synchronization time for new nodes and also increases the cost of every future operation on the chain⁴. Constraining the number of transactions per block and, hence, state growth is essential. For these reasons, only hard quantity constraints will be studied thereafter. As exemplified by the blog by Buterin (2024), there has been interest in considering multidimensional gas prices.

The blog mentions parallels to a problem central banks were confronted with during the 2007–2008 financial crisis. Central banks aimed to expand the range of acceptable collateral at liquidity auctions. Instead of accepting only one type of collateral, they allowed two types, each associated with different credit risks. The question then arose: How should these auctions be organized? Can a single-round auction combine more complicated preferences?

What was proposed by Klemperer (2008) and Klemperer (2013) and adopted after discussions by the Bank of England was a single-round sealed bid auction, where bidders could bid for a fixed amount but offer a choice of collateral. Each type of collateral had an associated borrowing rate to reflect its different creditworthiness. The Bank of England could then select what collateral mix to accept for the provided liquidity for each bidder.

Related ideas were also developed by Milgrom (2009), and linear programming provides the mathematical underpinning to solve such a constrained optimization problem. Klemperer, who also worked jointly with Milgrom and others on the proposal, provided a nice graphical way to determine an acceptable solution. In the section on our toy model, we will develop an analogous framework for gas pricing. Although the overlap is not exact, our interest lies primarily in their approach’s heuristics and graphical implementation rather than in the precise technical details.

In this analogy, the central bank corresponds to the block builders in the Ethereum network. The financial institutions requiring liquidity are analogous to the blockchain users who initiate transactions. Lastly, the collateral constraints financial institutions face can be likened to the hardware constraints block builders encounter.

In the Ethereum network, transaction fees are divided into the base fee, priority fee, and max fee; the base fee is a mandatory, algorithmically determined fee that adjusts based on network demand and is burned (destroyed) to reduce the total supply of ether (ETH). The priority fee is an optional fee set by users to incentivize miners to prioritize their transactions. It is paid directly to miners. The max fee is the maximum amount a user is willing to pay per unit of gas. It includes both the base fee and the priority fee (Figure 1).

Figure 1

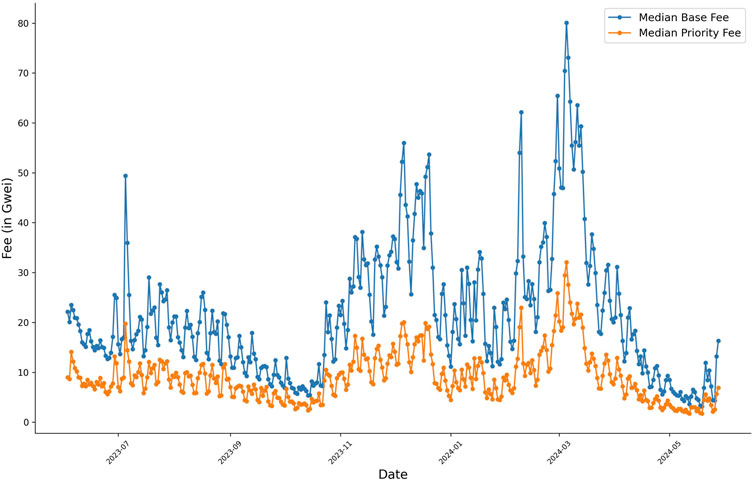
Figure 1. Daily median base fee and priority fee over time. The data were extracted from the Dune database, where daily median base fees were computed from block data, and daily median priority fees were computed from transaction data joined with block data. This analysis covers the past 360 days.

The effective fee per gas unit is the sum of the base fee and the priority fee. If the effective fee is less than the max fee, the user is refunded the difference. This mechanism tries to balance users’ wishes to prioritize their transactions with a hard limit on total cost to protect them from excessive spending.

The data utilized in this analysis were extracted from the Dune⁵ database, employing a structured query to calculate daily median base fees and median priority fees over the past 360 days. The extraction process involved two primary components. First, daily median base fees were computed by truncating the timestamps of block data to the nearest day and then calculating the median base fee per gas unit from the. Ethereum blocks table (Figure 1). Second, daily median priority fees were determined by joining transaction data from the Ethereum transactions table with block data, again truncating the timestamps to the nearest day and calculating the median difference between the maximum fee per gas and the base fee per gas. To achieve the median values, these computations were performed using the APPROX_PERCENTILE function. The final dataset was obtained by joining the daily median base fee and priority fee records on their respective dates. In the next section, we present a new gas model to improve the management of resource constraints.

3 Toy gas model for incorporating resource constraints

Until now, we have described properties of the blockchain. In this section, we take the next step and introduce a simplified supply model highlighting the multidimensional nature of the resources necessary for maintaining and expanding the blockchain. The core concept is as follows: Transactions included in the blockchain can be split into operations. Operations require resources, which are constrained and can be transformed into gas. Gas can be converted into a fee or cost payable in ether. We use the terms fee and cost interchangeably.

Let us define some additional terms. The gas cost paid for a transaction is a product of the amount of gas used and the cost per unit of gas. This can be further subdivided because gas splits in the model we consider into $M$ different resources. These are, for example, the amount of computation required or data stored, constituting the multidimensionality of gas. The availability of these resources adjusts on the time scale of months with technological progress and other external factors like electricity prices. Here, we assume that the limits per block for each of the $M$ resources are provided as an external input. Gas has the dimension of “units of gas” and is converted to ether by a quantity with the dimension “ether per units of gas.”

More about the different components that cost can be decomposed is described next. Each distinct operation involves the use of various resources. The “static gas” matrix captures this transformation. In addition to the static gas, there is a vector called “dynamic gas.” This vector will capture the individual resource constraints. It will be adjusted similarly to the “base fee” of EIP-1559, except that not the total amount of gas of the past block but the gas associated with a particular resource provides the condition for adjusting the particular dynamic factor.

The intuition is that EIP-1559 was approximately one overall constraint for gas implemented through the adjustment of the base fee, but here, we want to have a finer-grained constraint for individual resources. This is achieved by diversifying the conversion factor, that is, adding “dynamic gas.” Overall congestion will still affect the base fee, but fine-grained resource-specific congestion will affect the aggregate cost through the dynamic gas coefficients. This will allow multiple constraints without introducing multiple base or priority fees. The user experience will stay simple, while the, on average, more sophisticated blockbuilders are faced with marginally more computational effort.

For the precise terms of the current framework of Ethereum, see the Yellow Paper by Wood, 2024. The details of the applicable “Fee Schedule” can be found in the article’s appendix G. It allows the transformation of operations⁶ of transactions or blocks into what is called a “gas limit.” This is the scalar quantity, which we will assume to be subdivided into different buckets, each with its own constraint. To avoid confusion, we use, unlike the Yellow Paper, the term fee or cost, as stated above, always in connection and priced in ether (denominated in ETH, Gwei, or Wei, with $1ETH=10^{9}Gwei=10^{18}Wei$), and “resources” are denominated in gas. The term “transformation” describes turning resources underlying “operations” into gas, while “conversion” describes turning gas into cost in ether. This is to clarify the article’s idiosyncratic terminology, but it is otherwise of no importance.

Let us next turn the words into equations. For brevity, we sometimes use the Einstein convention, which assumes repeated indices are summed over even without the summation symbol and requires consistent application of indices. Vectors are written with an arrow overhead, while matrices carry a double arrow. Both are written in bold and capital letters. Coefficients of vectors and matrices use the same letters but in lowercase. The description is given in three forms: in more symbolic notation, index notation, and visual arrays. The different representations are equivalent and are simply added to benefit a diverse readership.

The gas cost $C_t$ of block $t$, where $t\in \{\mathrm{1,2,3},\dots \}$, a scalar in our toy model, is the product of multiple terms. It includes the scalar base fee and the vector priority fee, the $B_t\vec{\mathbf{I}}$⁷ and vector ${\vec{\mathbf{P}}}_t$, respectively, where both terms are block $t$ dependent, and the priority fee is in addition an $N$ dimensional vector. The $i$-th transaction uses the amount ${\stackrel{⃡}{\mathbf{\Pi }}}_t$, which is a $O_p$ times $N$ dimensional matrix⁸, of resources. The transformation of operations to resources is done by the matrix ${\stackrel{⃡}{\mathbf{G}}}_t$, which is $O_p$ times $M$ dimensional matrix⁹. This matrix is modified by the “dynamic gas” transposed vector ${\stackrel{⃖}{\mathbf{\Lambda }}}_t$, which is $M$ times one-dimensional¹⁰. Combining the different elements produces the equation for the cost of a block of

$C_t={\stackrel{⃖}{\mathbf{\Lambda }}}_t{\stackrel{⃡}{\mathbf{G}}}_t{\stackrel{⃡}{\mathbf{\Pi }}}_t\left(B_t\vec{\mathbf{I}}+{\vec{\mathbf{P}}}_t\right),$

which can be rewritten in terms of coefficients

$c_t={\lambda }_k\left(t\right)g_{kj}\left(t\right){\pi }_{ji}\left(t\right)\left(B_t{1}_i+p_i\left(t\right)\right),$

and in terms of arrays

$c=\left(\begin{array}{ccccc}\hfill {\lambda }_1\hfill & \hfill {\lambda }_2\hfill & \hfill {\lambda }_3\hfill & \hfill \dots \hfill & \hfill {\lambda }_M\hfill \end{array}\right)\left(\begin{array}{ccccc}\hfill g_{11}\hfill & \hfill g_{12}\hfill & \hfill g_{13}\hfill & \hfill \dots \hfill & \hfill g_{1O_p}\hfill \\ \hfill g_{21}\hfill & \hfill g_{22}\hfill & \hfill g_{23}\hfill & \hfill \dots \hfill & \hfill g_{2O_p}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill g_{M1}\hfill & \hfill g_{M2}\hfill & \hfill g_{M3}\hfill & \hfill \dots \hfill & \hfill g_{M{O}_p}\hfill \end{array}\right)\left(\begin{array}{ccccc}\hfill {\pi }_{11}\hfill & \hfill {\pi }_{12}\hfill & \hfill {\pi }_{13}\hfill & \hfill \dots \hfill & \hfill {\pi }_{O_{p}1}\hfill \\ \hfill {\pi }_{21}\hfill & \hfill {\pi }_{22}\hfill & \hfill {\pi }_{23}\hfill & \hfill \dots \hfill & \hfill {\pi }_{O_{p}2}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\pi }_{O_{p}1}\hfill & \hfill {\pi }_{O_{p}2}\hfill & \hfill {\pi }_{O_{p}3}\hfill & \hfill \dots \hfill & \hfill {\pi }_{O_{p}N}\hfill \end{array}\right)\left(\begin{array}{c}\hfill B_t+p_1\hfill \\ \hfill B_t+p_2\hfill \\ \hfill ⋮\hfill & \hfill \hfill \\ \hfill B_t+p_N\hfill \end{array}\right).$

In the last representation of the cost equation, the $t$ dependence was dropped for notational brevity.

If one wants to work with truly multidimensional gas such that users must pay separate fees for each of the $M$ resources, then instead of the vector $B_t\vec{\mathbf{I}}+{\vec{\mathbf{P}}}_t$ one would have to introduce a $N$ times $M$ dimensional matrix. The transposed vector ${\stackrel{⃖}{\mathbf{\Lambda }}}_t$ would be replaced by an $M$ times $M$ matrix ${\stackrel{⃡}{\mathbf{\Lambda }}}_t$, as a general dynamic gas, to allow cross-linked constraints and adaptation of the $M^2$ coefficients of ${\stackrel{⃡}{\mathbf{\Lambda }}}_t$ with congestion.

Next, we introduce hard block-by-block constraints as a $M$-dimensional vector of the form $\vec{\mathbf{L}}$ with coefficients $l_k$, we further assume that the sum ${\sum }_{k=1}^M{l}_k$ corresponds to the current number of target gas units per block¹¹. These values for the resource constraints are set externally and updated infrequently with technological advances and other changes influencing the EVM. Each of the dynamic gas coefficients ${\lambda }_k$ is deemed to start at one and ideally should mean revert around this value. How is this achieved? For a fixed $\widehat{k}$, if the block’s $k$-resource ${\sum }_{i=1}^N{g}_{\widehat{k}i}(t)$ is bigger than $l_{\widehat{k}}$, then the value of ${\lambda }_{\widehat{k}}$ applicable to the block $t+1$ will be increased, and, if it falls below the $l_{\widehat{k}}$, then the value will be proportionally decreased using a formula along the line of EIP-1559¹², but dependent on relative congestion in terms of the $\widehat{k}$-th resource instead of absolute congestion.

In the next paragraphs, we will show how block builders can fish the most profitable transactions from the mempool. As before, MEVs or other side deals are ignored. There is a simple graphical representation of transactions that enables easy comparison. Each transaction corresponds to a line that intercepts the resource axes. The points of intersection are chosen such that the priority fee is exclusively associated with only one resource consumed by the transaction. This leads to a hyperplane of $M-1$ dimensions for each of the $M$ constraints. If no cost of a particular kind is associated with a transaction, the line in the two-dimensional case is parallel to that axis.

In this paragraph, we delve deeper into the graphical representation. Assume the two-dimensional resource case and set the dynamic gas coefficients to one. Let us further assume that the transaction under consideration requires $x$ units of gas for storage and $y$ units of gas for computation. The priority fee is set to $z$ Gwei per unit of gas. The total amount of gas is given by $x+y$; the total priority cost is $(x+y)z$. The equation of the relevant line is given by $x\mathbf{S}+y\mathbf{C}=(x+y)z$, where $\mathbf{S}$ represents the storage resource and $\mathbf{C}$ represents the computational resource. The line shows how the total priority fee can be attributed to the two resources in different ways. Figure 2A depicts the case with $x$ equal to one, $y$ equal to two, and $z$ equal to $3/4$ because the line segment fits the equation $\mathbf{S}+\frac{1}{3}\mathbf{C}=1$.

Figure 2

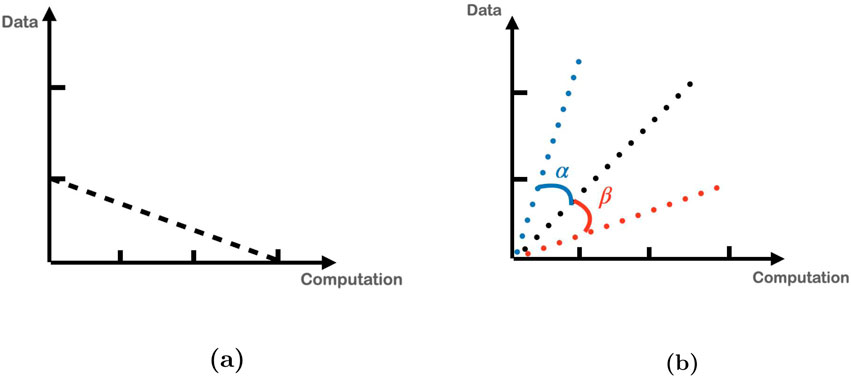
Figure 2. (A) The line segment intercepts the “storage” axis, where the normalized priority fee is assigned to “storage,” and intercepts the “computation” axis, where the normalized priority fee is assigned to “computation.” (B) The red line corresponds to the gas weighted resources vector; that is, the coefficients for each of the $M$ resources are equal to the amount of static gas associated. In contrast, the blue line is a reflection of the red line on the vector $(\mathrm{1,1},\dots ,1)$ and is the direction in which the optimal search is carried out.

This representation has the advantage that different transactions can be compared, and furthermore, transactions are represented by identical lines as long as they are related by a scale factor; that is, the same line represents the triplets $(x,y,z)$ and $(kx,ky,z)$. From the perspective of block builders, the identification of lines that have the same priority fee per unit of gas and the same ratio of resource requirements is reasonable because incorporating $k$-times the smaller transaction $(x,y,z)$ into a block is equivalent to the inclusion of one big transaction of the form $(kx,ky,z)$ in terms of base and priority fee as well as resource requirements¹³

Two further cases are considered in the two-dimensional criteria case to acquire an intuition. We compare two transactions with corresponding lines that intersect and do not intersect. Suppose the two lines do not intersect (see Figure 3). In that case, the transaction associated with the line closer to the origin is preferred independent of the constraints, assuming one is sufficiently far from any constraint boundary. If the two lines intersect (see Figure 3), then the choice depends on the relative size of the coefficients of the constraint vector $\vec{\mathbf{L}}$. The relevant direction of the vector that intersects the lines associated with the transactions is given in the two-dimensional case by $(L_2,L_1)$. As an example, if $\vec{\mathbf{L}}=(\mathrm{2,1})$, then the direction of the blue test vector shown in blue (for Figures 4A, B) is (1,2) starting from the origin. In the general case, with an original weight induced vector of $\vec{\mathbf{L}}$, relating the different constraints being reflected on the $(\mathrm{1,1},\dots ,1)$ vector will produce the new vector $\vec{\mathbf{T}}$. The equations determining the new vector are as follows: $\vec{\mathbf{T}}=\cos \alpha \vec{\mathbf{E}}-{\vec{\mathbf{E}}}_{\perp }$, with ${\vec{\mathbf{E}}}_{\perp }=\vec{\mathbf{L}}-\cos \alpha \vec{\mathbf{E}}$, and $\vec{\mathbf{T}}=2\cos \alpha \vec{\mathbf{E}}-\vec{\mathbf{L}}$ with $\cos \alpha ≔\vec{\mathbf{L}}\vec{\mathbf{E}}/\left(\Vert \vec{\mathbf{L}}\Vert \Vert \vec{\mathbf{E}}\Vert \right)$.

Figure 3

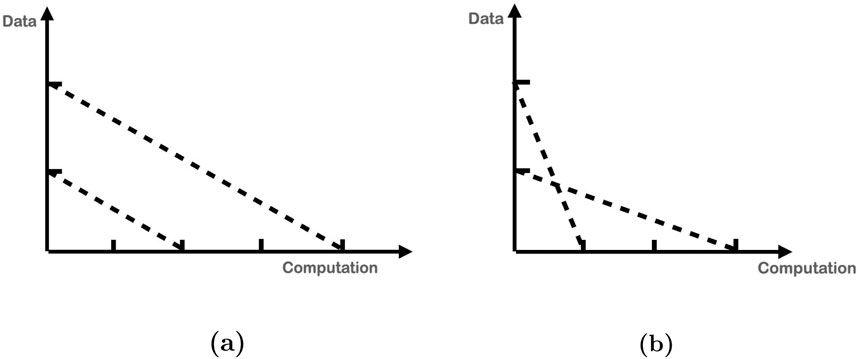
Figure 3. (A) Two line segments, each representing a type of transaction, with the one closer to the origin always being more attractive independent of the relative resource constraints. (B) Two intersecting line segments. The preferred transaction depends on the relative resource constraints.

Figure 4

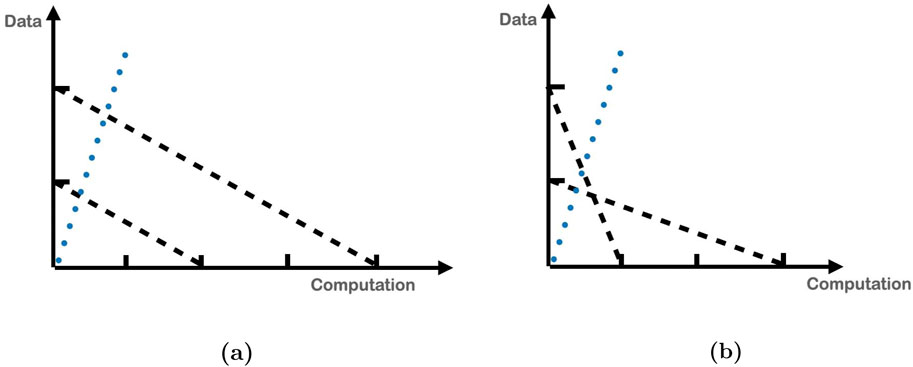
Figure 4. (A) The blue vector, independent of direction, always intersects one line first. (B) The line first intersected by the blue vector depends on the direction of the blue vector.

This toy model goes incrementally beyond EIP-1559 because it “start[s] with a base fee amount which is adjusted up and down by the protocol based on how congested the network is” (taken from the EIP-1559 proposal), but instead of having one quantity, it has $M+1$ quantities. The first $M$ limits adjust relatively slowly to technological advances, and the last constraint is the sum of the others. The decomposition and number of constraints will also evolve over longer time scales.

Which function is suitable for the modification of the dynamical factor ${\stackrel{⃖}{\mathbf{\Lambda }}}_t$, if one wants to go beyond the EIP-1559 adjustment mechanism applied to relative constraints, depends on the drift and volatility encountered in the demand for resources. One can use the sophisticated method described by Ernst et al. (2020) to discern a drift in noisy data. A simpler way is to smooth the data to generate stability but at a cost in reaction time. In general, if volatility is high, a faster response might be needed, but a correct response that avoids overreaction might be harder because observed volatility can be due to real market changes, that is, different contracts becoming popular or the irregular arrival of transactions.

Hardware questions that flow into the choice of resources to be considered and constraints to implement need to be discussed in a different setting geared toward engineering. We assume that the changing nature of hardware, software, and general infrastructure can be translated into a well-defined set of constraints at any point in time.

General transaction fee mechanism design, and EIP-1559 in particular, has been scrutinized by Chung and Shi (2021), Roughgarden (2021), and others. Some see it as an unalloyed success; others are more circumspect. See Kiayias et al. (2023) for the description of some challenges that are also applicable to the Bitcoin protocol. As an alternative, they propose a tiered mechanism as a solution for congestion and to enhance “egalitarianism,” where users can choose the urgency, and capacity is set aside for cheaper, low-latency demand. This prevents the withdrawal of lower-value transactions from a chain during high throughput. The authors compare their proposal to a service-dependent price, where a high price results in speedy execution, but a low price is prone to delays. The authors draw an analogy between this outcome and a multi-speed highway. To conduct experiments on queuing times, one can augment the number of channels and adjust their width. This comparison also evokes the image of a theme park with VIP lanes, where operators could delay standard ticket holders to provide preferential treatment to VIPs, ostensibly maximizing their perceived value. A problem remains: if endemic demand outstrips processing ability, then high-vaulting “inclusivity” intentions will not prevent the failure of some transactions to be processed. If demand-supply imbalances are temporary, then their scheme or similar schemes proposed by others might be an interesting way to allocate capacity. One could derive a possible inducement for deleting dormant smart contracts, which take up space on the blockchain, from what has been observed for the exercise times of options – American options with flexible exercise times versus European options with fixed exercise times. Under standard conditions ignoring dividends,¹⁴ it is best to exercise options at the latest possible time. This could be similar to applying for refunds and deletions of smart contracts under the current scheme. To encourage deletions, one could add a discount function or reduce the returned amount with each technological change that increases and cheapens storage and, therefore, devalues stored data¹⁵.

Next are some examples of the diverse blockchain network fee structures currently in fashion. On many blockchains, transaction size and demand determine fees. Bitcoin, the most prominent token, employs a transaction fee model. Fees are determined by the transaction size in bytes and current network demand. Users are incentivized to offer high enough fees so that miners select their transactions as they strive to maximize revenue. In contrast to Bitcoin, IOTA employs a highly unusual feeless transaction model using its Tangle architecture, a directed acyclic graph (DAG). Each transaction in the IOTA network confirms two previous transactions, thus eliminating the need for miners and transaction fees. Other blockchains allocate resources in dramatically different ways. EOS, for example, adopts a resource allocation model in which users stake tokens to access network resources such as CPU and RAM. Instead of paying per transaction, users can perform transactions “for free” within the limits of their staked resources. The above examples hint at the great variety on offer. In the next two sections, we switch to the demand side and consider a pre-determined gas price process.

4 Gas price dynamics: an introduction to the demand side

Gas prices, as observed for various tokens, show persistence and mean reversion (Figure 5). Fractional Ornstein–Uhlenbeck processes possess both these properties and seem a good candidate as a base process. This approach has also proven to be popular for temperature modeling in the field of weather derivatives. Similar to gas prices across blocks, direct investment in temperature across different time periods is not possible. Instead, gas prices can be observed and then incorporated into derivatives contracts.

Figure 5

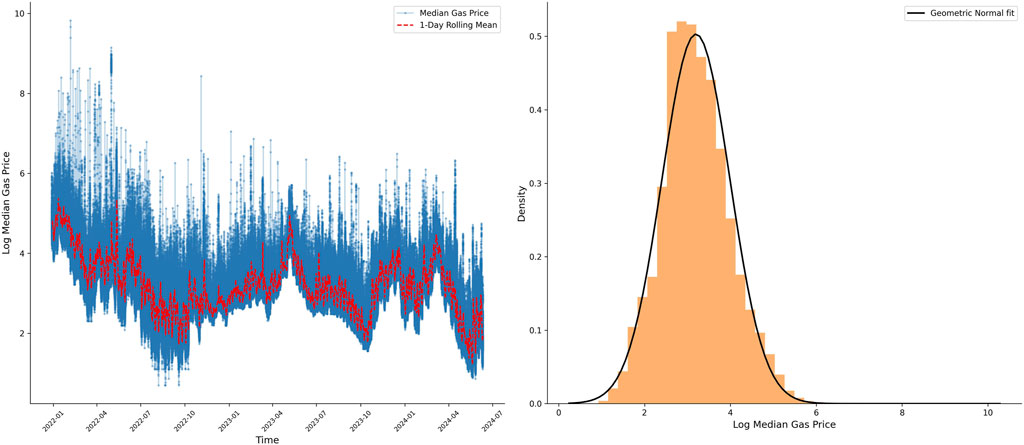
Figure 5. Motivation for a geometric fractional Ornstein–Uhlenbeck process. The left plot shows the median gas price over time, including minute-level data and a 1-day rolling mean to illustrate mean reversion. The right plot displays a histogram of the median gas prices with a log-normal fit, highlighting the goodness-of-fit metrics: $\mu ={\mu }_{\mathit{value}}$, $\sigma ={\sigma }_{\mathit{value}}$. The data were sourced from Dune.com and represent the minute-level data for approximately 900 days.

The relationship between Brownian motion and fractional Brownian motion is similar to the relationship between the Ornstein–Uhlenbeck and the fractional Ornstein–Uhlenbeck processes. In both cases, the fractional process represents a generalization by adding one parameter linked to the autocorrelation.

Various simplifying assumptions are applied when modeling gas fees. In each block, gas fees per unit of gas, in terms of base and priority fees, vary across included transactions. We could model the outliers, for example, the maximum or the minimum fee per block or some average. Under most conditions, due to a lower limit to the gas fee, the volatility of the maximal gas fee should be higher than the volatility of the mean, median, or minimal gas fee, even if counter examples can be constructed easily. Here, we take the median as the gas fee to be modeled. Higher-order moments of the gas are also not considered but are necessary for a comprehensive description of the problem.

The modeling raises several questions that will be discussed near the end of the article. For example, is it possible to simplify planning by creating a forward market for a position in the blockchain in addition to a spot market? In commodities, producers and users use forward markets to hedge risk.

5 A gas model: fractional Ornstein–Uhlenbeck process

In this section, fractional Brownian motion (fBM), a generalization of Brownian motion characterized by the Hurst exponent $H$, is formally introduced. It forms the basis of a mean-reverting fractional Ornstein–Uhlenbeck process that describes the temporal evolution of the gas price. The fBM is described in detail in the book by Biagini et al. (2008). The mean-reverting application to weather derivatives can be found in Brody et al. (2002), and their economic notion is used throughout the section. Fractional Brownian motion $W^H$, parameterized by the Hurst exponent $H\in (\mathrm{0,1})$, and with $H=1/2$ corresponding to the conventional Brownian motion, is a Gaussian stochastic process defined on $(\mathrm{\Omega },\mathcal{F},{\mathbb{P}}^H)$. The sample path of the process $W^H$ is continuous with $W_0^H=0$, and for $t\ge 0$,

$\mathbb{E}\left[W_t^H{W}_s^H\right]=\left(t^{2H}+s^{2H}-|t-s{|}^{2H}\right).$

For $H>1/2$, the correlation between the increments is positive, while for $H<1/2$, the correlation between the increments is negative. $W^H$ is “self-affine,” that is, $W_{\alpha t}^H$ has the same distribution as $\alpha W_t^H$ for every positive $\alpha$.

Some background about the fBM is given next. The Hurst exponent takes its name from the hydrologist H.E. Hurst, who studied the time series of water levels of the Nile in the middle of the last century. He noticed long-range dependencies and scaling behavior. This may not be surprising because cumulative precipitation in a river’s catchment area drives water levels downstream. Some decades later, Mandelbrot named the parameter $H$ in the fBM in honor of Hurst. The gas cost $X_t$ at time $t$ is now defined as the following process:

$d{X}_t=\kappa \left(\theta -X_t\right)dt+\sigma d{W}_t^H,X_0=x.$

The above equation can be solved under some simplifying assumptions for the parameters, as shown in Duncan et al. (2000) and developed by Hu and Øksendal (1999). If $\kappa ,\theta$ and $\sigma$ are bounded deterministic functions allowing us to write

$K_t=exp\left(-{\int }_0^t{\kappa }_{s}ds\right),$

then

$X_t=x{K}_t+K_t{\int }_0^t{\kappa }_s{\theta }_s{K}_s^{-1}ds+K_t{\int }_0^t{\sigma }_s{K}_s^{-1}d{W}_s^H,$

and further for $t\ge 0X_t$ is a normal random variable with mean $m_t^X=\mathbb{E}[X_t]$

$m_t^X=x{K}_t+K_t{\int }_0^t{\kappa }_s{\theta }_s{K}_s^{-1}ds,$

the variance $V_t^X=\mathcal{\upsilon }ar[X_t]$

$V_t^X=K_t^2{\int }_0^t{\int }_0^t{\sigma }_u{\sigma }_s{K}_u^{-1}{K}_s^{-1}\varphi \left(u,s\right)duds,$

with $\varphi (u,s)=H(2H-1)|u-s{|}^{2H-2}$. These results are all given without proof, which can be found in Brody et al. (2002). Assume for simplicity that gas prices are autocorrelated and form clusters of high and low prices. This can be achieved by a fractional Ornstein–Uhlenbeck model, where the gas price meanders around a predetermined value, which can be cyclical, like some seasonal commodity prices. The gas price $g_t$ (see Figure 6) is described by

$d{g}_t={\kappa }_t\left({\mu }_t-g_t\right)dt+{\sigma }_{t}d{W}_t^H$

Figure 6

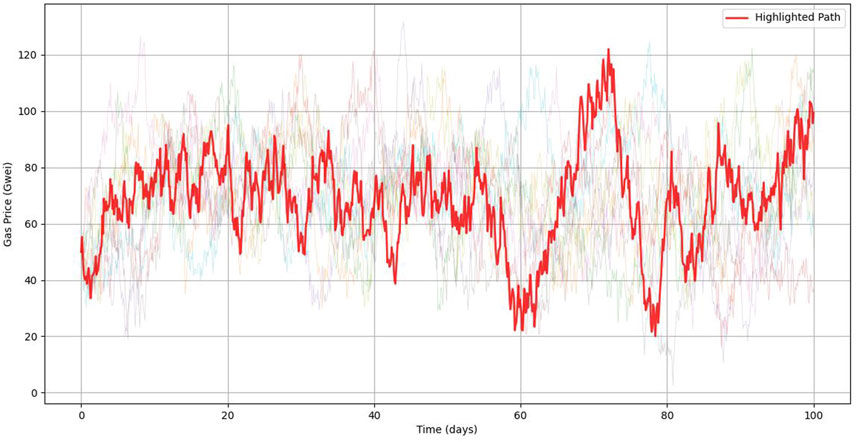
Figure 6. Simulated Ethereum gas price path trajectories as a fractional Ornstein–Uhlenbeck process.

with ${\mu }_t$ as the mean reversion level, $\kappa$ as the mean reversion speed or mean reversion rate, and $\sigma$ as the volatility.

As an aside, the gas cost of a single block can be defined in multiple ways. Is it the highest or the lowest cost transaction accepted by the block builder or is it the median or average cost? How are the volatilities of these different quantities related? Except under exceptional circumstances, which can be easily constructed¹⁶ but are not replicated in the data; the volatility of the different percentiles of cost can be ordered with the lowest percentile having the lowest volatility since the cost is bounded below by zero.

6 Gas price derivatives

This section explores different forms of gas fee derivatives. We use the fractional Ornstein–Uhlenbeck process developed in the previous section as the underlying price process. European and other option prices for assets following the Ornstein–Uhlenbeck price process, that is, $H=1/2$, can be found in Heston and Nandi (2000), Hilliard and Reis (1978), and Lioui (2006). The generalization to any $H\in (\mathrm{0,1})$ was considered for weather derivatives by Brody et al. (2002). Weather derivatives often involve the number of days a local temperature hovers above or below a fixed level. This is called heating or cooling degree days and has the form

$\begin{array}{ccc}\hfill P_t={\left(K-X_t\right)}^{+},& \hfill & \hfill \\ \hfill C_t={\left(X_t-K\right)}^{+}.& \hfill & \hfill \end{array}$

The same quantity is of interest also for gas derivatives, and the abstract evaluation formula of the two derivatives can be written, respectively, in the form

$\mathbb{E}\left[e^{-\delta \left(T-t\right)}{\int }_{T-S}^T{\left(K-X_t\right)}^{+}ds|{\mathcal{F}}_t^{\mathcal{X}}\right],$

In addition, one can define a modified derivative with an additional strike price $L$

$\mathbb{E}\left[e^{-\delta \left(T-t\right)}{\int }_{T-S}^T{\left({\left(K-X_t\right)}^{+}-L\right)}^{+}ds|{\mathcal{F}}_t^{\mathcal{X}}\right],$

in this or in other permutations. All these derivatives have been priced and the result can be found in Section 4 of Brody et al. (2002). An example of call option values for different initial gas prices and maturities is given in Figure 7. Since the underlying is in the gas case not directly tradable, the price of the derivatives cannot be simply replicated or the product directly hedged. Next comes a short conclusion rounding of the paper.

Figure 7

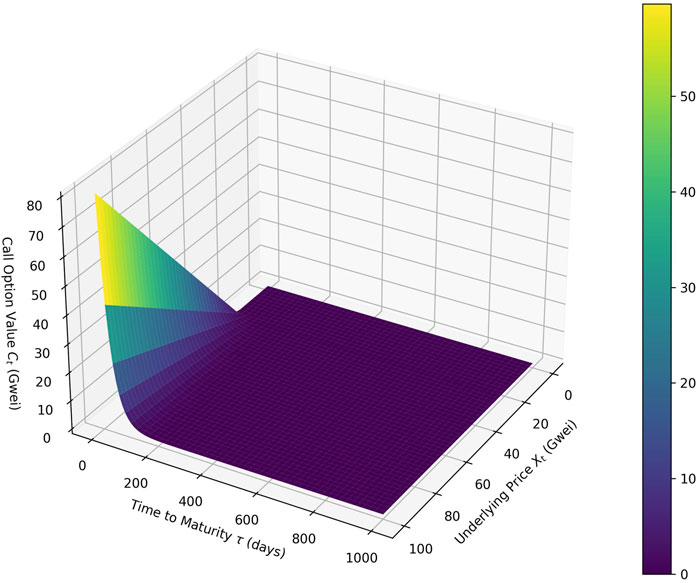
Figure 7. Call option values for different times to expiry and underlying prices (Ethereum gas), where the underlying asset follows a fractional Ornstein–Uhlenbeck process.

7 Conclusion

Gas is a determining factor not only for users in their choice of blockchain but also for token holders, stakers, and node operators. Each group has a different perspective. On the supply side, node operators must worry about shifting technological constraints and the costs involved. On the demand side, chains compete fiercely in Darwinian fashion.

In the toy model introduced in Section 2 and developed in Section 3, we showed how multiple constraints can be simply incorporated into the gas fee. Adopting multidimensional gas constraints will better align a blockchain with technological realities.

The subsequent sections focus on the demand side and how the fractional Ornstein–Uhlenbeck price process can act as a base for evaluating derivatives, similar to developments in weather derivatives. Temperature is a key variable in understanding the weather, but it is not directly tradable, unlike company ownership or obligations represented as stock or bond certificates¹⁷. The same can be said for the gas fee. The magnitude of the gas fee has economic consequences, but no gas fee certificate is directly investable or transferable between blocks. Consequently, the approximate continuous time series of gas fees does not have to follow a stochastic process that, under a change of measure, could turn into a martingale to avoid arbitrage. Instead, gas fees on the Ethereum blockchain, like temperature, show identifiable patterns and have properties of a mean-reverting fractional Ornstein–Uhlenbeck process. This is theoretically appealing and retains its plausibility after analyzing the data. One of the interesting features of this model is that if transactions are not time-sensitive, execution delays can be traded off for cost improvements. The cost improvement versus time delay can be read From the instantaneous drift of the fractional Ornstein–Uhlenbeck process. This helps users balance cost against time. Optimal investment strategies for an asset following the related Ornstein–Uhlenbeck process can be found in Lv and Meister (2009) and Lv and Meister (2010).

This raises the question of how users can hedge against potential gas fee spikes or the related questions of how one hedges an option when the underlying asset has a drift. How does one hedge gas cost because one cannot hand over block openings from block to block? How does one deal with blocks containing a whole host of transactions rather than only one? These more practical questions will be addressed in a separate report.

What are some of the limitations of the models proposed and related implementation challenges? The models were derived from first principles and justified by stylized facts. Only time will tell if a multidimensional gas fee model, as described in the article, will receive a positive reception. The same applies to gas fee forwards. The willingness of market participants to use such derivatives depends on the future cost and volatility of gas fees, which is dependent on the development of the Ethereum ecosystem. Both the future demand for blockchain space and protocol changes are inherently unknowable. Implementation challenges abound due to the uncertainties stated above.

One possible extension of the research, suggested to us by a referee, is to look at the basis risk between expected spot and forward gas fees. Basis risk is the mismatch between the asset or liability one wants to hedge and the contract one uses as a hedge. The cause of the imperfect substitution can be market forces related to supply and demand imbalances or discrepancies in the contract definitions. Initially, market makers are likely to have limited risk tolerance for gas fee forward contracts and will provide limited liquidity. As a consequence, imbalances in hedging demand and supply between blockchain users and stakers are likely to lead to mispricings and, consequently, basis risk.

Another possible extension of the research is to develop not only the various derivatives proposed and priced in the article but also forward contracts for gas prices at a time point or averaged over a time period in the future. Deployers and users of smart contracts would then be able to gain confidence that costs are predictable and hedgable. A short position in forward contracts has intrinsic attractiveness to stakers and block builders who are long with regard to gas fees and could limit their downside by locking in the forward price. This raises other questions. Could one pre-order block capacity through a forward market to reduce volatility? This benefits both sellers and buyers who wish to obtain fixed costs. These commitments could be enshrined for future reference in current blocks.

In general, assuming the fractional Ornstein–Uhlenbeck process is well suited to modeling gas prices, the question arises: Can one use the predictive nature inherent in the process to improve the block creation protocol to increase efficiency? This will be explored elsewhere.

Another hotly debated topic is how to rein in maximum extractable value (MEV). Reducing MEV might be in the purview of smart contract developers, who should have incentives to construct efficient marketplaces to attract business, and in the interest of blockchain designers, who want their chains to be competitive. Facts to consider: A block-updating rate of multiple seconds will, by default, be slow compared to what legacy finance (LeFi) can offer, and the same is true for limits in on-chain transaction throughput. These two constraints are structural and difficult to overcome. What may be fixable is the reordering of transactions by block builders, which can be guided toward a more beneficial outcome. MEV could, for example, be marginally impeded if the order of transactions in a block is fixed by a checkable deterministic algorithm. A deterministic ordering is clearly harder to manipulate than leaving the choice completely up to block builders. Unpredictability can be introduced either if the ordering is a function of components revealed as late as possible or given by a hard-to-invert function. It would be helpful, therefore, to have a one-way function that allows checking that the right process was carried out but makes predicting the block position fiendishly difficult. To achieve this, imagine a one-way function that takes all the proposed transactions and splits out an ‘unstable ordering;’ that is, if the transactions are slightly changed, the resulting order changes dramatically. An example would be calculating a hash function and using it to force an order. Even this would offer only limited protection against sandwich or other attacks because the block builder can try other similar block constructions if a particular combination of transactions does not give the right sandwich ordering. A particular order of three transactions, assuming that the rest of the block is neutral, is only one of six possible cases. If, instead, the aim is to combine dozens of transactions in a specific order, then the combinatorial possibilities multiply, and it becomes significantly harder for the block builder to deliver a particular outcome in the limited time available.

The main concern should instead not be the reordering or adding of transactions but rather the deliberate exclusion, which results in delays with costly economic consequences. As others have mentioned, this can lead to the liquidation of positions as margin payments¹⁸ are not received in time. This is especially worrisome at times of price volatility linked with natural chain congestion. Centralization facilitates this process because a payment proportional to the associated priority fee is required to motivate a block builder to disallow a transaction. This cost will eventually outweigh any gain for a manipulator if it must be paid out too many times.

Therefore, collusion is the likely consequence of restricting block building to a small group because, as Adam Smith wrote, “people of the same trade seldom meet together, even for merriment and diversion, but the conversation ends in a conspiracy against the public.”

Data availability statement

Publicly available datasets were analyzed in this study. These data can be found here: dune.com.

Author contributions

BM: writing–original draft and writing&review and editing. HP: writing–original draft and writing&review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported by the imperial college open access fund.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbloc.2024.1462666/full#supplementary-material

Footnotes

¹These are transactions that have been submitted to the mempool but have not yet been incorporated into the blockchain.

²For an analysis of the link between network activity and gas fees for Ethereum, see Koutmos (2023), Liu et al. (2022), Pierro and Rocha (2019), Donmez (2022), and Karaivanov (2024).

³This is reflected in the current choice of gas pricing, where writing to a new “slot” in a state costs a multiple of writing to an existing “slot” in state.

⁴Consequences of state growth are that the state no longer fits as easily into memory, and updating takes longer.

⁵dune.com.

⁶There are approximately three dozen types of operations, including refunds, with fees ranging from one unit of gas for a JUMPDEST operation to $\mathrm{32,000}$ units of gas for a CREATE operation.

⁷$\vec{\mathbf{1}}$ is the transposition of the vector $(\mathrm{1,1},\dots ,1)$.

⁸We define $O_p$ to be the number of distinct operations, as, for example, defined in the Fee Schedule of Appendix G of (Wood).

⁹We define $M$ as the number of distinct resources that each will have its own constraint

¹⁰We use $\stackrel{⃖}{\mathbf{A}}$ as the transposition of the vector $\vec{\mathbf{A}}$.

¹¹The current target gas is $15\times 10^6$ units of gas per block, while the hard cap gas limit is $30\times 10^6$ units of gas per block. It is worth noting that this is not a hard-coded cap but an arrangement agreed on by the validators en masse – see Ethereum research https://ethresear.ch/t/on-block-sizes-gas-limits-and-scalability/18444.

¹²The EIP-1559 base fee adjustment formula for overall congestion is given in terms of gas used, target gas, current base fee, updated base fee, and some constants. For details, see (Wood) and the many articles that analyze the proposal.

¹³Blockchain users view this differently because combining transactions can be beneficial; for example, there is a base cost for each transaction of currently 21,000 Gas. Access lists can also warm up storage for a transaction prior to accessing it (see EIP-2930: Optional access lists). To clarify and justify the scaling assumption for block builders, the resources charged and the resources consumed by block builders must match. An exception exists as a block approaches a hard limit for one of the resources; a block builder could prefer smaller transactions for added flexibility.

¹⁴Also ignoring other extraneous factors like stock borrow.

¹⁵This is similar to dividends in American options, which, under the right conditions, induce early exercise.

¹⁶The maximal cost can be held constant, while the minimal, average, and median cost can vary.

¹⁷Commodities are a directly investable quantity, but to understand their price processes, one must include storage cost and convenience yield (Kaldor, 1939).

¹⁸In the margining case, the trade-off between liquidation delays and risk for counterparties requires some new ideas. For example, can cross-chain links be utilized to allow margins to be replenished more flexibly? One of the authors, HCWP, thanks Numaan Ahmed for stimulating discussions and gives particular thanks to Jim McDonald for clarifying some less-known aspects of the Ethereum blockchain.

References

Biagini, F., Hu, Y., Øksendal, B., and Zhang, T. (2008). Series: probability and its applications. Springer-Verlag London.

Google Scholar

Brody, D. C., Syroka, J., and Zervos, M. (2002). Dynamical pricing of weather derivatives. Quant. Finance 2 (3), 189–198. doi:10.1088/1469-7688/2/3/302

CrossRef Full Text | Google Scholar

Buterin, V. (2018). Blockchain resource pricing. Available at: https://ethresear.ch/uploads/default/original/2X/1/197884012ada193318b67c4b777441e4a1830f49.pdf.

Google Scholar

Buterin, V. (2024). Multidimensional gas pricing. Available at: https://vitalik.eth.limo/general/2024/05/09/multidim.html.

Google Scholar

Buterin, V., Conner, E., Dudley, R., Slipper, M., and Norden, I. (2019). Ethereum improvement proposal 1559: fee market change for eth 1.0 chain. Available at: https://github.com/ethereum/EIPs/blob/master/EIPS/eip-1559.md.

Google Scholar

Chung, H., and Shi, E. (2021). “Foundations of transaction fee mechanism design,” in Foundations of transaction fee mechanism design hao Chung, carnegie mellon university elaine Shi. Carnegie Mellon University, 1474. Available at: https://eprint.iacr.org/2021/1474.

Google Scholar

Donmez, A. A. K. (2022). Transaction fee economics in the Ethereum blockchain. Econ. Inq. 60 (1), 265–292. doi:10.1111/ecin.13025

CrossRef Full Text | Google Scholar

Duncan, T. E., Hu, Y., and Pasik-Duncan, B. (2000). Stochastic calculus for fractional brownian motion I. Theory. Theory SIAM J. Control Optim. 38, 582–612. doi:10.1137/s036301299834171x

CrossRef Full Text | Google Scholar

Ernst, P. A., Peskir, G., and Zhou, Q. (2020). Optimal real-time detection of a drifting Brownian coordinate. Ann. Appl. Probab. 30 (3), 1032–1065. doi:10.1214/19-aap1522

CrossRef Full Text | Google Scholar

Heston, S. L., and Nandi, S. (2000). A closed-form GARCH option valuation model. Rev. Financ. Stud. 13, 585–625. doi:10.1093/rfs/13.3.585

CrossRef Full Text | Google Scholar

Hilliard, J. E., and Reis, J. (1978). Valuation of commodity futures and options under stochastic convenience yields, interest rates, and jump diffusions in the spot. J. Finance 12, 61–625. doi:10.2307/2331378

CrossRef Full Text | Google Scholar

Hu, Y., and Øksendal, B. (1999). Fractional white noise calculus and applications to finance Preprint 10. Department of Mathematics, University of Oslohttps://www.duo.uio.no/bitstream/handle/10852/42642/1/1999-10.pdf

Google Scholar

Johnson, P., Pedersen, J. L., Peskir, G., and Zucca, C. (2022). Detecting the presence of a random drift in Brownian motion. Stoch. Process. their Appl. 150, 1068–1090. doi:10.1016/j.spa.2021.05.006

CrossRef Full Text | Google Scholar

Kaldor, N. (1939). Speculation and economic stability. Rev. Econ. Stud. 7, 1–27. doi:10.2307/2967593

CrossRef Full Text | Google Scholar

Karaivanov, A. S. Z., (2024). Economic determinants of ethereum transaction fees in the priority fee and proof of stake periods (No. dp24-02).

Google Scholar

Kiayias, A., Koutsoupias, E., Lazos, P., and Panagiotakos, G. (2023). Tiered mechanisms for blockchain transaction fees. arXiv:2304, 06014. doi:10.48550/arXiv.2304.06014

CrossRef Full Text | Google Scholar

Klemperer, P. (2008). A new auction for substitutes: central Bank liquidity auctions, the U.S. TARP, and variable product-mix auctions. Oxford University: mimeo.

Google Scholar

Klemperer, P. (2013). The product-mix auction. Oxford University Press.

Google Scholar

Koutmos, D. (2023). Network activity and ethereum gas prices. J. Risk Financial Manag. 16 (10), 431–444. doi:10.3390/jrfm16100431

CrossRef Full Text | Google Scholar

Lioui, A. (2006). Black–Scholes–Merton revisited under stochastic dividend yields. J. Futur. Mark. 26, 703–732. doi:10.1002/fut.20208

CrossRef Full Text | Google Scholar

Liu, Y., Yuxuan, L., Kartik, N., Fan, Z., Luyao, Z., and Yinhong, Z. (2022). “Empirical analysis of eip-1559: transaction fees, waiting times, and consensus security,” in ACM SIGSAC conference on computer and communications security (Copenhagen, Denmark, November), 2099–2113. 2.

CrossRef Full Text | Google Scholar

Lv, Y. D., and Meister, B. K. (2009). Application of the kelly criterion to ornstein-uhlenbeck processes. LNICST 4, 1051–1062. doi:10.1007/978-3-642-02466-5_105

CrossRef Full Text | Google Scholar

Lv, Y. D., and Meister, B. K. (2010). Applications of the Kelly Criterion to multi-dimensional diffusion processes. Int. J. Theor. Appl. Finance 13, 93–112. doi:10.1142/s0219024910005693

CrossRef Full Text | Google Scholar

Milgrom, P. R. (2009). Assignment messages and exchanges. Am. Econ. J. Microeconomics 1, 95–113. doi:10.1257/mic.1.2.95

CrossRef Full Text | Google Scholar

Ndiaye, A., (2024). Blockchain price vs. quantity controls. arXiv preprint arXiv:2405.00235.

Google Scholar

Pierro, G. A., and Rocha, H. (2019). “The influence factors on ethereum transaction fees,” in 2019 IEEE/ACM 2nd international workshop on emerging trends in software engineering for blockchain (WETSEB) (IEEE), 24–31.

CrossRef Full Text | Google Scholar

Roughgarden, T., (2021). Transaction fee mechanism design. ACM SIGecom Exch., 19(1), pp.52–55. doi:10.1145/3476436.3476445

CrossRef Full Text | Google Scholar

Weitzman, M. L. (1974). Prices vs. Quantities. Rev. Econ. Stud. 41 (4), 477–491. doi:10.2307/2296698

CrossRef Full Text | Google Scholar

Wood, G. (2024). Ethereum: a secure decentralised generalised transaction ledger, Paris Version 705168a – 2024-03-04. https://ethereum.github.io/yellowpaper/paper.pdf

Google Scholar