DAO voting mechanism resistant to whale and collusion problems

With the widespread adoption of blockchain technology, a novel organizational structure known as Decentralized Autonomous Organizations (DAOs) has attracted considerable attention. DAOs facilitate decision-making through member voting, realizing the governance in a decentralized manner. However, DAOs face unique challenges compared to traditional organization. This paper focuses on two key challenges of governance within DAOs: the whale problem and collusion issue. The whale problem is characterized by the concentration of power among specific members, while for the collusion problem, voting results are distorted by fraudulent collaboration. In terms of voting, we consider Quadratic Voting, a voting system expected to deter the concentration of voting power among a subset of participants, analyzing its resistance to the collusion problem. We show with numerical examples that in comparison to Linear Voting, Quadratic Voting lacks resistance to collusion. Then, we propose a voting mechanism that integrates Quadratic Voting with the Vote escrow tokens, demonstrating the mitigation of the whale problem while acquiring resilience to collusion in the decision-making process. The numerical examples confirm the high efficacy of our proposed model.

1 Introduction

With the recent advancements in blockchain technology, there has been a growing interest in Decentralized Autonomous Organizations (DAOs). DAOs represent a form of self-governing entities running through smart contracts operating on the blockchain, eliminating centralized structures Wang et al. (2019). Smart contracts are programmable transaction execution functions implemented on the blockchain, automatically executing transactions based on pre-defined rules when specific conditions are satisfied. Transactions are processed without the need for the trust in the parties involved, that is traditionally required in commercial transactions¹. In addition, the code written in smart contracts is publicly accessible on the blockchain, allowing anyone to review it².

DAOs operated on such a mechanism differ from traditional centralized organizations, as they do not involve decision-making or the possession of assets and rights by a subset of participants. In centralized organizational structures, authority is concentrated in a few central administrators, leading to a lack of transparency due to decision-making processes and internal information control. This setup poses risks of fraudulent activities and erroneous decision-making through unilateral actions. In contrast, DAOs utilize smart contracts to govern the organization, make decisions, and provide services. This approach enables the construction of organizations that ensure transparency and reliability in their operations Wang et al. (2019).

In traditional organizations, when one entity (agent) makes decisions on behalf of another entity (principal), the Principal-Agent problem arises, where the interests of the agent and the principal do not align, leading the agent to prioritize their own interests. However, DAOs, benefiting from the transparency and decentralization aforementioned, have the potential to address the Principal-Agent problem that conventional organizations often face Qin et al. (2023). Moreover, the ability to make decisions reflecting a multitude of opinions provides DAOs with flexibility and adaptability to rapidly evolving technological innovations and dynamically changing markets Li and Wang (2023). In decision-making, incorporating diverse perspectives democratically maximizes the potential of DAOs based on collective intelligence. The shift from traditional centralized management to decentralized governance structure is also a core aspect of digital transformation which aims to leverage technology to decentralize and distribute control and decision-making processes Kraus et al. (2021), Zaoui and Souissi (2020).

DAOs require a distinct decision-making mechanism compared to the governance applied in traditional centralized organizations. Decision-making in DAOs is executed through participants’ voting, eliminating centralized decision-making structures. Voting in DAOs is conducted using governance tokens issued on the blockchain El Faqir et al. (2020), Kharitonova (2021). Given that decisions in DAOs deal with matters of importance such as project policies, service changes, and budget allocation, the voting mechanism plays a pivotal role in the healthy development of DAOs.

A significant challenge arises in blockchain networks, including Bitcoin, where users can participate and withdraw from the network anonymously. In traditional organizations, participants have employment contracts, establishing a structure where they bear responsibility for their activities. Such contractual relationships have the effect of restraining malicious behavior by participants. On the contrary, DAO participants operate in accordance with rules defined by smart contracts. Due to anonymity, however, it is difficult to hold participants accountable when they engage in malicious activities. In other words, as long as participants adhere to the rules specified in the smart contract, any form of misconduct is tolerated. In such a situation, the likelihood of engaging in malicious activities for short-term benefits becomes high. An actual incident illustrating this concern is an attack on a DAO called Beanstalk, where $182 million was stolen³. In this case, a proposal by a malicious user holding a significant amount of tokens was approved, leading to the theft of funds held by Beanstalk. Inadequately designed voting mechanisms for decision-making can become significant obstacles to the proper operation of DAOs. Therefore, the design of voting mechanisms with resistance to malicious activities and careful safety verification is crucial for the reliable governance of DAOs.

In this paper, we address two issues related to the voting mechanisms of DAOs: the dominance of whales and the collusion problem. In the former issue, the whales are DAO participants with a huge amount of governance tokens, wielding substantial influence in the decision-making processes of DAOs. For the collusion problem, malicious participants may engage in collusion using communication tools, exchanging bribes, and voting in favor of proposals that benefit themselves. Focusing on the voting of participants joining a DAO, we construct a mathematical model to elucidate the collusion resistance of existing voting systems. In our model, we assume the existence of honest participants and a malicious one with a huge amount of tokens, i.e., a whale, quantitatively evaluating the impact of malicious user manipulation on voting systems. We consider the utility of honest participants, which consists of the beneficial gain yielded from DAO services and the profit from the sale of tokens. Considering the existing voting systems of Linear Voting and Quadratic Voting for DAO decision-making, we derive the collusion cost under each voting system and compare the collusion resistance of the two voting systems. Finally, we propose a voting mechanism combining Quadratic Voting and the Vote Escrowed Token (veToken), in which tokens are locked for a certain period. We conduct numerical experiments to demonstrate that the proposed voting mechanism not only mitigates the whale problem but also achieves higher collusion resistance than Quadratic Voting.

The rest of the paper is structured as follows. Section 2 summarizes the related work, and in Section 3, we explain Quadratic Voting, which is the focus of this study. Section 4 provides an explanation of the mathematical model of DAOs and conducts an analysis of collusion resistance. Next, in Section 5, we describe the proposed voting mechanism, and Section 6 presents the results of the numerical evaluation. Finally, in Section 7, we conclude the paper and discuss future challenges.

2 Related work

Since DAOs are decentralized organizations formed on the Internet, anonymous participation is fundamental, making it challenging to directly control the actions of participants. Therefore, it is crucial to design DAOs such that DAOs encourage participants to autonomously take desirable actions.

2.1 Tokenomics

A fundamental element of DAOs is tokens. Also known as cryptocurrencies, tokens have market value. As DAOs are based on online participation, incentivizing contributors through token rewards is essential. Research on tokenomics has been conducted in the literature, e.g., Toyoda (2022), Pazos (2018), Akcin et al. (2022), Zhang and Liu (2021). Tokenomics, or token economics, focuses on the economic functions of tokens, exploring the sources of their monetary value Goutte et al. (2021). Since rewards are typically paid with tokens issued by the DAO, it is important for the study of DAO to analyze the economic value of tokens.

In Pazos (2018), Holden and Malani (2022), the authors focus on Initial Coin Offerings (ICOs), a method of fundraising by selling tokens, investigating the impact of ICOs on the token prices with the quantity theory of money. Pazos (2018) proposes a framework for determining a more transparent token offering price during ICOs, taking into account the growth potential of the services provided by DAOs. Holden and Malani (2022) models the dilemma faced by companies offering blockchain as a platform during ICOs. When reducing operational costs, such as mining rewards, the token price tends to decrease. To address this dilemma, the authors introduce a burn and mint system, which renders a part of the token unusable, proving it to be effective.

The control of token prices is also an important issue in tokenomics. Akcin et al. (2022) address the issue of initial participants accumulating tokens and reducing the incentive for new participants to join when there is an upper limit on the total token supply in the context of a blockchain-based infrastructure system. To continuously provide incentives while preventing inflation and issuing new tokens, the authors propose a system based on optimal control theory. This system controls the total token supply to maintain a sustainable incentive structure. Zhang and Liu (2021) propose a design model for algorithmic stablecoins. Stablecoins are a type of cryptocurrency designed to achieve a stable price in response to the high volatility of cryptocurrencies. Algorithmic stablecoins, in particular, operate independently of centralized assets or government currencies. They use algorithms and smart contracts to automatically adjust the token supply to maintain a stable price.

Toyoda (2022) considers the design of incentive mechanisms incorporating the prospect theory of behavioral economics, using the crypto-lottery game as an example. Given the economic value of tokens, understanding how to design incentive mechanisms that encourage participants to take desirable actions is crucial for the functioning of DAOs.

2.2 Voting system

There is extensive literature on voting systems for DAOs Kurniawan (2022), Ding et al. (2023), Dimitri (2023), Yu et al. (2019), Li et al. (2023). In Ding et al. (2023), a comprehensive survey on DAOs has been conducted, including the introduction of seven voting schemes and the analysis of voting mechanisms adopted in DAOs. The matters related to voting covered in the survey include eligibility, the voting process, incentive mechanisms, consensus mechanisms, and voting models. In terms of the eligibility, the authors consider three voting types: one person, one vote; a system where voting power is based on the amount of token holdings; and a restricted election where some voting rights are limited to certain participants. In Kurniawan (2022), a decision-making model is proposed for determining suitable voting mechanisms in DAOs. It clarifies the mechanisms and features that define how voting rights are weighted and the required quorum, comprehensively examining voting schemes for DAOs. Dimitri (2023) discusses the holographic consensus voting system. This system relaxes the quorum conditions for a vote to be effective through a staking mechanism, ensuring that decision-making is not delayed even when there are many participants, addressing the scalability issues of DAOs. In Yu et al. (2019), the Proof of Reputation (PoR) voting system is investigated. In PoR, participants’ reputations are calculated based on the amount of work contributed to the system, and voting power is determined based on reputation. The study shows that PoR has high resistance to known blockchain attacks, such as Sybil attacks. Li et al. (2023) statistically analyze Delegated-Proof-of-Stake (DPoS) based on actual projects. The study reveals differences in the length of delegation chains and the number of Sybil accounts operated by a single entity based on the nature of the project.

2.3 Governance

There is some literature on DAO governance models Han et al. (2023); Braun et al. (2022); Fritsch et al. (2022). Fritsch et al. (2022) analyze the distribution of voting power and voting behavior in several prominent DAOs that adopt Delegates. This study reports significant biases in voting power in the surveyed DAOs, highlighting issues with decentralized governance systems. Han et al. (2023) consider a mathematical model for DAO governance characterized by strategic token trading in voting. The analysis explores potential conflicts of interest between participants holding a large amount of tokens (whales) and a majority of participants holding a small amount of tokens. It is reported that the short-term, profit-driven voting actions of whales can lead to a decrease in token prices, and delaying token liquidity is proposed as an approach to mitigate these effects. Braun et al. (2022) focus on collusion issues in DAOs with staking mechanisms. The authors consider various mathematical models for staking amounts and voting systems to increase resistance against collusion. Note, however, that Braun et al. (2022) specifically consider staking mechanisms and do not address collusion prevention in non-staking-based voting. The present paper explores non-staking-based voting in general.

3 Quadratic voting

In blockchain networks adopting voting-based consensus algorithms like Proof-of-Stake, participants can vote based on the amount of tokens they hold. Two well-known methods for converting held tokens into voting power are Linear Voting and Quadratic Voting.

In Linear Voting, each token is equivalent to one vote, allowing participants to cast as many votes as the number of tokens they possess (e.g., using n tokens enables the casting of n votes). Note that the maximum number of votes a participant can cast is equivalent to the amount of tokens the participant holds. Linear Voting has the disadvantage of allowing the voting outcome to be influenced by the wishes of “whales,” the participants who hold a large number of tokens, since the amount of held tokens is converted directly into voting power. In cases where whales own more than half of the governance tokens in DAO, the voting outcome can be unilaterally determined by the whales, regardless of the votes from other participants. This situation compromises the decentralization of the DAOs and hinders their healthy development, making it important to implement measures to decentralize voting power.

Quadratic Voting, on the contrary, is a voting system designed to alleviate the whale problem arising in Linear Voting. In Quadratic Voting, similar to Linear Voting, each unit token is counted as one vote. However, to cast n votes, it is necessary to contribute n² tokens.

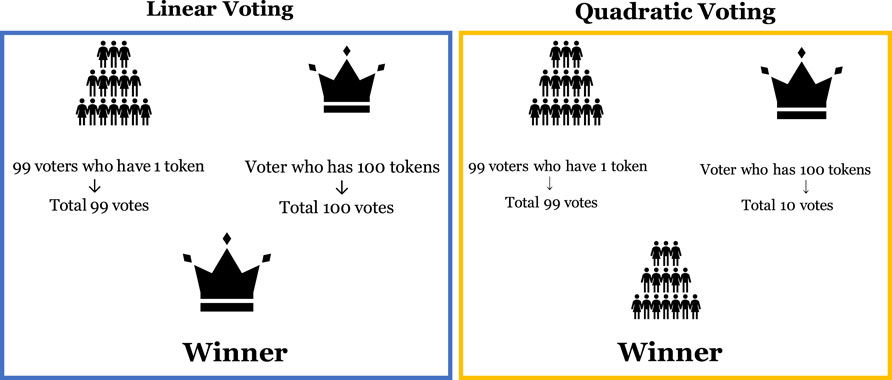
To illustrate the difference between Linear Voting and Quadratic Voting, consider a DAO decision-making scenario with a total of 100 participants. Among these participants, 99 individuals each possess only 1 token, while one participant holds 100 tokens (See Figure 1). Suppose that a project is proposed, in which there is a conflict of interest between the group of 99 participants with 1 token each and the single participant with 100 tokens. In the case of voting on the project, with Linear Voting, the participant holding 100 tokens can cast 100 votes, overpowering the 99 votes from the group of 99 participants. In Quadratic Voting, on the contrary, the voting power of the participant with 100 tokens is compressed to 10 votes, allowing the group of 99 participants to win with their 99 votes. Note that in Linear Voting, the cost of voting increases linearly, meaning each additional vote costs a constant amount. In contrast, in Quadratic Voting, the cost increases quadratically, where the cost for each additional vote grows at an increasing rate, making it more expensive to accumulate more votes Lalley and Weyl (2018). This mechanism weakens the voting power of participants holding a large number of tokens, making Quadratic Voting a system that tends to reflect the will of a larger number of participants.

Figure 1

Figure 1. Linear voting and quadratic voting.

As mentioned, the introduction of the Quadratic Voting mechanism can help mitigate the influence of whales. However, note that whales still possess a significant number of tokens, and there remains a possibility for them to engage in collusion by using their tokens as bribes. In the next section, we will analyze the potential for collusion by whales.

4 DAO mathematical model

In this section, we describe our mathematical model of voting for DAOs.

4.1 Scenario setup

In this paper, we consider a discrete-time model similar to Han et al. (2023). The time is discretized and denoted by $t\in \mathbb{N}\cup \{0\}$. Suppose that a DAO is formed and a project of services is proposed at t = 0. At t = 1, voting for decision-making is conducted, and then the DAO initiates its services at t = 2. For simplicity, we assume that the voting process occurs only once⁴.

Voting is conducted in response to proposals regarding the services provided by the DAO, and the accepted proposals are then implemented. We consider Linear Voting and Quadratic Voting for decision-making, and investigate their respective impacts on collusion resistance. In the following, we assume that each participant votes to maximize their utility at t = 2, just after the voting process.

The participants of the DAO are classified into two types. The first type is contributory participants who vote for proposals that benefit the DAO during decision-making. In the following, these participants are referred to as contributing users. The second type is participants who hold a substantial amount of tokens and pursue personal interests, prioritizing short-term self-interest over the overall benefit of the DAO. In the following, these participants are referred to as malicious users. We assume that there is only one malicious user, and at the time of project proposals, the malicious user suggests projects that benefit only themselves, causing harm to the entire DAO. There are N contributing users in the DAO. We define the set of all the participants $\mathcal{N}$ as

$\mathcal{N}=\left\{1,\dots ,N\right\}\cup \left\{m\right\},$

where m represents the malicious user.

4.2 Participants utility

At the formation of the DAO at t = 0, user $i\in \mathcal{N}$ possesses a quantity of tokens represented by x_i. Participants derive two types of utility: one from the usage of DAO services and the other from the proceeds of selling tokens.

The utility obtained from the services is assumed to be given by S(a)N_ex_i (a ∈ {H, M}). Here, S(a) represents the service efficiency and is determined by the adopted proposal a ∈ {H, M} through voting. Here, H indicates the adoption of a proposal that benefits the DAO, while M indicates the adoption of a proposal that harms the entire DAO. We assume S(H) > S(M). N_e represents the number of participants in the DAO. In our model, as the number of users utilizing the DAO increases, the value of the DAO platform also rises. For instance, in the case of a DAO providing social networking services, with a small number of participants, the limited communication opportunities may result in lower utility. With a large number of participants, on the other hand, users can connect with a diverse group, increasing the utility of the service. We also assume that participant i can obtain utility from the services in proportion to the quantity of tokens the participant hold, denoted by x_i.

Regarding the utility of profit from token sales, we assume that participant i sells all tokens at time T_a (>1) and obtains token sale profit of $P_{T_a}^{(a)}{x}_i$. Here, $P_t^{(a)}$ represents the market price of tokens at time t, increasing monotonically when a = H and decreasing monotonically when a = M. This implies that if a proposal that benefits the DAO is adopted, the value of the DAO improves, causing an increase in token prices. Conversely, if a proposal that harms the DAO is adopted, the token prices decrease as the value of the DAO diminishes.

Based on the considerations above, the utility $U_i^{(a)}(t)$ for participant i at time t (=2, … , T_a) is defined by the following expression:

$\begin{array}{ll}\hfill U_i^{\left(a\right)}\left(t\right)& ={\displaystyle \sum _{n=0}^{T_a-t}}{\delta }^{n}S\left(a\right)N_e{x}_i+{\delta }^{T_a-t}{P}_{T_a}^{\left(a\right)}{x}_i\hfill \\ \hfill & =\frac{1-{\delta }^{T_a-t+1}}{1-\delta }S\left(a\right)N_e{x}_i+{\delta }^{T_a-t}{P}_{T_a}^{\left(a\right)}{x}_i.\hfill \end{array}(1)$

Here, δ is the discount rate. Participants convert the utility derived from DAO services obtainable until the token selling time T_a and the utility from token sale profit into present value using the discount rate δ.

Next, we consider the utility of a contributing user i ∈ {1, … , N}. At t = 1, user i has two choices: either rejecting bribery and voting for a proposal that benefits the entire DAO or accepting bribery and voting for a malicious proposal. Since the voting is done to maximize the utility at t = 2, we consider the utility at t = 2. For contributing user’s choices, there are two possibilities: rejecting bribery and voting for proposal H, and accepting bribery from the malicious user and voting for proposal M.

If user i chooses not to accept bribery, from (Eq. 1), the utility at t = 2 is given by:

$U_i^{\left(H\right)}\left(2\right)=\frac{1-{\delta }^{T_H-1}}{1-\delta }S\left(H\right)N_e{x}_i+{\delta }^{T_H-2}{P}_{T_H}^{\left(H\right)}{x}_i,i\in \left\{1,\dots ,N\right\}.(2)$

On the contrary, if user i chooses to accept bribery, the utility is given by:

$U_i^{\left(M\right)}\left(2\right)=\frac{1-{\delta }^{T_M-1}}{1-\delta }S\left(M\right)N_e\left(x_i+b_i\right)+{\delta }^{T_M-2}{P}_{T_M}^{\left(M\right)}\left(x_i+b_i\right),i\in \left\{1,\dots ,N\right\},(3)$

where b_i is the bribery received from the malicious user m.

4.3 Bribe cost

We assume that bribes are paid through smart contracts as soon as the contributing users cast malicious votes. Therefore, contributing users are compelled to vote for malicious proposals. We also assume that the malicious user pays bribery using the tokens used in the DAO. A contributing user accepting the bribery and voting for proposal M occur when $U_i^{(M)}(2)>U_i^{(H)}(2)$. In this case, from Eqs 2, 3, the bribery b_i must satisfy the following inequality:

$b_i>\frac{\left(\left(1-{\delta }^{T_H-1}\right)S\left(H\right)-\left(1-{\delta }^{T_M-1}\right)S\left(M\right)\right)N_e+\left(1-\delta \right)\left({\delta }^{T_H-2}{P}_{T_H}^{\left(H\right)}-{\delta }^{T_M-2}{P}_{T_M}^{\left(M\right)}\right)}{\left(1-{\delta }^{T_M-1}\right)S\left(M\right)N_e+\left(1-\delta \right){\delta }^{T_M-2}{P}_{T_M}^{\left(M\right)}}{x}_i.(4)$

Note that the right side of the above inequality indicates that the bribery cost is proportional to the contributing user i’s current quantity of tokens x_i.

4.4 Total bribe cost

In this subsection, we quantitatively evaluate collusion resistance in two voting systems: Linear Voting and Quadratic Voting. When a project is proposed in the DAO, the adoption of the proposed project is decided by a majority vote, meaning that the proposed project is adopted when it receives more than half of the votes. Therefore, when colluding to determine the fate of a project, malicious user m needs to choose individuals to bribe in a way that secures more than half of the votes.

In most blockchain networks, there are costs associated with fees when sending transactions. For example, when conducting transactions on Ethereum, such as making remittance or interacting with smart contracts, there is a cost referred to as gas fees. In the following, such fee-related cost is denoted as c.

Let y_i $(i\in \mathcal{N}\backslash \{m\})$ denote the binary decision variable as

$y_i=\left\{\begin{array}{cc}\hfill 1,\hfill & \text{if\hspace{0.17em}the\hspace{0.17em}malicious\hspace{0.17em}user\hspace{0.17em}}m\text{\hspace{0.17em}decides\hspace{0.17em}to\hspace{0.17em}send\hspace{0.17em}}\text{a\hspace{0.17em}bribe\hspace{0.17em}to\hspace{0.17em}contributing\hspace{0.17em}user\hspace{0.17em}}i,\hfill \\ \hfill 0,\hfill & \text{otherwise}.\hfill \end{array}\right.$

Noting that the bribery given by the malicious user m to the contributing user i is b_i, the total bribery cost required for collusion by the malicious user m is given by ${\sum }_{i=1}^N(b_i+c)y_i$. A smaller total bribery cost makes collusion more likely, while a larger total bribery cost indicates higher resistance to collusion.

Here, from the perspective of the malicious user, the problem of minimizing the total bribery cost can be formalized as follows:

$\begin{array}{ccc}\hfill \mathbf{\text{Problem}}1:& \hfill & \hfill \\ \hfill \min & \hfill & {\displaystyle \sum _{i=1}^N}\left(b_i+c\right)y_i,\hfill \end{array}(5)$

$\text{s.t.}{y}_i\in \left\{\mathrm{0,1}\right\},(6)$

$⌊\frac{{\sum }_{i=1}^N{f}_V\left(v_i\right)}{2}⌋+1\le {\displaystyle \sum _{i=1}^N}{f}_V\left(v_i\right)y_i.(7)$

In the objective function (Eq. 5), we consider the set of users who receive bribes in a way that minimizes the total bribery cost. The constraint (Eq. 6) is followed by the definition of y_i. The constraint (Eq. 7) indicates that more than half of the total votes are cast for the malicious proposal. Here, the function f_V (⋅) represents the function converting the token quantity used for voting into the number of votes, and f_V (⋅) is expressed differently depending on the voting system. When a user uses a token quantity v for voting, in Linear Voting, f_V(v) = v, and in Quadratic Voting, $f_V(v)=\lfloor \sqrt{v}\rfloor$ (where ⌊⋅⌋ is the floor function). Also, let v_i be the token quantity used for voting by user i $(i\in \mathcal{N}\backslash \{m\})$. We assume v_i = x_i, meaning that contributing users vote with all the tokens they possess. Ideally, malicious users would also participate in voting and influence the results, but here, we do not consider the impact of malicious users on the voting process⁵.

4.5 Token selling strategy of a contributing user

We consider the optimal token selling time for a contributing user. From Eqs 2, 3, the optimal token selling time T_H for contributing user i can be expressed as follows:

$T_H=\underset{t\ge 2}{argmax}\frac{1-{\delta }^{t-1}}{1-\delta }S\left(H\right)N_e{x}_i+{\delta }^{t-2}{P}_t^{\left(H\right)}{x}_i.(8)$

In Eq. (8), $P_t^{\left(H\right)}$ is the token price given by Eq. 10 in the following subsection.

Note that bribe is given to contributing user i in a way where the inequality $U_i^{(M)}(2)>U_i^{(H)}(2)$ holds. In this situation, the utility $U_i^{(M)}(2)$ is constant regardless of when contributing user i sells tokens. Considering the contributing user’s utility for a proposal, which results from their own tokens, the bribed tokens compensate for the opportunity cost incurred by voting for proposal M. Therefore, the point at which the bribe is minimized is the point at which the utility is maximized if proposal M is adopted. The incentive for the malicious user is to minimize the bribes paid while aiming to win the vote. Thus, the malicious user instructs the contributing users, who receive the bribes, to sell their tokens at the time when the amount of the bribes are minimized. This observation yields T_M as:

$T_M=\underset{t\ge 2}{argmax}\frac{1-{\delta }^{t-1}}{1-\delta }S\left(M\right)N_e{x}_i+{\delta }^{t-2}{P}_t^{\left(M\right)}{x}_i.(9)$

Here, $P_t^{\left(M\right)}$ is the token price given by Eq. 11 in the following subsection.

4.6 Token price

Tokens are used when participants utilize the services provided by the DAO. Participants join the DAO not only to use the services but also in the hope that the services will continue to improve. It is important to note that when the quality of DAO services improves, leading to an increase in the number of participants, the token price $P_t^{(a)}$ also increases. Here, referring to Han et al. (2023), the market value P_market of tokens at time t = 1 can be defined by the following equation:

$P_{\mathit{market}}={\displaystyle \sum _{t=0}^{\infty }}{\delta }^{t}S\left(H\right)N_e=\frac{S\left(H\right)N_e}{1-\delta }.$

Based on P_market, the prices at time t ( ≥ 2) for two types of proposals are determined by the following equations.

$P_t^{\left(H\right)}=\left\{k_H\left(t-1\right)+1\right\}{P}_{\mathit{market}},(10)$

$P_t^{\left(M\right)}=k_M^{t-1}{P}_{\mathit{market}},(11)$

where k_a (a ∈ {H, M}) is a coefficient related to the price changes. When a = H, it is assumed that the token price increases linearly, and when a = M, it is assumed to decrease exponentially in the market.

4.7 Collusion resistance analysis

In this subsection, we analyze collusion resistance for the two voting mechanisms through computer simulations. Here, we assume that at t = 0, each contributing user i ∈ {1, … , N} holds x_i tokens. Let x^(total) denote the total amount of tokens held by all contributing users, given by

$x^{\left(total\right)}={\displaystyle \sum _{i\in \mathcal{N}\backslash \left\{m\right\}}}{x}_i.$

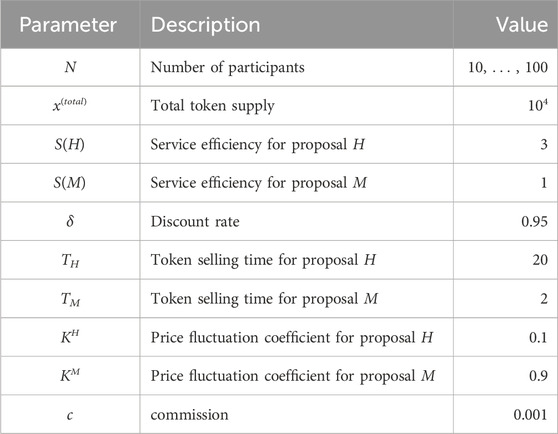
In the simulation, we randomly allocate x_i such that x^(total) remains constant⁶. The parameter values set for the simulation are shown in Table 1. Here, for simplicity, we assume that there are no restrictions on the number of tokens held by the malicious user m. This assumption allows the malicious user m to bear the total bribery cost (Eq. 5) required for collusion. Here, b_i is calculated by the right hand side of Eq. 4.

Table 1

Table 1. Parameter setting for simulation experiments.

Under these assumptions, we solved Problem 1 for both Linear Voting and Quadratic Voting using the PuLP Python library and CBC solver. We calculated the average values of the total bribery cost along with 95% confidence intervals.

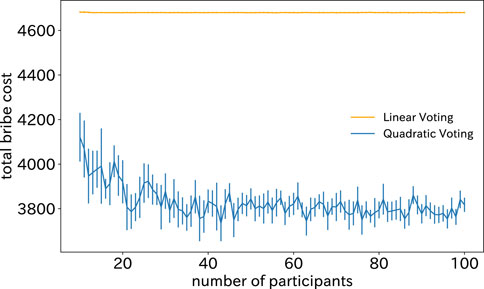
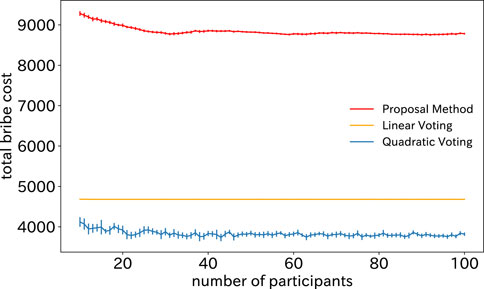
Figure 2 shows the total bribery cost for the two voting mechanisms concerning the number of contributing users N. From the figure, it can be observed that while Linear Voting takes on almost a constant value regardless of the number of participants, the total bribery cost in Quadratic Voting decreases with an increase in the number of participants.

Figure 2

Figure 2. The total bribery cost in Linear Voting and Quadratic Voting.

The reason why the total bribery cost in Quadratic Voting is lower than in Linear Voting is due to the fact that the total number of votes in Quadratic Voting is smaller than that in Quadratic Voting. When a user holds a large number of tokens, Quadratic Voting compresses the number of votes significantly, and the more tokens a user has, the greater the compression effect. It is important to note that the reduction in the total number of votes also reduces the number of votes required for collusion.

As a simple example, consider a situation with four contributing users and token holdings of (x₁, x₂, x₃, x₄) = (1, 1, 4, 9). In this case, the total number of votes is 15. For Linear Voting, the minimum number of votes required for collusion is 8. Therefore, in this case, the minimum total bribery cost can be achieved by bribing the user with a token quantity of 9. On the other hand, for Quadratic Voting, converting token quantity to votes yields (1, 1, 2, 3). The total number of votes is then 7, and the minimum number of votes required for collusion is 4. Consequently, bribery should be directed to two users with a token quantity of 1 and one user with a token quantity of 4. Assuming that the transaction cost c is sufficiently small and negligible, we can see that Quadratic Voting requires fewer tokens for collusion than Linear Voting.

Consider an alternative scenario where all participants have equal and completely distributed token holdings. Suppose that the token quantity per participant is n² $(n\in \mathbb{N})$. When applying Quadratic Voting, the number of votes becomes n. In this situation, regardless of Quadratic Voting or Linear Voting, to collude, it is necessary to bribe the majority of users, and the selection of users to bribe remains the same. Thus, in a fully decentralized DAO, collusion resistance is high.

5 Proposal voting mechanism

From the preliminary experiments in the previous section, it was revealed that Quadratic Voting is more vulnerable to collusion compared to Linear Voting. In this section, we propose a voting mechanism that combines Quadratic Voting with vote-escrowed tokens (veToken) to mitigate the influence of whales.

5.1 veToken

The veToken is a mechanism proposed to prevent malicious voting actions driven by participants’ short-term self-interest. Participants can acquire voting power weighted by the duration of token lockup, in exchange for locking their tokens for a specified period. Importantly, this voting power cannot be sold or transferred. Such a mechanism enables aligning participants’ voting behavior with the DAOs’ long-term objectives Lloyd et al. (2023).

To establish the relationship between voting power and the token lockup period, we refer to the Curve Finance calculation model⁷. In this model, for a token amount a locked for a duration t_l at the time of lockup, the voting power w at an elapsed time t_e (≤t_l) from the lockup is given by the following equation⁸:

$w=\frac{t_l-t_e}{t_{\mathit{max}}}\cdot a,0\le t_e\le t_l.$

In the veToken model, the lockup period is selectable, and the voting power is computed based on the token amount and how long the tokens are locked.

5.2 Proposal voting mechanisms and bribe costs

In the proposed voting mechanism, tokens are compressed with Quadratic Voting and then their voting power is determined with the lock period. Let $T_i^{(lock)}(\le T_{\mathit{Max}}^{(lock)})$ denote the lock period for user i ∈ {1, … , N}. The voting power of user i with token quantity x_i, incorporating the Quadratic Voting function $f_V(v)=\lfloor \sqrt{v}\rfloor$, is given by:

$\frac{T_i^{\left(lock\right)}-t_e}{T_{\mathit{Max}}^{\left(lock\right)}}\cdot f_V\left(x_i\right),$

where t_e represents the time when the vote is cast.

Now consider the minimum bribery cost for the proposed voting mechanism. The problem of minimizing the bribery cost for malicious users during voting in the proposed mechanism is formulated similarly to Problem 1.

$\begin{array}{ccc}\hfill \mathbf{\text{Problem}}2:& \hfill & \hfill \\ \hfill \min & \hfill & {\displaystyle \sum _{i=1}^N}\left(b_i+c\right)y_i,\hfill \end{array}(12)$

$\text{s.t.}{y}_i\in \left\{\mathrm{0,1}\right\},(13)$

$\frac{{\sum }_{i=1}^N\left(T_i^{\left(lock\right)}-t_e\right)}{T_{\mathit{Max}}^{\left(lock\right)}}{f}_V\left(x_i\right)\left(1-y_i\right)+\frac{1}{T_{\mathit{Max}}^{\left(lock\right)}}\le {\displaystyle \sum _{i=1}^N}\frac{T_m^{\left(lock\right)}-t_e}{T_{\mathit{Max}}^{\left(lock\right)}}{f}_V\left(x_i\right)y_i.(14)$

Here, the objective function of Eq. 12 and the constraint of Eq. 13 are the same as Problem 1. $T_m^{(lock)}$ in (Eq. 14) represents the lock period specified by malicious users offering bribes, while $T_i^{(lock)}$ denotes the lock period chosen by contributing users. $T_i^{(lock)}$ is constrained to be smaller than or equal to the token sale time T_H in Eq. 8, and it is given by $T_i^{(lock)}=\min (T_H,T_{\mathit{Max}}^{(lock)})$.

6 Numerical results

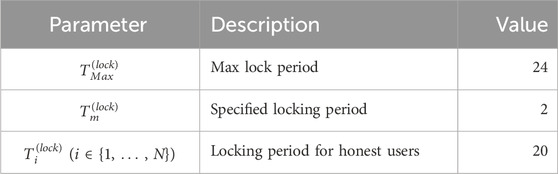
We conducted simulation experiments for analyzing collusion resistance for the proposed voting mechanism. For parameters common to Problem 1, the same parameter settings as in Table 1 were used. The other parameters introduced in this experiment are listed in Table 2. We assume that token locking is initiated at t = 0, and that voting occurs at t = 1, thus noting that t_e = 1. In Curve Finance, the maximum lock period is set to 4 years, and hence in this experiment, the range for $T_i^{(lock)}$ is set as $0\le T_i^{(lock)}\le T_{\mathit{lock}}^{(Max)}(=24)$. Throughout the experiments, $T_m^{(lock)}$ is set to the same value for all cases. The bribery cost b_i with respect to the lock period $T_i^{(lock)}$ can be computed by substituting T_M in Eq. 9 with $T_m^{(lock)}$. In the following, we compare the total bribery costs for Linear Voting, Quadratic Voting, and the proposed mechanism.

Table 2

Table 2. Parameter setting for Problem 2.

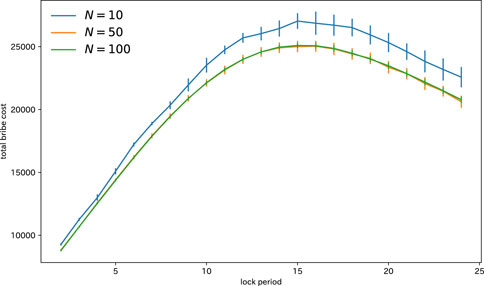
Figure 3 shows the total bribery cost for three voting mechanisms. The horizontal axis is the number of users participating the DAO. In this figure, the total bribery cost in the proposed mechanism is the largest among the three voting mechanisms. The primary reason for the substantial increase in the total bribery cost for the proposed mechanism is the remarkably increased voting power of users who reject bribes. Malicious users find themselves needing to offer bribes to a larger number of users compared to existing voting mechanisms. Consequently, the proposed mechanism allows for a substantial escalation in the total bribery cost, confirming a significant improvement in collusion resistance.

Figure 3

Figure 3. Comparison of the total bribe costs of three voting systems.

Next, we consider the relationship between the lock period and the total bribery cost. Figure 4 illustrates the trend of the total bribery cost with respect to the lock period. It is observed from this figure that for the three voting mechanisms, the total bribery cost increases and then decreases with increase in the lock period. Consequently, it is apparent that a malicious user’s optimal strategy is to specify $T_m^{(lock)}=2$ to minimize the total bribery cost necessary for collusion. This is the worst-case scenario for DAO developers who designing a voting mechanism against collusion. Even in such a worst-case scenario, the proposed method is effective for increasing the total bribery cost.

Figure 4

Figure 4. Total bribe costs over the lock period.

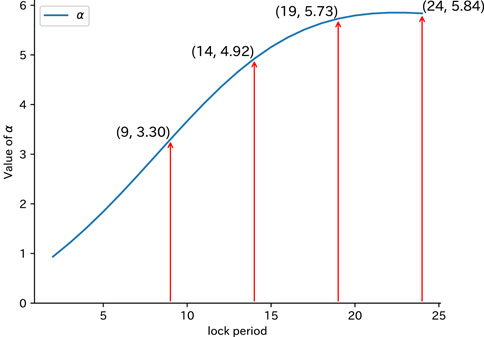
Regarding the relationship between the lock period and the total bribery cost, it is essential to consider the relationship between the bribery cost b_i and the lock period t_l. Let the bribery cost per unit token for user i be denoted as α(t_l) = b_i/x_i. Note that b_i in α(t_l) is a function of the lock period t_l, given by substituting T_M = t_l into (Eq. 4). Figure 5 illustrates the relationship between the lock period and α(t_l). When the lock period is small, α(t_l) increases significantly, leading to a decrease in the cost-effectiveness of the bribery cost b_i. When the lock period is large, on the contrary, the bribe becomes more cost-effective, leading to collusion with a small total bribery cost. This corresponds to the decreasing tendency in Figure 4.

Figure 5

Figure 5. The bribery cost per token with respect to the lock period.

Figure 6 shows the impact of the number of participants on the total bribery cost in cases of the lock periods 2, 13, and 24. It is observed from this figure that for the three lock-period cases, the total bribe cost remains constant with respect to the number of participants. This result confirms that the proposed voting mechanism is effective in preventing collusion regardless of the increase in the number of participants.

Figure 6

Figure 6. Comparison of total bribe costs for three lock periods.

7 Conclusion

In this paper, we tackled two prevalent issues in DAOs: the undue influence of whales and the problem of collusion among participants for mutual benefit. We constructed a mathematical model to assess the collusion resistance of current voting systems in DAOs, considering both honest participants and a malicious whale. Our analysis focused on the utility derived from DAO services and token sales, using Linear and Quadratic Voting systems to evaluate the cost of collusion and compare their resistance to it. Then we developed a novel voting mechanism that combines Quadratic Voting with veToken, where tokens are time-locked. We demonstrated through numerical experiments that this approach not only addresses the whale problem but also offers enhanced resistance to collusion compared to Quadratic Voting alone.

Quadratic Voting is known to be vulnerable to Sybil attacks. In blockchain, where anonymous participation is fundamental, an individual can create multiple accounts and infiltrate a DAO under different participant identities. The existence of Sybil accounts is pointed out in Li et al. (2023). Malicious users can diminish the impact of Quadratic Voting by distributing tokens among multiple participant aliases they control. In such cases, the proposed approach in this paper may not be sufficient. However, technologies like WorldCoin⁹, which utilize biometric authentication to provide unique IDs on the blockchain while protecting personal information (Proof of Personalhood), aim to prevent Sybil attacks. Considering the potential spread of such technologies, our study addressing the resistance of Quadratic Voting to collusion remains relevant.

Future challenges include the creation and analysis of mathematical models that consider repeated voting over a long span, token movement, and changes in the number of participants, moving beyond one-time voting scenarios.

In our mathematical model, we considered only one project proposal and the voting on its aceptance or rejection, assuming that bribes are paid in the same token. However, it is common for bribes to be paid in different tokens. We also considered simple functions for the token-price evolution. Extending the mathematical model to include these aspects are also an important research topic for future studies.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

ST: Conceptualization, Formal Analysis, Investigation, Software, Visualization, Writing–original draft. SK: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Supervision, Validation, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported in part by Japan Society for the Promotion of Science under Grant-in-Aid for Challenging Research (Exploratory) No. 22K19776 and Grant-in-Aid for Scientific Research (B) No. 24K02931.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Trust is an important concept in decentralized internet systems, and studies on the trustworthiness of Bitcoin have been conducted. In terms of the trust for commerce and digital currency, see Zarifis et al. (2014).

²https://ethereum.org/en/smart-contracts/

³https://medium.com/@nvy_0x/the-beanstalk-bean-exploit-b038f4d324ea

⁴We should consider the DAO voting-process model in which multiple projects are proposed and voting is conducted for each project proposal. In addition, the token price fluctuates based on the success or failure of projects, and that users determine the token-lock period for voting on the next project while taking into account these fluctuations of token value. For such voting model, however, we should carefully model the token-price process, project utility of honest users, and the incentive interaction among token-price, project utility and voting power. Because constructing such a model is challenging, as a first step, we have focused on a model specifically designed for collusion, targeting a single project only.

⁵In this paper, we assume that malicious users are whales. In the case of Linear Voting, a whale can adopt a malicious proposal M by voting only for themselves without colluding, making collusion unnecessary. Quadratic Voting is introduced to mitigate the arbitrary voting by whales, which was a drawback of Linear Voting. Here, for simplicity, we focus solely on the total bribery cost and do not consider the participation of malicious users in voting.

⁶Here, we generate uniform random numbers r_i from the interval [0,1], and we calculate x_i as x_i = x^(total) × r_i/W using the sum W = ∑_ir_i.

⁷https://classic.curve.fi/files/CurveDAO.pdf

⁸Since 0 ≤ t_l ≤ t_max, we have 0 ≤ w ≤ a, i.e., voting power is bounded by the amount of token to be locked. This implies that a user who regards a project as valuable will make w large by locking a large amount of tokens. Note that voting power is influenced by the interaction between the utility of the project’s success and the fluctuations in token value.

⁹https://whitepaper.worldcoin.org/

References

Akcin, O., Streit, R. P., Oommen, B., Vishwanath, S., and Chinchali, S. (2022). A control theoretic approach to infrastructure-centric blockchain tokenomics.

Google Scholar

Braun, A., Häusle, N., and Karpischek, S. (2022). Collusion-proof decentralized autonomous organizations. Available at SSRN 3760531.

Google Scholar

Dimitri, N. (2023). Voting in DAOs. Distributed Ledger Technolgies Reserch Pract. 2, 1–12. doi:10.1145/3624574

CrossRef Full Text | Google Scholar

Ding, Q., Liebau, D., Wang, Z., and Xu, W. (2023). A survey on decentralized autonomous organizations (DAOs) and their governance. SSRN J. Available at SSRN 4378966. doi:10.2139/ssrn.4378966

CrossRef Full Text | Google Scholar

El Faqir, Y., Arroyo, J., and Hassan, S. (2020). “An overview of decentralized autonomous organizations on the blockchain,” in Proceedings of the 16th international symposium on open collaboration (New York, NY, USA: Association for Computing Machinery). doi:10.1145/3412569.3412579

CrossRef Full Text | Google Scholar

Fritsch, R., Müller, M., and Wattenhofer, R. (2022). Analyzing voting power in decentralized governance: who controls DAOs? arXiv preprint arXiv:2204.01176.

Google Scholar

Goutte, S., Guesmi, K., and Saadi, S. (2021). Cryptofinance: a new currency for A new economy. World Scientific Publishing Company, 175.

Google Scholar

Han, J., Lee, J., and Li, T. (2023). Dao governance. Available at SSRN 4346581.

Google Scholar

Holden, R., and Malani, A. (2022). An examination of velocity and initial Coin offerings. Manag. Sci. 68, 9026–9041. doi:10.1287/mnsc.2022.4314

CrossRef Full Text | Google Scholar

Kharitonova, A. (2021). “Capabilities of blockchain technology in tokenization of economy,” in Proceedings of the 1st international scientific conference “legal regulation of the digital economy and digital relations: problems and prospects of development” (LARDER 2020) (Dordrecht, Netherlands: Atlantis Press), 28–32. doi:10.2991/aebmr.k.210318.006

CrossRef Full Text | Google Scholar

Kraus, S., Jones, P., Kailer, N., Weinmann, A., Chaparro-Banegas, N., and Roig-Tierno, N. (2021). Digital transformation: an overview of the current state of the art of research. Sage Open 11, 215824402110475. doi:10.1177/21582440211047576

CrossRef Full Text | Google Scholar

Kurniawan, W. (2022). Voting mechanism selection for decentralized autonomous organizations

Google Scholar

Lalley, S. P., and Weyl, E. G. (2018). Quadratic voting: how mechanism design can radicalize democracy. AEA Pap. Proc. 108, 33–37. doi:10.1257/pandp.20181002

CrossRef Full Text | Google Scholar

Li, C., Xu, R., and Duan, L. (2023). “Liquid democracy in DPoS blockchains,” in Proceedings of the 5th ACM international symposium on blockchain and secure critical infrastructure (New York, NY, USA: Association for Computing Machinery), 25–33. doi:10.1145/3594556.3594606

CrossRef Full Text | Google Scholar

Li, J., and Wang, F.-Y. (2023). The TAO of blockchain intelligence for intelligent Web 3.0. IEEE/CAA J. Automatica Sinica 10, 2183–2186. doi:10.1109/JAS.2023.124056

CrossRef Full Text | Google Scholar

Lloyd, T., O’Broin, D., and Harrigan, M. (2023). “Emergent outcomes of the veToken model,” in 2023 IEEE international conference on omni-layer intelligent systems (COINS), 1–6. doi:10.1109/COINS57856.2023.10189201

CrossRef Full Text | Google Scholar

Pazos, J. (2018). Valuation of utility tokens based on the quantity theory of money. J. Br. Blockchain Assoc. 1, 1–7. doi:10.31585/jbba-1-2-(2)2018

CrossRef Full Text | Google Scholar

Qin, R., Ding, W., Li, J., Guan, S., Wang, G., Ren, Y., et al. (2023). Web3-Based decentralized autonomous organizations and operations: architectures, models, and mechanisms. IEEE Trans. Syst. Man, Cybern. Syst. 53, 2073–2082. doi:10.1109/TSMC.2022.3228530

CrossRef Full Text | Google Scholar

Toyoda, K. (2022). Web3 meets behavioral economics: an example of profitable crypto lottery mechanism design. arXiv e-prints , arXiv:2206.03664. doi:10.48550/arXiv.2206.03664

CrossRef Full Text | Google Scholar

Wang, S., Ding, W., Li, J., Yuan, Y., Ouyang, L., and Wang, F.-Y. (2019). Decentralized autonomous organizations: concept, model, and applications. IEEE Trans. Comput. Soc. Syst. 6, 870–878. doi:10.1109/TCSS.2019.2938190

CrossRef Full Text | Google Scholar

Yu, J., Kozhaya, D., Decouchant, J., and Esteves-Verissimo, P. (2019). RepuCoin: your reputation is your power. IEEE Trans. Comput. 68, 1225–1237. doi:10.1109/TC.2019.2900648

CrossRef Full Text | Google Scholar

Zaoui, F., and Souissi, N. (2020). Roadmap for digital transformation: a literature review. Procedia Comput. Sci. 175, 621–628. doi:10.1016/j.procs.2020.07.090

CrossRef Full Text | Google Scholar

Zarifis, A., Efthymiou, L., Cheng, X., and Demetriou, S. (2014). “Consumer trust in digital currency enabled transactions,” in Business information systems workshops. Editors W. Abramowicz, and A. Kokkinaki (Cham: Springer International Publishing), 241–254.

CrossRef Full Text | Google Scholar

Zhang, L., and Liu, Y. (2021). Optimal algorithmic monetary policy. arXiv preprint arXiv:2104.07888.

Google Scholar