- Kleros Cooperative, Paris, France
We consider griefing factors, a system for measurement of the cost-effectiveness of sabotage, which have been used to analyze the attack resistance of blockchain systems. Attackers are said to “grief” if they accept economic harm to themselves in order to harm others; the griefing factor is the ratio of the harm done to the victim to the harm taken on by the attacker. In this work, we study the mathematical properties of this notion, particularly focusing on how the presence of players willing to engage in griefs at varying griefing factors impacts the equilibria present in games.
1 Introduction
There is a rich body of literature in economics examining strategies that rely on committing sabotage against other participants in games (Chowdhury and Gürtler, 2015). Indeed, in certain games, such as contests with a fixed prize that is awarded to one of a finite number of players, strategies based on attempting to reduce the chances of an opponent in order to improve one’s own can be incentivized (Konrad, 2000). Typically, existing research on this question adopts an approach that involves attempting to incorporate the incentives of participants to harm others directly into the payoff matrices of the games considered.
A related idea, introduced by Buterin (2018b) in the context of analyzing blockchain systems, defines a “grief” as a strategy that causes harm to both the participant executing this strategy and other participants in a game. The word “grief” draws upon the slang term used in video game communities for styles of play that seek to harm others despite not being useful or indeed being harmful to the player carrying them out (Leonardos et al., 2023). Buterin additionally provides a measure of the effectiveness of griefs, which he calls the “griefing factor,” indicating the ratio of the harm that an attack does and its cost to the attacker (Buterin, 2018b).
To illustrate this concept, we consider a game with two players Alice and Bob whose payoffs are given in Table 1. It is a (weakly) dominant strategy for each player to play A. If Alice thus expects Bob to play A, she can nonetheless play B. Playing this strategy requires Alice to accept a cost: she loses the opportunity to earn $1. However, by accepting this cost to herself, Alice can inflict even greater economic harm upon Bob, as she prevents him from receiving $2. Hence, Alice has the ability to grief Bob with a griefing factor of 2.
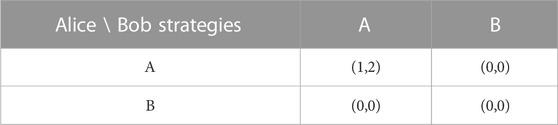
TABLE 1. The payoff table in a game between Alice and Bob. When Alice plays a strategy corresponding to a given row and Bob plays a strategy corresponding to a given column, they receive as payoffs the amounts in parentheses in the cell for that row and that column, with Alice receiving the amount given by the first coordinate and Bob receiving the amount given by the second coordinate. If Alice expects Bob to play A, she can play B even though this gives her a lower payout than playing A in order to grief Bob.
Griefing factors provide a useful measure in that they allow for identification of the presence of particularly effective sabotage strategies in a game. As griefing factors can be calculated in terms of the payoffs of the game, one does not need to know in advance what rewards an attacker may receive for successful sabotage in order to perform an analysis of available griefing factors. Thus, when designing a game, a mechanism designer can attempt to ensure that all of the griefing strategies available in that game have griefing factors that are as small as possible, implying that whatever external incentives an attacker may have would need to be correspondingly large in order for it to be worthwhile to perform an attack.
In this article, we analyze the mathematical properties of griefing factors. While this analysis is general, our examples are largely drawn from the setting of blockchains. Indeed, this notion is perhaps particularly relevant in the context of blockchain systems due to their heavy reliance on mechanism design, in consensus algorithms (Nakamoto, 2008; Buterin, 2014) as well as in applications. We note several additional reasons that a griefing factor perspective is natural in the setting of blockchain systems.
• Interactions with different blockchain applications on a smart contract platform such as Ethereum (Buterin, 2014) can be linked so that a transaction that attempts to make two interactions either executes both successfully or has no effect, permitting novelties such as flash loans (Qin et al., 2021). Thus, attackers will often have interests that are not well captured by the internal incentives of the game designed by any given developer. In Ford and Böhme (2019), it is argued that, for these reasons, permissionless systems that are designed to be resistant to attacks by economically rational actors must actually be resistant to attacks by Byzantine actors in order to be secure. However, if one can show that the griefing factors of any actions available to an attacker are sufficiently small, then one can recover useful notions of economic security even in the presence of external incentives, as long as one can assume some upper bounds on the external rewards that the attacker can realistically obtain.
• As the blockchain oracle problem (Beniiche, 2020) limits the information available to a given blockchain protocol, it can be difficult to identify parties as attackers and penalize them accordingly. This is the case in situations of “speaker–listener equivalence,” where it is observed in Buterin (2017) that there must always exist griefs with a griefing factor of at least one.
• The culture of current communities of blockchain users (Gladieux, 2021; Locke, 2021) is such that one might expect the presence of “trolls” who are willing to suffer small financial losses in order to grief others for social or ideological reasons, without necessarily requiring a financial incentive.
2 Related work
An extensive body of literature (Konrad, 2000; Chowdhury and Gürtler, 2015) considers games in which it is in the interests of players to cause harm to other participants. Further behavioral research (Abbink and Sadrieh, 2009) has shown that there are populations that do not require financial incentives in order to be incentivized to harm other players in economic games. This phenomenon is related to psychological studies on “trolls” (March 2019) who exert effort to antagonize others, particular in semi-anonymous Internet settings.
In defining griefing factors (Buterin, 2017; Buterin, 2018a; Buterin, 2018b), has provided a measure of a strategy’s effectiveness in doing harm to other participants relative to its cost that does not require a priori knowledge of what incentives participants may have to seek to do this harm. Buterin has discussed this concept principally in the context of analyzing blockchain settings. He notes in particular that griefs with griefing factors at least equal to one must exist in settings where there is “speaker–listener equivalence” (Buterin, 2017), and in Buterin (2018a), he considers the impact of a specific grief on economic equilibria of supply and demand for validators in a simplified model of a proof-of-stake system. Griefing factors have subsequently been used to analyze the effectiveness of specific attack strategies in various other blockchain systems, notably attacks on payment channels (Mazumdar et al., 2020; Mazumdar et al., 2022).
In Leonardos et al. (2023), griefing in a specific model of proof-of-work mining is related to a generalized notion of evolutionarily stable allocations explored in Schaffer (1988) in the context of games with a fixed reward. In that setting, it can be observed that participants are incentivized to act “spitefully” to drive competitors out of the competition. Indeed, Leonardos et al. (2023) observe that the unique Nash equilibrium in the mining game is not evolutionarily stable. Instead, evolutionarily stable allocations have a griefing factor of one with respect to the Nash equilibrium.
3 Contribution of this work
We expand on the mathematical framework allowing the study of notions of griefing and griefing factors. In Section 5 we illustrate these ideas by examining examples of griefs in several prominent blockchain applications. Notably, we provide a detailed analysis of various griefs between participants that are possible under the Ethereum consensus algorithm.
In Section 6.1 we explore questions on how the presence of players willing to engage in griefing affects the equilibria of a game. For any game, we define a collection of derived games in which the players obtain utility from griefing each other. As one varies the amount of utility that the different players derive from doing one unit of harm to other players (namely, the griefing factors at which the players are willing to engage in griefs), the equilibria in the derived games change. This can be represented geometrically through diagrams where each point in the diagram represents a given derived game in which the players are willing to grief at a given set of griefing factors. On this basis, one can consider the regions of the diagram where different equilibria are present and how the equilibria evolve as one moves along a path through the diagram. In Section 6.2 we present several results concerning the geometric structure of these regions. For example, we show in Proposition 4 that the boundaries of the region where a pure Nash equilibrium is present are defined by hyperplanes, although we see in Example 5 that the regions where mixed equilibria are present can have more complicated geometric structures. We consider examples illustrating how these results apply to blockchain applications. Notably, in Example 4 we extend results presented in Leonardos et al. (2023) to consider the equilibria that are present in the presence of griefers in a mining game that models proof-of-work systems.
4 Notation and model of actors
We consider games of the form (N, A, u), where.
• N is a finite set of players of cardinality |N| = n;
• for each i ∈ N, Ai is the finite set of actions of cardinality |Ai| that can be taken by i, and A = A1 ×⋯ × An is the set of possible assignments of an action to each player; and
•
We generally denote i’s action as xi ∈ Ai, and we denote the tuple of actions of the other users by x−i ∈ A−i, consisting of an action xj ∈ Aj for all j ≠ i. Sometimes we condense this by writing x = (xi, x−i). We can compute the utility of the jth participant given these actions as uj(x) = uj (xi, x−i) = uj (x1, … , xn) for any j ∈ N.
We take
as naturally identified with the set of mixed strategies that the participant i ∈ N can take; in particular, for si ∈ Δi and x ∈ Ai, we denote by si(x) the probability that i selects the alternative x while playing the mixed strategy si. Thus,
In Section 6 we consider utility functions that are modified to depend on the griefing factors at which participants are willing to perform griefs. Specifically, we will take a set of values (λ1, … , λn) where λi measures the willingness of i to grief. We will also take a tuple of “base” utility functions u1, … , un, and we will present various formulations in each of which we will have a tuple of derived utility functions that can depend on u1, … , un as well as λ1, … , λn, as described below in Eqs 4, 5. These derived utility functions are chosen in such a way as to take into account utility that griefing players derive from causing harm to other players playing the game, defined by u1, … , un. Players in a given game are assumed to be economically rational in that they seek to maximize their utility as given by the relevant derived utility functions that include this utility from griefing. We will suppose that players take actions simultaneously and independently unless otherwise noted. Finally, we assume that these rationality, independence, and simultaneity assumptions, as well as the utility functions considered (including both the “base” utility functions u1, … , un and the various derived utility functions), are common knowledge.
We fix definitions of griefing factors that follow those of Leonardos et al. (2023), covering both scenarios in which an attacker griefs another individual participant and those in which an attacker griefs the broader set of other participants.
Definition 1.
Let i, j ∈ N. Take x = (xi, x−i) ∈ A assigning an action to each player, namely, xi ∈ Ai and x−i ∈ A−i. Suppose
and the total griefing factor of the action
We can extend these concepts to the case where
Remark 1.
Note that we assume
for all
On the other hand, note that Definition 1 still allows for the possibility that
5 Examples of griefs on cryptoeconomic systems
We further illustrate the notion of griefing factors by calculating the griefing factors of several griefs on the Ethereum consensus protocol (Buterin, 2022).
Example 1.
We consider the economic games of the Ethereum Beacon Chain, as they are implemented after the Paris hard fork (“the merge”) (Buterin, 2021). In this game, validators perform several roles. Validators are randomly selected to produce new blocks, and additionally once per epoch (approximately 6.4 min) each validator is tasked with attesting to the most recent block in the preceding slot (a 1/32 division of an epoch) (Buterin et al., 2022; Bedawala and Salot, 2023). Also included in attestations are references to previous blocks, referred to as the “target” and the “source”. The information on target and source blocks that is provided in attestations is used in the process of determining when a block is finalized (see Buterin and Griffith, 2017). The system is calibrated so that if all actors, including block producers and attestors, perform their roles perfectly then each participant will earn on average a base reward of B per epoch (Buterin et al., 2022). This base reward is a function of the number of active validators, and as such it gradually changes over time as validators join or leave the network (Buterin, 2022).
In order for the attestation to be eligible for rewards, it must be “timely” (Buterin et al., 2022): that is, it must be provided in the next slot to obtain a reward for indicating the preceding block, in the next 32 slots to be rewarded for indicating the target, and in the next 5 slots to be rewarded for indicating the source. Attestors are rewarded
We analyze several griefs in this system. For all of these analyses, we assume that the result as to which blocks are finalized does not ultimately change. We express griefing factors in terms of B, m, and n. We also provide an approximate value of each griefing factor after the symbol “≈” based on current typical values for B, m, and n. As of June 2023, the current number of active validators is approximately 625000 (Bitfly, 2023), so we estimate that the number of participants in a given slot is n = 625000/32 = 19531. We also take m = 19336 so that the proportion of validators completing each task is
We determine griefing factors with respect to default strategies of honest participation. Specifically, in the notation of Definition 1, x−i corresponds to the m attestors other than i providing correct, timely attestations and block producers other than i providing blocks that include all possible attestations. The action xi corresponds to i also providing correct, timely information as an attestor or as a block producer when applicable, and
• The attestor i griefs the block producer and the other attestors by publishing her attestation beyond the timeliness deadline for indicating the previous block. This costs the griefer
This can also be considered as a grief against the block producer j individually, noting that the block producer is also an attestor.
• A block producer i can grief the community of attestors (other than herself) by not including an attestation from j, hence causing it to fall beyond the one-slot period for timely reporting of the previous block. This reduces i’s block-producer reward by
As a grief against the censored attestor j individually, this gives a griefing factor of
We see that the dependence on B can be canceled from the numerators and denominators of these expressions, so these griefing factors can be viewed as functions of m and n. Additionally, the two griefs against individuals are indistinguishable from the point of view of the consensus algorithm. Thus, they are an example of speaker–listener equivalence, as discussed in Buterin (2017); hence their griefing factors are reciprocals and, in particular, one of them must be at least one.
One can consider other griefs involving attestors not including correct, timely targets and sources. The griefing factors of these griefs are stated in Table 2 in terms of n and m and then using the approximate values of n and m indicated above. Note that under the current (Buterin et al., 2022) parameters for timeliness, failing to provide either a correct, timely target or source implies that the attestor also fails to provide a correct, timely previous block. Hence, the effects of failing to timely indicate the previous block are included in the griefing factors in the corresponding columns below. Additionally, note that block producers can only delay an attestation by one block, so it is not typically possible for them to prevent its inclusion within the time limits for timely targets and sources.
Another example of a grief on a cryptoeconomic system is considered in Leonardos et al. (2023) in the setting of proof-of-work mining games. We further consider this game in Example 4 using the tools that we develop in Section 6.1.
Note that it is also possible to have griefs that do harm that is not purely monetary. We present brief notes on cryptoeconomic systems in which griefers can expend resources to cause delays in the normal operation of the system.
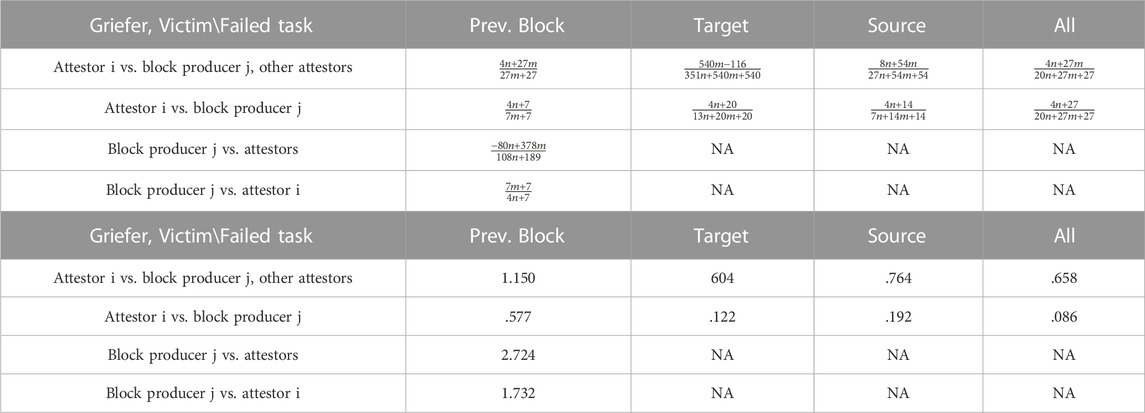
TABLE 2. Griefing factors that attestors and block producers under the Ethereum consensus algorithm can achieve in griefs against each other for actions that consist of intentionally failing to provide certain consensus algorithm information in a timely fashion as discussed in Example 1. In the first table above, these values are given in terms of the number of validators participating in a given slot m and the total validators assigned to participate in that slot n. In the second table, approximate values are calculating using estimates of m =19336 and n =19531, based on current network activity.
Example 2 (Delay griefs).
• In Arbitrum, if contrasting states of the rollup1 are submitted by validators, then there is a process designed to prove that at least one of them is incorrect (Offchain Labs Developers, 2022). As the final states differ, there is guaranteed to be some specific step in the off-chain computation on which the two parties disagree. Via an interactive game where parties progressively commit to points of disagreement in their series of computations, such a step can be identified and verified on-chain. Attackers can place malicious stakes that require the system to use this process and then use the maximum amount of time they are allowed before responding to each step of the interactive game, causing delays. The cost of such an attack is considered in Offchain Labs Developers (2022).
• The payment channels used in Bitcoin’s Lightning Network (Poon and Dryja, 2016) allow for incremental micro-payments to be exchanged between parties without the requirement to issue Bitcoin transactions on-chain for each micro-payment. For example, if Alice wants to establish a payment channel to be able to send micro-payments to Bob, she can create a “funding transaction” that sends some amount of bitcoin to an address that can be spent by a 2-of-2 multisig requiring both her signature and Bob’s. Before publishing this transaction, she ensures that Bob has also signed another transaction that reimburses her these funds but that is “timelocked”. Then Alice can send a series of transactions, each of which deducts progressively more of the locked funds to be sent to Bob and sends the balance to Alice. None of these intermediate transactions need to incur the transaction costs of being published on-chain. If Bob is cooperative, when A. wants to close the channel he will publish the last of these transactions, which sends the highest amount to himself. However, if Bob refuses to cooperate, he can force Alice to wait until the timelock expires and her original reimbursement transaction becomes valid. This inflicts a delay on Alice at the cost to Bob of the funds he was due from the payment channel. Moreover, if A. wants to send a payment to Charles, with whom she has not set up a direct link via a funding transaction, but where there is a path of participants between Alice and Charles, each participant having set up a channel with the next, she can use “Hash Timelocked Contracts” to send funds along this path in such a way that intermediate participants in the path are unable to steal the funds (Poon and Dryja, 2016). However, if Charles becomes inactive, he can cause every participant along the path to have funds locked up until a timelock expires. Thus, the griefing factor of such a delay attack scales with the length of the path used, and large attacks can stress the liquidity of the network. Such attacks are analyzed in Mazumdar et al. (2020, 2022) and mitigation approaches are considered in which participants place collateral that can be taken from griefers and used to compensate victims of such delay griefs. Similar delay griefs can also be possible in state channels (Coleman et al., 2018), which generalize this idea to applications beyond payments.
• In the blockchain-based dispute resolution system of Ast et al. (2021), small randomly selected groups of users are chosen from among token holders to provide subjective judgments on off-chain disputes. There is also an appeal system via which parties can invoke larger panels that are generally more statistically representative of the community of crowd-sourced participants. In the event that a party invokes the appeal process frivolously, she sacrifices appeal fees to delay the finalization of the decision in the case.
• Many blockchain-based curated lists, such as James (2021), make use of a mechanism whereby individuals submit elements to the list having certain fixed criteria for inclusion. Submitters include a deposit, and their submission can be “challenged” by other participants who also provide a deposit within some fixed period. In the event of a challenge, some blockchain oracle mechanism (for example, a vote by holders of some token) decides whether the entry satisfy the criteria, and either the submitter or the challenger loses their deposit accordingly. As the process of invoking the oracle is time-consuming, an attacker can sacrifice a deposit to frivolously challenge an entry, resulting in delaying its inclusion in the list.
6 Results
6.1 Equilibria in the presence of griefing
One can adopt the perspective that, if there are situations where i’s in-game reward is maximized by voting xi, but where she is willing to receive a lower reward by voting
For each i ∈ N, we think of the willingness of player i to grief as being characterized by a value λi ∈ (0, ∞). Then, i should be willing to engage in a grief if the griefing factor of that grief is at least equal to λi. Formally, our modified utility functions should have the following property.
Definition 2.
Let
and
Here the griefing factors are defined as in Definition 1 using the utility functions u1, … , un.
Note, however, that we can rearrange the inequality
It is natural to think of
Take
for any xi ∈ Ai, x−i ∈ A−i. As our notion of griefing in Definition 1 always compares two alternatives for a player i, we need the values of
Proposition 1.
Let
Proof. Let i ∈ N,
and
Thus, we see that
where we adopt the assumption that
We now consider the equilibria that arise in these modified games where each participant i is willing to engage in griefs with a griefing factor of at least λi.
Definition 3.
Take
Another related utility function we will consider is the following, in which i derives negative utility proportional to the utilities of other players:
for xi ∈ Ai, x−i ∈ A−i. We see that these utility functions give the same equilibria as
Proposition 2.
The (λ1, … , λn)-Nash-equilibria are independent of the choices of
In particular, even though the definition of griefing factors in Definition 1 makes reference to two profiles of participants’ actions in A, and Eq. (4) implicitly incorporates this comparison between two profiles (xi, x−i) and
Lemma 1. Consider two tuples of utility functions
for all xi ∈ Ai. Then u and u′ induce the same (pure and mixed) N. equilibria.
Proof. of Lemma 1.
Note that, for all x−i ∈ A−i,
where the expected value is taken over the potentially mixed strategies of other players.
We now have the tools to show the independence of the (λ1, … , λn)-Nash-equilibria of a game with respect to the choices of
Proof. of Proposition 2.
We note that, for all xi ∈ Ai, x−i ∈ A−i:
However, the right-hand side of this equation is independent of xi. Thus, by Lemma 1,
We denote the set of (λ1, … , λn)-Nash-equilibria by NE (λ1, … , λn). By representing the (λ1, … , λn)-Nash-equilibria for each choice of
Example 3.
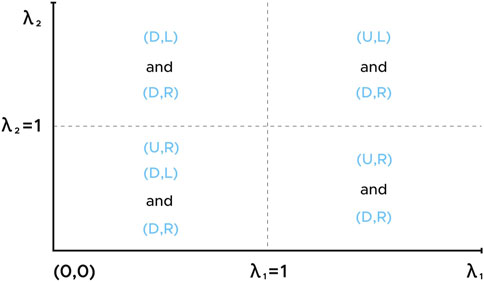
Consider the payoff table given in Table 3 (above) corresponding to some utility functions u1, u2 and the transformation of this payoff table that includes utility from griefs corresponding to utility functions
We can identity these diagrams as subsets of
This framework allows us to consider equilibria in games with attackers who have sabotage incentives, building on the work of Chowdhury and Gürtler (2015) and Konrad (2000), by giving us a tool to consider attackers with varying external incentives simultaneously.
Next, we consider the mining game studied in Leonardos et al. (2023) and Arnosti and Weinberg (2022), allowing us to develop upon the results of Leonardos et al. (2023) on griefs in proof-of-work mining.
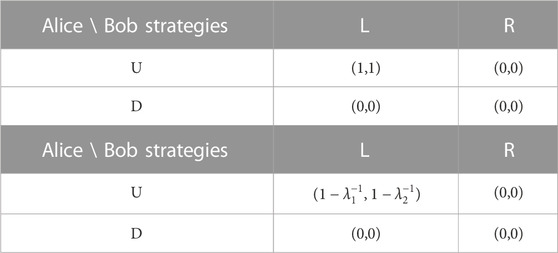
TABLE 3. The table on the above gives payoffs in a game between Alice and Bob, similar to Table 1. The table on the below gives the transformation of these payoffs to include utility from griefs as in Eq. 5.
Example 4 (Mining game).
Suppose that there exist
for each i ∈ N.
Then, a modified utility function as in Equation 5, reflecting the idea that a miner can grief other miners by spending additional energy to mine in excess of her natural equilibrium level, is given by
Following a generalization of the proof of Theorem 1 in Arnosti and Weinberg (2022) that considers the varying values of λ1, … , λn, we compute the equilibria of this game. Denote by
the percentage of mining power corresponding to i for a given profile x. Note that, for any i, the profiles given by xi = ϵ > 0 and xj = 0 for all j ≠ i are not equilibria. Indeed, in these cases
Next, note that
Then, as we note that
or when xi = 0. However, if ∑k≠i xi > 0, then xi = 0 ⇔ ri(x) = 0. Given that the case where xj = 0 for all j ≠ i is excluded, we deduce that there is a Nash equilibrium if and only if
for all i ∈ N.
As the proportions of hash power sum to 1, in equilibrium we have
which implies by Lemma 1 of Arnosti and Weinberg (2022) that
Thus, the diagram of (λ1, … , λn)-Nash-equilibria is
That is, it consists of a single equilibrium that varies continuously in
Note that when λi = n − 1 for all i, corresponding to the case of individual griefing factors of 1 for all participants against all other participants, we recover the allocation of Theorem 2iii of Leonardos et al. (2023).
6.2 Structure of diagrams of equilibria
In this section, we explore several results that limit the structure of the diagrams of equilibria introduced in Section 6.1. These results can provide a mechanism designer with insight into how a system may respond to griefs.
An initial result considers situations in which the diagram of equilibria is constant with respect to the willingness of actors to grief.
Proposition 3.
Consider a constant-sum game. The (pure and mixed) equilibria of this game are constant for all values of (λ1, … , λk).
Proof. Let s be the constant value of the sum of payoffs. Hence,
for all x ∈ A. In particular, for all i ∈ N,
On the other hand, the utility function given by Eq. (5) is given by:
Rearranging, we obtain
for all x ∈ A. Then, for any given choice of (λ1, … , λn), by Lemma 1,
Of course, while we have shown that constant-sum games have equilibria that are constant with respect to actors’ willingness to grief and hence provide ease of analysis for a mechanism designer, this constant equilibrium may nevertheless be an attack or otherwise undesirable.
Next, we analyze the possibilities of the boundaries in these diagrams between regions with different equilibria. For all values (x1, … , xn) ∈ A, we denote the regions where (x1, … , xn) is a (pure) Nash equilibrium by:
Proposition 4.
For all values (x1, … , xn) ∈ A, the boundaries of regions
for some
Proof. Note that
for all i ∈ N and xi ∈ Ai. However, Inequality 6 can be rewritten as
If
However, these boundary conditions are of the form of those in the statement.
Hence, the rectilinear boundaries of the regions observed in Figure 1 are typical of the regions where a given pure equilibrium is present. On the other hand, we note in the following example that regions in which mixed equilibria have a given support do not necessarily have boundaries given by hyperplanes.
Example 5. We consider a three-player coordination game in which
for each i = 1, 2, 3.
Then, transformed under the perspective of Equation 5, this gives a payoff table as shown in Table 4.
We notice that.
1. (n, n, n) is a pure Nash equilibrium for all λi.
Furthermore, noting that
2. (c, c, c) is a pure N. equilibrium if and only if λi ≥ 4 for all i = 1, 2, 3.
Next, we can compute all mixed equilibria of this game by exhaustively considering each possible choice of support. This gives.
3. A mixed equilibrium of
4. A mixed equilibrium of
5. A mixed equilibrium of
and.
6. A mixed equilibrium of (z1, z2, z3), where
•
•
•
We provide a visualization of these regions in Figure 2.
We see that there are richer possibilities for the structures of regions where a given mixed equilibrium is present than for those of pure equilibria. Further analysis of the geometry of these diagrams could provide additional insight into what constraints do or do not exist on the available griefs against a given game and is a potentially interesting avenue for future work.

TABLE 4. The modified payoff tables that correspond to the utility functions
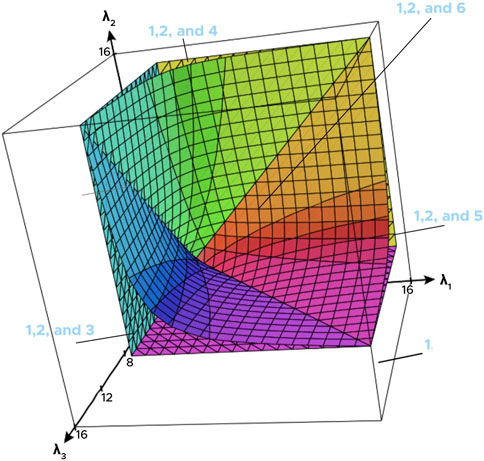
FIGURE 2. Diagram of equilibria in Example 5 following the numbering used above for the various pure and mixed equilibria in that example. Equilibrium 1 is present at all points. Note that the boundaries of Equilibrium 2, a pure equilibrium, are given by hyperplanes, whereas the boundaries of Equilibria 3, 4, 5, and 6 involve more complex surfaces. The surfaces in this image were generated using CalcPlot3D, https://c3d.libretexts.org/CalcPlot3D/index.html.
7 Conclusion
We have considered a variety of griefs, particularly those relating to blockchains and decentralized systems. Moreover, we have noted reasons that griefing might be particularly relevant in this setting. In order to gain insight into how the presence of griefing players can affect a given game, we have introduced a new geometric tool in the form of diagrams of (λ1, … , λn)-Nash-equilibria. We have shown that these diagrams are well-defined and that their structures obey certain basic constraints. Moreover, these diagrams should be able to provide mechanism designers with global insight into how stable a given game is with respect to griefing behaviors.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This research was funded by the Kleros Cooperative, a French-based Société coopérative d’intérêt collectif that is developing the open-source blockchain-based dispute resolution protocol Kleros. In particular, this work was partially financed through grant # DOS0101273/00 that the Kleros Cooperative received from the ‘‘Programme d’Investissements d’Avenir’’ (Future Investment Program) of BPIFrance Financement.
Acknowledgments
BPIFrance Financement did not actively participate in the research that led to this report, the writing of this report, or the decision to publish it. The author would also like to thank several members of the Kleros Cooperative who provided useful comments and feedback on preliminary versions of this work, as well as Karla Spanier for her help in designing Figures 1, 2.
Conflict of interest
The author is employed as a contractor by the Kleros Cooperative and is a holder of Kleros (PNK) tokens; the Kleros Cooperative is developing the Kleros protocol cited in Section 5.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1Arbitrum is an example of an optimistic rollup. That is, it is a secondary blockchain network whose state updates are periodically committed to on a primary, smart-contract-compatible blockchain (see Thibault et al., 2022). In the case of Arbitrum, this primary blockchain is Ethereum, and the integrity of state updates is ensured via an interactive validation game (Offchain Labs Developers, 2022).
References
Abbink, K., and Sadrieh, A. (2009). The pleasure of being nasty. Econ. Lett. 105, 306–308. doi:10.1016/j.econlet.2009.08.024
Arnosti, N., and Weinberg, S. M. (2022). Bitcoin: a natural oligopoly. Manage. Sci. 68, 4755–4771. doi:10.1287/mnsc.2021.4095
Ast, F., Lesaege, C., and George, W. (2021). Kleros long paper v2.0.2. Online, Available at: https://kleros.io/yellowpaper.pdf (Accessed June, 2023).
Bedawala, M., and Salot, A. (2023). Ethereum’s economics and stacking model. Online, Available at: https://usa.visa.com/solutions/crypto/cryptoeconomics.html (Accessed June, 2023).
Beniiche, A. (2020). A study of blockchain oracles. ArXiv Preprint. Available at: https://arxiv.org/abs/2004.07140 (Accessed June, 2023).
Bitfly (2023). Open source Ethereum 2.0 beacon chain explorer. Online, Available at: https://beaconcha.in/(Accessed June, 2023).
Buterin, V. (2018b). A griefing factor analysis model. Ethresear.ch Forum, Available at: https://ethresear.ch/t/a-griefing-factor-analysis-model/2338 (Accessed June, 2023).
Buterin, V. (2018a). Discouragement attacks. Github. Available at: https://github.com/ethereum/research/blob/master/papers/discouragement/discouragement.pdf, commit : 7e3482c532aee115c3850e5c7c0de3ecbc1ab3b5 (Accessed June, 2023).
Buterin, V. (2014). Ethereum, a next-generation smart contract and decentralized application platform. Online, Available at: https://ethereum.org/en/whitepaper/(Accessed June, 2023).
Buterin, V., Goldberg, D., and Dapplion, L. (2022). Ethereum 2.0 Altair beacon chain changes. Github, Available at: https://github.com/ethereum/annotated-spec/blob/master/altair/beacon-chain.md, commit : 3855127b22e989b52371188c830b1a4769eca762 (Accessed June, 2023).
Buterin, V., and Griffith, V. (2017). Casper the friendly finality gadget. ArXiv Preprint. Available at: https://arxiv.org/abs/1710 (Accessed June, 2023).09437.
Buterin, V. (2022). Serenity design rationale. Online, Available at: https://notes.ethereum.org/@vbuterin/serenity_design_rationale (Accessed June, 2023).
Buterin, V. (2021). The merge - the beacon chain. Github. Available at: https://github.com/ethereum/annotated-spec/blob/master/merge/beacon-chain.md,commit: 350a060826d31f9a030177a58b618906caf789dc (Accessed June, 2023).
Buterin, V. (2017). The triangle of harm. Online, Available at: https://vitalik.ca/general/2017/07/16/triangle_of_harm.html (Accessed June, 2023).
Chowdhury, S., and Gürtler, O. (2015). Sabotage in contests: a survey. Public Choice 164, 135–155. doi:10.1007/s11127-015-0264-9
Coleman, J., Horne, L., and Xuanji, L. (2018). Counterfactual: Generalized state channels. Online, Available at: https://www.bgp4.com/wp-content/uploads/2019/05/statechannels.pdf (Accessed June, 2023).
Ford, B., and Böhme, R. (2019). Rationality is self-defeating in permissionless systems. ArXiv Preprint. Available at: https://arxiv.org/pdf/1910.08820.pdf (Accessed June, 2023).
Gladieux, M. (2021). The stock market has always been a game. now Gen Z is learning to play. 34th Street Magazine. Available at: https://www.34st.com/article/2021/02/reddit-robinhood-gamestop-amc-dogecoin-stockmarket-stocks-stonks-meme-wallstreetbets-investment-trading-genz-game-corruption (Accessed June, 2023).
Heyman, J. L. (2019). On the computation of strategically equivalent games. Ph.D. thesis. Columbus: The Ohio State University.
James, S. (2021). Proof of humanity - an explainer. Kleros Blog. Available at: https://blog.kleros.io/proof-of-humanity-an-explainer/(Accessed June, 2023).
Konrad, K. A. (2000). Sabotage in rent-seeking contests. J. Law, Econ. Organ. 16, 155–165. doi:10.1093/jleo/16.1.155
Leonardos, S., Sridhar, S., Cheung, Y. K., and Piliouras, G. (2023). “Griefing factors and evolutionary in-stabilities in blockchain mining games,” in Mathematical research for blockchain economy, MARBLE 2022. Editors P. Pardalos, I. Kotsireas, Y. Guo, and W. Knottenbelt (Cham: Springer International Publishing), 75–94. doi:10.1007/978-3-031-18679-0_5
Locke, T. (2021). Younger investors are calling bitcoin “boomer coin” here’s why they prefer dogecoin and other altcoins. CNBC. Available at: https://www.cnbc.com/2021/05/20/some-millennials-call-bitcoin-boomer-coin-prefer-dogecoin-altcoins.html (Accessed June, 2023).
March, E. (2019). Psychopathy, sadism, empathy, and the motivation to cause harm: new evidence confirms malevolent nature of the internet troll. Personality Individ. Differ. 141, 133–137. doi:10.1016/j.paid.2019.01.001
Mazumdar, S., Banerjee, P., and Ruj, S. (2020). “Time is money: countering griefing attack in Lightning Network,” in IEEE 19th international conference on trust, security and privacy in computing and communications TrustCom. 1036–1043.
Mazumdar, S., Banerjee, P., Sinha, A., Ruj, S., and Roy, B. K. (2022). Strategic analysis of griefing attack in Lightning Network. IEEE Trans. Netw. Serv. Manag. 20, 1790–1803. doi:10.1109/TNSM.2022.3230768
Nakamoto, S. (2008). Bitcoin: a peer-to-peer electronic cash system. Online, Available at: https://bitcoin.org/bitcoin.pdf/(Accessed June, 2023).
Offchain Labs Developers (2022). Inside Arbitrum nitro. Online, Available at: https://developer.offchainlabs.com/inside-arbitrum-nitro (Accessed June, 2023).
Papon, P., Leblond, J., and Meijer, P. (2002). The physics of phase transition: Concepts and applications. Springer.
Poon, J., and Dryja, T. (2016). The bitcoin lightning network: Scalable off-chain instant payments draft. version 0.5.9.2. Online, Available at: https://lightning.network/lightning-network-paper.pdf (Accessed June, 2023).
Qin, K., Zhou, L., Livshits, B., and Gervais, A. (2021). “Attacking the defi ecosystem with flash loans for fun and profit,” in Financial cryptography and data security, FC2021. Editors N. Borisov, and C. Diaz (Springer Berlin Heidelberg), 3–32. Lecture Notes in Computer Science. doi:10.1007/978-3-662-64322-8_1
Schaffer, M. E. (1988). Evolutionarily stable strategies for a finite population and a variable contest size. J. Theor. Biol. 132 4, 469–478. doi:10.1016/S0022-5193(88)80085-7
Strogatz, S. H. (2000). Nonlinear dynamics and chaos: With applications to physics, biology, chemistry and engineering. Boulder: Westview Press.
Keywords: sabotage, griefing, equilibria, utility functions, blockchain
Citation: George W (2023) An analysis of griefs and griefing factors. Front. Blockchain 6:1137155. doi: 10.3389/fbloc.2023.1137155
Received: 04 January 2023; Accepted: 28 July 2023;
Published: 15 August 2023.
Edited by:
Giuseppe Destefanis, Brunel University London, United KingdomReviewed by:
Pietro Saggese, Complexity Science Hub Vienna (CSH), AustriaSubhra Mazumdar, Vienna University of Technology, Austria
Stefanos Leonardos, King’s College London, United Kingdom
Copyright © 2023 George. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: William George, d2lsbGlhbUBrbGVyb3MuaW8=
 William George
William George