- Department of Mathematics, Computer Science and Physics, University of Udine, Udine, Italy
Currently, the best known applications of blockchain technology are finance and art. In particular, the blockchain art market, born in early 2018 without fuss, went parabolic around 2021, also thanks to record-breaking sales of digital artworks associated with a Non-Fungible Token (NFT), mediated by the grand dames of auction houses Christie’s and Sotheby’s. In this contribution we merge art and finance on blockchain and explore the opportunity of buying blockchain art as a financial investment. While there exists a relatively large literature on traditional art as investment, the topic of investing in NFTs is still in its infancy. Thus, we provide methods (metrics) and tools (a Web app) to reason about opportunities, in terms of risks and returns, of investing in art on chain.
1 Introduction
Crypto art encompasses art forms that make use of the blockchain technology not only as a medium for the dissemination of artistic work but mainly for artistic creation (Franceschet et al., 2021). Crypto art has its roots in conceptual art (Finucane, 2018). It shares the immaterial and distributive nature of its artworks and the rejection of conventional art markets, institutions, and intermediaries. Crypto art is also much overlapping with net art (Quaranta, 2021); in fact, the two artistic movements have almost everything in common, except the market economy. Net art entirely lived in the gift economy. Blockchain technology and Non-Fungible Tokens (NFTs), on the other hand, have given rise to a thriving market for crypto art, made of artists and collectors that interact mediated by smart contracts deployed by digital galleries.
In this paper we consider a scenario of a crypto art gallery (also referred to as crypto art marketplace) with artists and collectors1. The life of a digital artwork in a marketplace is marked by the following events.
1. The artwork is created, or minted, by the artist in the gallery;
2. Collectors place bids in cryptocurrency to purchase the artwork;
3. If the artist is satisfied with the current bid, the sale happens: the NFT of the artwork moves from the artist’s wallet to the collector’s wallet and the agreed cryptocurrency moves in the opposite direction;
4. The artwork remains on the market and can be traded among collectors.
Each event triggers a transaction that is immutably recorded on the blockchain. Transactions are mediated by a smart contract - a program that executes the terms of a contract - developed by the marketplace and deployed on the blockchain2. The primary market of the gallery is the set of all first sales of artworks, those from the original artist to the first collector. The secondary market is the set of all future sales of artworks after the first one, hence moving the NFT from collector to collector. Every time an artwork is sold on the secondary market, the original artist receives a royalty (typically 10%) of the sale price3. Moreover, on some galleries, also collectors receive royalties when an artwork they sold is sold again on the secondary market.
All Time High in the City4, minted on SuperRare crypto art gallery in 2018, is one of the first artworks of digital artist XCOPY. London based artist XCOPY is considered an OG5 of crypto art. He explores death, dystopia and apathy through distorted visual loops. His artworks betray a powerful English humour and are highly prized by collectors and investors who are willing to spend large amounts of money to acquire them. The sale history of All Time High in the City became a case study about returns and royalties in crypto art and is summarized as follows:
1. The artwork is first sold in 2018 from XCOPY to artist and collector hex6c for 0.5Ξ6 (or 88$ back then);
2. After 1 year, hex6c sells the artwork to collector Moderats Art for 10Ξ (1,446$) with a return on investment (ROI) of 20x. XCOPY receives an artist royalty of 10% of the sale price (1Ξ);
3. In 2021 Moderats Art sells the artwork to collector superrare88 for a whopping 1000Ξ (2,923,871$) making a ROI of 100x. Interestingly, XCOPY gets an artist royalty of 10% (100Ξ), which is 200 times the price of the first sale on the primary market. Moreover, the first collector hex6c obtains a collector royalty of 1% of the sale price, that is 10Ξ, exactly the same amount he collected when he sold the artwork;
4. Finally, after a few months, superrare88 sells the artwork to collector rarecollector3000 for 1630Ξ (6,189,469$) The first and second collectors (hex6c and Moderats Art) each get a collector royalty of 0.5% of the sale price (8.15Ξ), while XCOPY still receives an artist royalty of 10% (163Ξ).
This case shows that when a work of crypto art is successful the proceeds are shared. Moreover, it shows how crypto art and NFTs more generally might be a good investment for several parties:
• the artist, who is paid for the artworks sold on the primary market and also receives a royalty on the sales of their artworks on the secondary market;
• the collector, who might resell a purchased artwork at a higher price and also receives a royalty when other collectors resell it in the future;
• the gallery, which earns a fee on every sale on the primary and secondary market.
In this paper, we are interested in exploring the possibility of buying crypto art (and more generally NFTs) as an investment. Our general attitude is the following: to provide methods and tools for the investor to reason about opportunities, in terms of risks and returns, of investing in crypto art. We will focus on a comparison rather than the usual ranking approach. More precisely, we are guided by the following question: given a pair of artists the investor is interested in, who has the higher potential return on investment?
Our contribution is twofold. On one hand, we propose a number of metrics to measure the return on investment in crypto art. Our flagship index - the RadaR index - measures the return adjusted by the risk of such an investment as a generalization of the popular Sharpe ratio used to assess a financial investment. Moreover, we develop a probabilistic method, called gain probabilities, to compare the returns of two given artists. Informally, the method measures the probability that an investment in one artist was more profitable than an investment in the other, given the history of sales of the two artists. We provide an algorithm to compute the gain probabilities for two artists, formally prove its correctness, and show that it is efficient in terms of computational complexity.
On the other hand, we developed a Web application called RadaR on which the investor can experiment with these metrics and many more. The application design revolved around a number of fundamental principles including extensibility, scalability, simplicity, user-friendliness, and low-cost production and management. In particular, scalability is achieved in terms of data volume and velocity, as well as number of galleries and users. Moreover, one of the aims was to demonstrate that it is possible to develop a minimum viable product in an economically sustainable manner (the cost of the application development is entirely self-financed).
The rest of the paper is as follows. In Section 2 we review the previous literature on (crypto) art as investment. In Section 3 we first propose a number of metrics to measure the return on investment in crypto art (Section 3.1). Then, we devise an algorithm to compute the gain probabilities for two artists, prove its correctness and analyse its complexity (Section 3.2). In Section 4 we describe the architecture of the RadaR web app, with a special focus on scalability. Moreover, we use the app to match a pair of notable artists and analyse the outcomes as a methodological case study. We conclude in Section 5 with a discussion of our contribution in the Web3 context.
2 Art as investment
There exists a relatively large literature on the possibility of buying traditional art for the sake of investment (Pommerehne and Frey, 1989). On the other hand, the literature on NFT art as investment is still in its infancy but rapidly growing.
One relevant subset of this literature concerns methods for art price estimation. These methods have mostly been developed for the purpose of constructing price indexes for investment. Two families of methods have emerged from economics: repeat-sales regression and hedonic regression (see Ginsburgh et al. (2006) for a general discussion about the two approaches). Repeat-sales regression uses the prices of the same object traded at two or more points in time. Hedonic regression, instead, regresses prices on characteristics of artworks (e.g., size, artist, style, and more) and uses the regression residuals - which can be considered as characteristic-free prices - to compute the price index. While repeat-sales regression allows bypassing the issue of measuring the heterogeneous characteristics of artworks entirely, hedonic regression allows estimating the price of artworks in the absence of a previous trading history.
Recently, Franceschet (2021) proposed a novel method based on network science to establish a rating for artists coupled with a rating for collectors, calculated independently from the characteristics of artworks, which can be hard to measure, and from re-sale history, which is often absent or limited. The rating system can therefore be used as the artist multiplier when applying pricing scripts in a gallery setting, and as a model variable for hedonic regression when considering price indexes or auctions.
The remaining literature mainly focuses on the risks and returns on investment in art, comparing with bond and stock investments and also with cryptocurrency in the case of NFTs. The general conclusion in the case of traditional art is that this kind of investment is not particularly attractive, since it presents high risks and a return which is comparable with bond but often lower than stock investments. Interestingly, the music changes when NFTs are taken into account. In this case, although even higher risks are acknowledged, the returns are quite impressive, beating both the stock and cryptocurrency markets.
As for traditional art, Goetzmann (1993) finds that while the returns to art investment has exceeded inflation for long periods, and returns in the second half of 20th century have rivalled the stock market, they are no higher than would be justified by the extraordinary risks they represent. He also notices that the demand for art increases with the wealth of art collectors, a common trait in the literature of art as investment, including that on NFTs. Burton and Jacobsen (1999) find that while most collectibles appear to yield positive real returns, the majority embody more risk and yield lower financial returns than stocks. Mei and Moses (2002) discover that art outperforms fixed income securities as an investment, though it significantly under-performs stocks in the US. However, art is also found to have lower volatility and lower correlation with other assets, making it more attractive for portfolio diversification than discovered in earlier research. Renneboog and Spaenjers (2013) observe that the art performance is similar to that of corporate bonds but at much higher risk and Korteweg et al. (2016) find that investing in a broad portfolio of paintings is not attractive, but targeting specific styles or top-selling artists may add value. Finally, Mandel (2009) analyses art as a conspicuous consumption good. The concept of conspicuous consumption is first illustrated by Veblen (2005) and refers to the consumption of costly goods or services for reputability. Mandel claims that art assets are appealing both for their ability to transfer consumption over time and for their use as signals of wealth. It follows that owning art might have both a financial and emotional reward, and the emotional dividend might justify the lower financial return and higher risk with respect to traditional investments.
A watershed between the case of investing in traditional and blockchain art is the paper by Whitaker and Kraeussl on fractional equity, blockchain, and the future of creative work (Whitaker and Kraeussl, 2020). The paper analyses the case of world-famous artists Jasper Johns and Robert Rauschenberg, finding out what their return would have been if they had retained 10% equity in their work when it was first sold. The proposed fractional equity model greatly outperforms the stock market and it offers tools for democratized access to the art market and help diversified investments, considering early-stage creative work as an act of investment of the artists in themselves. According to the authors, blockchain technology would succeed in enabling a future of work in which anyone can have fractional ownership of the upside they help to create.
The literature on NFT investment is growing fast (Kong and Lin, 2021; Mazur, 2021; Borri et al., 2022; Horky et al., 2022; Schaar and Kampakis, 2022; Schnoering and Inzirillo, 2022). As said above, this literature agrees that, in contrast with traditional art, investing in NFTs has higher returns than both stock and cryptocurrency vehicles, but the risk (measured as the volatility of returns) is also larger.
In particular, Kong and Lin (2021) study CryptoPunks, one of the earliest and largest NFT collections, and find that NFTs have higher returns than traditional financial assets. However, investing in NFTs comes along with extremely high volatility, leading to a comparable Sharpe ratio to the NASDAQ index. They also find that the movements of the NFT index are positively correlated with those of its native cryptocurrency exchange rate (ETH/USD) and stock indices, implying that most investors are more likely to bid up their investment in NFTs when aggregate wealth increases, and are negatively correlated with common hedging vehicles (i.e., gold and bonds), indicating that NFTs resemble risky investments in this regard. Interestingly, they argue that NFTs provide investors not only financial returns from resales but also emotional dividends from possession (in accordance with the theory of conspicuous consumption (Veblen, 2005)). Consequently, investors are more willing to accept such extremely high volatility in NFT investments. Horky et al. (2022) suggest that cryptocurrencies and NFTs are much more different, especially from a pricing perspective, than their common blockchain origins suggest. Thus, despite their young history, NFTs appear to be establishing themselves as financial assets in their own right in the blockchain cosmos. For policymakers, this indicates that any regulations concerning the crypto market will fall short if only classical cryptocurrencies are targeted. Moreover, Nadini et al. (2021) investigate the predictability of NFT sales using simple machine learning algorithms and find that, not surprisingly, sale history and, secondarily, visual features are good predictors for price.
Finally, Franceschet et al. (2021) applies the Lorenz curve and the Gini index to measure the concentration of the sale volume - the total amount of USD paid to buy art - on the crypto art gallery SuperRare. It turns out that the crypto art market is highly concentrated among few sellers and even rarer buyers with 80% of the sale volume dominated by 18% of the richest sellers (Gini index 0.79) and by 6% of the richest buyers (Gini index 0.91). Vasan et al. (2022) find a similar concentration on Foundation gallery observing that successful artists receive disproportional, repeated investment from a small group of collectors and underscoring the importance of artist-collector ties in the digital marketplace.
3 Return on investment
The crypto art market, as the traditional art market, is illiquid. This means that assets do not have a market price and cannot be immediately traded. So, how do we measure a return on investment for an illiquid asset? Let’s start by considering:
• each artist as the set of artworks minted by the artist;
• each artwork as the set of consecutive sales of the same artwork;
• each sale as a priced transaction trading the artwork NFT either on the primary or on the secondary market. It is worth noticing that a non-priced transfer, or donation, is not considered a sale in this context.
An artwork has always an implicit value that mainly depends on its intrinsic characteristics as well as on the popularity and success of the artist that made it. This value, however, is not explicit and can only be estimated during the rare moments when the artwork is traded. Hence, at the artwork level, the relevant information for the sake of investment is the time series of sales and resales of an artwork with the associated prices. More formally, each artwork is associated with a repeated sale sequence (t1, p1) (t2, p2), … (tn, pn), where t1 < t2 … < tn and each pair (ti, pi) refers to the sale of the artwork that happened at timestamp ti with price pi. Each artist is then associated with all the repeated sale sequences of the artworks they minted.
3.1 Metrics of return
In this section we propose a number of metrics measuring the return on investment on an artist based on the set of repeated sale sequences for the artist.
3.1.1 ROI
Given a sale on the secondary market, let P be the price of the sale and Q be the price of the previous sale in time for the same artwork. Then, the Return On Investment (ROI) of the sale is given by:
The ROI is positive (greater than 0) if the selling collector made a gain, it is negative (between -1 and 0) if the seller made a loss, or null if there was neither a gain nor a loss. For instance, if an artwork bought for 1Ξ is sold for 1.2Ξ, then there is a positive return of 0.2, or 20%. If the same artwork is sold for 0.5 instead, then there is a negative return of 0.5, that is 50%. Notice that any two consecutive sales for an artwork generate a ROI.
3.1.2 Temporalized ROI
We devise a Temporalized ROI (TROI) method that considers also the speed of the return. Intuitively, a return, either positive or negative, is larger if it happens faster. A resale time for an artwork is the time occurred between two consecutive sales for that artwork. Let t be a resale time and ROI be the corresponding return as defined above. We define
with
and percentile(t) is the percentile of t with respect to all resale times for some artwork in the gallery. Notice that 0.5 ≤ ρ(t) ≤ 1.5 and ρ(t) is low (close to 0.5) when the resale time is large, while ρ(t) is high (close to 1.5) when the resale time is small. If the resale time is the median in the gallery, then ρ(t) = 1 and the TROI is equal to the ROI. Hence, the multiplicative factor ρ(t) weighs the ROI by the resale speed.
3.1.3 RadaR index
The return of an investment always needs to the compared with its risk. For instance, in traditional finance, the popular Sharpe ratio is the average return earned per unit of volatility or total risk (Sharpe, 1966). Volatility is a measure of the price fluctuations of an asset or portfolio. As we have seen in Section 2, the literature agrees that both returns and risks of investment in NFTs are higher than in traditional investments.
We define the return set for an artist as the set of ROIs for all secondary sales of artworks created by the artist. Given a return set for artist X, we will consider the following components to assess the risk-adjusted return:
• the mean μX of the ROIs for X is the return factor;
• the standard deviation σX of the ROIs for X is one factor of risk that measures the volatility of the ROIs: the more the ROIs deviate from the mean, the more risky is an investment in X;
• the sale frequency πX of X, that is the number of items sold by X over the number of items minted by X in the gallery7, is another source of risk. The larger the sale frequency for an artist, the lower the risk of an investment in X;
• the overall risk factor is defined as ρX = σX/πX.
We define a risk-adjusted return ζX for artist X, called the RadaR index of X, as follows:
This is essentially the Sharpe ratio μX/σX weighted by the sale frequency πX of artist X. The ideal artist for an investor has large and stable returns and sold most of their creations. Risky investments are artists that either sold few items or that have quite volatile ROIs (or both). The risk can be compensated only by large returns. The temporalized RadaR index is defined in the same way but in terms of temporalized ROIs as described above.
If the distribution of returns for an artist is highly skewed, and in particular, if it contains large outliers, we advocate the use a different version of the RadaR index in which the average of ROIs is replaced by the median of ROIs and the standard deviation of ROIs is replaced by the median absolute deviation (mad) of ROIs. Both median and mad are robust statistics, being more resilient to outliers in a data set than average and standard deviation. In particular, in the standard deviation, the distances from the mean are squared, so large deviations are weighted more heavily, and thus outliers can heavily influence it. In the mad, the deviations of a small number of outliers are irrelevant.
3.1.4 Gain probabilities
One can use the above defined risk-adjusted return to rate and rank artists in a gallery. In this section, however, we propose a radically different method to compare the returns of artists. We devise a binary probabilistic method to compare the returns of two given artists called gain probabilities. Informally, the method measures the probability that an investment in one artist was more profitable than an investment in the other, given the history of sales of the two artists.
More formally, given the return sets X = {x1, … , xn} and Y = {y1, … , ym} for two artists X and Y, we define the gain probabilities as follows:
Notice that P(X > Y) + P(Y > X) + P(X = Y) = 1. We have that P (X > Y) is the probability that if we randomly choose one ROI from artist X and one ROI from artist Y, then the ROI for X is larger than the ROI for Y. In other terms, it is the probability that an investment on artist X was more profitable than an investment on artist Y. For instance, if X = {1, 2, 3} and Y = {1, 5}, then P(X > Y) = 2/6, P(Y > X) = 3/6, and P(X = Y) = 1/6. Hence, in 50% of cases investing in Y had a larger return than investing in X while in (about) 33% of cases investing in X was more profitable than investing in Y. For the rest of the cases, there was no difference.
3.2 An algorithm for gain probabilities
In this section we propose an algorithm to compute the gain probabilities for two artists, prove its correctness and analyse its complexity. Figure 1 contains the pseudo-code of the proposed algorithm. The algorithm inputs two tables A and B containing a column for the ROIs and one for an identifier of the artist. Tables A and B, which are originally sorted by the ROIs, are then merged into a table C, sorted again by the ROIs. Then the algorithm scans table C from tail to head updating the gain probabilities. The general idea is the following. If, during this scan in decreasing order of ROIs, the algorithm finds a ROI r1 for artist A such that the next ROI r2 in the scan is strictly lower than r1, and moreover we know that there are k ROIs of artist B to visit in the scan, then we can conclude that the ROI r1 for A is larger than each of the k ROIs for B. The tricky part is when r1 = r2, or, in general, when there is a group of equal ROIs. In this case we need to read the entire group of equal ROIs and then update the gain probabilities in terms of the number of ROIs of the two artists that have been found.
In the code we have used the following data structures. Variables A, B and C are tables with columns roi (containing a ROI) and artist (containing an identifier of an artist, either A or B). In particular, table A contains ROIs for artist A; table B contains ROIs for artist B. We assume that both tables A and B are sorted in increasing order by the ROI column; Table C is the sorted merge of A and B, hence it contains the ROIs sorted in increasing order for both artists A and B. For instance, C[0, artist] is the artist, either A or B, of the first row (indexed 0) of C and C[0, roi] is the ROI of the first row of C. Variables counters and groupCounters are named vectors containing integers with components A for artist A and B for artist B. For instance, counters[A] is the counter value for A. Variable counters contains, for each artist, the number of ROIs that still need to be visited in the scan of table C, while variable groupCounters records, for each artist, the number of ROIs encountered during a the visit of a group of equal ROIs. Finally, gainProbs is a named vector with components gainProbs[A] for the gain probability P(A > B), gainProbs[B] for the gain probability P(B > A), and gainProbs[E] for the gain probability P(A = B).
Before proving the correctness of the algorithm, we show its execution on a simple example. Suppose the ROI sequence to visit is the following:
with 4 instances of A and 3 instances of B. The code reads this sequence from right to left and reasons as follows.
1. The first instance of B is read; it is larger than 4 instances of A, hence gainProbs[B] = 4;
2. The next instance of A is read; it is larger than 2 instances of B, hence gainProbs[A] = 2;
3. Now the equality group containing 2 instances of A and 1 instance of B is read. The 2 instances of A are both larger than 1 other B instance, hence gainProbs[A] = 4, while the B instance is larger than 1 other A instance, hence gainProbs[B] = 5;
4. The next instance of B is read; it is larger than 1 instance of A, hence gainProbs[B] = 6;
5. The next instance of A is read and it is not larger than any other instance of B and the outer while loop terminates with gainProbs[A] = 4 and gainProbs[B] = 6;
6. Finally, over the 4 ⋅ 3 = 12 possible pairs of A and B instances, we have that P(A > B) = 4/12 = 1/3, P(B > A) = 6/12 = 1/2 and P(A = B) = 2/12 = 1/6.
In the following we formally prove that GainProbs algorithm computes the gains probabilities P(A > B), P(B > A), and P(A = B) for two ROI tables A and B. We first show the following:
Lemma 1. After each iteration of the outer while loop the following invariant holds:
• counters[A] and counters[B] contain the number of instances of A and B present in the head of the C table from index 0 to index i;
• gainProbs[A] and gainProbs[B] contain (up to a division by A.length * B.length) the gain probabilities P(A > B) and P(B > A) when only elements in the tail of the C table from index i + 1 to index C.length - 1 are considered.
Proof. We prove the statement by backward induction on the counter i in the code. The statement is true initially (i = C.length - 1), since counters[A] = A.length, counters[B] = B.length, both gainProbs[A] and gainProbs[B] are 0, and the tail of table C from i + 1 to to C.length - 1 is empty. The recursive case is as follows. Assuming the statement holds for i
1. Either there are no equal ROIs, that is, C[i, roi] is different from C[i-1, roi]. In this case we skip the inner while loop, or;
2. There is a group of cardinality at least 2 of equal ROIs, and hence we enter the inner while loop.
In the first case, the simpler one, suppose that C[i, artist] = A (the case for B is similar). Hence groupCounters[A] = 1, groupCounters[B] = 0, counters[A] is decremented by 1 (we have read one A) and counters[B] remains constant (we have read no B). Using the recursion hypothesis for the counters of A and B, the thesis holds for them. Thus, gainProbs[A] is incremented by counters[B], because we have read one A and we know that its ROI is larger than counters[B] ROIs of B in the remaining head of table C (recall that C is sorted in increasing order or ROIs). Finally gainProbs[B] is not changed. Therefore, using again the recursion hypothesis for the gain probabilities, also gainProbs[A] and gainProbs[B] contains the correct values.The second case is a generalization of the first one to a group of ROI equalities that contains more than one element. After the inner while loop, groupCounters[A] contains the number of visited A during the loop, hence counters[A] is decremented by this number and after this operation, using the recursion hypothesis, it contains the remaining number of A in the head of table C. Similarly for B. Hence the thesis holds for the counters of A and B. Then, gainProbs[A] is incremented by the number of visited A in the inner while (groupCounters[A]) multiplied by the remaining number of B in the head of the C table (counters[B]). Indeed, all these instances of A have an equal ROI that is larger than the ROIs of B in the remaining head of table C. Similarly for gainProbs[B]. Hence, using the recursion hypothesis, the gain probabilities are also correct and the overall thesis holds.Using the above Lemma, we can now easily show that the coded algorithm computes the gain probabilities for tables A and B.Theorem 1. Algorithm GainProbs computes the gain probabilities P(A > B), P(B > A), and P(A = B) for ROI tables A and B.
Proof. The outer while loop in GainProbs ends when i = 0. Using Lemma 1, when i = 0, gainProbs[A] and gainProbs[B] contain (up to a division by A.length * B.length) the gain probabilities P(A > B) and P(B > A) for all elements of table C after the first one. Notice that the first element of C, that at position 0, does not change the gain probabilities, since there are no other elements in C to compare with. Hence, at the end of the outer while loop, the gain probabilities are computed (up to a division by A.length * B.length) for the entire C table.Notice that A.length * B.length is the number of pairs (x, y) with x an A member and y a B member. After the division by A.length * B.length made outside the outer while loop, gainProbs[A] and gainProbs[B] contain the gain probabilities P(A > B) and P(B > A). Finally, the gain probability P(A = B) = 1 − P(A > B) − P(B > A).It is easy to show that GainProbs is not only correct, but also efficient.
Theorem 2. Assuming that A and B are sorted tables of length n and m, the computational complexity of the GainProbs algorithm is O(n + m).Proof. Merging tables A and B into table C costs O(n + m). The rest of the algorithm scans the rows of table C, whose length is n + m, making only constant-time operations, with a cost of O(n + m). Hence the total cost of the GainProbs algorithm is O(n + m).There exists in fact one simple optimization of the GainProbs algorithm that replaces the Boolean condition of the outer while loop (i
4 The RadaR web app
We developed a Web application called RadaR, accessible at https://niftyradar.app, that implements the return metrics proposed in Section 3. The application might be primarily useful for collectors seeking for the good investment in the NFT space. It might be also functional to crypto art galleries to feature some already onboarded artist or to inform the decision about the onboarding of a new artist8.
In this section we describe the architecture of the RadaR web app, with a special focus on scalability. Moreover, we thoroughly analyse a case study matching two notable artists of the crypto art space.
4.1 Architecture
The design phase of the RadaR app revolved around a number of fundamental principles:
• Extensibility and scalability: the Minimum Viable Product (MVP) was implemented to be easily extended and improved over time, with a long-term view of the entire project. In particular, scalability of the product along different dimensions has been a core goal of the development (we will discuss scalability in detail in Section 4.2);
• Cloud-based application: the potential of cloud computing was exploited in all aspects of application development and management, from storage to deployment. Specifically, the Amazon Web Services (AWS) platform was chosen;
• Simplicity and immediacy of the User Interface: RadaR was developed with a critical spirit and attention to the user-friendliness of the interface and effectiveness of data visualization;
• Cost management: the design mantra was to achieve a simple, elegant and extensible product while keeping costs to a minimum. In fact, one aim was to demonstrate that it is possible to develop an MVP in an economically sustainable manner, using open-source methodologies and tools that are scalable as needed. Notably, the cost of the project was entirely self-financed.
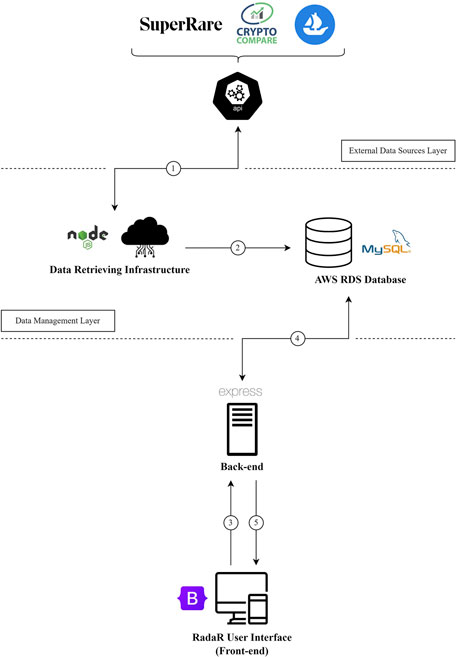
In the following we describe the different components of the RadaR application using a top-down approach (see Figure 2):
• Front-end. The information provided to the user has been organised in a pyramid fashion. The comparison between two artists through the use of gain probabilities is immediately displayed. The interested user can expand the visualization of each artist with further statistics, like those described in Section 3.1 and more. The experienced user can finally be guided by some tips on the use of metrics to fully understand the potential of each artist. The front-end implementation was realized with HTML/CSS and Javascript, using a Bootstrap template;
• Back-end. The back-end is responsible for these key operations:
• HTTP management: this part coordinates concurrent requests and responses and, in view of future developments, might include more specific and complex features (such as cookies and sessions);
• computation of gain probabilities: gain probabilities are computed in real time when a specific user request arrives. Pre-calculating the gain probabilities for each artist pair is not a viable solution given the quadratic number of artist pairs and the low probability that a user requests any specific comparison;
• database retrieval: the rest of the statistics shown in the interface are retrieved from the database (via specially created queries) on the basis of the HTTP request received and handled by the back-end.
The server-side programming of the web app is based on Node.js and the Express.js frameworks. The technologies were chosen for their efficiency and speed in managing and retrieving data: the asynchronous event-based execution makes this environment ideal for developing real-time web applications, especially on the cloud:
• Database. We store all data used by the web app in a MySQL relational database on the AWS cloud. Managing a proprietary database allows unlimited access to data and greater flexibility, especially in view of future adaptations and changes. In particular, being on the cloud, it is possible to adapt the size of the database according to need. The database is not limited to being a simple data container, but integrates a mechanism of triggers and stored procedures within it, which has the task of computing most of the statistics after each data insertion;
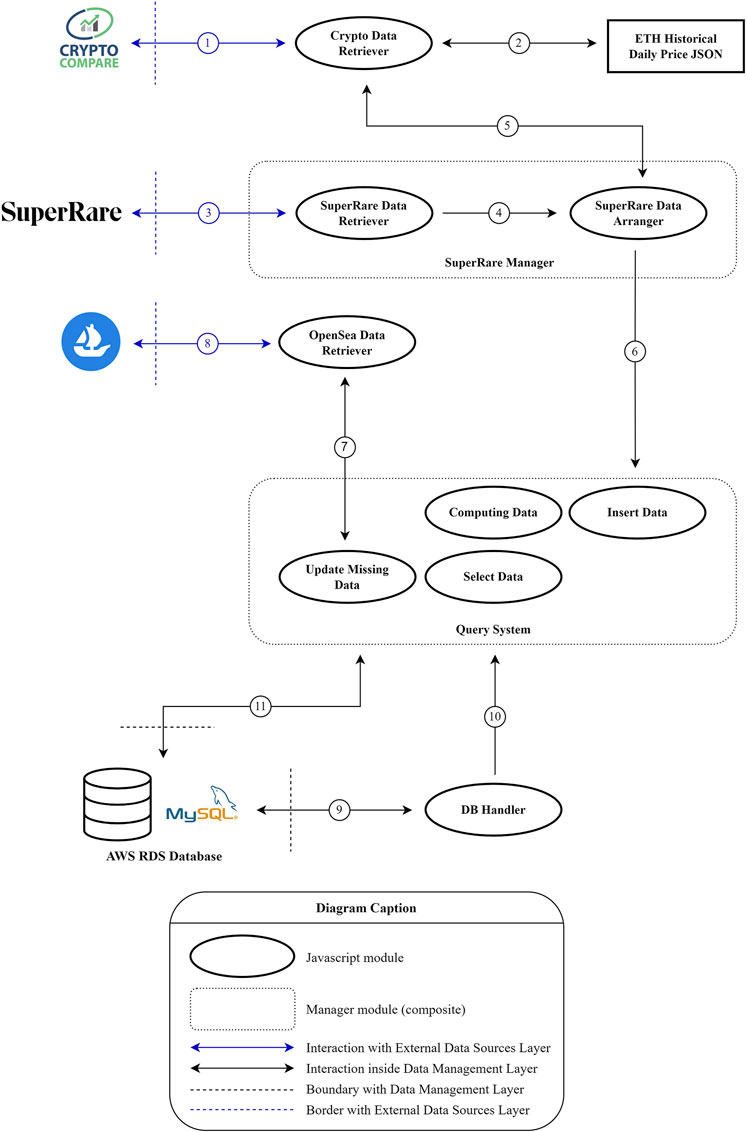
• Data retrieving infrastructure. This component is the heart of the system, as it allows the retrieval of data that will then be used by the web application (see Figure 3). Concretely, the data management infrastructure consists of a series of modules written in the Javascript language (Node.js framework) which, suitably integrated with each other, allow (i) to make HTTP requests to the APIs that provide the external data (e.g. the API of a marketplace); (ii) to process and structure the retrieved data with the goal of inserting them in the cloud database; (iii) to connect and update the database with the new data.
The data retrieving infrastructure was designed and implemented with the aim of running at regular time intervals. Increasing the frequency of retrieving data from external sources increases the freshness of the information provided by the front-end to users but also increases the computational load of the data retrieving component.
A crucial aspect of this component concerns re-usability: each marketplace is managed by an independent and dedicated module that retrieves, manages and formats the relevant data. In view of future developments, with the addition of new data sources, it will be sufficient to adapt this component to the new endpoint, while the rest of the infrastructure will remain unchanged.
4.2 Scalability
We developed the RadaR application with an eye at scalability. We achieved a scalable product using cloud computing, modular programming, and efficient algorithms that run both online and offline. More precisely, we identified three main scalability impact factors:
1. Increase in the number of data sources (marketplaces) and volume of data. The initial MVP considers only one marketplace (SuperRare) but we plan to extend to many more. As soon as a new marketplace has an endpoint exposing the relevant data, the integration with RadaR architecture is smooth. The exposed information must be, at minimum, data about NFTs (such as contract, id, name, creator, owner) and about sales (like timestamp, seller, buyer, price, exchanged token). To integrate a new marketplace, we will need to create a new module in the data retrieving infrastructure (an adaptation of the one for SuperRare) that makes the request to the endpoint and fetches the data to insert into the database. The rest of the architecture will not be affected. The resulting increase in data volume can be managed by leveraging on the cloud infrastructure of RadaR application, hence, if necessary, increasing the available space or scaling to distributed instances.
2. Increase in the number of online users of the Web application. The traffic of users playing with the application online is a point that should be evaluated early on, so that unpleasant system stalls and crashes can be avoided. More visitors means an increase in the amount of requests to be handled in the backend and, consequently, database queries. We leverage on the load balancing and auto scaling features of the cloud solution to dynamically adapt the performance of the app. Moreover, most of the computation is triggered offline at the time of update of the database with new data. The only real-time computation is the computation of gain probabilities, which is, however, very efficient (linear complexity);
3. Increase in the speed of arrival of data. The MVP updates the marketplace data every week, but imagine we want a finer granularity, leading towards stream computing akin to financial trading. This might be a bottleneck for our application, since much computation is done at update time. To consider this event, the computation following a database insert, for instance the update of the average ROI statistics for an artist, is done efficiently using database triggers. The triggers, when possible, merge the old data (for instance the old value of the ROI average) with the new data (a new ROI), hence they do not recompute the statistics from scratch. Moreover, to tackle an increase in velocity, we leverage on Node.js. Given its asynchronous, event-driven execution model, Node.js is an ideal environment for developing real-time Web applications, especially on the cloud, even when data rates are significantly increased.
4.3 The nifty clash
The front-end interface of the RadaR app is laid out as a clash between two artists chosen by the user or suggested by the app. For each artist, the app delivers three layers of information, where each consecutive layer expands and deepens the knowledge of the previous one.
1. Layer 1. This is the first layer that is accessed by all users that run the app. In this layer, we simply show the gain probabilities of the two chosen artists. The user obtains a straight-to-the-point indication of who among the two artists is potentially a more profitable investment.
2. Layer 2. This layer goes a bit deeper in the investigation. Here we compare the RadaR index for both artists, and explode it into its components as defined in Eq. 1: the average ROI, the standard deviation of ROIs and the sale frequency. The sale frequency is expanded into primary sale frequency - the relative number of artworks sold only on primary market, and secondary sale frequency - the relative number of artworks sold on the secondary market. Notice that the sale frequency is the sum of primary and secondary frequencies. Moreover, we show the unsold frequency, that is the relative number of unsold artworks, or the complement to 1 of the sale frequency. Since the ROI distribution is particularly telling to a potential investor, we also give: minimum, first quartile, median, third quartile, and maximum ROI. Moreover, we allow the user to switch between normal and temporalized RadaR index and corresponding components. Finally, we also provide the median/mad version of RadaR index, which is a more robust statistics in case of presence of heavy outliers in the data set.
3. Layer 3. This layer gives the usual suspects of metrics, plus a new one, borrowed from bibliometrics. We show, for each artist, the following statistics:
• OG-ness: the number of days that separate the minting of the first artwork of the artist and the minting of the first artwork in the gallery. The lower this number, the more OG is the artist;
• artworks: the number of artworks created by the artist;
• sales: the cumulative number of sales of artworks created by the artist. Notice that if an artwork is sold once on primary market and twice on secondary market, the count is 3;
• sale volume: the cumulative sale amounts of artworks created by the artist (in USD and ETH);
• mean sale price: the sale volume divided by the number of sales (in USD and ETH);
• minimum, first quartile, median, third quartile, and maximum sale price (in USD and ETH);
• h-index: the maximum value of h such that the artist has created h artworks that have each been sold for at least h ETH9. This mimics the popular h-index in bibliometrics (Hirsch, 2005).
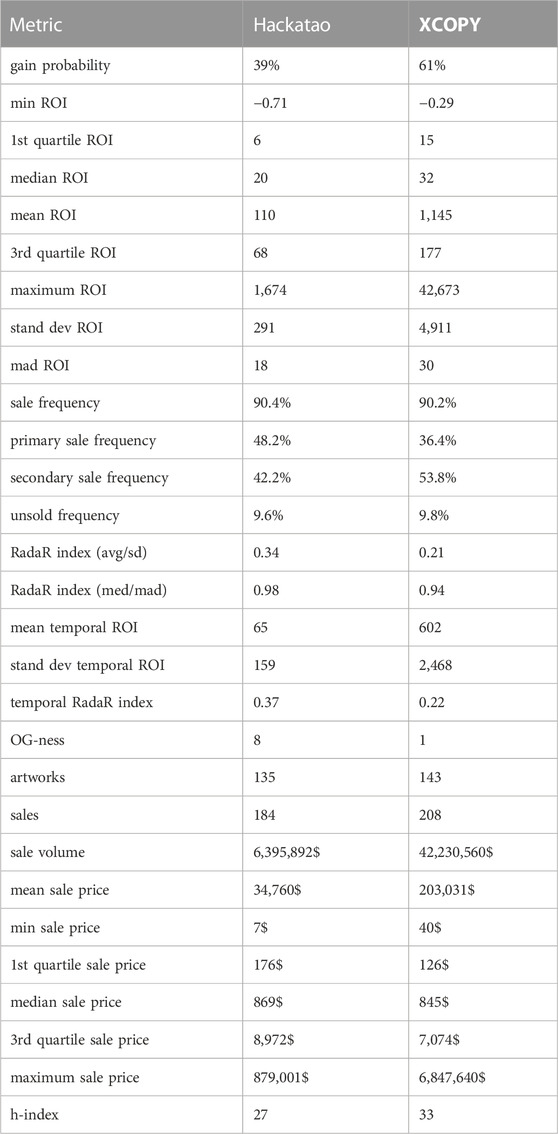
Hackatao10 and XCOPY11 are two of the most relevant OGs of crypto art. They were among the first artists in the world to join the NFT space and have both gained notable commercial success and social popularity within this space. On SuperRare gallery, in particular, they have minted and sold a comparable number of artworks. Hence, why not casting a match between these two superstars? Table 1 contains the outcomes based on data from 19 July 2022.
First of all, notice that the gain probabilities are in favour of XCOPY (61% vs. 39%). It means that 61% of the time an investment in XCOPY’s art was more profitable than an investment in Hackatao’s art. This might suggest how to split a budget for a future investment, in case the two artists are on the radar of an investor.
The second layer of metrics digs a little deeper. The mean return on resales in neatly is favour of XCOPY: 1,145 vs. 110. This means that the average XCOPY artwork has been resold with a price 1,145 higher than its purchase price, while this factor is (only) 110 for Hackatao’s art. The median ROI is more balanced, with XCOPY scoring 32 and Hackatao 20. In other terms, about 50% of the time an XCOPY (respectively, Hackatao) has made a return larger than 32 times (respectively, 20 times), with an impressive maximum ROI of 42,673 (respectively, 1,674). On the other hand, the risk, measured using the variability of the returns, is much higher for XCOPY (ROI standard deviation of 4,911 and ROI median absolute deviation of 30) than for Hackatao (ROI standard deviation of 291 and ROI median absolute deviation of 18). Since the sale probability for the two artists is similar, we have that the risk-adjusted return, or RadaR index (using average and standard deviation), is in fact in favour of Hackatao: 0.34 vs. 0.21. The RadaR index using median and median absolute deviation is more balanced but still in favour of Hackatao (0.98 vs. 0.94). In other words, the return per unit of risk is higher for an investment in Hackatao. On the other hand, XCOPY is an emblematic high-risk-high-return type of investment.
The temporal version of the RadaR index confirms the above conclusions. However, notice that the mean temporal ROI is in both cases about a half lower than the mean ROI. This means that these incredible returns we have noticed have taken a relative long time to realize. Indeed, we checked that the average resale time is large for both artists. This makes sense, since collectors of these blue chip artists have typically diamond hands: either they hodl the art or they wait enough time until they receive a highly profitable offer.
The third and last layer of metrics contains more traditional metrics plus the h-index. Both artists are OGs: XCOPY minted the first artwork the day after the genesis piece in SuperRare, while Hackatao after 8 days. XCOPY is still dominant in terms of sale volume, average and maximum sale price. However, both artists have sold artworks also for reasonably low prices: about 25% of artworks for less than two hundred dollars and about 50% of artworks for less than one thousand dollars (if you were far-sighted enough, you could have bought an XCOPY for 40$ and an Hackatao for, well, 7$). Finally, XCOPY has sold no more than 33 artworks each for at least 33 Ether, while the h-index of Hackatao is a bit lower (27).
5 Discussion
Blockchain technology initiated the so-called third iteration of the Web, namely Web3. Whereas in Web1 we only read static content, in Web2 we learned to write dynamic content through blogs and social networks. However, we missed the subtle fact that we were the product and failed to own our own content. Finally, in Web3 we become holders of our assets and learn how to value and monetize it.
Blockchain is a political technology that relies on the following principles:
• decentralisation: the system is not presided over by a central unit; it is a web without a spider;
• disintermediation: interaction takes place directly between the parties involved, without passing through an intermediary;
• transparency: information is public and verifiable by all;
• sovereignty of the individual: the individual fully owns what they create. This also implies a profound assumption of responsibility.
The proposal we have made in this article is in line with these principles. By leveraging data transparency, we have developed a nifty radar for the benefit of all those who want to collect and invest in digital art without going through expensive and opaque intermediaries, as is often the case in the traditional art world. A system that is also useful for artists themselves in order to assess their own position on the digital art market.
In this respect, we are planning to evolve the RadaR web app in the direction of Web3. This includes retrieving the data directly from the blockchain, instead of relying on programmatic interfaces from third parties. Moreover, the user will access the app with digital wallet identification and will interact with it using a token-based system. Users will spend RadaR tokens in order to clash the desired artists as well as to get additional, possibly personalized, statistics. Finally, RadaR will become a modular system that generates a plurality of statistics, composable with each other, to create narratives for the user, whether an artist, collector or curator. The system will not provide an absolute truth, but different perspectives, even opposed ones. It is up to the user to focus on one of these narratives, according to their level of knowledge, propensity for risk and return, and objective.
Data availability statement
Publicly available datasets were analysed in this study. This data can be found here: https://superrare.com.
Author contributions
MF devised the investment metrics and wrote the first draft of the manuscript. DDL designed and implemented the RadaR Web application. All authors contributed to manuscript revision, read, and approved the submitted version.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1We focus on the case of digital art but in fact artists can be creators on any type of NFT, for instance any gadget for an avatar in a decentralized metaverse.
2The most popular blockchains for crypto art are, at the moment, Ethereum and Tezos.
3In fact, royalties differ based on the marketplace and some marketplaces let the artist decide what the royalty is. Recently there has been a huge controversy around marketplaces like OpenSea making royalties optional and rebranding them as “fees”.
4Accessible at: https://superrare.co/artwork/all-time-high-in-the-city-11. Warning: flashing imagery.
5OG, short for Original Gangster, is a slang term for someone who is incredibly exceptional, authentic, or old-school.
6Ether, abbreviated as ETH with symbol Ξ, is the native currency of Ethereum blockchain.
7One might split the sale frequency in primary sale and secondary sale frequencies. In particular, the secondary sale frequency is interesting since it is the chance to make a resale, hence a ROI, with the artist's artwork. However, some collectors in the NFT space have diamond hands and they rarely sell what they bought. In this case, the primary sale frequency is also relevant.
8The revenue of a gallery on an artist is strictly correlated with the returns made by the artist's artworks.
9In practice, we rate each artwork with the maximum price for which it has been sold either on primary or secondary market. Then, for each artist, we sort the artwork ratings in decreasing order. Finally, we scroll down the list until the rating is lower than the list rank. The previous rank is the h-index.
10https://superrare.com/hackatao.
11https://superrare.com/xcopy.
References
Borri, N., Liu, Y., and Tsyvinski, A. (2022). The economics of non-fungible tokens. Rochester, NY: Social Science Research Network. SSRN Scholarly Paper ID 4052045.
Burton, B. J., and Jacobsen, J. P. (1999). Measuring returns on investments in collectibles. J. Econ. Perspect. 13, 193–212. doi:10.1257/jep.13.4.193
Finucane, B. P. (2018). “Creating with blockchain technology: The “provably rare” possibilities of crypto art,”. Master’s thesis (The University of British Columbia).
Franceschet, M., Colavizza, G., Smith, T., Finucane, B., Ostachowski, M. L., Scalet, S., et al. (2021). Crypto art: A decentralized view. Leonardo 54, 402–405. doi:10.1162/leon_a_02003
Franceschet, M. (2021). HITS hits art. Blockchain Res. Appl. 2, 100038. doi:10.1016/j.bcra.2021.100038
Ginsburgh, V., Mei, J., and Moses, M. (2006). The computation of prices indices. 11 edn. Elsevier, 947–979. chap. 27.
Goetzmann, W. N. (1993). Accounting for taste: Art and the financial markets over three centuries. Am. Econ. Rev. 83, 1370–1376.
Hirsch, J. E. (2005). An index to quantify an individual’s scientific research output. Proc. Natl. Acad. Sci. U. S. A. 102, 16569–16572. doi:10.1073/pnas.0507655102
Horky, F., Rachel, C., and Fidrmuc, J. (2022). Price dynamics of non-fungible tokens: The case of the digital arts market. Rochester, NY: Social Science Research Network. SSRN Scholarly Paper ID 4080372.
Kong, DR., and Lin, TC. (2021). Alternative investments in the fintech era: The risk and return of non-fungible token(nft). SSRN Electron. J. doi:10.2139/ssrn.3914085
Korteweg, A., Kräussl, R., and Verwijmeren, P. (2016). Does it pay to invest in art? A selection-corrected returns perspective. Rev. Financial Stud. 29, 1007–1038. doi:10.1093/rfs/hhv062
Mandel, B. R. (2009). Art as an investment and conspicuous consumption good. Am. Econ. Rev. 99, 1653–1663. doi:10.1257/aer.99.4.1653
Mazur, M. (2021). Non-fungible tokens (Nft). The analysis of risk and return. SSRN Electron. J. doi:10.2139/ssrn.3953535
Mei, J., and Moses, M. (2002). Art as an investment and the underperformance of masterpieces. Am. Econ. Rev. 92, 1656–1668. doi:10.1257/000282802762024719
Nadini, M., Alessandretti, L., Di Giacinto, F., Martino, M., Aiello, L. M., and Baronchelli, A. (2021). Mapping the NFT revolution: Market trends, trade networks, and visual features. Sci. Rep. 11, 20902. doi:10.1038/s41598-021-00053-8
Pommerehne, W. W., and Frey, B. S. (1989). Muses and markets: Explorations in the economics of the arts. Cambridge, Mass., USA: B. Blackwell.
Renneboog, L., and Spaenjers, C. (2013). Buying beauty: On prices and returns in the art market. Manag. Sci. 59, 36–53. doi:10.1287/mnsc.1120.1580
Schaar, L., and Kampakis, S. (2022). Non-fungible tokens as an alternative investment – evidence from cryptopunks. J. Br. Blockchain Assoc. 5, 1–12. doi:10.31585/jbba-5-1-(2)2022
Schnoering, H., and Inzirillo, H. (2022). Constructing a NFT price index and applications. doi:10.48550/ARXIV.2202.08966
Vasan, K., Janosov, M., and Barabási, A.-L. (2022). Quantifying NFT-driven networks in crypto art. Sci. Rep. 12, 2769. doi:10.1038/s41598-022-05146-6
Veblen, T. (2005). The theory of the leisure class: An economic study of institutions. Delhi: Aakar Books. OCLC: 297506670.
Keywords: blockchain, art investment, investment metrics, web applications (WebApps), non-fungible tokens
Citation: Franceschet M and Della Libera D (2023) Return on NFTs. Front. Blockchain 6:1101939. doi: 10.3389/fbloc.2023.1101939
Received: 18 November 2022; Accepted: 12 January 2023;
Published: 01 February 2023.
Edited by:
Andrea Pizzoferrato, University of Bath, United KingdomCopyright © 2023 Franceschet and Della Libera. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Massimo Franceschet, massimo.franceschet@uniud.it
 Massimo Franceschet
Massimo Franceschet Davide Della Libera
Davide Della Libera