Toward Quantifying Decentralization of Blockchain Networks With Relay Nodes

1 Introduction

Blockchain is an integral component of Distributed Ledger Technology (DLT), which enable decentralized and immutable data repositories among mutually non-trusted entities in a public or private setting. The first public blockchain was Bitcoin, and was introduced by Nakamoto in 2008 (Nakamoto, 2009) since then, DLT has continued to evolve through many more advanced public and private blockchains such as Ethereum (Wood, 2014) and Hyperledger Fabric (Androulaki et al., 2018). Despite vast differences in design, operation, and application, the fundamental properties of DLT remain network decentralization and data immutability.

In computer networks, decentralization comprises of shifting from the traditional client-server architecture to a peer-to-peer (P2P) networks in which all nodes have the same role. In blockchain networks, decentralization is usually expressed at the application layer as the execution and storage of transactions without a trusted third party, or at the consensus layer through a byzantine fault-tolerant protocol. However, an overlooked aspect is the decentralization of the public blockchain network itself, which is sensitive to the peer selection strategy and network protocol. In other words, even in a permission-less blockchain network where nodes can freely join and connect, the network can be more or less decentralized depending on how each node selects its neighbors to maintain connections to within the P2P network, since these connections affect how transactions, and blocks propagate throughout the system.

In practice, blockchain-based systems have encountered scalability and performance issues (Eyal and Sirer, 2014; Atzei et al., 2017; Brandenburger et al., 2018). Thus, there have been proposals for performance improvements, which range from attempts at speeding up the blockchain overlay networks (e.g., (Corallo, 2016; Fadhil et al., 2017; Pinar Ozisik et al., 2017; Klarman et al., 2018; Basu et al., 2019; Coralo, 2019)) to proposals for increasing the throughput of the system (e.g., (Croman et al., 2016; Yu et al., 2018; Gueta et al., 2019; Yang et al., 2019)). While it is clear that these proposals are beneficial to the blockchain systems in terms of performance, it is not yet known what impact (positive or negative) they have on the other fundamental property of blockchain, which is network decentralization. In this paper, we seek to address this gap by formally studying decentralization as a property of the P2P network graph.

Network decentralization is also overlooked in other common aspects of blockchain systems. For instance, Bitcoin uses a bootstrapping stage where participating nodes connect to seed nodes. This bootstrapping phase prevents blockchains from having a completely random topology, particularly, if the nodes remain connected to the seed nodes for a long time. This is important since a fully decentralization network should have a completely random topology where nodes have no preference when selecting a peer to maintain a connection. Relay nodes, which are the focus of this paper, can have the same impact on the network topology. As well, uneven geographical distribution is another cause of centrality if peers use proximity-aware connections.

While the main aim of blockchain-based systems is to remove the need for a trusted third party (TTP), a poorly decentralized blockchain network can be prone to be a single point of failure (network partitions) or vulnerable to denial of service (DoS) attacks. Furthermore, poor network decentralization can lead to governance issues, as a minority of central nodes can enforce a certain protocol version by limiting communication among nodes which support a different version. Therefore, a methodology for quantifying network decentralization is crucial in order to analyze these proposals deeply and ensure they do not have unintended side effects on network decentralization. Furthermore, our proposed criterion for analytical and numerical analysis of network decentralization will help blockchain designers compare multiple systems along that dimension.

In this paper, we focus our attention on studying the impact of relay networks on decentralization. Relay networks are sub-networks which consist of powerful nodes which maintain many connections simultaneously in order to reduce block and transaction propagation times (Basu et al., 2019; Coralo, 2019). Relay networks affect the peer selection strategy of the entire P2P network, which will preferentially connect to the relay nodes. To do so, we propose an analytical approach based on the random graph models of Barabási–Albert (BA) (Barabási and Albert, 1999) and Erdös-Rény (ER) (Erdős and Rényi, 1959), which are suitable for modeling permissionless blockchains with and without a relay network, respectively.

The contributions of this paper are as follows:

1 We present an analytical approach for quantifying the decentralization degree in blockchain networks based on the peer selection strategy (random vs. prioritizing relays) for blockchain networks with different architectures.

2 We verify our approach by implementing a complex network generator and running extensive simulations. Furthermore, we validate our model using an experimental dataset mined from the Bitcoin network.

3 We present simulation results and analysis of decentralization based on several important metrics such as average shortest path and average number of connections.

4 We provide a detailed comparison between blockchain networks with varying architectures and topologies with respect to decentralization and network speed.

5 We study the impact of the relay networks on the decentralization degree of the blockchain network.

The rest of this paper is organized as follows. Section 2 presents the most important works related to our paper. In Section 3, we briefly give background material required for understanding this paper. In Section 4, we describe the system and graph models applied in our paper. In Section 5.1, we verify our complex network generator and validate our simulation with the real Bitcoin network. Simulation results and related discussions are presented in Section 6. Finally, Section 7 concludes this paper.

2 Related Works

While the quantification of the decentralization degree at the application layer of blockchains has been widely studied in the literature, to the best of our knowledge, there have been a little or no work on quantifying and measuring the decentralization of the network layer of blockchain-based systems. Most of the existing works such as (Atzori, 2015; Swan, 2015; Cai et al., 2018; Puthal et al., 2018) are geared towards introducing P2P networks as a new architecture to replace traditional server-client centralized networks. Furthermore, some of the research works have reported the tendency of blockchain systems such as Bitcoin towards a centralized architecture due to existence of mining pools (Beikverdi and Song, 2015; Tschorsch and Scheuermann, 2016).

In (Wu et al., 2019), an information entropy-based approach for quantifying the degree of decentralization in Bitcoin and Ethereum is proposed. Using empirical data, the work compares the decentralization of mining and wealth in Bitcoin and Ethereum. However, it does not consider the networking aspects and configuration metrics of the blockchain networks.

In (Chu and Wang, 2018), another attempt for quantifying the decentralization degree in blockchain systems has been carried out. In this work, decentralization is defined using the fraction of the transactions performed by top nodes. With this definition and related analysis, Chu, et al. have concluded that achieving full decentralization in blockchain networks is very hard due to skewed mining power of the nodes. As well, they have claimed that a full decentralization comes at the expense of limited scalability. Our work in this paper is complementary as it studies the problem of decentralization from the perspective of the network.

(Li and Palanisamy, 2020) compares the decentralization degree of consensus protocols between Proof-of-Work (PoW) and Delegated Proof-of-Stake (DPoS). To accomplish this, the decentralization degree in Bitcoin and Steem is calculated using the Shannon entropy of the distribution of hash power and distribution of invested stake among stakeholders, respectively. According to this research work, Bitcoin is more decentralized between top miners but is overall less decentralized than Steem. Unlike our work, network characteristics like topology, and average number of connections per node are not considered.

(Gencer et al., 2018) presents a comparative measurement study on decentralization in Bitcoin and Ethereum. To accomplish this, this work relies on measurement of network resources and evaluates the impact of a relay network (Falcon network). Authors of this work have reported that Bitcoin has more clustered nodes and that mining processes are fairly centralized in both of them. This work is purely empirical and does not propose an analytical technique unlike our work. (Kwon et al., 2019) proves that it is impossible for a permissionless blockchain to be fully decentralized using a concept known as the Sybil cost. This theoretical proof is based on the consensus protocol and does not consider network decentralization, which is the focus of our research.

None of the research works mentioned above have proposed an analytical technique for quantifying and comparing the decentralization degree in the network layer of the blockchain-based systems using the design and configuration metrics (e.g., number of selected peers, network size etc).

3 Background

In this section, we briefly discuss the concepts required for understanding this paper.

3.1 Blockchain P2P Networks

Blockchain networks commonly operate over an unstructured P2P overlay network, where participating nodes are free to join the network by establishing a connection to any existing node in the network. After initial setup, each node continuously maintains a certain number of connections to other neighboring nodes according to a peer selection strategy, which can vary based on the blockchain implementation. Different parameters can be considered for selecting neighbors such as P2P bandwidth, delay, number of hops to the targeted peer, and or geographical distance. The peer selection strategy will strongly affect the topology of the network, and consequently, the decentralization of the network, as we will demonstrate in this paper. Furthermore, different typologies may exhibit different performance and scalability. In this paper, we focus on the number of P2P connections and path length from one node to others. For instance, in the Bitcoin network, each node can select up to 8 peers with outgoing connections as well as up to 117 peers with incoming connections.

3.2 Traffic Handling Overhead

In blockchain networks, a traffic handling protocol is required in order to efficiently disseminate information (i.e. transactions and blocks) over the network. In most public blockchains such as Bitcoin and Ethereum, an inventory-based protocol is implemented in order to avoid overwhelming the network with redundant messages (Corallo, 2016; Lange et al., 2016). According to these protocols, every node has to notify its neighbors that it has a new block/transaction to forward. The inventory message can be either a special message or hash of the block/transaction. If the targeted node does not have the new item, it will inform the inventory message sender, which will transfer the requested data. Therefore, each link in the network will transfer at least one inventory message to notify its neighbor about its content. Figure 1 depicts the inventory-based gossiping protocol of Bitcoin. The number of links is a good parameter to count the minimum number of inventory messages required for the block/transaction dissemination over the blockchain network. Note that the number of the links indicates the lower bound of the number of inventory messages and it can be more than this amount in practice.

FIGURE 1

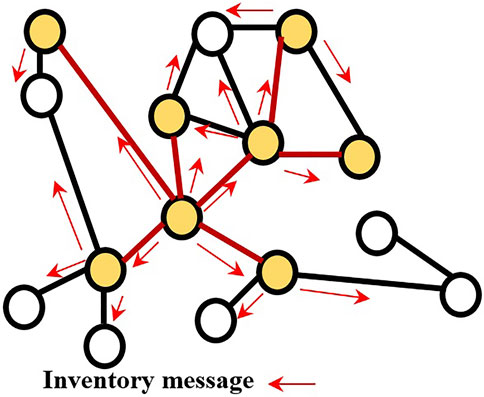
FIGURE 1. Information propagation in a permission-less blockchain such as Bitcoin. Colored nodes are the nodes that have already received the block/transaction. Colored links are the links that have been used for transferring block/transaction. Each link will carry at least one inventory message, but some of them will carry blocks/transactions.

3.3 Bitcoin Network

Bitcoin is a permissionless blockchain-based system that operates over an unstructured P2P network. The network protocol allows the participating nodes to join or leave the network at any time. At the time of joining the network for the first time, a newly arrived node has no knowledge of the IP address of the other nodes in the network. In order to enable the new nodes to discover the network during the bootstrapping phase, there are a number of domain name service (DNS) seeds being run by the volunteer nodes in the network such as a custom implementation of Berkeley Internet Name Daemon (BIND). As of the year 2017, the names of six different DNS seeds are hardcoded in the Bitcoin Core client (Satoshi Client Node Discovery, 2021).

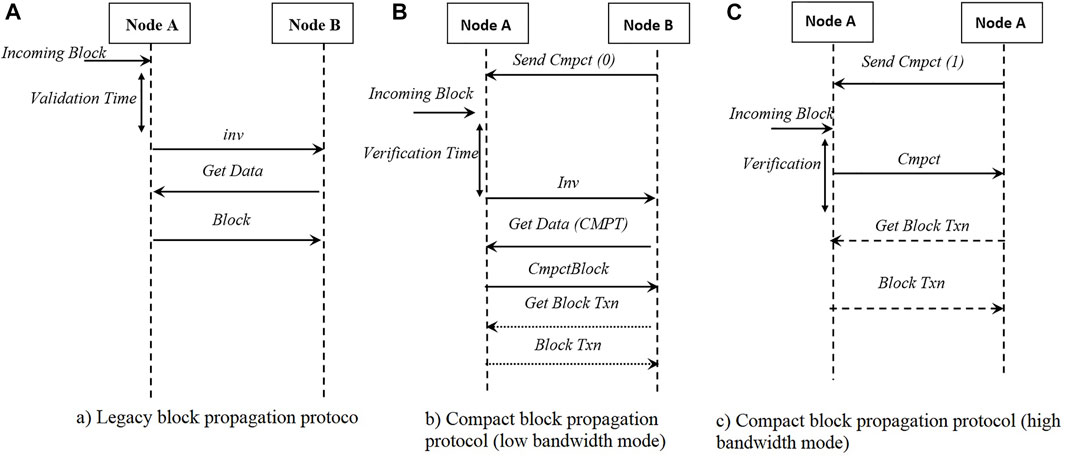
After discovering the network and finding other nodes, newcomer nodes are now able to maintain multiple connections to the neighboring nodes in order to maintain and update the ledger state. As already mentioned in Section 3.2, Bitcoin uses an inventory-based dissemination protocol. Currently, two dissemination protocols are being used in the Bitcoin network: the legacy protocol and the compact block protocol. The first one is almost obsoleted and the majority of the nodes are using the compact block protocol.

3.3.1 Legacy propagation protocol

When a certain block or transaction arrives and is verified by a node, it notifies the neighbors using an inventory (inv) message to let them know that a new block or transaction is available and ready to send. The inv message is consists of the hash of the mentioned block or transaction. This protocol is depicted in Figure 2A. When a node receives a inv message for a block or transaction that is not already seen by it, it replies the inv message by a getdata message. Upon receiving the getdata message, the node will transfer the block or transaction to the sender of this message.

FIGURE 2

FIGURE 2. Block propagation protocol in Bitcoin

3.3.2 Compact block protocol

This protocol was introduced as BIP-152 (Corallo, 2016) in 2016 and reduces the required bandwidth amount for block dissemination in the Bitcoin network. The main aim of this protocol is to let peers reconstruct a block instead of receiving it from other participating nodes. To accomplish this goal, the network should be fairly synchronized and peers should already have accumulated considerable number of transaction in their memory pool. The compact block protocol works in two modes of operation: low bandwidth mode (LBM) and high bandwidth mode (HBM). In LBM, as illustrated in Figure 2B, the receiver (i.e., node B) sends a sendcmp(0) message to the sender of the block (i.e. node A) and tells it that it wants to minimize the bandwidth usage. Whenever node A receives a new block, it informs node B about the reception of a new block via an inv message. If the node B has not already heard about that block, it will reply the inv message via a getdata(cmpct) message. Upon receiving this message, node A will send the hash of the new block, the hash of the transactions, and the transactions that node B is missing. If node B succeeds to reconstruct the block using the received information from node A, the protocol stops. Otherwise, node B will ask node A to send missing transactions. In HBM, as illustrated in Figure 2C, node B sends a sendcmp(1) message to node A and tells it that it wants to receive the block as fast as possible. Whenever a new block arrives, node A starts to do some basic validation (e.g., checking the block header) instead of a complete validation. After that, it will transfer the hash of the block and hash of transactions to node B. If the mentioned information is adequate, Node B will reconstruct the block successfully. Otherwise, it will request from node A to send the missing information (e.g., missing transactions).

3.4 Relay Networks

Relay networks are a set of nodes (or global gateways) deployed in the blockchain network with a large number of connections from the blockchain nodes (e.g., miners in PoW blockchains) and provide them with high-speed links that enables them to propagate their block or transaction as quickly as possible and thereby increasing the efficiency of information propagation. Currently, relay networks are being leveraged as a scalability solution for blockchain networks such as Bitcoin (Otsuki et al., 2019).

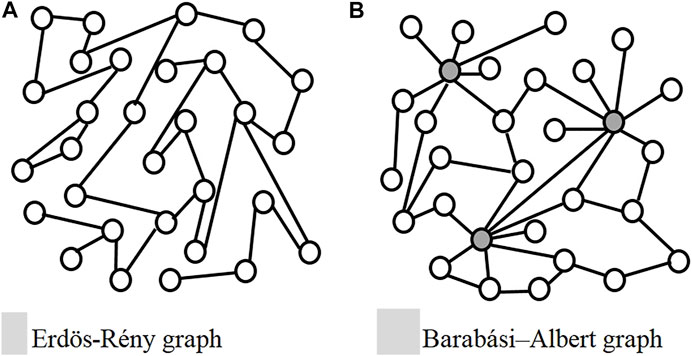
3.5 Erdös-Rény Model

The Erdös-Rény model (ER) is a random graph model for generating random graphs. In this model, in a network of N participants, two arbitrary nodes are connected to each other with the same probability of p in such a way that the average degree of nodes equals M. Hence,

$p=\frac{M}{N-1}(1)$

In other words, this graph is chosen uniformly at random from the set of all possible graphs with N nodes and M links per node on average. This model can be suitable for modeling the blockchain networks with no hubs or relay networks. As well it can be a suitable for modeling large scale public blockchains such as Bitcoin when the relay networks are not taken into account and instead, the average values of the network (e.g., average number of connections per node) are considered (Shahsavari et al., 2020).

The ER model does not exhibit a power-law degree distribution or preferential attachment. Instead, degree distribution in this model follows a Poisson distribution. A sample network generated with the ER model is depicted in Figure 3A.

FIGURE 3

FIGURE 3. ER and BA graphs

3.6 Barabási–Albert Model

Barabási–Albert (BA) is a random graph model with two defining features: preferential attachment and power law degree distribution. Networks with power-law degree distribution are also referred to as scale-free networks. Preferential attachment is also called the rich gets richer. This is because it is more likely for newly joining nodes to select peers with more connections, thereby increasing their already high number of connections. Hence, this peer selection strategy tends to produce networks where a limited number of hubs with a high degree can be found. A complete description of preferential attachment networks is presented in (Van Der Hofstad, 2016).

As a more formal definition, assume there exist N₀ initial nodes in the gradually growing network. Initially, these nodes are connected together as a complete graph with a degree of M₀. Suppose a new incoming node intends to establish m (m ≤ N₀) connections to the existing nodes. The probability that this node will select node i as a peer can be estimated as follows:

$p_i=\frac{m_i}{{\sum }_j{m}_j}(2)$

where m_i is the degree of the node i.

In this model, nodes with the highest degree are themselves more likely to be connected to each other according to Eq. 2. We propose BA graphs as a good model for public blockchain networks such as Bitcoin and Ethereum which employ a limited number of relay gateways, which use a high-speed backbone to efficiently transfer new blocks and transactions from one part of the network to another. A sample network generated using the Barabási–Albert model is depicted in Figure 3B.

4 System Model and Analysis

In this section, we first perform a decentralization analysis of permissionless blockchains using clustering coefficient. Then we propose the average shortest path as an indicator of the network speed. These two metrics represent the trade-off between decentralization and performance, respectively.

4.1 Decentralization Analysis

The clustering coefficient is a metric that captures the tendency of nodes in a graph to form a cluster. For a simple graph, the clustering coefficient is bounded between zero and one and is defined as local clustering coefficient (LCC) and global clustering coefficient (GCC).

Local clustering coefficient: this measure is also known as Watts—Strogatz (Watts and Strogatz, 1998) clustering coefficient and for any arbitrary node i in the network, the local clustering coefficient can be calculated as follows:

$c_i=\frac{2L_i}{k_i\left(k_i-1\right)}(3)$

where L_i denotes the number of edges between the k_i neighbors of the node i. Consequently, the average network clustering coefficient can be calculated as follows:

$C=\frac{1}{N}\sum _{i=1}^N{c}_i(4)$

where N is the number of participating nodes.

Global clustering coefficient: this measure is defined as follows:

$C=\frac{numberofclosedtriplets}{totalnumberoftriplets}(5)$

where the triplet is an ordered set of three nodes that are connected together by either two (in open triplets) or three (in closed triplets) edges.

Note that the average clustering coefficient defined in Eq. 4 and the global clustering coefficient defined in Eq. 5 are not equivalent. The local clustering coefficient reflects the fraction of pairs of neighbors of a given individual node that are connected together, and hence the average value of the tendency of the individual nodes to form a cluster, while the global clustering coefficient reflects the overall structure of the nodes in the network. Although both may exhibit the same behavior in most of the cases, nevertheless those can diverge in some extreme networks (Bollobás and Riordan, 2003; Estrada, 2016) which are out of scope of this paper. In this paper, we study both of the mentioned measures in blockchain networks.

According to the above, a higher clustering coefficient indicates a higher degree of decentralization due to the higher number of closed loops in the graph. Closed loops are trios of nodes that are fully connected together (i.e., to form a triangle). This kind of formation is beneficial for decentralization since the fully connected nodes can directly communicate without an intermediate node. In contrast, low values of clustering coefficient signify that there are less alternative paths in the system, hence, there exist some centralized nodes through which the traffic must necessarily flow.

4.2 Algorithm 1 Erdös-Rény Model Generation Algorithm

4.3 Algorithm 2 Barabási–Albert Model Generation Algorithm

4.4 Performance Analysis

The shortest path d_ij is the path between node i and node j with the least number of steps. The average shortest path length can be obtained from the following equation:

$D=\frac{1}{n\left(n-1\right)}\sum _{i\ne j}{d}_{ij}(6)$

In blockchain networks with a gossip protocol, the average shortest path plays a very important role in the speed of information propagation. Figure 4 demonstrates this fact by comparing three different networks together.

FIGURE 4

FIGURE 4. Importance of the average shortest path: in all of the networks above, the colored node is the initiator node that intends to disseminate its information using a gossip protocol. The initiator node in the network (A) is able to disseminate the information in only one gossip round. In the network (B), the initiator node will need two gossip rounds to disseminate the information. In the network (C) more than two gossip rounds are needed.

5 Verification and Validation

In this section we first verify our complex network generator which can be used for generating P2P networks with a given size and known average number of connections per node as well as specific conditions imposed by the blockchain protocol. Then, we validate our model by comparing with the real Bitcoin network.

5.1 Simulation Model and Verification

We now provide details on our methodology to generate networks which will satisfy the properties required to be considered a BA or ER graph. Our generator is very important for our analysis which requires many networks to be generated and studied in order to understand the impact of several network characteristics on decentralization. We show that the graph generated by our generator, has the same features as expected in theory We verify that our implementation is correct by running over 1,000 trials for each simulation with different initial random seeds. Furthermore, we carefully controlled the generated networks in order to ensure each generated network is unique.

5.1.1 ER Network

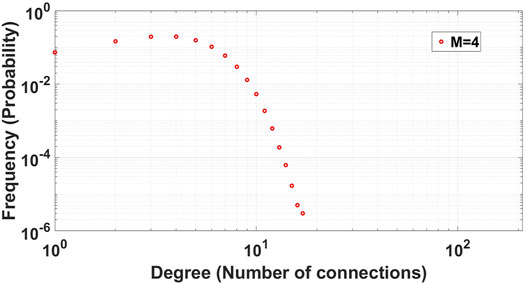
The methodology for generating the ER network is presented in Algorithm 1. This algorithm starts with an initiator node. Then rest of the nodes join the network respectively and get connected to existing nodes with a probability of p. We used this algorithm to generate an ER network of 1,000 nodes with a connection probability of p = 0.004. Regarding these values and Eq. 1, we expect the average degree of the nodes to be around 4 with a Poisson distribution. In fact, the majority of the nodes should have around 4 connections to other nodes. The degree distribution of nodes in 1,000 repeats of this algorithm is depicted in Figure 5, which validates our expectations. As mentioned, this model is suitable for blockchains with no relay networks deployed and nodes periodically refresh their connection pool and forget the initial seeds.

FIGURE 5

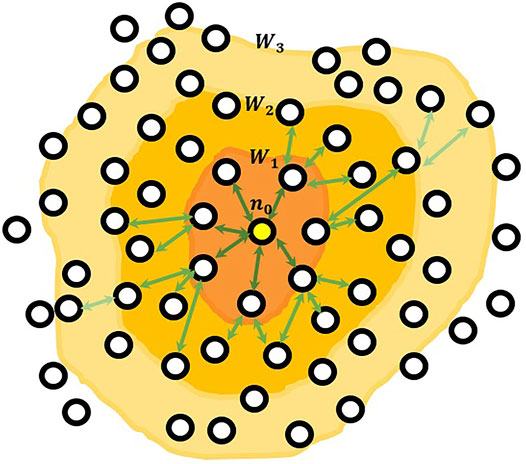
FIGURE 5. Degree distribution of nodes with M and M₀ set to 4 for ER network with a network size of N = 1000

5.1.2 BA Network

Algorithm 2 briefly describes the methodology we used to generate a power-law scale free network. This algorithm starts with M₀ initiator nodes connected together via M₀ − 1 links as a complete graph. Then, the rest of the nodes join the network respectively and one by one and get connected to each of the existing nodes with a probability of p_i as defined in Eq. 2. During the attachments, the algorithm controls the average degree of the nodes in order to keep it around M. In order to ensure that the generated network has the mentioned features, we conducted a simulation with 1,000 nodes. As shown in Figure 6, our generated network is a BA network according to (Barabási and Albert, 1999). This simulation is conducted for M = M₀ = 4. A few nodes appear with a high degree of connections and are labelled as hubs. In our experiments, we expect to observe few hubs around the number of initial seed size. Furthermore, the majority of the nodes have a degree around the average M.

FIGURE 6

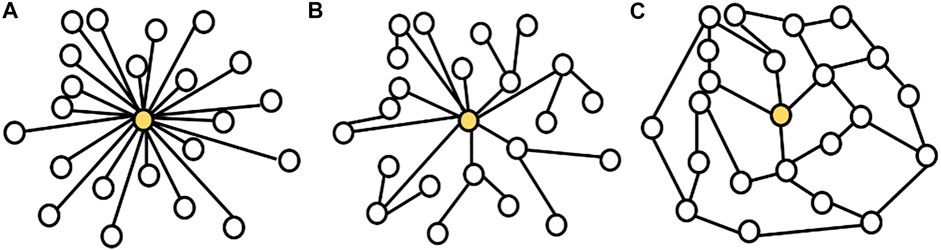
FIGURE 6. Degree distribution of nodes with M and M₀ set to 4 for BA network with a network size of N = 1000

5.2 Model Validation

We validate our generator against a simulation of the Bitcoin network. We set the maximum number of outgoing connections to 8 and the maximum number of incoming connections to 117, in accordance to the Bitcoin protocol. The average degree is set to 32 connections per node (Decker and Wattenhofer, 2013). We conduct the simulation 10,000 nodes, which is the real size of the Bitcoin network¹. A schematic of the generated network can be seen in Figure 7. The output result contains GCC, LCC, and the average shortest path length (ASPL) in each network as presented in Table 1. In order to compare our results with the experimental data mined from the Bitcoin network, we use the concept of dissemination waves (Shahsavari et al., 2020). Block propagation is modeled using a set of subsequent waves, each of which covers one hop in the Bitcoin P2P network. In this model, LBM is modeled as a set of long waves, and HBM is modeled as a set of short waves. Each block transfer in LBM equivalents roughly three block transfer in HBM. This concept is depicted in Figure 8. Our simulation results show the ASPL amounts of 3.05 and 3.22 for ER and BA models respectively. According to results reported in (Shahsavari et al., 2020), 100% of block propagation takes 3.33 waves (i.e., three long waves plus one short wave) which almost the same as BA algorithm results. But the ER algorithm underestimates it to 13 of a wave. Thus, the BA algorithm is a better choice for simulating the Bitcoin network.

FIGURE 7

FIGURE 7. Schematic of a generated network for Bitcoin

TABLE 1

TABLE 1. Simulation results for Bitcoin. Targeted M was 32.

FIGURE 8

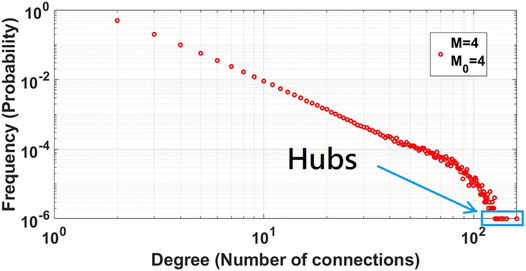
FIGURE 8. Concept of dissemination waves in the Bitcoin network. n₀ is the miner of the block and W₁, W₂, and W₃ are the first, second, and third dissemination waves.

6 Results and Analysis

In this section, we present simulation results and an analysis of network decentralization. We study the impact of several network parameters, such as average number of connections per node, peer selection strategy, and relay network size over the decentralization degree of the network, which is expressed in clustering coefficients.

6.1 Methodology

We conducted extensive simulations in order to study the impact of the network architecture and peer selection strategy including the average number of connections per node on the overall decentralization and speed of the blockchain networks. Simulations are carried out for a network with a size of 10,000 nodes.

6.2 Peer Selection Strategy

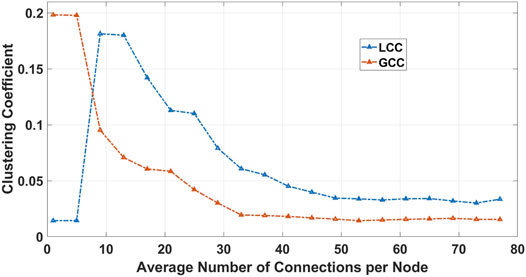
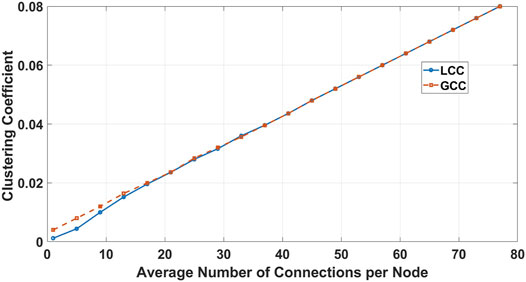
We first study the effect of the peer selection strategy and the average degree of the nodes on the decentralization degree of the blockchain networks. The ER network employs a uniformly random peer selection strategy, while the BA network employs preferential attachment to the relay nodes. The clustering coefficient measures the degree of decentralization of the system, and has a value between 0 and 1. With a value of 0, the network is completely centralized with a tree-like structure. With a value of 1, the network is a complete graph which is fully decentralized, since each node can communicate with any other node without any intermediary.

As seen in Figure 9, both GCC and LCC are decreased in a BA network with the increase of the average number of connection per node and then tend to a constant amount. For M = 32, GCC reaches the minimum amount. The network tends to form fewer closed loops and instead more star-like nodes with a higher degree of connections appear. This situation in the blockchain networks can be referred to the appearance of hub-like nodes such as relay gateways.

FIGURE 9

FIGURE 9. Local and global clustering coefficient of BA network for N = 10 000

In another test, we repeated the experiment above for an ER network. As can be seen in Figure 10, the decentralization degree increases linearly with the increase in the metric p (hence average number of connections per node). However, at the low values of M shown here, the ER networks have a worse absolute decentralization degree than the BA network counterpart at the same value of M. This is because at these low values of M, the ER network is sparsely connected, and thus the paths between nodes contain a lot of redundancy.

FIGURE 10

FIGURE 10. Local and global clustering coefficient of ER network for N = 10 000

At higher values of M, ER networks eventually outperform the BA networks. The reason is that in an ER graph, it tends to a complete graph with an increase of p. This means, in the absence of hubs and relay networks, when every node selects its peers randomly with the same probability, the degree of decentralization will increase.

In light of the above, we claim that relay networks hamper the decentralization degree in blockchain networks with a sufficiently high average number of connections per node.

6.3 Shortest Path Analysis

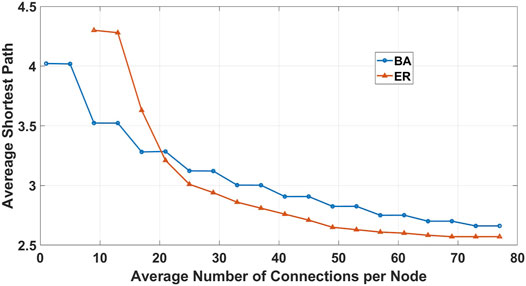
In the next experiment, we study the trade-off between decentralization and performance by analysing the shortest paths length of the ER and BA networks. As depicted in Figure 11 for both of the BA and ER networks, increasing the average degree of the network decreases the average shortest path length. Note that there are no results for M < 8 for an ER network because such networks are not fully connected. Partitioned networks returned amount of infinite for shortest path length and it led the amount of infinite for the average after extensive simulations. However, these networks contain a partition and cannot achieve consensus. Due to the gossiping protocol, a smaller average for the shortest path means faster information propagation. In particular, the result from the BA network experiment indicates that the growing presence of a relay network will improve performance, at the expense of decentralization (as seen in the previous graph Figure 9). In the ER network, increase of the number of connections has limited impact on the average shortest path, as the uniform random peer selection strategy does not efficiently leverage those additional connections to reduce the path length.

FIGURE 11

FIGURE 11. Average shortest path for ER and BA networks for N = 10 000

Note that we assume that all P2P connections have the same bandwidth and geographical distance. However, we can generalize our results by taking into account both additional parameters. Nevertheless, increasing the network speed by increasing the average number of connections per node is not a good idea since it comes at the cost of increased overheads such as traffic overhead in the network (Shahsavari et al., 2020).

6.4 Traffic Overhead Analysis

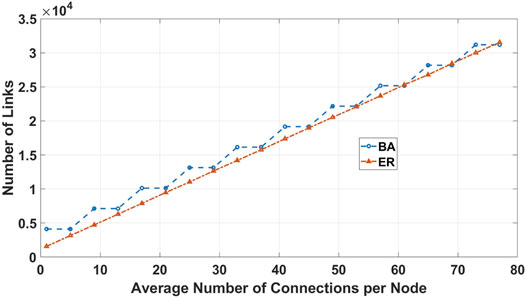
As mentioned in Section 3.2, the total number of links represents the lower bound of the traffic handling overhead. As shown in Figure 12, in both BA and ER networks, the total number of links increases with the increase of the average degree as a step-like and sub-linear function. The overall consequence is that in a BA network, the presence of a growing relay network (i.e., increase in the average degree of the network) will lead to a faster network but it comes at the cost of decentralization and minimum traffic handling overhead. But in an ER network, the trade-off is different as increasing the average number of connections improves the decentralization and network speed but increases the minimum traffic overhead.

FIGURE 12

FIGURE 12. Total number of links (traffic overhead) for N=10 000

6.5 Relay Network Size

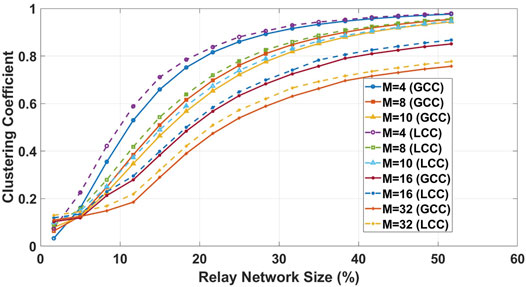
We also wish to understand the effect of the relay network size on the overall decentralization degree of the network. To accomplish this goal, we conducted another set of experiments in which the overall size of the network was kept constant (at N = 10,000), while varying the percentage of nodes participating in the relay network. We repeated the experiment for different amounts of the average degree of the network. The results are depicted in Figure 13. As it can be seen, for a constant network size, when the size of the relay network tends to 50%, the network tends to be fully decentralized. For M = 4, for a relay network size of 15%, the decentralization degree is around 70%. For M = 8 and M = 10, this amount is around 55 and 45% respectively. As well, for M = 16 and M = 32, this amount goes down to around 40 and 30% respectively. As a clear consequence, for a constant size of a blockchain network, a bigger percentage of the nodes participating as a relay node means a more decentralized network that is fairer.

FIGURE 13

FIGURE 13. Local and global clustering coefficient for a BA network with N = 10 000

7 Conclusion and Future Works

In this paper, we presented an analytical methodology for quantifying the decentralization degree in blockchain networks based on the peer selection strategy. To accomplish this, we implemented a complex blockchain network generator using two graph models: Barabási–Albert and Erdös-Rény. We analyzed and compared decentralization, average shortest path as an indicator of the network speed, and the number of links as an indicator of minimum traffic handling overhead in blockchain networks with different architectures through extensive simulations. The obtained results disclosed that the decentralization degree of the network extremely depends on the topology and the architecture of the network. We have proven that the use of hubs and relay networks drastically reduces the decentralization degree of the network. Although increasing the number of connections per node can decrease the average shortest path and consequently decrease the block propagation delay, nevertheless in networks with deployed relay nodes it comes at cost of a reduced amount of decentralization.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

This manuscript is prepared by YS as a Ph.D. student And He is the first author. KZ is the Supervisor of this research and he is the second author. As well, CT is the Co-supervisor of the research and third author. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹https://bitnodes.io/dashboard/?days=1825, Dec. 2021.

References

Androulaki, E., Barger, A., Bortnikov, V., Cachin, C., Christidis, K., De Caro, A., et al. (2018). “Hyperledger Fabric: a Distributed Operating System for Permissioned Blockchains,” in Proceedings of the Thirteenth EuroSys Conference. New York, NY: Association for Computing Machinery, 1–15.

Google Scholar

Atzei, N., Bartoletti, M., and Cimoli, T. (2017). “A Survey of Attacks on Ethereum Smart Contracts (Sok),” in International Conference on Principles of Security and Trust (Springer-Verlag Berlin, Heidelberg: Springer), 164–186. doi:10.1007/978-3-662-54455-6_8

CrossRef Full Text | Google Scholar

Atzori, M. (2015). Blockchain Technology and Decentralized Governance: Is the State Still Necessary?” Available at SSRN 2709713.

Google Scholar

Barabási, A. L., and Albert, R. (1999). Emergence of Scaling in Random Networks. science 286 (5439), 509–512. doi:10.1126/science.286.5439.509

PubMed Abstract | CrossRef Full Text | Google Scholar

Basu, S., Eyal, I., and Sirer, E. G. (2019). Falcon. Available at: https://www.falcon-net.org (accessed 05 26, 2019).

Google Scholar

Beikverdi, A., and Song, J. (2015). Trend of Centralization in Bitcoin’s Distributed Network in 2015 IEEE/ACIS 16th International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD), Takamatsu, Japan, Jun 1-3, 2015 (IEEE), 1–6.

Bollobás, B., and Riordan, O. M. (2003). “Mathematical Results on Scale-free Random Graphs,” in Handbook of Graphs and Networks: From the Genome to the Internet. Gemany: Wiley, 1–34.

Google Scholar

Brandenburger, M., Cachin, C., Kapitza, R., and Sorniotti, A. (2018). Blockchain and Trusted Computing: Problems, Pitfalls, and a Solution for Hyperledger Fabric,” arXiv preprint arXiv:1805.08541.

Google Scholar

Cai, W., Wang, Z., Ernst, J. B., Hong, Z., Feng, C., and Leung, V. C. M. (2018). Decentralized Applications: The Blockchain-Empowered Software System. IEEE Access 6, 53019–53033. doi:10.1109/access.2018.2870644

CrossRef Full Text | Google Scholar

Coralo, M. (2019). Bitcoin FIBRE Network. Available at: http://bitcoinfibre.org/public-network.html (Accessed 06 16, 2019).

Google Scholar

Chu, S., and Wang, S. (2018). The Curses of Blockchain Decentralization. arXiv preprint arXiv:1810.02937.

Google Scholar

Croman, K., Decker, C., Eyal, I., Gencer, A. E., Juels, A., Kosba, A., et al. (2016). “On Scaling Decentralized Blockchains,” in International Conference on Financial Cryptography and Data Security (Springer), 106–125. doi:10.1007/978-3-662-53357-4_8

CrossRef Full Text | Google Scholar

Corallo, M. (2016). Bip 152: Compact Block Relay,” See https://github.com/bitcoin/bips/blob/master/bip-0152.mediawiki.

Google Scholar

Decker, C., and Wattenhofer, R. (2013). “Information Propagation in the Bitcoin Network,” in IEEE P2P 2013 Proceedings, Trento, Italy (IEEE), 1–10. doi:10.1109/p2p.2013.6688704

CrossRef Full Text | Google Scholar

Erdős, P., and Rényi, A. (1959). On Random Graphs I. Publicationes Mathematicae (Debrecen) 6, 290–297.

Google Scholar

Estrada, E. (2016). When Local and Global Clustering of Networks Diverge. Linear Algebra its Appl. 488, 249–263. doi:10.1016/j.laa.2015.09.048

CrossRef Full Text | Google Scholar

Eyal, I., and Sirer, E. G. (2014). “Majority Is Not Enough: Bitcoin Mining Is Vulnerable,” in International Conference on Financial Cryptography and Data Security (Springer), 436–454. doi:10.1007/978-3-662-45472-5_28

CrossRef Full Text | Google Scholar

Fadhil, M., Owenson, G., and Adda, M. (2017). “Locality Based Approach to Improve Propagation Delay on the Bitcoin Peer-To-Peer Network,” in 2017 IFIP/IEEE Symposium on Integrated Network and Service Management (IM), Lisbon (IEEE), 556–559. doi:10.23919/inm.2017.7987328

CrossRef Full Text | Google Scholar

Gencer, A. E., Basu, S., Eyal, I., Van Renesse, R., and Sirer, E. G. (2018). “Decentralization in Bitcoin and Ethereum Networks,” in International Conference on Financial Cryptography and Data Security (Springer), 439–457. doi:10.1007/978-3-662-58387-6_24

CrossRef Full Text | Google Scholar

Gueta, G. G., Abraham, I., Grossman, S., Malkhi, D., Pinkas, B., Reiter, M., et al. (2019). “Sbft: a Scalable and Decentralized Trust Infrastructure,” in 2019 49th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN), Portland United States, Jun 24-27, 2019 (IEEE), 568–580. doi:10.1109/dsn.2019.00063

CrossRef Full Text | Google Scholar

Klarman, U., Basu, S., Kuzmanovic, A., and Sirer, E. G. (2018). “Bloxroute: A Scalable Trustless Blockchain Distribution Network Whitepaper.”

Google Scholar

Kwon, Y., Liu, J., Kim, M., Song, D., and Kim, Y. (2019). “Impossibility of Full Decentralization in Permissionless Blockchains,” in. Proceedings of the 1st ACM Conference on Advances in Financial Technologies. New York, NY: Association for Computing Machinery.

CrossRef Full Text | Google Scholar

Lange, F., Ballet, G., and Toulme, A. (2016). Ethereum Wire Protocol. See https://github.com/ethereum/devp2p/blob/master/caps/eth.md.

Google Scholar

Li, C., and Palanisamy, B. (2020). “Comparison of Decentralization in Dpos and Pow Blockchains,” in International Conference on Blockchain (Springer), 18–32. doi:10.1007/978-3-030-59638-5_2

CrossRef Full Text | Google Scholar

Nakamoto, S. (2009). Bitcoin: A Peer-To-Peer Electronic Cash System. [Online]. Available: http://www.bitcoin.org/bitcoin.pdf.

Google Scholar

Otsuki, K., Aoki, Y., Banno, R., and Shudo, K. (2019). “Effects of a Simple Relay Network on the Bitcoin Network,” in Proceedings of the Asian Internet Engineering Conference. New York, NY: Association for Computing Machinery, 41–46. doi:10.1145/3340422.3343640

CrossRef Full Text | Google Scholar

Pinar Ozisik, A., Andresen, G., Bissias, G., Houmansadr, A., and Levine, B. (2017). “Graphene: A New Protocol for Block Propagation Using Set Reconciliation,” in Data Privacy Management, Cryptocurrencies and Blockchain Technology (Springer), 420–428. doi:10.1007/978-3-319-67816-0_24

CrossRef Full Text | Google Scholar

Puthal, D., Malik, N., Mohanty, S. P., Kougianos, E., and Yang, C. (2018). The Blockchain as a Decentralized Security Framework [future Directions]. IEEE Consumer Electron. Mag. 7 (2), 18–21. doi:10.1109/mce.2017.2776459

CrossRef Full Text | Google Scholar

Satoshi Client Node Discovery (2021). Talk:Satoshi Client Node Discovery. Available at: https://en.bitcoin.it/wiki/Satoshi_Client_Node_Discovery (accessed 03 30, 2021).

Google Scholar

Shahsavari, Y., Zhang, K., and Talhi, C. (2020). “A Theoretical Model for Block Propagation Analysis in Bitcoin Network,” in IEEE Transactions on Engineering ManagementIEEE. doi:10.1109/tem.2020.2989170

CrossRef Full Text | Google Scholar

Swan, M. (2015). Blockchain Thinking : The Brain as a Decentralized Autonomous Corporation [Commentary]. IEEE Technol. Soc. Mag. 34 (4), 41–52. doi:10.1109/mts.2015.2494358

CrossRef Full Text | Google Scholar

Tschorsch, F., and Scheuermann, B. (2016). Bitcoin and beyond: A Technical Survey on Decentralized Digital Currencies. IEEE Commun. Surv. Tutorials 18 (3), 2084–2123. doi:10.1109/comst.2016.2535718

CrossRef Full Text | Google Scholar

Van Der Hofstad, R. (2016). Random Graphs and Complex Networks, Vol. 1. , Cambridge: Cambridge University Press.

Google Scholar

Watts, D. J., and Strogatz, S. H. (1998). Collective Dynamics of 'small-World' Networks. nature 393 (6684), 440–442. doi:10.1038/30918

PubMed Abstract | CrossRef Full Text | Google Scholar

Wood, D. D. (2014). Ethereum: A Secure Decentralised Generalised Transaction Ledger, 151, 1–32.

Google Scholar

Wu, K., Peng, B., Xie, H., and Huang, Z. (2019). “An Information Entropy Method to Quantify the Degrees of Decentralization for Blockchain Systems,” “ in 2019 IEEE 9th International Conference on Electronics Information and Emergency Communication (ICEIEC), Beijing, China, Jul 12-14, 2019 (IEEE). doi:10.1109/iceiec.2019.8784631

CrossRef Full Text | Google Scholar

Yang, L., Bagaria, V., Wang, G., Alizadeh, M., Tse, D., Fanti, G., et al. (2019). Prism: Scaling Bitcoin by 10,000 X,” arXiv preprint arXiv:1909.11261.

Google Scholar

Yu, H., Nikolic, I., Hou, R., and Saxena, P. (2018). Ohie: Blockchain Scaling Made Simple. arXiv preprint arXiv:1811.12628.

Google Scholar