- 1Kellogg School of Management, Northwestern University, Evanston, IL, United States
- 2Columbia Business School, Columbia University, New York, NY, United States
- 3Weizmann Institute of Science, Rehovot, Israel
Human decision making is often prone to biases and irrationality. Group decisions add dynamic interactions that further complicate the choice process and frequently result in outcomes that are suboptimal for both the individual and the collective. We show that an implementation of a Blockchain protocol improves individuals’ decision strategies and increases the alignment between desires and outcomes. The Blockchain protocol affords (1) a distributed decision, (2) the ability to iterate repeatedly over a choice, (3) the use of feedback and corrective inputs, and (4) the quantification of intrinsic choice attributes (i.e., greed, desire for fairness, etc.). We test our protocol’s performance in the context of the Public Goods Game. The game, a generalized version of the Prisoner’s Dilemma, allows players to maximize their own gain or act in ways that benefit the collective. Empirical evidence shows that participants’ cooperation in the game typically decreases once a single player favors their own interest at the expense of others’. In our Blockchain implementation, “smart contracts” are used to safeguard individuals against losses and, consequently, encourage contributions to the public good. Across different tested simulations, the Blockchain protocol increases both the overall trust among the participants and their profits. Agents decision strategies remain flexible while they act as each other’s source of accountability (which can be seen as formalized distributed “Ulysses contract”). To highlight the contribution of our protocol to society at large we incorporated an entity that represents the public good. This benevolent independent beneficiary of the contributions of all participants (e.g., a charity organization or a tax system) maximized its payoffs when the Blockchain protocol was implemented. We provide a formalized implementation of the Blockchain protocol and discuss potential applications that could benefit society by more accurately capturing individuals’ preferences. For example, the protocol could help maximize profits in groups, facilitate democratic election that better reflect the public opinion, or enable group decision in circumstances where a balance between anonymity, diverse opinions, personal preferences and loss-aversion play a role.
1. Introduction
Among the fundamental assumptions of traditional economic theory is the belief that individuals act to maximize the utility they receive from the decisions they make (Smith, 1776). Any deviation from that behavior is considered irrational. However, contrary to the traditional economic theory, years of research in behavioral economics have shown that people frequently behave irrationally (Thomas, 1993; Ariely, 2008). Examples for such irrational behaviors are seen in marketing, healthcare, dating, the legal system, and numerous other domains (Levy et al., 2010; Cerf et al., 2015; Mentovich et al., 2016).
One explanation for the reason individuals deviate from an optimal, utility maximizing, economic decision making model is the bias that emerges from psychological and sociological attributes of the decision. For example, individuals are likely to be influenced by the decisions of others around them, adhere to social norms, or conform to with a group majority despite their better judgment of a certain decision (Asch and Guetzkow, 1951; Cialdini and Goldstein, 2004). Whether a person manages to save money or eat healthily, for example, is not only determined by their mere rationality but also by the decisions made by those around them (Christakis and Fowler, 2007). Furthermore, people’s decisions are typically influenced by context, by their emotional state, or by situational factors. For example, people are more easily persuaded to behave in ways that violate their normal personality traits when they are in a good mood (Bless et al., 2001), or, on online dating platforms, are more likely to display preference toward users whose name sound like theirs, despite stating explicitly that their decisions were not biased (Levy et al., 2010).
Decision making is particularly prone to group influence if the decisions of individuals interdependently impact the outcomes of the entire group. Such decisions include elections, the division of shared resources, or contributions to public goods. Research has shown that individuals are more altruistic when cooperation benefits the public good rather than other individuals (Gächter et al., 2017). This is true for resources that are socioeconomic (i.e., a shared financial resources; Levin, 2014), ecological (i.e., climate change; Ostrom, 2010), or even at the level of micro-organisms (Nadell et al., 2008). Group effects such as spite, competitiveness, retribution, alongside compassion, prosociality and altruism have all been shown to alter the magnitude of adherence to norms in the context of decisions that cater toward a public good (Levin, 2014). Finally the likelihood of altruistic behavior (i.e., higher contributions to public goods) is Increased when decisions are not made Individually but as a team (Coxb and Stoddard, 2016). Altogether, prior works point to a delicate balance between the individual’s self-interest of maximizing their utility and their desire to adhere to social norms that signal cooperation.
A key component that influences individual decision making in a broader social context is trust. Individuals establish trust in order to form agreements, navigate personal relationships, create alliances, and maintain functioning societies (Gambetta, 1988; Fukuyama, 1995; Jones and George, 1998; Leana and van Buren, 1999). For example, numerous sovereign institutes rely on citizens’ trust in the governing body to enable a collective pooling of resources to aid the community as a whole. Governments collect taxes and use those taxes to build roads, subsidize healthcare or fund education. The citizens contribute their income to the collective pool via the taxation system with an implied trust that the government will make use of the funds to help the community. Similarly, people pay insurance companies regularly with the belief that if they encounter grave circumstances those insurance companies will use the money collected to pay for their needs. The core idea behind such systems is that social life can be managed more efficiently when resources are pooled rather than exploited individually.
In line with this proposition, empirical evidence shows that decision making at various social structures (e.g., companies or countries) becomes more efficient when these structures show greater levels of trust among individuals (e.g., employees, or citizens). For example, research has demonstrated that high levels of trust between business partners or firms is associated with a more pronounced focus on long-term relationships, higher levels of cooperation, and higher relationship satisfaction (Fukuyama, 1995; Coxb and Stoddard, 2016). Likewise, higher levels of trust on a country-level are related to a higher likelihood of citizens complying with the country’s laws (Jones, 2015), higher levels of prosociality (Zak and Knack, 2001), as well as higher GDP (Bjørnskov, 2012).
Contrary, the absence of trust can severely undermine the quality of decision making. Individuals in countries where the level of trust in the sovereign institutions is low are more likely to make decisions that are detrimental to their own long-term wellbeing (Jachimowicz et al., 2017). For example, if people do not trust that the money they deposited in a bank will be available to them in the future then they are unlikely to deposit it in the first place. This, in turn, leads to an increased likelihood that they will spend the money on impulsive immediate gratification rather than long-term goals, which often leads to shortage of income in dire times.
Despite the benefits of trust for both individuals and society at large, empirical evidence shows that trust is fragile and easily deteriorates (Schweitzer et al., 2006). All it takes is one single instance in which trust has been broken for individuals to make generalizations about the trustworthiness of others. At the same time, once trust is broken, it is difficult – and sometimes impossible – to repair (Johnson et al., 2001; Schweitzer et al., 2006; Smith and Freyd, 2014). Countries that suffer from systemic corruption tend to remain corrupt without intervention (Bjørnskov, 2012; Jachimowicz et al., 2017), negotiations that uncover a deceptive party often lead to retribution and a failure to reach an agreement (Johnson et al., 2001; Schweitzer et al., 2006), and couples who experience a betrayal in the form of cheating frequently end up in separation (Perel, 2017).
This led behavioral economists and researchers in psychology to suggest various scenarios that can model breakage of trust – allowing for the study of its antecedents and consequences (Gunnthorsdottir et al., 2007). A number of those scenarios involve a game played over multiple rounds [e.g., a multiple-iteration Prisoners Dilemma game, the Trust Game (Berg et al., 1995), or the Public Goods game; Ledyard, 1995; Hauert and Szabo, 2003; Camerer and Fehr, 2004; Levitt and List, 2007]. Typically, those games have two conceptual states of equilibria: complete trust and complete distrust (Hauert and Szabo, 2003). Empirical evidence, however, shows that while players typically initiate their behavior with complete trust (i.e., do not defect in the Prisoners Dilemma game on the first iteration), the games tend to converge toward a state of complete distrust (Levitt and List, 2007; McGinty and Milam, 2013). This is because a breakage of trust frequently leads to a loss for the players who were suffering the consequences. As a quid-pro-quo those players tend to become more cautious and less trusting in future rounds, which, in turn, leads the remaining players to become cautious too. The resulting decay toward the equilibrium of complete distrust is rapid and nearly impossible to reverse.
To withstand the challenges that emerge from lack of trust various protocols have been suggested to enforce a collective rule, to prevent trust breakage or to minimize the likelihood of dishonesty (Buterin et al., 2019). Those protocols rely on mathematics, cryptography and anonymized majority-rule to enable complete accountability by all participants. That is, each player acts as other players’ checks-and-balances and is able to call-out departure from the norm rapidly. One such protocol is Blockchain (Tapscott and Tapscott, 2016).
1.1. Blockchain
Blockchain is a protocol by which individuals are able to use an anonymized ledger to code, sign, and timestamp decisions. The individuals can generate contracts that incorporate a set of conditions which can revoke and nullify a commitment based on pre-determined criteria (Tapscott and Tapscott, 2016). For example, person A can state publicly within a shared ledger that they commit to giving person B an amount of money only if person C gives them a sum of money prior. All parties code the contract and honor it only if evidence for all transactions occur and are shared across the ledger. As such, Blockchain can function as mechanism by which all parties act as the others’ regulators. Consequently, Blockchain protocols can be used to improve the collective outcomes of all individual decision makers.
As a simple illustration of a Blockchain protocol, one can imagine the baggage claim belts at airports. While no single entity checks that arriving passengers only claim their own suitcase and not others’, the fact that all suitcases arrive together and that all suitcase-owners are looking for their personal belongings, effectively generates a way by which every person claims only their own luggage.
While Blockchain protocols have been used primarily in the financial domain (e.g., in the form of cryptocurrencies) the effective use of the protocol can go beyond the monetary use (Camerer and Fehr, 2004). Indeed, some groups have formed alliances that rely on Blockchain to enable collective decision making in the form of voting, supply-chain management, transportation management, and more (Hauert and Szabo, 2003).
Here we show an implementation of Blockchain protocol to allow multiple players in a generalized version of the Prisoner’s Dilemma, known as the “The Public Goods” Game (PG) (Camerer and Fehr, 2004). We first replicate the classical behavioral results of the PG game using a computer simulation. That is, we show that the game deteriorates to a state of complete and permanent distrust in nearly all conditions. Following, we test two hypotheses. First, we propose that the inclusion of a Blockchain protocol in the PG enables a recovery of trust after a violation by a defector (Hypothesis 1). Second, we propose that the Blockchain implementation yields a higher gain for a third-party entity that represents the public good (Hypothesis 2).
Across multiple simulations, we demonstrate that an implementation of the anonymous Blockchain protocol enables agents to regain trust in one another, generate higher payoffs, and increase the overall contribution to a collective pool. Additionally, we show that optimizing the Blockchain model – while allowing individuals to maximize their own interests – yields an increased reward for all agents as well as an independent 3rd-party beneficiary. That is, adding a representation of individuals’ personal preferences, while keeping within the reigns of the trust protocol, leads to an increase in trust even following a momentary betrayal. We suggest that the protocol effectively allows for a democratic decision making process that maximizes all individuals benefit while contributing to the public goods in an optimal fashion.
2. Materials and Methods
2.1. The Public Goods Game
To illustrate the conditions of our work, we first describe the protocol of the PG game. The PG game is typically portrayed in the context of a scenario where n players are working in a village and receive equal daily wages (w) for their work, every morning. For example, each of 10 players may receive a wage of $10. The total amount earned by all the players is then n x w (10 x $10 = $100).
Each player can decide, each morning, whether to keep their income, or to put it in a shared account (e.g., a collective savings account with fixed interest, or a bond that yields a static increase). Over the course of the day the shared account multiplies by a fixed amount (e.g., 600%). Once the day is over, the money in the shared account is divided equally among all players. Importantly, all players receive their dividend regardless of whether they contributed to the public good or not. The same procedure is repeated daily, and each player is free to decide every day whether or not to contribute their wages to the shared account. In the standard PG game protocol, all players can only contribute the full amount or nothing, and the decision is anonymous such that no player known who may have betrayed. This scenario is often seen as analogous to a taxation system, a shared mutual fund or pension plan, an insurance, or other systems that collect money from a group and use it to promote everyone interests equally.
In the outlined scenario (see Appendix 1 for complete breakdown of the game), if all players contribute their wages the shared account will end up having $600 ($100 × 600%) at the end of the day, and each of the 10 players will receive a cut of $60. This condition is termed “complete trust.” Complete trust is a state of equilibrium where players have no immediate incentive to change the status quo and would benefit from continuous contribution to the shared account. However, each player may increase their payoff if they chose to betray the public good. This can happen by electing to independently not share their wages with the remaining players. For example, in a scenario where one player chooses to not share their wages only nine players will contribute their wages and the shared account will hold 9 x $10 = $90. Multiplied by the interest, the daily total will be $540. This money would then be equally split among all the players, including the one who did not contribute. Each of the nine contributing players will receive $54 while the one player that betrayed the community would end up with $64 ($10 of the wages they kept, along with $54 from the joint contributions of everybody else).
Similar versions of the game have been developed, which highlight specific attributes of the overall experience. A version of the game with only a single iteration focuses on the behavior of individuals without the opportunity to engage in norm-enforcement and long-term planning (Gunnthorsdottir et al., 2007). Other versions force players to play without the veil of anonymity, thereby forcing transparent disclosures and group dynamics effects (i.e., emergence of group leaders, or increase in cooperation due to public shaming of defectors) (Rege and Telle, 2004). Other versions allow for alteration of the contributed amount by agents, asymmetry in the dividend yielded, asymmetry in punishment for defection, sequential versus simultaneous contributions, and the reframing of the public good’s meaning (i.e., instead of focusing on financial outcomes, the public goods can be seen as a climate outcome or a shared water resource) (Willinger and Ziegelmeyer, 1999; Andreoni et al., 2003; Sefton et al., 2007; Rand et al., 2009; Gächter et al., 2010). While the plurality of the works mentioned overwhelmingly replicate the results pertaining to decay in trust and cooperation, some studies have shown that under various conditions (i.e., larger groups of players) trust and cooperation may be restored after a decay (Isaac et al., 1994). This suggests that some variables of the game could be tuned to alter the behavior of individuals for prosocial outcomes. Those works, however, are still the minority. Finally, similar games such as the single/repeated-trials Prisoner’s Dilemma and the Trust Game have focused primarily on two-player interactions and show how an equilibrium of lack of cooperation and lack of trust are the more frequent outcome under most experimental conditions (Berg et al., 1995) [despite some differences in interpretation of the generalization of those games from two players to n players. See Barcelo and Capraro (2015) for discussion]. Recent works in neuroscience have investigated potential neural drivers of the decay in trust [i.e., in the context of peer influence (Van Hoorn et al., 2016), political outcomes (Barnett and Cerf, 2018) and even the view of public goods entities as human or not (Mentovich and Cerf, 2014)].
2.1.1. Additional Third-Party Beneficiary
We implemented a modified version of the PG game (see Table 1 for experimental parameters) with one additional element to amplify the fact that a shared account can be seen as a public good. We added an independent, benevolent entity that only stands to gain from the contribution of all players without the ability to hurt or be hurt by anyone. That is, in addition to dividing the total amount generated by the shared account among all the players we introduced an additional third-party beneficiary that receives a cut from the total amount without contributing. This third-party can be seen as representing a taxation body, a charity receiving donations, or fund manager receiving fees for their clever investments that yield the daily interests. We term the third-party beneficiary: Charity/3rd-Party Organization (C-3PO).
In our implementation the C-3PO receives 1/6 of the funds generated in each round (which is equal to the amount contributions by all players in the round). The remaining 5/6 of the funds are equally distributed among all n players. The game setup is illustrated in Figure 1. The main focus of our analyses will be the amount the C-3PO generates from the game after N consecutive iterations. This is a proxy of the overall utility of all players and the ability of the group to maximize profits.
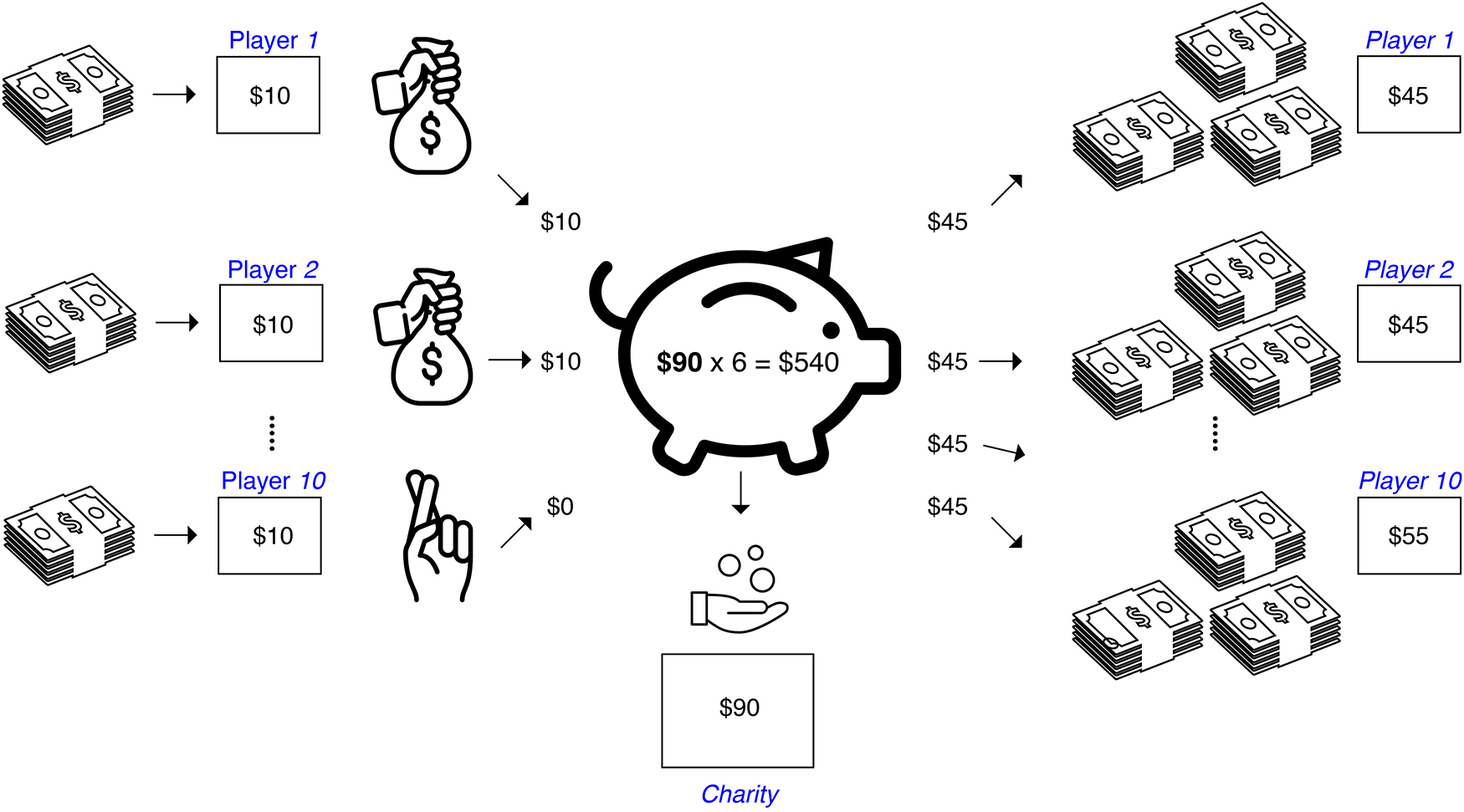
Figure 1. Illustration of the Iterative Public Goods Game with a Charity/3rd-Party Organization. Left: agents either contribute their wages into the shared account, or anonymously defect. The amount in the shared account is multiplied during the day. Center: A cut of the total yield is donated to Charity (/3rd-Party), and the rest (right) is divided equally among all players (including the defecting ones).
We define the game properties “parameters” and keep those constant (see Table 1) across all simulations.
To test the effect of the Blockchain protocol on the system and demonstrate that the performance is improved irrespective of the game conditions we test various experimental variables (Table 2). Our performance measures are the amount of money earned by the C-3PO at the end of N iterations and the average trust among all players. Specifically, we test the increase in earnings following the introduction of the Blockchain protocol and the optimal conditions that enable maximum increase in trust. All the codes for the simulations are available online at http://www.morancerf.com/publications.
2.1.2. Nomenclature
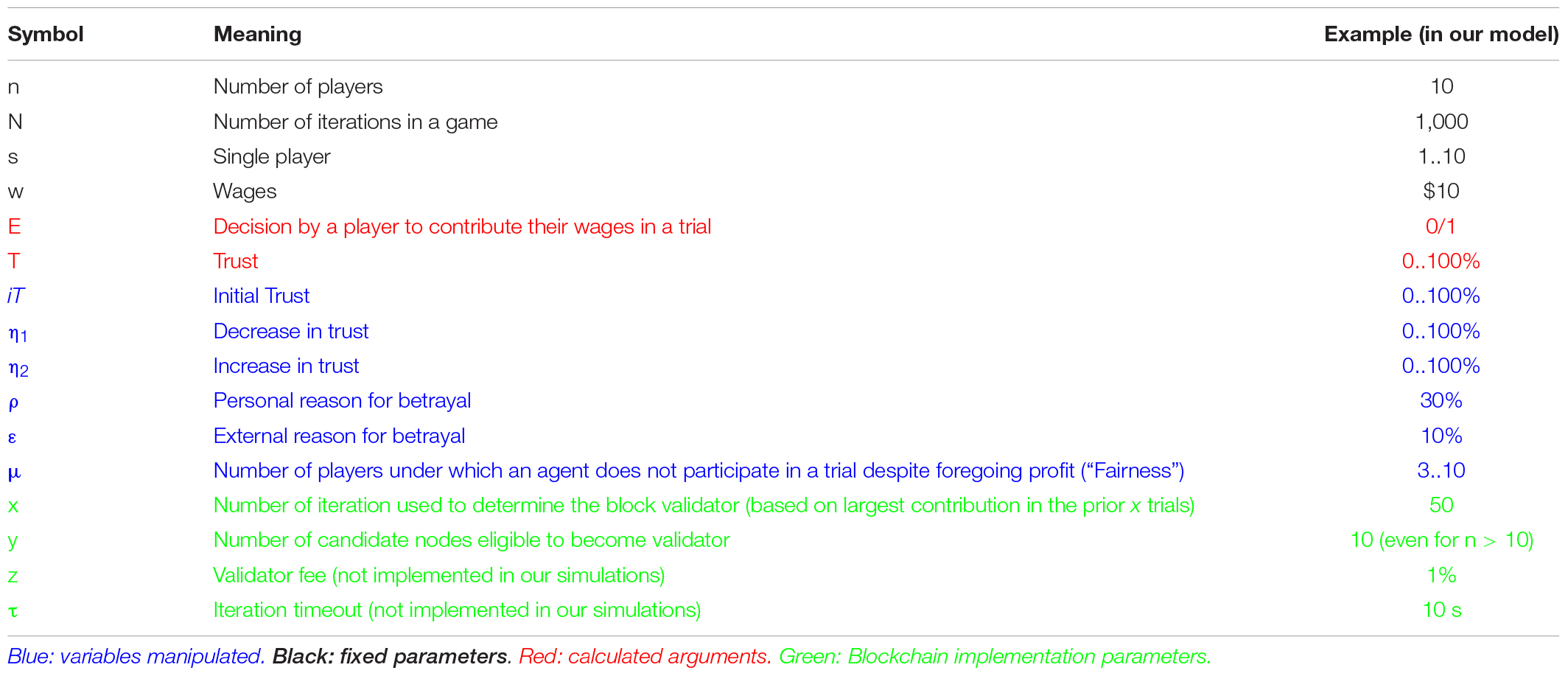
For ease of reading we used the following nomenclature throughout the work. For a complete list of all variables/parameters symbols used in the study, see Appendix 2.
- Simulation: one of four conditions we manipulate (i.e., Blockchain condition, Realistic condition).
- Game: a single N-iterations (i.e., 1,000 iteration) test with a fixed set of variables.
- Parameters: fixed arguments used in this work (i.e., number of participants).
- Variables: manipulated arguments tested in this work.
- Participants/players/subjects/people/persons: human individuals in a game.
- Agents: simulation/modeled individuals in a game.
- Nodes: individual clients in the Blockchain implementation.
- Trial/iteration/round: a single step, t, out of N, in each game.
2.2. Experimental Variables in the Simulations
We manipulated multiple decision making parameters to simulate how different levels of trust and personal variables impact the collective outcome (measured, primarily, as the dividend for the C-3PO) after N iterations of the adapted PG game in both a regular condition as well as three Blockchain conditions.
Recent empirical work investigating the behavior of agents in PG games identified four factors that contribute to an individual’s decision making in the game: self-interest, the behavior of others, the reaction to rewards, and the reaction to punishment (Dong et al., 2016). Of those four, financial rewards and punishments show the weakest effects. Consequently, we incorporated into our model elements that correspond to the following drivers of a decision: self-interest, group dynamics (the behavior of others), and external circumstances.
2.2.1. Trust
The main experimental variable we manipulated was individuals’ trust (T). Agents’ initial level of trust was set to a number ranging from 100% (complete trust) to 0% (no trust).
In each iteration an agent’s level of trust was calculated as a function of two variables:
(1) η1,s - the level of decay in trust by agent s in response to betrayal by other agents in the previous iteration (t-1).
(2) η2,s - the level of increase in trust in response to an increase of collective trust from trial t-2 to t-1.
The second variable, η2, corresponds to an increase in trust by an individual in response to a gradual creation of trust in the group. Therefore, as agents see that others are contributing to the game, they, too, will update their priors with respect to the group’s likelihood to trust one another.
Additionally, we varied the initial level of trust each agent had as the game started (iT). Effectively, an agent’s trust in each iteration, T, is modeled as a Bayesian Markov chain where each iteration depends on the previous one, starting with iT.
Notably, although we separated the decrease in group trust following a betrayal from the increase in group trust following a collective renewed belief in the system, the two variables can be observed as a single argument labeled as “change in trust” (η) corresponding to the sum of the two. This is because at any given trial either a decrease or increase in trust occurs – but not both. We elected to use two variables in our model since: (1) prior experimental data were shown to have dynamic ratio between people’s decrease in trust and increase in trust, and (2) because this closely aligns with the literature’s view of trust as a process that involves decrease and increase that are not necessarily identical in magnitude. Based on empirical evidence suggesting that individuals show a higher decline in trust after a betrayal than an incline after trust recovery (ηs,1 ≫ ηs,2) we modeled the parameters to reflect these conditions.
Trust in each iteration can therefore be operationalized as:
where, T1 = iT, η = η2∨η1 and t is the iteration number ∈ [1,1000]
In our simulations we varied the values of η1 and η2 from 95% (nearly complete trust) to 15% in decrement of 5%.
In each game we allocated the three variables to each of the n agents using a random distribution centered around the value, with standard deviation of 1%. That is, if in a certain game iT was set to 95%, then all n agents’ initial trust values were assigned from a normal distribution with mean 95% and standard-deviation 1%.
This decision simplifies the computations but is not mandated by the model. More complicated models can use different distributions thereby increasing the model’s degrees of freedom. Notably, given the large number of iterations compared to the number of agents starting with such distributions typically does not affect the results. Multiple tests using the same random selections should converge to the same trust values.
To give the reader an intuition about the effects of η1/η2 ratios on the trust outcome we illustrate three combination of values (Figure 2). When η1 is notably bigger than η2 the decrease following a betrayal is large, dropping the trust altogether to 0 rapidly. Lower levels of initial trust suggest a higher likelihood of betrayal by an agent, and therefore a faster decrease in trust as well. Effectively, the lower the initial trust, the faster the game will converge to complete distrust. Games that end with total distrust make for the plurality of empirical data (Ledyard, 1995; Hauert and Szabo, 2003; Camerer and Fehr, 2004). We, therefore, deem this condition the “realistic” scenario.
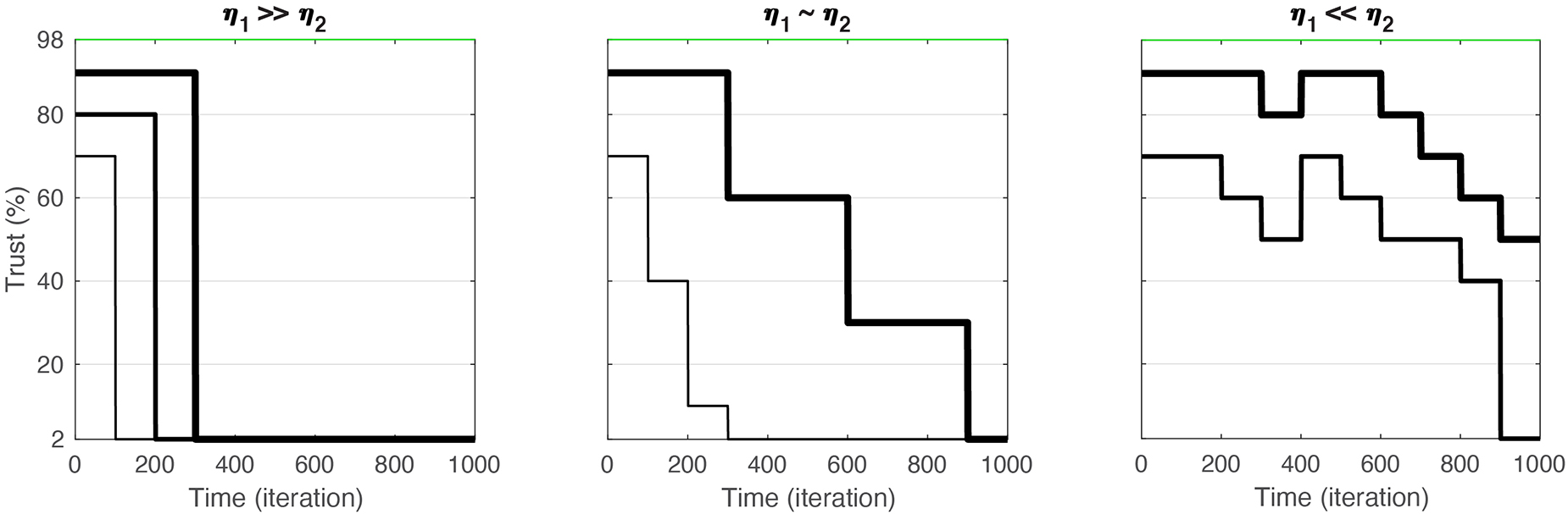
Figure 2. Illustration of three scenarions depicting ratios of η1/η2 in the PG game. While the three conditions show different styles of operation, “realistic” (left), “reciprocal” (middle), and “lovers” (right), all scenarios typically ultimately converge to a state of complete distrust. This is because of the disproportional opportunity for η1 (decrease in trust) to occur compared to η2 (increase in trust). The initial trust (iT) simply determines the speed of decay. Lower values of iT lead to faster convergence to distrust. Lines illustrate different trust trajectories across games.
When η1 is proportional to η2 trust converges to 0 as well. This is because the effect of even a single betrayal is a decrease in trust, whereas increase in trust requires multiple participants to elect to contribute their wages. Therefore, not only do games with η1 > η2 converge to complete distrust, but also games with similar sized η values. Same-sized η values games take more iterations to converge to 0. We name the scenario depicted in η1∼η2 games the “reciprocal” scenario.
Finally, when participants are playing in conditions where η2 is notably bigger than η1 they manifest a scenario where they do not see betrayal as a devastating behavior or a violation of trust. Participants are therefore likely to recover trust irrespective of prior trials. This scenario is uncommon in most situations of human relationship and reflect a uniquely psychological characteristic. This may be attributed to “lovers” who choose to confide in their partner despite momentary breakage of trust. This Ghandi/Jesus-like approach of “turning the other cheek” is not observed frequently in empirical data from the PG game. However, we can imagine situations by which it is the norm, primarily in places where trust is so fundamental and strong that even a momentary failure is seen as an anomaly. Nevertheless, even in those conditions, over time, the overall trust is likely to converge to a state of complete distrust, albeit over numerous iterations and while potentially demonstrating momentary increases in trust. The reason this scenario, too, converges to 0 is similar to reason in the “reciprocal” scenario: the number of opportunities for a betrayal to occur is approximately n times higher than the number of opportunities for random honesty of multiple players. Therefore, the small decreases in trust happen more frequently and are unlikely to be balanced by the infrequent increases in trust unless the ratio of η1/η2 is greater than n (i.e., a betray leads to a drop of 6% in trust, but a sign of honesty leads to a 60% increase).
2.2.2. Betrayal Due to Lack of Trust
To implement an agent’s decision to betray the public good in a given trial due to lack of trust we randomly selected a number between 0–100% from a uniform distribution, 𝕌(0,100), (i.e., 66%). If the random number was higher than the current trust level for the agent [i.e., T(3,21) = 60%, for the trust level of agent 3 in iteration 21] then we deemed the agent a “betrayer” on that trial. If the number was lower – the agent would not betray due to trust issues. Therefore, higher levels of trust would yield a likely selection to contribute the wages. Lower levels of trust are likely to lead to a withholding of the wages. This function of trust, f(T), ultimately yields a number, 0/1, indicating whether the agent chooses to betray, or not.
2.2.3. Betrayal Due to Reasons Independent of Trust
Participants can choose to not include their wages in the shared account for reasons outside of lack of trust. These reasons can be driven by external circumstances (i.e., a person may get ill and need to pay for his healthcare) or internal preferences (i.e., the person chooses to not contribute their wages despite the loss of profit in order to engage in norm-enforcement; behavioral economics suggest that such behavior plays significant role in people’s decision making Fehr et al., 2002; Fehr and Fischbacher, 2004a).
2.2.3.1. Betrayal due to external reasons
A person might be forced (rather than decide) to not contribute because an external circumstance does not allow them to do so. For example, a person could be forced to keep their initial wages because of an immediate need for liquid cash (e.g., the need to pay a mortgage in the morning may lead to an inability to wait a full day for the funds to multiply).
We incorporated in the model the ability for agents to manifest those external factors using a single variable, which we term “external reasons for betrayal” (ε). The value of ε is either 0 or 1, and is selected from a binomial distribution, 𝔹. We set the probability to betray as a result of external reasons to 10%. Importantly, the outcome of this variable does not depend on an agent’s level of trust. The value is calculated in each trial.
2.2.3.2. Betrayal due to internal reasons
In addition to external reasons over which the person has no control, there might also be internal reasons that result in a person deciding to not contribute. For example, a person might trust the other people in the game to contribute their wages, but decide against doing so themselves because he/she dislikes the other players. This could lead a player to make a decision that intentionally harms the other players in the game even if it comes at a personal cost. Similarly, people may consider not contributing their wages as a way to signal to other agents that they are willing to withstand an immediate financial loss as a way to elicit norm-enforcement (Fehr et al., 2002). In addition, people might simply make a mistake in their decision due to an incorrect estimate of anticipated payoffs. All of those options lead to a behavior that does not obey the classical utility functions, but incorporate psychological factors into the decision.
We incorporated these factors into the model as a term we call “internal reasons for betrayal” (ρ). Similar to the external reasons, the value of ρ is either 0 or 1 and is selected from a binomial distribution, 𝔹. The value of ρ is independent of the agent’s level of trust. Corresponding to the external factors, we set the probability to betray as a result of external reasons to 30%.
Altogether, our experimental variables are, show in Table 2.
2.3. Decision to Contribute in “Regular” Game
The equations determining the decision to contribute the wages in each iteration in a regular game are:
where s is the agent number ∈ [1,n] and t is the trial ∈ [1,N]
where Es,t ∈ [0,1] indicates whether agents will betray (0) in trial t, or not (1).
f(Ts,t) = 1 if Ts,t >𝕌(0,100), such that 𝕌(0,100) is a random number generated uniformly between 0-100.
The process of deciding whether to contribute can be described in the following way:
(1) First, an agent determines whether there are external circumstances that would force them to not contribute to the coming trial, ε. If the answer is “yes” [p(0) = 10%] then the agent does not contribute.
(2) Following, the agent determines whether they have personal internal reasons to not participate,. If the answer is “yes” [p(0) = 30%] then the agent does not contribute.
(3) Following, the agent determines whether they should contribute to the trial based on their trust in the group. This is determined according to their current value of T. If their current level of trust is higher than the randomly generated number, the agent does not contribute.
Consequently, for an agent to contribute in a given trial, three conditions need to be met simultaneously: The agent cannot have (1) external or (2) internal reasons for not playing, and they have to have (3) sufficiently high levels of trust. At the end of each trial all agents update their trust values based on the outcomes (number of agents betraying/contributing) of the previous trial. An increase in number of agents contributing in the previous trial (or maintenance of the maximal number of agents contributing in the previous trial) would yield an increase in trust, whereas a decrease in the number (or equal number that is lower than n) would yield a decrease in trust.
Our study is aimed at identifying the optimal combination of variables, in each condition that yield the highest profit for the C-3PO (an independent entity that cannot betray anyone, does not contribute to the shared account, and is perceived as benevolent by all other participants). Importantly, we sought a protocol that is realistic against the backdrop of real-world decision making and enables the participants to exert their “free will” (their individual independent decision making process) during each choice iteration (i.e., one can still elect to not contribute their wages in a trial for personal reasons).
2.4. Blockchain Protocols
The Blockchain implementation of the model adds a certification system that is monitored by all agents in the following way: a “smart contract” (a commitment to act in a certain way, Es,t, that is logged in a ledger shared by all players) is created in each trial, t, by each agent, s, such that the agent states, anonymously their intent to invest their wages in the fund. Every agent can then see how many of the n agents have committed to contribute () in the trial. The contract is executed only if a minimum number of agent, μ have agreed to contribute their wages. The value of μ is fixed, for each agent, throughout a game. See section “Discussion” for details on the Blockchain protocol’s implementation).
We test the Blockchain protocol under three different scenarios that vary in their level of resembles of real-world decision making and complexity:
2.4.1. Blockchain (Homo Economicus)
The first scenario assumes that the agents’ only goal in the game is to optimize their monetary utility from the game. That is, the goal of each agent is to leave the game with as much money as possible. This implies that participants are willing to accept contracts in which their payoff is bigger than their initial wage even if others are making a higher profit. In this “Blockchain – homo economicus” scenario, the threshold for executing the contract, μ, is equal to the lowest number of agents that need to contribute in order to yield a positive revenue for each contributing agent. The value of μ is similar for all agents.
For the parameters used in our simulations, μ = 3 is that lower cutoff. If at least 3 agents participated, the payoff at the end of the day is $15 (3 players x $10 wages x 600% interest - $30 C-3PO cut; divided by all 10 players), which is higher than the initial $10 wages.
Formalized, the equation to compute the minimal cutoff for agent to accept the contract is:
The homo economicus Blockchain protocol guarantees that no agent will lose money. If the minimal number of agents needed for the contract to be fulfilled is not reached, the contract is voided and none of the rows in the ledger are executed.
In this model, the certification system acts as an insurance against loss. Trust becomes less instrumental for the choice as one can participate in each trial with the assurance that no money is lost. However, the experience of trust T is still updated continuously as it is an indicator of the group dynamics. For example, low trust values signal that other agents may need liquid cash and cannot contribute to the public good, or that they are malevolent. Therefore, one may lower their trust in the group.
Practically, the model incentivizes agents to contribute their wages in every trial because it offers a safeguard against losing money. If agents elect not to do so they are likely driven by personal reasons, both internal (ρ) or external (ε). This shared understanding among all agents makes the collective trust increase over time even after a betrayal has occurred.
Equations 2–3 in the Blockchain model are, therefore, identical to the ones in the “regular” case. However, f(Ts,t) = 1 since trust is no longer affecting the decisions to contribute and there is no risk of losing money.
2.4.2. Blockchain (Homo Reciprocans)
The homo economicus Blockchain model assumes that the goal of players is to maximize their financial gains. If a player earns more than their initial wage (w = $10) they should be willing to accept the executed contract if they contributed their wages. However, as we have outlined in the introduction, prior research suggest that people make decisions that are not fully rational and that do not follow the logic of maximizing one’s economic utility (Dohmen et al., 2009). More so, research in behavioral economics argues that a rational actor in a repeated trials game may deliberately engage in a behavior that results in an immediate loss but maximizes long-term gain. Specifically, behavior that signals to other agents that some behavior is not tolerated may lead to norm-enforcement and future gains at the expense of a momentary loss (Fehr et al., 2002).
In the context of smart contracts facilitated by Blockchain technology, it is reasonable to assume that not everybody would be willing to accept the conditions put forward in the rational Blockchain model. That is, even though people stand to gain more than their initial wages if they contribute to a trial and are willing to execute a contract with only two other players, they might have moral standards that require the number of other people contributing to the game to be higher. These moral standards can be thought of as a person’s individual sense for fairness (Wang et al., 2010), for example. Fairness is known to be a fundamental human need that may place constraints on profit seeking (Wang et al., 2009; Perel, 2017). That said, the extent to which people desire and strive for fairness can vary (Dohmen et al., 2009). Having a relatively low sense of fairness might lead a person to accept a contract in which other participants benefit from free-riding the system (making more money than those contributing to the shared account). In contrast, a person with a higher sense of fairness might reject any contract that has less than maximum contributors – even they stand to lose potential payoff.
This more realistic homo reciprocans Blockchain scenario, in which people might forsake monetary gains in a trade-off against fairness, is implemented by varying the threshold between agents. That is, each agent is assigned a random variable, μs, ranging between μ and n (3–10 in our case) to reflect the degree to which they value fairness versus personal monetary gains (Table 3). Given that this threshold is considered to be a fundamental individual disposition, μs remains constant across all trials for each agent.
Effectively, this means that we add an additional variable to our model. We assign this variable randomly to each agent at the beginning of each game.
The result of this additional constraint is that both the levels of trust as well as the levels of payoffs to the C-3PO are expected to drop compared to the homo economicus Blockchain condition. This is because the additional constraint makes it less likely for the contract to be executed due to personal preferences. However, it is expected to outperform the regular model (without Blockchain) both with regards to trust and C-3PO payoffs. Additionally, it is expected to be more realistic in its depiction of human behavior. We term this model the “homo reciprocans” Blockchain model.
2.4.3. Blockchain (Optimized Homo Reciprocans)
While the homo reciprocans model provides a more realistic picture of human decision making, it also lowers both the trust and the profits compared to the homo economicus model. While still higher than the regular simulation, it may not benefit the public good in an optimal way. In order to optimize the yield of the public good, while offering individuals a chance to increase their yield and trust, we suggest an optimized version of the homo reciprocans model. In this model we include an intervention mechanism that benefits from the Blockchain implementation. This optimization allows agents to update their decision in each iteration (before the contract is executed) based on information on “what the market looks like” (i.e., the decisions of all the other agents, which determine the expected payoffs in each round). Effectively, this allows agents to keep updating their beliefs after all other participants have declared anonymously their intentions, in a way that maximizes profits and increases trust.
To illustrate the optimization we depict an agent that has decided to not contribute to the particular round due to internal reasons (ρ). The agent might wish to update their decision if they found out that 8 other agents are participating in the current round. They might change their mind since they learn that the group’s trust is increasing (more participants are willing to contribute their wages), that they may have made an irrational choice in not contributing (as others do not align with their preference to defect), or simply because the wave of support for the C-3PO by others may be contagious.
Either way, this update should depend on people’s personal standards and their sense of fairness (μs). If a person generally does not accept contracts with less than 8 people, they are unlikely to change their opinion if a given round has, say, 7 people contributing their wages. However, if a person generally accepts contracts with only 4 people playing, but was about to betray, they might change their mind if they see that 7 other players elected to contribute their wages. The person might be inclined to change their mind and contribute their wages as it both signals higher than expected levels of trust in the community, and yields higher profit.
Intuitively this means that the information on how many people choose to contribute to a round should update the person’s internal beliefs, manifested in our model as ρ. The higher the difference between one’s fairness level and the group’s willingness to express trust, the more likely the individual to change their mind, for example.
Operationalized, this is reflected in the following equation:
Simplified, this is equivalent to taking the difference between each agent’s fairness level, the group’s current willingness-to-participate, and updating the probability ρ both in the numerator and denominator.
As an example, let us use and agent s’s fairness level of μs=6. If, in a certain trial, 8 other agents are willing to contribute their wages (), then agent s will update their rationality value to
is embedded in equation 3 in each trial and returns to the initial value, ρs, before re-calculating the next iteration.
As this optimization suggests, agents are able to revisit their decisions repeatedly via the public ledger. The Blockchain therefore enables an anonymous update of the decision process such that agents maximize the alignment between their preferences and the outcomes.
Practically, this means that agents are allowed to repeatedly add rows to the ledger with updated information within a single iteration until all choices converge to a state that satisfies all participants. In our example the update happens only once (from ρs,t → ).
3. Results
We examine each model separately with the same fixed parameters (Table 1) and alternating variables (Table 2).
To illustrate the trust trajectory in the game we selected, first, a subset (n = 510) of all combinations of η1,η2,iT such that they focus on the realistic conditions that are reflected in behavioral games. The values reflect situations where, η1≫η2 and ones with, η1≈η2 which align with individuals’ tendency to decrease their trust after a betrayal and increase their trust in response to cooperation. This combinations selection corresponds to 10.38% of all 4,913 possible combinations of η1,η2,iT (17 x 17 x 17).
The η1,η2 pair combinations were selected from the following three options:
(1) both η1,η2 reflect small changes in trust (i.e., η1,η2∼15%).
(2) both η1,η2 reflect big changes in trust (i.e., η1,η2∼90%).
(3) the values of η1,η2 are of different magnitude (i.e., η1∼ 70%, η2∼15%).
We used the remaining possible combinations in following robustness checks. The probability of betraying due to external reasons (ε) was kept constant at p(1) = 90%.
We used the same η1/η2 combinations in all four models to demonstrate their effect on trust and on the income generated by the C-3PO across conditions. After depicting the results for subsets of the data, for ease of visualization (Figures 3–7), we show the broader case with all combinations of η1/η2 (Figure 8).
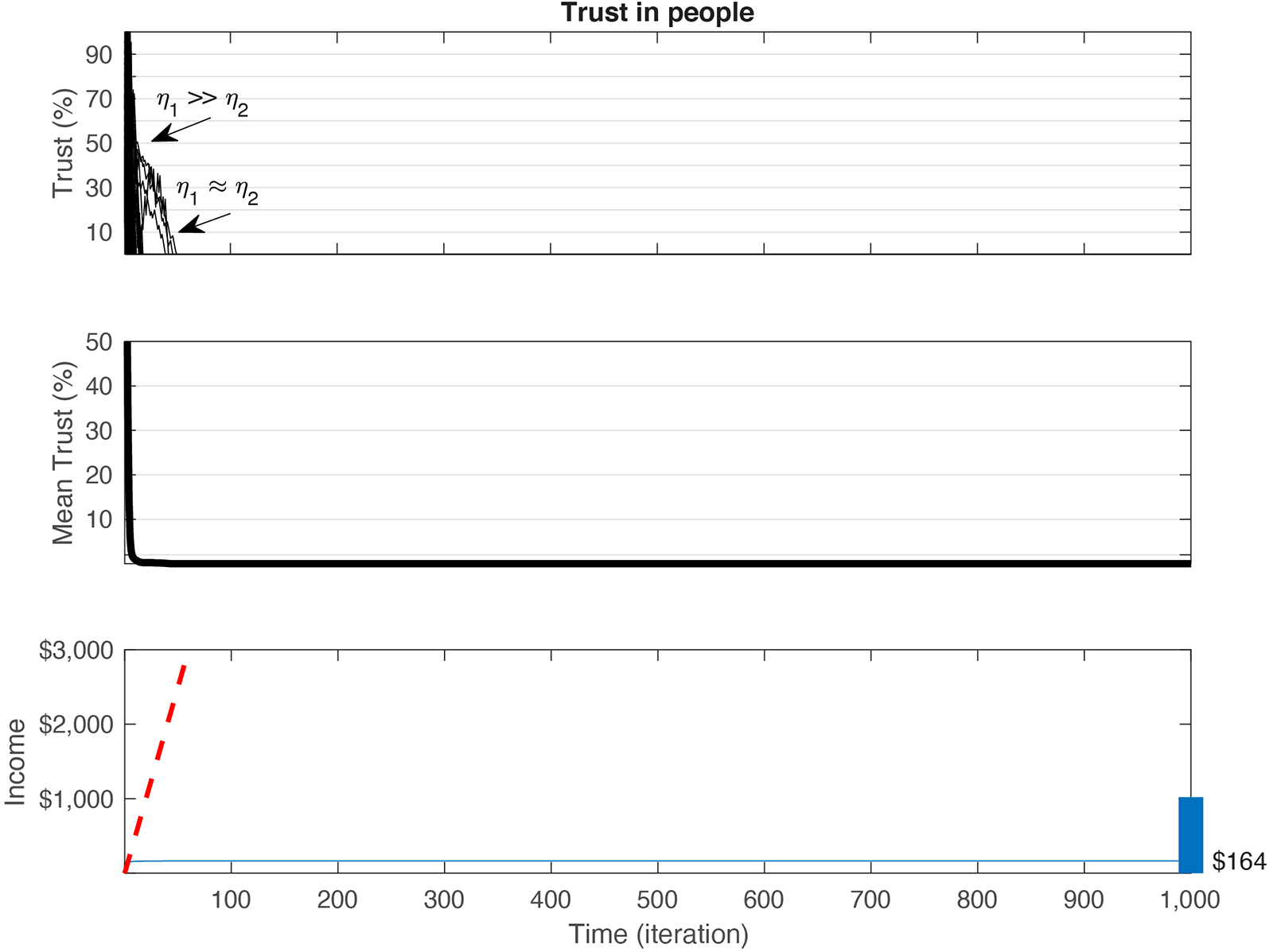
Figure 3. Simulation of regular PG games with varying values for η1 and η2. (Top) across 1,000 iterations, the trust (see equation 2) decays in all games and converges to 0, irrespective of the initial value (iT) and the ratio between η1 and η2. (Middle) Average trust across all games in the top panel. (Bottom) For each of the games and combinations of iT,η1,η2 we calculated the cumulative sum generated by the C-3PO (blue line). While the initial trials typically yield a steady revenue for the C-3PO, once trust breaks and converges to 0 no payoff is received by the C-3PO. Value of $164 correspond to the average scenario where in the first trial all agents contributed to C-3PO ($100 payoff to the C-3PO), followed by a few trials (ranging between 1 to 5 trials) where the income drops because of lower trust by participants, until the payoff decreased to 0 and remains 0 perpetually. Blue bar on the right axis depicts the range of income values generated by the C-3PO across all simulations ($0 – $1,020). Red dashed line marks the optimal cumulative sum if all agents maintained trust throughout the game.
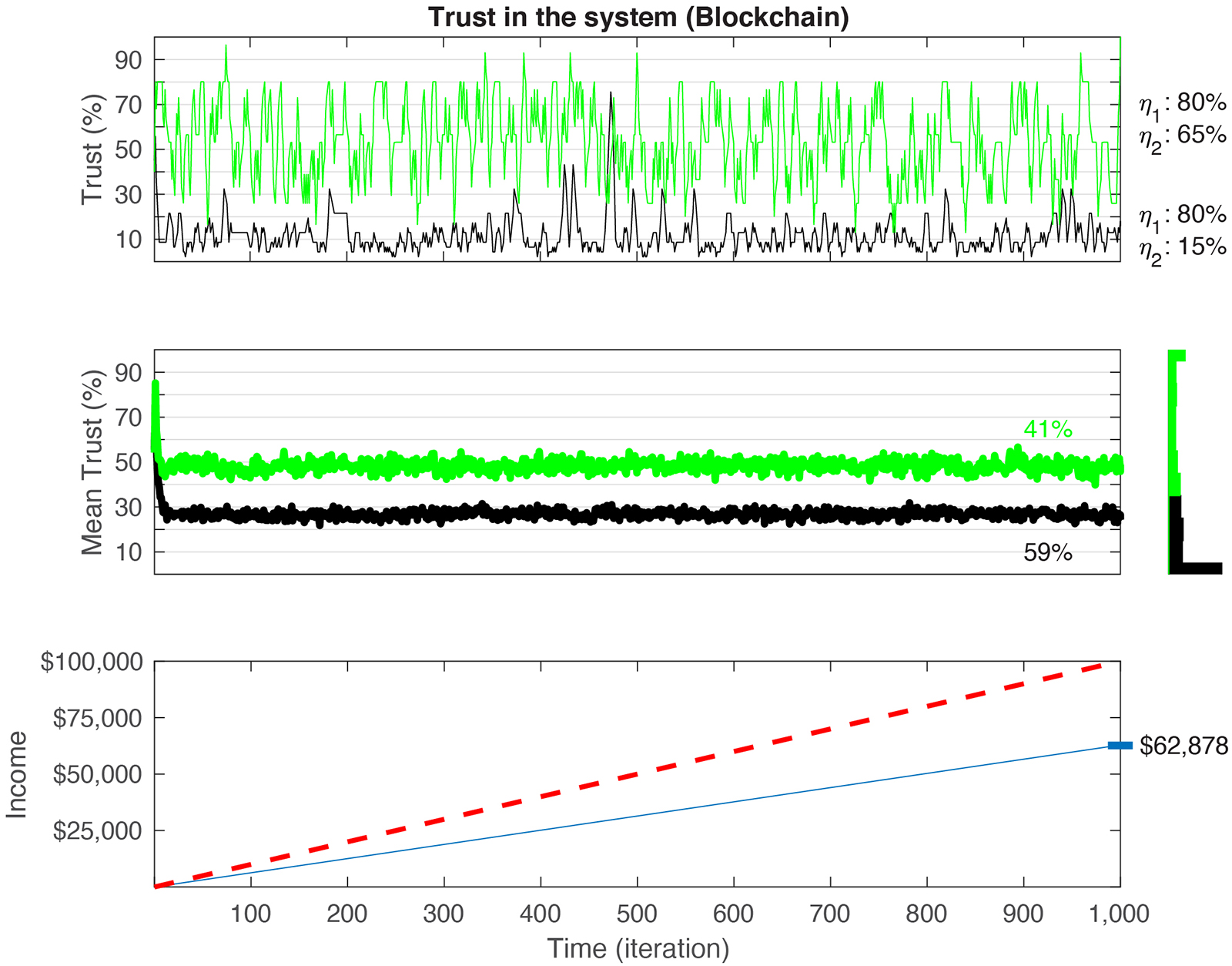
Figure 4. Simulation of Blockchain games with varying values of η1 and η2. (Top) Depiction of two examples of games with η1≫η2 and η1≈η2 ratios. (Middle) Trust (see equation 2) decays in 59% of games to a value lower than the mean (34%), irrespective of the initial trust and the ratio between η1 and η2 (black line in the Top, Middle). Green line corresponds to the average of all trials that ended with trust values above the mean. A histogram of all final trust values is shown on the right. While high trust values have broader range, convergence to 0 trust is still dominant. This, however, has no effect on the individual/C-3PO income. (Bottom) Blue line corresponds to the average cumulative sum in the Blockchain games. The total cumulative sum generated by the C-3PO is $62,878. Red dashed line depicts the optimal (“Full trust”) revenue that the C-3PO could generate if all 1,000 trials were played with maximum payoff (1,000 × $100). Thin blue rectangle on the right axis corresponds to the upper/lower boundaries of income generated by the C-3PO, across all games. The values are stable and range between $61,000 and $64,330.
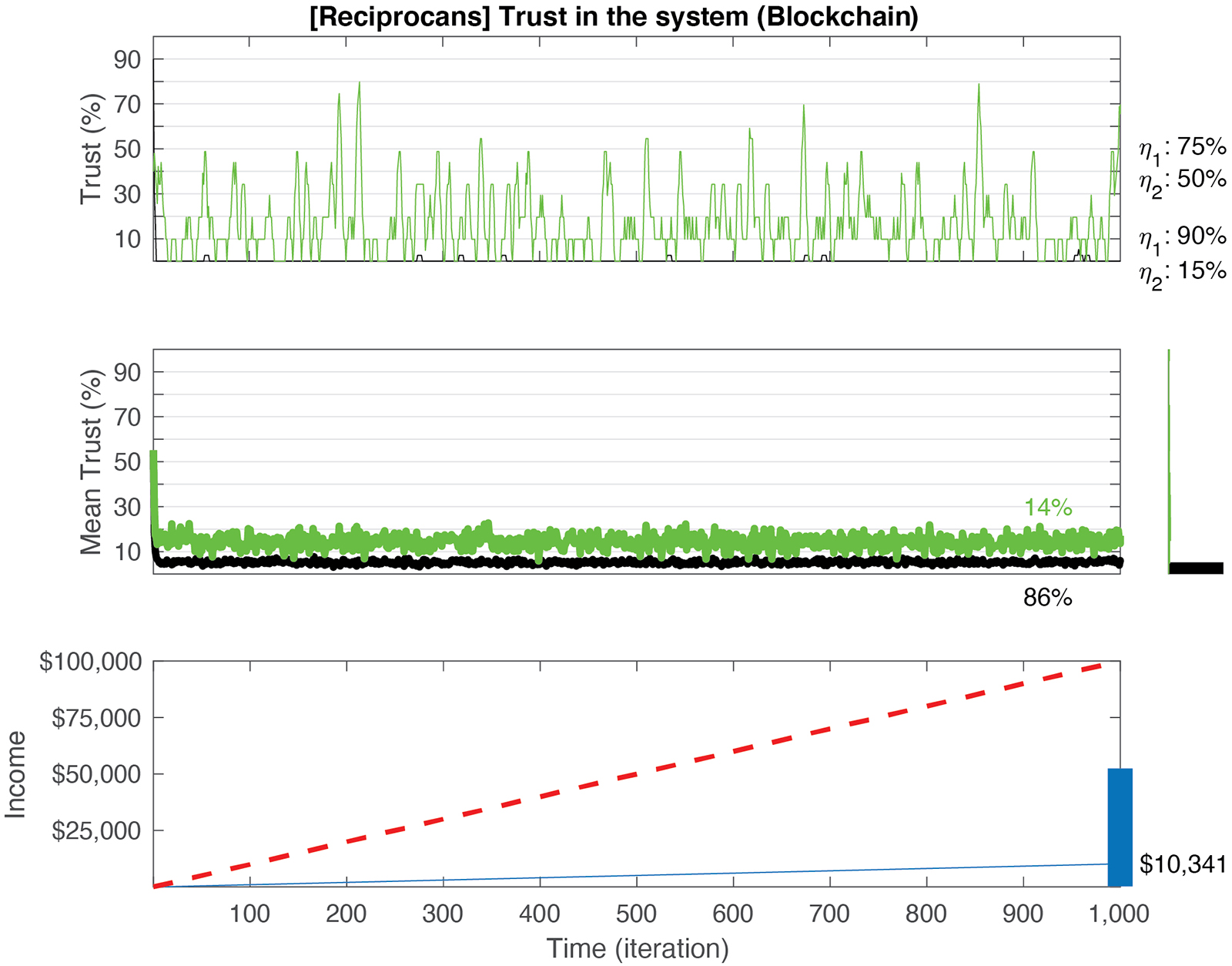
Figure 5. Simulation of reciprocans Blockchain games with varying values of η1 and η2. Top: depiction of two examples of games with η1≫η2 and η1≈η2 ratios. Middle: trust (see equation 2) decays in 86% of games to a value lower than the mean (7%), irrespective of the initial trust and the ratio between η1 and η2 (black line in the middle/top panels). Green (/black) line corresponds to the average of all trials that ended with trust values above (/below) the mean. A histogram of all final trust values is shown to the right. While high trust values have broader range, convergence to 0 trust is still dominant. This, however, has no effect on the individual/C-3PO income. Bottom: Blue line corresponds to the average cumulative sum in the games. The total cumulative sum generated by the C-3PO is $10,341. Red dashed line depicts the optimal (“Full trust”) revenue that the C-3PO can generate if all 1,000 trials were played with maximum payoff (1,000 × $100). The blue rectangle on the right axis corresponds to the upper/lower boundaries of income generated by the C-3PO, across all simulations. The values range between $256 and 52,435.
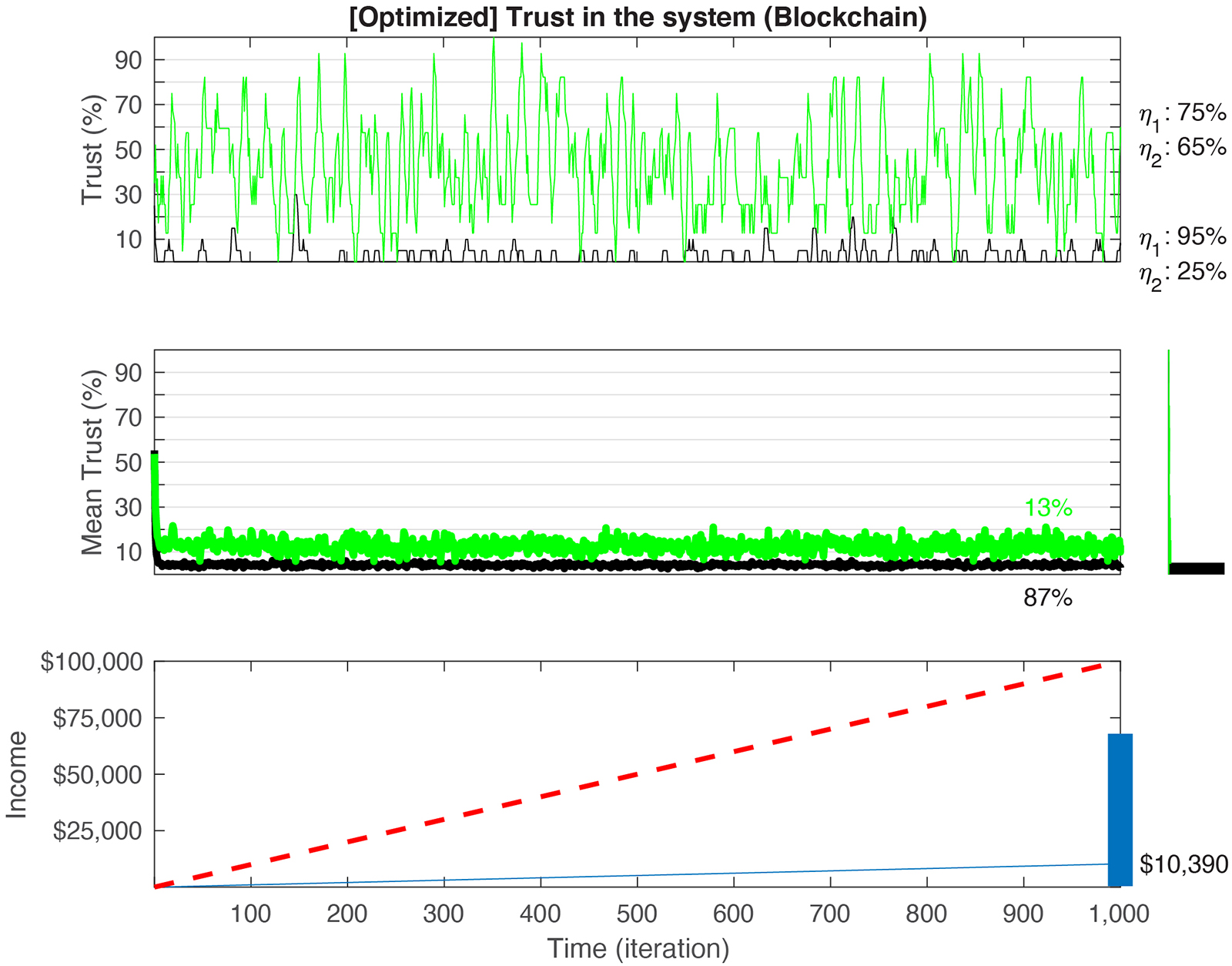
Figure 6. Simulation of optimized Blockchain games with varying values of η1 andη2. Top: depiction of two examples of games with η1≫η2 and η1≈η2 ratios. Middle: trust (see equation 2) decays in 87% of games to a value lower than the mean (5%), irrespective of the initial trust and the ratio between η1 and η2 (black line in the middle/top panels). Green line corresponds to the average of all trials that ended with trust values above the mean (Black: below the mean). A histogram of all final trust values is shown to the right. While high trust values have broader range, convergence to 0 trust is still dominant. Bottom: The total cumulative sum generated by the C-3PO is $10,390. Red dashed line depicts the optimal (“Full trust”) revenue that the C-3PO can generate if all 1,000 trials were played with maximum payoff (1,000 × $100). Blue rectangle on right axis corresponds to the upper/lower boundaries of income generated by the C-3PO, across all simulations. The values range between $462 and $67,895.
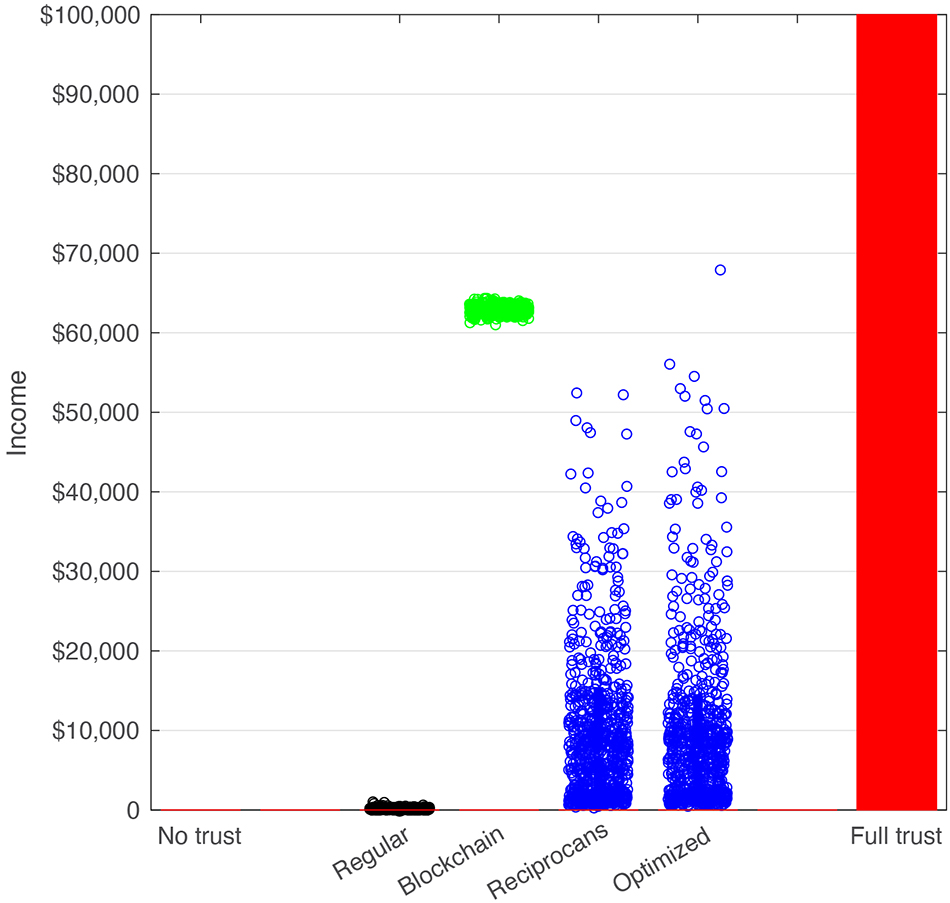
Figure 7. Profit generated by the C-3PO in each simulation condition. Red bar depicts the maximum possible payoff in a 1,000-iteration game with full trust, where each agent contributes all their wages to the shared account (1,000 × $100). Dots reflect the ultimate outcome of a game played with the simulation variables. “No trust” (left) yields $0 for the C-3PO. Regular games (black) yield low gains compared to the Blockchain (green), Reciprocans and Optimized (blue) implementations.
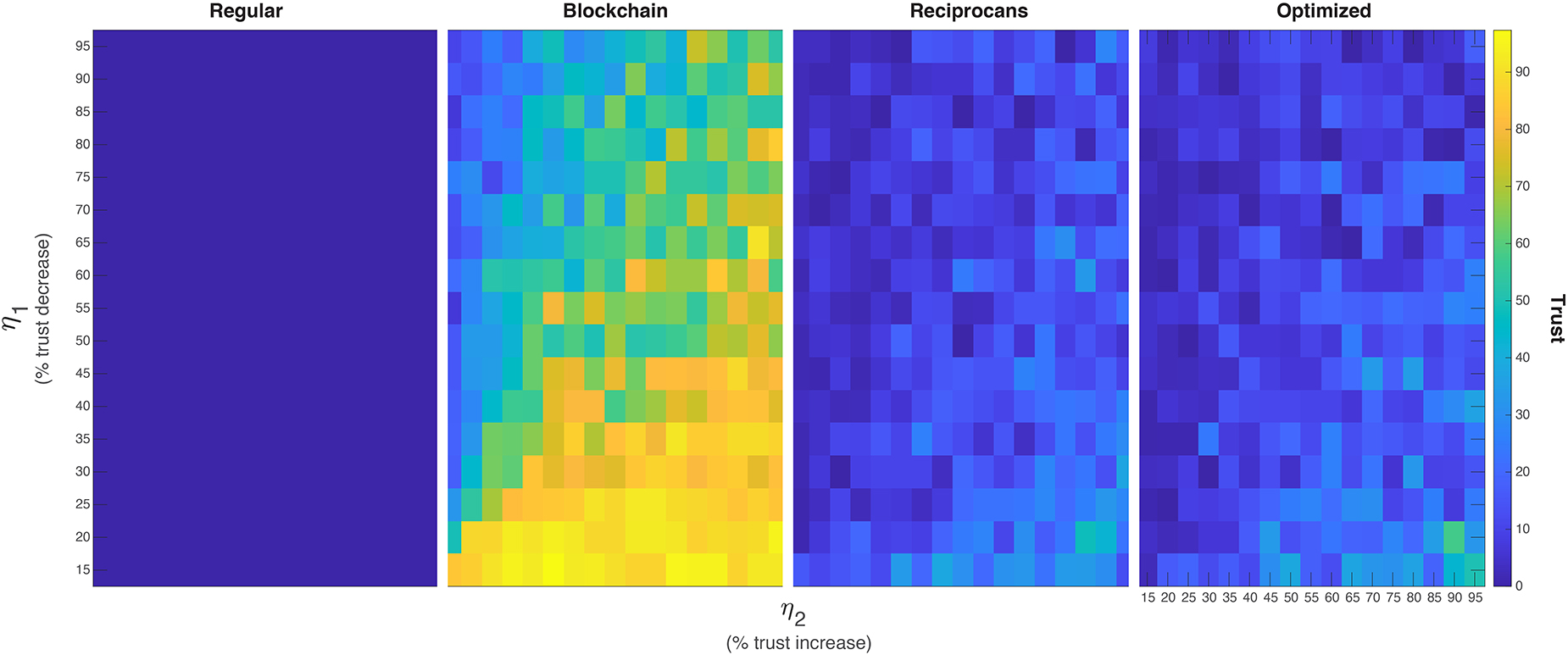
Figure 8. Ultimate trust value in all games for all variables. Each cell corresponds to the final trust value (after 1,000 iterations) in a simulation with a mix of the variables: iT,η1,η2, and μ. Left: ultimate trust value in the average of 4,913 (17 η1 × 17 η2 × 17 iT combinations) of regular games. Second from left: ultimate trust value in 4,913 conditions with regular Blockchain simulation. Second from Right: ultimate trust values in a reciprocans Blockchain condition. Rightmost panel: ultimate trust values in an optimized Blockchain simulation. The upper-left triangle in the “Blockchain,” “Reciprocans” and “Optimized” simulations are nearly same in their value. As these triangles correspond to a more realistic trust scenario (see Figure 2, left) we suggest that trust is increasing similarly in all conditions (albeit less frequently in the simulations that allow fairness as a variable). In games with “lovers” conditions (η2≫η1) all the trust outcomes are different that the norm, as is often the case with love.
3.1. Simulating a Regular Game
The standard model (i.e., model with no Blockchain) reflects the performance in a regular version of the PG game. Importantly, the results of this model resemble the results shown in empirical behavioral data (Ledyard, 1995; Hauert and Szabo, 2003; Camerer and Fehr, 2004). That is, in all combinations of η1 and η2 the trust converged to 0 (Figure 3). The decay in trust depended on the ratio between η1 and η2 and the initial trust (iT) of all agents. Values of η1 greater than η2 sped up the converge to 0, whereas η1 proportional to η2 slowed down the decay.
The average decay to 0 happened within 9 iterations for η1 > >η2, and within 41 iterations when η1≈η2.
Given that the C-3PO benefits from the public good only when agents contribute to the shared account, the yield in a regular game is low. Averaging the ultimate C-3PO payoff in 510 η1,η2,iT combinations after 1,000 iterations, yielded an income of $164 ± 116 (mean ± s.d.; Figure 3 Bottom). The slope of cumulative increase in revenue for the C-3PO is 0.16, compared to 100 in the ideal “full trust” condition.
3.1.1. Robustness Check
As a robustness check, we ran the model with alternative values of ρ [p(1) = 60, 80, 90%]. The average amount of money generated by the C-3PO in those cases is $139 ± 109, $188 ± 145, and $222 ± 114, respectively. The monetary gains for the C-3PO is affected by the level of different values ofρ, but these remain low compared to the values in the Blockchain cases. The maximum gain shown was $1,020 (1% of the ideal case). See Table 4 for summary of the results.
3.2. Simulating a Game With Blockchain
Adding a certification system in the form of a Blockchain contract allows agents to lower their reliance on trust and enable a steady payoff. Operationalized, the decision to contribute in a specific iteration still depends on one’s personal preferences and external drivers, ε and, ρ but not on their trust, T.
Agents effectively create a binding contract that minimized the likelihood of a betrayal by others. If at least two other players participate – then agent s is contributing, as the total of three players will yield a revenue for all agents (see equation 4). If less than three players declare their willingness to contribute their wages on the ledger then no deposit into the shared account is done by anyone. While trust itself fluctuates in response to the group dynamic in each trial, it is more likely to increase. This increase is due to the safety network provided by the Blockchain insurance, which allows agents to focus on their desire to maximize profits while assuming that others do the same.
The average ultimate trust (average of trust value on the 1,000th iteration) in a Blockchain game is 34% ± 36%. This is significantly different than the average trust in a regular game [Figure 4 Top; t(509) = 21.34, CI = (31 38), p < 10–10, t-test; Cohen’s D: 1.34]. Similarly, the income generated by the C-3PO is 383.4 times higher ($62,878 ± 516; Figure 4 Bottom) than in a regular game. The C-3PO, therefore, benefits from the agents’ desire to profit. While defections still lead to drop in income for the C-3PO, the chances of a contract with at least three people being executed is 99.2% [with ε = 90% and ρ = 70%; ]. Therefore, the expected payoff for the C-3PO in 1,000 iterations is $64,480 (992 iterations x $65 average yield per iteration — with minimum yield of $30 and maximum $100). Our results are within 2.4% of the expected estimate.
Overall, C-3PO is generating a steady increase in revenue (slope of 62.8) in a Blockchain-moderated game, suggesting that within up to three iterations the C-3PO can match the amount of money yielded in a regular game across the entire 1,000 iterations. That is, adding the Blockchain certification helps the C-3PO and the players increase their revenue and allows the group to increase their trust in one another.
3.2.1. Robustness Check
Similar to the robustness checks in the regular game, we ran the Blockchain model with alternative values of ρ [p(1) = 60, 80, 90%; Table 4]. The average amount of money generated by the C-3PO in those cases is $53,454 ± 564, $72,004 ± 426, and $81,017 ± 377, respectively. Altogether, the elasticity of ρ is therefore 117 (that is, an increase in 1% in rationality, ρ, increases the yield for the C-3PO by $117 dollars). Put differently, an increase of 1% in rationality in the Blockchain-enabled game is nearly equivalent to all the money generated by the C-3PO in the average regular game.
3.3. Simulating a Homo Reciprocans Blockchain Scenario
As expected, implementing a more realistic homo reciprocans model in which agents may elect to not contribute to a trial for reasons outside of profit, shows a drop in the financial performance and in trust. Here, agents are able to exhibit internal reasoning for betray and exercise a sense of fairness thereby foregoing profit (they may do so to signal that they are dissatisfied with the trust in the group, or because they may not be motivated purely by the financial gains). While trust may still recover after a betrayal it is overall lower than in the regular Blockchain implementation (7% ± 21%; Figure 5). Only 14% of the trials end up with a trust value above the mean. The mean trust itself is significantly lower than the one in the regular Blockchain simulation [t(509) = 14.27, CI = (23 31), p < 10–10, t-test; Cohen’s D: 0.91]. While the majority of games ended up with 0 trust, even those show an occasional, momentary recovery of trust. Accordingly, the income generated by the C-3PO is significantly higher (by an order of magnitude) compared to the regular game without Blockchain [t(509) = 21.84, CI = (9,164 10,975), p < 10–10, t-test; Cohen’s D: 1.37]. The financial performance is also significantly different than the yield in the regular Blockchain game [t(509) = 113.92, CI = (51,734 53,550), p < 10–10, t-test; Cohen’s D: 7.15].
3.3.1. Robustness Check
Similar to the previous specifications, we ran the model with alternative values of ρ [p(1) = 60, 80, 90%; Table 4]. The average amount of money the C-3PO yields is $4,586 ± 6,109, $18,913 ± 14,993, and $32,193 ± 19,378, respectively. The only trials where the yield for the C-3PO is not $100 happen when agents do not contribute due to personal reasons. That is, from the C-3PO perspective, the model performs best when agents exert more utility maximizing decision making and have no external demand for the wages (ε). The Blockchain model still yields higher trust values and higher financial yield for the public goods than the regular game, across all ε, ρ values. As a metric for the influence of personal reasons on the income we used the elasticity (increase of 1% in rationality’s effect on the C-3PO revenues). A quadratic fit of the ρ values (best fit for the data, with a norm of residuals of 422.8) shows that the differential value is 214. That is, while the regular Blockchain shows a higher income for the C-3PO than the reciprocans one, the effect of ρ in the regular Blockchain is smaller. Put differently, in the reciprocans case, an increasing tendency to maximize monetary utility by an agent helps the public good more than in the regular Blockchain model.
3.4. Simulating an Optimized Homo Reciprocans Blockchain Scenario
Finally, we tested a Blockchain simulation that not only protects agents from losing money, but also enables a dynamic updating of preferences and therefore a more effective recovery of trust based on common interests in maximizing profits.
Trust in the optimized Blockchain model is above 0 in 13% of trials (5% ± 17%, Figure 6). The C-3PO profit here is similar in magnitude compared to the one in the previous homo reciprocans Blockchain model. While trust in the optimized model is significantly different than in the regular game [t(509) = 7.29, CI = [4 7], p < 10–10, t-test; Cohen’s D: 0.46] and the regular Blockchain simulation [t(509) = 15.94, CI = (25 33), p < 10–10, t-test; Cohen’s D: 1.02] the regular and optimized homo reciprocans models are not significantly different from one another [t(509) = 1.63, CI = [0 4], p = 0.1, t-test]. However, with respect to the C-3PO yield, the ultimate maximum values for the optimized games are higher than the reciprocans ones. Some of the extreme values surpass even the regular Blockchain maximal values (Figures 6, 7).
3.4.1. Robustness Check
Running the model with alternative values of ρ shows similar improvement as in the previous models (see Table 4). p(1) = 60% yields an income of $5,180 ± 7,546 to the C-3POT. p(1) = 80%, yields $20,184 ± 17,780. And p(1) = 90% yields $35,566 ± 22,228. Fitting the values of ρ here (best done with a quadratic equation that minimizes the norm of residues to 224.5) shows that the elasticity is 195. That is, an increase of 1% in rationality yields an increase of $195 for the C-3PO.
Although the optimized version of the homo reciprocans model does not substantially increase the trust, it yields higher payoffs for the C-3PO. This suggests that the optimized model is less sensitive to individual agents’ decisions and maintains an overall higher profit across all games.
3.5. Identifying an Optimal Set of Variables
Comparing all the models (Figure 7) illustrates that the regular Blockchain model shows the highest financial gain for the C-3PO. The financial gain is not only higher but also most stable compared to the two other Blockchain models. However, as the two other models are more reflective of real-world human behavior (i.e., the desire for fairness) we suggest that improvement and optimizations of all three models should incorporate the identification of common levers that drive and influence such desired outcomes (both trust and payoffs).
To that effect we tested the various combinations of all manipulated variables to identify configurations that enabled ultimate trust recovery. That is, we observed the combinations of trust decay/increase values that yield maximal trust across all models (Figure 8).
The optimal conditions for our experimental variables (η1,η2,iT) were fixed for 4,913 combinations, with μs randomly selected for all n = 10 agents. For each combination of variables, we examined the final value of trust after 1,000 iterations in all the four models (regular, Blockchain, reciprocans Blockchain, and optimized Blockchain; Figure 8). We varied η1,η2,iT from 15 to 95% in steps of 5% (17 conditions each).
Trust in the regular game converges to 0 for all variable combinations (regardless of the initial trust and ratio between η1 and η2). The incorporation of Blockchain shows an improvement in mean trust throughout the game. The outcome is driven by the ratio of η1/η2. When η2 is notably higher than η1 (a large increase in trust following a cooperative game, and a small decay following a betray, which we termed earlier the “lovers” setting) the ultimate trust is highest. This is replicated in all three Blockchain implementations.
Manipulating ε across all four conditions shows that the optimal combination of η1, η2 emerges always when η2 > >η1 (the typical scenario for regular games with no Blockchain) and that external reasons do not alter the results in a robust way.
4. Discussion
4.1. Summary
We incorporated a Blockchain smart contract into a simulation of the Public Goods game. We show that the smart contracts help agents improve their decision making, and, in turn, the outcomes of the decision (in terms of financial gains, fairness, cooperation and trust). We tested multiple implementations of the Blockchain protocol and varied the degree to which they reflected the real world. The outcomes were compared to a simulation of empirical behavioral data from humans playing the PG game.
To explicitly estimate the improvement of our model we investigated two main outcomes: (1) the level of trust among the group members, and (2) the financial profits yielded by a 3rd-party that was defined as independent and benevolent.
Our results show that, overall, the implementation of a Blockchain smart contract in the game leads to a recovery of trust after a betrayal and significantly higher payoffs for the 3rd-party entity. In all Blockchain implementations the ultimate payoffs were two orders of magnitude higher than in the regular game. This is primarily driven by the fact that the Blockchain protocol removes the risk of losing money. The model that yielded the highest levels of trust and payoffs was a Blockchain model in which people accept any contract that allows them to make a profit. This model (“homo economicus”) yielded an over 38,000% increase in payoff for the public good compared to the regular model without Blockchain. When introducing additional constraints that reflect the fact that people are not always maximizing immediate gains, and, at times, forsake monetary utility to fulfill their desire for norm-enforcement or fairness (termed: “homo reciprocans” model; Fehr and Schmidt, 1999), the levels of trust and payoffs dropped, but still remained significantly higher than those observed in the regular game. Specifically, the “homo reciprocans” Blockchain model yields a 6,305% increase in payoff for the public good compared to the regular model without Blockchain. However, given that this model incorporates human decision making that is not driven by a desire to maximize monetary utility, it inevitably falls short compared to the initial Blockchain model. The payoffs for the 3rd-party are over six times lower, and the trust is converging to 0 in 86% of the games, compared to 59% in the standard Blockchain.
In an attempt to recover some of this drop in trust and profits, we implemented an optimized Blockchain model that allows agents to update their own preferences as a function of how profitable and “trusting” the market seems in each round. Allowing such feedback loops within each trial results in a model that yields 6,335% higher payoffs for the public good than the regular model without Blockchain. While the average payoffs are similar to the ones in the regular “homo reciprocans” model, the breadth of outcomes (standard deviation) is higher, with some tests outperforming even the regular Blockchain model. Effectively, the optimized model adds to the regular “homo reciprocans” model a property that allows agents to benefit from a key feature of the repeated games – the ability to norm-enforce and adapt the agent’s behavior to the group. Repeated trial games typically engage with such norm-enforcing and adaptive behavior across trials (i.e., agents act in trial t in behaviors that respond to action in trial t-1 in hopes of changing the behavior of others in trials t+1). The benefit of the optimized model is that it allows for such signaling and adaptive behavior within a single trial. The combination of the fairness variable (intrinsic property of the agent that does not change, but responds to group behavior), with trust (changes based on behavior in previous trials), and the anonymity afforded by the Blockchain protocol enable agents to maximize their benefit while signaling to others about their preferred outcomes. The unique property of the Blockchain’s smart contract mechanism allows for an effective communication under the veil of anonymity. This, we argue, is an improvement upon existing protocols that either: (1) limit the communication and signaling to ones that happen across-trials, or (2) force agents to not be anonymous in order to engage in norm-enforcing behavior, or (3) require a dynamic alteration of the fairness variable to align with the groups’. Effectively, the optimized model allows for the group’s behavior to stabilize within a trial. It allows agents to defect or to increase their contribution to the public good in response to a combination of fairness and utility maximization. The rational, purely economic and utility-maximizing behavior, that is often exhibited in single trial games differs from the one shown in multi-trial games. An optimized Blockchain model serves as a way to allow the benefits or signaling and dynamic group adaptations that are seen in repeated trials games even within a single trial.
Finally, we see that in all Blockchain implementations trust can increase even after it converged to 0.
In short, adding a Blockchain implementation to a public goods function (1) contributes to the likelihood that a multi-player system will recover its trust after a betrayal, and (2) increases the rewards yield by a public goods entity (charity, income tax, etc.). While various models have shown improved mechanisms for increased financial gains, recovery of trust after a breach of honesty is rare.
4.2. Recovery of Trust
Prior research on trust has shown that it is a challenge to restore trust after a betrayal (Schweitzer et al., 2006). The main methods shown to increase trust after a breach of honesty involve: (1) apologizing, (2) accepting blame, and (3) demonstrating consistent honest behavior over long periods of time (Schweitzer et al., 2006). Importantly, while accepting blame is helpful in restoring trust, studies have shown that this only works if the breach of trust is framed as the outcome of an incompetence rather than dishonesty or immoral behavior (Kim et al., 2004). Given that the first two trust-recovery methods require communication between the parties, these methods cannot always be implemented (i.e., in situations where signaling or communication between all parties are difficult to accomplish). Consequently, the Blockchain protocols suggested in this paper could provide a new alternative to recover trust that does not rely on any of the previously suggested mechanisms. The protocol makes it easier for collective trust to recover as the systemic nature of Blockchain technology partially replaces the need for individual accountability. It is noteworthy that the Blockchain implementation allows for trust increase while maintaining full anonymity of the individuals. This is important as recent discussion on mechanisms to improve trust have raised debates on whether transparency is useful for trust increase (Walker, 2016). While longstanding belief among researchers was that increased transparency leads to increased trust (Grimmelikhuijsen, 2012b), some works argue that indeed the opposite is true (Grimmelikhuijsen, 2012a). Countries where transparency is opaque (i.e., China) actually show high levels of trust in the government among citizens (Edelman trust barometer, 2019). It is suggested that this is because of the fact that the break of trust is not disclosed to the citizens (Edelman trust barometer, 2019). Similarly, countries where transparency is high (i.e., the United States) has also exposed its citizens to a plethora of fake news and misinformation that are fueled by lack of rein on exposure.
4.3. Contributions to the Scientific Literature
Our findings contribute to the existing scientific literature in a number of ways.
First, our findings contribute to the literature on trust and decision making while introducing a technological solution to collectively align individual’s interests more efficiently. The Blockchain implementation assures high levels of trust among a particular population. These trust levels supersede the current existing best-case scenarios for trust recovery in the literature.
While the public goods game has been studied for decades and resulted in a substantial body of work exploring the antecedents and consequences of trust in collaborative-competitive decision making contexts (Levitt and List, 2007; Cerf, 2009) the vast majority of these works show that a breakage of trust usually leads to a downward spiral with potentially devastating consequences for both individuals and groups (Boles et al., 2000; Kim et al., 2004; Schweitzer et al., 2006; Wang et al., 2009). Against this backdrop of decades of research, our findings suggest that technological solutions such as Blockchain technology can positively impact trust through an assurance that one cannot be exploited by others. This might open the door to a new line of research that investigates ways in which human decision making in a context that is both competitive and cooperative can be facilitated by similar technologies.
Second, our findings contribute to the growing literature on Blockchain. Specifically, they highlight an application of this technology which could have a tremendous positive impact on individuals, societies and groups. We show that interventional model (the “optimized” model, where individuals are able to repeatedly reflect on their preferences) improves upon models that do not allow for iterative optimization. The optimized model uses the Blockchain not just as a passive database that collects historical data, but rather a signaling mechanism for all participants on the status of the collective. It allows participants to improve their estimates pertaining to the group dynamics. More complex implementations of such signaling mechanism (i.e., additional corrective steps within each iteration) could optimize the performance of the Blockchain usage further.
Therefore, the elucidation of the specific levers for trust increase should be investigated further, and our work offers a first brick in this exploration.
4.4. Practical Implementation of Blockchain in Interdependent Decision Making Contexts
We implement the suggested Blockchain models using an architecture akin to the ones featured in Ethereum and in probabilistic collaborative decision making (Salman et al., 2018).
The key functionality used by those architectures is the smart contract, which allow each node to apply the set of rules suggested in a transaction and execute the transaction.
A complete transaction works in the following way:
(1) Each node in the architecture operates a client that, first, executes the internal processing of the agent’s decision to contribute. An agent uses their own internal/external reasons to betray, their fairness level, and their trust state to decide whether they are interested in contributing the coming trial. (note: in an architecture with n users, there would be n+2 nodes, including one node pertaining to the shared account – the recipient of the daily wages, before they multiply – and another node for the C-3PO).
(2) After an agent’s decision is made, they initiate a transaction that is communicated over the Blockchain protocol (peer-to-peer) to all other nodes. The transaction details are (Table 5):
(3) The smart contract is then implemented. This may include multiple iterations, depending on the model executed. In the “reciprocans” model only one iteration occurs. In the “optimized” model a repeated back and forth between the agents and the clients enables all nodes to ensure that their entry logic is applied.
(4) Note that our implementation includes only the entry decision, E, and fairness, μ, as variables of the transaction. More complicated models may include also the exact amount of money contributed (i.e., instead of a fixed $10 amount one may select a different number), a punishment mechanism applied toward a specific node, or even a string that can be used to communicate and signal desired behaviors directly.
(5) Once the smart contract was validated by all nodes, the “block” that includes the final entry/contribution decisions is being sent to a validator to sign. Signing implies working through all the final transactions and ensuring that all nodes indeed have the funds needed for the transaction. Effectively, this moves from the “logical implementation” (the smart contract) to the transaction validation.
(a) A block can have as little as n entries (in the regular game implementation) and as many as allowed by the optimization algorithm. If the algorithm allows, for example, for multiple updates by nodes based on their updates the block may have multiple entries from each user. The final entry – based on timestamp – is the one that is used by the validator.
(b) If the model is implemented with a “timeout” rather than a finite set of iterations within a trial, then all transactions which arrived by the timeout are included. Transactions that did not arrive by the time are considered as E = 0.
(c) To avoid errors on noisy networks, the transaction can add a field: “last” (= 1/0) where a user can indicate whether they are still iterating or are ready to seal their entry decision. Similarly, a “counter” field can be used to maintain the agreed number of iterations.
(6) Once the validator receives the entries block, they go over the ledger and check that all users indeed have the funds and are part of the network. This ensures that no double spending is occurring and that all users are indeed legitimate players. The validator is selected from within the participating nodes based on the contribution amounts (“Proof of Stake”). That is, users that contributed the most in the last x trials has the highest probability of becoming the validator. The choice of validator occurs randomly from within the top y players. In our implementation we selected x as 50 (i.e., whoever contributed the most in the last 50 trials has the highest probability of becoming the validator in each trial) and y = 10 (i.e., all players may become validators). The numbers x,y should be selected either based on the number of iterations expected, or as a function of the desired time for each round.
(7) Once the validator has approved the block, they send to all nodes a transaction that includes the payoffs for each user (in our case – equal amount), and the hash of the block. All users update their ledger with the corresponding hash. Validators receive a fee from the total as an additional reward, z (i.e., 1% of the value of the iteration). This incentivizes users to desire becoming the validators, which in turn incentivizes contribution to the shared account. If the validator does not sign the block (either stating that the block contains invalid transactions or fails to sign by the specified timeout) the block is not included in the ledger and the trial restarts.
(8) [boundary condition]: as the first transaction(s) (before the x transaction) may not have enough contributions to determine who should be the validator, the shared account acts as the constant validator of all rounds. Once a stake has been established – the validation happens by the contributing nodes.
Note that the user ID in our implementation corresponds to the username, however, the Blockchain implementation allows for anonymous user names (using public key rather than plain names).
4.4.1. Selection of Parameters
Our Blockchain implementation incorporates a number of decisions that require explanation.
First, we chose “Proof of Stake” as our consensus algorithm (as opposed to other algorithms such as “Proof of Work,” where all nodes act as each other’s validators). This choice was driven by the following reasons:
(1) Efficiency and speed. A single validator rather than n validators means that less computation power and energy (and with those, environmental burdens) are exerted.
(2) Encourages contribution. Given that validators receive a small fee for signing the block, there is an incentive to become the validator. The validator is chosen among the top y highest contributors and, accordingly, users are encouraged to increase the contribution. This, in turn, also increases the yield for the C-3PO.
(3) Encourages participation. Given that the validator receives a fee from the entire contribution in each iteration, they have an incentive not only to validate the iteration, but also to increase the number of nodes. More participants mean higher total contribution (n x w). And since the validator fee, z, is a percentage of the total contribution all nodes would presumably be interested in convincing new agent to join. This, too, yields higher income for the C-3PO.
(4) Scalability. The consensus algorithm is invariant to the size of the network. A single validator out of x (a fixed, small, predetermined number) is selected in each iteration irrespective of the number of nodes. This means that larger n will not slow down each transaction and the implementation can maintain a fixed time. The choice of time (τ), and number of candidate validators (y) can ensure an efficient transaction.
Second, our transactions are noted by username rather than agent’s name (using public key as identifiers rather than full name/IP Address). This implementation allows for anonymity of the agents and of their strategies.
Third, given our desire to anonymize not only the user identity but also their strategy, we further incorporate an IPFS hash Blockchain. That is, nodes do not keep the full transactions ledger, but rather a chain of hashed blocks. Only one user (the validator) sees the actual transactions in each block. This means that no user can easily work out other users’ transactions behavior by reading the ledger. This is implemented in the following way: if user A (“Bob”) is validating the 4th block in a chain for the first time, then their ledger would include the transactions pertaining to the specific block but not others. Their ledger would therefore be: Hash1 → Hash2 → Hash3 → Block4 data. Once Bob validates the transaction, he sends all other users only the hash of the 4th block (“Hash4”). Other users (i.e. “Alice”) incorporate the hash into their ledger. Alice’s ledger would, therefore, be: Hash1 → Hash2 → Hash3 → Hash4. If in the next iteration Alice is acting as the validator, then Bob’s ledger would show: Hash1 → Hash2 → Hash3 → Block4 data → Hash5, while Alice’s will be: Hash1 → Hash2 → Hash3 → Hash4 → Block5 data. Accordingly, neither Bob nor Alice can derive the full ledger’s history and all users’ contribution strategies. The hashed ledger is also smaller in size and, therefore, more efficient in handling, size and processing power (/energy).
Fourth, our architecture does not favor existing players inherently in their chances of earning the additional fees. This is because: (1) the validators are chosen based on the contribution in the last x iterations alone (i.e., if a new user joined the network at iteration 500 and contributed most between iterations 500–550 they are more likely to become the validator than users who contributed a large amount prior to iteration 500). This makes the architecture fairer and more balanced toward incoming participants rather than favoring large contributors overall. The choice of x can be larger/smaller based on the desire to encourage more new entrants (lower x) or favor stable validators (higher x).
In line with the second and fourth points, our architecture does not require any information on new participants other than a proof that they have the funds (i.e., are recipients of the daily wages). This, too, enables total anonymity and encourages natural strategies that benefit from such anonymity.
Fifth, the choice of architecture requires a calibrated balance between the variables: x (number of iterations to integrate toward the choice of validator), y (number of ranked validators within the × iterations to consider), and z (reward for validation). The choice of those variables, alongside the number of allowed corrections within each iteration, the number of nodes, n, and the time allotted for each iteration, τ, determine the efficiency of the network. If users want faster iterations, then lower values of x, y,τ should be used. Alternatively, higher value of z may encourage users to dedicate more resources to the validation and increase speed. In our implementation with n = 10 all those values were negligible and the bottleneck was always in the client entry decision calculation end. Lower values of τ or a fixed number of corrections within a trial would force users to speed up this calculation.
Finally, our architecture benefits from all the traditional advantages of Blockchain platforms: (1) it is immutable, (2) it yields high performance with low overhead, (3) it surpasses geographical boundaries (users can be remote and participate), (4) it allows for micro-transactions (e.g., of less than a cent) given the digital nature of the currency, which opens the architecture to low-income contributors as well, and (5) it allows for complex contracts that are not easily possible in classical PG games (for example, an agent can indicate that they want to contribute only if another specific agent does so – even without knowing the other agent’s identity).
Taken together, we believe that this architecture offers a realistic, efficient and improved way to implement the PG game – with the added advantages that benefit all users and the C-3PO.
4.5. Limitations
Our work suffers from a number of limitations. First and foremost, besides the choice of parameters that is arbitrary (despite being grounded in the science of decision making), we recognize that our implementation of the public goods game is specific to certain conditions that may be limited. The public goods game can have numerous additional variants that we did not incorporate into the model. For example, some variants of the game incorporate only a single iteration games and thereby amplify the importance of one’s initial choice. Alternative implementations make the game fully transparent, where players see one another. This transparency is known to change behavior dramatically such that people are less likely to betray (Fiala and Suetens, 2017). Yet, other implementations allow players to choose how much of their wages to allocate rather than forcing them to contribute the entire sum or not contribute anything (and, in doing so, to generate internal safety mechanisms), or to enable post-trial punishments, where betrayers can be costly to the betraying individual (Andreoni et al., 2003).
All of these deviations have been shown to impact trust and payoffs in real-world scenarios. Therefore, our implementation may not speak to those alternative cases. Real-world implementations of taxation, for example, are different than ours since the government has the ability to identify tax-evaders and punish them. Consequently, our model is not necessarily generalizable to cases outside of iterative decision making processes such as charitable donations or collective fund management.
Second, our work lacks human behavioral verification. While the choice of parameters in the regular game replicates the outcomes of empirical studies, we do not have data that speaks to the behavior of subjects in natural settings under the Blockchain implementations. We cannot rule out a scenario where the introduction of the Blockchain settings will alter key variants of the behavior of humans and shift the outcomes outside of the theoretical framework we laid out. For example, existing work in decision making during behavioral economics games have shown that saliency of information and outcomes may drive choices more than purely strategic reasoning (Einhäuser et al., 2009; Wang et al., 2010).
Third, while our work argues for Blockchain as a mechanism for trust recovery, it is noteworthy that, as we suggest earlier, most of the established methods for trust recovery involve direct communication (i.e., in the form of an apology or reframing of the dishonest act as a mistake). Blockchain’s anonymity makes such mechanisms challenging. That is, the resulting increase in trust is a product of collective optimization of interests rather than genuine forgiveness or confidence in one another. While one can argue that in some situations where collective distrust is grave this may be the optimal solution our test did not pit those options against one another and cannot speak to that.
4.6. Future Work
Besides additional tests related to the outlined limitations – primarily the need for actual behavioral experiments testing the Blockchain implementations – we would like to highlight one key direction for future work that has applications beyond the context of trust and public good: the adaptation of the optimized Blockchain model for iterative decision making.
In our implementation, we allowed players to correct their decision, following the exposure of information about the group preferences (“optimized homo reciprocans” model). Players could maximize their profit after learning about the group selection. We constrained our implementation by forcing players who already elected to contribute their wages to remain in the contract and by allowing others to reverse a decision to betray. Once the update has happened all the contracts were executed.
However, the model does not mandate that the update to the ledger can only happen once. One could offer repeated updates to allow for more optimal convergence. That is, one can establish an iterative process by which the ledger gets updated with a secondary choice and, once those choices are revealed, a third choice, and so on. This process can continue until all choices are settled, or until a set threshold of time/iterations has been reached.
The tradeoff in repeated updates is that between efficiency/speed and higher alignment of preferences. That is, every iteration of updates may increase the alignment between the players’ preferences and the outcomes, but will take longer and require more changes of the ledger. Future works can therefore offer: (1) an incorporation of a fixed counter which will enable a set number of repeated optimization steps, or (2) a counter that will dynamically adjust the number of iterations allotted for a decision (presumably, proportional to the number of players, n, or the payoff generated by the C-3PO), or a (3) time-dependent counter. Notably, a time-dependent counter (one that allows updates in a certain, fixed, period of time; i.e., 10 min of updates for each iteration) resembles the implementation of coin minting in Bitcoin implementation. In this implementation, a new coin is minted every set fixed of minutes (i.e., 10 in regular Bitcoin, compared to 2.5 in Litecoin). The timing is proportional to the number of nodes on the ledger, the overall CPU power of all nodes, and the time it took for the last coin to be Hashed (Nakamoto, 2008). Similar implementation may render the decision making process optimal.
Finally, additional work could investigate the effect of the C-3PO’s inclusion on trust, independent of the Blockchain implementation. Our work focused on the inclusion of the Blockchain protocol and did not model any additional effects of the benevolent recipient on the agents’ behaviors. The agents in our simulations effectively acted as if there is no C-3PO in their decision making strategies. Prior works looking at the change in dynamics due to the introduction of 3rd party recipient show that the external party often alters the game dynamics (i.e., in 3rd party dictator game, 3rd party prisoner’s dilemma, 3rd party punishing agents, or games with observers/audience the inclusion of a 3rd party typically changes the group behavior, Fehr and Fischbacher, 2004b). Testing of the effect of the C-3PO alone would help understand the weighted contribution of the Blockchain implementation and the tuning levers that drive agents to behave differently in their contribution merely because of their (dis)interest in helping the benevolent benefactor.
4.7. Managerial and Policy Implications
The abovementioned implementation of optimized Blockchain with repeated updates has bearing in reality as some processes of collective decision making involve such iterative updates. Below we highlight some of those. These are all real-world cases which can be seen as field-studies supporting the theoretical ideas proposed in the work, or as suggestions for improvements of existing frameworks that may benefit from an implementation of the models.
4.7.1. Caucuses Voting
One case we suggest is that of Primary elections using Caucuses. In those elections (implemented currently in various countries such as Australia, New Zealand, Canada, Nepal, United States, and South Africa) a group of voters are gathered at a certain time/place to vote on a topic (i.e., select a candidate out of a number of options in a U.S. state such as Iowa). Initially, each voter makes their decision (implemented, at times, by physically standing next to their preferred candidate’s sign). Once voters see that other candidates may have more votes, or as they are called by their peers to join their ranks, they gradually update their selection. Over time, candidates with low voter counts dwindle down and the voters gradually move to other locations, thereby converging toward the winner. This iterative process yields a candidate selection over multiple rounds of decision and through group dynamics.
One challenge of this method of voting, which is frequently used as a criticism of the method, is that it removes the anonymity of the process and therefore is subject to external influence (i.e., individuals with more power may drive the voting decisions of ones with less power against their interest). In addition, caucuses often require people to be in the same place physically and spend a considerable amount of time during the process of continuous updates.
Our Blockchain implementation can resolve this in an efficient manner that does not require voters to be in the same location, and allows anonymity. The ledger will include all the details of each step, and voters would be able to update their preferences based on current data (or submit a ranking of their candidates ahead of time) without the need to disclose their identity.
4.7.2. Stokvel
Stokvel are clubs of, typically, about dozen people, who are prevalent primarily among low-income individuals in South Africa. Stokvels allow a group of people to increase their financial power by aggregating and pooling the resources of all members (Schulze, 1997). Effectively, the Stokvel operates such that in every fixed period of time (e.g., monthly) all members give a fixed sum of money to one member who uses the fund as they please. That is, every member gets a boost in income once every couple of months. This is used as a mechanisms to exert peer pressure to save (as individuals who do not have the money to donate are scrutinized by the other members), yields higher purchasing-power by the individual who has the collected money, and creates a sense of community among all participants (Schulze, 1997). The implementation of Stokvel, however, is often technically challenging and is therefore frequently limited to communities that are able to physically meet. This means that individuals that are more isolated geographically, or are not as social, suffer greatly from their inability to join a Stokvel. Our Blockchain implementation could be used as a technological way to generate Stokvels outside of a geography and even across countries.
4.7.3. Negotiations
In negotiations, making the first offer can be an advantage or a disadvantage. One the one hand, making the first offer anchors the other side and sets the tone for the remainder of the conversation (Kristensen and Gärling, 1997; Galinsky and Mussweiler, 2001). On the other hand, it can result in less than optimal outcomes, if one does not have enough information about how much the other side values a particular item or issue (Maaravi and Levy, 2017). A Blockchain implementation in the context of negotiations could act as an “escrow” that allows all parties (two or more) to submit their initial offer independently and have all the offers either be revealed simultaneously, or even updated iteratively across players in a fashion similar to the one we depicted in the optimized Blockchain model.
4.7.4. General Election
Finally, the protocol can facilitate truly democratic elections that reflect the group preferences in an optimally democratic way. That is, we suggest that the optimized Blockchain implementation can be generalized to the context of voting. Whereas in many elections the decision by a voter is done in an isolated moment, and is independent of the choice of others, the protocol suggested here can offer a way to calibrate the outcomes to the group preferences in a gradual process.
Imagine the following scenario: a voter in California believes that, based on historical data on prior Presidential elections in the U.S., the state will end up with a majority for the Democratic candidate. Although she is a supporter of the Democratic party, she decides to skip the voting altogether and stay at home (e.g., because she is ill and prefers not to vote given that she is certain of the outcome). At the close of the ballots in the evening she learns that numerous voters acted similarly, and that the low turnout of the Democrats has led to a majority of Republicans in California. The state, to many voters’ surprise, ends up with a Republican electorate. Had the voter known that this was the case, she tells herself, she would have surely voted. However, her choice cannot be exercised anymore as the current voting system does not allow for correction after the ballots are closed. An alternative Blockchain-based implementation of voting can afford voters “conditional decisions.” That is, the voter can indeed behave as she did before, but if the outcomes are different than those expected, she can post-hoc alter her decision and exercise her vote to help tilt the decision toward her preferred candidate. This suggest that, once the results fully converge, with no more changes (or: a small enough number of changes by the entire group, a timeout, or a number of alterations that is lower than a fixed threshold) the outcome will reflect more of the public opinion.
Polling data from the so-called “Brexit” vote in England suggest that a similar situation have led to the outcome of “Leave” vote. The majority of voters did not exercise their voting right, with the assumption that the “Remain” vote will win (polling data supported this belief). The outcome was a surprise to those voters. If they had the option to reverse their decisions to not vote, they would have exercised the right and may have altered the outcome.
Similarly, one can imagine a conditional vote where a constituent in a certain location wishes to exercise a protest vote (i.e., vote for a candidate with a low probability of winning; say, Jill Stein in Michigan during the 2012 U.S. Presidential election). The voter engages in the protest vote with the underlying belief that the state will end up with a majority that aligns with the polls (in the specific case: an expected significant win for candidate Clinton). If, to their surprise, the state ends up with a majority that is different than the one expected (as indeed was the case) then the voter may say that they wish they were able to “go back in time” and vote for candidate Clinton. Again, while this is not possible in current voting conditions a Blockchain system that resembles the optimized simulation shown here would allow individuals such conditional voting. The ledger will carry all options and all voters will act as each other’s’ guarantors of the stated contract.
Smart voting contracts could enable voters not only to change their decisions based on outcomes, but also aim for specific voting proportions (i.e., “I would like to include my vote such that candidate Macron wins the vote, but does not win by over 60% majority, so that it does not seem like I have no reservations about his policies”) and even determine their votes conditionally (i.e., “I would like to vote like my wife, and do not need to know what I end up voting for”).
Finally, in countries where proportional representation methods are used (i.e., Argentina, Turkey, Israel, Hong-Kong, Germany, or Netherlands) the Blockchain voting mechanism can be used to ensure that no votes are lost. In those countries a cutoff is set based on the number of citizens who voted to determine a bar for entry into the parliament. That is, once all votes are cast a fixed number is set (proportional to the number of voters) that indicates what is the least number of votes necessary to be included in the parliament. Parties that received a lower number of votes are disqualified and the votes attributed to them are not included in the final tally. Here, again, a conditional Blockchain-driven voting can insert into the ledger a “replacement” choice. The iterative process can include multiple steps of voting and, ultimately, an outcome that is more reflective of the democratic process, the majority decision, and the overall public good.
A number of platforms, such as “FollowMyVote” (a blockchain venture allowing for secure, anonymous voting), and “Agora” (a blockchain voting service that was recently used across 280 polling locations in Sierra Leone’s Wester District) have demonstrated real-world implementations of the suggested architecture. Similarly, a concept termed “liquid democracy” is currently discussed among political technologists as a mechanism to allow voters to give feedback on policy issues or pieces of new legislation based on knowledge and availability, in real time. Under liquid democracy platforms, voters can select a personal representative who has the authority to be a proxy for their vote. The proxy can be changed as voter’s interests change. Additionally, a proxy can have a proxy of their own – creating a directed network graph that connects multiple voters to politicians. When a need for a collective decision occurs, individuals (or their proxies) offer their opinion in the form of a rapid vote – allowing their representatives to get an accurate sense of the public opinion.
In alignment with our suggested implementations, voting can use a smart contract to align one’s ideals with experts that the agent identifies. The smart contract will ensure that the agent’s interests are taken into account and provide a signed evidence for the voter proxy’s decision after it was made. When legislators are voting on topics that the individual may not have an informed opinion on, such a system can be used to maximize their utility and interests-alignment, without the need to engage with every decision. This, in turn, may yield better representation and more accurate reflection of the popular view.
In alignment with the voting implementations of our architecture, recent platforms have been developed also for healthcare solutions. In these platforms, healthcare ecosystem allow providers and individuals to access, move and share their healthcare data over a Blockchain protocol and reach consensus decision on ideal care outcomes. Users are able to trust unknown providers and practitioners, get opinions from multiple sources, share records with various groups in ways that benefit both the patients but also the collective (i.e., share symptoms and care outcomes without disclosing the identity of the patient), and iterate over a decision multiple times if they are not satisfied with the initial opinion.
Finally, in the context of consumer goods, architectures similar to the one implemented in this paper were suggested to allow users to buy/sell tickets for shows/events without the risk of fraud. The collective interest in honest and trustworthy exchange of tickets benefits all participants and provides reliable mechanisms to avoid price hiking and ensure the integrity of the sale. As an additional benefit, the platform provides higher accuracy in the data used by event planners with respect to attendance, audience engagement and customer experiences. The participants maintain the integrity of all transactions while the various nodes in the system allow for convergence to optimal ticket prices, maximizing of the number of tickets used, and rapid exchange.
Taken together, these recent examples all show that the suggested Blockchain platform can be used for implementations beyond the mere allocation of funds toward a third party while maintaining the agent’s interest, but rather for an interactive decision making that benefits all parties as well as the collective.
It has not escaped our noticed that the implementation laid out in the above cases may give rise to an entirely alternative mechanism for group decision making and public trust recovery. While the PG game was paralleled to investment groups (Shane et al., 2019), collective purchase groups, crowd funding and numerous financial implementations, we see the work as instrumental in its offering to both increase trust and allow individuals to better align their preferences with their outcomes.
Given the strong positive correlation between GDP and trust, and the inverse correlation between trust and corruption (Edelman trust barometer, 2019) we suggest that an implementation of Blockchain protocols similar to the one suggested here can help regain trust in a collective way, even at the country level. In countries where profit maximization is valued (i.e., Capitalistic countries such as the United States) the protocol can help people generate higher individual payoffs. In countries where shared interests are valued (i.e., Socialistic countries such as Sweden) the fact that the C-3PO maximizes the yield would be seen as valuable), and in countries where corruption is widespread and disbelief in centralized entities prevails (i.e., Zimbabwe) the protocol can be useful to gradually rebuild trust in collective institutions.
As measures of trust show a decline in institutional trust (Edelman trust barometer, 2019), the reliance on mathematics could provide a reliable remedy for our world. As stated by one of the pioneers of the Blockchain technology: “who do you trust more – the governments or mathematics.”
Data Availability Statement
All the codes for the simulations are available online at http://www.morancerf.com/publications.
Author Contributions
MC conceived the study. MC, SM, and AB designed the simulation. AB conducted the simulations. MC and AB conducted the analyses. MC, AB, and SM discussed the results, and wrote the manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors wish to thank Kent Grayson for valuable comments on the manuscript, to Phillip Kotler for conversations on the application to the public good, and to Dan Ariely for conversations about trust which initiated the study.
Appendices
Appendix 1
A set of n players (for the sake of the example, we use n = 10) are working in a village and receive equal salary for their work, daily, in the morning. The daily wage for each player, w, is $10. Therefore, the total money earned by the players is 10 x $10 = $100 (n x $w). Each individual can choose to keep their income or to contribute it to shared account (e.g., a collective savings account with fixed interest). The shared account generates an interest and multiplies the amount 6x (600%) over the course of the day (note: prior research investigated the ratio between the number of players and the multiplier shows varying behaviors pertaining to these proportions. See Gunnthorsdottir et al. (2007).
If all players contributed their wages in the fund ($100), the interest would increase the shared amount to $600 at the end of the day.
Out of the total, an amount equivalent to the total sum contributed by the players initially ($100 out of the $600) is donates to a 3rd party (e.g., a charity, a tax, or a fee collected by a fund manager). The remainder of the sum in the shared account is divided by all players, regardless of whether they contributed their wages or not. Each player therefore receives 1/n shares of the fund’s total left after the donation to the charity.
Mathematically, this can be annotated:
The total money earned by each player is then:
Players can contribute their wages to the shared account or keep the money and benefit from the wages of their peers.
To illustrate the outcomes of the game, we highlight three scenarios:
(1) Complete trust. If all (n = 10) players contribute their wages to the shared account ($100) then the total amount yielded at the end of the day would be $600. Of this amount, $100 goes to the charity, and the remaining $500 is divided equally by all players. Therefore, each player started the day with $10 and ended with $50. This is one equilibrium state.
(2) Complete distrust. If all players do not contribute their wages to the fund ($0) then the total yield at the end of the day is $0. The charity therefore gets nothing, and the players receive no additional income outside of their initial wages. The total for each player is then $10.
(3) Betrayal. If, say, one player chooses to betray the public good, while all others still act in “complete trust,” then the shared account receives $10 × 9 (players) = $90. Multiplied 6 times the total is $540. The charity gets $90 and each player gets ($540 – $90)/10 = $45. However, the one player who betrayed the public good and did not contribute their wages benefits from receiving both the dividend and maintaining the original wage. Their total income for the day is therefore $10 + $45 = $55.
Notice, versions of the game exist where players can choose to also contribute part of their money (i.e., only $3 out of their $5). These are analogous to a version of Ultimatum games.
Below is a table for payoffs to each individual across various scenarios in a game with a charity and n = 10 players.
Appendix 2
List of all variables/parameters used in the work:
References
Andreoni, J., Harbaugh, W., and Vesterlund, L. (2003). The carrot or the stick: rewards, punishments, and cooperation. Am. Econ. Rev. 93, 893–902. doi: 10.1257/000282803322157142
Asch, S. E., and Guetzkow, H. (1951). “Effects of group pressure upon the modification and distortion of judgments,” in Documents of Gestalt Psychology, ed. H. Guetzkow, (Pittsburgh, PA: Carnegie Press), 222–236.
Barcelo, H., and Capraro, V. (2015). Group size effect on cooperation in one-shot social dilemmas. Sci. Rep. 5:7937. doi: 10.1038/srep07937
Barnett, S. B., and Cerf, M. (2018). Trust the Polls? Neural and recall responses provide alternative predictors of political outcomes. Adv. Consum. Res. 46, 374–377.
Berg, J., Dickhaut, J., and McCabe, K. (1995). Trust, reciprocity, and social history. Games Econ. Behav. 10, 122–142. doi: 10.1006/game.1995.1027
Bjørnskov, C. (2012). How does social trust affect economic growth? South. Econ. J. 78, 1346–1368. doi: 10.4284/0038-4038-78.4.1346
Bless, H., Bohner, G., Schwarz, N., and Strack, F. (2001). “Mood and persuasion: a cognitive response analysis,” in Emotions in Social Psychology: Essential Readings, ed. W. G. Parrott, (Philadelphia, PA: Psychology Press), 216–226.
Boles, T. L., Croson, R. T., and Murnighan, J. K. (2000). Deception and retribution in repeated ultimatum bargaining. Organ. Behav. Hum. Decis. Process. 83, 235–259. doi: 10.1006/obhd.2000.2908
Buterin, V., Hitzig, Z., and Weyl, E. G. (2019). A flexible design for funding public goods. Manage. Sci. 65, 4951–5448.
Camerer, C. F., and Fehr, E. (2004). “Measuring social norms and preferences using experimental games: a guide for social scientists,” in Foundations of Human Sociality, eds J. Henrich, R. Boyd, S. Bowles, C. Camerer, E. Fehr, and H. Gintis, (Oxford: Oxford University Press), 55–95. doi: 10.1093/0199262055.003.0003
Cerf, M. (2009). Competition and Attention in the Human Brain Eye-Tracking and Single-Neuron Recordings in Healthy Controls and Individuals with Neurological and Psychiatric Disorders. Ph.D. thesis, California Institute of Technology, Pasadena, CA.
Cerf, M., Greenleaf, E., Meyvis, T., and Morwitz, V. G. (2015). Using single-neuron recording in marketing: opportunities, challenges, and an application to fear enhancement in communications. J. Mark. Res. 5, 530–545. doi: 10.1509/jmr.13.0606
Christakis, N. A., and Fowler, J. H. (2007). The spread of obesity in a large social network over 32 years. N. Engl. J. Med. 357, 370–379. doi: 10.1056/nejmsa066082
Cialdini, R. B., and Goldstein, N. J. (2004). Social influence: Compliance and conformity. Annu. Rev. Psychol. 55, 591–621. doi: 10.1146/annurev.psych.55.090902.142015
Coxb, C. A., and Stoddard, B. (2016). Strategic thinking in public goods games with teams. J. Public Econ. 161, 31–43. doi: 10.1016/j.jpubeco.2018.03.007
Dohmen, T., Falk, A., Huffman, D., and Sunde, U. (2009). Homo reciprocans: survey evidence on behavioural outcomes. Econ. J. 119, 592–612. doi: 10.1111/j.1468-0297.2008.02242.x
Dong, Y., Zhang, B., and Tao, Y. (2016). The dynamics of human behavior in the public goods game with institutional incentives. Sci. Rep. 6:28809. doi: 10.1038/srep28809
Edelman Trust Barometer (2019). Edelman Trust Barometer. Available online at: https://www.edelman.com/sites/g/files/aatuss191/files/2019-02/2019_Edelman_Trust_Barometer_Global_Report.pdf (accessed January 20, 2019).
Einhäuser, W., Schumann, F., Vockeroth, J., Bartl, K., Cerf, M., Harel, J., et al. (2009). Distinct roles for eye and head movements in selecting salient image parts during natural exploration. Ann. N. Y. Acad. Sci. 1164, 188–193. doi: 10.1111/j.1749-6632.2008.03714.x
Fehr, E., and Fischbacher, U. (2004a). Social norms and human cooperation. Trends Cogn. Sci. 8, 185–190. doi: 10.1016/j.tics.2004.02.007
Fehr, E., and Fischbacher, U. (2004b). Third-party punishment and social norms. Evol. Hum. Behav. 25, 63–87. doi: 10.1016/s1090-5138(04)00005-4
Fehr, E., Fischbacher, U., and Gächter, S. (2002). Strong reciprocity, human cooperation, and the enforcement of social norms. Hum. Nat. 13, 1–25. doi: 10.1007/s12110-002-1012-7
Fehr, E., and Schmidt, K. M. (1999). A theory of fairness, competition, and cooperation. Q. J. Econ. 114, 817–868. doi: 10.1162/003355399556151
Fiala, L., and Suetens, S. (2017). Transparency and cooperation in repeated dilemma games: a meta study. Exp. Econ. 20, 755–771. doi: 10.1007/s10683-017-9517-4
Fukuyama, F. (1995). Trust: The Social Virtues and the Creation of Prosperity. New York, NY: Free press.
Gächter, S., Kölle, F., and Quercia, S. (2017). Reciprocity and the tragedies of maintaining and providing the commons. Nat. Hum. Behav. 1, 650–656. doi: 10.1038/s41562-017-0191-5
Gächter, S., Nosenzo, D., Renner, E., and Sefton, M. (2010). Sequential vs. simultaneous contributions to public goods: experimental evidence. J. Public Econ. 94, 515–522. doi: 10.1016/j.jpubeco.2010.03.002
Galinsky, A. D., and Mussweiler, T. (2001). First offers as anchors: the role of perspective-taking and negotiator focus. J. Pers. Soc. Psychol. 81, 657–669. doi: 10.1037/0022-3514.81.4.657
Grimmelikhuijsen, S. (2012a). A good man but a bad wizard. About the limits and future of transparency of democratic governments. Inf. Polity 17, 293–302. doi: 10.3233/ip-2012-000288
Grimmelikhuijsen, S. (2012b). Linking transparency, knowledge and citizen trust in government: an experiment. Int. Rev. Adm. Sci. 78, 50–73. doi: 10.1177/0020852311429667
Gunnthorsdottir, A., Houser, D., and McCabe, K. (2007). Disposition, history and contributions in public goods experiments. J. Econ. Behav. Organ. 62, 304–315. doi: 10.1016/j.jebo.2005.03.008
Hauert, C., and Szabo, G. (2003). Prisoner’s dilemma and public goods games in different geometries: compulsory versus voluntary interactions. Complexity 8, 31–38. doi: 10.1002/cplx.10092
Isaac, R. M., Walker, J. M., and Williams, A. W. (1994). Group size and the voluntary provision of public goods: experimental evidence utilizing large groups. J. Public Econ. 54, 1–36.
Jachimowicz, J. M., Chafik, S., Munrat, S., Prabhu, J. C., and Weber, E. U. (2017). community trust reduces myopic decisions of low-income individuals. Proc. Natl. Acad. Sci. U.S.A. 114, 5401–5406. doi: 10.1073/pnas.1617395114
Johnson, S. M., Makinen, J. A., and Millikin, J. W. (2001). Attachment injuries in couple relationships: a new perspective on impasses in couples therapy. J. Marital Fam. Ther. 27, 145–155. doi: 10.1111/j.1752-0606.2001.tb01152.x
Jones, D. R. (2015). Declining trust in congress: effects of polarization and consequences for democracy. Forum 13, 375–394.
Jones, G. R., and George, J. M. (1998). The experience and evolution of trust: implications for cooperation and teamwork. Acad. Manag. Rev. 23, 531–546. doi: 10.5465/amr.1998.926625
Kim, H., Ferrin, D. L., Cooper, C. D., and Dirks, K. T. (2004). Removing the shadow of suspicion: the effects of apology versus denial for repairing competence-versus integrity-based trust violations. J. Appl. Psychol. 89, 104–118. doi: 10.1037/0021-9010.89.1.104
Kristensen, H., and Gärling, T. (1997). The effects of anchor points and reference points on negotiation process and outcome. Organ. Behav. Hum. Decis. Process. 71, 85–94. doi: 10.1006/obhd.1997.2713
Leana, C. R., and van Buren, H. J. (1999). Organizational social capital and employment practices. Acad. Manag. Rev. 24, 538–555. doi: 10.5465/amr.1999.2202136
Ledyard, J. (1995). “Public goods: a survey of experimental research,” in Handbook of Experimental Economics içinde, eds J. Kagel and A. Roth, (Princeton NJ: Princeton University Press).
Levin, S. A. (2014). Public goods in relation to competition, cooperation, and spite. Proc. Natl. Acad. Sci. U.S.A. 111, 10838–10845. doi: 10.1073/pnas.1400830111
Levitt, S. D., and List, J. A. (2007). What do laboratory experiments measuring social preferences reveal about the real world? J. Econ. Perspect. 21, 153–174. doi: 10.1257/jep.21.2.153
Levy, J., Markell, D., and Cerf, M. (2010). Polar similars: using massive mobile dating data to predict dating preferences. Front. Psychol. 10:2010. doi: 10.3389/fpsyg.2019.02010
Maaravi, Y., and Levy, A. (2017). When your anchor sinks your boat: Information asymmetry in distributive negotiations and the disadvantage of making the first offer. Judgm. Decis. Mak. 12, 420–429.
McGinty, M., and Milam, G. (2013). Public goods provision by asymmetric agents: experimental evidence. Soc. Choice Welfare 40, 1159–1177. doi: 10.1007/s00355-012-0658-2
Mentovich, A., and Cerf, M. (2014). “A psychological perspective on punishing corporate entities,” in Regulating Corporate Criminal Liability, eds D. Brodowski, M. Espinoza de los Monteros de la Parra, K. Tiedemann, and J. Vogel, (Cham: Springer), 33–45. doi: 10.1007/978-3-319-05993-8_4
Mentovich, A., Huq, A., and Cerf, M. (2016). The psychology of corporate rights: perception of corporate versus individual rights to religious liberty, privacy, and free speech. Law Hum. Behav. 40, 195–210. doi: 10.1037/lhb0000163
Nadell, C. D., Bassler, B. L., and Levin, S. A. (2008). Observing bacteria through the lens of social evolution. J. Biol. 7:27. doi: 10.1186/jbiol87
Nakamoto, S. (2008). Bitcoin: A Peer-to-Peer Electronic Cash System. Available online at: https://bitcoin.org/bitcoin.pdf (accessed October 31, 2008).
Ostrom, E. (2010). Polycentric systems for coping with collective action and global environmental change. Glob. Environ. Chang. 20, 550–557. doi: 10.1016/j.gloenvcha.2010.07.004
Perel, E. (2017). The State of Affairs: Rethinking Infidelity-A Book for Anyone who has Ever Loved. New York, NY: Hachette.
Rand, D. G., Dreber, A., Ellingsen, T., Fudenberg, D., and Nowak, M. A. (2009). Positive interactions promote public cooperation. Science 325, 1272–1275. doi: 10.1126/science.1177418
Rege, M., and Telle, K. (2004). The impact of social approval and framing on cooperation in public good situations. J. Public Econ. 88, 1625–1644. doi: 10.1016/s0047-2727(03)00021-5
Salman, T., Jain, R., and Gupta, L. (2018). “Probabilistic Blockchains: A Blockchain Paradigm for Collaborative Decision-Making,” in Proceedings of the 9th IEEE Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, 457–465.
Schulze, W. G. (1997). The origin and legal nature of the Stokvel (Part 1). S. Afr. Merc. Law J. 9, 18–29.
Schweitzer, M. E., Hershey, J. C., and Bradlow, E. T. (2006). Promises and lies: Restoring violated trust. Organ. Behav. Hum. Decis. Process. 101, 1–19. doi: 10.1016/j.obhdp.2006.05.005
Sefton, M., Shupp, R., and Walker, J. M. (2007). The effect of rewards and sanctions in provision of public goods. Econ. Inq. 45, 671–690. doi: 10.1111/j.1465-7295.2007.00051.x
Shane, S., Drover, W., Clingingsmith, D., and Cerf, M. (2019). Founder passion, neural engagement and informal investor interest in startup pitches: an fMRI study. J. Bus. Ventur. 35, 105949. doi: 10.1016/j.jbusvent.2019.105949
Smith, C., and Freyd, J. J. (2014). Institutional betrayal. Am. Psychol. 69, 575–587. doi: 10.1037/a0037564
Tapscott, D., and Tapscott, A. (2016). Blockchain Revolution: How the Technology Behind Bitcoin is Changing Money, Business, and the World. New York, NY: Penguin Random House.
Thomas, G. (1993). How We Know What Isn’t So: The Fallibility of Human Reason in Everyday Life. New York, NY: The Free Press.
Van Hoorn, J., Van Dijk, E., Güroðlu, B., and Crone, E. A. (2016). Neural correlates of prosocial peer influence on public goods game donations during adolescence. Soc. Cogn. Affect. Neurosci. 11, 923–933. doi: 10.1093/scan/nsw013
Walker, K. L. (2016). Surrendering information through the looking glass: Transparency, trust, and protection. J. Public Policy Mark. 35, 144–158. doi: 10.1509/jppm.15.020
Wang, C. S., Galinsky, A. D., and Murnighan, J. K. (2009). Bad drives psychological reactions, but good propels behavior: responses to honesty and deception. Psychol. Sci. 20, 634–644. doi: 10.1111/j.1467-9280.2009.02344.x
Wang, J. T., Spezio, M., and Camerer, C. F. (2010). Pinocchio’s pupil: using eyetracking and pupil dilation to understand truth telling and deception in sender-receiver games. Am. Econ. Rev. 100, 984–1007. doi: 10.1257/aer.100.3.984
Willinger, M., and Ziegelmeyer, A. (1999). Framing and cooperation in public good games: an experiment with an interior solution. Econ. Lett. 65, 323–328. doi: 10.1016/s0165-1765(99)00177-9
Keywords: Blockchain, decision making, trust, public goods game (PGG), simulation, behavioral economics
Citation: Cerf M, Matz S and Berg A (2020) Using Blockchain to Improve Decision Making That Benefits the Public Good. Front. Blockchain 3:13. doi: 10.3389/fbloc.2020.00013
Received: 01 November 2019; Accepted: 03 March 2020;
Published: 31 March 2020.
Edited by:
Natalie Geld, MedNeuro, Inc., United StatesReviewed by:
Reza Parizi, Kennesaw State University, United StatesClifford D. Saron, University of California, Davis, United States
Alea Corin Skwara, University of California, Davis, United States, in collaboration with reviewer CS
Copyright © 2020 Cerf, Matz and Berg. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Moran Cerf, bW9yYW5AbW9yYW5jZXJmLmNvbQ==
 Moran Cerf
Moran Cerf Sandra Matz
Sandra Matz Aviram Berg
Aviram Berg