
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Bioeng. Biotechnol. , 01 October 2024
Sec. Biomechanics
Volume 12 - 2024 | https://doi.org/10.3389/fbioe.2024.1476473
This article is part of the Research Topic Biomechanics in Orthopaedic Diseases and Surgery, Volume II View all 12 articles
Introduction: Woven bone, a heterogeneous and temporary tissue in bone regeneration, is remodeled by osteoblastic and osteoclastic activity and shaped by mechanical stress to restore healthy tissue properties. Characterizing this tissue at different length scales is crucial for developing micromechanical models that optimize mechanical parameters, thereby controlling regeneration and preventing non-unions.
Methods: This study examines the temporal evolution of the mechanical properties of bone distraction callus using nanoindentation, ash analysis, micro-CT for trabecular microarchitecture, and Raman spectroscopy for mineral quality. It also establishes single- and two-parameter power laws based on experimental data to predict tissue-level and bulk mechanical properties.
Results: At the macro-scale, the tissue exhibited a considerable increase in bone fraction, controlled by the widening of trabeculae. The Raman mineral-to-matrix ratios increased to cortical levels during regeneration, but the local elastic modulus remained lower. During healing, the tissue underwent changes in ash fraction and in the percentages of Calcium and Phosphorus. Six statistically significant power laws were identified based on the ash fraction, bone fraction, and chemical and Raman parameters.
Discussion: The microarchitecture of woven bone plays a more significant role than its chemical composition in determining the apparent elastic modulus of the tissue. Raman parameters were demonstrated to provide more significant power laws correlations with the micro-scale elastic modulus than mineral content from ash analysis.
During skeletal tissue differentiation processes such as distraction osteogenesis, fracture healing, adaptation to skeletal implants, bone development and regeneration, the structure and composition of the mineralized bone tissue, referred to as woven bone or immature bone, continually change due to growth and responses to the tissue environment, including physical, chemical, and mechanical factors (Wehrle et al., 2014; Tourolle Né Betts et al., 2020; Mora-Macías et al., 2021; Blázquez-Carmona et al., 2021a; Paul et al., 2022). The organic and inorganic matrices of woven bone are highly dynamic and undergo alterations in their structure and composition (Isaksson et al., 2010; Turunen et al., 2011; Martínez-Reina et al., 2018; Reznikov et al., 2018). The inorganic phase is primarily composed of nonstoichiometric hydroxyapatite crystals. This mineral content is deposited in two phases: an initial phase in which 70% of the final mineral content is incorporated within a few weeks, followed by a second phase in which the mineral content increases over months and years (Roschger et al., 2020). The organic phase is predominantly composed of type I collagen, along with various biomacromolecules, including proteoglycans and non-collagenous proteins (Boskey and Robey, 2013). During the initial stages of healing, naïve collagen fibers are randomly oriented due to their rapid formation. As the maturation progresses, these fibers increase in density, reorient, and structurally mature (Blázquez-Carmona et al., 2022). This maturation is understood as the process in which the fibers are crosslinked and packaged to accommodate mineralization. These microstructure arrangements result in a time-dependent mechanical behavior of the tissue, with initial stiffness much lower than that of the matured cortical and trabecular bones.
The microstructure and composition of bone play crucial roles in its macroscopic structural and mechanical behavior. Their relationship has been extensively studied in cortical and trabecular bones (Schaffler and Burr, 1988; Rho et al., 1995; Sevostianov and Kachanov, 2000; Budyn et al., 2012). It has been shown that the elastic modulus of the mature bones strongly depends on mineral content, while toughness correlates with the quality of the collagen matrix (Zioupos and Currey, 1998). Correlations between the elastic modulus and the bone mineral density have been established to estimate mechanical properties from the image-based measurements of the bone mineral density at both the organ and tissue scales (Nobakhti and Shefelbine, 2018). At the organ level, the elastic modulus (E) is related to the apparent mineral density
Various techniques have been developed to assess the bone inorganic matrix at macroscopic scale to measure bone mineral density or mineral content: computed tomography (Snyder and Schneider, 1991; Rho et al., 1995), micro-computed tomography, dual-energy X-ray absorptiometry (Hodgskinson and Currey, 1993; Bouxsein and Radloff, 1997), ashing the sample (Currey, 1988; Martínez-Reina et al., 2018) or weighing it (Schaffler and Burr, 1988; Martin and Boardman, 1993; Keller, 1994; Nicholson et al., 1997). To account for local variations in mineral content, scanning small angle X-ray scattering and wide angle X-ray scattering have been used to measure mineral crystal length and thickness (Roschger et al., 2020). Quantitative back-scattered electron microscopy is a validated method for determining spatially resolved calcium content (Roschger et al., 2020), and Fourier Transform infrared microspectroscopy and Raman microspectroscopy have been widely used to study the inorganic chemical compositional changes of the bone (Tarnowski et al., 2002; Akkus et al., 2004; McCreadie et al., 2006; Yerramshetty et al., 2006; Morris and Mandair, 2011), including mineralization, crystallinity, or carbonate substitution amongst others. For instance, investigating the inorganic chemical compositional changes during bone ageing using infrared and Raman microspectroscopy, it was concluded that Raman microspectroscopy is more sensitive for the inorganic matrix (Turunen et al., 2011). Bone healing processes have also been monitored with Raman spectroscopy (Uthgenant et al., 2007; Gamulin et al., 2013; Ahmed et al., 2018). Ahmed et al. (2018) studied early healing in calvarial defects, which heal spontaneously, with Raman Spectroscopy. They showed an increase in mineral/matrix and crystallinity ratios and a reduction in the carbonate/phosphate ratio after 14 days of healing. However, the long-term temporal evolution of the mechanical, chemical and morphological properties of woven bone during healing in critical-sized bone defects remains unknown. Beyond ash analysis, using Raman spectra or back-scattered electron signals as reliable input data for building power laws to predict the mechanical properties of bone tissue has not been explored to date.
Methods for evaluating the mechanical properties of bone tissue are more standardized. Macroscopic mechanical properties of cortical and trabecular bones have been traditionally evaluated through different mechanical testing including tension, compression, torsion, three-point bending, or buckling (Townsend et al., 1975; Ryan and Williams, 1989; Woo et al., 1991; Bayraktar et al., 2004; Beaupied et al., 2007). Local mechanics of mature tissue has been also assessed with ultrasound microscopy (Eriksen et al., 1994; Hengsberger et al., 2002; Bala et al., 2013), nanoindentation (Rho et al., 1995; 1999; Rho and Pharr, 1999; Zysset et al., 1999; Thurner, 2009) or atomic force microscopy (Asgari et al., 2019). However, for woven bone and its evolutionary properties, studies have used both in vivo (Dwyer et al., 1996; Aarnes et al., 2005; Mora-Macías et al., 2015a; b; Blázquez-Carmona et al., 2021a) and ex vivo approaches (Ohyama et al., 1994; Floerkemeier et al., 2010; Blázquez-Carmona et al., 2022) to provide values of local and apparent stiffness at different time-points during healing. Typically, in vivo mechanical properties are indirectly measured through instrumentation of surgically implanted fixations (Dwyer et al., 1996; Aarnes et al., 2005; Mora-Macías et al., 2015a; b; Blázquez-Carmona et al., 2021a). For ex vivo techniques, nanoindentation tests have proven valid to account for nanoscale heterogeneity and examine bone quality at a lower scale (Leong and Morgan, 2008; Manjubala et al., 2009; Mora-Macías et al., 2017; Mora-Macías et al., 2021). For instance, Manjubala et al. (2009) and Mora-Macías et al. (2017) measured the nanoindentation modulus for woven bone during fracture healing and bone transport processes, respectively.
In silico models are valuable for the understanding the course of healing from a mechanobiological perspective. Many researchers have sought to establish relationships between the mechanical properties of undifferentiated tissue and ultimate tissue phenotype formed in a wide variety of bone regeneration processes, such as fracture healing (Borgiani et al., 2017; Ghiasi et al., 2017), distraction osteogenesis (Isaksson et al., 2007; Reina-Romo et al., 2011; 2012) or tissue engineering (Byrne et al., 2007; Stops et al., 2010), amongst others. As a limitation, all these works develop phenomenological rules based on empirical observations and input parameters that are not sufficiently validated with experimental data, leaving room for improvement in accuracy. In particular, most of these models assumed constant values for the elastic modulus and porosity of the woven bone, regardless of its mineralization state or degree of matrix organization, which is not explicitly modeled. A constant porosity value of 80% and an elastic modulus of 1,000 MPa are typically assigned to the woven bone in most of these mechanobiological evolutionary models (Lacroix and Prendergast, 2002; Isaksson et al., 2007; Burke and Kelly, 2012).
The main aim of this study is to identify time-related changes at the macro- and micro-scales at the chemical, mechanical, and morphological properties of the woven bone during healing of a critical-size bone defect. There is a need for a better understanding of the woven bone micromechanics and the development of a reliable mechanical model of this tissue to improve the prediction of its stiffness. For this purpose, at the microscopic scale, micromechanical properties will be measured with nanoindentation; mineral and organic characteristics will be quantified through Raman spectroscopy; and structural features through micro-CT. At the macroscopic scale, ash and element analyses will be assessed together with a numerical model to reproduce the woven bone bulk mechanical behavior based on physical measurements. All these experimental data will be used to build power laws relating the elastic modulus with the structural and chemical properties of the woven bone for the first time.
The woven bone samples analyzed in the current study originate from previous in vivo distraction osteogenesis experiments conducted on the right-back metatarsi of six skeletally-mature female Merino sheep (Blázquez-Carmona et al., 2021a; b). The animals followed a surgical intervention and a bone lengthening protocol approved by the Animal Ethics of the University of Córdoba (Reference 2021PI/21), in compliance with the European (2010/63/UE) and national (RD 1201/2005) regulations. During the surgery, an Ilizarov-type external fixator was implanted in the metatarsus, and a cross-sectional osteotomy was performed in an intermediate section of the diaphysis. Consequently, each metatarsus was divided into two initially unconnected bone fragments, with their alignment ensured by the fixator device. After a 15-day latency period during which the bone healing begins by way of a preliminary soft callus formation, the fragments were distracted at rate of 1 mm/day during 15 days (Figure 1A). The resulting 15-mm bone callus was then allowed to mineralize over time. The specimens were sacrificed at different time-points of the distraction and consolidation phases to analyze ex vivo different states of callus ossification: days 18, 29, 47, 64, 112 and 161 after surgery. More details on the design of the external fixator and the distraction protocol were provided in previous works (Blázquez-Carmona et al., 2020; 2021b). After sacrifice, operated limbs were immediately stored at −80°C.
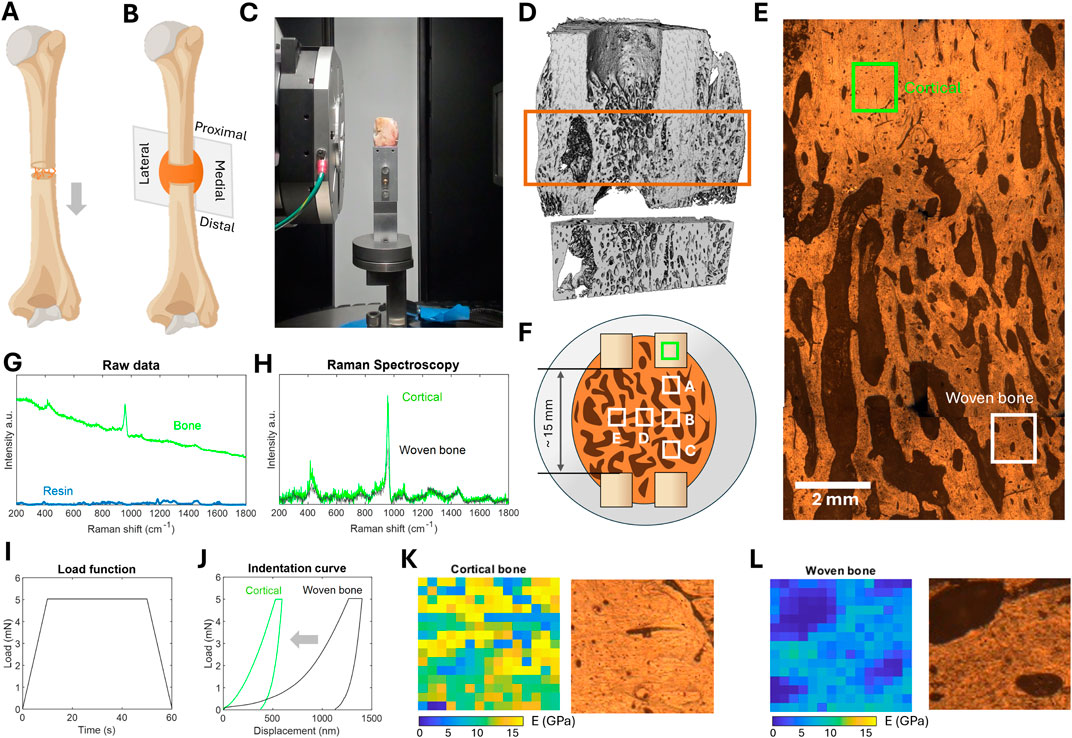
Figure 1. (A) Scheme of the osteotomized metatarsus and the distracion protocol, (B) scheme of the frontal plane sliced and analyzed from each operated limb, (C) image of a bone callus sample being imaged in the tomography, (D) 3D reconstruction of one of the bone calluses and volume of interest structurally analyzed, (E) visualization of microscope image of a bone callus sample. An example of cortical and woven bone areas to be analyzed by Raman Spectroscopy and nanoindentation are indicated, (F) scheme of the embedded bone callus samples and the areas analyzed, (G) example of a raw Raman spectra of the bone and the embedding resin, (H) comparison of corrected Raman spectra between cortical and woven bones, (I) load function applied by the indenter during a nanoindentation measure, (J) comparison of the indentation curve between cortical and woven bones, (K) nanoindentation of a cortical bone area, (L) nanoindentation of a woven bone area.
Two slices of each bone callus, each approximately 3 mm thick, were cut in the frontal plane to address potential differences in the lateral-medial direction (Figure 1B). These cuts were performed using a Femi FM-785XL band saw (Femi, Castel Guelfo, Bologna, Italy) while the sample was freshly taken out of the freezer to maintain the integrity of both the surrounding soft tissues and the callus itself. The first slice was used for micro-CT, Raman Spectroscopy and nanoindentation analysis. For micro-CT, the sample was analyzed in the same condition as cut. However, the other techniques required embedding and subsequent surface polishing to achieve flat and parallel surfaces. For embedding, a 40-mm diameter cylindrical polypropylene mold (FixiForm, Struers, California, United States) and a slow-curing epoxy resin (Epofix, Struers, California, United States) were employed. This resin hardens at room temperature in 24 h, thus avoiding alterations in the mechanical or chemical properties of the sample due to high curing temperatures. Following a bone polishing guidelines provided in the literature (Mora-Macías et al., 2017), the surfaces of the embedded samples were polished by means of carbide papers (P600 to P4000) and diamond slurry (from 3 to 0.25 µm), cleaning them ultrasonically with distilled water after each polishing step. The second slice was used to analyze the chemical composition of each bone callus, for which the cortical fragments were excised. No additional preparation was needed for this second slice. After the slicing, samples were stored in PBS-soaked gauze and plastic wrap at −80°C until the testing day. They were thawed by placement in PBS at room temperature for 1 h prior to every test. Throughout the brief intervals between micro-CT, nanoindentation, and Raman spectroscopy tests, the samples were consistently kept hydrated in PBS-soaked gauze and plastic wrap at 4°C. As a reference for the interpretation and discussion of the micro-CT results, six trabecular and six cortical samples from the operated ovine metatarsus were also cut and preserved as detailed above. Similarly, as a control for the chemical analysis, cortical fragments of each operated metatarsus were prepared.
Micro-CT images were taken using a Cougar tomography® (Y.Cougar SMT, Yxlon, Hudson, Ohio, United States) with the following settings: ×4 optical magnification; exposure time of 9 s; voxel size of 3.72 µm); source setting of 50 kV and 90.02 µm); and a physical size of approximately 25 × 25 × 25 mm. An image of one of the samples in the micro-CT during imaging is provided for reference (Figure 1C). The tomographies were processed using the image analysis platform Thermo Scientific Avizo Software (Thermo Fisher Scientific, Waltham, Massachusetts, United States). A median filter (3D interpretation, 6 neighborhood pixels, 3 iterations) was initially applied to reduce the contrast, soften the edges of the woven bone, and facilitate segmentation. A mixed automatic-manually interactive thresholding was performed, followed by a small noise spot removal with a maximum size of 100 px. The 3D structures were cropped into an inner cube covering the entire bone callus volume. An example of a thresholded sample and the cropped bone callus volume of interest is provided (Figure 1D). From each 3D reconstructed callus, several parameters were determined: bone volume over total volume (BV/TV, module Volume Fraction), average trabecular thickness (Tb.Th, module Average Object Thickness), average trabecular separation (Tb.Sp, module Average Space Thickness), trabecular number (Tb.Nm, module Average Object Number per slice), degree of anisotropy (DA, module Degree of Anisotropy), and Structural Model Index (SMI, module Structure Model Index), which defines the relative prevalence of rods and plates in the structure.
The connectivity of the woven trabecular networks (Conn.D) was calculated using the Euler-Poincaré formula for a 3D structure
where
Control trabecular and cortical bone samples (n = 6 per tissue type) were also measured and analyzed using micro-CT. However, BV/TV was the only parameter calculated in cortical samples due to the absence of trabecular structures in this tissue.
For the spectroscopy and nanoindentation tests, six rectangular regions of interest (800 × 800 µm) were selected in both woven and cortical tissues from each of the embedded and polished bone callus samples. An example locations of a composition of images taken with the microscope to select these areas of interest is provided for reference (Figure 1E), highlighting examples of cortical and woven tissue. One area was always located in the proximal cortical fragment as a control reference (Figure 1F). The other five zones were positioned to cover the proximal-distal (A-B-C) and medial-distal (B-D-E) directions.
Raman Spectroscopy analysis was performed using a LabRAM Horiba Jobin Yvon (HORIBA, Kyoto, Japan) confocal Raman microscope. The embedded samples were periodically sprayed with PBS on their surface to maintain hydration. Spectra were collected with a 785 nm red laser at ×100 magnification, with a 5-s integration time and 20 accumulations. The spectral range was from 200 to 1800
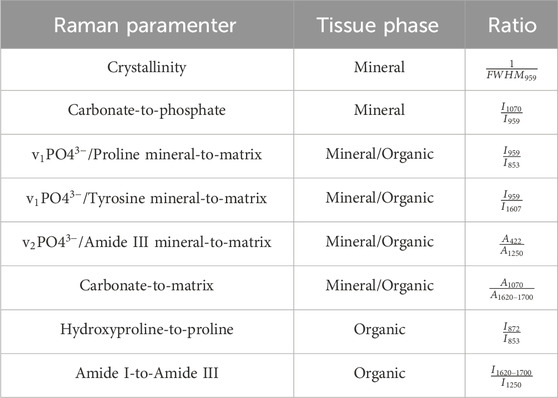
Table 1. Raman parameters in cortical and woven bone tissues calculated for each Raman spectra. I: maximum peak intensity, A: area under the peaks, FWHM: full width at half maximum. the subscript indicates the Raman shift position (
The elastic modulus of the tissue was determined by nanoindentation tests on the same regions of interest described in section 2.3, including the cortical zones. Nanoindentation was performed using a Nanotest indenter (Nanotest, Micro Materials Ltd. Wrexham, United Kingdom) equipped with a Berkovich diamond indenter. In each area, 16 × 16 indentations were made, spaced 50 µm apart in both directions, corresponding to the minimum trabecula thickness of naïve woven bone tissue (López-Pliego et al., 2016). Thus, a total of 256 indentations were performed per area, covering the entire region of interest. Samples were sprayed with PBS from time to time to preserve their hydration. The load applied to each indentation point was increased at a rate of 0.5 mN/s to a maximum of 5 mN (Figure 1I). Once the maximum load was reached in approximately 10 s, it was held constant for 40 s. The unloading was performed at the same rate. The indentation depth, or the indenter’s displacement, is a variable parameter that depends on the hardness of the tissue, being lower in cortical bone (Figure 1J). The Oliver and Pharr method was used to calculate the elastic modulus
The second slice was employed for ash analysis and elemental analysis. The samples were initially ground with a sterilized pestle and mortar. They were then immediately dried in a BINDER VD 23 vacuum drying chamber (BINDER GmbH, Tuttlingen, Germany) using heating cycles at 105
An elemental analysis was also performed on the ashed samples to measure the calcium (Ca) mass percentage and trace element substitutions, mainly stable isotopes of carbon with oxygen in the carbonate (
The elemental analysis of the carbon content was conducted using a TruSpec Micro analyzer (LECO Corporation, Michigan, United States). The calcium and phosphorus contents were measured with an inductively coupled plasma optical emission spectrometer SpectroBLUE (Spectro Analytical Instruments, Kleve, Germany) after the samples were dissolved in hydrochloric acid. As stated in section 2.1, one cortical slice from each metatarsal diaphysis was also prepared and analyzed using the methodology detailed above (six cortical fragments in total).
The ex vivo experiments described in the previous sections will elucidate the evolution of the mechanical and chemical properties of woven bone during healing at the tissue scale, as well as the structural changes at the apparent level towards a cortical microarchitecture. In the literature, ash fraction or calcium content have been shown to be effective predictors of cancellous and cortical bone’s mechanical properties (Currey, 1988; Hernandez et al., 2001; García-Rodríguez and Martínez-Reina, 2017). Therefore, these parameters were used to define single-parameter powers laws that predict the woven bone elastic modulus over the regeneration time, following Equation 4:
where
Given that the experimental data used to fit the empirical coefficients were measured at the micro-scale, the previous models predict the elastic modulus at the tissue scale. Consequently, a two-parameter power law function was also proposed in Equation 5 to differentiate the influence of bone volume (BV/TV) and ash fraction
To adjust the coefficients of this second model, the volume fraction (BV/TV) measured by micro-CT were employed. Moreover, the apparent elastic modulus was taken by the model provided by Blázquez-Carmona et al. (2021a) and shown in Equation 6, which is based on experimental gait force data measured in vivo through instrumented external fixators and a load platform during gait tests on the same animals whose bone calluses were used in this work (R-square = 0.933, p-value
where t is the day after surgery, and
The evolution of the structural parameters in the 3D reconstructed woven bone calluses were measured from the micro-tomographic images (Figure 2). The BV/TV raised during the mineralization process (Figure 2A). The calluses were partially mineralized shortly after the surgery, comprising 44.59
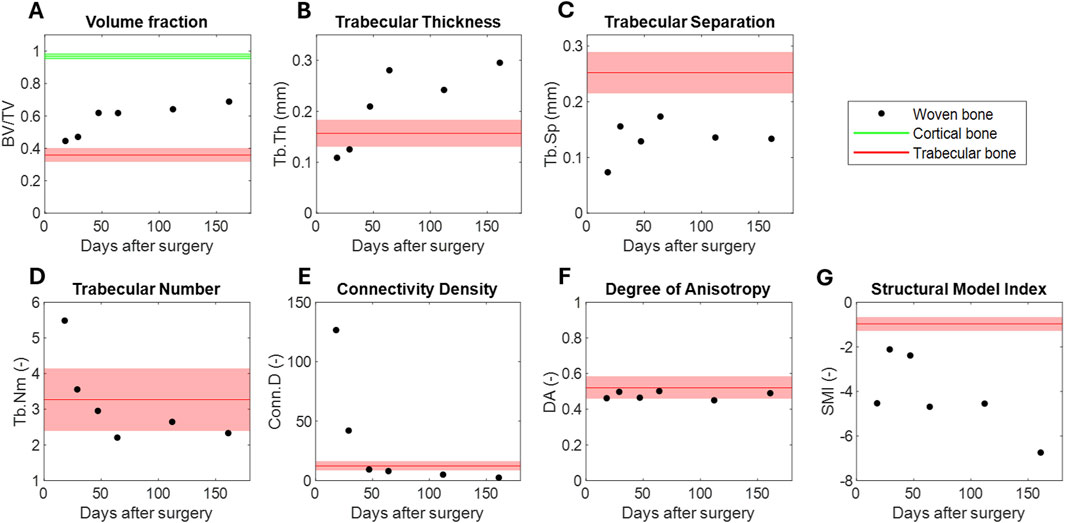
Figure 2. Evolution of the woven bone’s microarchiture measured from micro-tomographic images: (A) volume fraction, (B) trabecular thickness, (C) trabecular separation, (D) trabecular number, (E) connectivity density, (F) degree of anisotropy, (G) structural model index. The average value and standard deviation of the cortical and trabecular data is provided as a reference in green and red, respectively.
The average and standard deviation of the elastic modulus were calculated in each analyzed area, including the cortical region (Figure 3A). Additionally, nanoindentation maps of the analyzed zones, along with their corresponding microscopic reference images, are provided in the Supplementary Material (Supplementary Figure S1). Overall, no remarkable differences were found between the areas in any analyzed direction of the callus, either the proximal-distal direction (A-B-C) or the medial-lateral direction (B-D-E). In all samples, the elastic modulus of cortical tissue is double or triple that of woven bone. The temporal evolution of the elastic modulus of the samples was also analyzed as the global average of all regions of interest (Figure 3B). Note that the control cortical data provided in Figure 3B encompasses the mean and standard deviation from all cortical nanoindentations across all samples/animals (256 cortical indentations per sample, 1,536 in total). Initially, the elastic modulus ranged from 3.07 to 6.32 GPa in the first weeks after surgery, and it increased slightly to 9.25 GPa after 6 months. During the analyzed period, the mechanical properties of woven bone remained notably lower than those of cortical bone, whose elastic modulus was 16.44
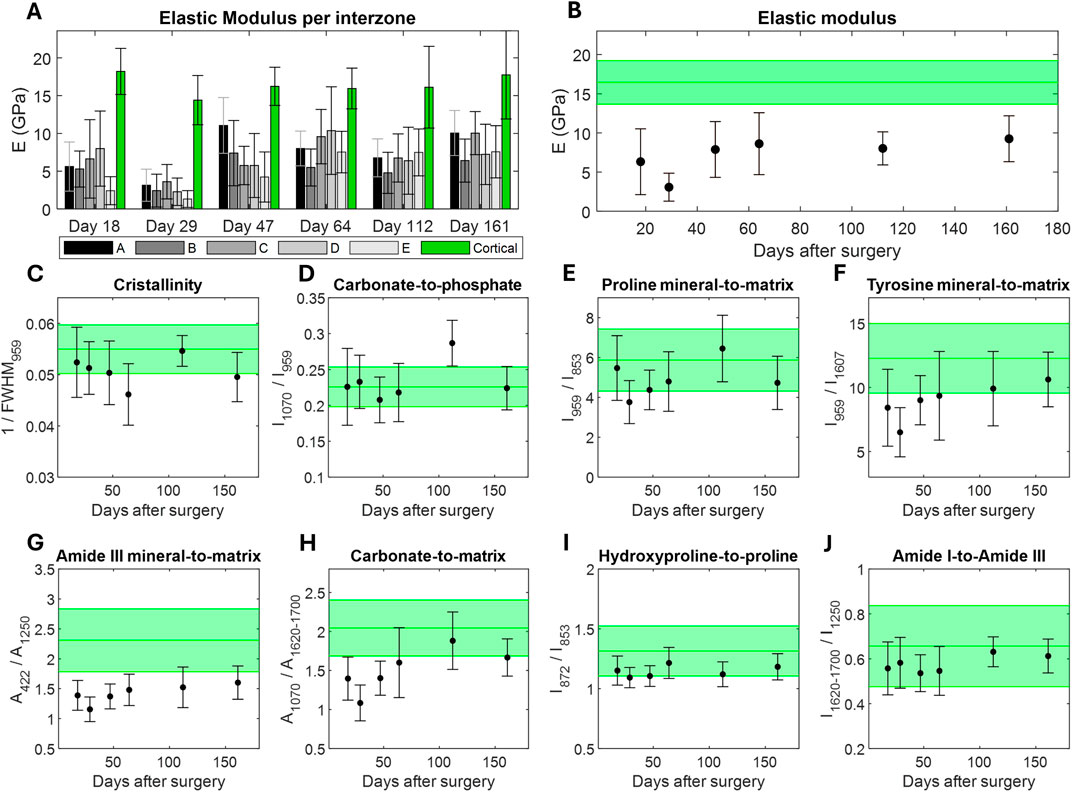
Figure 3. Evolution of the micro-scale woven bone’s elastic modulus and chemical composition measured by nanoindentation and Raman Spectroscopy, respectively. Mechanical properties: (A) elastic modulus by callus zones in each of the samples analyzed, (B) average elastic modulus of all the indentations made in all analyzed areas of the sample. Chemical structure: (C) Cristallinity, (D) Carbonate-to-phosphate, (E) Proline mineral-to-matrix, (F) Tyrosine mineral-to-matrix, (G) Amide III mineral-to-matrix, (H) Carbonate-to-matrix, (I) Hydroxyproline-to-proline, (J) Amide I-to-Amide III. Data from cortical bone (mean and standard deviation) is provided in green.
In this study, the chemical structures of woven and cortical bones were analyzed on both micro- and macro-scales. On the micro-scale, the evolution of the Raman parameters were calculated for each woven bone sample (Figure 3). The data is provided as the average ratios of all zones and all spectra taken from each. The control cortical data provides the average ratios of all spectra measured in all samples (6 spectra per sample, 36 in total). The results per areas of each sample is also provided in the Supplementary Material (Supplementary Figure S2). In both figures, the ratios calculated for the reference cortical tissue are shown in green. The naïve woven bone tissue exhibited a degree of crystallinity comparable to that of cortical tissue from few days after surgery, without appreciable evolution over time (Figure 3C). During regeneration, the carbonate-to-phosphate ratio was also similar to that of cortical bone, without noteworthy differences in their standard deviation (Figure 3D). The mineral amount of Phosphate v1 and v2 was normalized by the organic components of the matrix: Proline (Figure 3E), Tyrosine (Figure 3F), and Amide III (Figure 3G), respectively. Although no trend was observed when normalizing by Proline compared to the cortical tissue, the ratios against the other organic phases began notably lower in woven bone compared to mature bone tissue, tending to approach cortical values during the regeneration phase. The carbonate content of the newly formed bone tissue also increased relative to the organic phase until reaching cortical values (Figure 3H). No trend was found in the Hydroxyproline-to-Proline (Figure 3I) and Amide I-to-Amide III (Figure 3J) ratios, but their standard deviations were lower than those calculated for the same ratios in cortical bone.
Regarding the macro-scale chemical composition, the evolution of the ash fraction over the regeneration time was investigated (Figure 4A). The results obtained from the six control cortical fragments are also provided as a mean and standard deviation (green data). The mass fraction of the mineral component versus the organic component of the tissue increased as the collagen template mineralized over time. Consequently, the ash fraction increased progressively from 0.15 to 0.29 in the less mature calluses to 0.57 in the most ossified ones. This more consolidated callus reached an ash fraction similar to that of cortical tissue, 0.66
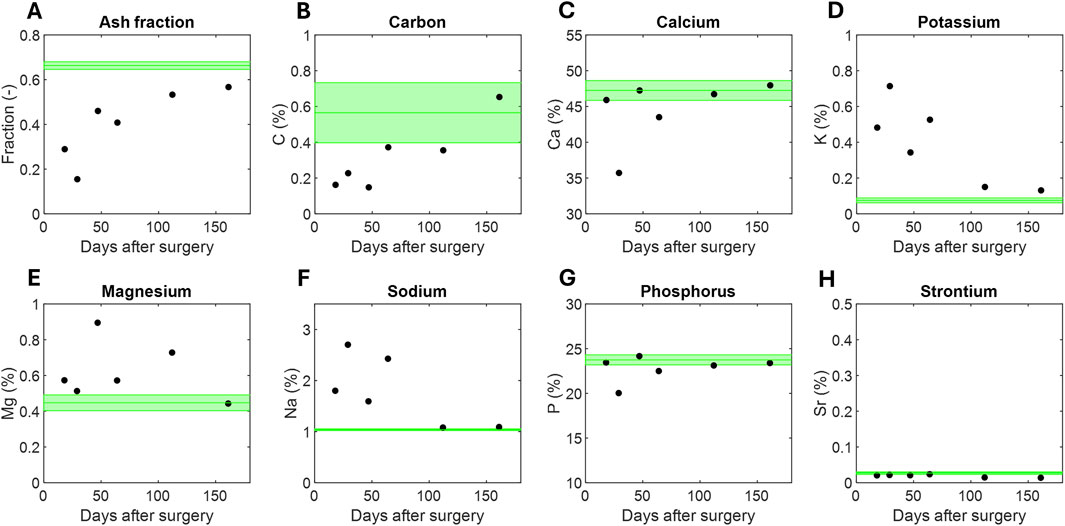
Figure 4. Evolution of the macro-scale woven bone’s chemical composition measured with micro-analysis: (A) ash fraction, (B) carbon percentage, (C) calcium percentage, (D) potassium percentage, (E) magnesium percentage, (F) sodium percentage, (G) phosphorus percentage, (H) strontium percentage. Cortical data (mean and standard deviation) is provided as a reference in green lines.
The micro-elemental determinations of the chemical components specified in section 2.5 are also provided (Figures 4B–H). The carbon content (C
Table 2 presents the different power laws, the value of the empirical constants after adjustment with the experimental data, as well as the goodness-of-fit parameters: the R-square and the p-value. Additionally, these best-fit power law models of the tissue and apparent elastic modulus was also graphically represented as functions of the predictor parameters, plotted against the experimental data (Figure 5). All single-parameter adjustments demonstrated high predictive strength of the tissue elastic modulus, with all R-square values exceeding 0.5 and most of p-values below 0.05. The highest degrees of significance were observed in correlation based on Raman parameters. The largest resulting predictor exponent values were found in the Calcium content measured by chemical analysis (b
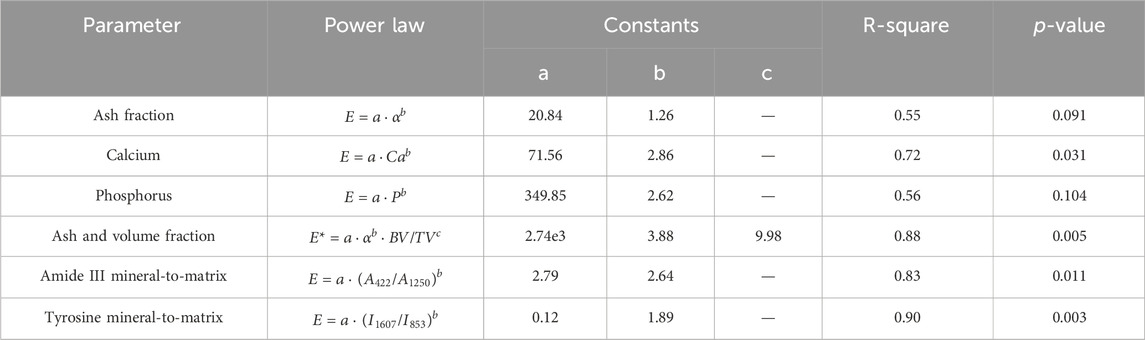
Table 2. Definition of the power laws of the tissue and apparent elastic modulus (
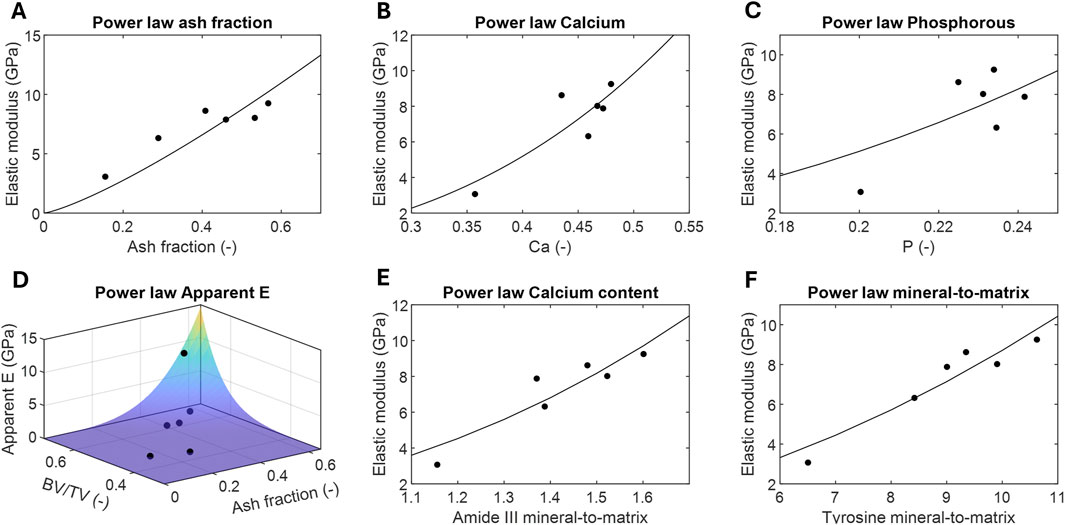
Figure 5. Correlations of the power laws defined in Table 2 to predict the tissue or apparent elastic modulus from the following structural and chemical parameters measured ex vivo: (A) ash fraction from chemical analysis, (B) calcium content from chemical analysis, (C) phosphorus content from chemical analysis, (D) ash fraction from chemical analysis and volume fraction from micro-CT, (E)
The two-parameter power law model based on the ash fraction and bone volume fraction measured in the current study, alongside the macro-scale apparent elastic modulus provided by Blázquez-Carmona et al. (2021a) (Figure 5D), was also found to be highly significant (R-square = 0.88 and p-value = 0.005). Furthermore, the best-fit volume fraction exponent value was nearly 3-fold the ash fraction exponent value, at 9.98 versus 3.88.
Quantifying the structural, chemical, and mechanical properties of the woven bone is crucial for understanding the mechanobiology behind bone regeneration and assessing the effectiveness of ortophaedic approaches for healing critical-sized bone defects. Equally important is the parallel development of numerical models that optimize key engineering parameters to control this biological process and prevent non-unions. There is a notable lack of micromechanical models of woven bone in the literature based on ex vivo experimental data that consider changes in tissue properties at different regeneration phases. The multiscale research presented here analyzed the evolution of the trabeculae organization in this immature tissue through micro-CT, its elastic modulus using nanoindentation, its mineral quality via Raman spectroscopy, and its chemical composition with ash analysis. From these experiments, power laws based on physical measurements were defined for the first time, relating the elastic modulus of the woven bone with its porosity and mineralization state. In addition, the data and power laws provided in this study are highly extrapolated to human bone tissues due to the ovine nature of the samples. High similarities in bone composition were reported between mature sheep and humans in the literature (Newman et al., 1995). Similarly, comparable metabolic and bone remodeling rates were found using dual energy X-ray absorptiometry (den Boer et al., 1999). The results obtained in this study also try to address some open questions in the field: Why is the stiffness of woven bone lower than that of cortical bone? Is it solely due to the mineral content, or is it influenced by the structural factors as well? Do structural and mineral changes equally contribute to the bulk mechanical properties of woven bone? Are Raman spectra valid inputs for defining power laws?
The mechanical properties of the woven bone tissue exhibited a slight increase over the analyzed regeneration period, as indicated by the elastic modulus measured by nanoindentation, which ranged from 3.07 to 9.25 GPa (Figures 3A, B; Supplementary Figure S1). However, the stiffness levels characteristic of cortical tissue, approximately 16.44
The mineral content in woven bone has been previously examinated in the literature. Manjubala et al. (2009) measured calcium content directly from back-scattered electron microscopic images (2D mineral content), showing inhomogeneity in the callus mineralization with a maximum Ca content of 20% of Ca that saturates at week 9 after surgery. In cortical bone, Turunen et al. (2011) investigated the temporal evolution of mineral content during aging with Infrared and Raman spectroscopy. They found that while mineralization increases over time, hydroxyapatite crystals mature more slowly. Ahmed et al. (2018) reported an increase in the mineral-to-matrix and crystallinity ratios during the first 14 days of healing in calvarial defects through Raman Spectroscopy. In our study, bone mineralization during healing was quantified at the microscopic scale using several Raman parameters, including mineral-to-matrix and carbonate-to-matrix ratios. Figure 3 demonstrates the positive correlation between the Tyrosine and Amide III mineral-to-matrix and healing time, reaching values comparable to those of cortical bone at day 161. These measurements provide a quantitative assessment of the extent of bone mineralization, directly related to ash weight (Gourion-Arsiquaud et al., 2009). Crystallinity, which is a measure of the crystal size development (Turunen et al., 2011), remained nearly constant during the consolidation phase, with values similar to those of the cortical bone (Figure 3C). Given that osteoid is deposited by osteoblasts at different locations and timing within the callus, this finding suggests that the maximum crystal size is obtained in an early stage of regeneration. Despite the increase in the carbonate-to-matrix ratio (Figure 3H), the carbonate-to-phosphate ratio (Figure 3D) showed no trend during the consolidation phase, maintaining values akin to those of cortical bone. Similar results were reported in calvarian healing (Ahmed et al., 2018). This ratio represents type-B carbonate substitution into hydroxyapatite, a process not fully understood but associated with increased solubility and decreased mechanical performance of the tissue (Pan and Darvell, 2010). Literature suggests this substitution is more related to aging, as carbonate peak areas and intensities increase with age (Boskey and Robey, 2013; Turunen et al., 2013). Regarding the hydroxyproline-to-proline ratio, the literature proved that it negatively correlates with the maturation of the tissue (Shah et al., 2019). However, it keeps constant in woven bone and within the standard deviation range of cortical bone (Figure 3G). A similar trend was observed for the Amide I-to-Amide III ratio, which remained approximately constant above 1 (Figure 3J). It follows a very similar trend to crystallinity, as both processes are closely correlated with the bone formation. Initially, naïve collagen fibers are created followed by an enzymatically crosslinking (Knott and Bailey, 1998). These fibers then mineralized and served as scaffolds for the nucleation and growth of the additional mineral crystals (Gourion-Arsiquaud et al., 2009). A high Amide I-to-Amide III ratio indicates a predominance of functional and mature collagen crosslinks, whereas a predominance of Amide III suggests high activity of nonfunctional precursor collagen with reducible crosslinks (Coelho et al., 2014; Mandair and Morris, 2015; Fraulob et al., 2020). Thus, woven bone exhibits an increase in procollagen molecules and immature crosslinks during the analyzed regeneration phase.
Figure 4 also reported the chemical analysis performed by ash analysis and elemental study. The ash fraction, phosphorous and calcium content increased nonlinearly with healing time with a plateau nearly the cortical reference values. Phosphorous and calcium contents are also in line with the infrared and X-ray analysis on natural hydroxyapatite (Janicki et al., 2012). Numerous substitutors were reported in hydroxyapatite crystals in the literature, including carbon, potassium, magnesium, sodium, or strontium (Bergstrom and Wallace, 1954; Buddhachat et al., 2016; Katzenberg, 2020). For potassium and sodium, the decrease with time was quantified (Figures 4D, F). However, none of the above substitutes seems to play a key role during the bone regeneration process.
Regarding the structural features of the woven bone at the trabecular scale, as measured by micro-CT, the BV/TV increased up to 0.69. This increase is primarily due to an increased in the trabecuale thickness (Tb.Th) as the different mineralization fronts advance (Figure 2). Previous studies have already examined bone volume fraction using different techniques and length scales. For instance, Blázquez-Carmona et al. (2021a) and Mora-Macías et al. (2021) measured the bone volume fraction from CT macroscopic images in bone lengthening and bone transport, respectively. In these studies, the volume fraction ranged from 88.18% to 93.97% in bone lengthening and 87.55%–100% in bone transport at days 121–161 after surgery. The lower values in our study are more consistent with estimates reported in bone transport calluses (Mora-Macías et al., 2021), which used direct segmentation of 2D micrographs based on x-ray grey-scale images. Thus, the porosity at the trabecular scale appears to significantly impact the estimation of the bulk volume fraction. This structural feature likely contributes to the differences found in the same period of time between the micro-scale elastic modulus measured in this study (3.07–9.25 GPa), and the lower apparent elastic modulus measured in vivo by Blázquez-Carmona et al. (2021a) (0.01–8.53 GPa), input in a later discussed power law. Compared to the trabecular tissue, woven bone only exhibits BV/TV levels similar to those observed in this study or those reported in femoral bone at the early stages of regeneration (Mittra et al., 2005; Teo et al., 2007). The other three-dimensional microarchitectural parameters of woven bone (Figure 2) could not be directly compared to other regenerating tissues due to the lack of reported data in the literature, to our knowledge. Therefore, comparisons are limited to cancellous bone tissue data from this study or literature sources (Mittra et al., 2005; Teo et al., 2007; Turunen et al., 2013). The aforementioned increase in Tb.Th above cancellous values occurs alongside a progressive reduction of the number (Tb.Nm) and interconnectivity (Conn.D) of woven trabeculae, more similar to that of healthy metatarsal trabecular tissue, 3.26
The previous experimental data facilitated the definition of the power laws presented in Table 2, which serve as valuable tools for predicting the elastic modulus of woven bone in future in silico models at both macro- and micro-scales. The varied laws allow for the assignment of woven bone tissue mechanical properties based on different experimental results, not necessarily mechanical testing. Except for the current study, woven bone correlations have never been established using mechanical, structural and chemical parameters measured directly from ex vivo samples. The exponents of these expressions (
There are several limitations associated with the methodology employed in this study. Firstly, it is expected that the mechanical, structural and chemical parameters analyzed ex vivo are not significantly influenced by differences in bone maturity of sheep during the regeneration period in vivo since the longest experiment (161 days) represents only around 4% of the animal life cycle. Secondly, the methods used for the indentation test (Oliver and Pharr, 1992) assume linear elastic behavior in the tissue, despite the possibility that the woven bone could exhibit viscoelastic behavior in some callus interzones, particularly during early stage of mineralization. However, the mechanical characterization performed in this study is focused on the mineralized phase, where the influence of the viscoelastic behavior should not be significant compared to a soft tissue (Blázquez-Carmona et al., 2021b). Using the Oliver-Pharr method in the evaluation of the nanoindentations also presents several limitations. The elastic modulus of surrounding tissue sub-domains, along with the presence of microcracks or defects, may influence the homogenized and averaged elastic modulus measured by the indenter (Kariem et al., 2015; Pastrama et al., 2018; Königsberger et al., 2022). Additionally, the use of different specimens for each time-point introduces an inevitable source of variation in the measurements. Despite this, the results appear to follow logical trends, and the power laws derived are significant. Finally, a higher number of animals would have enhanced the statistical significance of the conclusions of this study. As previously mentioned, the authors prioritized the use of an ovine animal model, whose results are crucial for construction of more realistic micromechanical models and whose conclusions can be readily extrapolated to human clinical cases.
In conclusion, this work contributes to the development of novel micromechanical models applicable to numerical simulations of bone regeneration processes. It also enhances the understanding of the relationship between chemical composition, structural morphology, and the mechanical properties of woven bone at different length scales by combining multiple ex vivo techniques: micro-CT, nanoindentation, Raman spectroscopy, and chemical and elemental analysis. Addressing the questions posed at the beginning of the discussion, woven bone exhibited a significant increase in bone volume, primarily controlled by the thickening and unification of trabeculae, alongside a simultaneous increase in apparent ash fraction, calcium, and phosphate content. The power law established for the bulk elastic modulus highlights a more significant influence of the evolving trabecular microarchitecture on the apparent mechanical behavior of the bone callus. At the tissue scale, the Raman mineral-to-matrix ratio increased over the analyzed regeneration period, reaching values and crystallinity levels comparable to those of cortical bone. However, the local elastic modulus did not increase sufficiently to reach cortical values, potentially due to the role of microporosities within the trabeculae. Power laws predicting the evolution of the woven bone elastic modulus at this scale demonstrated that Raman parameters correlate better with the elastic modulus than apparent mineral content measured through ash analysis and elemental studies. Therefore, we advocate for the combined use of Raman spectroscopy and nanoindentation in constructing future power laws for regenerating tissue, potentially strengthened by including a second parameter to account for structural features at the microscale.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
The animal study was approved by Animal Ethics of the University of Córdoba (Reference 2021PI/21). The study was conducted in accordance with the local legislation and institutional requirements.
PB-C: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Visualization, Writing–original draft, Writing–review and editing. JM-M: Conceptualization, Funding acquisition, Methodology, Project administration, Supervision, Writing–review and editing. AP: Investigation, Methodology, Writing–review and editing. ÁM: Data curation, Writing–review and editing. ER-R: Conceptualization, Formal Analysis, Funding acquisition, Project administration, Supervision, Writing–original draft, Writing–review and editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Grant PID 2020-113790RB-I00 funded by MICIU/AEI/10.13039/501100011033.
Micro-CT imaging and chemical analysis of the bone samples were performed in the University of Seville Research, Technology and Innovation Centre (CITIUS).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbioe.2024.1476473/full#supplementary-material
Aarnes, G., Steen, H., Ludvigsen, P., Waanders, N., Huiskes, R., and Goldstein, S. (2005). In vivo assessment of regenerate axial stiffness in distraction osteogenesis. J. Orthop. Res. 23, 494–498. doi:10.1016/j.orthres.2004.08.024
Ahmed, R., Law, A., Cheung, T., and Lau, C. (2018). Raman spectroscopy of bone composition during healing of subcritical calvarial defects. Biomed. Opt. express 9, 1704–1716. doi:10.1364/boe.9.001704
Akkus, O., Adar, F., and Schaffler, M. B. (2004). Age-related changes in physicochemical properties of mineral crystals are related to impaired mechanical function of cortical bone. Bone 34, 443–453. doi:10.1016/j.bone.2003.11.003
Asgari, M., Abi-Rafeh, J., Hendy, G. N., and Pasini, D. (2019). Material anisotropy and elasticity of cortical and trabecular bone in the adult mouse femur via afm indentation. J. Mech. Behav. Biomed. Mater. 93, 81–92. doi:10.1016/j.jmbbm.2019.01.024
Bala, Y., Farlay, D., and Boivin, G. (2013). Bone mineralization: from tissue to crystal in normal and pathological contexts. Osteoporos. Int. 24, 2153–2166. doi:10.1007/s00198-012-2228-y
Bayraktar, H., Morgan, E., Niebur, G., Morris, G., Wong, E., and Keaveny, T. (2004). Comparison of the elastic and yield properties of human femoral trabecular and cortical bone tissue. J. Biomech. 37, 27–35. doi:10.1016/s0021-9290(03)00257-4
Beaupied, H., Lespessailles, E., and Benhamou, C. (2007). Evaluation of macrostructural bone biomechanics. Jt. Bone Spine 74, 233–239. doi:10.1016/j.jbspin.2007.01.019
Bergstrom, W. H., and Wallace, W. M. (1954). Bone as a sodium and potassium reservoir. J. Clin. Investigation 33, 867–873. doi:10.1172/jci102959
Blázquez-Carmona, P., Mora-Macías, J., Morgaz, J., Fernández-Sarmiento, J. A., Domínguez, J., and Reina-Romo, E. (2021a). Mechanobiology of bone consolidation during distraction osteogenesis: bone lengthening vs. bone transport. Ann. Biomed. Eng. 49, 1209–1221. doi:10.1007/s10439-020-02665-z
Blázquez-Carmona, P., Mora-Macías, J., Sanz-Herrera, J. A., Morgaz, J., Navarrete-Calvo, R., Domínguez, J., et al. (2021b). Mechanical influence of surrounding soft tissue on bone regeneration processes: a bone lengthening study. Ann. Biomed. Eng. 49, 642–652. doi:10.1007/s10439-020-02592-z
Blázquez-Carmona, P., Sanchez-Raya, M., Mora-Macías, J., Gómez-Galán, J. A., Domínguez, J., and Reina-Romo, E. (2020). Real-time wireless platform for in vivo monitoring of bone regeneration. Sensors 20, 4591. doi:10.3390/s20164591
Blázquez-Carmona, P., Sanz-Herrera, J. A., Mora-Macías, J., Morgaz, J., Domínguez, J., and Reina-Romo, E. (2022). Time-dependent collagen fibered structure in the early distraction callus: imaging characterization and mathematical modeling. Ann. Biomed. Eng. 50, 1798–1809. doi:10.1007/s10439-022-02992-3
Borgiani, E., Duda, G., and Checa, S. (2017). Multiscale modeling of bone healing: toward a systems biology approach. Front. Physiol. 8, 287. doi:10.3389/fphys.2017.00287
Boskey, A. L., and Robey, P. G. (2013). “The composition of bone,” in Primer on the metabolic bone diseases and disorders of mineral metabolism, 49–58.
Bouxsein, M., and Radloff, S. (1997). Quantitative ultrasound of the calcaneus reflects the mechanical properties of calcaneal trabecular bone. J. Bone Min. Res. 12, 839–846. doi:10.1359/jbmr.1997.12.5.839
Buddhachat, K., Klinhom, S., Siengdee, P., Brown, J. L., Nomsiri, R., Kaewmong, P., et al. (2016). Elemental analysis of bone, teeth, horn and antler in different animal species using non-invasive handheld x-ray fluorescence. PLoS One 11, e0155458. doi:10.1371/journal.pone.0155458
Budyn, E., Jonvaux, J., Funfschilling, C., and Hoc, T. (2012). Bovine cortical bone stiffness and local strain are affected by mineralization and morphology. J. Appl. Mech. 79 (011008–1). doi:10.1115/1.4004644
Burke, D. P., and Kelly, D. J. (2012). Substrate stiffness and oxygen as regulators of stem cell differentiation during skeletal tissue regeneration: a mechanobiological model. PLoS ONE 7, e40737. doi:10.1371/journal.pone.0040737
Byrne, D. P., Lacroix, D., Planell, J. A., Kelly, D. J., and Prendergast, P. J. (2007). Simulation of tissue differentiation in a scaffold as a function of porosity, young’s modulus and dissolution rate: application of mechanobiological models in tissue engineering. Biomaterials 28, 5544–5554. doi:10.1016/j.biomaterials.2007.09.003
Coelho, N. P. M. d. F., Raniero, L., Costa, C. L. S. d., Maia Filho, A. L. M., Martins, M., Martin, A. A., et al. (2014). Ft-Raman spectroscopic study of skin wound healing in diabetic rats treated with cenostigma macrophyllum tul. Rev. Bras. Eng. Biomédica 30, 47–53. doi:10.4322/rbeb.2013.047
Currey, J. (1988). The effect of porosity and mineral content on the young’s modulus of elasticity of compact bone. J. Biomech. 21, 131–139. doi:10.1016/0021-9290(88)90006-1
den Boer, F. C., Patka, P., Bakker, F. C., Wippermann, B. W., van Lingen, A., Vink, G. Q., et al. (1999). New segmental long bone defect model in sheep: quantitative analysis of healing with dual energy x-ray absorptiometry. J. Orthop. Res. 17, 654–660. doi:10.1002/jor.1100170506
Dwyer, J., Owen, P., Evans, G., Kuiper, J., and Richardson, J. (1996). Stiffness measurements to assess healing during leg lengthening. a preliminary report. J. Bone Jt. Surg. Br. 78, 286–289. doi:10.1302/0301-620x.78b2.0780286
Eriksen, E., Axelrod, D., and Melsen, F. (1994). Bone histomorphometry. New York, United States: Raven Press.
Floerkemeier, T., Thorey, F., Hurschler, C., Wellmann, M., Witte, F., and Windhagen, H. (2010). Stiffness of callus tissue during distraction osteogenesis. Orthop. Traumatol. Surg. Res. 96, 155–160. doi:10.1016/j.otsr.2009.11.005
Fraulob, M., Pang, S., Le Cann, S., Vayron, R., Laurent-Brocq, M., Todatry, S., et al. (2020). Multimodal characterization of the bone-implant interface using Raman spectroscopy and nanoindentation. Med. Eng. & Phys. 84, 60–67. doi:10.1016/j.medengphy.2020.07.013
Fritsch, A., and Hellmich, C. (2007). universal’microstructural patterns in cortical and trabecular, extracellular and extravascular bone materials: micromechanics-based prediction of anisotropic elasticity. J. Theor. Biol. 244, 597–620. doi:10.1016/j.jtbi.2006.09.013
Gamulin, O., Serec, K., Bilić, V., Balarin, M., Kosović, M., Drmić, D., et al. (2013). Monitoring the healing process of rat bones using Raman spectroscopy. J. Mol. Struct. 1044, 308–313. doi:10.1016/j.molstruc.2013.01.049
García-Rodríguez, J., and Martínez-Reina, J. (2017). Elastic properties of woven bone: effect of mineral content and collagen fibrils orientation. Biomechanics Model. Mechanobiol. 16, 159–172. doi:10.1007/s10237-016-0808-z
Ghiasi, M. S., Chen, J., Vaziri, A., Rodriguez, E. K., and Nazarian, A. (2017). Bone fracture healing in mechanobiological modeling: a review of principles and methods. Bone Rep. 6, 87–100. doi:10.1016/j.bonr.2017.03.002
Gourion-Arsiquaud, S., Burket, J., Havill, L., DiCarlo, E., Doty, S., Mendelsohn, R., et al. (2009). Spatial variation in osteonal bone properties relative to tissue and animal age. J. bone mineral Res. official J. Am. Soc. Bone Mineral Res. 24, 1271–1281. doi:10.1359/jbmr.090201
Hamed, E., Lee, Y., and Jasiuk, I. (2010). Multiscale modeling of elastic properties of cortical bone. Acta Mech. 213, 131–154. doi:10.1007/s00707-010-0326-5
Hellmich, C., Ukaj, N., Smeets, B., Van Oosterwyck, H., Filipovic, N., Zelaya-Lainez, L., et al. (2022). Hierarchical biomechanics: concepts, bone as prominent example, and perspectives beyond. Appl. Mech. Rev. 74, 030802. doi:10.1115/1.4055032
Hengsberger, S., Kulik, A., and Zysset, P. (2002). Nanoindentation discriminates the elastic properties of individual human bone lamellae under dry and physiological conditions. Raven Press 30, 178–184. doi:10.1016/s8756-3282(01)00624-x
Hernandez, C. J., Beaupré, G. S., Keller, T. S., and Carter, D. R. (2001). The influence of bone volume fraction and ash fraction on bone strength and modulus. Bone 29, 74–78. doi:10.1016/s8756-3282(01)00467-7
Hildebrand, T., and Rüegsegger, P. (1997). Quantification of bone microarchitecture with the structure model index. Comput. Methods Biomechanics Bio Med. Eng. 1, 15–23. doi:10.1080/01495739708936692
Hodgskinson, R., and Currey, J. (1993). Separate effects of osteoporosis and density on the strength and stiffness of human cancellous bone. Clin. Biomech. 8, 262–268. doi:10.1016/0268-0033(93)90036-h
Isaksson, H., Comas, O., van Donkelaar, C., Mediavilla, J., Wilson, W., Huiskes, R., et al. (2007). Bone regeneration during distraction osteogenesis: mechano-regulation by shear strain and fluid velocity. J. Biomech. 40, 2002–2011. doi:10.1016/j.jbiomech.2006.09.028
Isaksson, H., Turunen, M. J., Rieppo, L., Saarakkala, S., Tamminen, I., Rieppo, J., et al. (2010). Infrared spectroscopy indicates altered bone turnover and remodeling activity in renal osteodystrophy. J. bone mineral Res. 25, 1360–1366. doi:10.1002/jbmr.10
Janicki, T., Sobczak-Kupiec, A., Skomro, P., and Wzorek, Z. (2012). Surface of root cementum following air-polishing with bioactive hydroxyapatite (ca and p mapping). a pilot study. Acta Bioeng. Biomech. 14, 31–38.
Kariem, H., Pastrama, M.-I., Roohani-Esfahani, S. I., Pivonka, P., Zreiqat, H., and Hellmich, C. (2015). Micro-poro-elasticity of baghdadite-based bone tissue engineering scaffolds: a unifying approach based on ultrasonics, nanoindentation, and homogenization theory. Mater. Sci. Eng. C 46, 553–564. doi:10.1016/j.msec.2014.10.072
Katzenberg, M. A. (2020). “Bone: chemical analysis,” in Encyclopedia of global archaeology (Springer), 1560–1565.
Keller, T. (1994). Predicting the compressive mechanical behavior of bone. J. Biomech. 27, 1159–1168. doi:10.1016/0021-9290(94)90056-6
Knott, L., and Bailey, A. (1998). Collagen cross-links in mineralizing tissues: a review of their chemistry, function, and clinical relevance. Bone 22, 181–187. doi:10.1016/s8756-3282(97)00279-2
Königsberger, M., Zelaya-Lainez, L., Lahayne, O., Pichler, B. L., and Hellmich, C. (2022). Nanoindentation-probed oliver-pharr half-spaces in alkali-activated slag-fly ash pastes: multimethod identification of microelasticity and hardness. Mech. Adv. Mater. Struct. 29, 4878–4889. doi:10.1080/15376494.2021.1941450
Kumbolder, V., Morin, C., Scheiner, S., and Hellmich, C. (2024). Hierarchical elastoplasticity of cortical bone: observations, mathematical modeling, validation. Mech. Mater. 198, 105140. doi:10.1016/j.mechmat.2024.105140
Lacroix, D., and Prendergast, P. (2002). A mechano-regulation model for tissue differentiation during fracture healing: analysis of gap size and loading. J. Biomech. 35, 1163–1171. doi:10.1016/s0021-9290(02)00086-6
Leong, P., and Morgan, E. (2008). Measurement of fracture callus material properties via nanoindentation. Acta Biomater. 4, 1569–1575. doi:10.1016/j.actbio.2008.02.030
López-Pliego, E. M., Giráldez-Sánchez, M. Á., Mora-Macías, J., Reina-Romo, E., and Domínguez, J. (2016). Histological evolution of the regenerate during bone transport: an experimental study in sheep. Injury 47, S7–S14. doi:10.1016/s0020-1383(16)30600-3
Mandair, G. S., and Morris, M. D. (2015). Contributions of Raman spectroscopy to the understanding of bone strength. BoneKEy Rep. 4, 620. doi:10.1038/bonekey.2014.115
Manjubala, I., Liu, Y., Epari, D., Roschger, P., Schell, H., Fratzl, P., et al. (2009). Spatial and temporal variations of mechanical properties and mineral content of the external callus during bone healing. Bone 45, 185–192. doi:10.1016/j.bone.2009.04.249
Martin, R., and Boardman, D. (1993). The effects of collagen fiber orientation, porosity, density, and mineralization on bovine cortical bone bending properties. J. Biomech. 26, 1047–1054. doi:10.1016/s0021-9290(05)80004-1
Martínez-Reina, J., García-Rodríguez, J., Mora-Macías, J., Domínguez, J., and Reina-Romo, E. (2018). Comparison of the volumetric composition of lamellar bone and the woven bone of calluses. Proc. Institution Mech. Eng. Part H J. Eng. Med. 232, 682–689. doi:10.1177/0954411918784085
McCreadie, B. R., Morris, M. D., Chen, T. C., Sudhaker Rao, D., Finney, W. F., Widjaja, E., et al. (2006). Bone tissue compositional differences in women with and without osteoporotic fracture. Bone 39, 1190–1195. doi:10.1016/j.bone.2006.06.008
Mittra, E., Rubin, C., and Qin, Y.-X. (2005). Interrelationship of trabecular mechanical and microstructural properties in sheep trabecular bone. J. biomechanics 38, 1229–1237. doi:10.1016/j.jbiomech.2004.06.007
Mora-Macías, J., García-Florencio, P., Pajares, A., Miranda, P., Domínguez, J., and Reina-Romo, E. (2021). Elastic modulus of woven bone: correlation with evolution of porosity and x-ray greyscale. Ann. Biomed. Eng. 49, 180–190. doi:10.1007/s10439-020-02529-6
Mora-Macías, J., Pajares, A., Miranda, P., Domínguez, J., and Reina-Romo, E. (2017). Mechanical characterization via nanoindentation of the woven bone developed during bone transport. J. Mech. Behav. Biomed. Mater. 74, 236–244. doi:10.1016/j.jmbbm.2017.05.031
Mora-Macías, J., Reina-Romo, E., and Domínguez, J. (2015a). Distraction osteogenesis device to estimate the axial stiffness of the callus in vivo. Med. Eng. Phys. 37, 969–978. doi:10.1016/j.medengphy.2015.07.008
Mora-Macías, J., Reina-Romo, E., López-Pliego, M., Giráldez-Sánchez, M., and Domínguez, J. (2015b). In vivo mechanical characterization of the distraction callus during bone consolidation. Ann. Biomed. Eng. 43, 2663–2674. doi:10.1007/s10439-015-1330-7
Morris, M. D., and Mandair, G. S. (2011). Raman assessment of bone quality. Clin. Orthop. Relat. Res. 469, 2160–2169. doi:10.1007/s11999-010-1692-y
Newman, E., Turner, A., and Wark, J. (1995). The potential of sheep for the study of osteopenia: current status and comparison with other animal models. Bone 16, S277–S284. doi:10.1016/8756-3282(95)00026-a
Nicholson, P., Cheng, X., Loweta, G., Boonen, S., Davie, M., Dequeker, J., et al. (1997). Structural and material mechanical properties of human vertebral cancellous bone. Med. Eng. Phys. 19, 729–737. doi:10.1016/s1350-4533(97)00030-1
Nobakhti, S., and Shefelbine, S. (2018). On the relation of bone mineral density and the elastic modulus in healthy and pathologic bone. Curr. Osteoporos. Rep. 16, 404–410. doi:10.1007/s11914-018-0449-5
Odgaard, A., and Gundersen, H. (1993). Quantification of connectivity in cancellous bone, with special emphasis on 3-d reconstructions. Bone 14, 173–182. doi:10.1016/8756-3282(93)90245-6
Ohyama, M., Miyasaka, Y., Sakurai, M., Yokobori Jr, A., and Sasaki, S. (1994). The mechanical behavior and morphological structure of callus in experimental callotasis. Biomed. Mater. Eng. 4, 273–281. doi:10.3233/bme-1994-4403
Oliver, W. C., and Pharr, G. M. (1992). An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 7, 1564–1583. doi:10.1557/jmr.1992.1564
Pan, H., and Darvell, B. W. (2010). Effect of carbonate on hydroxyapatite solubility. Cryst. Growth & Des. 10, 845–850. doi:10.1021/cg901199h
Pastrama, M.-I., Blanchard, R., Clement, J. G., Pivonka, P., and Hellmich, C. (2018). Modal analysis of nanoindentation data, confirming that reduced bone turnover may cause increased tissue mineralization/elasticity. J. Mech. Behav. Biomed. Mater. 84, 217–224. doi:10.1016/j.jmbbm.2018.05.014
Paul, G. R., Vallaster, P., Rüegg, M., Scheuren, A. C., Tourolle, D. C., Kuhn, G. A., et al. (2022). Tissue-level regeneration and remodeling dynamics are driven by mechanical stimuli in the microenvironment in a post-bridging loaded femur defect healing model in mice. Front. cell Dev. Biol. 10, 856204. doi:10.3389/fcell.2022.856204
Reina-Romo, E., Gómez-Benito, M. J., Domínguez, J., and García-Aznar, J. M. (2012). A lattice-based approach to model distraction osteogenesis. J. biomechanics 45, 2736–2742. doi:10.1016/j.jbiomech.2012.09.004
Reina-Romo, E., Gómez-Benito, M. J., Sampietro-Fuentes, A., Domínguez, J., and García-Aznar, J. M. (2011). Three-dimensional simulation of mandibular distraction osteogenesis: mechanobiological analysis. Ann. Biomed. Eng. 39, 35–43. doi:10.1007/s10439-010-0166-4
Reznikov, N., Bilton, M., Lari, L., Stevens, M. M., and Kröger, R. (2018). Fractal-like hierarchical organization of bone begins at the nanoscale. Science 360, eaao2189. doi:10.1126/science.aao2189
Rho, J., Hobato, M., and Ashman, R. (1995). Relations of mechanical properties to density and ct numbers in human bone. Med. Eng. Phys. 5, 347–355. doi:10.1016/1350-4533(95)97314-f
Rho, J., and Pharr, G. (1999). Effects of drying on the mechanical properties of bovine femur measured by nanoindentation. J. Mater. Sci. Mater. Med. 10, 485–488. doi:10.1023/a:1008901109705
Rho, J., Zioupos, P., Currey, J., and Pharr, G. (1999). Variations in the individual thick lamellar properties within osteons by nanoindentation. Bone 25, 295–300. doi:10.1016/s8756-3282(99)00163-5
Rice, J., Cowin, S., and Bowman, J. (1988). On the dependence of the elasticity and strength of cancellous bone on apparent density. J. Biomech. 21, 155–168. doi:10.1016/0021-9290(88)90008-5
Roschger, A., Gamsjaeger, S., Hofstetter, B., Masic, A., Blouin, S., Messmer, P., et al. (2014). Relationship between the v 2 po 4/amide iii ratio assessed by Raman spectroscopy and the calcium content measured by quantitative backscattered electron microscopy in healthy human osteonal bone. J. Biomed. Opt. 19, 065002. doi:10.1117/1.jbo.19.6.065002
Roschger, A., Wagermaier, W., Gamsjaeger, S., Hassler, N., Schmidt, I., Blouin, S., et al. (2020). Newly formed and remodeled human bone exhibits differences in the mineralization process. Acta Biomater. 104, 221–230. doi:10.1016/j.actbio.2020.01.004
Ryan, S., and Williams, J. (1989). Tensile testing of rodlike trabeculae excised from bovine femoral bone. J. Biomech. 22, 351–355. doi:10.1016/0021-9290(89)90049-3
Schaffler, M., and Burr, D. (1988). Stiffness of compact bone: effects of porosity and density. J. Biomech. 21, 13–16. doi:10.1016/0021-9290(88)90186-8
Sevostianov, I., and Kachanov, M. (2000). Impact of the porous microstructure on the overall elastic properties of the osteonal cortical bone. J. Biomech. 33, 881–888. doi:10.1016/s0021-9290(00)00031-2
Shah, F. A., Sayardoust, S., Thomsen, P., and Palmquist, A. (2019). Extracellular matrix composition during bone regeneration in the human dental alveolar socket. Bone 127, 244–249. doi:10.1016/j.bone.2019.06.003
Snyder, S., and Schneider, E. (1991). Estimation of mechanical properties of cortical bone by computed tomography. J. Orthop. Res. 9, 422–431. doi:10.1002/jor.1100090315
Stops, A., Heraty, K., Browne, M., O’Brien, F., and McHugh, P. (2010). A prediction of cell differentiation and proliferation within a collagen-glycosaminoglycan scaffold subjected to mechanical strain and perfusive fluid flow. J. Biomech. 43, 618–626. doi:10.1016/j.jbiomech.2009.10.037
Tarnowski, C. P., Ignelzi, M. A. J., and Morris, M. D. (2002). Mineralization of developing mouse calvaria as revealed by Raman microspectroscopy. J. bone mineral Res. official J. Am. Soc. Bone Mineral Res. 17, 1118–1126. doi:10.1359/jbmr.2002.17.6.1118
Teo, J., Si-Hoe, K., Keh, J., and Teoh, S. (2007). Correlation of cancellous bone microarchitectural parameters from microct to ct number and bone mechanical properties. Mater. Sci. Eng. C 27, 333–339. doi:10.1016/j.msec.2006.05.003
Thurner, P. (2009). Atomic force microscopy and indentation force measurement of bone. Nanomed. Nanobiotechnol 1, 624–649. doi:10.1002/wnan.56
Tourolle Né Betts, D., Wehrle, E., Paul, G., Kuhn, G., Christen, P., Hofmann, S., et al. (2020). The association between mineralised tissue formation and the mechanical local in vivo environment: time-lapsed quantification of a mouse defect healing model. Sci. Rep. 10, 1100. doi:10.1038/s41598-020-57461-5
Townsend, P., Rose, R., and Radin, E. (1975). Buckling studies of single human trabeculae. J. Biomech. 8, 199–201. doi:10.1016/0021-9290(75)90025-1
Turunen, M., Saarakkala, S., Rieppo, L., Helminen, H., Jurvelin, J., and Isaksson, H. (2011). Comparison between infrared and Raman spectroscopic analysis of maturing rabbit cortical bone. Appl. Spectrosc. 65, 595–603. doi:10.1366/10-06193
Turunen, M. J., Prantner, V., Jurvelin, J. S., Kröger, H., and Isaksson, H. (2013). Composition and microarchitecture of human trabecular bone change with age and differ between anatomical locations. Bone 54, 118–125. doi:10.1016/j.bone.2013.01.045
Uthgenant, B. A., Kramer, M. H., Hwu, J. A., Wopenka, B., and Silva, M. J. (2007). Skeletal self-repair: stress fracture healing by rapid formation and densification of woven bone. ournal bone mineral Res. official J. Am. Soc. Bone Mineral Res. 22, 1548–1556. doi:10.1359/jbmr.0070614
Wehrle, E., Wehner, T., Heilmann, A., Bindl, R., Claes, L., Jakob, F., et al. (2014). Distinct frequency dependent effects of whole-body vibration on non-fractured bone and fracture healing in mice. J. Orthop. Res. 32, 1006–1013. doi:10.1002/jor.22629
Woo, S.-Y., Hollis, J., Adams, D., Lyon, R., and Takai, S. (1991). Tensile properties of the human femur-anterior cruciate ligament-tibia complex: the effects of specimen age and orientation. Am. J. Sports Med. 19, 217–225. doi:10.1177/036354659101900303
Yerramshetty, C. J. S., Lind, , and Akkus, O. (2006). The compositional and physicochemical homogeneity of male femoral cortex increases after the sixth decade. Bone 39, 1236–1243. doi:10.1016/j.bone.2006.06.002
Zioupos, P., and Currey, J. D. (1998). Changes in the stiffness, strength, and toughness of human cortical bone with age. Bone 22, 57–66. doi:10.1016/s8756-3282(97)00228-7
Keywords: woven bone, nanoindentation, micro-CT, Raman sprectroscopy, composition, distraction osteogenesis, elastic modulus, power law
Citation: Blázquez-Carmona P, Mora-Macías J, Pajares A, Mármol Á and Reina-Romo E (2024) On the influence of structural and chemical properties on the elastic modulus of woven bone under healing. Front. Bioeng. Biotechnol. 12:1476473. doi: 10.3389/fbioe.2024.1476473
Received: 05 August 2024; Accepted: 19 September 2024;
Published: 01 October 2024.
Edited by:
Jingwei Zhang, Shanghai Jiao Tong University, ChinaReviewed by:
Sacha Cavelier, Queensland University of Technology, AustraliaCopyright © 2024 Blázquez-Carmona, Mora-Macías, Pajares, Mármol and Reina-Romo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Pablo Blázquez-Carmona, cGJjYXJtb25hQHVzLmVz
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.