- 1Department of Engineering and Geology, University “G. D’Annunzio” of Chieti-Pescara, Pescara, Italy
- 2Institute for Biomechanics, ETH-Zurich, Zurich, Switzerland
- 3Future Health Technologies Programme, Singapore-ETH Centre, CREATE campus, Singapore, Singapore
- 4Faculty of Electrical and Computer Engineering, University of Iceland, Reykjavik, Iceland
Background: The success of using bone mineral density and/or FRAX to predict femoral osteoporotic fracture risk is modest since they do not account for mechanical determinants that affect bone fracture risk. Computed Tomography (CT)-based geometric, densitometric, and finite element-derived biomarkers have been developed and used as parameters for assessing fracture risk. However, to quantify these biomarkers, segmentation of CT data is needed. Doing this manually or semi-automatically is labor-intensive, preventing the adoption of these biomarkers into clinical practice. In recent years, fully automated methods for segmenting CT data have started to emerge. Quantifying the accuracy, robustness, reproducibility, and repeatability of these segmentation tools is of major importance for research and the potential translation of CT-based biomarkers into clinical practice.
Methods: A comprehensive literature search was performed in PubMed up to the end of July 2024. Only segmentation methods that were quantitatively validated on human femurs and/or pelvises and on both clinical and non-clinical CT were included. The accuracy, robustness, reproducibility, and repeatability of these segmentation methods were investigated, reporting quantitatively the metrics used to evaluate these aspects of segmentation. The studies included were evaluated for the risk of, and sources of bias, that may affect the results reported.
Findings: A total of 54 studies fulfilled the inclusion criteria. The analysis of the included papers showed that automatic segmentation methods led to accurate results, however, there may exist a need to standardize reporting of accuracy across studies. Few works investigated robustness to allow for detailed conclusions on this aspect. Finally, it seems that the bone segmentation field has only addressed the concept of reproducibility and repeatability to a very limited extent, which entails that most of the studies are at high risk of bias.
Interpretation: Based on the studies analyzed, some recommendations for future studies are made for advancing the development of a standardized segmentation protocol. Moreover, standardized metrics are proposed to evaluate accuracy, robustness, reproducibility, and repeatability of segmentation methods, to ease comparison between different approaches.
1 Introduction
Hip fractures account for significantly higher disability, mortality and socio-economic costs compared to other skeletal fractures. Approximately 20-25% of elderly patients die within 6-months post-fracture and the majority of survivors do not return to their pre-fracture state (Haleem et al., 2008). Therefore, effective early screening of patients at risk of developing a fragility fracture is important, as hip fracture incidence is expected to increase to 6.3 million in 2050, in the aging North American, European, and other industrialized countries' populations. Notably, it is projected that more than 50% of hip fractures will occur in Asia by the year 2050 (Cong and Walker, 2014).
A major contributor to elevated fracture risk at the hip is osteoporosis, affecting mostly the elderly population. The current clinical standard for diagnosing osteoporosis is the use of areal bone mineral density (aBMD) derived from dual-energy X-ray absorptiometry (DXA) scans, with an aBMD of more than 2.5 standard deviations lower than the mean of the healthy young adult female (T-score ≤ -2.5) as the threshold for a positive diagnosis (Kanis et al., 2008). However, aBMD lacks both sensitivity and specificity, as around 50% of incident fractures occur in individuals who do not have osteoporosis at the time when the scan is acquired and around 50% of individuals diagnosed with osteoporosis will not sustain a hip fracture during a study’s follow-up period (Schuit et al., 2004; Stone et al., 2003; Wainwright et al., 2005). Another fracture risk assessment tool, which is a part of the clinical guidelines in many countries, is the FRAX-score, used with or without aBMD (https://frax.shef.ac.uk/FRAX/). However, the performance of FRAX in identifying cases at high risk of fracture compared to aBMD is controversial and depends on the intervention threshold. In some studies, FRAX was found to be sensitive in terms of identifying subjects at risk of sustaining a major osteoporosis fracture, whereas an opposite result was found for some studies (Jiang et al., 2017).
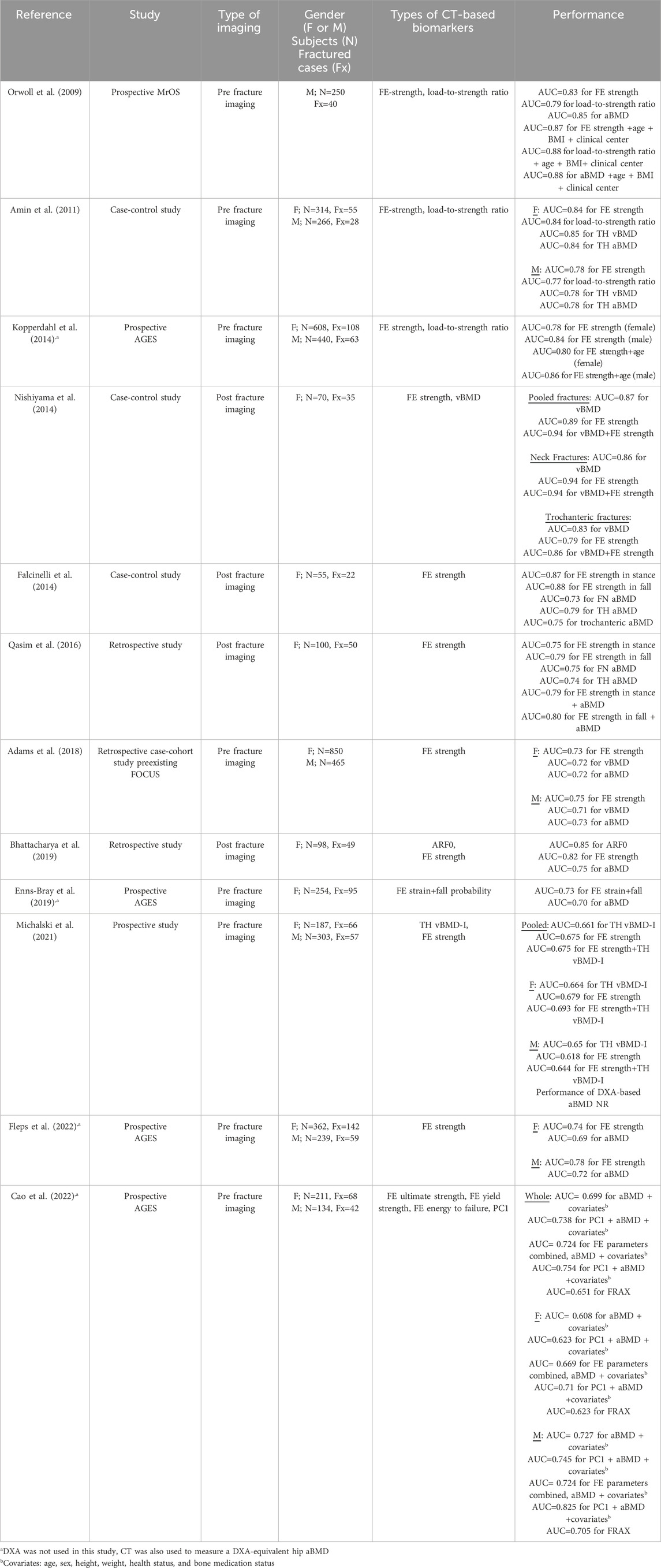
The current standards for assessing hip fracture risk do not directly include information on material and structural determinants, such as bone and soft tissue geometry, mechanical properties, and loading, that are factors known to affect bone fracture risk (Bouxsein, 2005; Keaveny et al., 2020). For these reasons, there exists a need for developing more accurate image-based biomarkers for quantifying hip fracture risk that take some or all these factors into account. To this end, Computed Tomography (CT)-based methods have been developed to derive geometric and densitometric biomarkers, such as cortical thickness (Treece et al., 2015), volumetric bone mineral density (vBMD) (Black et al., 2008), bone mass (Treece et al., 2015), and bone volume (Cheng et al., 2007). The predictive power of CT-based biomarkers has been quantified in several studies (Table 1), demonstrating a significant association with hip fracture risk. However, in most studies, CT-derived measures alone or in combination with other markers, did not classify fractures significantly better than DXA-derived aBMD (Black et al., 2008; Chalhoub et al., 2016; Cheng et al., 2007). In contrast, CT-based finite element (FE)-derived biomarkers enable more accurate representation of heterogeneous distribution of bone density and strength based on the bone geometry. CT-based subject-specific FE models have been studied extensively and demonstrated to accurately predict the mechanical response of the proximal femur under loading (Bessho et al., 2007; Dall’Ara et al., 2013; Dragomir-Daescu et al., 2011; Duchemin et al., 2008; Grassi et al., 2012; Keyak, 2001; Keyak et al., 2005; Koivumäki et al., 2012; Nishiyama et al., 2013; Schileo et al., 2020; 2014; 2007; Varga et al., 2016; Yosibash et al., 2014) and the response of the whole hip region under simulated impact (Fleps et al., 2019). There exists ample evidence to suggest that most hip fractures, in vulnerable populations at least, are the result of a fall from standing height or lower (Hayes et al., 1996; Parkkari et al., 1999; Scott et al., 2010). As such, FE-derived strength or load-to-strength ratio computed through CT-based subject-specific FE models have been used as parameters for assessing osteoporotic hip fracture risk (Table 2). However, the improvement over DXA-based aBMD in predicting hip fracture risk is not uniform and depends on the patient cohort analyzed. When tested on pre-fracture cohorts, most studies found that FE-derived predictors performed equivalently to DXA-derived aBMD in classifying incidence hip fractures with the exception of two studies. Fleps et al. (2022) found FE models to be a better classifier than aBMD in the AGES Reykjavik study cohort. Moreover, Yosibash et al. (2023) showed that 7/11 of subjects that had DXA imaging who subsequently fractured had non-osteoporotic aBMD score. When post-fracture CT images have been used, CT-based FE strength estimates performed significantly better than aBMD in classifying fracture cases (Bhattacharya et al., 2019; Falcinelli et al., 2014; Qasim et al., 2016).
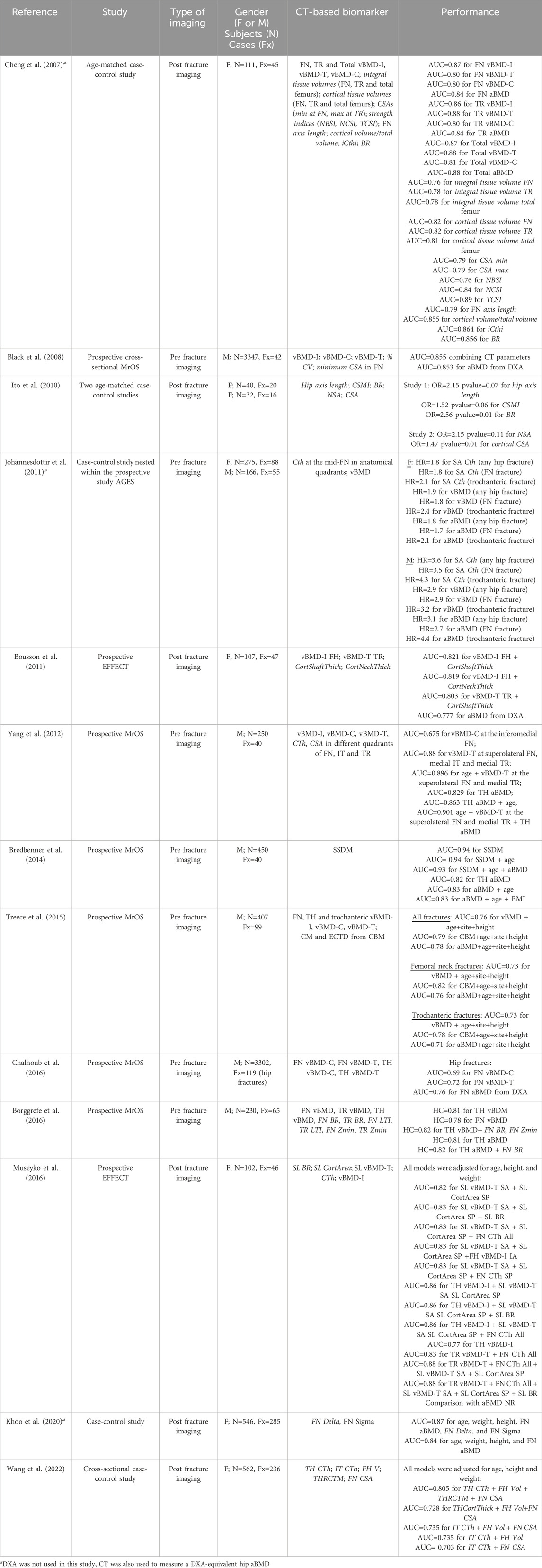
Table 1. Literature overview of CT-derived densitometric (plain text) and geometric biomarkers (italic) used to classify osteoporotic hip fractures.
Although CT-derived biomarkers for assessing hip fracture risk have shown good potential for improving the performance of aBMD and T-score (Tables 1 and 2), the largest studies on CT-derived biomarkers are a couple of orders of magnitudes smaller in terms of the number of subjects, than the largest studies on FRAX and aBMD. This is related to the fact that to quantify many of the CT-based biomarkers, segmentation of the bones in the hip from the CT data is needed. When the segmentation is done manually or semi-automatically, which is known to be labor intensive and expensive, this essentially prevents these biomarkers from being adopted in clinical practice. In recent years, however, fully automated methods for segmenting CT data have started to emerge (Besler et al., 2021; Bjornsson et al., 2023; Yosibash et al., 2020). Quantifying the accuracy, robustness, reproducibility, and repeatability of these segmentation tools is of major importance for research and potential down-stream translation of CT-based biomarkers into clinical practice. Here, we define.
• accuracy, as the ability of the method to predict ground truth segmentation;
• robustness, as the ability of the method to produce accurate results across varied cohorts (e.g. healthy vs. pathological) and across scanners;
• reproducibility, as the ability of the method to produce consistent results using the same CT dataset, thus pertaining to e.g. inter- and intra- operator variability;
• repeatability, as the ability of the method to produce the same results for the same subject and same scanner, in two separate imaging sessions.
It is important to highlight that besides fracture risk assessment, CT-based biomarkers may be valuable in quantifying the effects of treatments in a more detailed way than DXA-based approaches. For example, some clinical research studies have already demonstrated the ability of CT-based FE-derived biomarkers in monitoring treatment responses in individual patients and detecting changes that were missed by DXA (Keaveny et al., 2020). As such, fully automating the segmentation of CT images, to make the process fast and clinically applicable for image-based and FE-based biomarkers, is crucial for guiding personalized treatments.
The aim of this work was to systematically review the literature on clinical CT image segmentation methods for the bones in the human hip, to establish the current level of evidence to support the use of these methods for quantifying image-based bone biomarkers in large clinical cohorts. To this end we focused on the general conclusions that can be drawn from the literature on accuracy, robustness, reproducibility, and repeatability, and finally the availability of these segmentation methods for use in research and clinical practice.
2 Methods
2.1 Literature search
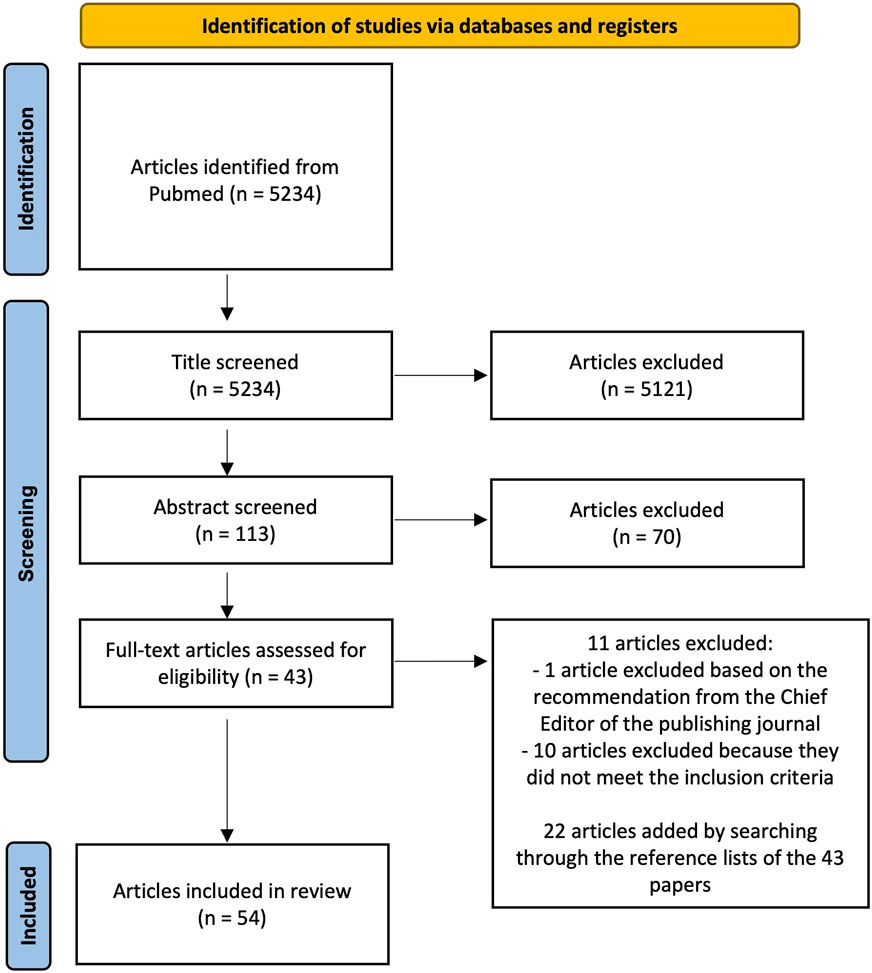
We conducted an electronic literature search on PubMed to identify relevant articles published until the end of July 2024. The following keywords were used as search terms: “image segmentation”, “femur segmentation”, “pelvis segmentation”, “automatic segmentation”, “convolutional neural network”, “fracture risk”, “computed-tomography”, “thresholding”, “statistical shape model”, “graph-cut”, “multi-atlas”, “deep-learning”, “bone strength”. The search terms were combined as follows: (((image segmentation) OR (femur segmentation) OR (pelvis segmentation)) AND ((automatic segmentation) OR (convolutional neural network) OR (thresholding) OR (statistical shape model) OR (graph-cut) OR (multi-atlas) OR (deep-learning)) AND ((computed-tomography) OR (fracture risk) OR (bone strength))). This resulted in 5234 articles. Using inclusion and exclusion criteria, authors CF and BH independently screened the studies based on title and subsequently, they compared their lists. Any disagreement between the two lists was resolved through discussion without in depth analysis of the content of the papers to reach a consensus leading to a total of 113 papers that were identified as being relevant for further review. These papers were subsequently screened based on their abstract by authors CF and BH independently, which further reduced the number of relevant articles to 43. During this second screening, any disagreement regarding the inclusion of papers was solved through a discussion. Finally, the full text of the 43 articles was evaluated to verify whether they met the inclusion criteria. This evaluation was performed independently by three different authors (CF, BH, VSC). In case of a disagreement, consensus on which articles to include was reached through discussion. If necessary, a fourth author (LME) was consulted to make the final decision. One paper among the 43 was excluded based on the recommendation from the Chief Editor of the publishing journal. Searching through the reference lists of these papers, additional publications of interest were found, resulting in a total of 54 papers being included in this review (Figure 1).
2.2 Inclusion and exclusion criteria
Studies that reported development of segmentation methods, validated on human femurs and/or pelvises were included in the review. Studies on other bones were excluded, as well as studies on fractured bones. Segmentation methods validated on both clinical and non-clinical CT data were included. Studies that used micro-CT images or data from other imaging modalities than clinical CT, were excluded. Only studies that reported a quantitative comparison between the study segmentation method and manual segmentation were included. Studies that did not report validation outcomes and/or resolution of images were excluded.
2.3 Comparing studies
All the papers included in this review were gathered into four tables, two for studies on the femur and two for studies on the pelvis. In terms of accuracy, four main metrics were extracted from the studies, i.e., DSC, JAC, HD, and its 95th percentile variant (HD95). All four metrics aim to quantify different aspects of the difference between ground truth and the segmented structures. The DSC measures the spatial overlap between the ground truth mask and the predicted mask and is given by the following equation (Dice, 1945):
where GT is the ground truth mask and MS the predicted mask (DSC=0, no overlap and DSC=1, full overlap). The JAC index represents a measure of similarity between two objects and is defined by the following equation:
where GT is the ground truth and MS the predicted mask (JAC=0, the segmentations have no common member, JAC=1, the segmentations are identical). The HD and its 95% percentile variant represent the distance between the ground truth and the resulting segmentation. The Hausdorff distance is the maximum of all shortest distances for all points from one object’s boundary to the other. Assuming that
with
DSC, JAC, and HD with HD95 have been chosen because they represent the state-of-the-art metrics when quantifying the accuracy of medical image segmentation methods, evaluated on ground truth data. However, not all studies have used these accuracy metrics. Thus, for those works, the accuracy measures used by the authors’ have been reported. In addition to the accuracy, based on the definitions reported in Section 1, robustness, reproducibility and repeatability outcomes of different studies were qualitatively compared.
2.4 Risk of bias
The risk of bias was evaluated in the following manner. First, for the four main topics investigated in this review (i.e., accuracy, robustness, reproducibility, and repeatability) authors CF and BH identified parameters that may affect the results reported in the studies. The type of CT dataset (i.e., if the dataset was obtained by scanning a homogeneous population or non-homogeneous population), and number of CT scanners used in the studies, were judged to be parameters that could bias the evaluation of the accuracy and robustness of the segmentation method. In terms of reproducibility, the risk of bias was evaluated to be associated with lack of quantification of inter- and intra-operator variability. Here, of importance are the number of operators involved in evaluating the inter-operator variability and the number of times each operator analyzed a CT dataset for the intra-operator variability. In terms of repeatability, the risk of bias was evaluated to be associated with absence of re-scanning of the same patient using the same scanner. An important aspect of the re-scanning procedure is the time between two imaging sessions, as changes in bone mass are time dependent due to e.g. use of pharmacological agents or simply due to aging. Subsequently, each study included in the review was independently evaluated by the two authors (CF and BH) based on the presence of these potential sources of bias. If a study reported a given parameter, it was labeled with a ‘Yes’, otherwise with a ‘No’. Articles that reported 0 or 1 parameters were classified as high risk of bias, whereas studies that reported 2 or 3 parameters were considered a source of medium risk of bias. If the articles reported all 4 parameters, they were assessed as providing low risk of bias.
3 Results
3.1 Search outcome
Supplementary Tables S1, S2 report the studies that validated segmentation methods on human femurs, whereas Tables 3, 4 include the studies validated on human pelvises. The studies are grouped in the tables based on the type of segmentation method under evaluation, i.e.: 1) threshold-based; 2) statistical shape method (SSM)-based; 3) atlas-based; 4) graph-cut based; and 5) convolutional neural network-based (CNN) methods (see Appendix A). In Supplementary Table S1 and Table 3 for each study the following information has been included: reference to the study, number of datasets segmented and type of material, scanning parameters and image resolution, metrics used for the assessment of accuracy, robustness, reproducibility, repeatability and remarks. The remarks column includes information that may be useful to the reader, such as the processing speed (when available), whether the method is fully automatic or semi-automatic, and whether the method is available under an open-source or a commercial license. In Supplementary Table S2; Table 4, the quantitative results for reported accuracy, robustness, reproducibility and repeatability have been reported for each study.

Table 3. Segmentation methods developed for the pelvis from the studies included in the review. The table shows the following information: reference of study; number of datasets N and type of material segmented; type of CT scanner, scanning parameters, and image resolution; segmentation method; metrics used to evaluate accuracy, robustness, reproducibility and repeatability; and remarks. NR: not reported
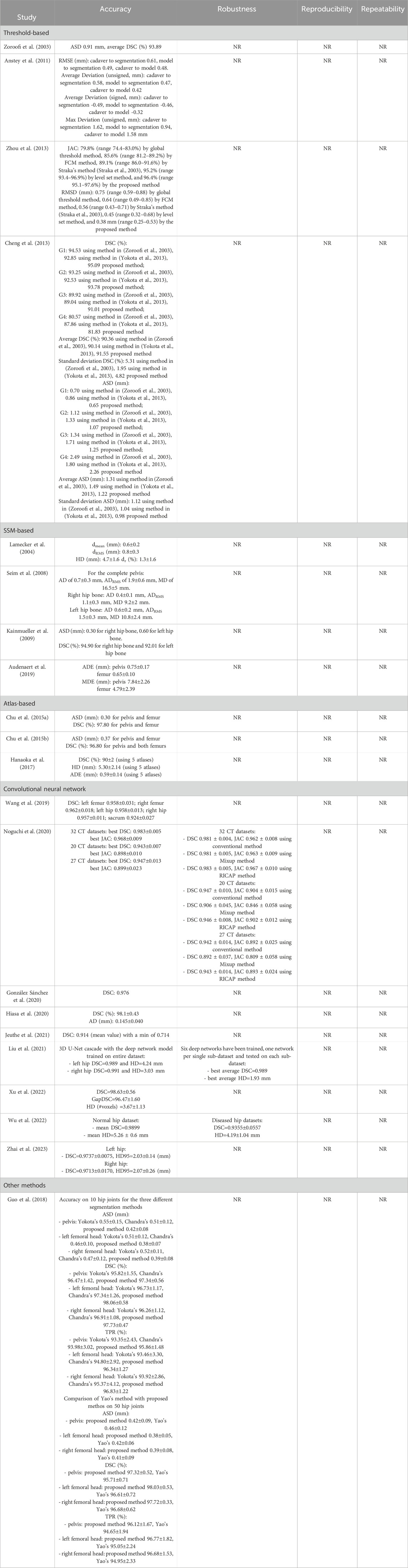
Table 4. Segmentation methods developed for the pelvis from the studies included in the review. The table shows the quantitative results obtained from each study for evaluating accuracy, robustness, reproducibility and repeatability. NR: not reported.
3.2 Accuracy
By comparing the state-of-the-art accuracy metrics used in medical image segmentation (i.e., DSC, JAC and HD/HD95), it can be observed that no studies evaluated the accuracy using all these metrics. In addition, in some studies, these metrics have not been used but other metrics quantified instead. More specifically, some studies used different distance-based metrics from HD, such as the average surface distance, the root mean-square average symmetric distance, the average distance error, and adopted volumetric-based metrics (e.g. volumetric overlap global error, volume difference). Furthermore, although HD95 represents a metric widely used in the field of image segmentation for its ability to handle outliers (Chen et al., 2021; Fick et al., 2021; Li et al., 2022; Van Den Oever et al., 2022), its use is not common for femur/pelvis segmentation. Only three studies reported this metric (Bjornsson et al., 2023; Kuiper et al., 2022; Zhai et al., 2023). Figures 2, 3 show the level of accuracy reached by the segmentation methods for the femur (Figure 2) and the pelvis (Figure 3) in terms of DSC. Only the studies that have used these metrics have been included when generating these figures.
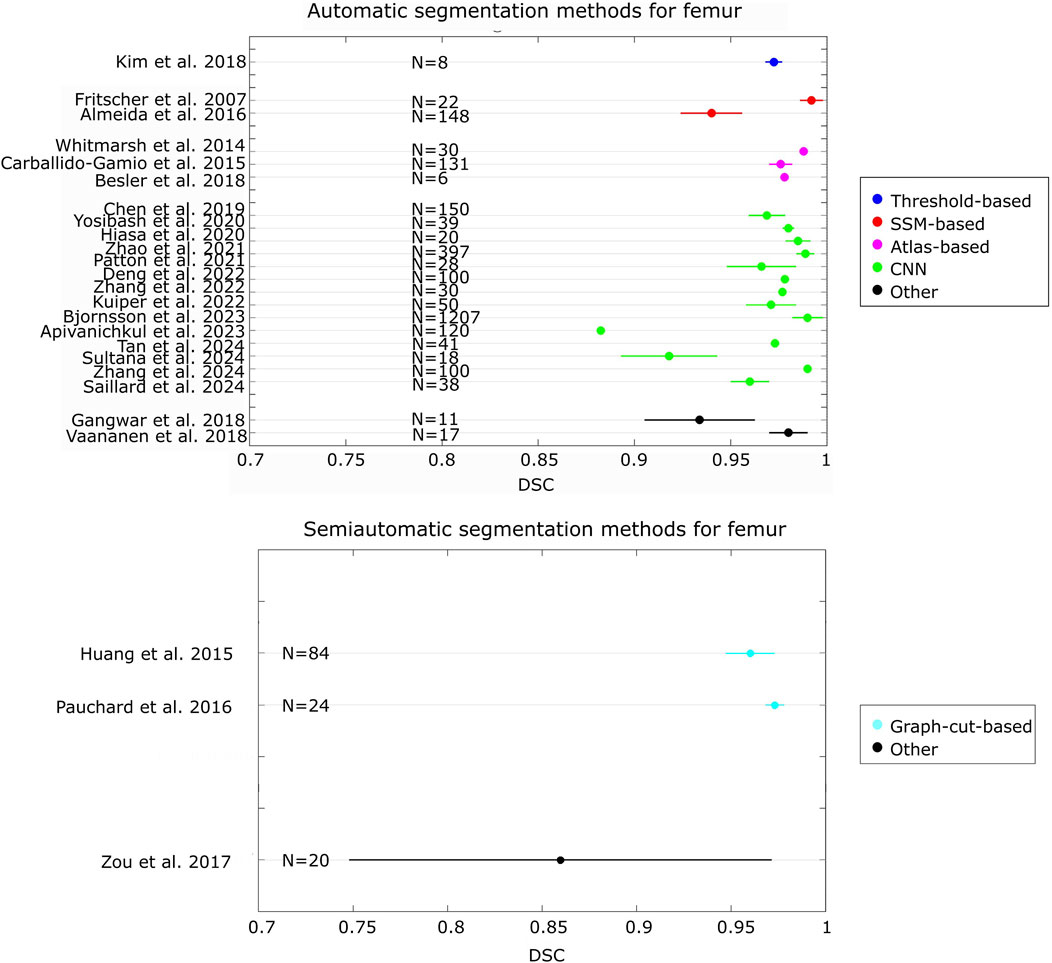
Figure 2. Forest plot that presents the level of DSC achieved by the automatic and semiautomatic segmentation methods developed for the femur. For each study, the number (N) of samples has been reported
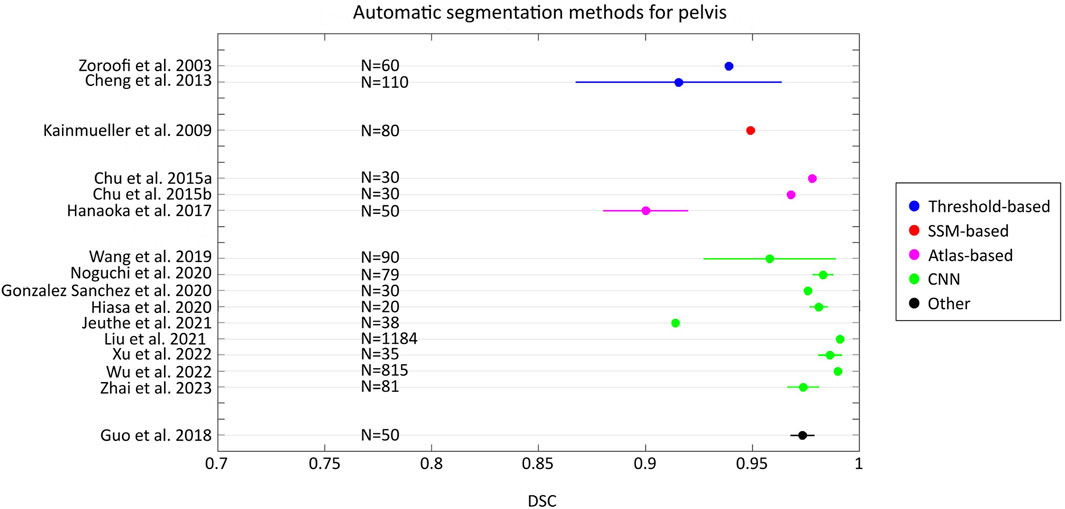
Figure 3. Forest plot that presents the level of DSC achieved by the automatic segmentation methods developed for the pelvis. For each study, the number (N) of samples has been reported
3.3 Robustness
Only a few of the studies attempted to quantify robustness. In the study performed by Kang et al. (2003) on human femurs, the robustness of the segmentation method was assessed with respect to the image noise. Gaussian noise was artificially added to the CT data of the European Spine Phantom (ESP) that was used to calibrate the CT data. The authors showed that an increase in noise caused an increase in the segmented periosteal volume. Moreover, they showed that the segmented endosteal volume was initially constant at low noise but then increased with increasing noise. They also showed that the effect of noise increase was more pronounced when the cortical thickness was smaller. The authors also added noise to a CT dataset of femurs and showed that only in the noisiest image a sub-optimal segmentation was obtained, and user interaction became necessary. To test the robustness of the segmentation method, Fritscher et al. (2007) added image artifacts that imitated screws inside the femur and a black blob. They concluded that the segmentation of this dataset resulted in closely similar segmentation results for the same dataset without artifacts, demonstrating the robustness of the method. However, they did not report a quantitative evaluation of robustness. Carballido-Gamio et al. (2015) demonstrated the robustness of their atlas-based method using 80 scans of older women from two different clinical sites and two highly anisotropic spatial resolutions and reported a mean DSC of 0.976, a mean SYM of 0.203 mm, and a mean modified HD of 0.253 mm (HD=3.928 mm). Almeida et al. (2016) reported the robustness of their developed SSM-based method in terms of the percentage of successfully completed segmentations. They obtained a success rate of 98% from 148 datasets; only 3 (i.e. 2% of datasets) failed to converge, despite the significant variability in gender and age-related bone loss. Väänänen et al. (2019) tested their automatic segmentation method on in-vivo and ex-vivo CT datasets, which were acquired using different CT scanners and with different scanning parameters, thus corroborating the robustness of the method against changes in imaging parameters. They reported the robustness results in terms of DSC obtaining values of 0.93±0.02 and 0.98±0.01 for the in-vivo and ex-vivo CT datasets, respectively. In the study performed by Noguchi et al. (2020), the robustness of their CNN-based automatic segmentation was demonstrated by considering three different datasets, i.e. in-house dataset (32 CT datasets), secondary dataset (20 CT datasets) and public dataset (27 CT datasets), and testing three types of data augmentation techniques (conventional method, Mixup and RICAP). For the in-house dataset they reported a DSC of 0.983±0.005 and a JAC index of 0.968±0.009 without using data augmentation, with none of the three data augmentation techniques improving the results. On the secondary dataset, their method achieved a DSC of 0.943±0.007 and a JAC index of 0.898±0.010. In this case, conventional augmentation and RICAP improved the prediction accuracy (small improvements with the DSC increase of 0.002–0.004). In contrast, Mixup worsened the results. On the public dataset, using a combination of conventional augmentation and RICAP, a DSC of 0.947±0.013 and a JAC index of 0.899±0.023 were obtained. The robustness of the method developed by Liu et al. (2021) was assessed by using a large dataset of pelvic CT images pooled from multiple sources with which the authors performed a series of experiments. First, they tested the segmentation approach using all CT images together from all sources. Subsequently, they trained six deep networks, one network per single sub-dataset, and then tested them on each sub-dataset. Zhao et al. (2021) did not report any robustness quantification of their deep learning-based approach but they stated that the robustness of the method had been guaranteed by performing the data augmentation since the sample size was insufficient to train a precise 3D segmentation model. Data augmentation used to improve the robustness of the method has been also used by Deng et al. (2022). However, according to the authors’ opinion, using only data augmentation was not enough to guarantee the robustness of the method. It was crucial to perform additional tests, such as evaluating the method on a different dataset or cohort. Wu et al. (2022) validated their segmentation method using different CT datasets that included normal and pathological hip joints. They obtained DSC values of 0.9899±0.0014 and 0.9355±0.0557 on normal and diseased hip CT datasets, respectively. Bjornsson et al. (2023) evaluated the robustness of their method by involving two different samples of the AGES data set (a first sample characterized by 48 gold standard manually delineated proximal femur segmentations from 24 CT images and a second sample characterized by 1207 manually delineated segmentations, generated with a semi-automated delineation protocol). They quantified the robustness in terms of the DSC and HD95 reporting a mean DSC of 0.990±0.008 and a mean value of HD95 of 0.999±0.331 mm. Kuiper et al. (2022) proposed a deep-learning-based approach for automatic segmentation of bones. They used 50 CT datasets for both training and initial evaluation of the networks. Then, to evaluate the robustness of the method, they selected 10 CT datasets taken from a different image database with respect to the database from which the 50 CT datasets have been selected, in which the CT images have been acquired with different acquisition parameters and characterized by different subject demographics. The robustness was quantified in terms of mean absolute surface distance (MASD) and HD. For femurs, they reported values of 0.58±0.07 mm and 5.03±3.20 mm for MASD and HD, respectively.
3.4 Reproducibility
Four studies investigated reproducibility. Testi et al. (2001) evaluated the reproducibility using an in-vivo femur CT dataset and by extracting from the dataset 19 images uniformly distributed along the scanning plan. For every slice, both the endosteal and periosteal surfaces were extracted using both the border-tracing method developed by the authors and a threshold-based method. The geometry extraction was executed three times for both methods. The distance between the contours was reported in terms of HD. Three sets of contours for both extraction procedures were obtained. The comparison among the contours were reported in terms of RMSE of the HD for all slices. They showed that the border-tracing algorithm improved the reproducibility by about 40% with respect to the threshold-based method with a mean RMSE that decreased from 2.29 mm to 1.41 mm. Furthermore, Testi et al. (2001) performed a reproducibility study by using 6 CT data sets of patients in need of a custom-made prosthesis (CMP), considering only the first five proximal slices from every dataset. All images had been traced three times by both border-tracing and threshold-based methods. The inner and outer contours were compared to each other in terms of HD. The border-tracing method improved the HD from 5 to 1.5 mm with respect to the threshold-based procedure. Kang et al. (2003) performed an inter- and intra-operator study analyzing the datasets of 9 patients and evaluating the CVRMS of the bone volume and cortical thickness within a sphere centered at the femoral neck. For the inter-operator variability, three operators analyzed each data set once, blinded to the results of the other operators. For the intra-operator variability, one operator analyzed each dataset three times. For inter- and intra-operator variability, the CVRMS was always lower than 1% for trabecular and total bone volumes (0.27% ± 0.15% and 0.73% ± 0.43%, respectively, for inter-operator variability; 0.29% ± 0.17% and 0.64% ± 0.37%, respectively, for intra-operator variability) and below 2% for cortical thickness (1.71% ± 1.10% for inter-operator variability; 1.54% ± 1.10% for intra-operator variability). No significant differences were detected for inter- and intra-operator analyses. Pauchard et al. (2016) performed an inter-operator reproducibility study on 12 femurs involving three operators. Average mean surface-to-surface distance, DSC and HD were calculated between graph cut segmentations and manual segmentations from three operators in pair-wise manner. Pair-wise comparison of segmentation methods between operators indicated that HD measurements were consistently smaller between manual segmentations (maximum value 3.09 mm for manual segmentations vs. 3.49 mm for graph-cut segmentations). In contrast, mean surface-to-surface differences were consistently smaller, and DSC was higher between graph cut segmentations (maximum value of mean surface-to-surface distance 0.378 mm for manual segmentations vs. 0.006 mm for graph-cut segmentations; maximum value of DSC coefficient 0.980 for manual segmentations vs. 0.995 for graph-cut segmentations). Besler et al. (2021) evaluated the inter-operator reproducibility (three operators) measuring the SDRMS (absolute units) and CVRMS (%) for volume, integral density, and failure load in both cadaveric and in-vivo CT images, showing that their proposed segmentation algorithm considerably improved inter-operator reproducibility for all three outcomes (SDRMS (CVRMS) equal to 9.58 mL (5.41%), 2.02 mg/cc (0.65%), and 70.10 N (5.17%) for volume, density, and failure load, respectively, using in-vivo CT datasets, and equal to 7.26 mL (4.10%), 1.86 mg/cc (0.92%), and 34.10 N (6.43%) in cadaveric CT datasets).
3.5 Repeatability
We found only two studies that investigated the repeatability of the segmentation method, in terms of its ability to produce the same results on the same subject and the same scanner, from two separate imaging sessions (Carballido-Gamio et al., 2015; Zhang et al., 2024). In that study (Carballido-Gamio et al., 2015), repeatability was evaluated using repeated scans after repositioning, on 22 subjects obtained on CT imaging systems from two manufacturers. Reproducibility was assessed with CVRMS for ten compartmental vBMD parameters, seven compartmental tissue volume parameters, FE-derived bone strength under two loading conditions, three compartmental surface-based cortical bone thickness parameters, and three compartmental surface-based cortical vBMD parameters. Repeatability was also assessed in a local manner for three surface-based cortical bone thicknesses and three surface-based cortical vBMD parameters. In the study by Zhang et al. (Zhang et al., 2024) repeatability was assessed using 5 subjects, by repeating CT scans after repositioning and quantifying regional vBMD measures. The study showed a nominal value of around -0.01% for the mean difference between vBMD estimates from baseline and repeated scans. Moreover, the authors reported an intraclass correlation coefficient (ICC) between vBMD values measured from baseline scans and those obtained from repeated scans equal to 0.996, and a root-mean-square coefficient of variation of 0.72%.
3.6 Additional remarks
We made several additional observations based on Supplementary Tables S1, S2 and Tables 3, 4. First, only a few of the studies reviewed provided information about total operator time required to process each image (see Supplementary Tables S1 and Table 3). However, this information is essential for translation into clinical practice. Second, the segmentation methods have in some of the studies been evaluated on a downstream FE modelling workflow, to assess the ability of these methods in predicting femoral strength and strains. Väänänen et al. (2019) showed a good agreement between FE predicted strains derived from their automatic segmentation method using the Stradwin segmentation tool, and the corresponding ex-vivo measurements (R2=0.89, maximum error=27%, normalized RMSE=6%). A graph-cut segmentation (Pauchard et al., 2016) and CNN segmentation (Bjornsson et al., 2023) resulted in high correlation between FE predicted femoral strength compared to FE predicted strength derived from manual segmentation (R2=0.98 in (Pauchard et al., 2016); R2=0.988, RMSE=212.2 N, max difference=25.3% for left femurs and R2=0.986, RMSE=177 N, max difference=30.1% for right femurs in Bjornsson et al. (2023)). These results demonstrate the potential of these methods in producing reliable segmentations that can be used in an FE workflow for fracture risk assessment. The potential of automatic segmentation methods for FE-based femur fracture risk assessment was also demonstrated by Kim et al. (2018) that showed that their automatic segmentation method based on the complementary characteristics between the thresholding method and watershed algorithm was able to obtain a fracture risk prediction close to that obtained by the manual segmentation with an average relative error of 4.99%. Finally, the studies included in this review used different CT scanners, CT scanning parameters and resolutions. It is challenging to determine how these variables affect accuracy and robustness, as the scanner and scanning parameters are rarely used as isolated study variables. Similar conclusions can be drawn for the reproducibility and repeatability, which we found only sparsely addressed in the literature.
3.7 Risk of bias
Table 5 lists the summary of the risk of bias assessment. As can be observed, most of the studies presented a high risk of bias, whereas a small portion of the works demonstrated a medium risk. Most studies scored poorly on inter- and/or intra-operator variability and re-scanning of the same patient using the same CT scanner. These results can be explained by the fact that the studies included in the review did not quantify the accuracy, robustness, reproducibility, and repeatability of the segmentation method at the same time, but they focused on one or two of these metrics.
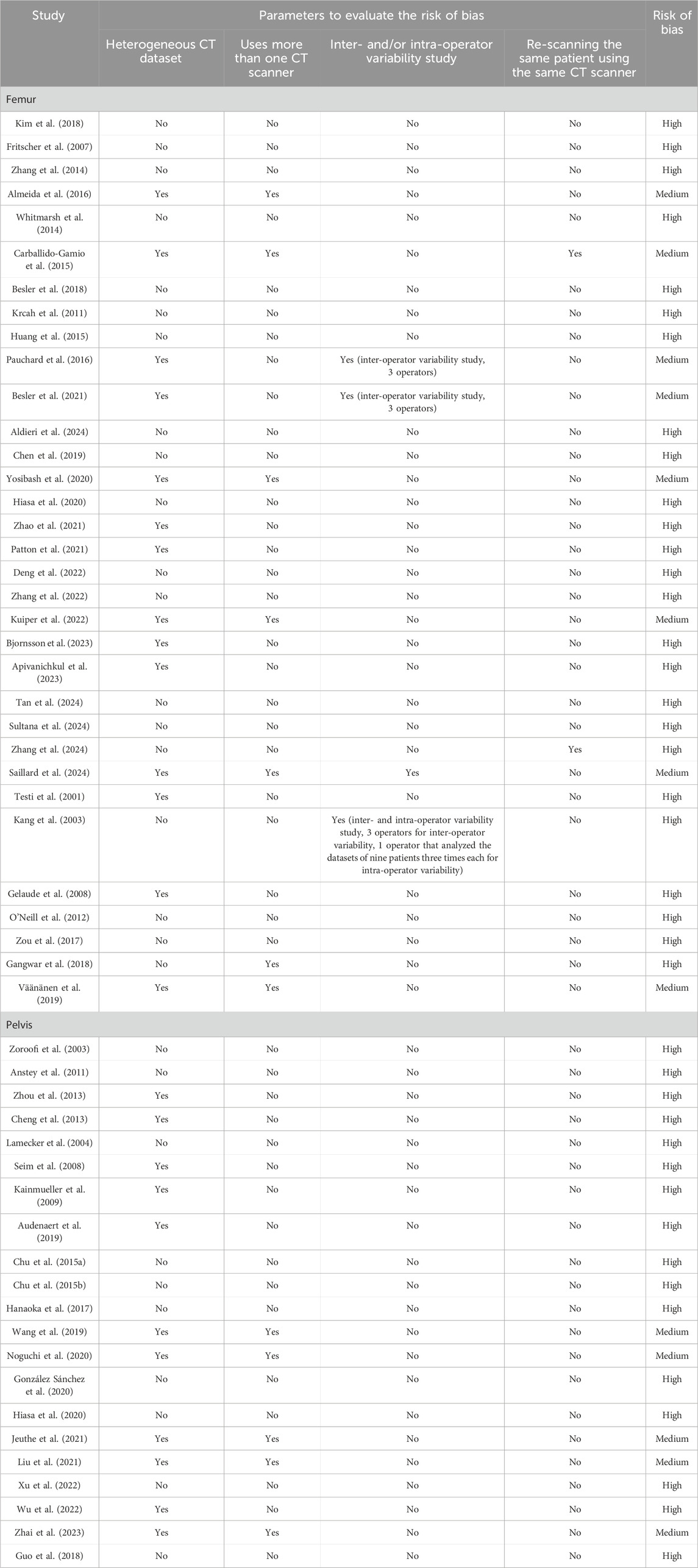
Table 5. Risk of bias assessment summary. The studies are reported in the same order as in Supplementary Tables S1, S2; Tables 3, 4.
4 Discussion
The aim of the present work was to systematically review the literature on clinical CT image segmentation methods for the bones in the human hip to establish the current level of evidence on accuracy, robustness, reproducibility and repeatability, to support the use of these methods for quantifying image-based bone biomarkers in large clinical cohorts. We found that studies that reported the accuracy of segmentation of the femur and the pelvis used different metrics, making inter-study comparison challenging. However, even though there may exist a need to standardize reporting of accuracy across studies, the accuracy of automatic segmentation methods in terms of predicting ground truth manual segmentation appears to be as high, if not higher than has been achieved with semi-automated methods. This is a positive finding as automation is essential for the translation of any segmentation method to clinical practice. With respect to robustness of the automated or semi-automated segmentation methods that we reviewed, we found reporting to be sparse, with only one paper on automatic segmentation reporting robustness as a percentage of successfully completed segmentations but not reporting robustness across different scanners. Finally, we found reproducibility and repeatability generally not to be reported in the segmentation studies and only a few studies reported reproducibility in the form of inter-operator differences. Here, interestingly, but perhaps not surprisingly, one of the few studies that reported inter-operator differences found it to be larger for manual segmentation than for a semi-automatic graph cut segmentation protocol (Pauchard et al., 2016). This points to the weakness of using manual segmentation from a single rater as the ground truth when validating segmentation methods.
We believe that the present study clearly shows that further work is necessary to investigate which is the best automatic segmentation method to integrate into a clinical workflow for estimating CT-based biomarkers for femur fracture risk assessment, not only in terms of accuracy, robustness, reproducibility, and repeatability, but also in terms of computational cost. However, in the authors’ opinion, artificial intelligence-based approaches, such as deep-learning-based or machine learning-based methods, may represent the most promising methods for developing fully automated workflow for deriving CT-based biomarkers. The advantages of such methods are related to decreasing human interaction and reducing the computational cost with respect to other non-machine learning based automated methods, which are two essential requirements for clinical application of segmentation methods. This is supported by the fact that recently, AI-based methods for segmentation have been implemented into commercial software platforms (e.g. Mimics, Simpleware). However, to the authors’ knowledge, there is no work that has have evaluated the accuracy, robustness, reproducibility, and repeatability of these methods in the femur and the pelvis.
It is important to highlight that there are some limitations associated with this review. First, not all studies reported the CT imaging specifications and parameters, which might influence the segmentation results. Second, not all studies used the same metrics to assess the segmentation accuracy and they were evaluated on datasets of very different sizes and demographics, which makes inter-study comparison challenging. As such, in future studies, the use of standardized metrics, and perhaps, publicly available test datasets, would ease the comparison across methods. Moreover, not all studies reported computation time and the memory requirements for the segmentation process. This is crucial information for understanding the cost associated with acquiring the segmentations and the ease of incorporating them into clinical practice. Finally, it is important to highlight that most of the studies included in this review were limited to methods applied to non-pathological femur and/or pelvis. However, approaches successfully applied to other skeletal sites and not yet applied to femur/pelvis can be found in the literature. Some examples based on convolutional neural networks and successfully applied to vertebra are reported in (Lessmann et al., 2019; Sekuboyina et al., 2021). Due to the emergence of several artificial intelligence-based approaches applied to specific skeletal districts and also across multiple regions of interests (Mazurowski et al., 2023) the interesting point will be to evaluate if such methods are sufficiently accurate for the creation of FE models for any bone in the body.
5 Recommendations
Bearing in mind the need in the field of image-based bone biomarker research and clinical practice to have access to accurate, robust, reproducible and repeatable automatic methods to segment bones, we propose that future work puts emphasis on the acquisition of high-quality datasets, preferably published in an open-access repository, for advancing the development of a standardized segmentation protocol. Human donor specimens with soft tissue attached could be scanned to replicate the beam hardening effect of soft tissue in clinical scans. Thereafter, the same specimens could be scanned in high accuracy optical scanners after removal of soft tissues and the resulting hard tissue surfaces used as ground truth. This option could be useful to establish the accuracy of the segmentation methods. However, the scans should preferably be taken soon after death to maintain a similar texture and noise level as an in-vivo scan. To assess the robustness and reproducibility of segmentation methods, repeated in-vivo scans on human subjects on multiple scanners could be acquired. Moreover, to investigate repeatability, the data acquisition could include sessions of rescanning with repositioning. In the case of using in-vivo CT scans, the ground truth could be obtained by using the STAPLE method (Warfield et al., 2004), which generates ground truth data by combining (“stapling”) multiple segmentations from different expert raters, to address the inter-rater variability in manual segmentation that is used to derive the gold standard.
To correct for partial volume effect (PVE) that represents an important issue when CT images at clinical resolution are used to segment the femur, leading to errors in surface reconstruction, we suggest performing a comparison across imaging modalities of different resolutions such as micro-CT, HR-pQCT and CT with the ultimate aim to develop segmentation methods that are able to directly correct for PVE. To validate the segmentation methods, we propose the use of the HD metric for quantifying accuracy, as the ultimate goal of any segmentation method is to accurately capture the surface of the organ under investigation. Moreover, we suggest reporting HD metric in different regions i.e., femoral neck, head, and shaft. The femoral neck and head represent critical regions to be segmented due to their thin cortical thickness and thus a lower accuracy in such regions would be more critical than in the shaft, especially in view of using the segmentations in FE analysis. To quantify robustness, we propose the use of percentage of segmentations that achieved HDs that are smaller than the in-plane resolution of the image data. To evaluate the reproducibility and repeatability, CVRMSE of HD may be quantified to investigate the consistency of the results using the same CT dataset, the inter- and intra-operator differences, and the effect of a re-scanning taken several days apart.
6 Conclusions
In conclusion, we found that automatic segmentation tools developed to date have produced at least as accurate outcomes as methods that require manual intervention. The development of automatic segmentation tools has thus matured far enough to suggest their use for quantifying image-based bone biomarkers in large clinical cohorts, as these methods can be operator independent and process images at low cost. However, only few studies systematically investigated the robustness of automatic segmentation methods, and limited data is available on their reproducibility and repeatability. These aspects require a more in-depth investigation in future studies. To this end, the development of open-access CT data and standardized metrics for quantifying accuracy, robustness, reproducibility, and repeatability in future works is recommended. Access to the CT data could be provided under the condition that methods developed or validated on the data be released as open source.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
CF: Conceptualization, Writing–original draft, Writing–review and editing. VSC: Conceptualization, Writing–review and editing. LME: Conceptualization, Writing–review and editing. BH: Conceptualization, Supervision, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Funding by the European Union - Fondo Sociale Europeo - PON Ricerca e Innovazione 2014-2020 (azione IV.6) - FSE-REACT EU. This research was supported by the National Research Foundation Singapore (NRF) under its Campus for Research Excellence and Technological Enterprise (CREATE) program. This work was also supported by The Icelandic Centre for Research (RANNIS) through grant 2422582-601.
Acknowledgments
CF acknowledges the support of the Italian National Group for Mathematical Physics (GNFM-INdAM). The research was in part conducted at the Future Health Technologies at the Singapore-ETH Centre, which was established collaboratively between ETH Zurich and the National Research Foundation Singapore.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbioe.2024.1446829/full#supplementary-material
References
Adams, A. L., Fischer, H., Kopperdahl, D. L., Lee, D. C., Black, D. M., Bouxsein, M. L., et al. (2018). Osteoporosis and hip fracture risk from routine computed tomography scans: the fracture, osteoporosis, and CT utilization study (FOCUS). J. Bone Miner. Res. 33 (7), 1291–1301. doi:10.1002/jbmr.3423
Aldieri, A., Biondi, R., La Mattina, A. A., Szyszko, J. A., Polizzi, S., Dall’Olio, D., et al. (2024). Development and validation of a semi-automated and unsupervised method for femur segmentation from CT. Sci. Rep. 14, 7403. doi:10.1038/s41598-024-57618-6
Almeida, D. F., Ruben, R. B., Folgado, J., Fernandes, P. R., Audenaert, E., Verhegghe, B., et al. (2016). Fully automatic segmentation of femurs with medullary canal definition in high and in low resolution CT scans. Med. Eng. Phys. 38 (12), 1474–1480. doi:10.1016/j.medengphy.2016.09.019
Amin, S., Kopperdhal, D.L., Melton, L.J., Achenbach, S.J., Therneau, T.M., Riggs, B.L., et al. (2011). Association of hip strength estimates by finite-element analysis with fractures in women and men. J. Bone Min. Res. 26, 1593–1600. doi:10.1002/jbmr.347
Anstey, J.B., Smith, E.J., Rasquinha, B., Rudan, J.F., and Ellis, R.E. (2011). On the use of laser scans to validate reverse engineering of bony anatomy. Stud. Health Technol. Inf. 163, 18–24. doi:10.3233/978-1-60750-706-2-18
Apivanichkul, K., Phasukkit, P., Dankulchai, P., Sittiwong, W., and Jitwatcharakomol, T. (2023). Enhanced deep-learning-based automatic left-femur segmentation scheme with attribute augmentation. Sensors 23, 5720. doi:10.3390/s23125720
Audenaert, E.A., Van Houcke, J., Almeida, D.F., Paelinck, L., Peiffer, M., Steenackers, G., et al. (2019). Cascaded statistical shape model based segmentation of the full lower limb in CT. Comput. Methods Biomech. Biomed. Engin. 22, 644–657. doi:10.1080/10255842.2019.1577828
Besler, B.A., Michalski, A.S., Forkert, N.D., and Boyd, S.K. (2018). “Automatic full femur segmentation from computed tomography datasets using an atlas-based approach,” in Computational methods and clinical applications in musculoskeletal imaging, lecture notes in computer science. Editors B. Glocker, J. Yao, T. Vrtovec, A. Frangi, and G. Zheng (Cham: Springer International Publishing), 120–132. doi:10.1007/978-3-319-74113-0_11
Besler, B.A., Michalski, A.S., Kuczynski, M.T., Abid, A., Forkert, N.D., and Boyd, S.K. (2021). Bone and joint enhancement filtering: application to proximal femur segmentation from uncalibrated computed tomography datasets. Med. Image Anal. 67, 101887. doi:10.1016/j.media.2020.101887
Bessho, M., Ohnishi, I., Matsuyama, J., Matsumoto, T., Imai, K., and Nakamura, K. (2007). Prediction of strength and strain of the proximal femur by a CT-based finite element method. J. Biomech. 40, 1745–1753. doi:10.1016/j.jbiomech.2006.08.003
Bhattacharya, P., Altai, Z., Qasim, M., and Viceconti, M. (2019). A multiscale model to predict current absolute risk of femoral fracture in a postmenopausal population. Biomech. Model. Mechanobiol. 18, 301–318. doi:10.1007/s10237-018-1081-0
Bjornsson, P.A., Baker, A., Fleps, I., Pauchard, Y., Palsson, H., Ferguson, S.J., et al. (2023). Fast and robust femur segmentation from computed tomography images for patient-specific hip fracture risk screening. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 11, 253–265. doi:10.1080/21681163.2022.2068160
Black, D.M., Bouxsein, M.L., Marshall, L.M., Cummings, S.R., Lang, T.F., Cauley, J.A., et al. (2008). Proximal femoral structure and the prediction of hip fracture in men: a large prospective study using qct. J. Bone Min. Res. 23, 1326–1333. doi:10.1359/jbmr.080316
Borggrefe, J., de Buhr, T., Shrestha, S., Marshall, L.M., Orwoll, E., Peters, K., et al. (2016). For the osteoporotic fractures in men (MrOS) study research Group, 2016. Association of 3D geometric measures derived from quantitative computed tomography with hip fracture risk in older men: QCT-DERIVED 3D GEOMETRIC MEASURES ASSOCIATED WITH HIP FRACTURE. J. Bone Min. Res. 31, 1550–1558. doi:10.1002/jbmr.2821
Bousson, V.D., Adams, J., Engelke, K., Aout, M., Cohen-Solal, M., Bergot, C., et al. (2011). In vivo discrimination of hip fracture with quantitative computed tomography: results from the prospective European Femur Fracture Study (EFFECT). J. Bone Min. Res. 26, 881–893. doi:10.1002/jbmr.270
Bouxsein, M.L. (2005). Determinants of skeletal fragility. Best. Pract. Res. Clin. Rheumatol. 19, 897–911. doi:10.1016/j.berh.2005.07.004
Bredbenner, T.L., Mason, R.L., Havill, L.M., Orwoll, E.S., and Nicolella, D.P. (2014). For the osteoporotic fractures in men (MrOS) study, 2014. Fracture risk predictions based on statistical shape and density modeling of the proximal femur: FRACTURE risk predictions based on SSDM of the proximal femur. J. Bone Min. Res. 29, 2090–2100. doi:10.1002/jbmr.2241
Cao, X., Keyak, J.H., Sigurdsson, S., Zhao, C., Zhou, W., Liu, A., et al. (2022). A new hip fracture risk index derived from FEA-computed proximal femur fracture loads and energies-to-failure. SSRN Electron. J., doi:10.2139/ssrn.4290884
Carballido-Gamio, J., Bonaretti, S., Saeed, I., Harnish, R., Recker, R., Keyak, J. H., et al. (2015). Automatic multi-parametric quantification of the proximal femur with quantitative computed tomography. Quantitative Imaging Med. Surg. 5, 552–568. doi:10.3978/j.issn.2223-4292.2015.08.02
Carballido-Gamio, J., Bonaretti, S., Saeed, I., Harnish, R., Recker, R., Keyak, J.H., et al. (2015). Automatic multi-parametric quantification of the proximal femur with quantitative computed tomography. Quant. Imaging Med. Surg. 5, 552–568. doi:10.3978/j.issn.2223-4292.2015.08.02
Chalhoub, D., Orwoll, E.S., Cawthon, P.M., Ensrud, K.E., Boudreau, R., Greenspan, S., et al. (2016). Areal and volumetric bone mineral density and risk of multiple types of fracture in older men. Bone 92, 100–106. doi:10.1016/j.bone.2016.08.014
Chandra, S.S., Xia, Y., Engstrom, C., Crozier, S., Schwarz, R., and Fripp, J. (2014). Focused shape models for hip joint segmentation in 3D magnetic resonance images. Med. Image Anal. 18, 567–578. doi:10.1016/j.media.2014.02.002
Chen, F., Liu, J., Zhao, Z., Zhu, M., and Liao, H. (2019). Three-dimensional feature-enhanced network for automatic femur segmentation. IEEE J. Biomed. Health Inf. 23, 243–252. doi:10.1109/JBHI.2017.2785389
Chen, X., Sun, S., Bai, N., Han, K., Liu, Q., Yao, S., et al. (2021). A deep learning-based auto-segmentation system for organs-at-risk on whole-body computed tomography images for radiation therapy. Radiother. Oncol. 160, 175–184. doi:10.1016/j.radonc.2021.04.019
Cheng, X., Li, J., Lu, Y., Keyak, J., and Lang, T. (2007). Proximal femoral density and geometry measurements by quantitative computed tomography: association with hip fracture. Bone 40, 169–174. doi:10.1016/j.bone.2006.06.018
Cheng, Y., Zhou, S., Wang, Y., Guo, C., Bai, J., and Tamura, S. (2013). Automatic segmentation technique for acetabulum and femoral head in CT images. Pattern Recognit. 46, 2969–2984. doi:10.1016/j.patcog.2013.04.006
Chu, C., Bai, J., Wu, X., and Zheng, G. (2015a). MASCG: multi-Atlas Segmentation Constrained Graph method for accurate segmentation of hip CT images. Med. Image Anal. 26, 173–184. doi:10.1016/j.media.2015.08.011
Chu, C., Chen, C., Liu, L., and Zheng, G. (2015b). FACTS: fully automatic CT segmentation of a hip joint. Ann. Biomed. Eng. 43, 1247–1259. doi:10.1007/s10439-014-1176-4
Cong, E., and Walker, M.D. (2014). The Chinese skeleton: insights into microstructure that help to explain the epidemiology of fracture. Bone Res. 2, 14009. doi:10.1038/boneres.2014.9
Dall’Ara, E., Luisier, B., Schmidt, R., Kainberger, F., Zysset, P., and Pahr, D. (2013). A nonlinear QCT-based finite element model validation study for the human femur tested in two configurations in vitro. Bone 52, 27–38. doi:10.1016/j.bone.2012.09.006
Deng, Y., Wang, L., Zhao, C., Tang, S., Cheng, X., Deng, H.-W., et al. (2022). A deep learning-based approach to automatic proximal femur segmentation in quantitative CT images. Med. Biol. Eng. Comput. 60, 1417–1429. doi:10.1007/s11517-022-02529-9
Dice, L.R. (1945). Measures of the amount of ecologic association between species. Ecology 26, 297–302. doi:10.2307/1932409
Dragomir-Daescu, D., Op Den Buijs, J., McEligot, S., Dai, Y., Entwistle, R.C., Salas, C., et al. (2011). Robust QCT/FEA models of proximal femur stiffness and fracture load during a sideways fall on the hip. Ann. Biomed. Eng. 39, 742–755. doi:10.1007/s10439-010-0196-y
Duchemin, L., Mitton, D., Jolivet, E., Bousson, V., Laredo, J.D., and Skalli, W. (2008). An anatomical subject-specific FE-model for hip fracture load prediction. Comput. Methods Biomech. Biomed. Engin. 11, 105–111. doi:10.1080/10255840701535965
Enns-Bray, W.S., Bahaloo, H., Fleps, I., Pauchard, Y., Taghizadeh, E., Sigurdsson, S., et al. (2019). Biofidelic finite element models for accurately classifying hip fracture in a retrospective clinical study of elderly women from the AGES Reykjavik cohort. Bone 120, 25–37. doi:10.1016/j.bone.2018.09.014
Falcinelli, C., Schileo, E., Balistreri, L., Baruffaldi, F., Bordini, B., Viceconti, M., et al. (2014). Multiple loading conditions analysis can improve the association between finite element bone strength estimates and proximal femur fractures: a preliminary study in elderly women. Bone 67, 71–80. doi:10.1016/j.bone.2014.06.038
Fick, T., Van Doormaal, J.A.M., Tosic, L., Van Zoest, R.J., Meulstee, J.W., Hoving, E.W., et al. (2021). Fully automatic brain tumor segmentation for 3D evaluation in augmented reality. Neurosurg. Focus 51, E14. doi:10.3171/2021.5.FOCUS21200
Fleps, I., Guy, P., Ferguson, S.J., Cripton, P.A., and Helgason, B. (2019). Explicit finite element models accurately predict subject-specific and velocity-dependent kinetics of sideways fall impact. J. Bone Min. Res. 34, 1837–1850. doi:10.1002/jbmr.3804
Fleps, I., Pálsson, H., Baker, A., Enns-Bray, W., Bahaloo, H., Danner, M., et al. (2022). Finite element derived femoral strength is a better predictor of hip fracture risk than aBMD in the AGES Reykjavik study cohort. Bone 154, 116219. doi:10.1016/j.bone.2021.116219
Fritscher, K.D., Grünerbl, A., and Schubert, R. (2007). 3D image segmentation using combined shape-intensity prior models. Int. J. Comput. Assist. Radiol. Surg. 1, 341–350. doi:10.1007/s11548-007-0070-z
Gangwar, T., Calder, J., Takahashi, T., Bechtold, J.E., and Schillinger, D. (2018). Robust variational segmentation of 3D bone CT data with thin cartilage interfaces. Med. Image Anal. 47, 95–110. doi:10.1016/j.media.2018.04.003
Gelaude, F., Vander Sloten, J., and Lauwers, B. (2008). Accuracy assessment of CT-based outer surface femur meshes. Comput. Aided Surg. 13, 188–199. doi:10.3109/10929080802195783
González Sánchez, J.C., Magnusson, M., Sandborg, M., Carlsson Tedgren, Å., and Malusek, A. (2020). Segmentation of bones in medical dual-energy computed tomography volumes using the 3D U-Net. Phys. Med. 69, 241–247. doi:10.1016/j.ejmp.2019.12.014
Grassi, L., Schileo, E., Taddei, F., Zani, L., Juszczyk, M., Cristofolini, L., et al. (2012). Accuracy of finite element predictions in sideways load configurations for the proximal human femur. J. Biomech. 45, 394–399. doi:10.1016/j.jbiomech.2011.10.019
Guo, H., Song, S., Wang, J., Guo, M., Cheng, Y., Wang, Y., et al. (2018). 3D surface voxel tracing corrector for accurate bone segmentation. Int. J. Comput. Assist. Radiol. Surg. 13, 1549–1563. doi:10.1007/s11548-018-1804-9
Haleem, S., Lutchman, L., Mayahi, R., Grice, J.E., and Parker, M.J. (2008). Mortality following hip fracture: trends and geographical variations over the last 40 years. Injury 39, 1157–1163. doi:10.1016/j.injury.2008.03.022
Hanaoka, S., Masutani, Y., Nemoto, M., Nomura, Y., Miki, S., Yoshikawa, T., et al. (2017). Landmark-guided diffeomorphic demons algorithm and its application to automatic segmentation of the whole spine and pelvis in CT images. Int. J. Comput. Assist. Radiol. Surg. 12, 413–430. doi:10.1007/s11548-016-1507-z
Hayes, W.C., Myers, E.R., Robinovitch, S.N., Van Den Kroonenberg, A., Courtney, A.C., and McMahon, T.A. (1996). Etiology and prevention of age-related hip fractures. Bone 18, S77–S86. doi:10.1016/8756-3282(95)00383-5
Hiasa, Y., Otake, Y., Takao, M., Ogawa, T., Sugano, N., and Sato, Y. (2020). Automated muscle segmentation from clinical CT using bayesian U-net for personalized musculoskeletal modeling. IEEE Trans. Med. Imaging 39, 1030–1040. doi:10.1109/TMI.2019.2940555
Huang, J., Griffith, J.F., Wang, D., and Shi, L. (2015). Graph-cut-based segmentation of proximal femur from computed tomography images with shape prior. J. Med. Biol. Eng. 35, 594–607. doi:10.1007/s40846-015-0079-7
Ito, M., Wakao, N., Hida, T., Matsui, Y., Abe, Y., Aoyagi, K., et al. (2010). Analysis of hip geometry by clinical CT for the assessment of hip fracture risk in elderly Japanese women. Bone 46, 453–457. doi:10.1016/j.bone.2009.08.059
Jeuthe, J., Sánchez, J.C.G., Magnusson, M., Sandborg, M., Tedgren, Å.C., and Malusek, A. (2021). SEMI-AUTOMATED 3D SEGMENTATION OF PELVIC REGION BONES IN CT VOLUMES FOR THE ANNOTATION OF MACHINE LEARNING DATASETS. Radiat. Prot. Dosim. 195, 172–176. doi:10.1093/rpd/ncab073
Jiang, X., Gruner, M., Trémollieres, F., Pluskiewicz, W., Sornay-Rendu, E., Adamczyk, P., et al. (2017). Diagnostic accuracy of FRAX in predicting the 10-year risk of osteoporotic fractures using the USA treatment thresholds: a systematic review and meta-analysis. Bone 99, 20–25. doi:10.1016/j.bone.2017.02.008
Johannesdottir, F., Poole, K.E.S., Reeve, J., Siggeirsdottir, K., Aspelund, T., Mogensen, B., et al. (2011). Distribution of cortical bone in the femoral neck and hip fracture: a prospective case-control analysis of 143 incident hip fractures; the AGES-REYKJAVIK Study. Bone 48, 1268–1276. doi:10.1016/j.bone.2011.03.776
Kainmueller, D., Lamecker, H., Zachow, S., and Hege, H.-C. (2009). “An articulated statistical shape model for accurate hip joint segmentation,” in 2009 annual international conference of the IEEE engineering in medicine and biology society. Presented at the 2009 annual international conference of the IEEE engineering in medicine and biology society (Minneapolis, MN: IEEE), 6345–6351. doi:10.1109/IEMBS.2009.5333269
Kang, Y., Engelke, K., and Kalender, W.A. (2003). A new accurate and precise 3-D segmentation method for skeletal structures in volumetric CT data. IEEE Trans. Med. Imaging 22, 586–598. doi:10.1109/TMI.2003.812265
Kanis, J.A., Burlet, N., Cooper, C., Delmas, P.D., Reginster, J.-Y., Borgstrom, F., et al. (2008). European guidance for the diagnosis and management of osteoporosis in postmenopausal women. Osteoporos. Int. 19, 399–428. doi:10.1007/s00198-008-0560-z
Keaveny, T.M., Clarke, B.L., Cosman, F., Orwoll, E.S., Siris, E.S., Khosla, S., et al. (2020). Biomechanical Computed Tomography analysis (BCT) for clinical assessment of osteoporosis. Osteoporos. Int. 31, 1025–1048. doi:10.1007/s00198-020-05384-2
Keyak, J.H. (2001). Improved prediction of proximal femoral fracture load using nonlinear finite element models. Med. Eng. Phys. 23, 165–173. doi:10.1016/S1350-4533(01)00045-5
Keyak, J.H., Kaneko, T.S., Tehranzadeh, J., and Skinner, H.B. (2005). Predicting proximal femoral strength using structural engineering models. Clin. Orthop. NA, 219–228. doi:10.1097/01.blo.0000164400.37905.22
Khoo, B.C.C., Wang, L., Lewis, J.R., Brown, K., Cheng, X., and Prince, R.L. (2020). Anatomical factors associated with femoral neck fractures of elderly Beijing women. Arch. Osteoporos. 15, 112. doi:10.1007/s11657-020-00780-x
Kim, J.J., Nam, J., and Jang, I.G. (2018). Fully automated segmentation of a hip joint using the patient-specific optimal thresholding and watershed algorithm. Comput. Methods Programs Biomed. 154, 161–171. doi:10.1016/j.cmpb.2017.11.007
Koivumäki, J.E.M., Thevenot, J., Pulkkinen, P., Kuhn, V., Link, T.M., Eckstein, F., et al. (2012). Ct-based finite element models can be used to estimate experimentally measured failure loads in the proximal femur. Bone 50, 824–829. doi:10.1016/j.bone.2012.01.012
Kopperdahl, D.L., Aspelund, T., Hoffmann, P.F., Sigurdsson, S., Siggeirsdottir, K., Harris, T.B., et al. (2014). Assessment of incident spine and hip fractures in women and men using finite element analysis of CT scans: INCIDENT FRACTURE ASSESSMENT USING FEA OF CT SCANS. J. Bone Min. Res. 29, 570–580. doi:10.1002/jbmr.2069
Krcah, M., Szekely, G., and Blanc, R. (2011). “Fully automatic and fast segmentation of the femur bone from 3D-CT images with no shape prior,” in 2011 IEEE international symposium on biomedical imaging: from nano to macro. Presented at the 2011 8th IEEE international symposium on biomedical imaging (ISBI 2011) (Chicago, IL, USA: IEEE), 2087–2090. doi:10.1109/ISBI.2011.5872823
Kuiper, R.J.A., Sakkers, R.J.B., van Stralen, M., Arbabi, V., Viergever, M.A., Weinans, H., et al. (2022). Efficient cascaded V-net optimization for lower extremity CT segmentation validated using bone morphology assessment. J. Orthop. Res. 40, 2894–2907. doi:10.1002/jor.25314
Lamecker, H., Seebass, M., Hege, H.-C., and Deuflhard, P. (2004). “A 3D statistical shape model of the pelvic bone for segmentation,” in Presented at the medical imaging 2004. Editors J.M. Fitzpatrick, and M. Sonka (San Diego, CA), 1341. doi:10.1117/12.534145
Lessmann, N., Van Ginneken, B., De Jong, P. A., and Išgum, I. (2019). Iterative fully convolutional neural networks for automatic vertebra segmentation and identification. Med. Image Anal. 53, 142–155. doi:10.1016/j.media.2019.02.005
Li, Y., Rao, S., Chen, W., Azghadi, S.F., Nguyen, K.N.B., Moran, A., et al. (2022). Evaluating automatic segmentation for swallowing-related organs for head and neck cancer. Technol. Cancer Res. Treat. 21, 153303382211057. doi:10.1177/15330338221105724
Liu, P., Han, H., Du, Y., Zhu, H., Li, Y., Gu, F., et al. (2021). Deep learning to segment pelvic bones: large-scale CT datasets and baseline models. Int. J. Comput. Assist. Radiol. Surg. 16, 749–756. doi:10.1007/s11548-021-02363-8
Mazurowski, M. A., Dong, H., Gu, H., Yang, J., Konz, N., and Zhang, Y. (2023). Segment anything model for medical image analysis: an experimental study. Med. Image Anal. 89, 102918. doi:10.1016/j.media.2023.102918
Michalski, A.S., Besler, B.A., Burt, L.A., and Boyd, S.K. (2021). Opportunistic CT screening predicts individuals at risk of major osteoporotic fracture. Osteoporos. Int. 32, 1639–1649. doi:10.1007/s00198-021-05863-0
Museyko, O., Bousson, V., Adams, J., Laredo, J.-D., and Engelke, K. (2016). QCT of the proximal femur—which parameters should be measured to discriminate hip fracture?. Osteoporos. Int. 27, 1137–1147. doi:10.1007/s00198-015-3324-6
Nishiyama, K.K., Gilchrist, S., Guy, P., Cripton, P., and Boyd, S.K. (2013). Proximal femur bone strength estimated by a computationally fast finite element analysis in a sideways fall configuration. J. Biomech. 46, 1231–1236. doi:10.1016/j.jbiomech.2013.02.025
Nishiyama, K.K., Ito, M., Harada, A., and Boyd, S.K. (2014). Classification of women with and without hip fracture based on quantitative computed tomography and finite element analysis. Osteoporos. Int. 25, 619–626. doi:10.1007/s00198-013-2459-6
Noguchi, S., Nishio, M., Yakami, M., Nakagomi, K., and Togashi, K. (2020). Bone segmentation on whole-body CT using convolutional neural network with novel data augmentation techniques. Comput. Biol. Med. 121, 103767. doi:10.1016/j.compbiomed.2020.103767
O’Neill, G.T., Lee, W.-S., and Beaulé, P. (2012). Segmentation of cam-type femurs from CT scans. Vis. Comput. 28, 205–218. doi:10.1007/s00371-011-0636-1
Orwoll, E.S., Marshall, L.M., Nielson, C.M., Cummings, S.R., Lapidus, J., Cauley, J.A., et al. (2009). Finite element analysis of the proximal femur and hip fracture risk in older men. J. Bone Min. Res. 24, 475–483. doi:10.1359/jbmr.081201
Parkkari, J., Kannus, P., Palvanen, M., Natri, A., Vainio, J., Aho, H., et al. (1999). Majority of hip fractures occur as a result of a fall and impact on the greater trochanter of the femur: a prospective controlled hip fracture study with 206 consecutive patients. Calcif. Tissue Int. 65, 183–187. doi:10.1007/s002239900679
Patton, D.M., Henning, E.N., Goulet, R.W., Carroll, S.K., Bigelow, E.M.R., Provencher, B., et al. (2021). Deep learning-based segmentation of high-resolution computed tomography image data outperforms commonly used automatic bone segmentation methods (preprint). Bioengineering. doi:10.1101/2021.07.27.453890
Pauchard, Y., Fitze, T., Browarnik, D., Eskandari, A., Pauchard, I., Enns-Bray, W., et al. (2016). Interactive graph-cut segmentation for fast creation of finite element models from clinical ct data for hip fracture prediction. Comput. Methods Biomech. Biomed. Engin. 19, 1693–1703. doi:10.1080/10255842.2016.1181173
Qasim, M., Farinella, G., Zhang, J., Li, X., Yang, L., Eastell, R., et al. (2016). Patient-specific finite element estimated femur strength as a predictor of the risk of hip fracture: the effect of methodological determinants. Osteoporos. Int. 27, 2815–2822. doi:10.1007/s00198-016-3597-4
Saillard, E., Gardegaront, M., Levillain, A., Bermond, F., Mitton, D., Pialat, J.-B., et al. (2024). Finite element models with automatic computed tomography bone segmentation for failure load computation. Sci. Rep. 14, 16576. doi:10.1038/s41598-024-66934-w
Schileo, E., Balistreri, L., Grassi, L., Cristofolini, L., and Taddei, F. (2014). To what extent can linear finite element models of human femora predict failure under stance and fall loading configurations?. J. Biomech. 47, 3531–3538. doi:10.1016/j.jbiomech.2014.08.024
Schileo, E., Pitocchi, J., Falcinelli, C., and Taddei, F. (2020). Cortical bone mapping improves finite element strain prediction accuracy at the proximal femur. Bone 136, 115348. doi:10.1016/j.bone.2020.115348
Schileo, E., Taddei, F., Malandrino, A., Cristofolini, L., and Viceconti, M. (2007). Subject-specific finite element models can accurately predict strain levels in long bones. J. Biomech. 40, 2982–2989. doi:10.1016/j.jbiomech.2007.02.010
Schuit, S.C.E., van der Klift, M., Weel, A.E.A.M., de Laet, C.E.D.H., Burger, H., Seeman, E., et al. (2004). Fracture incidence and association with bone mineral density in elderly men and women: the Rotterdam Study. Bone 34, 195–202. doi:10.1016/j.bone.2003.10.001
Scott, V., Wagar, L., and Elliott, S. (2010). “Falls & related injuries among older Canadians: fall-related hospitalizations & intervention initiatives,” in Prep. Behalf public health agency can. Div. Aging Sr. Vic. BC vic. Scott consult.
Seim, H., Kainmueller, D., Heller, M., Lamecker, H., and Zachow, S. (2008). “Automatic segmentation of the pelvic bones from CT data based on a statistical shape model,” in Eurographics workshop on visual computing for biomedicine. doi:10.2312/VCBM/VCBM08/093-100
Sekuboyina, A., Husseini, M. E., Bayat, A., Löffler, M., Liebl, H., Li, H., et al. (2021). VerSe: a Vertebrae labelling and segmentation benchmark for multi-detector CT images. Med. Image Anal. 73, 102166. doi:10.1016/j.media.2021.102166
Stone, K.L., Seeley, D.G., Lui, L.-Y., Cauley, J.A., Ensrud, K., Browner, W.S., et al. (2003). BMD at multiple sites and risk of fracture of multiple types: long-term results from the study of osteoporotic fractures. J. Bone Min. Res. 18, 1947–1954. doi:10.1359/jbmr.2003.18.11.1947
Straka, M., LaCruz, A., Fleischmann, D., and Dimitrov, L.I. (2003). Bone segmentation in CT-angiography data using a probabilistic atlas. Proc. Vis. Model. Vis. Conf. 121, 19–21.
Sultana, J., Naznin, M., and Faisal, T. R. (2024). SSDL—an automated semi-supervised deep learning approach for patient-specific 3D reconstruction of proximal femur from QCT images. Med. Biol. Eng. Comput 62, 1409–1425. doi:10.1007/s11517-023-03013-8
Tan, D., Yao, Z., Peng, X., Ma, H., Dai, Y., Su, Y., et al. (2024). Multi-level medical image segmentation network based on multi-scale and context information fusion strategy. IEEE Trans. Emerg. Top. Comput. Intell. 8, 474–487. doi:10.1109/TETCI.2023.3306250
Testi, D., Zannoni, C., Cappello, A., and Viceconti, M. (2001). Border-tracing algorithm implementation for the femoral geometry reconstruction. Comput. Methods Programs Biomed. 65, 175–182. doi:10.1016/S0169-2607(00)00125-5
Treece, G.M., Gee, A.H., Tonkin, C., Ewing, S.K., Cawthon, P.M., Black, D.M., et al. (2015). Predicting hip fracture type with cortical bone mapping (CBM) in the osteoporotic fractures in men (MrOS) study. J. Bone Min. Res. 30, 2067–2077. doi:10.1002/jbmr.2552
Väänänen, S.P., Grassi, L., Venäläinen, M.S., Matikka, H., Zheng, Y., Jurvelin, J.S., et al. (2019). Automated segmentation of cortical and trabecular bone to generate finite element models for femoral bone mechanics. Med. Eng. Phys. 70, 19–28. doi:10.1016/j.medengphy.2019.06.015
Van Den Oever, L.B., Van Veldhuizen, W.A., Cornelissen, L.J., Spoor, D.S., Willems, T.P., Kramer, G., et al. (2022). Qualitative evaluation of common quantitative metrics for clinical acceptance of automatic segmentation: a case study on heart contouring from CT images by deep learning algorithms. J. Digit. Imaging 35, 240–247. doi:10.1007/s10278-021-00573-9
Varga, P., Schwiedrzik, J., Zysset, P.K., Fliri-Hofmann, L., Widmer, D., Gueorguiev, B., et al. (2016). Nonlinear quasi-static finite element simulations predict in vitro strength of human proximal femora assessed in a dynamic sideways fall setup. J. Mech. Behav. Biomed. Mater. 57, 116–127. doi:10.1016/j.jmbbm.2015.11.026
Wainwright, S.A., Marshall, L.M., Ensrud, K.E., Cauley, J.A., Black, D.M., Hillier, T.A., et al. (2005). Hip fracture in women without osteoporosis. J. Clin. Endocrinol. Metab. 90, 2787–2793. doi:10.1210/jc.2004-1568
Wang, C., Connolly, B., De Oliveira Lopes, P.F., Frangi, A.F., and Smedby, Ö. (2019). “Pelvis segmentation using multi-pass U-net and iterative shape estimation,” in Computational methods and clinical applications in musculoskeletal imaging, lecture notes in computer science. Editors T. Vrtovec, J. Yao, G. Zheng, and J.M. Pozo (Cham: Springer International Publishing), 49–57. doi:10.1007/978-3-030-11166-3_5
Wang, L., Yang, M., Liu, Y., Ge, Y., Zhu, S., Su, Y., et al. (2022). Differences in hip geometry between female subjects with and without acute hip fracture: a cross-sectional case-control study. Front. Endocrinol. 13, 799381. doi:10.3389/fendo.2022.799381
Warfield, S.K., Zou, K.H., and Wells, W.M. (2004). Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation. IEEE Trans. Med. Imaging 23, 903–921. doi:10.1109/TMI.2004.828354
Whitmarsh, T., Treece, G.M., and Poole, K.E.S. (2014). “Automatic segmentation and discrimination of connected joint bones from CT by multi-atlas registration,” in Comput. Methods clin. Editor Li Yao J Klinder T (Cham: Appl. Spine Imaging Lect. Notes Comput. Vis. Biomech. Springer), 117, 199–207. doi:10.1007/978-3-319-07269-2_17
Wu, D., Zhi, X., Liu, X., Zhang, Y., and Chai, W. (2022). Utility of a novel integrated deep convolutional neural network for the segmentation of hip joint from computed tomography images in the preoperative planning of total hip arthroplasty, J. Orthop. Surg. 17, 164. doi:10.1186/s13018-022-02932-w
Xu, P., Moshfeghifar, F., Gholamalizadeh, T., Nielsen, M.B., Erleben, K., and Darkner, S. (2022). Auto-segmentation of hip joints using MultiPlanar UNet with transfer learning, 153–162. doi:10.1007/978-3-031-16760-7_15
Yang, L., Burton, A.C., Bradburn, M., Nielson, C.M., Orwoll, E.S., and Eastell, R. (2012). Distribution of bone density in the proximal femur and its association with hip fracture risk in older men: the osteoporotic fractures in men (MrOS) study. J. Bone Min. Res. 27, 2314–2324. doi:10.1002/jbmr.1693
Yao, W., Abolmaesumi, P., Greenspan, M., and Ellis, R.E. (2005). An estimation/correction algorithm for detecting bone edges in CT images. IEEE Trans. Med. Imaging 24, 997–1010. doi:10.1109/TMI.2005.850541
Yokota, F., Okada, T., Takao, M., Sugano, N., Tada, Y., Tomiyama, N., et al. (2013). “Automated CT segmentation of diseased hip using hierarchical and conditional statistical shape models,” in Advanced information systems engineering, lecture notes in computer science. Editors C. Salinesi, M.C. Norrie, and Ó. Pastor (Berlin Heidelberg, Berlin, Heidelberg: Springer), 190–197. doi:10.1007/978-3-642-40763-5_24
Yosibash, Z., Myers, K., Trabelsi, N., and Sternheim, A. (2020). Autonomous FEs (AFE) - a stride toward personalized medicine. Comput. Math. Appl. 80, 2417–2432. doi:10.1016/j.camwa.2020.03.012
Yosibash, Z., Plitman Mayo, R., Dahan, G., Trabelsi, N., Amir, G., and Milgrom, C. (2014). Predicting the stiffness and strength of human femurs with real metastatic tumors. Bone 69, 180–190. doi:10.1016/j.bone.2014.09.022
Yosibash, Z., Trabelsi, N., Buchnik, I., Myers, K. W., Salai, M., Eshed, I., et al. (2023). Hip fracture risk assessment in elderly and diabetic patients: combining autonomous finite element analysis and machine learning. J. Bone Mineral Res. 38, 876–886. doi:10.1002/jbmr.4805
Zhai, H., Chen, Z., Li, L., Tao, H., Wang, Jinwu, Li, K., et al. (2023). Two-stage multi-task deep learning framework for simultaneous pelvic bone segmentation and landmark detection from CT images. Int. J. Comput. Assist. Radiol. Surg. 19, 97–108. doi:10.1007/s11548-023-02976-1
Zhang, J., Malcolm, D., Hislop-Jambrich, J., Thomas, C.D.L., and Nielsen, P.M.F. (2014). An anatomical region-based statistical shape model of the human femur. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2, 176–185. doi:10.1080/21681163.2013.878668
Zhang, X., Nadeem, S. A., DiCamillo, P. A., Shibli-Rahhal, A., Regan, E. A., Barr, R. G., et al. (2024). Ultra-low dose hip CT-based automated measurement of volumetric bone mineral density at proximal femoral subregions. Med. Phys., 17319. doi:10.1002/mp.17319
Zhang, X., Zheng, Y., Bai, X., Cai, L., Wang, L., Wu, S., et al. (2022). Femoral image segmentation based on two-stage convolutional network using 3D-DMFNet and 3D-ResUnet. Comput. Methods Programs Biomed. 226, 107110. doi:10.1016/j.cmpb.2022.107110
Zhao, C., Keyak, J.H., Tang, J., Kaneko, T.S., Khosla, S., Amin, S., et al. (2021). ST-V-Net: incorporating shape prior into convolutional neural networks for proximal femur segmentation. Complex Intell. Syst. 9, 2747–2758. doi:10.1007/s40747-021-00427-5
Zhou, S., Cheng, Y., Wang, Y., Dong, K., Guo, C., Bai, J., et al. (2013). Segmentation of the hip joint in CT volumes using adaptive thresholding classification and normal direction correction. J. Chin. Inst. Eng. 36, 1059–1072. doi:10.1080/02533839.2012.747064
Zoroofi, R.A., Sato, Y., Sasama, T., Nishii, T., Sugano, N., Yonenobu, K., et al. (2003). Automated segmentation of acetabulum and femoral head from 3-D CT images. IEEE Trans. Inf. Technol. Biomed. 7, 329–343. doi:10.1109/TITB.2003.813791
Zou, Z., Liao, S.-H., Luo, S.-D., Liu, Q., and Liu, S.-J. (2017). Semi-automatic segmentation of femur based on harmonic barrier. Comput. Methods Programs Biomed. 143, 171–184. doi:10.1016/j.cmpb.2017.03.005
Appendix A
In the following, a brief description of the main segmentation methods adopted for femur/pelvis has been reported.
a) Threshold-based method. In this approach, the pixels are binarized depending on their intensity value. The segmentation is achieved by grouping all pixels with intensities greater than the threshold into one class and all other pixels into another class.
b) Statistical shape model-based method. This method aims to use prior knowledge about the shape to segment images and describes the anatomical variation observed in medical images. To create a statistical shape model, a training dataset that corresponds to a database of ground truth segmentations is used to compute the mean shape and extract the variation. The mean shape that represents the knowledge about the general shape is computed as the shape to which all other shapes in the training dataset have minimal distance to. The principal modes of variation, that corresponds to the knowledge about how much the shape differs between subjects, is extracted using principal component analysis by computing the eigenvectors of the covariance matrix. The eigenvectors corresponding to the eigenvalues of the covariance matrix are the directions of variation present in the data.
c) Atlas-based method. This method is based on the atlas that is assumed as a reference image and in which the region of interest has been accurately segmented, generating the binary mask. To segment a new image, the atlas is first registered to the new image, and then the binary mask is deformed from the atlas onto the new image to segment it.
d) Graph-cut method. This method represents an energy-based method in which an image is converted to a graph and the image segmentation problem is transformed into a cost function minimization problem. A graph of an image consists of a set of vertices and edges that connect them. Each image voxel corresponds to a vertex in the graph. Besides these vertices, there are two additional vertices, called terminal vertices that are used to represent the object and the background. Two kinds of edges can be identified: n-edges that connect two neighboring voxels, and t-edges that link each voxel to the terminal vertices. All edges in the graph are assigned some cost. The cost of n-edges corresponds to a penalty for discontinuity between the voxels, whereas the cost of a t-edge corresponds to a penalty for assigning the corresponding label to the voxel. An s-t cut is defined as a subset of edges such that the terminal vertices become completely separated. The idea of the method is to compute the best cut that would furnish the optimal segmentation. Thus, to find the optimal segmentation the cut that has the minimum cost among all cuts must be found.
e) Deep-learning method. This method uses deep neural networks to automatically perform the segmentation. An essential phase of such a method is the training of the networks. The most common approach in medical image segmentation is to use ground truth data to train the network to perform the desired segmentation task. For the training, it is important to use datasets that contain a variety of data that can be found in clinical practice.
Glossary
Anatomical abbreviations
All union of all quadrants
FH femoral head
FN femoral neck
IA inferior-anterior quadrant
IT intertrochanter
SA supero-anterior quadrant
SP superior-posterior quadrant
TH total hip
TR trochanter
Densitometric abbreviations
aBMD areal bone mineral density
BMD bone mineral density
ECTD average density in the trabecular compartment close to the cortex
vBMD volumetric bone mineral density
vBMD-C cortical volumetric BMD
vBMD-I integral volumetric BMD
vBMD-T trabecular volumetric BMD
Measurements and indices abbreviations
AD average symmetric surface distance
ADE average distance error
ADRMS average symmetric roots mean square surface distance
ASD average surface distance
BMI body mass index
BR buckling ratio
CM cortical mass per unit cortical surface area
CortShaftThick cortical thickness of shaft
CortNeckThick cortical thickness of neck
CortArea cortical area
CSA cross-sectional area
CSMI cross-sectional moment of inertia
CTh cortical thickness
CV coefficient of variation
%CV percent cortical volume
CVRMS root mean square coefficient variation
dcort vertebral cortical thickness
dmean mean distance
dr area deviation
dRMS root mean square distance
DS surface distance
DSC Dice similarity coefficient
FN Delta the displacement between the geometric center of the mineral mass projection profile and its centre of mass
FN Sigma standard deviation of the mineral mass projection profile
FNG false negatives
FO false overlap
FP false positives
HD Hausdorff distance
HR Hazard Ratio
JAC Jaccard similarity index
LTI local thinning index
MAE mean absolute error
MD maximum distance
MDE maximal distance error
ME mean error
M-HD modified Hausdorff distance
MO mean overlap
NBSI FN bending/torsional strength index
NCSI FN compressive strength index
TCSI trochanteric compressive strength index
NSA neck-shaft angle
OR odds ratio
R2 coefficient of determination
RE relative error
RMSD root-mean-squared distance error
RMSE root mean square error
RMS-SYM root mean-square average symmetric distance
rtot radii of the vertebral body
rtrab radii of the vertebral trabecular compartment
SD standard deviation
SDRMS root-mean-square standard deviation
SSDgAvg symmetric surface distance global average
SSDMax symmetric surface distance maximal surface distance
SSDSAvgAvg symmetric surface distance average of slice averages
SYM average symmetric distance
THRCTM ratio between cortical and trabecular mass of total hip
TN true negatives
TP true positives
V volume
VD volume difference
VOEg volumetric overlap global error
VOESAvg average slice error
VOESmax slice maximum error
VOESmin slice minimum error
X±SD absolute difference mean and standard deviation
Other abbreviations
ARF0 predicted absolute risk of current fracture (from multi-scale modelling)
CBM cortical bone mapping
CM cortical bone mass
DCD directional cut discrepancy
EFFECT European Femur Fracture Study
F female
FL failure load
FRAX fracture risk assessment tool
HC Harrells C
L1, L2 and L3 vertebral levels
M male
MrOS Osteoporotic Fractures in Men Study
N number
NR not reported
PA pixel accuracy
PC1 principal component analysis to develop a global FE-derived risk index based on the FE parameters which were mutually correlated
SL values were computed as means over the corresponding clusters of selected slices
SSDM statistical shape and density modeling
Zmin section modulus along the weakest axis
Keywords: segmentation, finite element modeling, hip fracture risk, computed tomography, osteoporosis, CT-derived biomarkers
Citation: Falcinelli C, Cheong VS, Ellingsen LM and Helgason B (2024) Segmentation methods for quantifying X-ray Computed Tomography based biomarkers to assess hip fracture risk: a systematic literature review. Front. Bioeng. Biotechnol. 12:1446829. doi: 10.3389/fbioe.2024.1446829
Received: 10 June 2024; Accepted: 30 September 2024;
Published: 23 October 2024.
Edited by:
Ron Noah Alkalay, Harvard Medical School, United StatesReviewed by:
Martino Pani, University of Portsmouth, United KingdomAlessandra Aldieri, Polytechnic University of Turin, Italy
Copyright © 2024 Falcinelli, Cheong, Ellingsen and Helgason. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Cristina Falcinelli, Y3Jpc3RpbmEuZmFsY2luZWxsaUB1bmljaC5pdA==
 Cristina Falcinelli
Cristina Falcinelli Vee San Cheong
Vee San Cheong Lotta Maria Ellingsen
Lotta Maria Ellingsen Benedikt Helgason
Benedikt Helgason