Application of numerical simulation studies to determine dynamic loads acting on the human masticatory system during unilateral chewing of selected foods

Introduction: This paper presents its kinematic-dynamic computational model (3D) used for numerical simulations of the unilateral chewing of selected foods. The model consists of two temporomandibular joints, a mandible, and mandibular elevator muscles (the masseter, medial pterygoid, and temporalis muscles). The model load is the food characteristic (i), in the form of the function F_i = f(Δh_i)−force (F_i) vs change in specimen height (Δh_i). Functions were developed based on experimental tests in which five food products were tested (60 specimens per product).

Methods: The numerical calculations aimed to determine: dynamic muscle patterns, maximum muscle force, total muscle contraction, muscle contraction corresponding to maximum force, muscle stiffness and intrinsic strength. The values of the parameters above were determined according to the mechanical properties of the food and according to the working and non-working sides.

Results and Discussion: Based on the numerical simulations carried out, it can be concluded that: (1) muscle force patterns and maximum muscle forces depend on the food and, in addition, the values of maximum muscle forces on the non-working side are 14% lower than on the working side, irrespective of the muscle and the food; (2) the value of total muscle contraction on the working side is 17% lower than on the non-working side; (3) total muscle contraction depends on the initial height of the food; (4) muscle stiffness and intrinsic strength depend on the texture of the food, the muscle and the side analysed, i.e., the working and non-working sides.

1 Introduction

Food consumption is one of the most important activities (Lund, 1991), necessary to sustain life processes at the same time as a complex kinematic-dynamic process (Daumas et al., 2005; Hedjazi et al., 2013; Peck et al., 2000; Piancino et al., 2008; Slager et al., 1997; Stróżyk and Balchanowski, 2018), which is controlled by the central nervous system (Dellow and Lund, 1971; Lund, 1991). Mastication is also a multi-parametric issue encompassing many complex and synchronised processes for preparing a bolus for swallowing. The most important processes may include: 1) the dynamic processing of the food (Stokes et al., 2013) dependent on its position on the dental arch (Manns and Díaz, 1988), 2) the continuous change in the geometric dimensions and mechanical properties of the food (Lenfant et al., 2009; Lillford, 2000; Lucas et al., 2004; Mioche et al., 2002; Stokes et al., 2013) and 3) the performance of complex movements by the mandible during chewing (Hylander, 2006; Koolstra, 2002; Piancino et al., 2012; Posselt, 1952; Quintero et al., 2013; Slavicek, 2010; Weinberg, 1963).

There are many papers in the literature where the authors (Çakir et al., 2011; Hutchings et al., 2012; Kohyama et al., 2007; Kohyama et al., 2008; Santana-Mora et al., 2014; Wang et al., 2010) focus on various parameters related to the act of chewing, e.g., 1) change in food texture, 2) chewing effort, 3) muscle activity, 4) some cycles needed to prepare a bolus of food, 5) degree of wetting of food with saliva, 6) age, 7) pathogenic changes, but most importantly 8) loads that occur during chewing of food. On the other hand, based on the data reported by (Agrawal et al., 1998; Hiiemae et al., 1996; Koolstra, 2002; Mathevon et al., 1995; Shimada et al., 2012), it appears that the mechanical properties of food are important for the function of the masticatory system during symmetric incisal biting and chewing. Furthermore, the work results (Mioche et al., 1999; Stróżyk and Bałchanowski, 2018) indicate that food imposes individual patterns of muscular force that must adapt to different functional requirements (Fitts et al., 1991). Their values are controlled by the central nervous system (Dellow and Lund, 1971; Lund, 1991), based on remembered external stimuli (patterns) perceived by different receptors (Quintero et al., 2013) so that it is adapted to the food consumed (Hiiemae et al., 1996; Knudson, 2007; Murray, 2004).

One of the main ways to determine muscle forces is through electromyography (EMG)-based method and mathematical equations (Ferrario and Sforza, 1996; Itoh et al., 1997; Mioche et al., 1999; Murray et al., 1999; Pruim et al., 1980; Weijs and Hillen, 1985). The method is mainly applied to the masseter muscle and the temporalis muscle. In the case of the medial and lateral pterygoid muscles, measurements are more difficult because they cannot be externally accessed (Koole et al., 1990; Murray et al., 1999; Widmalm et al., 1987; Wood et al., 1986). Consequently, determining muscle forces requires intra-oral access, which makes measurements during chewing difficult due to the possibility of interference with the natural act of chewing.

Since using EMG during chewing makes it impossible to determine the forces in all the mandibular elevator muscles, it is a good option to use a numerical computational model of the masticatory system. The model developed for numerical calculations provides reproducibility but requires the preparation of basic data, e.g., the geometry of the mandible, the muscle attachment sites, the muscle model and the mode of support. As chewing is a dynamic issue, a model should be developed based on solid mechanics, i.e., a kinematic-dynamic model (Stróżyk and Bałchanowski, 2016; Stróżyk and Bałchanowski, 2018; Stróżyk and Bałchanowski, 2020). The load of the model should be the characteristics of the food in the form of the function F_i = f(Δh_i)—force (F_i) vs. change in specimen height (Δh_i), determined during experimental tests, while the movement of the mandible is set in the path of mastication determined for the tested food.

Preliminary analysis of the function of the masticatory system in terms of: 1) the position of the food (bite force) on the dental arch, 2) the number of cycles and 3) the muscle activity on the left and right sides of the mandible indicate that, in mechanical terms, unilateral chewing will be an interesting case of physiological load on the masticatory system.

In the literature, it is possible to find publications in which the authors model unilateral chewing, but these are static models in which the position of the mandible corresponds to the closure of the mouth (Korioth et al., 1992; Pinheiro and Alves, 2015; Pachnicz and Stróżyk, 2021; Reina et al., 2007). Interesting information on unilateral chewing can be found in (Harrison et al., 2014). However, the authors focus on dynamic changes in the mechanical properties of the food rather than on changes in the values of the muscular forces acting on the masticatory system. Analysing other publications on chewing (Choi et al., 2005; Jahadakbar et al., 2016; Lee et al., 2017; Luo et al., 2017; Marková and Gallo, 2016; Reina et al., 2007), we find that none of them present changes in muscle force values (muscle functioning patterns) to dynamic changes occurring in the food during mastication.

The primary aim of this study was to determine computational model of unilateral chewing, loaded with the dynamic patterns of food (i) determined in experimental tests. The model prepared in this way made it possible to determine, firstly, selected dynamic parameters of the mandibular elevator muscles, i.e., total muscle contraction (q_i) and dynamic muscle forces (F_i) as functions, q_i = qi(t) and F_i = F_i(t), respectively. The parameters obtained allowed the determination of muscle dynamic patterns in the function F_i = f(q_i). From the results obtained, parameters such as muscle stiffness (K_i) and intrinsic strength (k_i) were also determined as a function of food.

As mastication is a complex mechanical process (Stokes et al., 2013), the study was limited to first cycle.

The results demonstrate the feasibility of using a hybrid model (based on experimental tests of food and numerical simulation of unilateral chewing) to show how the dynamic parameters of the mastication system change as a function of the mechanical properties of the food and its geometric dimensions.

The proposed computational model, the adopted boundary conditions and the calculation method can be one possibility for determining muscular forces. On the other hand, the results obtained can be used to model complex issues concerning the biomechanics of the masticatory system requiring knowledge of loads.

2 Materials and methods

The use of numerical simulation to determine force patterns for the mandibular elevator muscles (the masseter muscle-M, the medial pterygoid muscle-MP and the temporalis muscle-T) during unilateral chewing required, first of all, the construction of a numerical model of the human masticatory system consisting of the mandible, TMJ and muscles. In addition, this necessitated: 1) determining how to support the model and 2) defining and determining the parameters (input data) responsible for the load and initial position (for time t = 0s) of the model.

2.1 Determination of model load and food characteristics

During the numerical simulations, forces in the muscles were determined for loads corresponding to different foods; therefore the basic parameter responsible for the mandibular force is the food characteristic (i), in the form of the function F_i =f(Δh_i)—force (F_i) vs. change in high of food specimen (Δh_i), determined in experimental studies. In the numerical model, the above function is decomposed into two functions in which force and change in high of food specimen are time-dependent, i.e., F_i(t) and Δh_i(t).

The general algorithm for determining food characteristics was similar to that presented in (Stróżyk and Bałchanowski 2018). Five foods were prepared for the study (i = c, a, d, b, s): 1) vegetables—carrot (c); 2) fruits—apple (a); 3) sweets—dark chocolate (d) and a chocolate bar (b) and 4) meat and cold cuts—sausage (s), different in terms of structure, mechanical properties and method of production (natural and artificial). The products were purchased from a single selected grocery shop and stored at 7°C until the specimens were prepared. The specimens were then normalised at 21°C for approximately 60 min until the tests began.

The aim of the experimental study was not to determine typical mechanical parameters but only the function F_i =f(Δh_i). The specimens in terms of dimensions [height (h_i), width (w_i). and length (l_i)] were similar to a typical bite of food, while the shape depended on the product (Table 1). To determine the characteristics, 60 specimens were prepared for each food.

TABLE 1

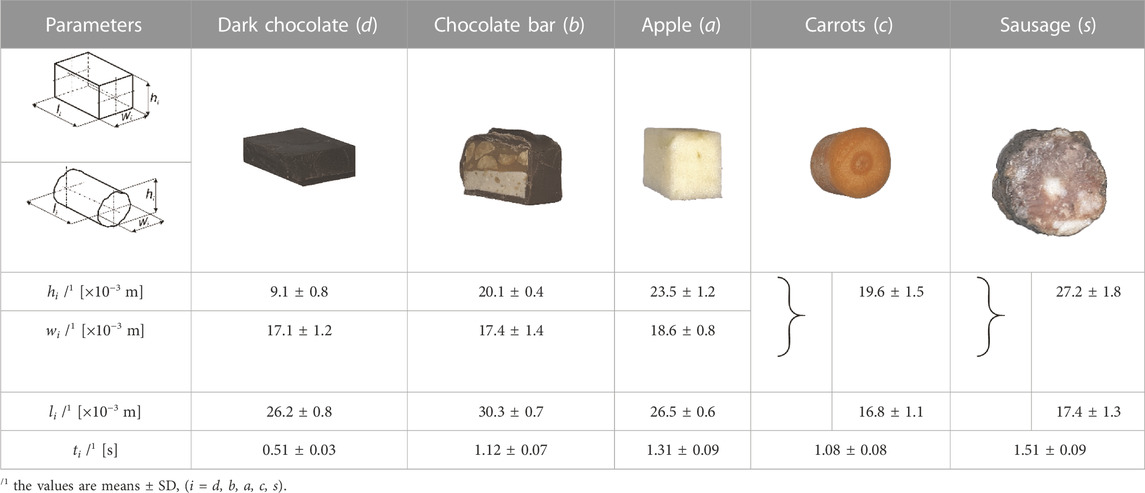
TABLE 1. Food product (i), its mean height (h_i), width (w_i) and length (l_i) and mean chewing time (t_i).

In the experimental tests, we used our own test stand design (Figure 1) [developed on the basis of a patent application—(Stróżyk, 2021)], consisting of two measuring heads, i.e., upper (maxilla) and lower (mandible), imitating fragments of the dental arches.

FIGURE 1

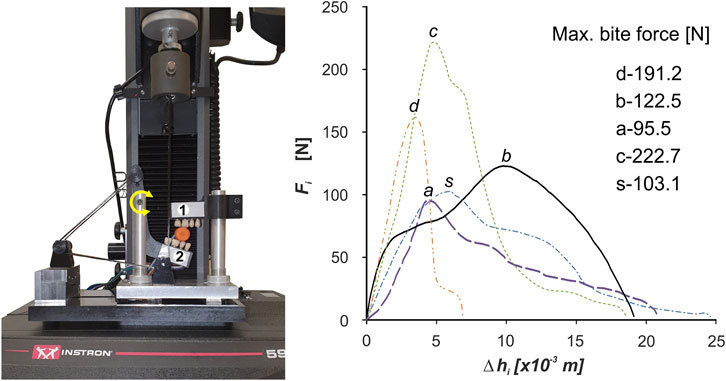
FIGURE 1. Unilateral chewing measuring system used in the experimental study to determine the characteristics of food products (i) in the form of the function F_i =f(Δh_i) (i = dark chocolate (d), chocolate bar (b), apple (a), carrots (c) and sausage (s)]; 1–upper head (maxilla), 2–lower head (mandible).

The lower head is mounted on a cantilever and thus can perform a rotational. In addition, acrylic dental prostheses, used in dental prosthetics, were attached to the heads to make the act of chewing similar to natural chewing. During testing, the test stand was mounted on an Instron 5944 test machine.

Based on the information provided in (Fitts et al., 1991; Dick and Wakeling, 2017; Koolstra, 2002), muscle force is dependent on the speed of mandibular movement, while speed is dependent on the mechanical parameters of the food, i.e., high force and low speed (hard food) or low force and high speed (soft food). Furthermore, based on the analysis of (Anderson et al., 2002; Foegeding and Drake, 2007; Foster et al., 2006; Meullenet et al., 2002; Williams et al., 2005) it appeared that the range of reported mandibular movement speeds (in this case, chewing speed) for different foods is extensive. Therefore, it was decided that all foods would be masticated at a constant velocity of v_t = 0.02 m/s (Stróżyk and Bałchanowski, 2016; Stróżyk and Bałchanowski, 2018; Stróżyk and Bałchanowski, 2020). Maintaining a constant v_t required performing a kinematic analysis of the simulator and, based on this, developing a control program for the Instron 5944 machine (Bluehill ver. 3). In addition, the chewing time (t_i) was determined for each food product based on the nominal food height h_i) and the set velocity v_t (Table 1).

Figure 1 shows the characteristics of selected products (i), in the form of the function F_i = f(Δh_i), developed on the basis of measurement results and elementary statistical calculations.

2.2 Numerical model of the human masticatory system

In order to carry out a kinetostatic analysis of the chewing process of selected foods, a computational model of the human masticatory system was developed, consisting of two elements: a fixed skull (Synbone 8500) and a movable mandible (Synbone 8596). The temporomandibular joints (TMJ) were modelled as shaped joints, with constraints in the form of contact forces between the articular surface of the condyle of the mandible and the articular tuber of the temporal bone (Strozyk and Balchanowski, 2018). The forces in the muscles were modelled using non-linear force vectors applied at the anatomical points of muscle attachment.

The numerical model had 4 degrees of freedom, which means that 4 active muscle force unknowns can be determined from the equilibrium equations. Hence, the model assumed the unknowns were the two temporalis muscle forces (FT_Wi, FT_Ni). In contrast, the forces in the masseter muscle (FM_Wi, FM_Ni) and the medial pterygoid muscles (FMP_Wi, FMP_Ni) were replaced by the resultant forces (FV_Wi, FV_Ni) (Prium et al., 1980), on the left and right sides (Figure 2).

FIGURE 2

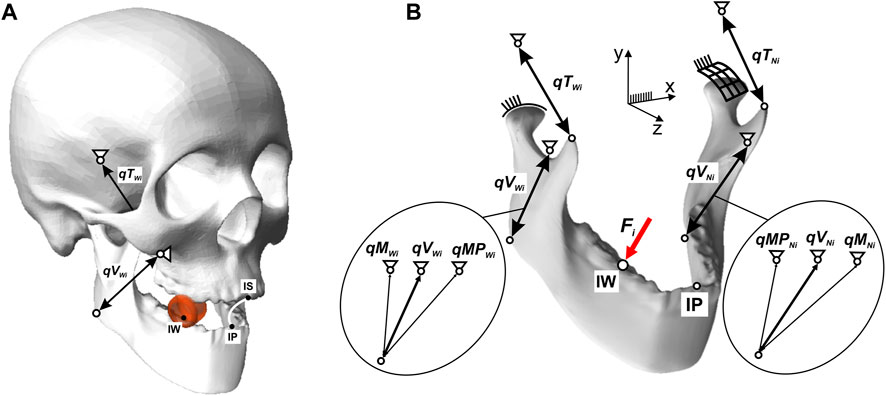
FIGURE 2. Computational model of the human masticatory system: (A) general view, (B) force forcing diagram of the mandible.

The muscles were modelled using linear kinematic excursions to simulate the elongation and contraction of the muscles that allow the mandible to move in relation to the maxilla during mastication. In the numerical model of the skull−mandible, four linear kinematic excursions were used for the temporalis muscle and the resultant. The active forces FT_Wi, FT_Ni, in the enforcing qT_Wi, qT_Ni represent the temporalis muscle, while the active forces FV_Wi, FV_Ni in the enforcing qV_Wi and qV_Ni represent the results of the masseter and medial pterygoid muscles (Figure 2).

The external force on the model [modelling the occlusal force (Stróżyk et al., 2018; Stróżyk and Bałchanowski, 2016; Stróżyk and Bałchanowski, 2018)] was the force F_i, as a function of F_i= f(Δh_i), applied at point IW on the occlusal surface of the first molar (46) (Figure 2).

2.3 Boundary conditions for the numerical model

Based on an analysis based on solid mechanics and analytical geometry, it appears that the parameters that will have a significant effect on the alignment of the mandible with respect to the maxilla will be: 1) product height (h_i) and 2) unilateral contraction of the lateral pterygoid muscle. The height of h_i is responsible for establishing the distance between the upper and lower incisors, whereas contraction of the muscle on the non-working side (N) is responsible for lateral movement of the mandible, resulting in the appearance of a path of mastication and asymmetrical displacement of the processes in the TMJ during unilateral chewing. Since there is a lack of data in the available literature on the preload (muscle force) and corresponding stiffness of the lateral pterygoid muscle, it was decided to use the effect of its action as a parameter defining mandibular preposition and movement.

The appropriate association of the height of the h_i and the mastication path (effect) and the appropriate alignment of the mandibular processes at the TMJ enable the initial position of the model to be determined during unilateral chewing.

Based on the analysis of data reported in (Bhatka et al., 2004; Buschang et al., 2007; Nishigawa et al., 1997; Piancino et al., 2012; Slavicek, 2010), a hypothetical path of mastication was prepared for each product, in the frontal plane (Figure 3A), in shape close to an ellipse (Hedjazi et al., 2013), in such a way that its geometric parameters (height and width) were synchronised with the food height (h_i), i.e., the initial distance between a pair of corresponding first molars.

FIGURE 3

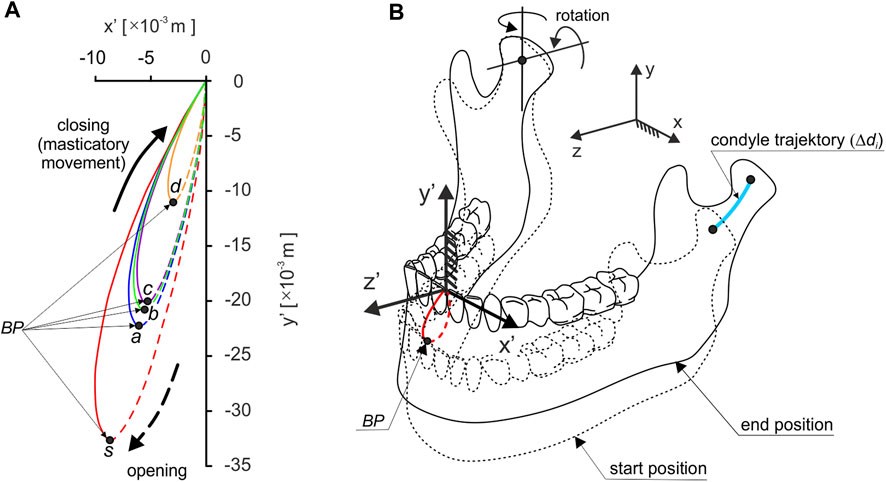
FIGURE 3. Trajectory of: (A) the incisal point in the frontal plane (path of chewing), depending on the foods and (B) the mandibular condyle on the non-working side during unilateral chewing; Black point (BP) indicates the point at which chewing begins.

The path of mastication prepared in this way are the parameter by which it is possible to reproduce the trajectory of the incisal point during a single or one cycle of unilateral chewing.

The results of preliminary calculations showed that the introduction of the mastication path significantly affects the values of the length of the condylar trajectories (Δd_i). In addition, analysis of the results showed that the condyles move according to the mandibular kinematics reported in (Weinberg, 1963), i.e., the working condylar rotates and little lateral Bennett’s movement. In contrast, the non-working condylar movement is sloped downward, forward, and medially.

For the non-working side, the length of the trajectory of the condylar is: chocolate Δd_d = 0.0031 m, chocolate bar Δd_b = 0.0068 m, apple Δd_a = 0.0079 m, carrot Δd_c = 0.0065 m, and sausage Δd_s = 0.0102 m, and is on average as much as seven times greater than on the working side. Therefore, in the numerical simulation, it was assumed that there would be a fixed centre of rotation of the mandible in the condylar on the working side, through which the instantaneous axes of rotation would pass. On the non-working side, on the other hand, the condylar will have the possibility of rotation and translation (Figure 3B).

The mandibular model is fixed in the TMJ and the origin attachment sites of the masseter, medial pterygoid, and temporalis muscles. Based on the developed chewing paths, there are kinematic contact pairs with 5 degrees of freedom (3 rotations and 2 displacements) in the TMJ on the working and non-working sides. The displacement values depend on the type of food and the chewing side (Table 1).

The proposed way of supporting the model, especially in the TMJ, made it possible to simulate the complex movement of the lower incisors during chewing (Figures 2, 3). A detailed description of the model is given in (Stróżyk and Bałchanowski, 2018).

2.4 Numerical simulations of unilateral chewing

Simulation studies consisted in moving the incisal point from the lower position (point IP Figure 2A) to the endpoint IS (the origin of the coordinate system Figure 2).

During the simulation of food chewing, the molar to which the force F_i has applied moves with a constant velocity v_t = 0.02 m/s. The developed numerical model is universal and can model variable (nonlinear) chewing velocity. In the simulation studies chewing was modelled at a constant speed because the food patterns were determined experimentally on a testing machine for such speed.

Numerical simulations were carried out in three stages. In the first, the inverse task of the kinematics of motion of the mandibular-cranial system was solved. This consisted in applying a forced mandibular movement along the longitudinal mastication path and determining the mandibular movement at the TMJ on the W and N sides. During this simulation, the changes in muscle length (contractions) necessary to force the mandibular closure movement were also determined (Figure 4).

FIGURE 4

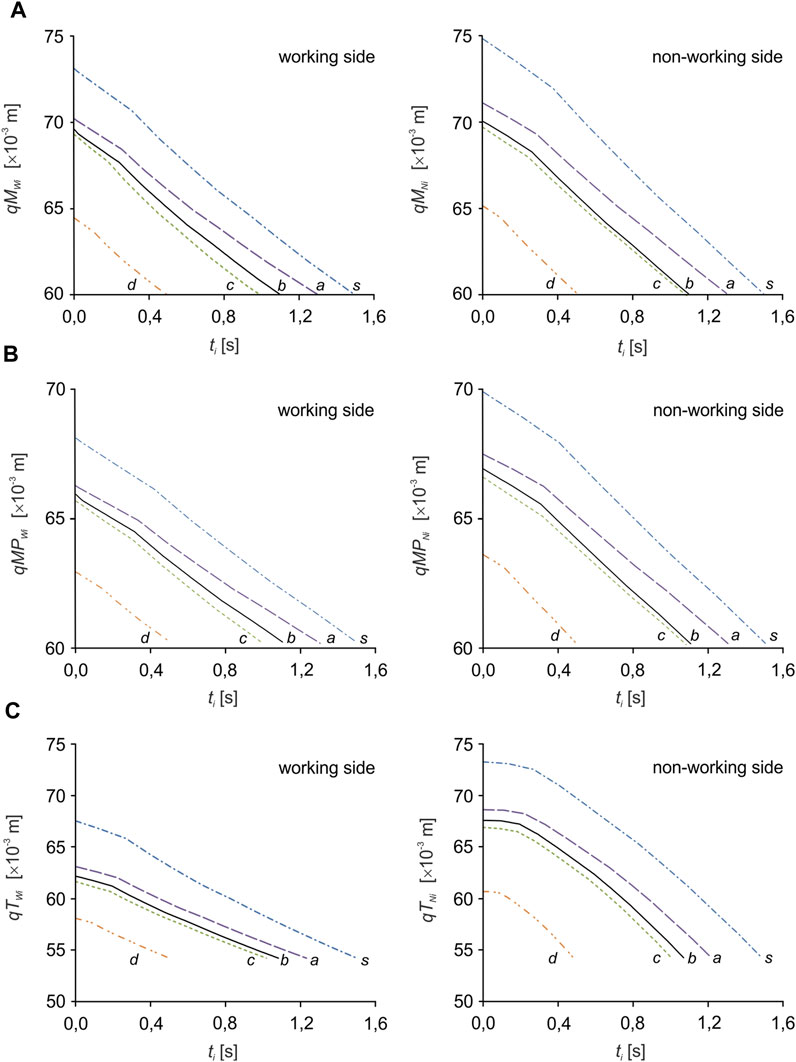
FIGURE 4. Kinematic characteristics of the change in muscle length: (A) the masseter muscle (qM_Wi, qM_Ni), (B) the medial pterygoid muscle (qMP_Wi, qMP_Ni) and (C) the temporalis muscle (qT_Wi, qT_Ni) depending on the food product (i).

In the second stage, proper calculations were performed modelling a simple dynamics task simulating mandibular closure resulting from muscle contractions. Forcing qT_Wi, qT_Ni, qV_Wi and qV_Ni were used as changes in muscle length (contractions) determined in the simple task. As a result of calculations, the unknown muscle forces were determined: FM_Wi, FM_Ni, FMP_Wi, FMP_Ni and FT_Wi, FT_Ni. Simulations were performed separately for each food.

In the third step, based on elementary trigonometric calculations, the principal vector of the temporalis muscle was decomposed (FT_Ni) into three components, respectively for: the anterior temporalis (FAT_Ni), the middle temporalis (FMT_Ni) and the posterior temporalis (FPT_Ni). The distribution was performed based on the assumption that muscle force is proportional to physiological cross-sectional area (PCSA) (Koolstra et al., 1988); Figure 5A shows the schematic position of the temporalis muscle (outline—ABC) in relation to the sagittal plane. On the other hand, Figure 5B shows the position of the temporalis muscle (outline—A'B'C) in the sagittal plane and gives the angles determining the position of the B'C edge (α = 11°) and the line of action of FT_Ni (ϕ = 58°) and its components, i.e., FAT_Ni (θ = 76°), FMT_Ni (γ = 42°) and FPT_Ni (β = 22°), in relation to the sagittal axes.

FIGURE 5

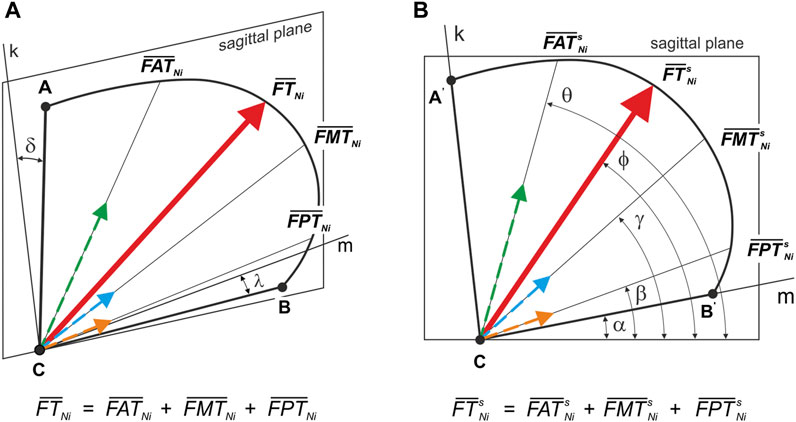
FIGURE 5. Position of the principal vector of the temporalis muscle and its components–working and non-working side: (A) relative to the sagittal plane ($\overline{{FT}_{Ni}}$; $\overline{{FAT}_{Ni}}$; $\overline{{FMT}_{Ni}}$; $\overline{{FPT}_{Ni}}$) and (B) on the sagittal plane ($\overline{{FT}_{Ni}^s}$; $\overline{{FAT}_{Ni}^s}$; $\overline{{FMT}_{Ni}^s}$; $\overline{{FPT}_{Ni}^s}$). (δ = 20° i λ = 20°); Line k and m lie in the sagittal plane.

3 Results

Based on the determined food characteristics (Figure 1), the developed model of the masticatory system (Figure 2), the chewing path (Figure 3), the determined changes in muscle length (Figure 4) and numerical calculations, muscle force patterns were determined, for the masseter muscle, the medial pterygoid muscle and the temporalis muscle and its components (the anterior temporalis, the middle temporalis, the posterior temporalis) (Figure 6). In addition, Tables 2, 3 give the values for maximum bite force and the corresponding values for muscle contraction and total muscle contraction. In contrast, Tables 4, 5 show muscle stiffness and intrinsic strength values.

FIGURE 6

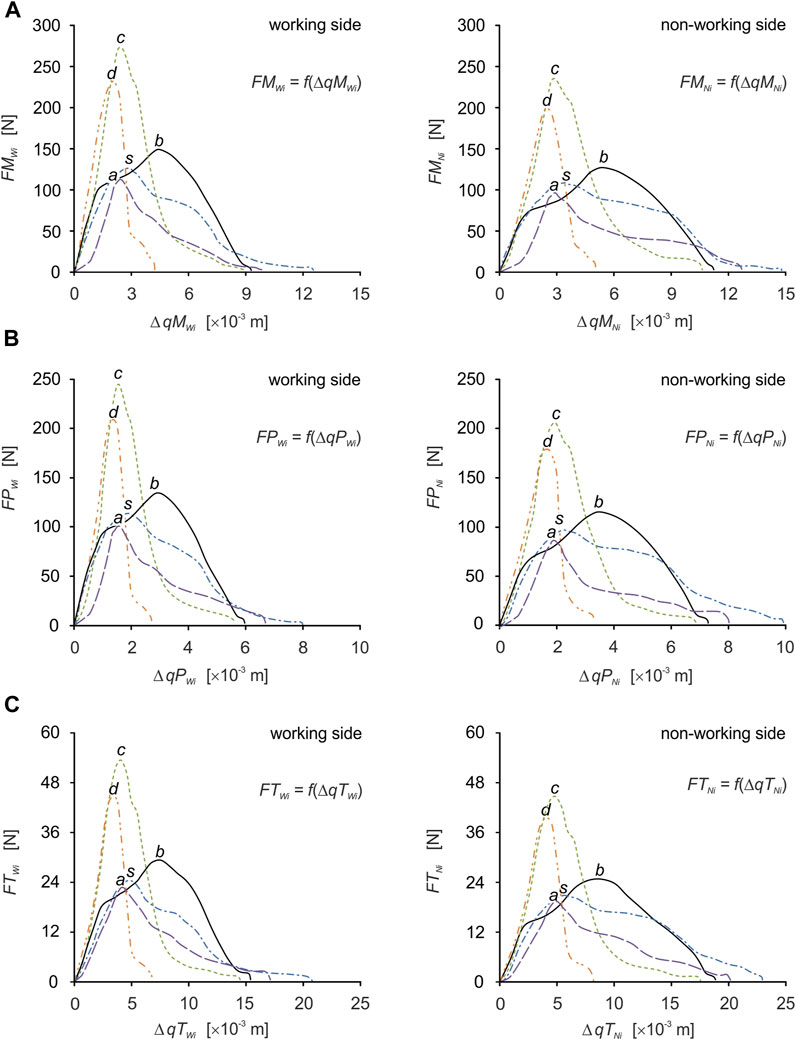
FIGURE 6. Muscle force patterns as a function of muscle force vs. muscle contraction for: (A) the masseter muscle [FM_Wi = f(ΔqM_Wi), FM_Ni = f(ΔqM_Ni)], (B) the medial pterygoid muscle [FMP_Wi = f(ΔqMP_Wi), FP_Ni = f(ΔqMP_Ni)] and (C) the temporalis muscle [FT_Wi = f(ΔqT_Wi), FT_Ni = f(ΔqT_Ni)], during unilateral food chewing (i).

TABLE 2

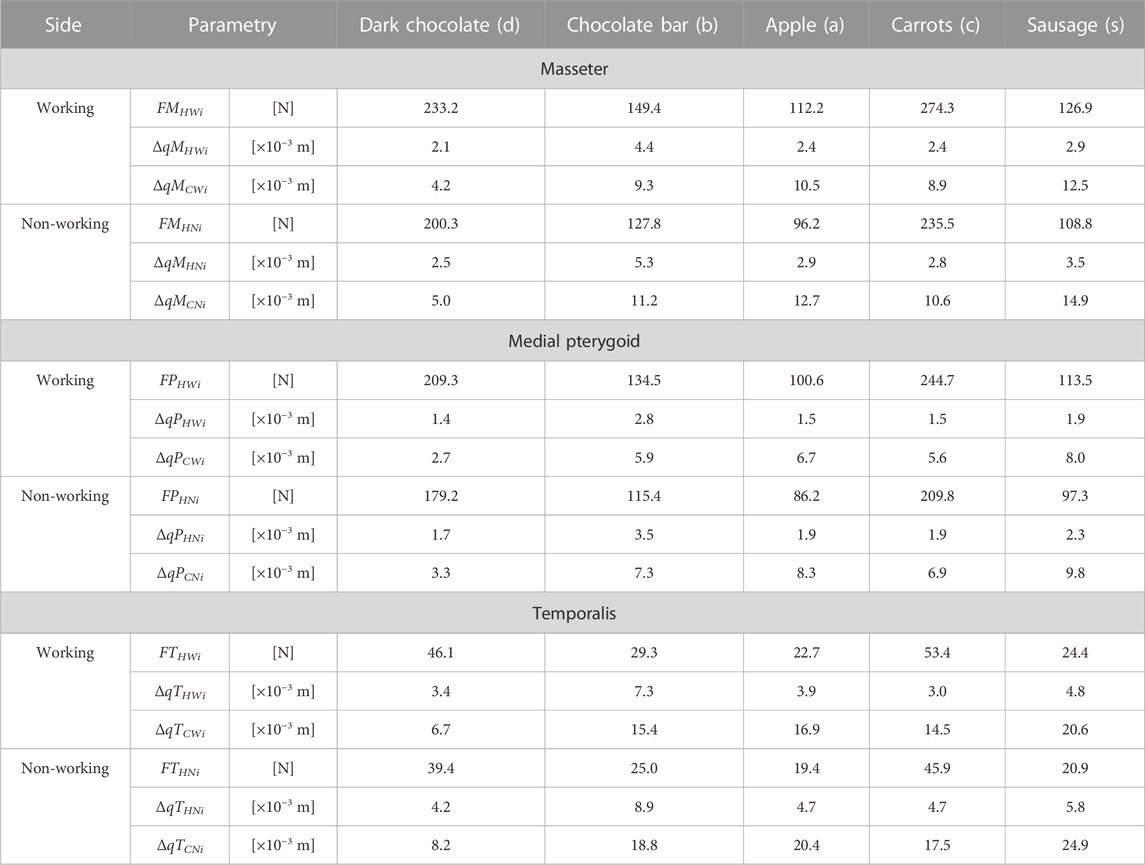
TABLE 2. Maximum muscle force, contraction corresponding to maximum force and total contraction, respectively for: the masseter muscle [(FM_HWi, FM_HNi), (ΔqM_HWi, ΔqM_HNi), (ΔqM_CWi, ΔqM_CNi)], the medial pterygoid muscle [(FMP_HWi, FMP_HNi), (ΔqMP_HWi, ΔqMP_HNi), (ΔqMP_CWi, ΔqMP_CNi)] and the temporalis muscle [(FT_HWi, FT_HNi), (ΔqT_HWi, ΔqT_HNi), (ΔqT_CWi, ΔqT_CNi)], depending on a product (i).

TABLE 3

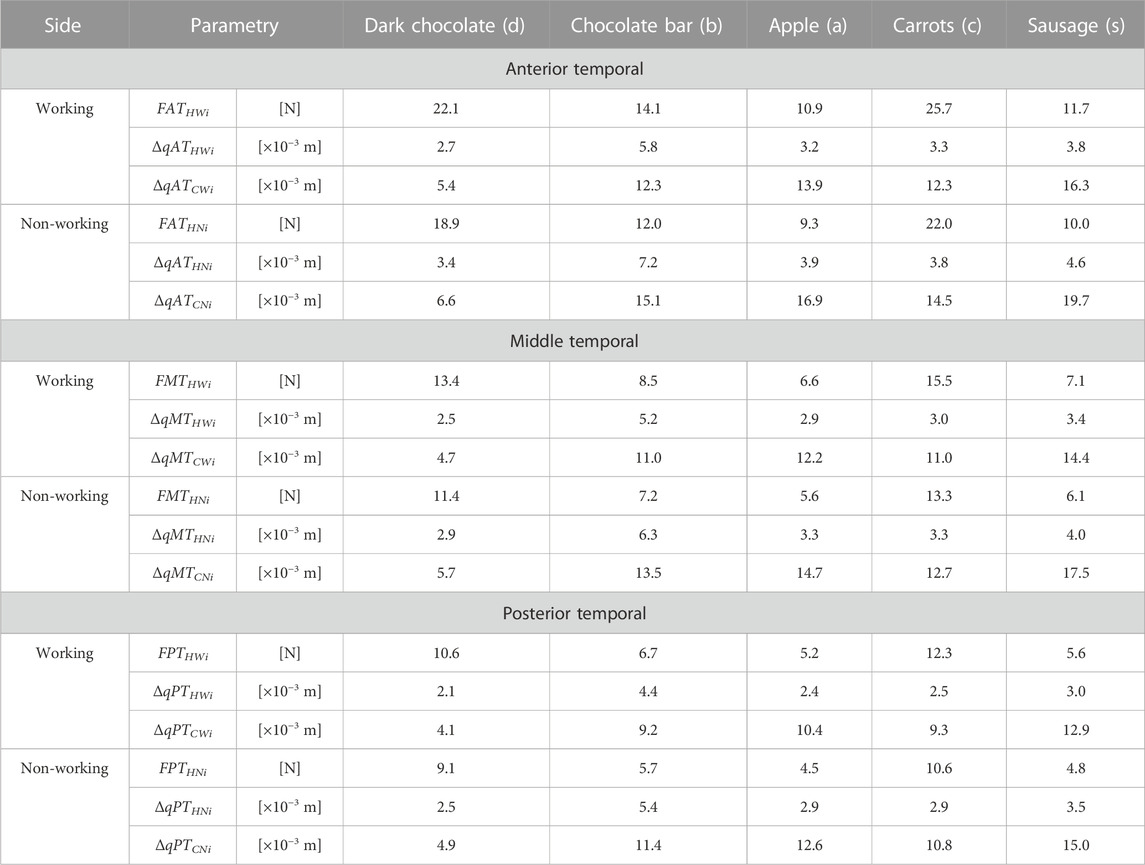
TABLE 3. Maximum muscle force, contraction corresponding to maximum force and total contraction respectively for: the anterior temporalis [(FAT_HWi, FAT_HNi), (ΔqAT_HWi, ΔqAT_HNi), (ΔqAT_CWi, ΔqAT_CNi)], the middle temporalis [(FMT_HWi, FMT_HNi), (ΔqMT_HWi, ΔqMT_HNi), (ΔqMT_CWi, ΔqMT_CNi)] and the posterior temporalis [(FPT_HWi, FPT_HNi), (ΔqPT_HWi, ΔqPT_HNi), (ΔqPT_CWi, ΔqPT_CNi)] depending on a product (i).

TABLE 4

TABLE 4. Values of stiffness (K_Wi, K_Ni) for selected muscles in relation to food.

TABLE 5

TABLE 5. Intrinsic strength values (k_Wi, k_Ni) for selected muscles in relation to food.

In the general case, the total contraction of the muscle (Δq_C), the contraction corresponding to the maximum force (Δq_H) and the muscle contraction (Δq_E) were determined from Eqs 1–3. During the calculations, the equations were modified in such a way that the above parameters could be determined on selected muscles depending on the food, separately for the working and non-working sides.

$\Delta q_C=\left|\mathrm{q}\left(t\right)-q\left(0\right)\right|(1)$

$\Delta q_H=\left|\mathrm{q}\left(t_H\right)-q\left(0\right)\right|(2)$

$\Delta q_E=\left|\mathrm{q}\left(t_E\right)-q\left(0\right)\right|(3)$

where:

q(0)—initial muscle length for time t = 0s—open mouth,

q(t)—muscle end length for time t—closed mouth,

q(t_H)—muscle length for time t_H, corresponding to the position of the mandible in which the muscle force reaches its maximum value (F_H),

q(t_E)—muscle length determined for time t_E from the interval 0÷t,

3.1 Muscle force patterns

Preliminary analysis indicates significant differences between patterns, force values and contractions. The variation in muscle behaviour is not surprising, as the diversity of characteristics (Figure 1) generates individual conditions for the masticatory system (Mioche et al., 1999), adapted to functional requirements, depending on the input data (Fitts et al., 1991).

For efficient interpretation of the results, muscle patterns were prepared separately for each muscle (Figure 7) and for the components of the temporalis muscle (Figure 5), and separately for the working and non-working sides. Thanks to this, there are 5 muscle patterns on each graph, depending on the food, while the data are given in Tables 2, 3 enable the determination of additional mechanical parameters characterising the muscle functioning.

FIGURE 7

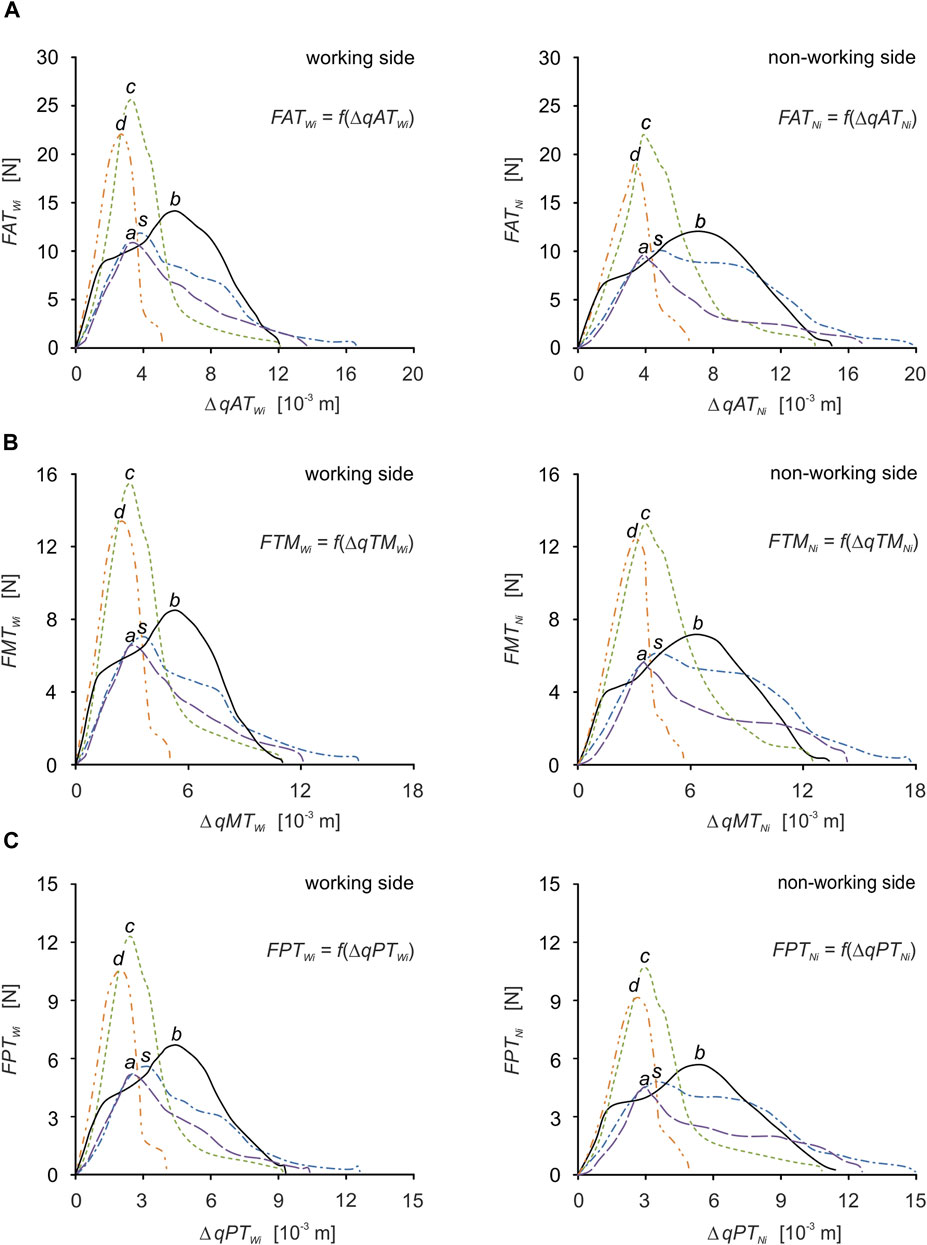
FIGURE 7. Muscle force patterns as a function of muscle force vs. muscle contraction for: (A) the anterior temporalis [FAT_Wi = f(ΔqAT_Wi), FAT_Ni = f(ΔqAT_Ni)], (B) the middle temporalis [FMT_Wi = f(ΔqMT_Wi), FMT_Ni = f(ΔqMT_Ni)] and (C) the posterior temporalis [FPT_Wi = f(ΔqPT_Wi), FPT_Ni = f(ΔqPT_Ni)] during unilateral food chewing (i).

3.2 Stiffness of the muscle

In the general case, the stiffness (K) is determined from the elementary Eq. 4, in which the force (F) and displacement (x) are directly proportional to each other.

$K=F/x\left[\mathrm{N}/\mathrm{m}\right](4)$

Eq. 4 is linear, so its use is limited to problems with a linear relationship between F and x. This means that the stiffness determined for a range of load (0÷F) or displacement (0÷x) has a constant value.

The above equation can be used for issues of a non-linear nature, but then the stiffness is only determined for a specific value of F or x. Therefore, the value of stiffness has the characteristics of a comparative parameter based on which it is possible to assess the influence of various factors on the functioning of the muscular system, e.g., 1) different ways of biting, 2) the geometry of the masticatory system resulting from individual characteristics and pathological conditions, 3) foods, 4) the state of dentition and 5) changes resulting from surgical procedures (Pachnicz and Stróżyk, 2021).

Based on the considerations above, this paper is limited only to the determination of muscle stiffness (Eq. 4) for the maximum muscle forces (Table 2, 3) for the working (K_Wi) and non-working (K_Ni) sides, respectively.

Of course, Eq. 4 was adjusted so that stiffness could be determined for selected muscles, i.e., F→F_H and x→ΔqH.

3.3 Intrinsic strength

Based on publications (Koolstra et al., 1988; Korioth and Hannam, 1990; May et al., 2001; Pruim et al., 1980) it can be stated that intrinsic strength (k), is used to determine maximum muscle force (F_H) based on Eq. 5 and the relationship between muscle force (F) and EMG measurements according to Eq. 6.

$F_H=k\times PCSA(5)$

$F=k\times PCSA\times EM{G}_F(6)$

where: (EMG_F)—scale factor

To calculate intrinsic strength, Eq. 5 was used, which was adjusted for the selected muscles depending on the selected foods, for the working (k_Wi) and non-working (k_Ni) sides, respectively—Table 5. To determine intrinsic strength, the data given in Table 1–3 were used and it was assumed that the PCSA values on the working and non-working sides are the same.

The values of the temporalis muscle components are not included in Table 5 because their values are identical to those of the principal vector.

4 Discussion

In the work presented here, we used our model of unilateral chewing (Figure 2) developed based on: 1) the anatomical structure of the masticatory system (Synbone skull 8500 and mandible 8596), 2) food patterns Figures 1, 3 chewing paths Figure 3A.

Based on the assumptions made, dynamic patterns were determined for the mandibular elevator muscles in the form of muscle forces and corresponding contractions. Furthermore, the results obtained allowed the calculation of stiffness of the muscle and intrinsic strength. All values of the above parameters were determined in relation to the food and the working and non-working sides for a single chewing cycle.

4.1 Limitations of the model

The model proposed and the assumptions made are a compromise between a correctly anatomical structure of the masticatory system and the physiological mechanism of mastication (act of chewing) and the possibility of reproducing the conditions (parameters) necessary to reproduce physiologically correct unilateral chewing.

Despite the use of simplifications (e.g., same chewing velocity, the muscle is represented by a single principal vector, no friction coefficients, no consideration of the muscle damping coefficient, use of a single geometrical model of the mandible, mechanically correct but basic in terms of the anatomical structure temporomandibular joint), the model meets the basic requirements to carry out calculations in accordance with the principles of solid mechanics and function of the masticatory system.

Since the model does not take into account all the parameters responsible for the correct course of the chewing process, it must be assumed that the results of the calculations show how the mandibular elevator muscles may function during the first unilateral chewing cycle.

4.2 Dynamic patterns of muscle forces

Similar to the authors’ previous work (Stróżyk and Bałchanowski 2016; Stróżyk and Bałchanowski, 2018; Stróżyk and Bałchanowski, 2020) and other publications (Agrawal et al., 1998; Hiiemae et al., 1996; Koolstra, 2002; Mathevon et al., 1995; Shimada et al., 2012) and the present study, it has been shown that mechanical [F_i = f(Δh_i)] and geometric [height (h_i)] food parameters have a significant influence on the function of the masticatory system, especially the muscular system.

Based on the elementary comparative analysis of the food characteristics (Figure 1) with the muscle force patterns (Figures 6, 7), it can be shown that there is a high similarity between them related to the course of the graphs. Such a relationship occurs in the so-called simple mechanisms (Stróżyk and Bałchanowski, 2016; Stróżyk and Bałchanowski, 2018; Stróżyk and Bałchanowski, 2020) characterised by the fact that the response of the system is in the form of displacements and enforcing forces (muscle forces) is correlated with the force (resistance force posed by food). The correlation between the above-mentioned parameters is manifested, among other things, by their values increasing at the same rate and reaching maximum values at the same time. Of course, the above statement is fulfilled for the kinematically correct movement of the masticatory system.

Furthermore, it can also be seen that the patterns of the same muscle on the working and non-working sides have similar characteristics but different values (Tables 2, 3). This is due to the asymmetrical alignment of the mandible concerning the sagittal plane, which is a consequence of including the chewing path.

In addition, significant differences can be observed, irrespective of the muscle, between the values of maximal muscle forces and maximal contractions, depending on the food. However, the comparison of the values of the contractions corresponding to the maximum forces shows that the differences are not as explicit as for the muscle forces (Tables 2, 3).

4.2.1 Maximum muscle force

The results indicate that not only muscle force patterns but also maximum muscle forces are dependent on food (mechanical parameters). Moreover, analysing their values (Tables 2, 3) it was observed that on the working side, they are higher than on the non-working side. This result proves the correctness of the obtained results and compliance with the elementary static principle, from which it follows that the resultant of external forces (occlusion force) is located closer to the components (muscular forces) with higher values.

A detailed analysis taking into account the values of the maximum muscle forces shows that the forces on the non-working side are on average 14% lower than those on the working side, irrespective of the muscle (the masseter, medial pterygoid and temporalis muscles), the division of the temporalis muscle (Figure 5) and the food (Table 1). The difference is not large, but it balances the non-working and the working side, allowing a stable mandible elevation during unilateral chewing for the given boundary conditions.

The knowledge of the maximum muscle forces (F_HWi and F_HNi) and the maximum occlusion forces (F_i,_max) made it possible to show that there is a correlation between them, which can be presented in the form of their ratio (Table 6), corresponding for the working (R_FW) and non-working (R_FN) sides. Based on the data (Figure 1; Tables 2, 3) R_FW and R_FN can be determined considering: (1) the principal vectors of the masseter, medial pterygoid and temporalis muscles (case I) and/or (2) the principal vectors of the masseter muscle and the medial pterygoid muscle with simultaneous consideration of the division of the temporalis muscle into three parts (case II)—(Figure 5). The results given in Table 6 indicate that the values of R_FW and R_FN are constant for the muscles and components of the primary vector of the temporalis muscle, of food, but different for the working and non-working sides.

TABLE 6

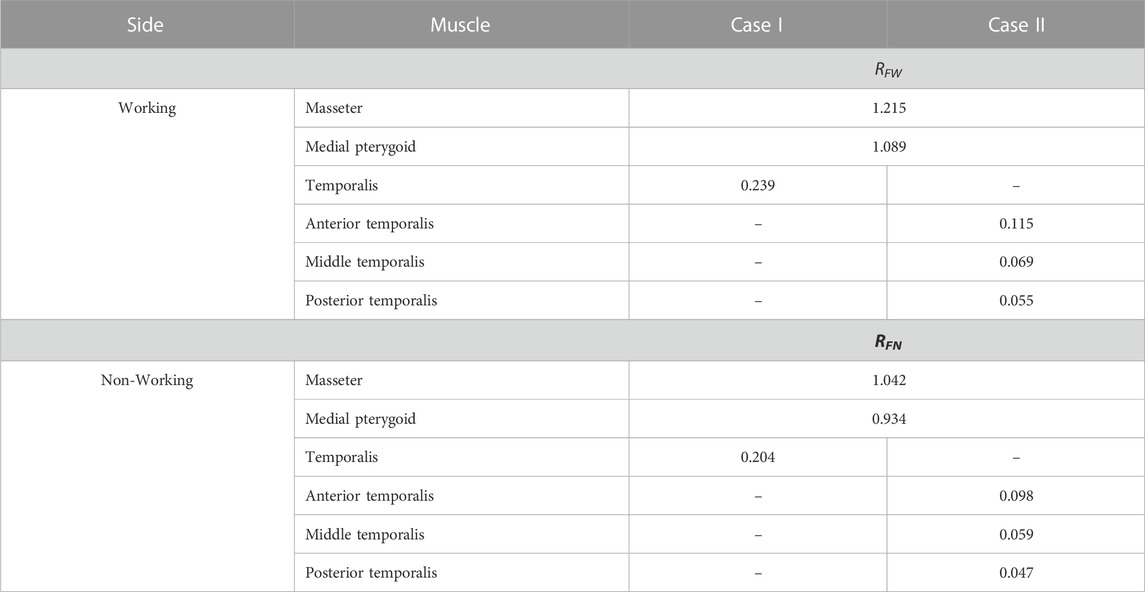
TABLE 6. The value of proportionality coefficients R_FW and R_FN for selected muscles, depending on cases I and II.

The relationship between maximum muscle force and maximum occlusion force can also be represented by a linear relationship (Eqs 7, 8) in which the proportionality coefficient is R_FW and R_FN.

$F_{HWi}=R_{FW}\times F_{i,\mathit{max}}(7)$

$F_{HNi}=R_{FN}\times F_{i,\mathit{max}}(8)$

In the literature, it is possible to find publications in which authors model bilateral and unilateral chewing, among others (Choi et al., 2005; Pinheiro and Alves, 2015; Jahadakbar et al., 2016; Lee et al., 2017; Luo et al., 2017; Marková and Gallo, 2016; Orassi et al., 2021; Pachnicz and Stróżyk, 2021; Reina et al., 2007); however, these are models corresponding to static occlusion and the muscle force values used are based, primarily, on the data reported in (Korioth et al., 1992; Korioth and Hannam, 1994) and in (Ferrario et al., 2004).

Despite the use of static models in the above-mentioned publications, it was decided to relate the obtained maximum values of muscle forces to those works in which the authors take into account the unilateral loading of the mandible—Table 7. Taking into account the data provided by (Pinheiro and Alves, 2015), it follows that the values of forces in the muscles differ significantly from those reported in Tables 2, 3. According to the authors of the above-mentioned publication, the main role in generating occlusal force is played by the temporalis muscle, which muscular force is greater than that of the masseter muscle and the medial pterygoid muscle, both on the working and non-working sides. On the basis of the results obtained in Tables 2, 3, it follows that during unilateral chewing the muscle forces generated by the masseter muscle and the medial pterygoid muscle are significantly greater than the values determined for the temporalis muscle. A similar regularity regarding the values of muscle forces can be found in the work of (Korioth et al., 1992).

TABLE 7

TABLE 7. Values of muscle forces corresponding to unilateral chewing.

Based on the muscle force values reported by (Reina et al., 2007), it appears that the medial pterygoid muscle is the dominant muscle. The analysis performed indicates that on the working side, the medial pterygoid muscle has the highest values, while the superficial the masseter muscle and the temporalis muscle have similar values. On the non-working side, the medial pterygoid muscle and the posterior temporalis muscle have similar values, while the masseter muscle has a value ∼2 times lower than them. In contrast, the results are shown in Tables 2, 3 indicate that regardless of the product and side, the masseter muscle has the highest value, and the temporalis muscle has the lowest value. The muscle force values of the medial pterygoid muscle are only 10% less than those of the masseter muscle.

Furthermore, in the works (Korioth et al., 1992; Reina et al., 2007), the temporalis muscle is decomposed into 3 components (Table 7), between which there is the same relationship as shown in Table 3, i.e., the anterior temporalis muscle has the highest value of muscle force, the middle temporalis muscle intermediate and the posterior temporalis muscle the lowest, regardless of the side.

4.2.2 Muscle contraction

On the basis of the data given in Tables 2, 3, it can be shown that for the working side, the total contraction of the mandibular elevator muscles is 17% lower on average than on the non-working side.

Analysis of the results also showed that total contraction was dependent on the initial food height (Table 1), i.e., the distance between a pair of corresponding molars.

Detailed analysis showed that the height of the food influences: 1) the size of the chewing path (mainly height, but also width (Figure 3) and 2) muscle contractions (Tables 2, 3). The relationship between food height and chewing path height in the sagittal plane can be described by Tales’ theorem. On the other hand, the relationship between the height of the food (h_i) and the total muscle contraction (Δq_Ci) can be determined: 1) by solving tasks in which the movable part (mandible) is suspended on a tendon (muscle) and is simultaneously supported at a point corresponding to the TMJ or 2) using a parameter that is the ratio (ratio) of their values (Δq_Ci/h_i). The ratio was determined separately for the working side (R_qW) and the non-working side (R_qN). The results of the calculations (Table 8) showed that the values of R_qW and R_qN are: 1) constant for each muscle and 2) dependent on the considered side, i.e., working or non-working side. Considering the temporalis muscle (Figure 5), the values of R_qW and R_qN (Table 8) can be presented for 2 cases: 1) without considering the division of the temporalis muscle (case I) and 2) with considering the division of the temporalis muscle into three parts (case II) (Figure 5).

TABLE 8

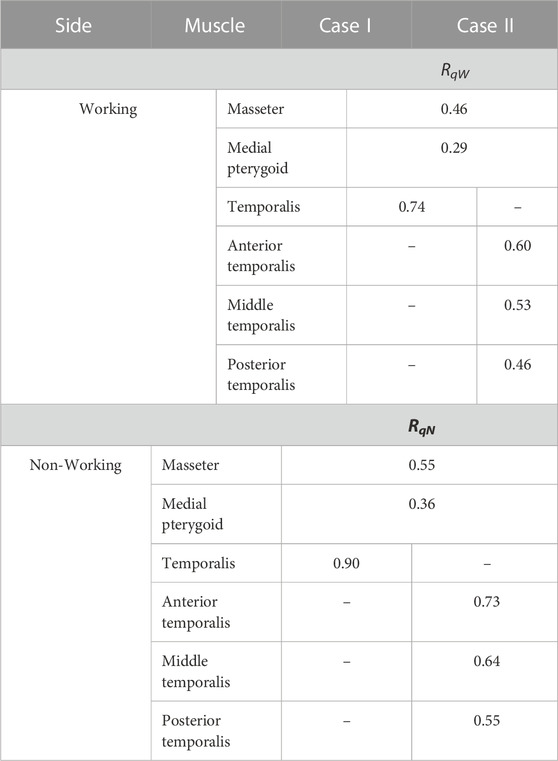
TABLE 8. Values of proportionality coefficients R_qW and R_qN for selected muscles, depending on cases I and II.

The relationship between (Δq_Ci) and (h_i) can be represented by the linear relationship (Eqs 9, 10) in which the proportionality coefficient is R_qW and R_qN.

$\Delta q_{CWi}=R_{qW}\times h_i(9)$

$\Delta q_{CNi}=R_{qN}\times h_i(10)$

Based on the results presented, it can be assumed that the muscle contraction during unilateral chewing, with the dimensions of the masticatory system fixed, depends on the height of the food bite. Since the height (h_i) changes during biting, therefore, the contraction can be written in the form of a function Δq_E = f(Δh_i) - the muscle contraction (Δq_E) vs. the height of food specimen (Δh_i). Moreover, the above parameters are time-dependent, i.e., Δq_E(t) and Δh_i(t). The above conclusion can also be applied to symmetric incisal biting of foodstuffs.

There was no clear relationship between maximum force and corresponding contraction (Tables 2, 3).

4.3 Stiffness of the muscle

As with the other parameters, the stiffness of the muscle (K) is also strongly dependent on: 1) the mechanical properties of the food (texture), 2) the muscle analysed and 3) the side analysed, i.e., working and/or non-working.

Preliminary analysis of the results indicates that similar values of stiffness of the muscle (Table 4) can be obtained for products different in texture, characteristics (Figure 1) and method of manufacture. The results given in Table 4 indicate that with respect to K the selected products can be divided into two groups, i.e., 1) chocolate and carrot and 2) bar, apple and sausage. It can also be observed that the K in the first group is, on average 2.7 times higher than that of the second group, irrespective of the type of muscle and the working and non-working side. Furthermore, analysing the K values in relation to the side, it can be seen that the stiffness of the muscles is lower under the non-working side (K_Ni), compared to the working side (K_Wi), by an average of 29%.

Analysis of the results given in Tables 2–4 indicates that the greater the stiffness of the muscle, the greater the maximum muscle force.

It should be added that the determined patterns of muscle forces (Figures 6, 7) enable the determination of the non-linear stiffness (K_i) according to the general Eq. 11. However, first, with the help of an appropriate tool (mathematical program), an appropriate mathematical equation should be fitted to the data (patterns), i.e., F_Ei = f(ΔqEi) or F_Ei = F_Ei(ΔqEi) (muscle force vs. muscle contraction).

$K_i=d{F}_{Ei}/d\left(\Delta qi\right)(11)$

where: dF_Ei—muscle force gains in relation to food and side of the mandible, d(Δqi)—increases in muscle contraction according to food and side of the mandible

The resulting K_Wi and K_Ni values can be used in numerical calculations where the muscle is modelled as a spring only (Antic et al., 2015; Pachnicz and Stróżyk, 2021). If the calculations involve static loading, it is sufficient to provide a single value corresponding to a given bite force or muscle force, depending on the target. In dynamic calculations, the non-linear function of the muscle must be taken into account (Figure 6), so the stiffness must be entered as a function according to the requirements of the programme. On the other hand, an accurate representation of the performance characteristics of the muscle requires the use of complex models, e.g., 1) Maxwell model, 2) Voigth model, 3) Kelvin model, and 4) Hill model, in which additional parameters regarding elements such as spring elements, damping elements, contractile element and parallel elastic element (elements describing the passive elastic properties of the muscle fibres) must be taken into account (Romero and Alonso, 2016). It is also possible to use the model proposed by Röhrle and Pullan (2007), in which the muscle is a viscoelastic material.

4.4 Intrinsic strength

Analysis of the data given in Table 5 has shown that the values of intrinsic strength (k): 1) depend on the food, above all on its mechanical properties, 2) depend on the side analysed, i.e., working and/or non-working, 3) regardless of the side and food considered, are the highest for the temporalis muscle and the lowest for the medial pterygoid muscle. However, for the masseter muscle they are smaller than the medial pterygoid muscle by an average of 28%, and 4) they are identical both for the main vector of the temporalis muscle and its components (this results from an assumption related to the decomposition of the main vector into its components (Figure 5).

In the available literature (in recent years), there are few publications concerning the determination of the k-parameter, especially in relation to physiological forces. An interesting publication on the k-parameter, despite the passage of more than 40 years, is the paper by Pruim et al., 1980. In the above-mentioned paper, the authors provide k values determined during experimental studies (in vivo) but during bilateral static occlusion at different levels of occlusion force. Moreover, the authors assume the same k value for all muscles, which makes it difficult to compare the results. However, taking the values obtained for chocolate as a reference (lowest height and maximum occlusion force reached in the mandibular position close to the close-up of the teeth) and considering the temporalis muscle (lowest k), it was decided to compare the results given by Pruim et al., 1980 with the values presented in Table 5. Analysis of the value of the k parameter showed that during unilateral chewing, the temporalis muscle has significantly lower average values (more than 20 times lower than bilateral chewing). Considering the masseter muscle and the medial pterygoid muscle, it turns out that the mean values are also smaller, respectively: 4-fold and 3-fold.

Taking into account some of the oldest data concerning the parameter k given in the works by Fick et al. (1904)-1 × 10⁶ N/m², Morris (1948)-0.9 × 10⁶ N/m², Ikai and Fukunaga (1968)-0.7 × 10⁶ N/m² it follows that a value close to the data given in Table 5 is 0.4 × 10⁶ N/m² determined by Hettinger. (2017). A similar value in the 1980s was given by Weijs and Hillen (1985) i.e., k = 0.37 × 10⁶ N/m², which is widely used by many authors (Hattori et al., 2003; Koolstra et al., 1988; Koolstra and Eijden, 1992; Korioth and Hannam, 1990; Langenbach and Hannam, 1999; Peck et al., 2000; Zheng et al., 2019). Analysis of the aforementioned papers indicates that the authors use only one value of k = 0.37 × 10⁶ N/m² or 0.4 × 10⁶ N/m², although the paper (Slager et al., 1997) used k = 0.35 × 10⁶ N/m². Furthermore, the authors used one value of k for all muscles. However, according to the data given in Table 5, it follows that the values of k are different and depend on the food product. This indicates that the mechanical parameters of the product also have a significant influence on the values of the k parameter. The same observations but concerning chewing, can be found in (Stróżyk and Bałchanowski, 2018).

It should also be added that the equations (Eqs 5, 6) from which the value of k was determined are linear and restricted to a point only, i.e., F_H.

It is interesting to note that k is very strongly dependent on PCSA, i.e., for the same muscle force but different values of PCSA, different values of k can be obtained, and each will bear the hallmarks (or give the impression) of a correct value.

It is also worth noting that there is an analogy between intrinsic strength (k) and the classical definition of strain (σ), i.e., the same formula and the same physical unit in the SI system. Considering the general function σ = f(ε) (tension vs. strain), which is used for the mathematical notation of the characteristics obtained in the classical compression test, it is possible, on its basis, to propose an elementary function for the parameter k, i.e., k = f(ε), where:ε = Δq_E/q(0). On the basis of the above function, it can be shown that k is not a constant value during muscle contraction and changes with the change in load similarly to σ. The equation k = f(ε), does not change the physical meaning of intrinsic strength but extends its applications to the full range of changes in muscle force values, not only the maximum values.

5 Conclusion

The present work shows that the use of a hybrid model based on numerical simulation and experimental studies can provide an advanced (promising) tool for modelling complex processes such as the act of chewing. This paper also shows that muscle forces and mechanical parameters of food can be represented as functions, F_i = f(q_i) and F_i = f(Δh_i), respectively. In addition, the advantage of the presented model is that it allows rapid modification of geometric parameters and loading functions tailored to individual patient characteristics. The results of such calculations will allow for better fabrication and fitting of implants or prosthetic components to the patient.

The determined muscle or food force patterns can also be used in numerical simulations based on deformable body mechanics. Such simulations will make it possible to determine stress, strain and displacement at selected points in the mandible, maxilla, teeth and temporomandibular joint.

The conclusions of the present study confirm and complement theories about the mechanisms of the masticatory system during chewing. On the other hand, the computational technique used, using inverse kinematics and dynamics analysis and the application of food patterns, made it possible to understand the influence of mechanical food parameters on muscle force patterns.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

PS and JB designed the study. PS conducted the experimental studies and determined the food characteristics. JB developed the computational models and collected the data. Both authors interpreted the data and wrote and revised the manuscript. In addition, they agree to be responsible for all aspects of the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This paper was supported by Grants-in-Aid from the Wrocław University of Science and Technology, Faculty of Mechanical Engineering, Poland; (K58 and K61—No. 821 1104 160).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agrawal, K. R., Lucas, P. W., Bruce, I. C., and Prinz, J. F. (1998). Food properties that influence neuromuscular activity during human mastication. J. Dent. Res. 77, 1931–1938. doi:10.1177/00220345980770111101

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson, K., Throckmorton, G. S., Buschang, P., and Hayasaki, H. (2002). The effects of bolus hardness on masticatory kinematics. J. Oral Rehabil. 29, 689–696. doi:10.1046/j.1365-2842.2002.00862.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Antic, S., Vukicevic, A. M., Milasinovic, M., Saveljic, I., Jovicic, G., Filipovic, N., et al. (2015). Impact of the lower third molar presence and position on the fragility of mandibular angle and condyle: A three-dimensional finite element study. J. Craniomaxillofac Surg. 43, 870–878. doi:10.1016/j.jcms.2015.03.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhatka, R., Throckmorton, G. S., Wintergerst, A. M., Hutchins, B., and Buschang, P. H. (2004). Bolus size and unilateral chewing cycle kinematics. Arch. Oral Biol. 49, 559–566. doi:10.1016/j.archoralbio.2004.01.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Buschang, P. H., Throckmorton, G. S., Austin, D., and Wintergerstd, A. M. (2007). Chewing cycle kinematics of subjects with deepbite malocclusion. Am. J. Orthod. Dentofac. Orthop. 131, 627–634. doi:10.1016/j.ajodo.2005.06.037

PubMed Abstract | CrossRef Full Text | Google Scholar

Çakir, E., Koç, H., Vinyard, C. H. J., Essick, G., Daubert, C. H. R., Drake, M., et al. (2011). Evaluation of texture changes due to compositional differences using oral processing. J. Texture Stud. 43, 257–267. doi:10.1111/j.1745-4603.2011.00335.x

CrossRef Full Text | Google Scholar

Choi, A. H., Ben-Nissan, B., and Conway, R. C. (2005). Three–dimensional modelling and finite element analysis of the human mandible during clenching. Aust. Dent. J. 50, 42–48. doi:10.1111/j.1834–7819.2005.tb00084.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Daumas, B., Xu, W. L., and Bronlund, J. (2005). Jaw mechanism modeling and simulation. Mech. Mach. Theory. 40, 821–833. doi:10.1016/j.mechmachtheory.2004.12.011

CrossRef Full Text | Google Scholar

Dellow, P. G., and Lund, J. P. (1971). Evidence for central timing of rhythmical mastication. J. Physiol. 215, 1–13. doi:10.1113/jphysiol.1971.sp009454

PubMed Abstract | CrossRef Full Text | Google Scholar

Dick, T. J. M., and Wakeling, J. M. (2017). Shifting gears: Dynamic muscle shape changes and force-velocity behavior in the medial gastrocnemius. J. Appl. Physiol. 123, 1433–1442. doi:10.1152/japplphysiol.01050.2016

PubMed Abstract | CrossRef Full Text | Google Scholar

Ferrario, V. F., and Sforza, C. (1996). Coordinated electromyographic activity of the human masseter and temporalis anterior muscles during mastication. Eur. J. Oral. Sci. 104, 511–517. doi:10.1111/j.1600-0722.1996.tb00134.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Ferrario, V., Sforza, C., Serrao, G., Dellavia, C., and Tartaglia, G. (2004). Single tooth bite forces in healthy young adults. J. Oral Rehabil. 31, 18–22. doi:10.1046/j.0305-182x.2003.01179.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Fick, H. (1904). Handbuch der Anatomie und Mechanik der Gelenke G. Fischer Classic reprint–forgotten books. https://www.forgottenbooks.com/en (Accessed February 14, 2018).

Google Scholar

Fitts, R. H., McDonald, K. S., and Schluter, J. M. (1991). The determinants of skeletal muscle force and power: Their adaptability with changes in activity pattern. J. Biomech. 24, 111–122. doi:10.1016/0021-9290(91)90382-W

PubMed Abstract | CrossRef Full Text | Google Scholar

Foegeding, E. A., and Drake, M. A. (2007). Invited review: Sensory and mechanical properties of cheese texture. J. Dairy Sci. 90, 1611–1624. doi:10.3168/jds.2006-703

PubMed Abstract | CrossRef Full Text | Google Scholar

Foster, K. D., Woda, A., and Peyron, M. A. (2006). Effect of texture of plastic and elastic model foods on the parameters of mastication. J. Neurophysiol. 95, 3469–3479. doi:10.1152/jn.01003.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Harrison, S. M., Paul, W., Cleary, P. W., Eyres, G., Sinnotta, M. D., and Lundinc, L. (2014). Challenges in computational modelling of food breakdown and flavour release. Food Funct. 5, 2792–2805. doi:10.1039/c4fo00786g

PubMed Abstract | CrossRef Full Text | Google Scholar

Hattori, Y., Satoh, C., Seki, S., Watanabe, Y., Ogino, Y., and Watanabe, M. (2003). Occlusal and TMJ loads in subjects with experimentally shortened dental arches. J. Dent. Res. 82, 532–536. doi:10.1177/154405910308200709

PubMed Abstract | CrossRef Full Text | Google Scholar

Hedjazi, L., Guessasma, S., Yven, C., Della Valle, G., and Salles, C. (2013). Preliminary analysis of mastication dynamics and fragmentation during chewing of brittle cereal foods. Food Res. Int. 54, 1455–1462. doi:10.1016/j.foodres.2013.09.041

CrossRef Full Text | Google Scholar

Hettinger, T. (2017). Physiology strength. This edition is published by Muriwai Books – www.pp-publishing.com. Text originally published in 1961 under the same title. (Editor by M. H. Thurlwell) Charles C Thomas, Springfield. Illinois.

Google Scholar

Hiiemae, K., Heath, M. R., Heath, G., Kazazoglu, E., Murray, J., Sapper, D., et al. (1996). Natural bites, food consistency and feeding behaviour in man. Arch. Oral Biol. 41, 175–189. doi:10.1016/0003-9969(95)00112-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Hutchings, S. C., Foster, K. D., Bronlund, J. E., Lentle, R. G., Jones, J. R., and Morgenstern, M. P. (2012). Particle breakdown dynamics of heterogeneous foods during mastication: Peanuts embedded inside different food matrices. J. Food Eng. 109, 736–744. doi:10.1016/j.jfoodeng.2011.11.011

CrossRef Full Text | Google Scholar

Hylander, V. L. (2006). “Functional anatomy and biomechanics of the masticatory apparatus,” in Temporomandibular disorders: An evidenced approach to diagnosis and treatment. Editors D. M. Laskin, C. S. Greene, and W. L. Hylander (Hanover Park, IL: Quintessence Publishing Co, Inc.).

Google Scholar

Ikai, M., and Fukunaga, T. (1968). Calculation of muscle strength per unit cross-sectional area of human muscle by means of ultrasonic measurement. Int. Z. Angew. Physiol. 26, 26–32. doi:10.1007/BF00696087

PubMed Abstract | CrossRef Full Text | Google Scholar

Itoh, K., Hayashi, T., and Miyakawa, M. (1997). Controllability of temporomandibular joint loading by coordinative activities of masticatory muscles: A two-dimensional static analysis. Front. Med. Biol. Eng. 8, 123–138. doi:10.1109/IEMBS.1996.651895

PubMed Abstract | CrossRef Full Text | Google Scholar

Jahadakbar, A., Moghaddam, N. S., Amirhesam Amerinatanzi, A., Dean, D., Karaca, H. E., and Elahinia, M. (2016). Finite element simulation and additive manufacturing of stiffness–matched niti fixation hardware for mandibular reconstruction surgery. Bioengineering 3, 36. doi:10.3390/bioengineering3040036

PubMed Abstract | CrossRef Full Text | Google Scholar

Knudson, D. (2007). Fundamentals of biomechanics. New York: Springer Science+Business Media.

Google Scholar

Kohyama, K., Nakayama, Y., Yamaguchi, I., Yamaguchi, M., Hayakawa, F., and Sasaki, T. (2007). Mastication efforts on block and finely cut foods studied by electromyography. Food Qual. prefer. 18, 313–320. doi:10.1016/j.foodqual.2006.02.006

CrossRef Full Text | Google Scholar

Kohyama, K., Sasaki, T., and Hayakawa, F. (2008). Characterization of food physical properties by the mastication parameters measured by electromyography of the jawclosing muscles and mandibular kinematics in young adults. Biosci. Biotechnol. Biochem. 72, 1690–1695. doi:10.1271/bbb.70769

PubMed Abstract | CrossRef Full Text | Google Scholar

Koole, P., Beenhakker, F., de Jongh, H. J., and Boering, G. (1990). A standardized technique for the placement of electrodes in the two heads of the lateral pterygoid muscle. J. Craniomandib. Pract. 8, 154–162. doi:10.1080/08869634.1990.11678309

PubMed Abstract | CrossRef Full Text | Google Scholar

Koolstra, J. H. (2002). Dynamics of the human masticatory system. Crit. Rev. Oral Biol. Med. 13, 366–376. doi:10.1177/154411130201300406

PubMed Abstract | CrossRef Full Text | Google Scholar

Koolstra, J. H., and van Eijden, T. M. G. J. (1992). Application and validation of a three–dimensional mathematical model of the human masticatory system in vivo. J. Biomech. 25, 175–187. doi:10.1016/0021–9290(92)90274–5

PubMed Abstract | CrossRef Full Text | Google Scholar

Koolstra, J. H., van Eijden, T. M. G. J., Weijs, W. A., and Naeije, M. (1988). A three-dimensional mathematical model of the human masticatory system predicting maximum possible bite forces. J. Biomech. 21, 563–576. doi:10.1016/0021–9290(88)90219–9

PubMed Abstract | CrossRef Full Text | Google Scholar

Korioth, T. W. P., and Hannam, A. G. (1994). Deformation of the human mandible during simulated tooth clenching. J. Dent. Res. 73, 56–66. doi:10.1177/00220345940730010801

PubMed Abstract | CrossRef Full Text | Google Scholar

Korioth, T. W. P., and Hannam, A. G. (1990). Effect of bilateral asymmetric tooth clenching on load distribution at the mandibular condyles. J. Prosthet. Dent. 64, 62–73. doi:10.1016/0022-3913(90)90154-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Korioth, T. W. P., Romilly, D. P., and Hannam, A. G. (1992). Three-dimensional finite element stress analysis of the dentate human mandible. Am. J. Phys. Anthropol. 88, 69–96. doi:10.1002/ajpa.1330880107

PubMed Abstract | CrossRef Full Text | Google Scholar

Langenbach, G. E. J., and Hannam, A. G. (1999). The role of passive muscle tensions in a three-dimensional dynamic model of the human jaw. Arch. Oral Biol. 44, 557–573. doi:10.1016/s0003–9969(99)00034–5

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, J. H., Han, H. S., Kim, Y. Ch., Lee, J. Y., and Lee, B. K. (2017). Stability of biodegradable metal (Mg–Ca–Zn alloy) screws compared with absorbable polymer and titanium screws for sagittal split ramus osteotomy of the mandible using the finite element analysis model. J. Craniomaxillofac Surg. 45, 1639–1646. doi:10.1016/j.jcms.2017.06.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Lenfant, F., Loret, C., Pineau, N., Hartmann, C., and Martin, N. (2009). Perception of oral food breakdown. The concept of sensory trajectory. Appetite 52, 659–667. doi:10.1016/j.appet.2009.03.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Lillford, P. J. (2000). The materials science of eating and food breakdown. MRS Bull. 25, 38–43. doi:10.1557/mrs2000.252,

CrossRef Full Text | Google Scholar

Lucas, P. W., Prinz, J. F., Agrawal, K. R., and Bruce, I. C. (2004). Food texture and its effect on ingestion, mastication and swallowing. J. Text. Stud. 35, 159–170. doi:10.1111/j.1745-4603.2004.tb00831.x

CrossRef Full Text | Google Scholar

Lund, P. J. (1991). Mastication and its control by the brain stem. Crit. Rev. Oral Biol. Med. 2, 33–64. doi:10.1177/10454411910020010401

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, D., Rong, Q., and Chen, Q. (2017). Finite-element design and optimization of a three-dimensional tetrahedral porous titanium scaffold for the reconstruction of mandibular defects. Med. Eng. Phys. 47, 176–183. doi:10.1016/j.medengphy.2017.06.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Manns, A., and Díaz, G. (1988). Sistema Estomatognático. Santiago de Chile: Sociedad Gráfica Almagro Ltda.

Google Scholar

Marková, M., and Gallo, L. M. (2016). The influence of the human TMJ eminence inclination on predicted masticatory muscle forces. Hum. Mov. Sci. 49, 132–140. doi:10.1016/j.humov.2016.06.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Mathevon, E., Mioche, L., Brown, W. E., and Culioli, J. (1995). Texture analysis of beef cooked at various temperatures by mechanical measurements, sensory assessments and electromyography. J. Text. Stud. 26, 175–192. doi:10.1111/j.1745-4603.1995.tb00792.x

CrossRef Full Text | Google Scholar

May, B., Saha, S., and Saltzman, M. (2001). A three–dimensional mathematical model of temporomandibular joint loading. Clin. Biomech. 16, 489–495. doi:10.1016/s0268–0033(01)00037–7

PubMed Abstract | CrossRef Full Text | Google Scholar

Meullenet, J. F., Finney, M. L., and Gaud, M. (2002). Measurement of biting velocities, and predetermined and individual crosshead speed instrumental imitative tests for predicting cheese hardness. J. Texture Stud. 33, 45–58. doi:10.1111/j.1745-4603.2002.tb01334.x

CrossRef Full Text | Google Scholar

Mioche, L., Bourdiol, P., Martin, J. F., and Noël, Y. (1999). Variations in human masseter and temporalis muscle activity related to food texture during free and side imposed mastication. Arch. Oral Biol. 44, 1005–1012. doi:10.1016/s0003-9969(99)00103-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Mioche, L., Bourdiol, P., Monier, S., and Martin, J. F. (2002). The relationship between chewing activity and food bolus properties obtained from different meat textures. Food Qual. prefer. 13, 583–588. doi:10.1016/S0950-3293(02)00056-3

CrossRef Full Text | Google Scholar

Morris, C. B. (1948). The measurement of the strength of muscle relative to the cross-section. Res. Q. Am. Assoc. Hlth Phys. Educ. 19, 295–303. doi:10.1080/10671188.1948.10621004

PubMed Abstract | CrossRef Full Text | Google Scholar

Murray, G. (2004). “Jaw movement and its control,” in Occlusion and clinical practice an evidence based approach. Editors I. Klineberg, and J. Rob (London: Elsevier Health Sciences), 13–22.

Google Scholar

Murray, G. M., Orfanos, T., Chan, J. Y., Wanigaratne, K., and Klineberg, I. J. (1999). Electromyographic activity of the human lateral pterygoid muscle during contralateral and protrusive jaw, movements. Arch. Oral Biol. 44, 269–285. doi:10.1016/s0003-9969(98)00117-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Nishigawa, K., Nakano, M., and Bando, E. (1997). Study of jaw movement and masticatory muscle activity during unilateral chewing with and without balancing side molar contacts. J. Oral Rehabil. 24, 691–696. doi:10.1046/j.1365-2842.1997.00553.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Orassi, V., Duda, G. N., Heiland, M., Fischer, H., Rendenbach, C., and Checa, S. (2021). Biomechanical assessment of the validity of sheep as a preclinical model for testing mandibular fracture fixation devices. Front. Bioeng. Biotechnol. 9, 672176. doi:10.3389/fbioe.2021.672176

PubMed Abstract | CrossRef Full Text | Google Scholar

Pachnicz, D., and Stróżyk, P. (2021). A biomechanical analysis of muscle force changes after bilateral sagittal split osteotomy. Front. Physiol. 12, 679644. doi:10.3389/fphys.2021.679644

PubMed Abstract | CrossRef Full Text | Google Scholar

Peck, C. C., Langenbach, G. E. J., and Hannam, A. G. (2000). Dynamic simulation of muscle and articular properties during human wide jaw opening. Arch. Oral Biol. 45, 963–982. doi:10.1016/s0003-9969(00)00071–6

PubMed Abstract | CrossRef Full Text | Google Scholar

Piancino, M. G., Bracco, P., Vallelonga, T., Merlo, A., and Farina, D. (2008). Effect of bolus hardness on the chewing pattern and activation of masticatory muscles in subjects with normal dental occlusion. J. Electromyogr. Kinesiol. 18, 931–937. doi:10.1016/j.jelekin.2007.05.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Piancino, M. G., Isola, G., Merlo, A., Dalessandri, D., Debernardi, C., and Bracco, P. (2012). Chewing pattern and muscular activation in open bite patients. J. Electromyogr. Kinesiol 22, 273–279. doi:10.1016/j.jelekin.2011.12.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Pinheiro, M., and Alves, J. L. (2015). The feasibility of a custom-made endoprosthesis in mandibular reconstruction: Implant design and finite element analysis. J. Craniomaxillofac Surg. 43, 2116–2128. doi:10.1016/j.jcms.2015.10.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Posselt, U. (1952). “Studies in the mobility of the human mandible,” in Acta odontologica scandinavica (Copenhagen: Supplementum).

Google Scholar

Pruim, G. J., de Jongh, H. J., and ten Bosch, J. J. (1980). Forces acting on the mandible during bilateral static bite at different bite force levels. J. Biomech. 13, 755–763. doi:10.1016/0021–9290(80)90237–7

PubMed Abstract | CrossRef Full Text | Google Scholar

Quintero, A., Ichesco, E., Myers, C., Schutt, R., and Gerstner, G. E. (2013). Brain activity and human unilateral chewing. an fMRI study. J. Dent. Res. 92, 136–142. doi:10.1177/0022034512466265

PubMed Abstract | CrossRef Full Text | Google Scholar

Reina, J. M., Garcia-Aznar, J. M., Dominguez, J., and Doblaré, M. (2007). Numerical estimation of bone density and elastic constants distribution in a human mandible. J. Biomech. 40, 828–836. doi:10.1016/j.jbiomech.2006.03.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Romero, F., and Alonso, F. J. (2016). A comparison among different Hill-type contraction dynamics formulations for muscle force estimation. Mech. Sci. 7, 19–29. doi:10.5194/ms-7-19-2016

CrossRef Full Text | Google Scholar

Röhrle, O., and Pullana, A. J. (2007). Three-dimensional finite element modelling of muscle forces during mastication. J. Biomech. 40, 3363–3372. doi:10.1016/j.jbiomech.2007.05.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Santana-Mora, U., Martínez-Ínsua, A., Santana-Penín, U., del Palomar, A. P., Banzo, J. C., and Mora, M. J. (2014). Muscular activity during isometric incisal biting. J. Biomech. 47, 3891–3897. doi:10.1016/j.jbiomech.2014.09.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Shimada, A., Yamabe, Y., Torisu, T., Baad-Hansen, L., Murata, H., and Svensson, P. (2012). Measurement of dynamic bite force during mastication. J. Oral Rehabil. 39, 349–356. doi:10.1111/j.1365-2842.2011.02278.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Slager, G. E. C., Otten, E., van Eijden, T. M. G. J., and van Willigen, J. D. (1997). Mathematical model of the human jaw system simulating static biting and movements after unloading. J. Neurophysiol. 78, 3222–3233. doi:10.1152/jn.1997.78.6.3222

PubMed Abstract | CrossRef Full Text | Google Scholar

Slavicek, G. (2010). Human mastication. Int. J. Stomatol. Occlusion Med. 3, 29–41. doi:10.1007/s12548-010-0044-6

CrossRef Full Text | Google Scholar

Stokes, J. R., Boehm, M. W., and Baier, S. K. (2013). Oral processing, texture and mouthfeel: From rheology to tribology and beyond. Curr. Opin. Colloid Interface Sci. 18, 349–359. doi:10.1016/j.cocis.2013.04.010

CrossRef Full Text | Google Scholar

Stróżyk, P., and Bałchanowski, J. (2020). Effect of foods on selected dynamic parameters of mandibular elevator muscles during symmetric incisal biting. J. Biomech. 2020, 109800. doi:10.1016/j.jbiomech.2020.109800

PubMed Abstract | CrossRef Full Text | Google Scholar

Stróżyk, P., and Bałchanowski, J. (2016). Effect of foodstuff on muscle forces during biting off. Acta Bioeng. Biomech. 18, 81–91. doi:10.5277/ABB-00305-2015-03

PubMed Abstract | CrossRef Full Text | Google Scholar

Stróżyk, P., and Bałchanowski, J. (2018). Modelling of the forces acting on the human stomatognathic system during dynamic symmetric incisal biting of foodstuffs. J. Biomech. 79, 58–66. doi:10.1016/j.jbiomech.2018.07.046

PubMed Abstract | CrossRef Full Text | Google Scholar

Stróżyk, P., Bałchanowski, J., and Szrek, J. (2018). “Modelling of the dynamic loads of the human stomatognathic system during biting off,” in 24th International Conference–Engineering Mechanics. Institute of Theoretical and Applied Mechanics of the Czech Academy of Sciences, Svratka, Czech Republic, May 14 – 17.

Google Scholar

Stróżyk, P. (2021). The patent application (WIP ST 10/C PL436928 patent Office of the Republic of Poland).

Google Scholar

Wang, M. Q., He, J. J., Zhang, J. H., Wang, K., Svensson, P., and Widmal, S. E. (2010). SEMG activity of jaw closing muscles during biting with different unilateral occlusal supports. J. Oral Rehabil. 37, 719–725. doi:10.1111/j.1365-2842.2010.02104.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Weijs, W. A., and Hillen, B. (1985). Cross–sectional areas and estimated intrinsic strength of the human jaw muscles. Acta Morphol. Neerl Scand. 23, 267–274.

PubMed Abstract | Google Scholar

Weinberg, L. A. (1963). An evaluation of basic articulators and their concepts. J. Prosthet. Dent. 13, 622–644. doi:10.1016/0022-3913(63)90133-1

CrossRef Full Text | Google Scholar

Widmalm, S. E., Lillie, J. H., and Ash, M. M. (1987). Anatomical and electromyographic studies of the lateral pterygoid muscle. J. Oral Rehabil. 14, 429–446. doi:10.1111/j.1365-2842.1987.tb00738.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, S. H., Wright, B. W., Truong, V. D., Daubert, C. R., and Vinyard, C. J. (2005). Mechanical properties of foods used in experimental studies of primate masticatory function. Am. J. Primatol. 67, 329–346. doi:10.1002/ajp.20189

PubMed Abstract | CrossRef Full Text | Google Scholar

Wood, W. W., Takada, K., and Hannam, A. G. (1986). The electromyographic activity of the inferior part of the human lateral pterygoid muscle during clenching and chewing. Arch. Oral Biol. 31, 245–253. doi:10.1016/0003-9969(86)90056-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, K., Liao, Z., Yoda, N., Fang, J., Chen, J., Zhang, Z., et al. (2019). Investigation on masticatory muscular functionality following oral reconstruction–An inverse identification approach. J. Biomech. 90, 1–8. doi:10.1016/j.jbiomech.2019.04.007

PubMed Abstract | CrossRef Full Text | Google Scholar