
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Bioeng. Biotechnol., 22 November 2023
Sec. Biosensors and Biomolecular Electronics
Volume 11 - 2023 | https://doi.org/10.3389/fbioe.2023.1280233
 Nunzio Camerlingo1
Nunzio Camerlingo1 Ilaria Siviero2
Ilaria Siviero2 Martina Vettoretti1
Martina Vettoretti1 Giovanni Sparacino1
Giovanni Sparacino1 Simone Del Favero1
Simone Del Favero1 Andrea Facchinetti1*
Andrea Facchinetti1*Introduction: The retrospective analysis of continuous glucose monitoring (CGM) timeseries can be hampered by colored and non-stationary measurement noise. Here, we introduce a Bayesian denoising (BD) algorithm to address both autocorrelation of measurement noise and temporal variability of its variance.
Methods: BD utilizes adaptive, a-priori models of signal and noise, whose unknown variances are derived on partially-overlapped CGM windows, via smoothing approach based on linear mean square estimation. The CGM signal and noise variability profiles are then reconstructed using a kernel smoother. BD is first assessed on two simulated datasets, DS1 and DS2. On DS1, the effectiveness of accounting for colored noise is evaluated by comparison against a literature algorithm; on DS2, the effectiveness of accounting for the noise variance temporal variability is evaluated by comparison against a Butterworth filter. BD is then evaluated on 15 CGM timeseries measured by the Dexcom G6 (DR).
Results: On DS1, BD allows reducing the root-mean-square-error (RMSE) from 8.10 [6.79–9.24] mg/dL to 6.28 [5.47–7.27] mg/dL (median [IQR]); on DS2, RMSE decreases from 6.85 [5.50–8.72] mg/dL to 5.35 [4.48–6.49] mg/dL. On DR, BD performs a reasonable tracking of noise variance variability and a satisfactory denoising.
Discussion: The new algorithm effectively addresses the nature of CGM measurement error, outperforming existing denoising algorithms.
The use of continuous glucose monitoring (CGM) sensors is rapidly growing in diabetes therapy management and research. This is due to the capability of CGM sensors to provide almost continuous glucose concentration measurements (e.g., every 5 min) over prolonged periods, such as days or weeks (Kumar Das et al., 2022). In the past years, the retrospective analysis of CGM timeseries proved to be important for tuning/refining diabetes therapies and, in turn, for improving the overall glycemic control (Klonoff, 2005; Scheiner, 2016). For example, the offline analysis of trends and patterns in the post-prandial CGM profiles can help optimizing insulin dosages (Battelino et al., 2022), suggesting strategies for taking rescue carbohydrates (Camerlingo et al., 2019), evaluating glucose variability (Service, 2013), quantifying the effectiveness of therapies through, e.g., the computation of time-in-ranges indices (Battelino et al., 2019; Camerlingo et al., 2021), and visualizing clinically-relevant CGM patterns (Danne et al., 2017).
Despite the advancements in sensors technology that have led to increased accuracy, CGM measurements are inevitably impacted by random non-stationary measurement noise, which typically dominates the true signal at high frequencies (Breton and Kovatchev, 2008; Lunn et al., 2011; Laguna et al., 2014; Vettoretti et al., 2019a; Vettoretti et al., 2019b). As a non-stationary random process, the statistical properties of the CGM measurement noise vary over time, or in response to different conditions (both internal mechanisms, such as electromagnetic interferences, electrode degradation, chemical contamination of the sensor surface, and related to the sensor-user interface, such as physical activity, compression, or site insertion inflammation), thus hampering data interpretation.
The signal-to-noise ratio (SNR) in CGM measurements can be improved by utilizing appropriate denoising algorithms. This would enhance the reliability of the clinical conclusions that can be derived from the retrospective analysis of CGM data. To address this issue, a variety of digital filtering and smoothing techniques have been proposed in the literature (Lee et al., 2021; Zhang et al., 2021). Low-pass digital filters, such as Butterworth filters have been often used in the literature (Sparacino et al., 2007; Pérez-Gandía et al., 2010; Mhaskar et al., 2017), as they represent a straightforward way to separate noise bands. However, since signal and noise spectra of CGM measurements normally overlap, it is not possible to remove the random measurement noise without distorting the true glucose values. Kalman filters (Knobbe and Buckingham, 2005; Bequette, 2018), instead, benefit of a maximum likelihood estimation step to determine the parameters of a state space system, modelling the true glucose signal and the measurement noise but, notably, prior knowledge about their statistical properties is needed. In offline setting, the Kalman smoother can be used to get further improvement of the estimates (Staal et al., 2019; Rabby et al., 2021). However, in the above-mentioned methods, the key parameters of the algorithms (e.g., the cutoff frequency for the Butterworth filter) are fixed once for all. This constraint makes such filters unable to adapt their “aggressiveness” to the temporal variations of the CGM measurement error statistical properties (e.g., the variance or the autocorrelation), which have been recently observed on CGM data (Facchinetti et al., 2014; Biagi et al., 2017; Vettoretti et al., 2019b), thus resulting in suboptimal denoised profiles, with oversmoothed or undersmoothed portions.
Despite several adaptive filtering/smoothing algorithms have been proposed in different research fields (Dixit and Nagaria, 2017; Sharma and Pachori, 2018), to the best of our knowledge only few attempts have been made to account for the variability of the SNR in CGM data (Facchinetti et al., 2010; Facchinetti et al., 2011; Zhao et al., 2018; Yadav et al., 2020).
For example, Facchinetti et al. (Facchinetti et al., 2010; Facchinetti et al., 2011) proposed the use of Bayesian estimation approach, where the a priori models of measurement error and glucose concentration time course are given by white noise with unknown variance and multiple integration of a white noise with unknown variance, respectively. Both the aforementioned unknown variances can be estimated, with once for all during a burn in interval (Facchinetti et al., 2010), or at specific times (Facchinetti et al., 2011), by using appropriate probabilistic smoothing criteria. Once the values of the models’ variances are determined, the denoised profile can be obtained through linear mean square estimation. While the algorithm of Facchinetti et al. allows to update the filter parameters at user-specified time points, Zhao et al. (2018) proposed later a strategy to update the filter parameters only after a significant change in the noise level, as quantified by an expectation-maximization algorithm, resulting in a significantly shorter computational time. While these adaptive algorithms update the parameters of a state space system to account for the SNR variability, Yadav et al. (2020) proposed an adaptive Savitzky-Golay filter, which can automatically adjust the parameters of a polynomial model (i.e., model order and length of frame), in accordance with the changes in the sampling or cut-off frequency. However, compared to the optimization of the nonparametric models used in (Facchinetti et al., 2010; Facchinetti et al., 2011; Zhao et al., 2018), the optimization of the parametric polynomial model might be computationally expensive, especially if the underlying signal is approximated by a high-order polynomial. Finally, to note, all the above-mentioned algorithms assumed a white Gaussian measurement noise.
Optimality of Bayesian approaches, of course, relies on how accurate the used a priori information on the signals into play is. While the expected regularity of glucose time-course is well described by the multiple integration of a white noise (with an unknown variance to be determined from the data), recent research has shown that for certain CGM sensors, the measurement noise cannot be assumed as white, but should be assumed as colored instead. Indeed, a temporal correlation between consecutive samples of CGM measurement noise has been identified in (Biagi et al., 2017; Vettoretti et al., 2019a; Vettoretti et al., 2019b). Specifically, Vettoretti et al. (Vettoretti et al., 2019a) focused on a recent factory-calibrated CGM sensor, the Dexcom G6 (Dexcom, Inc., San Diego, CA), and described its random measurement noise using a second order autoregressive (AR) model, which is consistent with findings reported in (Vettoretti et al., 2019b) for the Dexcom SEVEN Plus (Dexcom, Inc. San Diego, CA) CGM sensor, and in (Biagi et al., 2017) for the Medtronic Paradigm Veo Enlite (Medtronic, Inc., Northridge, CA) CGM sensor. As far as we know, there are no denoising approaches in the literature that can effectively handle colored, non-stationary, measurement error in CGM data. The goal of this paper is to present and evaluate a Bayesian denoising algorithm for retrospective use on CGM data (off-line) which:
1. explicitly accounts for the temporal correlation among measurement noise samples;
2. iteratively estimates the CGM measurement variance in order to adapt its “aggressiveness” to the temporal variability of the SNR.
The proposed algorithm will be thoroughly evaluated against existing algorithms in a simulated environment, where the true underlying signal is known. The performance of the algorithm will be also demonstrated through its application to real-world data, using 15 traces acquired with the Dexcom G6 CGM sensor.
In this section, a step-by-step description of the proposed Bayesian Denoising (BD) algorithm is provided. First, a mathematical formulation of the problem is given, and the notations introduced. Then, the prior information used for the Bayesian estimation is documented, and the estimation step is described. Finally, the flowchart of the algorithm is explained.
Let us assume that the CGM measurements are collected in
where
Let us define the vectors
In the Bayesian framework, if
Obtaining the linear mean square estimate thus requires knowledge of the a priori covariance matrices
As far as the model of
where
From Eq. 3,
where
As far as the CGM measurement error
where
From Eq. 5,
where
Once defined
where, as discussed in (De Nicolao et al., 1997),
where
while the estimate of
To account for the intra-individual variability of the SNR, the algorithm is applied to consecutive partially-overlapped CGM windows. An optimal “smoothing aggressiveness” is automatically determined for each window, based on the estimated level of noise accounted by
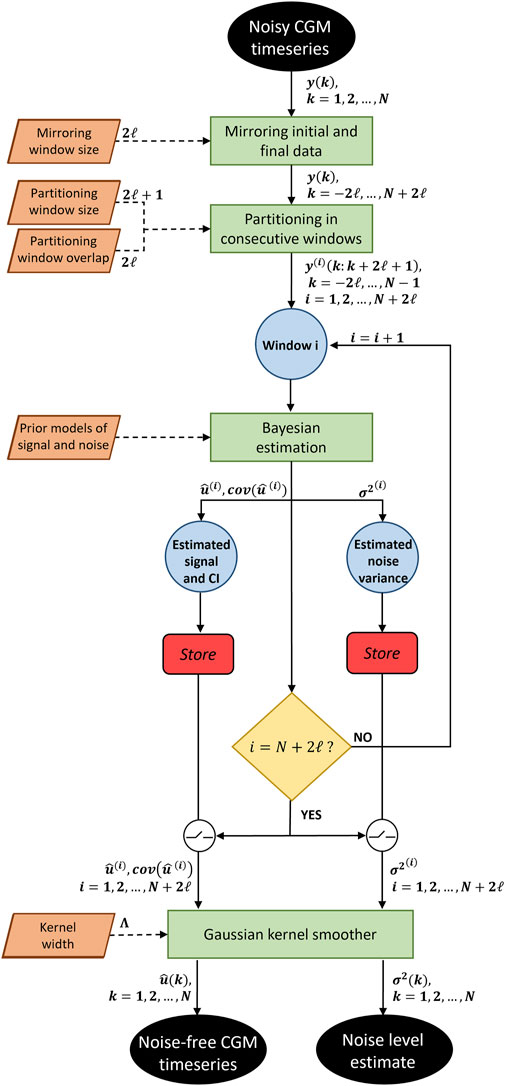
FIGURE 1. Flowchart of the proposed algorithm. A noisy CGM timeseries is given as input to the algorithm. After mirroring the input data and partitioning it in consecutive windows, a Bayesian estimation is performed for each window, providing the denoised signal with its confidence interval, and the noise variance. Once all windows have been processed, a Gaussian kernel smoother recombine the estimated signals. The algorithm gives as output the noise-free CGM timeseries and the noise level timeseries.
Step 1: The algorithm partitions a CGM timeseries into windows of
Step 2: For each window, the mean square estimation is computed, as illustrated in Section 2.1.3. The algorithm estimates
Step 3: Once noisy data in all windows have been smoothed, the algorithm reconstructs the estimated signal in the overlapped regions by implementing a KS. This strategy effectively eliminates any jumps or discontinuities around the boundaries of neighboring windows. Let us consider a kernel
For example, the first point of the smoothed signal
Step 4: Step 3 is repeated to reconstruct a continuous profile of
Since the signals estimated in windows centered in point
The strategy proposed so far does not allow to obtain the final estimates
The proposed BD algorithm, presents two hyperparameters that need to be set:
The proposed BD methodology is first assessed on two synthetic datasets of 100 traces each, namely,
The assessment pipeline implemented therein is incremental. The first dataset
Finally, the proposed BD methodology is evaluated on the real dataset
A set of 100 reference noise-free 1-min sampled glucose profiles of 1-day duration were first generated.
A time-correlated noise profile
The final synthetic dataset
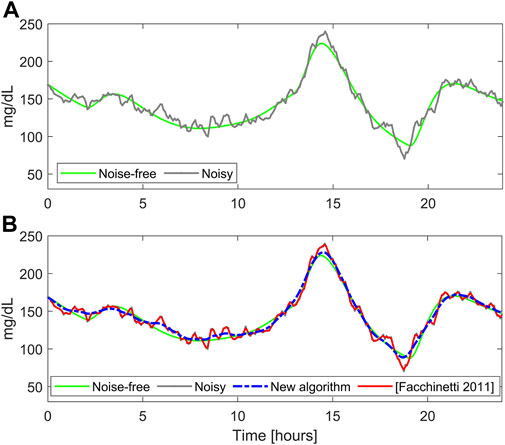
FIGURE 2. A representative simulated glucose profile with stationary measurement noise. Panel (A): noise-free (green) and noisy CGM data (gray). Panel (B) smoothed traces obtained with the literature algorithm (Facchinetti et al., 2011) (red) and BD (blue).
The new BD algorithm is compared against the literature algorithm of Facchinetti et al. (Facchinetti et al., 2011), that assumes white measurement noise (i.e., the matrix
and the mean-absolute-relative-difference (MARD) computed as
Finally, a Wilcoxon signed rank test with significance level of 1% is performed to test statistical difference among RMSE and MARD distributions.
A set of 100 reference noise-free 1-min sampled glucose profiles of 14-day duration were first generated, as performed for the dataset
with amplitude
The final synthetic dataset
The new BD algorithm is compared against two literature Butterworth filters: the first is the one used in Sparacino et al. (Sparacino et al., 2007), that will be referred to as BW1, and the second is that employed in Perez-Gandia et al. (Pérez-Gandía et al., 2010), that will be referred to as BW2. Both BW1 and BW2 are first-order low-pass filters, with BW1 more aggressive than BW2 (cutoff frequency normalized to half sampling rate equal to 0.05 for BW1 and 0.1 for BW2). Note that the comparison against the algorithm of Facchinetti et al. (Facchinetti et al., 2011) on
To evaluate the reliability of BD in denoising the traces of the dataset
Figure 2B shows the smoothed traces obtained with the literature algorithm (red) and BD (dashed blue), for a representative simulated profile. It is well visible that the literature algorithm performs undersmoothing, reducing only slightly the noise fluctuations, while the new algorithm provides a reliable estimate of the noise-free profile (reported in green). This happens because the literature algorithm underestimates the noise variance (
Similar considerations can be drawn considering the overall synthetic dataset
Figure 3 displays the comparison between true and estimated
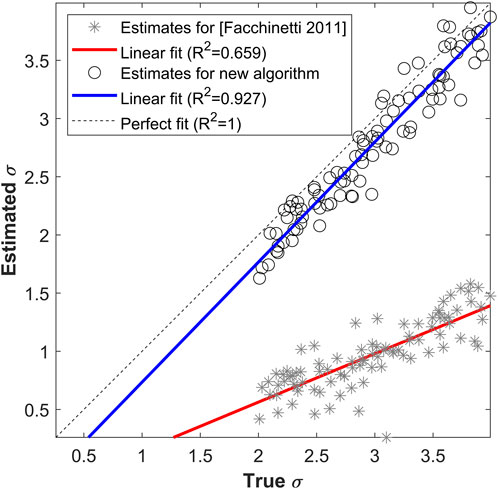
FIGURE 3. True vs. estimated
The percent absolute relative error in the estimation of
Figure 4A reports the smoothed profile obtained with BD (dashed blue) and the Butterworth filter BW2 (orange solid line). BD performs a satisfactory denoising, being the estimated profile very close to the reference noise-free trace, while BW2 performs undersmoothing for most of the trace. The time course of the estimated
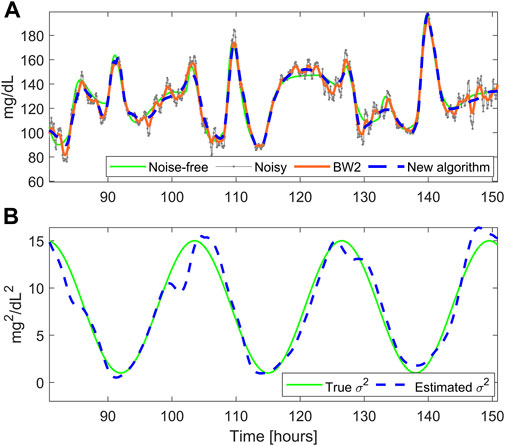
FIGURE 4. A representative simulated glucose profile with non-stationary measurement noise. Panel (A): noise-free data (green), noisy CGM data (gray), smoothed trace obtained with the new BD (dashed blue), and the Butterworth filter BW2 (orange). Panel (B) simulated
To quantify the improvement given by BD, in Table 1 we report, for the 100 simulated traces of the dataset

TABLE 1. RMSE [mg/dL] and MARD [%] computed between the noise-free “ground-truth” profiles and the noisy simulated traces (first column), the traces provided by the filter BW1 (second column), BW2 (third column), and BD (fourth column), for 100 simulated traces.
The Butterworth filter BW1 provides higher RMSE and MARD values. This happens because it is too aggressive (i.e., too low cutoff frequency), thus performing oversmoothing in almost all the traces. Instead, the Butterworth filter BW2 provides acceptable RMSE and MARD values. Finally, the new BD algorithm provides the lowest RMSE and MARD values, thus outperforming all comparator algorithms, and resulting significantly different from those provided by the Butterworth filter BW2 (p-value<0.0001 for both RMSE and MARD).
Figure 5 reports a comparison between the smoothed traces obtained with the new BD algorithm and the filter BW2, in two different portions of the dataset
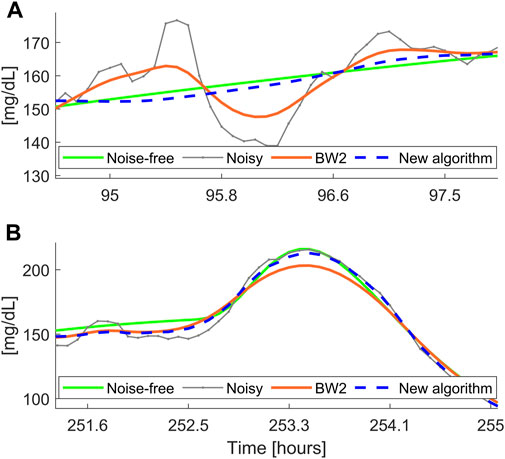
FIGURE 5. Two representative simulated noise-free (green) and noisy (gray) profiles, with non-stationary measurement noise, filtered with the new algorithm (dashed blue) and the Butterworth filter BW2 (orange). Panel (A): example of undersmoothing of BW2; Panel (B): example of oversmoothing of BW2.
Figure 6 illustrates the application of the new BD algorithm to two representative portions of the traces of
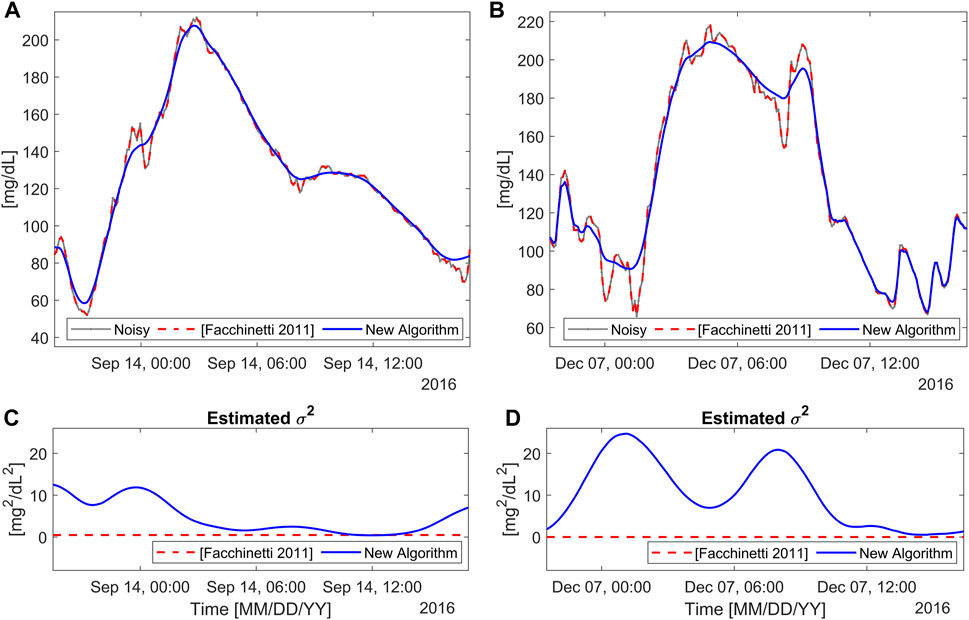
FIGURE 6. Two representative real profiles from
These considerations outlined for the representative data hold for the entire real dataset.
The simulation analysis performed in this paper to assess the performance of the proposed algorithm involved simulated data mimicking the measurement noise corrupting the Dexcom G6 CGM device, as it is the only CGM device available on the market with a publicly available statistical model of the measurement noise. While statistical models of old generation CGM devices are available in the literature (e.g., for the Dexcom SEVEN Plus (Facchinetti et al., 2014), the Medtronic Paradigm Veo Enlite (Biagi et al., 2017), the Dexcom G4 (Facchinetti et al., 2015)), these devices are outdated, and the proposed algorithm should be adapted to cope with other limitations of older technologies, for instance the manual calibration, which would create periodic discontinuities in the CGM traces, affecting the reconstruction of the denoised signal. Statistical models of the measurement noise for other new generation CGM devices (such as Medtronic Guardian Connect, Abbott FreeStyle Libre 3, Ascensia Eversense E3) are not publicly available, and their development would require ad hoc datasets with frequently sampled blood glucose values collected in clinic. Although the proposed methodology has not been designed for a specific CGM model, and it is expected to work properly with any colored and non-stationary measurement noise, its assessment on different CGM devices will be performed when the statistical models of their measurement noise will become available.
In addition, the model used in this work assumes the measurement noise to be additive, and signal and noise to be mutually uncorrelated. While these assumptions have been widely used in the literature for biological signals (Facchinetti et al., 2010; Facchinetti et al., 2011; Bequette, 2018; Zhao et al., 2018; Yadav et al., 2020), removing them would require the algorithm to be redesigned.
Finally, the proposed algorithm is retrospective, as it denoises a CGM measurement using data collected before and after that measurement. For this reason, it cannot be applied in real-time. However, in the future we will explore the advantages of implementing the algorithm periodically, for example, every night to denoise the CGM measurements collected in the previous 24 h.
The retrospective analysis of CGM timeseries is useful to evaluate the effectiveness of diabetes treatments and, in turn, to design personalized therapies. However, the presence of measurement noise may complicate this evaluation. To improve the quality of CGM signals, denoising approaches can be employed. Unfortunately, most approaches exploit digital filters with fixed parameters that cannot cope with neither the inter- nor the intra-individual variability of the SNR in CGM timeseries. In addition, recent investigations showed that, for several CGM sensors, the measurement noise is not only non-stationary, but also colored.
In the present paper we proposed an algorithm which accounts for both autocorrelation and non-stationarity of CGM measurement noise, by leveraging the Bayesian theory. The performance of the new algorithm was assessed on both simulated and real data. Simulation results proved the effectiveness of the method and its superiority versus literature approaches, being effective in correctly estimating the measurement noise variance and tracking its time-variability. Application on real data showed that the measurement noise variance determined by the new algorithm over time was in agreement with the SNR qualitatively perceivable by eye inspection. In summary, the new algorithm can be used to effectively perform retrospective denoising of CGM timeseries, providing a reliable estimate of both the glucose profile and the measurement noise variance time-variable pattern.
Notably, being the proposed algorithm devised in a Bayesian framework, it is theoretically and practically possible to obtain also the confidence interval of the estimated CGM denoised profiles. Future work will explore the use of confidence intervals as a measure of reliability and how this feature could be exploited in practical challenges related to CGM sensors, such as identifying pressure-induces artifacts. Finally, we will also investigate how to adapt the proposed algorithm to smooth different biological signals, such as heart rate or blood pressure, and to quantify the amount of measurement noise present on these timeseries.
In conclusion, we contend that the algorithm presented in this work represents a significant advance in the field of retrospective denoising of CGM timeseries. Indeed, as opposite to the literature algorithms accounting for the non-stationarity of CGM timeseries (Facchinetti et al., 2011; Zhao et al., 2018; Yadav et al., 2020), which assumed the measurement noise to be white, the proposed algorithm represents the first attempt to simultaneously account for both the non-stationarity and the time-correlation of the measurement noise.
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://github.com/NunzioCamer/Bayesian-Denoising-CGM.
NC: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Validation, Visualization, Writing–original draft, Writing–review and editing. IS: Data curation, Formal Analysis, Investigation, Validation, Visualization, Writing–review and editing. MV: Methodology, Supervision, Writing–review and editing. GS: Methodology, Supervision, Writing–review and editing. SDF: Conceptualization, Methodology, Supervision, Writing–review and editing. AF: Conceptualization, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Writing–review and editing.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. Dexcom, Inc. (San Diego, CA, United States) provided financial support to the research presented in this work. This work was also partially supported by MIUR, under the initiative “PRIN: Programmi di Ricerca Scientifica di Rilevante Interesse Nazionale (2020)”, project ID: 2020X7XX2P, project title: “A noninvasive tattoo-based continuous GLUCOse Monitoring electronic system FOR Type-1 diabetes individuals (GLUCOMFORT)”.
Dexcom, Inc. (San Diego, CA, United States) is acknowledged for having kindly provided the dataset used in this study.
The authors declare no conflict of interest. Dexcom, Inc. (San Diego, CA, United States) did not edit or influenced the material presented therein. None of the data, or data or analysis derived from the data, are derived using Dexcom, Inc. proprietary algorithms in any way. Nor does anything in this paper, including descriptions of algorithms and the state-of-the-art, purport to describe or use such proprietary algorithms. However, the algorithms disclosed in this paper may be covered by one or more US and international pending patents and applications.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbioe.2023.1280233/full#supplementary-material
Battelino, T., Alexander, C. M., Amiel, S. A., Arreaza-Rubin, G., Beck, R. W., Bergenstal, R. M., et al. (2022). Continuous glucose monitoring and metrics for clinical trials: an international consensus statement. Lancet Diabetes Endocrinol. 11, 42–57. doi:10.1016/S2213-8587(22)00319-9
Battelino, T., Danne, T., Bergenstal, R. M., Amiel, S. A., Beck, R., Biester, T., et al. (2019). Clinical targets for continuous glucose monitoring data interpretation: recommendations from the international consensus on time in range. Diabetes Care 42, 1593–1603. doi:10.2337/dci19-0028
Bequette, B. W. (2018). Optimal estimation applications to continuous glucose monitoring. IEEE Trans. Biomed. Eng. 1, 958–962. doi:10.23919/ACC.2004.1383731
Biagi, L., Ramkissoon, C. M., Facchinetti, A., Leal, Y., and Vehi, J. (2017). Modeling the error of the medtronic Paradigm Veo enlite glucose sensor. Sensors 17, 1361. doi:10.3390/S17061361
Breton, M., and Kovatchev, B. (2008). Analysis, modeling, and simulation of the accuracy of Continuous glucose sensors. J. Diabetes Sci. Technol. 2, 853–862. doi:10.1177/193229680800200517
Camerlingo, N., Vettoretti, M., Del Favero, S., Cappon, G., Sparacino, G., and Facchinetti, A. (2019). A real-time continuous glucose monitoring–based algorithm to trigger hypotreatments to prevent/mitigate hypoglycemic events. Diabetes Technol. Ther. 21, 644–655. doi:10.1089/dia.2019.0139
Camerlingo, N., Vettoretti, M., Sparacino, G., Facchinetti, A., Mader, J. K., Choudhary, P., et al. (2021). Design of clinical trials to assess diabetes treatment: minimum duration of continuous glucose monitoring data to estimate time-in-ranges with the desired precision. Diabetes Obes. Metab. 23, 2446–2454. doi:10.1111/DOM.14483
Danne, T., Nimri, R., Battelino, T., Bergenstal, R. M., Close, K. L., DeVries, J. H., et al. (2017). International consensus on use of continuous glucose monitoring. Diabetes Care 40, 1631–1640. doi:10.2337/dc17-1600
De Nicolao, G., Sparacino, G., and Cobelli, C. (1997). Nonparametric input estimation in physiological systems: problems, methods, and case studies. Automatica 33, 851–870. doi:10.1016/S0005-1098(96)00254-3
Dixit, S., and Nagaria, D. (2017). LMS adaptive filters for noise cancellation: a review. Int. J. Electr. Comput. Eng. (IJECE) 7, 2520–2529. doi:10.11591/IJECE.V7I5.PP2520-2529
Facchinetti, A., Del Favero, S., Sparacino, G., Castle, J. R., Ward, W. K., and Cobelli, C. (2014). Modeling the glucose sensor error. IEEE Trans. Biomed. Eng. 61, 620–629. doi:10.1109/TBME.2013.2284023
Facchinetti, A., Simone, ·, Favero, D., Sparacino, G., and Cobelli, C. (2015). Model of glucose sensor error components: identification and assessment for new Dexcom G4 generation devices. Med. Biol. Eng. Comput. 53, 1259–1269. doi:10.1007/s11517-014-1226-y
Facchinetti, A., Sparacino, G., and Cobelli, C. (2010). An online self-tunable method to denoise CGM sensor data. IEEE Trans. Biomed. Eng. 57, 634–641. doi:10.1109/TBME.2009.2033264
Facchinetti, A., Sparacino, G., and Cobelli, C. (2011). Online denoising method to handle intraindividual variability of signal-to-noise ratio in continuous glucose monitoring. IEEE Trans. Biomed. Eng. 58, 2664–2671. doi:10.1109/TBME.2011.2161083
Klonoff, D. C. (2005). Continuous glucose monitoring. Diabetes Care 28, 1231–1239. doi:10.2337/DIACARE.28.5.1231
Knobbe, E. J., and Buckingham, B. (2005). The extended kalman filter for continuous glucose monitoring. Diabetes Technol. Ther. 7, 15–27. doi:10.1089/DIA.2005.7.15
Kulemann, D., Jain, A., and Schon, S. (2021). “Evaluation and comparison of different motion models for flight navigation,” in 15th European Conference on Antennas and Propagation, Dusseldorf, Germany, 22-26 March 2021 (IEEE).
Kumar Das, S., Nayak, K. K., Krishnaswamy, P. R., Kumar, V., and Bhat, N. (2022). Review—electrochemistry and other emerging technologies for continuous glucose monitoring devices. ECS Sensors Plus 1, 031601. doi:10.1149/2754-2726/AC7ABB
Laguna, A. J., Rossetti, P., Ampudia-Blasco, F. J., Vehí, J., and Bondia, J. (2014). Postprandial performance of Dexcom® SEVEN® PLUS and Medtronic® Paradigm® VeoTM: modeling and statistical analysis. Biomed. Signal Process Control 10, 322–331. doi:10.1016/J.BSPC.2012.12.003
Lee, I., Probst, D., Klonoff, D., and Sode, K. (2021). Continuous glucose monitoring systems - current status and future perspectives of the flagship technologies in biosensor research. Biosens. Bioelectron. 181, 113054. doi:10.1016/J.BIOS.2021.113054
Lunn, D. J., Wei, C., and Hovorka, R. (2011). Fitting dynamic models with forcing functions: application to continuous glucose monitoring in insulin therapy. Stat. Med. 30, 2234–2250. doi:10.1002/SIM.4254
Mahmoudi, Z., Cameron, F., Poulsen, N. K., Madsen, H., Bequette, B. W., and Jørgensen, J. B. (2019). Sensor-based detection and estimation of meal carbohydrates for people with diabetes. Biomed. Signal Process Control 48, 12–25. doi:10.1016/J.BSPC.2018.09.012
Mhaskar, H. N., Pereverzyev, S. V., and van der Walt, M. D. (2017). A deep learning approach to diabetic blood glucose prediction. Front. Appl. Math. Stat. 3, 1–11. doi:10.3389/fams.2017.00014
Palerm, C. C., Willis, J. P., Desemone, J., and Bequette, B. W. (2005). Hypoglycemia prediction and detection using optimal estimation. Diabetes Technol. Ther. 7, 3–14. doi:10.1089/DIA.2005.7.33
Pérez-Gandía, C., Facchinetti, A., Sparacino, G., Cobelli, C., Gómez, E. J., Rigla, M., et al. (2010). Artificial neural network algorithm for online glucose prediction from continuous glucose monitoring. Diabetes Technol. Ther. 12, 81–88. doi:10.1089/dia.2009.0076
Rabby, M. F., Tu, Y., Hossen, M. I., Lee, I., Maida, A. S., and Hei, X. (2021). Stacked LSTM based deep recurrent neural network with kalman smoothing for blood glucose prediction. BMC Med. Inf. Decis. Mak. 21, 101–115. doi:10.1186/s12911-021-01462-5
Scheiner, G. (2016). CGM retrospective data analysis. Diabetes Technol. Ther. 18, S2. doi:10.1089/dia.2015.0281
Sharma, R. R., and Pachori, R. B. (2018). Baseline wander and power line interference removal from ECG signals using eigenvalue decomposition. Biomed. Signal Process Control 45, 33–49. doi:10.1016/J.BSPC.2018.05.002
Sparacino, G., Milani, S., Arslan, E., and Cobelli, C. (2002). A Bayesian approach to estimate evoked potentials. Comput. Methods Programs Biomed. 68, 233–248. doi:10.1016/S0169-2607(01)00175-4
Sparacino, G., Zanderigo, F., Corazza, S., Maran, A., Facchinetti, A., and Cobelli, C. (2007). Glucose concentration can be predicted ahead in time from continuous glucose monitoring sensor time-series. IEEE Trans. Biomed. Eng. 54, 931–937. doi:10.1109/TBME.2006.889774
Staal, O. M., Salid, S., Fougner, A., and Stavdahl, O. (2019). Kalman smoothing for objective and automatic preprocessing of glucose data. IEEE J. Biomed. Health Inf. 23, 218–226. doi:10.1109/JBHI.2018.2811706
Vettoretti, M., Battocchio, C., Sparacino, G., and Facchinetti, A. (2019a). Development of an error model for a factory-calibrated continuous glucose monitoring sensor with 10-day lifetime. Sensors Switz. 19, 5320–5417. doi:10.3390/s19235320
Vettoretti, M., Battocchio, C., Sparacino, G., and Facchinetti, A. (2019b). Development of an error model for a factory-calibrated continuous glucose monitoring sensor with 10-day lifetime. Sensors 19, 5320. doi:10.3390/S19235320
Vettoretti, M., Facchinetti, A., Sparacino, G., and Cobelli, C. (2018). Type-1 diabetes patient decision simulator for in silico testing safety and effectiveness of insulin treatments. IEEE Trans. Biomed. Eng. 65, 1281–1290. doi:10.1109/TBME.2017.2746340
Wadwa, R. P., Laffel, L. M., Shah, V. N., and Garg, S. K. (2018). Accuracy of a factory-calibrated, real-time continuous glucose monitoring system during 10 days of use in youth and adults with diabetes. Diabetes Technol. Ther. 20, 395–402. doi:10.1089/dia.2018.0150
Yadav, J., Srivastav, N., Agarwal, S., and Rani, A. (2020). Denoising of continuous glucose monitoring signal with adaptive SG filter. Adv. Intelligent Syst. Comput. 1053, 1041–1053. doi:10.1007/978-981-15-0751-9_96
Yue, L., Abdel-Aty, M. A., Wu, Y., and Yuan, J. (2020). An augmentation function for active pedestrian safety system based on crash risk evaluation. IEEE Trans. Veh. Technol. 69, 12459–12469. doi:10.1109/TVT.2020.3017131
Zhang, Y., Sun, J., Liu, L., and Qiao, H. (2021). A review of biosensor technology and algorithms for glucose monitoring. J. Diabetes Complicat. 35, 107929. doi:10.1016/J.JDIACOMP.2021.107929
Keywords: Bayesian denoising, continuous glucose monitoring, correlation, stationarity, Butterworth filter
Citation: Camerlingo N, Siviero I, Vettoretti M, Sparacino G, Del Favero S and Facchinetti A (2023) Bayesian denoising algorithm dealing with colored, non-stationary noise in continuous glucose monitoring timeseries. Front. Bioeng. Biotechnol. 11:1280233. doi: 10.3389/fbioe.2023.1280233
Received: 19 August 2023; Accepted: 07 November 2023;
Published: 22 November 2023.
Edited by:
Giorgio Pennazza, Campus Bio-Medico University, ItalyReviewed by:
Rishi Raj Sharma, Defence Institute of Advanced Technology (DIAT), IndiaCopyright © 2023 Camerlingo, Siviero, Vettoretti, Sparacino, Del Favero and Facchinetti. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Andrea Facchinetti, ZmFjY2hpbmVAZGVpLnVuaXBkLml0
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.