
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Bioeng. Biotechnol. , 31 August 2023
Sec. Biomechanics
Volume 11 - 2023 | https://doi.org/10.3389/fbioe.2023.1241135
 Yi Huang1
Yi Huang1 Liang Jiang1
Liang Jiang1 Xue Chen1
Xue Chen1 Qing Sun1*
Qing Sun1* Xiao Zhang1
Xiao Zhang1 Xunan Tan2
Xunan Tan2 Yan Du2
Yan Du2 Fangtong Zhang2
Fangtong Zhang2 Nannan Wang1
Nannan Wang1 Rufeng Su3
Rufeng Su3 Feng Qu2
Feng Qu2 Guoqing Zhang1
Guoqing Zhang1 Bo Huo3*
Bo Huo3*Introduction: Musculoskeletal simulation has been widely used to analyze athletes’ movements in various competitive sports, but never in ski jumping. Aerodynamic forces during ski jumping take-off have been difficult to account for in dynamic simulation. The purpose of this study was to establish an efficient approach of musculoskeletal simulation of ski jumping take-off considering aerodynamic forces and to analyze the muscle function and activity.
Methods: Camera-based marker-less motion capture was implemented to measure the take-off kinematics of eight professional jumpers. A suitable full-body musculoskeletal model was constructed for the simulation. A method based on inverse dynamics iteration was developed and validated to estimate the take-off ground reaction force. The aerodynamic forces, which were calculated based on body kinematics and computational fluid dynamics simulations, were exerted on the musculoskeletal model as external forces. The activation and joint torque contributions of lower extremity muscles were calculated through static optimization.
Results: The estimated take-off ground reaction forces show similar trend with the results from past studies. Although overall inconsistencies between simulated muscle activation and EMG from previous studies were observed, it is worth noting that the activation of the tibialis anterior, gluteus maximus, and long head of the biceps femoris was similar to specific EMG results. Among lower extremity extensors, soleus, vastus lateralis, biceps femoris long head, gluteus maximus, and semimembranosus showed high levels of activation and joint extension torque contribution.
Discussion: Results of this study advanced the understanding of muscle action during ski jumping take-off. The simulation approach we developed may help guide the physical training of jumpers for improved take-off performance and can also be extended to other phases of ski jumping.
Ski jumping has been one of the competitive disciplines in the very first Olympic Winter Game in 1924 (Braghin et al., 2016). The ski jumping movement sequence is divided into the following four phases: in-run, take-off, flight, and landing. Among these phases, take-off has been considered the most important one as it determines the initial state of the flight phase (Chardonnens et al., 2014).
Previous biomechanical studies on take-off have been mainly focused on body kinematics and dynamics. Throughout the take-off, body velocity, acceleration, angular velocity, angular momentum, energy, and joint torque were reported, among which the acceleration at the center of mass and forward somersaulting angular velocity were important for performance (Arndt et al., 1995; Sasaki et al., 1997; Sasaki et al., 2005; Virmavirta and Komi, 2010; Chardonnens et al., 2014). Some other studies have been carried out on ground reaction force (GRF). Measuring devices such as force plate installed on the ski jumping platform or insole pressure sensors were once used, but never popularized due to their high cost (Virmavirta and Koml, 1993a; b; Virmavirta et al., 2001). Later studies focused more on data-driven GRF estimation methods (Fritz et al., 2019; Nam et al., 2023). Although these studies have revealed the correlation of take-off kinematics and dynamics with athletes’ performance, the activity and function of lower extremity muscle during take-off have not yet been fully elucidated.
Aerodynamics is another vital factor in ski jumping. Past aerodynamic studies have focused more on the flight phase of ski jumping because of the significant aerodynamic effects involved (Barnes et al., 2022; Yamamoto et al., 2022). The role of aerodynamics during take-off has not been studied extensively (Braghin et al., 2016). Virmavirta et al. (Virmavirta et al., 2011) have compared take-off characteristic under nonwind and wind condition through wind tunnel experiment. Differences in body posture, take-off time and GRF between the two conditions were reported. Yamamoto et al. reported an aerodynamic resultant force of over 100 N at the end of take-off (Yamamoto et al., 2016), which could bring a substantial impact on body dynamics of jumpers. However, aerodynamic effects have rarely been considered in previous studies of take-off dynamics.
Electromyography (EMG) has been the most commonly used approach to study muscle activation patterns. However, there are only a few EMG studies on hill jumps with a limited number of muscles that are measured. Virmavirta et al. (Virmavirta et al., 2001; Virmavirta and Komi, 2001) have reported the EMG results of several lower body muscles during take-off. Their studies indicated that the gluteus maximus and vastus lateralis are major contributors to the take-off, while ankle plantar flexors play a limited role. There might be two reasons for the limitation of such studies. Firstly, the large displacement of jumpers during hill jumps brings difficulties to the signal transmission and reception of the EMG sensor. Secondly, athletes’ movements can be severely affected when equipped with EMG sensors, and the risk of injury may therefore increase.
Human locomotion simulation based on musculoskeletal model is another practical approach for estimating muscle state, which is useful for athletes’ physical training, motion optimization, and injury risk prediction. This technique has been applied to various competitive sports, such as basketball (Akhundov et al., 2022), golf (Mahadas et al., 2019), cross-country sit-skiing (Chen et al., 2023), swimming (Langholz et al., 2016), etc. Musculoskeletal simulation of ski jumping take-off has not yet been reported so far, possibly due to the difficulty of kinematic and external forces (GRF and aerodynamic force) acquisition in-field. However, these difficulties are expected to be overcome in view of recent research advances. The accuracy of vision-based marker-less motion capture methods has continued to improve with advances in AI and computer vision. Drazan et al. verified the consistency between the kinematics derived from marker-less motion-capture and marker-based motion capture during vertical jumping (Drazan et al., 2021). Further, Nam et al. predicted a GRF close to the measured one based on the kinematics acquired by a marker-less motion capture system and applied it to in-field take-off (Nam et al., 2023). In terms of aerodynamics, although it is difficult to measure the aerodynamics of a specific jump directly, researchers have established a method to estimate posture-corresponding aerodynamic forces based on a series of wind tunnel test results. Jung et al. have performed ballistics studies using this method to optimize flight attitude and investigate the effect of wind (Jung et al., 2014; Jung et al., 2019). Considering that these studies have provided methods for acquiring or estimating the basic data (kinematics, GRF, and aerodynamics) required, a data-driven musculoskeletal simulation of in-field take-off seems feasible.
In this study, we aim to develop an effective approach for musculoskeletal simulation which considers both GRF and aerodynamic forces during the take-off phase of in-field ski jumping. Based on the musculoskeletal simulation, muscle activity and function were analyzed. Using this simulation model, it becomes feasible to study muscle activation and function during ski jumping, particularly in the situations where GRF and aerodynamic forces are challenging to measure.
At the normal hill (hill size = 86 m) in Akita Japan, take-offs of eight male professional jumpers (23 ± 7.7 years old, 176 ± 4.3 cm, 62 ± 6.5 kg) from Chinese national ski jumping team were filmed after being informed. The trial protocol was reviewed and approved by the ethics committee of Capital University of Physical Education and Sports (approval number: 2022A41). Twenty-seven jumps (three or four jumps per participant) were recorded at 120 fps using two cameras positioning in front of the table edge. A 3D radial calibration frame (QFS-28 DLT Calibration Frame, HuiAnMing Sciences Co., Ltd., Beijing, China) was set up on the table and filmed for camera calibration. The equipment layout is shown in Figure 1A.

FIGURE 1. Acquisition of take-off kinematics. (A) Take-off trial equipment layout. (B) An example result of 2D automatic pose estimation aided with manual correction.
Videos from two cameras were synchronized based on the frame in which jumpers’ heels left the table edge. Video digitization was implemented through an automatic algorithm assisted with manual corrections. A 2D pose estimation algorithm (Motion-3D V1.2.5, Fastmove, Dalian, China) was used to identify 20 joint points of human body automatically (Figure 1B). Joint points with weak estimation accuracy were then corrected manually. Based on images of the calibration frame, 3D trajectories of 20 joint points were calculated by triangulation and will be used as the raw kinematics data for the following musculoskeletal simulation.
It is critical for our simulation to use a suitable musculoskeletal model. The model developed by Lai et al. (Lai et al., 2017) was used as base model because of its’ refined lower extremity musculature. This model modified the range of knee flexion and properties of several muscles on the basis of the model published by Rajagopal et al., making it suitable for movements involving substantial knee and knee flexion, such as ski jumping take-off. In addition, since the external forces in this simulation would be calculated based on full-body kinematics, the model we used should also be capable of full-body movements tracking. Thus, the lumbar spine of the FBLS model (Raabe and Chaudhari, 2016), the head and neck of the MASI model (Cazzola et al., 2017), and the shoulder construction from the model developed by Blana et al. (Blana et al., 2008) were combined into the original Lai model to enable it to track full-body movements. While combining these models, inertial properties of each body were also adjusted to meet the mass distribution of a human body. Additionally, since the raw kinematic data was not enough to determine the movements of subtalar and metatarsal-phalangeal joints, these two joints were locked in the simulation.
The general model constructed above was then scaled based on athletes’ height and weight through scaling module of OpenSim (Scott L et al., 2007). Since these professional athletes have higher muscle strength than ordinary people, it is necessary to increase the muscle strength. The maximum isometric forces of all muscles were first doubled and then multiplied by a scaling factor based on the height and weight of each athlete (Handsfield et al., 2014).
Due to equipment limitations, we were unable to measure the GRF directly during the take-off. However, we developed a general method based on inverse dynamics iteration to estimate the GRF from kinematic data. Given kinematics and kinetics, inverse dynamics solves the equations of motion and calculates generalized forces (Kuo, 1998), which include the compensating forces and torques directly acting on the pelvis to satisfy Newton’s second law, called residuals. These residuals represent dynamic inconsistencies between kinematics and kinetics, and consist of six components, namely, the components of force and torque along three orthogonal axes, denoted by
where superscript
In order to verify this method under standard in-lab motion capture trial procedure, an imitation jump trial was implemented. After being informed the trial procedure, three healthy adult men (29 ± 2.2 years old, 172 ± 0.04 cm, 83 ± 2.83 kg) from local college agreed to participate. The trial protocol was reviewed and approved by the ethics committee of Capital University of Physical Education and Sports (approval number: 2022A41). Participants were asked to perform 3 jumps each. Thirty-nine reflective markers were attached to multiple anatomical landmarks all over the body. Raw marker kinematics data were collected by a 12-camera motion capture system (Optitrack Prime 22, NaturalPoint, Corvallis, United States) with 200 fps, while the GRF were collected synchronously with 1,000 Hz by two force plates (Multicomponent Force Plate 9260AA, Kistler, Winterthur, Switzerland). GRF estimated by the above method was compared with the result of force plates.
The high-speed nature of ski jumping makes the aerodynamic effects significant enough to be considered in the simulation. In our case, aerodynamic forces during take-off were estimated based on body kinematics and CFD simulations.
CFD simulations were carried out under various possible ski jumping postures. Seven representative posture angles with a significant impact on jumper aerodynamic properties were selected (Figure 2A, including the angle between legs
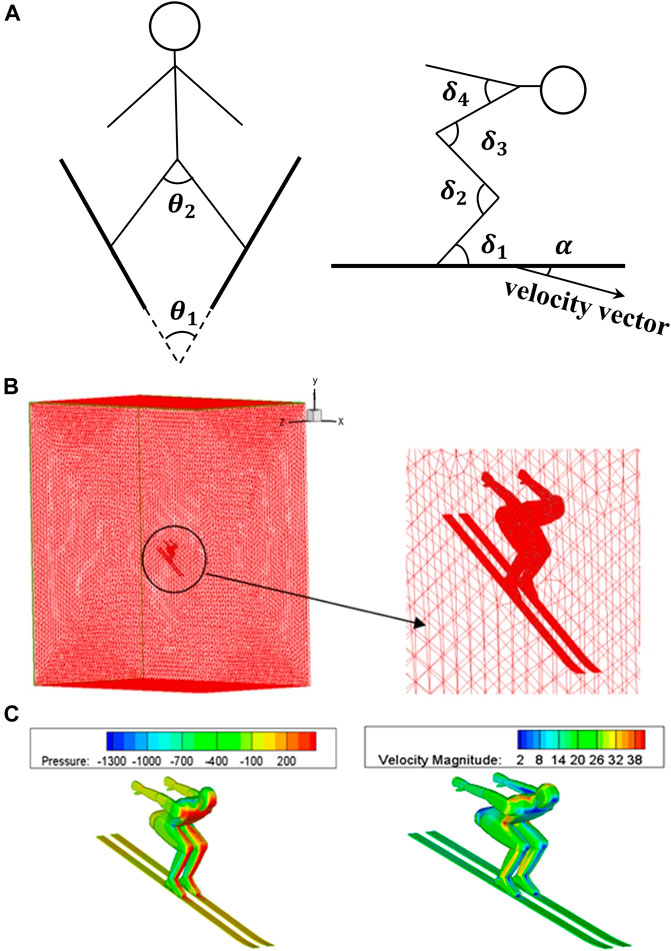
FIGURE 2. Schematic diagram of CFD simulation setup. (A) Posture angles definition. (B) Flow field meshing. (C) Boundary condition settings.
Aerodynamic forces were estimated by matching the measured body motion sequences with the postures in the database. The above posture angles during the take-off were calculated based on model and marker set kinematics. Wherein, ski postures were calculated by markers on heels and toes. The angles in each frame were linearly interpolated in the multidimensional posture space to calculate the corresponding aerodynamic force. Flow velocity and body size were set as constant values in the above CFD simulations. To reflect these effects, the following empirical formula was used:
where
All data processing procedures were implemented through OpenSim 4.1 (Stanford University, Stanford, United States) shown in Figure 4. Movements within 0.1s before release were simulated. Firstly, full-body kinematics were calculated from joint points trajectories through inverse kinematics (Lu and O'Connor, 1999). An example of model motion sequence from inverse kinematics is shown in Figure 5. Then, GRFs and aerodynamic forces were calculated through the method established above. The GRF components in the medial-lateral direction and all moment components were ignored, which allows
Measured and estimated GRFs of simulated jumps were normalized to body weight (Figure 6). They were similar in the anterior-posterior and vertical directions, while the differences were larger in the medial-lateral direction. The mean root mean square error (RMSE) between the measured and estimated GRFs was 39.92 N, 106.41 N, and 19.44 N in the anterior-posterior, vertical, and medial-lateral directions, respectively.
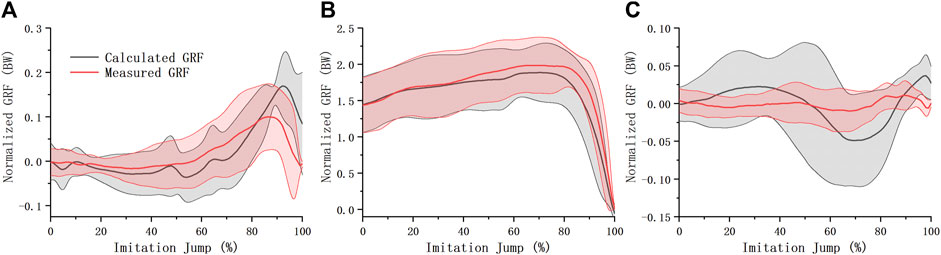
FIGURE 6. GRF of imitation jump. Estimated imitation jump GRF (mean ± S.D.) were compared with measured one in the anterior-posterior (A), vertical (B), and medial-lateral (C) direction.
The mean RMSE between the coordinates of the simulated markers derived from inverse kinematics and the measured one was 3.13 cm, which was slightly larger than the reported result using a marker-based motion capture system (1.38–2.03 cm) (Glover et al., 2021).
Take-off GRF (normalized to body weight) component perpendicular to the table from our calculation was reported and compared with the GRF from 2 previous studies (Virmavirta and Koml, 1993b; Kaps et al., 1997) (Figure 7). The take-off GRFs all share a similar trend, that is, decrease as the take-off process. The GRF from our estimation reduced more rapidly than that of Virmavirta and Komi.
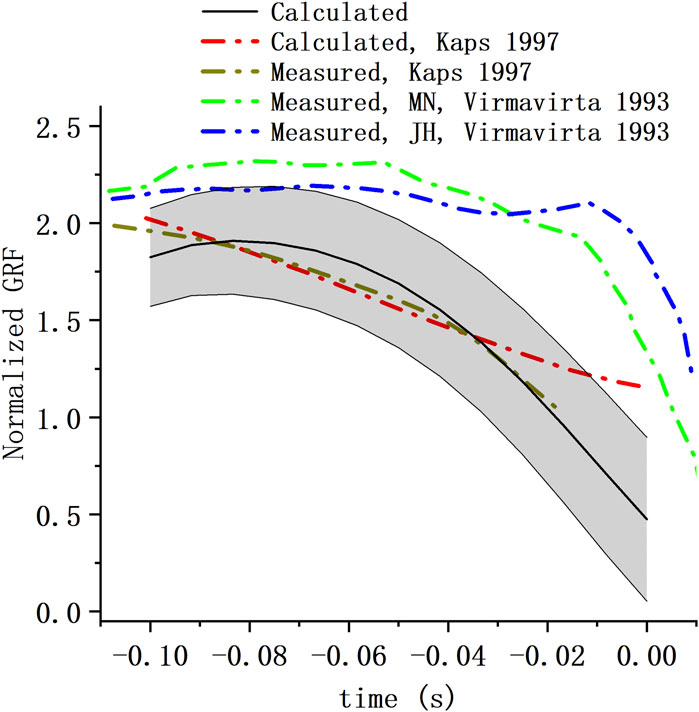
FIGURE 7. Take-off GRF of hill jump. Take-off GRF perpendicular to the table from our calculation (mean ± S.D.) were compared with GRF from the study of Kaps et al. (Kaps et al., 1997) and that of Virmavirta and Komi (Virmavirta and Koml, 1993b) (MN and JH represent the two athletes tested in the study).
The calculated take-off aerodynamic resultant force (mean ± S.D.) was shown in Figure 8A, where

FIGURE 8. Calculated aerodynamic force (mean ± S.D.) for the whole body (A), trunk (B), forearm (C), upper arm (D), calf and ski (E), and thigh (F).
Simulated mean muscle activation was reported and compared with EMG (Figure 9) from study of Virmavirta et al. (Virmavirta et al., 2001) (EMG of jumper VML and ML on hill K-90) and that of Virmavirta and Komi (Virmavirta and Komi, 2001) (mean EMG of ten jumpers on hill K-100). The simulated activation of the tibialis anterior showed a similar trend to both the EMG data of the jumper VML and the mean EMG data of ten athletes (Figure 9A). Similarly, the simulated activation of the gluteus maximus was similar to the EMG data of jumper ML (Figure 9B), and the activation of the biceps femoris long head was similar to the mean EMG of ten athletes (Figure 9E). As for other muscles, the simulated activation was less consistent with EMG.
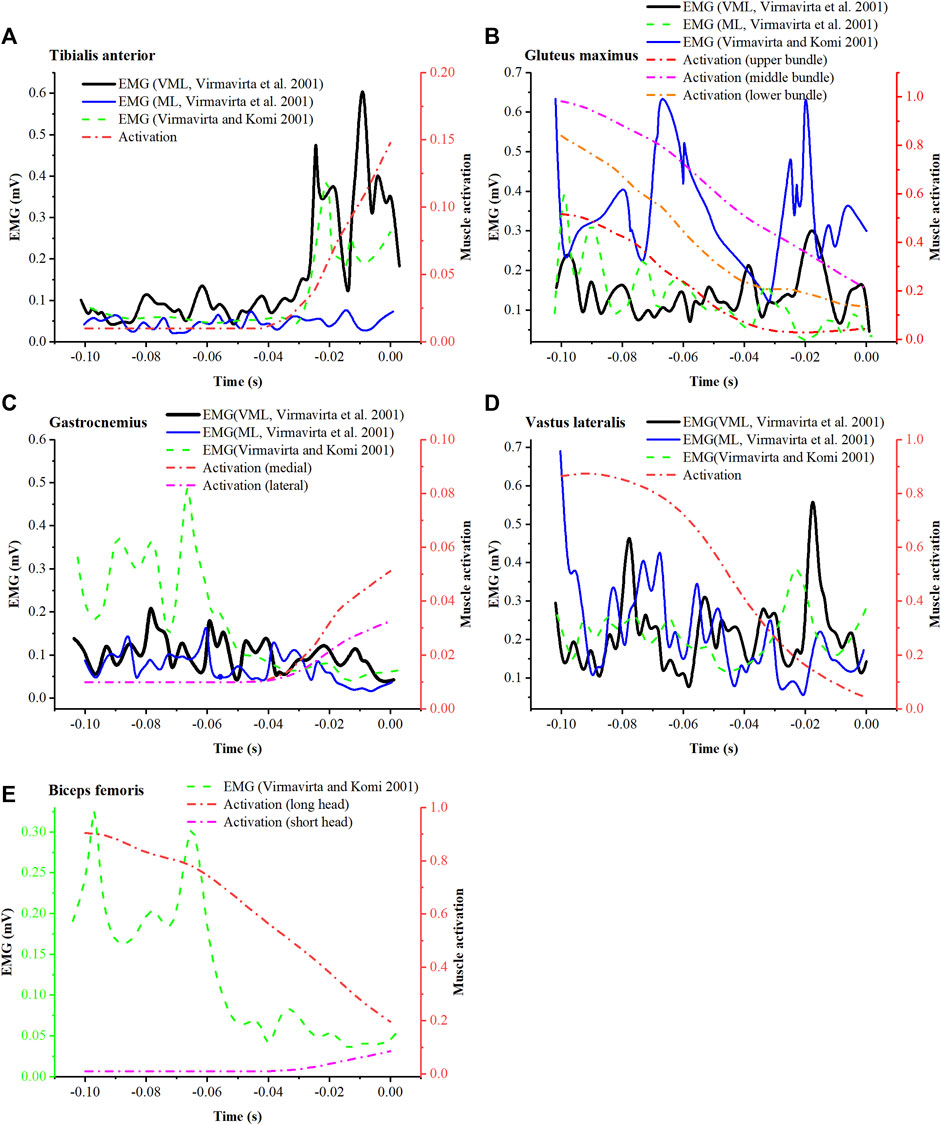
FIGURE 9. Comparison between simulated muscle activation (mean) and EMG from the research of Virmavirta et al. (2001) (VML and ML represent 2 jumpers in the study) and the research of Virmavirta and Komi (2001) for tibialis anterior (A), gluteus maximus (B), gastrocnemius (C), vastus lateralis (D), and biceps femoris (E).
Simulated activation of selected lower limb muscles was shown in Figure 10. Muscles with the function of lower limb extension were selected and grouped as ankle plantar flexors, knee extensors, and hip extensors to plot. Activation level of the ankle plantar flexors was relatively low (Figure 10A). The soleus was activated until the end of the take-off, where the gastrocnemius began to activate slightly. The activation level of quadriceps decreased with take-off progress (Figure 10B). Similarly, the activation level of the hip extensors also decreased with take-off progress, among which lower bundles of gluteus maximus and biceps femoris long head showed higher activation level than the others (Figure 10C).
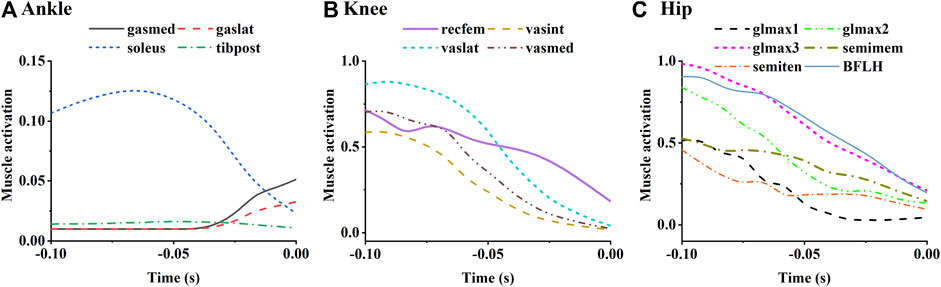
FIGURE 10. Simulated mean muscle activation of the ankle (A), knee (B) and hip (C) extensors. Ankle plantar flexors include medial gastrocnemius (gasmed), lateral gastrocnemius (gaslat), soleus, and tibialis posterior (tibpost). Knee extensor muscles include rectus femoris (recfem), vastus lateralis (vaslat), vastus medialis (vasmed), and vastus intermedius (vasint). Hip extensors include gluteus maximus, semimemem (semiten), and biceps femoris long head (BFLH). Gluteus maximus is constructed in the musculoskeletal model as upper (glmax1), middle (glmax2), and lower (glmax3) bundles.
The torque contributions of the lower extremity muscles to the ankle, knee, and hip joints are shown in Figure 11. The relative magnitudes of the extension torques produced by the ankle plantar flexors and knee extensors on their corresponding joints (Figures 11A,B) were approximately consistent with the relative magnitudes of their activation levels. As for the hip joint (Figure 11C), the extension torque produced by the long head of the biceps femoris, gluteus maximus, and semimembranosus were similar, although the activation level of the biceps femoris was higher than the others. In addition, the biceps femoris long head and semimembranosus were found to generate large flexion torques on the knee, while the rectus femoris produces large flexion torque on the hip.
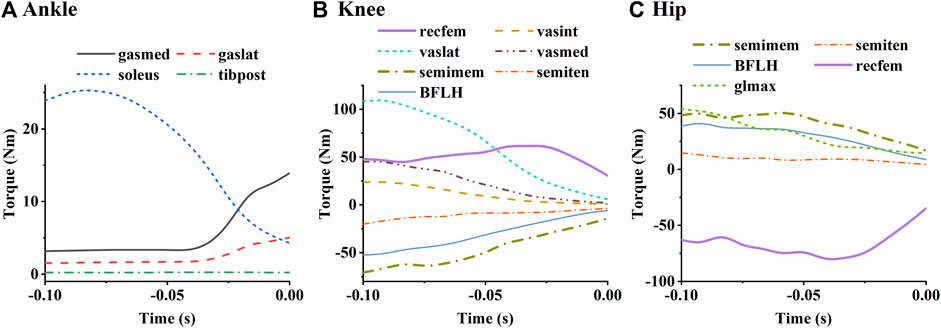
FIGURE 11. Simulated mean torques of each muscle to the ankle (A), knee (B), and hip (C). The labels in the figure are the same as those in Figure 8.
In this study, we applied musculoskeletal simulation to ski jumping take-off. With newly developed methods, GRFs and aerodynamic forces were calculated and used in the simulation. The GRF estimation method was verified through in-lab trial and showed results close to the measurements. Calculated aerodynamic forces were also reported. Simulated GRFs and muscle activation were compared with the results from previous studies to demonstrate the validity of this simulation. The simulation results showed high activation levels and large extension torque contributions for the soleus, vastus lateralis, gluteus maximus, semimembranosus, and biceps femoris long head.
The deviation between the estimated and measured GRFs in the medial-lateral direction during the simulated jump was large (Figure 6C), probably because the GRFs in this direction were relatively small and were covered by errors. Previous studies of Data-driven GRF estimation to the take-off (Kaps et al., 1997; Logar and Munih, 2015; Fritz et al., 2019; Nam et al., 2023) share the same theoretical basis as ours, that is, the inverse dynamics analysis for multibody models. The computational accuracy of this type of method depends on the quality of the raw kinematics data and how well the model is able to track the kinematics. Compared with two-dimensional models in previous studies, the three-dimensional model we used is able to capture the potential asymmetry of body movements. By taking coupled joint motion of shoulders, neck and spine into account, the model we used has a better ability to track the upper body motion than simplified head-torso models previously reported. Additionally, the GRF estimation pipeline was merged with inverse dynamics analysis of Opensim, making the estimated GRF can be conveniently used in subsequent musculoskeletal simulations.
Rigorous musculoskeletal simulation validation requires agreement between simulated muscle activation and measured EMG of the same movements. However, due to the limitations of the ski jump field environment, it was challenging to set up laboratory-grade equipment on-site. Additionally, considering the safety concerns in ski jumping, athletes were not permitted to wear any measurement devices. We were unable to perform synchronous motion capture and EMG testing. Therefore, simulated muscle activation can only be assessed by comparison with measured EMG from previous studies. Overall low agreement between simulated muscle activation and measured EMG was observed (Figure 9). These differences could be caused by trial condition differences, individual motion differences, and simulation errors. Differences in hill size may not affect the comparison significantly, as the data being compared are close in hill size (K-86, K-90, and K-100). The inconsistency between activation and EMG could be primarily caused by individual differences, since Virmavirta et al. (Virmavirta et al., 2001) reported significant inter-individual differences in muscle activation patterns under the same test conditions. In addition, the errors of kinetic and kinematic data may also lead to unrealistic muscle activity. Nonetheless, similarities between activation and EMG in the tibialis anterior, gluteus maximus, and biceps femoris long head (Figures 9A,B,E) demonstrate the ability of musculoskeletal simulations to characterize the activity of some muscles.
Muscle activation levels are influenced by muscle function, muscle strength, as well as by force-velocity and force-length effects determined from body kinematics. As the muscles with high strength are more likely to be recruited, soleus among ankle plantar flexors, vastus lateralis among knee extensors, as well as biceps femoris long head, gluteus maximus, and semimembranosus among hip extensors showed high levels of activation (Figure 10). Increasing the strength of these muscles may contribute to greater joint extension torque and higher take-off speed. Biarticular muscles (acting as extensors in one joint and flexors in the other) tend to have relatively low activation levels, such as the gastrocnemius and semitendinosus. However, the rectus femoris, the long head of the biceps femoris, and the semimembranosus, which also function in 2 joints, showed high activation levels for their torque contributions are necessary for motion execution (Figures 11B,C). Activity of these muscles can potentially limit athletes’ take-off speed.
There are some limitations in this study. Firstly, the mean RMSE between the measured marker trajectories and the simulated ones indicates that the overall kinematic error of the marker-less motion capture system is slightly larger than that of marker-based motion capture systems such as Vicon or Qualisys. It is possible to further improve kinematic accuracy through personalized anthropometric measurements, better performing joint point estimation systems, or higher resolution cameras. The effect of less precise raw kinematics on subsequent dynamics and muscle state simulations remains to be further investigated. Secondly, the musculoskeletal simulations were not rigorously validated in this study, which limited the explanatory power of our results for take-off muscle action. Simulated muscle activation pattern needs to be further verified by comparison with the synchronously measured EMG. Finally, this is a group study of multiple jumpers. It can only reflect the common characteristics of take-off. Future research may focus on individual take-off dynamics, muscle activity and their impact on ski jumping performance.
This is a preliminary study that implemented musculoskeletal simulation of professional jumpers during take-off considering aerodynamic forces for the purpose of approach validation and muscle action analysis. The simulated GRFs were similar to both in-lab GRFs from force plates and in-field GRFs from previous studies. Although there were inconsistencies between the results of some muscle activation in the simulation and EMG from previous studies in general, it is worth noting that the activation of the tibialis anterior, gluteus maximus, and long head of the biceps femoris was similar to specific EMG results. This approach may be further used to explore the musculoskeletal dynamics of other ski jumping movements.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
The studies involving humans were approved by the ethics committee of Capital University of Physical Education and Sports (approval number: 2022A41). The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study. Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.
BH and YH contributed to conception and design of the study. LJ, XC, QS, and XZ conducted the in-lab imitation jump trial. FQ, XT, YD, and FZ conducted the in-field take-off trial. NW and GZ performed the computational fluid dynamics simulation. YH performed the musculoskeletal simulation and analyzed the data. BH, QS, RS, and YH wrote the manuscript. All authors contributed to the article and approved the submitted version.
This work was supported by the National Key Research and Development Program of China under Grant [2018YFF0300800 (BH)].
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbioe.2023.1241135/full#supplementary-material
Akhundov, R., Saxby, D. J., Diamond, L. E., Snodgrass, S., Clausen, P., Drew, M., et al. (2022). Game-play affects hamstring but not adductor muscle fibre mechanics in elite U20 basketball athletes. Sports Biomech., 1–17. doi:10.1080/14763141.2022.2133006
Arndt, A., Brüggemann, G.-P., Virmavirta, M., and Komi, P. (1995). Techniques used by olympic ski jumpers in the transition from takeoff to early flight. J. Appl. Biomechanics 11 (2), 224–237. doi:10.1123/jab.11.2.224
Barnes, J., Tuplin, S., and Walker, A. D. (2022). Flight dynamics of ski jumping: wind tunnel testing and numerical modeling to optimize flight position. Proc. Institution Mech. Eng. Part P J. Sports Eng. Technol. 0 (0), 175433712211116. doi:10.1177/17543371221111625
Blana, D., Hincapie, J. G., Chadwick, E. K., and Kirsch, R. F. (2008). A musculoskeletal model of the upper extremity for use in the development of neuroprosthetic systems. J. Biomechanics 41 (8), 1714–1721. doi:10.1016/j.jbiomech.2008.03.001
Braghin, F., Cheli, F., and Maldi Fa Ssi, S. (2016). The engineering approach to winter sports. New York: Springer.
Cazzola, D., Holsgrove, T. P., Preatoni, E., Gill, H. S., and Trewartha, G. (2017). Cervical spine injuries: A whole-body musculoskeletal model for the analysis of spinal loading. PLOS ONE 12 (1), e0169329. doi:10.1371/journal.pone.0169329
Chardonnens, J., Favre, J., Cuendet, F., Gremion, G., and Aminian, K. (2014). Measurement of the dynamics in ski jumping using a wearable inertial sensor-based system. J. Sports Sci. 32 (6), 591–600. doi:10.1080/02640414.2013.845679
Chen, X., Huang, Y., Jiang, L., Sun, Q., Tian, Y., Zhou, Z., et al. (2023). Bilateral upper extremity trunk model for cross-country sit-skiing double poling propulsion: model development and validation. Med. Biol. Eng. Comput. 61 (2), 445–455. doi:10.1007/s11517-022-02724-8
Drazan, J. F., Phillips, W. T., Seethapathi, N., Hullfish, T. J., and Baxter, J. R. (2021). Moving outside the lab: markerless motion capture accurately quantifies sagittal plane kinematics during the vertical jump. J. Biomechanics 125, 110547. doi:10.1016/j.jbiomech.2021.110547
Fritz, J., Kröll, J., and Schwameder, H. (2019). Influence of body segment parameter estimation on calculated ground reaction forces in highly dynamic movements. J. Biomechanics 84, 11–17. doi:10.1016/j.jbiomech.2018.12.008
Gasser, H.-H. (2018). Jumping hills construction norm 2018, implementing provisions for art. 411 of the icr ski jumping [online]. Oberhofen: International Ski Federation.
Glover, N. A., Kakar, R. S., and Chaudhari, A. M. W. (2021). Effects of spinal coupling and marker set on tracking of spine models during running. J. Biomechanics 116, 110217. doi:10.1016/j.jbiomech.2020.110217
Handsfield, G. G., Meyer, C. H., Hart, J. M., Abel, M. F., and Blemker, S. S. (2014). Relationships of 35 lower limb muscles to height and body mass quantified using MRI. J. Biomechanics 47 (3), 631–638. doi:10.1016/j.jbiomech.2013.12.002
Jung, A., Muller, W., and Staat, M. (2019). Optimization of the flight technique in ski jumping: the influence of wind. J. Biomechanics 88, 190–193. doi:10.1016/j.jbiomech.2019.03.023
Jung, A., Staat, M., and Muller, W. (2014). Flight style optimization in ski jumping on normal, large, and ski flying hills. J. Biomechanics 47 (3), 716–722. doi:10.1016/j.jbiomech.2013.11.021
Kaps, P., Schwameder, H., and Engstler, C. (1997). “Inverse dynamic analysis of take-off in ski-jumping,” in Skiing and science (London: E&FN Spon), 72–87.
Kuo, A. D. (1998). A least-squares estimation approach to improving the precision of inverse dynamics computations. J. Biomech. Eng. 120 (1), 148–159. doi:10.1115/1.2834295
Lai, A. K. M., Arnold, A. S., and Wakeling, J. M. (2017). Why are antagonist muscles co-activated in my simulation? A musculoskeletal model for analysing human locomotor tasks. Ann. Biomed. Eng. 45 (12), 2762–2774. doi:10.1007/s10439-017-1920-7
Langholz, J. B., Westman, G., and Karlsteen, M. (2016). Musculoskeletal modelling in sports - evaluation of different software tools with focus on swimming. Procedia Eng. 147, 281–287. doi:10.1016/j.proeng.2016.06.278
Logar, G., and Munih, M. (2015). Estimation of joint forces and moments for the in-run and take-off in ski jumping based on measurements with wearable inertial sensors. Sensors (Basel) 15 (5), 11258–11276. doi:10.3390/s150511258
Lu, T. W., and O'Connor, J. J. (1999). Bone position estimation from skin marker co-ordinates using global optimisation with joint constraints. J. Biomech. 32 (2), 129–134. doi:10.1016/s0021-9290(98)00158-4
Mahadas, S., Mahadas, K., and Hung, G. K. (2019). Biomechanics of the golf swing using OpenSim. Comput. Biol. Med. 105, 39–45. doi:10.1016/j.compbiomed.2018.12.002
Nam, Y., Do, Y., Kim, J., Lee, H., and Kim, D.-N. (2023). A hybrid framework to predict ski jumping forces by combining data-driven pose estimation and model-based force calculation. Eur. J. Sport Sci. 23 (2), 221–230. doi:10.1080/17461391.2022.2028013
Raabe, M. E., and Chaudhari, A. M. W. (2016). An investigation of jogging biomechanics using the full-body lumbar spine model: model development and validation. J. Biomechanics 49 (7), 1238–1243. doi:10.1016/j.jbiomech.2016.02.046
Sasaki, T., Tsunoda, K., and Koike, T. (2005). “Kinetic analysis of ski jumping in the period of transition area,” in Science and skiing III (Oxford: Meyer and Meyer Sport), 367–380.
Sasaki, T., Tsunoda, K., Uchida, E., Hoshino, H., and Ono, M. (1997). “Joint power production in take-off action during ski jumping,” in Science and skiing (London: E and FN Spon), 309–319.
Scott, L. D., Frank C, A., Allison S, A., Peter, L., Ayman, H., T, J. C., et al. (2007). OpenSim: open-source software to create and analyze dynamic simulations of movement. IEEE Trans. Biomed. Eng. 54 (11), 1940–1950. doi:10.1109/tbme.2007.901024
Thelen, D. G., and Anderson, F. C. (2006). Using computed muscle control to generate forward dynamic simulations of human walking from experimental data. J. Biomechanics 39 (6), 1107–1115. doi:10.1016/j.jbiomech.2005.02.010
Virmavirta, M., Kivekäs, J., and Komi, P. (2011). Ski jumping takeoff in a wind tunnel with skis. J. Appl. Biomechanics 27 (4), 375–379. doi:10.1123/jab.27.4.375
Virmavirta, M., and Komi, P. V. (2010). “Kinetics and muscular function in ski jumping,” in Neuromuscular aspects of sport performance, 91–102.
Virmavirta, M., and Komi, P. V. (2001). Plantar pressure and EMG activity of simulated and actual ski jumping take-off. Scand. J. Med. Sci. Sports 11 (5), 310–314. doi:10.1034/j.1600-0838.2001.110510.x
Virmavirta, M., and Koml, P. V. (1993a). Measurement of take-off forces in ski jumping: part II. Scand. J. Med. Sci. Sports 3 (4), 237–243. doi:10.1111/j.1600-0838.1993.tb00388.x
Virmavirta, M., and Koml, P. V. (1993b). Measurement of take-off forces in ski jumping: part1. Scand. J. Med. Sci. Sports 3 (4), 229–236. doi:10.1111/j.1600-0838.1993.tb00387.x
Virmavirta, M., Perttunen, J., and Komi, P. V. (2001). EMG activities and plantar pressures during ski jumping take-off on three different sized hills. J. Electromyogr. Kinesiol. 11 (11), 141–147. doi:10.1016/s1050-6411(00)00047-x
Yamamoto, K., Nishino, T., Bale, R., Shimada, T., Miyamoto, N., and Tsubokura, M. (2022). Numerical study of transient aerodynamic forces acting on a ski jumper considering dynamic posture change from takeoff to landing. Sports Biomech., 1–15. doi:10.1080/14763141.2022.2154256
Keywords: ski jumping, take-off, musculoskeletal simulation, aerodynamics, muscle activation, joint torque, ground reaction force
Citation: Huang Y, Jiang L, Chen X, Sun Q, Zhang X, Tan X, Du Y, Zhang F, Wang N, Su R, Qu F, Zhang G and Huo B (2023) Musculoskeletal simulation of professional ski jumpers during take-off considering aerodynamic forces. Front. Bioeng. Biotechnol. 11:1241135. doi: 10.3389/fbioe.2023.1241135
Received: 16 June 2023; Accepted: 21 August 2023;
Published: 31 August 2023.
Edited by:
Peter A. Federolf, University of Innsbruck, AustriaReviewed by:
Emanuel Andrada, Friedrich Schiller University Jena, GermanyCopyright © 2023 Huang, Jiang, Chen, Sun, Zhang, Tan, Du, Zhang, Wang, Su, Qu, Zhang and Huo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bo Huo, aHVvYm9AY3VwZXMuZWR1LmNu; Qing Sun, NzUyMDIxMDAwM0BiaXQuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.