- Key Laboratory of Exercise and Health Sciences of Ministry of Education, Shanghai University of Sport, Shanghai, China
Introduction: Patellofemoral joint stress (PFJS) is an important parameter for understanding the mechanism of patellofemoral joint pain, preventing patellofemoral joint injury, and evaluating the therapeutic efficacy of PFP rehabilitation programs. The purpose of this systematic review was to identify and categorize the non-invasive technique to evaluate the PFJS.
Methods: Literature searches were conducted from January 2000 to October 2022 in electronic databases, namely, PubMed, Web of Science, and EBSCO (Medline, SPORTDiscus). This review includes studies that evaluated the patellofemoral joint reaction force (PJRF) or PFJS, with participants including both healthy individuals and those with patellofemoral joint pain, as well as cadavers with no organic changes. The study design includes cross-sectional studies, case-control studies, and randomized controlled trials. The JBI quality appraisal criteria tool was used to assess the risk of bias in the included studies.
Results: In total, 5016 articles were identified in the database research and the citation network, and 69 studies were included in the review.
Discussion: Researchers are still working to improve the accuracy of evaluation for PFJS by using a personalized model and optimizing quadriceps muscle strength calculations. In theory, the evaluation method of combining advanced computational and biplane fluoroscopy techniques has high accuracy in evaluating PFJS. The method should be further developed to establish the “gold standard” for PFJS evaluation. In practical applications, selecting appropriate methods and approaches based on theoretical considerations and ecological validity is essential.
1 Introduction
Patellofemoral pain (PFP), a frequent complaint in orthopedic practice, is associated with 25%–40% of knee injuries (Liao et al., 2015). This pain is aggravated by various activities that load the joint (e.g., squatting, running, ascending/descending stairs), greatly limiting the daily activities of individuals with PFP (Fick et al., 2022). There is no consensus on the exact mechanism of PFP development (Vannatta and Kernozek, 2015). However, a prevailing theory holds that PFP develops in response to increased patellofemoral joint stress (PFJS) (Salsich and Perman, 2007). Chronic overuse of the patellofemoral joint has been related to increased intraosseous pressures and pain, microfractures, increased bone metabolism, and increased bone water content, all of which have pathologically detrimental effects on the subchondral bone (Ho et al., 2014). Studies have reported that individuals with PFP exhibit elevated PFJS during walking and running when compared with those in pain-free individuals (Farrokhi et al., 2011b; Liao et al., 2015). Based on the associations, PFJS seems to be an important factor in assessing the load on the patellofemoral joint. It can be helpful in preventing patellofemoral joint injuries, evaluating the effectiveness of PFP rehabilitation programs.
The analytical model is currently the most widely used method for evaluating the PFJS, which is based on the formula obtained from previous cadaver experiments. The classic analytical model has several significant limitations, including the failure to account for the synergistic contraction of knee joint muscles and the consideration of only sagittal plane factors in relation to PFJS (Bonacci et al., 2014; Atkins et al., 2019). To achieve greater accuracy in assessing PFJS, various methods have been developed, including musculoskeletal models, discrete element analysis (DEA), and finite element analysis (FEA). Nunes et al. systematically reviewed the literature which was utilized analytical models to evaluate PFJS and described the possible best paradigm to evaluate PFJS (Nunes et al., 2018). An important limitation of the review is its relatively narrow definition of the methods of PFJS. Nunes et al. do not take into consideration the methods of musculoskeletal modeling, DEA, and FEA. It is necessary to carry out a new literature review due to the progress of PFJS evaluation technology and the increase in the number of studies since the publication of the previous review.
The primary goal of the present systematic review was to identify and categorize the methods developed and used to evaluate PFJS comprehensively by taking into consideration all important aspects of PFJS (e.g., synergistic contraction, variables of the coronal plane, and 3D geometry of bones). This paper will help researchers fully understand the assessment schemes for patellofemoral joint stress and different optimization strategies, while also proposing future research directions.
2 Methods
While conducting this review, we followed the recommendations of the PRISMA statement (Supplementary Table S6) (Liberati et al., 2009).
2.1 Search strategy
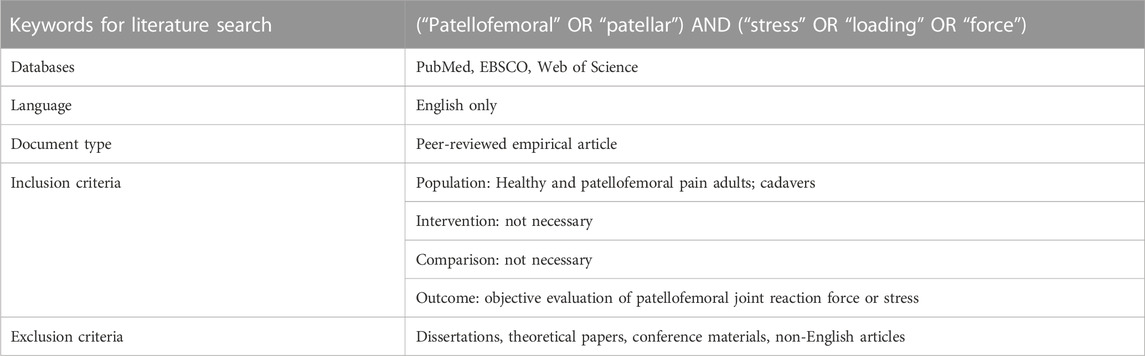
Literature searches were conducted from January 2000 to October 2022 in electronic databases, namely, PubMed, Web of Science, and EBSCO (Medline, SPORTDiscus). The following search terms were used: (“patellofemoral” OR “patellar”) AND (“stress” OR “loading” OR “force”). In addition, the reference lists of the included articles were investigated to detect additional relevant articles that could not be found via the initial electronic search strategy.
2.2 Inclusion and exclusion criteria
Those studies evaluating the patellofemoral joint reaction force (PJRF) or PFJS were included, whose participants were healthy individuals, individuals with patellofemoral joint pain, and cadavers (no organic change) (Table 1). Studies published in any language other than English, review papers, book chapters, conference abstracts, commentaries, and study protocols were excluded.
Two researchers evaluated the search results independently, resolving any differences through consultation. The first step involved eliminating duplicate articles, which was carried out using EndNote and focused on the titles and abstracts. Next, the researchers conducted an initial screening of the titles and removed irrelevant articles. They then read the abstracts and full texts of relevant articles to screen for inclusion based on predefined criteria. Finally, the researchers confirmed the articles that met the criteria and made the final decision on inclusion.
2.3 Evaluation of the methodological quality
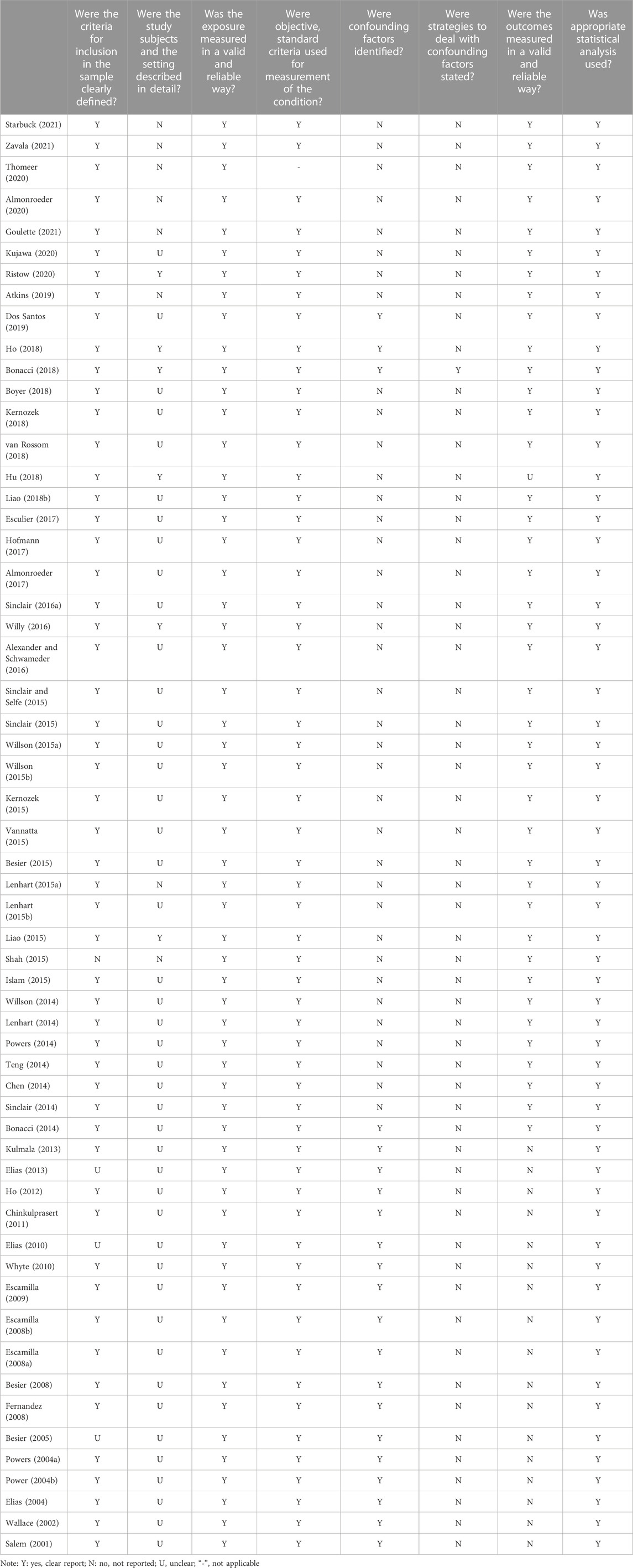
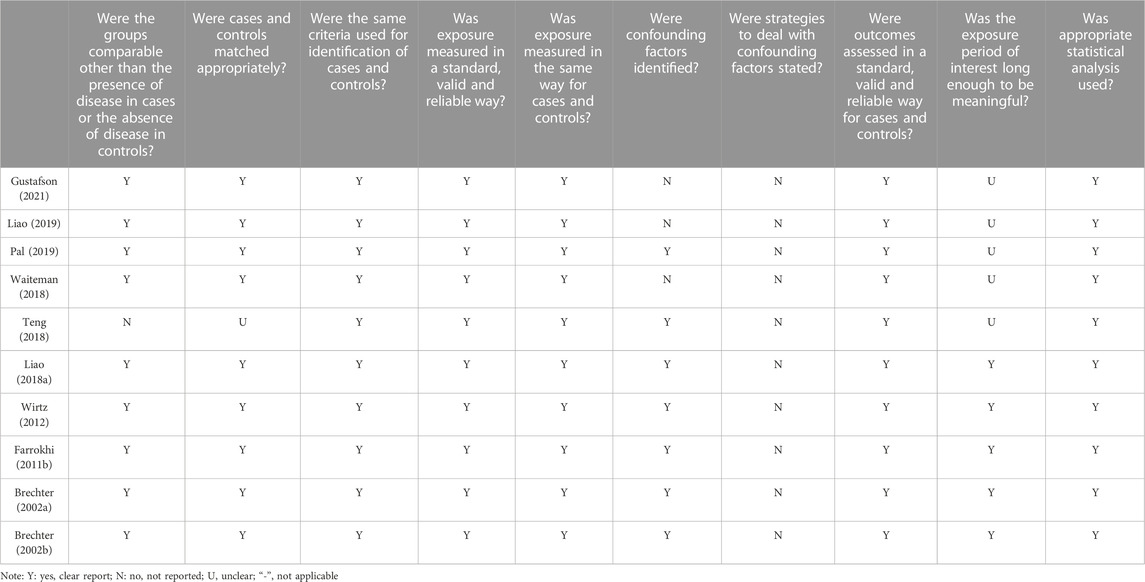
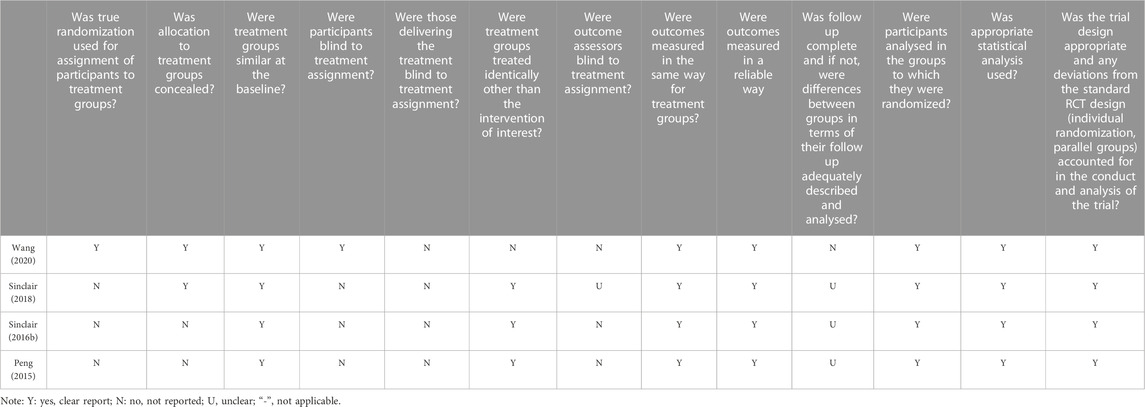
The included studies were subjected to quality assessment based on the JBI quality appraisal criteria (Barker et al., 2023). The assessment criteria comprised 8–13 items, including the source and characteristics of the study population, control of confounding factors, measurement of outcome indicators, and other relevant aspects. Evaluators provided judgments of “yes”, “no”, “unclear”, or “not applicable” for each item. To evaluate the quality of the included studies, two independent reviewers conducted assessments, and a third reviewer was consulted when there was disagreement.
2.4 Data extraction
The basic information (i.e., population, gender, age, height, weight) of participants, PJRF and PFJS calculation methods (quadriceps muscle strength, quadriceps muscle effective lever arm, musculoskeletal model, cartilage mechanics, etc.) and primary outcomes (peak knee flexion moment, peak PJRF, peak PFJS, etc.) were extracted. For studies of setting up training or additional equipment interventions, only the PJRF or PFJS before training or without equipment factors were extracted. Where necessary, WebPlotDigitizer v4.5 was used to extract means and standard deviation from figures in the manuscripts (Whitehead et al., 2018).
3 Results
3.1 Included studies
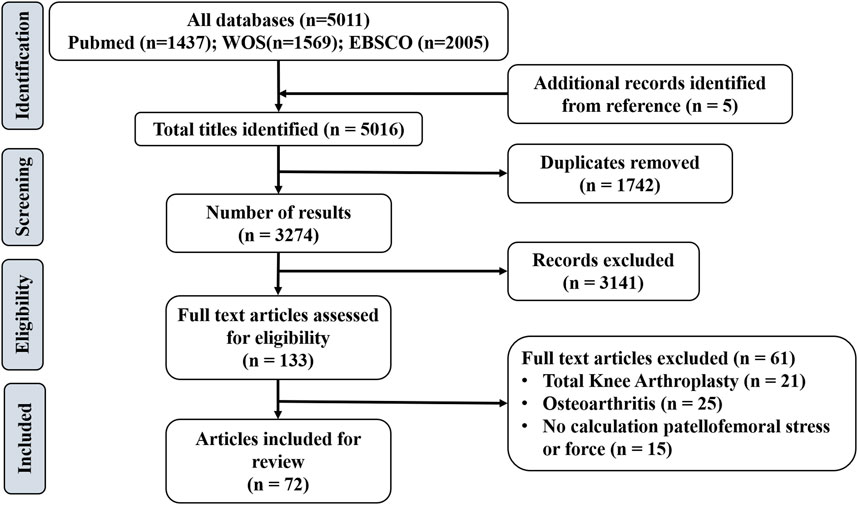
A total of 5,016 articles were identified overall based on database search and citation network analysis. After removing the duplicates, 3,274 remained. After reading the titles/abstracts, a further 3,141 articles were excluded because they did not meet the inclusion criteria. Based on the full texts of the remaining 133 articles, 61 studies were excluded. In total, 72 studies were included in the review (Figure 1). Among them, 48 studies evaluated PFJS by analytical model; eight studies evaluated PJRF or PFJS by establishing a musculoskeletal model; four studies evaluated PJRF or PFJS by DEA; 12 studies evaluated PJRF or PFJS by FEA.
3.2 Study characteristics
Regarding the methodological quality of the included studies, the majority of studies scored well in terms of the source and characteristics of the study population, measurement of outcome indicators, and other relevant aspects. However, there was a significant deficiency in considering and controlling for confounding factors (Tables 2–4). Among the 72 included studies, 1,432 participants (453 males and 979 females) and 27 cadaveric knees were evaluated regarding PFJS. Two studies assessed PFJF or PFJS in older adults (Hu et al., 2018; Gustafson et al., 2021) (67.7–70 years) and 66 studies assessed PFJF or PFJS calculations in younger adults (18.3–37.1 years). Among the 69 included studies, the health condition of the participants included two categories: 1) individuals with PFP (n = 204); 2) individuals without knee injury (n = 1,228). The activity condition of the population includes: 1) active population (n = 113); 2) high-level athletes (n = 88); 3) recreational runners (n = 498); 4) no mention of physical activity (n = 703) (Supplementary Table S1).
3.3 Analytical model
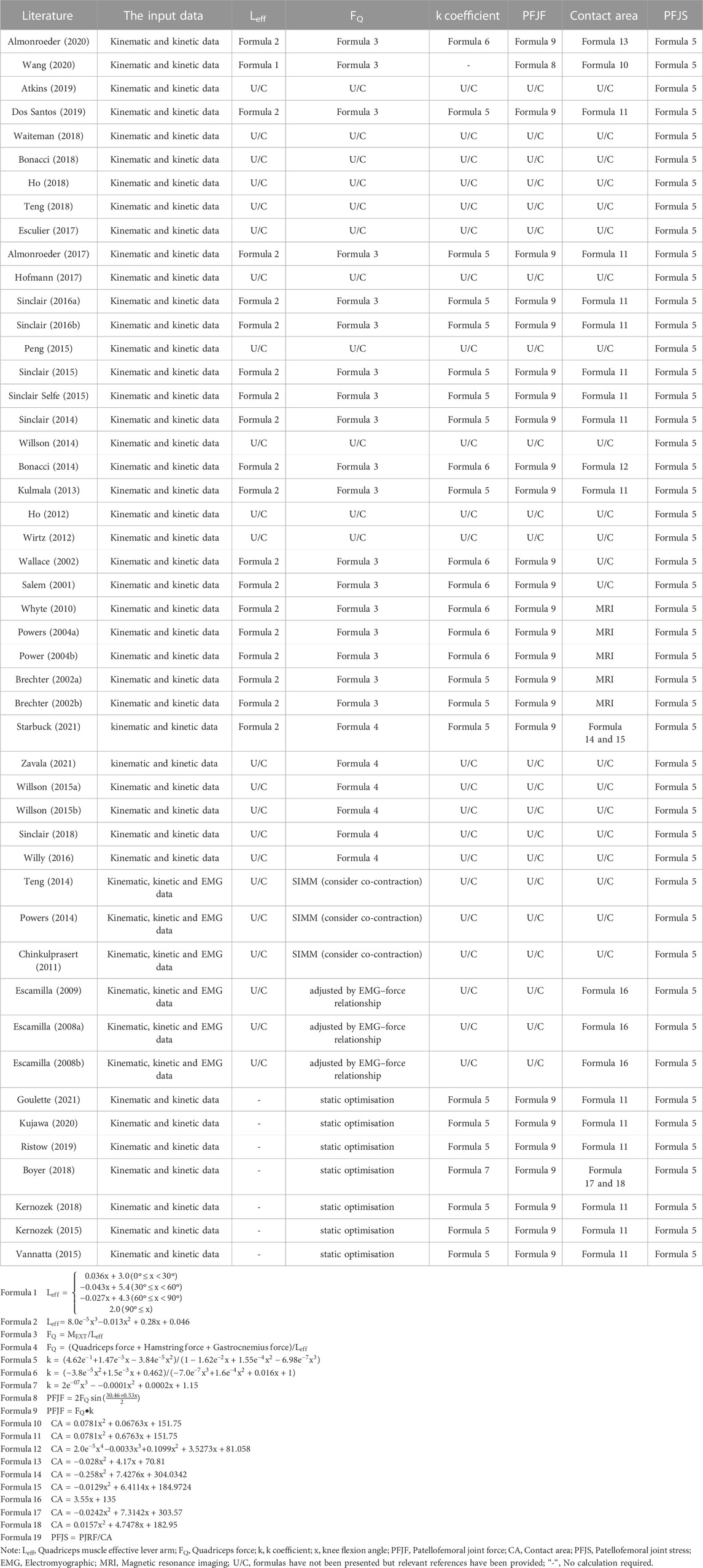
The analytical model is based on functional relationships obtained from previous cadaver studies to evaluate PFJS. The computational process of the mathematical model is straightforward, and the input variables (knee flexion angle and knee extension moment) are easily obtainable. Twenty-four studies evaluated the PFJS of running, walking, squatting, lunging, ascending, descending, landing, and ballet dance activities by the analytical model (Table 5). The analytical model process includes:
1) The effective lever arm (Leff) of the quadriceps muscle is calculated using nonlinear formulas (formulas 1, 2) based on the degree of knee flexion angle (x).
2) quadriceps muscle force (FQ) is calculated by dividing the knee extension moment (MEXT) by the effective moment arm (formulas 3, 4).
3) the coefficient k of defining the relation between quadriceps force and PJRF is calculated based on the formulas of knee flexion angle (formulas 5formulas –formulas 7).
4) the PJRF is obtained by multiplying the quadriceps muscle force by the coefficient k or by a function of the knee joint flexion angle (formulas 8, 9).
5) the patellofemoral joint contact area (CA) is calculated based on the formula of knee flexion angle (e10formulas –formulas 18).
6) the PFJS is obtained by dividing the PJRF by the patellofemoral joint contact area (formula 19).
Fourteen out of 24 studies evaluated the PFJS of recreational runners during running at speeds ranging from 2.3 to 4 m/s, and the result of PFJS was 6.00–20.6 MPa (Wirtz et al., 2012; Kulmala et al., 2013; Bonacci et al., 2014; Sinclair, 2014; Willson et al., 2014; Sinclair and Selfe, 2015; Sinclair J. et al., 2016; Sinclair J. K. et al., 2016; Almonroeder and Benson, 2017; Esculier et al., 2017; Bonacci et al., 2018; Ho et al., 2018; Dos Santos et al., 2019; Wang et al., 2020). One out of 24 studies evaluated the PFJS of healthy females during ascend stair, and the result of PFJS was 6.61–9.99 MPa (Atkins et al., 2019). One out of 24 studies evaluated the PFJS of females with PFP and pain free during descent stair, and the result of PFJS was 9.2–12.5 MPa (Waiteman et al., 2018). Three out of 24 studies evaluated the PFJS of healthy participants at squat, and the result of PFJS was 8.8–12.34 MPa (Salem and Powers, 2001; Wallace et al., 2002; Almonroeder and Benson, 2017). Two out of 24 studies evaluated the PFJS of healthy individuals at walking, and the result of PFJS was 2.6–3.5 MPa (Ho et al., 2012; Teng et al., 2018). Three out of 24 studies evaluated the PFJS at lunges (Hofmann et al., 2017), ballet (Peng et al., 2015) and landings (Sinclair et al., 2015), and the result of PFJS was 7.17–26.71 MPa (Supplementary Table S2).
Five studies evaluated PFJS based on the analytical model but adjusted for patellofemoral contact area using magnetic resonance imaging (MRI) (Table 5). Two of these studies evaluated the PFJS during walking, and the result of PFJS was 2.33–6.61 MPa (Brechter and Powers, 2002b; Powers et al., 2004a). Two of these studies evaluated the PFJS at ascending, and the result of PFJS was 6.46–6.97 MPa (Brechter and Powers, 2002a; Powers et al., 2004b). One of these studies evaluated the PFJS at squat, and the result of PFJS was 23.62 ± 6.89 MPa (Whyte et al., 2010) (Supplementary Table S2).
Twelve studies calculated a quadriceps muscle strength by modified methods, which accounted for co-contraction of the hamstrings and gastrocnemius muscles (Table 5). Six of these studies evaluated the PFJS during running, and the result of PFJS was 5.1–21.5 MPa (Teng and Powers, 2014; Willson et al., 2015a; Willson et al., 2015b; Willy et al., 2016; Sinclair et al., 2018; Starbuck et al., 2021). Three of these studies evaluated the PFJS at squat, and the result of PFJS was 7.09–12.3 MPa (Escamilla et al., 2009; Powers et al., 2014; Zavala et al., 2021). Two of these studies evaluated the PFJS in the lunge, and the result of PFJS was 5.09–5.45 MPa (Escamilla et al., 2008a; Escamilla et al., 2008b). One of these studies evaluated the PFJS at ascending and the result of PFJS was 9.49 MPa (Chinkulprasert et al., 2011) (Supplementary Table S2).
Six studies estimated the muscle strength forces from joint moments by minimizing a static cost function (Kernozek et al., 2015; Vannatta and Kernozek, 2015; Boyer and Derrick, 2018; Kernozek et al., 2018; Kujawa et al., 2020; Goulette et al., 2021) (Table 5). The total quadriceps force was obtained by summing the muscle forces of the rectus femoris, vastus medialis, vastus lateralis, and vastus intermedius. Studies evaluated the PFJS at running (Vannatta and Kernozek, 2015; Boyer and Derrick, 2018; (Kujawa et al., 2020), squatting (Kernozek et al., 2015; Kernozek et al., 2018), lunge (Goulette et al., 2021) activities, respectively, and the result of PFJS was 5.0–20.1 MPa (Supplementary Table S2).
3.4 Musculoskeletal model
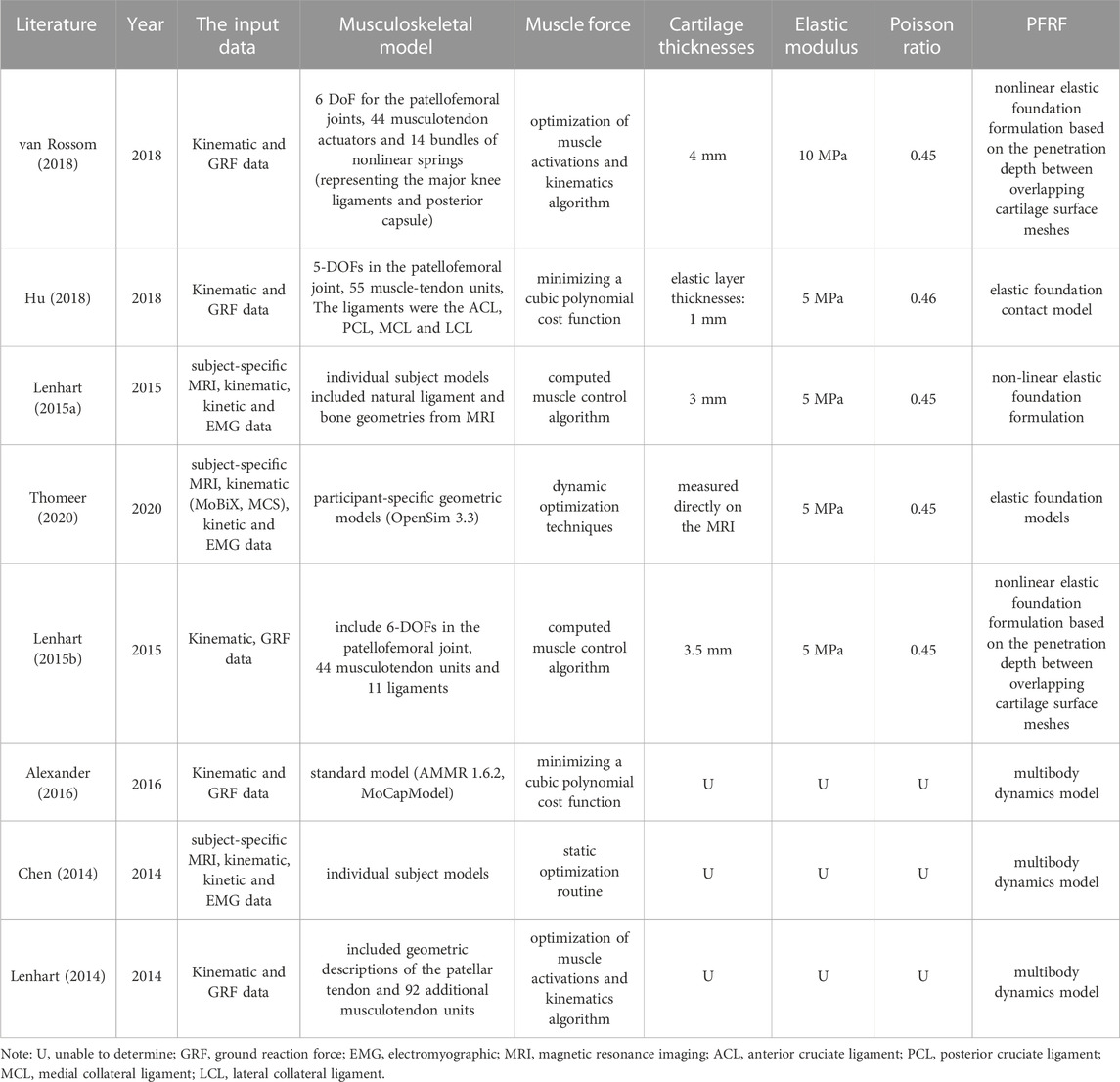
A musculoskeletal model can provide an accurate estimate and more detailed and valid information on lower limb muscle and joint loads (Steele et al., 2012; Haight et al., 2014). The computed forces are useful for understanding the relative demands on muscles and joints, as well as the potential risk and pathologies for injuries (Erdemir et al., 2007). Eight studies built the musculoskeletal models of the knee to evaluate PJRF. Five of these studies performed PFJF calculations for running (Lenhart et al., 2015b), walking (Lenhart et al., 2015a; Hu et al., 2018; van Rossom et al., 2018; Thomeer et al., 2020), squatting (van Rossom et al., 2018), and lunging (van Rossom et al., 2018) based on elastic foundation models, and the result of PJRF was 0.57–5.59 BW (Supplementary Table S3). The elastic modulus of the cartilage used was 5 MPa (Lenhart et al., 2015a; Lenhart et al., 2015b; Hu et al., 2018; Thomeer et al., 2020), 10 MPa (van Rossom et al., 2018), and the Poisson’s ratio was 0.45 (Lenhart et al., 2015a; Lenhart et al., 2015b; van Rossom et al., 2018; Thomeer et al., 2020), 0.46 (Hu et al., 2018). Hu et al. (2018) set the cartilage thickness to 1 mm, Lenhart et al. (2015a) set it to 3 mm, 3.5 mm (Lenhart et al., 2015b), and van Rossom et al. set it to 4 mm (van Rossom et al., 2018). Thomeer et al. (2020) calculated cartilage thickness directly from the MR images (the shortest distance between the bone-cartilage interface in various regions of the knee joint). Three of these studies performed PFJF calculations for running (Chen and Powers, 2014; Lenhart et al., 2014), walking (Chen and Powers, 2014; Alexander and Schwameder, 2016), stair climbing (Chen and Powers, 2014), and descending (Chen and Powers, 2014) based on multibody dynamics and the result of PJRF is 0.86–6.72 BW. Among them, Seven studies used the concurrent optimization of muscle activations and kinematics algorithm (Chen and Powers, 2014; Lenhart et al., 2014 (Lenhart et al., 2015b; Alexander and Schwameder, 2016; van Rossom et al., 2018); or used a computed muscle control algorithm to determine the muscle excitations needed to produce the computed kinematic trajectories (Lenhart et al., 2015a; Thomeer et al., 2020). One of eight studies did not describe the method of calculating muscle force (Hu et al., 2018) (Table 6).
3.5 Discrete element analysis
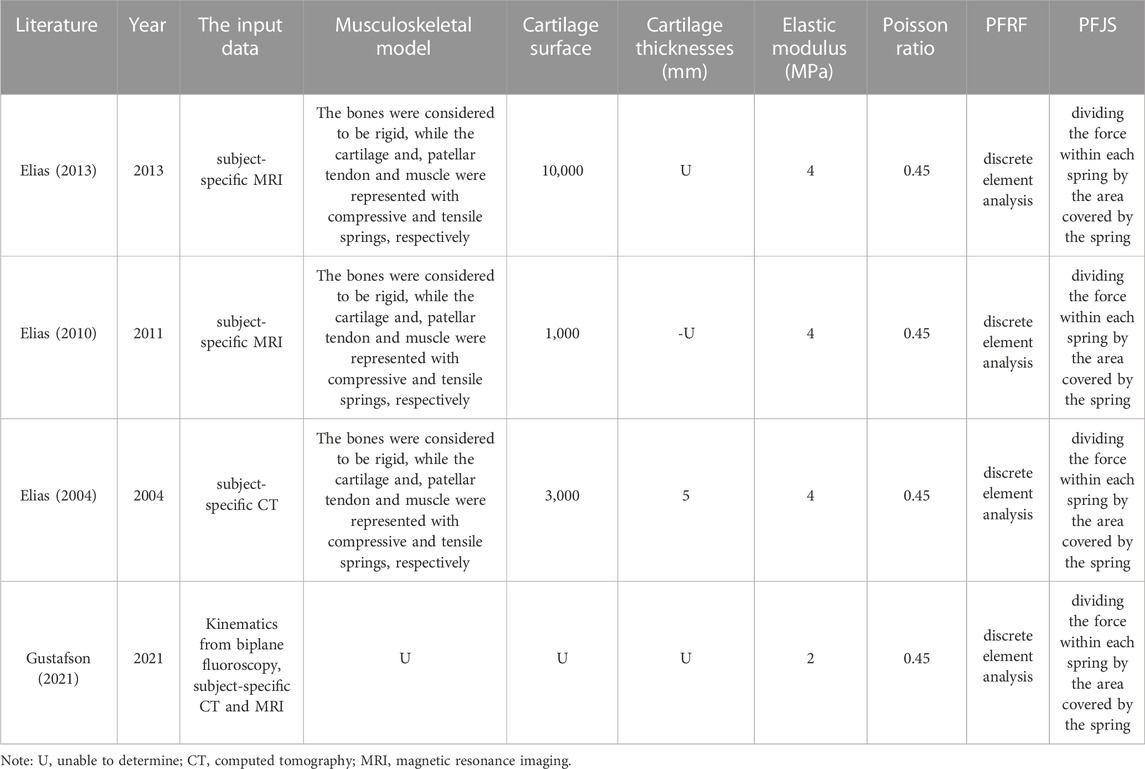
DEA is a technique that is often used to evaluate joint stress distribution and determine influencing factors. DEA treat the patellofemoral cartilage as a layer of compressive springs separating rigid bones, with the soft tissue restraints treated as tensile springs. Four studies evaluated the PFJS of knee flexion (Elias et al., 2010; Elias and Saranathan, 2013), squat (Elias et al., 2004; Besier et al., 2005), and walk (Gustafson et al., 2021) activities by DEA (Table 7). For each DEA model, cartilage was assigned isotropic linear-elastic material properties, which were assigned an elastic modulus of 2 or 4 MPa, and a Poisson’s ratio of 0.45. The output variables of the DEA include lateral and medial facets PFJS. The result of lateral facet PFJS was 2.55–6.81 MPa. The result of medial facet PFJS was 2.41–4.68 MPa (Supplementary Table S4).
3.6 Finite element analysis
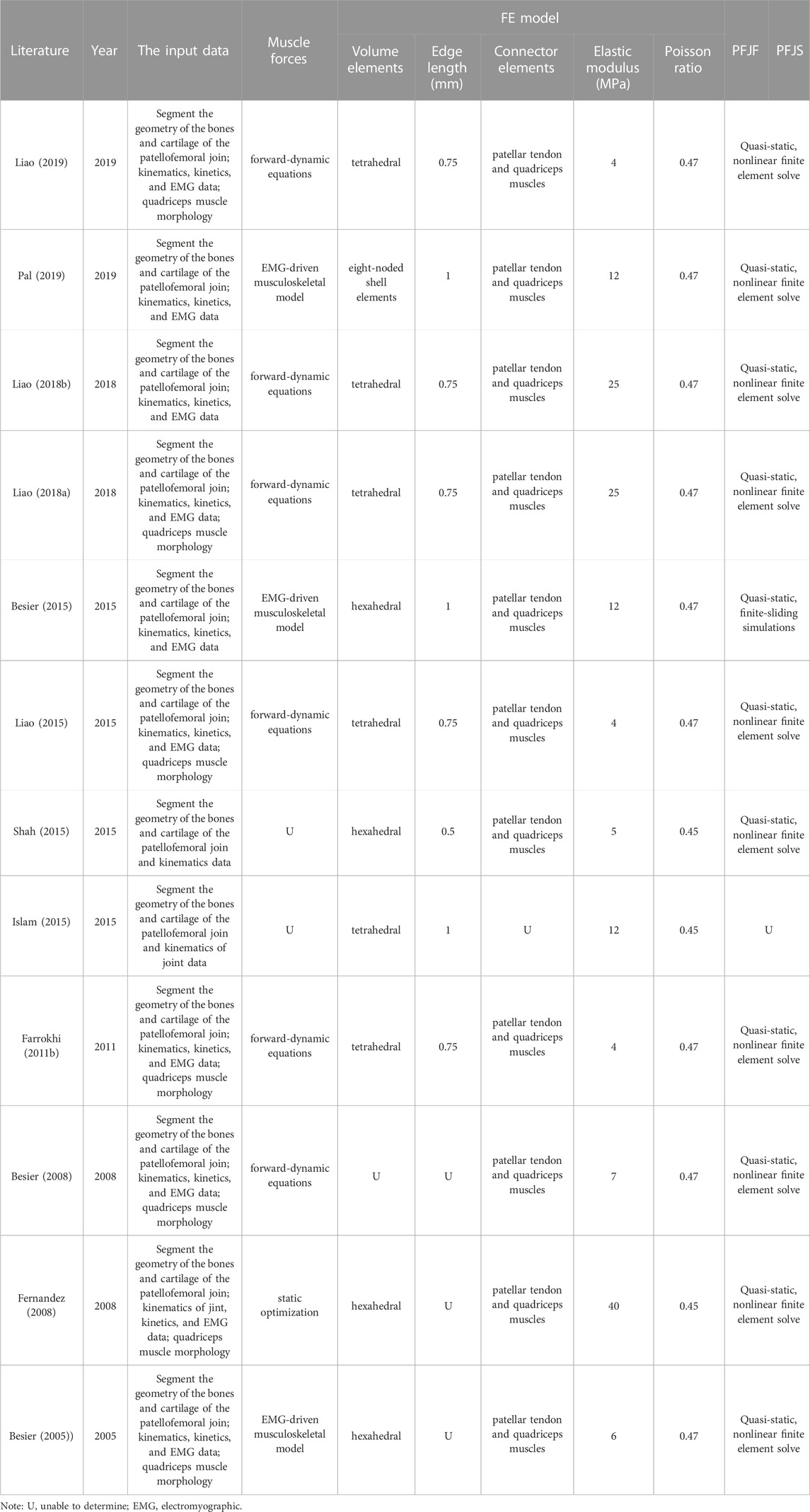
FEA are refined computational models that allow the integration of subject-specific musculoskeletal parameters and in vivo experimental data, and are of great value for understanding stress distributions in complex biological structures (Fernandez et al., 2008; Farrokhi et al., 2011b). Eleven studies evaluated the PFJS of ascending stair (Fernandez et al., 2008; (Besier et al., 2015; Pal et al., 2019), running (Liao et al., 2018a; Liao and Powers, 2019), and squat (Besier et al., 2008; Fernandez et al., 2008; (Farrokhi et al., 2011b; (Islam et al., 2015 (Liao et al., 2015; Shah et al., 2015); by FEA (Table 8). The cartilage of patella was modeled using homogeneous isotropic tetrahedral or hexahedral continuum elements with an elastic modulus of 4, 5, 7, 12, 25, and 40 MPa and a Poisson ratio of 0.45, 0.46, and 0.47. Concerning the muscle strength calculations, nine studies calculated quadriceps muscle strength by inputting kinematics, kinetics, and EMG data (Liao and Powers, 2019). A study performed FEA simulations by using specific quadriceps muscle strength values (Shah et al., 2015). Another study used a three-dimensional registration technique and linear mapping to investigate the PFJS: the depth of virtual penetration of the patellar cartilage surface into the femoral cartilage surface, which does not require the calculation of muscle strength (Islam et al., 2015) (Supplementary Table S5).
4 Discussion
Studies of the patellofemoral joint mechanism have particularly concerned the forces and stresses in the joint (van Eijden et al., 1986). Non-invasive evaluation of PFJS will provide important information on the factors contributing to joint load in a special population and may provide data that can be used to guide treatment (Brechter and Powers, 2002b). Thus, it is necessary to evaluate the PFJF or PFJS non-invasively. This review aims to identify and categorize methods used to evaluate PFJS non-invasively, and we found four methodologies: analytical model musculoskeletal model, DEA, and FEA.
At present, there is still no “gold standard” for PFJS assessment because it is impossible to measure the PFJS directly in vivo. Accurate assessment of PFJS will aid engineers in the design of better tissue-engineered constructs for cartilage replacement and assist physiotherapists to evaluate the PFP patient’s recovery and design a more effective intervention. Researchers have adopted some techniques to optimize the PFJS assessment program to improve the accuracy of PFJS or expand its scope of application. It is mainly aimed at patella kinematics and quadriceps muscle strength optimization.
The geometry or alignment of the patella affects kinematics, contact mechanics, and strain in the patellar bone, potentially leading to PFP (Brechter and Powers, 2002b; Fitzpatrick and Rullkoetter, 2012). The differences in subject-specific anatomy among the population will cause errors in the process of calculating the PFJS. Researchers use personalized programs to eliminate errors. In the analytical model evaluation scheme, the patellofemoral contact area was estimated using a function of knee flexion angles from 0° to 90°, as previously described in past cadaver studies. It is not clear whether the cadaveric data can represent the characteristics of the patellofemoral joint in vivo. Furthermore, in studies of patellofemoral bracing, it is not appropriate to calculate the patellar joint contact area by formula because the patellofemoral bracing will affect the patellar trajectory and change the patellofemoral contact area (Powers et al., 2004a). This implies that the generalized equation for the patellofemoral contact area may not be fully accurate (Zavala et al., 2021). A analytical model based on MRI technology was applied to establish a regression equation of contact area based on their respective sample (Brechter and Powers, 2002a; b; Powers et al., 2004a; Whyte et al., 2010). However, the MRI assessment protocol still has some limitations. For example, participants completed the scan in a relaxed quadriceps state to avoid motion artifacts in the MRI, which may not reflect the patellofemoral joint contact area when the quadriceps is contracted.
The accurate prediction of patellofemoral joint kinematics is a key prerequisite prior to investigating the effects of evaluating the impact of injury and physical activity on the PFJS. The geometry of the patella and femur is an important factor affecting the kinematics of the patella. Yu et al. (2019) study revealed that soft tissue plays a critical role in adjusting patellar tracking during the early stages of knee flexion, while the morphology of the trochlear groove and patellar face determines the relative position of the patella and femur as the knee flexion angle increases. Among the eight included studies that used musculoskeletal models to evaluate PFJF or PFJS, two musculoskeletal models were used. The first is the standard model available in simulation software (e.g., AMMR 1.6.2, MoCapModel) (Alexander and Schwameder, 2016), including patella, femur, and tendon, and the model was scaled to match each participant’s anthropometry and mass (Andersen et al., 2010). The second is a subject-specific musculoskeletal model based on subject-specific bone geometry, cartilage surface, and muscle fiber orientation (from MRI) (Chen and Powers, 2014; Lenhart et al., 2015a). Similarly, the included studies of PFJS evaluation using DEA and FEA also adopted the subject-specific model based on the radiation image. Using standardized models to evaluate PFJS may lack biofidelity. The subject-specific model may contribute to more accurately predicting patella tracking and PFJS evaluation (Mesfar and Shirazi-Adl, 2005).
During active knee flexion, the force of the quadriceps muscle is transmitted to the patellar tendon to generate stress on the contact surface of the patellofemoral joint. The researchers used several methods to estimate quadriceps muscle strength. The simplest method is to divide the knee extension moment by the effective lever arm of the quadriceps muscle (from radiography or magnetic resonance imaging). This method does not consider the co-activation of the hamstring and quadriceps during the activity. The second method used net joint moments and muscle moment arms (function of joint angles) to derive hamstring, quadriceps, and gastrocnemius muscle forces (Willson et al., 2015a; Willson et al., 2015b; Willy et al., 2016; Sinclair et al., 2018; Starbuck et al., 2021; Zavala et al., 2021). The third method is to modify the quadriceps muscle forces by the muscle’s cross-sectional area, maximum voluntary contraction force per unit cross-sectional area, and the EMG-force relationship (Escamilla et al., 2008a; Escamilla et al., 2008b; Escamilla et al., 2009). The fourth method is to estimate quadriceps muscle strength by summing the knee flexion moment and the net moment calculated by inverse kinematics. The knee flexion moment was estimated by SIMM software based on the individual’s lower extremity kinematics, the velocity of muscle contraction, and flexor muscle EMG (Chinkulprasert et al., 2011; Powers et al., 2014; Teng and Powers, 2014). The fifth method is computed muscle control algorithm that modifies muscle excitations by using feedforward and feedback control to follow recorded joint angle trajectories (Thelen et al., 2014). In addition, the researchers used static optimization techniques to estimate quadriceps muscle strength. Specifically, an active force adjustment, passive force adjustment, and velocity adjustment were interpolated from Arnold et al. (2010) curves for a given fiber length and velocity. The maximal dynamic muscle force was then calculated from the maximal isometric muscle force (Kernozek et al., 2015). From the perspective of the calculation principle, the quadriceps muscle force calculated by the coordinated contraction adjustment, computed muscle control algorithm, and static optimization techniques, while not flawless in their ability to represent muscle force in vivo, is more accurate than the force calculated from the net moment of knee extension and moment arm. However, it is still difficult to accurately solve the muscle force because the musculoskeletal system is redundant (the identical joint moment can frequently result from an unlimited number of combinations of muscle forces) (Johnson et al., 2022). And the motion simulation depends on experimental data and various uncertainty parameters, such as the variability of marker position, motion artifact, how to normalize EMG, and collecting EMG from deep muscles (Ackermann and van den Bogert, 2010; Burden, 2010). An earlier study has shown that the muscle is activated but does not produce effective muscle force in individuals with PFP (Herzog, 2000). Muscle force is a major factor affecting PFJS, and inaccurate quantification of muscle force may lead to misinterpretation of contact stress patterns. Islam et al. used three-dimensional registration techniques and linear mapping to measure the virtual penetration depth from the patellar cartilage surface to the femoral cartilage surface, combined with a FEA to estimate PFJS (Islam et al., 2015). The method provided by Islam et al. does not require the calculation of muscle force but provides accurate kinematics data of the patella and femur. However, the scanning space of MRI technology is narrow, and it is difficult to capture dynamic functional activities (walking, running, etc.). The development of biplane fluoroscopy systems has provided a method for directly measuring the kinematic data of the patella relative to the femur during functional activity (Wheatley et al., 2020). Gustafson et al. (2021) used a DEA model driven by high-precision kinematic data collected by a biplane fluoroscopy system to evaluate the PFJS during walk tasks. The method of DEA driven by high-precision kinematic data can estimate the PFJS at a subject-specific level without estimating the muscle force, avoiding the source of error. Therefore, the method for evaluating PFJS has a theoretically high accuracy. At the same time, this method can provide information on the change in the stress curve and distribution of the patellofemoral joint during the entire functional activity period, thereby promoting the understanding of PFP and the innovation of rehabilitation methods. The methods described are applicable for studying individuals with abnormal patellar trajectories and additional knee joint load.
FEA and DEA are refined computational models that allow the integration of subject-specific musculoskeletal parameters and experimental data, and are of great value for understanding stress distributions in complex biological structures (Fernandez et al., 2008; Farrokhi et al., 2011b; Gustafson et al., 2019). The researchers believe that shear stress is related to cartilage degeneration and damage, and higher shear stress in cartilage may also be the cause of damage to the exciting nociceptors present in the subchondral bone plate of the patella (Wojtys et al., 1990; (Besier et al., 2008). The FEA has been used to calculate the shear stress of PFP patients and healthy people during activities, and it was found that PFP patients have a higher level of shear stress (Farrokhi et al., 2011b). The studies of FEA and DEA included in this review conducted MRI or CT scans to obtain specific bone geometries to build subject-specific models. The material properties of cartilage are determined using constitutive models of varying complexity. These models range from linear spring models, which are described by a single constant, to isotropic, linear elastic models with two material constants, and a biphasic model with three material constants (Keenan et al., 2013). The studies used a linear elastic material model, which is widely accepted as valid due to the cartilage’s short-term elastic response during activities with loading frequencies over 0.1 Hz, such as walking (Higginson and Snaith, 1979). The average element size in the FEA was 0.5–1 mm, and previous studies on convergence analysis have shown that element sizes smaller than 0.75 mm did not result in significant stress changes but resulted in longer simulation times (Farrokhi et al., 2011b; Liao et al., 2015). The cartilage material properties of Young’s modulus and Poisson’s ratio are important factors affecting stress distribution of cartilage. Unfortunately, researchers do not seem to have reached a consensus about the material properties of cartilage. The minimum elastic modulus used in the included literature is 2 MPa, and the maximum is 40 MPa. Indentation testing is the main means of measuring the properties of materials. Although the indentation test is very accurate for determining material properties, researchers have not yet reached a consensus on cartilage properties. The thickness of cartilage, dehydration of the cartilage, contact area of the indentation test, and strain rate will affect the stiffness of cartilage. Kempson et al. reviewed the study of measuring the cartilage elastic modulus and gave the range of the cartilage elastic modulus under different working conditions (Kempson, 1980). Although the elastic modulus used in most studies related to PFJS evaluation is within this range, the elastic modulus used in some studies is beyond this range, and the basis for the elastic modulus was not provided. It should also be noted that changes in cartilage thickness will affect biomechanical properties (Shaktivesh et al., 2019). Individuals with PFP have been confirmed to have a possible loss of cartilage thickness (Farrokhi et al., 2011a). The rationality of using the same elastic modulus as that of healthy people to evaluate the PFJS of individuals with PFP needs further study. However, there is currently no research directly assessing the mechanical properties of articular cartilage in patients with PFP. The main technical limitation is the inability to directly estimate the mechanical performance of articular cartilage through non-invasive assessments such as MRI (Brenneman Wilson et al., 2023). Indirect prediction methods based on cartilage composition, such as quantitative MRI (Hatcher et al., 2017) and Raman spectroscopy (Bonifacio et al., 2010) and numerical simulations for performance prediction (Gupta et al., 2009), have shown promising potential in non-invasively assessing the mechanical properties of cartilage. In future research, these indirect prediction methods can be used to predict the mechanical properties of cartilage in patients with PFP, thereby promoting the development of stress calculation models for the patellofemoral joint.
In summary, the evaluation of PFJS using analytical models remains the most commonly used approach. Currently, researchers are enhancing the accuracy of PFJS evaluations by combining analytical models with MRI or musculoskeletal models. Musculoskeletal simulations, FEA, and DEA offer more detailed information on stress distribution. FEA can compute stress variations throughout the depth of the cartilage and estimate shear stress, which may be a key indicator of pain. Compared to analytical models, these three approaches consider more PFJS influencing factors and reduce sources of error. However, they are more time-consuming and require technical expertise. The evaluation of PFJS is undoubtedly a complex task. If the goal is to achieve high accuracy in evaluating PFJS, combining advanced imaging technologies (such as biplane fluoroscopy system) with advanced computational techniques (DEA and FEA) would be a good option. The method should be further developed to establish the “gold standard” for PFJS evaluation. If the focus is on exploring the impact of changes in muscle strength on PFJS, utilizing musculoskeletal models would be a suitable approach. For those seeking a simpler computational solution, analytical models would be appropriate. However, there is no clear boundary in the application scope of the aforementioned approaches. In practical applications, the appropriate technical means and evaluation approaches need to be selected based on theoretical considerations and/or ecological validity. Furthermore, the insufficient consideration of confounding factors remains a key limitation to the current research quality. There are multiple factors that impact PFJS such as sub-group classification of PFP patients (Selfe et al., 2013) and foot posture (Neal et al., 2014). In future studies, it is necessary to exercise better control over variables and minimize the influence of confounding factors. These measures will contribute to an improved level of evidence in research.
This study has potential limitations. A total of 69 studies were included in this review and the PFJF and PFJS data of included studies were extracted, but it was not possible to quantitatively analyze the calculation results between different methods due to the high heterogeneity (population, task).
5 Conclusion
There are four methods to evaluate patellofemoral joint reaction force and patellofemoral joint stress, including the analytical model, musculoskeletal model, discrete element analysis, and finite element analysis. At present, there is still no “gold standard” for PFJS. And researchers are still trying to improve the evaluation accuracy of PFJS. This is mainly achieved through using a personalized model and optimizing (or avoiding) quadriceps muscle strength calculation. In theory, the evaluation scheme of combining advanced computational and biplane fluoroscopy techniques has high accuracy in evaluating PFJS. Additionally, in practical applications, it is important to select the appropriate technical methods and evaluation approaches based on theoretical considerations and/or ecological validity. In the future, researchers can develop relevant model frameworks to accurately calculate PFJS and provide technical solutions for a better understanding of the mechanism of patellofemoral joint pain and optimization of the patellofemoral joint treatment program.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
BW and SZ contributed to conception and design of the study. BW, JG, and SZ took part in selection process. BW wrote the first draft of the manuscript. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by the key R&D plan of China for Winter Olympics (Ministry of Science and Technology of the People’s Republic of China, Grant No. 2020YFF0303800).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbioe.2023.1197014/full#supplementary-material
References
Ackermann, M., and van den Bogert, A. J. (2010). Optimality principles for model-based prediction of human gait. J. Biomech. 43 (6), 1055–1060. doi:10.1016/j.jbiomech.2009.12.012
Alexander, N., and Schwameder, H. (2016). Lower limb joint forces during walking on the level and slopes at different inclinations. Gait Posture 45, 137–142. doi:10.1016/j.gaitpost.2016.01.022
Almonroeder, T. G., and Benson, L. C. (2017). Sex differences in lower extremity kinematics and patellofemoral kinetics during running. J. Sports Sci. 35 (16), 1575–1581. doi:10.1080/02640414.2016.1225972
Almonroeder, T. G., Watkins, E., and Widenhoefer, T. (2020). Verbal instruction reduces patellofemoral joint loading during bodyweight squatting. J. Sport Rehabil. 29 (4), 463–468. doi:10.1123/jsr.2018-0157
Andersen, M. S., Damsgaard, M., MacWilliams, B., and Rasmussen, J. (2010). A computationally efficient optimisation-based method for parameter identification of kinematically determinate and over-determinate biomechanical systems. Comput. Methods Biomech. Biomed. Engin 13 (2), 171–183. doi:10.1080/10255840903067080
Arnold, E. M., Ward, S. R., Lieber, R. L., and Delp, S. L. (2010). A model of the lower limb for analysis of human movement. Ann. Biomed. Eng. 38 (2), 269–279. doi:10.1007/s10439-009-9852-5
Atkins, L. T., Smithson, C., Grimes, D., and Heuer, N. (2019). The influence of sagittal trunk posture on the magnitude and rate of patellofemoral joint stress during stair ascent in asymptomatic females. Gait Posture 74, 121–127. doi:10.1016/j.gaitpost.2019.08.016
Barker, T. H., Stone, J. C., Sears, K., Klugar, M., Leonardi-Bee, J., Tufanaru, C., et al. (2023). Revising the JBI quantitative critical appraisal tools to improve their applicability: An overview of methods and the development process. JBI Evid. Synth. 21 (3), 478–493. doi:10.11124/jbies-22-00125
Besier, T. F., Gold, G. E., Delp, S. L., Fredericson, M., and Beaupré, G. S. (2008). The influence of femoral internal and external rotation on cartilage stresses within the patellofemoral joint. J. Orthop. Res. 26 (12), 1627–1635. doi:10.1002/jor.20663
Besier, T. F., Gold, G. E., Beaupré, G. S., and Delp, S. L. (2005). A modeling framework to estimate patellofemoral joint cartilage stress in vivo. Med. Sci. Sports Exerc 37 (11), 1924–1930. doi:10.1249/01.mss.0000176686.18683.64
Besier, T. F., Pal, S., Draper, C. E., Fredericson, M., Gold, G. E., Delp, S. L., et al. (2015). The role of cartilage stress in patellofemoral pain. Med. Sci. Sports Exerc 47 (11), 2416–2422. doi:10.1249/mss.0000000000000685
Bonacci, J., Vicenzino, B., Spratford, W., and Collins, P. (2014). Take your shoes off to reduce patellofemoral joint stress during running. Br. J. Sports Med. 48 (6), 425–428. doi:10.1136/bjsports-2013-092160
Bonacci, J., Hall, M., Fox, A., Saunders, N., Shipsides, T., and Vicenzino, B. (2018). The influence of cadence and shoes on patellofemoral joint kinetics in runners with patellofemoral pain. J. Sci. Med. Sport 21 (6), 574–578. doi:10.1016/j.jsams.2017.09.593
Bonifacio, A., Beleites, C., Vittur, F., Marsich, E., Semeraro, S., Paoletti, S., et al. (2010). Chemical imaging of articular cartilage sections with Raman mapping, employing uni- and multi-variate methods for data analysis. Analyst 135 (12), 3193–3204. doi:10.1039/c0an00459f
Boyer, E. R., and Derrick, T. R. (2018). Lower extremity joint loads in habitual rearfoot and mid/forefoot strike runners with normal and shortened stride lengths. J. Sports Sci. 36 (5), 499–505. doi:10.1080/02640414.2017.1321775
Brechter, J. H., and Powers, C. M. (2002b). Patellofemoral stress during walking in persons with and without patellofemoral pain. Med. Sci. Sports Exerc 34 (10), 1582–1593. doi:10.1097/00005768-200210000-00009
Brechter, J. H., and Powers, C. M. (2002a). Patellofemoral joint stress during stair ascent and descent in persons with and without patellofemoral pain. Gait Posture 16 (2), 115–123. doi:10.1016/s0966-6362(02)00090-5
Brenneman Wilson, E. C., Quenneville, C. E., and Maly, M. R. (2023). Integrating MR imaging with full-surface indentation mapping of femoral cartilage in an ex vivo porcine stifle. J. Mech. Behav. Biomed. Mater 139, 105651. doi:10.1016/j.jmbbm.2023.105651
Burden, A. (2010). How should we normalize electromyograms obtained from healthy participants? What we have learned from over 25 years of research. J. Electromyogr. Kinesiol 20 (6), 1023–1035. doi:10.1016/j.jelekin.2010.07.004
Chen, Y. J., and Powers, C. M. (2014). Comparison of three-dimensional patellofemoral joint reaction forces in persons with and without patellofemoral pain. J. Appl. Biomech. 30 (4), 493–500. doi:10.1123/jab.2011-0250
Chinkulprasert, C., Vachalathiti, R., and Powers, C. M. (2011). Patellofemoral joint forces and stress during forward step-up, lateral step-up, and forward step-down exercises. J. Orthop. Sports Phys. Ther. 41 (4), 241–248. doi:10.2519/jospt.2011.3408
Dos Santos, A. F., Nakagawa, T. H., Serrão, F. V., and Ferber, R. (2019). Patellofemoral joint stress measured across three different running techniques. Gait Posture 68, 37–43. doi:10.1016/j.gaitpost.2018.11.002
Elias, J. J., Kilambi, S., and Cosgarea, A. J. (2010). Computational assessment of the influence of vastus medialis obliquus function on patellofemoral pressures: Model evaluation. J. Biomech. 43 (4), 612–617. doi:10.1016/j.jbiomech.2009.10.039
Elias, J. J., and Saranathan, A. (2013). Discrete element analysis for characterizing the patellofemoral pressure distribution: Model evaluation. J. Biomech. Eng. 135 (8), 81011. doi:10.1115/1.4024287
Elias, J. J., Wilson, D. R., Adamson, R., and Cosgarea, A. J. (2004). Evaluation of a computational model used to predict the patellofemoral contact pressure distribution. J. Biomech. 37 (3), 295–302. doi:10.1016/s0021-9290(03)00306-3
Erdemir, A., McLean, S., Herzog, W., and van den Bogert, A. J. (2007). Model-based estimation of muscle forces exerted during movements. Clin. Biomech. (Bristol, Avon) 22 (2), 131–154. doi:10.1016/j.clinbiomech.2006.09.005
Escamilla, R. F., Zheng, N., MacLeod, T. D., Edwards, W. B., Hreljac, A., Fleisig, G. S., et al. (2008a). Patellofemoral compressive force and stress during the forward and side lunges with and without a stride. Clin. Biomech. (Bristol, Avon) 23 (8), 1026–1037. doi:10.1016/j.clinbiomech.2008.05.002
Escamilla, R. F., Zheng, N., Macleod, T. D., Edwards, W. B., Hreljac, A., Fleisig, G. S., et al. (2008b). Patellofemoral joint force and stress between a short- and long-step forward lunge. J. Orthop. Sports Phys. Ther. 38 (11), 681–690. doi:10.2519/jospt.2008.2694
Escamilla, R. F., Zheng, N., Macleod, T. D., Edwards, W. B., Imamura, R., Hreljac, A., et al. (2009). Patellofemoral joint force and stress during the wall squat and one-leg squat. Med. Sci. Sports Exerc 41 (4), 879–888. doi:10.1249/MSS.0b013e31818e7ead
Esculier, J. F., Dubois, B., Bouyer, L. J., McFadyen, B. J., and Roy, J. S. (2017). Footwear characteristics are related to running mechanics in runners with patellofemoral pain. Gait Posture 54, 144–147. doi:10.1016/j.gaitpost.2017.03.010
Farrokhi, S., Colletti, P. M., and Powers, C. M. (2011a). Differences in patellar cartilage thickness, transverse relaxation time, and deformational behavior: A comparison of young women with and without patellofemoral pain. Am. J. Sports Med. 39 (2), 384–391. doi:10.1177/0363546510381363
Farrokhi, S., Keyak, J. H., and Powers, C. M. (2011b). Individuals with patellofemoral pain exhibit greater patellofemoral joint stress: A finite element analysis study. Osteoarthr. Cartil. 19 (3), 287–294. doi:10.1016/j.joca.2010.12.001
Fernandez, J. W., Akbarshahi, M., Kim, H. J., and Pandy, M. G. (2008). Integrating modelling, motion capture and x-ray fluoroscopy to investigate patellofemoral function during dynamic activity. Comput. Methods Biomech. Biomed. Engin 11 (1), 41–53. doi:10.1080/10255840701551046
Fick, C. N., Jiménez-Silva, R., Sheehan, F. T., and Grant, C. (2022). Patellofemoral kinematics in patellofemoral pain syndrome: The influence of demographic factors. J. Biomech. 130, 110819. doi:10.1016/j.jbiomech.2021.110819
Fitzpatrick, C. K., and Rullkoetter, P. J. (2012). Influence of patellofemoral articular geometry and material on mechanics of the unresurfaced patella. J. Biomech. 45 (11), 1909–1915. doi:10.1016/j.jbiomech.2012.05.028
Goulette, D., Griffith, P., Schiller, M., Rutherford, D., and Kernozek, T. W. (2021). Patellofemoral joint loading during the forward and backward lunge. Phys. Ther. Sport 47, 178–184. doi:10.1016/j.ptsp.2020.12.001
Gupta, S., Lin, J., Ashby, P., and Pruitt, L. (2009). A fiber reinforced poroelastic model of nanoindentation of porcine costal cartilage: A combined experimental and finite element approach. J. Mech. Behav. Biomed. Mater 2 (4), 326–338. doi:10.1016/j.jmbbm.2008.09.003
Gustafson, J. A., Elias, J. J., Debski, R. E., and Farrokhi, S. (2019). Development and validation of a kinematically-driven discrete element model of the patellofemoral joint. J. Biomech. 88, 164–172. doi:10.1016/j.jbiomech.2019.03.032
Gustafson, J. A., Elias, J. J., Fitzgerald, G. K., Tashman, S., Debski, R. E., and Farrokhi, S. (2021). Combining advanced computational and imaging techniques as a quantitative tool to estimate patellofemoral joint stress during downhill gait: A feasibility study. Gait Posture 84, 31–37. doi:10.1016/j.gaitpost.2020.11.016
Haight, D. J., Lerner, Z. F., Board, W. J., and Browning, R. C. (2014). A comparison of slow, uphill and fast, level walking on lower extremity biomechanics and tibiofemoral joint loading in obese and nonobese adults. J. Orthop. Res. 32 (2), 324–330. doi:10.1002/jor.22497
Hatcher, C. C., Collins, A. T., Kim, S. Y., Michel, L. C., Mostertz, W. C., Ziemian, S. N., et al. (2017). Relationship between T1rho magnetic resonance imaging, synovial fluid biomarkers, and the biochemical and biomechanical properties of cartilage. J. Biomech. 55, 18–26. doi:10.1016/j.jbiomech.2017.02.001
Herzog, W. (2000). Skeletal muscle mechanics: From mechanisms to function. Hoboken, New Jersey, United States: John Wiley & Sons.
Higginson, G., and Snaith, J. J. E. (1979). The mechanical stiffness of articular cartilage in confined oscillating compression. Eng. Med. 8 (1), 11–14. doi:10.1243/emed_jour_1979_008_005_02
Ho, K. Y., Blanchette, M. G., and Powers, C. M. (2012). The influence of heel height on patellofemoral joint kinetics during walking. Gait Posture 36 (2), 271–275. doi:10.1016/j.gaitpost.2012.03.008
Ho, K. Y., French, T., Klein, B., and Lee, Y. (2018). Patellofemoral joint stress during incline and decline running. Phys. Ther. Sport 34, 136–140. doi:10.1016/j.ptsp.2018.09.010
Ho, K. Y., Hu, H. H., Colletti, P. M., and Powers, C. M. (2014). Running-induced patellofemoral pain fluctuates with changes in patella water content. Eur. J. Sport Sci. 14 (6), 628–634. doi:10.1080/17461391.2013.862872
Hofmann, C. L., Holyoak, D. T., and Juris, P. M. (2017). Trunk and shank position influences patellofemoral joint stress in the lead and trail limbs during the forward lunge exercise. J. Orthop. Sports Phys. Ther. 47 (1), 31–40. doi:10.2519/jospt.2017.6336
Hu, J., Chen, Z., Xin, H., Zhang, Q., and Jin, Z. (2018). Musculoskeletal multibody dynamics simulation of the contact mechanics and kinematics of a natural knee joint during a walking cycle. Proc. Inst. Mech. Eng. H. 232 (5), 508–519. doi:10.1177/0954411918767695
Islam, K., Duke, K., Mustafy, T., Adeeb, S. M., Ronsky, J. L., and El-Rich, M. (2015). A geometric approach to study the contact mechanisms in the patellofemoral joint of normal versus patellofemoral pain syndrome subjects. Comput. Methods Biomech. Biomed. Engin 18 (4), 391–400. doi:10.1080/10255842.2013.803082
Johnson, R. T., Lakeland, D., and Finley, J. M. (2022). Using Bayesian inference to estimate plausible muscle forces in musculoskeletal models. J. Neuroeng Rehabil. 19 (1), 34. doi:10.1186/s12984-022-01008-4
Keenan, K. E., Pal, S., Lindsey, D. P., Besier, T. F., and Beaupre, G. S. (2013). A viscoelastic constitutive model can accurately represent entire creep indentation tests of human patella cartilage. J. Appl. Biomech. 29 (3), 292–302. doi:10.1123/jab.29.3.292
Kempson, G. E. (1980). “5 - the mechanical properties of articular cartilage,” in The joints and synovial fluid. Editor L. Sokoloff (Cambridge, Massachusetts, United States: Academic Press), 177–238.
Kernozek, T. W., Gheidi, N., Zellmer, M., Hove, J., Heinert, B. L., and Torry, M. R. (2018). Effects of anterior knee displacement during squatting on patellofemoral joint stress. J. Sport Rehabil. 27 (3), 237–243. doi:10.1123/jsr.2016-0197
Kernozek, T. W., Vannatta, C. N., and van den Bogert, A. J. (2015). Comparison of two methods of determining patellofemoral joint stress during dynamic activities. Gait Posture 42 (2), 218–222. doi:10.1016/j.gaitpost.2015.05.017
Kujawa, M., Goerlitz, A., Rutherford, D., and Kernozek, T. W. (2020). Patellofemoral joint stress during running with added load in females. Int. J. Sports Med. 41 (6), 412–418. doi:10.1055/a-1088-5467
Kulmala, J. P., Avela, J., Pasanen, K., and Parkkari, J. (2013). Forefoot strikers exhibit lower running-induced knee loading than rearfoot strikers. Med. Sci. Sports Exerc 45 (12), 2306–2313. doi:10.1249/MSS.0b013e31829efcf7
Lenhart, R. L., Kaiser, J., Smith, C. R., and Thelen, D. G. (2015a). Prediction and validation of load-dependent behavior of the tibiofemoral and patellofemoral joints during movement. Ann. Biomed. Eng. 43 (11), 2675–2685. doi:10.1007/s10439-015-1326-3
Lenhart, R. L., Smith, C. R., Vignos, M. F., Kaiser, J., Heiderscheit, B. C., and Thelen, D. G. (2015b). Influence of step rate and quadriceps load distribution on patellofemoral cartilage contact pressures during running. J. Biomech. 48 (11), 2871–2878. doi:10.1016/j.jbiomech.2015.04.036
Lenhart, R. L., Thelen, D. G., Wille, C. M., Chumanov, E. S., and Heiderscheit, B. C. (2014). Increasing running step rate reduces patellofemoral joint forces. Med. Sci. Sports Exerc 46 (3), 557–564. doi:10.1249/MSS.0b013e3182a78c3a
Liao, T. C., Keyak, J. H., and Powers, C. M. (2018a). Runners with patellofemoral pain exhibit greater peak patella cartilage stress compared with pain-free runners. J. Appl. Biomech. 34 (4), 298–305. doi:10.1123/jab.2017-0229
Liao, T. C., and Powers, C. M. (2019). Tibiofemoral kinematics in the transverse and frontal planes influence the location and magnitude of peak patella cartilage stress: An investigation of runners with and without patellofemoral pain. Clin. Biomech. (Bristol, Avon) 62, 72–78. doi:10.1016/j.clinbiomech.2019.01.003
Liao, T. C., Yang, N., Ho, K. Y., Farrokhi, S., and Powers, C. M. (2015). Femur rotation increases patella cartilage stress in females with patellofemoral pain. Med. Sci. Sports Exerc 47 (9), 1775–1780. doi:10.1249/mss.0000000000000617
Liao, T. C., Yin, L., and Powers, C. M. (2018b). The influence of isolated femur and tibia rotations on patella cartilage stress: A sensitivity analysis. Clin. Biomech. (Bristol, Avon) 54, 125–131. doi:10.1016/j.clinbiomech.2018.03.003
Liberati, A., Altman, D. G., Tetzlaff, J., Mulrow, C., Gøtzsche, P. C., Ioannidis, J. P., et al. (2009). The PRISMA statement for reporting systematic reviews and meta-analyses of studies that evaluate healthcare interventions: Explanation and elaboration. Bmj 339, b2700. doi:10.1136/bmj.b2700
Mesfar, W., and Shirazi-Adl, A. (2005). Biomechanics of the knee joint in flexion under various quadriceps forces. Knee 12 (6), 424–434. doi:10.1016/j.knee.2005.03.004
Neal, B. S., Griffiths, I. B., Dowling, G. J., Murley, G. S., Munteanu, S. E., Franettovich Smith, M. M., et al. (2014). Foot posture as a risk factor for lower limb overuse injury: A systematic review and meta-analysis. J. Foot Ankle Res. 7 (1), 55. doi:10.1186/s13047-014-0055-4
Nunes, G. S., Scattone Silva, R., Dos Santos, A. F., Fernandes, R. A. S., Serrão, F. V., and de Noronha, M. (2018). Methods to assess patellofemoral joint stress: A systematic review. Gait Posture 61, 188–196. doi:10.1016/j.gaitpost.2017.12.018
Pal, S., Besier, T. F., Gold, G. E., Fredericson, M., Delp, S. L., and Beaupre, G. S. (2019). Patellofemoral cartilage stresses are most sensitive to variations in vastus medialis muscle forces. Comput. Methods Biomech. Biomed. Engin 22 (2), 206–216. doi:10.1080/10255842.2018.1544629
Peng, H. T., Chen, W. C., Kernozek, T. W., Kim, K., and Song, C. Y. (2015). Influences of patellofemoral pain and fatigue in female dancers during ballet jump-landing. Int. J. Sports Med. 36 (9), 747–753. doi:10.1055/s-0035-1547220
Powers, C. M., Ho, K. Y., Chen, Y. J., Souza, R. B., and Farrokhi, S. (2014). Patellofemoral joint stress during weight-bearing and non-weight-bearing quadriceps exercises. J. Orthop. Sports Phys. Ther. 44 (5), 320–327. doi:10.2519/jospt.2014.4936
Powers, C. M., Ward, S. R., Chen, Y. J., Chan, L. D., and Terk, M. R. (2004b). Effect of bracing on patellofemoral joint stress while ascending and descending stairs. Clin. J. Sport Med. 14 (4), 206–214. doi:10.1097/00042752-200407000-00003
Powers, C. M., Ward, S. R., Chen, Y. J., Chan, L. D., and Terk, M. R. (2004a). The effect of bracing on patellofemoral joint stress during free and fast walking. Am. J. Sports Med. 32 (1), 224–231. doi:10.1177/0363546503258908
Ristow, A., Besch, M., Rutherford, D., and Kernozek, T. W. (2020). Patellofemoral joint loading during single-leg hopping exercises. J. Sport Rehabil. 29 (8), 1131–1136. doi:10.1123/jsr.2019-0135
Salem, G. J., and Powers, C. M. (2001). Patellofemoral joint kinetics during squatting in collegiate women athletes. Clin. Biomech. (Bristol, Avon) 16 (5), 424–430. doi:10.1016/s0268-0033(01)00017-1
Salsich, G. B., and Perman, W. H. (2007). Patellofemoral joint contact area is influenced by tibiofemoral rotation alignment in individuals who have patellofemoral pain. J. Orthop. Sports Phys. Ther. 37 (9), 521–528. doi:10.2519/jospt.2007.37.9.521
Selfe, J., Callaghan, M., Witvrouw, E., Richards, J., Dey, M. P., Sutton, C., et al. (2013). Targeted interventions for patellofemoral pain syndrome (TIPPS): Classification of clinical subgroups. BMJ Open 3 (9), e003795. doi:10.1136/bmjopen-2013-003795
Shah, K. S., Saranathan, A., Koya, B., and Elias, J. J. (2015). Finite element analysis to characterize how varying patellar loading influences pressure applied to cartilage: Model evaluation. Comput. Methods Biomech. Biomed. Engin 18 (14), 1509–1515. doi:10.1080/10255842.2014.921814
Shaktivesh, S., Malekipour, F., and Lee, P. V. S. (2019). Shock absorbing ability in healthy and damaged cartilage-bone under high-rate compression. J. Mech. Behav. Biomed. Mater 90, 388–394. doi:10.1016/j.jmbbm.2018.10.023
Sinclair, J. (2014). Effects of barefoot and barefoot inspired footwear on knee and ankle loading during running. Clin. Biomech. (Bristol, Avon) 29 (4), 395–399. doi:10.1016/j.clinbiomech.2014.02.004
Sinclair, J., Hobbs, S. J., and Selfe, J. (2015). The influence of minimalist footwear on knee and ankle load during depth jumping. Res. Sports Med. 23 (3), 289–301. doi:10.1080/15438627.2015.1040917
Sinclair, J., Janssen, J., Richards, J. D., Butters, B., Taylor, P. J., and Hobbs, S. J. (2018). Effects of a 4-week intervention using semi-custom insoles on perceived pain and patellofemoral loading in targeted subgroups of recreational runners with patellofemoral pain. Phys. Ther. Sport 34, 21–27. doi:10.1016/j.ptsp.2018.08.006
Sinclair, J. K., Selfe, J., Taylor, P. J., Shore, H. F., and Richards, J. D. (2016b). Influence of a knee brace intervention on perceived pain and patellofemoral loading in recreational athletes. Clin. Biomech. (Bristol, Avon) 37, 7–12. doi:10.1016/j.clinbiomech.2016.05.002
Sinclair, J., Richards, J., Selfe, J., Fau-Goodwin, J., and Shore, H. (2016a). The influence of minimalist and maximalist footwear on patellofemoral kinetics during running. J. Appl. Biomech. 32 (4), 359–364. doi:10.1123/jab.2015-0249
Sinclair, J., and Selfe, J. (2015). Sex differences in knee loading in recreational runners. J. Biomech. 48 (10), 2171–2175. doi:10.1016/j.jbiomech.2015.05.016
Starbuck, C., Bramah, C., Herrington, L., and Jones, R. (2021). The effect of speed on Achilles tendon forces and patellofemoral joint stresses in high-performing endurance runners. Scand. J. Med. Sci. Sports 31 (8), 1657–1665. doi:10.1111/sms.13972
Steele, K. M., Demers, M. S., Schwartz, M. H., and Delp, S. L. (2012). Compressive tibiofemoral force during crouch gait. Gait Posture 35 (4), 556–560. doi:10.1016/j.gaitpost.2011.11.023
Teng, H. L., Pedoia, V., Link, T. M., Majumdar, S., and Souza, R. B. (2018). Local associations between knee cartilage T(1ρ) and T(2) relaxation times and patellofemoral joint stress during walking: A voxel-based relaxometry analysis. Knee 25 (3), 406–416. doi:10.1016/j.knee.2018.02.016
Teng, H. L., and Powers, C. M. (2014). Sagittal plane trunk posture influences patellofemoral joint stress during running. J. Orthop. Sports Phys. Ther. 44 (10), 785–792. doi:10.2519/jospt.2014.5249
Thelen, D. G., Won Choi, K., and Schmitz, A. M. (2014). Co-simulation of neuromuscular dynamics and knee mechanics during human walking. J. Biomech. Eng. 136 (2), 021033. doi:10.1115/1.4026358
Thomeer, L. T., Lin, Y. C., and Pandy, M. G. (2020). Load distribution at the patellofemoral joint during walking. Ann. Biomed. Eng. 48 (12), 2821–2835. doi:10.1007/s10439-020-02672-0
van Eijden, T. M., Kouwenhoven, E., Verburg, J., and Weijs, W. A. (1986). A mathematical model of the patellofemoral joint. J. Biomech. 19 (3), 219–229. doi:10.1016/0021-9290(86)90154-5
van Rossom, S., Smith, C. R., Thelen, D. G., Vanwanseele, B., Van Assche, D., and Jonkers, I. (2018). Knee joint loading in healthy adults during functional exercises: Implications for rehabilitation guidelines. J. Orthop. Sports Phys. Ther. 48 (3), 162–173. doi:10.2519/jospt.2018.7459
Vannatta, C. N., and Kernozek, T. W. (2015). Patellofemoral joint stress during running with alterations in foot strike pattern. Med. Sci. Sports Exerc 47 (5), 1001–1008. doi:10.1249/mss.0000000000000503
Waiteman, M. C., Briani, R. V., Pazzinatto, M. F., Ferreira, A. S., Ferrari, D., de Oliveira Silva, D., et al. (2018). Relationship between knee abduction moment with patellofemoral joint reaction force, stress and self-reported pain during stair descent in women with patellofemoral pain. Clin. Biomech. (Bristol, Avon) 59, 110–116. doi:10.1016/j.clinbiomech.2018.09.012
Wallace, D. A., Salem, G. J., Salinas, R., and Powers, C. M. (2002). Patellofemoral joint kinetics while squatting with and without an external load. J. Orthop. Sports Phys. Ther. 32 (4), 141–148. doi:10.2519/jospt.2002.32.4.141
Wang, B., Yang, Y., Zhang, X., Wang, J., Deng, L., and Fu, W. (2020). Twelve-Week gait retraining reduced patellofemoral joint stress during running in male recreational runners. Biomed. Res. Int. 2020, 1–9. doi:10.1155/2020/9723563
Wheatley, M. G. A., Rainbow, M. J., and Clouthier, A. L. (2020). Patellofemoral mechanics: A review of pathomechanics and research approaches. Curr. Rev. Musculoskelet. Med. 13 (3), 326–337. doi:10.1007/s12178-020-09626-y
Whitehead, S., Till, K., Weaving, D., and Jones, B. (2018). The use of microtechnology to quantify the peak match demands of the football codes: A systematic review. Sports Med. 48 (11), 2549–2575. doi:10.1007/s40279-018-0965-6
Whyte, E. F., Moran, K., Shortt, C. P., and Marshall, B. (2010). The influence of reduced hamstring length on patellofemoral joint stress during squatting in healthy male adults. Gait Posture 31 (1), 47–51. doi:10.1016/j.gaitpost.2009.08.243
Willson, J. D., Loss, J. R., Willy, R. W., and Meardon, S. A. (2015a). Sex differences in running mechanics and patellofemoral joint kinetics following an exhaustive run. J. Biomech. 48 (15), 4155–4159. doi:10.1016/j.jbiomech.2015.10.021
Willson, J. D., Ratcliff, O. M., Meardon, S. A., and Willy, R. W. (2015b). Influence of step length and landing pattern on patellofemoral joint kinetics during running. Scand. J. Med. Sci. Sports 25 (6), 736–743. doi:10.1111/sms.12383
Willson, J. D., Sharpee, R., Meardon, S. A., and Kernozek, T. W. (2014). Effects of step length on patellofemoral joint stress in female runners with and without patellofemoral pain. Clin. Biomech. (Bristol, Avon) 29 (3), 243–247. doi:10.1016/j.clinbiomech.2013.12.016
Willy, R. W., Halsey, L., Hayek, A., Johnson, H., and Willson, J. D. (2016). Patellofemoral joint and achilles tendon loads during overground and treadmill running. J. Orthop. Sports Phys. Ther. 46 (8), 664–672. doi:10.2519/jospt.2016.6494
Wirtz, A. D., Willson, J. D., Kernozek, T. W., and Hong, D. A. (2012). Patellofemoral joint stress during running in females with and without patellofemoral pain. Knee 19 (5), 703–708. doi:10.1016/j.knee.2011.09.006
Wojtys, E. M., Beaman, D. N., Glover, R. A., and Janda, D. (1990). Innervation of the human knee joint by substance-P fibers. Arthroscopy 6 (4), 254–263. doi:10.1016/0749-8063(90)90054-h
Yu, Z., Yao, J., Wang, X., Xin, X., Zhang, K., Cai, H., et al. (2019). Research methods and progress of patellofemoral joint kinematics: A review. J. Healthc. Eng. 2019, 1–13. doi:10.1155/2019/9159267
Keywords: patellofemoral joint stress, analytical model, musculoskeletal model, discrete element analysis, finite element analysis
Citation: Wang B, Mao Z, Guo J, Yang J and Zhang S (2023) The non-invasive evaluation technique of patellofemoral joint stress: a systematic literature review. Front. Bioeng. Biotechnol. 11:1197014. doi: 10.3389/fbioe.2023.1197014
Received: 30 March 2023; Accepted: 20 June 2023;
Published: 29 June 2023.
Edited by:
Amir Esrafilian, University of Eastern Finland, FinlandReviewed by:
Jonathan Gustafson, Rush University Medical Center, United StatesUriel Zapata, EAFIT University, Colombia
Hannah Lundberg, Rush University, United States
Copyright © 2023 Wang, Mao, Guo, Yang and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shengnian Zhang, emhhbmdzbnhAMTYzLmNvbQ==
 Baofeng Wang
Baofeng Wang Zheng Mao
Zheng Mao Jin Yang
Jin Yang