- 1Cyber-Physical Systems Laboratory, Department of ICT and Natural Sciences, Norwegian University of Science and Technology (NTNU), Ålesund, Norway
- 2Ålesund Biomechanics Lab, Ålesund General Hospital, Møre and Romsdal Hospital Trust, Ålesund, Norway
- 3Division of Biomechanics, Department of Structural Engineering, Norwegian University of Science and Technology (NTNU), Trondheim, Norway
- 4Department of Orthopaedic Surgery, Medi3, Ålesund, Norway
In this paper, we examine the region- and layer-specific collagen fiber morphology via second harmonic generation (SHG) in combination with planar biaxial tension testing to suggest a structure-based constitutive model for the human meniscal tissue. Five lateral and four medial menisci were utilized, with samples excised across the thickness from the anterior, mid-body, and posterior regions of each meniscus. An optical clearing protocol enhanced the scan depth. SHG imaging revealed that the top samples consisted of randomly oriented fibers with a mean fiber orientation of 43.3o. The bottom samples were dominated by circumferentially organized fibers, with a mean orientation of 9.5o. Biaxial testing revealed a clear anisotropic response, with the circumferential direction being stiffer than the radial direction. The bottom samples from the anterior region of the medial menisci exhibited higher circumferential elastic modulus with a mean value of 21 MPa. The data from the two testing protocols were combined to characterize the tissue with an anisotropic hyperelastic material model based on the generalized structure tensor approach. The model showed good agreement in representing the material anisotropy with a mean r2 = 0.92.
1 Introduction
The meniscus is a crescent-shaped tissue present between the femoral condyle and the tibial plateau of the human knee joint. This fibrocartilaginous soft tissue plays a crucial role in load distribution and structural stability. It also acts as a shock absorber and provides lubrication and nutrition to the knee joint (Makris et al., 2011; Fox et al., 2012). The human knee joint has two menisci; the C-shaped medial meniscus is on the inner side of the knee joint, and the O-shaped lateral meniscus is on the outer side of the knee. The medial meniscus is restricted in its range of motion and more susceptible to injury than the lateral meniscus, as it is tightly attached to the knee joint capsule (Lento and Akuthota, 2000). This difference, along with the shape of the menisci, and variation in applied loading, contributes to the anatomical location specificity in material properties. When viewed from above, three distinct regions can be identified in both menisci. The dissimilarity of width in these anterior, mid-body, and posterior regions together with differing load distributions, produces various stress concentrations, which result in the region-specific material properties (Danso et al., 2017). In the cross-sectional view, the topmost layer, so-called the superficial layer, is characterized by randomly arranged fibers. Lamellar collagen fibrils make up the second layer, referred to as the lamellar layer. The central main layer, underneath the lamellar layer, has predominant bundles of circumferentially arranged fibers (Fithian et al., 1990; Petersen and Tillmann, 1998; Fox et al., 2012). This depth-wise heterogeneity in fiber quantity and fiber orientation controls the layer-specific material properties. The anisotropic tissue behavior resulting from this region- and layer-specificity must be incorporated into material models for accurate biomechanical characterization.
The formulation of tissue mechanical behavior led to the development of constitutive models, which are mathematical frameworks based on fundamental physical principles. These models aid in understanding structure-function relationships and, as a result, help predict the mechanical response of the tissue to different loading (Imeni et al., 2020). These are valuable in medical applications such as tissue engineering and the design of synthetic replacement alternatives (Kahlon et al., 2015). The awareness of biomechanical function also helps in studying the meniscus injury mechanism, which leads to the selection of suitable repair strategies (Lento and Akuthota, 2000). Additionally, the computational models of the knee joint, including the constitutive framework of the menisci, assist in assessing the impact of meniscus geometry (Luczkiewicz et al., 2018), meniscal tears, meniscectomy, and osteoarthritis (Li et al., 2020) on the biomechanics of the knee joint. The fidelity of these knee joint models is tied directly to the constitutive model parameters, which must be well characterized by the mechanical response of the material (Morrow et al., 2010). For this, mechanical testing has commonly been the gold standard.
Numerous studies have reported region-wise differences in the material properties of the meniscus, but only a few have focused on layer-wise mechanical characterization. The indentation test exhibited higher elastic moduli (Danso et al., 2015; Gaugler et al., 2015; Danso et al., 2017), higher strain-dependent fibril network modulus (Danso et al., 2017), and higher permeability (Danso et al., 2017) in the anterior horn of the medial menisci. However, estimating anisotropic behavior and developing a mathematical model from indentation test data is extremely challenging (Navindaran et al., 2023). Unconfined compression testing on human menisci showed a significantly lower compressive modulus than the tensile modulus (Chia and Hull, 2008). In contrast to the direct correlation of the tensile characteristics with the collagen orientation (Bursac et al., 2006), it has little effect on the compressive moduli (Leslie et al., 2000; Chia and Hull, 2008). Uniaxial tensile testing on human menisci revealed the greater circumferential tensile modulus (Lechner et al., 2000) as well as higher elastic and viscous dynamic moduli (Bursac et al., 2006) of the anterior region of the medial menisci. In addition to the region-specificity implied in these studies, the variation of elastic and viscous properties across the meniscus (which indicates layer-specificity) was demonstrated using uniaxial testing on porcine menisci (Maritz et al., 2021). However, stretching the tissue fibers in the uniaxial direction causes compression of the fibers in the lateral directions, which is undesirable. This can be overcome by biaxial testing, which can better replicate the complex in vivo loading conditions (Jacobs et al., 2013). Kahlon et al. (2015) studied regional and depth variability of porcine meniscus properties through biaxial testing, and noticed higher Young’s moduli in the layers near to femur and tibia. Understanding this location-specific material behavior is crucial for comprehending the macroscopic behavior of the meniscus and developing appropriate constitutive models (Barrera et al., 2018).
The constitutive models that do not incorporate information from fiber families are not able to capture the stress-strain response of different layers accurately (Gasser et al., 2005). Many imaging modalities have been used to quantitatively describe the three-dimensional structural morphology of collagen fibers at the micro-nano scale. Light microscopy (Andrews et al., 2014; Bonomo et al., 2020), electron microscopy (Fithian et al., 1990), scanning electron microscopy (SEM) (Vetri et al., 2019), micro-computed tomography (μCT) (Agustoni et al., 2021), and multiphoton microscopy (MPM) (Vetri et al., 2019; Sancataldo et al., 2022) studies elucidated the complex inhomogeneous architecture of the human meniscal tissue. According to a prior spectroscopic investigation (Danso et al., 2017), the anterior region of the medial menisci has a larger collagen content, which explains the higher elastic moduli reported in many studies. In addition to this, they observed a lower collagen orientation angle at the top layer of the menisci. Collagen fibers in the layers adjacent to the femoral condyle and tibial plateau were randomly aligned in μCT investigations of the mid-body of the lateral meniscus, whereas collagen fibers with a 30° alignment were observed in the deep interior layer (Agustoni et al., 2021). Maritz et al. (2021) demonstrated that this random alignment of the collagen fibers in the superficial layers results in stiffer mechanical responses compared to internal regions. These investigations are all consistent in showing the heterogeneity of the meniscus in a width-wise (region-specificity) and depth-wise (layer-specificity) manner. However, deep imaging in complex environments is an important challenge in these imaging modalities. The imaging modality used in identifying region-and layer-specific collagen details should be capable of producing ultra-high resolution images deep within optically thick samples. Multiphoton microscopy (Williams et al., 2001) is well-suited for this purpose. In addition, second harmonic generation (SHG) (Freund and Deutsch, 1986) enables direct imaging of collagen fibers. These imaging techniques can be employed simultaneously to image intrinsic tissue indicators like collagen, which have a high degree of hyperpolarizability (Zipfel et al., 2003). MPM and SHG studies on the human meniscus, for example, have shown that collagen bundles are stacked in compartments with a honeycomb-like pattern in the cross-section of the meniscal tissue (Vetri et al., 2019). Another intriguing observation achieved utilizing MPM on the bovine meniscus was the arborization of “tie-fibers” and its association with circumferential fibers (Andrews et al., 2014). SHG imaging is also an effective tool for diagnosing osteoarthritis, even in its early stages, by analyzing the thickness and organization of collagen fibers in different layers (Hui Mingalone et al., 2018). Therefore, in this paper, we employed an SHG via MPM-enabled imaging of collagen fiber morphology to obtain data for constitutive modeling.
A wide variety of numerical models of the meniscus tissue have been reported, ranging from simple isotropy to complex anisotropy consideration (Imeni et al., 2020; Elmukashfia et al., 2022). Previous mechanical studies suggested a plane of isotropy for the material properties (Chia and Hull, 2008), which led to models that took transverse isotropy into account (Spilker et al., 1992; LeRoux and Setton, 2002). Fibril-reinforced modeling has been included in a few studies (LeRoux and Setton, 2002; Abraham et al., 2011; Danso et al., 2015; Danso et al., 2017; Seyfi et al., 2018). Freutel et al. (2015) and Seyfi et al. (2018) presented a constitutive model that takes the local collagen network into account based on the strain energy density (SED) function proposed by Holzapfel et al. (2000). Both of these studies used the inverse finite element method to determine the regional variation in material properties. Despite having the advantage of allowing materials to be tested non-invasively while retaining in vivo conditions, this technique has the disadvantage of requiring a large number of simulations (Bäker and Shrot, 2013). Abraham et al. (2011) presented an anisotropic hyperelastic model based on circumferential and radial fibers in different regions, however, the samples were extracted only from the central main layer, indicating a lack of layer specificity. Moreover, all of the aforementioned constitutive models have been on animal menisci. For a detailed review of the available constitutive models applied to the meniscus tissue and their sensitivity analysis, the reader is redirected to Elmukashfia et al. (2022).
The observations from mechanical testing and histology examinations confirm variations in the mechanical behavior of the different layers within the regions of the menisci, suggesting the significance of defining distinct region- and layer specificity as well as taking direction dependence into account when modeling the meniscus (Seyfi et al., 2018). The constitutive model based on this data would be advantageous in total knee simulations, which require the capture of the highly complex material behavior of the meniscus with high accuracy. This study is a part of developing a digital twin for human knee joint for practicing arthroscopic surgery (Bjelland et al., 2022). Probing meniscus is a common task in meniscectomy to ascertain the tissue characteristic as being hard or soft (Hu and Desai, 2004), which usually serves as the initial guide for surgeons to diagnose degenerative meniscus (Anetzberger et al., 2014). Hence, the quasi-static deformation must be modeled accurately for providing accurate haptic feedback to the surgeon in surgical training and simulation (Tuijthof et al., 2011). The material model for the meniscus used in the digital twin must be realistic enough to replicate the differing deformation in each layer within the region during the in-vivo probe-meniscus interaction, as the success of pre-operative planning hinges on every aspect of the surgical simulation. In this regard, a constitutive framework for human menisci is presented here based on the strain energy density function proposed by Holzapfel et al. (2015). The mechanical characterization is done by in situ biaxial tensile testing in different layers of each region of the lateral and medial menisci. As our study focused on quasi-static behavior, special attention was given to minimizing the viscoelastic and poroelastic effects. The dispersed collagen orientation is characterized by multi-photon microscopy based on second harmonic imaging. Finally, the material data obtained from these two approaches were incorporated into the constitutive equation. The results help in identifying the anisotropy of different tissue layers in different regions in both menisci. This region- and layer-specific constitutive model aids surgeons in better decision-making and the design of more realistic meniscal prostheses. The paper is organized as follows: The methods section provides an overview of the experimental setup and post-processing of the obtained data. The results section demonstrates novel findings in terms of both collagen organization, regional non-linear anisotropic mechanical response, and structure-function relationships. The discussion section presents the main contributions, comparisons to existing literature, and limitations of the current study. Finally, the overall conclusions and future perspectives are presented.
2 Methods
2.1 Sample preparation and storage
In this study, a total of nine human menisci were examined including five lateral menisci and four medial menisci. The tissues were procured from human cadavers with an average age of 75 years. The research was approved by Regionale komiteer for medisinsk og helsefaglig forskningsetikk (REK midt), Trondheim, Norway dated 27.01.2021 with reference number 214114. This study has followed the ethical principles for medical research involving human subjects outlined in the World Medical Association’s Declaration of Helsinki. The tissues were transported in an ice chamber to minimize any degradation during transport. Once in the laboratory, they were stored in a freezer operating at −28°C. Brief storage of soft tissues in this freezing condition was shown to have minimal effects on the observed biaxial mechanics in previous studies (Duginski et al., 2020). On the day of mechanical testing, the tissues were thawed in phosphate-buffered saline (PBS) solution at room temperature (20°C). To prepare repeatable samples, the following slicing procedure is used: First, the circumferential length is measured using a thread from the tip of the anterior region to the end of the posterior region. Then, the meniscus is sliced into three regions based on one-third of the circumferential measurement (Figure 1A) using a surgical knife. Next, each region is cut into halves (the top half layer and the bottom half layer) using a half-cut plane, as shown in Figure 1B. Finally, the top sample of dimension 10 × 10 mm is extracted from the top half layer, starting from the superior meniscal surface (the surface near the femoral condyle) and extending to around 2 mm (2.1 ± 0.1 mm) normal to it. In the same way, the bottom sample is extracted from the bottom half layer but starting from the half-cut plane. This is to ensure the top sample is representative of a combined superficial and lamellar layer and the bottom sample is from the central-main layer. The sample thickness was ensured to be constant within the central region (2 mm), however, it was intricate to ensure uniform thickness for the whole sample using a surgical knife. A better method could be the protocol presented in Bonomo et al. (2020). In total, six samples were tested per meniscus to quantify their mechanical behavior.
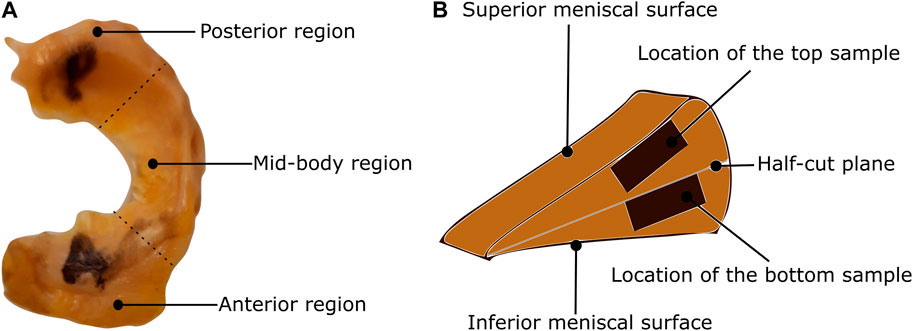
FIGURE 1. Classification of the meniscus tissue into three regions and two layers (A) The top view of the lateral meniscus of the left knee with identification of the posterior, mid-body, and anterior regions. (B) The location of the samples on the cross-sectional view.
2.2 Biaxial mechanical testing
Once the menisci samples were thawed, they were marked with indicative markers using a tissue marking dye (Leica Biosystems, Germany). This ensures a proper distinction between the circumferential and radial directions during testing and imaging. The sample thickness was then measured three times with a caliper (0.01 mm resolution), whereby the average value is reported. Finally, the sample was attached to four barbless hooks (Ahrex, Denmark) on each side, using a 3D-printed template for consistency. The 10 × 10 mm sample was additionally marked with four fiducial markers in the center, with an approximate area of 2 × 2 mm, as shown in Figure 2A. The samples were submerged in a PBS bath heated to 36°C for the entire duration of the biaxial mechanical test. Doing so ensures that the sample is hydrated in an isotonic solution that mimics the in-vivo conditions and minimizes fluid leakage/drying up of the tissue. The hooks are connected to the handle mechanism with surgical Gore-Tex CV5 sutures (Gore Medicals, United States). The custom-designed handle mechanism consists of a rotatable base with two 1 mm thick bars representing the sutures’ attachment sites. These bars can rotate freely around the base axis, which is equipped with an all-ceramic bearing (SMB Bearings, United Kingdom). This mechanism enables self-alignment when mounting the sample and minimizes the shear forces during the experiments (Sommer et al., 2015). The custom-built biaxial machine (see Figure 2B) is equipped with four step motors that are individually controlled via an inductive displacement sensor (BAW M18MG, Balluff, Germany). The loads are also measured with an axial load transducer (U9C/50 HBM, Germany). Using a custom software for digital image correlation (Fagerholt et al., 2013), the fiducial markers are tracked during the test and synchronized with the measured forces at a frequency of 2 Hz. Before starting the test, preconditioning of five loading-unloading cycles at a rate of 0.1 mm/s was applied up to a stretch of 1.30. Additionally, the sample was subjected to a preload of 0.01 N in both directions to remove any tissue slack. Three sets of displacement-controlled tests, each repeated three times, were carried out at a speed of 0.1 mm/s up to the maximum load 1 N. The total loading cycle varied from sample to sample with an average time of 40 s. The chosen quasi-static loading rate ensures that the measured mechanical response corresponds to the passive-elastic properties of the tissue, with minimal relaxation and creep effects (Wang et al., 2018). However, pausing the test momentarily for microstructure imaging for instance would affect the stress-stretch response as seen in Pukaluk et al. (2023). Sufficient care was taken in the design of the experiment to only measure the elastic response of the tissue and minimize any relaxation effects. Further, the damping effect has not been measured using cyclic testing. The displacement configurations used in the three test sets represent a different displacement ratio of circumferential to radial direction (1 : 1, 1 : 1.2, 1.2 : 1). The acquired force and deformation data are then used to compute the stress-stretch curves of the sample.

FIGURE 2. Sample preparation and mounting protocol for biaxial tension testing (A) The sample is placed on a 3D-printed template. The sample is attached with barbless hooks and sutures, marked using tissue marking dye. (B) Custom-built biaxial tensile test set-up. The sample is submerged in PBS. (C) The sample after optical tissue clearing.
2.3 Optical tissue clearing
The same samples that were subjected to biaxial tension were chemically fixed prior to the microscopy investigations. Samples were chemically fixed in a 4% formaldehyde solution for a minimum of 36 h and also dehydrated based on graded absolute ethanol: 50%, twice 70%, twice 95%, and twice 100% with each step lasting 30 min (Schriefl et al., 2013). The fixation and dehydration were performed in an automated vacuum tissue processor (ASP 300, Leica Biosystems, Germany). Once the tissue sample was chemically fixated, it was then subjected to an optical clearing protocol called SeeDB (Ke et al., 2013). The tissue samples were treated in graded solutions of fructose: 4–8 in 20%, 4–8 in 40%, 4–8 in 60%, 12 in 80%, 12 in 100%, and 24 h in SeeDB solution. The solutions were maintained at room temperature while being mixed uniformly on a tube rotator for the entire duration of the clearing. A representative cleared sample is shown in Figure 2C.
2.4 Second harmonic generation imaging
SHG imaging of collagen fibers was performed using a Leica SP8 confocal microscope (Leica Microsystem, Germany). Before the SHG acquisition, the measurement of the entire thickness was verified with the bright field microscope in the Leica SP8 to ensure that the SHG scanning occurs through the entire thickness of the samples. To induce the second harmonic of collagen fiber, the laser excitation was set to 890 nm. The Leica HCX IRAPO 25×, NA 0.95 water objective with a working distance of 2.4 mm was used for image acquisition. To compensate for scattering at greater depth, the laser power was increased linearly (z compensation). The scanning took place at the center of the sample with an area of 465 × 465 μm and a resolution of 0.45 μm/pixel from the top side (superior). Imaging was performed at 2 μm intervals across the entire thickness of the sample. The optically cleared samples were imaged up to a depth of 500 μm with an excellent resolution of the collagen fiber network, compared to around 150 μm for non-cleared tissue samples.
2.5 Collagen fiber morphology quantification
A user-defined Matlab script based on the method documented in Polzer et al. (2013) is used to quantify the collagen fiber dispersion in each layer. Prior to the analysis, a 2D Tukey (tapered cosine) window was applied to the image. Each image was then Fourier transformed and multiplied by its complex conjugate to form the power spectral density, which distinguishes the fiber direction by frequency and orientation. A wedge-shaped filter was used to extract the fiber orientations at a certain angle θ. The wedge-shaped filter ranges from −89.5° to 89.5° with an increment of 1° to determine the relative amplitude of the fiber distribution. A moving average filter with a range of 5° was applied to the angle θ to smooth the data. For a certain anisotropic fiber morphology, the fiber distribution is then fitted by a von Mises probability distribution as defined in Eq. 1 and Eq. 2.
Here, a is the concentration parameter defining the dispersion of the fiber family, and μ is the mean orientation angle of the fiber family. Finally, I0(a) is a zero-order Bessel function of type I, which acts as a normalization parameter. The number of images recorded for each sample varied based on the signal-to-noise ratio and the amount of information that could be extracted. As the scan depth increased, the noise dominated the images, which were therefore discarded. The accepted MPM scan images were then analyzed independently to extract the fiber morphology. To get a representative fiber morphology of the entire tissue stack, the average orientation distribution over the entire image stack was computed and used in the modeling process. In addition to that, the relative amplitude of the orientation quantified on all the slices of the entire stack was compiled together to create 3D intensity plots in Matlab as in Cavinato et al. (2017). For this, the obtained relative amplitude values were normalized between 0 and 255 (8-bit image) to produce the color map of the stack’s orientation distributions. An example of a 3D intensity plot and its relation to the planar fiber distribution of a given image slice is shown in Figure 3.
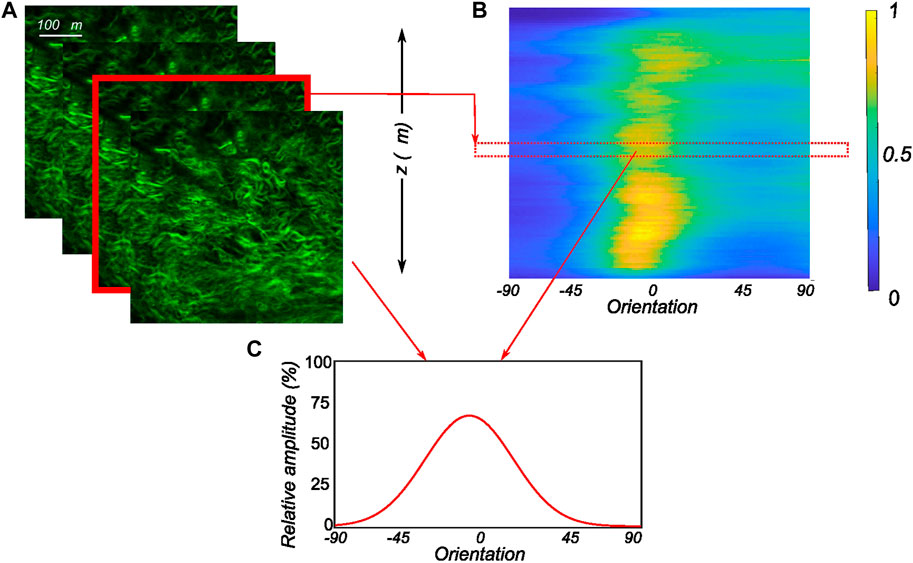
FIGURE 3. Postprocessing of the obtained MPM image stacks (A) The recorded SHG signals through the thickness of the tissue in 2 μm intervals with each image in the stack analyzed to extract the planar orientation distribution. (B) The computed orientation distributions of all images of the MPM stack as an intensity plot with 1 representing the peak of collagen intensity and 0 representing low collagen intensity. (C) The corresponding planar orientation distribution of an individual slice of the MPM stack along with its relative position in the 3D intensity plot.
2.6 Constitutive model
An anisotropic hyperelastic constitutive model as presented in Holzapfel et al. (2015) is used for describing the mechanical behavior of the human menisci. The deformation gradient F is defined in relation to an undeformed reference configuration, that is, assumed to be stress-free. The right Cauchy-Green tensor is then calculated as C = FTF. The modified counterpart of C with first invariant I1 = tr(C) can be written as
The isotropic function is assumed as the neo-Hookean model and ψiso is given by
where c1 > 0 is a material parameter. The anisotropic part of the strain energy density function is described as follows:
where k1 is a parameter with the dimensions of stress and k2 a dimensionless parameter, while
where I is the second-order identity tensor, M is a unit vector in the direction of the mean orientation of the fiber family, and γ is the dispersion parameter of the fiber family. The dispersion parameter is related to the von Mises concentration parameter through the equation
Given the planar biaxial loading, we denote the subscripts c and r to represent the two in-plane orthogonal directions: circumferential and radial, respectively. The out-of-plane axis is represented by the subscript z. The stretch components λc and λr are computed from the DIC measurements. The condition of incompressibility gives λz =
The mean fiber orientation unit vector can be written as M = cos(μ)ec + sin(μ)er, where μ is the angle between M and ec. The unit vectors ec and er are along the circumferential and radial direction, respectively. We define h = FHFT such that tr(h) = tr(CH), whose diagonal components are defined in Eq. 8.
Hence, the anisotropic components of the Cauchy stress tensor can be written as:
The isotropic components of the Cauchy stress tensor are
Together with Eq. 9 and Eq. 10, the non-zero components of the Cauchy stress are
where c and r represent the circumferential and radial components respectively. It is to be noted that the stress components in Eq. 11 are derived by enforcing an incompressibility constraint, meaning the isotropic component is not a direct derivative of Eq. 4. The isotropic material parameter is presumed to account for the contributions of the ground matrix and elastin. Based on MPM investigations, a single fiber family was chosen for the layers of the menisci, whose stress components are described by Eq. 9 and Eq. 10.
2.7 Inverse material parameter identification
Quantified fiber morphology derived from MPM image stacks reduced the number of parameters to be identified. A cost function representative of the standard error of estimate (SEOE) (Peddada et al., 2005), based on the experimental and analytical stress-stretch responses, was used in the optimization process. The structural parameters: mean fiber orientation and fiber dispersion were identified from the SHG image stacks. The material mechanical parameters (c1, k1, k2) were inversely identified in the parameter optimization process. Constraints were imposed based on the parameters in order to ensure a uniform sampling of the initial population. Multiple runs of the optimization algorithm as well as the second-order derivatives at the optimized point aimed at avoiding the identified parameter set that did not correspond to local minima. The identified parameter set obtained by minimizing the cost function was accepted as the optimal value.
In the above equation, n is the number of data points considered for each sample, following a spatial discretization of stretch (n > 20). σexp and σanalytical are the experimental and analytical stress values at each point on the discretized stretch domain.
3 Results
3.1 Biaxial mechanical response of human menisci
We observed the typical non-linear, anisotropic membrane stress-stretch response of the meniscal layers under all loading protocols. For the top samples, the radial and the circumferential directions displayed similar extensibility. The coupling between the two tissue directions was also evidenced in the non-equibiaxial tension protocols. For example, under circumferentially dominant tension protocols, radial stress decreased while circumferential stress increased. The mechanical response varied significantly with the region and layer of the sample. Figure 4 shows the delineated mechanical response of samples tested from a lateral and a medial meniscus, respectively. Comparing the two menisci as a whole, the medial menisci were found to be stiffer in the circumferential direction (upto 14%), while the radial direction was not significantly different among the two menisci (the difference is ≤3.4% across all the biaxial loading protocols).
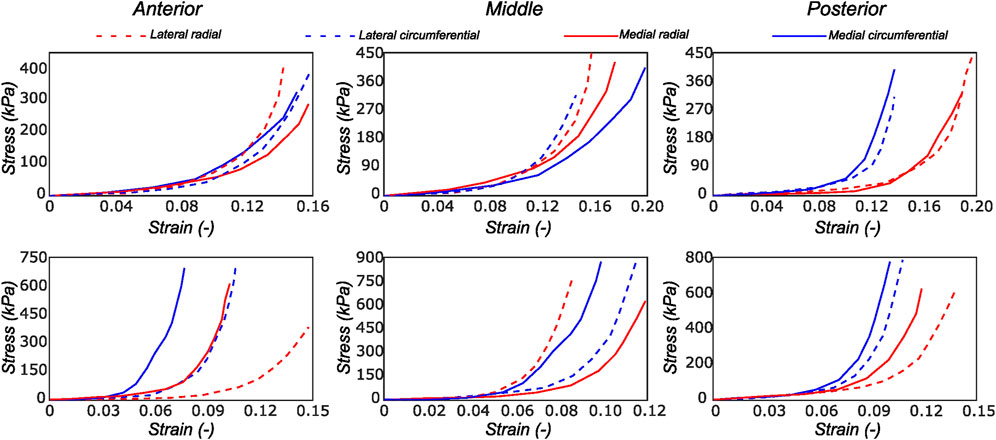
FIGURE 4. Computed Cauchy stress-strain curves for the meniscus samples (LM1 and MM1) obtained from the biaxial testing protocol. The top and bottom rows of subplots represent the samples from the top and bottom samples, respectively. Column-wise, they represent the anterior, mid-body, and posterior regions.
3.2 Quantification of collagen fiber morphology
The thickness of human menisci can go up to 6 mm. Although imaging of the collagen fiber architecture through the whole thickness is extremely challenging, the optical clearing technique used in this study enabled us to image individual layers up to 500 μm.
3.2.1 Lateral menisci
The collagen fiber morphology through the imaged thickness for samples obtained from different regions of a representative lateral meniscus is shown in Figure 5 as a contour plot. The color bar depicts the relative intensity of the fibers along a given orientation (x-axis) and a given depth (y-axis). As illustrated in Figure 5, all samples show rich collagen content with their orientation evolving through the thickness of the top layer. The distinctive characteristic of the top samples was the presence of randomly organized fibers, with the mean fiber orientation varying with the anatomical regions as shown in the top row subplots of Figure 5. The mean fiber orientation (μ in Table 1) of samples from the top layer was −33.2 ± 12.8° in the anterior region, to −40.1 ± 10.2° in the mid-body, and 36.7 ± 15.7° in the posterior region. On the contrary, the samples from the bottom layer were characterized by densely packed collagen fibers predominantly oriented in the circumferential direction. This was observed for all thicknesses and for the three anatomical regions (anterior, mid-body, and posterior), as illustrated in the bottom row profiles of Figure 5. The mean fiber orientation was 4.7° in the anterior region, −2.4° in the mid-body, and −8.5° in the posterior region. Within each region, the variation in computed dispersion of collagen fiber orientations was
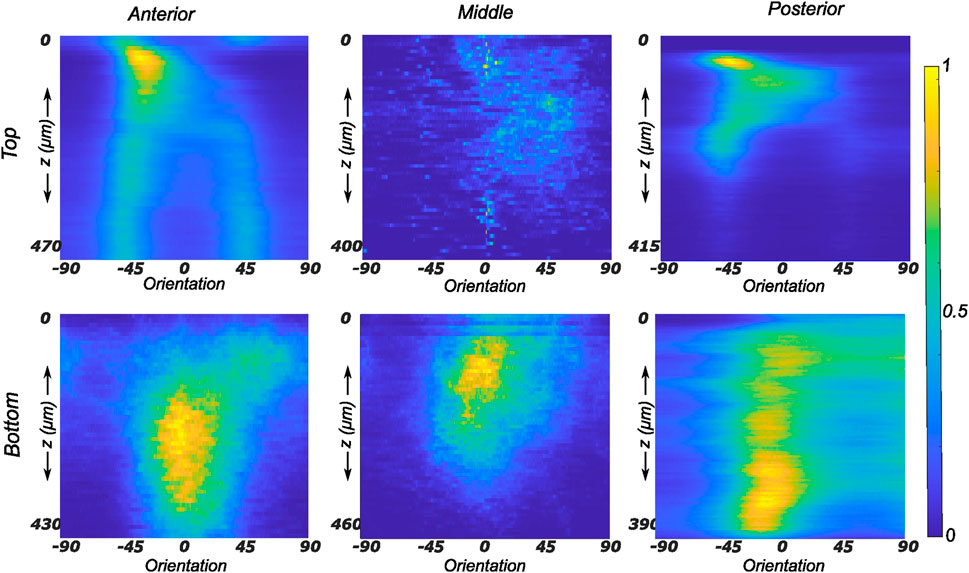
FIGURE 5. Depth profile of collagen fiber intensity of samples obtained from the lateral meniscus. The images recorded on the entire stack were analyzed individually and compiled together in Matlab to produce an intensity plot representative of the transmural variation in collagen fiber morphology. The top and bottom rows of subplots represent the top and bottom samples, respectively. Column-wise, they represent the anterior, mid-body, and posterior regions.
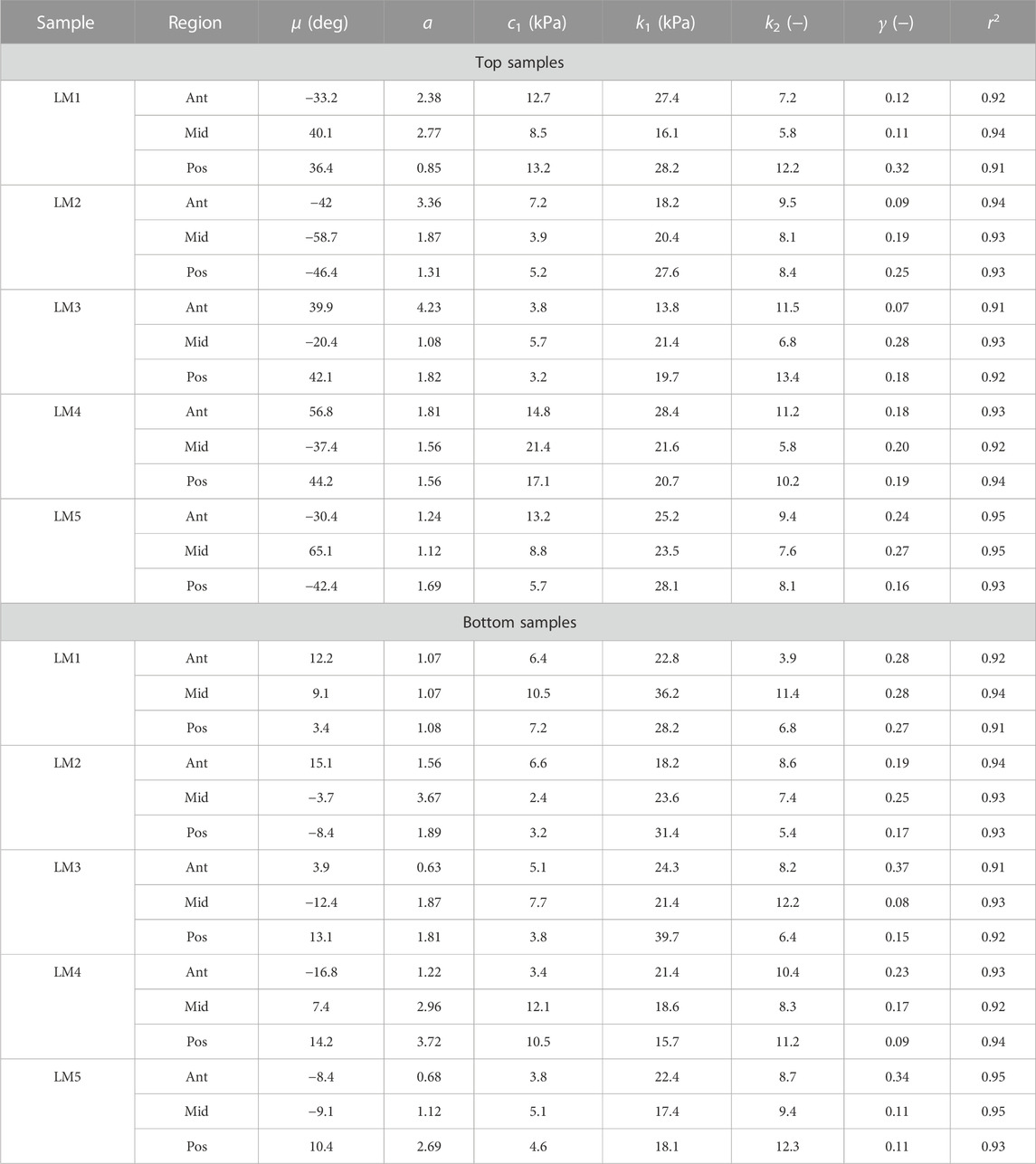
TABLE 1. Collagen morphology and tissue material parameters for top and bottom samples from lateral menisci. LM denotes lateral meniscus.
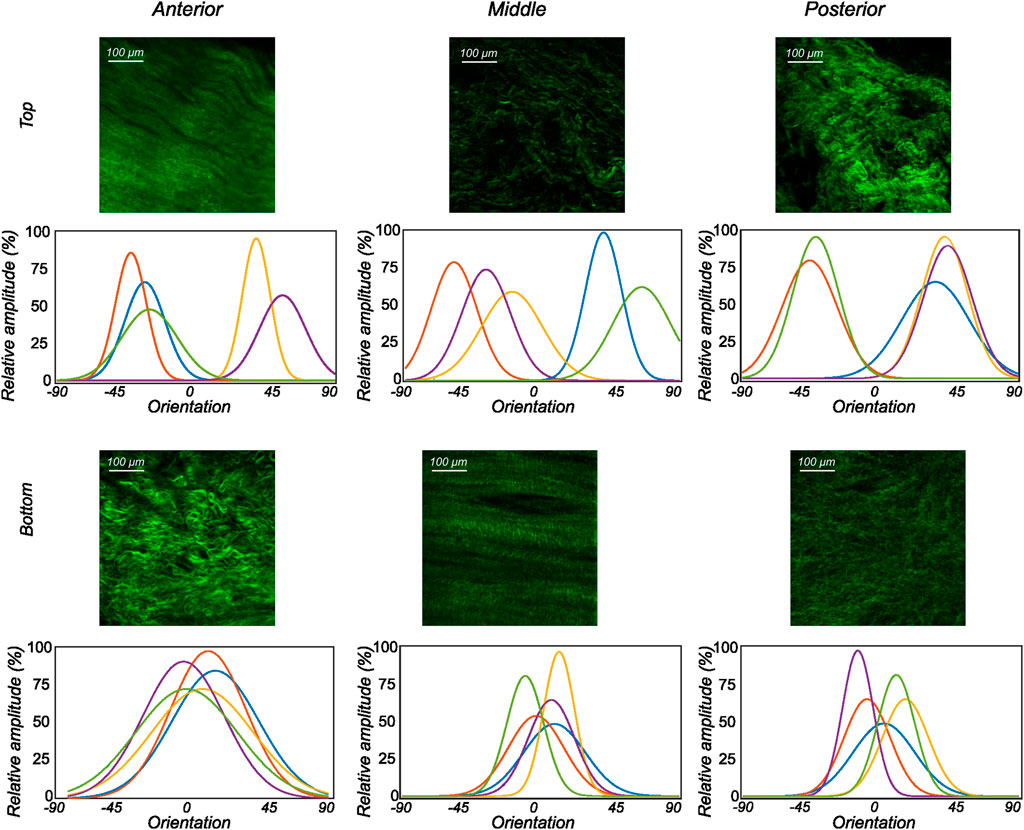
FIGURE 6. The orientation distribution computed on each image slice of individual image stacks was averaged through the thickness to obtain the representative collagen orientation distribution of the sample. Here, the computed orientation distribution for samples excised from lateral menisci is shown. The top and bottom profiles represent the samples from the top and bottom samples, respectively. Column-wise, they represent the anterior, mid-body, and posterior regions.
3.2.2 Medial menisci
The fiber morphology in the medial menisci showed similar characteristics to the lateral menisci. The fibers in the top samples were sparsely arranged, and the preferred orientation varied between different regions and among different menisci. For instance, as shown in the top row profiles of Figure 7, the mean fiber orientation (μ in Table 2) of samples from the top layer varied from −60.8 ± 13.6° in the anterior region to 55.6 ± 17.1° in the middle, to 49.4 ± 20.2° in the posterior region. Within the bottom layer, in terms of their preferred orientation, the fibers were aligned close to the circumferential direction (bottom row profiles in Figure 7). The mean fiber orientation was computed to be 9.4° in the anterior region, 9.2° in the mid-body, and 9.1° in the posterior region (absolute value away from 0). The dispersion of fibers in both layers was observed to be similar, contrary to lateral menisci. The medial menisci were found to have a significantly higher dispersion of fibers within the top and bottom samples than the lateral menisci (18.3 vs. 11.6°). In contrast to the lateral menisci, the fiber morphology of bottom samples showed a higher degree of variation among the medial menisci, as shown in Figure 8. The corresponding von Mises distribution parameters as well as the inversely identified anisotropic material parameters for four medial menisci are tabulated in Table 2.
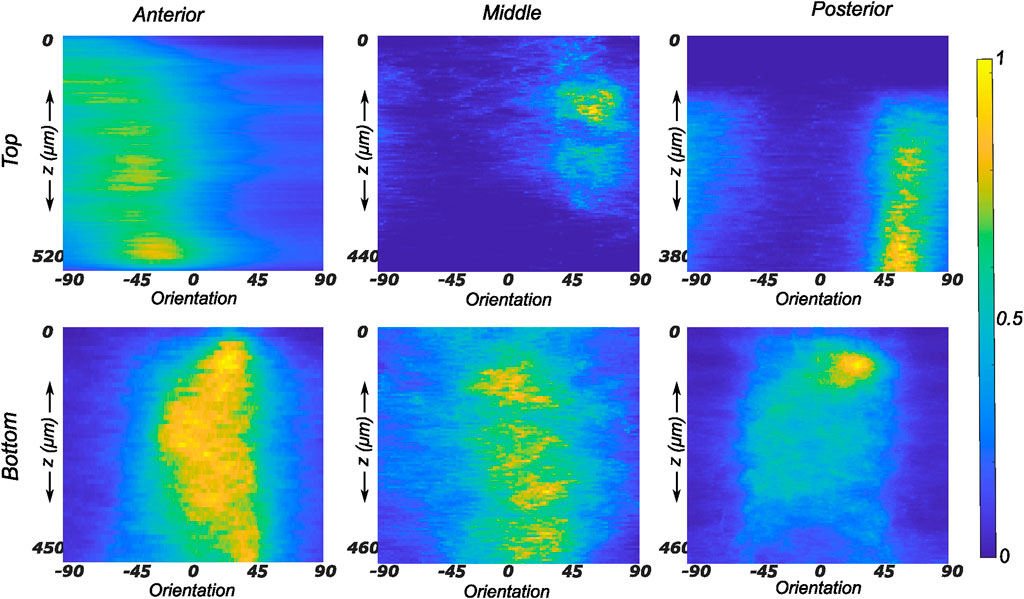
FIGURE 7. Depth profile of collagen fiber intensity of samples obtained from the medial meniscus. The images recorded on the entire stack were analyzed individually and compiled together in Matlab to produce an intensity plot representative of the transmural variation in collagen fiber morphology. The top and bottom rows of subplots represent the top and bottom samples, respectively. Column-wise, they represent the anterior, mid-body, and posterior regions.
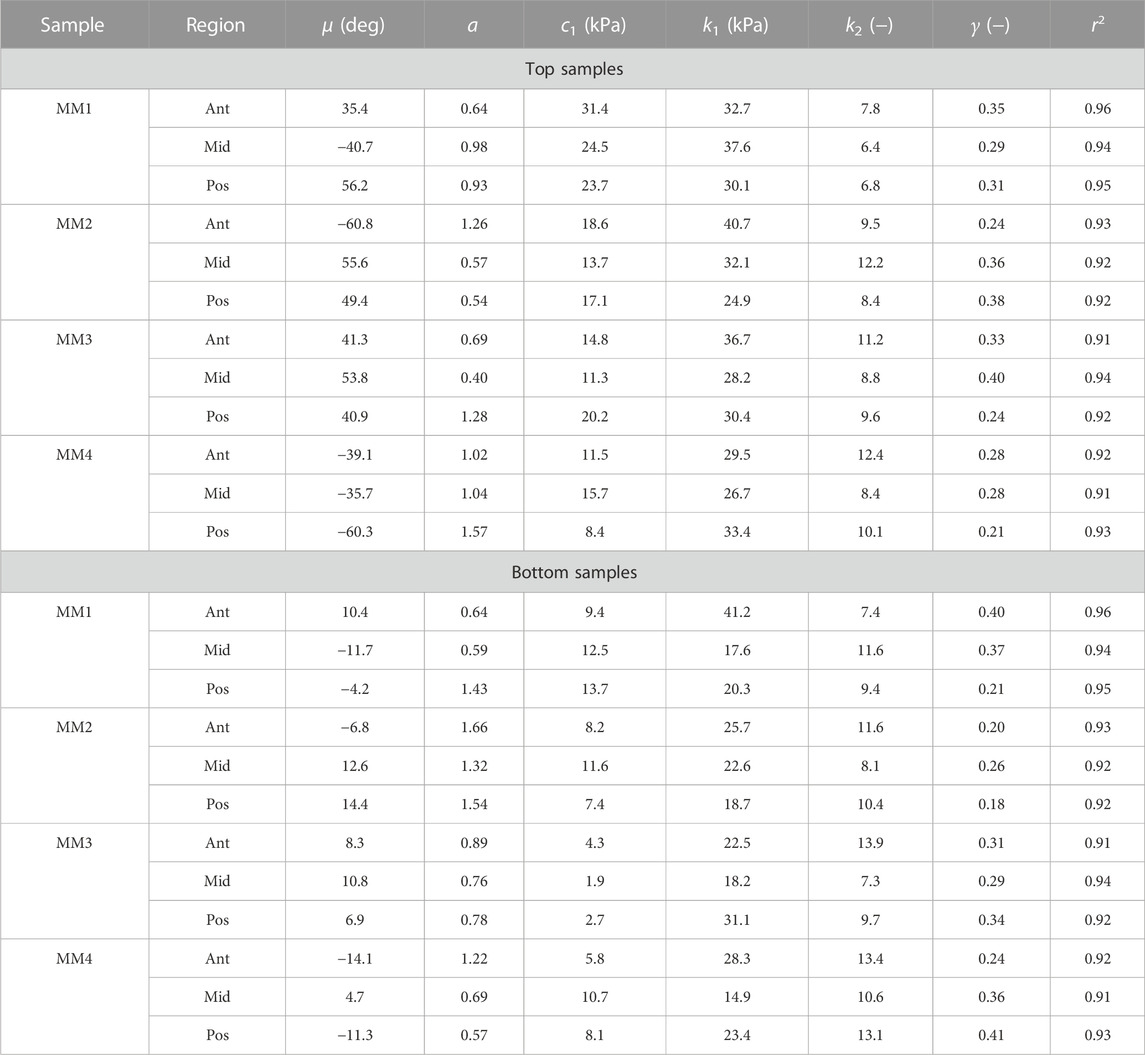
TABLE 2. Collagen morphology and tissue material parameters for top and bottom samples from medial menisci. MM denotes medial meniscus.
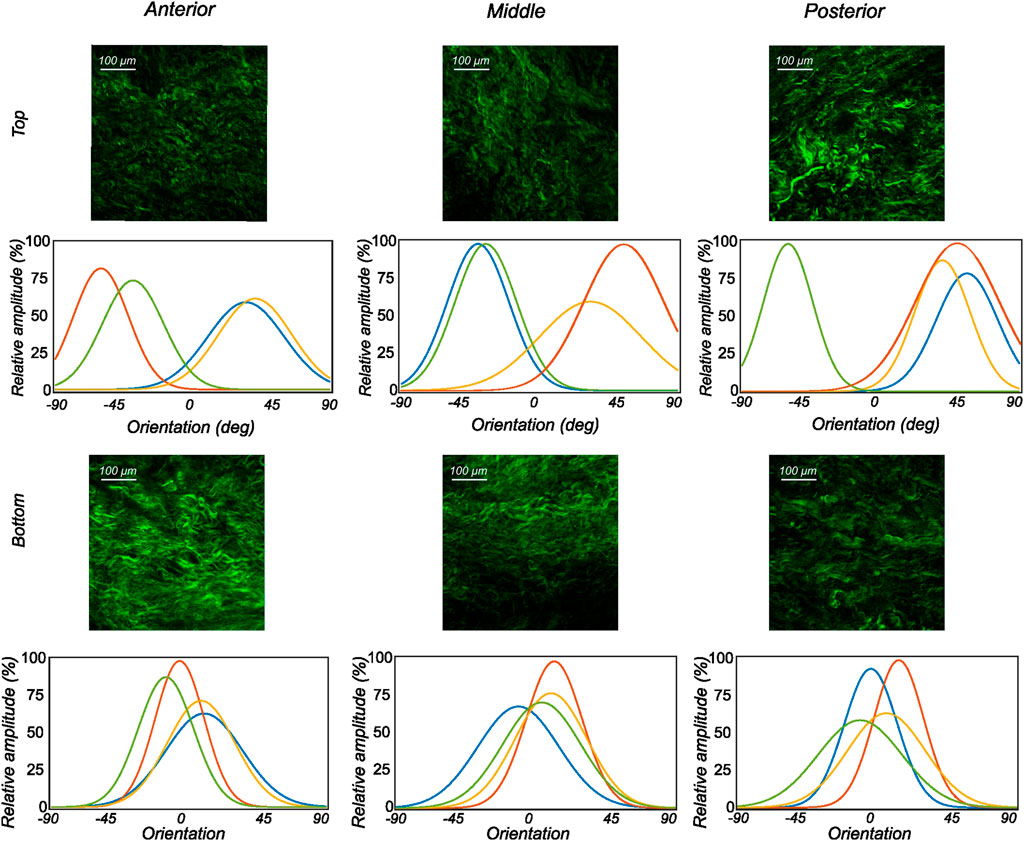
FIGURE 8. The orientation distribution computed on each image slice of individual image stacks was averaged through the thickness to obtain the representative collagen orientation distribution of the sample. Here, the computed orientation distribution for samples excised from medial menisci is shown. The top and bottom profiles represent the samples from the top and bottom samples, respectively. Column-wise, they represent the anterior, mid-body, and posterior regions.
3.3 Constitutive modeling
The proposed constitutive model in Section 2.6 takes into account the mean fiber morphology in the tested tissue sample to better describe the anisotropy of the meniscal tissue. Figure 9 illustrates the predictive capability of the constitutive model on a single sample, and it is evident that the model is in good agreement with the experiment data. The constitutive model parameters for the top and bottom samples from the anterior, mid-body, and posterior regions of each lateral and medial meniscus are tabulated in Table 1 and Table 2, respectively. The derived von Mises distribution parameters are included in columns 5, 6, and 7. In almost all samples examined, a single fiber family was deemed sufficient to satisfactorily represent the collagen fiber morphology within the tissue. However, the anterior segment from lateral meniscus 2 (LM2) was found to have two perpendicular mean fiber orientations across its thickness. To simplify, the fiber orientations were averaged into a single vector, thereby approximating it with a single fiber family. Nonetheless, a single representative fiber family in a constitutive tissue model could adequately capture the mechanical behavior of the sample. The constitutive model predicts the mechanical behavior of the tissue samples with good agreement, and an average r2-value is 0.94. Overall, the isotropic material constant for the extracellular matrix was found to be relatively small (10.4 ± 5.8 kPa). The anatomical specificity, including the region and depth variability, is obvious from Table 1 and Table 2.
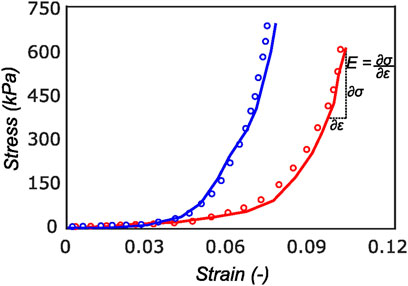
FIGURE 9. Cauchy stress versus strain for a sample in the radial (red curve) and circumferential direction (blue curve). The experimental data (solid curve) is well represented by the model (dotted curve) with r2 of 0.94. On the final loading regime of the red curve, the computation of linear elastic modulus is illustrated. Most of the tissue stiffness in this loading region is assumed to be contributed by fibers.
4 Discussion
In this paper, the structure-based mechanics of human menisci are quantified using an anisotropic hyperelastic material model. The collagen fiber morphology is examined within five lateral menisci and four medial menisci at three different anatomic regions and two layers through the depth of the tissue. SHG imaging combined with planar biaxial testing permits a high degree of coupling between the material’s anisotropic mechanical response and the underlying collagen fiber morphology. To the best of our knowledge, this is the first study to explore the collagen fiber morphology throughout the human meniscal tissue and incorporate it into the tissue’s mechanical response.
We found that using the SeeDB (Ke et al., 2013) optical clearing protocol, it is possible not only to visualize, but also to quantitatively analyze the local microstructural organization of collagen network in anterior, mid-body, and posterior regions of the human menisci in 3D. Each sample was imaged to a depth of up to 500 μm through the thickness. An FFT (Fast Fourier Transform)-based automatic algorithm was used to quantify the distribution of collagen fibers. The automated process ensures high reproducibility but poses some challenges. The Fourier transform assumes a periodic signal, so a window should be applied to the images before the Fourier transform. In the current study, a tapered cosine window is used to minimize the loss of information at the edges of each image (layer). The results of the local microstructural orientation analysis indicate that there are substantial differences in collagen organization in the top samples. The mean orientation was often computed to be around the diagonal direction (±45°) with high dispersion. Conversely, the samples from the bottom layer showed consistent collagen fiber organization close to the circumferential direction with varying dispersion. Evidently, the majority of collagen found in the bottom layers of the human menisci was organized into circumferential bundles with some randomly oriented fibers.
This study has refined the understanding of collagen fiber structure in the human meniscus. Several imaging techniques have been previously utilized to characterize the collagen fiber morphology in meniscus tissue; including polarized light microscopy (PLM) (Kiraly et al., 1997; Danso et al., 2017), second harmonic generation (SHG) via multiphoton microscopy (Brown et al., 2014; Vetri et al., 2019), small-angle x-ray diffraction (Aspden et al., 1985; Moger et al., 2007), scanning electron microscopy (Zhu et al., 2021), and μCT (Karjalainen et al., 2021). Apart from μCT examinations, all other studies were limited to an imaging depth of 100 μm in human meniscus tissue. The μCT investigation covers a volume of interest of 1800 μm3. At this point, direct comparisons could be made. The X-ray diffraction conducted on two human samples (Aspden et al., 1985) showed that the top superficial layer is dominated by a mixture of radial and randomly oriented collagen fibers, extending up to a depth of 100 μm. Beyond this depth, they report circumferentially oriented fiber bundles within the bulk of the tissue. The SHG imaging conducted in Vetri et al. (2019) describes in detail the collagen fiber architecture in both circumferential and radially oriented samples, with the transmural imaging scan depth limited to 60 μm as compared to 500 μm in the current study. However, their results from the circumferential sections of a human lateral meniscus are in agreement with our observations, where the mean orientation of collagen fibers is 9.5 ± 3.2° compared to their 11°. While their study was extensively focused on explaining the micro-scale and nano-scale architecture of collagen fibers in the human menisci, we are more interested in combining the mean collagen morphology with the tissue’s mechanical response.
Due to the non-homogeneous composition and the anisotropic mechanical properties of the meniscus, the local stress–strain response varies greatly with location. Therefore, the experimental testing apparatus should encompass tensile, compressive, and shear stresses and strains. Confined compression tests conducted on the tissue (Proctor et al., 1989; Joshi et al., 1995) are important to better understand the bi-phasic environment of the meniscus. Biomechanical parameters such as compressive stiffness, tissue permeability, and aggregate water content could be derived from such testing protocols, which are all complex material modeling and simulations. Dynamic shear testing (Anderson et al., 1991) reveals the aggregate region-specific shear modulus of the tissue given that shear loading is one of the primary mechanisms for meniscus tear (Siegel, 1988). However, considering that the meniscus is rich in collagen fibers which do not contribute to compressive load bearing, tensile testing is important for understanding their role in the maintenance, degeneration, and repair of the meniscus. The majority of tensile testing was limited to uniaxial testing protocols (Proctor et al., 1989; Tissakht and Ahmed, 1995; Goertzen et al., 1997), which limits the understanding of material in-homogeneity and anisotropy. In the current study, we quantify the biaxial tensile material properties of nine human menisci with respect to regional and depth-wise variations. This is a necessary improvement on existing literature as the tissue undergoes in-vivo loading in multiple directions simultaneously (Walker and Erkiuan, 1975).
Based on our region- and layer-specific studies of the human menisci, we can conclude that its mechanical response is highly anisotropic. Therefore, the constitutive model should be complex enough to reflex this behavior. Early studies were limited to the premise of linear elasticity (Tissakht and Ahmed, 1995), but based on the results of experimental testing, transversely isotropic (Wheatley et al., 2015) and anisotropic hyperelastic material models (Abraham et al., 2011) have been developed (tension, indentation, shear, etc.). The extent of non-linear anisotropic hyperelastic material models used for describing the mechanics of meniscal tissue is either limited to phenomenological descriptions (Haemer et al., 2012) or structure-based models that take into account the morphology of collagen fibers in the tissue (Freutel et al., 2015; Seyfi et al., 2018; Abraham et al., 2011). However, the studies reported in Freutel et al. (2015); Seyfi et al. (2018) are based on inverse finite element modeling using indentation testing data, which is not sufficient to capture the complex anisotropic behavior of the tissue. Moreover, they did not conduct any histological imaging but identified collagen fiber morphology parameters inversely, which can be misleading. On the other hand, the study on the bovine menisci reported in Abraham et al. (2011) utilizes previously reported micro-structural imaging data (Hutton, 1993) and assumed two perpendicular fiber families in their modeling process. While this is well-founded, the consideration of collagen fiber dispersion could further enhance the material modeling. In the current study, we incorporated region-specific and layer-specific collagen fiber morphology in the constitutive model to better explain the structure-function relationship in the tissue’s mechanical response. We included fiber dispersion details in addition to the fiber orientation; both of these material parameters are indicators of collagen fiber morphology and were derived from SHG imaging. This is intuitive since the amount of reorganization of fibers during loading influences the mechanical response in different directions, which cannot be expressed by just considering the mean fiber orientation.
The estimated values of k1 and k2 in Table 1 and Table 2 represent the fiber properties, which are stress-like and dimensionless parameters, respectively. The average values of these parameters for the lateral meniscus are 23.3 ± 5.9 kPa and 8.8 ± 2.3; and for the medial meniscus, they are 27.8 ± 7.2 kPa and 9.9 ± 2.1. This indicates the anatomical specificity of the human meniscus, with the medial meniscus being stiffer than the lateral meniscus. The average fiber properties of samples from six locations tabulated in Table 3 confirm the width- and depth-wise difference in material properties. This variation is stronger in the medial menisci than in the lateral menisci. Among the samples from the top layer in the medial menisci, the anterior region showed higher values of fiber properties (k1 and k2 are 34.9 ± 4.8 kPa and 10.2 ± 2.0, respectively), while in the lateral menisci, the posterior region displayed higher values (k1 and k2 are 24.8 ± 4.2 kPa and 10.4 ± 2.3, respectively). This pattern was also observed in the bottom layer sample. When anatomical specificity was compared along with region- and layer-specificity, the top layer from the anterior horn of the medial menisci had the marginally highest stiffness with average k1 and k2 values (34.9 ± 4.8 kPa and 10.2 ± 2.0).
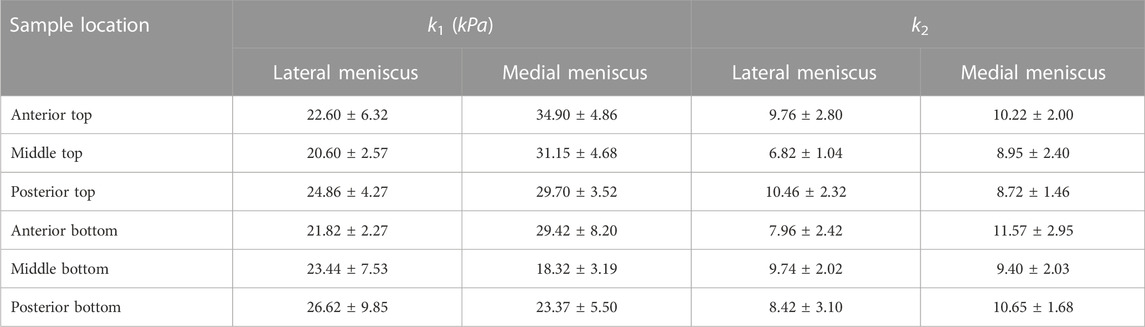
TABLE 3. The average values of k1 and k2 for samples from different locations of the lateral and medial menisci.
The tangent modulus in the final loading regime (see Figure 9) has been computed to take into account the stiffness of tissue post collagen fiber engagement. The overall pooled results show that the circumferential direction was significantly stiffer than the radial direction. This was expected given the presence of primarily arranged circumferential fiber bundles in all the bottom-layer samples and a mixture of circumferential and near-diagonally oriented fiber bundles in top samples. This is in accordance with previously conducted tensile tests (Tissakht and Ahmed, 1995; Kahlon et al., 2015). Further assessment of the regional and layer-specific results revealed substantially higher circumferential elastic moduli in the anterior regions of both menisci (lateral and medial) within bottom-layered samples (see Figure 10 and Figure 11). A similar trend was not observed in the top samples, with both circumferential and radial moduli being comparable to each other. Within both the top and bottom samples, the medial menisci displayed a slightly higher modulus compared to the lateral menisci. An interesting comparison to note here is the study by Proctor et al. (1989), where uniaxial tension tests in the superficial layer revealed a near isotropic behavior with a mean elastic modulus of 59.4 MPa. The reported decrease in radial elastic modulus with the depth of the tissue is not seen in our observations, as shown in Figure 12. This could possibly be due to two reasons: firstly, regional sectioning data was not mentioned in their study, which could create some ambiguity; secondly, fiber kinematics are not well represented in uniaxial tension, which often leads to an underestimation of elastic modulus in directions away from principle fiber orientations. Our findings demonstrate that both the circumferential and radial moduli increase with depth, while the circumferential modulus showed more increment. A one-way ANOVA test was used to evaluate the statistical significance between different groups of elastic moduli in lateral and medial menisci (anterior, middle, and posterior regions; top and bottom layers), as shown in Figures 10, 11. Within each layer, all three regions were compared independently in circumferential and radial directions. A p − value < 0.05 was considered to be representative of statistical significance. As shown in Figure 10, the elastic moduli in the top layer were found to vary significantly between regions in the circumferential direction, while the elastic moduli in radial direction were found to vary significantly between anterior and middle regions. Similarly, in the bottom layer, elastic moduli were found to vary significantly between regions in the radial direction, while the elastic moduli in circumferential direction were found to vary significantly between middle and posterior regions. With reference to Figure 11, the radial elastic moduli were found to be significantly different between all regions in the top layer, while significance was only observed between anterior and middle regions for circumferential elastic moduli. Within the bottom layer, statistical significance was observed between anterior and middle, middle and posterior regions for circumferential and radial elastic moduli respectively. However, it is to be noted that the sample size utilized to conduct this analysis is low (n = 4/5) and should be updated as and when more samples are tested. Moreover, the reported range of elastic modulus in our study
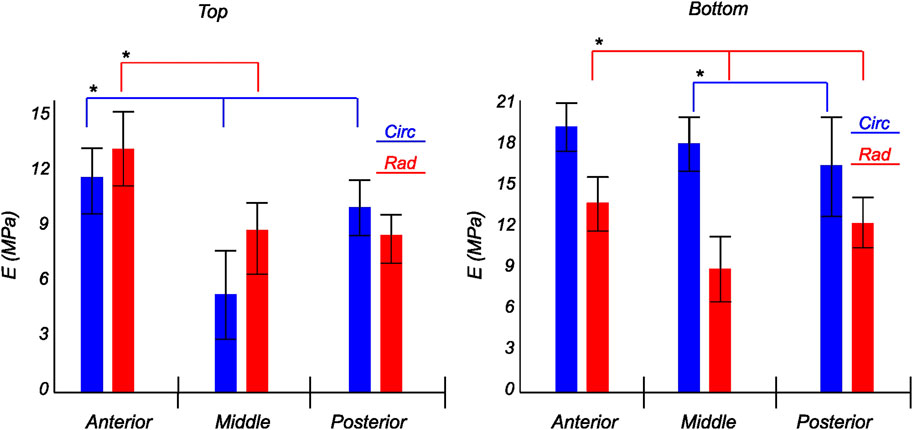
FIGURE 10. Computed elastic modulus of a human lateral meniscus in the final loading regime: top layer (left), and bottom layer (right). The anisotropic nature of the material is shown with the circumferential stiffness represented in blue and the radial stiffness represented in red. Within each layer, the anterior, middle, and posterior regions are presented to see the regional variations. * indicates statistical significance from a one-way ANOVA test with p-value
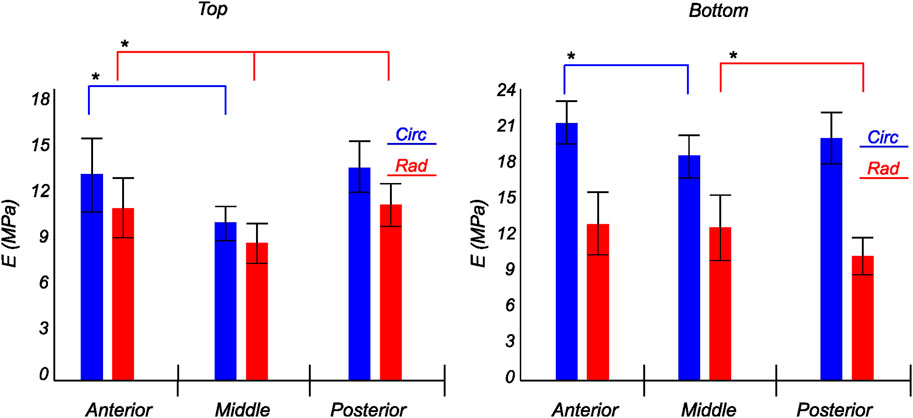
FIGURE 11. Computed elastic modulus of a human medial meniscus in the final loading regime: top layer (left), and bottom layer (right). The anisotropic nature of the material is shown with the circumferential stiffness represented in blue and the radial stiffness represented in red. Within each layer, the anterior, middle, and posterior regions are presented to see the regional variations. * indicates statistical significance from a one-way ANOVA test with p-value
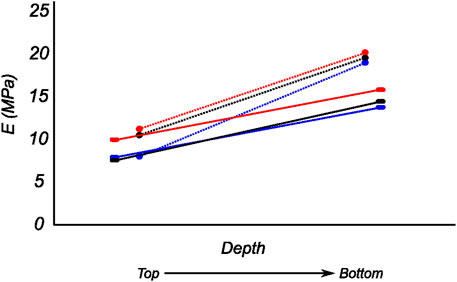
FIGURE 12. Computed biaxial elastic modulus of all meniscus samples showing regional and depth-wise variation. The circumferential and radial moduli are shown as dotted and solid lines respectively. Regions anterior (red), middle (blue), and posterior (black) are presented here.
Our study has the following limitations. The samples used in our study represented a geriatric group because of the difficulties in obtaining younger cadaveric subjects. Even if we used cadavers with no history of arthritis and discarded the ones with visible tears, we cannot guarantee the non-degeneracy of the tissue as it is from elderly people. Using the model herein, we could model both young and old tissue, but it requires sample studies from donors of different age groups (Haskett et al., 2010). Therefore, against the background of patient-specificity based on demography, this study is limited to the older population. Further, we assumed the outcomes of in vitro and in vivo studies do not contradict much as we used biaxial testing which can better replicate the complex in vivo loading conditions (Jacobs et al., 2013; Kahlon et al., 2015). Even though the previous studies reported three distinct layers (Petersen and Tillmann, 1998) such as a superficial, lamellar, and central main layer, our study discards the individual characteristics of superficial and lamellar layers. The superficial layer thickness is approximately 150–200 μm, and the depth of the layer decreases to 20–30 μm towards the internal circumference (Petersen and Tillmann, 1998). Therefore, obtaining samples from this layer by manual slicing was not practicable. Hence, we collected the top samples in each region from an approximate zone that combined the superficial and lamellar layers to circumvent the challenge of cutting samples from this paper-thin layer while still including the biomechanical aspects of both layers in our model. However, we paid special attention to extracting the bottom sample from the central main layer by removing other layers from the inferior surface of the meniscus. A consistent, repeatable tissue slicing protocol for irregularly shaped tissues such as the meniscus is presented in Bonomo et al. (2020). As an extension to the current study, the protocol could be adopted to improve the sample preparation protocol. For this study, however, since the excised tissue samples do not have a constant thickness, the principal stresses were assumed to be uniform through the thickness, with minimal alterations.
The field of view of SHG imaging (465 × 465 μm) is too small compared to the sample size used in biaxial testing. Even though the optical clearing procedure greatly increased the depth of the image stacks, the whole thickness of the tissue was still not captured. Therefore, further improvement in clearing and imaging protocols could enrich our current findings. Along with regulating elastic recoil, elastin fibers also contribute to the load-bearing properties of the tissue. More information may be gained from their structural organization, which was not considered in this study. Although the samples used in the biaxial investigation had a non-uniform thickness that was brought about by the manual slicing of the tissue, our study assumed a uniform stress distribution through the thickness during the post-processing of test data. The constitutive model utilized here only considers the morphology of collagen fibers, disregarding the density of collagen, fiber waviness, and the number of crosslinks. All of these are important factors that control the mechanics of the tissue at the microscale. However, quantifying these parameters is beyond the scope of the current study. The model further assumes affine fiber kinematics, which has been shown not to be the case for soft tissues with a dense network of collagen fibers (Krasny et al., 2017). Moreover, despite the fact that the meniscus tissue is also known to exhibit poroelastic and viscoelastic behavior (Myers et al., 2018; Bulle et al., 2021; Maritz et al., 2021), the current study primarily seeks to advance our understanding of the quasi-static mechanics of the tissue.
The chemical fixation and microscopy protocol is applied to the samples after they undergo biaxial testing. Possible alterations could have been induced to the collagen fiber morphology due to this. The amount of change, if any, has not been quantified in this study. Further, the main advantage of using MPM for imaging collagen is its non-destructive, non-invasive nature. The optical clearing agent SeeDB highly limits the amount of tissue shrinkage in comparison to other clearing methods (Azaripour et al., 2016), while greatly improving the scan depth. However, any changes induced to the collagen morphology are not known/reported at this moment.
5 Conclusion
In this study, the collagen structure of meniscal tissue regions was quantified through the thickness with high transmural resolution. The majority of collagen fibers in human menisci are circumferential in nature. The mean fiber angle and collagen dispersion were found to vary across the thickness and within the anterior, mid-body, and posterior regions. Additionally, planar biaxial mechanical tests were performed to characterize the mechanical behavior of meniscal tissue within the regions. Biaxial test results confirmed that the menisci have a significantly higher tensile strength in the circumferential direction than the transverse direction, which explains the injury mechanisms in commonly occurring meniscal tears such as the horizontal flap tear, the vertical longitudinal tear, and the bucket-handle tear (Patel et al., 2021). The biaxial results further affirmed the region- and layer-specific variations in material properties, which emphasize the highly anisotropic nature of the tissue. Furthermore, it was found that the tissue matrix is compliant and that collagen is the main load carrier. The medial menisci exhibited a slightly higher modulus than the lateral menisci, which may be attributed to its stiffer connections with the knee joint capsule and the medial collateral ligament. Hence, the mechanical and morphological observations in our study agree with the clinical findings. Despite the variation in collagen morphology, a constitutive tissue model with a single representative fiber family adequately captured the mechanical behavior of the meniscal tissue. This material model is based on a strain-energy function that accommodates both the mechanical and structural features of the menisci.
The presented constitutive model parameter is extremely important in order to understand the macroscopic behavior of the human menisci and for developing a reality-based model for medical simulators to facilitate adequate training. Knee arthroscopy simulators based on our model could provide realistic tactile feedback during the meniscal probing. The region- and layer-specific material data enables realistic tissue manipulation with respect to applied probing force. Moreover, the slightest variation in tissue behavior during different probing tasks, such as push and continuous run on the superior meniscal surface and pull on the inferior meniscal surface (Tuijthof et al., 2011), could be easily analyzed, as such detailing is essential to ascertain the tissue stiffness. This procedure helps the orthopedic surgeons make decisions regarding whether the meniscus should be repaired or resected (Anetzberger et al., 2014).
In our research, we utilized the menisci with no apparent signs of degeneration or injury. As patient-specificity is one of the notions of our envisioned digital twin for knee arthroscopic surgery (Bjelland et al., 2022), including patient demographics is a future consideration. Collagen fibers in degenerative tissues differ in composition and structure from those in healthy tissues (Hui Mingalone et al., 2018). Age also affects the collagen fiber’s extensibility (Nesbitt et al., 2021). This necessitates the tuning of parameters in the proposed model in accordance with the age and health condition of the patient. Moreover, the constitutive model should be modified to accommodate gender details, as all of these are crucial in developing a digital twin for a specific patient. However, the presented model would be adequate for studying generic meniscal tear mechanisms, designing meniscal repair procedures, simulating existing or innovative arthroscopic meniscal repair techniques, and designing implants.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving human participants were reviewed and approved by Regionale komiteer for medisinsk og helsefaglig forskningsetikk (REK midt), Trondheim, Norway dated 27.01.2021 with reference number 214114. This study has followed the ethical principles for medical research involving human subjects outlined in the World Medical Association’s Declaration of Helsinki. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements.
Author contributions
BR and VA equally contributed to experiment implementation, writing—original draft, writing—review and editing, and conceptualization. VA also contributed to data curation. TV helped with harvesting menisci from human cadavers and provided the medical background for the study. US and HS assisted with writing—review and editing, supervision.
Acknowledgments
We would like to thank Aleksander Larsen Skrede (Ph.D. scholar, Department of ICT and Natural Sciences, NTNU, Ålesund, Norway) for his assistance in sample extraction from human cadavers.
Conflict of interest
Author TV was employed by the company Medi3.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abraham, A. C., Edwards, C. R., Odegard, G. M., and Donahue, T. L. (2011). Regional and fiber orientation dependent shear properties and anisotropy of bovine meniscus. J. Mech. Behav. Biomed. Mater. 4, 2024–2030. doi:10.1016/J.JMBBM.2011.06.022
Agustoni, G., Maritz, J., Kennedy, J., Bonomo, F. P., Bordas, S. P., and Barrera, O. (2021). High resolution micro-computed tomography reveals a network of collagen channels in the body region of the knee meniscus. Ann. Biomed. Eng. 49, 2273–2281. doi:10.1007/S10439-021-02763-6
Anderson, D. R., Woo, S. L.-Y., Kwan, M. K., and Gershuni, D. H. (1991). Viscoelastic shear properties of the equine medial meniscus. J. Orthop. Res. 9, 550–558. doi:10.1002/jor.1100090411
Andrews, S. H., Rattner, J. B., Abusara, Z., Adesida, A., Shrive, N. G., and Ronsky, J. L. (2014). Tie-fibre structure and organization in the knee menisci. J. Anat. 224, 531–537. doi:10.1111/JOA.12170
Anetzberger, H., Birkenmaier, C., and Lorenz, S. (2014). Meniscectomy: Indications, procedure, outcomes, and rehabilitation. J. Orthop. Res. 6, 1–9. doi:10.2147/orr.s54669
Aspden, R., Yarker, Y., and Hukins, D. (1985). Collagen orientations in the meniscus of the knee joint. J. Anat. 140, 371–380.
Azaripour, A., Lagerweij, T., Scharfbillig, C., Jadczak, A. E., Willershausen, B., and Van Noorden, C. J. (2016). A survey of clearing techniques for 3d imaging of tissues with special reference to connective tissue. Prog. Histochem. Cytochem. 51, 9–23. doi:10.1016/j.proghi.2016.04.001
Bäker, M., and Shrot, A. (2013). Inverse parameter identification with finite element simulations using knowledge-based descriptors. Comput. Mater. Sci. 69, 128–136. doi:10.1016/j.commatsci.2012.11.059
Barrera, O., Bologna, E., Zingales, M., and Alotta, G. (2018). “Experimental characterization of the human meniscal tissue,” in 2018 IEEE 4th International Forum on Research and Technology for Society and Industry (RTSI), Palermo, Italy, 10-13 September 2018. doi:10.1109/RTSI.2018.8548369
Bjelland, O., Rasheed, B., Schaathun, H. G., Pedersen, M. D., Steinert, M., Hellevik, A. I., et al. (2022). Toward a digital twin for arthroscopic knee surgery: A systematic review. IEEE Access 10, 45029–45052. doi:10.1109/ACCESS.2022.3170108
Bonomo, F. P., Gregory, J. J., and Barrera, O. (2020). A procedure for slicing and characterizing soft heterogeneous and irregular-shaped tissue. Mater. Today Proc. 33, 2020–2026. doi:10.1016/j.matpr.2020.07.624
Brown, C. P., Houle, M.-A., Popov, K., Nicklaus, M., Couture, C.-A., Laliberté, M., et al. (2014). Imaging and modeling collagen architecture from the nano to micro scale. Biomed. Opt. express 5, 233–243. doi:10.1364/boe.5.000233
Bulle, R., Alotta, G., Marchiori, G., Berni, M., Lopomo, N. F., Zaffagnini, S., et al. (2021). The human meniscus behaves as a functionally graded fractional porous medium under confined compression conditions. Appl. Sci. 11, 9405. doi:10.3390/app11209405
Bursac, P., York, A. M., Deuerling, J. M., Kuzina, P. M., and Bianchi, J. R. (2006). Dynamic and static mechanical properties of human meniscus in tension and compression: Relationships with tissue composotion. Annu. Meet. Orthop. Res. Soc. 52, 2003.
Cavinato, C., Helfenstein-Didier, C., Olivier, T., Du Roscoat, S. R., Laroche, N., and Badel, P. (2017). Biaxial loading of arterial tissues with 3d in situ observations of adventitia fibrous microstructure: A method coupling multi-photon confocal microscopy and bulge inflation test. J. Mech. Behav. Biomed. Mater. 74, 488–498. doi:10.1016/j.jmbbm.2017.07.022
Chia, H. N., and Hull, M. L. (2008). Compressive moduli of the human medial meniscus in the axial and radial directions at equilibrium and at a physiological strain rate. J. Orthop. Res. 26, 951–956. doi:10.1002/JOR.20573
Danso, E. K., Mäkelä, J. T., Tanska, P., Mononen, M. E., Honkanen, J. T., Jurvelin, J. S., et al. (2015). Characterization of site-specific biomechanical properties of human meniscus-Importance of collagen and fluid on mechanical nonlinearities. J. Biomechanics 48, 1499–1507. doi:10.1016/j.jbiomech.2015.01.048
Danso, E. K., Oinas, J. M., Saarakkala, S., Mikkonen, S., Töyräs, J., and Korhonen, R. K. (2017). Structure-function relationships of human meniscus. J. Mech. Behav. Biomed. Mater. 67, 51–60. doi:10.1016/J.JMBBM.2016.12.002
Duginski, G. A., Ross, C. J., Laurence, D. W., Johns, C. H., and Lee, C.-H. (2020). An investigation of the effect of freezing storage on the biaxial mechanical properties of excised porcine tricuspid valve anterior leaflets. J. Mech. Behav. Biomed. Mater. 101, 103438. doi:10.1016/j.jmbbm.2019.103438
Elmukashfia, E., Marchiorib, G., Bernic, M., Cassiolasd, G., Lopomod, N. F., Rappelg, H., et al. (2022). Model selection and sensitivity analysis in the biomechanics of soft tissues: A case study on the human knee meniscus. Adv. Appl. Mech. 55, 425–511. doi:10.1016/bs.aams.2022.05.001
Fagerholt, E., Børvik, T., and Hopperstad, O. (2013). Measuring discontinuous displacement fields in cracked specimens using digital image correlation with mesh adaptation and crack-path optimization. Opt. Lasers Eng. 51, 299–310. doi:10.1016/j.optlaseng.2012.09.010
Fithian, D. C., Kelly, M. A., and Mow, V. C. (1990). Material properties and structure-function relationships in the menisci. Clin. Orthop. Relat. Res. 19, 19–31. doi:10.1097/00003086-199003000-00004
Fox, A. J., Bedi, A., and Rodeo, S. A. (2012). The basic science of human knee menisci: Structure, composition, and function. Sports Health 4, 340–351. doi:10.1177/1941738111429419
Freund, I., and Deutsch, M. (1986). Second-harmonic microscopy of biological tissue. Opt. Lett. 11, 94. doi:10.1364/OL.11.000094
Freutel, M., Galbusera, F., Ignatius, A., and Dürselen, L. (2015). Material properties of individual menisci and their attachments obtained through inverse FE-analysis. J. biomechanics 48, 1343–1349. doi:10.1016/J.JBIOMECH.2015.03.014
Gasser, T. C., Ogden, R. W., and Holzapfel, G. A. (2005). Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J. R. Soc. Interface 3, 15–35. doi:10.1098/RSIF.2005.0073
Gaugler, M., Wirz, D., Ronken, S., Hafner, M., Beat, , , Niklaus, G, et al. (2015). Fibrous cartilage of human menisci is less shock-absorbing and energy-dissipating than hyaline cartilage. Knee Surg. Sports Traumatol. Arthrosc. 1141, 1141–1146. doi:10.1007/s00167-014-2926-4
Goertzen, D. J., Budney, D. R., and Cinats, J. G. (1997). Methodology and apparatus to determine material properties of the knee joint meniscus. Med. Eng. Phys. 19, 412–419. doi:10.1016/S1350-4533(97)00011-8
Haemer, J. M., Carter, D. R., and Giori, N. J. (2012). The low permeability of healthy meniscus and labrum limit articular cartilage consolidation and maintain fluid load support in the knee and hip. J. biomechanics 45, 1450–1456. doi:10.1016/j.jbiomech.2012.02.015
Haskett, D., Johnson, G., Zhou, A., Utzinger, U., and Vande Geest, J. (2010). Microstructural and biomechanical alterations of the human aorta as a function of age and location. Biomechanics Model. Mechanobiol. 9, 725–736. doi:10.1007/s10237-010-0209-7
Holzapfel, G. A., Gasser, T. C., and Ogden, R. W. (2000). A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. 61, 1–48. doi:10.1023/a:1010835316564
Holzapfel, G. A., Niestrawska, J. A., Ogden, R. W., Reinisch, A. J., and Schriefl, A. J. (2015). Modelling non-symmetric collagen fibre dispersion in arterial walls. J. R. Soc. interface 12, 20150188. doi:10.1098/rsif.2015.0188
Hu, T., and Desai, J. P. (2004). “Characterization of soft-tissue material properties: Large deformation analysis,” in International symposium on medical simulation (Berlin, Germany: Springer), 28–37.
Hui Mingalone, C. K., Liu, Z., Hollander, J. M., Garvey, K. D., Gibson, A. L., Banks, R. E., et al. (2018). Bioluminescence and second harmonic generation imaging reveal dynamic changes in the inflammatory and collagen landscape in early osteoarthritis. Laboratory investigation; a J. Tech. methods pathology 98, 656–669. doi:10.1038/S41374-018-0040-9
Hutton, C. W. (1993). Knee meniscus: basic and clinical foundations. Ann. Rheum. Dis. (BMJ Publishing Group) 52 (8), 556.
Imeni, M., Seyfi, B., Fatouraee, N., and Samani, A. (2020). Constitutive modeling of menisci tissue: A critical review of analytical and numerical approaches. Biomechanics Model. Mechanobiol. 19, 1979–1996. doi:10.1007/S10237-020-01352-1
Jacobs, N. T., Cortes, D. H., Vresilovic, E. J., and Elliott, D. M. (2013). Biaxial tension of fibrous tissue: Using finite element methods to address experimental challenges arising from boundary conditions and anisotropy. J. Biomechanical Eng. 135, 021004. doi:10.1115/1.4023503
Joshi, M. D., Suh, J.-K., Marui, T., and Woo, S. L.-Y. (1995). Interspecies variation of compressive biomechanical properties of the meniscus. J. Biomed. Mater. Res. 29, 823–828. doi:10.1002/jbm.820290706
Kahlon, A., Hurtig, M. B., and Gordon, K. D. (2015). Regional and depth variability of porcine meniscal mechanical properties through biaxial testing. J. Mech. Behav. Biomed. Mater. 41, 108–114. doi:10.1016/J.JMBBM.2014.10.008
Karjalainen, V.-P., Kestilä, I., Finnilä, M., Folkesson, E., Turkiewicz, A., Önnerfjord, P., et al. (2021). Quantitative three-dimensional collagen orientation analysis of human meniscus posterior horn in health and osteoarthritis using micro-computed tomography. Osteoarthr. Cartil. 29, 762–772. doi:10.1016/j.joca.2021.01.009
Ke, M.-T., Fujimoto, S., and Imai, T. (2013). Seedb: A simple and morphology-preserving optical clearing agent for neuronal circuit reconstruction. Nat. Neurosci. 16, 1154–1161. doi:10.1038/nn.3447
Kiraly, K., Hyttinen, M., Lapvetelainen, T., Elo, M., Kiviranta, I., Dobai, J., et al. (1997). Specimen preparation and quantification of collagen birefringence in unstained sections of articular cartilage using image analysis and polarizing light microscopy. Histochem. J. 29, 317–327. doi:10.1023/a:1020802631968
Krasny, W., Morin, C., Magoariec, H., and Avril, S. (2017). A comprehensive study of layer-specific morphological changes in the microstructure of carotid arteries under uniaxial load. Acta biomater. 57, 342–351. doi:10.1016/j.actbio.2017.04.033
Lechner, K., Hull, M. L., and Howell, S. M. (2000). Is the circumferential tensile modulus within a human medial meniscus affected by the test sample location and cross-sectional area? J. Orthop. Res. 18, 945–951. doi:10.1002/JOR.1100180614
Lento, P. H., and Akuthota, V. (2000). Meniscal injuries: A critical review. J. back Musculoskelet. rehabilitation 15, 55–62. doi:10.3233/BMR-2000-152-302
LeRoux, M. A., and Setton, L. A. (2002). Experimental and biphasic FEM determinations of the material properties and hydraulic permeability of the meniscus in tension. J. biomechanical Eng. 124, 315–321. doi:10.1115/1.1468868
Leslie, B. W., Gardner, D. L., McGeough, J. A., and Moran, R. S. (2000). Anisotropic response of the human knee joint meniscus to unconfined compression. Proc. Institution Mech. Eng. 214, 631–635. doi:10.1243/0954411001535651
Li, L., Yang, L., Zhang, K., Zhu, L., Wang, X., and Jiang, Q. (2020). Three-dimensional finite-element analysis of aggravating medial meniscus tears on knee osteoarthritis. J. Orthop. Transl. 20, 47–55. doi:10.1016/J.JOT.2019.06.007
Luczkiewicz, P., Daszkiewicz, K., Witkowski, W., Chróścielewski, J., Ferenc, T., and Baczkowski, B. (2018). The influence of a change in the meniscus cross-sectional shape on the medio-lateral translation of the knee joint and meniscal extrusion. PLoS ONE 13, e0193020–20. doi:10.1371/journal.pone.0193020
Makris, E. A., Hadidi, P., and Athanasiou, K. A. (2011). The knee meniscus: Structure-function, pathophysiology, current repair techniques, and prospects for regeneration. Biomaterials 32, 7411–7431. doi:10.1016/J.BIOMATERIALS.2011.06.037
Maritz, J., Agustoni, G., Dragnevski, K., Bordas, S. P., and Barrera, O. (2021). The functionally grading elastic and viscoelastic properties of the body region of the knee meniscus. Ann. Biomed. Eng. 49, 2421–2429. doi:10.1007/s10439-021-02792-1
Moger, C., Barrett, R., Bleuet, P., Bradley, D., Ellis, R., Green, E., et al. (2007). Regional variations of collagen orientation in normal and diseased articular cartilage and subchondral bone determined using small angle x-ray scattering (saxs). Osteoarthr. Cartil. 15, 682–687. doi:10.1016/j.joca.2006.12.006
Morrow, D. A., Donahue, T. H., Odegard, G. M., and Kaufman, K. R. (2010). A method for assessing the fit of a constitutive material model to experimental stress–strain data. Comput. Methods Biomech. Biomed. Engin. 13, 247–256. doi:10.1080/10255840903170686
Myers, E. R., Zhu, W., and Mow, V. C. (2018). “Viscoelastic properties of articular cartilage and meniscus,” in Collagen: Volume II biochemistry and biomechanics (Boca Raton, Florida, United States: CRC Press), 267–288.
Navindaran, K., Kang, J. S., and Moon, K. (2023). Techniques for characterizing mechanical properties of soft tissues. J. Mech. Behav. Biomed. Mater. 138, 105575. doi:10.1016/J.JMBBM.2022.105575
Nesbitt, D. Q., Siegel, D. N., Nelson, S. J., and Lujan, T. J. (2021). Effect of age on the failure properties of human meniscus: High-speed strain mapping of tissue tears. J. biomechanics 115, 110126. doi:10.1016/J.JBIOMECH.2020.110126
Patel, H., Skalski, M. R., Patel, D. B., White, E. A., Tomasian, A., Gross, J. S., et al. (2021). Illustrative review of knee meniscal tear patterns, repair and replacement options, and imaging evaluation. Clin. Imaging 69, 4–16. doi:10.1016/J.CLINIMAG.2020.06.045
Peddada, S. D., Dunson, D. B., and Tan, X. (2005). Estimation of order-restricted means from correlated data. Biometrika 92, 703–715. doi:10.1093/biomet/92.3.703
Petersen, W., and Tillmann, B. (1998). Collagenous fibril texture of the human knee joint menisci. Anat. embryology 197, 317–324. doi:10.1007/s004290050141
Polzer, S., Gasser, T. C., Forsell, C., Druckmüllerova, H., Tichy, M., Staffa, R., et al. (2013). Automatic identification and validation of planar collagen organization in the aorta wall with application to abdominal aortic aneurysm. Microsc. Microanal. 19, 1395–1404. doi:10.1017/s1431927613013251
Proctor, C. S., Schmidt, M. B., Whipple, R. R., Kelly, M. A., and Mow, V. C. (1989). Material properties of the normal medial bovine meniscus. J. Orthop. Res. 7, 771–782. doi:10.1002/JOR.1100070602
Pukaluk, A., Wolinski, H., Viertler, C., Regitnig, P., Holzapfel, G. A., and Sommer, G. (2023). Changes in the microstructure of the human aortic adventitia under biaxial loading investigated by multi-photon microscopy. Acta Biomater. 161, 154–169. doi:10.1016/j.actbio.2023.02.027
Sancataldo, G., Barrera, O., and Vetri, V. (2022). “Two-photon imaging,” in Principles of light microscopy: From basic to advanced (Berlin, Germany: Springer), 215–241.
Schriefl, A. J., Wolinski, H., Regitnig, P., Kohlwein, S. D., and Holzapfel, G. A. (2013). An automated approach for three-dimensional quantification of fibrillar structures in optically cleared soft biological tissues. J. R. Soc. Interface 10, 20120760. doi:10.1098/rsif.2012.0760
Seyfi, B., Fatouraee, N., and Imeni, M. (2018). Mechanical modeling and characterization of meniscus tissue using flat punch indentation and inverse finite element method. J. Mech. Behav. Biomed. Mater. 77, 337–346. doi:10.1016/J.JMBBM.2017.09.023
Siegel, I. M. (1988). Injury and repair of the musculoskeletal soft tissues. JAMA 260, 2304. doi:10.1001/jama.1988.03410150152053
Sommer, G., Haspinger, D. C., Andrä, M., Sacherer, M., Viertler, C., Regitnig, P., et al. (2015). Quantification of shear deformations and corresponding stresses in the biaxially tested human myocardium. Ann. Biomed. Eng. 43, 2334–2348. doi:10.1007/s10439-015-1281-z
Spilker, R. L., Donzelli, P. S., and Mow, V. C. (1992). A transversely isotropic biphasic finite element model of the meniscus. J. biomechanics 25, 1027–1045. doi:10.1016/0021-9290(92)90038-3
Tissakht, M., and Ahmed, A. (1995). Tensile stress-strain characteristics of the human meniscal material. J. biomechanics 28, 411–422. doi:10.1016/0021-9290(94)00081-e
Tuijthof, G. J., Horeman, T., Schafroth, M. U., Blankevoort, L., and Kerkhoffs, G. M. (2011). Probing forces of menisci: What levels are safe for arthroscopic surgery. Knee Surg. sports Traumatol. Arthrosc. 19, 248–254. doi:10.1007/s00167-010-1251-9
Vetri, V., Dragnevski, K., Tkaczyk, M., Zingales, M., Marchiori, G., Lopomo, N. F., et al. (2019). Advanced microscopy analysis of the micro-nanoscale architecture of human menisci. Sci. Rep. 9, 18732. doi:10.1038/s41598-019-55243-2
Walker, P. S., and Erkiuan, M. J. (1975). The role of the menisci in force transmission across the knee. Clin. Orthop. Relat. Research 109, 184–192. doi:10.1097/00003086-197506000-00027
Wang, D., He, C., Wu, C., and Zhang, Y. (2018). Mechanical behaviors of tension and relaxation of tongue and soft palate: Experimental and analytical modeling. J. Theor. Biol. 459, 142–153. doi:10.1016/j.jtbi.2018.10.001
Wheatley, B. B., Fischenich, K. M., Button, K. D., Haut, R. C., and Donahue, T. L. H. (2015). An optimized transversely isotropic, hyper-poro-viscoelastic finite element model of the meniscus to evaluate mechanical degradation following traumatic loading. J. biomechanics 48, 1454–1460. doi:10.1016/j.jbiomech.2015.02.028
Williams, R. M., Zipfel, W. R., and Webb, W. W. (2001). Multiphoton microscopy in biological research. Curr. Opin. Chem. Biol. 5, 603–608. doi:10.1016/S1367-5931(00)00241-6
Zhu, S., Tong, G., Xiang, J.-p., Qiu, S., Yao, Z., Zhou, X., et al. (2021). Microstructure analysis and reconstruction of a meniscus. Orthop. Surg. 13, 306–313. doi:10.1111/os.12899
Keywords: human menisci, constitutive modeling, biaxial testing, second harmonic imaging, multi-photon microscopy, collagen fiber, fiber distribution, surgery simulation
Citation: Rasheed B, Ayyalasomayajula V, Schaarschmidt U, Vagstad T and Schaathun HG (2023) Region- and layer-specific investigations of the human menisci using SHG imaging and biaxial testing. Front. Bioeng. Biotechnol. 11:1167427. doi: 10.3389/fbioe.2023.1167427
Received: 16 February 2023; Accepted: 04 April 2023;
Published: 18 April 2023.
Edited by:
Seungik Baek, Michigan State University, United StatesReviewed by:
Gioacchino Alotta, Mediterranea University of Reggio Calabria, ItalyOlga Barrera, Oxford Brookes University, United Kingdom
Copyright © 2023 Rasheed, Ayyalasomayajula, Schaarschmidt, Vagstad and Schaathun. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bismi Rasheed, YmlzbWkucmFzaGVlZEBudG51Lm5v
†These authors have contributed equally to this work
 Bismi Rasheed
Bismi Rasheed Venkat Ayyalasomayajula
Venkat Ayyalasomayajula Ute Schaarschmidt
Ute Schaarschmidt Terje Vagstad1,2,4
Terje Vagstad1,2,4