Exploring the effects of skeletal architecture and muscle properties on bipedal standing in the common chimpanzee (Pan troglodytes) from the perspective of biomechanics

Introduction: It is well known that the common chimpanzee, as both the closest living relative to humans and a facultative bipedal, has the capability of bipedal standing but cannot do so fully upright. Accordingly, they have been of exceeding significance in elucidating the evolution of human bipedalism. There are many reasons why the common chimpanzee can only stand with its hips–knees bent, such as the distally oriented long ischial tubercle and the almost absent lumbar lordosis. However, it is unknown how the relative positions of their shoulder–hip–knee–ankle joints are coordinated. Similarly, the distribution of the biomechanical characteristics of the lower-limb muscles and the factors that affect the erectness of standing as well as the muscle fatigue of the lower limbs remain a mystery. The answers are bound to light up the evolutional mechanism of hominin bipedality, but these conundrums have not been shed much light upon, because few studies have comprehensively explored the effects of skeletal architecture and muscle properties on bipedal standing in common chimpanzees.

Methods: Thus, we first built a musculoskeletal model comprising the head-arms-trunk (HAT), thighs, shanks, and feet segments of the common chimpanzee, and then, the mechanical relationships of the Hill-type muscle-tendon units (MTUs) in bipedal standing were deduced. Thereafter, the equilibrium constraints were established, and a constrained optimization problem was formulated where the optimization objective was defined. Finally, thousands of simulations of bipedal standing experiments were performed to determine the optimal posture and its corresponding MTU parameters including muscle lengths, muscle activation, and muscle forces. Moreover, to quantify the relationship between each pair of the parameters from all the experimental simulation outcomes, the Pearson correlation analysis was employed.

Results: Our results demonstrate that in the pursuit of the optimal bipedal standing posture, the common chimpanzee cannot simultaneously achieve maximum erectness and minimum muscle fatigue of the lower limbs. For uni-articular MTUs, the relationship between muscle activation, relative muscle lengths, together with relative muscle forces, and the corresponding joint angle is generally negatively correlated for extensors and positively correlated for flexors. For bi-articular MTUs, the relationship between muscle activation, coupled with relative muscle forces, and the corresponding joint angles does not show the same pattern as in the uni-articular MTUs.

Discussion: The results of this study bridge the gap between skeletal architecture, along with muscle properties, and biomechanical performance of the common chimpanzee during bipedal standing, which enhances existing biomechanical theories and advances the comprehension of bipedal evolution in humans.

1 Introduction

Apart from modern humans (Homo sapiens), there are various other species of primates, such as the common chimpanzee (Pan troglodytes), that have acquired the ability of bipedal standing; however, they cannot stand fully upright (Jenkins, 1972). As our closest living relative (Goodman, 1999; Waterson et al., 2005), common chimpanzees (chimps) share with us the post-cranial features related to orthograde modes of locomotion (Hunt, 1991) while lacking the human-like skeletal architecture that aligns the shoulder, hip, knee, and ankle joints in the sagittal plane (Thorpe et al., 1999; Payne et al., 2006b; Pontzer, 2018). Circumscribed to the distally oriented long ischial tubercle and the almost absent lumbar lordosis (Robinson, 1972; McHenry, 1975), chimps are unable to extend their hip joint so that they stand bipedally in a bent-hip, bent-knee manner, a position in which the center of mass (CoM) is located anterior to the hip (Sockol et al., 2007). When a human stands upright, the CoM, hip, knee, and ankle joints approximately line up (Neumann, 2013), diminishing the necessity for the lower-limb muscles to be activated (Pontzer et al., 2009). In the case of a chimp, muscle activation of the hind limbs is required to generate muscle forces and joint moments on account of balance when it comes to standing on two feet. However, how do chimps coordinate the relative positions of their shoulder, hip, knee, and ankle joints? How is the muscle activation of the hind limbs assigned in pursuit after maintaining balance? How do biomechanical factors such as skeletal architecture and muscle properties affect the erectness of standing? Although the bipedal locomotion pattern of chimps has been studied since 1944 (Elftman, 1944), few studies have explored this topic in depth.

The road to uncovering the aforementioned questions is paved with challenging puzzles. Although laboratory-based experiments have been widely conducted in the bipedal walking or running of chimps (Demes et al., 2015; Thompson et al., 2015; Kozma et al., 2018), their application remains unfeasible in bipedal standing since it is barely possible to keep untrained chimps standing bipedally for a sufficient amount of time (Doran, 1992a; Doran, 1992b; Hunt, 1992; Hunt, 1994). Training may not be a feasible alternative either because trained primates have been proven to develop changes in the musculoskeletal structure (Nakatsukasa, 2004). Modeling and simulation can not only overcome these problems but can also provide internal parameters that are difficult to measure. However, existing musculoskeletal models (Yamazaki, 1985; O'Neill et al., 2013; O'Neill et al., 2015; O'Neill et al., 2018; O'Neill et al., 2022; Sellers et al., 2013) are still far from effective for investigating the biomechanical performance of chimps during bipedal standing. Yamazaki (1985) measured the net joint moments of chimps during bipedal locomotion under controlled conditions and derived the corresponding muscle forces using computer simulations. However, Yamazaki assumed constant values of the muscle moment arms that apparently vary with joint angles and did not specify whether anatomical or physiological cross-sectional areas were used to estimate muscle forces from stresses. O'Neill et al. (2013, 2015, 2018, 2022) quantified the variation in moment arms and muscle forces of hind limb muscles with joint angles during bipedal locomotion in chimps through modeling and simulations on the OpenSim platform, combined with detailed muscle–tendon parameters. However, their model merely contained the pelvis and hind limbs and could not predict the maximum erectness that chimps can achieve during bipedal standing and the corresponding posture. Sellers et al. (2013) established a whole-body model of the common chimpanzee on the GaitSym platform to explore changes in performance, such as footfall sequences, locomotion velocity, and energy expenditure during quadrupedal locomotion within the domain. However, their model simplified the pattern of muscle activation according to the motor function, which is solely applicable to rhythmic movements.

Numerical optimization is recognized as a viable technique for predicting animal behavior (Pandy, 2001), where it is crucial to translate appropriate biomechanical metrics into optimization objectives (Lee and Umberger, 2016). Experimental studies have indicated that the larger the hip and knee joint angles, that is, the greater the erectness, the smaller the activation volume of the hind limb muscles during bipedal walking in chimps (Pontzer et al., 2014). This implies that erectness and muscle activation can be considered as the objective function for optimization. Furthermore, muscle fatigue, as a pivotal biomechanical indicator, can be regarded as an objective function that characterizes muscle activation (Crowninshield and Brand, 1981). The constrained optimization is thus applicable for exploring the bipedal standing postures (BSPs) of chimps and corresponding biomechanical factors. This methodology thoroughly assesses multiple biomechanical factors of the skeletal muscles, such as the isometric force, deformation, and muscle fatigue. To the best of our knowledge, this approach is the first-ever attempt to predict the optimal bipedal standing posture of chimps and is a valuable complement to existing biomechanical theories.

This study aimed to investigate the biomechanical effects of skeletal architecture and muscle properties on bipedal standing in chimps. First, a musculoskeletal model based on anatomical data comprising the head–arms–trunk (HAT), thighs, shanks, and feet segments of the common chimpanzee was developed. Second, the static relationships among the Hill-type muscle–tendon units (MTUs) in bipedal standing were deduced. Next, the equilibrium constraints and the optimization objective were set up, which transformed the investigation into a constrained optimization problem. Subsequently, thousands of simulations of bipedal standing experiments in chimps were conducted. Finally, the optimal posture that simultaneously maximizes erectness and minimizes muscle fatigue of the hind limbs was determined via numerical searching within the domain, and MTU parameters including muscle activation, muscle length, and muscle force were drawn. In addition, the biomechanical effects under investigation were stipulated by the Pearson correlation analysis of the outcomes from simulating experiments.

2 Materials and methods

2.1 Musculoskeletal modeling

In the strictest sense, the analysis of bipedal standing in chimps should be conducted in three dimensions. However, reckoning with the reality that the mechanical behaviors of bipedal standing in chimps mainly occur in the sagittal plane, we subsequently generated the musculoskeletal model in the sagittal plane.

2.1.1 Segmental and skeletal properties

The body of the common chimpanzee can be represented as seven segments: the HAT (including the pelvis), bilateral thighs (including femurs), bilateral shanks (including tibias and fibulas), and bilateral feet.

Without loss of generality and to ensure computational efficiency, the following hypotheses were presented: 1) the thigh length and femur length were the same; 2) the shank length was the same as the tibia length; 3) the foot was subdivided into the forefoot, midfoot, and rearfoot, and the midfoot and rearfoot were integrated as one rigid piece; 4) the hip joint connecting the HAT and the thigh, the knee joint connecting the thigh and the shank, the ankle joint connecting the shank and the foot, and the metatarsophalangeal (MP) joint connecting the forefoot and midfoot were all simplified as smooth hinges; 5) the ground reaction force was evaluated as a resultant force and its acting point at the foot was the center of pressure (CoP); and 6) the external force only involved the gravitational force and the support force from the ground, and friction was neglected.

The segments, CoMs, joints, segmental angles, and ground reaction force (GRF) are shown in Figure 1A. Annotations of the segmental parameters and joint angles are shown in Figure 1B. The precise values of the segmental parameters are listed in Supplementary Table S1, and their sources are disclosed in Section 2.1.3. The positive direction of the joint angles was defined as the hip joint extension, knee joint extension, and ankle joint extension. Given that the hip joint of chimps cannot be entirely extended owing to the orientation and length of the ischium (Kozma et al., 2018), the acute angle between the ischium and HAT was fixed as a constant $\mathrm{\beta }$.

FIGURE 1

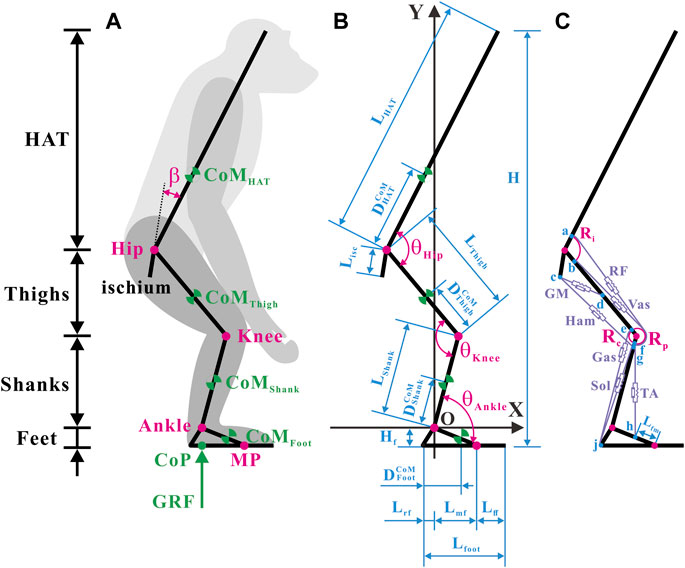
FIGURE 1. Musculoskeletal model of a bipedally standing common chimpanzee in the sagittal plane. (A) The skeletal elements include seven segments (HAT, bilateral thighs, bilateral shanks, and bilateral feet) and the ischium, with mobile articulations at the hip, knee, ankle, and metatarsal-phalangeal joints. (B) Annotations of segmental parameters (length of each segment and sub-segment, and position of CoM in each segment) and joint angles. (C) The muscular elements include the primary extensors and flexors of each lower limb [gluteus maximus (GM), hamstrings (Ham) (biceps femoris long head, semimembranosus, and semitendinosus), vastus (Vas), rectus femoris (RF), gastrocnemius (Gas) (gastrocnemius lateralis and gastrocnemius medialis), soleus (Sol), and tibialis anterior (TA)]. Blue dots: a) anterior-inferior iliac spine; b) the combined origin point of the vastus intermedius, vastus lateralis, and vastus medialis; c) midpoint of the most superior and to the most inferior points of the ischial tuberosity face; d) midpoint of the posterior femur shaft; e) medial and lateral femoral condyles and knee capsule; f) patella; g) fibular head; h) proximal end of the metatarsal I; j) distal end of the rear foot. Adapted from Diogo et al. (2013), Thorpe et al. (1999), Payne et al. (2006b), Myatt et al. (2011).

Considering computational efficiency, a global Cartesian coordinate system with the rotation center of the ankle joint as the origin was created.

2.1.2 Muscle geometry and Hill-type MTU

Conscientious observations of the anatomy of chimps (Thorpe et al., 1999; Payne et al., 2006b; Myatt et al., 2011; Diogo et al., 2013) have revealed that the extensor and flexor muscles, which primarily produce forces and joint moments in the sagittal plane in each hind limb, incorporate a total of 10 muscles in seven muscle groups, as shown in Figure 1C. It should be noted that the gluteus maximus (GM) only comprises the gluteus maximus ischiofemoralis according to Stern (1972), Tuttle et al. (1978), and Lieberman et al. (2006).

After careful estimation of bone landmarks and muscle maps of chimps (Thorpe et al., 1999; Payne et al., 2006b; Myatt et al., 2011; Diogo et al., 2013), the points of origin and insertion for each muscle were designated, located as close to the center of the attachment area as possible, as shown in Figure 1C. In accordance with the attachment points and wrapping paths of muscles, the functional relationship between the lengths and moment arms of muscles with respect to joint angles can be verified. In particular, because the femoral condyle contour in chimps is significantly more circular than that in humans (Heiple and Lovejoy, 1971), the femoral condyle was approximated as a circular arc in the sagittal plane. The tibia was presumed to move wholly along the femoral condyle contour, and the patella was presumed to move completely along the femoral–tibial condyle contour (O'Neill et al., 2013). Consequently, the moment arms of the rectus femoris (RF) and vastus (Vas) around the knee joint were constant ($R_p$), and the moment arm of gastrocnemius lateralis and gastrocnemius medialis (Gas) around the knee joint was constant ($R_e$) when tangential to the femoral condyle. With reference to the measurements (Thorpe et al., 1999; Payne et al., 2006a), the moment arm of RF about the hip joint was assumed constant ($R_i$).

A generic Hill-type model (Zajac, 1989) was applied to enumerate metrics such as the lengths and forces of muscles and tendons in each hind limb under isometric contraction as the joint angle changed (Sawicki and Khan, 2015), as illustrated in Figure 2. It was the posture of bipedal standing that this study intended to analyze. Therefore, the muscle contraction velocity $v^M$ was approximated to zero, and the bipedal standing of the common chimpanzee was statically analyzed.

FIGURE 2

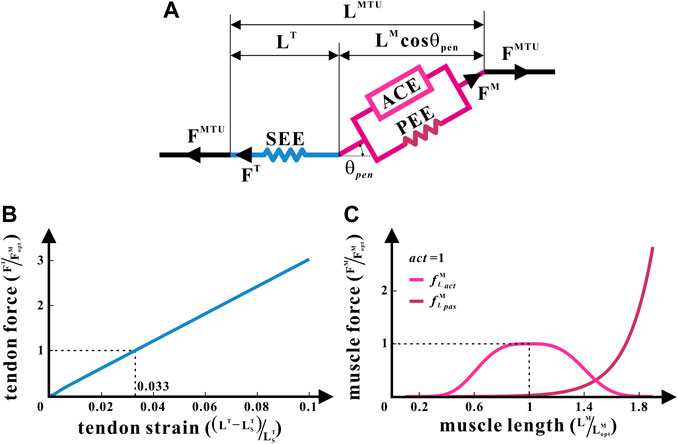
FIGURE 2. Hill-type MTU of the common chimpanzee. (A) Structure of the Hill-type MTU. (B) Non-linear relationship between the tendon force and tendon strain for SEE. (C) Non-linear relationships between the relative muscle force and relative muscle length, respectively, for ACE and PEE.

The Hill-type model treats each muscle as an MTU. Every MTU consists of two portions: a part associated with the traits of the muscle fibers and another part equated to the tendon. They are in series with each other, between which is the pennation angle ${\theta }_{pen}$. The muscle part is composed of an active contractile element (ACE) arranged in parallel with a passive non-linear elastic element (PEE), while the tendon part consists of a series elastic unit (SEE). Because no ${\theta }_{pen}$ of any MTU in chimps is greater than $30°$, which means $\cos {\theta }_{pen}\approx 1$ (Thorpe et al., 1999), all ${\theta }_{pen}$ were approximated to zero (Payne et al., 2006). Furthermore, the muscle and tendon in MTUs were confined to the following force and length relationships:

$\begin{array}{c}{F}^{MTU}=F^M=F^T\end{array},(1)$

$\begin{array}{c}{L}^{MTU}=L^M+L^T\end{array},(2)$

where $F^{MTU}$ denotes the force of MTU, $F^M$ denotes the muscle force, $F^T$ denotes the tendon force, $L^{MTU}$ denotes the length of MTU, $L^M$ denotes the muscle length, and $L^T$ denotes the tendon length.

The biomechanical characteristics of each MTU were confirmed by five internal parameters: the mass of MTU ($m^{MTU}$), optimal fiber length ($L_{opt}^M$), physiological cross-sectional area ($PCSA$), optimal isometric muscle force ($F_{opt}^M$), and tendon slack length ($L_S^T$), the values of which are shown in Table 1 and explained in Section 2.1.3.

TABLE 1

TABLE 1. Hill-type MTU parameters.

With the aforementioned parameters, $F^M$ and $F^T$ can be addressed by the following formula:

$\begin{array}{c}{F}^M=F_{opt}^M\bullet \left(act\bullet f_L^M{}_{act}+f_L^M{}_{pas}\right)\end{array},(3)$

$\begin{array}{c}{F}^T=K^T\bullet \left(L^T-L_S^T\right)\end{array},(4)$

where $act$ is the muscle activation between $\left[\mathrm{0,1}\right]$, $f_L^M{}_{act}$ is the active coefficient of the muscle force–length relationship, $f_L^M{}_{pas}$ is the passive coefficient of the muscle force–length relationship, and $K^T$ is the coefficient of the tendon stiffness. In addition, $f_L^M{}_{act}$ and $f_L^M{}_{pas}$ are both functions of $L^M$. $K^T$ is a function of $F^T$, and $F^T=F_{opt}^M$ when $\raisebox{1ex}{$\left(L^T-L_S^T\right)$}\!\left/ \!\raisebox{-1ex}{$L_S^T$}\right.=0.033$ (Zajac, 1989). Subsequently, under circumstances wherein every $L^{MTU}$ has been counted from ${\theta }_{Hip}$, ${\theta }_{Knee}$, and ${\theta }_{Ankle}$, together with the knowledge of $L_{opt}^M$, $F_{opt}^M$, and $L_S^T$, all the unknown variables in MTUs can be articulated as functions of $L^M$.

2.1.3 Musculoskeletal dataset

Full sets of anatomical data of the common chimpanzee are limited (Zihlman and Cramer, 1978; Thorpe et al., 1999; Wang and Crompton, 2004; Isler et al., 2006; Kozma et al., 2018), among which source sample Chimp 95 (Thorpe et al., 1999) stands out for integrity. To construct the complete dataset of the skeletal and muscular parameters in need, the anatomical data from other sources were scaled to match that of sample Chimp 95 (Thorpe et al., 1999), depending on the geometric similarity between different individuals of the same species.

The segmental masses of sample Pa1 in Table 3 from Isler et al. (2006) were scaled according to the ratio of the mass of Chimp 95 $m_{Chimp95}$ to that of Pa1 $m_{Pa1}$ for obtaining the corresponding head mass $m_{Head}$, trunk mass $m_{Trunk}$, upper arm mass $m_{Uarm}$, forearm mass $m_{Farm}$, hand mass $m_{Hand}$, thigh mass $m_{Thigh}$, shank mass $m_{Shank}$, and foot mass $m_{Foot}$ of Chimp 95. The HAT mass $m_{HAT}$ of Chimp 95 was calculated as follows:

$\begin{array}{c}{m}_{HAT}=m_{Head}+m_{Trunk}+2\times \left(m_{Uarm}+m_{Farm}+m_{Hand}\right)\end{array}.(5)$

The segmental lengths of sample Pa1 in Table 3 from Isler et al. (2006) were scaled according to the ratio of masses as ${\left(\frac{m_{Chimp95}}{m_{Pa1}}\right)}^{\frac{1}{3}}$ for attaining the corresponding head length $l_{Head}$, trunk length $l_{Trunk}$, and foot length $l_{Foot}$ of Chimp 95. The HAT length $L_{HAT}$ of Chimp 95 was calculated as follows:

$\begin{array}{c}{L}_{HAT}=l_{Head}+l_{Trunk}\end{array}.(6)$

The relative position of each segmental CoM of sample Pa1 in Table 3 from Isler et al. (2006) was, respectively, multiplied by the segmental lengths of Chimp 95 worked out previously to attain the corresponding segmental CoM positions of Chimp 95, that is, the distance from the HAT CoM to the hip joint $D_{HAT}^{CoM}$, the distance from the thigh CoM to the knee joint $D_{Thigh}^{CoM}$, the distance from the shank CoM to the ankle joint $D_{Shank}^{CoM}$, and the distance from the foot CoM to the heel $D_{Foot}^{CoM}$.

The average fibular length ${\overline{X}}_{fibula}$ of samples Pan troglodytes in Table 1 from Zihlman and Cramer (1978) was scaled according to the ratio of the tibial length of Chimp 95 $L_{tibia}$ to the average tibial length of Pan troglodytes ${\overline{X}}_{tibia}$ for obtaining the corresponding fibula length $L_{fibula}$ of Chimp 95.

The foot length parameters of the chimpanzee species in Table 1 in the paper by Wang and Crompton (2004) were scaled by the ratio of the foot length of Chimp 95 $L_{Foot}$ to that of the species chimpanzee $FL$ for attaining the corresponding foot height $H_f$, rearfoot length $L_{rf}$, midfoot length $L_{mf}$, forefoot length $L_{ff}$, and third metatarsal length $L_{fm}$ of Chimp 95.

To obtain the corresponding ischial length $L_{isc}$ of Chimp 95, the ischial lengths of the 20 samples of Pan troglodytes in Supplementary Table S1 from the study by Kozma et al. (2018) were averaged.

The value of $\mathrm{\beta }$ was elicited from the maximum hip angle ($162°$) in the presence of the dimensionless mechanical advantage of samples of Pan troglodytes in Table S1 from Kozma et al. (2018):

$\begin{array}{c}\beta =180°-162°=18°\end{array}.(7)$

The values of $m^{MTU}$, $L_{opt}^M$, and $PCSA$ were obtained from sample Chimp 95 by Thorpe et al. (1999). The value of $F_{opt}^M$, which characterizes the capacity of muscle force production, can be acquired by multiplying the $PCSA$ with the maximum isometric muscle stress, which was set to 0.3 MPa according to previous studies (Wells, 1965; Thorpe et al., 1999). The value of $L_S^T$ was obtained using the constrained non-linear optimization function (fmincon) in the MATLAB optimization toolbox (MathWorks, Natick, MA, United States) (O'Neill et al., 2013), following the force and length relationships between muscles and tendons in MTUs (Zajac, 1989; Manal and Buchanan, 2004; Sawicki and Khan, 2015).

2.2 Search of solutions

It is well-known that chimps, like any primate, are constrained in their erectness when standing bipedally by their skeletal architecture and muscle properties; for example, they must maintain balance and stability, and their muscles and tendons should not exceed the force ranges (O'Neill et al., 2013). These constraints were translated into numerical boundaries merged with the geometric and mechanical relationships of the musculoskeletal system, as described in Section 2.1. Subsequently, the objective function was interpreted in accordance with the principle of simultaneously maximizing erectness and minimizing the muscle fatigue of the hind limbs. Finally, the constrained optimization was carried out through random initial values and random directions within the domain, and this process was repeated to globally search for the bipedal standing postures (BSPs) of chimps. During the procedure, every set of optimization results was equivalent to one simulation experiment of bipedal standing in chimps.

2.2.1 Biomechanical constraints

To guarantee the stability of bipedal standing, the overall CoM of the common chimpanzee was assumed to be maintained directly above the ankle joint:

$\begin{array}{c}{X}^{CoM}=0\end{array},(8)$

where $X^{CoM}$ is the horizontal coordinate of the CoM about the origin, which is a function of ${\theta }_{Hip}$, ${\theta }_{Knee}$, and ${\theta }_{Ankle}$.

To ensure the balance of bipedal standing in chimps, the MTU of the hind limbs must be able to produce the torque desired by the hip, knee, and ankle joints:

$\begin{array}{c}{M}_i^{need}=M_i^{prod}\\ \left(i=Hip,Knee,Ankle\right),\end{array}(9)$

where $M_i^{need}$ is the required moment of the hip, knee, and ankle joints, and $M_i^{prod}$ is the moment produced by the hip, knee, and ankle joints. Referring to Figure 1A, $M_i^{need}$ can be expressed as a function of ${\theta }_{Hip}$, ${\theta }_{Knee}$, and ${\theta }_{Ankle}$. Referring to Figure 1C, combined with Section 2.1, $M_i^{prod}$ can be, respectively, expressed as functions of ${\theta }_{Hip}$, ${\theta }_{Knee}$, ${\theta }_{Ankle}$, and $L^M$.

2.2.2 Constrained optimization

Considering that chimps seek the maximum erectness and minimum muscle fatigue of hind limbs during bipedal standing, the optimization objective was defined as the square of the ratio of erectness to the muscle fatigue of hind limbs:

$\begin{array}{c}Object=\raisebox{1ex}{${Erectness}^2$}\!\left/ \!\raisebox{-1ex}{${Fatigue}^2$}\right.\end{array},(10)$

where $Erectness$ is the ratio of height to the full length of the body during bipedal standing:

$\begin{array}{c}Erectness=\frac{H}{H_f+L_{Shank}+L_{Thigh}+L_{HAT}}\end{array},(11)$

where $H$ is the height during bipedal standing. Thus, $Erectness$ is a function of ${\theta }_{Hip}$, ${\theta }_{Knee}$, and ${\theta }_{Ankle}$.

The muscle fatigue of hind limbs was manifested as follows (Anderson and Pandy, 2001):

$\begin{array}{c}Fatigue={\displaystyle \sum }_i{\left({act}_i\right)}^2\\ \left(i=GM,bflh,semimem,semiten,Vas,RF,Gasl,Gasm,Sol,TA\right).\end{array}(12)$

Consequently, $Fatigue$ is a function of $L^M$.

To sum up, $Object$ is a function of ${\theta }_{Hip}$, ${\theta }_{Knee}$, ${\theta }_{Ankle}$, and $L^M$.

2.2.3 Data analysis

To obtain the numerical solution of $Object$ that is as close to the global optimal solution as possible, the values of ${\theta }_{Hip}$, ${\theta }_{Knee}$, ${\theta }_{Ankle}$, and $L^M$ were randomly initiated within the range of $0.60\le Erectness\le 1$ and every variable threshold. In addition, the search direction was randomly selected on the foundation of the gradient descent method; this process was repeated 3,536 times. The largest $Object$ among these 3,536 sets of numerical results was approximated as the global optimal solution. During the course, other sets of optimization results were also weighted as simulation experiments of bipedal standing in chimps.

Probing deeper into the relationship between each pair of the biomechanical parameters, the Pearson correlation analysis of the outcomes from simulating experiments was accomplished.

3 Results

In this study, the effects of skeletal architecture and muscle properties on bipedal standing in chimps were investigated using modeling and simulation. The global optimal solution of $Object$ was achieved from 3,536 sets of optimization results to ascertain the optimal posture for bipedal standing in chimps. It is worth noting that these 3,536 sets of numerical results can also be considered as 3,536 simulations of bipedal standing experiments. Based on these simulations, the numerical relationships among $Object$, $Erectness$, and $Fatigue$ can be analyzed, and the biomechanical relationships among the hip, knee, and ankle joint angles; muscle activation; muscle lengths; and muscle forces of the hind limbs can be further analyzed.

3.1 Numerical trade-offs between erectness and fatigue

Taking $Object$ as the objective function, simultaneously maximizing $Erectness$ and minimizing $Fatigue$, numerical optimization was conducted 3,536 times, and 3,536 randomized simulations of bipedal standing experiments in chimps were performed.

As shown in Figures 3A–C, the same degree of $Erectness$ may correspond to different degrees of $Fatigue$, and in turn, the same degree of $Fatigue$ may correspond to different degrees of $Erectness$. As the value of $Object$ gradually increased from a minimum of 0.096 to a maximum of 4.480, the degree of $Fatigue$ generally decreased from a maximum of 3.060 to a minimum of 0.407, whereas the degree of $Erectness$ did not show a clear pattern of change. When $Object$ reached a maximum of 4.480, which is the optimal BSP, although $Fatigue$ also reached a minimum of 0.407 (the easiest BSP), $Erectness$ reached neither the minimum of 0.600 nor the maximum of 0.959, but 0.861. This indicated that $Fatigue$ is higher than 0.407 when $Erectness$ is either less than or more than 0.861, so that $Object$ is reduced. Moreover, when $Fatigue$ reached a maximum of 3.060 (the hardest BSP), $Erectness$ was 0.947, which is not significantly different from its maximum of 0.959. Additionally, the degree of $Fatigue$ was higher at the maximum value of $Erectness$ (the highest BSP) than at the minimum value of $Erectness$ (the lowest BSP), which were 2.702 and 1.486, respectively. This result is rather counterintuitive, indicating that too high a degree of $Erectness$ would not lead to a decrease in $Fatigue$. These results contrast with those for humans, where the optimal BSP corresponds to both the highest $Erectness$ and the lowest $Fatigue$ (Pontzer et al., 2009), with $Erectness$ and $Fatigue$ being almost negatively correlated (Neumann, 2013).

FIGURE 3

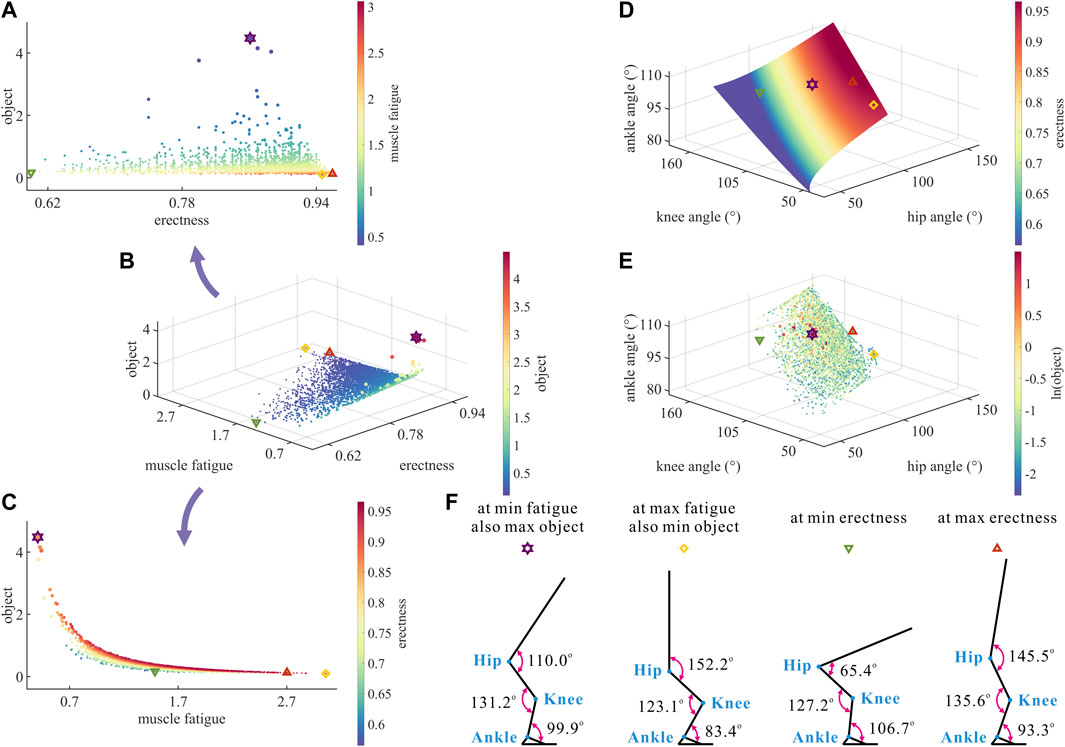
FIGURE 3. (A–C) Results of optimization objective, standing erectness, and muscle fatigue of the lower limb in the 3,536 simulation experiments of bipedal standing. Marked points: purple hexagram: both the optimal and easiest BSP; yellow diamond: both the worst and hardest BSP; green downward-pointing triangle: lowest BSP; red upward-pointing triangle: highest BSP. (D) Domain of the hip, knee, and ankle joint angles. (E) Results of the hip, knee, and ankle joint angles in the 3,536 simulation experiments of bipedal standing. (F) Joint angles, respectively, at (purple hexagram) both the optimal and easiest BSP, (yellow diamond) both the worst and hardest BSP, (green downward-pointing triangle) lowest BSP, and (red upward-pointing triangle) highest BSP.

As a result, there is a numerical trade-off between the degree of $Erectness$ and the degree of $Fatigue$ in the quest of the optimal BSP for chimps.

Although $Object$ is the ratio of $Erectness$ to $Fatigue$, the latter two are not completely independent variables. The degree of $Erectness$ is directly dependent on ${\theta }_{Hip}$, ${\theta }_{Knee}$, and ${\theta }_{Ankle}$. The degree of $Fatigue$ is directly dependent on the muscle activation of hind limb MTUs ${act}_i$ ($i=GM,bflh,semimem,semiten,Vas,RF,Gasl,Gasm,Sol,TA$), which indirectly depends on $L^{MTU}$ and $L^M$ (see Section 2.1.2 for details). Because $L^{MTU}$ depends directly on ${\theta }_{Hip}$, ${\theta }_{Knee}$, and ${\theta }_{Ankle}$, $Fatigue$ is indirectly affected by ${\theta }_{Hip}$, ${\theta }_{Knee}$, ${\theta }_{Ankle}$, and $L_i^M$ ($i=GM,bflh,semimem,semiten,Vas,RF,Gasl,Gasm,Sol,TA$).

In summary, the numerical trade-off between the degree of $Erectness$ and the degree of $Fatigue$ requires a comprehensive consideration of ${\theta }_{Hip}$, ${\theta }_{Knee}$, ${\theta }_{Ankle}$, $act$, and $L^M$.

3.2 Numerical trade-offs among hip–knee–ankle angles by skeletal architecture

As shown in Figure 3D, the degree of $Erectness$ increased with ${\theta }_{Hip}$, ${\theta }_{Knee}$, and ${\theta }_{Ankle}$, wherein the change caused by ${\theta }_{Hip}$ was the most evident. This is attributable to the fact that the hip, knee, and ankle joints, respectively, drive the HAT, thigh, and shank segments, among which the HAT segment is the longest.

As shown in Figure 3E, the motion range of ${\theta }_{Hip}$ was $105.59\pm 48.49°$, the motion range of ${\theta }_{Knee}$ was $118.07\pm 43.83°$, and the motion range of ${\theta }_{Ankle}$ was $95.42\pm 17.05°$ in 3,536 simulation experiments of bipedal standing in chimps.

As shown in Figure 3F, the corresponding ${\theta }_{Hip}$, ${\theta }_{Knee}$, and ${\theta }_{Ankle}$ of the optimal BSP and easiest BSP were, respectively, $110.02°$, $131.19°$, and $99.92°$, which is consistent with the existing measurement data of the middle stance during bipedal walking in chimps (Jenkins, 1972; O'Neill et al., 2015).

Taking the optimal BSP as the benchmark, the lowest BSP showed a significant decrease in ${\theta }_{Hip}$ ($-40.60\%$) and insignificant changes in ${\theta }_{Knee}$ ($-3.07\%$) and ${\theta }_{Ankle}$ ($+6.80\%$), while the highest BSP showed a significant increase in ${\theta }_{Hip}$ ($+32.24\%$) and insignificant changes in ${\theta }_{Knee}$ ($+3.36\%$) and ${\theta }_{Ankle}$ ($-6.59\%$). This is not only consistent with the pattern shown in Figure 3D, but also suggests that ${\theta }_{Hip}$, ${\theta }_{Knee}$, and ${\theta }_{Ankle}$ cannot be increased or decreased at the same time compared to the optimal BSP in the effort to maintain balance in chimps.

It is noteworthy that the maximum degree of $Fatigue$ (the hardest BSP) did not correspond to the highest or lowest BSP, whereas ${\theta }_{Hip}$ increased significantly ($+38.32\%$), ${\theta }_{Knee}$ decreased slightly ($-6.18\%$), and ${\theta }_{Ankle}$ decreased significantly ($-16.55\%$) compared to the optimal BSP. This signifies that simultaneous changes in ${\theta }_{Hip}$ and ${\theta }_{Ankle}$ cause a greater degree of $Fatigue$ than simultaneous changes in ${\theta }_{Hip}$ and ${\theta }_{Knee}$.

Therefore, there is a numerical trade-off between the hip–knee–ankle joint angles in the quest of the optimal BSP for chimps.

The hip–knee–ankle joint angles directly decided $L^{MTU}$ of the hind limbs, thereby influencing the range of values for $L^M$, which, in turn, indirectly influenced the value of the degree of $Fatigue$.

For uni-articular MTUs, the larger the ${\theta }_{Hip}$ was, the smaller the $L^{MTU}$ of the extensor GM; the larger the ${\theta }_{Knee}$ was , the smaller the $L^{MTU}$ of the extensor Vas; the larger the ${\theta }_{Ankle}$ was, the smaller the $L^{MTU}$ of the extensor Sol and the larger the $L^{MTU}$ of the flexor TA.

For bi-articular MTUs, bflh, semimem, and semiten were both hip extensors and knee flexors, RF was both the hip flexor and knee extensor, and gasl and gasm were both knee flexors and ankle extensors. The variation in the $L^{MTU}$ in bi-articular MTUs depended on the specific magnitude of the angular variations.

As shown in Figures 5–7, as long as ${\theta }_{Hip}$, ${\theta }_{Knee}$, ${\theta }_{Ankle}$, and $L_i^M$ ($i=GM,bflh,semimem,semiten,Vas,RF,Gasl,Gasm,Sol,TA$) were settled, ${act}_i$ ($i=GM,bflh,semimem,semiten,Vas,RF,Gasl,Gasm,Sol,TA$) could be uniquely certified. Ergo, $Fatigue$ can be derived.

To summarize, the numerical trade-offs between ${\theta }_{Hip}$, ${\theta }_{Knee}$, and ${\theta }_{Ankle}$ also demand the contemplation of muscle activation of lower-limb MTUs.

3.3 Numerical trade-offs among muscle parameters of MTUs by muscle properties

The distribution and value ranges of the activation, relative muscle lengths, and relative muscle forces of the lower-limb MTUs in the 3,536 experimental simulations are shown in Figure 4.

FIGURE 4

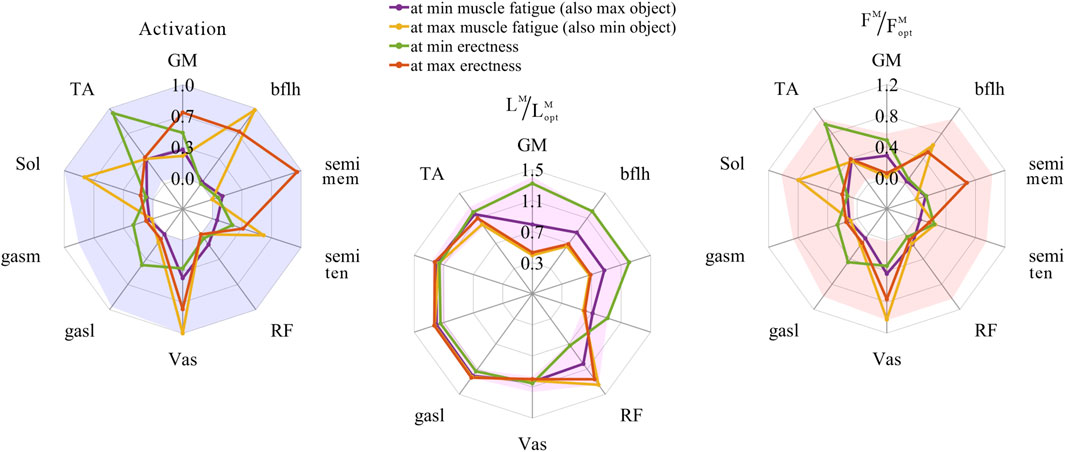
FIGURE 4. Distribution and value ranges of activation, relative muscle lengths, and relative muscle forces of the lower-limb MTUs. Marked lines: purple: both the optimal and easiest BSP; yellow: both the worst and hardest BSP; green: lowest BSP; red: highest BSP.

3.3.1 Relative muscle lengths

According to Section 2.1.2, the degree of muscle activation in the lower-limb MTUs directly depends on the relative muscle lengths.

As shown in Figures 5, 8, 9, for uni-articular MTUs, there was a correspondence between the relative muscle lengths and joint angles. For the hip extensor GM, $\frac{l_m^{GM}}{l_{opt}^{GM}}$ was negatively correlated with ${\theta }_{Hip}$ ($r=-1.00$, $p<0.05$). For the knee extensor Vas, $\frac{l_m^{Vas}}{l_{opt}^{Vas}}$ was negatively correlated with ${\theta }_{Knee}$ ($r=-0.95$, $p<0.05$). For the ankle extensor Sol, $\frac{l_m^{Sol}}{l_{opt}^{Sol}}$ was negatively correlated with ${\theta }_{Ankle}$ ($r=-0.78$, $p<0.05$). For the ankle flexor TA, $\frac{l_m^{TA}}{l_{opt}^{TA}}$ was positively correlated with ${\theta }_{Ankle}$ ($r=0.99$, $p<0.05$).

FIGURE 5

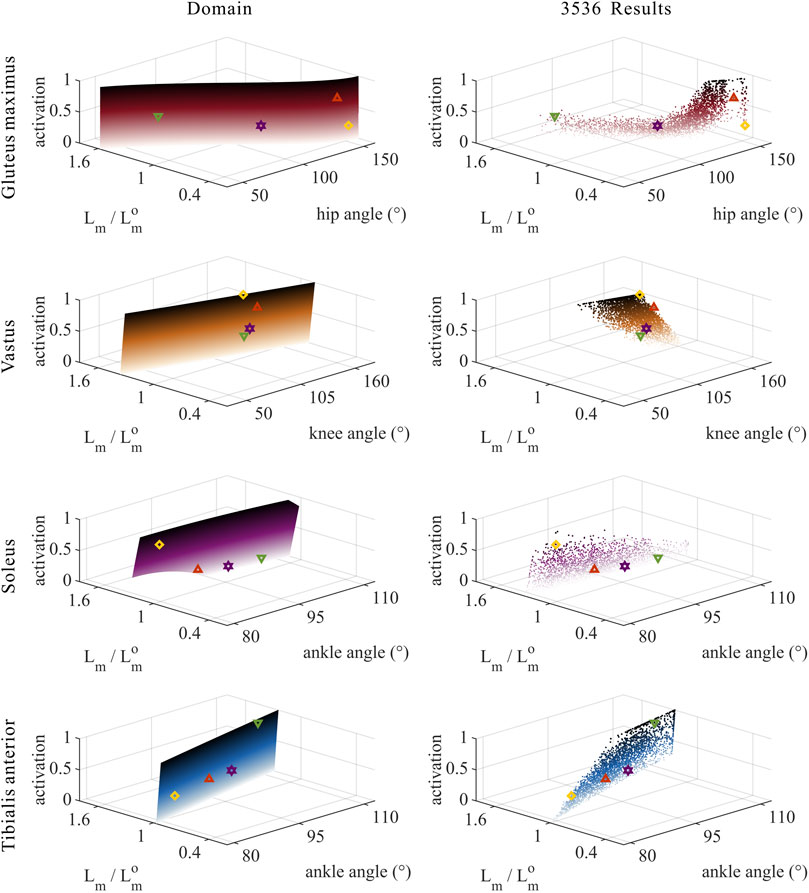
FIGURE 5. Domains (surfaces) and results in the 3,536 simulation experiments (scatters) of activation, relative muscle lengths, and joint angles for the uni-articular MTUs (gluteus maximus, vastus, soleus, and tibialis anterior). Marked points: purple hexagram: both the optimal and easiest BSP; yellow diamond: both the worst and hardest BSP; green downward-pointing triangle: lowest BSP; red upward-pointing triangle: highest BSP.

As shown in Figures 6, 7, 10, 11, and 12, for bi-articular MTUs, the correspondence between the relative muscle lengths and joint angles still existed but the degree varied among joints. For bflh, semimem, and semiten, which are both hip extensors and knee flexors, the relative muscle lengths were negatively correlated with ${\theta }_{Hip}$ ($\frac{l_m^{bflh}}{l_{opt}^{bflh}}$: $r=-0.98$, $p<0.05$; $\frac{l_m^{semimem}}{l_{opt}^{semimem}}$: $r=-0.98$, $p<0.05$; $\frac{l_m^{semiten}}{l_{opt}^{semiten}}$: $r=-0.97$, $p<0.05$) and less correlated with ${\theta }_{Knee}$ ($\frac{l_m^{bflh}}{l_{opt}^{bflh}}$: $r=-0.31$, $p<0.05$; $\frac{l_m^{semimem}}{l_{opt}^{semimem}}$: $r=-0.30$, $p<0.05$; $\frac{l_m^{semiten}}{l_{opt}^{semiten}}$: $r=-0.30$, $p<0.05$). For RF, both the hip flexor and knee extensor, the relative muscle length was positively correlated with ${\theta }_{Hip}$ ($\frac{l_m^{RF}}{l_{opt}^{RF}}$: $r=0.90$, $p<0.05$) and less correlated with ${\theta }_{Knee}$ ($\frac{l_m^{RF}}{l_{opt}^{RF}}$: $r=0.07$, $p<0.05$). For gasl and gasm, which are both knee flexors and ankle extensors, the relative muscle lengths were positively correlated with ${\theta }_{Knee}$ ($\frac{l_m^{Gasl}}{l_{opt}^{Gasl}}$: $r=0.57$, $p<0.05$; $\frac{l_m^{Gasm}}{l_{opt}^{Gasm}}$: $r=0.59$, $p<0.05$) and less correlated with ${\theta }_{Ankle}$ ($\frac{l_m^{Gasl}}{l_{opt}^{Gasl}}$: $r=0.20$, $p<0.05$; $\frac{l_m^{Gasm}}{l_{opt}^{Gasm}}$: $r=0.21$, $p<0.05$).

FIGURE 6

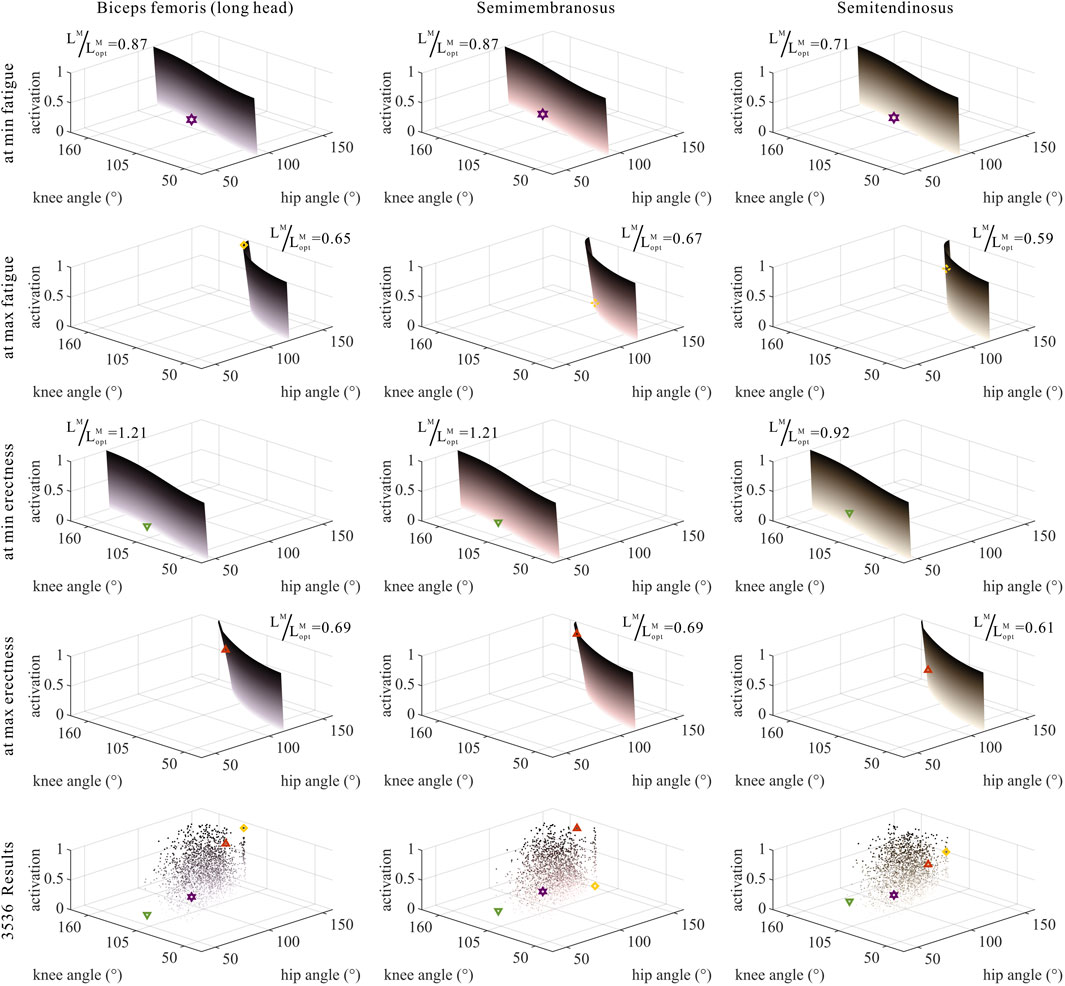
FIGURE 6. Domains (surfaces) and results in the 3,536 simulation experiments (scatters) of activation, relative muscle lengths, and joint angles for bi-articular MTUs [biceps femoris (long head), semimembranosus, and semitendinosus]. Marked points: purple hexagram: both the optimal and easiest BSP; yellow diamond: both the worst and hardest BSP; green downward-pointing triangle: lowest BSP; red upward-pointing triangle: highest BSP.

FIGURE 7

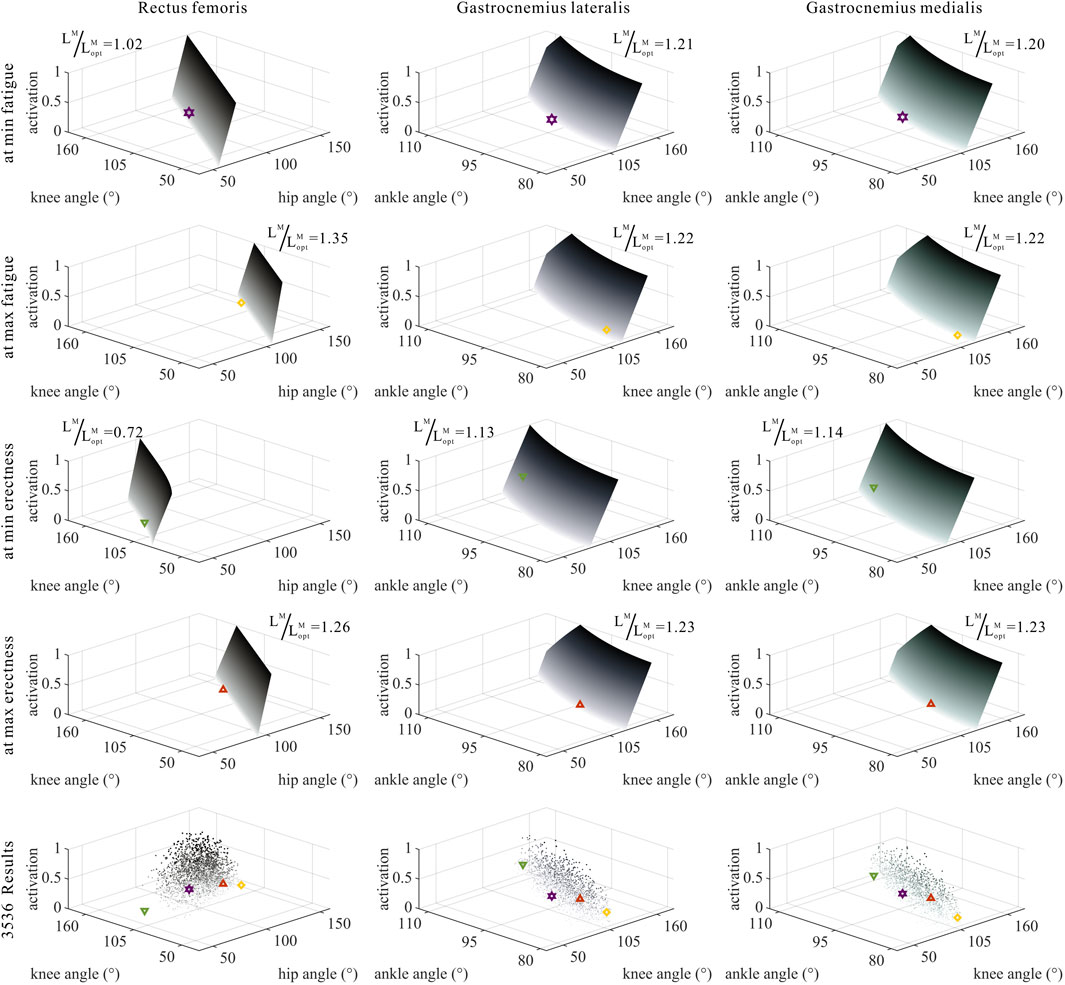
FIGURE 7. Domains (surfaces) and results in the 3,536 simulation experiments (scatters) of activation, relative muscle lengths, and joint angles for bi-articular MTUs (rectus femoris, gastrocnemius lateralis, and gastrocnemius medialis). Marked points: purple hexagram: both the optimal and easiest BSP; yellow diamond: both the worst and hardest BSP; green downward-pointing triangle: lowest BSP; red upward-pointing triangle: highest BSP.

3.3.2 Muscle activation

As shown in Figures 5, 9, for uni-articular MTUs, there was a correspondence between the muscle activation and joint angles. For the hip extensor GM, ${act}^{GM}$ was positively correlated with ${\theta }_{Hip}$ ($r=0.56$, $p<0.05$). For the knee extensor Vas, ${act}^{Vas}$ was negatively correlated with ${\theta }_{Knee}$ ($r=-0.80$, $p<0.05$). For the ankle extensor Sol, ${act}^{Sol}$ was negatively correlated with ${\theta }_{Ankle}$ ($r=-0.40$, $p<0.05$). For the ankle flexor TA, ${act}^{TA}$ was positively correlated with ${\theta }_{Ankle}$ ($r=0.66$, $p<0.05$). Among them, GM did not satisfy the rule that muscle activation is negatively correlated with joint angles for extensors and positively correlated with joint angles for flexors, which will be discussed in detail in Section 4.

As shown in Figures 6, 7, 12, for bi-articular MTUs, the correspondence between the muscle activation and joint angles still existed in some but the degree was much lower. For bflh, semimem, and semiten, which are both hip extensors and knee flexors, the muscle activation was positively correlated with ${\theta }_{Hip}$ (${act}^{bflh}$: $r=0.20$, $p<0.05$; ${act}^{semimem}$: $r=0.14$, $p<0.05$; ${act}^{semiten}$: $r=0.09$, $p<0.05$) and also positively correlated with ${\theta }_{Knee}$ (${act}^{bflh}$: $r=0.28$, $p<0.05$; ${act}^{semimem}$: $r=0.26$, $p<0.05$; ${act}^{semiten}$: $r=0.18$, $p<0.05$). For RF, both the hip flexor and knee extensor, the muscle activation was negatively correlated with ${\theta }_{Hip}$ (${act}^{RF}$: $r=-0.29$, $p<0.05$) and also negatively correlated with ${\theta }_{Knee}$ (${act}^{RF}$: $r=-0.22$, $p<0.05$). For gasl and gasm, which are both knee flexors and ankle extensors, the correlation was neglectable.

These results suggest that the corresponding relationship between muscle activation and joint angles in bi-articular MTUs does not match that in uni-articular MTUs. It was speculated that bi-articular MTUs play a paramount role in regulating balance during bipedal standing in chimps.

3.3.3 Relative muscle forces

As shown in Figures 8, 9, for uni-articular MTUs, there was a correspondence between the relative muscle forces and joint angles. For the hip extensor GM, $\frac{F_m^{GM}}{F_{opt}^{GM}}$ was negatively correlated with ${\theta }_{Hip}$ ($r=-0.68$, $p<0.05$). For the knee extensor Vas, $\frac{F_m^{Vas}}{F_{opt}^{Vas}}$ was negatively correlated with ${\theta }_{Knee}$ ($r=-0.81$, $p<0.05$). For the ankle extensor Sol, $\frac{F_m^{Sol}}{F_{opt}^{Sol}}$ was negatively correlated with ${\theta }_{Ankle}$ ($r=-0.44$, $p<0.05$). For the ankle flexor TA, $\frac{F_m^{TA}}{F_{opt}^{TA}}$ was positively correlated with ${\theta }_{Ankle}$ ($r=0.66$, $p<0.05$).

FIGURE 8

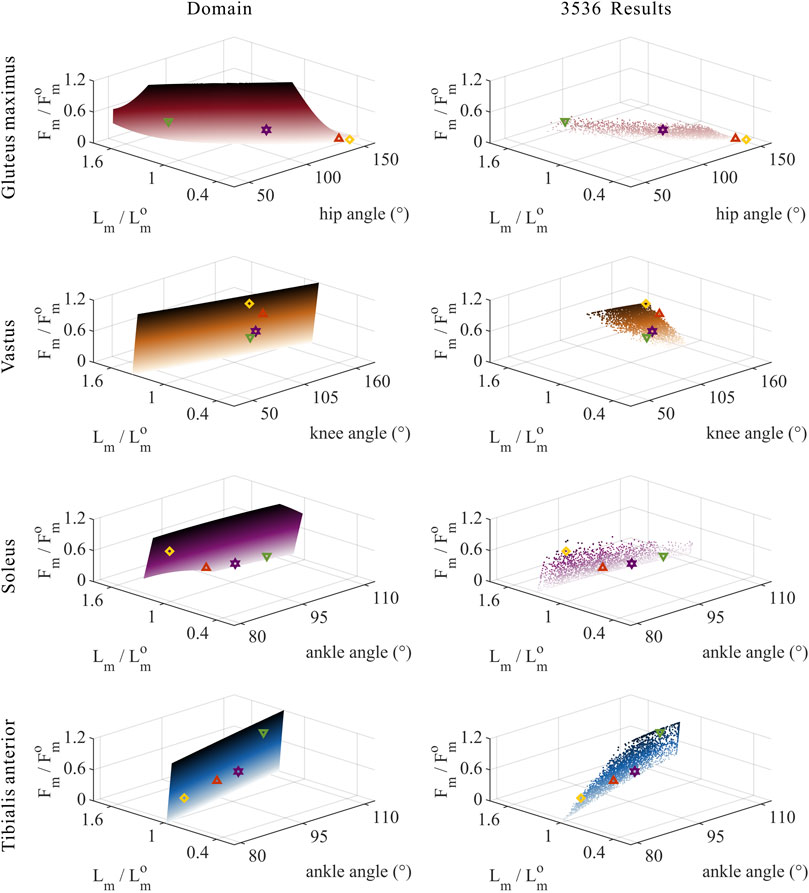
FIGURE 8. Domains (surfaces) and results in the 3,536 simulation experiments (scatters) of relative muscle forces, relative muscle lengths, and joint angles for uni-articular MTUs (gluteus maximus, vastus, soleus, and tibialis anterior). Marked points: purple hexagram: both the optimal and easiest BSP; yellow diamond: both the worst and hardest BSP; green downward-pointing triangle: lowest BSP; red upward-pointing triangle: highest BSP.

FIGURE 9

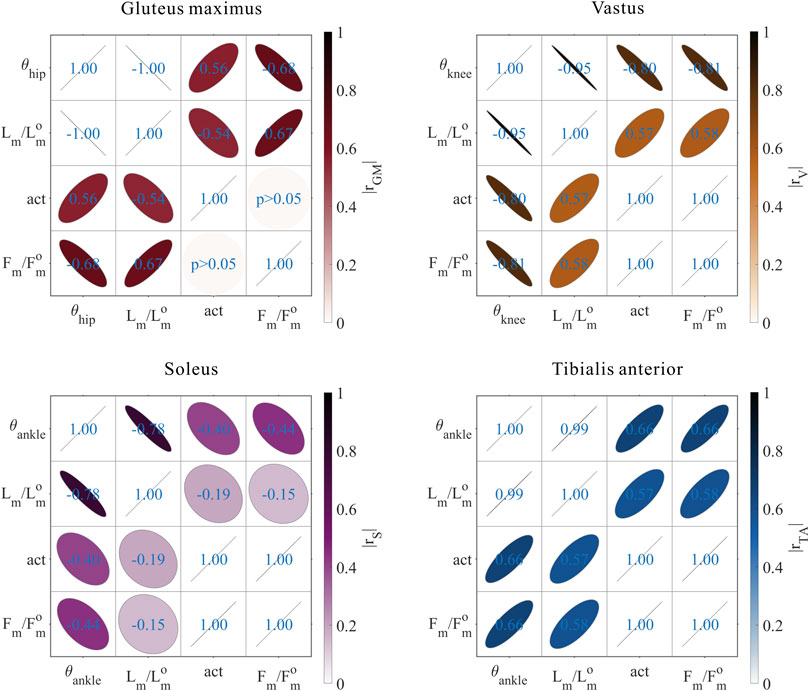
FIGURE 9. Results of the correlation analysis of joint angles, relative muscle lengths, activation, and relative muscle forces among the 3,536 simulation experiments for the uni-articular MTUs (gluteus maximus, vastus, soleus, and tibialis anterior).

These results satisfied the rule that relative muscle forces are negatively correlated with joint angles for extensors and positively correlated with those for flexors.

As shown in Figures 10, 11, 12, for bi-articular MTUs, the correspondence between the relative muscle forces and joint angles was too weak to form a pattern. These results indicate that the relative muscle forces of bi-articular MTUs cannot be conjectured directly from ${\theta }_{Hip}$, ${\theta }_{Knee}$, and ${\theta }_{Ankle}$, which likewise took the next step in validating that bi-articular MTUs play a fundamental role in regulating balance during bipedal standing in chimps.

FIGURE 10

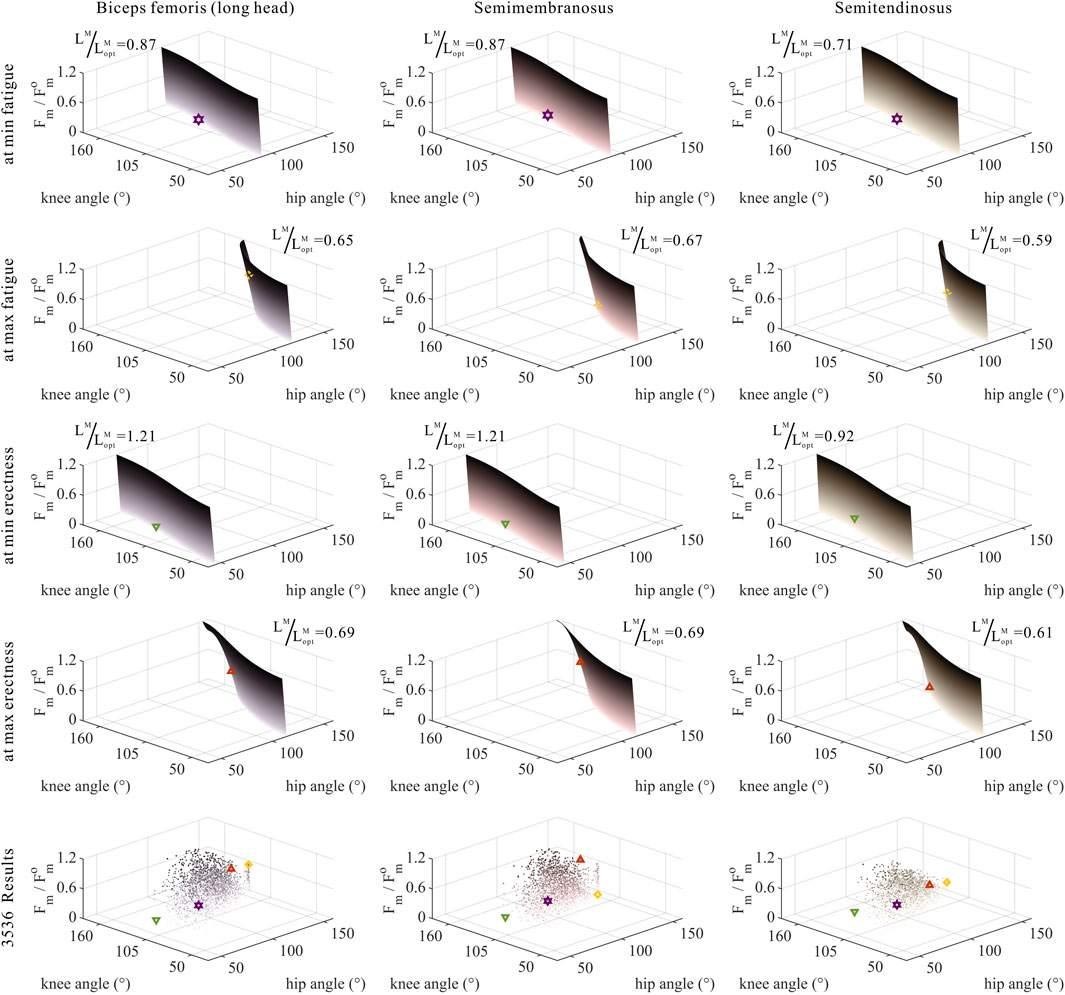
FIGURE 10. Domains (surfaces) and results in the 3,536 simulation experiments (scatters) of relative muscle forces, relative muscle lengths, and joint angles for bi-articular MTUs [biceps femoris (long head), semimembranosus, and semitendinosus]. Marked points: purple hexagram: both the optimal and easiest BSP; yellow diamond: both the worst and hardest BSP; green downward-pointing triangle: lowest BSP; red upward-pointing triangle: highest BSP.

FIGURE 11

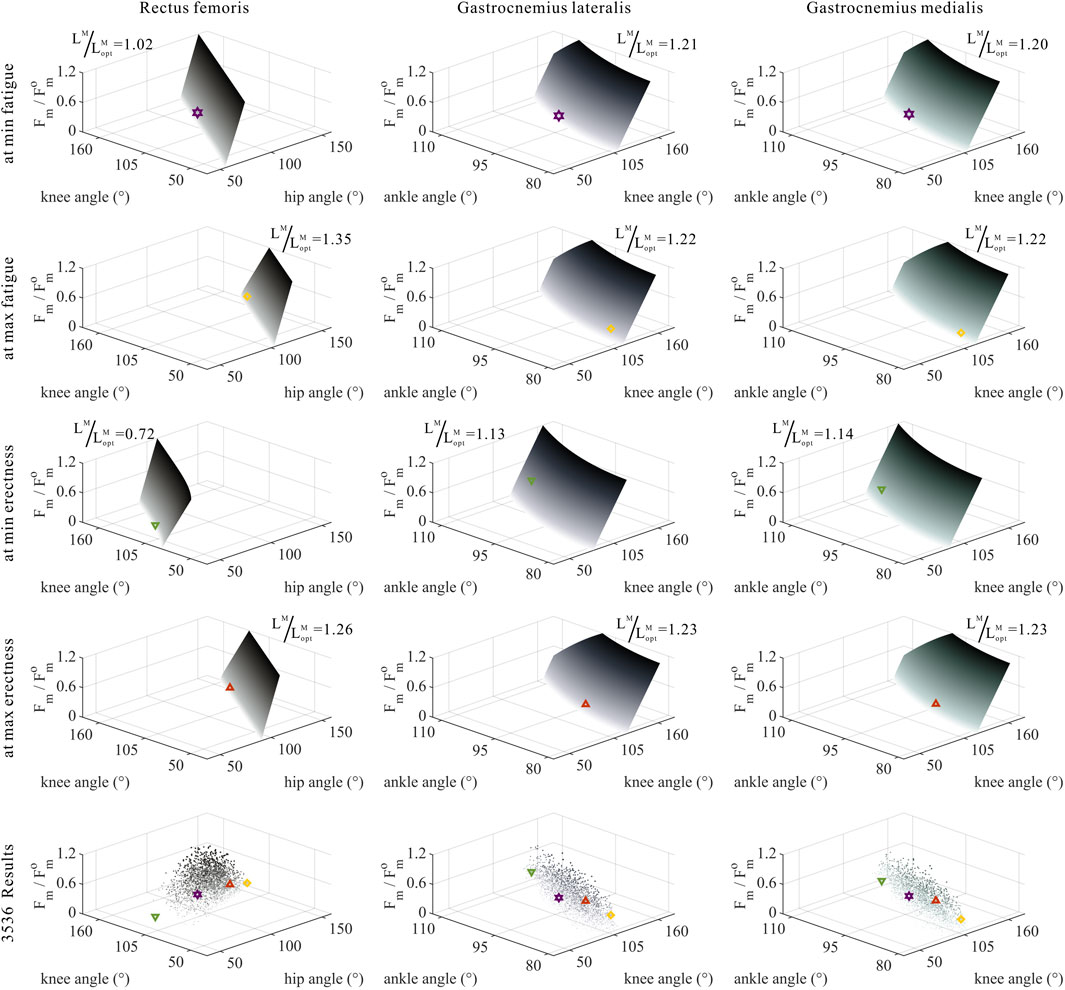
FIGURE 11. Domains (surfaces) and results in the 3,536 simulation experiments (scatters) of relative muscle forces, relative muscle lengths, and joint angles for bi-articular MTUs (rectus femoris, gastrocnemius lateralis, and gastrocnemius medialis). Marked points: purple hexagram: both the optimal and easiest BSP; yellow diamond: both the worst and hardest BSP; green downward-pointing triangle: lowest BSP; red upward-pointing triangle: highest BSP.

FIGURE 12

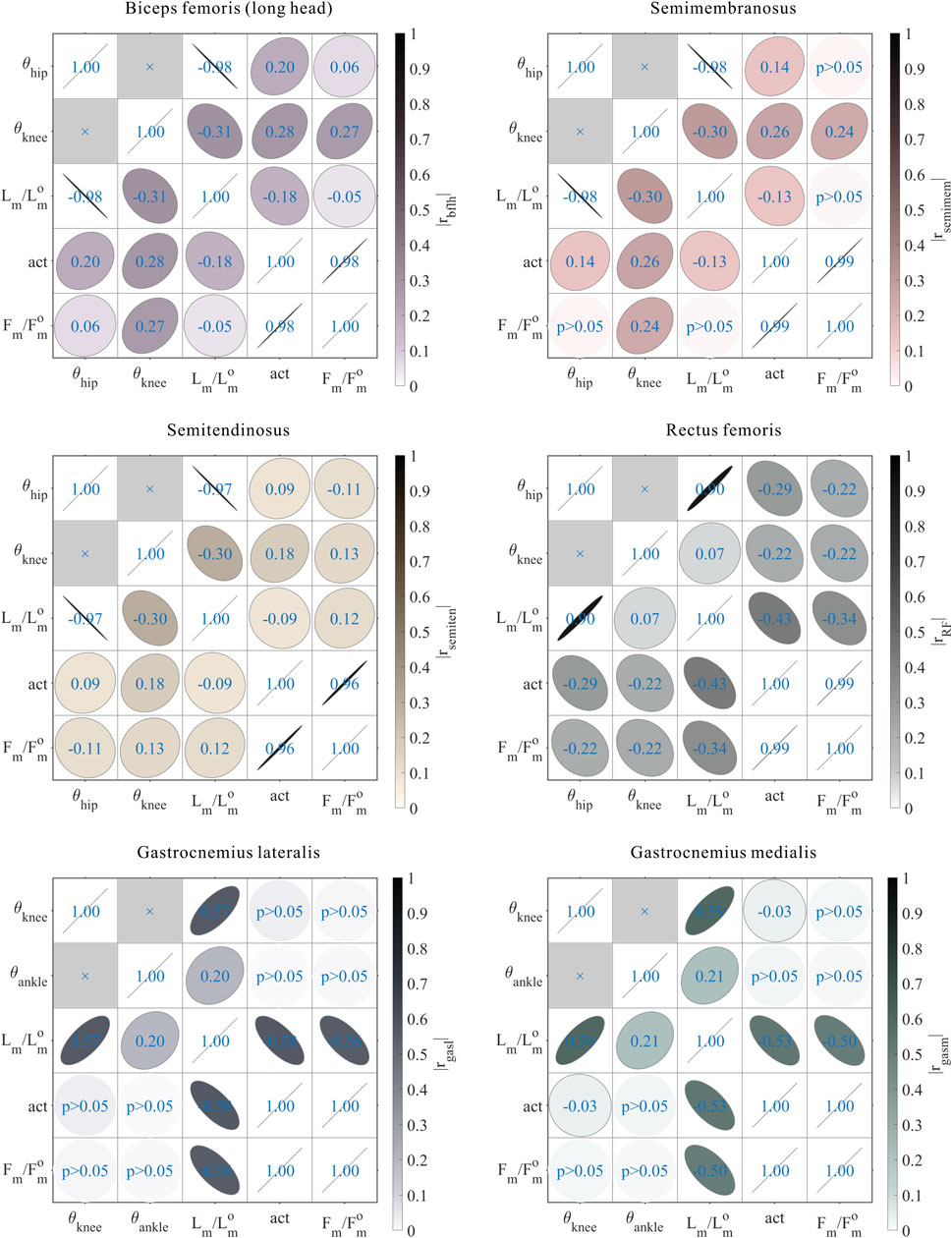
FIGURE 12. Results of the correlation analysis of joint angles, relative muscle lengths, activation, and relative muscle forces among the 3,536 simulation experiments for the bi-articular MTUs [biceps femoris (long head), semimembranosus, semitendinosus, rectus femoris, gastrocnemius lateralis, and gastrocnemius medialis].

4 Discussion

Our study substantiated the premise that when the common chimpanzee is bipedal standing, 1) it cannot simultaneously achieve the maximum $Erectness$ and the minimum $Fatigue$, and excessive $Erectness$ would not lead to the reduction of $Fatigue$; 2) the hip–knee–ankle joint angles corresponding to the optimal BSP are consistent with the measurement data (Jenkins, 1972; O'Neill et al., 2015) of the middle stance during bipedal walking of chimps; 3) for uni-articular MTUs, the relationship between the muscle activation and the corresponding joint angle, that between the relative muscle lengths and the corresponding joint angle, together with that between the relative muscle forces and the corresponding joint angle is, generally negatively correlated for extensors and positively correlated for flexors; and 4) for bi-articular MTUs, the relationship between the relative muscle lengths and the corresponding joint angles is still negatively correlated for extensors and positively correlated for flexors, but that between the muscle activation and the corresponding joint angles, coupled with the relationship between the relative muscle forces and the corresponding joint angles, is hardly correlated.

4.1 Biomechanical effects of skeletal architecture on the bipedal standing posture of chimps

The lumbar lordosis is absent in chimps; their almost-rigid lumbar spine restrains further extension of the HAT, which compels the lower-limb MTUs to bear greater lumbar-bending stresses during bipedal standing (Lovejoy et al., 2009). In this study, the pelvis was included in the HAT segment, and not as a separate segment, when we established the musculoskeletal model, ignoring the degree of freedom between the lumbar spine and pelvis.

The lower limbs of chimps are evidently shorter than the slender legs of humans (Schultz, 1937; Young et al., 2010); evidently, their HAT segment is longer than the thigh and shank segments. The results presented in Section 3.1 unmasked that this very skeletal architecture leads to the variation in the degree of $Erectness$, which was induced mainly by the hip joint angle.

The elongated and laterally oriented ischia of chimps limit the range of motion of the hip joint. When the hip joint is extended, the moment arms of the GM and hamstrings (bflh, semimem, and semiten), together with the length of the GM, rapidly decrease (Robinson, 1972; McHenry, 1975; Kozma et al., 2018). The results obtained in Section 3.3.1 suggest that this very skeletal architecture leads to the relative muscle lengths of bi-articular MTUs that span the hip and knee joints, namely, the bflh, semimem, semiten, and RF, to be more susceptible to the hip joint angle.

The elongated and dorsally oriented ilia of chimps entail that only the movement of the gluteus maximus ischiofemoralis is regulated in the sagittal plane, whereas the movement of the gluteus maximus poprius is mainly curbed in the coronal plane (Stern, 1972; Tuttle et al., 1979; Lieberman et al., 2006). The results obtained in Section 3.3.2 indicate that this skeletal architecture leads to a positive correlation between the muscle activation of GM, uni-articular extensor, and hip joint angle, in contrast to the pattern satisfied by other uni-articular MTUs, where muscle activation was negatively correlated with joint angles for extensors and positively correlated with joint angles for flexors.

4.2 Biomechanical effects of muscle properties on the bipedal standing posture of chimps

The structure of the MTU governs its muscle–tendon length distribution and its ability to produce force (Biewener and Roberts, 2000; Charles et al., 2022). For instance, the MTU with a shorter muscle and longer tendon is designed to generate more economic force, and that with a longer muscle and shorter tendon is suitable for maintaining the stability of joints. The skeletal muscles of chimps have, on average, longer muscle fibers (Isler, 2005); thus, the maximum dynamic force output in muscles of the same size is 1.35 times greater than that of humans (O’Neill et al., 2017). The results presented in Section 3.3.2 and Section 3.3.3 suggest that this muscle property leads the muscle activation and relative muscle forces of bi-articular MTUs to the violation of the pattern conformed by uni-articular MTUs, where these parameters were negatively correlated with joint angles for extensors and positively correlated with joint angles for flexors. It was meditated that during the bipedal standing of chimps, bi-articular MTUs mainly played a role in harmonizing balance, owing to the longer muscle fibers than those of uni-articular MTUs.

The gluteus maximus of chimps originates from the sacro-iliac region, coccyx, sacrotuberous ligament, and ischial tuberosity, while it inserts in the vastus lateralis aponeurosis (a part of the iliotibial tract) and along the lateral side of the femoral diaphysis (Stern, 1972). Therefore, compared with humans, the gluteus maximus of chimps faces more laterally and then acts more in the coronal plane than that in the sagittal plane (Lovejoy et al., 2002). The results of Section 3.3.2 indicated that this muscle property leads to a positive correlation between the muscle activation and the hip joint angle for the uni-articular extensor GM, in contrast to the pattern met by other uni-articular MTUs where muscle activation was negatively correlated with joint angles for extensors and positively correlated with joint angles for flexors.

The gluteus maximus of chimps is considerably smaller than that of humans, deteriorating the complementary function of the hamstrings in extending the hip joint (Stern and Susman, 1981; Lieberman et al., 2006). The results presented in Section 3.3.2 and Section 3.3.3 indicate that this muscle property leads to a further increase in both the muscle activation and muscle forces of the hamstrings when the hip joint is extended.

Unlike humans, chimps lack the external Achilles tendon in the triceps surae (gasl, gasm, and Sol), the PCSAs of which are relatively small. Therefore, the force production of all these MTUs is small within the motion range of the ankle joint (Thorpe et al., 1999; Payne et al., 2006b).

4.3 Limitations and practical implications

Due to the incompleteness of anatomical information from a single specimen of the common chimpanzee, multiple different specimens were used to build the musculoskeletal model. Therefore, parameters of the skeletal architecture and muscle properties were scaled based on the principle of geometric similarity, which might not be an appropriate assumption. Muscle force-generating capacities of mammals in general were found to be proportional to the body mass raised to the power of 0.8 (Alexander et al., 1981) and to differ in divergent muscles. However, research studies also suggested that while peak isometric muscle forces calculated by the scaling method significantly differed from those measured, the gleaned muscle-force functions were quite similar (Scovil et al., 2006; Redl et al., 2007; Correa & Pandy, 2011). This indication supports the application of mass–length scaling in the musculoskeletal model development.

Though mainly lower-limb MTUs were considered in the musculoskeletal model, core muscles, such as multifidus, also play a critical role in the bipedalism (Wang et al., 2023). Research studies implied that multifidus controls trunk movement primarily in the sagittal plane during the bipedal and quadrupedal movements in chimps (Shapiro & Jungers, 1988; Shapiro & Jungers, 1994). Consequently, multifidus is worth being used in the model, only if the anatomical data are available.

The musculoskeletal model proposed in this paper is able to predict how changes in the skeletal architecture and muscle properties could alter the force-generating capacity of MTUs. This will enhance the understanding of causal relationships between the musculoskeletal system and locomotor characteristics in primates and advance the comprehension of bipedal evolution in humans.

The biomechanical limitations of the common chimpanzee were elucidated in this paper, which inspire the design of prosthetic devices and assistive technologies for people with impaired mobility, and of robotic systems that better mimic the movements of humans.

5 Conclusion

In this study, to explore the effects of skeletal architecture and muscle properties on bipedal standing in chimps from the perspective of biomechanics, we established a whole-body musculoskeletal model of the common chimpanzee and developed experimental simulations of bipedal standing. Chimps bipedally stand in a “bent-hip, bent-knee” posture due to their skeletal architecture, such as the almost rigid lumbar spine, relatively long HAT segment, elongated and laterally oriented ischia, and elongated and dorsally oriented ilia. The relationship between muscle activation, relative muscle lengths, together with relative muscle forces, and the corresponding joint angle varies between uni-articular and bi-articular MTUs because of muscle properties, such as the muscle–tendon length distribution, insertion, and shape. It would appear that bi-articular MTUs chiefly contribute to balance. Future research could continue to complete the anatomical dataset of chimps, refine the relationships between the musculoskeletal system and locomotor characteristics in primates, and even design wearable equipment or bipedal robotics based on the drawn mechanism.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

CHX conceived and directed the study. XWX, WBC, CHX, BH, and LFC constructed the model. XWX collected the data, wrote the codes, conducted the simulation, and performed the statistical analysis. XWX, WBC and CHX interpreted the results. XWX, WBC, CHX, BH, LFC, and BYS wrote the manuscript. All authors approved the submitted version.

Funding

This work was partially supported by the National Natural Science Foundation of China (grant no. 52027806, U1913601).

Acknowledgments

The authors would like to thank Dr. Di Hu, Dr. Chang He, Dr. Lei He, Dr. Jun Fan, Quan-Lin Li, Jin-Hao Yang, and Han-Wen Zhang for their academic advice and technical assistance during the study.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbioe.2023.1140262/full#supplementary-material

References

Alexander, R. M., Jayes, A., Maloiy, G., and Wathuta, E. (1981). Allometry of the leg muscles of mammals. J. Zool 194, 539–552. doi:10.1111/j.1469-7998.1981.tb04600.x

CrossRef Full Text | Google Scholar

Anderson, F. C., and Pandy, M. G. (2001). Static and dynamic optimization solutions for gait are practically equivalent. J. Biomech 34, 153–161. doi:10.1016/s0021-9290(00)00155-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Biewener, A. A., and Roberts, T. J. (2000). Muscle and tendon contributions to force, work, and elastic energy savings: A comparative perspective. Exerc. Sport Sci. Rev 28, 99–107.

PubMed Abstract | Google Scholar

Charles, J., Kissane, R., Hoehfurtner, T., and Bates, K. T. (2022). From fibre to function: Are we accurately representing muscle architecture and performance? Biol. Rev 97, 1640–1676. doi:10.1111/brv.12856

PubMed Abstract | CrossRef Full Text | Google Scholar

Correa, T. A., and Pandy, M. G. (2011). A mass–length scaling law for modeling muscle strength in the lower limb. J. Biomech. 44, 2782–2789. doi:10.1016/j.jbiomech.2011.08.024

PubMed Abstract | CrossRef Full Text | Google Scholar

Crowninshield, R. D., and Brand, R. A. (1981). A physiologically based criterion of muscle force prediction in locomotion. J. Biomech 14, 793–801. doi:10.1016/0021-9290(81)90035-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Demes, B., Thompson, N. E., O’Neill, M. C., and Umberger, B. R. (2015). Center of mass mechanics of chimpanzee bipedal walking. Am. J. Phys. Anthropol 156, 422–433. doi:10.1002/ajpa.22667

PubMed Abstract | CrossRef Full Text | Google Scholar

Diogo, R., Potau, J. M., and Pastor, J. F. (2013). Photographic and descriptive musculoskeletal atlas of chimpanzees: With notes on the attachments, variations, innervation, function and synonymy and weight of the muscles. Boca Raton, FL, USA: CRC Press.

Google Scholar

Doran, D. M. (1992a). Comparison of instantaneous and locomotor bout sampling methods: A case study of adult male chimpanzee locomotor behavior and substrate use. Am. J. Phys. Anthropol 89, 85–99. doi:10.1002/ajpa.1330890108

PubMed Abstract | CrossRef Full Text | Google Scholar

Doran, D. M. (1992b). The ontogeny of chimpanzee and pygmy chimpanzee locomotor behavior: A case study of paedomorphism and its behavioral correlates. J. Hum. Evol 23, 139–157. doi:10.1016/0047-2484(92)90104-H

CrossRef Full Text | Google Scholar

Elftman, H. (1944). The bipedal walking of the chimpanzee. J. Mammal 25, 67–71. doi:10.2307/1374722

CrossRef Full Text | Google Scholar

Goodman, M. (1999). The genomic record of Humankind’s evolutionary roots. Am. J. Hum. Genet 64, 31–39. doi:10.1086/302218

PubMed Abstract | CrossRef Full Text | Google Scholar

Heiple, K. G., and Lovejoy, C. O. (1971). The distal femoral anatomy of Australopithecus. Am. J. Phys. Anthropol 35, 75–84. doi:10.1002/ajpa.1330350109

PubMed Abstract | CrossRef Full Text | Google Scholar

Hunt, K. D. (1991). Positional behavior in the hominoidea. Int. J. Primatol 12, 95–118. doi:10.1007/BF02547576

CrossRef Full Text | Google Scholar

Hunt, K. D. (1992). Positional behavior of Pan troglodytes in the Mahale Mountains and Gombe stream national parks, Tanzania. Am. J. Phys. Anthropol 87, 83–105. doi:10.1002/ajpa.1330870108

PubMed Abstract | CrossRef Full Text | Google Scholar

Hunt, K. D. (1994). The evolution of human bipedality: Ecology and functional morphology. J. Hum. Evol 26, 183–202. doi:10.1006/jhev.1994.1011

CrossRef Full Text | Google Scholar

Isler, K. (2005). 3D-kinematics of vertical climbing in hominoids. Am. J. Phys. Anthropol 126, 66–81. doi:10.1002/ajpa.10419

PubMed Abstract | CrossRef Full Text | Google Scholar

Isler, K., Payne, R. C., Günther, M. M., Thorpe, S. K., Li, Y., Savage, R., et al. (2006). Inertial properties of hominoid limb segments. J. Anat 209, 201–218. doi:10.1111/j.1469-7580.2006.00588.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Jenkins, F. A. (1972). Chimpanzee bipedalism: Cineradiographic analysis and implications for the evolution of gait. Science 178, 877–879. doi:10.1126/science.178.4063.877

PubMed Abstract | CrossRef Full Text | Google Scholar

Kozma, E. E., Webb, N. M., Harcourt-Smith, W. E. H., Raichlen, D. A., D’Août, K., Brown, M. H., et al. (2018). Hip extensor mechanics and the evolution of walking and climbing capabilities in humans, apes, and fossil hominins. Proc. Natl. Acad. Sci. U. S. A 115, 4134–4139. doi:10.1073/pnas.1715120115

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, L. F., and Umberger, B. R. (2016). Generating optimal control simulations of musculoskeletal movement using OpenSim and MATLAB. PeerJ 4, e1638. doi:10.7717/peerj.1638

PubMed Abstract | CrossRef Full Text | Google Scholar

Lieberman, D. E., Raichlen, D. A., Pontzer, H., Bramble, D. M., and Cutright-Smith, E. (2006). The human gluteus maximus and its role in running. J. Exp. Biol 209, 2143–2155. doi:10.1242/jeb.02255

PubMed Abstract | CrossRef Full Text | Google Scholar

Lovejoy, C. O., Meindl, R. S., Ohman, J. C., Heiple, K. G., and White, T. D. (2002). The maka femur and its bearing on the antiquity of human walking: Applying contemporary concepts of morphogenesis to the human fossil record. Am. J. Phys. Anthropol 119, 97–133. doi:10.1002/ajpa.10111

PubMed Abstract | CrossRef Full Text | Google Scholar

Lovejoy, C. O., Suwa, G., Simpson, S. W., Matternes, J. H., and White, T. D. (2009). The great divides: Ardipithecus ramidus reveals the postcrania of our last common ancestors with African apes. Science 326, 73–106. doi:10.1126/science.1175833

PubMed Abstract | CrossRef Full Text | Google Scholar

Manal, K., and Buchanan, T. S. (2004). Subject-specific estimates of tendon slack length: A numerical method. J. Appl. Biomech 20, 195–203. doi:10.1123/jab.20.2.195

CrossRef Full Text | Google Scholar

McHenry, H. M. (1975). The ischium and hip extensor mechanism in human evolution. Am. J. Phys. Anthropol 43, 39–46. doi:10.1002/ajpa.1330430107

PubMed Abstract | CrossRef Full Text | Google Scholar

Myatt, J. P., Crompton, R. H., and Thorpe, S. K. (2011). Hindlimb muscle architecture in non-human great apes and a comparison of methods for analysing inter-species variation. J. Anat 219, 150–166. doi:10.1111/j.1469-7580.2011.01383.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakatsukasa, M. (2004). Acquisition of bipedalism: The miocene hominoid record and modern analogues for bipedal protohominids. J. Anat 204, 385–402. doi:10.1111/j.0021-8782.2004.00290.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Neumann, D. A. (2013). Kinesiology of the musculoskeletal system: Foundations for rehabilitation. St. Louis, MO, USA: Elsevier Inc.

Google Scholar

O'Neill, M. C., Demes, B., Thompson, N. E., Larson, S. G., Stern, J. T., and Umberger, B. R. (2022). Adaptations for bipedal walking: Musculoskeletal structure and three-dimensional joint mechanics of humans and bipedal chimpanzees (Pan troglodytes). J. Hum. Evol 168, 103195. doi:10.1016/j.jhevol.2022.103195

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Neill, M. C., Demes, B., Thompson, N. E., and Umberger, B. R. (2018). Three-dimensional kinematics and the origin of the hominin walking stride. J. R. Soc. Interface 15, 20180205. doi:10.1098/rsif.2018.0205

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Neill, M. C., Lee, L. F., Demes, B., Thompson, N. E., Larson, S. G., Stern, J. T., et al. (2015). Three-dimensional kinematics of the pelvis and hind limbs in chimpanzee (Pan troglodytes) and human bipedal walking. J. Hum. Evol 86, 32–42. doi:10.1016/j.jhevol.2015.05.012

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Neill, M. C., Lee, L. F., Larson, S. G., Demes, B., Stern, J. T., and Umberger, B. R. (2013). A three-dimensional musculoskeletal model of the chimpanzee (Pan troglodytes) pelvis and hind limb. J. Exp. Biol 216, 3709–3723. doi:10.1242/jeb.079665

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Neill, M. C., Umberger, B. R., Holowka, N. B., Larson, S. G., and Reiser, P. J. (2017). Chimpanzee super strength and human skeletal muscle evolution. Proc. Natl. Acad. Sci. U. S. A 114, 7343–7348. doi:10.1073/pnas.1619071114

PubMed Abstract | CrossRef Full Text | Google Scholar

Pandy, M. G. (2001). Computer modeling and simulation of human movement. Annu. Rev. Biomed. Eng 3, 245–273. doi:10.1146/annurev.bioeng.3.1.245

PubMed Abstract | CrossRef Full Text | Google Scholar

Payne, R. C., Crompton, R. H., Isler, K., Savage, R., Vereecke, E. E., Günther, M. M., et al. (2006a). Morphological analysis of the hindlimb in apes and humans. II. Moment arms. J. Anat 208, 725–742. doi:10.1111/j.1469-7580.2006.00564.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Payne, R. C., Crompton, R. H., Isler, K., Savage, R., Vereecke, E. E., Günther, M. M., et al. (2006b). Morphological analysis of the hindlimb in apes and humans. I. Muscle architecture. J. Anat 208, 709–724. doi:10.1111/j.1469-7580.2006.00563.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Pontzer, H. (2018). “Locomotor ecology and evolution in chimpanzees and humans,” in Chimpanzees and human evolution. Editors M. Muller, R. Wrangham, and D. Pilbeam (Cambridge, MA, USA: Harvard University Press).

Google Scholar

Pontzer, H., Raichlen, D. A., and Rodman, P. S. (2014). Bipedal and quadrupedal locomotion in chimpanzees. J. Hum. Evol 66, 64–82. doi:10.1016/j.jhevol.2013.10.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Pontzer, H., Raichlen, D. A., and Sockol, M. D. (2009). The metabolic cost of walking in humans, chimpanzees, and early hominins. J. Hum. Evol 56, 43–54. doi:10.1016/j.jhevol.2008.09.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Redl, C., Gfoehler, M., and Pandy, M. G. (2007). Sensitivity of muscle force estimates to variations in muscle-tendon properties. HumanMovementScience 26, 306–319. doi:10.1016/j.humov.2007.01.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Robinson, J. T. (1972). Australopithecine anatomy: Early hominid posture and locomotion. Chicago, IL, USA: University of Chicago Press.

Google Scholar

Sawicki, G. S., and Khan, N. S. (2016). A simple model to estimate plantarflexor muscle–tendon mechanics and energetics during walking with elastic ankle exoskeletons. IEEE Trans. Bio Med. Eng 63, 914–923. doi:10.1109/TBME.2015.2491224

CrossRef Full Text | Google Scholar

Schultz, A. H. (1937). Proportions, variability and asymmetries of the long bones of the limbs and the clavicles in man and apes. Hum. Biol 9, 281–328.

Google Scholar

Scovil, C. Y., and Ronsky, J. L. (2006). Sensitivity of a Hill-based muscle model to perturbations in model parameters. J. Biomech 39, 2055–2063. doi:10.1016/j.jbiomech.2005.06.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Sellers, W. I., Margetts, L., Bates, K. T., and Chamberlain, A. T. (2013). Exploring diagonal gait using a forward dynamic three-dimensional chimpanzee simulation. Folia Primatol. (Basel) 84, 180–200. doi:10.1159/000351562

PubMed Abstract | CrossRef Full Text | Google Scholar

Shapiro, L. J., and Jungers, W. L. (1988). Back muscle function during bipedal walking in chimpanzee and gibbon: Implications for the evolution of human locomotion. Am. J. Phys. Anthropol 77, 201–212. doi:10.1002/ajpa.1330770208

PubMed Abstract | CrossRef Full Text | Google Scholar

Shapiro, L. J., and Jungers, W. L. (1994). Electromyography of back muscles during quadrupedal and bipedal walking in primates. Am. J. Phys. Anthropol 93, 491–504. doi:10.1002/ajpa.1330930408

PubMed Abstract | CrossRef Full Text | Google Scholar

Sockol, M. D., Raichlen, D. A., and Pontzer, H. (2007). Chimpanzee locomotor energetics and the origin of human bipedalism. Proc. Natl. Acad. Sci. U. S. A 104, 12265–12269. doi:10.1073/pnas.0703267104

PubMed Abstract | CrossRef Full Text | Google Scholar

Stern, J. T. (1972). Anatomical and functional specializations of the human gluteus maximus. Am. J. Phys. Anthropol 36, 315–339. doi:10.1002/ajpa.1330360303

PubMed Abstract | CrossRef Full Text | Google Scholar

Stern, J. T., and Susman, R. L. (1981). Electromyography of the gluteal muscles in Hylobates, Pongo, and Pan: Implications for the evolution of hominid bipedality. Am. J. Phys. Anthropol 55, 153–166. doi:10.1002/ajpa.1330550203

CrossRef Full Text | Google Scholar

Thompson, N. E., Demes, B., O’Neill, M. C., Holowka, N. B., and Larson, S. G. (2015). Surprising trunk rotational capabilities in chimpanzees and implications for bipedal walking proficiency in early hominins. Nat. Commun. 6, 8416. doi:10.1038/ncomms9416

PubMed Abstract | CrossRef Full Text | Google Scholar

Thorpe, S. K., Crompton, R. H., Günther, M. M., Ker, R. F., and McNeill Alexander, R. (1999). Dimensions and moment arms of the hind-and forelimb muscles of common chimpanzees (Pan troglodytes). Am. J. Phys. Anthropol 110, 179–199. doi:10.1002/(SICI)1096-8644(199910)110:2<179:AID-AJPA5>3.0.CO;2-Z

PubMed Abstract | CrossRef Full Text | Google Scholar

Tuttle, R. H., Basmajian, J. V., and Ishida, H. (1978). Activities of pongid thigh muscles during bipedal behavior. Am. J. Phys. Anthropol 50, 123–135. doi:10.1002/ajpa.1330500113

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, K., Deng, Z., Chen, X., Shao, J., Qiu, L., Jiang, C., et al. (2023). The role of multifidus in the biomechanics of lumbar spine: A musculoskeletal modeling study. Bioengineering 10, 67. doi:10.3390/bioengineering10010067

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, W. J., and Crompton, R. H. (2004). Analysis of the human and ape foot during bipedal standing with implications for the evolution of the foot. J. Biomech 37, 1831–1836. doi:10.1016/j.jbiomech.2004.02.036

PubMed Abstract | CrossRef Full Text | Google Scholar

Waterson, R. H., Lander, E. S., and Wilson, R. K. (2005). Initial sequence of the chimpanzee genome and comparison with the human genome. Nature 437, 69–87. doi:10.1038/nature04072

PubMed Abstract | CrossRef Full Text | Google Scholar

Wells, J. B. (1965). Comparison of mechanical properties between slow and fast mammalian muscles. J. Physiol 178, 252–269. doi:10.1113/jphysiol.1965.sp007626

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamazaki, N. (1985). “Primate bipedal walking: Computer simulation,” in Primate morphophysiol. Locomot. Anal. Human biped (Tokyo: University of Tokyo Press).

Google Scholar

Young, N. M., Wagner, G. P., and Hallgrímsson, B. (2010). Development and the evolvability of human limbs. Proc. Natl. Acad. Sci. U. S. A 107, 3400–3405. doi:10.1073/pnas.0911856107

PubMed Abstract | CrossRef Full Text | Google Scholar

Zajac, F. E. (1989). Muscle and tendon: Properties, models, scaling, and application to biomechanics and motor control. Crit. Rev. Biomed. Eng 17, 359–411.

PubMed Abstract | Google Scholar

Zihlman, A. L., and Cramer, D. L. (1978). Skeletal differences between pygmy (Pan paniscus) and common chimpanzees (Pan troglodytes). Folia Primatol. (Basel) 29, 86–94. doi:10.1159/000155830

PubMed Abstract | CrossRef Full Text | Google Scholar