Zhiqian Zheng
Yang Liu
Aobo Zhang
Hao Chen
Qian Wan
Lei Zhong
Qing Han
Jincheng Wang- Department of Orthopedics, The Second Hospital of Jilin University, Changchun, China
Background: Poor prosthesis alignment during total knee arthroplasty could cause problems such as polyethylene spacer wear, leading to surgical failure and revision surgery. The problems caused by the malalignment of the tibial plateau prosthesis in the medial and lateral planes are unclear. We aimed to investigate the stress distribution and micromotion of the tibia when the tibial plateau prosthesis is translated 1 and 2 mm medially and laterally, respectively, using finite element analysis (FEA).
Method: A non-homogeneous tibia model was created and load conditions when standing on two legs were applied using FEA to simulate the misaligned prosthesis. The stresses, stress distribution, and micromotion of the proximal tibia were analyzed in five positions of the tibial plateau prosthesis: Lateral-2 mm; Lateral-1 mm; Medium; Medial-2 mm; Medial-1 mm.
Result: The maximum stress in the five groups with different misalignments of the platform was 47.29 MPa (Lateral-2 mm). The maximum micromotion among the five groups in different positions was 7.215 μm (Lateral-2 mm).
Conclusion: When placing the tibial plateau prosthesis during total knee arthroplasty, an error of 2 mm or less is acceptable as long as it does not overhang.
1 Introduction
Several studies have shown that total knee arthroplasty (TKA) is an effective and durable treatment for end-stage knee arthritis (Vessely et al., 2006; Guo et al., 2012). The primary goals of TKA include reducing knee pain, re-aligning the femur and tibia, maintaining knee stability, and preserving joint flexibility. Despite the great clinical results of TKA, revision rates remain high due to poorly aligned prosthetic components, resulting in aseptic loosening, instability, and polyethylene wear (Dalury et al., 2013).
To predict and avoid the problems mentioned above and thus improve the prognosis of surgery, the analytical approach (Jin et al., 1995), experimental measurement (Liau et al., 1999) and finite element analysis (Popescu et al., 2019; Dong et al., 2020; Park et al., 2021) (FEA) have been widely used in the field of orthopedics. Matsuda et al. (1999) investigated the effect of varus tilt on contact stresses in total knee prostheses using electronic pressure sensors; Liau et al. (1999) studied the effect of tibiofemoral joint contact alignment of knee prosthesis using Fuji pressure-sensitive film in an in vitro biomechanical test. They also explored the effect of the tibial polyethylene component of the total knee prosthesis on stresses using FEA (Liau et al., 2002). Different misalignment conditions are tested by FEA by simulating angles, friction, and stresses. These findings are applied in preoperative planning to prevent potential TKA failure (Perillo-Marcone and Taylor, 2007; Minh et al., 2013). To our knowledge, there have been few studies examining the effect of medial-lateral translational misalignment of the tibial plateau prosthesis on the tibia.
Inoue et al. (2016) showed that the risk of medial tibial condylar fractures increases with increased tilt of the valgus angle of the tibial prosthesis. If the tibial prosthesis is poorly rotated, firstly, the riser of the polyethylene prosthesis will be worn further and, since the femoral and tibial prostheses are no longer matched in the same position, the soft tissue will be twisted during flexion and extension activities, resulting in a stiff knee (Bedard et al., 2011). Secondly, internal rotation can bring about lateral patellar subluxation and wear of the lateral patellofemoral joint, while external rotation can cause inward patellar trajectory, internal tibial rotation, or a change in gait (Perillo-Marcone et al., 2000; Ishii et al., 2015). Any errors that cause asymmetric loading of the joint, such as misalignment or instability of the prosthesis, could lead to increased wear rates, resulting in surgical failure and revision (Fraser et al., 2015).
We aimed to investigate the stress distribution and micromotion of the tibia when the tibial plateau prosthesis is translated 1 mm and 2 mm medially and laterally, respectively, using FEA. This may contribute to the reduction of TKA revision rates and improved satisfaction of patients after TKA.
2 Materials and methods
2.1 Establishment of a non-homogeneous three-dimensional (3D) tibia model and surgical simulation
Computed tomography (CT) scan data were recorded from a 49-year-old male volunteer. The images were imported into Mimics (v21.0, Materialise, Leuven, Belgium), and the right tibia was rebuilt as a 3D model. This research was approved by the Ethics Committee of the Second Hospital of Jilin University and the volunteer provided informed consent.
The 3D model of the right tibia and the tibial plateau prosthesis (Ai Kang A3)were prepared as STL format files, and the simulated surgery was performed in Magics (v21.0, Materialise, Leuven, Belgium). The posterior slope was set to 5°, and the tibial model was resected in the traditional surgical fashion (Indelli et al., 2016; Maderbacher et al., 2017), by removing the tibia 6 mm below the medial tibial articular surface, perpendicular to the mechanical axis. The application of this study focused on the stress distribution during the interaction of the proximal bone with the platform prosthesis, so the distal tibia was separated from the system to reduce the calculation time.
After installing the tibial plateau prosthesis, the prosthesis was moved medially and laterally by 1 mm and 2 mm, respectively, to simulate a slippage dislocation. The prosthesis is shown in the middle position, as well as translated 2 mm to the medial and lateral side, in Figure 1.
FIGURE 1. Prosthesis in different positions. (A) Lateral-2 mm; (B) Medium; (C) Medial-2 mm.
In the Mimics software, the 3D model of the tibia with inhomogeneous material properties was defined based on the grayscale values of the CT scans. Following previous studies, the material properties of the tibia were determined according to the following equations (Rho et al., 1995):
in which E is the modulus of elasticity, ρ is the bone density, and GV is the gray value of the bone in the CT data. According to other previous studies (Thompson et al., 2016), the Poisson’s ratio of the bone was set to 0.3 and the modulus of elasticity of the tibial plateau prosthesis was set to 114,500 MPa with a Poisson’s ratio of 0.3. To differentiate, the tibia was divided into ten colored regions, and the material properties are shown in Figure 2.
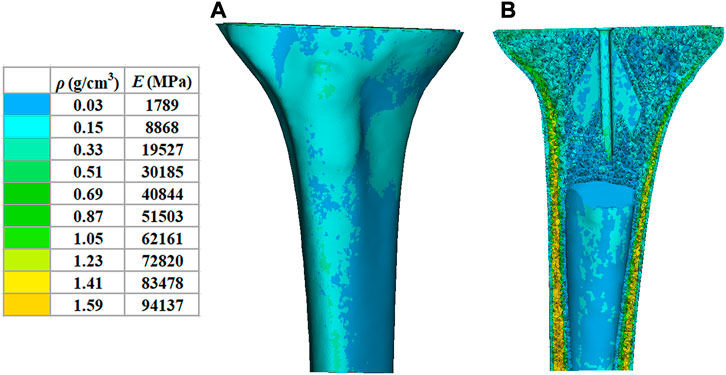
FIGURE 2. Material properties of the inhomogeneous tibia. (A) External material properties of the tibia. (B) Internal material properties of the tibia. ρ: bone density. (E) elastic modulus.
2.2 Meshing and load setting
All components were imported into Hypermesh (14.0, Altair, Troy, MI) to create triangular meshes with the element type C3D4. The number of elements in the bone and prosthesis are 420,036 and 117,094 respectively. A non-linear friction model with surface-surface contact was established between the superior surface of the tibia and the inferior surface of the prosthesis, and the friction coefficient was set to 0.2 (Li et al., 2019). A static analysis of the tibia was performed under a load condition of 963 N to simulate a two-legged stance (Kutzner et al., 2010). According to a previous study (Lin et al., 2017), the ratio of force between the lateral and medial tibial plateau is 40%:60%, respectively, so the force was divided into 385 N and 578 N and loaded with rigid bar element 3 (Rbe3) to transfer the force uniformly. The inferior surface of the distal tibia was constrained in all directions (Figure 3).
FIGURE 3. Loads and constraints of the tibia. The distal tibia is constrained completely.
3 Results
3.1 Finite element analysis
3.3.1 Stress
Figure 4 shows the maximum von Mises stress in the tibia for five sets of platforms in different positions. The highest stress peak of 47.29 MPa can be seen when the platform is misaligned by 2 mm to the lateral side, followed by the stress peak of 20.90 MPa when the platform is misaligned by 2 mm to the medial side. The remaining three data groups were not significantly different compared to each other.
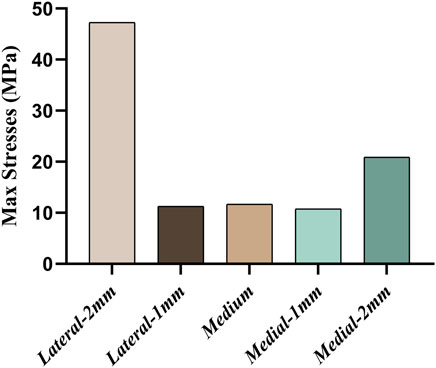
FIGURE 4. Comparison of maximum stresses when five groups of platforms are in different misalignment positions.
The proximal tibia was divided into seven regions to analyze the stress distribution (Figure 5). All cell points in each region were extracted separately and the data was analyzed using SPSS software. Since the data does not obey a normal distribution, the results were analyzed using the Kruskal–Wallis test. According to the stress distribution in the first six regions, the data statistics were obtained as shown in Figure 6. Significant differences were found between the groups except for those labeled p > 0.05. The largest median of 1.43 MPa occurred in the case of a 2 mm medial misalignment in the F region, while the smallest median of 0.075 MPa was seen in the B region where the prosthesis was in the middle position. It can be seen that the red part of the high stress was concentrated in the lower part of the proximal tibia which was the G region.
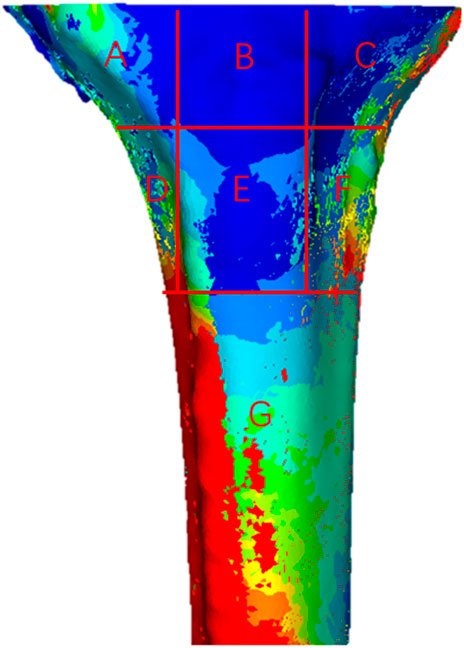
FIGURE 5. Distribution of von Mises stress in the proximal tibia. (A–G) Seven different regions of stress.
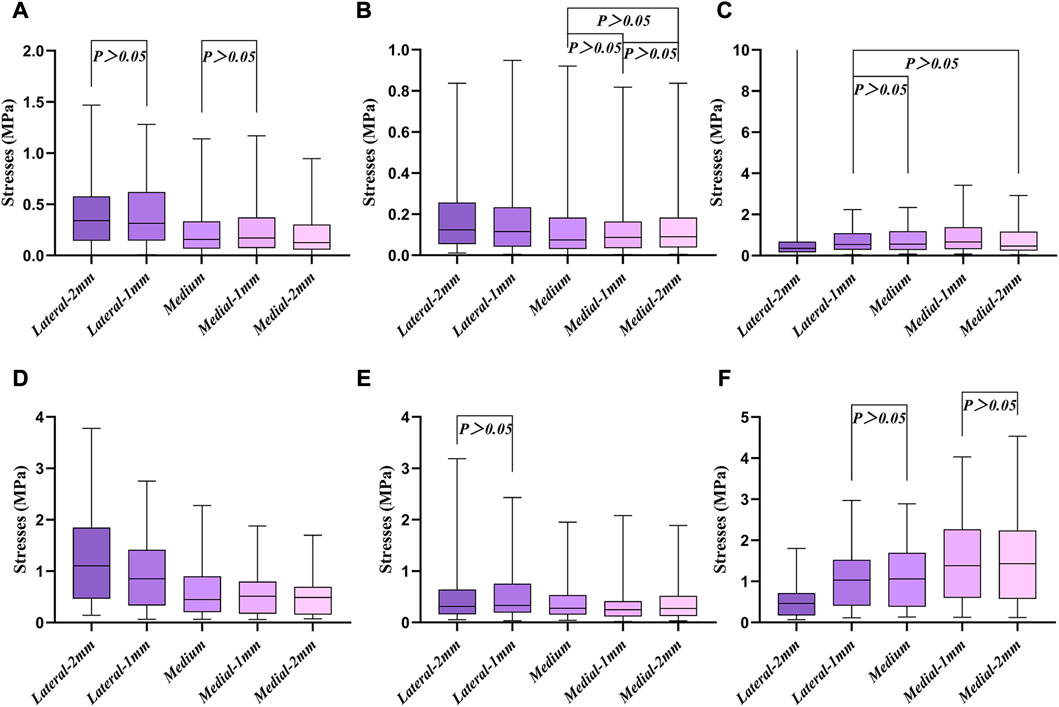
FIGURE 6. Box diagram of the first six different regions. (A–F) Six different regions of stress, corresponding to Figure 5, respectively.
A representative evaluation path was defined for qualitative and quantitative comparison among the different positions of stresses at the region of the tibia plateau. Figure 7 shows stresses along the path defined at the stem cavity border. The major differences along this path pertain to the extreme values at the distance of 25–50 mm. The maximum stress along the defined path occurred in the lateral-2 mm group; the maximum stress in this case was 6.43 MPa. In the same location, the least stress model represents the medium group, with the maximum value of 1.38 MPa.
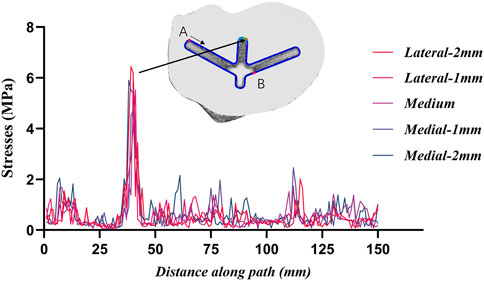
FIGURE 7. Stresses along the border of the stem cavity. Point A is the starting point and point B is the 100 mm position.
3.2 Micromotion
Figure 8 shows the micromotion clouds of one of the groups and Figure 9 demonstrates the micromotion of the five sets of platforms for different misalignment situations. When the platform was misaligned to the lateral side by 2 mm, its micromotion of 7.215 μm was significantly larger than the remaining four groups. Additionally, while the platform was misaligned 2 mm medially, its micromotion of 2.869 μm was the smallest among the five groups. The middle three groups of micromotions are almost half of the first group, respectively. Figure 10 shows the micromotion at different misalignment positions of the plateau and stem. The largest micromotion of 3.854 um occurred on the plateau when the platform was misaligned 1 mm medially.
FIGURE 8. Micromotion cloud map when the platform is misaligned 1 mm to the lateral side.
FIGURE 9. Micromotion at different misalignment positions of the platform.
FIGURE 10. Micromotion at different misalignment positions of the plateau and stem.
4 Discussion
Addressing the problems caused by the wear of prostheses in TKA remains a challenge for orthopedic surgeons. In previous studies, varus-valgus, anterior-posterior tilt, and internal and external rotation misalignment of the prosthesis were included (Fraser et al., 2015). However, no studies have been conducted to investigate the medial-lateral translational misalignment of the prosthesis.
FEA is an effective tool to evaluate the mechanical properties of prostheses and bone. The accuracy of the analysis depends on the veracity of the model. In this study, a non-homogeneous 3D tibia model was used, which means that it will be closer to real human bone than a homogeneous bone model, making the results of the study more realistic (Venalainen et al., 2016; Ün and Çalık, 2016). According to Ruggiero et al. (2019) we can learn that the quality of the hexahedral mesh is better than that of the tetrahedral one, especially in the dynamic condition. But based on the static conditions of our study and the fact that we draw the relatively small mesh, the accuracy is guaranteed even if we use the tetrahedral mesh in this study.
The comparison of the five groups of maximum stresses shows that the maximum stress was 47.29 MPa, which is less than the ultimate stress of 80 MPa in cortical bone (Maslov et al., 2021). This indicates that translational misalignments of 2 mm or less do not result in fractures. As can be seen in Figure 6, the stresses in the A and D regions were high when the platform prosthesis was misaligned to the lateral side, which was in line with our expectations. A similar pattern could be seen in regions C and F, when the tibial plateau prosthesis was transferred medially. Even with these stress concentrations, the stresses were not sufficient to cause significant effects on the proximal tibia (Maslov et al., 2021). Figure 7 demonstrates that, at the stem cavity border, the stresses are concentrated at the rear. Figure 9 shows that the largest micromovement was 7.215 μm, which was much smaller than 28 μm, showing that all five groups could have good bone growth in the future (Pilliar et al., 1986; Jasty et al., 1997). From Figure 10 it can be seen that the plateau presents more micromotion than the stem.
In summary, there is no significant effect on the proximal tibia whether the tibial plateau prosthesis is misaligned medially or laterally by 2 mm or 1 mm. However, according to the current study, the tibial plateau prosthesis should be properly aligned on the tibial surface. A prosthesis overlapping the bony surface will have a negative impact on the surrounding soft tissues, such as the medial and lateral collateral ligaments, and especially upon the popliteal tendon (Bonnin et al., 2017). Dowson and Jin, (1986) showed that in synovial joints, micro-elastohydrodynamic action largely smooths the initial roughness of the cartilage surface, which was then considered a form of lubrication responsible for the significant tribological properties of synovial joints. Later, Ruggiero, (2020) reviewed several theories on the natural synovial lubrication phenomenon in human joints that have been proposed over the years. These indicated that the synovial soft tissue was also closely related to friction. In order to achieve basic stability during the postoperative period without the formation of an alignment, the resistance to movement between the bone and the implant is optimized by increasing the friction at the interface. This is necessary because excessive relative movements can inhibit bone growth due to wear and tear of the bone and formation of fibrous tissue at the implant interface, which can lead to loosening and pain (de Vries et al., 2022). Therefore, oversizing or malposition should be avoided when installing a tibial plateau prosthesis during TKA.
This study has some limitations. First, we applied the stress under static conditions, without introducing dynamic factors such as squatting or walking. And no additional loading conditions such as maximum force in the gait cycle were added in this study. Second, we did not consider the impact on the muscles and ligaments. Third, no synovial lubrication phenomena were considered in this study. Apart from these, Affatato et al. (2019) used in-vitro experimental investigation in the study of femoral prosthesis roughness. Such in-vitro experiments were not used in our study. In future studies, if the above details are included in the experiments, the results obtained may be more appropriate to clinical settings.
5 Conclusion
FEA of stress distribution and micromotion results showed that misalignment of the tibial plateau prosthesis by 2 or 1 mm medially or laterally during TKA did not significantly negatively affect the stress upon the proximal tibia. However, to prevent postoperative pain and stiffness due to impingement on the surrounding soft tissues and ligaments, it is important to consider and design the most appropriate prosthesis and ensure proper positioning for different patients.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving human participants were reviewed and approved by the Ethics committee of The Second Hospital of Jilin University. The patients/participants provided their written informed consent to participate in this study.
Author contributions
ZZ: Investigation, methodology, visualization, writing—original draft, writing—review and editing; YL: Investigation, methodology, supervision, validation, visualization, writing—review and editing; AZ: Software, validation, writing—review and editing. hc: software, validation, writing—review and editing. LZ: Clinical data collection, project administration. xw: clinical data collection, project administration. QW: Clinical data collection. qh: conceptualization, funding acquisition, project administration, resources, supervision, validation, writing—review and editing. JW: Conceptualization, funding acquisition, project administration, resources, supervision, validation.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Affatato, S., Merola, M., and Ruggiero, A. (2019). Tribological performances of total knee prostheses: Roughness measurements on medial and lateral compartments of retrieved femoral components. Measurement 135, 341–347. doi:10.1016/j.measurement.2018.11.072
Bedard, M., Vince, K. G., Redfern, J., and Collen, S. R. (2011). Internal rotation of the tibial component is frequent in stiff total knee arthroplasty. Clin. Orthop. Relat. Res. 469 (8), 2346–2355. doi:10.1007/s11999-011-1889-8
Bonnin, M. P., de Kok, A., Verstraete, M., Van Hoof, T., Van Der Straten, C., Saffarini, M., et al. (2017). Popliteus impingement after TKA may occur with well-sized prostheses. Knee Surg. Sports Traumatol. Arthrosc. 25 (6), 1720–1730. doi:10.1007/s00167-016-4330-8
Dalury, D. F., Pomeroy, D. L., Gorab, R. S., and Adams, M. J. (2013). Why are total knee arthroplasties being revised? J. Arthroplasty 28 (8), 120–121. doi:10.1016/j.arth.2013.04.051
de Vries, E., Sanchez, E., Janssen, D., Matthews, D., and van der Heide, E. (2022). Predicting friction at the bone - implant interface in cementless total knee arthroplasty. J. Mech. Behav. Biomed. Mater 128, 105103. doi:10.1016/j.jmbbm.2022.105103
Dong, Y., Zhang, Z., Dong, W., Hu, G., Wang, B., and Mou, Z. (2020). An optimization method for implantation parameters of individualized TKA tibial prosthesis based on finite element analysis and orthogonal experimental design. BMC Musculoskelet. Disord. 21 (1), 165. doi:10.1186/s12891-020-3189-5
Dowson, D., and Jin, Z. M. (1986). Micro-elastohydrodynamic lubrication of synovial joints. Eng. Med. 15 (2), 63–65. doi:10.1243/emed_jour_1986_015_019_02
Fraser, J. F., Werner, S., and Jacofsky, D. J. (2015). Wear and loosening in total knee arthroplasty: A quick review. J. Knee Surg. 28 (2), 139–144. doi:10.1055/s-0034-1398375
Guo, L., Yang, L., Briard, J. L., Duan, X. J., and Wang, F. Y. (2012). Long-term survival analysis of posterior cruciate-retaining total knee arthroplasty. Knee Surg. Sports Traumatol. Arthrosc. 20 (9), 1760–1765. doi:10.1007/s00167-011-1758-8
Indelli, P. F., Graceffa, A., Marcucci, M., and Baldini, A. (2016). Rotational alignment of the tibial component in total knee arthroplasty. Ann. Transl. Med. 4 (1), 3. doi:10.3978/j.issn.2305-5839.2015.12.03
Inoue, S., Akagi, M., Asada, S., Mori, S., Zaima, H., and Hashida, M. (2016). The valgus inclination of the tibial component increases the risk of medial tibial condylar fractures in unicompartmental knee arthroplasty. J. Arthroplasty 31 (9), 2025–2030. doi:10.1016/j.arth.2016.02.043
Ishii, Y., Noguchi, H., Sato, J., Todoroki, K., and Toyabe, S. (2015). Rotational alignment of tibial components in mobile-bearing TKA: Posterior substituted vs. PCL retaining. Arch. Orthop. Trauma Surg. 135 (9), 1299–1305. doi:10.1007/s00402-015-2275-x
Jasty, M., Bragdon, C., Burke, D., O'Connor, D., Lowenstein, J., and Harris, W. H. (1997). In vivo skeletal responses to porous-surfaced implants subjected to small induced motions. J. bone Jt. Surg. Am. volume 79 (5), 707–714. doi:10.2106/00004623-199705000-00010
Jin, Z. M., Dowson, D., and Fisher, J. (1995). Contact pressure prediction in total knee joint replacements. Part 1: General elasticity solution for elliptical layered contacts. Proc. Inst. Mech. Eng. H. 209 (1), 1–8. doi:10.1243/PIME_PROC_1995_209_311_02
Kutzner, I., Heinlein, B., Graichen, F., Bender, A., Rohlmann, A., Halder, A., et al. (2010). Loading of the knee joint during activities of daily living measured in vivo in five subjects. J. Biomech. 43 (11), 2164–2173. doi:10.1016/j.jbiomech.2010.03.046
Li, Y. R., Gao, Y. H., Yang, C., Ding, L., Zhang, X., Chen, H., et al. (2019). Finite-element analysis of the proximal tibial sclerotic bone and different alignment in total knee arthroplasty. BMC Musculoskelet. Disord. 20 (1), 617. doi:10.1186/s12891-019-3008-z
Liau, J. J., Cheng, C. K., Huang, C. H., Lee, Y. M., Chueh, S. C., and Lo, W. H. (1999). The influence of contact alignment of the tibiofemoral joint of the prostheses in in vitro biomechanical testing. Clin. Biomech. (Bristol, Avon) 14 (10), 717–721. doi:10.1016/s0268-0033(99)00027-3
Liau, J. J., Cheng, C. K., Huang, C. H., and Lo, W. H. (2002). The effect of malalignment on stresses in polyethylene component of total knee prostheses-a finite element analysis. Clin. Biomech. (Bristol, Avon) 17 (2), 140–146. doi:10.1016/s0268-0033(01)00109-7
Lin, Y., Ma, L., Zhu, Y., Lin, Z., Yao, Z., Zhang, Y., et al. (2017). Assessment of fracture risk in proximal tibia with tumorous bone defects by a finite element method. Microsc. Res. Tech. 80 (9), 975–984. doi:10.1002/jemt.22899
Maderbacher, G., Baier, C., Springorum, H. R., Maderbacher, H., Birkenbach, A. M., Benditz, A., et al. (2017). Impact of axial component alignment in total knee arthroplasty on lower limb rotational alignment: An in vitro study. J. Knee Surg. 30 (4), 372–377. doi:10.1055/s-0036-1592148
Maslov, L., Borovkov, A., Maslova, I., Soloviev, D., Zhmaylo, M., and Tarasenko, F. (2021). Finite element analysis of customized acetabular implant and bone after pelvic tumour resection throughout the gait cycle. Mater. (Basel) 14 (22), 7066. doi:10.3390/ma14227066
Matsuda, S., Whiteside, L. A., and White, S. E. (1999). The effect of varus tilt on contact stresses in total knee arthroplasty: A biomechanical study. Orthopedics 22 (3), 303–307. doi:10.3928/0147-7447-19990301-06
Minh, H. L., Park, W. M., Kim, K., Son, S.-W., Lee, S.-H., and Kim, Y. H. (2013). A new patient-specific planning method based on joint contact force balance with soft tissue release in total knee arthroplasty. Int. J. Precis. Eng. Manuf. 14 (12), 2193–2199. doi:10.1007/s12541-013-0297-2
Park, H. J., Bae, T. S., Kang, S. B., Baek, H. H., Chang, M. J., and Chang, C. B. (2021). A three-dimensional finite element analysis on the effects of implant materials and designs on periprosthetic tibial bone resorption. PLoS One 16 (2), e0246866. doi:10.1371/journal.pone.0246866
Perillo-Marcone, A., and Taylor, M. (2007). Effect of varus/valgus malalignment on bone strains in the proximal tibia after TKR: An explicit finite element study. J. Biomech. Eng. 129 (1), 1–11. doi:10.1115/1.2401177
Perillo-Marcone, A., Barrett, D. S., and Taylor, M. (2000). The importance of tibial alignment: Finite element analysis of tibial malalignment. J. Arthroplasty 15 (8), 1020–1027. doi:10.1054/arth.2000.17941
Pilliar, R. M., Lee, J. M., and Maniatopoulos, C. (1986). Observations on the effect of movement on bone ingrowth into porous-surfaced implants. Clin. Orthop. Relat. Res. 208 (208), 108–113. doi:10.1097/00003086-198607000-00023
Popescu, R., Haritinian, E. G., and Cristea, S. (2019). Relevance of finite element in total knee arthroplasty - literature review. Chir. (Bucur) 114 (4), 437–442. doi:10.21614/chirurgia.114.4.437
Rho, J. Y., Hobatho, M. C., and Ashman, R. B. (1995). Relations of mechanical properties to density and CT numbers in human bone. Med. Eng. Phys. 17 (5), 347–355. doi:10.1016/1350-4533(95)97314-f
Ruggiero, A., D'Amato, R., and Affatato, S. (2019). Comparison of meshing strategies in THR finite element modelling. Mater. (Basel) 12 (14), 2332. doi:10.3390/ma12142332
Ruggiero, A. (2020). Milestones in natural lubrication of synovial joints. Front. Mech. Eng. 6. doi:10.3389/fmech.2020.00052
Thompson, S. M., Yohuno, D., Bradley, W. N., and Crocombe, A. D. (2016). Finite element analysis: A comparison of an all-polyethylene tibial implant and its metal-backed equivalent. Knee Surg. Sports Traumatol. Arthrosc. 24 (8), 2560–2566. doi:10.1007/s00167-015-3923-y
Ün, K., and Çalık, A. (2016). Relevance of inhomogeneous–anisotropic models of human cortical bone: A tibia study using the finite element method. Biotechnol. Biotechnol. Equip. 30 (3), 538–547. doi:10.1080/13102818.2016.1154803
Venalainen, M. S., Mononen, M. E., Vaananen, S. P., Jurvelin, J. S., Toyras, J., Viren, T., et al. (2016). Effect of bone inhomogeneity on tibiofemoral contact mechanics during physiological loading. J. Biomech. 49 (7), 1111–1120. doi:10.1016/j.jbiomech.2016.02.033
Keywords: total knee arthroplasty, malalignment, finite element analysis, tibial stress, wear rates
Citation: Zheng Z, Liu Y, Zhang A, Chen H, Wan Q, Zhong L, Wang X, Han Q and Wang J (2023) Medial-lateral translational malalignment of the prosthesis on tibial stress distribution in total knee arthroplasty: A finite element analysis. Front. Bioeng. Biotechnol. 11:1119204. doi: 10.3389/fbioe.2023.1119204
Received: 08 December 2022; Accepted: 20 February 2023;
Published: 02 March 2023.
Edited by:
Richard Mark Hall, University of Leeds, United KingdomReviewed by:
Alessandro Ruggiero, University of Salerno, ItalyRui B. Ruben, Polytechnic Institute of Leiria, Portugal
Copyright © 2023 Zheng, Liu, Zhang, Chen, Wan, Zhong, Wang, Han and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qing Han, bXkuaGFucWluZ0AxNjMuY29t; Jincheng Wang, amluY2hlbmd3YW5namx1QDE2My5jb20=
†These authors have contributed equally to this work and share first authorship