Surface Defect Segmentation Algorithm of Steel Plate Based on Geometric Median Filter Pruning

Problems such as redundancy of detection model parameters make it difficult to apply to factory embedded device applications. This paper focuses on the analysis of different existing deep learning model compression algorithms and proposes a model pruning algorithm based on geometric median filtering for structured pruning and compression of defect segmentation detection networks on the basis of structured pruning. Through experimental comparisons and optimizations, the proposed optimization algorithm can greatly reduce the network parameters and computational effort to achieve effective pruning of the defect detection algorithm for steel plate surfaces.

1 Introduction

Applying defect detection segmentation algorithms to real industrial production scenarios, hardware resources are a challenge that must be faced (Tang et al., 2017; Liu H. et al., 2020; Hao et al., 2021). Complex models often mean better detection capabilities, but the high memory space footprint and huge consumption of computational resources doom it to ineffective application in resource-limited hardware platforms (Sun H. et al., 2020, Sun et al., 2022c; Tao et al., 2022; Wu et al., 2022; Zhao et al., 2022). Therefore, compression of redundant neural network models is essential.

Model pruning is a fast and effective way to compress neural networks by cutting out unimportant neurons or filters to obtain a small network model with small storage capacity and fast inference. Model pruning can inherit the weights of the network before pruning, so the model can be pruned to achieve better optimization results.

Model pruning is a fast and effective way to compress neural networks by cutting out unimportant neurons or filters to obtain a network model with small storage capacity and fast inference. Model pruning inherits the weights of the network before pruning, so model pruning allows for better mobile deployment and better optimization.

For real-time applications such as surface EMG signal processing (Li et al., 2019b, Li et al., 2020; Sun et al., 2020a; Qi et al., 2020; Yang et al., 2021), gesture recognition (Duan et al., 2021, Liu X. et al., 2022, Liu et al., 2022a, Liu et al., 2022b, Luo et al., 2020, Jiang et al., 2019a, b, Xu et al., 2022, Sun et al., 2022a) and quality inspection (Chen et al., 2021a, Chen et al., 2021b, Huang L. et al., 2021, Jiang et al., 2021a, Jiang et al., 2021b, Sun et al., 2021b, Chen et al., 2022a, Chen et al., 2022b, Chen et al., 2022c, Huang et al., 2022, Sun et al., 2022b, Yun et al., 2022b, Zhang et al., 2022), model compression effectively reduces the memory and computational power consumed by the original large neural network, and improves the training and inference speed. Moreover, the compressed models are conducive to deployment and timely updates on embedded and mobile devices with limited storage space, facilitating the development of smart factories (Li et al., 2019a; Li et al., 2019c; Yun et al., 2022a).

The key contributions of this work are:

1) A model pruning method based on improved geometric median filter pruning is proposed on the basis of structured pruning.

2) The pruning method and pruning process are improved by performing model acceleration and fine-tuning in the structured pruning process, and determining whether the pruning end condition is satisfied by the evaluation function to improve the pruning compression efficiency.

3) After experimental comparison, the improved geometric median filter model-based pruning method proposed in this paper outperforms other classical pruning methods. And the pruning algorithm has better detection performance and pruning efficiency in steel plate surface defect segmentation detection.

The rest of this paper is organized as follows: Section 2 discusses related work on model compression in recent years. Section 3 analyses model pruning methods and clarifies in detail the advantages and disadvantages of unstructured pruning and structured pruning methods; and as a basis, proposes a structured model pruning method based on geometric median filtering for pruning and compressing steel plate surface defect models. After a brief introduction of the open source steel plate surface defect dataset and the configuration of the experimental environment, Section 4 presents an experimental comparison of the proposed pruning algorithm with other pruning algorithms to demonstrate the effectiveness of the structured pruning algorithm. Section 5 concludes the paper with a prospect.

2 Related Work

In recent years, in order to perform more complex information processing tasks, deep learning-based neural network models have become deeper and deeper, also making them increasingly computationally intensive, making it difficult to deploy neural networks on devices with scarce computational resources or with strict latency requirements (Liu H. et al., 2022). As a result, compression of neural network models is becoming increasingly important. For applications such as steel plate surface defect detection, where real-time requirements are particularly stringent, it is even more important to reduce the computational cost and storage requirements and to speed up the computation. Currently, there are five main neural network model compression methods that are widely used (Gao et al., 2021): Low rank decomposition, structural design, knowledge distillation, parameter quantization and model pruning, and the relevant short descriptions are shown in Table 1.

TABLE 1

TABLE 1. Model compression methods.

Liu M. et al. (2020) proposed a joint optimization model of low-rank matrix bi-factor decomposition and structured sparse matrix decomposition, and applied it to saliency target detection with low time complexity. Zhang and Chen (2019) modelled the detection of defects on the track surface as a low-rank matrix decomposition problem, and calculated the row accumulation of the sparse matrix obtained from the decomposition, and searched for the maximum connected region to determine the defect location, realizing automatic detection and localization of defects. Wang et al. (2018) used multiple independent and complementary information in the multi-view feature space to outperform single information, and proposed that by decomposing the potential low-dimensional data cluster representations to present structured low-rank representations and improve clustering performance by exploring multi-view consensus structures beyond low-rank with an efficient alternating minimization strategy function. Ouyang (2021) proposed an improved autoencoder architecture based on an extreme learning machine that uses low-rank matrix decomposition to learn optimal low-dimensional features. The representational and non-linear capabilities of the features are enhanced. However, due to the large arithmetic size of matrix decomposition, it inherently takes longer training time and requires more hardware resources.

DenseNet (Huang et al., 2017) is a densely connected neural network, with connections between any two layers of the network, combining information from all previous layers as input features for the next layer and introducing a feature channel scaling factor and a resolution scaling factor into the network, further reducing the computational effort of the network. Inception (Szegedy et al., 2016), on the other hand, uses mainly 1 × 1 filters instead of 3 × 3 filters, saving the number of parameters in the network. To randomly disrupt the feature channels, ShuffleNet (Xin et al., 2021) divides the feature channels into multiple groups and convolves them to increase the information exchange between different feature channels. MobileNet (Sun et al., 2021a) designs a deeply separable convolution module and fuses the information of different feature channels by 1 × 1 convolution. In addition, researchers often introduce 1 × 1 filters between 3 × 3 filters to reduce the number of input and output channels of the feature map. Although lightweight networks are effective in reducing the computational complexity of the network, there is still a large amount of redundancy in the network and the design requirements are high.

Huang J. et al. (2021) replaced the traditional static convolution by constructing a dynamic convolution module incorporating an attention mechanism to transfer dynamic feature knowledge from the teacher network back to the student network, thus achieving high accuracy recognition of defects while significantly reducing model inference time. Liu et al. (2021) proposed a neural network compression algorithm based on knowledge distillation and adversarial learning, and allowed the teacher network and student network to learn from each other in the second half of training, enabling the student network to explore its own optimal solution space. Park and Yong (2020) proposed to apply channel and spatial correlation loss functions and adaptive cross-entropy loss functions to train the light network and use the heavy network for semantic segmentation. Knowledge distillation from the heavy network as the teacher to the light network as the student can be used as a way to improve the performance of the student network. Zhang et al. (2021) proposed a novel two-branch network that took three pairs of original transformed images as input and incorporated a class activation graph to drive the network to mine the most relevant class-specific regions. This strategy ensured that the network generated differentiated embeddings and a round of self-knowledge distillation was set up to prevent overfitting and improve performance. However, compared to other compression methods (Sarakon et al., 2021), the whole training process of knowledge distillation takes longer and is only applicable to neural networks with softmax layers.

Rao et al. (2019) proposed a deep neural network compression method based on dynamic quantization coding, in which the quantization codebook is updated simultaneously during the training of the model, so that the codebook minimizes the error caused by quantization of larger weight parameters. Sun H. et al. (2020) proposed a lightweight image compression neural network based on parameter quantization, quantizing the model parameters from 32-bit floating-point to 8-bit integer, saving 73% of storage space compared to the original model. Chen et al. (2019) proposed an efficient convolutional neural network-based fast decision method for quantization parameter selection for video coding by comparing the rate distortion cost to calculate the optimal quantization parameters, saving the encoding time of the video. Feature extraction is important for steganalysis of content-adaptive JPEG steganography, Xu et al. (2018) proposed a scale covariance matrix feature based on a two-dimensional Gabor filter and used diverse quantization of filter residuals to improve detection performance.

Jin et al. (2018) proposed a hybrid pruning method combining weight pruning and convolutional kernel pruning; the convolutional kernels that contribute less to the overall accuracy of the convolutional neural network are pruned first, and then the pruned model is weight pruned to achieve further model compression. Wei et al. (2021) obtained a deep convolutional neural network model with sparse parameters by training the convolutional neural network model with sparse regularization, and combined the sparsity of the convolutional and batch regression layers to perform structured pruning to remove redundant filters. Ziani et al. (2018) proposed a vertical partition pruning method based on the maximum frequent item set, which effectively prunes the potential search space to search for optimal solutions. Zhang H. et al. (2020) performed model compression by enforcing channel-level sparsity pruning in a YOLOv3 network, and tested the effect of different gradient optimizers on model pruning before finally using the Adam optimizer to optimize the model. Jia et al. (2021) proposed a novel solution for minutely significant target object detection, which evaluates the parameters in the training model based on significant energy levels as a way to distinguish between background parameters in the model as a way to distinguish between background and salient objects.

The above-mentioned deep learning-based model compression methods still have problems such as requiring large hardware resources for acceleration, high redundancy, the stability and robustness of the network after model compression is difficult to be guaranteed in complex environments, and the network model has insufficient self-adaptability.

3 Improved Geometric Median Filter Based Pruning Algorithm

3.1 Model Pruning Methods

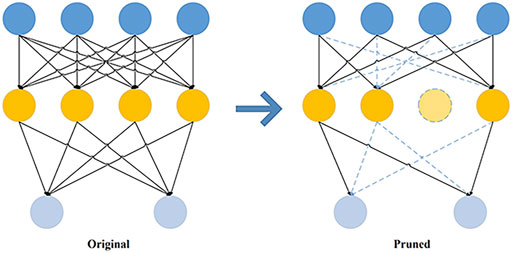
There are two main types of model pruning methods: unstructured pruning and structured pruning. Unstructured pruning prunes the neuron or connection weights, which means that some non-0 elements in the network calculation are set to 0, or the dense connections of the network are turned into sparse connections, turning the original dense matrix operation into a sparse matrix operation, as shown in Figure 1. In Figure 1, the dashed box is a pruning of the neurons to 0, and the dashed connection is a pruning of the dense connections to sparse connections, i.e. pruning weights.

FIGURE 1

FIGURE 1. Unstructured pruning diagram.

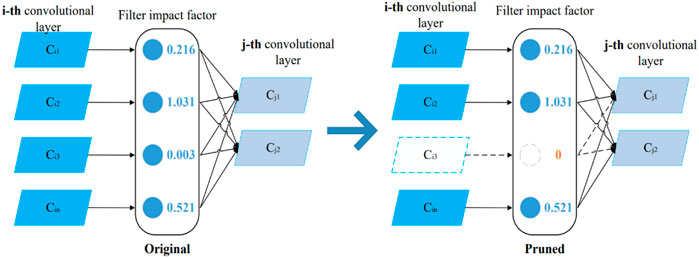
Structured pruning is a type of pruning at the filter level, which focuses on pruning the filters with smaller contributions in each layer of the network. When the filter van value (the filter's impact factor) is less than a set range, the network is structured to prune redundant filters according to the van value, as shown in Figure 2. In the figure, the jth convolutional layer is the i + 1th convolutional layer. Thus, structured pruning can effectively reduce the network model size without destroying the convolutional structure.

FIGURE 2

FIGURE 2. Structured pruning diagram.

Since the convolution kernel obtained after pruning is sparse, and most GPUs today do not provide additional acceleration for sparse matrix operations, this results in a pruned network that is not accelerated in any way compared to the original network, but may be slower.

Therefore, structured pruning is now a more general approach, and is relatively more efficient than unstructured pruning methods. For the use of the pruned network does not require the support of specific hardware platforms, computational libraries, effectively avoiding the drawbacks of unstructured pruning and enabling direct deployment on the mainstream deep learning frameworks nowadays (Liu et al., 2017).

3.2 Geometric Median Filtering Based Detection Model Pruning Algorithm

Model-structured pruning requires a criterion to select the filter to be pruned, i.e. the filter’s magnitude value. The most common pruning criterion is that the filter's parametric value is compared to some threshold value and if it is below the threshold, the filter is set to zero, i.e., the filter is pruned and pruned.

He et al. (2019) proposed a new filter pruning method for pruning models by geometric median filter pruning, which is a type of structured pruning.

Unlike the previous methods, geometric median filter-based pruning compresses the convolutional neural network model by removing redundant filters. Geometric median filtering works by calculating the geometric median of the filters within the same layer and, depending on the properties of the geometric median, filters near the geometric median can be represented by the remaining filters. Therefore, pruning the geometric median filter does not have a substantial negative impact on the model performance.

In d-dimensional space, given any set of n points: ${\mathrm{a}}^{\left(1\right)},\mathrm{..},{\mathrm{a}}^{\left(n\right)}$, and ${\mathrm{a}}^{\left(\text{i}\right)}\in R^d$, there exists a point $x^{\ast }$ such that the sum of the Euclidean distances (Euclidean distances) to each point is minimized, and the point $x^{\ast }$ is referred to as the Geometric Median (GM) point and is calculated as:

$x^{\ast }=\underset{x\in R^d}{\arg \min }f\left(x\right)(1)$

$f\left(x\right)\stackrel{def}{=}{\displaystyle \sum _{i\in \left[1,n\right]}{\Vert x-a^{\left(i\right)}\Vert }_2}(2)$

In which,

$x^{\ast }\in R^d$, and $x^{\ast }$ is referred to as the geometric median point;

$\arg \min$ denotes the value of the variable at which the objective function $f\left(x\right)$ is made to take its minimum valu;

[1, n] = {1, …, n}; def means that the $f\left(x\right)$ function is defined as ${\displaystyle \sum _{i\in \left[1,n\right]}{\Vert x-a^{\left(i\right)}\Vert }_2}$.

The geometric median is a classical robust estimator of data centeredness in Euclidean space and is used when pruning the model to obtain common information about all filters within a single layer i as the geometric median for that layer $F_i^{GM}$.

$F_i^{GM}=\underset{x\in R^{N_i\times H_i\times W_i}}{\arg \min }g\left(x\right)(3)$

$g\left(x\right)\stackrel{def}{=}{\displaystyle \sum _{j^{\prime }\in \left[1,N_{i+1}\right]}{\Vert x-F_{i,j^{\prime }}\Vert }_2}(4)$

In which, $g\left(x\right)$ denotes the sum of the Euclidean distances of all filters within tensor $x$ to layer i.$x\in R^{N_i\times H_i\times W_i}$ denotes that $x$ exists within input tensor $N_i\times H_i\times W_i$, and $N_i$, $H_i$ and $W_i$ denote the number of channels, height and width of the input tensor within layer i, respectively.$N_{i+1}$ indicates that the output is $N_{i+1}$ when the input is $N_i$.

The core idea of geometric median filtering is that if there are filters within layer i that are close to geometric median $F_i^{GM}$, then these filters are redundant and clipping these redundant filters will not have a large impact on network performance. In layer i, these redundant filters are:

$F_{i,j^{\ast }}=\underset{j^{\prime }\in \left[1,N_{i+1}\right]}{\arg \min }{\Vert F_{i,j^{\prime }}-F_i^{GM}\Vert }_2(5)$

And these redundant filters are close to the geometric median $F_i^{GM}$.

${\Vert F_{i,j^{\ast }}-F_i^{GM}\Vert }_2=0(6)$

That is, Eq. 5 is equivalent to

$\begin{array}{l}{F}_{i,j^{\ast }}\sim \underset{j^{\prime },j^{\ast }\in \left[1,N_{i+1}\right]}{\arg \min }{\Vert F_{i,j^{\prime }}-F_{i,j^{\ast }}\Vert }_2\\ =\underset{j^{\prime },j^{\ast }\in \left[1,N_{i+1}\right]}{\arg \min }{\Vert x-F_{i,j^{\prime }}\Vert }_2\\ =\underset{j^{\prime },j^{\ast }\in \left[1,N_{i+1}\right]}{\arg \min }g\left(x\right)\end{array}(7)$

In Eq. 7, $x\in \left\{F_{i,1},\mathrm{...},F_{i,N_{i+1}}\right\}$。

The geometric median is a classical robust estimator of data-centricity in Euclidean space. This shows that the information of the selected filter $F_{i,j^{\ast }}$ can be replaced by other filters. After fine-tuning, the network can easily recover its original performance. Therefore, the neural network is pruned to have little impact on the final result of the detection.

The pruning flow chart based on geometric median structured pruning is shown in Figure 3. First, a pre-trained detection model with the required compression is input and the pruning rate and pruning layers are set. The pruning rate can be set to 0–1 and the pruning layers can be set to convolutional layers, fully connected layers, Batchnorm layers, etc.

FIGURE 3

FIGURE 3. Structured pruning flow chart.

The structured pruning process in this paper includes updating the mask, updating the indirect sparsity and updating the module. After the pruning process, the model is accelerated and refined to optimize the model. Finally, an evaluation score is calculated to determine whether the end condition is met. If the end condition is met, the pruned and compressed model is output; if not, the pruning process continues.

Geometric median filtering algorithms can effectively improve the compression rate of neural networks and reduce detection model redundancy. The pruned detection model can be deployed to portable devices for faster processing (Ran et al., 2022).

In this paper, a model pruning algorithm based on geometric median filtering is used to compress the steel plate surface defect detection network and implement a model pruning defect segmentation detection algorithm based on geometric median filtering to reduce the number of parameters and computational effort of the detection model.

4 Experimental Results and Analysis

4.1 Open Source Surface Defect Dataset for Steel Plates

The Severstal dataset was released open source on the competition platform Kaggle. The Severstal dataset contains 12,568 images from the training set and 1,801 images from the test set. There are 5,902 defect-free images and 6,666 defective images in the training set. The number of defective and non-defective images in the dataset is roughly equal, and most of the images have no defects or contain only one type of defect (Hao et al., 2022).

All images in the Severstal dataset have a vertical and horizontal resolution of 256 and 1,600 respectively. There are four types of steel surface defects in the Severstal dataset, as shown in Figure 4: A) Pit defects, B) Edge crack defects, C) Scratch and scrape defects, D) Rolled-in scale defects and E) Non-defect images.

FIGURE 4

FIGURE 4. Surface defect data for Severstal plates. (A) Pit defects, (B) Edge crack defects, (C) Scratch and scrape defects, (D) Rolled-in scale defects and (E) Non-defect images.

The Severstal dataset contains a large variation in morphology between different defects on the surface of steel plates, both large defects such as scratches and scrapes, and very small defects such as pits and edge cracks.

The extremely large span of defect scales places high demands on the defect detection segmentation algorithm: it has to focus on the details to achieve fine segmentation; and it has to focus on the global picture and have sufficient sensory field for large scale defects. These factors make feature extraction and detection segmentation of the network difficult and lead to the need for pruning and compression of the defect detection model.

4.2 Experimental Environment Configuration

The algorithm research and network training in this paper were conducted on a laboratory server. The specific computer systems used and the configuration of the experimental environment are shown in Table 2.

TABLE 2

TABLE 2. Experimental environment configuration.

This paper uses relevant open source libraries and toolkits to implement the overall algorithmic procedure based on the good ecology and scalability of the Python language and the open source framework PyTorch (Bai et al., 2021).

These open source tools greatly save the development time of the defect detection and segmentation procedure in this paper, thus allowing more time and effort to be devoted to the research, improvement and experimentation of the structured pruning algorithm.

4.3 Experiments on Surface Defect Segmentation Detection of Steel Plates Based on Structured Pruning

In order to verify the practical effectiveness of the proposed defect segmentation algorithm based on geometric median filter pruning, experiments with different pruning rates were conducted on different models under the same conditions to test the effect of different pruning rates on the accuracy of the models.

Since the main network layer of the pruned model is the convolutional layer, this paper only detects pruning on the convolutional layer of the detection model, and does not perform pruning experiments on the fully connected layers, Batchnorm layers, etc.

The input size of the model only affects the computational volume of the model and does not affect the number of model parameters. Therefore, the input size was set to [3, 64, 64] for the model pruning experiments, i.e., the simulated input image size was 64 × 64 for the 3-channel image.

The ResNet50 model has good performance in image recognition and localization tasks (He et al., 2016). The ResNeXt50 model is a grouped convolution based on the ResNet50 model, which can greatly reduce the number of parameters and is more effective in many visual recognition tasks (Xie et al., 2017).

The FPN-ResNeSt50 model is an improved fusion of the FPN (Feature pyramid networks) and the ResNeSt50 model (Lin et al., 2017; Zhang Y. et al., 2020), with powerful feature extraction and fusion capabilities, and have good detection capability for defect segmentation detection tasks on steel plate surfaces.

In this paper, ResNet50, ResNeXt50 and FPN-ResNeSt50 are used as the detection models for defects on the surface of steel plates, and pruning experiments and validation are performed on them.

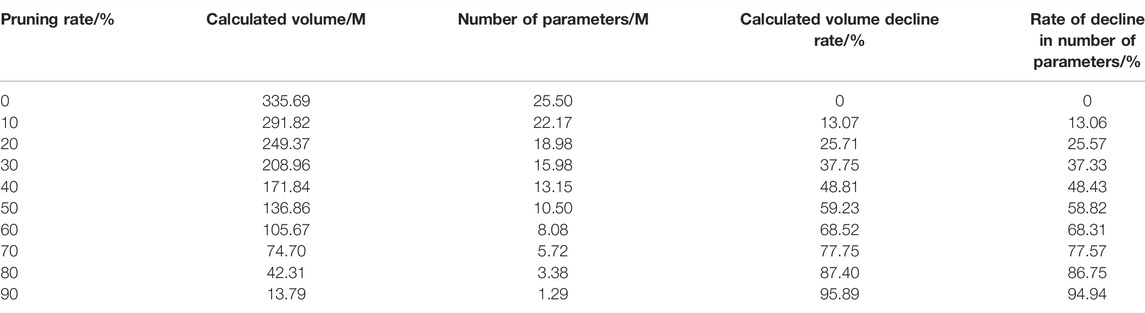
The effect of different pruning rates on the ResNet50 model is shown in Table 3. A pruning rate of 0% indicates that no pruning is applied to the model. For example, when the pruning rate is 40%, the computation of the model is $171.84\times {10}^6$, which is 48.81% lower than the computation of the original model, and the number of parameters of the model is $13.15\times {10}^6$, which is 48.43% lower than the number of parameters of the original model.

TABLE 3

TABLE 3. Effect of different pruning rates on the ResNet50 model.

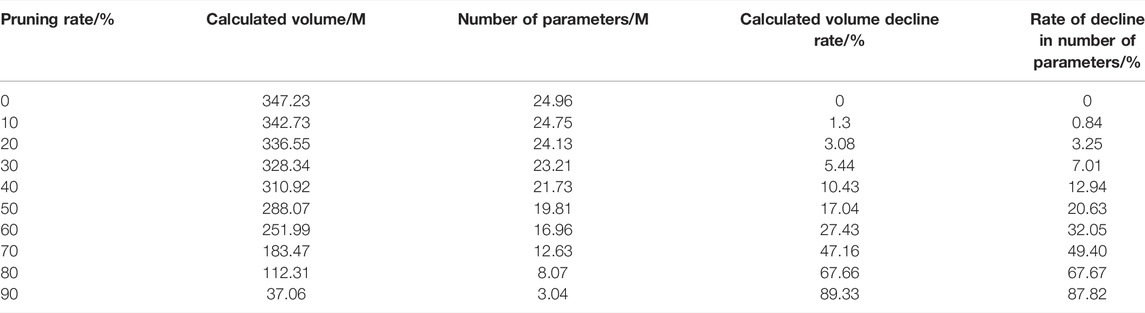
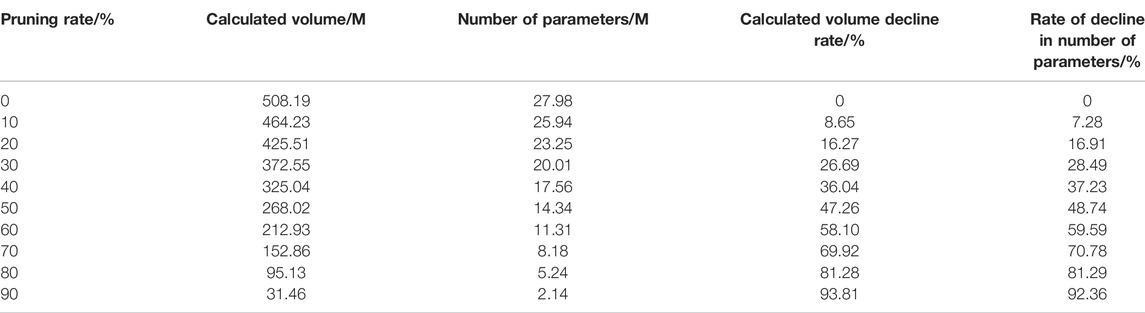
The effect of different pruning rates on the ResNeXt50 (32 × 4d) model is shown in Table 4. As the pruning rate increases, the computational volume and number of parameters of the network decreases and the rate of decrease in computational volume and number of parameters increases.

TABLE 4

TABLE 4. Effect of different pruning rates on the ResNeXt50 (32 × 4d) model.

However, the structured pruning effect of the model was not evident at smaller pruning rates in the early stages due to the ResNeXt50 (32 × 4d) model having a 32-component group convolution, resulting in a smaller pruning rate.

The effects of different pruning rates on the FPN-ResNeSt50 model are shown in Table 5.

TABLE 5

TABLE 5. Effect of different pruning rates on the FPN-ResNeSt50 model.

Comparing Tables 3, 4, 5, the results of the pruning experiments prove that the more grouped convolutions a network model has, the lower the compression rate of its pruning. Since grouped convolutions can greatly reduce the number of model parameters, the more groupings exist for grouped convolutions, the lower the pruning compression rate.

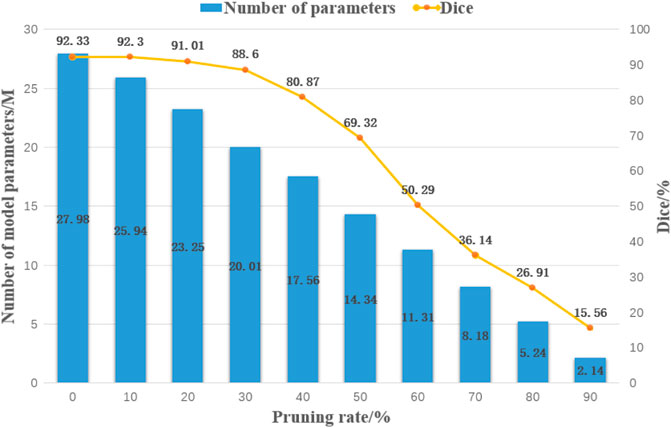
The model pruning algorithm based on geometric median filtering prunes and compresses the steel plate surface defect segmentation model based on depth feature fusion, and experiments with different pruning rates were conducted on it under the same conditions to test the effect of different pruning rates on the accuracy of the FPN-ResNeSt50 model, and the detection results are shown in Figure 5.

FIGURE 5

FIGURE 5. Plot of test results for different pruning rates.

At a pruning rate of 40%, the defect detection accuracy starts to gradually decline, so at a pruning rate greater than 40%, it will lead to the loss of important parameters of the model, resulting in a serious decline in accuracy. In contrast, at a pruning rate of 10%–30%, the model accuracy is able to maintain a low loss of accuracy.

The test results show that when the pruning rate is small, pruning brings regularization to the network and enhances the generalization performance of the network; when the pruning rate is large, the characterization ability of the network is severely damaged and the performance of the model decreases significantly.

5 Conclusion

In order to solve the problems of large number of model parameters and difficulty in applying the model to actual plant equipment, this paper investigates the defect segmentation detection algorithm based on geometric median filter pruning. Based on the structured pruning, a model pruning algorithm based on geometric median filtering is proposed to prune and compress the defect segmentation detection network, which greatly reduces the network parameters and computational effort and improves the generalization ability of the model. Through experimental comparisons and optimizations, the detection accuracy of steel surface defects is improved. Meanwhile, the parameters and computation of the detection model are reduced. The pruning and compression algorithm proposed in this paper has good prospects for application in the segmentation and detection of defects on steel plate surfaces. Good pruning algorithms can be applied to a variety of factory embedded or portable mobile devices and can meet the demand for real-time scene detection. In the future, there is still a long way to go in model pruning and compression research.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

ZH and ZW provide research ideas and write programs for experiments. XT is responsible for collecting data and analyzing and interpreting the simulation results; DB improves the algorithm. DB and XT as corresponding authors, were responsible for writing the paper and approved the final submission.

Funding

This work was supported by grants of the National Natural Science Foundation of China (Grant Nos.. 52075530, 51575407, 51505349, 51975324, and 61733011, 41906177); the Grants of Hubei Provincial Department of Education (D20191105); the Grants of National Defense Pre-Research Foundation of Wuhan University of Science and Technology (GF201705) and Open Fund of the Key Laboratory for Metallurgical Equipment and Control of Ministry of Education in Wuhan University of Science and Technology (2018B07, 2019B13).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai, D., Sun, Y., Tao, B., Tong, X., Xu, M., Jiang, G., et al. (2021). Improved Single Shot Multibox Detector Target Detection Method Based on Deep Feature Fusion. Concurrency Comput. 34 (4), e6614. doi:10.1002/cpe.6614

CrossRef Full Text | Google Scholar

Chen, L., Wang, B., Yu, W., and Fan, X. (2019). CNN-based Fast HEVC Quantization Parameter Mode Decision. Comput. Mater. Continua 61 (3), 115–126. doi:10.32604/jnm.2019.08581

CrossRef Full Text | Google Scholar

Chen, T., Jin, Y., Yang, J., and Cong, G. (2022a). Identifying Emergence Process of Group Panic Buying Behavior under the COVID-19 Pandemic. J. Retail. Consumer Serv. 67, 102970. doi:10.1016/j.jretconser.2022.102970

CrossRef Full Text | Google Scholar

Chen, T., Peng, L., Yang, J., Cong, G., and Li, G. (2021a). Evolutionary Game of Multi-Subjects in Live Streaming and Governance Strategies Based on Social Preference Theory during the COVID-19 Pandemic. Mathematics 9 (21), 2743. doi:10.3390/math9212743

CrossRef Full Text | Google Scholar

Chen, T., Qiu, Y., Wang, B., and Yang, J. (2022b). Analysis of Effects on the Dual Circulation Promotion Policy for Cross-Border E-Commerce B2B Export Trade Based on System Dynamics during COVID-19. Systems 10 (1), 13. doi:10.3390/systems10010013

CrossRef Full Text | Google Scholar

Chen, T., Rong, J., Yang, J., and Cong, G. (2022c). Modeling Rumor Diffusion Process with the Consideration of Individual Heterogeneity: Take the Imported Food Safety Issue as an Example during the COVID-19 Pandemic. Front. Public Health 10, 781691. doi:10.3389/fpubh.2022.781691

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, T., Yin, X., Yang, J., Cong, G., and Li, G. (2021b). Modeling Multi-Dimensional Public Opinion Process Based on Complex Network Dynamics Model in the Context of Derived Topics. Axioms 10 (4), 270. doi:10.3390/axioms10040270

CrossRef Full Text | Google Scholar

Duan, H., Sun, Y., Cheng, W., Jiang, D., Yun, J., Liu, Y., et al. (2021). Gesture Recognition Based on Multi‐modal Feature Weight. Concurr. Comput. Pract. Exper 33 (5), e5991. doi:10.1002/cpe.5991

CrossRef Full Text | Google Scholar

Gao, H., Tian, Y., Xu, F., and Zhong, S. (2021). Overview of Deep Learning Model Compression and Acceleration. J. Softw. 32 (1), 69–92. doi:10.13328/j.cnki.jos.006096

CrossRef Full Text | Google Scholar

Hao, Z., Wang, Z., Bai, D., Tao, B., Tong, X., and Chen, B. (2022). Intelligent Detection of Steel Defects Based on Improved Split Attention Networks. Front. Bioeng. Biotechnol. 9, 810876. doi:10.3389/fbioe.2021.810876

PubMed Abstract | CrossRef Full Text | Google Scholar

Hao, Z., Wang, Z., Bai, D., and Zhou, S. (2021). Towards the Steel Plate Defect Detection: Multidimensional Feature Information Extraction and Fusion. Concurr. Comput. Pract. Exper 33 (4), e6384. doi:10.1002/cpe.6384

CrossRef Full Text | Google Scholar

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep Residual Learning for Image Recognition. Available at: https://arxiv.org/abs/1512.03385.

CrossRef Full Text | Google Scholar

He, Y., Liu, P., Wang, Z., Hu, Z., and Yang, Y. (2019). Filter Pruning via Geometric Median for Deep Convolutional Neural Networks Acceleration. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), 4335–4344. doi:10.1109/CVPR.2019.00447

CrossRef Full Text | Google Scholar

Huang, G., Liu, Z., Van Der Maaten, L., and Weinberger, K. Q. (2017). “Densely Connected Convolutional Networks,” in IEEE Conference on Computer Vision and Pattern R-ecognition (CVPR), Honolulu, HI, USA, 21-26 July 2017, 2261–2269. doi:10.1109/CVPR.2017.243

CrossRef Full Text | Google Scholar

Huang, J., Zhang, H., Li, Y., Zhao, H., Wang, H., and Feng, C. (2021). Defect Recognition Method for Hydraulic Tunnels Based on Dynamic Feature Distillation. Comput. Appl. 41 (8), 2358–2365. doi:10.11772/j.issn.1001-9081.2020101596

CrossRef Full Text | Google Scholar

Huang, L., Chen, C., Yun, J., Sun, Y., Tian, J., Hao, Z., et al. (2022). Multi-scale Feature Fusion Convolutional Neural Network for Indoor Small Target Detection. Front. Neurorobot. 16, 881021. doi:10.3389/fnbot.2022.881021

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, L., Fu, Q., He, M., Jiang, D., and Hao, Z. (2021). Detection Algorithm of Safety Helmet Wearing Based on Deep Learning. Concurr. Comput. Pract. Exper 33 (13), e6234. doi:10.1002/cpe.6234

CrossRef Full Text | Google Scholar

Jia, F., Wang, X., Guan, J., Li, H., Qiu, C., and Qi, S. (2021). WRGPruner: A New Model Pruning Solution for Tiny Salient Object Detection. Image Vis. Comput. 109 (3), 104143. doi:10.1016/j.imavis.2021.104143

CrossRef Full Text | Google Scholar

Jiang, D., Li, G., Sun, Y., Hu, J., Yun, J., and Liu, Y. (2021a). Manipulator Grabbing Position Detection with Information Fusion of Color Image and Depth Image Using Deep Learning. J. Ambient. Intell. Hum. Comput. 12 (12), 10809–10822. doi:10.1007/s12652-020-02843-w

CrossRef Full Text | Google Scholar

Jiang, D., Li, G., Sun, Y., Kong, J., and Tao, B. (2019a). Gesture Recognition Based on Skeletonization Algorithm and CNN with ASL Database. Multimed. Tools Appl. 78 (21), 29953–29970. doi:10.1007/s11042-018-6748-0

CrossRef Full Text | Google Scholar

Jiang, D., Li, G., Tan, C., Huang, L., Sun, Y., and Kong, J. (2021b). Semantic Segmentation for Multiscale Target Based on Object Recognition Using the Improved Faster-RCNN Model. Future Gener. Comput. Syst. 123, 94–104. doi:10.1016/j.future.2021.04.019

CrossRef Full Text | Google Scholar

Jiang, D., Zheng, Z., Li, G., Sun, Y., Kong, J., Jiang, G., et al. (2019b). Gesture Recognition Based on Binocular Vision. Clust. Comput. 22 (Suppl. 6), 13261–13271. doi:10.1007/s10586-018-1844-5

CrossRef Full Text | Google Scholar

Jin, L., Yang, W., Wang, S., Cui, Z., Chen, X., and Chen, L. (2018). A Hybrid Pruning Method for Convolutional Neural Network Compression. Small Microcomput. Syst. 39 (12), 2596–2601. doi:10.3969/j.issn.1000-1220.2018.12.007

CrossRef Full Text | Google Scholar

Li, C., Li, G., Jiang, G., Chen, D., and Liu, H. (2020). Surface EMG Data Aggregation Processing for Intelligent Prosthetic Action Recognition. Neural Comput. Applic 32 (22), 16795–16806. doi:10.1007/s00521-018-3909-z

CrossRef Full Text | Google Scholar

Li, G., Jiang, D., Zhou, Y., Jiang, G., Kong, J., and Manogaran, G. (2019b). Human Lesion Detection Method Based on Image Information and Brain Signal. IEEE Access 7, 11533–11542. doi:10.1109/ACCESS.2019.2891749

CrossRef Full Text | Google Scholar

Li, G., Li, J., Ju, Z., Sun, Y., and Kong, J. (2019a). A Novel Feature Extraction Method for Machine Learning Based on Surface Electromyography from Healthy Brain. Neural Comput. Applic 31 (12), 9013–9022. doi:10.1007/s00521-019-04147-3

CrossRef Full Text | Google Scholar

Li, J., Zhao, Y., Xue, Z., Cai, Z., and Li, Q. (2019c). Overview of Deep Neural Network Model Compression. J. Eng. Sci. 41 (10), 1229–1239. doi:10.13374/j.issn2095-9389.2019.03.27.002

CrossRef Full Text | Google Scholar

Lin, T.-Y., Dollar, P., Girshick, R., He, K., Hariharan, B., and Belongie, S. (2017). “Feature Pyramid Networks for Object Detection,” in IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Honolulu, HI, USA, 21-26 July 2017, 936–944. doi:10.1109/CVPR.2017.106

CrossRef Full Text | Google Scholar

Liu, H., Ding, W., and Huang, Q. (2022). Research on Defect Detection Method of Photovoltaic Cell Based on Lightweight Convolutional Neural Network. Appl. Opt. 43 (1), 87–94. doi:10.5768/JAO202243.0103003

CrossRef Full Text | Google Scholar

Liu, H., Liu, A., Zhou, S., Liu, H., and Yang, J. (2020). Research on Defect Detection Algorithm of Solar Cell Modules Based on Deep Neural Networks. Appl. Opt. 41 (2), 327–336. doi:10.5768/JAO202041.0202006

CrossRef Full Text | Google Scholar

Liu, J., Li, Q., and Li, X. (2021). Neural Network Compression Algorithm Based on Adversarial Learning and Knowledge Distillation. Comput. Eng. Appl. 57 (21), 180–187. doi:10.3778/j.issn.1002-8331.2105-0295

CrossRef Full Text | Google Scholar

Liu, M., Qiu, W., and Sun, W. (2020). Fast Salient Object Detection Algorithm Based on Binary Decomposition of Low-Rank Matrix. Comput. Appl. Res. 37 (7), 2210–2216. doi:10.19734/j.issn.1001-3695.2018.11.0911

CrossRef Full Text | Google Scholar

Liu, X., Jiang, D., Tao, B., Jiang, G., Sun, Y., Kong, J., et al. (2022). Genetic Algorithm-Based Trajectory Optimization for Digital Twin Robots. Front. Bioeng. Biotechnol. 9, 793782. doi:10.3389/fbioe.2021.793782

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y., Jiang, D., Tao, B., Qi, J., Jiang, G., Yun, J., et al. (2022a). Grasping Posture of Humanoid Manipulator Based on Target Shape Analysis and Force Closure. Alexandria Eng. J. 61 (5), 3959–3969. doi:10.1016/j.aej.2021.09.017

CrossRef Full Text | Google Scholar

Liu, Y., Jiang, D., Yun, J., Sun, Y., Li, C., Jiang, G., et al. (2022b). Self-tuning Control of Manipulator Positioning Based on Fuzzy PID and PSO Algorithm. Front. Bioeng. Biotechnol. 9, 817723. doi:10.3389/fbioe.2021.817723

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Z., Li, J., Shen, Z., Huang, G., Yan, S., and Zhang, C. (2017). Learning Efficient Convolutional Networks through Network Slimming. IEEE Int. Conf. Comput. Vis. (ICCV), 2755–2763. doi:10.1109/ICCV.2017.298

CrossRef Full Text | Google Scholar

Luo, B., Sun, Y., Li, G., Chen, D., and Ju, Z. (2020). Decomposition Algorithm for Depth Image of Human Health Posture Based on Brain Health. Neural Comput. Applic 32 (10), 6327–6342. doi:10.1007/s00521-019-04141-9

CrossRef Full Text | Google Scholar

Ouyang, T. (2021). Feature Learning for Stacked ELM via Low-Rank Matrix Factorization. Neurocomputing 448 (7553), 82–93. doi:10.1016/j.neucom.2021.03.110

CrossRef Full Text | Google Scholar

Park, S., and Heo, Y. S. (2020). Knowledge Distillation for Semantic Segmentation Using Channel and Spatial Correlations and Adaptive Cross Entropy. Sensors 20 (16), 4616. doi:10.3390/s20164616

PubMed Abstract | CrossRef Full Text | Google Scholar

Qi, J., Jiang, G., Li, G., Sun, Y., and Tao, B. (2020). Surface EMG Hand Gesture Recognition System Based on PCA and GRNN. Neural Comput. Applic 32 (10), 6343–6351. doi:10.1007/s00521-019-04142-8

CrossRef Full Text | Google Scholar

Ran, G., Li, Z., and Li, L. (2022). Research on FPGM Pruning Algorithm Based on Sensitivity Analysis. Comput. Appl. Res. 39 (1), 141–145. doi:10.19734/j.issn.1001-3695.2021.06.0246

CrossRef Full Text | Google Scholar

Rao, C., Chen, L., Xu, R., and Liu, L. (2019). A Deep Neural Network Compression Method Based on Dynamic Quantization Coding. J. Automation 45 (10), 1960–1968. doi:10.16383/j.aas.c180554

CrossRef Full Text | Google Scholar

Sarakon, P., Kawano, H., Shimonomura, K., and Serikawa, S. (2021). Improvement of Shrinking CNN Architecture Using Weight Sharing and Knowledge Distillation for Tactile Object Recognition. ICIC Express Lett. 12 (7), 627–633. doi:10.24507/icicelb.12.07.627

CrossRef Full Text | Google Scholar

Sun, H., Wang, W., and Chen, H. (2020). Research on Lightweight Image Compression Neural Network Based on Parameter Quantization. Inf. Technol. 44 (10), 87–91. doi:10.13274/j.cnki.hdzj.2020.10.016

CrossRef Full Text | Google Scholar

Sun, Y., Hu, J., Jiang, G., Bai, D., Liu, X., Cao, Y., et al. (2022b). Multi-objective Location and Mapping Based on Deep Learning and Visual Slam. Front. Bioeng. Biotechnol. 10, 903261. doi:10.3389/fbioe.2022.90326110.3389/fbioe.2022.865820

CrossRef Full Text | Google Scholar

Sun, Y., Hu, J., Li, G., Jiang, G., Xiong, H., Tao, B., et al. (2020a). Gear Reducer Optimal Design Based on Computer Multimedia Simulation. J. Supercomput 76 (6), 4132–4148. doi:10.1007/s11227-018-2255-3

CrossRef Full Text | Google Scholar

Sun, Y., Huang, P., Cao, Y., Jiang, G., Yuan, Z., Bai, D., et al. (2022a). Multi-objective Optimization Design of Ladle Refractory Lining Based on Genetic Algorithm. Front. Bioeng. Biotechnol. 10, 900655. doi:10.3389/fbioe.2022.90065510.3389/fbioe.2022.865820

CrossRef Full Text | Google Scholar

Sun, Y., Ma, S., Sun, S., Liu, P., Zhang, L., Ouyang, J., et al. (2021a). Partial Discharge Pattern Recognition of Transformers Based on mobileNets Convolutional Neural Network. Appl. Sci. 11 (15), 6984. doi:10.3390/app11156984

CrossRef Full Text | Google Scholar

Sun, Y., Xu, C., Li, G., Xu, W., Kong, J., Jiang, D., et al. (2020b). Intelligent Human Computer Interaction Based on Non Redundant EMG Signal. Alexandria Eng. J. 59 (3), 1149–1157. doi:10.1016/j.aej.2020.01.015

CrossRef Full Text | Google Scholar

Sun, Y., Yang, Z., Tao, B., Jiang, G., Hao, Z., and Chen, B. (2021b). Multiscale Generative Adversarial Network for Real‐world Super‐resolution. Concurr. Comput. Pract. Exper 33 (21), e6430. doi:10.1002/CPE.6430

CrossRef Full Text | Google Scholar

Sun, Y., Zhao, Z., Jiang, D., Tong, X., Tao, B., Jiang, G., et al. (2022c). Low-illumination Image Enhancement Algorithm Based on Improved Multi-Scale Retinex and ABC Algorithm Optimization. Front. Bioeng. Biotechnol. 10, 865820. doi:10.3389/fbioe.2022.865820

PubMed Abstract | CrossRef Full Text | Google Scholar

Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., and Wojna, Z. (2016). “Rethinking the Inception Architecture for Computer Vision,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27-30 June 2016, 2818–2826. doi:10.1109/CVPR.2016.308

CrossRef Full Text | Google Scholar

Tang, B., Kong, J., and Wu, S. (2017). A Review of Machine Vision Surface Defect Detection. Chin. J. Image Graph. 22 (12), 1640–1663. doi:10.11834/jig.160623

CrossRef Full Text | Google Scholar

Tao, B., Wang, Y., Qian, X., Tong, X., He, F., Yao, W., et al. (2022). Photoelastic Stress Field Recovery Using Deep Convolutional Neural Network. Front. Bioeng. Biotechnol. 10, 818112. doi:10.3389/fbioe.2022.818112

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Wu, L., Lin, X., and Gao, J. (2018). Multiview Spectral Clustering via Structured Low-Rank Matrix Factorization. IEEE Trans. Neural Netw. Learn. Syst. 29 (10), 4833–4843. doi:10.1109/TNNLS.2017.2777489

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, Y., Chen, S., Zhu, F., and Xiong, G. (2021). Pruning Method of Convolutional Neural Network Model Based on Sparse Regularization. Comput. Eng. 47 (10), 61–66. doi:10.19678/j.issn.1000-3428.0059375

CrossRef Full Text | Google Scholar

Wu, X., Jiang, D., Yun, J., Liu, X., Sun, Y., Tao, B., et al. (2022). Attitude Stabilization Control of Autonomous Underwater Vehicle Based on Decoupling Algorithm and PSO-ADRC. Front. Bioeng. Biotechnol. 10, 843020. doi:10.3389/fbioe.2022.843020

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, S., Girshick, R., Dollar, P., Tu, Z., and He, K. (2017). “Aggregated Residual Transformations for Deep Neural Networks,” in IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Honolulu, HI, USA, 21-26 July 2017, 5987–5995. doi:10.1109/CVPR.2017.634

CrossRef Full Text | Google Scholar

Xin, W., Hao, H., Bu, M., Lan, Y., Huang, J., and Xiong, X. (2021). Real-time Recognition of Static Gestures Based on ShuffleNetv2-YOLOv3 Model. J. Zhejiang Univ. Eng. Ed. 55 (10), 1815–1824. doi:10.3785/j.issn.1008-973X.2021.10.003

CrossRef Full Text | Google Scholar

Xu, M., Zhang, Y., Wang, S., and Jiang, G. (2022). Genetic-Based Optimization of 3D Burch-Schneider Cage with Functionally Graded Lattice Material. Front. Bioeng. Biotechnol. 10, 819005. doi:10.3389/fbioe.2022.819005

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, X., Song, X., Yang, C., Zhao, W., and Zhao, R. (2018). Steganalysis of Content-Adaptive JPEG Steganography Based on Scale Co-occurrence Matrix with Diverse Quantization. J. Electron. Imag. 27 (6), 1. doi:10.1117/1.JEI.27.6.063004

CrossRef Full Text | Google Scholar

Yang, Z., Jiang, D., Sun, Y., Tao, B., Tong, X., Jiang, G., et al. (2021). Dynamic Gesture Recognition Using Surface EMG Signals Based on Multi-Stream Residual Network. Front. Bioeng. Biotechnol. 9, 779353. doi:10.3389/fbioe.2021.779353

PubMed Abstract | CrossRef Full Text | Google Scholar

Yun, J., Jiang, D., Liu, Y., Sun, Y., Tao, B., Kong, J., et al. (2022a). Real-Time Target Detection Method Based on Lightweight Convolutional Neural Network. Front. Bioeng. Biotechnol. 10, 861286. doi:10.3389/fbioe.2022.861286

CrossRef Full Text | Google Scholar

Yun, J., Sun, Y., Li, C., Jiang, D., Tao, B., Li, G., et al. (2022b). Self-adjusting Force/bit Blending Control Based on Quantitative Factor-Scale Factor Fuzzy-PID Bit Control. Alexandria Eng. J. 61 (6), 4389–4397. doi:10.1016/j.aej.2021.09.067

CrossRef Full Text | Google Scholar

Zhang, H., Wu, C., Zhang, Z., Zhu, Y., Zhang, Z., Lin, H., et al. (2020). ResNeSt: Split-Attention Networks, 08955v2. Available at: https://arxiv.org/abs/2004.08955.

Google Scholar

Zhang, L., and Cen, Y. (2019). Low-rank Matrix Factorization Defect Detection of Rail Images. Signal Process. 35 (4), 667–675. doi:10.16798/j.issn.1003-0530.2019.04.018

CrossRef Full Text | Google Scholar

Zhang, P., Li, Y., Wang, D., and Wang, J. (2021). RS-SSKD: Self-Supervision Equipped with Knowledge Distillation for Few-Shot Remote Sensing Scene Classification. Sensors 21 (5), 1566. doi:10.3390/s21051566

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Xiao, F., Tong, X., Yun, J., Liu, Y., Sun, Y., et al. (2022). Time Optimal Trajectory Planing Based on Improved Sparrow Search Algorithm. Front. Bioeng. Biotechnol. 10, 852408. doi:10.3389/fbioe.2022.852408

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Zhu, B., Ma, Q., and Wang, H. (2020). Effects of Gradient Optimizer on Model Pruning. IOP Conf. Ser. Mat. Sci. Eng. 711 (1), 012095. doi:10.1088/1757-899X/711/1/012095

CrossRef Full Text | Google Scholar

Zhao, G., Jiang, D., Liu, X., Tong, X., Sun, Y., Tao, B., et al. (2022). A Tandem Robotic Arm Inverse Kinematic Solution Based on an Improved Particle Swarm Algorithm. Front. Bioeng. Biotechnol. 10, 832829. doi:10.3389/fbioe.2022.832829

PubMed Abstract | CrossRef Full Text | Google Scholar

Ziani, B., Ouinten, Y., and Bouakkaz, M. (2018). Maxpart: An Efficient Search-Space Pruning Approach to Vertical Partitioning. cai 37 (4), 915–945. doi:10.4149/cai.2018.4_91510.4149/cai_2018_4_915

CrossRef Full Text | Google Scholar