- 1School of Aeronautics and Astronautics, Xiamen University, Xiamen, China
- 2School of Mechanical and Automotive Engineering, Xiamen University of Technology, Xiamen, China
- 3Department of Mechanical Science and Engineering, Graduate School of Engineering, Nagoya University, Nagoya, Japan
- 4Chalmers University of Technology, Gothenburg, Sweden
Compared with the young, the elderly (age greater than or equal to 60 years old) vulnerable road users (VRUs) face a greater risk of injury or death in a traffic accident. A contributing vulnerability is the aging processes that affect their brain structure. The purpose of this study was to investigate the injury mechanisms and establish head AIS 4+ injury tolerances for the elderly VRUs based on various head injury criteria. A total of 30 elderly VRUs accidents with detailed injury records and video information were selected and the VRUs’ kinematics and head injuries were reconstructed by combining a multi-body system model (PC-Crash and MADYMO) and the THUMS (Ver. 4.0.2) FE models. Four head kinematic-based injury predictors (linear acceleration, angular velocity, angular acceleration, and head injury criteria) and three brain tissue injury criteria (coup pressure, maximum principal strain, and cumulative strain damage measure) were studied. The correlation between injury predictors and injury risk was developed using logistical regression models for each criterion. The results show that the calculated thresholds for head injury for the kinematic criteria were lower than those reported in previous literature studies. For the brain tissue level criteria, the thresholds calculated in this study were generally similar to those of previous studies except for the coup pressure. The models had higher (>0.8) area under curve values for receiver operator characteristics, indicating good predictive power. This study could provide additional support for understanding brain injury thresholds in elderly people.
Introduction
The Global Status Report on Road Safety (2018) shows that 1.35 million people die each year from road traffic accidents (World Health Organization, 2018) and that more than half of the global deaths were vulnerable road users (VRUs) (specifically 23% of pedestrians, 3% of cyclists, and 28% of motorized 2–3 wheelers). In China, there were 63,772 deaths caused by traffic accidents in 2017, in which elderly people (the age ≥ 60 years) accounted for 30.35% (TABC, 2017).
Brain injuries have been observed as the most fatal factor to the VRUs and have been investigated thoroughly in the past five decades (Gadd, 1966; Nahum et al., 1977; Ward et al., 1980; Hertz, 1993; Arbogast et al., 1995; Hardy et al., 2001; Melvin and Lighthall, 2002; Shi et al., 2020). Due to the complexity of the head anatomical structure, many head injury tolerances (Nusholtz et al., 1984; Margulies and Thibault, 1992; Bain and Meaney, 2000; Zhang et al., 2004) and head injury criteria (HIC) (Versace, 1971; Newman, 1986; Newman and Shewchenko, 2000; Willinger and Baumgartner, 2003; Marjoux et al., 2008; Takhounts et al., 2011, 2013; Kimpara and Iwamoto, 2012) have been proposed for evaluating the human head injury risk under various crash conditions. Two types of HIC have been proposed for evaluating head injury risk; one is based on head kinematics and the other on local tissue stress and strain information. Kinematic-based criteria include the head injury criterion (HIC) (National Highway Traffic Safety Administration (NHTSA), 1972), the Brain Injury Criteria (BRIC) (Takhounts et al., 2011, 2013), the Generalized Acceleration Model for Brain Injury Threshold (GAMBIT) (Newman, 1986), and the head impact power (HIP) (Newman and Shewchenko, 2000). The development of computer technology and finite element (FE) head models facilitated brain tissue-based injury criteria such as the von Mises stress, shear stress (Donnelly and Medige, 1997; Kang et al., 1997; Darvish and Crandall, 2001), pressure, the maximal principal strain (MPS), the cumulative strain damage measure (CSDM) (Bandak and Eppinger, 1994; Takhounts et al., 2003), and the dilatation damage measure (DDM) (Nusholtz et al., 1995). For the elderly, as the brain size decreases and the subdural space increases (Genarelli and Thibault, 1982), the relative motion between the skull and the brain increases significantly under various impact conditions, which would lead to a greater risk of vein rupture and hematoma (Kleiven and Holst, 2001; Richards and Carroll, 2012). However, there are few studies on the head injury tolerances for the elderly.
Brain injury criteria and mechanism tolerances based on biomechanical experiments (Melvin and Lighthall, 2002) and indepth accident reconstructions (Yao et al., 2008; Peng et al., 2012; Bourdet et al., 2014; Giordano and Kleiven, 2014; Nie and Yang, 2014; Sahoo et al., 2016) have been intensively investigated. Shi et al. (2020) investigated the effectiveness of the various HIC in the prediction of VRUs severe head injuries caused by ground impact in 10 accidents and showed that predictors like angular acceleration, linear acceleration, HIC, coup pressure, MPS, and CSDM had good capability to predict severe head injuries. However, the correlation between those injury predictors and injury risk still needs more analyzing. With more real-world accident cases collected and reconstructed with high accuracy, the purpose of the current study was to establish the head AIS 4+ injury tolerance of elderly people based on various HIC. A total of 30 detailed real-world elderly VRU accidents with video information from the TRaffic Accident database with Video (VRU-TRAVi) (Han et al., 2018; Shi et al., 2020) was used.
Materials and Methods
Vulnerable Road Users Accident Data
A total of 30 real-world VRU accident cases were selected and reconstructed from the VRU-TRAV database. This database was established in 2015, and more than 1,500 cases of video information have been collected at present. Among them, about 1,300 cases (only video information) were downloaded from the Internet (Youku, YouTube, Tencent, etc.). In addition, more than 220 in-depth accidents (contains video and detailed medical records) were obtained from National Automobile Accident In-Depth Investigation System (NAIS) and Academy of Forensic Science (AFS). NAIS and AFS meet the ethical procedures for incident data collection. We have intensive cooperation with NAIS workstations (Shanghai University of Engineering and Technology and Xihua University) and AFS to obtain these accident data. The selection standards for VRU accidents were:
(a) All cases were for the elderly (age ≥ 60 years).
(b) Each case has detailed accident sketches, vehicle damage photos, video information from the vehicle recorder or road monitoring, and detailed head injury reports.
(c) The contact area between the VRU’s head and the vehicle front-end structure (such as the A-pillar, bonnet, windshield, or ground) could be obtained from the above information.
(d) From the video records, the kinematic motion of the vehicle and the VRU kinematics before/during/after collisions could be observed clearly.
(e) The injury report should record details of the type of head injury and the severity of the head injuries having been classified and coded by using the maximum degree of injury severity (MAIS) (Association for the Advancement Automotive Medicine, 2005).
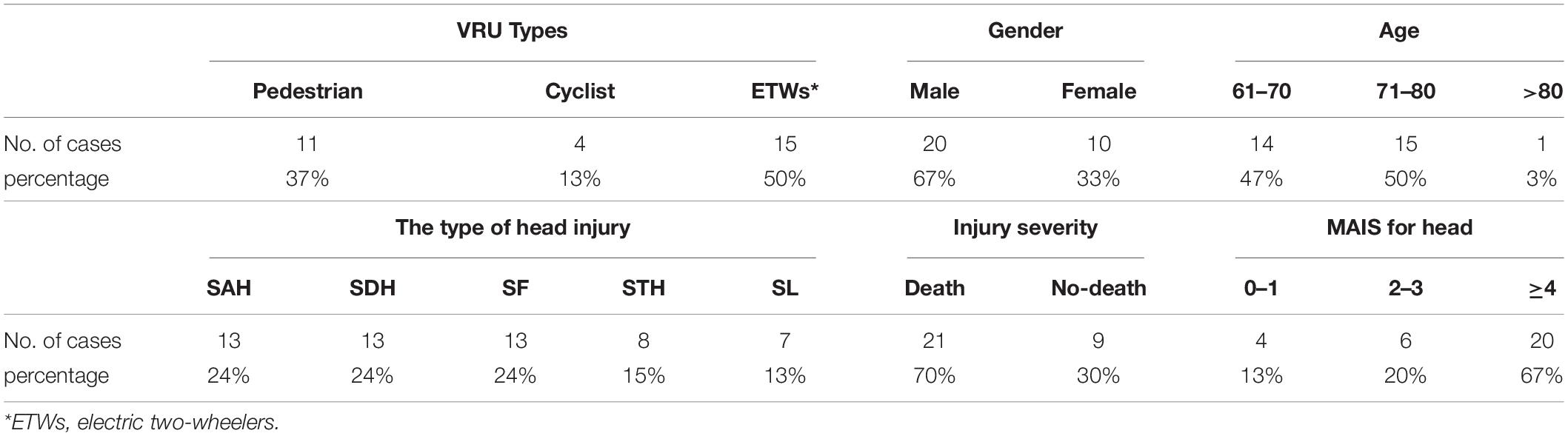
Table 1 shows the basic information of the 30 accidents (detailed information listed in Supplementary Table 1), in which the VRU’s age was mainly distributed between 60 and 80 years old, and the five most common types of head injuries (detailed head injury information listed in Supplementary Table 2) were subarachnoid hemorrhage (SAH), subdural hematoma (SDH), skull fracture (SF), soft tissue hematoma (STH), and scalp laceration (SL).
Accident Reconstruction
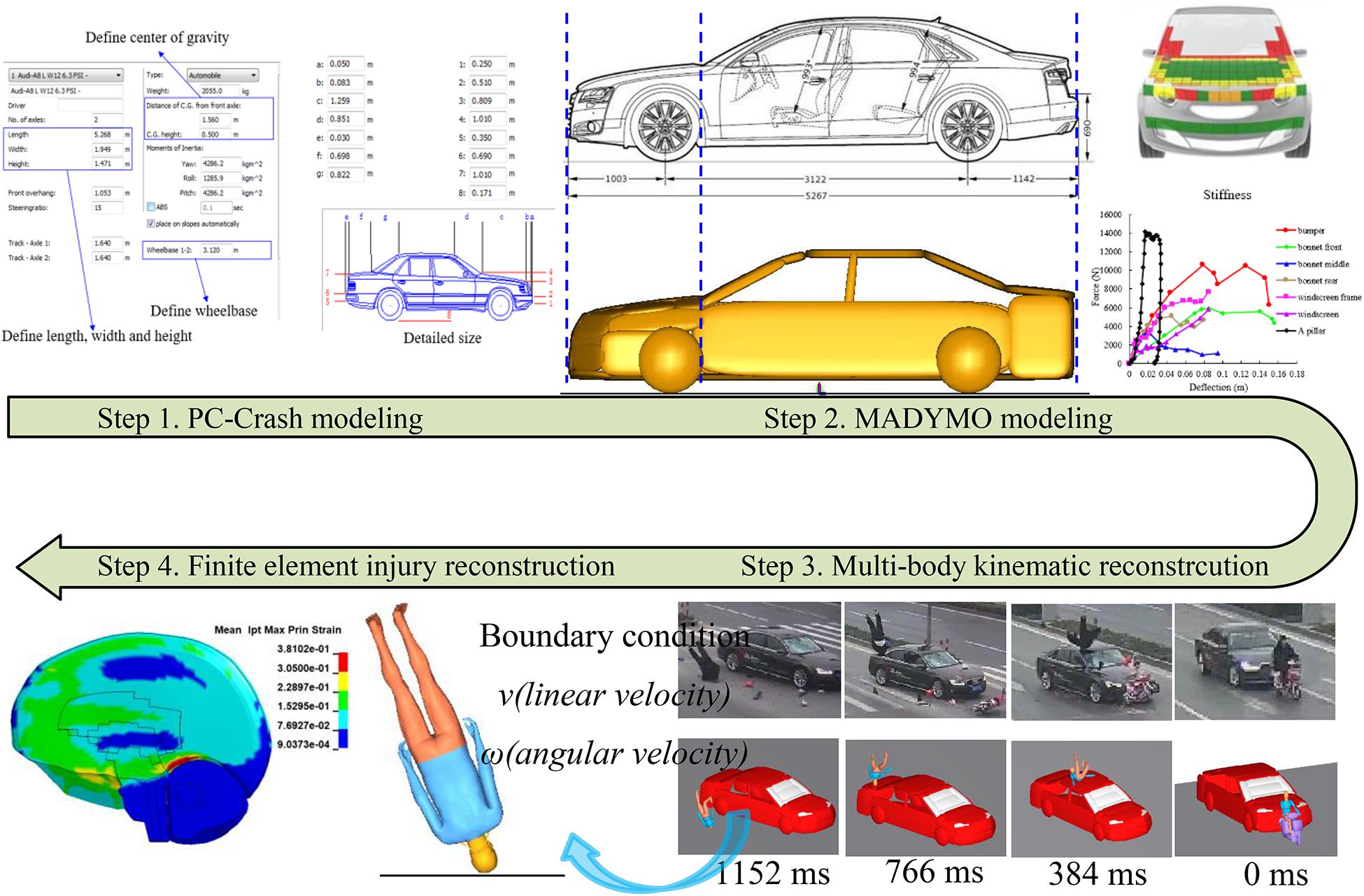
Shi et al. (2020) described the accident reconstruction flow shown in Figure 1. There are four steps to reconstruct the kinematic and head injury severity of the VRUs by coupling multi-body system and FE models.
Step 1: PC-Crash Modeling
The multi-body vehicle and VRUs models were reconstructed based on vehicle and VRU size information in the accident files, and the estimation of vehicle speed was obtained by the video frame-by-frame analysis method (Han et al., 2019) and direct linear transformation (DLT) method (Han X. Y. et al., 2012). The initial impact position between vehicle and VRUs were mainly determined by the video and pictures of vehicle damage parts.
Step 2: MADYMO Modeling
The vehicle multi-body model used was developed based on the detailed vehicle structural dimensions using ellipsoids, and the front-end stiffnesses were defined based on Euro-NCAP test data (Martinez et al., 2007). For the pedal bicycle and electric two-wheelers, six hinges were used to simulate the motion between each component, and the stiffness characteristics were defined based on the studies of McLundie (2007) and Maki and Kajzer (2000). The VRU’s gender, stature, and weight were similarly reconstructed to the accident victims by using the scaling method on the baseline model of the 50th Chalmers Pedestrian Model (CPM) (Young, 1997; Yang et al., 2000). For the contact simulation, the elastic contact model was used to represent the contact between different multi-body models, and the friction coefficient was specified to be 0.2 between the VRU and the vehicles models, and 0.58 between the VRUs and the ground (Wood and Simms, 2000; Shi et al., 2018).
Step 3: Multi-body Kinematic Reconstruction
The final position of the vehicle and VRU was reconstructed based on the accident sketch by using PC-Crash and MADYMO code. The VRUs’ kinematic in both vehicle and ground contact were reproduced by comparing with the accident video information.
Step 4: Finite Element Injury Reconstruction
The head and torso boundary conditions pre-impact were defined by the output from running the multi-body kinematic reconstruction. These boundary conditions included three-axis linear and angular velocities of the head, chest, and pelvis centers of gravity (CG) and the relative position between the pedestrian to vehicle and ground impact. Some cases have both head-to-vehicle and head-to-ground impacts, some have only ground impacts, and the types of vehicles involved in the 30 cases are mainly sedan, SUV, and MPV. To make the FE vehicle model used for simulation match the dimensions of the accident vehicle as much as possible, a total of five FE vehicle models (Han X. Y. et al., 2012; Han Y. et al., 2012; Shi et al., 2018, 2019) were selected and used for the head-to-vehicle impacts simulations, and the ground surface was the asphalt road and defined as a rigid body (Tamura et al., 2014; Huang et al., 2020).
Head Injury Criteria
All FE simulations were performed using the LS-DYNA MPP R9.3.0 (LSTC, Livermore, CA, United States) software. Eight HIC were computed with the THUMS V4.0.2 pedestrian model. The head kinematic-based criteria were the angular velocity, the angular and linear acceleration, and HIC (Versace, 1971; National Highway Traffic Safety Administration (NHTSA), 1972). The brain tissue level-based injury criteria were the coup pressure, MPS (Thibault et al., 1990; Bain and Meaney, 2000), and CSDM (Bandak and Eppinger, 1994; Takhounts et al., 2003). The estimated injury risks were compared with the injury records with AIS codes, and their effectiveness to predict severe head injuries was examined.
Statistical Analysis
In this study, a single logistic regression method was used to establish the relationship between the head AIS 4+ injury risk and different evaluation criteria in the elderly. The injury risk curves are a sigmoid function derived based on Eq. 1 as follows:
Where P(x) is the probability of head AIS 4+ injuries for a value of injury criterium lower than or equal to x, α0 is the intercept, and α1 is the regression coefficient of x. Receiver operating characteristic (ROC) curves and area under curves (AUC) were further used to assess the predictive capability of the regression models. In this study, we used a confusion matrix to obtain the ROC curves and AUC. Confusion matrix (Li, 2012) is a concept from machine learning and is a measure of the performance of a classification model, which has two dimensions, one of which represents the actual value and the other the predicted value. Table 2 shows the expression of the confusion matrix for a typical binary classification problem. True positive (TP) means that the actual value is positive and the predicted value is also positive. False negative (FN) means that the actual value is positive and the predicted value is negative. Similarly, False positive (FP) and True negative (TN) indicated that the actual values are negative, and the predicted values are positive and negative, respectively.
To plot the ROC curves, we first need to define two measures, namely false positive rate (FPR) and true positive rate (TPR). FPR refers to the ratio of false-positive cases (the cases that predicted positive but are actually negative) out of all negative cases, it is defined by:
True positive rate refers to the ratio of true-positive cases (the cases that predicted positive and actually are positive too) out of all positive cases, it is defined by:
In the binary classification task, the classification result can be obtained by setting a threshold. If the predicted value is higher than the threshold, it is classified as positive, and classified as negative if lower than the threshold. By setting different thresholds, we can get different confusion matrices, and then multiple pairs of FPR and TPR values can be calculated with FPR as the X-axis and TPR as the Y-axis, thus the ROC curve can be obtained by connecting them. The ROC indicates the predictive power with AUC 1.0 indicating a perfect model.
Results
Kinematic Response of Accident Reconstructions
Based on the clear and complete accident video information, the kinematic response before/during/after the collision was reconstructed for a total of 30 elderly cases. Figure 2 shows the results of comparing the reconstruction kinematic response with the video information in case 9 (others are summarized in Supplementary Figure 1). The reconstructed pedestrian kinematics showed consistent results with the video records, including the relative position between the pedestrian and the vehicle, the pedestrian rotation angle (Shi et al., 2018), the pedestrian body region contact to the ground, the subsequent order of contacts (Han et al., 2018), and the final position (Wu et al., 2020). The reconstructed kinematic of the VRUs show consistency with the observed kinematics in the video records for all cases.
Results of VRU Head Injury Simulations
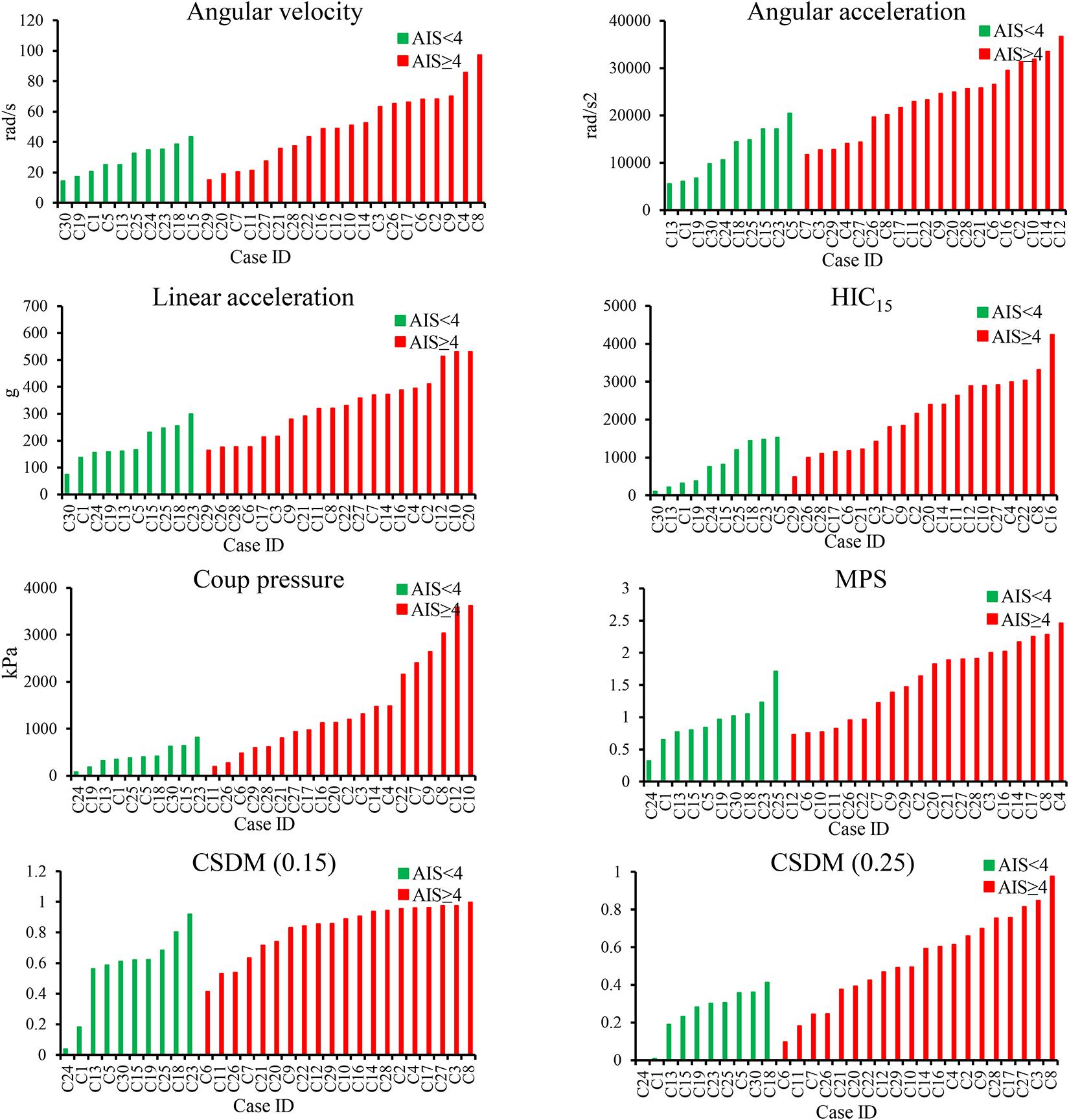
For the 30 real-world VRU accident reconstructions, the simulated results of the four kinematic-based HIC and four brain tissue-based criteria are shown in Figure 3. The histograms were reordered in terms of the magnitude of the calculated injury criterion values according to the AIS < 4 cases (in the green columns) and the cases resulting in head AIS 4+ injuries (in the red columns). For each head kinematics-based and brain tissue-based criteria, the simulated values in green columns were globally lower than those simulated for the red columns. The ranges for the kinematic-based criteria consisting of the head angular velocity and acceleration, linear acceleration, and HIC15 were 14.4–97.3 rad/s, 5,550–36,688 rad/s2, 73–530.3 g, 103–4,238, respectively. The ranges for the brain tissue-based criteria consisting of the coup pressure, MPS, CSDM (0.15), and CSDM (0.25) were 78.44–3,618 kPa, 0.32–2.46, 0.04–0.996, and 0.001–0.98, respectively. The detailed parameter values for all head kinematics-based criteria and brain tissue-based criteria as determined from the simulations are listed in Supplementary Table 2.
Injury Risk Curves for All Head Injury Criteria
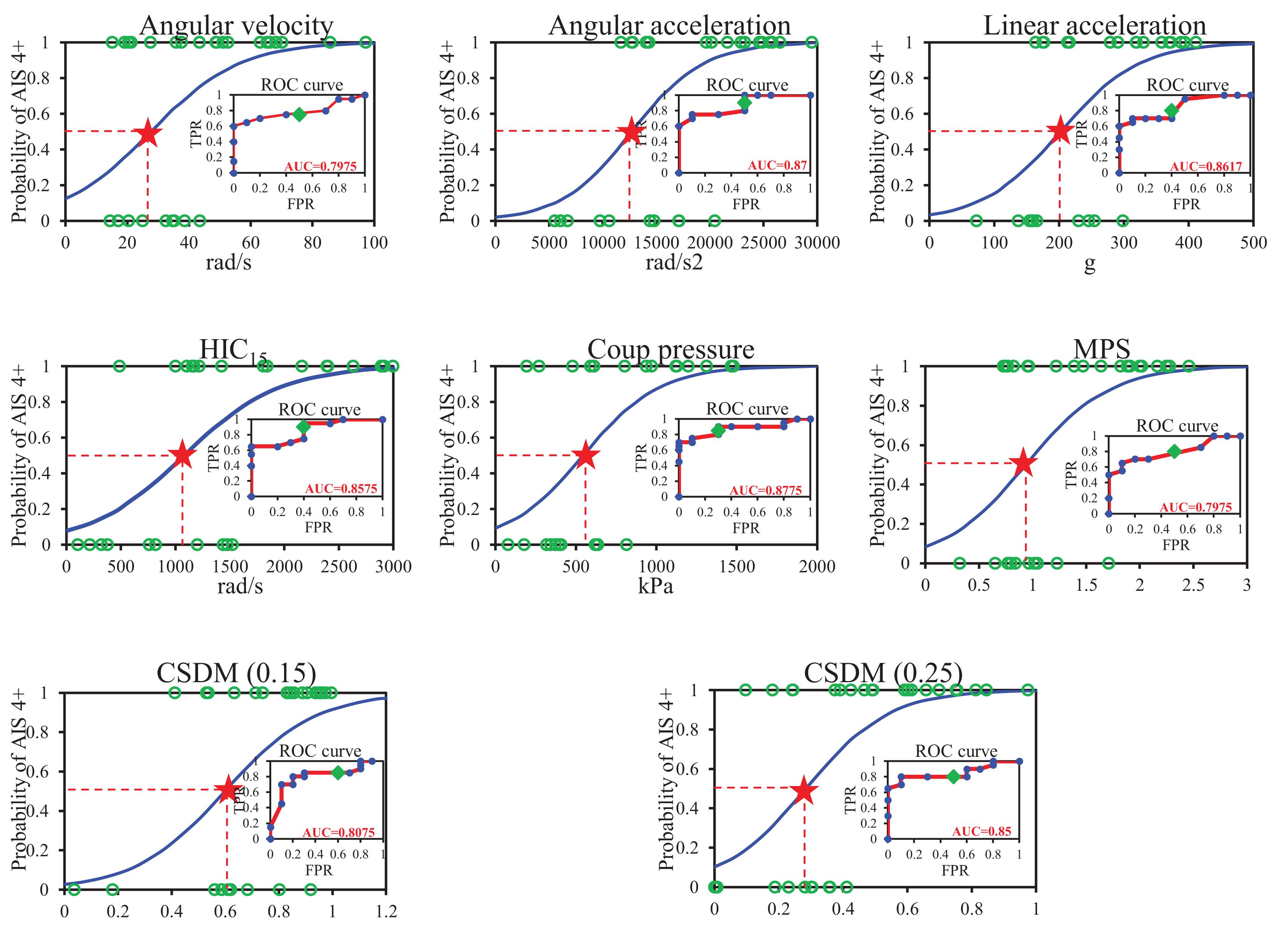
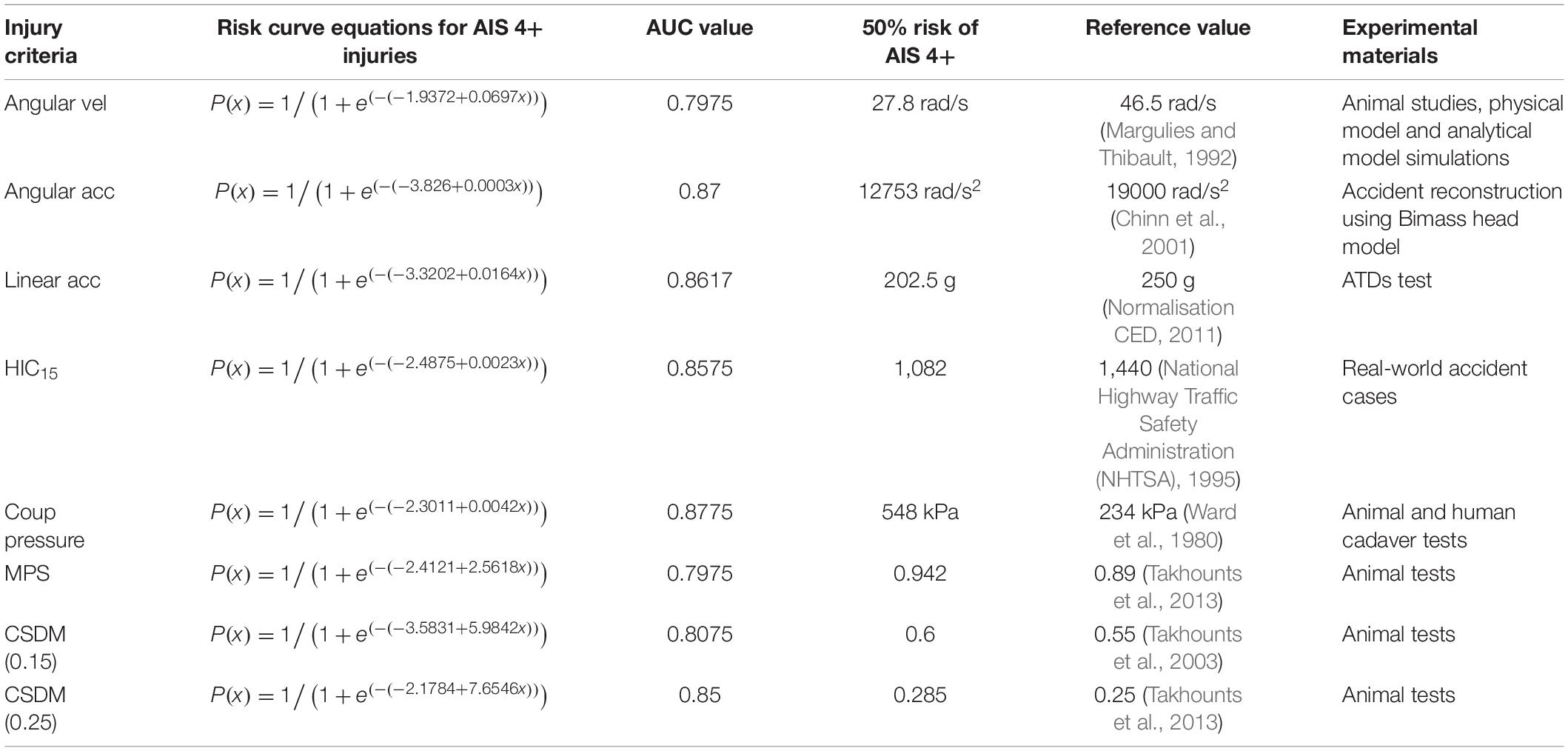
The injury risk curves for the four head kinematic based criteria and the four brain tissue based criteria were developed based on the regression of the histograms, and the resulting curves are shown in Figure 4, where the green circles are the experimental data, and the red pentagrams are the threshold at 50% AIS 4+ injury risk for each criterion. The subplots are the ROC curves, the blue dots are the FPR and TPR coordinates at different thresholds, and the green dots represent the FPR and TPR coordinates when the threshold is 0.5. The closer the ROC curve is to the upper left corner, and the closer the AUC = 1, the better the predictive capability of the regression equation. The AUC value for the kinematic-based criteria consisting of the head angular velocity and acceleration, linear acceleration, and HIC15 were 0.7975, 0.87, 0.8617, and 0.8575, respectively. Similarly, the AUC value for the brain tissue-based criteria consisting of the coup pressure, MPS, CSDM (0.15), and CSDM (0.25) were 0.8775, 0.7975, 0.8075, and 0.85, respectively. The logistic regression risk equations, the AUC value, and the 50% probability of head AIS 4+ injury for all HIC are summarized in Table 3.
Discussion
The Reliability of the Accident Reconstructions
The “accident reconstructions” using the real-world accident data to reproduce the collision process and human injuries can be used to alleviate the lack of real data to some extent (Kleiven, 2007; Yao et al., 2008). The traditional accident reconstruction methods were mostly based on police investigation records, including the objective vehicle trajectory traces developed from the investigation of the collision and the subjective information such as the comments and opinions garnered from the participants involved in the accident (Yao et al., 2008; Badea-Romero and Lenard, 2013). However, due to the lack of video information, factors exist regarding the uncertainty which influences the quality and reliability of the reconstruction. These include such factors as the VRUs’ kinematics, vehicle dynamics, impact area, impact angle, and landing posture, and the factors affecting the uncertainty could be alleviated by analyzing the videos for use in undertaking the accident reconstruction.
In the current study, the real-world VRU accidents with video information were selected and reconstructed by using a multi-body system (PC-Crash and MADYMO) and FE methods. Initially, the collision speed could be calculated more accurately using the video images and the DLT method. Then, the reconstructed kinematics could be verified against video frame by frame. Finally, the head impact conditions and injury outcomes could be more objectively compared with the hospital injury reports. In some cases (e.g., in case 18), it is difficult to observe the whole process of VRUs’ kinematic response after collision due to the perspective of the video; therefore, the kinematic response of the obscured part could be inferred by comparing the final position (Pascoletti et al., 2019a) and the observed kinematic response at the next moment. The 5th and 50th percentile THUMS models have different size and material properties, which could change the impact locations with the vehicle and injury severity of the head. But in this study, only the 50th percentile of THUMS was used for injury reconstruction in both male and female cases. The reasons are as follows: firstly, we used the CPM model to reconstruct the VRU’s kinematic response (including the impact location of the head), and the CPM model was scaled strictly according to the VRU’s height, weight, and gender in the real accident, and the reconstruction results were compared with the video information and vehicle damage photos. Then, the multi-body reconstruction results were input into the THUMS model as boundary conditions for injury reconstruction (shown in section “Accident Reconstruction”). Therefore, it can be ensured that the head-to-vehicle impact locations are consistent with the actual accident. Also, with the same loading boundary conditions (including the same linear and angular velocity, impact angle, and location), the little differences in the severity of head injury caused by the fifth and 50th THUMS models were observed, especially to simulate head impact with the ground.
Regression Models Evaluation
For the unbalanced sample of head injury level (the number of head AIS 4+ was 20 cases and no head AIS 4+ was 10 cases), the performance of the regression models was evaluated using ROC curves (shown in Figure 5) and AUC values (listed in Table 3) in this study. For all regression models, the values of AUC ranged from 0.8 to 0.88, indicating a good predictive capability. However, by comparing with previous studies (National Highway Traffic Safety Administration (NHTSA), 1995; Mertz et al., 1996), the initial probability (the probability when the horizontal coordinate is zero) of the regression model obtained in this study was slightly higher (the corresponding AIS 4+ probability was not zero (from 0.02 to 0.12) when the injury value was zero), and this phenomenon was one of the possible reasons why the AUC value could not be very close to 1. There are two reasons to explain this phenomenon: one is the insufficient sample size used to fit the regression model, and another is the unbalanced sample size and the number of on-head AIS 4+ only 10 cases. The main purpose of this study was to obtain the threshold of head AIS 4+ injury in elderly people, so the effect of the initial probability on the threshold was not significant, and the authors will subsequently increase the sample size further to obtain a more optimal regression model.
For the study of brain injuries tolerance, most human tolerance limits were constrained in the mild or moderate brain injuries (Rowson et al., 2012) because the head injury data used were mostly for football players, and there were limited data available with severe injuries, especially for the elderly. In this study, each criterion injury threshold of a 50% risk of an AIS 4+ severe brain injury for elderly people (listed in Table 3) was compared with those published in the literature for this field.
Rotational Motion-Based Criteria (Angular Velocity and Angular Acceleration)
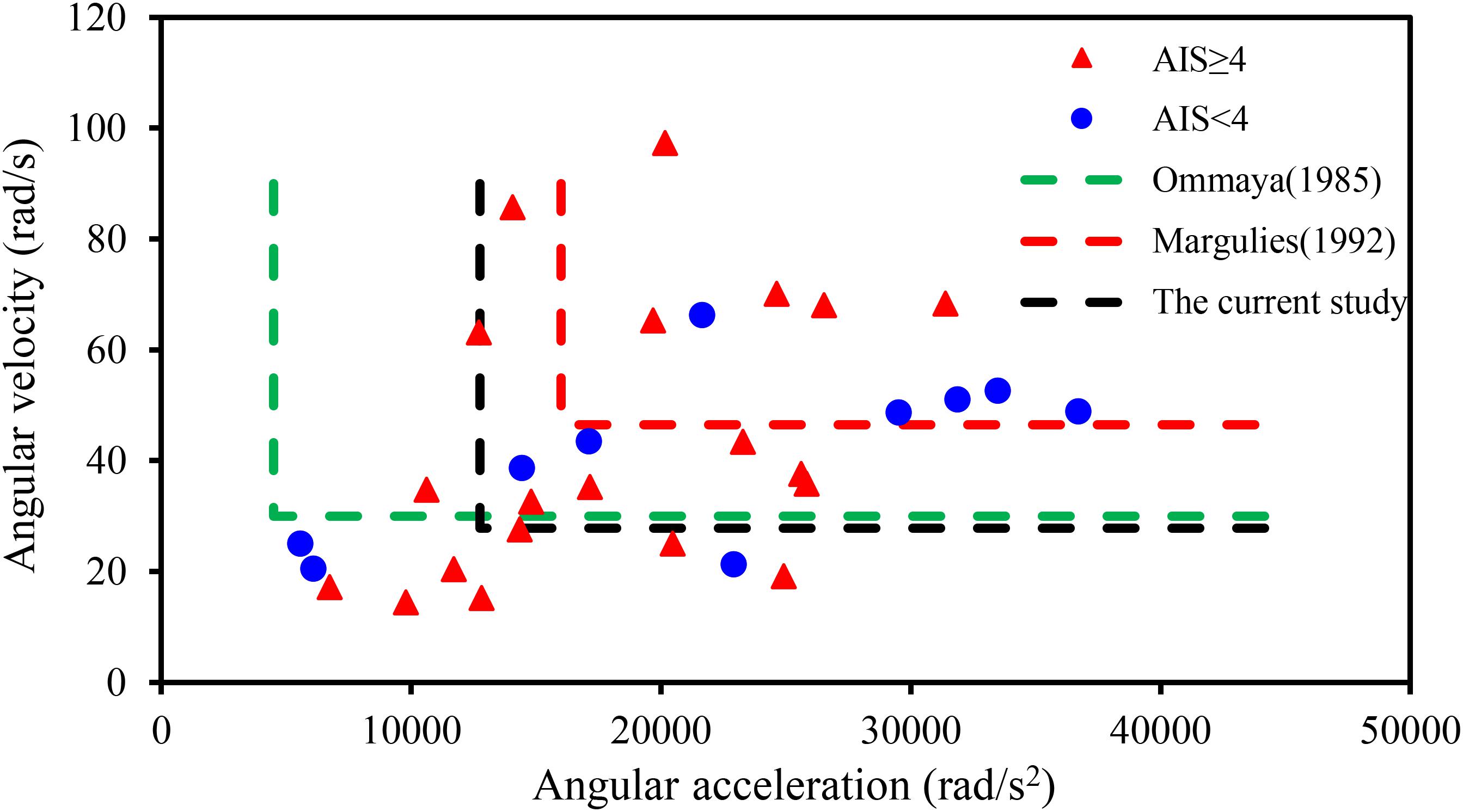
Based on animal experiments, Unterharnscheidt (1971) indicated that a rotational acceleration of 101–150 krad/s2 leads to no injury and when the accelerations up to 197 krad/s2, subdural hematomas combined with neurological injuries, could be observed. Ommaya (1985) used a primate model and suggested an injury threshold for sagittal plane rotation of the head of 4,500 rad/s2 when rotational velocity is less than 30 rad/s. Pincemaille et al. (1989), based on experimental data from volunteer boxers, found that the concussion thresholds for angular acceleration and angular velocity were in the range of 13.6–16, 25–48 rad/s, respectively. Margulies and Thibault (1992) utilized a primate model and proposed a DAI-tolerance limit (AIS 4+) for humans of 46.5 rad/s with an angular acceleration of 16,000 rad/s2. Patton et al. (2012) reported maximum rotational acceleration, respectively, a velocity of 4.5 krad/s2, 33 rad/s as a threshold for short or no loss of consciousness, based on a set of American football players’ head impact analyses. In this current study, the thresholds of angular velocity and angular acceleration (listed in Table 3) for the head injury level of AIS 4+ in the elderly were obtained based on logistic regression of the reconstruction results of 30 accidents, which were 27.8 rad/s and 12,753 rad/s2, respectively (shown in Figure 5). These thresholds were only similar to the concussion thresholds derived by Pincemaille et al. (1989) and Patton et al. (2012) and were much lower than those derived by Unterharnscheidt (1971) and Ono et al. (1980) for subdural hematoma and brain contusion. Those suggested that the probability of brain injury was higher in the elderly under the same impact conditions.
Linear Motion-Based Criteria (Maximum Resultant Linear Acceleration and HIC)
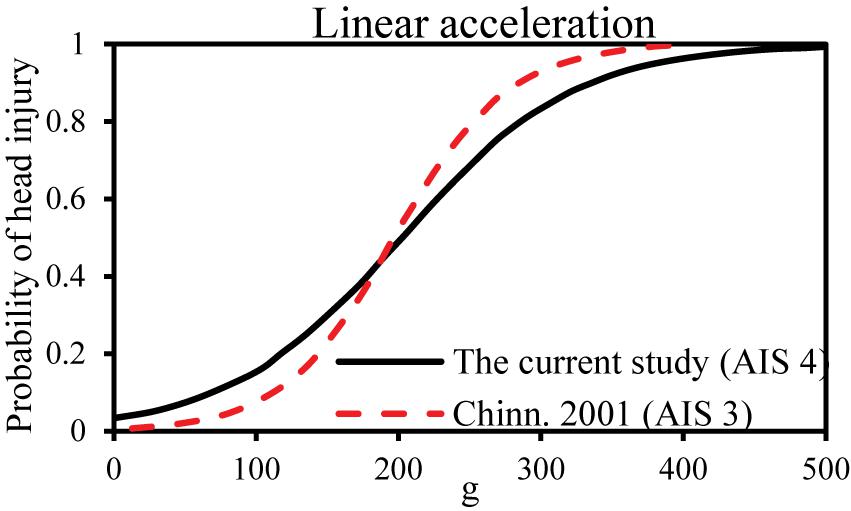
Early HIC were maximum resultant head acceleration because of their simplicity. The head accelerations of 200 and 250 g causing an AIS 3 and AIS 4 head injury were confirmed with previous studies (Newman, 1980; Chinn et al., 2001). However, this criterion does not take into account the time duration of the impact, so HIC was developed as a new HIC based on the Wayne state tolerance curve. The National Highway Traffic Safety Administration (National Highway Traffic Safety Administration (NHTSA), 1995) developed the HIC curves for various AIS injury levels, and HIC = 1,440 means a 50% probability of head AIS 4+ injury. Mertz et al. (1996) established a risk curve for HIC15 and skull fracture based on cadaver’s data and knowing that HIC = 1,420 means a 50% probability of skull fracture. The comparison of the linear acceleration and HIC risk curves for a head injury derived from these studies is shown in Figures 6, 7. In this current study, the critical value of 50% probability of head AIS 4+ injury for linear acceleration and HIC15 were 202.5 g and 1,082, respectively, which were slightly lower than (linear acceleration and HIC15 in this study were 19 and 24.86% lower than the earlier studies, respectively) the threshold of previous studies (Chinn et al., 2001; National Highway Traffic Safety Administration (NHTSA), 1995; Mertz et al., 1996).
Stress-Based Criteria
Ward et al. (1980) simulated the head impacts in animal and human cadaver tests in aircraft accidents by using an original FE brain model and showed that the serious and fatal injuries would occur when the intracranial pressure exceeded 234 kPa. In the current study, the critical value of the pressure for a 50% risk brain injury was 548 kPa, which is much higher (the pressure threshold in this study was 134.2% higher) than Ward’s and his colleagues’ study. One reason for this large difference may be the difference in the material properties used, and another may the intense head-to-ground impact due to the ground being considered as a rigid body.
For the strain-based criteria, such as MPS and CSDM, Takhounts et al. (2003, 2011, 2013) proposed the 50% thresholds for MPS, CSDM0.15, and CSDM0.25 to predict concussion and DAI, which were 0.89, 0.55, and 0.25, respectively. The research was performed based on the animal experimental data simulated by the SIMon head model. It should be noted that the anatomical structure of the SIMon model was quite simplified compared to the real human head and the skull was assumed to be a rigid body. In this current study, the 50% risk of head AIS 4+ injury for MPS, CSDM0.15, and CSDM0.25 of 0.94, 0.6, and 0.285, respectively, in which these thresholds are very close to proposed by Takhounts et al. (2003, 2011, 2013).
According to the comparison with previous studies in the literature using different sources, it could be found that the threshold for head AIS 4+ injury in the elderly computed by the global kinematic criteria is generally lower than those of previous studies; for the brain tissue level criteria, the thresholds calculated were generally similar to those of previous studies except for the coup pressure. One reason is that all accidents involved elderly people, and another reason is that the injury threshold for all criteria in this study was obtained from the THUMS head model (Ver. 4.0.2); therefore, the model differences should be carefully considered in the future when applying the threshold.
Limitation
The first limitation was that the accident cases are too limited and the number of head AIS 4+ cases (20 cases) and no head AIS 4+ cases (10 cases) were not equivalent in this research due to the high selection standards. The second limitation was that the kinematics could not be completely replicated according to the video information due to the limitations of the CPM model. Since not all deaths were analyzed anatomically, there existed some cases (six cases in total) without weight information. Admittedly, a more accurate numerical model also requires road user weight (Pascoletti et al., 2019b) in addition to the height and age, which is another limitation in this article. The variables in the regression models were only injury criteria and head AIS level, and did not include age and sex, mainly because of the small number of cases and the unbalanced proportion of sex and age groups (listed in Supplementary Table 1). Moreover, for some cases, the head collided with both the vehicle and the ground, but only the collision that caused the more severe head injury was included and the cumulative effect caused by another collision was not considered (Determine the collision that caused the more serious head injury using two aspects: Firstly, the specific position of the head impact with the vehicle and the ground can be derived from the video information. Then compared to the position of head injury in the injury report to determine whether the most serious head injury was caused by the vehicle or the ground. In addition, the values for each HIC were calculated for VRU during the vehicle impact and ground impact phases based on the THUMS 4.02 model, and the head injury values resulting from the vehicle and ground impact phases were compared to determine in which impact phase that caused the more severe head injury). And the THUMS head model represents a 50th male adult, the brain tissue mass and volume were not scaled according to the different ages and genders. The head injury models also did not consider the potential difference in tissue properties (e.g., skull stiffness), which was another limitation.
Conclusion and Perspectives
Thirty in-depth VRUs accident cases with video records were reconstructed with high reliability by using a multi-body system (PC-Crash and MADYMO) and the THUMS (Ver. 4.0.2) head FE model. The kinematic-based injury criteria (linear acceleration, angular velocity, and acceleration, HIC) and brain tissue-based injury criteria (coup pressure, MPS, and CSDM) were investigated for predicting the head AIS 4+ injuries in elderly VRUs. The predictive ability of the logistic regression models was evaluated using the ROC curve and AUC, where the AUC ranged from 0.8 to 0.88, indicating a good correlation between all criteria and head AIS 4+ injury in the elderly. Thereby, the relevance of their capability to predict AIS 4+ brain injuries could therefore be compared with the AIS 4+ injury thresholds determined in the previous studies identified in the literature.
In this study, the determined injury threshold could alleviate the limited data on previously available brain tolerance. Also, the injury value acquired from in-depth real-world accident investigations could provide additional support for understanding brain injury mechanisms in elderly people. What’s more, the authors recommend that the comprehensive kinematic-based and tissue-based injury criteria should be considered for future VRUs’ safety studies.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
YH conceptualization, methodology, writing original draft preparation, and writing reviewing and edition. HW software. HW, BW, and DP cases analysis, investigation, and joint writing the original draft preparation. YH and RT methodology, writing draft, and revising. KM conceptualization, supervision, and revising. All authors contributed to the article and approved the submitted version.
Funding
The authors would like to acknowledge support of the Natural Science Foundation of China (Grant Number 51775466), Fujian Provincial Science foundation for distinguished young scholars (Grant Number 2019J06022), the State Key Laboratory of Automotive Safety and Energy under Project No. KF2005, and the Natural Science Foundation of Fujian Province (Grant Number 2020J05235).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbioe.2021.682015/full#supplementary-material
References
Arbogast, K., Meaney, F., and Thibault, L. (1995). Biomechanical Characterization Of The Constitutive Relationship For The Brainstem. SAE Technical Paper. 952716. Warrendale, PA: SAE.
Association for the Advancement Automotive Medicine (2005). The Abbreviated Injury Scale–Copyright 2005. Barrington, IL: Association for the Advancement of Automotive Medicine, 60011.
Badea-Romero, A., and Lenard, J. (2013). Source of head injury for pedestrians and pedal cyclists: striking vehicle or road? Accid. Anal. Prev. 50, 1140–1150. doi: 10.1016/j.aap.2012.09.024
Bain, A., and Meaney, D. (2000). Tissue-level thresholds for axonal damage in an experimental model of central nervous system white matter injury. J. Biomech. Eng. 122, 615–622. doi: 10.1115/1.1324667
Bandak, F. A., and Eppinger, R. H. (1994). A three-dimensional finite element analysis of the human brain under combined rotational and translational accelerations. SAE Trans. 103, 1708–1726.
Bourdet, N., Deck, C., Serre, T., Perrin, C., Llari, M., and Willinger, R. (2014). In-depth real-world bicycle accident reconstructions. Int. J. Crashworthiness 19, 222–232. doi: 10.1080/13588265.2013.805293
Chinn, B., Canaple, B., Derler, S., Doyle, D., Otte, D., Schuller, E., et al. (2001). Cost 327 Motorcycle Safety Helmets. Brussels: European Commission.
Darvish, K., and Crandall, J. (2001). Nonlinear viscoelastic effects in oscillatory shear deformation of brain tissue. Med. Eng. Phys. 23, 633–645. doi: 10.1016/s1350-4533(01)00101-1
Donnelly, B. R., and Medige, J. (1997). Shear properties of human brain tissue. J. Biomech. Eng. Trans. ASME 119, 423–432. doi: 10.1115/1.2798289
Gadd, C. (1966). Use of a Weighted-Impulse Criterion For Estimating Injury Hazard. SAE Technical Paper. 660793. Warrendale, PA: SAE.
Genarelli, T. A., and Thibault, L. E. (1982). Biomechanics of acute subdural hematoma. J. Trauma 22, 680–686.
Giordano, C., and Kleiven, S. (2014). Evaluation of axonal strain as a predictor for mild traumatic brain injuries using finite element modeling. Stapp Car Crash J. 58, 29–61.
Han, X. Y., Jin, X. L., Zhang, X. Y., and Miao, X. (2012). Vehicle movement information reconstruction based on video images and DLT theory. Automot. Eng. 12, 1145–1149.
Han, Y., Li, Q., Qian, Y. B., Zhou, D. Y., and Svensson, M. (2018). Comparison of the landing kinematics of pedestrians and cyclists during ground impact determined from vehicle collision video records. Int. J. Veh. Saf. 10, 212–234. doi: 10.1504/ijvs.2018.10018889
Han, Y., Li, Q., Wang, F., Wang, B. Y., Mizuno, K., and Zhou, Q. (2019). Analysis of pedestrian kinematics and ground impact in traffic accidents using video records. Int. J. Crashworthiness 24, 211–220. doi: 10.1080/13588265.2018.1429520
Han, Y., Yang, J. K., Nishimoto, K., Mizuno, K., Matsui, Y., Nakane, D., et al. (2012). Finite element analysis of kinematic behaviour and injuries to pedestrians in vehicle collisions. Int. J. Crashworthiness 17, 141–152. doi: 10.1080/13588265.2011.632243
Hardy, W., Foster, C., Mason, M., Yang, K., King, A., and Tashman, S. (2001). Investigation of head injury mechanisms using neutral density technology and high-speed biplanar X-ray. Stapp Car Crash J. 45, 337–368.
Hardy, W., Mason, M., Foster, C., Shah, C. S., Kopacz, J., Yang, K., et al. (2007). A study of the response of the human cadaver head to impact. Stapp Car Crash J. 51, 17–80.
Hertz, E. (1993). “A note on the head injury criterion (HIC) as a predictor of the risk of skull fracture,” in Proceedings of the Association for the Advancement of Automotive Medicine Annual Conference (San Antonio, TX: AAAM).
Huang, Y., Zhou, Q., Koelper, C., Li, Q., and Nie, B. (2020). Are riders of electric two-wheelers safer than bicyclists in collisions with motor vehicles? Accid Anal. Prev. 134, 105336. doi: 10.1016/j.aap.2019.105336
Kang, H. S., Willinger, R., Diaw, B. M., and Chinn, B. (1997). Validation of a 3D Anatomic Human Head Model And Replication Of Head Impact In Motorcycle Accident By Finite Element Modeling. Warrendale, PA: SAE Transactions, 3849–3858.
Kimpara, H., and Iwamoto, M. (2012). Mild traumatic brain injury predictors based on angular accelerations during impacts. Ann. Biomed. Eng. 40, 114–126. doi: 10.1007/s10439-011-0414-2
Kleiven, S. (2007). Predictors for traumatic brain injuries evaluated through accident reconstructions. Stapp Car Crash J. 51, 81–114.
Kleiven, S., and Holst, H. (2001). “Consequences of brain size following impact in prediction of subdural hematoma evaluated with numerical techniques,” in Proceedings of the International IRCOBI Conference (Isle of Mann: IRCOBI).
Maki, T., and Kajzer, J. (2000). The behavior of bicyclists in frontal and rear crash accidents with cars. JSAE Rev. 22, 357–363. doi: 10.1016/s0389-4304(01)00112-6
Margulies, S. S., and Thibault, L. (1992). A proposed tolerance criterion for diffuse axonal injury in man. J. Biomech. 25, 917–923. doi: 10.1016/0021-9290(92)90231-o
Marjoux, D., Baumgartner, D., Deck, C., and Willinger, R. (2008). Head injury prediction capability of the hic, hip, simon and ulp criteria. Accid. Anal. Prev. 40, 1135–1148. doi: 10.1016/j.aap.2007.12.006
Martinez, L., Guerra, L., Ferichola, G., Garcia, A., and Yang, J. K. (2007). “Stiffness corridors of the european fleet for pedestrian simulations,” in Proceedings of the 20th International Technical Conference on the Enhanced Safety of Vehicles (ESV) (Washington, DC: National Highway Traffic Safety Administration.NHTSA).
McLundie, W. (2007). Investigation of Two-Wheeled Road Traffic Accidents Using Explicit FE Techniques. PhD’s thesis. Bedford: Cranfield university.
Melvin, J., and Lighthall, J. W. (2002). “Brain-injury biomechanics,” in Accidental Injury, eds A. M. Nahum and J. W. Melvin (New York, NY: Springer), 277–302. doi: 10.1007/978-0-387-21787-1_13
Mertz, H., Motors, G., and Nushdh, G. (1996). Head Injury Risk Assessment for Forehead Impacts. SAE Technical Papers. 960099. Warrendale, PA: SAE.
Nahum, A., Smith, R., and Ward, C. (1977). Intracranial Pressure Dynamics During Head Impact. SAE Technical Paper. 770922. Warrendale, PA: SAE.
National Highway Traffic Safety Administration (NHTSA) (1972). Occupant Crash Protection-Head Injury Criterion. (S6. 2 of FMVSS 571.208). Washington, DC: National Highway Traffic Safety Administration.
National Highway Traffic Safety Administration (NHTSA) (1995). Final Economic Assessment, FMVSS No. 201, Upper Interior Head Protection. Office of Regulatory Analysis, Plans and Policy. Washington DC: National Highway Traffic Safety Administration.
Newman, J. (1980). Head Injury Criteria In Automotive Crash Testing. Warrendale, PA: SAE Transactions, 4098–4115.
Newman, J. (1986). “A generalized acceleration model for brain injury threshold (GAMBIT),” in Proceedings of the International IRCOBI Conference (Isle of Mann: IRCOBI).
Newman, J., and Shewchenko, N. (2000). A proposed new biomechanical head injury assessment function-the maximum power index. Stapp Car Crash J. 44, 215–247.
Nie, J., and Yang, J. K. (2014). A study of bicyclist kinematics and injuries based on reconstruction of passenger car–bicycle accident in China. Acci. Anal. Prev. 71, 50–59. doi: 10.1016/j.aap.2014.04.021
Normalisation CED (2011). Head and Neck Impact, Burn And Noise Injury Criteria—A Guide For Cen Helmet Standards Committees. CEN/TR 16148. Brussels: Comite Europeen de Normalisation.
Nusholtz, G. S., Lux, P., Kaiker, P., and Janicki, M. A. (1984). Head impact response-skull deformation and angular accelerations. SAE Technical Paper. doi: 10.4271/841657
Nusholtz, G. S., Wylie, B., and Glascoe, L. G. (1995). Cavitation/boundary effects in a simple head impact model. Aviat. Space Environ. Med. 66, 661–667.
Ommaya, A. K. (1985). “Biomechanics of head injury: experimental aspects,” in The Biomechanics of Trauma (Norwalk, CT: Appleton & Lange), 245–258.
Ono, K., Kikuchi, A., Nakamura, M., Kabayashi, H., and Nakamura, N. (1980). Human Head Tolerance To Sagittal Impact: Reliable Estimation Deduced From Experimental Head Injury Using Primates And Human Cadaver Skulls, SAE Technical Paper, No: 801303. Warrendale, PA: SAE.
Pascoletti, G., Catelani, D., Conti, P., Cianetti, F., and Zanetti, E. M. (2019a). A multibody simulation of a human fall: model creation and validation. Procedia Struct. Integr. 24, 337–348. doi: 10.1016/j.prostr.2020.02.031
Pascoletti, G., Catelani, D., Conti, P., Cianetti, F., and Zanetti, E. M. (2019b). Multibody models for the analysis of a fall from height: accident, suicide, or murder? Front. Bioeng. Biotechnol. 7:419. doi: 10.3389/fbioe.2019.00419
Patton, D., McIntosh, A., Kleiven, S., and Frechede, B. (2012). Injury data from unhelmeted football head impacts evaluated against critical strain tolerance curves. J. Sports Eng. Technol. 226, 177–186. doi: 10.1177/1754337112438305
Peng, Y., Chen, Y., Yang, J. K., Otte, D., and Willinger, R. (2012). A study of pedestrian and bicyclist exposure to head injury in passenger car collisions based on accident data and simulations. Saf. Sci. 50, 1749–1759. doi: 10.1016/j.ssci.2012.03.005
Pincemaille, Y., Trosseille, X., Mack, P., Tarrière, C., Breton, F., and Renault, B. (1989). Some New Data Related To Human Tolerance Obtained From Volunteer Boxers. SAE Technical Paper, No: 892435. Warrendale, PA: SAE.
Richards, D., and Carroll, J. (2012). Relationship between types of head injury and age of pedestrian. Acci. Anal. Prev. 47, 16–23. doi: 10.1016/j.aap.2012.01.009
Rowson, S., Duma, S. M., Beckwith, J. G., Chu, J. J., Greenwald, R. M., Crisco, J. J., et al. (2012). Rotational head kinematics in football impacts: an injury risk function for concussion. Ann. Biomed. Eng. 40, 1–13. doi: 10.1007/s10439-011-0392-4
Sahoo, D., Deck, C., and Willinger, R. (2016). Brain injury tolerance limit based on computation of axonal strain. Acci. Anal. Prev. 92, 53–70. doi: 10.1016/j.aap.2016.03.013
Shi, L., Han, Y., Huang, H., He, W., Wang, F., and Wang, B. Y. (2019). Effects of vehicle front-end safety countermeasures on pedestrian head injury risk during ground impact. Proc. Instit. Mech. Eng. D J. Automob. Eng. 233, 0954407019828845. doi: 10.1177/0954407019828845
Shi, L., Han, Y., Huang, H., Li, Q., Wang, B., and Mizuno, K. (2018). Analysis of pedestrian-to-ground impact injury risk in vehicle-to-pedestrian collisions based on rotation angles. J. Saf. Res. 64, 37–47. doi: 10.1016/j.jsr.2017.12.004
Shi, L., Han, Y., Huang, H. W., Davidsson, J., and Thomson, R. (2020). Evaluation of injury thresholds for predicting severe head injuries in vulnerable road users resulting from ground impact via detailed accident reconstructions. Biomech. Model. Mechanobiol. 19, 1845–1863. doi: 10.1007/s10237-020-01312-9
TABC (2017). Statistics of Road Traffic Accidents in PR of China. Chongqing: Traffic Administration Bureau of China.
Takhounts, E., Craig, M., Moorhouse, K., Mcfadden, J., and Hasija, V. (2013). Development of brain injury criteria (BrIC). Stapp Car Crash J. 57, 243–266.
Takhounts, E., Eppinger, R., Campbell, J., Tannous, R., Power, E., and Shoo, L. (2003). On the development of the simon finite element head model. Stapp Car Crash J. 47, 107–133.
Takhounts, E., Hasija, V., Ridella, S., Rowson, S., and Duma, S. (2011). “Kinematic rotational brain injury criterion (BRIC),” in Proceedings of the 22nd Enhanced Safety Of Vehicles (ESV) Conference (Washington, DC: ESV).
Tamura, A., Koide, T., and Yang, K. H. (2014). Effects of ground impact on traumatic brain injury in a fender vault pedestrian crash. Int J Veh Saf 8, 85–100. doi: 10.1504/ijvs.2015.066278
Thibault, L., Gennarelli, T., Margulies, S., Marcus, J., and Eppinger, R. (1990). “The strain dependent pathophysiological consequences of inertial loading on central nervous system tissue,” in Proceedings of the International Conference on the Biomechanics of Impacts (IRCOBI) (Bron), IRCOBI. doi: 10.4103/2468-5690.191932
Unterharnscheidt, F. (1971). Translational Versus Rotational Acceleration: Animal Experiments With Measured Input. SAE Technical Paper, No: 710880. Warrendale, PA: SAE.
Versace, J. (1971). A Review Of The Severity Index. SAE Technical Paper, No: 710881. Warrendale, PA: SAE.
Ward, C., Chan, M., and Nahum, A. (1980). Intracranial Pressure-A Brain Injury Criterion. SAE Technical Paper, No: 801304. Warrendale, PA: SAE.
Willinger, R., and Baumgartner, D. (2003). Human head tolerance limits to specific injury mechanisms. Int. J. Crashworthiness 8, 605–617. doi: 10.1533/ijcr.2003.0264
World Health Organization (2018). Global Status Report On Road Safety 2018. Geneva: World Health Organization.
Wu, H., Han, Y., Shi, L., and Xu, W. (2020). Research on high-precision accident reconstruction method based on video information. Automot. Eng. 42, 74–79+88.
Yang, J. K., Lövsund, P., Cavallero, C., and Bonnoit, J. (2000). A human-body 3d mathematical model for simulation of car-pedestrian impacts. J. Crash Prev. Inj. Control 2, 131–149. doi: 10.1080/10286580008902559
Yao, J. F., Yang, J. K., and Otte, D. (2008). Investigation of head injuries by reconstructions of real-world vehicle-versus-adult-pedestrian accidents. Saf. Sci. 46, 1103–1114. doi: 10.1016/j.ssci.2007.06.021
Young, J. K. (1997). “Development and validation of a human-body mathematical model for simulation of car-pedestrian collisions,” in Proceedings of the International Conference on the Biomechanics of Impacts (IRCOBI) (Isle of Mann: IRCOBI).
Keywords: the elderly, accident reconstruction, video information, head injury criteria, vulnerable road user
Citation: Wu H, Han Y, Pan D, Wang B, Huang H, Mizuno K and Thomson R (2021) The Head AIS 4+ Injury Thresholds for the Elderly Vulnerable Road User Based on Detailed Accident Reconstructions. Front. Bioeng. Biotechnol. 9:682015. doi: 10.3389/fbioe.2021.682015
Received: 17 March 2021; Accepted: 26 May 2021;
Published: 23 June 2021.
Edited by:
Francisco J. Lopez-Valdes, Comillas Pontifical University, SpainReviewed by:
Elisabetta M. Zanetti, University of Perugia, ItalyDeclan A. Patton, Children’s Hospital of Philadelphia, United States
Jalaj Maheshwari, Center for Injury Research and Prevention, The Children’s Hospital of Philadelphia, United States, in collaboration with reviewer DP
Copyright © 2021 Wu, Han, Pan, Wang, Huang, Mizuno and Thomson. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yong Han, eW9uZ2hhbkB4bXV0LmVkdS5jbg==
 He Wu
He Wu Yong Han
Yong Han Di Pan
Di Pan Bingyu Wang
Bingyu Wang Hongwu Huang
Hongwu Huang Koji Mizuno
Koji Mizuno Robert Thomson
Robert Thomson