Carbon Acidity in Enzyme Active Sites

Mechanistic enzymologists have made great strides over the past decades in deciphering the fundamental principles of enzyme catalysis. Nevertheless, a quantitative accounting of the contributions to rate enhancement has not yet been achieved (Machleder et al., 2010; Wolfenden, 2011; Herschlag and Natarajan, 2013; Richard, 2013; Warshel and Bora, 2016). One of the most fundamental catalytic mechanisms available to enzymes is general acid/base catalysis by amino acid side chains in active sites (Jencks, 1987; Richard, 1998; Frey and Hegeman, 2007). Deprotonation of carbon acids (C-H bonds of substrates) is an especially important and difficult reaction requiring base catalysis (Richard and Amyes, 2001; Richard, 2012). Enzymologists have measured the pK_a values of many active site catalytic residues through pH-rate profiles (Cook and Cleland, 2007), and these can frequently be assigned to specific residues in combination with additional information, but substrate C-H pK_a values have remained elusive.

Many enzymatic reactions involve deprotonation of carbon as a central step in the catalytic mechanism, yet there are no examples in the literature where the pK_a of a substrate C-H has been established experimentally. The closest example known to this author is that of uridine monophosphate bound to orotidine monophosphate decarboxylase (Amyes et al., 2008). In that work, the authors estimated the pK_a of the product (≤22) by isotope exchange kinetics, which generates via deprotonation the same vinyl carbanion resulting from decarboxylation. It is generally appreciated that enzymes must substantially lower pK_as of carbon acids at active sites to achieve observed rate enhancements (Gerlt et al., 1991; Gerlt and Gassman, 1992, 1993a,b; Richard et al., 2014). A full understanding of the thermodynamics, including the pK_a values for both the general acid/base catalyst and the substrate C-H bond is needed to account quantitatively for enzyme catalysis.

Here, a recently introduced method for free energy profile (FEP) determination (Toney, 2013) is applied to five enzymes, employing experimental data reported in the literature. The FEPs allow calculation of proton transfer equilibrium constants in active sites. Additionally, literature FEPs and spectroscopic information are used to calculate proton transfer equilibrium constants for six additional enzymes. Combining proton transfer equilibrium constants with pK_as for catalytic active site residues allows one to solve for active site-bound substrate C-H pK_as, which are in the range ~6 to ~16 for the enzymes discussed here.

Methods

Here, FEP determination involves optimizing the agreement between several calculated and observed experimental measurements simultaneously. The freely available biochemical simulation and analysis software COPASI was used for all optimizations (Hoops et al., 2006; Mendes et al., 2009). The procedure used here does not involve time-consuming numerical integration of differential rate equations. Instead, the adjustable parameters (rate constants) are altered by the chosen algorithm and the new parameters are used to calculated a new value of the target function (see below) (Toney, 2013). This is much less computationally demanding than fitting to primary kinetic data via numerical integration, allowing essentially exhaustive exploration of parameter space. Global optimization algorithms fall into four main categories: random, deterministic, stochastic (e.g., simulated annealing), and heuristic (e.g., genetic algorithms, swarm algorithms) (Moles et al., 2003). COPASI implements examples of all these categories. The COPASI input files used here for FEP determinations are included in the Supplementary Material.

A critical step to defining enzymatic FEPs by global optimization is the specification of the target function to be minimized. A sum-of-squared absolute values of residuals between calculated and experimental values, divided by the experimental value, was used. Equation (1) shows the target function used for alanine racemase.

$\begin{array}{l}SSR={\left|\frac{k_L^{calc}-k_L^{expt}}{k_L^{expt}}\right|}^2+{\left|\frac{k_D^{calc}-k_D^{expt}}{k_D^{expt}}\right|}^2+{\left|\frac{K_L^{calc}-K_L^{expt}}{K_L^{expt}}\right|}^2\\ +{\left|\frac{K_D^{calc}-K_D^{expt}}{K_D^{expt}}\right|}^2+{\left|\frac{Vis{c}^{calc}-Vis{c}^{expt}}{Vis{c}^{expt}}\right|}^2+etc.& (1)\end{array}$

Here, k_L is k_cat for the L → D direction, K_L is K_M for the L → D direction, “Visc” is the effect of viscosity on relative k_cat/K_M values, etc. Central to the procedure, random initial values for all parameters were assigned automatically by COPASI at the beginning of each individual optimization run. The use of the mean normalized difference between calculated and observed values weights the different experimental measurements equally. This is essentially a sum of chi-squared statistics (Greenwood and Nikulin, 1996). It is analogous to the commonly used relative weighting scheme in non-linear regression (Motulsky and Christopoulos, 2004).

Microscopic rate constants and intrinsic kinetic isotope effects (KIEs) (where applicable) were adjustable parameters. For bimolecular rate constants, the lower bound was k_cat/K_M for the respective direction, and the upper bound was 10⁹ M⁻¹s⁻¹ (diffusion limit). For unimolecular constants, the lower bound was k_cat for the respective direction, and the upper bound was 10¹² s⁻¹ (vibrational limit). The values of intrinsic deuterium KIEs were limited to the semi-classical range of 1–6. The application of these limits is important for restricting the parameter space searched to a productive one.

The search of parameter space was performed in two phases. First, a broad search over the rate constant limits given above was performed using the “genetic algorithm” in COPASI. Second, a focused search was performed to define well the sum of squared residuals (SSR) surface at the lower SSR values: narrower limits on each parameter (corresponding to a 50-fold increase in SSR from the lowest values obtained in the first search) were set. The latter employed the “particle swarm” algorithm in COPASI. A complete search was comprised of 10⁵-10⁶ independent calculations. Each calculation started with random initial values for the parameters, within the specified limits. This was automated using the “parameter scan” task in COPASI.

Results and Discussion

The calculation of C-H pK_a values in enzymes active sites reported here employs the relationship between reactant and product pK_a values for a simple proton transfer reaction:

$\begin{array}{cc}p{K}_{eq}=p{K}_a^{reactant}-p{K}_a^{product}& (2)\end{array}$

The equilibrium constant (pK_eq) for the proton transfer between a carbon acid and an acid/base catalyst in the active site and the pK_a of the product must be known to solve for the reactant (C-H) pK_a. For general base catalysis by an active site amino acid side chain, the pK_a of the product is the pK_a of the protonated form of the side chain in the enzyme-substrate complex, which is readily obtained from k_cat vs. pH profiles: k_cat/K_M vs. pH profiles provide pK_a values for free enzyme and free substrate, while k_cat vs. pH profile provides pK_a values for enzyme-substrate complexes. The latter are relevant to the calculation of substrate C-H pK_as in active sites and are used here.

The equilibrium constant is generally more difficult to obtain. The simplest method, but applicable only to select classes of enzymes, is to use spectroscopic information (e.g., absorbance and extinction coefficient) that is specific to the carbanionic intermediate to calculate the equilibrium constant. Pyridoxal phosphate (PLP) dependent enzymes constitute an especially favorable case since the highly resonance stabilized carbanionic “quinonoid” intermediate has long wavelength absorption bands (~500 nm) with high a extinction coefficient (~40,000 M⁻¹cm⁻¹) that allow it to be readily identified and quantified (Metzler et al., 1988; Mozzarelli et al., 2000).

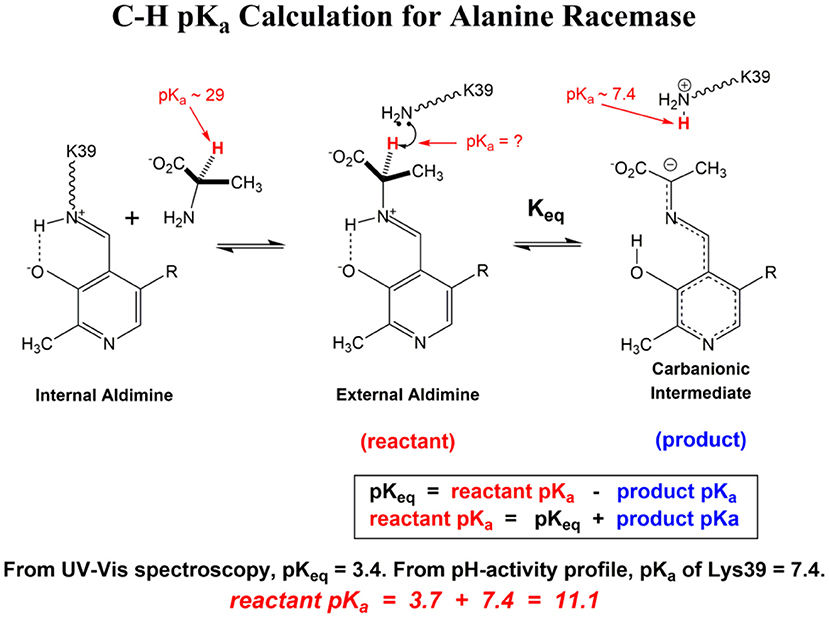
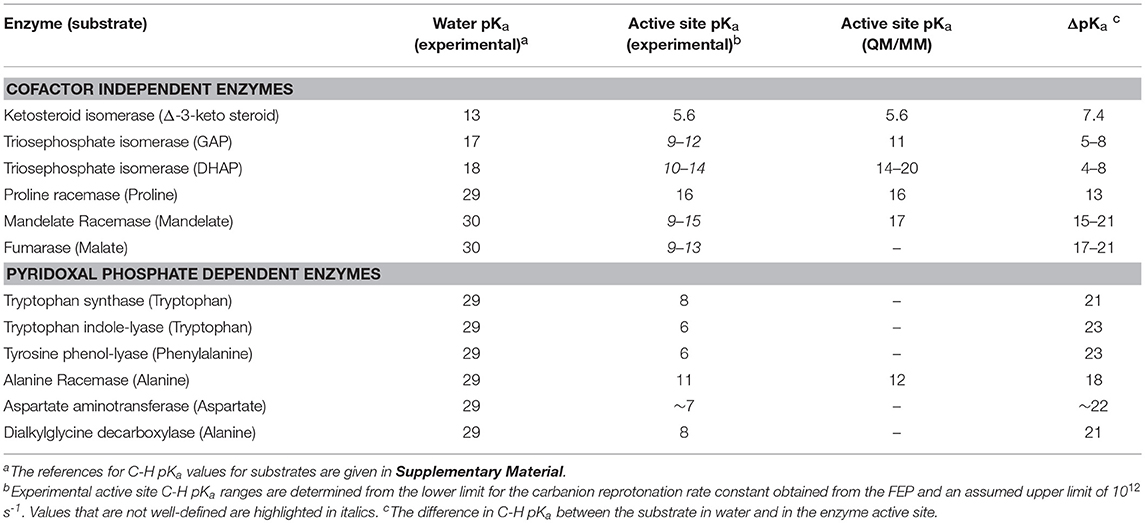
Scheme 1 Illustrates the calculation of the C-H pK_a for alanine bound to alanine racemase (AR) based on spectroscopic information. From published pH profiles for k_cat, one can deduce a pK_a of 7.4 for Lys39 in the substrate-bound active site (Sun and Toney, 1999). From UV-vis spectroscopy of AR saturated with alanine, one can calculate pK_eq = 3.4 for proton transfer based on the 500 nm absorption band of the carbanionic quinonoid intermediate (Toney, 2013). Thus, the external aldimine C-H pK_a = 3.7 + 7.4 = 11.1. The C-H pK_a values of 12 active site-bound substrates are presented in Table 1, along with the corresponding pK_as in water, the difference in pK_a for free vs. active site bound substrates, and pK_as calculated via QM/MM simulations where available.

SCHEME 1

Scheme 1. C-H pK calculation for Alanine Racemase.

TABLE 1

Table 1. Carbon Acid (Substrate C-H) pK_a values.

A general method for evaluating the proton transfer equilibrium constant is to calculate a FEP for the complete enzyme catalyzed reaction, then take the ratio of the deprotonation to reprotonation rate constants as the proton transfer equilibrium constant. Historically, the determination of FEPs for enzymes was a laborious process requiring a variety of enzyme-specific experiments, generally including pre-steady-state kinetic measurements. Recently, this author showed that enzymatic FEPs are readily obtained by combining the information obtained from a variety of commonly employed enzyme kinetic experiments (Toney, 2013). The types of information combined include, for example, k_cat and K_M, KIEs, viscosity effects, washout vs. turnover ratios, etc. The key is that these different experimental measurements provide information on various components of the reaction sequence constituting the enzymatic mechanism. The experimental data are combined in a target function for global optimization, in which the individual rate constants for the enzymatic mechanism are optimized via a minimization algorithm (e.g., genetic algorithm, particle swarm, Hooke, and Jeeves, etc.) to achieve best-fit agreement between calculated and experimental observations.

This method was employed here to calculate five new enzymatic FEPs. All FEPs were calculated with COPASI (Hoops et al., 2006; Mendes et al., 2009). The COPASI input files used here are provided separately as Supplementary Material. The general mechanism used for the analysis of all the enzymes considered here is:

$\begin{array}{cc}E+S\underset{k2}{\overset{k1}{\rightleftharpoons }}ES\underset{k4}{\overset{k3}{\rightleftharpoons }}EI\underset{k6}{\overset{k5}{\rightleftharpoons }}EP\underset{k8}{\overset{k7}{\rightleftharpoons }}E+P& (3)\end{array}$

Ketosteroid Isomerase (3-Oxo-Δ5-Steroid Isomerase) FEP

Pollack et al. extensively studied the reaction catalyzed by ketosteroid isomerase (KSI). Their work resulted in a nearly complete FEP calculated from a variety of different experiments (Hawkinson et al., 1991). They were unable to define a precise value for the energy of the enolate (enol) intermediate, only a lower limit. Therefore, FEP calculations to define these values was undertaken using global optimization. The experimental data employed included k_cat and K_M values for the forward reaction, the partitioning ratio for the intermediate going backward to substrate vs. forward to product, KIEs, the equilibrium constant for the reaction, the product dissociation constant, and two rate constant ratios (k₁₋/k₂, and k₋₂/k₃). The details of FEP calculations are provided in Supplementary Material.

Figure 1 shows the results of global optimization with KSI. The graph presents the sum-of-squared residuals (SSR), which is a measure of the goodness-of-fit to experimental data for a series of independent optimization runs, plotted against the fitted values of the rate constants. Each independent global optimization run results in a set of parameters (rate constants, KIE) with a common SSR value (identical y-axis value). The lower the value of the SSR, the better the optimized rate constants predict the experimental results.

FIGURE 1

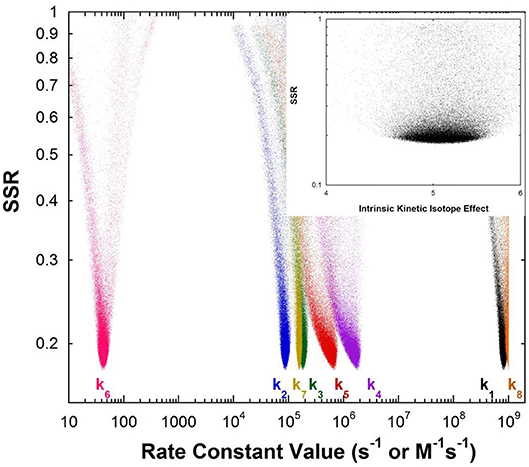
Figure 1. Results of global optimization with KSI. SSR, sum of squared residuals of the fit to the target function. Each point results from an independent optimization run. The figure was generated from ~100,000 independent runs, each starting from randomized sets of rate constants. The inset presents the intrinsic KIE resulting from global optimization.

Fundamentally, the graph shows how sensitive the goodness-of-fit is to the values of the fitted parameters (i.e., rate constants and intrinsic KIEs): rate constants with narrower SSR “peaks” at the bottom of the distributions are better defined. For example, the inset shows the SSR vs. the value of the intrinsic KIE on the deprotonation step. The lowest values of SSR occur at an intrinsic KIE of ~5, but the wide distribution shows that the fit to the experimental data is not very sensitive to the value of this parameter, and it is therefore not well-defined. On the other hand, k₇ has a narrow SSR “peak” and its value is well-defined.

Each independent optimization run generates 8 rate constants and the intrinsic KIE (if KIE measurements are included). Crucially, ~100,000 independent optimization runs are presented in the graph, each starting from a set of random initial rate constant values (within reasonable chemical limits: >k_cat/K_M and < 10⁹ M⁻¹s⁻¹ for second order rate constants, and >k_cat and < 10¹² s⁻¹ for first order rate constants), constituting an essentially exhaustive search of rate constant space. The randomization of the initial guesses for the rate constants combined with the user-specified global optimization termination conditions provide the distribution of values that allow the “SSR surface” to be defined (i.e., not all fits advance to the absolute SSR minimum).

The resulting rate constant values for KSI are: k₁ = 8.3 × 10⁸ M⁻¹s⁻¹, k₂ = 8.6 × 10⁴ s⁻¹, k₃ = 1.8 × 10⁵ s⁻¹, k₄ = 1.7 × 10⁶ s⁻¹, k₅ = 6.4 × 10⁵ s⁻¹, k₆ = 43 s⁻¹, k₇ = 1.5 × 10⁵ s⁻¹, k₈ = 1 × 10⁹ M⁻¹s⁻¹. These agree well with those reported by Pollack et al, and show that global optimization can additionally define the rate constants for carbanion reprotonation (k₄ and k₅) that were previously not well-defined. The equilibrium constant for proton transfer (K_eq) calculated from k₃ and k₄ is 0.11. This is in agreement with the previously calculated value of 0.3 ± 0.2 (Hawkinson et al., 1994).

The value of pK_eq for the reaction of 5-androstene-3,17-dione is 0.96 while that for 4-androstene-3,17-dione is 4.2. These values correspond to ΔG₀ for proton transfer of 1.3 and 5.7 kcal/mol. They can be combined with the pK_a (4.6) of the general acid/base catalyst in the active site (Asp38) to give calculated active site C-H pK_a values of 5.6 for 5-androstene-3,17-dione and 8.8 for 4-androstene-3,17-dione. The pK_a of 5-androstene-3,17-dione in solution is 12.7 (Pollack et al., 1989).

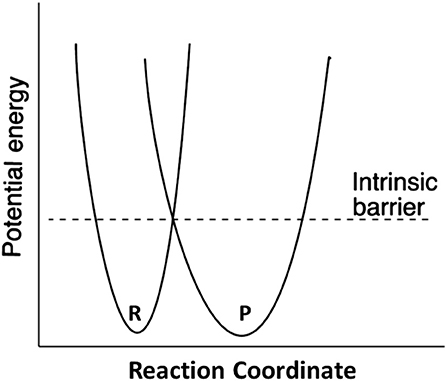
Marcus theory for electron transfer has been extended to a variety of other reactions including proton transfers and enzymatic reactions (Silverman, 2000; Bearne and Spiteri, 2005). In its simplest form, the theory describes a reaction in terms of an intrinsic reaction barrier (Scheme 2), which is the barrier for the reaction when ΔG⁰ = 0 (kinetic component), and the difference in free energy between reactants and products (thermodynamic component). The theory has been extended to include work terms to describe the energy required to bring reactants together into the reactive ground state complex; this term is ignored here since enzymes form the reactive complex in a separate substrate binding step (i.e., substrate binding energy pays for the work required to form the reactive complex), and the calculations for the non-enzymatic reactions correct the measured second order rate constants for reactive complex formation by using an association constant of 0.017 M⁻¹ estimated by Hine and commonly employed in the literature (Hine, 1971). The form of the Marcus equation used here is given in Equation (4), where ΔG^‡ is the observed free energy of activation, ΔG⁰ is the energy difference between reactants and products, and Δ${\text{G}}_0^{\text{‡}}$ is the intrinsic reaction barrier.

$\begin{array}{cc}\Delta G^{‡}={(1+\Delta G^o/4\Delta G_o^{‡})}^2\Delta G_o^{‡}& (4)\end{array}$

SCHEME 2

Scheme 2. Definition of the Marcus intrinsic barrier.

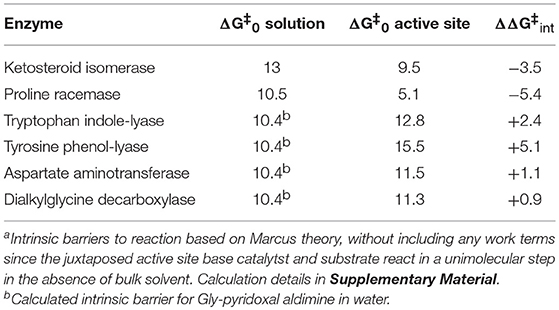
The Δ${\text{G}}_0^{\text{‡}}$ values for proton abstraction in ketosteroid isomerization were previously estimated to be 10 kcal/mol for the enzymatic reaction and 13 kcal/mol for the reaction in solution (Hawkinson et al., 1994). The rate constant values derived here from global optimization allow calculation of Δ${\text{G}}_0^{\text{‡}}$ = 9.5 kcal/mol for the enzymatic reaction (Table 2), in agreement with the previously calculated value.

TABLE 2

Table 2. Marcus intrinsic barriers (kcal/mol)^a.

Mandelate Racemase (MR) FEP

Multiple KIE experiments provide good evidence for a carbanionic intermediate in mandelate racemase catalysis (Mitra et al., 1995), as does the partitioning of an alternative substrate between racemization and bromide elimination (Lin et al., 1988). This justifies the use of the mechanism in Equation (2) with MR. The FEP for MR was determined by combining k_cat and K_M for both directions of racemization with viscosity effects, KIEs, and intermediate partitioning (Whitman et al., 1985; Powers et al., 1991; St Maurice and Bearne, 2002). The global optimization results are presented in Figure 2. The pK_a of the active site acid/base catalyst is 6.4 (Kallarakal et al., 1995). From the results presented in Figure 2, the rate constant for deprotonation of (S)-mandelate in the active site (k₃) is 800 s⁻¹ while the reprotonation rate constant (k₄) is in the range of 10⁵ and 10¹² s⁻¹. These values translate into a C-H pK_a range of 8.5–15.5, reported as 9–15 in Table 1. The reverse isomerization reaction occurs with a deprotonation rate constant (k₆) of 3,300 s⁻¹, while reprotonation (k₅) is in the range of 10⁶-10¹² s⁻¹. These values correspond to C-H pK_a values of 9–15.

FIGURE 2

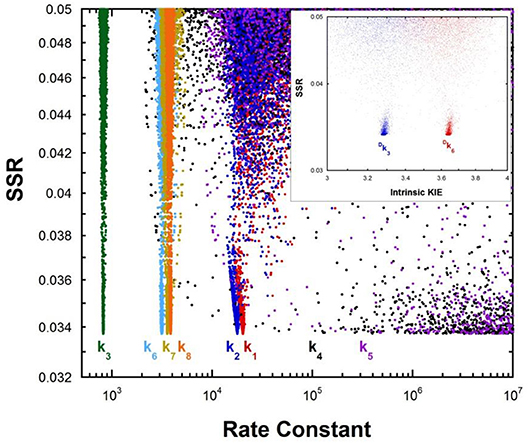
Figure 2. Results of global optimization with mandelate racemase. SSR, sum of squared residuals of the fit to the target function. Each point results from an independent optimization run. The figure was generated from ~40,000 independent runs, each starting from randomized sets of rate constants. The inset presents the intrinsic kinetic isotope effect resulting from global optimization. The fit to the target function is shows significant sensitivity to the values of k₄ and k₅ when they are < 10⁶ s⁻¹. Therefore, these are the lower limits on the values of these rate constants.

The C-H pK_a of mandelate (monoanion) in water is calculated by assuming the rate constants for deprotonation catalyzed by hydronium and hydroxide ions are equal at pH 7 and 25°C, given the pH independence of the reaction rate in this region (Bearne and Wolfenden, 1997). The rate constant for proton exchange at pH 7 and 25°C is 3 × 10⁻¹³ s⁻¹, or 1.5 × 10⁻¹³ s⁻¹ for the hydroxide catalyzed component. This value, divided by the concentration of hydroxide at pH 7, gives a rate constant of 1.5 × 10⁻⁶ M⁻¹s⁻¹, which can be used with the correlation between log(k_OH) and carbon acid pK_a presented by Richard (Richard et al., 2001) to give an estimated solution C-H pK_a of 30 for mandelate. This value is in agreement with others estimated in the literature (Gerlt et al., 1991). It can be compared to the C-H pK_a of 22 for mandelic acid (Chiang et al., 1990).

Fumarase FEP

The fumarase FEP for pH 7 was calculated by global optimization, employing k_cat and K_M for both directions of the reaction, viscosity effects, the equilibrium constant, and rate constant ratios and commitments to catalysis determined by KIE analyses (Alberty and Peirce, 1957; Brant et al., 1963; Blanchard and Cleland, 1980; Sweet and Blanchard, 1990). The global optimization results are presented in Figure 3. The rate constant for deprotonation of malate in the active site (k₃) is 1.1 × 10⁵ s⁻¹, while the reprotonation rate constant (k₄) is 10⁷-10¹² s⁻¹. These values allow calculation of a C-H pK_a of 8.5–13 in the active site (reported as 9–13 in Table 2), given the active site acid/base catalyst pK_a of 6.4 (Brant et al., 1963).

FIGURE 3

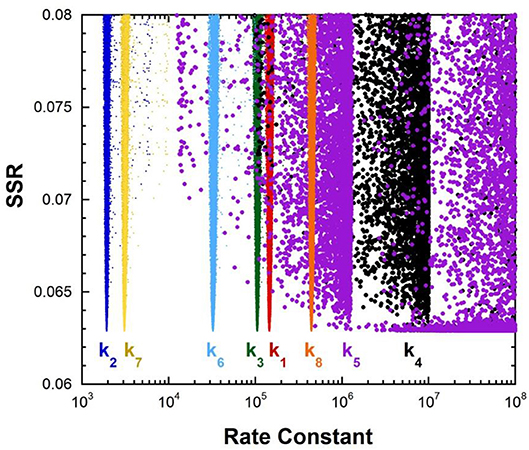
Figure 3. Results of global optimization with fumarase. SSR, sum of squared residuals of the fit to the target function. The figure was generated from ~40,000 independent runs, each starting from randomized sets of rate constants. The fit to the target function is shows significant sensitivity to the values of k₄ and k₅ when they are < 10⁷ s⁻¹ and < 10⁸ s⁻¹. Therefore, these are the lower limits on the values of these rate constants.

Aspartate Aminotransferase FEP

Previous studies with aspartate aminotransferase defined rate constants for a mechanism in which the central 1,3-prototropic shift occurs as a concerted double proton transfer, avoiding the carbanionic quinonoid intermediate (Goldberg and Kirsch, 1996). A more recent study proved the existence of the quinonoid intermediate on the productive pathway (Hill et al., 2010). Therefore, a FEP including the quinonoid intermediate on the reaction pathway was determined by global optimization. Only the aspartate/oxalacetate half-reaction was analyzed. The experimental observations used in global optimization included pre-steady-state k_max and K_app from stopped-flow experiments, KIEs, viscosity dependence, intermediate partitioning (i.e., isotopic washout vs. turnover), the equilibrium constant, and the absorbance of the quinonoid intermediate, which were used in the previous study on the concerted mechanism. The results are presented in Figure 4.

FIGURE 4

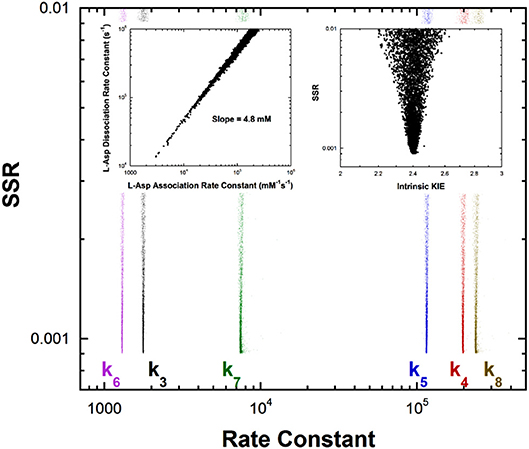
Figure 4. Results of global optimization for the L-asp/oxalacetate half-reaction of aspartate aminotransferase. SSR, sum of squared residuals of the fit to the target function. The figure was generated from ~40,000 independent runs, each starting from randomized sets of rate constants. The insets show that the correlation between the association and dissociation rate constants for L-Asp binding. The individual rate constants are not well-determined, but their ratio is over a broad range of values, indicating rapid equilibrium binding. The observed ratio of the rate constants is 4.8mM, which is the K_M value for L-Asp. The intrinsic KIE calculated in the global optimization is also presented as an inset.

The left inset to Figure 4 presents the correlation between the L-Asp association rate constant (k₁) and the dissociation rate constant (k₂). These composite rate constants include the steps leading from the free enzyme and free substrate up to and including external aldimine intermediate formation via transimination. The tight correlation between the rate constants, as well as the large value of k₂ compared to k₃, demonstrates that these steps are essentially at equilibrium with respect to the remainder of the half-reaction. The slope of the line (i.e., calculated equilibrium binding constant) is 4.8 mM, which is equal to the experimental K_app in stopped-flow analyses.

The remaining rate constants (k₃-k₈) in the mechanism are very well-defined by global analysis. The rate constant for external aldimine deprotonation is 1,800 s⁻¹, while reprotonation occurs at 200,000 s⁻¹. The value of pK_eq calculated from these rate constants is 2.0, close to the value of 2.3 calculated from UV-vis spectral data (Goldberg and Kirsch, 1996). The pK_a of the active site acid/base catalyst (Lys258) is taken here to be ~5.5, which is the value observed in the pH profile for k_cat with mutant enzymes (Y225F and K258C-EA) (Gloss and Kirsch, 1995). The value of k_cat for wild type and L-Asp shows pH dependence but the activity does not go to zero below the acidic pK_a, making it unlikely that this ionization is that of Lys258, which is critical to catalysis (Toney and Kirsch, 1993). The combination of pK_eq = 2 and pK_a = ~5.5 gives an active site C-H pK_a for the external aldimine of 7.5, which is reported as ~7 in Table 1 due to the uncertainty in the pK_a of Lys258.

The FEP also allows calculation of the C-H pK_a for the C4′-H bond of the oxaloacetate ketimine intermediate. The pK_eq for C4′ deprotonation is calculated from the deprotonation rate constant of 1,300 s⁻¹ and the reprotonation rate constant of 115,000 s⁻¹ to be 2.0. Combined with the pK_a of ~5.5 for Lys258 this give a C4′-H pK_a of ~7.5 in the active site.

For enzymatic deprotonation of the external aldimine intermediate, ΔG^‡ = 12.9 kcal/mol and ΔG₀ = 2.7 kcal/mol for proton transfer. These values give Δ${\text{G}}_0^{\text{‡}}$ = 11.5 kcal/mol (Table 2).

Dialkylglycine Decarboxylase FEP

This unusual PLP enzyme catalyzes the oxidative decarboxylation of 2,2-dialkylglycines in the first half-reaction of a ping-pong mechanism and the transamination of pyruvate to L-alanine in the second (Toney et al., 1995). The L-alanine transamination half-reaction was analyzed by global optimization. The experimental data included k_max, K_app, and rate constant ratios from stopped-flow experiments and intermediate partitioning (washout vs. turnover) (Zhou et al., 2001). The results are presented in Figure 5.

FIGURE 5

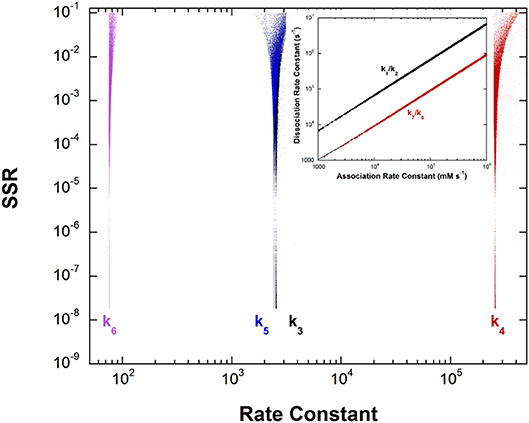
Figure 5. Results of global optimization for the L-Ala/pyruvate half-reaction of dialkylglycine decarboxylase. SSR, sum of squared residuals of the fit to the target function. The figure was generated from ~40,000 independent runs, each starting from randomized sets of rate constants. The inset shows the ratios of the association and dissociation rate constants for both L-Ala and pyruvate binding. The linear correlation over a very large range of values indicates rapid equilibrium binding of both.

The inset shows that, as with aspartate aminotransferase, the formation of the external aldimine intermediate is at equilibrium (k₁/k₂). Additionally, the hydrolysis of the pyruvate ketimine intermediate and pyruvate dissociation (k₇/k₈) is also at equilibrium, with the slopes of the lines equaling the experimental values of K_app for these substrates in stopped-flow experiments.

The four remaining rate constants (k₃-k₆) are well-defined by global analysis. The pK_eq value calculated from the deprotonation/reprotonation rate constant ratio for the L-Ala external aldimine intermediate (2,600/255,000 s⁻¹) is 2.0. The pK_a of the active site catalyst was determined from pH dependence studies to be < 6 (Zhou and Toney, 1999). Here, it is assumed to be 6. Combined, these values allow calculation of an L-Ala external aldimine C-H pK_a of 8.0. The C4′-H pK_eq is similarly calculated from the deprotonation/reprotonation rate constant ratio for the pyruvate ketimine intermediate (77/2,400 s⁻¹) to be 1.5, corresponding to a C4′-H pK_a of 7.5.

For enzymatic deprotonation of the L-Ala external aldimine, ΔG^‡ = 12.7 kcal/mol, while ΔG₀ = 2.7 kcal/mol for proton transfer. These values give Δ${\text{G}}_0^{\text{‡}}$ = 11.3 kcal/mol (Table 2).

Additional enzymes Details of the calculations of the C-H pK_a values and intrinsic barriers for the other enzymes reported in Tables 1, 2 are provided in the Supplementary Material.

Active Site C-H Acidity

The decrease in substrate C-H pK_a going from water to enzyme active site (i.e., ΔpK_a in Table 1) varies from ~7 for ketosteroid isomerase to ~23 for the PLP dependent enzymes tryptophan indole-lyase and tyrosine phenol-lyase. The average value for the cofactor independent enzymes is 12 ± 6 (using mean values of ranges) which corresponds to ~16 kcal/mol of carbanion stabilization by the enzymes, while that for the PLP dependent enzymes is 21 ± 2 which corresponds to ~29 kcal/mol of carbanion stabilization by the enzymes.

Richard et al. have shown that, in water, the pyridoxal protonation state used by enzymes lowers the C_α-H pK_a of amino acids from ~29 to ~17 (Toth and Richard, 2007; Richard et al., 2009). Adjusting for this factor, the protein components of PLP enzymes reduce the C_α-H pK_a of amino acids by an average of 9 ± 1 units, which is similar to the value for the cofactor independent enzymes. Thus, PLP itself provides the lion's share of carbanion stabilization in PLP dependent enzymes. The protein components provide ~12 kcal/mol of carbanion stabilization. In terms of potential active site interactions, this translates into ~6 hydrogen bonds, or ~3 salt bridges, or a combination thereof, that selectively stabilize the carbanion product over the reactant.

The calculated pK_a of the C_α-H bond in the active site of aspartate aminotransferase is ~7. Bronsted analysis of the aspartate external aldimine intermediate in aspartate aminotransferase gave a β value of 0.62, and demonstrated strong steric hindrance toward exogenous catalysts, as expected for a reactant sequestered from solvent (Toney and Kirsch, 1989, 1992). Based on this Bronsted analysis, one can calculate a second-order rate constant for deprotonation of the active site-bound substrate by water and compare it to an experimentally estimated value for a resonance-stabilized carbon acid with pK_a = 7.

The second order rate constant for external aldimine deprotonation by water calculated from the previously reported analysis (log k_B = 0.62 × pK_a−0.047 × molecular volume −2.1) when steric hindrance by the active site is eliminated (by assuming molecular volume = 0) is 7 × 10⁻⁴ M⁻¹s⁻¹. The experimentally derived rate constant for deprotonation of a resonance-stabilized C-H with pK_a = 7 is ~0.02 s⁻¹, or ~4 × 10⁻⁴ M⁻¹s⁻¹ accounting for the concentration of water (Pearson and Dillon, 1953). The agreement between these independently derived values of the C-H deprotonation rate constants corroborates at least the aspartate aminotransferase pK_a reported in Table 1. In terms of Marcus theory, the similarity in the rate constants suggests that aspartate aminotransferase does little to reduce the intrinsic kinetic barrier to deprotonation compared to that in water, which is discussed further below.

QM/MM studies have been performed on several of the enzymes discussed here, providing theoretical estimates of C-H acidity in active sites through calculated FEPs. A study on ketosteroid isomerase gave a value of pK_eq that is essentially identical to the value calculated from the global optimization FEP reported here, providing excellent C-H pK_a agreement between theory and experiment (van der Kamp et al., 2013).

Proline racemase and similar cofactor-independent, two-cysteine amino acid racemases have been examined computationally (Stenta et al., 2008, 2009; Puig et al., 2009; Rubinstein and Major, 2009). The general conclusion from the computational studies is that no stable carbanionic intermediate exists, but that the reaction is a highly asynchronous, double proton transfer with the transition state essentially a fleeting carbanion. Based on experimental data, Albery and Knowles argued that a carbanionic intermediate does exists, although barely (Albery and Knowled, 1986). From molecular orbital considerations, electrophilic substitution reactions preferentially occur by front-side attack (Cram et al., 1955; Jensen and Gale, 1960; Sayre and Jensen, 1979). Therefore, it is reasonable to conclude that back-side double proton transfer in the proline racemase reaction effectively occurs through a carbanion, either a very short-lived intermediate or a transition state. The pK_a of this carbanionic species is calculated to be 15.8 from a DFT treatment and 21.6 from a semi-empirical one (Stenta et al., 2008). The former value agrees well with the experimental value reported in Table 1.

QM/MM calculations on the triosephophate isomerase reactions have produced a variety of energetic profiles, from which C-H pK_a values from ~14 to 20 for dihydroxyacetone phosphate, and a C-H pK_a value of 11 for glyceraldehyde phosphate, are calculated (Cui and Karplus, 2002; Guallar et al., 2004; Wang et al., 2006; Xiang and Warshel, 2008). The range for dihydroxyacetone phosphate is in general agreement with the experimental upper limit presented in Table 1, calculated from a refined experimental FEP (Toney, 2013). Mandelate racemase showed a shallow well in QM/MM studies for the carbanionic intermediate at 14 kcal/mol (Prat-Resina et al., 2005). This translates into a C-H pK_a value of 17, close to the upper limit of the experimental range. Finally, QM/MM calculations on alanine racemase yield a C-H pK_a value (12) that is in good agreement with experiment (11) (Major and Gao, 2006; Major et al., 2006). In general, QM/MM studies appear to provide accurate values for proton transfer equilibrium constants, and thereby accurate active site C-H pKa values.

The rates of proton transfers between heteroatoms such as nitrogen and oxygen are fast. For simple weak acids such as amines, carboxylic acids, alcohols, and water, proton association with the conjugate base is generally diffusion limited (10¹⁰-10¹¹ M⁻¹s⁻¹). Acidity is determined by the wide variation in rate constants for proton dissociation from the acid form. For example, the rate constants for proton dissociation from acetic acid (pK_a = 4.8) in water is 7.8 × 10⁵ s⁻¹, while that for p-nitrophenol (pK_a = 7.1) is 2.6 × 10³ s⁻¹ (Isaacs, 1995).

The ionization of carbon acids is more complex. For example, a carbon acid with a pK_a similar to acetic acid (~5) dissociates a proton with a rate constant of ~1 s⁻¹ in water (Pearson and Dillon, 1953). The large difference in the rates of ionization of heteroatoms vs. carbon exists because carbanions generally must be resonance stabilized to lower their pK_as to those of heteroatom-based acids. Scheme 1 shows the extensive resonance that occurs with PLP, where the carbanionic intermediate is stabilized via the azaallylic group as well as the pyridine ring.

The kinetic consequences of increasing carbon acidity by resonance delocalization have been elaborated by Bernasconi and given the name the “Principle of Non-perfect Synchronization” (Bernasconi, 1987, 1992, 2010). This principle can be summarized by noting that full resonance stabilization, which occurs only in the product and accounts for low pK_a values (i.e., thermodynamic stability of carbanions), requires full p orbital character at the reacting carbon. Conversely, transition states necessarily have only partial p orbital character, and are therefore only partially resonance stabilized compared to the product.

Marcus theory casts activation free energy (ΔG^‡) in terms of the thermodynamic driving force of the reaction (ΔG₀), and the intrinsic reaction barrier (Δ${\text{G}}_0^{\text{‡}}$; activation free energy for reaction when ΔG₀ = 0) (Kresge and Silverman, 1999; Silverman, 2000). An excellent discussion of Marcus theory applied to enzymes is presented by Bearne and Spiteri (2005). In terms of Marcus theory, the intrinsic barrier to proton transfer is greater for carbon acids compared to heteroatom acids because of the late development of resonance stabilization with carbon.

Table 2 presents the intrinsic barriers to enzymatic proton transfers for which well-defined non-enzymatic and enzymatic values can both be calculated (see Supplementary Material). One fundamental catalytic mechanism that enzymes employ is selective stabilization (binding) of an intermediate, thereby lowering ΔG₀ (Albery and Knowles, 1976). A second, equally important mechanism for catalysis is selective stabilization of transition states (catalysis of an individual step) (Albery and Knowles, 1976), thereby lowering Δ${\text{G}}_0^{\text{‡}}$. Within this context, the values in Table 2 show distinct behaviors for cofactor independent and PLP dependent enzymes.

Compared to non-enzymatic reactions, the two cofactor independent enzymes decrease intrinsic barriers to proton transfer by ~5 kcal/mol, while the PLP dependent enzymes increase intrinsic barriers by 2.4 ± 1.7 kcal/mol. The cofactor independent enzymes enhance the rate of proton transfer by stabilizing both the carbanion product (as evidenced by decreases in substrate C-H pK_as in active sites; Table 1) and the transition state leading to it (as evidenced by decreases in Δ${\text{G}}_0^{\text{‡}}$; Table 2). On the other hand, the PLP dependent enzymes presented in Table 2 (all of which employ PLP in the pyridine N-protonated form) achieve high rates of deprotonation exclusively by selective stabilization of the carbanionic intermediate (C-H pK_a reduction). Indeed, the high degree of carbanion stabilization on PLP enzymes is likely achieved by augmenting resonance stabilization through active site interactions with the cofactor, which inevitably leads to increased intrinsic barriers seen in Table 2.

Gerlt et al. (1991), Gerlt and Gassman (1992, 1993a,b), previously addressed a conundrum posed by carbon acid deprotonation in enzyme active sites: the large difference in pK_as of active site acid/base residues and substrate C-H makes deprotonation unfavorable. Central to their analysis is the idea that the intrinsic barriers to C-H deprotonation in active sites are similar to those in water (Gerlt and Gassman, 1992). If this were the case, then C-H pK_as would have to be reduced to that of the active site acid/base in order to account for the observed rates of enzymatic deprotonation. The authors championed concerted acid-base catalysis leading to enol intermediates in deprotonation of α-carbonyl compounds to account for the drastically reduced pK_as of substrates. The present analysis shows that enzymes can indeed lower intrinsic barriers to C-H deprotonation compared to reactions in water. This reduction in intrinsic barrier can be as large as ~7 kcal/mol in the case of proline racemase (Table 2), corresponding to a rate enhancement of ~10⁵ fold. For proline racemase, the experimental and computational evidence points to the transition state being a fleeting carbanion (Albery and Knowled, 1986; Stenta et al., 2008). As discussed in the Supplementary Material, this corresponds to a C-H pK_a of 16 in the active site (Table 1) and a difference in pK_a of ~9 units between the active site cysteine acid/base catalyst and the substrate. The enzyme achieves a high rate of C-H deprotonation not simply by lowering the C-H pK_a to that of the acid/base catalyst, but by coordinately lowering both ΔG₀ and Δ${\text{G}}_0^{\text{‡}}$, as has been discussed previously (Bearne and Spiteri, 2005). For proline racemase, ΔΔG_rxn is ~-18 kcal/mol while ΔΔ${\text{G}}_0^{\text{‡}}$ ~-7 kcal/mol.

In conclusion, FEPs based on experimental data allow the calculation of substrate C-H pK_as in enzyme active sites based on the relation between pK_eq for the proton transfer and known pK_as of catalytic active site residues. The decreases in C-H pK_a provided by active sites ranges from moderate (~7 units) for relatively reactive substrates such as ketosteroids and triosephosphates to large (~20) for amino acids in PLP enzyme active sites. Calculations of Marcus intrinsic barriers for several reactions show that enzymes alter both intrinsic reaction barriers (catalysis of an individual step) and carbanion stability (selective binding of an intermediate) to achieve their impressive rate enhancements. The results presented here are an important step toward a complete quantitative understanding of the fundamental origins of enzyme catalysis.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbioe.2019.00025/full#supplementary-material

Supplementary Material includes details of calculations of FEPs, C-H pKas, and intrinsic barriers for the enzymes discussed (Data Sheet 1), as well as the COPASI input files used for global optimizations.

References

Alberty, R. A., and Peirce, W. H. (1957). Studies of the enzyme fumarase. V.1 calculation of minimum and maximum values of constants for the general fumarase mechanism2. J. Am. Chem. Soc. 79, 1526–1530. doi: 10.1021/ja01564a002

CrossRef Full Text | Google Scholar

Albery, W. J., and Knowled, J. R. (1986). Energetics and mechanism of proline racemase. Biochemistry 25, 2572–2577. doi: 10.1021/bi00357a043

PubMed Abstract | CrossRef Full Text | Google Scholar

Albery, W. J., and Knowles, J. R. (1976). Free-energy profile of the reaction catalyzed by triosephosphate isomerase. Biochemistry 15, 5627–5631. doi: 10.1021/bi00670a031

PubMed Abstract | CrossRef Full Text | Google Scholar

Amyes, T. L., Wood, B. M., Chan, K., Gerlt, J. A., and Richard, J. P. (2008). Formation and stability of a vinyl carbanion at the active site of orotidine 5 ′-monophosphate decarboxylase: pK(a) of the C-6 proton of enzyme-bound UMP. J. Am. Chem. Soc. 130, 1574–1575. doi: 10.1021/ja710384t

CrossRef Full Text | Google Scholar

Bearne, S. L., and Spiteri, R. J. (2005). Reduction of intrinsic kinetic and thermodynamic barriers for enzyme-catalysed proton transfers from carbon acid substrates. J. Theor. Biol. 233, 563–571. doi: 10.1016/j.jtbi.2004.11.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Bearne, S. L., and Wolfenden, R. (1997). Mandelate racemase in pieces: effective concentrations of enzyme functional groups in the transition state. Biochemistry 36, 1646–1656. doi: 10.1021/bi9620722

PubMed Abstract | CrossRef Full Text | Google Scholar

Bernasconi, C. F. (1987). Intrinsic barriers of reactions and the principle of nonperfect synchronization. Accounts Chem. Res. 20, 301–308. doi: 10.1021/ar00140a006

CrossRef Full Text | Google Scholar

Bernasconi, C. F. (1992). The principle of nonperfect synchronization. Adv. Phys. Org. Chem. 27, 119–238. doi: 10.1016/S0065-3160(08)60065-9

CrossRef Full Text | Google Scholar

Bernasconi, C. F. (2010). The principle of nonperfect synchronization: recent developments. Adv. Phys. Org. Chem. 44, 223–324. doi: 10.1016/S0065-3160(08)44005-4

CrossRef Full Text | Google Scholar

Blanchard, J. S., and Cleland, W. W. (1980). Use of isotope effects to deduce the chemical mechanism of fumarase. Biochemistry 19, 4506–4513. doi: 10.1021/bi00560a019

PubMed Abstract | CrossRef Full Text | Google Scholar

Brant, D. A., Barnett, L. B., and Alberty, R. A. (1963). The temperature dependence of the steady state kinetic parameters of the fumarase reaction. J. Am. Chem. Soc. 85, 2204–2209. doi: 10.1021/ja00898a003

CrossRef Full Text | Google Scholar

Chiang, Y., Kresge, A. J., Pruszynski, P., Schepp, N. P., and Wirz, J. (1990). The enol of Mandelic-acid, detection, acidity in aqueous-solution, and estimation of the Keto-enol equilibrium-constant and carbon acidity of Mandelic-acid, Angew. Chem. Int. Edit. 29, 792–794.

Google Scholar

Cook, P. F., and Cleland, W. W. (2007). Enzyme Kinetics and Mechanism. London; New York, NY: Garland Science.

Google Scholar

Cram, D. J., Allinger, J., and Langemann, A. (1955). Stereochemical paths available for electrophilic aliphatic substitution at saturated carbon. Chem. Ind Lond. 19, 919–920.

Google Scholar

Cui, Q., and Karplus, M. (2002). Quantum mechanics/molecular mechanics studies of triosephosphate isomerase-catalyzed reactions: effect of geometry and tunneling on proton-transfer rate constants. J. Am. Chem. Soc. 124, 3093–3124. doi: 10.1021/ja0118439

PubMed Abstract | CrossRef Full Text | Google Scholar

Frey, P. A., and Hegeman, A. D. (2007). Enzymatic Reaction Mechanisms. Oxford; New York, NY: Oxford University Press.

Google Scholar

Gerlt, J. A., and Gassman, P. G. (1992). Understanding enzyme-catalyzed proton abstraction from carbon acids - details of stepwise mechanisms for beta-elimination reactions. J. Am. Chem. Soc. 114, 5928–5934. doi: 10.1021/ja00041a004

CrossRef Full Text | Google Scholar

Gerlt, J. A., and Gassman, P. G. (1993a). An explanation for rapid enzyme-catalyzed proton abstraction from carbon acids - importance of late transition-states in concerted mechanisms. J. Am. Chem. Soc. 115, 11552–11568. doi: 10.1021/ja00077a062

CrossRef Full Text | Google Scholar

Gerlt, J. A., and Gassman, P. G. (1993b). Understanding the rates of certain enzyme-catalyzed reactions - proton abstraction from carbon acids, Acyl-transfer reactions, and displacement-reactions of phosphodiesters. Biochemistry 32, 11943–11952. doi: 10.1021/bi00096a001

PubMed Abstract | CrossRef Full Text | Google Scholar

Gerlt, J. A., Kozarich, J. W., Kenyon, G. L., and Gassman, P. G. (1991). Electrophilic catalysis can explain the unexpected acidity of carbon acids in enzyme-catalyzed reactions. J. Am. Chem. Soc. 113, 9667–9669. doi: 10.1021/ja00025a039

CrossRef Full Text | Google Scholar

Gloss, L. M., and Kirsch, J. F. (1995). Use of site-directed mutagenesis and alternative substrates to assign the prototropic groups important to catalysis by Escherichia coli aspartate aminotransferase. Biochemistry 34, 3999–4007. doi: 10.1021/bi00012a018

PubMed Abstract | CrossRef Full Text | Google Scholar

Goldberg, J. M., and Kirsch, J. F. (1996). The reaction catalyzed by Escherichia coli aspartate aminotransferase has multiple partially rate-determining steps, while that catalyzed by the Y225F mutant is dominated by ketimine hydrolysis. Biochemistry 35, 5280–5291. doi: 10.1021/bi952138d

PubMed Abstract | CrossRef Full Text | Google Scholar

Greenwood, P. E., and Nikulin, M. S. (1996). A Guide to Chi-Squared Testing. New York, NY: Wiley.

Google Scholar

Guallar, V., Jacobson, M., McDermott, A., and Friesner, R. A. (2004). Computational modeling of the catalytic reaction in triosephosphate isomerase. J. Mol. Biol. 337, 227–239. doi: 10.1016/j.jmb.2003.11.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Hawkinson, D. C., Eames, T. C., and Pollack, R. M. (1991). Energetics of 3-oxo-delta 5-steroid isomerase: source of the catalytic power of the enzyme. Biochemistry 30, 10849–10858. doi: 10.1021/bi00109a007

PubMed Abstract | CrossRef Full Text | Google Scholar

Hawkinson, D. C., Pollack, R. M., and Ambulos, N. P. (1994). Evaluation of the internal equilibrium constant for 3-oxo-delta 5-steroid isomerase using the D38E and D38N mutants: the energetic basis for catalysis. Biochemistry 33, 12172–12183. doi: 10.1021/bi00206a021

PubMed Abstract | CrossRef Full Text | Google Scholar

Herschlag, D., and Natarajan, A. (2013). Fundamental challenges in mechanistic enzymology: progress toward understanding the rate enhancements of enzymes. Biochemistry 52. 2050–2067. doi: 10.1021/bi4000113

PubMed Abstract | CrossRef Full Text | Google Scholar

Hill, M. P., Carroll, E. C., Vang, M. C., Addington, T. A., Toney, M. D., and Larsen, D. S. (2010). Light-enhanced catalysis by pyridoxal phosphate-dependent aspartate aminotransferase. J. Am. Chem. Soc. 132, 16953–16961. doi: 10.1021/ja107054x

PubMed Abstract | CrossRef Full Text | Google Scholar

Hine, J. (1971). Rate and equilibrium in the addition of bases to electrophilic carbon and in SN1 reactions. J. Am. Chem. Soc. 93, 3701–3708. doi: 10.1021/ja00744a025

CrossRef Full Text | Google Scholar

Hoops, S., Sahle, S., Gauges, R., Lee, C., Pahle, J., Simus, N., et al. (2006). COPASI–a COmplex PAthway Simulator. Bioinformatics 22, 3067–3074. doi: 10.1093/bioinformatics/btl485

PubMed Abstract | CrossRef Full Text | Google Scholar

Isaacs, N. S. (1995). Physical Organic Chemistry, 2nd Edn. Harlow; New York, NY: Longman Scientific & Technical; Wiley and Sons, Burnt Mill.

Google Scholar

Jencks, W. P. (1987). Catalysis in Chemistry and Enzymology. New York, NY: Dover.

Google Scholar

Jensen, F. R., and Gale, L. H. (1960). Electrophilic aliphatic substitution.4. Organomercurials.2. A stereochemical study of the cleavage of organomercurials by various brominating agents. J. Am. Chem. Soc. 82, 148–151. doi: 10.1021/ja01486a034

CrossRef Full Text | Google Scholar

Kallarakal, A. T., Mitra, B., Kozarich, J. W., Gerlt, J. A., Clifton, J. G., Petsko, G. A., et al. (1995). Mechanism of the reaction catalyzed by mandelate racemase: structure and mechanistic properties of the K166R mutant. Biochemistry 34, 2788–2797.

PubMed Abstract | Google Scholar

Kresge, A. J., and Silverman, D. N. (1999). Application of Marcus rate theory to proton transfer in enzyme-catalyzed reactions, Methods Enzymol. 308, 276–297.

PubMed Abstract | Google Scholar

Lin, D. T., Powers, V. M., Reynolds, L. J., Whitman, C. P., Kozarich, J. W., and Kenyon, G. L. (1988). Evidence for the Generation of Alpha-Carboxy-Alpha-Hydroxy-Para-Xylylene from Para-(Bromomethyl)Mandelate by Mandelate Racemase. J. Am. Chem. Soc. 110, 323–324. doi: 10.1021/ja00209a069

CrossRef Full Text | Google Scholar

Machleder, S. Q., Pineda, E. T., and Schwartz, S. D. (2010). On the origin of the chemical barrier and tunneling in enzymes. J. Phys. Org. Chem. 23, 690–695. doi: 10.1002/poc.1688

PubMed Abstract | CrossRef Full Text | Google Scholar

Major, D. T., and Gao, J. (2006). A combined quantum mechanical and molecular mechanical study of the reaction mechanism and alpha-amino acidity in alanine racemase. J. Am. Chem. Soc. 128, 16345–16357. doi: 10.1021/ja066334r

PubMed Abstract | CrossRef Full Text | Google Scholar

Major, D. T., Nam, K., and Gao, J. (2006). Transition state stabilization and alpha-amino carbon acidity in alanine racemase. J. Am. Chem. Soc. 128, 8114–8115. doi: 10.1021/ja062272t

PubMed Abstract | CrossRef Full Text | Google Scholar

Mendes, P., Hoops, S., Sahle, S., Gauges, R., Dada, J., and Kummer, U. (2009). Computational modeling of biochemical networks using COPASI. Methods Mol. Biol. 500, 17–59. doi: 10.1007/978-1-59745-525-1_2

PubMed Abstract | CrossRef Full Text | Google Scholar

Metzler, C. M., Harris, A. G., and Metzler, D. E. (1988). Spectroscopic studies of quinonoid species from pyridoxal 5'-phosphate. Biochemistry 27, 4923–4933. doi: 10.1021/bi00413a050

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitra, B., Kallarakal, A. T., Kozarich, J. W., Gerlt, J. A., Clifton, J. G., Petsko, G. A., et al. (1995). Mechanism of the reaction catalyzed by mandelate racemase: importance of electrophilic catalysis by glutamic acid 317. Biochemistry 34, 2777–2787. doi: 10.1021/bi00009a006

PubMed Abstract | CrossRef Full Text | Google Scholar

Moles, C. G., Mendes, P., and Banga, J. R. (2003). Parameter estimation in biochemical pathways: a comparison of global optimization methods. Genome Res. 13, 2467–2474. doi: 10.1101/gr.1262503

PubMed Abstract | CrossRef Full Text | Google Scholar

Motulsky, H., and Christopoulos, A. (2004). Fitting Models to Biological Data Using Linear and Nonlinear Regression: A Practical Guide to Curve Fitting. Oxford; New York, NY: Oxford University Press.

Google Scholar

Mozzarelli, A., Peracchi, A., Rovegno, B., Dalè, G., Rossi, G. L., and Dunn, M. F. (2000). Effect of pH and monovalent cations on the formation of quinonoid intermediates of the tryptophan synthase alpha(2)beta(2) complex in solution and in the crystal. J. Biol. Chem. 275, 6956–6962. doi: 10.1074/jbc.275.10.6956

PubMed Abstract | CrossRef Full Text | Google Scholar

Pearson, R. G., and Dillon, R. L. (1953). Rates of ionization of pseudo acids.4. Relation between Rates and Equilibria. J. Am. Chem. Soc. 75, 2439–2443. doi: 10.1021/ja01106a048

CrossRef Full Text | Google Scholar

Pollack, R. M., Zeng, B. F., Mack, J. P. G., and Eldin, S. (1989). Determination of the microscopic rate constants for the base-catalyzed conjugation of 5-Androstene-3,17-Dione. J. Am. Chem. Soc. 111, 6419–6423. doi: 10.1021/ja00198a066

CrossRef Full Text | Google Scholar

Powers, V. M., Koo, C. W., Kenyon, G. L., Gerlt, J. A., and Kozarich, J. W. (1991). Mechanism of the reaction catalyzed by mandelate racemase. 1. Chemical and kinetic evidence for a two-base mechanism. Biochemistry 30, 9255–9263. doi: 10.1021/bi00102a018

PubMed Abstract | CrossRef Full Text | Google Scholar

Prat-Resina, X., Gonzalez-Lafont, A., and Lluch, J. M. (2005). Reaction mechanism of the mandelate anion racemization catalyzed by mandelate racemase enzyme: a QM/MM molecular dynamics free energy study. J. Phys. Chem. B 109, 21089–21101. doi: 10.1021/jp052239d

PubMed Abstract | CrossRef Full Text | Google Scholar

Puig, E., Mixcoha, E., González-Viloca, M., Gonzalez-Lafont, A., and Lluch, J. M. (2009). How the substrate D-Glutamate drives the catalytic action of Bacillus subtilis glutamate racemase. J. Am. Chem. Soc. 131, 3509–3521. doi: 10.1021/ja806012h

PubMed Abstract | CrossRef Full Text | Google Scholar

Richard, J. P. (1998). The enhancement of enzymatic rate accelerations by Bronsted acid-base catalysis. Biochemistry 37, 4305–4309. doi: 10.1021/bi972655r

PubMed Abstract | CrossRef Full Text | Google Scholar

Richard, J. P. (2012). A paradigm for enzyme-catalyzed proton transfer at carbon: triosephosphate isomerase. Biochemistry 51, 2652–2661. doi: 10.1021/bi300195b

PubMed Abstract | CrossRef Full Text | Google Scholar

Richard, J. P. (2013). Enzymatic rate enhancements: a review and perspective. Biochemistry 52, 2009–2011. doi: 10.1021/bi3017119

PubMed Abstract | CrossRef Full Text | Google Scholar

Richard, J. P., and Amyes, T. L. (2001). Proton transfer at carbon. Curr. Opin. Chem. Biol. 5, 626–633. doi: 10.1016/S1367-5931(01)00258-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Richard, J. P., Amyes, T. L., Crugeiras, J., and Rios, A. (2009). Pyridoxal 5'-phosphate: electrophilic catalyst extraordinaire. Curr. Opin. Chem. Biol. 13, 475–483. doi: 10.1016/j.cbpa.2009.06.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Richard, J. P., Amyes, T. L., Goryanova, B., and Zhai, X. (2014). Enzyme architecture: on the importance of being in a protein cage. Curr. Opin. Chem. Biol. 21, 1–10. doi: 10.1016/j.cbpa.2014.03.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Richard, J. P., Amyes, T. L., and Toteva, M. M. (2001). Formation and stability of carbocations and carbanions in water and intrinsic barriers to their reactions. Accounts Chem Res 34, 981–988. doi: 10.1021/ar0000556

PubMed Abstract | CrossRef Full Text | Google Scholar

Rubinstein, A., and Major, D. T. (2009). Catalyzing racemizations in the absence of a cofactor: the reaction mechanism in proline racemase. J. Am. Chem. Soc. 131, 8513–8521. doi: 10.1021/ja900716y

PubMed Abstract | CrossRef Full Text | Google Scholar

Sayre, L. M., and Jensen, F. R. (1979). Mechanism in electrophilic aliphatic substitution - kinetic and stereochemical study of bromodemercuration with bromide ion catalysis. J. Am. Chem. Soc. 101, 6001–6008. doi: 10.1021/ja00514a022

CrossRef Full Text | Google Scholar

Silverman, D. N. (2000). Marcus rate theory applied to enzymatic proton transfer. Biochim. Biophys. Acta 1458, 88–103. doi: 10.1016/S0005-2728(00)00061-X

PubMed Abstract | CrossRef Full Text | Google Scholar

St Maurice, M., and Bearne, S. L. (2002). Kinetics and thermodynamics of mandelate racemase catalysis. Biochemistry 41, 4048–4058. doi: 10.1021/bi016044h

PubMed Abstract | CrossRef Full Text | Google Scholar

Stenta, M., Calvaresi, M., Altoè, P., Spinelli, D., Garavelli, M., and Bottoni, A. (2008). The catalytic activity of proline racemase: a quantum mechanical/molecular mechanical study. J. Phys. Chem. B 112, 1057–1059. doi: 10.1021/jp7104105

PubMed Abstract | CrossRef Full Text | Google Scholar

Stenta, M., Calvaresi, M., Altoè, P., Spinelli, D., Garavelli, M., Galeazzi, R., et al. (2009). Catalytic mechanism of diaminopimelate epimerase: a QM/MM investigation. J. Chem. Theory Comput. 5, 1915–1930. doi: 10.1021/ct900004x

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, S., and Toney, M. D. (1999). Evidence for a two-base mechanism involving tyrosine-265 from arginine-219 mutants of alanine racemase. Biochemistry 38, 4058–4065. doi: 10.1021/bi982924t

PubMed Abstract | CrossRef Full Text | Google Scholar

Sweet, W. L., and Blanchard, J. S. (1990). Fumarase: viscosity dependence of the kinetic parameters. Arch. Biochem. Biophys. 277, 196–202. doi: 10.1016/0003-9861(90)90569-K

PubMed Abstract | CrossRef Full Text | Google Scholar

Toney, M. D. (2013). Common enzymological experiments allow free energy profile determination. Biochemistry 52, 5952–5965. doi: 10.1021/bi400696j

PubMed Abstract | CrossRef Full Text | Google Scholar

Toney, M. D., Hohenester, E., Keller, J. W., and Jansonius, J. N. (1995). Structural and mechanistic analysis of two refined crystal structures of the pyridoxal phosphate-dependent enzyme dialkylglycine decarboxylase. J. Mol. Biol. 245, 151–179. doi: 10.1006/jmbi.1994.0014

PubMed Abstract | CrossRef Full Text | Google Scholar

Toney, M. D., and Kirsch, J. F. (1989). Direct Bronsted analysis of the restoration of activity to a mutant enzyme by exogenous amines. Science 243, 1485–1488. doi: 10.1126/science.2538921

PubMed Abstract | CrossRef Full Text | Google Scholar

Toney, M. D., and Kirsch, J. F. (1992). Bronsted analysis of aspartate aminotransferase via exogenous catalysis of reactions of an inactive mutant. Protein Sci. 1, 107–119.

PubMed Abstract | Google Scholar

Toney, M. D., and Kirsch, J. F. (1993). Lysine 258 in aspartate aminotransferase: enforcer of the Circe effect for amino acid substrates and general-base catalyst for the 1,3-prototropic shift, Biochemistry 32, 1471–1479.

PubMed Abstract | Google Scholar

Toth, K., and Richard, J. P. (2007). Covalent catalysis by pyridoxal: evaluation of the effect of the cofactor on the carbon acidity of glycine. J. Am. Chem. Soc. 129, 3013–3021. doi: 10.1021/ja0679228

PubMed Abstract | CrossRef Full Text | Google Scholar

van der Kamp, M. W., Chaudret, R., and Mulholland, A. J. (2013). QM/MM modelling of ketosteroid isomerase reactivity indicates that active site closure is integral to catalysis. FEBS J. 280, 3120–3131. doi: 10.1111/febs.12158

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, M., Lu, Z., and Yang, W. (2006). Nuclear quantum effects on an enzyme-catalyzed reaction with reaction path potential: proton transfer in triosephosphate isomerase. J. Chem. Phys. 124:124516. doi: 10.1063/1.2181145

PubMed Abstract | CrossRef Full Text | Google Scholar

Warshel, A., and Bora, R. P. (2016). Perspective: defining and quantifying the role of dynamics in enzyme catalysis. J. Chem. Phys. 144:180901. doi: 10.1063/1.4947037

PubMed Abstract | CrossRef Full Text | Google Scholar

Whitman, C. P., Hegeman, G. D., Cleland, W. W., and Kenyon, G. L. (1985). Symmetry and asymmetry in mandelate racemase catalysis. Biochemistry 24, 3936–3942. doi: 10.1021/bi00336a020

PubMed Abstract | CrossRef Full Text | Google Scholar

Wolfenden, R. (2011). Benchmark reaction rates, the stability of biological molecules in water, and the evolution of catalytic power in enzymes. Annu. Rev. Biochem. 80, 645–667. doi: 10.1146/annurev-biochem-060409-093051

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiang, Y., and Warshel, A. (2008). Quantifying free energy profiles of proton transfer reactions in solution and proteins by using a diabatic FDFT mapping. J. Phys. Chem. B 112, 1007–1015. doi: 10.1021/jp076931f

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, X., Jin, X., Medhekar, R., Chen, X., Dieckmann, T., and Toney, M. D. (2001). Rapid kinetic and isotopic studies on dialkylglycine decarboxylase. Biochemistry 40, 1367–1377. doi: 10.1021/bi001237a

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, X., and Toney, M. D. (1999). pH studies on the mechanism of the pyridoxal phosphate-dependent dialkylglycine decarboxylase. Biochemistry 38, 311–320. doi: 10.1021/bi981455s

PubMed Abstract | CrossRef Full Text | Google Scholar