Characterization of protein–protein interfaces through a protein contact network approach

Introduction

Protein–protein interactions play a key role in the biological signaling pathways; however, they were considered difficult to study in terms of their chemo-physical and structural properties. For a long time, scientists simply relied on the functional properties of protein complexes, disregarding the physical details of protein–protein interactions. This restriction had drastically limited the therapeutic interventions impinging on such interactions. This situation changed because of increased structural information; therefore, drugs specifically designed to target protein–protein interactions have reached the market (Arkin et al., 2014).

Once key residues (hot-spot residues) at protein–protein interfaces (PPIs) are identified, PPIs become challenging pharmacological targets with a huge potential in structure-based drug design (Wells and McClendon, 2007). Hot-spot residues largely contribute to the protein–protein binding energy and could be spread over wider “cold regions,” which comprise residues slightly contributing to complex stability (Clackson and Wells, 1995). Hot-spot residues are experimentally identified by mutating residues to alanine: hot spots are those residues that, if mutated, lead to a change in protein–protein binding energy >2.0 kcal/mol (Thorn and Bogan, 2001).

Experimental methods are generally expensive and time-consuming, and predictive computational methods may largely reduce time and cost by guiding the mutagenesis of putative hot-spot residues (Morrow and Zhang, 2012). Computational methods for prediction of hot-spot residues include computational alanine scanning, molecular dynamics, and machine learning-based methods (Morrow and Zhang, 2012); however, often it is necessary to combine methods in order to reach successful predictions.

The computational approach based on protein contact networks (PCNs) has been recently applied to study protein complexes (Di Paola et al., 2015). Although PCN is a minimalist tool, it is an efficient way to study protein structure–function relationships (Di Paola et al., 2013; Cheng et al., 2015). PCN formalism considers protein structures as networks whose nodes are amino acid residues, and two nodes (residues) are in contact if their distance in the 3D structure is within 4–8 Å. PCN helps in elucidating key processes, such as folding (Plaxco et al., 2000) and ligand binding (De Ruvo et al., 2012). Additional methods are based on centrality metrics and graph-spectral clustering, which are based on network partition into clusters of highly interconnected residues, through the analysis of global properties of PCNs (Brinda and Vishveshwara, 2005). PCN is also effective in the localization of hot-spot residues, by means of identification of highly connected hubs (residues) and clusters of nodes (residues), which corresponds to evolutionary conserved residues (Karain and Qaraeen, 2015). Furthermore, analysis of molecular dynamics, based on elastic network models, revealed that hot-spot residues show a moderate-high flexibility, which accounts for conformational accommodation upon binding (Chennubhotla et al., 2005).

Indeed, PCN approach has a high potential of applicability to the study of protein structures by means of simplified representations, e.g., networks and cluster maps. Therefore, we hereby propose an approach that links topology of PPIs to complex stability through the PCN formalism. We applied this method to complexes of protective agent (PA) bounded with lethal factor (LF) and CMG2. Furthermore, we analyzed monomeric and octameric PA. The analysis of PPIs for these complexes will open up the possibility to develop anthrax antidotes and possibly new anti-angiogenic agents.

The attention on anthrax toxicity raised when, in 2001, 22 people were exposed to mail envelopes contaminated by anthrax spores (Jernigan et al., 2001, 2002; Goel, 2015). The possibility of anthrax diffusion induced a widespread terror in the population, calling for huge attention from public authorities (Wein et al., 2003). Anthrax could be easily spread as bio-weapon, because of its low cost and high stability; moreover, anthrax spores can cause different forms of infection with a high mortality rate.

The molecular machinery behind the Bacillus anthracis toxicity relies on a trimeric protein complex (Young and Collier, 2007), which is composed of PA, LF, and edema factor (EF). Anthrax exerts its toxicity through the following steps: PA binding to extracellular domain of anthrax receptors (ANTXRs), PA oligomerization, binding of EF and LF, and endocytosis. EF and LF translocation through the PA pre-pore is promoted by low pH in the endosome (Young and Collier, 2007). So far, two ANTXRs have been cloned: the tumor endothelial marker 8 or anthrax receptor 1 (TEM8/ANTXR1) and the CMG2, also named as ANTXR2.

Toxicity of PA is mainly related to the activation of CMG2 receptor, because of its wider expression and higher affinity for PA compared to the TEM8 receptor. A key residue, leucine 56 in TEM8 mutated into alanine in CMG2, seems to influence PA affinity for ANTXR1 receptor (Fu et al., 2010). Indeed, the designing of drugs, which target PA/LF and PA/ANTXRs interfaces, could represent a key step in the development of an anthrax antidote. Furthermore, TEM8 and CMG2 receptors play a role in epithelial and endothelial cell functions, so that mutations of TEM8 and CMG2 lead to very rare diseases, whose pathological mechanism is still largely unknown (Deuquet et al., 2011). TEM8 is involved in the regulation of expression of vascular endothelial growth factor receptors (VEGFRs), playing a role in angiogenesis that, in turn, is detrimental in cancer progression (Deuquet et al., 2011). CMG2 is involved in the regulation cytoskeleton structure and might have a role in cancer spreading (Cryan and Rogers, 2011). The physiological functions of ANTXRs suggest that drugs targeting them would have a therapeutic potential for diseases where angiogenesis is detrimental (i.e., cancer and retinal neovascular diseases) (Cryan and Rogers, 2011).

The computational approach hereby presented aims at characterizing the homomeric and heteromeric interactions of PA. A PCN method was applied to crystal structures of the aforementioned complexes and was successful in finding “hot-spot” residues.

Analysis was focused on both global network stability (e.g., graph energy, flexibility, and robustness) and local features (e.g., participation coefficient, centrality, and degree). PCN approach has been further applied to evaluate complex stability, inferred from network resilience, or vulnerability (Oliva et al., 2013). The participation coefficient P was the topological parameter that mostly affected the PCNs’ vulnerability of all structures; meaning that, residues important for the protein–protein interactions are also involved in the inter-module communication. Inter-module communication is crucial for either allosteric mechanisms or cooperative events, which in turn play a key role in supramolecular interactions (Keskin et al., 2005). Therefore, identification of high P residues will help the rational drug design of molecules targeting supramolecular (protein–protein) interactions of anthrax complexes.

Materials and Methods

Protein Data Set

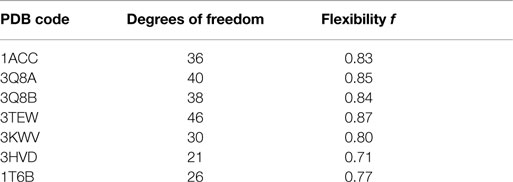
A series of X-ray structures were analyzed (Table 1). Structures are indexed with their own Protein Data Bank (PDB) code. The data set included monomeric and multimeric forms of PA, PA bound to LF (PDB: 3KWV), and to human receptor CMG2 (PDB: 1T6B).

TABLE 1

Table 1. Protein data set.

Protein Contact Network

In PCN methodology, the protein structure is considered as a graph $\mathcal{G}$ = {V, ε}, where the set V includes the nodes v₁…, v_n (i.e., the amino acid residues) and ε is the set of links (v_i, v_j), the link describes a specific relationship between i-th and j-th nodes. Topological descriptors of a PCN quantitatively describe the network that corresponds to a given protein structure (Csermely et al., 2013).

Protein contact networks were built on the base of three dimensional coordinates of α-carbons exported from PDB files (Table 1). Nodes of the network correspond to residues connected by links if the Euclidean distance between α-carbons is in the range of 4–8 Å; this range has been chosen because it includes only significant non-covalent intra-molecular interactions (da Silveira et al., 2009). PCN building is based only on the adjacency binary matrix A, whose rows and columns list residues ordered on the base of the protein primary sequence. A generic element A_ij of the adjacency matrix A is set to 1 if i-th and j-th nodes are connected by a link, otherwise A_ij is set to 0.

Protein structures, translated into a PCN, were then described in terms of (Csermely et al., 2013) (Table 2):

• local network descriptors that describe single residues properties (Table 2, upper part);

• global network descriptors that correspond to properties of the whole structure (average on the whole graph) (Table 2, lower part).

TABLE 2

Table 2. Topological descriptors.

Additionally, we computed two metrics of centrality:

• betweenness centrality: the number of shortest paths passing through each node. Nodes characterized by high betweenness centrality are crucial for signal transmission and, if placed in the PPI, likely responsible for inter-chain communication;

• closeness centrality: the sum of distances (shortest paths) of each node from other nodes. Indeed, high closeness centrality nodes are connected through few links to any other node of the network.

Furthermore, we applied a spectral clustering procedure in order to divide networks into clusters of nodes (Tasdighian et al., 2014). This procedure is based on eigenvalue decomposition. First of all, Laplacian matrix L of PCN is defined as the difference between the adjacency matrix A and the degree matrix D, which is a diagonal matrix, whose generic element D_ii is the i-th node degree. The eigenvalue decomposition is applied to L; therefore, eigenvectors are ordered according to the descending order of the corresponding eigenvalue. The reference for the spectral clustering decomposition is the second minor eigenvalue v₂. The whole range of v₂ values is divided into as many sub-ranges as the number of clusters (given as input); therefore, a node is placed in a cluster according to which sub-range its v₂ value belongs.

The relevance of this approach, to study the structural basis of allosteric regions, was previously reported (De Ruvo et al., 2012; Di Paola and Giuliani, 2015). Once the PCN is partitioned into clusters, each node (residue) can be characterized in terms of its propensity to form inter-cluster or intra-cluster connections, by means of two descriptors:

• the participation coefficient P, defined as:

$P_{\text{i}}=1-{\left(\frac{k_{\text{si}}}{k_{\text{i}}}\right)}^2$ (1)

k_si is the node degree in its own cluster. P measures the inter-cluster connectivity of nodes. P has been found to shift from non-null to null values in regions close to an allosteric site (De Ruvo et al., 2012);

• z-score of intra-cluster connectivity, defined as:

$z_{\text{i}}=\frac{k_{\text{i}}-{\overline{k}}_{\text{si}}}{{\mathrm{\sigma }}_{\text{si}}}$ (2)

${\overline{k}}_{\text{si}}$ and σ_si are, respectively, the average and the SD of degree in the cluster to which the i-th node belongs. Therefore, z-score describes the propensity of a node to establish links with nodes belonging to its own cluster.

According to P and z values, nodes can be classified into seven categories, which cover specific regions in the P–z plane. This representation, called Guimerà–Amaral cartography (Guimerà and Nunes Amaral, 2005), characterizes the topological role of nodes in the PCN, according to their function in signal transmission across the network (Cumbo et al., 2014). The methodology is based on an evolution of the degree concept, which accounts for the ability of the nodes to link different regions of the network. This perspective is particularly well suited for PCNs, which are characterized by a strong small-world character; average shortest path in small-world networks scales logarithmically with the total number of vertices due to long-range contacts between residues far in sequence (Watts and Strogatz, 1998; Atilgan et al., 2004; Paci et al., 2012). P–z maps (representation of nodes distribution on the P–z planes) show a peculiar shape, referred to as “dentist’s chair,” which represents the PCNs of the folded protein structures. The “dentist’s chair” shape is conserved for a large number of structures, and reveals a common architecture of protein folds regardless of protein function and size (Krishnan et al., 2007). Clustering partition, through a clustering color map, was hereby represented as a 2D map clusters of residues (Tasdighian et al., 2014), where each cluster is represented by a different color and projections of clusters correspond to long-range interactions. This representation helps in characterizing the match between clusters and chains, or protein domains.

Flexibility and Vulnerability Assessment

The flexibility index f of a network with c degrees of freedom is defined as (Thorpe and Kuhn, 2000):

$f=\frac{c-6}{c}$ (3)

because the maximum number of degrees of freedom in a rigid network in 3D is 6.

The f index was calculated accordingly to Eq. 3 (Table 3) and degrees of freedom of PCNs were calculated accordingly to the method of Zelazo et al. (2012). The vulnerability of PCNs was computed in terms of size reduction of the largest giant component (LGC) of each PCN (Holme et al., 2002; Oliva et al., 2013); this reduction of size is defined also as “biggest fall.” The LGC of the graph is the set of connected nodes with the maximum number of nodes. The reduction profile of the size of LGC depends on the specific strategy of nodes removal: nodes with decreasing or increasing values of a given network descriptor are removed. A huge fall in LGC size, due to a small fraction of removed nodes, identifies a network vulnerable to a given removal strategy, whereas the network is robust if a smooth and regular degradation is measured.

TABLE 3

Table 3. Flexibility analysis results.

The synthetic index of vulnerability, the Degradation Index DI, (Oliva et al., 2013), is defined as the normalized metric of the effectiveness of different removal strategies:

$\text{DI}=\frac{\text{Difference in giant component size}}{\text{Fraction of removed nodes}}$ (4)

The index is computed at the first discontinuity in size of the giant component and accounts for the magnitude of the fall of the LGC and for the fraction of removed nodes that generated the fall.

Figures, graphs, and statistics

Figures of the protein structures were obtained via PyMOL Molecular Graphics System, Version 1.7.4. Values of the molecular descriptors of residues were mapped in each structure by adding the column corresponding to the b-factor in the PDB file. Graphs and statistics were obtained with Matlab 2014a environment.

Results

Protein Contact Networks General Properties

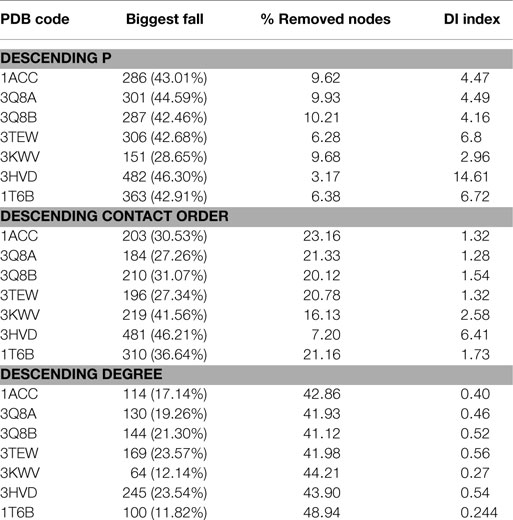
Global topological descriptors of PCNs (Table 4) of monomeric forms were not markedly different from descriptors of complexes; this result suggested that PPIs would not influence the overall topology of PCNs. The parameter that best described PPIs is the inter-chain energy of the graph E_C. The percentage of residues involved in inter-chain contacts (IC) varied from 8.7% (PDB: 3KWV) to 4.4% (PDB: 1T6B), whereas the inter-chain energy E_C normalized per inter-chain contacts (E_C /IC) substantially did not vary; meaning that E_C only depends on the number of residues in the PPIs and not on their nature (contact length and type). Greater E_C values described complexes bearing homomeric PA interactions (PDB: 3HVD and 3KWV).

TABLE 4

Table 4. Topological and structural descriptors.

“Hot-Spots” Recognition by Mesoscopic Topological Descriptors

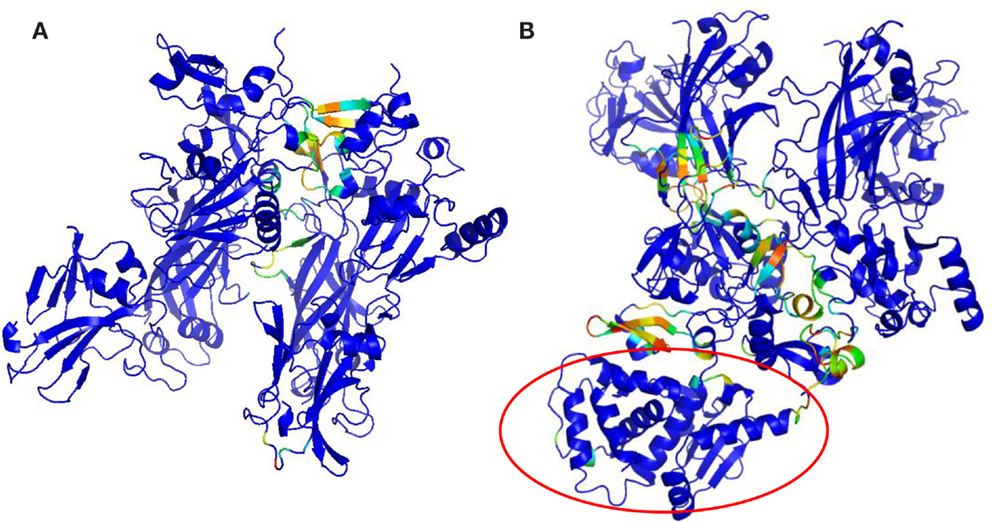
Protective agent bound to LF (PDB: 3KWV) and to receptor CMG2 (PDB: 1T6B) was analyzed (Figure 1), because drugs targeting key residues of such complexes may be developed as anthrax antidotes or novel anti-angiogenic molecules.

FIGURE 1

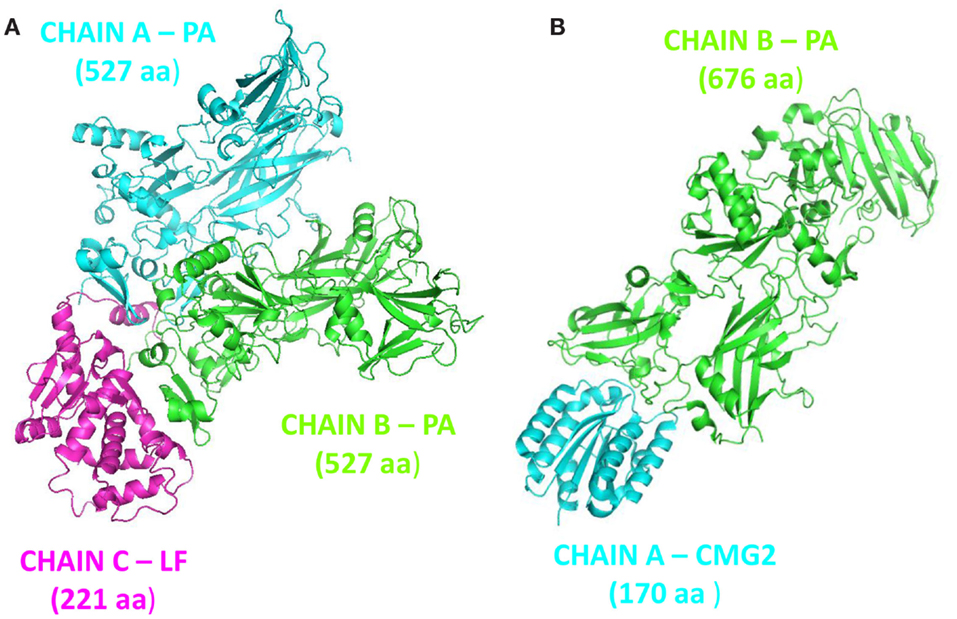
Figure 1. Complex structures: (A) PA–PA–LF trimeric complex (PDB: 3KWV); (B) dimeric complex PA–CMG2 (PDB: 1T6B).

The clustering of PCN of 3KWV, accordingly to graph-spectral method, was carried out (Figure 2). The protein network was divided into three clusters. The clustering helped for the identification of protein modules of the complex. The two chains of PA were not recognized as two different clusters; otherwise, each PA chain was divided into two functional modules: the red cluster (Figure 2A) is the protein module far from PPI (red cartoon Figure 2B), the yellow cluster (Figure 2A) is the protein module near the PPI (yellow cartoon Figure 2B) and in contact to the LF (green cartoon Figure 2B). The red and yellow clusters were substantially intermingled (Figure 2A).

FIGURE 2

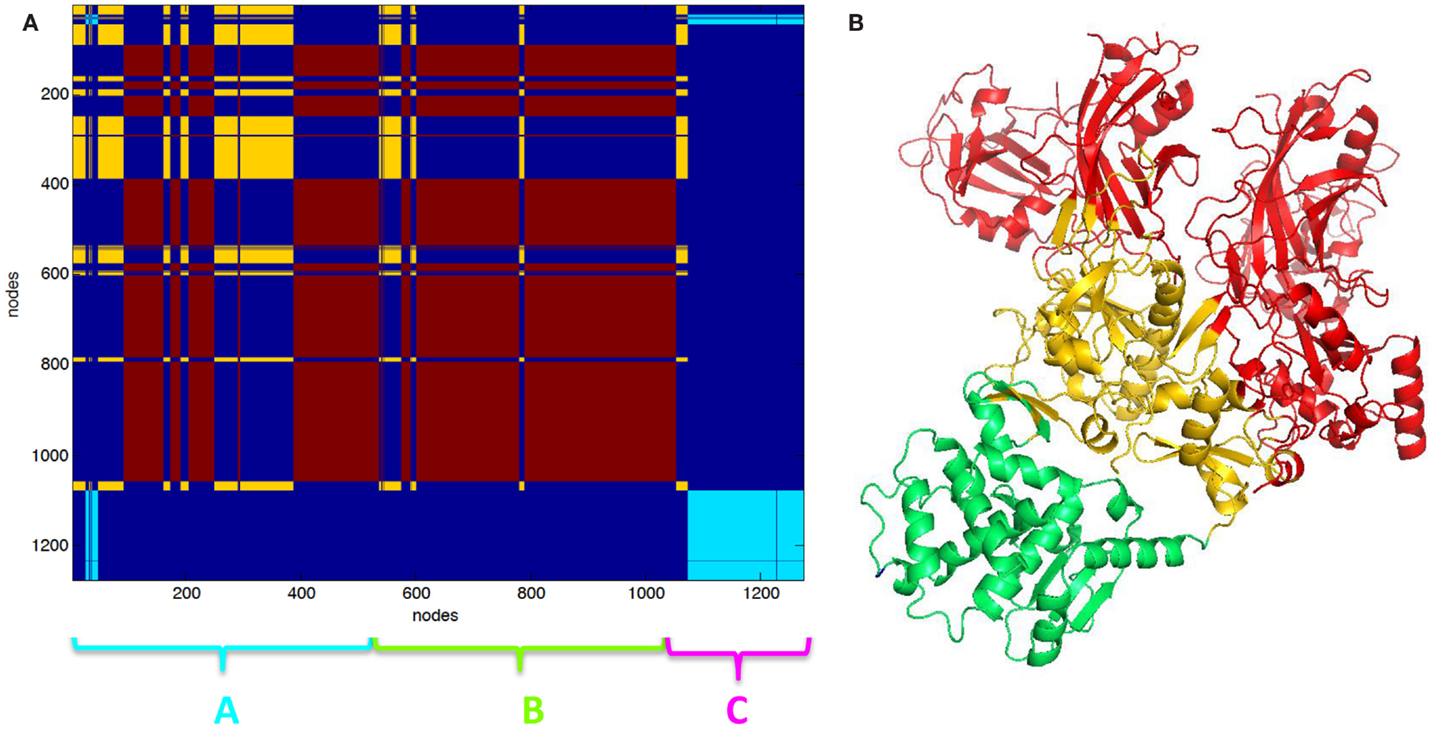
Figure 2. Clustering partition of PA–PA–LF complex: (A) clustering color map, the length of the three chains is reported for reference; (B) cartoon representation of clusters the green cartoon corresponds to the light blue cluster in (A). The lethal factor (LF) is highlighted by the empty circle.

Partition in three clusters of PA–CMG2 complex (1T6B) was also carried out. In 1T6B, a single PA chain is bound to CMG2. PA is divided into two intermingled functional domains, such as the yellow and the red clusters (Figures 3A,B). The light blue (Figure 3A) cluster includes the CGM2 and a domain of PA (cartoon Figure 3B).

FIGURE 3

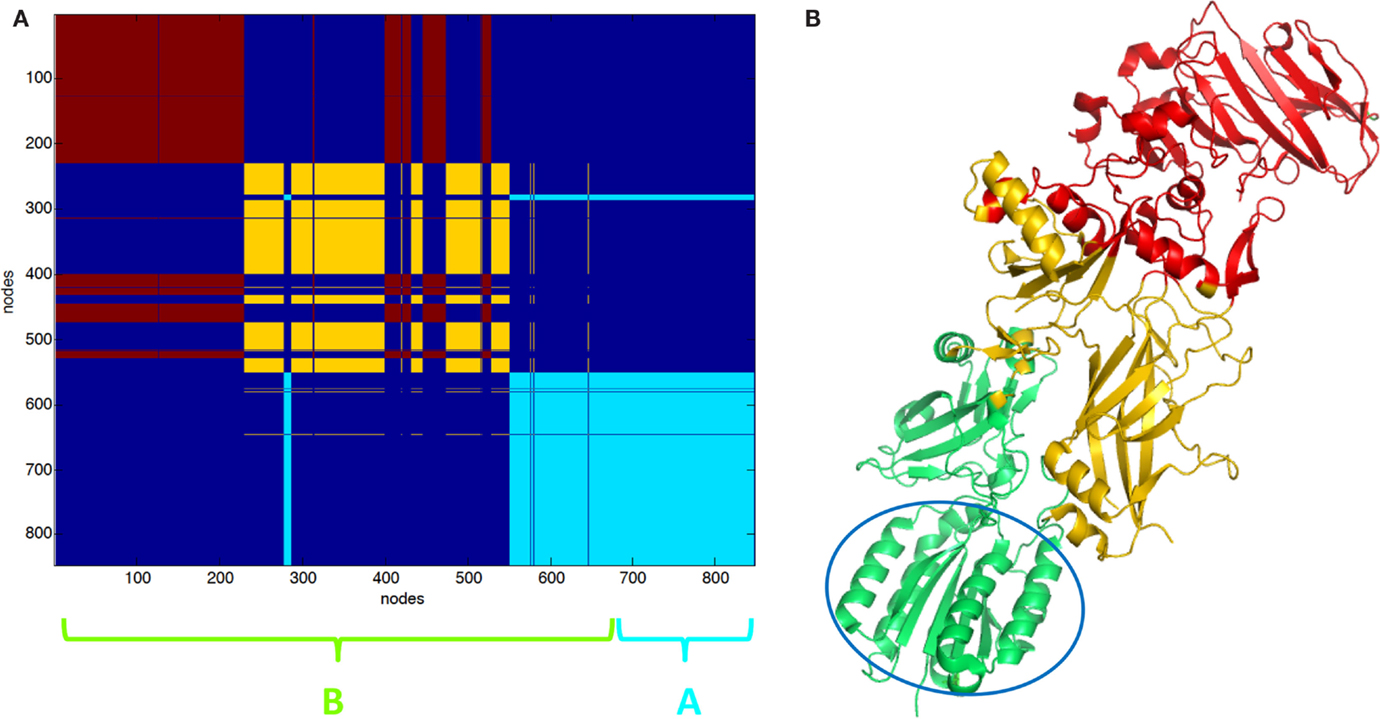
Figure 3. Clustering partition of PA–CMG2 complex: (A) clustering color map, the length of the three chains is reported for reference; (B) cartoon representation of clusters the green cartoon corresponds to the light blue cluster in (A). The CMG2 receptor is highlighted by the empty circle.

Key PCN descriptors were mapped in the molecular representation of PA–PA–LF (PDB: 3KWV) and PA–CGM2 (PDB: 1T6B) (Figures 4 and 5). In 3KWV, the residues with highest closeness centrality (Figures 4C and 5C) belong to the center of mass of the complex, where the residues have the lowest flexibility. In fact, high closeness corresponds to high rigidity of the residue. Conversely, betweenness centrality (Figures 4A and 5A) and participation coefficient P (Figures 4B and 5B) identify residues at the PPIs, which would be good candidates as hot-spot residues. Betweenness centrality and participation coefficient P maps also highlighted residues far from interfaces, in regions with possible allosteric function. Finally, the inter-chain degree (Figure 4D) identified the residues in PPIs easily. The role of inter-chain degree in the identification of residues at PPIs (PA–LF, PA–PA, and PA–CMG2) confirmed the results about the role of E_c in description of PPIs of complexes.

FIGURE 4

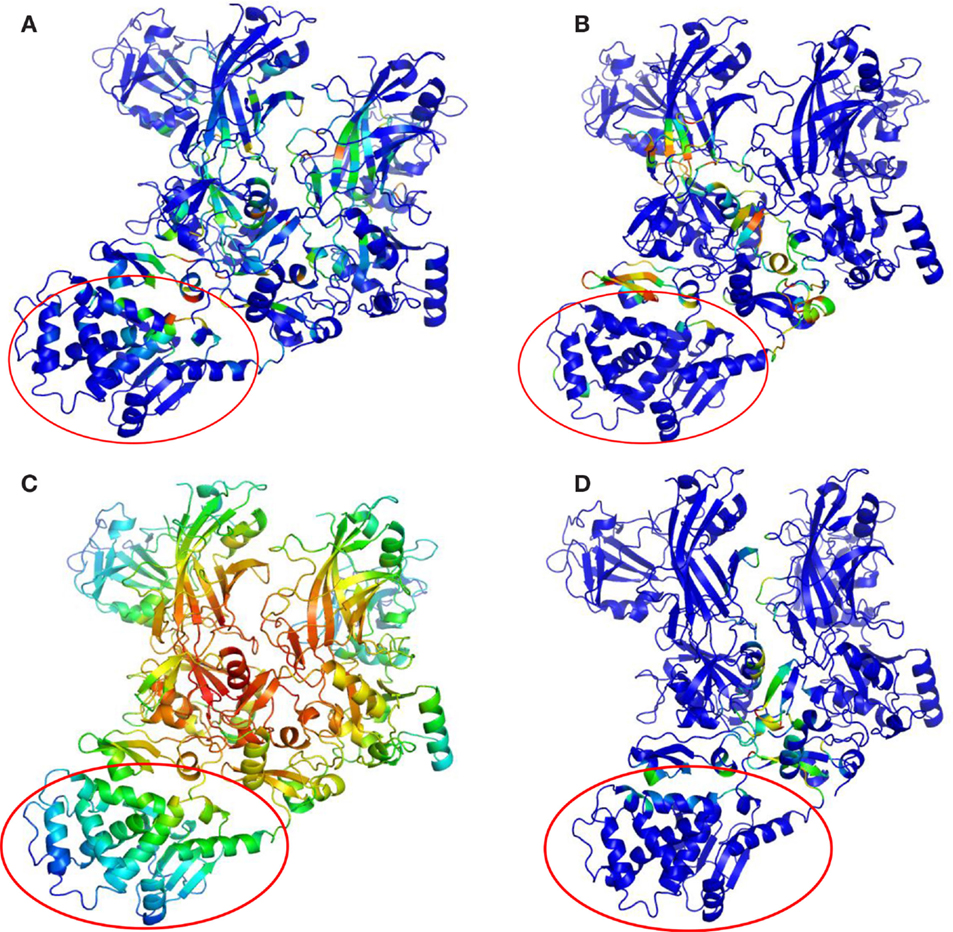
Figure 4. Maps of PCN descriptors on protein structures: complex PA–PA–LF (PDB: 3KWV): (A) betweenness centrality; (B) participation coefficient P; (C) closeness centrality; (D) inter-chain degree. The lethal factor (LF) is highlighted by the empty circle.

FIGURE 5

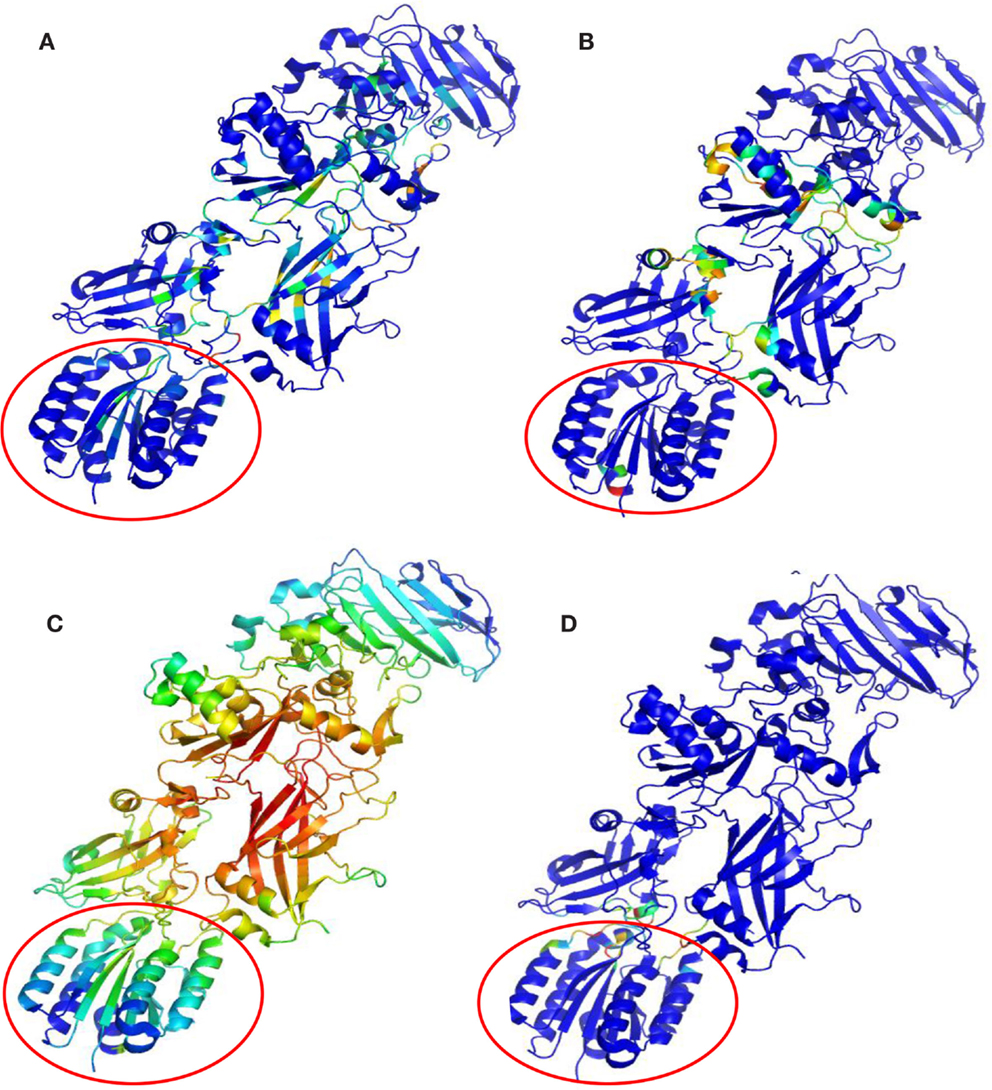
Figure 5. Maps of PCN descriptors on protein structures: complex PA–CGM2 (PDB: 1T6B): (A) betweenness centrality; (B) participation coefficient P; (C) closeness centrality; (D) inter-chain degree. The CMG2 receptor is highlighted by the empty circle.

Protein Contact Networks Rigidity and Vulnerability Analysis

All structures showed a flexibility index f (Table 3) >0.7, albeit with some differences. 3TEW was the most flexible (f = 0.8696), and 3HVD was the most rigid (f = 0.7143). Flexibility was high in monomeric forms of PA, and decreased with increasing number of interacting chains. In fact, flexibility was lowest in 3HVD where eight chains of PA are interacting. The comparison of flexibility of PA–PA–LF (PDB: 3KWV) and PA–CMG2 (PDB: 1T6B) revealed that the number of PA chains did not decrease the flexibility of 3KWV; although, the difference in values was not high.

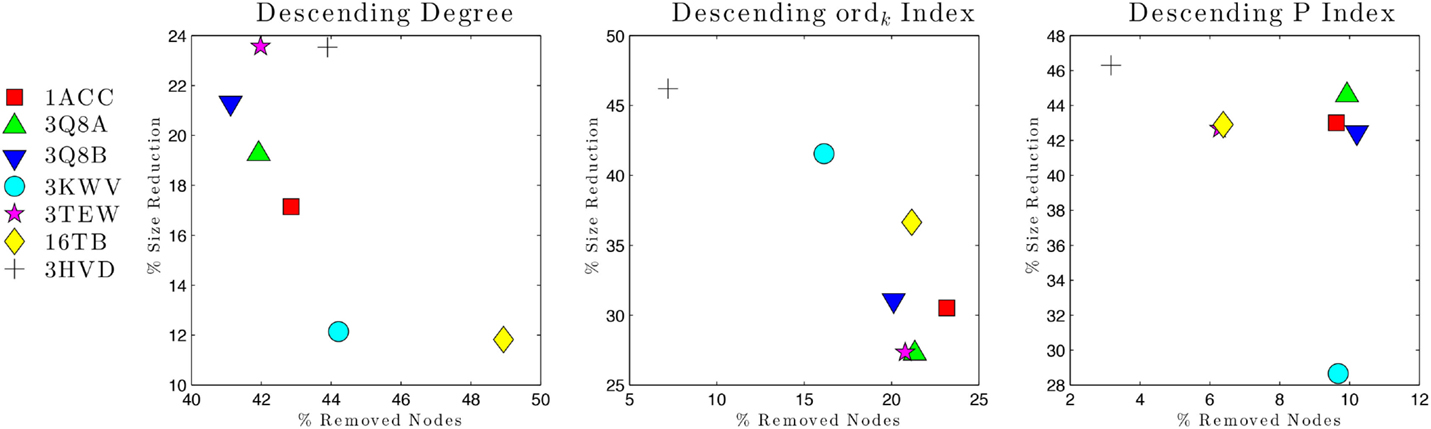
Vulnerability analysis was done by removing nodes with decreasing values of P, contact order, and degree (Table 5; Figures 6 and 7). The P removal strategy significantly influenced the dimension of LGC, i.e., the biggest fall of LGC is associated to the lowest percentage of removed nodes. In all structures, the participation coefficient P was the parameter with the highest influence on PCN robustness. The most vulnerable structure was the octameric PA (PDB: 3HVD), which showed the biggest fall with 3% of removed nodes. The PA–PA–LF complex was less vulnerable than PA–CGM2; meaning that PA–PA interaction were not crucial in the participation coefficient P vulnerability strategy, at least for heteromeric interactions. The contact order removal strategy was substantially detrimental for network robustness of the octameric structure of PA (PDB: 3HVD) (7% of removed nodes) and of PA–PA–LF complex (PDB: 3KWV) (16% of removed nodes); in this case, PA–PA interaction influenced the robustness of PCNs. Finally, the degree removal strategy did not influence the robustness of all PCNs. The influence of P parameter was different in homomeric (PDB: 3HVD) and heteromeric complexes (PDB: 3KWV). Map of residues with high P values in the homomeric (Figure 7A) and heteromeric (Figure 7B) complexes of PA is reported in Figure 7. High P residues were at PA–PA interfaces; however, high P values in 3KWV were localized also at PA–LF interface.

TABLE 5

Table 5. Vulnerability analysis.

FIGURE 6

Figure 6. Network vulnerability upon nodes removal strategies.

FIGURE 7

Figure 7. P maps on protein structures: (A) 3HVD, octamer of PA; (B) 3KWV, PA–PA–LF complex.

Discussion

Crystal structures of unbound anthrax PA, octameric form of PA, PA–PA–LF, and PA–CMG2 complexes were analyzed using a PCN approach. This methodology was used in order to identify residues (hot-spots) that influence significantly the stability of complexes.

Protein–protein interface properties were largely independent from global topology descriptor of the systems. For this reason, local (single residue) properties of PCNs were analyzed in detail.

Local topological descriptors that better described PPIs were the betweenness centrality, the participation coefficient P, and the inter-chain degree. Furthermore, hot-spot residues with the highest betweenness centrality and the participation coefficient were localized in regions with allosteric functions. This result complies with previous works, hot-spot residues are not necessarily placed PPIs, and they can be localized in other regions of the complex acting through allosteric mechanisms (Reynolds et al., 2011). Residues far from PPIs (Reynolds et al., 2011) modulate the small-world properties of PCNs explaining the allosteric nature of PPIs (Brinda et al., 2002).

Thus, the general wiring architecture of PCNs provides a mesoscopic framework (clustering, small-world nature) influencing the “hot-spot” character of residues. This result is in accordance with the previous findings about the modular feature of protein structures (Di Paola et al., 2012; Tasdighian et al., 2014).

Analysis of global PCN vulnerability identified which residues have a crucial role in the stability of anthrax complexes. The PCN vulnerability assessment showed that high P residues played a key role in the network stability of all analyzed protein structures. Furthermore, participation coefficient P and the contact order described residues likely to be involved in cooperative binding. In the PA octamer (3HVD), the most vulnerable structure, high P residues were mostly localized at PPIs; this means that inter-module communication guide cooperative binding and influence PCN robustness. In the PA–PA–LF complex, high P residues were specifically at PA–LF and PA–PA interfaces and also in allosteric regions. Furthermore, PA–CMG2 complex was more vulnerable than PA–PA–LF based on P removal strategy. Thus, the participation coefficient P accounted for overall structural stability and high P residues were localized at PPIs and in allosteric regions. Furthermore, the participation coefficient P partially explained cooperative events. However, the parameter that mostly explained cooperative events was the contact order, because the most vulnerable structures were the octameric PA and the PA–PA–LF complexes, where there are homomeric PA–PA interactions. Interestingly, all analyzed structures were similarly resistant to node removal based on decreasing degree, which is known to be highly effective for scale-free networks (Holme et al., 2002). In conclusion, network vulnerability assessment identified high P residues, distributed both at PPIs and regions far from PPIs, as the most essential for global stability.

The identification of high P residues, crucial for supramolecular interactions, would have a perspective application as a guide for site-directed mutagenesis and other experimental approaches, aimed at functional characterization of PPIs. Furthermore, this approach will help medicinal chemists to identify cavities for molecular-docking studies, in order to design effective drugs targeting protein–protein interactions. Indeed, finding of high P residues will open additional scenarios to drug discovery applications. Drugs may not target PPIs, often scarcely accessible. Additionally, drugs would be designed to bind allosteric regions, influencing supramolecular interactions with efficacy comparable or higher than drugs targeting only protein–protein interfaces.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors wish to thank the reviewers and the editor for their comments, which contributed to improve the manuscript considerably. Dr. CP would like to thank Prof. Filippo Drago, chair of the Department of Biomedical and Biotechnological Sciences (BIOMETEC) of University of Catania, where part of the work on this paper was done.

References

Arkin, M. R., Tang, Y., and Wells, J. A. (2014). Small-molecule inhibitors of protein-protein interactions: progressing toward the reality. Chem. Biol. 21, 1102–1114. doi:10.1016/j.chembiol.2014.09.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Atilgan, A. R., Akan, P., and Baysal, C. (2004). Small-world communication of residues and significance for protein dynamics. Biophys. J. 86(1 Pt 1), 85–91. doi:10.1016/S0006-3495(04)74086-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Brinda, K. V., Kannan, N., and Vishveshwara, S. (2002). Analysis of homodimeric protein interfaces by graph-spectral methods. Protein Eng. 15, 265–277. doi:10.1093/protein/15.4.265

PubMed Abstract | CrossRef Full Text | Google Scholar

Brinda, K. V., and Vishveshwara, S. (2005). Oligomeric protein structure networks: insights into protein-protein interactions. BMC Bioinformatics 6:296. doi:10.1186/1471-2105-6-296

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheng, S., Fu, H.-L., and Cui, D.-X. (2015). Characteristics analyses and comparisons of the protein structure networks constructed by different methods. Interdiscip. Sci. 1–10. doi:10.1007/s12539-015-0106-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Chennubhotla, C., Rader, A., Yang, L.-W., and Bahar, I. (2005). Elastic network models for understanding biomolecular machinery: from enzymes to supramolecular assemblies. Phys. Biol. 2, S173–S180. doi:10.1088/1478-3975/2/4/S12

PubMed Abstract | CrossRef Full Text | Google Scholar

Clackson, T., and Wells, J. (1995). A hot spot of binding energy in a hormone-receptor interface. Science 267, 383–386. doi:10.1126/science.7529940

PubMed Abstract | CrossRef Full Text | Google Scholar

Cryan, L. M., and Rogers, M. S. (2011). Targeting the anthrax receptors, TEM-8 and CMG-2, for anti-angiogenic therapy. Front. Biosci. (Landmark Ed.) 16:1574–1588. doi:10.2741/3806

PubMed Abstract | CrossRef Full Text | Google Scholar

Csermely, P., Korcsmáros, T., Kiss, H. J., London, G., and Nussinov, R. (2013). Structure and dynamics of molecular networks: a novel paradigm of drug discovery: a comprehensive review. Pharmacol. Ther. 138, 333–408. doi:10.1016/j.pharmthera.2013.01.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Cumbo, F., Paci, P., Santoni, D., Di Paola, L., and Giuliani, A. (2014). GIANT: a cytoscape plugin for modular networks. PLoS ONE 9:e105001. doi:10.1371/journal.pone.0105001

PubMed Abstract | CrossRef Full Text | Google Scholar

da Silveira, C. H., Pires, D. E. V., Minardi, R. C., Ribeiro, C., Veloso, C. J. M., Lopes, J. C. D., et al. (2009). Protein cutoff scanning: a comparative analysis of cutoff dependent and cutoff free methods for prospecting contacts in proteins. Proteins 74, 727–743. doi:10.1002/prot.22187

PubMed Abstract | CrossRef Full Text | Google Scholar

De Ruvo, M., Giuliani, A., Paci, P., and Santoni, D. (2012). Shedding light on protein-ligand binding by graph theory: the topological nature of allostery. Biophys. Chem. 16, 21–29. doi:10.1016/j.bpc.2012.03.001

CrossRef Full Text | Google Scholar

Deuquet, J., Lausch, E., Superti-Furga, A., and van der Goot, F. G. (2011). The dark sides of capillary morphogenesis gene 2. EMBO J. 31, 3–13. doi:10.1038/emboj.2011.442

CrossRef Full Text | Google Scholar

Di Paola, L., De Ruvo, M., Paci, P., Santoni, D., and Giuliani, A. (2013). Protein contact networks: an emerging paradigm in chemistry. Chem. Rev. 113, 1598–1613. doi:10.1021/cr3002356

CrossRef Full Text | Google Scholar

Di Paola, L., and Giuliani, A. (2015). Protein contact network topology: a natural language for allostery. Curr. Opin. Struct. Biol. 31, 43–48. doi:10.1016/j.sbi.2015.03.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Di Paola, L., Mei, G., Di Venere, A., and Giuliani, A. (2015). Exploring the stability of dimers through protein structure topology. Curr. Protein Pept. Sci.

PubMed Abstract | Google Scholar

Di Paola, L., Paci, P., Santoni, D., De Ruvo, M., and Giuliani, A. (2012). Proteins as sponges: a statistical journey along protein structure organization principles. J. Chem. Inf. Model. 52, 474–482. doi:10.1021/ci2005127

PubMed Abstract | CrossRef Full Text | Google Scholar

Feld, G. K., Kintzer, A. F., Tang, I. I., Thoren, K. L., and Krantz, B. A. (2012). Domain flexibility modulates the heterogeneous assembly mechanism of anthrax toxin protective antigen. J. Mol. Biol. 415, 159–174. doi:10.1016/j.jmb.2011.10.035

PubMed Abstract | CrossRef Full Text | Google Scholar

Feld, G. K., Thoren, K. L., Kintzer, A. F., Sterling, H. J., Tang, I. I., Greenberg, S. G., et al. (2010). Structural basis for the unfolding of anthrax lethal factor by protective antigen oligomers. Nat. Struct. Mol. Biol. 17, 1383–1390. doi:10.1038/nsmb.1923

PubMed Abstract | CrossRef Full Text | Google Scholar

Fu, S., Tong, X., Cai, C., Zhao, Y., Wu, Y., Li, Y., et al. (2010). The structure of tumor endothelial Marker 8 (TEM8) extracellular domain and implications for its receptor function for recognizing anthrax toxin. PLoS ONE 5:e11203. doi:10.1371/journal.pone.0011203

PubMed Abstract | CrossRef Full Text | Google Scholar

Goel, A. K. (2015). Anthrax: a disease of biowarfare and public health importance. World J. Clin. Cases 3, 20. doi:10.12998/wjcc.v3.i1.20

PubMed Abstract | CrossRef Full Text | Google Scholar

Guimerà, R., and Nunes Amaral, L. A. (2005). Functional cartography of complex metabolic networks. Nature 433, 895–900. doi:10.1038/nature03288

PubMed Abstract | CrossRef Full Text | Google Scholar

Holme, P., Kim, B. J., Yoon, C. N., and Han, S. (2002). Attack vulnerability of complex networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 65, 056109. doi:10.1103/PhysRevE.65.056109

PubMed Abstract | CrossRef Full Text | Google Scholar

Jernigan, D. B., Raghunathan, P. L., Jernigan, D. B., Bell, B. P., Brechner, R., Raghunathan, P. L., et al. (2002). Investigation of bioterrorism-related anthrax, United States, 2001: epidemiologic findings. Emerging Infect. Dis. 8, 1019–1028. doi:10.3201/eid0810.020353

PubMed Abstract | CrossRef Full Text | Google Scholar

Jernigan, J. A., Stephens, D. S., Ashford, D. A., Omenaca, C., Topiel, M. S., Galbraith, M., et al. (2001). Bioterrorism-related inhalational anthrax: the first 10 cases reported in the United States. Emerging Infect. Dis. 7, 933–944. doi:10.3201/eid0706.010604

PubMed Abstract | CrossRef Full Text | Google Scholar

Karain, W. I., and Qaraeen, N. I. (2015). Weighted protein residue networks based on joint recurrences between residues. BMC Bioinformatics 16:173. doi:10.1186/s12859-015-0621-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Keskin, O., Ma, B., Rogale, K., Gunasekaran, K., and Nussinov, R. (2005). Protein-protein interactions: organization, cooperativity and mapping in a bottom-up systems biology approach. Phys. Biol. 2, S24–S35. doi:10.1088/1478-3975/2/2/S03

PubMed Abstract | CrossRef Full Text | Google Scholar

Kintzer, A. F., Thoren, K. L., Sterling, H. J., Dong, K. C., Feld, G. K., Tang, I. I., et al. (2009). The protective antigen component of anthrax toxin forms functional octameric complexes. J. Mol. Biol. 392, 614–629. doi:10.1016/j.jmb.2009.07.037

PubMed Abstract | CrossRef Full Text | Google Scholar

Krishnan, A., Giuliani, A., Zbilut, J. P., and Tomita, M. (2007). Network scaling invariants help to elucidate basic topological principles of proteins. J. Proteome Res. 6, 3924–3934. doi:10.1021/pr070162v

PubMed Abstract | CrossRef Full Text | Google Scholar

Morrow, J. K., and Zhang, S. (2012). Computational prediction of protein hot spot residues. Curr. Pharm. Des. 18, 1255–1265. doi:10.2174/138161212799436412

PubMed Abstract | CrossRef Full Text | Google Scholar

Oliva, G., Di Paola, L., Giuliani, A., Pascucci, F., and Setola, R. (2013). “Assessing protein resilience via a complex network approach,” in IEEE 2nd International Workshop on Network Science. West Point, NY. 131–137. doi:10.1109/NSW.2013.6609209

CrossRef Full Text | Google Scholar

Paci, P., Di Paola, L., Santoni, D., De Ruvo, M., and Giuliani, A. (2012). Structural and functional analysis of hemoglobin and serum albumin through protein long-range interaction networks. Curr. Proteom. 9, 160–166. doi:10.2174/157016412803251815

CrossRef Full Text | Google Scholar

Petosa, C., Collier, R. J., Klimpel, K. R., Leppla, S. H., and Liddington, R. C. (1997). Crystal structure of the anthrax toxin protective antigen. Nature 385, 833–838. doi:10.1038/385833a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Plaxco, K. W., Simons, K. T., Ruczinski, I., and Baker, D. (2000). Topology, stability, sequence, and length: defining the determinants of two-state protein folding kinetics. Biochemistry 39, 11177–11183. doi:10.1021/bi000200n

PubMed Abstract | CrossRef Full Text | Google Scholar

Rajapaksha, M., Lovell, S., Janowiak, B. E., Andra, K. K., Battaile, K. P., and Bann, J. G. (2012). pH effects on binding between the anthrax protective antigen and the host cellular receptor CMG2. Protein Sci. 21, 1467–1480. doi:10.1002/pro.2136

PubMed Abstract | CrossRef Full Text | Google Scholar

Reynolds, K. A., McLaughlin, R. N., and Ranganathan, R. (2011). Hot spots for allosteric regulation on protein surfaces. Cell 147, 1564–1575. doi:10.1016/j.cell.2011.10.049

PubMed Abstract | CrossRef Full Text | Google Scholar

Santelli, E., Bankston, L. A., Leppla, S. H., and Liddington, R. C. (2004). Crystal structure of a complex between anthrax toxin and its host cell receptor. Nature 430, 905–908. doi:10.1038/nature02763

PubMed Abstract | CrossRef Full Text | Google Scholar

Tasdighian, S., Di Paola, L., De Ruvo, M., Palumbo, P., Paci, P., Santoni, D., et al. (2014). Modules identification in protein structures: the topological and geometrical solutions. J. Chem. Inf. Model. 54, 159–168. doi:10.1021/ci400218v

PubMed Abstract | CrossRef Full Text | Google Scholar

Thorn, K. S., and Bogan, A. A. (2001). ASEdb: a database of alanine mutations and their effects on the free energy of binding in protein interactions. Bioinformatics 17, 284–285. doi:10.1093/bioinformatics/17.3.284

PubMed Abstract | CrossRef Full Text | Google Scholar

Thorpe, M. F., and Kuhn, L. (2000). Rigidity in glasses and proteins. Periodica Mathematica Hungarica 39, 241–252. doi:10.1023/A:1004867612889

CrossRef Full Text | Google Scholar

Watts, D. J., and Strogatz, S. H. (1998). Collective dynamics of “small-world” networks. Nature 393, 440–442. doi:10.1038/30918

CrossRef Full Text | Google Scholar

Wein, L. M., Wein, L. M., Craft, D. L., Kaplan, E. H., Craft, D. L., and Kaplan, E. H. (2003). Emergency response to an anthrax attack. Proc. Natl. Acad. Sci. U.S.A. 100, 4346–4351. doi:10.1073/pnas.0636861100

PubMed Abstract | CrossRef Full Text | Google Scholar

Wells, J. A., and McClendon, C. L. (2007). Reaching for high-hanging fruit in drug discovery at protein-protein interfaces. Nature 450, 1001–1009. doi:10.1038/nature06526

CrossRef Full Text | Google Scholar

Young, J. A. T., and Collier, R. J. (2007). Anthrax toxin: receptor binding, internalization, pore formation, and translocation. Annu. Rev. Biochem. 76, 243–265. doi:10.1146/annurev.biochem.75.103004.142728

PubMed Abstract | CrossRef Full Text | Google Scholar

Zelazo, D., Franchi, A., Allgower, F., Bulthoff, H. H., and Robuffo Giordano, P. (2012). Rigidity maintenance control for multi-robot systems. In N. Roy, N. Newman, and S. Srinivasa (473–480). Sidney, NSW: MIT Press. Available at: http://www.ist.uni-stuttgart.de/~zelazo/papers/2012g-ZelFraAlgBueRob-preprint.pdf

Google Scholar