
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Bioinform., 04 March 2024
Sec. Genomic Analysis
Volume 4 - 2024 | https://doi.org/10.3389/fbinf.2024.1306244
This article is part of the Research TopicComputational Methods for Analysis of DNA Methylation Data, Volume IIView all 6 articles
 Claudia Sala1*†
Claudia Sala1*† Pietro Di Lena2†
Pietro Di Lena2† Danielle Fernandes Durso3
Danielle Fernandes Durso3 Italo Faria do Valle4
Italo Faria do Valle4 Maria Giulia Bacalini5
Maria Giulia Bacalini5 Daniele Dall’Olio5
Daniele Dall’Olio5 Claudio Franceschi6
Claudio Franceschi6 Gastone Castellani1‡
Gastone Castellani1‡ Paolo Garagnani1‡
Paolo Garagnani1‡ Christine Nardini7‡
Christine Nardini7‡Introduction: DNA methylation clocks presents advantageous characteristics with respect to the ambitious goal of identifying very early markers of disease, based on the concept that accelerated ageing is a reliable predictor in this sense.
Methods: Such tools, being epigenomic based, are expected to be conditioned by sex and tissue specificities, and this work is about quantifying this dependency as well as that from the regression model and the size of the training set.
Results: Our quantitative results indicate that elastic-net penalization is the best performing strategy, and better so when—unsurprisingly—the data set is bigger; sex does not appear to condition clocks performances and tissue specific clocks appear to perform better than generic blood clocks. Finally, when considering all trained clocks, we identified a subset of genes that, to the best of our knowledge, have not been presented yet and might deserve further investigation: CPT1A, MMP15, SHROOM3, SLIT3, and SYNGR.
Conclusion: These factual starting points can be useful for the future medical translation of clocks and in particular in the debate between multi-tissue clocks, generally trained on a large majority of blood samples, and tissue-specific clocks.
DNA methylation clocks are powerful tools in translational medicine as they carry the potential to estimate biological age (methylage) and predict the risk of early-onset frailty and mortality (Oblak et al., 2021). Indeed, the ability to identify markers of accelerated aging carries the potential to develop strategies to prevent non-communicable age-related diseases (NCDs), whose burden worldwide has been by now defined as a silent pandemic (Saha and Alleyne, 2018). In particular, cancer being among the most deadly NCDs, research studies on epigenetic clocks have very often concentrated on the early identification of persons at high risk of cancer development and on the stratification of subtypes of oncological patients with different prognoses (Zheng et al., 2016; Durso et al., 2017a; Durso et al., 2017b; Johnstone et al., 2022). From the pioneering work of Hannum et al. (2013), Horvath (2013), and Weidner et al. (2014), numerous new clocks (see EstimAge for a recent summary (Di Lena et al., 2021)) and variants (Levine et al., 2018; Lu et al., 2019; Belsky et al., 2020) have been designed. In the translational perspective, the most appealing approach relies on minimally invasive one-catch-all blood clocks, representing the holy grail of cost-effective prevention, owing to the limited invasiveness (blood drawn) and savings associated with effective prevention. However, with the epigenome being among the most specific cell-defining features, it is to be expected that tissue-specific clocks may better express divergences from physiology. Despite their added invasiveness and risks (pain, bleeding, and infection), understanding in detail the differential performances of the two (blood versus tissue-specific) approaches offers an important insight into the real potential of epigenetic clocks and the bases for the construction of more efficient tools. Focusing on the ability of epigenetic clocks to provide methylage estimates that are correlated with chronological age in healthy subjects, we offer a broad analysis of the dependency of the performance of epigenetic clocks on a number of relevant variables, including regression model, size of the training set, sex, and sample tissue of origin. Our work builds on existing research aiming at the exploitation of methylage as a predictor of frailty, lifespan, and other clinically relevant parameters and intends to assess the impact of covariates that may hamper the real comparability of such translational performances. These variables are parameters by which we assess the clock performance and include the regression model, the size of the training set, the impact of sex, the tissue specificity, and in particular, given the expectations toward these techniques, the differential performance of tissue-specific and blood-specific tissues. This latter analysis is, in fact, deemed relevant to gain a clear understanding of the performance of the so-called multi-tissue clocks. Indeed, despite their name, multi-tissue clocks are, in general, trained on a very large majority of blood samples, thus leaving so far the actual predictive power of such universal models unclear, which might be erroneously interpreted as derived from multiple tissues. Our results represent a solid foundation to quantify the clock performance at the state-of-the-art in this continuously active research field, potentially paving the way for the development of better performing epigenetic clocks.
In order to implement tissue-specific methylage clocks, we retrieved all the DNA methylation datasets previously used by Di Lena et al. (2020). These include all the DNA methylation datasets obtained using the Illumina HumanMethylation450 BeadChip (platform GPL13534) for which β-values are available on the NCBI database Gene Expression Omnibus (Edgar et al., 2002). The list of datasets was updated on 12 December 2020. All datasets were carefully filtered according to the following criteria using a combination of automatic and manual curation to ensure that samples from healthy subjects would be selected (for instance, excluding normal tissues adjacent to cancer tissues from oncologic patients): only datasets for which tissue and subject age, sex, and categorization based on health status (control or case) were available were retained; samples from subjects younger than (≤) 20 years or older than
First, for each dataset, we imputed the missing data with metyhLImp (Di Lena et al., 2019). Then, we selected a reference dataset for each tissue, and we used regRCPqn (Sala et al., 2020) to normalize the data. Within each tissue, before proceeding with the training of the model, we selected only the CpGs present both in the training and validation sets, and we filtered out the remaining CpGs with missing values, as well as the unreliable CpGs, as defined by Zhou et al. (2017), the rs (SNP) control probes, and all CpGs on the X and Y chromosomes. The final number of CpGs used to train each clock is given in Supplementary Table S1. Finally, we converted the processed β-values into M-values using the logit2 transformation (M-value = log2(β/(1 − β))) because of their more desirable statistical properties (Du et al., 2010).
We obtained tissue-specific predictive models of methylage considering three possible types of penalized linear regressions: ridge (L2 penalization), lasso (L1 penalization), and elastic-net [equally weighted L1 and L2 penalizations as in the studies by Hannum et al. (2013); Horvath (2013); Horvath et al. (2018); Levine et al. (2018); Zhang et al. (2019); Lee et al. (2020); Shireby et al. (2020); and Voisin et al. (2020)]. Model fitting and prediction were performed using the cv.glmnet function of the glmnet library v4.1.2 in R v4.2.2 and selecting the penalty parameter that minimized the mean-squared error. Each model was trained using the default parameters but with nlambda = 50 rather than 100 to lower the RAM usage. Moreover, an internal 10-fold cross-validation was performed when the number of samples was at least 10, while a leave-one-out cross-validation was performed when the number of samples was lower than 10.
To assess the predictive accuracy of the models on external datasets, a further leave-one-out cross-validation in which each dataset is iteratively left out from the training set was performed within each tissue. It should be noted that a clock was only computed when there were at least three samples in both the training set and validation set. In order to test how the model performance changes with the number of samples in the training set, we performed a stratified subsampling (by age) of the training set of each clock considering various possible dimensions, i.e., 25; 50; 75; 100; 125; 150; 175; 200; 300; 400; 500; 750; 1,000; 1,250; 1,750; 2,000; 2,250; 2,500; and 2,750 samples (when available in the training set), plus the dimension of the training set itself, which was used as the maximum dimension. When the size of the subsample was smaller than that of the training set, some samples were excluded from the training set and formed the test set. For each tissue, each clock was computed by considering males and females either jointly or separately. Finally, the clock trained on all blood samples was also evaluated on samples from other tissues to verify the possible advantage of tissue-specific clocks.
In order to evaluate the performance of the trained clock, we fitted a linear regression model of the computed methylage as a function of chronological age:
where θ1 and θ2 are the intercept and slope of the model, respectively. A visualization of the model is shown in Supplementary Figure S1.
Then, we evaluated the goodness of fit of such a model by computing two assessment measurements (generally called Score in the following sections): the root mean-squared error (RMSE) and the adjusted-R2.
Given n observations yi (Methylage) and given the predicted values
A graphical representation of the meaning of yi (Methylage) and
The RMSE, hence, describes how far apart the observed values are from the regression line (predicted values), on average. The lower the RMSE, the better the model fits the data, meaning that it is possible to accurately predict Methylage based on Age.
The adjusted-R2 in Eq. 3 is a modified version of the R2 that takes into account the number of predictors in the model (K = 2). It is computed as
where
In order to compare the performance of clocks computed under different scenarios, we fitted a series of mixed-effect models described in the following sections. The fitting was performed using the lmer function of the lme4 library v1.1.31 in R. In each model, a random intercept was introduced to take into account the dataset of origin of the samples (GSE). This is indicated as (1|GSE) in the formula of the models. Moreover, in all models, both the dependent and independent variables were always standardized, ensuring the interpretation of the partial slopes as partial correlations. Finally, in all models, we used the logarithm of the sample size instead of the sample size itself due to the skewness of its distribution.
To verify whether the predictive accuracy (Score) of the model evaluated on the validation set depends on the number of samples in the training set (Sample size), we considered all clocks trained and validated on males and females jointly and separately for each tissue and each penalty. In detail, we computed the mixed-effects model in Eq. 4 as follows:
The partial slope relative to log(Sample size) was then evaluated to assess the dependence of the Score on the sample size.
To evaluate which among the ridge, lasso, and elastic-net penalization allowed us to obtain the clock with better predictive performance, we considered all the clocks trained and validated on males and females jointly, and we evaluated the relationship between the Score and the Penalty type by fitting for each tissue a -effects model as in Eq. 5
where log(Sample size) is added to adjust the model for the number of samples in the training set. For each pair of penalties, a dummy variable Penalty is created so that its partial slope indicates how much the Score changes when choosing one penalty or the other.
To evaluate the possible advantage of a sex-specific clock, we considered for each tissue the results (Score) obtained training the elastic-net model on males and females jointly or separately. In both cases, the model was validated separately on males and females. Specifically, for each tissue, we fitted a mixed-effects model as follows in Eq. 6:
where Sex.specific indicates whether the clock was sex-specific (1) or trained on males and females jointly (0) and log(Sample size) is added to adjust the model for the number of samples in the training set.
In order to compare the predictive performance obtained in different tissues, for each pair of tissues, we fitted a mixed-effects model as follows in Eq. 7:
where Tissue is a dummy variable appropriately defined for each pair of tissues and log(Sample size) is added to adjust the model for the number of samples in the training set. Here, we considered the Score obtained when keeping males and females jointly in the training and validation sets. Moreover, elastic-net-only results are presented owing to the better performance obtained, as per Results described below.
In order to compare the predictive performance of a tissue-specific clock and a clock trained on blood samples, for each tissue (except blood and whole blood, see “Datasets and tissues summary” in Results for their definition), we fitted a model as in Eq. 8
where Tissue.specific is a dummy variable equal to 0 if the model was trained on blood samples and to 1 if it was trained on the specific tissue and log(Sample size) is added to adjust the model for the number of samples in the training set. Here, we considered clocks trained on males and females jointly. Moreover, elastic-net-only results are presented owing to the better performance obtained, as per Results described below.
In all models, one-sample Student’s t-test was used to test the null hypothesis that the model coefficients are equal to zero. p-values were then adjusted using the Benjamini–Yekutieli (BY) approach (Benjamini and Yekutieli, 2001).
Methylage estimated by previously existing clocks was obtained using the EstImage webserver (Di Lena et al., 2021). These include Horvath13 (Horvath, 2013); PhenoAge (Levine et al., 2018); Zhang19.enpred and Zhang19.blupred (Zhang et al., 2019); Horvath18 (Horvath et al., 2018); Weidner14 (Weidner et al., 2014); Hannum13 (Hannum et al., 2013); ABEC, eABEC, and cABEC (Lee et al., 2020); Vidal (Vidal-Bralo et al., 2016); CorticalClock (Shireby et al., 2020); and MEAT (Voisin et al., 2020). A detailed description of all such clocks is given by Di Lena et al. (2022). The performance of the tissue-specific elastic-net clocks trained on males and females jointly (i.e., using the best performing setting according to our results) was then graphically compared with those of previously existing clocks using box plots.
As detailed in Supplementary Table S1, we found DNA methylation data of healthy samples passing our filters for four tissue categories: digestive system (A03), nervous system (A08), blood (A12.207.152), and adipose tissue (A10.165.114). However, only six samples (four females and two males) were available for the adipose tissue. Hence, this tissue was not included in the analysis. Table 1 summarizes the number of samples (females and males) found for each specific tissue.
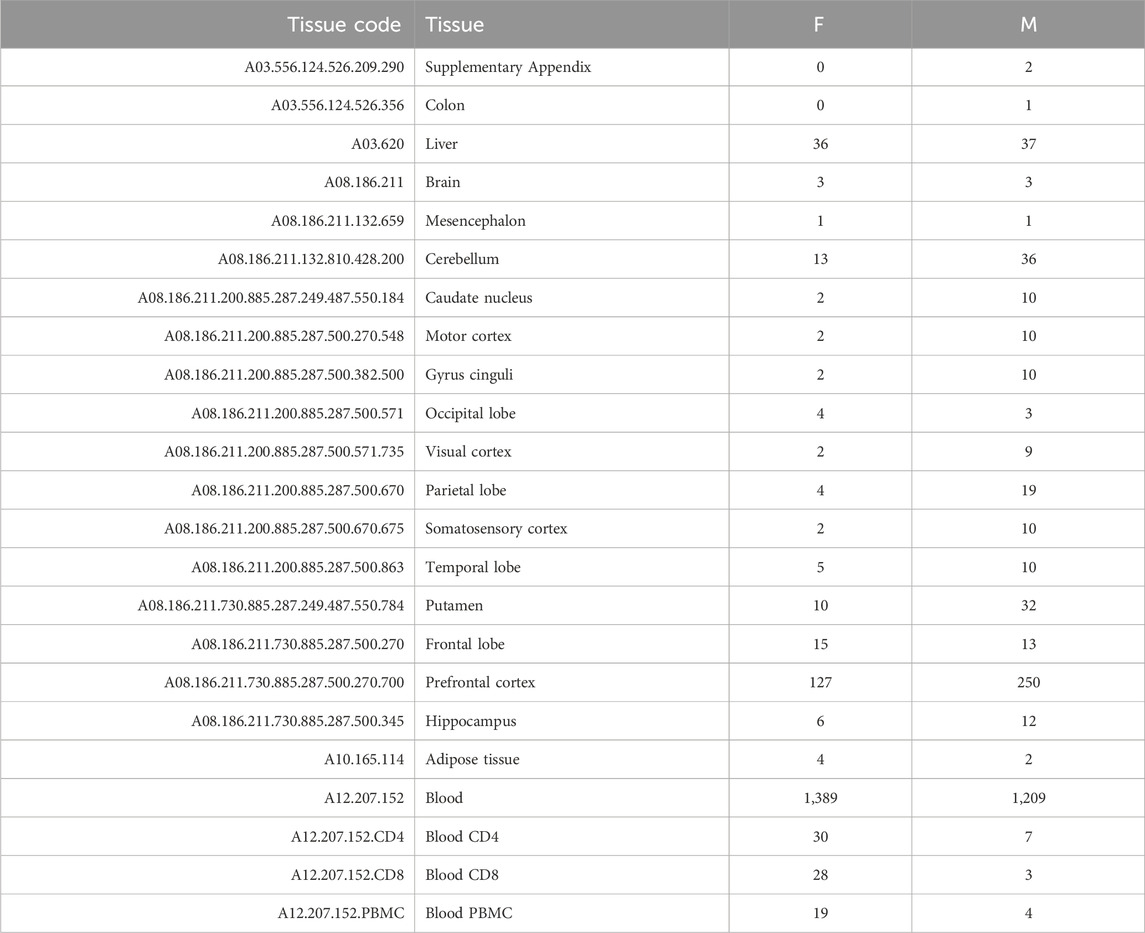
TABLE 1. Summary of the number of samples found for each specific tissue for females (F) and males (M).
Based on the number of samples per tissue, we focused our analysis on three tissues (liver, prefrontal cortex, and whole blood) and three aggregated tissues (digestive system, nervous system, and blood). In the second case, we also classified as blood samples those including only specific subsets of blood cells (CD4, CD8, or PBMC), and we included in the digestive system and nervous system all tissues that belong to such systems, according to the MeSH vocabulary (Lipscomb, 2000). Tables 2, 3 provide the number of samples available for each tissue.
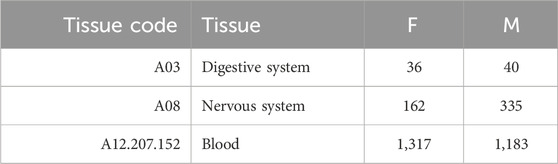
TABLE 3. Summary of the number of samples for each aggregated tissue. Here, blood also includes samples with only specific subsets of blood cells (CD4, CD8, or PBMC).
Using the approach described in Materials and methods, we statistically evaluated the dependency of the clock performance on the sample size (Supplementary Figures S2–S7 provide an overview of such dependency). The partial correlations between each Score and the logarithm of the sample size (log(Sample size)) are reported in Supplementary Table S2, which includes results obtained in the validation set and the training and test sets. The results for the adjusted-R2 and RMSE obtained in the validation set are shown in Figure 1. Figure 1A shows that, overall, a positive correlation (Partial.Corr) exists between the model adjusted-R2 on the validation set and the number of samples in the training set. The effect is evident for all three types of penalization, and it is statistically significant in blood, whole blood, the nervous system, and prefrontal cortex but not in the digestive system and liver. Figure 1B shows that, overall, the RMSE on the validation set decreases as the number of samples in the training set increases (negative Partial.Corr), confirming that the performance of the model on the validation set improves when the sample size of the training set increases. More precisely, such a trend is not visible when using ridge penalization, where the only statistically significant result is in blood and shows an opposite behavior, while the results obtained with the lasso and elastic-net are in agreement with the overall trend, although no statistical significance is found in the digestive system and liver when using the lasso and in the prefrontal cortex and liver when using the elastic-net penalization.
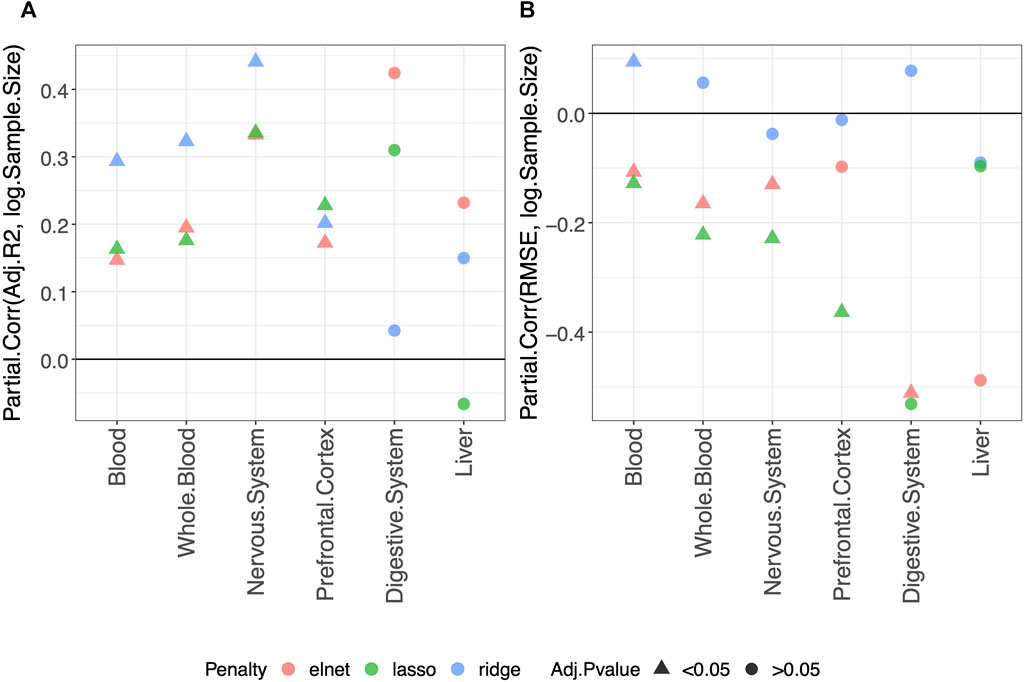
FIGURE 1. Model performance and sample size. Partial correlation (Partial.Corr) between the score of the model performance (adjusted-R2 in (A) and RMSE in (B)), and the number of samples in the training set (log-transformed). As indicated in the legend, different colors refer to models trained with different penalties, while different symbols refer to one-sample t-test BY adjusted p-values (Adj.p-value) greater or smaller than the significance threshold 0.05 (see Materials and methods for details). As expected, the performance improves when the sample size is increased.
It should be noted that the non-significant effect of the sample size in the digestive system and liver is possibly due to the small number of samples available for such tissues (Tables 2, 3 show for the number of samples available for each tissue and aggregated tissue, and Supplementary Table S1 shows the number of studies for each tissue and the number of samples available within each study).
We evaluated the impact of using different penalties on the predictive performance of the clock computing the partial correlation between the Score and the Penalty of the clocks, as described in Materials and methods. Specifically, for each pair of penalties, we obtained an estimate of the partial correlation (Partial.Corr) describing how much the Score changes when changing the Penalty.
We considered the Score values obtained on the validation set. However, results on the training and test sets are also available and given in Supplementary Table S3.
Average values of adjusted-R2 and RMSE per penalty within each tissue are given in Supplementary Tables S4, S5.
Regarding the comparison between the lasso and elastic-net penalization, Figure 2 shows that both adjusted-R2 and RMSE improve when using the elastic-net, but the differences are not statistically significant. Choosing the ridge penalization over the lasso or the elastic-net, on the other hand, reduces the RMSE while also reducing the adjusted-R2. This implies that the correlation between methylage and real age is lower when using the ridge penalization, even though the uncertainty of such correlations is also reduced.
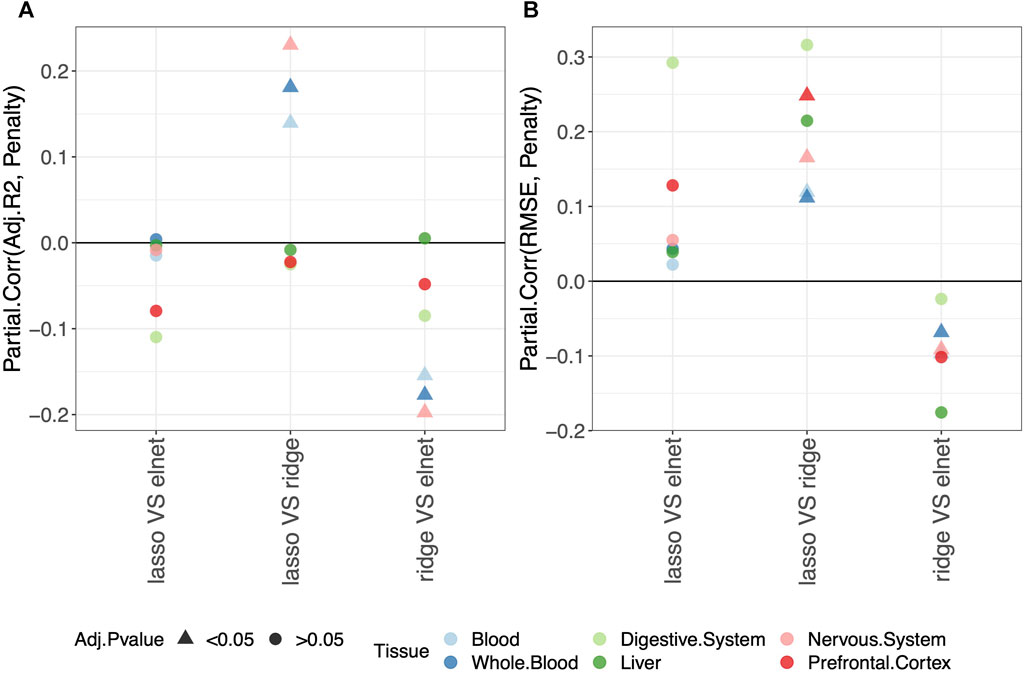
FIGURE 2. Model performance and penalty. Partial correlation between score (adjusted-R2 in (A) and RMSE in (B)) and penalty. The model was fitted (and validated) considering males and females jointly. The dummy variables in the model are labeled as follows: “ridge V elnet” means ridge = 1, elnet = 0; “lasso VS elnet” means lasso = 1, elnet = 0; and “lasso VS ridge” means lasso = 1, ridge = 0. As indicated in the legend, different colors refer to different tissues, while different symbols refer to one-sample t-test BY adjusted p-values (Adj.p-value) greater or smaller than the significance threshold 0.05 (see Materials and methods for details). Overall, choosing the elastic-net penalization does not affect the clock performance.
It should be noted that when considering the digestive system or the liver, all p-values are
Overall, we conclude that the common choice of using the elastic-net penalization does not impact the results when aiming to obtain a predictive model of methylage that is in agreement with the real age. Hence, in the following sections, we focus on this penalization. The results for the other penalizations are reported in Supplementary Tables, as detailed in the following sections.
For each tissue, we evaluated the possible advantage of a sex-specific clock in predicting methylage in the validation set, using the approach described in Materials and methods. The results comparing the clocks trained on males and females jointly or separately for males and females are shown in Supplementary Table S6. Average values of adjusted-R2 and RMSE per tissue and per sex (i.e., sex selected in the training and validation sets) are shown in Supplementary Tables S7, S8.
Overall, we do not detect any statistically significant difference in the predictive performance of clocks when fitting a sex-specific clock or a clock for males and females jointly (Figure 3).
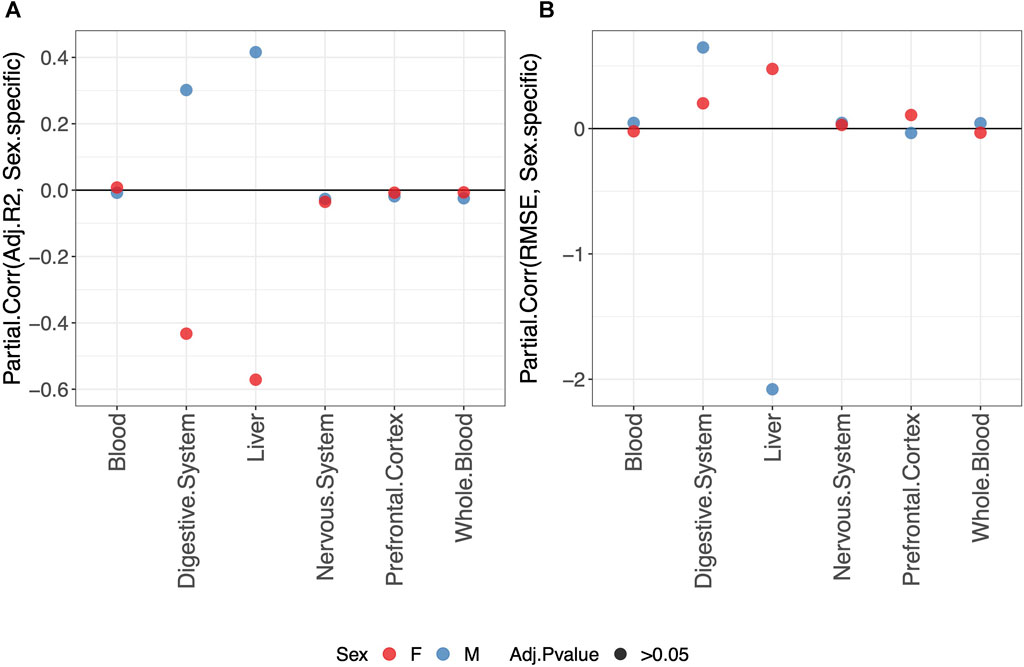
FIGURE 3. Partial correlation between the score (adjusted-R2 in (A) and RMSE in (B) and model either fitted jointly on males and females (0) or separately for males (blue) or females (red) (1). The model was trained using the elastic-net penalization. The results are shown for the validation set. A positive partial correlation for the adjusted-R2 means that the performance is higher when fitting a sex-specific clock. The opposite holds for RMSE. In all cases, the one-sample t-test BY adjusted p-value (Adj.p-value) is
We compared the predictive performance on the validation set of each pair of tissues, as described in Materials and methods. The results are shown in Supplementary Table S9. The average values of adjusted-R2 and RMSE per tissue are shown in Supplementary Tables S10, S11.
Considering the results on the validation set (orange dots in Figure 4), we do not detect any difference in the performance of different tissue-specific clocks.

FIGURE 4. Partial correlation between the score (adjusted-R2 in (A) and RMSE in (B) and having fitted/validated the model on one tissue or the other. As indicated in the legend, different colors refer to results obtained for the training or validation set, while different symbols refer to one-sample t-test BY adjusted p-values (Adj.p-value) greater or smaller than the significance threshold 0.05 (see Materials and methods for details). The model was trained on males and females jointly using the elastic-net penalization. Given the label “tissue1 VS tissue2,” a negative Partial.Corr for the adjusted-R2 means that the performance is lower in the first tissue (tissue1), while the opposite holds for the RMSE.
Considering the easier clinical translatability of a clock computed on blood compared to other tissues, we evaluated whether methylation information from blood samples is already effective in making blood-specific clocks comparable to their tissue-specific counterparts. To this aim, for each tissue (except blood and whole blood), we compared the predictive performance on such tissues of a model trained on blood or on the specific tissue. The details are provided in Materials and methods. The results comparing the clocks trained on blood or on specific tissues are shown in Supplementary Table S12. Average values of adjusted-R2 and RMSE per tissue are shown in Supplementary Tables S13, S14.
Overall, our results show that tissue-specific clocks perform better than the blood-specific clock. Figure 5 shows, in fact, that fitting a tissue-specific clock results in an increase in the adjusted-R2 and a decrease in the RMSE. The results for the digestive system and liver are not statistically significant due to the small sample size but have the same trend observed for the nervous system and prefrontal cortex.
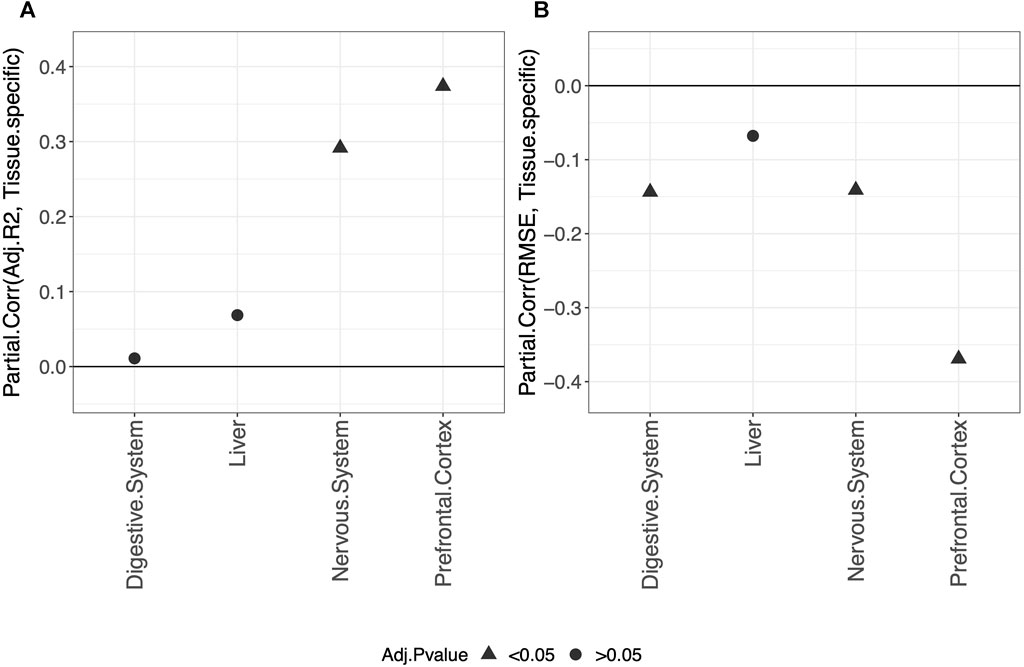
FIGURE 5. Partial correlation between the score (adjusted-R2 in (A) and RMSE in (B) and having trained the model on the specific tissue (1) or on blood (0). As indicated in the legend, different symbols refer to one-sample t-test BY adjusted p-values (Adj.p-value) greater or smaller than the significance threshold 0.05 (see Materials and methods for details). The model was trained on males and females jointly using elastic-net penalization. The performance was evaluated on the validation set (tissue indicated in the x-axis). A positive partial correlation for adjusted-R2 means that the performance is higher when fitting a tissue-specific clock, while the opposite holds for the RMSE.
Based on the previous results, we selected the elastic-net tissue-specific clocks trained on males and females jointly (this setting was chosen because of their better performance, knowing that joint male and female individuals increase the sample size) and without performing any subsampling, and we compared the performance of such clocks with that of previously existing clocks by evaluating the concordance between methylage and real age on the validation sets using the adjusted-R2 and RMSE. Supplementary Figures S8, S13 show the results for each tissue. Overall, the performance on the validation set has high variability for most clocks. The graphical comparison provided by the box plots highlights the utility of tissue-specific clocks. While the elastic-net clocks trained on the liver and digestive system provide worse predictions than multi-tissue and blood-specific clocks (Supplementary Figures S8, S9), possibly due to the small sample size of the training set, the tissue-specific elastic-net models for the nervous system and prefrontal cortex achieve particularly good performance, together with the CorticalClock, a clock specific for the cerebral cortex (Supplementary Figures S10, S11). Regarding the blood-specific elastic-net clock, Supplementary Figures S12, S13 show that the results obtained using the elastic-net model are comparable with those obtained using most of the other blood-specific clocks (except for Weidner14 and Vidal, two clocks based on the methylation value of only a few CpGs: three in the case of Weidner14 and eight in the case of Vidal), as well as with multi-tissue clocks.
Considering, as in the previous section, the tissue-specific elastic-net models trained on males and females jointly and without performing any subsampling, we retrieved the list of CpGs selected by each clock for the computation of methylage. Overall, we observe that the number of selected CpGs increases with the sample size of the training set. This is an expected result related to an increase in the test power. The selected CpGs and their partial effects within each clock are shown in Supplementary Figures S14–S19. Here, all coefficients between −0.1 and 0.1 were set to 0 to simplify the heatmaps. Moreover, the less stable CpGs were discarded by removing the CpGs with non-zero coefficients in less than 10% of the clocks within a certain tissue.
The list of the CpGs selected by all elastic-net clocks for each separate tissue is given in Supplementary Table S15. Overall, no CpG is selected by all elastic-net clocks in all tissues. The Venn diagram given in Figure 6A shows that, while a couple of CpGs are selected both in blood and the digestive system or nervous system, none of them are shared between the last two tissues. A very similar result is obtained when grouping the CpGs at the gene level (Figure 6B) or when considering more specific tissues (Figure 7). Our results confirm the high heterogeneity of the selected CpGs and genes. An overview of the genes selected by both previously existing clocks and those found in our elastic-net tissue-specific models is provided in Supplementary Table S15.
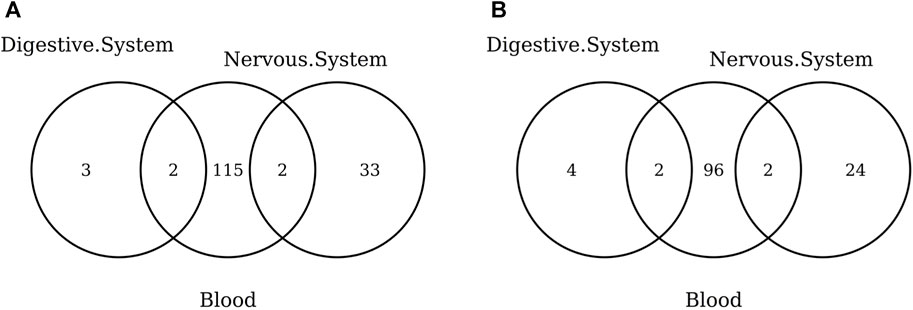
FIGURE 6. Venn diagram of CpGs (A) and genes (B) shared in blood, the nervous system, and digestive system. Here, we considered the results obtained using the elastic-net tissue-specific clocks trained on males and females jointly and without performing any subsampling. The Venn diagrams were then obtained taking into account only the CpGs selected in all the training sets for each tissue.
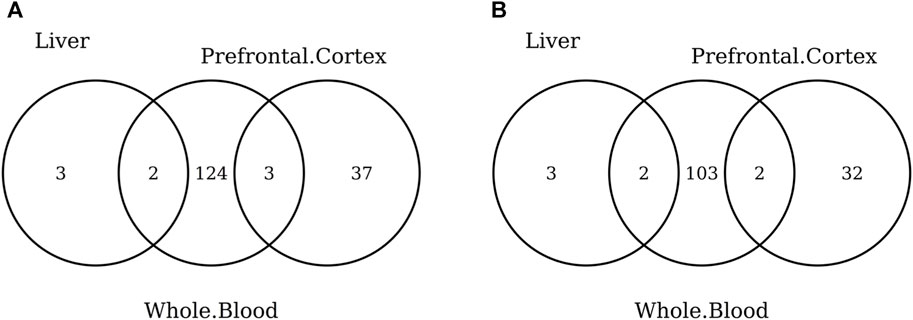
FIGURE 7. Venn diagram of CpGs (A) and genes (B) shared in whole blood, the prefrontal cortex, and liver. Here, we considered the results obtained using the elastic-net tissue-specific clocks trained on males and females jointly and without performing any subsampling. The Venn diagrams were then obtained taking into account only the CpGs selected in all the training sets for each tissue.
When considering the CpGs selected in at least one elastic-net clock, we find some CpGs shared by each pair of tissues but no CpG shared by all the three tissues (Figures 8A, 9A). Figures 8B, 9B show instead that, when aggregating the CpGs at the gene level, we identify 11 genes that are selected in all the three aggregated tissues (CPT1A, EIF5A2, ELOVL2, FHL2, FLJ45983, GATA3, MMP15, SHROOM3, SLC9A3, SLIT3, and SYNGR3) and 5 genes that are selected in all the 3 specific tissues (CPLX2, HAS3, MMP15, RPA2, and SYNGR3). Interestingly, ELOVL2 and FHL2 are well-known as epigenomic markers of aging (Garagnani et al., 2012) and are also selected by various other existing methylage clocks (Table 4). Furthermore, Table 4 shows that among the remaining 12 genes, 7 are also selected by at least 1 other methylage clock, while 5 are uniquely identified by the elastic-net clocks (CPT1A, MMP15, SHROOM3, SLC9A3, and SLIT3).
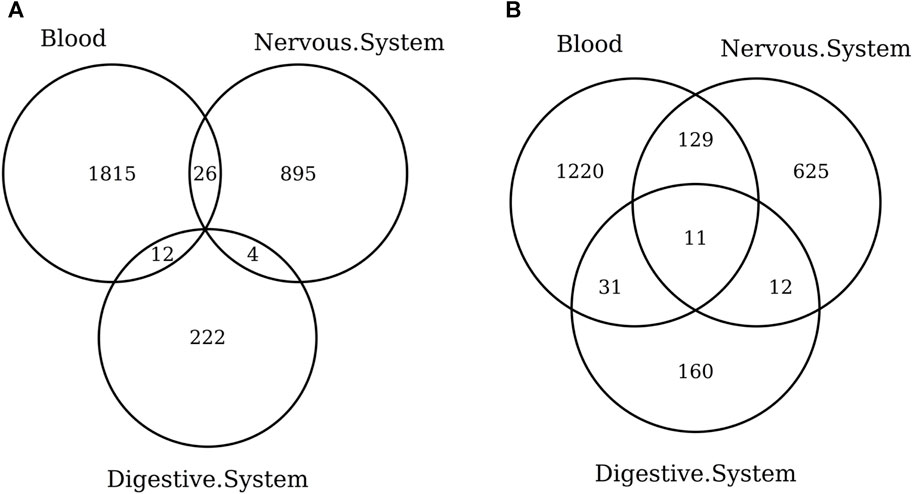
FIGURE 8. Venn diagram of CpGs (A) and genes (B) shared in blood, the nervous system, and digestive system. Here, we considered the results obtained using the elastic-net tissue-specific clocks trained on males and females jointly and without performing any subsampling. The Venn diagrams were then obtained taking into account all the CpGs selected in at least one of the training sets for each tissue.
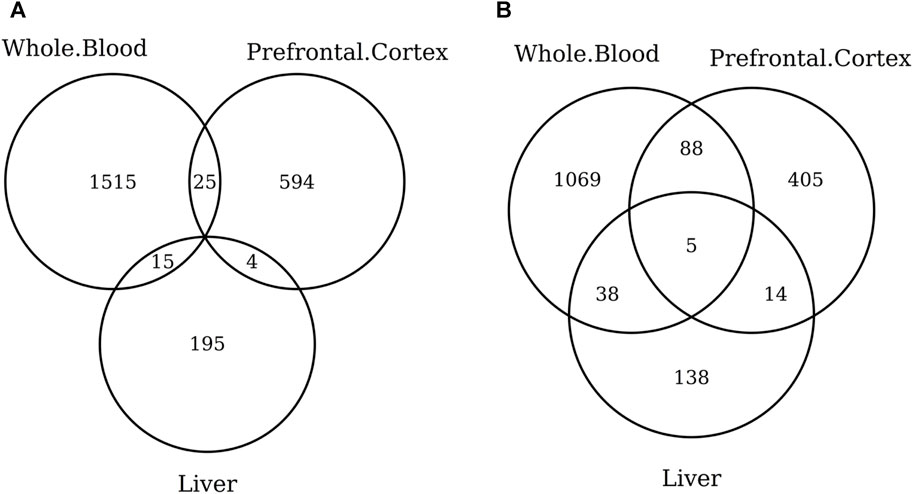
FIGURE 9. Venn diagram of CpGs (A) and genes (B) shared in whole blood, the prefrontal cortex, and liver. We considered the results obtained using the elastic-net tissue-specific clocks trained on males and females jointly and without performing any subsampling. The Venn diagrams were then obtained taking into account all the CpGs selected in at least one of the training sets for each tissue.
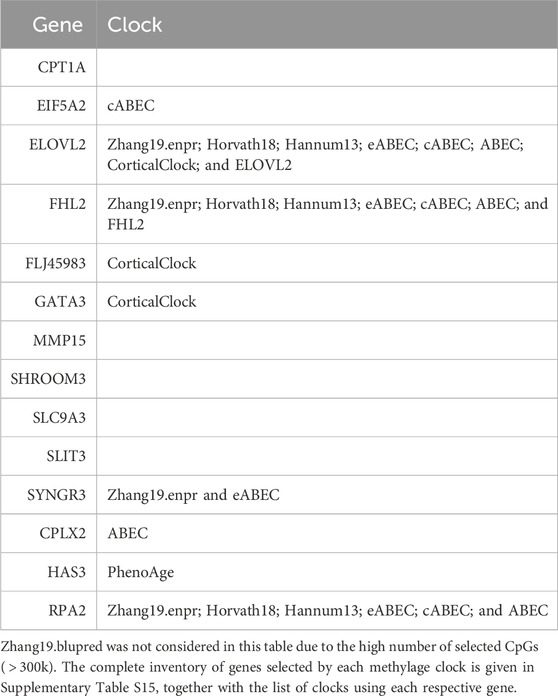
TABLE 4. Column “Gene” lists the 14 genes found in at least 1 clock in all 3 tissues or aggregated tissues. For each gene, column “Clock” lists the previously existing clocks in which such a gene was also used for the computation of methylage.
Methylage clocks are novel biomarkers of aging (He et al., 2021), which exploit DNA methylation to estimate biological age. A common approach to develop such clocks is to fit a penalized linear regression model that relates the chronological age of individuals with their DNA methylation values, considering a training set of control samples. In addition to the relevance of methylage clocks, important aspects of their computational strategy are not well-defined. These include the criteria by which the training set samples are selected (e.g., males and females jointly or separately, samples from a specific tissue or from different tissues) and the model specifications (e.g., the type of penalty). Our work aims at providing a broad analysis of the dependency of methylage clock performance on a number of relevant variables and identifies different significant aspects. Among such aspects, the sample size of the training set is indeed a critical point; as expected, a larger sample size improves the predictive performance of the clock. For what regards the choice of the penalty type, no statistically significant difference is observed among the ridge, lasso, and elastic-net penalization, confirming the suitability of the most commonly used elastic-net approach. In addition to the well-known differences in the aging process in males and females (Yusipov et al., 2020; Hägg and Jylhävä, 2021; Iannuzzi et al., 2023), our results do not find a significant advantage in computing a sex-specific clock, meaning that methylage clocks capture a broader signal, which is sex-independent. Another kind of unexpected result is that the performance of diverse tissue-specific clocks is not different. Since the aging process is linked to multiple cellular alterations, which frequently exhibit specificity for particular tissues (Ferrucci et al., 2020; Nie et al., 2022), we might expect to obtain stronger signatures of aging in some tissues than in others. However, this is not the case for methylage clocks, according to our results. Interestingly, on the other hand, tissue-specific clocks perform better than a generic clock trained on blood. Blood is indeed a favored tissue for the computation of methylage clocks due to its ease of sampling. However, such differences in performance should be taken into account when generalizing the results obtained on blood to other tissues or the whole body. The importance of tissue specificity also emerges when comparing the results obtained with our clocks with those achieved with other existing clocks. For instance, despite the high variability in the predictive performance of the clocks, it emerges that the CorticalClock works better than clocks trained on other tissues when predicting the age of prefrontal cortex and nervous system samples.
Finally, our results show a high variability in the biological signal taken into account by different clocks. Considering the sets of selected CpGs, we find, for instance, that no CpG is shared by all tissue-specific clocks. However, when we shift at the gene level and compare the genes to which the selected CpGs are associated, we find some commonality: 5 genes are selected in all the clocks obtained from the 3 considered specific tissues (liver, prefrontal cortex, and whole blood), while 11 genes are selected in all the clocks obtained from the 3 considered aggregated tissues (digestive system, nervous system, and blood). Among those common genes, ELOVL2 and FHL2 stand out since they are two well-known markers of aging (Garagnani et al., 2012). Moreover, the majority of genes (9 out of 14) are also selected by other existing clocks. On the other hand, CPT1A, MMP15, SHROOM3, SLC9A3, and SLIT3 are first identified within our clocks. Although the identification of such genes can be considered by no means conclusive as to their power as methylage markers, they remain a robust set of hypotheses for further (experimental) testing.
To conclude, we mention that the limits of our study are clearly related to the usage of data obtained using a single technology (Illumina HumanMethylation450 BeadChip) and model (penalized linear regression), as well as to the data availability per tissue. Furthermore, additional experiments like assessing the performance of blood clocks using only CpGs linked to genes expressed in all tissues, or pre-selected according to other biological criteria (for instance, the remarkable case of genes associated with sex-specific hormones), or testing tissue-specific models on different tissues, represent as many questions that could provide additional insights into the mechanisms of methylage. Nevertheless, such a systematic analysis represents a useful and needed evidence-based ground for additional and further exploration in the translation of epigenetic clocks.
Publicly available datasets were analyzed in this study. These data can be found at: Gene Expression Omnibus (GEO) repository (https://www.ncbi.nlm.nih.gov/geo/) under the IDs listed in Supplementary Table S1.
CS: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing–original draft, and writing–review and editing. PD: conceptualization, data curation, formal analysis, software, writing–original draft, and writing–review and editing. DF: data curation, software, and writing–review and editing. IF: data curation, software, and writing–review and editing. MB: conceptualization, data curation, and writing–review and editing. DD’O: methodology, software, and writing–review and editing. CF: conceptualization and writing–review and editing. GC: conceptualization, supervision, and writing–review and editing. PG: conceptualization, supervision, and writing–review and editing. CN: conceptualization, methodology, project administration, resources, supervision, writing–original draft, and writing–review and editing.
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbinf.2024.1306244/full#supplementary-material
Belsky, D. W., Caspi, A., Arseneault, L., Baccarelli, A., Corcoran, D. L., Gao, X., et al. (2020). Quantification of the pace of biological aging in humans through a blood test, the DunedinPoAm DNA methylation algorithm. eLife 9, e54870. doi:10.7554/elife.54870
Benjamini, Y., and Yekutieli, D. (2001). The control of the false discovery rate in multiple testing under dependency. Ann. statistics 29, 1165–1188. doi:10.1214/aos/1013699998
Di Lena, P., Sala, C., and Nardini, C. (2021). Estimage: a webserver hub for the computation of methylation age. Nucleic Acids Res. 49, W199–W206. doi:10.1093/nar/gkab426
Di Lena, P., Sala, C., and Nardini, C. (2022). Evaluation of different computational methods for dna methylation-based biological age. Briefings Bioinforma. 23, bbac274. doi:10.1093/bib/bbac274
Di Lena, P., Sala, C., Prodi, A., and Nardini, C. (2019). Missing value estimation methods for dna methylation data. Bioinformatics 35, 3786–3793. doi:10.1093/bioinformatics/btz134
Di Lena, P., Sala, C., Prodi, A., and Nardini, C. (2020). Methylation data imputation performances under different representations and missingness patterns. BMC Bioinforma. 21, 268–322. doi:10.1186/s12859-020-03592-5
Du, P., Zhang, X., Huang, C.-C., Jafari, N., Kibbe, W. A., Hou, L., et al. (2010). Comparison of beta-value and m-value methods for quantifying methylation levels by microarray analysis. BMC Bioinforma. 11, 587–589. doi:10.1186/1471-2105-11-587
Durso, D. F., Bacalini, M. G., do Valle, I. F., Pirazzini, C., Bonafe, M., Castellani, G., et al. (2017a). Aberrant methylation patterns in colorectal cancer: a meta-analysis. Oncotarget 8, 12820–12830. doi:10.18632/oncotarget.14590
Durso, D. F., Bacalini, M. G., Sala, C., Pirazzini, C., Marasco, E., Bonafe, M., et al. (2017b). Acceleration of leukocytes’ epigenetic age as an early tumor and sex-specific marker of breast and colorectal cancer. Oncotarget 8, 23237–23245. doi:10.18632/oncotarget.15573
Edgar, R., Domrachevù, M., and Lash, A. E. (2002). Gene expression omnibus: ncbi gene expression and hybridization array data repository. Nucleic acids Res. 30, 207–210. doi:10.1093/nar/30.1.207
El Khoury, L. Y., Gorrie-Stone, T., Smart, M., Hughes, A., Bao, Y., Andrayas, A., et al. (2019). Systematic underestimation of the epigenetic clock and age acceleration in older subjects. Genome Biol. 20, 283–310. doi:10.1186/s13059-019-1810-4
Ferrucci, L., Gonzalez-Freire, M., Fabbri, E., Simonsick, E., Tanaka, T., Moore, Z., et al. (2020). Measuring biological aging in humans: a quest. Aging Cell 19, e13080. doi:10.1111/acel.13080
Garagnani, P., Bacalini, M. G., Pirazzini, C., Gori, D., Giuliani, C., Mari, D., et al. (2012). Methylation of ELOVL2 gene as a new epigenetic marker of age. Aging Cell 11, 1132–1134. doi:10.1111/acel.12005
Hägg, S., and Jylhävä, J. (2021). Sex differences in biological aging with a focus on human studies. Elife 10, e63425. doi:10.7554/elife.63425
Hannum, G., Guinney, J., Zhao, L., Zhang, L., Hughes, G., Sadda, S., et al. (2013). Genome-wide methylation profiles reveal quantitative views of human aging rates. Mol. Cell 49, 359–367. doi:10.1016/j.molcel.2012.10.016
He, X., Liu, J., Liu, B., and Shi, J. (2021). The use of dna methylation clock in aging research. Exp. Biol. Med. 246, 436–446. doi:10.1177/1535370220968802
Horvath, S. (2013). Dna methylation age of human tissues and cell types. Genome Biol. 14, R115–R120. doi:10.1186/gb-2013-14-10-r115
Horvath, S., Oshima, J., Martin, G. M., Lu, A. T., Quach, A., Cohen, H., et al. (2018). Epigenetic clock for skin and blood cells applied to hutchinson gilford progeria syndrome and ex vivo studies. Aging (Albany NY) 10, 1758–1775. doi:10.18632/aging.101508
Iannuzzi, V., Bacalini, M. G., Franceschi, C., and Giuliani, C. (2023). The role of genetics and epigenetics in sex differences in human survival. Genus 79, 1. doi:10.1186/s41118-023-00181-1
Johnstone, S. E., Gladyshev, V. N., Aryee, M. J., and Bernstein, B. E. (2022). Epigenetic clocks, aging, and cancer. Science 378, 1276–1277. doi:10.1126/science.abn4009
Lee, Y., Haftorn, K. L., Denault, W. R., Nustad, H. E., Page, C. M., Lyle, R., et al. (2020). Blood-based epigenetic estimators of chronological age in human adults using dna methylation data from the illumina methylationepic array. BMC genomics 21, 747–813. doi:10.1186/s12864-020-07168-8
Levine, M. E., Lu, A. T., Quach, A., Chen, B. H., Assimes, T. L., Bandinelli, S., et al. (2018). An epigenetic biomarker of aging for lifespan and healthspan. Aging 10, 573–591. doi:10.18632/aging.101414
Lu, A. T., Quach, A., Wilson, J. G., Reiner, A. P., Aviv, A., Raj, K., et al. (2019). DNA methylation GrimAge strongly predicts lifespan and healthspan. Aging 11, 303–327. doi:10.18632/aging.101684
Nie, C., Li, Y., Li, R., Yan, Y., Zhang, D., Li, T., et al. (2022). Distinct biological ages of organs and systems identified from a multi-omics study. Cell Rep. 38, 110459. doi:10.1016/j.celrep.2022.110459
Oblak, L., van der Zaag, J., Higgins-Chen, A. T., Levine, M. E., and Boks, M. P. (2021). A systematic review of biological, social and environmental factors associated with epigenetic clock acceleration. Ageing Res. Rev. 69, 101348. doi:10.1016/j.arr.2021.101348
Saha, A., and Alleyne, G. (2018). Recognizing noncommunicable diseases as a global health security threat. Bull. World Health Organ. 96, 792–793. doi:10.2471/BLT.17.205732
Sala, C., Di Lena, P., Fernandes Durso, D., Prodi, A., Castellani, G., and Nardini, C. (2020). Evaluation of pre-processing on the meta-analysis of dna methylation data from the illumina humanmethylation450 beadchip platform. Plos one 15, e0229763. doi:10.1371/journal.pone.0229763
Shireby, G. L., Davies, J. P., Francis, P. T., Burrage, J., Walker, E. M., Neilson, G. W., et al. (2020). Recalibrating the epigenetic clock: implications for assessing biological age in the human cortex. Brain 143, 3763–3775. doi:10.1093/brain/awaa334
Vidal-Bralo, L., Lopez-Golan, Y., and Gonzalez, A. (2016). Simplified assay for epigenetic age estimation in whole blood of adults. Front. Genet. 7, 126. doi:10.3389/fgene.2016.00126
Voisin, S., Harvey, N. R., Haupt, L. M., Griffiths, L. R., Ashton, K. J., Coffey, V. G., et al. (2020). An epigenetic clock for human skeletal muscle. J. cachexia, sarcopenia muscle 11, 887–898. doi:10.1002/jcsm.12556
Weidner, C. I., Lin, Q., Koch, C. M., Eisele, L., Beier, F., Ziegler, P., et al. (2014). Aging of blood can be tracked by dna methylation changes at just three cpg sites. Genome Biol. 15, R24–R12. doi:10.1186/gb-2014-15-2-r24
Yusipov, I., Bacalini, M. G., Kalyakulina, A., Krivonosov, M., Pirazzini, C., Gensous, N., et al. (2020). Age-related dna methylation changes are sex-specific: a comprehensive assessment. Aging (Albany NY) 12, 24057–24080. doi:10.18632/aging.202251
Zhang, Q., Vallerga, C. L., Walker, R. M., Lin, T., Henders, A. K., Montgomery, G. W., et al. (2019). Improved precision of epigenetic clock estimates across tissues and its implication for biological ageing. Genome Med. 11, 54–11. doi:10.1186/s13073-019-0667-1
Zheng, S. C., Widschwendter, M., and Teschendorff, A. E. (2016). Epigenetic drift, epigenetic clocks and cancer risk. Epigenomics 8, 705–719. doi:10.2217/epi-2015-0017
Keywords: methylage, DNA methylation, aging, biological age, epigenetic clock, Illumina HumanMethylation450 BeadChip
Citation: Sala C, Di Lena P, Fernandes Durso D, Faria do Valle I, Bacalini MG, Dall’Olio D, Franceschi C, Castellani G, Garagnani P and Nardini C (2024) Where are we in the implementation of tissue-specific epigenetic clocks?. Front. Bioinform. 4:1306244. doi: 10.3389/fbinf.2024.1306244
Received: 03 October 2023; Accepted: 14 February 2024;
Published: 04 March 2024.
Edited by:
Keith A. Crandall, George Washington University, United StatesReviewed by:
Idil Yet, Hacettepe University, TürkiyeCopyright © 2024 Sala, Di Lena, Fernandes Durso, Faria do Valle, Bacalini, Dall’Olio, Franceschi, Castellani, Garagnani and Nardini. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Claudia Sala, Y2xhdWRpYS5zYWxhM0B1bmliby5pdA==
†These authors share first authorship
‡These authors share last authorship
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.