- 1Department of Mathematics, College of Natural and Computational Sciences, Mattu University, Mattu, Ethiopia
- 2Department of Mathematics, College of Natural and Computational Sciences, Wallaga University, Nekemte, Ethiopia
- 3Department of Mathematics, College of Natural Sciences, Jimma University, Jimma, Ethiopia
Malaria remains a serious and potentially fatal vector-borne disease, consistently ranking among the world’s deadliest infections. This study presents a systematic review of age-structured malaria transmission models. Articles were sourced from PubMed, Google Scholar, and the Research Gate Library, resulting in the identification and inclusion of eleven papers in the review. The findings highlight that children under the age of five are more susceptible to malaria than adults, due to their still-developing immune systems. The highest rates of morbidity and mortality are seen in youngsters, pregnant women, and people with impaired immune systems, making age structure a critical factor in the spread of malaria within populations. Personal protection and vector control are key strategies in reducing the transmission of malaria in communities. The study also suggests that the use of fractional operators in modeling could offer new insights into the dynamics of malaria transmission and potential control strategies.
1 Introduction
Malaria remains one of the world’s deadliest vector-borne diseases, posing a serious and potentially fatal threat, particularly in tropical and subtropical regions (1). This infectious disease is a significant global cause of morbidity and mortality, often associated with poverty and contributing to the inhibition of economic growth in affected areas (2). Malaria is especially devastating in endemic regions, where it disproportionately impacts children under five, pregnant women, and non-immune adults. According to the World Health Organization (WHO) (3), there were an estimated 249 million cases of malaria and 608,000 deaths worldwide. Children under the age of five accounted for 76% of all malaria-related deaths. Furthermore, 94% of cases and 95% of deaths occurred in the African region, with children under five representing 78% of the fatalities in this region (3).
Malaria is caused by Plasmodium parasites, a group of protozoa transmitted primarily through the bites of infected female Anopheles mosquitoes (4). Five species of Plasmodium infect humans, with Plasmodium falciparum being the most prevalent and lethal, particularly in Africa and Southeast Asia (5–7). Symptoms of malaria typically appear within weeks of infection and include fever, chills, sweating, vomiting, abdominal pain, rapid heartbeat, and headaches. Some species of the parasite can remain dormant in the liver, causing relapses months or even years after the initial infection (8). Early diagnosis and treatment are critical for survival, and malaria control strategies, such as insecticide-treated bed nets, anti-malarial medications, and indoor residual spraying, have proven effective in reducing transmission (9–11). While newborns receive temporary immunity from their mothers (12), a multifaceted approach is essential to control the spread of malaria and work toward the ultimate goal of eradicating this preventable disease.
Climatic variability, particularly temperature and rainfall, significantly influences malaria transmission dynamics. Temperature affects both mosquito and parasite behavior (13–17). Higher temperatures lead to more frequent mosquito feeding due to quicker blood digestion (13), but also shorten mosquito lifespan (14). Furthermore, the maturation period of malaria parasites within the mosquito decreases with rising temperatures, from nineteen days at 22°C to eight days at 30°C (16). Temperature fluctuations can also affect malaria transmission rates, either lowering or speeding them up (17). Rainfall plays a crucial role in mosquito breeding and survival (18, 19). While warm, moist conditions in the tropics support stable transmission, excessive rainfall can negatively impact mosquito breeding by flushing away breeding sites (19). Conversely, moderate rainfall can provide suitable breeding habitats for mosquitoes, increasing larval populations (7). These factors demonstrate the complex interplay between climate and malaria transmission, highlighting the need to consider climate variability in public health strategies.
Malaria is preventable and curable, though no single prevention method exists. Various control strategies, including insecticide treated nets (ITNs), treatment of infected individuals, and adulticide, can reduce transmission. Optimal control theory has been applied to identify effective combinations of these strategies, with studies demonstrating the potential for disease eradication using four control strategies such as LLINs, treatment of symptomatic and asymptomatic infections, and IRS (20). A study (21) the cost-effectiveness of optimal control strategies for malaria, considering partial immunity and protected travelers, and incorporating ITNs, prophylaxis, treatment, and vector control.
Vaccination is an effective way of preventing and controlling the prevalence of infectious diseases (22). Recent breakthroughs in malaria vaccines include the WHO’s October 2021 recommendation for broad use of RTS and S/AS01 (the first malaria vaccine) in children from moderate to high malaria transmission. In October 2023, the R21/Matrix-M (R21) malaria vaccine became the second vaccine recommended by WHO to prevent malaria in children living in areas of risk (3).
Recently, mathematical models have become increasingly important for understanding infectious disease dynamics (23–25) and remain a powerful tool for controlling infectious diseases like malaria (26–32). Deterministic and stochastic models are used to study transmission mechanisms, design control strategies, and forecast outbreaks (26–32). Early models by Ross and Macdonald highlighted the importance of mosquito control, with Ross suggesting eradication is possible by reducing mosquito populations below a certain threshold (29). Macdonald’s model, incorporating an exposed class in the mosquito population, showed that reducing mosquito numbers has limited impact in areas with intense transmission (28). These models introduced the concept of the basic reproduction number which represents the average number of new infections caused by one infected individual (26).
The vulnerability of children under five years to malaria, due to their lack of immunity, makes age structure a significant factor in transmission dynamics (1, 33). Recent models incorporating age-structure have provided insights into control strategies (20, 34–37). Models have highlighted the importance of targeting asymptomatic carriers and utilizing various control measures, including mosquito nets with long-lasting treatment, indoor residual spraying, and the screening and care of both symptomatic and asymptomatic people (20). Other studies have shown that increasing mosquito lifespan and birth rate can lead to higher infection and mortality rates (34). The incorporation of age-structure into models has also been applied to other infectious diseases, such as SARS (38), and has been used to explore the effectiveness of optimal control strategies (39). Further research exploring nonlinear incidence and infection age in malaria transmission has revealed complex interactions that impact the stability of disease states (40).
Fractional calculus, a generalization of classical calculus, has emerged as a valuable tool for modeling real world problems, including infectious disease dynamics (41–47). The most common definitions of fractional derivatives, such as Caputo-fractional and Riemann-Liouville, utilize power decay and derivatives as kernels (41, 45). However, the Atangana-Baleanu and Caputo-Fabrizio operators, with non-singular kernels and non-power law distributions, offer superior modeling capabilities for complex systems, including infectious disease models (42, 43, 46). The Atangana-Baleanu derivative, in particular, is well-suited for modeling real world problems due to its non-singular and non-local kernel properties (42).
Fractional order calculus is increasingly popular for its ability to capture memory effects and hereditary properties present in biological systems, which are not adequately represented by integer-order derivatives (41, 43, 48–50). Models incorporating fractional order derivatives have been developed for malaria transmission, considering factors such as vaccination, anti-malarial drugs, and mosquito control strategies (51–55) and the references therein. This systematic review focuses on age-structured malaria transmission models published between 2019 and 2024.
2 Methods
2.1 Study design
A document analysis review design method was employed in the study.
2.2 Search strategy
A systematic literature search was carried out using the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) guidelines (56). This search was carried out by using the PubMed, Google Scholar, and Research Gate databases from January 2019 and May 30, 2024. We utilized various keywords and Boolean operators in a systematic manner, including “age-structured” OR “class-age structured,” as well as “malaria” AND “model*.” The Mendeley software was employed to categorize and remove duplicate references (see Figure 1).
2.3 Inclusion and exclusion criteria
• The study used the following inclusion criteria to determine study eligibility:
Deterministic modeling approach.
Articles published in English.
Full text of studies available.
Latest published articles from 2019–2024.
Studies indexed by PubMed, Google Scholar, and Research Gate.
• Studies meeting the following criteria were excluded from the review:
Stochastic modeling approach
Article is not published in English
The full text of the study is not available.
Articles published before 2019.
Studies not indexed in PubMed, Google Scholar, and Research Gate.
Text book or book series is not included.
3 Results
By taking into account all of the aforementioned inclusion and exclusion criteria, a database search engine on age-structured malaria models found 1,097 (one thousand ninety-seven) published articles. Following that, a total of 51 (fifty-one) duplicate research articles were eliminated out of a total of 1,097 (one thousand ninety-seven) that were searched. The titles and abstracts of 1,046 (one thousand forty-six) studies were then used to filter them. Ultimately, eleven of the 35 (thirty-five) articles that we had read through to the end were deemed suitable for this systematic review. The included studies are classified as age-structured malaria transmission models, optimal control and cost effectiveness of age-structured malaria transmission models, and fractional order of age-structured malaria transmission models, which are listed in the following Tables 1–3.
4 Discussion
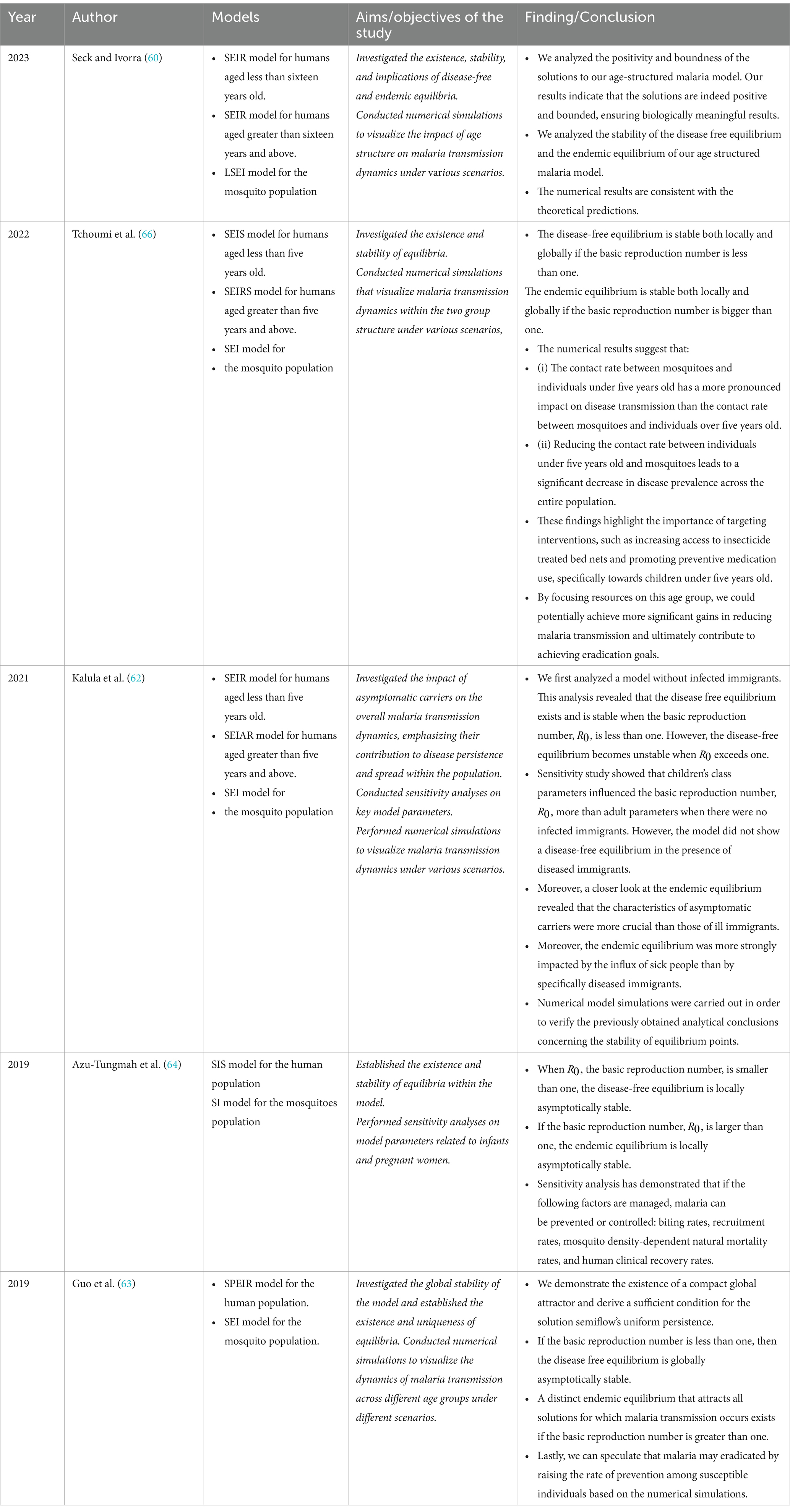
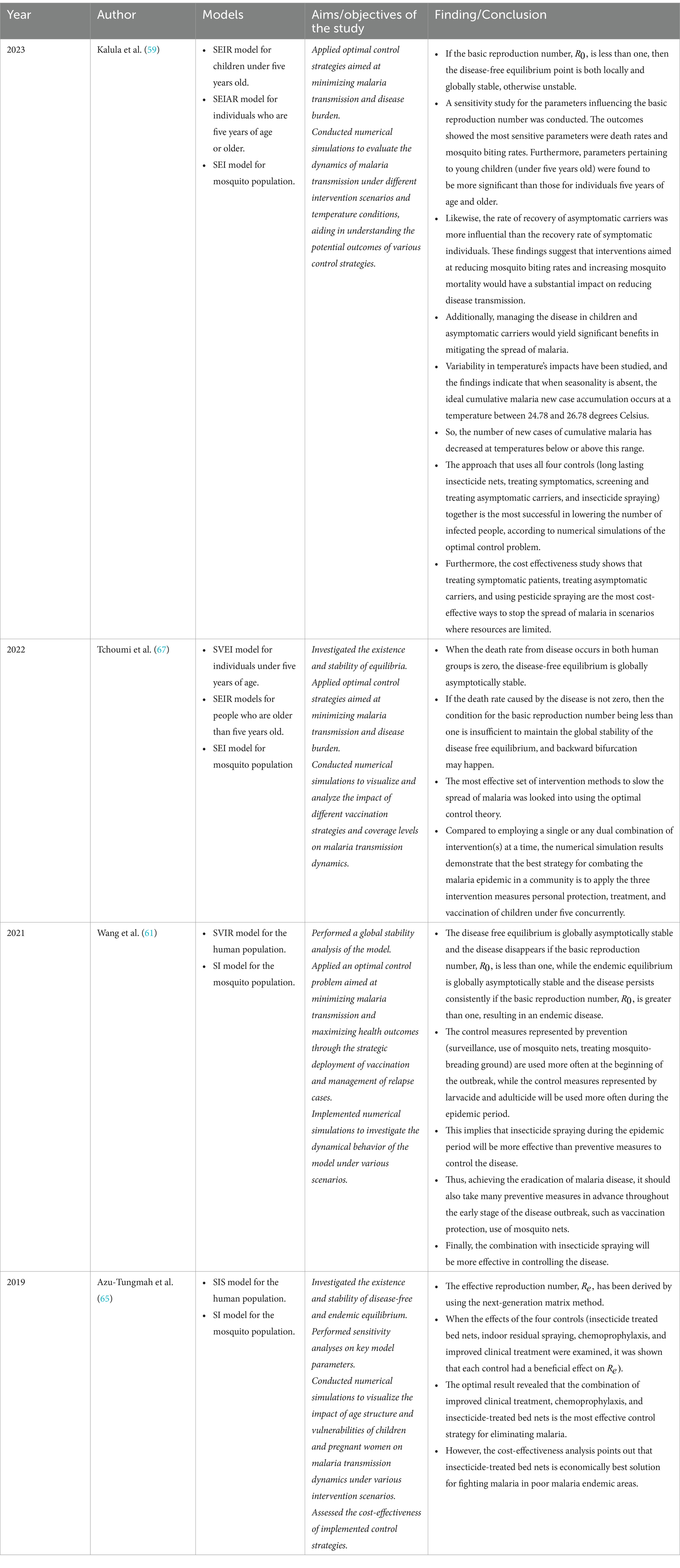
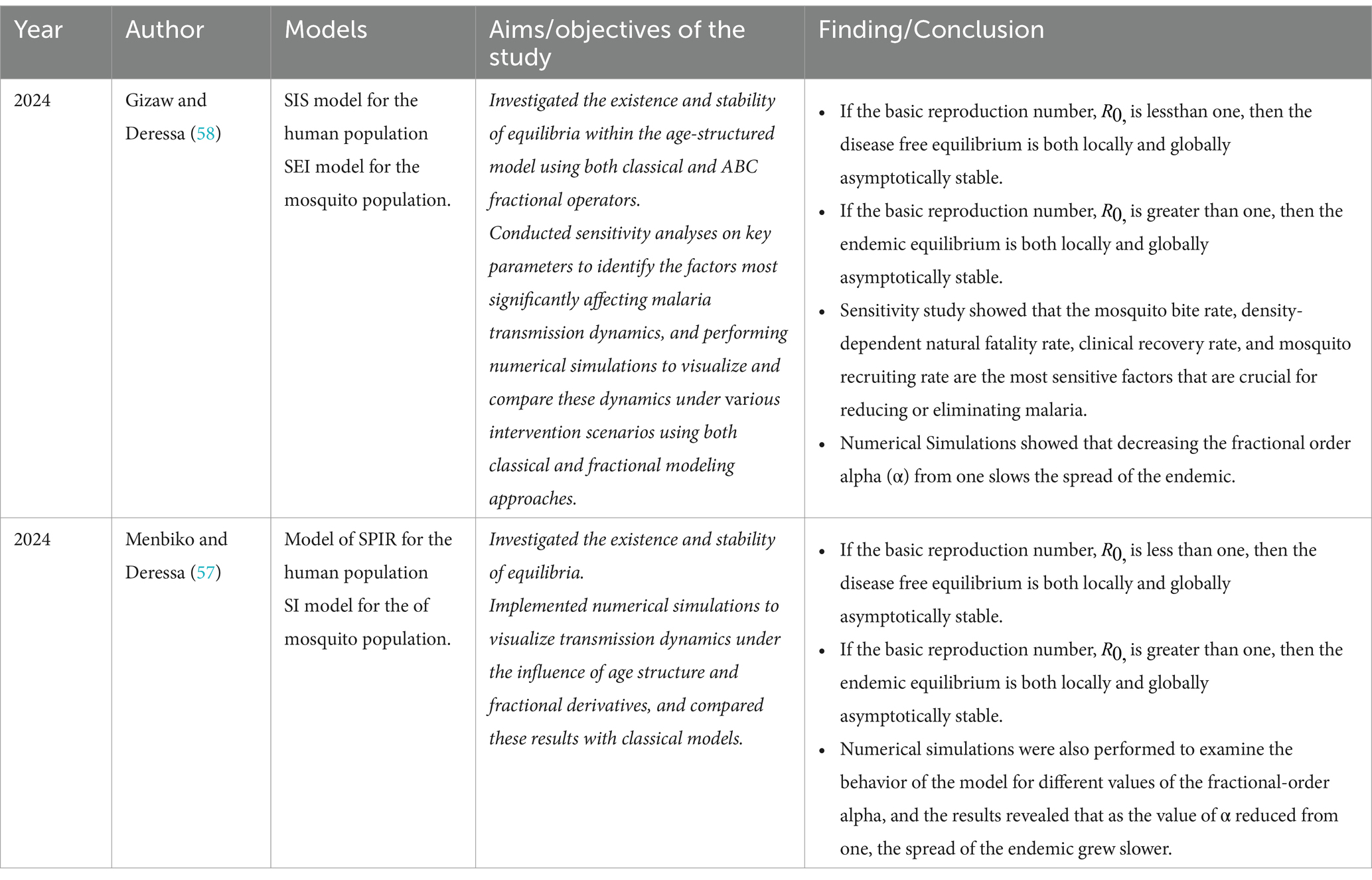
• In order to investigate the dynamics of malaria transmission, Menbiko and Deressa (57) used a mathematical model that included age structure and made use of the Atangana Baleanu fractional derivative. The author included classical and Atangana Baleanu fractional operators in the transmission model details section. The author employed a system of ordinary differential equations along with the SPIR model for the human population and the SI model for the mosquito population. The stability of the endemic and disease-free equilibriums was examined, and the basic reproduction number was calculated. Additionally, numerical simulations are run to investigate the model’s behavior for various values of the fractional order alpha. The outcome showed that the endemic spread slows down when the value of α decreases from 1.
• In order to comprehend the dynamics of malaria transmission, Gizaw and Deressa (58) investigated mathematical models using both fractional order and classical (integer order) derivatives. By adding classical and ABC fractional operators, the author expanded on “Analysis of an age structured malaria model incorporating infants and pregnant women.” The author employed a system of ordinary differential equations along with the SIS model for the human population and the SEI model for the mosquito population. The basic reproduction number was determined, and the stability of both disease free and endemic equilibrium was explored. Using numerical simulations, the behavior of the model for various values of the fractional order alpha was investigated. The findings showed that when the value α decreases from one, the spread of the endemic grows slower.
• According to Kalula et al. (59), an age-structured deterministic model for malaria transmission that includes symptomatic carriers, temperature variability, and its optimal control and effectiveness was studied. The model was analyzed when temperature-dependent parameters are kept constant and a system of ordinary differential equations is used. The basic reproduction number of the model was determined, as was the stability of both disease-free and endemic equilibrium.
• According to the findings of a sensitivity study, the most sensitive criteria for the basic reproduction number are the rates of mosquito bites and deaths. Furthermore, it has been noted that factors pertaining to individuals under the age of five hold greater significance than those relating to those aged five and above. The recovery rate of carriers who do not exhibit symptoms is also comparatively more significant than the recovery rate of persons who do exhibit symptoms. As a result, efforts to lower mosquito bite rates and raise mosquito mortality rates have a bigger effect on lowering the spread of disease.
• Controlling the condition in children and carriers who exhibit symptoms will also have a significant impact. Numerical simulations of the optimal control problem indicate that treating symptomatics, treating asymptomatic carriers, implementing long-lasting insecticide nets, and insecticide spraying is the most effective strategy for reducing the number of infected individuals. The cost-effectiveness analysis also shows that treating symptomatic patients, identifying and treating asymptomatic carriers, and applying pesticide spraying are the most cost-effective ways to stop the spread of malaria in scenarios where resources are limited.
• Seck and Ivorra (60), studied a mathematical model to understand how malaria spreads within a population, specifically considering the influence of age on disease transmission. The author employed a system of ordinary differential equations along with the LSEI model for the mosquito population and the SEIRS model for the human population. The next-generation matrix approach was used to calculate the fundamental reproduction number, and the stability of the endemic and disease-free equilibrium was examined.
• Tchoumi et al. (2022), conducted a theoretical analysis and formulation of a two group malaria model structured by age, wherein individuals under five years old receive vaccine. The author employed a system of ordinary differential equations, the SVEI and SEIR models in the human population, and the SEI model in the mosquito population. The next generation matrix approach was utilized to calculate the basic reproduction number. When the disease induced death rate in both human groups is zero, the disease free equilibrium is globally asymptotically stable; otherwise, backward bifurcation may happen. The outcomes of the numerical simulation showed that the three intervention measures personal protection, treatment, and vaccination of children under five should be implemented concurrently in order to effectively combat the malaria outbreak in a community.
• Tchoumi et al. (66), studied how malaria spread within a population that was divided into two distinct groups. They used the SEI(R)S model for the human population, the SEI model for the mosquito population, and a system of ordinary differential equations. The next generation matrix approach was used to calculate the basic reproduction number, and equilibrium stability was explored. On the other hand, when an endemic equilibrium coexists with a disease free equilibrium, the model may display the phenomena of backward bifurcation under specific circumstances. According to the numerical result, there is a greater sensitivity in the contact rate between mosquitoes and people under five years old than there is between mosquitoes and people over five. Lastly, increasing the effort to combat malaria in children under five has a higher effect on reducing the disease’s spread throughout the population, which may result in better progress toward the disease’s eventual mitigation and eradication.
• Wang et al. (61), examined how to understand and manage malaria transmission using a mathematical model that integrates age structure, immunization, and the occurrence of relapse. The author employed a system of ordinary and partial differential equations, the SVIR model for the human population, and the SI model for the mosquito population. The basic reproduction was calculated, and the disease free equilibrium was both locally and globally asymptotically stable, otherwise unstable, because the basic reproduction number is smaller than unity. According to the numerical result, controlling the disease in combination with insecticide spraying will be more successful.
• According to Kalula et al. (62), malaria spreads in a population, considering the influence of age, infected immigrants, and asymptomatic carriers. The author used the SEI(A)R model for the human population, the SEI model for the mosquito population, and a system of ordinary differential equations. The basic reproduction number was computed, and the stability of the disease-free and endemic equilibrium was discussed. Besides, the sensitivity of the basic reproduction number shows that children’s class parameters are more sensitive than those of adults. In the presence of infected immigrants, the model does not admit a disease-free equilibrium. The numerical results indicate that the asymptomatic carriers have more impacts than the infected immigrants on malaria dynamics.
• Using a mathematical model, Guo et al. (63) investigated the long-term (global) effects of preventive measures on malaria transmission while taking into account the distinct vulnerabilities of different age groups. The author used the SPEIR model for the human population and the SEI model for the mosquito populations, and the model was described as a system of both ordinary and partial differential equations. The author clearly explained well-posedness and uniform persistence. The basic reproduction number was computed, and both local and global stability were discussed. Finally, the author concluded that the basic reproduction number decreased as the rate of prevention increased; that is, increasing the degree of prevention could lead to malaria becoming extinct.
• Azu-Tungmah et al. (64, 65) investigated how the prevalence of malaria in humans varies with age and gender. The author did an extension of “Analysis of an age-structured malaria transmission model” or Wang et al. (36) by incorporating an infectious compartment for pregnant women and avoiding the recovered compartment from Addawe and Lope’s model. The author used the SIS model for the human population, the SI model for the mosquito population, and a system of ordinary differential equations. The basic reproduction number confirmed that the disease-free and endemic equilibrium is both locally and globally stable. Sensitivity analysis has proved that malaria can be controlled or eliminated if the following parameters are controlled: biting rates, recruitment rate, density-dependent natural mortality rate for mosquitoes, and clinical recovery rates for humans.
• The most effective and efficient methods of preventing malaria transmission were investigated by Azu-Tungmah et al. (64, 65), with a particular emphasis on the special vulnerability of pregnant women and children under five. By including optimal control, the author expanded on “Analysis of an age structured malaria model incorporating children under five years and pregnant women.” For the human population, the author employed the SIS model, and for the mosquito population, the SI model. The system of ordinary differential equations was used to define the model. The next generation approach was used to determine the effective reproduction number. The impact of the controls was examined, and it was found that each of the four controls had a positive effect.
5 Conclusion
This systematic review examined the transmission dynamics of malaria in age-structured populations, revealing the crucial role of age in shaping disease spread. Children under five, due to their weaker immune responses, are significantly more susceptible to malaria than adults. The highest rates of morbidity and mortality are seen in youngsters, pregnant women, and people with impaired immune systems. The distribution of age groups plays a crucial role in the spread of malaria within communities, with different age groups contributing uniquely to transmission patterns. Moreover, effective control strategies including personal protection methods, targeted treatment regimens, and vector control interventions have demonstrated a substantial impact in reducing malaria transmission. The application of fractional operators in mathematical models offers further insights into the complexities of malaria transmission and may provide new approaches for optimizing control strategies. Overall, this review underscores the intricate relationship between age structure, demographic factors, and control measures in shaping malaria transmission dynamics. These findings provide valuable guidance for public health efforts aimed at minimizing the global malaria burden.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
DD: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. TK: Conceptualization, Methodology, Supervision, Validation, Writing – review & editing. CD: Conceptualization, Methodology, Resources, Supervision, Validation, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Acknowledgments
The authors would like to thank the reviewers and editors for their valuable comments and suggestions which improved the quality of the paper.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Gen AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. WHO, “Guidelines for malaria. Geneva: World Health Organization; 2022” 1–396, (2022). Available at: https://www.who.int/publications/i/item/; https://www.who.int/teams/global-malaria-programme/reports/world-malaria-report-2022
2. Koutou, O, Traoré, B, and Sangaré, B. Mathematical model of malaria transmission dynamics with distributed delay and a wide class of nonlinear incidence rates. Cogent Math Stat. (2018) 5:1564531. doi: 10.1080/25742558.2018.1564531
3. World Health Organization (WHO), World Malaria World Malaria Report. (2023). Available at: https://www.wipo.int/amc/en/mediation/; https://www.who.int/teams/global-malaria-programme/reports/world-malaria-report-2023
4. Mandal, S, Sarkar, R, and Sinha, S. Mathematical models of malaria—a review. Malar J. (2011) 10:1–19. doi: 10.1186/1475-2875-10-202
5. Ababa, A. Diagnosis and treatment guidelines for health workers in Ethiopia 2nd edition. Heal. (2004) 1:1–62. doi: 10.1186/1475-2875-1-14
6. Traoré, B, Koutou, O, and Sangaré, B. A global mathematical model of malaria transmission dynamics with structured mosquito population and temperature variations. Nonlinear Anal. Real World Appl. (2020) 53:103081. doi: 10.1016/J.Nonrwa.2019.103081
7. Yiga, V, Nampala, H, and Tumwiine, J. Analysis of the model on the effect of seasonal factors on malaria transmission dynamics. J Appl Math. (2020) 2020:1–19. doi: 10.1155/2020/8885558
8. Agusto, FB, Marcus, N, and Okosun, KO. Application of optimal control to the epidemiology of malaria. Elect. J. Differ. Equations. (2012) 81:1–22. doi: 10.1142/S179355712250005X
9. Agusto, FB, del Valle, SY, Blayneh, KW, Ngonghala, CN, Goncalves, MJ, Li, N, et al. The impact of bed-net use on malaria prevalence. J Theor Biol. (2013) 320:58–65. doi: 10.1016/J.Jtbi.2012.12.007
10. Chu, CS, and White, NJ. The prevention and treatment of plasmodium Vivax malaria. PLoS Med. (2021) 18:1–21. doi: 10.1371/Journal.Pmed.1003561
11. Makinde, OD, and Okosun, KO. Impact of chemo-therapy on optimal control of malaria disease with infected immigrants. Biosystems. (2011) 104:32–41. doi: 10.1016/J.Biosystems.2010.12.010
12. Abiodun, G. J., “A mathematical model for studying the impact of climate variability on malaria epidemics in South Africa”. Available at: http://etd.uwc.ac.za/xmlui/handle/11394/5436
13. Altizer, S, Dobson, A, Hosseini, P, Hudson, P, Pascual, M, and Rohani, P. Seasonality and the dynamics of infectious diseases. Ecol Lett. (2006) 9:467–84. doi: 10.1111/J.1461-0248.2005.00879.X
14. Egbendewe-Mondzozo, A, Musumba, M, Mccarl, BA, and Wu, X. Climate change and vector-borne diseases: an economic impact analysis of malaria in Africa. Int J Environ Res Public Health. (2011) 8:913–30. doi: 10.3390/Ijerph8030913
15. Garba, SM, and Danbaba, UA. Modeling the effect of temperature variability on malaria control strategies. Math Model Nat Phenom. (2020) 15:65. doi: 10.1051/Mmnp/2020044
16. Githeko, AK, Lindsay, SW, Confalonieri, UE, and Patz, JA. Climate change and vector-borne diseases: a regional analysis. Bull World Health Organ. (2000) 78:1136–47.
17. Mafwele, BJ, and Lee, JW. Relationships between transmission of malaria in Africa and climate factors. Sci Rep. (2022) 12:1–8. doi: 10.1038/S41598-022-18782-9
18. Jepson, WF, Moutia, A, and Courtois, C. The malaria problem in Mauritius: the bionomics of Mauritian Anophelines. Bull Entomol Res. (1947) 38:177–208. doi: 10.1017/S0007485300030273
19. Paaijmans, KP, Wandago, MO, Githeko, AK, and Takken, W. Unexpected high losses of Anopheles Gambiae larvae due to rainfall. PLoS One. (2007) 2:e1146. doi: 10.1371/Journal.Pone.0001146
20. Mwanga, GG, Haario, H, and Capasso, V. Optimal control problems of epidemic systems with parameter uncertainties: application to a malaria two-age-classes transmission model with asymptomatic carriers. Math Biosci. (2015) 261:1–12. doi: 10.1016/J.Mbs.2014.11.005
21. Olaniyi, S, Okosun, KO, Adesanya, SO, and Lebelo, RS. Modelling malaria dynamics with partial immunity and protected Travellers: optimal control and cost-effectiveness analysis. J Biol Dyn. (2020) 14:90–115. doi: 10.1080/17513758.2020.1722265
22. Siehler, EG. American journal of philology. Caesar Cicero Ferrero. (2019) 161:379–99. doi: 10.31826/9781463222413-001
23. Deressa, CT, Mussa, YO, and Duressa, GF. Optimal control and sensitivity analysis for transmission dynamics of coronavirus. Results Phys. (2020) 19:103642. doi: 10.1016/J.Rinp.2020.103642
24. Pal, KK, Rai, RK, Tiwari, PK, and Kang, Y. Role of incentives on the dynamics of infectious diseases: implications from a mathematical model. Eur Phys J Plus. (2023) 138:1–25. doi: 10.1140/Epjp/S13360-023-04163-2
25. Pal, KK, Sk, N, Rai, RK, and Tiwari, PK. Examining the impact of incentives and vaccination on COVID-19 control in India: addressing environmental contamination and seasonal dynamics. Eur Phys J Plus. (2024) 139:1–29. doi: 10.1140/Epjp/S13360-024-04997-4
26. Diekmann, O, Heesterbeek, JAP, and Metz, JAJ. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J Math Biol. (1990) 28:365–82. doi: 10.1007/BF00178324
27. Kamgang, JC, and Sallet, G. Stabilité Globale Et Asymptotique De L’équilibre Sans Maladie Des Modèles Épidémiologiques. Comptes Rendus Math. (2005) 341:433–8. doi: 10.1016/J.Crma.2005.07.015
29. Ross, R. Some a priori Pathometric equations. Br Med J. (1915) 1:546–7. doi: 10.1136/Bmj.1.2830.546
30. Simon, CP, and Jacquez, JA. Reproduction numbers and the stability of equilibria of SI models for heterogeneous populations. SIAM J Appl Math. (1992) 52:541–76. doi: 10.1137/0152030
31. Smith, DL, Battle, KE, Hay, SI, Barker, CM, Scott, TW, and Mckenzie, FE. Ross, Macdonald, and a theory for the dynamics and control of mosquito-transmitted pathogens. PLoS Pathog. (2012) 8:e1002588. doi: 10.1371/Journal.Ppat.1002588
32. Van Den Driessche, P, and Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci. (2002) 180:29–48. doi: 10.1016/S0025-5564(02)00108-6
33. Schumacher, RF, and Spinelli, E. Malaria in children. Medit J Hematol Infect Dis. (2012) 4:73. doi: 10.4084/MJHID.2012.073
34. Forouzannia, F, and Gumel, AB. Mathematical analysis of an age-structured model for malaria transmission dynamics. Math Biosci. (2014) 247:80–94. doi: 10.1016/J.Mbs.2013.10.011
35. Liu, L, Wang, J, and Liu, X. Global stability of an SEIR epidemic model with age-dependent latency and relapse. Nonlinear Anal Real World Appl. (2015) 24:18–35. doi: 10.1016/J.Nonrwa.2015.01.001
36. Wang, X, Chen, Y, and Liu, S. Global dynamics of a vector-borne disease model with infection ages and general incidence rates. Comput Appl Math. (2018) 37:4055–80. doi: 10.1007/S40314-017-0560-8
37. Wang, L, Liu, Z, and Zhang, X. Global dynamics for an age-structured epidemic model with media impact and incomplete vaccination. Nonlinear Anal. Real World Appl. (2016) 32:136–58. doi: 10.1016/J.Nonrwa.2016.04.009
38. Magal, P, Mccluskey, CC, and Webb, GF. Lyapunov functional and global asymptotic stability for an infection-age model. Appl Anal. (2010) 89:1109–40. doi: 10.1080/00036810903208122
39. Khan, A, and Zaman, G. Optimal control strategy of SEIR endemic model with continuous age-structure in the exposed and infectious classes. Optim Control Appl. Methods. (2018) 39:1716–27. doi: 10.1002/Oca.2437
40. Wang, X, Chen, Y, and Liu, S. Dynamics of an age-structured host-vector model for malaria transmission. Math. Methods Appl. Sci. (2018) 41:1966–87. doi: 10.1002/Mma.4723
41. Abboubakar, H, Kumar, P, Rangaig, NA, and Kumar, S. A malaria model with Caputo-Fabrizio and Atangana-Baleanu derivatives. Int J Model Simul Sci Comput. (2021) 12:2150013. doi: 10.1142/S1793962321500136
42. Akyildiz, FT, and Alshammari, FS. Complex mathematical SIR model for spreading of COVID-19 virus with Mittag-Leffler kernel. Adv. Differ. Equations. (2021) 2021:1–17. doi: 10.1186/S13662-021-03470-1
43. Boukhouima, A, Hattaf, K, Lotfi, EM, Mahrouf, M, Torres, DFM, and Yousfi, N. Lyapunov functions for fractional-order systems in biology: methods and applications. Chaos Solitons Fractals. (2020) 140:110224. doi: 10.1016/J.Chaos.2020.110224
44. Devi, AS, Pal, KK, and Tiwari, PK. Exploring fractional dynamical probes in the context of gender-structured Hiv–Tb coinfection: a study of control strategies. J Biol Syst. (2024) 32:719–69. doi: 10.1142/S0218339024500256
45. Helikumi, M, and Lolika, PO. Global dynamics of fractional-order model for malaria disease transmission. Asian Res. J. Math. (2022) July:82–110. doi: 10.9734/Arjom/2022/V18i930409
46. Toufik, M, and Atangana, A. New numerical approximation of fractional derivative with non-local and non-singular kernel: application to chaotic models. Eur Phys J Plus. (2017) 132:1–16. doi: 10.1140/Epjp/I2017-11717-0
47. Yavuz, M, and Bonyah, E. New approaches to the fractional dynamics of schistosomiasis disease model. Phys Stat Mech Its Appl. (2019) 525:373–93. doi: 10.1016/J.Physa.2019.03.069
48. Ali, A, Islam, S, Khan, MR, Rasheed, S, Allehiany, FM, Baili, J, et al. Dynamics of a fractional order Zika virus model with mutant. Alex Eng J. (2022) 61:4821–36. doi: 10.1016/J.Aej.2021.10.031
49. Shikrani, R, Hashmi, MS, Khan, N, Ghaffar, A, Nisar, KS, Singh, J, et al. An efficient numerical approach for space fractional partial differential equations. Alex Eng J. (2020) 59:2911–9. doi: 10.1016/J.Aej.2020.02.036
50. Simelane, SM, and Dlamini, PG. A fractional order differential equation model for hepatitis B virus with saturated incidence. Results Phys. (2021) 24:104114. doi: 10.1016/J.Rinp.2021.104114
51. Altaf Khan, M, Ullah, S, and Farooq, M. A new fractional model for tuberculosis with relapse via Atangana–Baleanu derivative. Chaos Solitons Fractals. (2018) 116:227–38. doi: 10.1016/J.Chaos.2018.09.039
52. Deressa, CT, and Duressa, GF. Analysis of Atangana–Baleanu fractional-order SEAIR epidemic model with optimal control. Adv Differ Equations. (2021) 2021:174. doi: 10.1186/S13662-021-03334-8
53. Kumar, D, Singh, J, Al Qurashi, M, and Baleanu, D. A new fractional SIRS-SI malaria disease model with application of vaccines, antimalarial drugs, and spraying. Adv Differ Equations. (2019) 2019:1–19. doi: 10.1186/S13662-019-2199-9
54. Shah, SAA, Khan, MA, Farooq, M, Ullah, S, and Alzahrani, EO. A fractional order model for hepatitis B virus with treatment via Atangana–Baleanu derivative. Phys Stat Mech Appl. (2020) 538:122636. doi: 10.1016/J.Physa.2019.122636
55. Tilahun, GT, Woldegerima, WA, and Mohammed, N. A fractional order model for the transmission dynamics of hepatitis B virus with two-age structure in the presence of vaccination. Arab J Basic Appl Sci. (2021) 28:87–106. doi: 10.1080/25765299.2021.1896423
56. Page, MJ, McKenzie, JE, Bossuyt, PM, Boutron, I, Hoffmann, TC, Mulrow, CD, et al. The PRISMA 2020 statement: an updated guideline for reporting systematic reviews. BMJ. (2021) 372:1–8. doi: 10.1136/Bmj.N71
57. Menbiko, DK, and Deressa, CT. Modeling and analysis of an age-structured malaria model in the sense of Atangana-Baleanu fractional operators. J Undergrad Math. (2024) 2024:1–30. doi: 10.1155/2024/6652037
58. Gizaw, AK, and Deressa, CT. Analysis of age-structured mathematical model of malaria transmission dynamics via classical and ABC fractional operators. Math Probl Eng. (2024) 2024:1–24. doi: 10.1155/2024/3855146
59. Kalula, A, Mureithi, E, Marijani, T, and Mbalawata, I. Optimal control and cost-effectiveness analysis of age-structured malaria model with asymptomatic carrier and temperature variability. J Biol Dyn. (2023) 17:1–36. doi: 10.1080/17513758.2023.2199766
60. Seck, R., and Ivorra, B., “A mathematical model for studying the malaria transmission with age-structured populations. Application to some areas of Senegal, (2023). 1–33. doi: 10.13140/RG.2.217866.64963
61. Wang, SF, Hu, L, and Nie, LF. Global dynamics and optimal control of an age-structure malaria transmission model with vaccination and relapse. Chaos Solitons Fractals. (2021) 150:111216. doi: 10.1016/J.Chaos.2021.111216
62. Kalula, AS, Mureithi, E, Marijani, T, and Mbalawata, I. An age-structured model for transmission dynamics of malaria with infected immigrants and asymptomatic carriers. Tanzania J Sci. (2021) 47:953–68. doi: 10.4314/Tjs.V47i3.7
63. Guo, Z, Huo, H, and Xiang, H. Global dynamics of an age-structured malaria model with prevention (2019) 16:1625–53. doi: 10.3934/mbe.2019078
64. Azu-Tungmah, GT, Oduro, FT, and Okyere, GA. Analysis of an age-structured malaria model incorporating infants and pregnant women. J Adv Math Comput Sci. (2019) 30:1–21. doi: 10.9734/Jamcs/2019/46649
65. Azu-Tungmah, GT, Oduro, FT, and Okyere, GA. Optimal control analysis of an age-structured malaria model incorporating children under five years and pregnant women. J Adv Math Comput Sci. (2019):1–23. doi: 10.9734/Jamcs/2019/V30i630096
66. Tchoumi, SY, Dongmo, EZ, Kamgang, JC, and Tchuenche, JM. Dynamics of a two-group structured malaria transmission model. Inform Med Unlocked. (2021) 29:100897. doi: 10.1016/J.Imu.2022.100897
Keywords: malaria, deterministic model, age-structure, control strategies, systematic review
Citation: Dinsa DW, Keno TD and Deressa CT (2024) A systematic review of age-structured malaria transmission models (2019–2024). Front. Appl. Math. Stat. 10:1512390. doi: 10.3389/fams.2024.1512390
Edited by:
Hua Nie, Shaanxi Normal University, ChinaReviewed by:
Pankaj Tiwari, University of Kalyani, IndiaZhiguo Wang, Shaanxi Normal University, China
Copyright © 2024 Dinsa, Keno and Deressa. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dechasa Wegi Dinsa, ZGVjaDIwMDNAZ21haWwuY29t
 Dechasa Wegi Dinsa
Dechasa Wegi Dinsa Temesgen Duressa Keno
Temesgen Duressa Keno Chernet Tuge Deressa3
Chernet Tuge Deressa3