Analysis of school bullying menace incorporating family education: a mathematical modeling approach

School bullying is a severe social problem that has an unfavorable impact on students development and behavior. Based on family education and students memory of having been bullied or witnessed bullying, this work established a mathematical model for analyzing school bullying dynamics. By employing the Caputo fractional derivative, the model incorporates students' memory in the interactional patterns of bullying, which provides for improved emulation of the impacts of previous episodes on future behaviors. An Adams-Bashforth method numerical scheme is presented, offering a robust approach for scenario simulations under the Caputo fractional operator. Scenario simulations shows the impact of family education on the prevalence and dynamics of school bullying. It is noticed that the behavior of students who lack and with family education and not involving bullying under different values of fractional order. The trajectory changes with the fractional order, suggesting that the system's sensitivity to initial conditions or recent changes decreases as fractional order reduce from the normal dynamics (integer order). Essentially, a lower fractional order makes the system less reactive to short-term fluctuations and more stable.

1 Introduction

Bullying is a pervasive issue that affects individuals across ages, genders, and cultures. It includes the intentional and persistent use of physical force, emotional or psychological aggressiveness to injure, threaten, or dominate another individual. While bullying has always existed, its prevalence and severity have increased in recent years due to the widespread use of technology and social media. This has become a common problem in schools (institutions of learning at different levels) and communities that has negative effects on the victims and society as a whole. Bullying can take different forms such as physical, verbal, relational, and cyberbullying. This literature review aims to examine the current state of research on bullying, its prevalence, effects on victims, and interventions to prevent and address bullying.

Bullying can lead the victim to commit crime, start engaging in drugs and smoking, and has psychological effects. These social vices have been studied extensively in the literature. In Nwajeri et al. [1], the authors studied the co-dynamic of drug trafficking and money laundering using fractional derivatives and also in Ngungu et al. [2], authors considered smoking in different age groups using fractal fractional derivatives and how government can intervene to curb the menace. In Alaka et al. [3], authors considered the psychological effect of the Coronavirus disease outbreak in a given population.

Bullying is a complex phenomenon that can be difficult to define, as it involves a wide range of behaviors and motivations. Some definitions emphasize the repetitive nature of bullying, while others focus on the power imbalance between the bully and the victim (or bullied). According to the Centers for Disease Control and Prevention (CDC), bullying is characterized as persistent, unwelcome aggressive behavior from one young individual or a group of youths who are not related or in current dating relationships. This behavior entails a perceived or observable power imbalance and occurs repeatedly or is highly anticipated [4].

1.1 Effects on victims/impacts

Bullying has non-positive impacts on the mental-physical health, academic outcome, and social relationships of the victims. Bullying victims are more prone to suffer from sadness, anxiety, low self-esteem, and suicidal thoughts, and post-traumatic stress disorder (PTSD) and sometimes leading to mental health issues than non-victims [5]. Others include physical injuries. Bullying can also have a negative influence on academic performance, with victims reporting lower grades, decreased motivation, and decreased attendance. These effects can also have an impact on the victims' social interactions, resulting in social isolation and difficulty forming friends.

1.2 Interventions

A range of interventions are being created to avoid and combat bullying, with varying degrees of success. School-based interventions often involve a union of classroom-based curricula, school-wide policies and procedures, and parent education and involvement. One effective approach is the Olweus Bullying Prevention Program, which involves a whole-school approach to bullying prevention and includes teacher training, parent education, and student-centered interventions [6]. Another promising approach is restorative justice, which aims to address the harm caused by bullying through dialogue and community-building. Restorative justice involves bringing together the victim, the perpetrator, and other relevant parties to discuss the harm caused and develop a plan for making amends. This approach can be particularly effective in cases where the victim and perpetrator have an ongoing relationship, such as in school or community settings [7]. The following are some additional interventions: social-emotional learning (SEL) programs, which work to develop students' social and emotional competencies in order to deter bullying and encourage pro-social conduct. These programs impart abilities like self-awareness, empathy, and problem-solving [8, 9]. School-wide initiatives are designed to make all students feel protected and supported. The Positive Behavioral Interventions and Supports (PBIS) program is one example of a program that involves the entire school community, including teachers, students, and parents, in promoting positive behavior and combating bullying [10–13].

1.3 Prevalence

Bullying is a widespread problem that affects individuals across ages, genders, and cultures. This is a major issue in schools and communities all across the world. The incidence of bullying in schools ranges from 9 to 98%, with an average prevalence of 35%, according to a meta-analysis of 80 studies [14]. Prevalence rates vary depending on the population studied, the definition of bullying used, and the method of data collection. However, research indicates that bullying is a pervasive issue that impacts a significant portion of the population. In schools, estimates suggest that up to 30% of students have experienced bullying at some point [15, 16]. Bullying takes various kinds, both bodily harm and verbal, relational, and cyberbullying [17–20]. While all forms of bullying are harmful, cyberbullying has emerged as a particularly concerning issue, given its potential for anonymity and widespread dissemination of hurtful messages or images. The prevalence of bullying is not limited to schools, as it also occurs in the workplaces, among adults, and in online communities. In a study of American adults, 31% reported experiencing bullying in the workplace, with women and racial minorities being at higher risk [21–23]. In online communities, cyberbullying is a growing concern, with one study finding that 70% of young people aged 13–22 reported experiencing [24–26]. It is important to note that prevalence rates may underestimate the true extent of the problem, as many victims may not report bullying due to fear of retaliation, stigma, or a lack of trust in authorities. The prevalence of bullying is higher among middle and high school students than elementary school students, and boys are more likely to be involved in bullying than girls. Additionally, some populations may be at higher risk of experiencing bullying, including individuals with disabilities [27–29], members of the LGBTQ+ community [30–32], students of color and those from marginalized racial and ethnic groups or minority students.

1.4 Effect of bullying on persons with family background

In this paper, we consider the effect of bullying on students incorporating the influence of family education. Bullying can have significant impacts on individuals, including those who lack family education. Family factors such as parenting practices, family relationships, and family conflict can influence an individual's vulnerability to bullying and their ability to cope with its effects. Research has shown that children who experience high levels of family conflict, low levels of parental support, and harsh or inconsistent parenting are more likely to experience bullying [33, 34]. Additionally, family conflict and a lack of parental support can make it harder for children to cope with the effects of bullying, leading to increased psychological distress and lower self-esteem [35]. For children from immigrant families, bullying can be particularly challenging, as they may face additional stressors such as language barriers, cultural differences, and discrimination. It is imperative to note that immigrant children who experience bullying may be more likely to experience psychological distress, lower academic achievement, and social isolation. Furthermore, the effects of bullying can extend beyond the individual to their family members. For example, parents of children who have experienced bullying may experience heightened stress, anxiety, and feelings of helplessness and guilt [36, 37]. Siblings of children who have experienced bullying may also be affected, with some research indicating that they may experience increased psychological distress and lower self-esteem [38–40]. Having to understand the family background is not only a point of consideration but also a necessary step to investigate the effect or importance of a person coming from a family with an education. Hence the reason why we introduce the knowledge of mathematical modeling as a tool to analytically and numerically study this effect.

1.5 Mathematical modeling of bullying

Mathematical Modeling has been used to study the dynamics of various social phenomena, including the spread of infectious diseases [2, 41], the evolution of social networks [42], [Addai11] and the emergence of collective behaviors [43]. Recent research has looked at mathematical modeling to better understand the dynamics of bullying and to develop effective strategies for prevention and intervention. Mathematical modeling is a way of representing a real-world phenomenon, in this case bullying, through mathematical formulas and equations. This helps to create a more accurate prediction of how bullying dynamics will develop over time. It can also be used to identify potential weaknesses in anti-bullying strategies, as well as potential solutions. Mathematical modeling can also be used to determine the effectiveness of various anti-bullying policies. By predicting the impact of different policies and strategies in different scenarios, it is possible to develop a comprehensive and effective set of measures for preventing and intervening in bullying situations. Recently, a mathematical model was created to analyze the phenomenon of bullying, with the aim of understanding the mechanisms underlying its occurrence and developing effective interventions to prevent it [44]. Another approach to modeling bullying is to use game-theoretic models, which allow researchers to study the interactions between individuals in a social context. Game theory can be used to model situations in which individuals have to make strategic decisions, taking into account the decisions of others. In the context of bullying, game-theoretic models can be used to study how the decisions of bullies, victims, and bystanders influence the occurrence and persistence of bullying behaviors. Other approaches to modeling bullying are network models which will be considered later in the future.

1.6 Mathematical modeling of bullying and its effect on students with family education

To date, there is limited research on the mathematical modeling of bullying and its effects specifically on students with family education. However, the use of mathematical modeling to study bullying can be useful in understanding the complex dynamics of bullying, and how it affects a person with family backgrounds. To implement this, we will employ the Caputo fractional operator.

The Caputo fractional derivative operator is a generalization of the classical derivative operator to non-integer orders, and it has been used in various applications in physics, engineering, mathematics, and the modeling of complex phenomena such as social behavior. The versatility of fractional derivatives, particularly the Caputo form, lies in their ability to capture long-range dependencies and memory effects, which makes them well-suited for modeling systems with memory or hereditary properties. These characteristics are crucial when modeling real-world systems where the history of the process significantly influences the present and future states of the system.

The Caputo fractional derivative was selected over other fractional derivative such as Caputo-Fabrizio, Atangana-Baleanu, Hadamard because of its suitability for initial value problems where the conditions of the system at earlier times directly influence the evolution of the model. In the context of bullying dynamics, the Caputo derivative enables a representation of how historical exposure to bullying influences current behavior patterns, accounting for how these influences accumulate gradually. Unlike classical differential models, which assume that only the current state of an individual determines their behavior, the fractional-order model incorporates a more realistic aspect by accounting for the cumulative impact of past experiences, thus making it particularly useful in capturing the essence of complex social interactions such as bullying.

Moreover, the memory effect captured by the fractional order relates directly to the dynamics of bullying in that it emphasizes the enduring nature of the behavioral tendencies formed through prolonged exposure to family education. This means that a student's current predisposition toward either bullying or avoiding it is influenced by not just recent experiences but by the cumulative history of family upbringing. For example, the support or lack thereof provided by a family in educating a student about social skills, empathy, and conflict resolution creates a type of "memory" that continuously influences their responses to bullying situations. Through this model, it becomes possible to simulate scenarios where stronger family support (as represented by the fractional order parameters) leads to reduced vulnerability to bullying or diminished propensity for becoming a bully, capturing the nuanced and long-term nature of behavioral development.

Ashi et al. [44] investigated the theoretical analysis of bullying by considering the stability analysis of school bullying in adolescents being bullied by other students. The authors gave good insight but this insight is not enough to draw inference as it does not consider other factors in the model, hence our work improved the model by considering a root cause. Our work is the first to investigate the possible source of bullying attributed to family eduction. We hypothesize that bullying does not occur without a fault which means it has a root and we decided that the root could possibly be as a result of family background which is aligned to the education status in the family. After carefully introducing the effect of victims, interventions, prevalence, effects of bullying on persons with family background, we propose a mathematical model that investigates the effects of family education on student bullying.

2 Model formulation

For the purpose of the model under consideration, we divide the total student population into four compartments: namely the students with lack of family education X₁, that is, students who lack family education and not involving bullying; students with family education X₂, that is, student who have family education and not involving bullying; the bully students with lack of family education Y₁; the bully students with family education Y₂. The following nonlinear ordinary differential equations are generated by considering the interplay between the compartments:

$\begin{array}{ll}\{\begin{array}{l}\frac{d{X}_1}{dt}=(1-m)A+{\xi }_2{X}_2(t)-({\lambda }_1+{\xi }_1)X_1-{\mu }_1{X}_1(t)Y_1(t),\hfill \\ \frac{d{X}_2}{dt}=(m)A+{\xi }_1{X}_1(t)-({\lambda }_2+{\xi }_2)X_2-{\mu }_2{X}_2(t)Y_2(t),\hfill \\ \frac{d{Y}_1}{dt}={\beta }_1{X}_1(t)Y_1(t)+\psi Y_2(t)-({\nu }_1+\varphi )Y_1(t),\hfill \\ \begin{array}{l}\frac{d{Y}_2}{dt}={\beta }_2{X}_2(t)Y_2(t)+\varphi Y_1(t)-({\nu }_2+\psi )Y_2(t).\hfill \end{array}\hfill \end{array}& (1)\end{array}$

where the total population at time is

$N(t)=X_1(t)+X_2(t)+Y_1(t)+Y_2(t).$

The corresponding non-negative initial conditions to the Equation 1 are given below

$X_1(0)\ge 0,X_2(0)\ge 0,Y_1(0)\ge 0,Y_2(0)\ge 0.$

The recruitment rates of school enrollment in the Equation 1 is denoted by $A$. m denote the rate of students who lack education from their families while ξ₁ and ξ₂ are progression to X₂ from X₁ and to X₁ from X₂, respectively. The rate of X₁ and X₂ graduate from schools are denoted as λ₁ and λ₂, respectively. The non-negative parameters μ₁ and μ₂ measure students who leave school due to the harassment of the bullies. The rates at which Y₁ and Y₂ bullies on other students are measured by β₁ and β₂, respectively. The rate of Y₁ and Y₂ who are expelled from school are denote by ν₁ and ν₂. Parameters ψ and ϕ measure the proportion of Y₂ who become Y₁ and proportion of Y₁ who become Y₂, respectively.

The key parameters associated with family education are:

1. m: The rate of students who lack education from their families. This parameter represents the proportion of students entering the school environment without sufficient family support or education.

2. ξ₁ and ξ₂: These represent the rates of progression between the compartments. Specifically, ξ₁ is the rate at which students without family education (X₁) gain sufficient family support and transition to students with family education (X₂). Conversely, ξ₂ represents the regression from X₂ to X₁, indicating instances where family support diminishes.

3. μ₁ and μ₂: These parameters measure the rates at which students leave school due to bullying. They are influenced by the level of family education, which is assumed to impact resilience against bullying behavior. For instance, students with family education (X₂) may be better equipped to cope with bullying and less likely to drop out compared to those without such support (X₁).

The inclusion of family education is built on several underlying assumptions:

1. Family education as a protective factor: we assume that family education plays a significant role in providing the necessary social and emotional tools for students to avoid involvement in bullying, either as victims or perpetrators. This is based on evidence suggesting that strong family support is associated with reduced vulnerability to bullying and a higher likelihood of coping effectively with bullying scenarios.

2. Dynamic interaction: the model assumes that family education is not static but can change over time. This is represented by the transition rates ξ₁ and ξ₂, which allow students to move between the compartments of having and not having family education. This reflects real-life scenarios where family circumstances may improve or worsen over time, influencing a student's vulnerability to bullying.

3. Impact on bullying behavior: we incorporate family education's influence directly into the interaction terms, such as β₁X₁Y₁ and β₂X₂Y₂, where β₁ and β₂ represent the bullying rate by students without and with family education, respectively. The presence of family education is assumed to decrease the likelihood of students becoming bullies or being bullied, thereby influencing these interaction terms.

Tilahun et al. [45] discuss the power law correlation function and its implications for a time-dependent kernel. This discussion allows us to integrate the Caputo fractional order derivative into our model. As a result, the ordinary differential Equation 1 is reformulated into a Caputo fractional-order system as shown below:

$\begin{array}{ll}\{\begin{array}{l}{}_0{}^C{{\displaystyle D}}_t^{\alpha }{X}_1(t)=(1-m)A+{\xi }_2{X}_2(t)-({\lambda }_1+{\xi }_1)X_1-{\mu }_1{X}_1(t)Y_1(t),\hfill \\ {}_0{}^C{{\displaystyle D}}_t^{\alpha }{X}_2(t)=(m)A+{\xi }_1{X}_1(t)-({\lambda }_2+{\xi }_2)X_2-{\mu }_2{X}_2(t)Y_2(t),\hfill \\ {}_0{}^C{{\displaystyle D}}_t^{\alpha }{Y}_1(t)={\beta }_1{X}_1(t)Y_1(t)+\psi Y_2(t)-({\nu }_1+\varphi )Y_1(t),\hfill \\ {}_0{}^C{{\displaystyle D}}_t^{\alpha }{Y}_1(t)={\beta }_2{X}_2(t)Y_2(t)+\varphi Y_1(t)-({\nu }_2+\psi )Y_2(t).\hfill \end{array}& (2)\end{array}$

where t∈[0, η], $T\in ℝ$, and ${}_0{}^C{{\displaystyle D}}_t^{\alpha }$ denotes the Caputo fractional derivative of order α, where the memory index is denoted as α, 0 < α ≤ 1. Note that when α = 1 the fractional-order model reduces to the ordinary differential model (Equation 1). It is commonly known that Caputo's derivative offers greater dependability and adaptability in analytical applications. Due to initial condition properties, which are more physically interpretable for most problems, many researchers consider the Caputo operator over other derivatives. Consequently, we represented the dynamics of the bullying using fractional theory. Table 1 describe and defines the system parameters.

Table 1

Table 1. Meaning of parameters in the model.

3 Preliminaries

The section details various key definitions, lemmas, and ideas that are required to comprehend our proposed model.

Definition 2.1 [46, 47] Given an integrable function u:ℝ⁺ → ℝ, and α∈(n−1, n), n∈N. The left Caputo fractional derivative of order α of the function u is defined as

${}_0{}^C{{\displaystyle D}}_t^{\alpha }(u(t))=\frac{1}{\Gamma (n-\alpha )}{\displaystyle {\int }_0^t{u}^n}(\Theta ){(t-\Theta )}^{n-\alpha -1}d\Theta$

Definition 2.2 [47] The appropriate Riemann-Liouville fractional integral for the power-law kernel is given as

$C_0{I}_t^{\alpha }(u(t))=\frac{1}{\Gamma (\alpha )}{\displaystyle {\int }_0^t{(t-\Theta )}^{\alpha -1}}u(\Theta )d\Theta ,t>0.$

Lemma 2.3 [47] Assuming there is a function u(t)∈C([c, d], ℝ) of order α∈(0, 1). The existence-uniqueness of the fractional differential equation

$\{\begin{array}{l}{}_0{}^C{{\displaystyle D}}_t^{\alpha }u(t)=\Upsilon (t,u(t)),t\in [0,T],\hfill \\ u(0)=u_0,\hfill \end{array}$

is continuous and bounded and satisfies a Lipschitz condition.

4 Existence and uniqueness

This section will present solutions for the existence and uniqueness of the Caputo model for the Equation 2. Suppose that there exists a set of real valued Banach space functions denoted $G$ on the interval $B=\left[0,T\right]$ and let denote $M=G(B)\times G(B)\times G(B)\times G(B)$ with norm ||(X₁, X₂, Y₁, Y₂)|| = ||X₁||+||X₂||+||Y₁||+||Y₂||, where $\left|\right|X_1\left|\right|=\underset{t\in B}{sup}\left|X_1\right|,\left|\right|X_2\left|\right|=\underset{t\in B}{sup}\left|X_2\right|,\left|\right|Y_1\left|\right|=\underset{t\in B}{sup}\left|Y_1\right|,\left|\right|Y_2\left|\right|=\underset{t\in B}{sup}\left|Y_2\right|.$ We reformulate the right-hand side of Equation 2 as follows:

$\begin{array}{ll}\{\begin{array}{l}{D}_1(\vartheta ,X_1,X_2,Y_1,Y_2)=(1-m)A+{\xi }_2{X}_2(t)-({\lambda }_1+{\xi }_1)X_1\hfill \\ -{\mu }_1{X}_1(t)Y_1(t),\hfill \\ D_2(\vartheta ,X_1,X_2,Y_1,Y_2)=(m)A+{\xi }_1{X}_1(t)-({\lambda }_2+{\xi }_2)X_2\hfill \\ -{\mu }_2{X}_2(t)Y_2(t),\hfill \\ D_3(\vartheta ,X_1,X_2,Y_1,Y_2)={\beta }_1{X}_1(t)Y_1(t)+\psi Y_2(t)-({\nu }_1+\varphi )Y_1(t),\hfill \\ D_4(\vartheta ,X_1,X_2,Y_1,Y_2)={\beta }_2{X}_2(t)Y_2(t)+\varphi Y_1(t)-({\nu }_2+\psi )Y_2(t).\hfill \end{array}& (3)\end{array}$

From understanding in Equation 3, our proposed Caputo fractional Equation 2 can be expressed as

$\begin{array}{ll}\{\begin{array}{l}{}_0{}^C{{\displaystyle D}}_t^{\alpha }D(\vartheta )=\Upsilon (\vartheta ,D(\vartheta )), \vartheta \in [0,T], 0<\alpha \le 1,\hfill \\ D(0)=D_0,\hfill \end{array}& (4)\end{array}$

where

$\begin{array}{ll}D(\vartheta )=\{\begin{array}{l}{X}_1(\vartheta ),\hfill \\ X_2(\vartheta ),\hfill \\ Y_1(\vartheta ),\hfill \\ \begin{array}{l}{Y}_2(\vartheta ),\hfill \end{array}\hfill \end{array}{D}_0=\{\begin{array}{l}{X}_1(0),\hfill \\ X_2(0),\hfill \\ Y_3(0),\hfill \\ Y_2(0),\hfill \end{array}& (5)\end{array}$

and

$\begin{array}{ll}\Upsilon (\vartheta ,D(\vartheta ))=\{\begin{array}{l}{D}_1(\vartheta ,X_1,X_2,Y_1,Y_2),\hfill \\ D_2(\vartheta ,X_1,X_2,Y_1,Y_2),\hfill \\ D_3(\vartheta ,X_1,X_2,Y_1,Y_2),\hfill \\ D_4(\vartheta ,X_1,X_2,Y_1,Y_2).\hfill \end{array}& (6)\end{array}$

Using the ideas in Lemma 2.3, Equation 4 yields

$\begin{array}{ll}D(\vartheta )=D_0(\vartheta )+\frac{1}{\Gamma (\alpha )}{\displaystyle \underset{0}{\overset{\vartheta }{\int }}}\Upsilon (\nu ,D(\nu )){(\vartheta -\nu )}^{\alpha -1}d\nu .& (7)\end{array}$

From here, our aim is to find the existence and uniqueness solutions, we assume the function vector

$\begin{array}{ll}B=\left[0,T\right]\times {ℝ}_{+}^4\to {ℝ}_{+}& (8)\end{array}$

as:

$(H_1)$ ∃ ${\Omega }_B,{\Theta }_B$ such that

$\begin{array}{ll}\Upsilon (\vartheta ,D(\vartheta ))\le {\Omega }_B\left|D\right|+{\Theta }_B.& (9)\end{array}$

$(H_2)$ ∃ ${\mathbf{\text{L}}}_B>0$ such that if $D,\tilde{D}\in M$, then

$\begin{array}{ll}|\Upsilon (\vartheta ,D(\vartheta ))-\Upsilon (\vartheta ,\tilde{D}(\vartheta ))|\le {\text{L}}_B\left[|D-\tilde{D}|\right].& (10)\end{array}$

Theorem 4.1. Under the continuity of $B$ together with $(H_1)$, Equation 4 has at least one solution.

Proof . We shall arrive at the required conclusion using the Schauder fixed point theorem. Let us take a closed subset $G$ of $B$ as $W_B=\left\{D\in B:\left|\right|D\left|\right|\le ℝ,ℝ>0\right\}$, where $W_B$ is the operator defined as $W_B:G\to G$ such that

$\begin{array}{ll}{W}_B(D)=D_0(\vartheta )+\frac{1}{\Gamma (\alpha )}{\displaystyle \underset{0}{\overset{\vartheta }{\int }}}\Upsilon (\nu ,D(\nu )){(\vartheta -\nu )}^{\alpha -1}d\nu ,& (11)\end{array}$

which means that

$\begin{array}{l}|W_{ℬ}(D)(\vartheta )|\le \left|D_0\right|+\frac{1}{\Gamma (\alpha )}{\displaystyle {\int }_0^{\vartheta }|}\Upsilon (\nu ,D(\nu ))|(\vartheta -\nu {)}^{\alpha -1}d\nu ,\\ \le \left|D_0\right|+\frac{1}{\Gamma (\alpha )}{\displaystyle {\int }_0^{\vartheta }{(\vartheta -\nu )}^{\alpha -1}}[{\Omega }_{ℬ}|D|+{\Theta }_{ℬ}]d\nu ,\\ \le \left|D_0\right|+\frac{T^{\alpha }}{\Gamma (\alpha +1)}[{\Omega }_{ℬ}|\left|D\right||+{\Theta }_{ℬ}].& (12)\end{array}$

From Equation 12, it follows that $|\Omega (D)|\le \left|D_0\right|+\frac{T^{\alpha }}{\Gamma (\alpha +1)}\left[{\Omega }_B\left|\right|D\left|\right|+{\Theta }_B\right]$ and also $W_B\in G$ such that $W_B(D)\subset G.$ Also it reveals that the operator $W_B(D)$ is bounded. For completely continuity we proceed as follows. Let ${\vartheta }_2<{\vartheta }_1\in \left[0,T\right]$ such that

$\begin{array}{l}|W_{ℬ}(D)({\vartheta }_2)|-|W_{ℬ}(D)({\vartheta }_1)|\\ \le |\frac{1}{\Gamma (\alpha )}{\displaystyle {\int }_0^{{\vartheta }_2}\Upsilon }(\nu ,D(\nu ))({\vartheta }_2-\nu {)}^{\alpha -1}d\nu \\ -\frac{1}{\Gamma (\alpha )}{\displaystyle {\int }_0^{{\vartheta }_1}\Upsilon }(\nu ,D(\nu ))({\vartheta }_1-\nu {)}^{\alpha -1}d\nu |\\ \le \frac{1}{\Gamma (\alpha )}[{{\displaystyle \int }}_0^{{\vartheta }_1}[({\vartheta }_1-\nu {)}^{\alpha -1}-({\vartheta }_2-\nu {)}^{\alpha -1}]\Upsilon (\nu ,D(\nu ))d\nu \\ +{\displaystyle {\int }_{{\vartheta }_1}^{{\vartheta }_2}{({\vartheta }_2-\nu )}^{\alpha -1}}\Upsilon (\nu ,D(s))d\nu ],\\ \le \frac{A_qℛ+B_q}{\Gamma (\alpha +1)}[({\vartheta }_2^{\alpha }-{\vartheta }_1^{\alpha })+2({\vartheta }_2-{\vartheta }_1{)}^{\alpha }].& (13)\end{array}$

Basically, we can see from Equation 13 that $\left|W_B(D)({\vartheta }_2)\right|-\left|W_B(D)({\vartheta }_1)\right|\to 0$ as ϑ₂ → ϑ₁. Hence, $W_B$ is an equicontinuous operator. With the help of the Arzela Ascoli theorem, we know that function $W_B$ is a completely continuous function and uniformly bounded. Again, by Schauder's fixed point theorem, we conclude that our proposed system has at least one solution.

Theorem 4.2. Suppose that $(H_2)$ holds. Then the considered Equation 1 has a unique solution if

$\begin{array}{ll}\frac{T^{\alpha }}{\Gamma (\alpha +1)}{\text{L}}_B<1.& (14)\end{array}$

Proof . If $D,\tilde{D}\in G$, then

$\begin{array}{l}\left|\right|W_{ℬ}(D)-W_{ℬ}(\tilde{D})\left|\right|\le {\sup }_{\vartheta \in [0,T]}|\frac{1}{\Gamma (\alpha )}{\int }_0^{\vartheta }\\ \Upsilon (\nu ,D(\nu ))(\vartheta -\nu {)}^{\alpha -1}d\nu \\ -\frac{1}{\Gamma (\alpha )}{\displaystyle {\int }_0^t\Upsilon }(\nu ,\tilde{D}(\nu ))(\vartheta -\nu {)}^{\alpha -1}d\nu |,\\ \le \frac{T^{\alpha }}{\Gamma (\alpha +1)}{L}_{ℬ}\left|\right|D-\tilde{D}\left|\right|.& (15)\end{array}$

Hence, $\left|\right|W_B(D)-W_B(\tilde{D})\left|\right|\le \frac{T^{\alpha }}{\Gamma (\alpha +1)}{\mathbf{\text{L}}}_B\left|\right|D-\tilde{D}\left|\right|$, which completes the proof: from the contraction principle, the operator has a unique fixed point and, consequently, our proposed model has a unique solution.

5 Hyers-Ulam stability results

In this section we examine the stability results of our proposed system. Hyers-Ulam (HU) stability is a significant concept in the analysis fractional equations, which includes models like the one for bullying dynamics among students. It pertains to the stability of functional equations when subjected to small perturbations, indicating that if a function nearly satisfies a functional equation, there exists a precise solution near this approximate one. This principle can be utilized for ordinary differential equations (ODEs) to guarantee that small alterations in initial conditions. By proving that the model is Hyers-Ulam stable, the study underlines the suitability of fractional-order modeling for social behavior systems like bullying, where the past influences present behavior. This is crucial for justifying the choice of fractional calculus in the proposed model, ensuring that the memory aspect contributes to a robust representation of the system dynamics. The stability analysis also implies that interventions based on the model's predictions can be implemented with the understanding that minor variations in their execution will not drastically affect the overall outcomes. This is important for policymakers and educators who need to rely on the model for decision-making, as it implies a degree of resilience to unexpected variations in program implementation or conditions. For stability of our proposed model we consider the following Lemma 3 and Theorem 4:

Lemma 3. The function $D(\vartheta )$ is a solution of

$\begin{array}{l}{}_0{}^C{{\displaystyle D}}_{\vartheta }^{\alpha }D(\vartheta )={\rm Y}(\vartheta ,D(\vartheta ))+\Omega (\vartheta ),\\ D(0)=D_0,& (16)\end{array}$

satisfies the given relation

$\begin{array}{ll}\begin{array}{c}D(\vartheta )-D_0(\vartheta )+\frac{1}{\Gamma (\alpha )}{\displaystyle \underset{0}{\overset{\vartheta }{\int }}}\Upsilon (\vartheta ,D(\vartheta )){(\vartheta -\nu )}^{\alpha -1}d\nu \\ \le \frac{T^{\alpha }}{\Gamma (\alpha +1)}ϵ=\delta ϵ,\end{array}& (17)\end{array}$

Proof. The proof is very common in literature so we omit it, see Ngungu et al. [2].

Theorem 4. The Caputo fractional model under consideration is HU stable, if there exists

$\begin{array}{l}\Pi =\frac{T^{\alpha }}{\Gamma (\alpha +1)}{\text{L}}_B<1.\end{array}$

Proof. Let $D\in G$ be any solution and $\tilde{D}\in G$ be a unique solution, then

$\begin{array}{l}|D(\vartheta )-\tilde{D}(\vartheta )|\\ =|D(\vartheta )-(D_0(\vartheta )+\frac{1}{\Gamma (\alpha )}{\displaystyle {\int }_0^{\vartheta }\Upsilon }(\vartheta ,\tilde{D}(\vartheta ))(\vartheta -\nu {)}^{\alpha -1}d\nu )|\\ \le |D(\vartheta )-(D_0(\vartheta )+\frac{1}{\Gamma (\alpha )}{\displaystyle {\int }_0^{\vartheta }\Upsilon }(\vartheta ,\tilde{D}(\nu ))(\vartheta -\nu {)}^{\alpha -1}d\nu )|\\ +|\frac{1}{\Gamma (\alpha )}{\displaystyle {\int }_0^{\vartheta }\Upsilon }(\vartheta ,\tilde{D}(\vartheta ))(\vartheta -\nu {)}^{\alpha -1}d\nu \\ -\frac{1}{\Gamma (\alpha )}{\displaystyle {\int }_0^{\vartheta }\Upsilon }(\vartheta ,\tilde{D}(\vartheta ))(\vartheta -\nu {)}^{\alpha -1}d\nu |\\ \le \delta ϵ+\Pi |D-\tilde{D}|.& (18)\end{array}$

Thus,

$|D-\tilde{D}|\le \frac{\delta }{1-\Pi }ϵ.$

Hence, we conclude that the Caputo fractional model under consideration is HU stable.

6 Numerical schemes

Here, using Adams-Bashforth method, we provide the numerical algorithms for the Caputo fractional model under consideration. The formula for the Cauchy problem of the Caputo derivative is

$\begin{array}{ll}\begin{array}{c}{}_0{}^{\text{C}}{{\displaystyle D}}_{\vartheta }^{\alpha }D(\vartheta )=\Upsilon (\vartheta ,D(\vartheta )),\\ D(0)=D_0.\end{array}& (19)\end{array}$

From principle of the Caputo integral, Equation 19 is rewrite as

$\begin{array}{ll}D(\vartheta )-D(0)=\frac{1}{\Gamma (\alpha )}{\displaystyle \underset{0}{\overset{\vartheta }{\int }}}\Upsilon (\nu ,D(\nu )){(\vartheta -\nu )}^{\alpha -1}d\nu .& (20)\end{array}$

At the point ϑ_p+1 = (p+1)h and ϑ_p = ph, p = 0, 1, 2, 3, 4, ..., with h being the time step, Equation 20 will then be rewrite as:

$\begin{array}{lll}D({\vartheta }_{p+1})-D(0)=& \frac{1}{\Gamma (\alpha )}{\displaystyle \underset{0}{\overset{{\vartheta }_{p+1}}{\int }}}\Upsilon (\nu ,D(\nu )){({\vartheta }_{p+1}-\nu )}^{\alpha -1}d\nu ,& (21)\end{array}$

which is the same as

$\begin{array}{lll}D({\vartheta }_{p+1})=& D(0)+\frac{1}{\Gamma (\alpha )}{\displaystyle \sum _{q=0}^p}{\displaystyle \underset{{\vartheta }_q}{\overset{{\vartheta }_{q+1}}{\int }}}\Upsilon (\nu ,D(\nu )){({\vartheta }_{p+1}-\nu )}^{\alpha -1}d\nu .& (22)\end{array}$

For simplicity we take the right hand side of Equation 22 and using the Lagrange polynomial, Equation 22 can now be written as

$\begin{array}{l}{D}_{p+1}=D_0+\frac{1}{\Gamma (\alpha )}\\ {\displaystyle \sum _{q=0}^p\left\{\begin{array}{c}\frac{\Upsilon ({\vartheta }_q,D_q)}{h}{\displaystyle {\int }_{{\vartheta }_q}^{{\vartheta }_{q+1}}(\nu -{\vartheta }_{q-1}){({\vartheta }_{p+1}-\nu )}^{\alpha -1}}d\nu \\ -\frac{\Upsilon ({\vartheta }_{q-1},D_{q-1})}{h}{\displaystyle {\int }_{{\vartheta }_q}^{{\vartheta }_{q+1}}(\nu -{\vartheta }_q){({\vartheta }_{p+1}-\nu )}^{\alpha -1}}d\nu \end{array}\right\}}.& (23)\end{array}$

where Equation 23 can be written as

$\begin{array}{l}{D}_{p+1}=D_0+\frac{1}{\Gamma (\alpha )}{\displaystyle \sum _{q=0}^p\frac{\Upsilon ({\vartheta }_q,D_q)}{h}}\\ {\displaystyle {\int }_{{\vartheta }_q}^{{\vartheta }_{q+1}}(\nu -{\vartheta }_{q-1}){({\vartheta }_{p+1}-\nu )}^{\alpha -1}}d\nu \\ -\frac{1}{\Gamma (\alpha )}{\displaystyle \sum _{q=0}^p\frac{\Upsilon ({\vartheta }_{q-1},D_{q-1})}{h}}\\ {\displaystyle {\int }_{{\vartheta }_q}^{{\vartheta }_{q+1}}(\nu -{\vartheta }_q){({\vartheta }_{p+1}-\nu )}^{\alpha -1}}d\nu .& (24)\end{array}$

For simplicity we evaluate the integrals in Equation 24, hence we have:

$\begin{array}{l}{\displaystyle \underset{{\vartheta }_q}{\overset{{\vartheta }_{q+1}}{\int }}}(\nu -{\vartheta }_{q-1}){({\vartheta }_{p+1}-\nu )}^{\alpha -1}d\nu \\ =\frac{h^{\alpha -1}}{\alpha (\alpha +1)}\left[\begin{array}{c}{(p-q+1)}^{\alpha }(p-q+2+\alpha )\\ -{(p-q)}^{\alpha }(p-q+2+2\alpha )\end{array}\right],& (25)\end{array}$

$\begin{array}{l}{\displaystyle \underset{{\vartheta }_q}{\overset{{\vartheta }_{q+1}}{\int }}}(\nu -{\vartheta }_q){({\vartheta }_{p+1}-\nu )}^{\alpha -1}d\nu \\ =\frac{h^{\alpha -1}}{\alpha (\alpha +1)}\left[\begin{array}{c}{(p-q+1)}^{\alpha +1}\\ -{(p-q)}^{\alpha }(p-q+1+\alpha )\end{array}\right].& (26)\end{array}$

For simple substitution of Equations 25, 26 into Equation 24, we get the numerical algorithm for the Caputo derivative is as follows

$\begin{array}{ll}\begin{array}{l}{D}_{p+1}=D_0+\frac{h^{\alpha }}{\Gamma (\alpha +2)}{\displaystyle \sum _{q=0}^p\Upsilon }(t_q,{\Phi }_q)\hfill \\ \left[\begin{array}{c}{(p-q+1)}^{\alpha }(p-q+2+\alpha )\\ -{(p-q)}^{\alpha }(p-q+2+2\alpha )\end{array}\right]\hfill \\ -\frac{h^{\alpha }}{\Gamma (\alpha +2)}{\displaystyle \sum _{q=0}^p\Upsilon }({\vartheta }_{q-1},D_{q-1})\hfill \\ \left[\begin{array}{c}{(p-q+1)}^{\alpha +1}\\ -{(p-q)}^{\alpha }(p-q+1+\alpha )\end{array}\right].\hfill \end{array}& (27)\end{array}$

Thus, in terms of our Caputo fractional social epidemiological model for the bullying, we get:

$\begin{array}{l}{X}_{1_{p+1}}=X_{1_0}+\frac{h^{\alpha }}{\Gamma (\alpha +2)}{\displaystyle \sum _{q=0}^p}\Upsilon ({\vartheta }_q,X_{1_q})\\ \left[\begin{array}{c}{(p-q+1)}^{\alpha }(p-q+2+\alpha )\\ -{(p-q)}^{\alpha }(p-q+2+2\alpha )\end{array}\right]\\ -\frac{h^{\alpha }}{\Gamma (\alpha +2)}{\displaystyle \sum _{q=0}^p}\Upsilon ({\vartheta }_{q-1},X_{1_{q-1}})\\ \left[\begin{array}{c}{(p-q+1)}^{\alpha +1}\\ -{(p-q)}^{\alpha }(p-q+1+\alpha )\end{array}\right],\\ X_{2_{p+1}}=X_{2_0}+\frac{h^{\alpha }}{\Gamma (\alpha +2)}{\displaystyle \sum _{q=0}^p}\Upsilon ({\vartheta }_q,X_{2_q})\\ \left[\begin{array}{c}{(p-q+1)}^{\alpha }(p-q+2+\alpha )\\ -{(p-q)}^{\alpha }(p-q+2+2\alpha )\end{array}\right]\\ -\frac{h^{\alpha }}{\Gamma (\alpha +2)}{\displaystyle \sum _{q=0}^p}\Upsilon ({\vartheta }_{q-1},X_{2_{q-1}})\\ \left[\begin{array}{c}{(p-q+1)}^{\alpha +1}\\ -{(p-q)}^{\alpha }(p-q+1+\alpha )\end{array}\right],\\ Y_{1_{p+1}}=Y_{1_0}+\frac{h^{\alpha }}{\Gamma (\alpha +2)}{\displaystyle \sum _{q=0}^p}\Upsilon ({\vartheta }_q,Y_{1_q})\\ \left[\begin{array}{c}{(p-q+1)}^{\alpha }(p-q+2+\alpha )\\ -{(p-q)}^{\alpha }(p-q+2+2\alpha )\end{array}\right]\\ -\frac{h^{\alpha }}{\Gamma (\alpha +2)}{\displaystyle \sum _{q=0}^p}\Upsilon ({\vartheta }_{q-1},Y_{1_{q-1}})\\ \left[\begin{array}{c}{(p-q+1)}^{\alpha +1}\\ -{(p-q)}^{\alpha }(p-q+1+\alpha )\end{array}\right],\\ Y_{2_{p+1}}=Y_{2_0}+\frac{h^{\alpha }}{\Gamma (\alpha +2)}{\displaystyle \sum _{q=0}^p}\Upsilon ({\vartheta }_q,Y_{2_q})\\ \left[\begin{array}{c}{(p-q+1)}^{\alpha }(p-q+2+\alpha )\\ -{(p-q)}^{\alpha }(p-q+2+2\alpha )\end{array}\right]\\ -\frac{h^{\alpha }}{\Gamma (\alpha +2)}{\displaystyle \sum _{q=0}^p}\Upsilon ({\vartheta }_{q-1},Y_{2_{q-1}})\\ \left[\begin{array}{c}{(p-q+1)}^{\alpha +1}\\ -{(p-q)}^{\alpha }(p-q+1+\alpha )\end{array}\right],& (28)\end{array}$

7 Numerical simulation and discussion

The diagram of our proposed model under the Caputo fractional operator is depicted in Figure 1, using the Adams-Bashforth method and taking into account the following initial conditions: X₁(0) = 500, X₂(0) = 110, Y₁(0) = 35, Y₂(0) = 20 with parameter values in Table 2. The goal of this section is to investigate the influence of changes in the values of these input parameters on system behavior. Our goal in studying many scenarios is to obtain a thorough grasp of how the system responds to changing conditions. By examining these numerical results, we hope to highlight the system's robustness and sensitivity to varied input variations. This section is critical in demonstrating the system's functioning under diverse situations, which deepens understanding of its responses and provides significant insights for scientific applications.

Figure 1

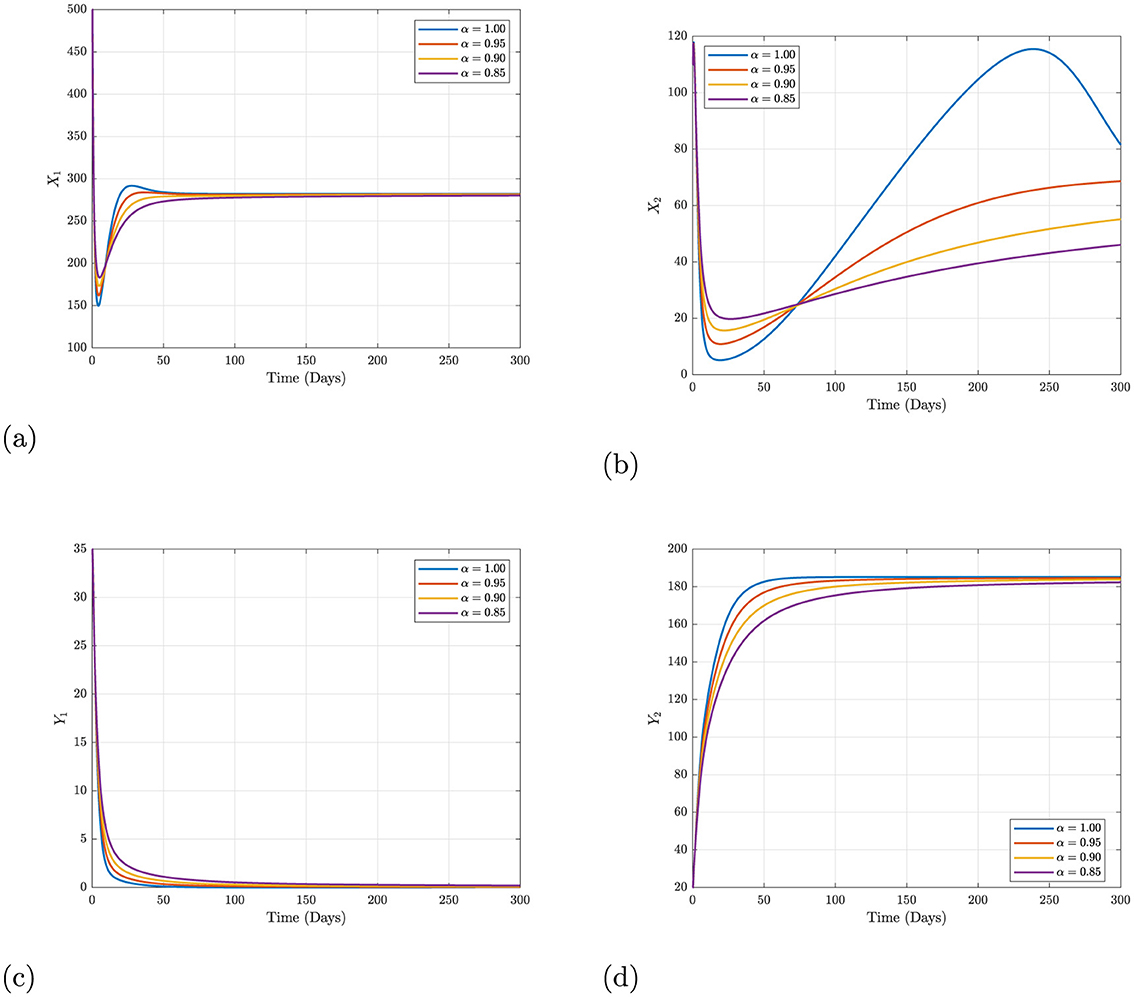
Figure 1. Numerical trajectory for school bullying under Caputo fractional operator. (A) Dynamics of students with lack of family education. (B) Dynamics of students with family education. (C) Dynamics of bullying students with lack of family education. (D) Dynamics of bullying students with family education.

Table 2

Table 2. Valuation of parameters in the model.

In the first simulation presented in Figures 1A, B, we noticed that the behavior of students who lack and with family education and not involving bullying under different values of fractional order. The trajectory changes with the fractional order, suggesting that the system's sensitivity to initial conditions or recent changes decreases as fractional order reduce from 1. Essentially, a lower fractional order makes the system less reactive to short-term fluctuations and more stable.

In Figures 1C, D, we illustrated the solution pathways of students with/without parental control and bullying other students of the system. In this simulation, we observed from Figure 1C that a fractional order is associated with a increase in bullying, unlike Figure 1D where a lower fractional order is associated with a decrease in bullying, these trajectories imply that interventions that have a more prolonged effect or that contribute to the “memory” of the system such as consistent policy enforcement or cultural shifts against bullying could be more effective than short-term solutions.

In Figures 2, 3, the effects of varying different parameters associated with family education are analyzed, providing insights into how changes in family dynamics and educational background influence the prevalence of bullying over time. Figures 2A, B present the dynamics of students without and with family education respectively, showing how the parameter variations (ξ₁ and ξ₂)impact students' stability. These parameters represent the rates of transition between having and lacking family education. The pink trajectory represents higher transition rates, indicating quicker movement from lacking family education to gaining it and vice versa. In both cases, the pink curves stabilize at higher values compared to the blue curve, indicating quicker movement from lacking family education to gaining it and vice versa. In both cases, the pink curves stabilize at higher values compared to the blue curves. This suggests that policies that facilitate family engagement or provide external support to simulate family education (e.g., community programs or school counseling) can lead to better stability and outcomes in students' behaviors. Improving family education rates will potentially reduce students' vulnerability to adverse behaviors by enhancing resilience against bullying. Figures 2C, D demonstrate the dynamics of bullying among students lacking family education and those with family education, respectively. The dynamics show that a higher rate of transition into a supportive environment leads to reduced numbers of bullying incidents over time. These results highlight the importance of family involvement as a preventative factor against bullying. Schools could collaborate with parents to strengthen family education programs, provide workshops on parenting skills, and offer resources aimed at creating supportive home environments. Furthermore, the transition rates (ξ₁ and ξ₂) could be influenced by school-led initiatives that directly involve parents in students' lives.

Figure 2

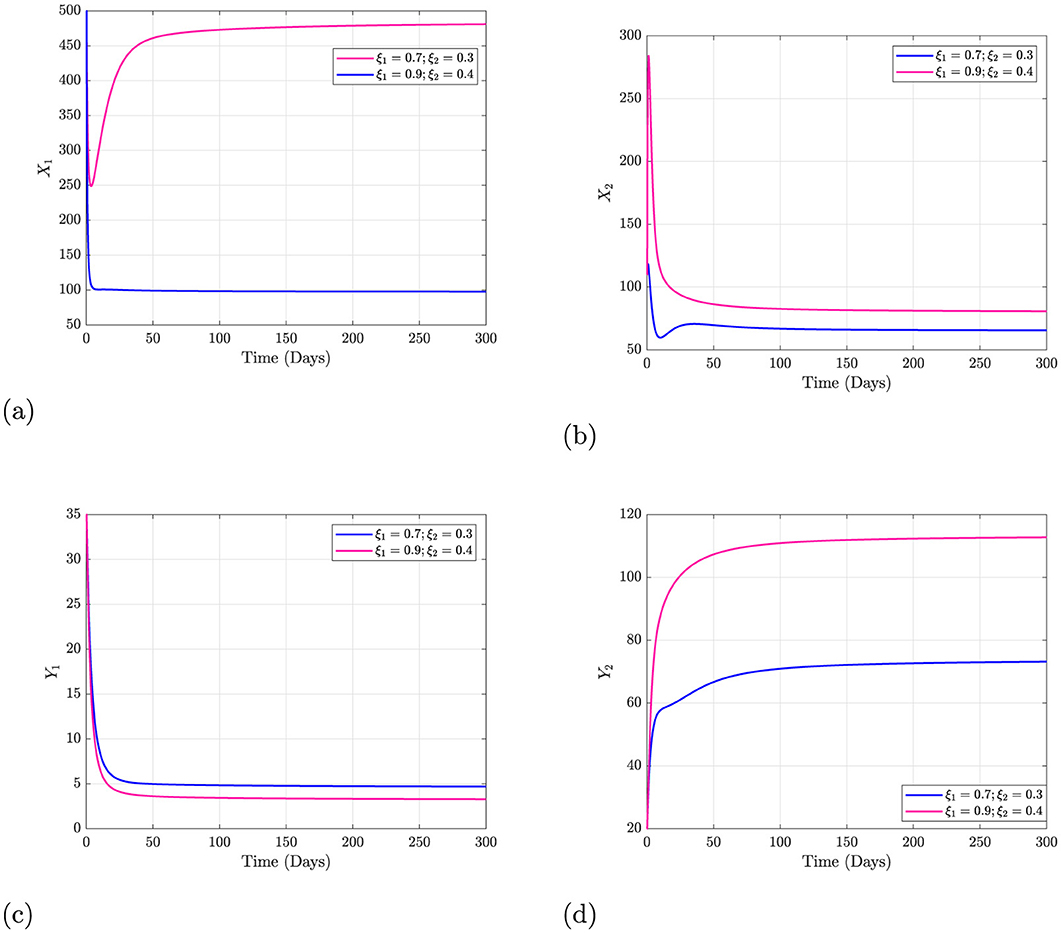
Figure 2. Effect of varying ξ₁ and ξ₁ when Caputo fractional operator is 0.95. (A) Dynamics of students with lack of family education. (B) Dynamics of students with family education. (C) Dynamics of bullying students with lack of family education. (D) Dynamics of bullying students with family education.

Figure 3

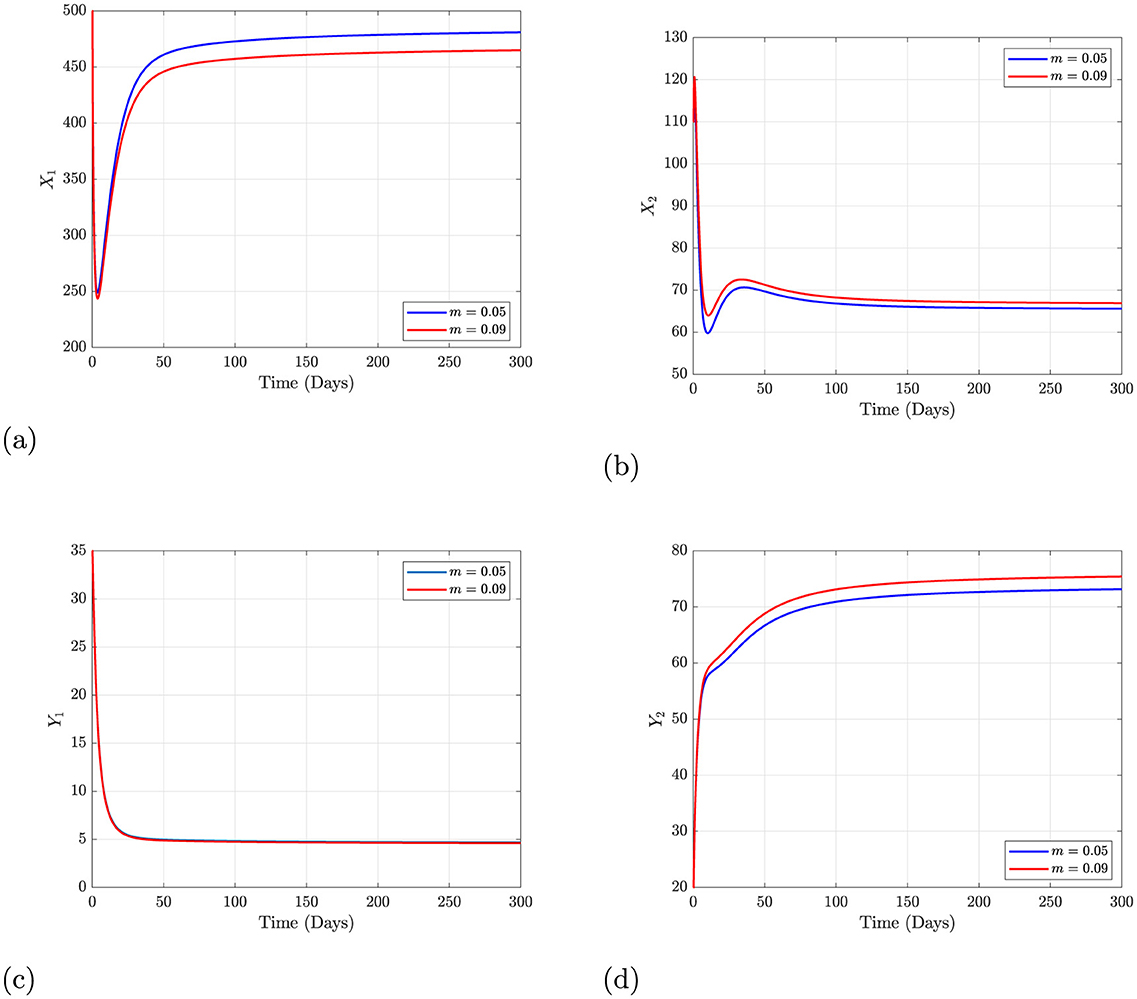
Figure 3. Effect of varying m when Caputo fractional operator is 0.95. (A) Dynamics of students with lack of family education. (B) Dynamics of students with family education. (C) Dynamics of bullying students with lack of family education. (D) Dynamics of bullying students with family education.

In Figures 3A, B depict the dynamics of students with and without family education for varying values of m which represents the rate of students lacking family education. When m increases from 0.05 to 0.09, it can be observed that the number of students without family education increases, as seen in the red curves. Conversely, the number of students with family education decreases, implying a growing population of students who lack sufficient support from their families. These figures show that increasing the rate of students without family education negatively impacts the student population's dynamics, increasing vulnerability. In real-world settings, this points to the need for government and school authorities to intervene with targeted programs for families that struggle to provide sufficient education and support. Policies aimed at subsidizing educational resources or counseling services could reduce m and improve student outcomes. Figures 3C, D show the dynamics of bullying incidents among students with and without family education as the rate m changes. With increased m the number of bullying incidents among students without family education also rises. This relationship indicates that when more students lack family education, the likelihood of involvement in bullying, either as a perpetrator or as a victim, also increases. For this results, schools and educational policymakers should focus on interventions that provide additional support to students who lack family education, such as mentorship programs, peer support initiatives, and after-school activities. These can serve as compensatory measures for students who are at higher risk due to a lack of family support. Providing targeted emotional and social learning initiatives in schools can also help mitigate bullying behaviors among students who may be predisposed to such behavior due to their family background.

In our ever more interconnected world, the capacity to model and anticipate the spread of bullying is essential for global readiness. Utilizing mathematical models, early identification and containment strategies can be guided, playing a crucial role in averting the swift global dissemination of bullying. Understanding the dynamics of a bullying model can aid in communicating the importance of preventive measures to the public. When people grasp how a bullying spreads among students, they are more likely to adhere to recommended behaviors like parental education and other preventive polices.

The students with lack of family education X₁, that is, students who lack family education and not involving bullying; students with family education X₂, that is, student who have family education and not involving bullying; the bully students with lack of family education Y₁; the bully students with family education Y₂.

8 Conclusion

Bullying has non-positive impacts on the mental-physical health, academic outcome, and social relationships of the victims. Those who are bullied face higher rates of sadness, anxiety, low self-esteem, and thoughts of suicide and post-traumatic stress disorders (PTSD) sometimes leading to mental health pathologies in the victims, prompting the need for a comprehensive examination of its cause and dynamics. This research has investigated the dynamics of bullying by introducing a parental education and has employed the fractional Caputo operator to model the system. The fractional Caputo model has been derived, and key findings related to this fractional model have been presented. Notably, stability analysis has been conducted, and the uniqueness and existence of the solution for the bully system have been examined. A novel numerical approach has been introduced to explore the system of bullying. The use of different orders of derivatives has revealed that the hypothesized model with the Caputo derivative has yielded more accurate and efficient graphical results. From the outcome of our result numerically, we have been able to show interventions have effect on reducing the prevalence of bullying; such interventions could campaign or policy shifts which gives better result than [44]. The outcomes of this study are expected to have provided valuable insights for policymakers, parents, and school authorities in their efforts to combat the spread of bullying in their communities or schools. Additionally, future iterations of this model may incorporate time-dependent control strategies based on optimal control theory to enhance bullying management and also test the model with real data by using the non-spatial form of the model developed at small spatial scales to understand the effect of bullying at different district schools in places like the USA at the census tract level.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

AA: Conceptualization, Formal analysis, Investigation, Methodology, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. EA: Conceptualization, Formal analysis, Investigation, Methodology, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. SM: Formal analysis, Investigation, Methodology, Resources, Supervision, Validation, Visualization, Writing – review & editing. KM: Investigation, Methodology, Resources, Supervision, Validation, Visualization, Writing – review & editing. JA: Formal analysis, Investigation, Methodology, Validation, Visualization, Writing – review & editing. KO: Formal analysis, Investigation, Methodology, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors thank the Tshwane University of Technology and Department of Higher Education and Technology for giving the platform and support.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Nwajeri U, Fadugba S, Ohaeri E, Oshinubi K, Ogunrinde R, Ogunrinde R. Co-dynamic model of drug trafficking and money laundering coupled with fractional derivative. Int J Appl Comput Math. (2023) 9:73. doi: 10.1007/s40819-023-01539-x

Crossref Full Text | Google Scholar

2. Ngungu M, Addai E, Adeniji A, Adam UM, Oshinubi K. Mathematical epidemiological modeling and analysis of monkeypox dynamism with non-pharmaceutical intervention using real data from United Kingdom. Front Public Health. (2023) 11:203. doi: 10.3389/fpubh.2023.1101436

PubMed Abstract | Crossref Full Text | Google Scholar

3. Alaka SA, Oshinubi K, Fasakin I, Akintande OJ. Factors associated with psychological impact of coronavirus disease 2019 (COVID-19) outbreak in Nigeria: regression-based approach. J Math Comput Sci. (2022) 12. doi: 10.3389/fpsyt.2021.565190

PubMed Abstract | Crossref Full Text | Google Scholar

4. Green JG, Furlong MJ, Felix ED. Defining and measuring bullying across the life course. In:Bradshaw CP, , editor. Handbook on Bullying Prevention: A Life Course Perspective. Boston, MA: National Association of School Social Workers (2017), p. 7–20.

PubMed Abstract | Google Scholar

5. Klomek AB, Sourander A, Elonheimo H. Bullying by peers in childhood and effects on psychopathology, suicidality, and criminality in adulthood. Lancet Psychiatry. (2015) 2:930–41. doi: 10.1016/S2215-0366(15)00223-0

PubMed Abstract | Crossref Full Text | Google Scholar

6. GR G, Olweus D. Bullying at School: What We Know and What We Can Do. Malden, MA: Malden Blackwell Publishing (1993).

PubMed Abstract | Google Scholar

7. Sherman L, Strang H. Restorative Justice: The Evidence. Lake Success, NY: Smith Institute (2007).

Google Scholar

8. Elbertson NA, Brackett MA, Weissberg RP. School-based social and emotional learning (SEL) programming: current perspectives. In:Hargreaves A, Lieberman A, Fullan M, Hopkins D, , editors. Second International Handbook of Educational Change. Cham: Springer (2009), p. 1017–32. doi: 10.1007/978-90-481-2660-6_57

Crossref Full Text | Google Scholar

9. Lawlor MS. Mindfulness and social emotional learning (SEL): a conceptual framework. In:Schonert-Reichl K, Roeser R, , editors. Handbook of Mindfulness in Education: Integrating Theory and Research into Practice. Cham: Springer (2016), p. 65–80. doi: 10.1007/978-1-4939-3506-2_5

Crossref Full Text | Google Scholar

10. Bradshaw CP, Koth CW, Bevans KB, Ialongo N, Leaf PJ. The impact of school-wide positive behavioral interventions and supports (PBIS) on the organizational health of elementary schools. Sch Psychol Q. (2008) 23:462. doi: 10.1037/a0012883

PubMed Abstract | Crossref Full Text | Google Scholar

11. Pugh R, Chitiyo M. The problem of bullying in schools and the promise of positive behaviour supports. J Res Spec Educ Needs. (2012) 12:47–53. doi: 10.1111/j.1471-3802.2011.01204.x

Crossref Full Text | Google Scholar

12. Bradshaw CP. Preventing bullying through positive behavioral interventions and supports (PBIS): a multitiered approach to prevention and integration. Theory Pract. (2013) 52:288–95. doi: 10.1080/00405841.2013.829732

Crossref Full Text | Google Scholar

13. Letendre J, Ostrander JA, Mickens A. Teacher and staff voices: implementation of a positive behavior bullying prevention program in an urban school. Child Sch. (2016) 38:235–43. doi: 10.1093/cs/cdw032

Crossref Full Text | Google Scholar

14. Modecki KL, Minchin J, Harbaugh AG, Guerra NG, Runions KC. Bullying prevalence across contexts: a meta-analysis measuring cyber and traditional bullying. J Adolesc Health. (2014) 55:602–11. doi: 10.1016/j.jadohealth.2014.06.007

PubMed Abstract | Crossref Full Text | Google Scholar

15. Ttofi MM, Farrington DP. Effectiveness of school-based programs to reduce bullying: a systematic and meta-analytic review. J Exp Criminol. (2011) 7:27–56. doi: 10.1007/s11292-010-9109-1

Crossref Full Text | Google Scholar

16. Gaffney H, Ttofi MM, Farrington DP. Evaluating the effectiveness of school-bullying prevention programs: an updated meta-analytical review. Aggress Violent Behav. (2019) 45:111–33. doi: 10.1016/j.avb.2018.07.001

Crossref Full Text | Google Scholar

17. Ybarra ML, Boyd D, Korchmaros JD, Oppenheim JK. Defining and measuring cyberbullying within the larger context of bullying victimization. J Adolesc Health. (2012) 51:53–8. doi: 10.1016/j.jadohealth.2011.12.031

PubMed Abstract | Crossref Full Text | Google Scholar

18. Waasdorp TE, Bradshaw CP. The overlap between cyberbullying and traditional bullying. J Adolesc Health. (2015) 56:483–8. doi: 10.1016/j.jadohealth.2014.12.002

PubMed Abstract | Crossref Full Text | Google Scholar

19. Olweus D, Limber SP, Breivik K. Addressing specific forms of bullying: a large-scale evaluation of the Olweus bullying prevention program. Int J Bullying Prev. (2019) 1:70–84. doi: 10.1007/s42380-019-00009-7

Crossref Full Text | Google Scholar

20. Çalışkan Z, Evgin D, Bayat M, Caner N, Kaplan B, Öztürk A, et al. Peer bullying in the preadolescent stage: frequency and types of bullying and the affecting factors. J Pediatr Res. (2019) 6:169–79. doi: 10.4274/jpr.galenos.2018.26576

Crossref Full Text | Google Scholar

21. Namie G, Namie R. Risk factors for becoming a target of workplace bullying and mobbing. In:Duffy M, Yamada DC, , editors. Workplace bullying and mobbing in the United States, Vol. 1. Santa Barbara, CA: ABC-CLIO, LLC (2018), p. 53–74.

Google Scholar

22. Misawa M, Andrews JL, Jenkins KM. Women's experiences of workplace bullying: a content analysis of peer-reviewed journal articles between 2000 and 2017. New Horiz Adult Educ Hum Resour Dev. (2019) 31:36–50. doi: 10.1002/nha3.20263

Crossref Full Text | Google Scholar

23. Salin D. Workplace bullying and gender: an overview of empirical findings. In:D'Cruz P, Noronha E, Caponecchia C, Escartín J, Salin D, Tuckey MR, , editors. Dignity and Inclusion at Work. Cham: Springer (2021), 331–361. doi: 10.1007/978-981-13-0218-3_12

PubMed Abstract | Crossref Full Text | Google Scholar

24. Patchin JW, Hinduja S. Measuring cyberbullying: Implications for research. Aggress Violent Behav. (2015) 23:69–74. doi: 10.1016/j.avb.2015.05.013

Crossref Full Text | Google Scholar

25. Hase CN, Goldberg SB, Smith D, Stuck A, Campain J. Impacts of traditional bullying and cyberbullying on the mental health of middle school and high school students. Psychol Sch. (2015) 52:607–17. doi: 10.1002/pits.21841

Crossref Full Text | Google Scholar

26. Hinduja S, Patchin JW. Connecting adolescent suicide to the severity of bullying and cyberbullying. J Sch Violence. (2019) 18:333–46. doi: 10.1080/15388220.2018.1492417

Crossref Full Text | Google Scholar

27. Raskauskas J, Modell S. Modifying anti-bullying programs to include students with disabilities. Teach Except Child. (2011) 44:60–7. doi: 10.1177/004005991104400107

Crossref Full Text | Google Scholar

28. Rose CA, Stormont M, Wang Z, Simpson CG, Preast JL, Green AL. Bullying and students with disabilities: examination of disability status and educational placement. Sch Psych Rev. (2015) 44:425–44. doi: 10.17105/spr-15-0080.1

Crossref Full Text | Google Scholar

29. Earnshaw VA, Reisner SL, Menino DD, Poteat VP, Bogart LM, Barnes TN, et al. Stigma-based bullying interventions: a systematic review. Devel Rev. (2018) 48:178–200. doi: 10.1016/j.dr.2018.02.001

PubMed Abstract | Crossref Full Text | Google Scholar

30. Earnshaw VA, Reisner SL, Juvonen J, Hatzenbuehler ML, Perrotti J, Schuster MA. LGBTQ bullying: translating research to action in pediatrics. Pediatrics. (2017) 140. doi: 10.1542/peds.2017-0432

PubMed Abstract | Crossref Full Text | Google Scholar

31. Gower AL, Rider GN, McMorris BJ, Eisenberg ME. Bullying victimization among LGBTQ youth: critical issues and future directions. Curr Sex Health Rep. (2018) 10:246–54. doi: 10.1007/s11930-018-0169-y

PubMed Abstract | Crossref Full Text | Google Scholar

32. Reisner SL, Sava LM, Menino DD, Perrotti J, Barnes TN, Humphrey DL, et al. Addressing LGBTQ student bullying in Massachusetts schools: perspectives of LGBTQ students and school health professionals. Prev Sci. (2020) 21:408–21. doi: 10.1007/s11121-019-01084-4

PubMed Abstract | Crossref Full Text | Google Scholar

33. Perren S, Ettekal I, Ladd G. The impact of peer victimization on later maladjustment: Mediating and moderating effects of hostile and self-blaming attributions. J Child Psychol Psychiatry. (2013) 54:46–55. doi: 10.1111/j.1469-7610.2012.02618.x

PubMed Abstract | Crossref Full Text | Google Scholar

34. Perren S, Hornung R. Bullying and delinquency in adolescence: Victims' and perpetrators' family and peer relations. Swiss J Psychol. (2005) 64:51–64. doi: 10.1024/1421-0185.64.1.51

Crossref Full Text | Google Scholar

35. O'Moore M, Kirkham C. Self-esteem and its relationship to bullying behaviour. Aggress. Behav. (2001) 27:269–83. doi: 10.1002/ab.1010

Crossref Full Text | Google Scholar

36. Shetgiri R. Bullying and victimization among children. Adv Pediatr. (2013) 60:33–51. doi: 10.1016/j.yapd.2013.04.004

PubMed Abstract | Crossref Full Text | Google Scholar

37. Shetgiri R, Lin H, Flores G. Trends in risk and protective factors for child bullying perpetration in the United States. Child Psychiatry Hum Dev. (2013) 44:89–104. doi: 10.1007/s10578-012-0312-3

PubMed Abstract | Crossref Full Text | Google Scholar

38. Wolke D, Tippett N, Dantchev S. Bullying in the family: sibling bullying. Lancet Psychiatry. (2015) 2:917–29. doi: 10.1016/S2215-0366(15)00262-X

PubMed Abstract | Crossref Full Text | Google Scholar

39. Vrijen C, Wiertsema M, Ackermans MA, van der Ploeg R, Kretschmer T. Childhood and adolescent bullying perpetration and later substance use: a meta-analysis. Pediatrics. (2021) 147. doi: 10.1542/peds.2020-034751

PubMed Abstract | Crossref Full Text | Google Scholar

40. deLara EW. Family bullying in childhood: consequences for young adults. J Interpers Violence. (2022) 37:NP2206–26. doi: 10.1177/0886260520934450

PubMed Abstract | Crossref Full Text | Google Scholar

41. Oshinubi K, Ibrahim F, Rachdi M, Demongeot J. Functional data analysis: application to daily observation of COVID-19 prevalence in France. AIMS Math. (2022) 7:5347–85. doi: 10.3934/math.2022298

Crossref Full Text | Google Scholar

42. Oshinubi K, Elumalero GO, Omosebi T, Komolafe OO, Afolabi BB, Odiwo H, et al. Data analysis of orphanage homes fund distribution in Nigeria. J Math Comput Sci. (2022) 12.

Google Scholar

43. Naldi G, Pareschi L, Toscani G. Mathematical Modeling of Collective Behavior in Socio-economic and Life Sciences. Cham: Springer Science & Business Media (2010). doi: 10.1007/978-0-8176-4946-3

Crossref Full Text | Google Scholar

44. Ashi H. Stability analysis of a simple mathematical model for school bullying. AIMS Math. (2022) 7:4936–45. doi: 10.3934/math.2022274

Crossref Full Text | Google Scholar

45. Tilahun GT, Woldegerima WA, Mohammed N. A fractional order model for the transmission dynamics of hepatitis B virus with two-age structure in the presence of vaccination. Arab J Basic Appl Sci. (2021) 28:87–106. doi: 10.1080/25765299.2021.1896423

Crossref Full Text | Google Scholar

46. Ahmed I, Baba IA, Yusuf A, Kumam P, Kumam W. Analysis of Caputo fractional-order model for COVID-19 with lockdown. Adv Differ Equ. (2020) 2020:394. doi: 10.1186/s13662-020-02853-0

PubMed Abstract | Crossref Full Text | Google Scholar

47. Addai E, Zhang L, Preko AK, Asamoah JKK. Fractional order epidemiological model of SARS-CoV-2 dynamism involving Alzheimer's disease. Healthc Anal. (2022) 2:100114. doi: 10.1016/j.health.2022.100114

PubMed Abstract | Crossref Full Text | Google Scholar