- Department of Applied Mathematics, Adama Science and Technology University, Adama, Ethiopia
The main challenge in solving clustering problems using mathematical optimization techniques is the non-smoothness of the distance measure used. To overcome this challenge, we used Nesterov's smoothing technique to find a smooth approximation of the ℓ1 norm. In this study, we consider a bi-level hierarchical clustering problem where the similarity distance measure is induced from the ℓ1 norm. As a result, we are able to design algorithms that provide optimal cluster centers and headquarter (HQ) locations that minimize the total cost, as evidenced by the obtained numerical results.
1 Introduction
Clustering, a widely studied field with applications across various scientific and engineering domains, often grapples with non-smooth and non-convex problems that defy traditional gradient descent algorithms. The discrete and combinatorial nature of clustering adds another layer of complexity, making optimality challenging to attain.
The synergy of Nesterov's smoothing technique [16], DC programming, and the difference of convex algorithm (DCA) [10] has created a fertile ground for investigating into non-convex and non-smooth optimization problems. The efficacy of the DC algorithm in addressing non-convex clustering problems has been well-established in previous studies [1, 5, 14, 17, 22] and cited references. Notable among these is the exploration of a DC optimization approach for constrained clustering with ℓ1 norm [6], tackling problems such as the minimum sum of squares clustering [2], bi-level hierarchical clustering [8], and multicast network design [13]. Recent studies have extended DC algorithms to solve multifacility location problems [4] and addressed similar issues using alternative approaches [21].
While previous methods often resorted to meta-heuristic algorithms, which are challenging to analyze for optimality, recent advancements have seen a shift toward more robust techniques. In 2003, Jia et al. [9] introduced three models of hierarchical clustering based on the Euclidean norm and employed the derivative-free method developed in [3] to solve the problem in ℝ2. In [21], DCA which was developed in [19, 20] was utilized by replacing ℓ2 norm by squared ℓ2 norm and applied to higher dimensional problems. However, the need for further enhancements led to the incorporation of new way in Nesterov's smoothing techniques in [8, 13] to overcome certain limitations identified in [9].
In real-world scenarios, the ℓ1 distance measure frequently provides a more accurate reflection of ground realities than the Euclidean distance. This study extends the investigation of the bi-level hierarchical clustering model proposed in [8, 13] by modifying the objective function and constraints using the ℓ1 norm. Employing Nesterov's partial smoothing techniques and a suitable DC decomposition tailored for the ℓ1 norm, we leverage the DC Algorithm (DCA). In addition, constraints are introduced to ensure that cluster centers and the headquarters lie on actual nodes in the datasets. To limit the search space, the headquarter is strategically placed in the region average to the cluster centers that minimize the overall distance of the network.
The study is organized as follows: Section 2 introduces the basic tools of convex analysis applied to DC functions and DCA. Sections 3 and subsequent subsections delve into the formulation and exploration of bi-level hierarchical clustering problems, along with the development of DCA algorithms that address the model using Nesterov's smoothing technique. Section 4 showcases numerical simulation results with artificial data, and concluding remarks are presented in Section 5.
2 Fundamentals of convex analysis
In this section, we will introduce fundamental results and definitions from convex analysis, crucial for understanding the subsequent discussions in this study. For in-depth technical proofs and additional readings, we recommend referring to [11, 12].
Definition 1. An extended real-valued function f : ℝn → (−∞, ∞] is called a DC function, if it can be represented as a difference of two convex functions g and h.
Moreover, the optimization problem
referred to as a DC optimization problem, and it can be addressed using the difference of convex algorithm introduced by Tao and An[19, 20] as follows.
The function g* referred in the DCA is the Fenchel Conjugate of g, and it is defined as in [18]
and it is always convex regardless of whether g is convex or not.
Theorem 1. [18] Let g : ℝn → (−∞, ∞] be a proper extended real-valued function, for x, y ∈ ℝn. Then, x ∈ ∂g*(y) if and only if y ∈ ∂g(x).
Definition 2. [12] A vector v ∈ ℝn is a sub-gradient of a convex function f : ℝn → (−∞, ∞], at , if it satisfies the inequality
The set of all sub-gradients of f at , denoted as , is known as the sub-differential of f at , that is,
Theorem 2. Let be a proper and extended real-valued convex function on ℝn, where i = 1, 2, …, m and [12]. Then for all ,
2.1 The max, min, and convergence of the DCA
The maximum function is defined as the point-wise maximum of convex functions. For i = 1, 2, 3, …, m, let the functions be closed and convex. Then, the maximum function
is also closed and convex. On the other hand, the minimum function f(x), defined by
may not be convex. However, it can always be represented as a difference of two convex functions as follows:
Lemma 3. [12] Let functions fi(x), i = 1 … m be closed and convex. Then, the maximum function
is also closed and convex. Moreover, for any , we have
where I(x) = {i : fi(x) = f(x)}.
Definition 3. [14] A function f : ℝn → ℝ is ρ-strongly convex if there exists ρ > 0 such that the function
is convex. In particular, if f is strongly convex, then f is also strictly convex, in the sense that f(λx1 + (1 − λ)x2) < λf(x1) + (1 − λ)f(x2) for all λ ∈ (0, 1).
Theorem 4. [14, 20] Let f be as defined in problem (1), and let {xk} be a sequence generated by the DCA Algorithm 1. Suppose that g and h are ρ1 and ρ2 strongly convex, respectively. Then, at every iteration number k of the DCA, we have
Moreover, if f is bounded from below and if {xk} is bounded, then all sub-sequential limits of {xk} converge to a stationary point of f.
2.2 Nesterov's smoothing approximation of the ℓ1 Norm
Definition 4. [12, 14] Let F be a non-empty closed subset of ℝn and let x ∈ ℝn.
1. Define the distance between x and set F by
2. The set of all Euclidean projection from x to F is defined by
It is well-known that P(x; F) is non-empty when F ⊂ ℝn is closed. If we assume in addition that F is convex, than P(x; F) is a singleton.
Proposition 5. [11, 15] Given any a ∈ ℝn and γ > 0, Nesterov's smoothing approximation of φ(x) = ||x − a||1 has the representation
where F is the closed unit box of ℝn, that is, F : for i = 1, …, n}. Moreover,
where P is the Euclidean projection from onto unit box F, and e ∈ ℝn is a vector with one in each coordinate and zero elsewhere. In addition, .
3 Problems formulation
To define our problems, consider a set A of m data points, that is, A = {ai ∈ Rn:i = 1, …, m} and k variable cluster centers denoted by x1, …, xk. We model a two-level hierarchical clustering problem by choosing k separate cluster centers from which one is the headquarter that serves the centers. Other members of the data will be assigned to one of the cluster based on the ℓ1 norm between the data points and centers. Thus, nodes are grouped into k variable centers by minimizing the ℓ1 distances from all node to k centers. Then, a headquarter is a center that minimizes the overall distance of the network and also serves as a cluster center. Then, headquarter is defined to be mean of xj for j = 1, .., k, that is, . This constraint limits the search region for headquarter to mean of selected centers or node near mean. Mathematically, the problem is defined as follows:
is minimized, where,
In addition, to insure the centers are real node, the points should satisfy the following condition:
Thus, the problem is formulated as
subject to
where xk+1 in the summation is . The constraints in (8) are used to force the centers to lie on real node and to force headquarter to be on or near mean of the centers based on minimum distance.
We can write (7) as unconstrained problem using penalty parameter τ > 0, as follows:
Writing (9) as the sum and maximum of convex functions using the formula in (4) as follows:
Expressing (9) as DC function, we have
where
Since f is DC function based on Proposition 5 and ℓ1 smoothing studied in [11], we obtain a Nesterov's approximation of ||x − a||1 as
The main goal is to minimize the partially smoothed objective given by,
That is
In addition, gγ is the sum of convex functions defined as
where
And hγ is also the sum of four convex functions defined as
where
For the calculation of gradient and sub-gradient, consider a data matrix A with ai, i = 1, ..., m, in the ith row and a variable matrix X with xj,j = 1, 2, ..., k + 1 in the jth row.
Since X and A belongs to a linear space of real matrices, we can apply inner product such that
And the Frobenius norm on ℝk×m is given by
To calculate the gradient of gγ in (13), let X be of size (k + 1) × n is variable matrix. Then,
where is a matrix of all ones. As g1γ is smooth, then
Again consider g2γ which is differentiable function,
where Ekk is a k × k matrix with elements all ones. Then, the gradients of g2γ are given by
Next, we focus on X ∈ ∂g*(Y) where g* is a Fenchel conjugate defined in (2) and can be calculated using the fact that X ∈ ∂g*(Y)⇔Y ∈ ∂g(X). Since gγ is differentiable. Thus,
where a = (1 + τ)m + 1 and b = 1.
Let N = a𝕀 − bH, then N is invertible as N−1 = α𝕀 + βH where
(see Lemma 5.1 of [8]). Therefore,
Next, we find the sub-gradient in (14) and this can be done by search Y ∈ ∂hγ(X). Given a smooth functions h1γ and h2γ, the partial gradient at xj for j = 1, …, k + 1 is
Thus, ∇h1γ(X)) is a matrix with dimension (k + 1) × n with jth row is .
The gradients of at X are given by
The projections in (17) and (18) are the Euclidean projection from v ∈ ℝn onto a unit closed box F which are defined as
where e ∈ ℝn is a vector with one in each coordinate and zero elsewhere.
Since we use ℓ1 norm, next we illustrate how to find the sub-gradient Y ∈ ∂hγ(X) for the case where F is the closed unit box in ℝn.
For a given x ∈ ℝ, we define
Then, we define sign(x): = (sign(x1), …, sign(xn)) for Note that the sub-gradients of f(x) = ||x||1 at x ∈ ℝn are si = sign(x) if xi ≠ 0 and si ∈ [−1, 1] if xi = 0.
The sub-gradients of the non-smooth functions h3γ and h4γ are calculated as the sub-differential of point-wise maximum functions,
where, for i = 1, …, m,
To do this, for each i = 1, …, m, we first find Ui ∈ ∂ϕi(X) according to Lemma 3. Then, we define to get a sub-gradient of the function h3γ at X by the sub-differential sum rule. To accomplish this goal, we first choose an index r* from the index set {1, …, k} such that
Using the familiar sub-differential formula of the ℓ1 norm function, the jth row for j ≠ r* of the matrix Ui is determined as follows:
The r*th row of the matrix Ui is .
Similarly, the sub-gradient of h4γ is given by
where, for j = 1, …, k,
To do this, for each j = 1, …, k, we first find Wj ∈ ∂ψj(X). Then, we define to get a sub-gradient of the function h4γ at X by the sub-differential sum rule. To accomplish this goal, we first choose an index s* from the index set {1, …, m} such that
The s*th row of the matrix Wj is .
Thus, the sub-gradient of h4γ is defined as
From the sub-gradient calculated above we have,
Now, we have in position to implement DCA algorithm that will solve the problem as shown in DCA Algorithm 2.
4 Simulation results
The numerical simulation was performed on an HP laptop with an Intel(R) Core(TM) i7-8565U at 1.80 GHz 1.99 GHz processor, 8.00 GB RAM with MATLAB version R2017b. Various parameters were used during the simulation, among others we used a large increasing penalty parameter τ and a decay smoothing parameter γ. These parameters are updated during iteration as in [6]; τi+1 = σ1τi, σ1 > 1 and γi+1 = σ2γi, 0 < σ2 < 1 and ϵ = 1e − 6. We chose the initial penalty parameter () and the initial smoothing parameter γ0 = 1. In addition, after varying the parameters, we chose as the growth factor of the penalty parameter, σ2 = 0.5 the decrease factor of the smoothing parameter, and the stopping criterion for inner for loop. To implement the algorithms, we used randomly selected default cluster centers from the datasets.
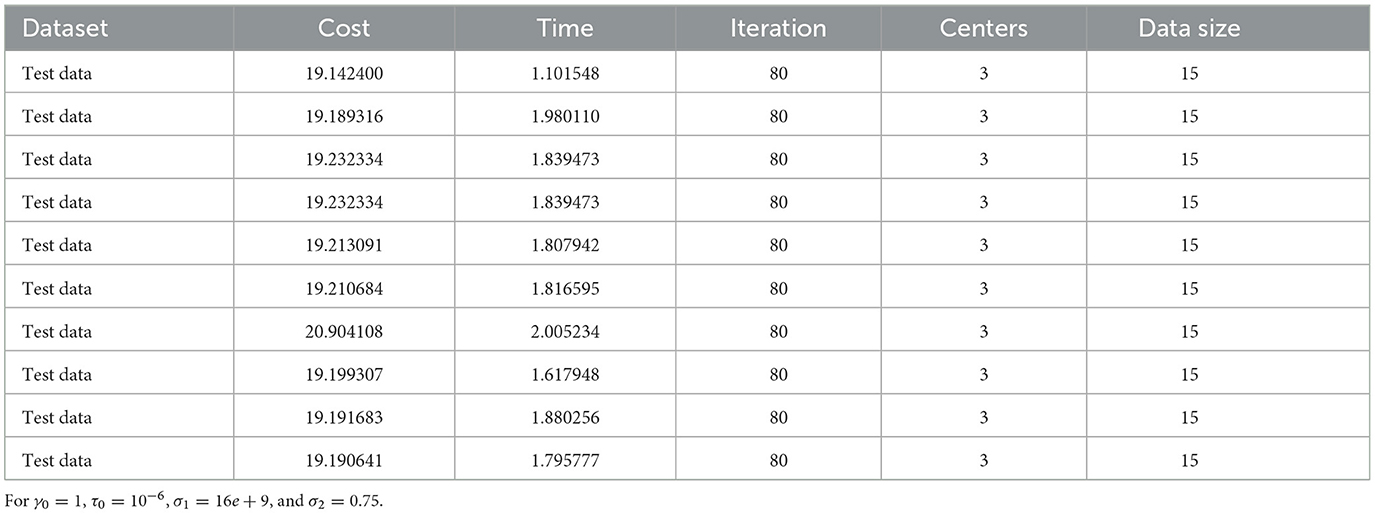
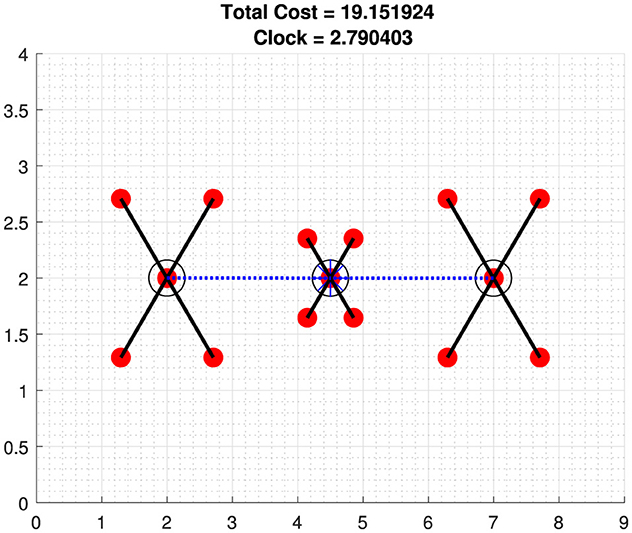
The performance of the DCA Algorithm 2 was tested with different datasets. We first tested the algorithm on a small dataset taken from [8], and the result shows that it converges to the same cluster centers as in [8] with a different objective value due to the ℓ1 norm. Since the ℓ1 distance is greater than or equal to the Euclidean distance, it depends on the data points. As shown in Table 1, the algorithm converges to the optimal point approximately 85.71%. This means that out of 7 iterations, 6 of them converge to the same objective valve.
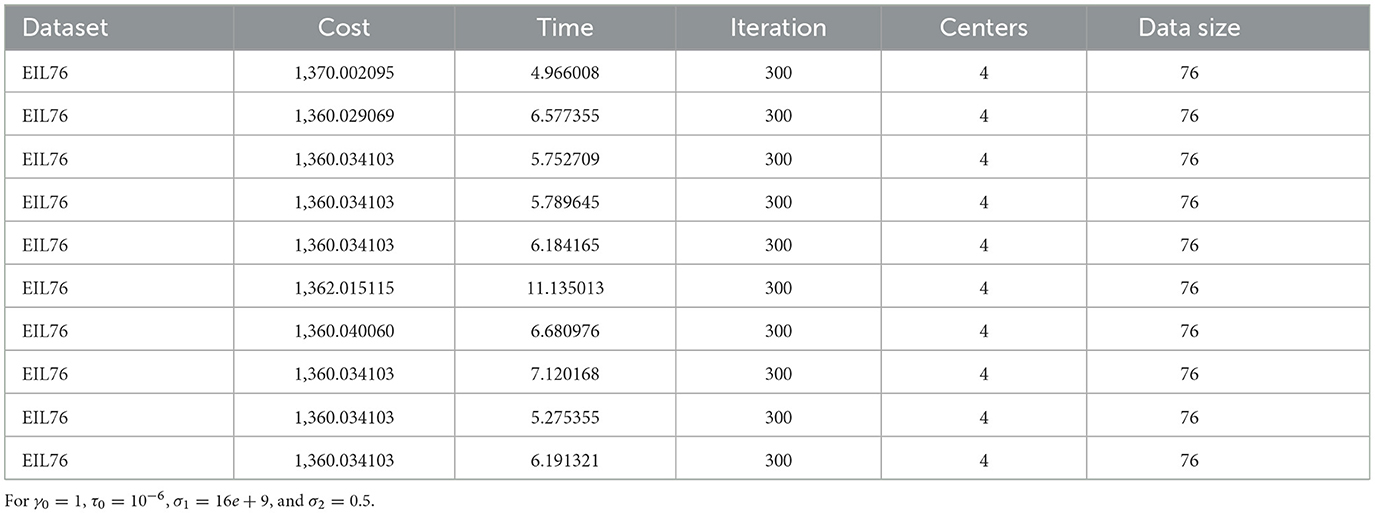
Second, we tested the proposed algorithm with EIL76 (The 76 City Problem) datasets taken from [7] with four clusters, one of which serves as HQ, which converge to near-optimal cluster centers in a reasonable time compared to study [8, 13] (see Figure 1).
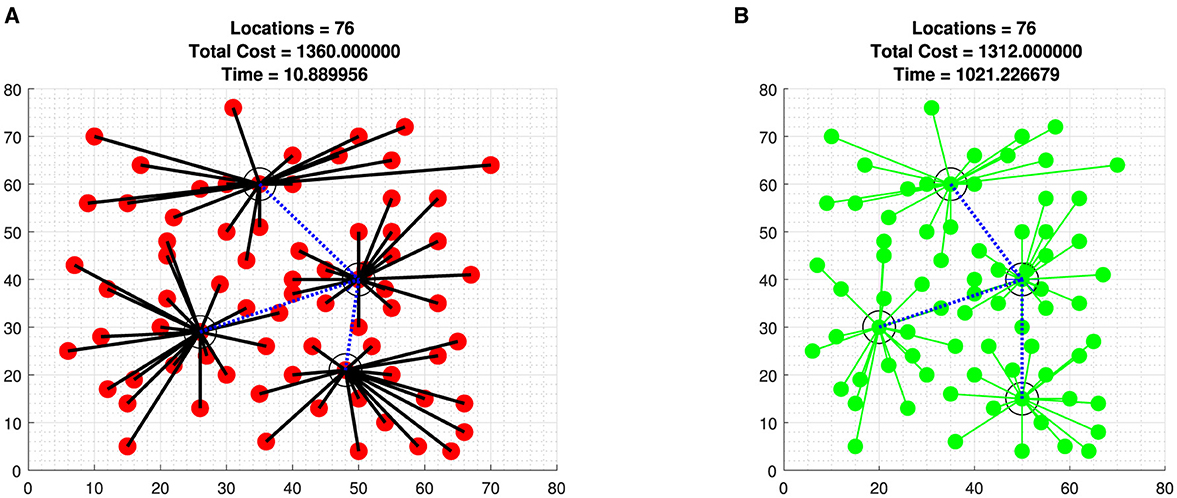
Figure 1. Optimal cost of EIL76 (The 76 City Problem) data taken from [7] with four clusters one serves as HQ. (A) A EIL76 data with Algorithm 2. (B) A EIL76 data with brute-force iteration.
It is also observed in the EIL76 (The 76 City Problem) data which converge to the same or close cluster centers with higher objective cost, fewer iterations, and almost the same time compared to the study of [8] iterated using MATLAB (see Table 2).
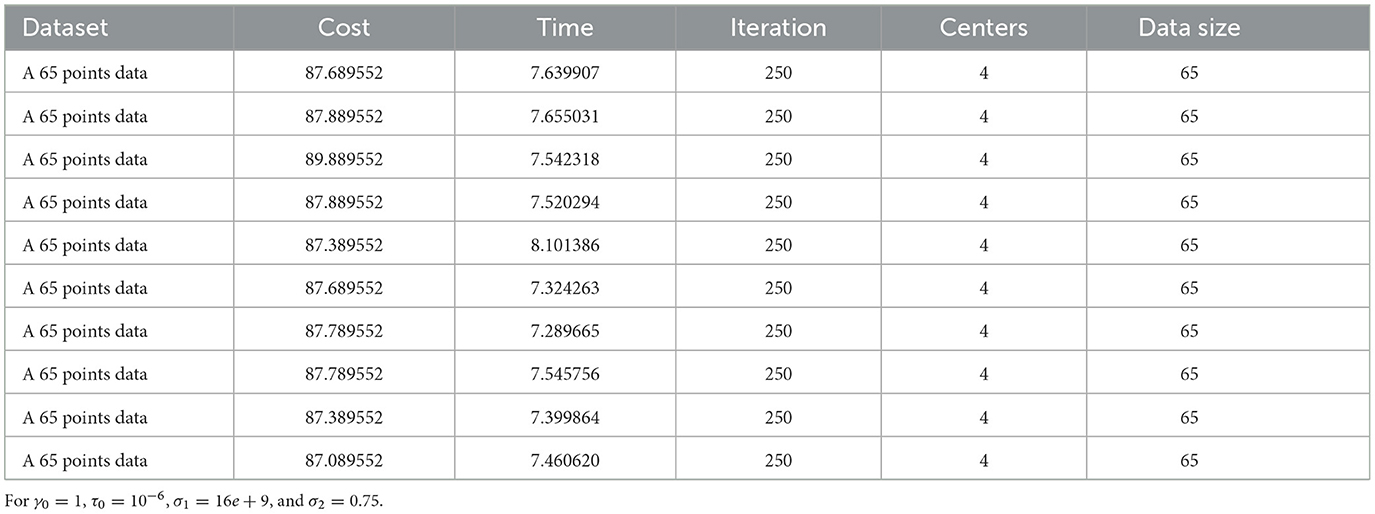
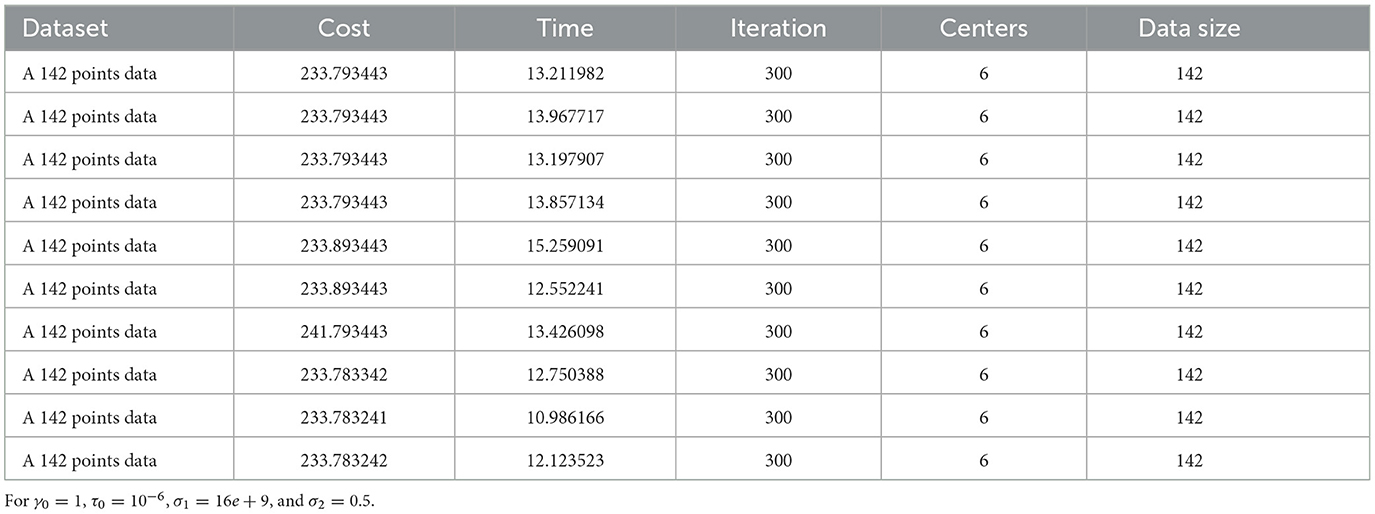
Third, we applied our proposed algorithm to a GPS data from 142 cities and towns in Ethiopia with more than 7,000 inhabitants, including 65 in Oromia regional state. We tested the algorithm with 65 nodes, 4 cluster centers, one of which serves as HQ, and 142 nodes with six clusters (see Figures 2, 3), which converge 86% to the optimal solution. This means that out of 7 iterations, 6 of them converge to the near-optimal values shown in Tables 3, 4.
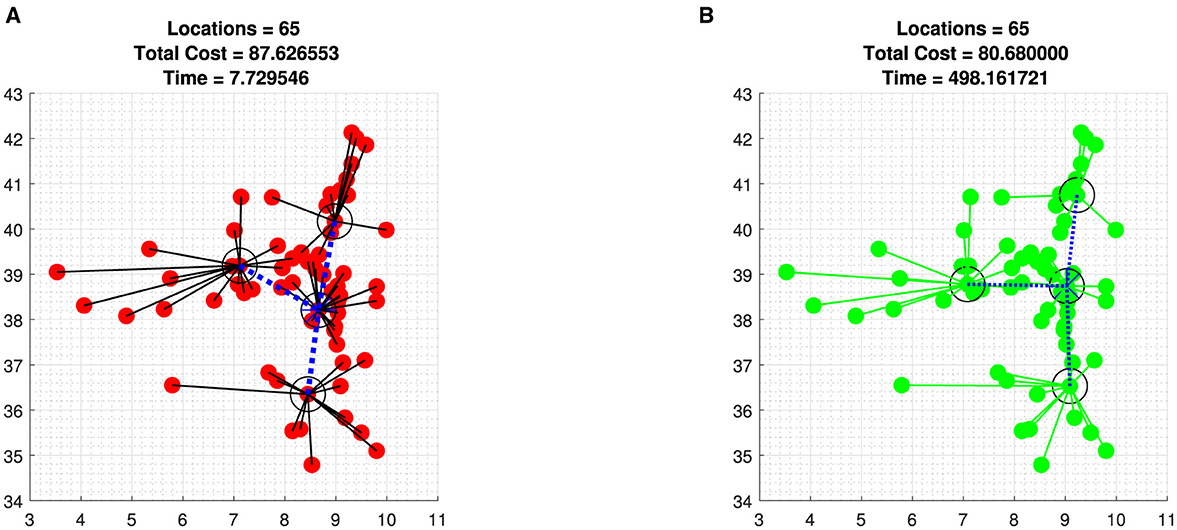
Figure 2. Datasets of 65 Oromia regional cities and towns with four clusters one serves as HQ. (A) Sixty-five data points using Algorithm 2. (B) Sixty-five data points with brute-force iteration.
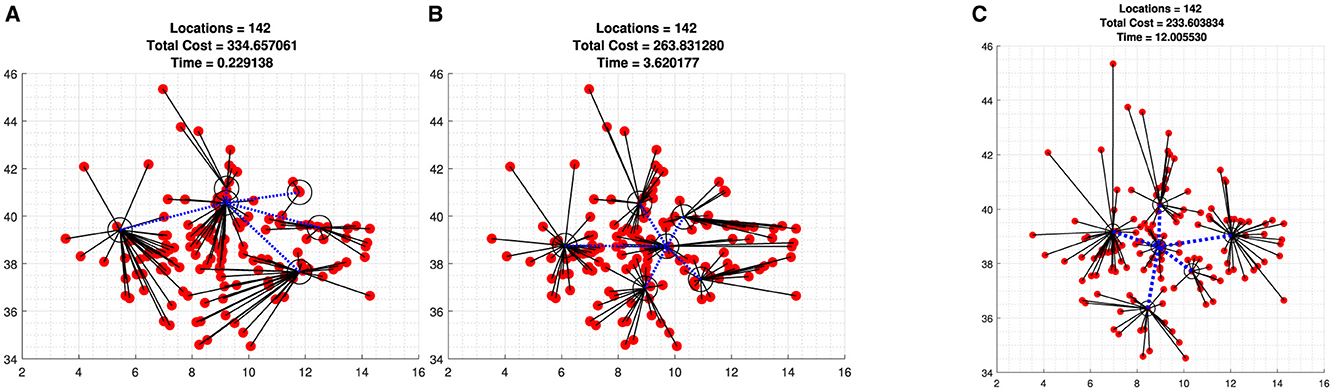
Figure 3. Datasets of 142 Ethiopian towns and cities with six clusters one serves as HQ. (A) Beginning of iterations. (B) Few iterations. (C) Optimal iterations.
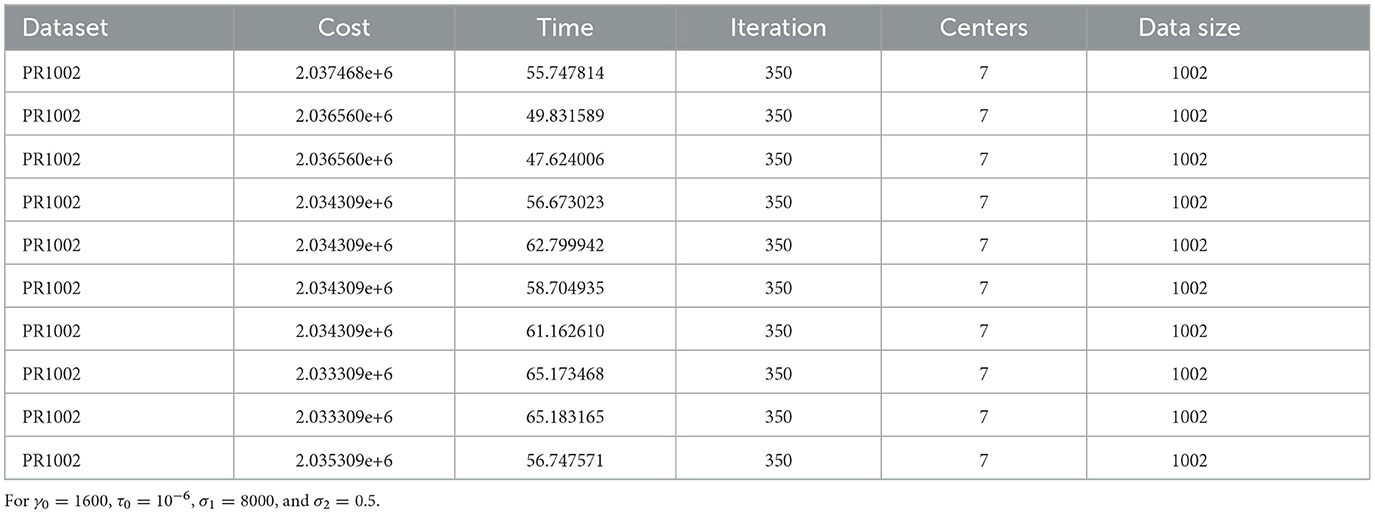
Fourth, we tested the proposed algorithm with PR1002 (The 1002 City Problem) datasets taken from [7] with seven clusters, one of which serves as HQ, which converge to near-optimal cluster centers in a reasonable time compared to study [8, 13] (see Table 5 and Figure 4).
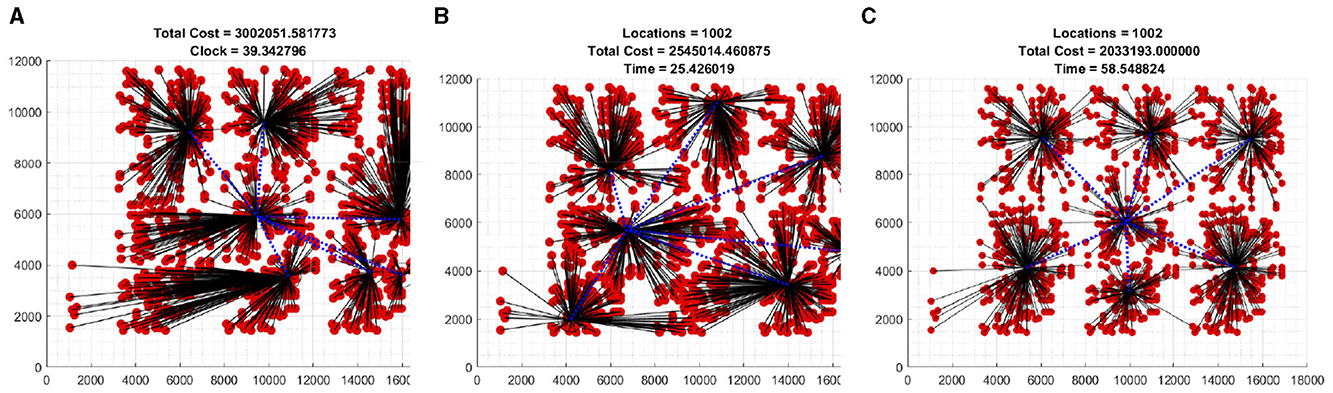
Figure 4. Datasets of PR1002 (The 1002 City Problem) taken from [7] with seven clusters and one serving as HQ. (A) Beginning of iteration. (B) Few iteration. (C) Optimal iteration.
To show how the objective functions improved with iteration, we include a plot of the first few iterations of Figures 3, 4, which shows the dynamics of the algorithm (see Figures 3A, B, 4A, B).
In general, since the algorithm is a modified DCA and DCA is a local search algorithm, there is no guarantee that our algorithms converge to the global optimal solution. However, we compared our result with ℓ2 norm in [8, 13], and it shows that our proposed algorithm converges with fewer iteration but relatively the same computational time for data iterated with MATLAB in [8]. In addition, we compared our result with brute-force generated solutions for datasets with fewer nodes (see Figures 1A, B, 2A, B) which converge to a near-optimal value with reasonable time compared to the brute-force iterations.
We expect that our method used in this study to solve the two-level clustering problem with the ℓ1 norm is less sensitive to outliers compared to the ℓ2 norm, which minimizes possible clustering errors. In addition, it can be used to solve other non-smooth and non-convex optimization problems in signal processing, such as image pixel clustering for image segmentation and compressed sensing.
For the following tables, we conducted an experiment with fixed iteration numbers for each dataset and initial cluster centers were randomly selected from the datasets. The cost is obtained by minimizing Equation (7).
Figure 5 shows the optimal cost of test data taken from [8] with optimal clusters centers and HQ,
In Figure 1 the selected cluster centers and HQ are
In Figure 2 the selected cluster centers and HQ are
In Figure 3 the selected cluster centers and HQ are
For this particular dataset, we used γ0 = 1600 and σ1 = 8000. In Figure 4 the selected cluster centers and HQ are
5 Conclusion
In this study, we used a continuous formulation of discrete two-level hierarchical clustering, where the distance between two data points is measured by the ℓ1 norm. As a result, it became non-smooth and non-convex, on which Nesterov's smoothing and DC-based algorithms were implemented. We observe that parameter selection is the decisive factor in terms of accuracy and speed of convergence of our proposed algorithms. The performance of Algorithm 2 highly depends on the initial values set to the penalty and smoothing parameter.
The algorithm was tested with real and known source datasets of different sizes in MATLAB. Starting from different random initial cluster centers, the algorithm converges to a near-optimal value in a reasonable time. As a result, improved iteration time for large-scale problems and convergence to a near-optimal solution were observed.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
AG: Investigation, Software, Writing – original draft, Conceptualization, Data curation, Formal analysis, Funding acquisition, Methodology, Project administration, Resources, Supervision, Validation, Visualization, Writing – review & editing. LO: Conceptualization, Formal analysis, Supervision, Validation, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Acknowledgments
Authors are grateful to the referees and handling editor for their constructive comments.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2024.1445390/full#supplementary-material
References
1. An LTH, Belghiti MT, Tao PD. A new efficient algorithm based on DC programming and DCA for clustering. J Global Optimizat. (2007) 37:593–608. doi: 10.1007/s10898-006-9066-4
2. Bagirov AM, Taheri S, Ugon J. Nonsmooth DC programming approach to the minimum sum-of-squares clustering problems. Pattern Recognit. (2016) 53:12–24. doi: 10.1016/j.patcog.2015.11.011
3. Bagirov A. Derivative-free methods for unconstrained nonsmooth optimization and its numerical analysis. Investigacao Operacional. (1999) 19:75–93.
4. Bajaj A, Mordukhovich BS, Nam NM, Tran T. Solving a continuous multifacility location problem by DC algorithms. Optimizat Meth Softw. (2022) 37:338–60. doi: 10.1080/10556788.2020.1771335
5. Barbosa GV, Villas-Boas SB, Xavier AE. Solving the two-level clustering problem by hyperbolic smoothing approach, and design of multicast networks. In: The 13th World Conference on Transportation Research was organized on July 15–18, 2013 by COPPE - Federal University of Rio de Janeiro, Brazil. WCTR RIO (2013).
6. Fita A, Geremew W, Lemecha L. A DC optimization approach for constrained clustering with l1-norm. Palest J Mathem. (2022) 11:3.
7. Reinelt G. TSPLIB: A traveling salesman problem library. ORSA J Comp. (1991) 3:376–84. doi: 10.1287/ijoc.3.4.376
8. Geremew W, Nam NM, Semenov A, Bogniski V, Psailio E. A DC programming approach for solving multicast network design problems via the Nesterov smoothing technique. J Global Optimizat. (2018) 72:705–29. doi: 10.1007/s10898-018-0671-9
9. Jia L, Bagirov A, Ouveysi I, Rubinov M. Optimization based clustering algorithms in Multicast group hierarchies. In: Proceedings of the Australian Telecommunications, Networks and Applications Conference (ATNAC) (2003).
10. Le Thi HA, Pham Dinh T. DC programming and DCA: thirty years of developments. Mathemat Program. (2018) 169:5–68. doi: 10.1007/s10107-018-1235-y
11. Mau Nam N, Hoai An LT, Giles D, An NT. Smoothing techniques and difference of convex functions algorithms for image reconstructions. Optimization. (2020) 69:1601–33. doi: 10.1080/02331934.2019.1648467
12. Mordukhovich BS, Nam NM. An Easy Path to Convex Analysis and Applications. Cham: Springer. (2014).
13. Nam NM, Geremew W, Reynolds S, Tran T. Nesterov's smoothing technique and minimizing differences of convex functions for hierarchical clustering. Optimizat Lett. (2018) 12:455–73. doi: 10.1007/s11590-017-1183-0
14. Nam NM, Rector RB, Giles D. Minimizing differences of convex functions with applications to facility location and clustering. J Optim Theory Appl. (2017) 173:255–78. doi: 10.1007/s10957-017-1075-6
15. Nesterov Y. Smooth minimization of non-smooth functions. Mathem Program. (2005) 103:127–52. doi: 10.1007/s10107-004-0552-5
16. Nesterov Y. Lectures on Convex Optimization. Cham: Springer. (2018). doi: 10.1007/978-3-319-91578-4
17. Nguyen PA, Le Thi HA. DCA approaches for simultaneous wireless information power transfer in MISO secrecy channel. Optimizat Eng. (2023) 24:5–29. doi: 10.1007/s11081-020-09570-3
19. Tao PD, An LTH. A DC optimization algorithm for solving the trust-region subproblem. SIAM J Optimizat. (1998) 8:476–505. doi: 10.1137/S1052623494274313
20. Tao PD, An LH. Convex analysis approach to DC programming: theory, algorithms and applications. Acta Mathematica Vietnamica. (1997) 22:289–355.
21. An LTH, Minh LH, Tao PD. Optimization based DC programming and DCA for hierarchical clustering. Eur J Operation Res. (2007) 183:1067–85. doi: 10.1016/j.ejor.2005.07.028
Keywords: clustering, DC programming, bi-level hierarchical, headquarter, smoothing
Citation: Gabissa AF and Obsu LL (2024) A DC programming to two-level hierarchical clustering with ℓ1 norm. Front. Appl. Math. Stat. 10:1445390. doi: 10.3389/fams.2024.1445390
Received: 17 June 2024; Accepted: 09 August 2024;
Published: 12 September 2024.
Edited by:
Lixin Shen, Syracuse University, United StatesReviewed by:
Jianqing Jia, Syracuse University, United StatesRongrong Lin, Guangdong University of Technology, China
Copyright © 2024 Gabissa and Obsu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Adugna Fita Gabissa, YWR1Z25hLmZpdGFAYXN0dS5lZHUuZXQ=
 Adugna Fita Gabissa
Adugna Fita Gabissa Legesse Lemecha Obsu
Legesse Lemecha Obsu