A new Steiner symmetrization defined by a subclass of analytic function in a complex domain

In this effort, we present a new definition of the Steiner symmetrization by using special analytic functions in a complex domain (the open unit disk) with respect to the origin. This definition will be used to optimize the class of univalent analytic functions. Our method is based on the concept of differential subordination and the Carathéodory theory. Examples are illustrated in the sequel involving the modified Libera–Livingston–Bernardi integral operator over the open unit disk. The result gives that this integral satisfies the definition of bounded turning function (univalent analytic function).

1 Introduction

In convex geometry, the process of “Steiner symmetrization” is used to change an existing convex body into a symmetric one when compared with a particular axis or plane. Steiner symmetrization takes a convex body and replaces every point with the midpoint of the line segment that goes from that point to its reflection across the selected axis or plane. Because the resultant symmetric body and the original body share some geometric features, analysis of the half plane becomes simpler. This transformation may streamline computations and provide insightful findings in specific situations, such as geometric inequalities and optimization issues affecting convex bodies. The definition of Steiner symmetrization in a complex domain admits many formulas. Smith et al. [1] suggested some Poincare domains Ω to define Steiner symmetrization, which are as follows:

$\begin{array}{l}{\Omega }^{*}=\left\{\zeta =\chi +iy:|y|<\frac{{\Omega }_{\chi }}{2}<\infty ,\Omega \ne Ø\right\}\end{array}$

Peretz [2] considered the formula in the open unit disk Ω: = {ζ ∈ ℂ:|ζ| < 1} as follows:

$\begin{array}{l}{\Omega }^{*}=\left\{\zeta \in \Omega :\Re (\zeta )>0\right\}.\end{array}$

The above definitions can sometimes yield loss in information when symmetrizing a shape or function. This situation might not be desired, especially if the original shape or function's features or properties are crucial for analysis or interpretation. Depending on the original form or function being symmetrical, Steiner symmetrization may or may not be successful. The application of this type of approach may be limited by some geometries or functions that are not well suited for symmetrization using this method. Moreover, the computational cost of Steiner symmetrization can be high, particularly for intricate forms or functions. For some applications, especially those that call for real-time or very real-time analysis, this computing expense can render it unfeasible. Therefore, we aim to enhance the above definitions using special functions.

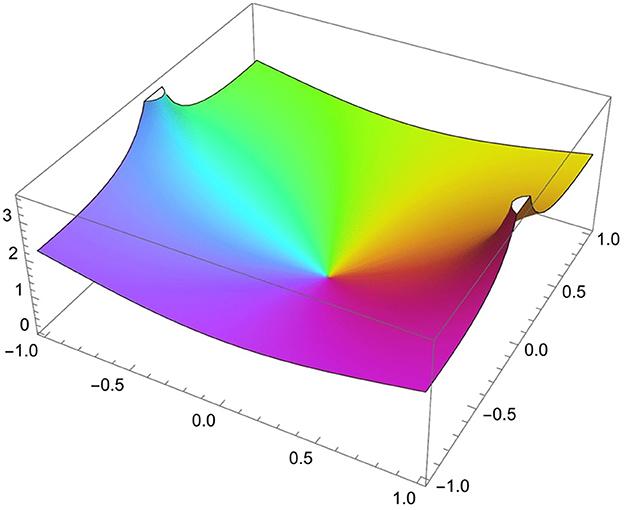
In this study, we consider the function (see Figure 1) as follows:

$\begin{array}{l}L(\zeta )=log\left(\frac{1+\zeta }{1-\zeta }\right),\left|\zeta \right|<1,L(0)=0.\end{array}$

Figure 1

Figure 1. The ComplexPlot3D of $log\left(\frac{1+\zeta }{1-\zeta }\right)$.

This function maps Ω conformally onto the horizontal strip Π = {ζ:|ℑζ| < π/2}. Moreover, this function maps the hyperbolic geodesic (−1, 1) onto the real axis, and it maps the curves equidistant from (−1, 1) onto the horizontal lines Π. To define the Steiner symmetrization, we need the following function:

$\begin{array}{l}S(\zeta )=1+log\left(\frac{1+\zeta }{1-\zeta }\right)\\ =1+2\zeta +\frac{(2{\zeta }^3)}{3}+\frac{(2{\zeta }^5)}{5}+O({\zeta }^6),\end{array}$

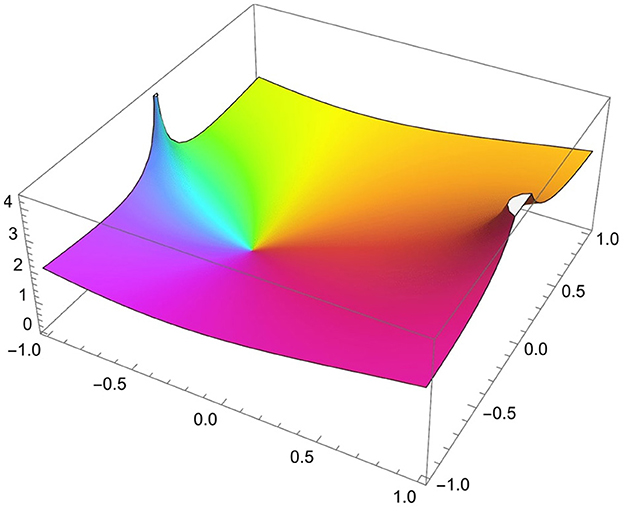
where S(0) = 1 (see Figure 2). Then, the Steiner symmetrization becomes

$\begin{array}{l}{\Omega }_{\phi }^{*}=\left\{\phi \in P:|\phi (\zeta )|\le 1+log\left(\frac{1+r}{1-r}\right),0<r<1\right\},\end{array}$

where φ is analytic function in $\Omega \in \mathcal{P}$, where $\mathcal{P}$ is the class of analytic function with the power series

$\phi (\zeta )=1+a_1\zeta +a_2{\zeta }^2+....$

such that φ(0) = 1. A good example of this function (or the extreme function of this class) is the Janowski function [3], which will be investigated in the next section.

Figure 2

Figure 2. The ComplexPlot3D of $1+log\left(\frac{1+\zeta }{1-\zeta }\right)$.

Our goal is to maximize the class of analytic functions that are univalent. The Carathéodory theory and the idea of differential subordination serve as the foundation for our approach. In the sequel, illustrations are given. The study is organized as follows: Section 2 deals with preliminaries and Section 3 involves the main results.

2 Methods

For two analytic functions, f₁(ζ) and f₂(ζ) in Ω are called subordinated denoting by f₁(ζ) ≺ f₂(ζ) if they satisfy f₁(0) = f₂(0) and the inclusion property f₁(Ω) ⊂ f₂(Ω) (see [4]). As an application, Ma-Minda formula for some special classes

$\left(\frac{\zeta f^{\prime }(\zeta )}{f(\zeta )}\right)\prec \varrho (\zeta ),\varrho (\zeta )=1+{\varrho }_1\zeta +{\varrho }_2{\zeta }^2+...\in P$

for starlike functions, and

$\left(1+\frac{\zeta f^{″}(\zeta )}{f^{\prime }(\zeta )}\right)\prec \rho (\zeta ),\rho (\zeta )=1+{\rho }_1\zeta +{\rho }_2{\zeta }^2+...\in P$

for convex functions, where ρ has a positive real part in Ω, ρ(0) = 1 and $f(\zeta )\in \mathcal{N}(\Omega ),$ the normalized class of analytic functions in Ω with f(0) = 0 and f′(0) = 1. Thus, f admits the power series

$\begin{array}{l}f(\zeta )=\zeta +{\displaystyle \sum _{n=2}^{\infty }}{a}_n{\zeta }^n,\zeta \in \Omega .\end{array}$

In fact, the function f is starlike whenever $\left(\frac{\zeta f^{\prime }(\zeta )}{f(\zeta )}\right)\in \mathcal{P}$, and it is convex when $\left(1+\frac{\zeta f^{″}(\zeta )}{f^{\prime }(\zeta )}\right)\in \mathcal{P}.$

The function $log\left(\frac{1-\zeta }{1+\zeta }\right)$ is starlike whenever −1 < ℜ(ζ) < 0 or 0 < ℜ(ζ) < 1. Moreover, it is convex whenever, −1 < ℜ(ζ) < 1 and

$-\sqrt{1-\Re {(\zeta )}^2}<\Im (\zeta )<\sqrt{1-\Re {(\zeta )}^2},\zeta \in \Omega .$

This function is considered for symmetrization in the study mentioned in Betsakos et al. [5]. While for the function $1+\left(log\left(\frac{1+\zeta }{1-\zeta }\right)\right)$ is starlike and convex when −1 < ℜ(ζ) < 0 or 0 < ℜ(ζ) < 1. Note that $\left(\frac{1+\zeta }{1-\zeta }\right)$ is an extreme Janowski function.

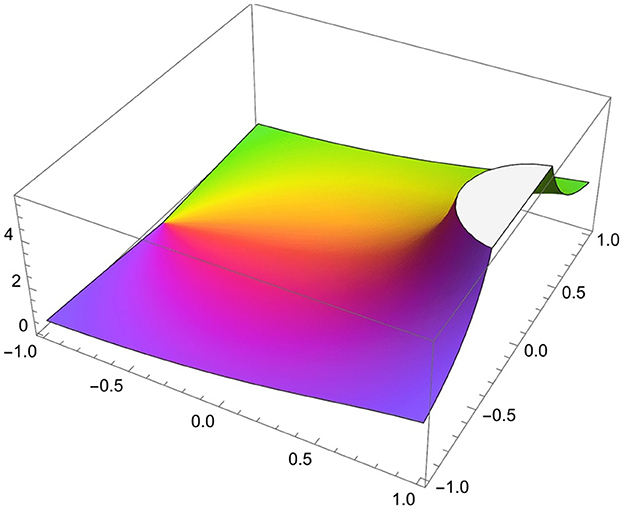
In our investigation, we concern about the Carathéodory function (a function that maps Ω onto the right half plane), φ(ζ), which is involved in the inequalities (see Figure 3):

$1+{\sigma }_k\left(\frac{\zeta {\phi }^{\prime }(\zeta )}{{\left[\phi (\zeta )\right]}^k}\right)\prec \frac{1+\zeta }{1-\zeta },k=0,1,2,$

where φ(0) = 1 and ℜ(φ) > 0.

Figure 3

Figure 3. ComplexPlot3D of $\frac{1+\zeta }{1-\zeta }$.

Our aim is to determine the upper bound of the parameter σ, where the function ϱ ∈ Ω is analytic such that ϱ(0) = 1 and ℜ(ϱ(ζ)) > 0. Note that the condition of ${\Omega }_{\phi }^{*},$ where φ(0) = 1, ℜ(φ) > 0 is equivalent to achieve the inequality:

$\phi (\zeta )\prec 1+log\left(\frac{1+\zeta }{1-\zeta }\right),\zeta \in \Omega ,$

where the function $\frac{1+\zeta }{1-\zeta }$ is a Carathéodory function. Moreover, the function $1+log\frac{1+\zeta }{1-\zeta }$ has a root $\zeta =\frac{1+e}{1-e}$ and two branch points at ζ = ±1, with the power series at ζ = −1

$\begin{array}{l}1+\log \left(\frac{1+\zeta }{1-\zeta }\right)=(\log (\zeta +1)+1-\\ \log (2))+\frac{(\zeta +1)}{2}+\frac{1}{8}(\zeta +1{)}^2\\ +\frac{1}{24}(\zeta +1{)}^3+\frac{1}{64}(\zeta +1{)}^4+O((\zeta +1{)}^5)\end{array}$

and at ζ = 1 when $\Im (\frac{1}{(1-\zeta )})>0$

$\begin{array}{l}1+\log \left(\frac{1+\zeta }{1-\zeta }\right)=(\log (-2/(\zeta -1))+\frac{(\zeta -1)}{2}-\\ \frac{1}{8}(\zeta -1{)}^2+\frac{1}{24}(\zeta -1{)}^3-\frac{1}{64}(\zeta -1{)}^4\\ +\frac{1}{160}(\zeta -1{)}^5-\frac{1}{384}(\zeta -1{)}^6+\\ O((\zeta -1{)}^7){)}^{*}+1.\end{array}$

The notion of the Carathéodory function, often referred to as the Carathéodory kernel function, is principally used in the theory of univalent functions, which are complex functions that are holomorphic (analytic) and injective (one-to-one).

3 Results

In this part, we illustrate the main results.

Theorem 3.1. Assume that the function φ ∈ Ω is analytic such that φ(0) = 1 and ℜ(φ(ζ)) > 0. If

$\begin{array}{ll}1+{\sigma }_k\left(\frac{\zeta {\phi }^{\prime }(\zeta )}{{\left[\phi (\zeta )\right]}^k}\right)\prec \frac{1+\zeta }{1-\zeta },k=0,1,2& (1)\end{array}$

then

$\begin{array}{ll}\phi (\zeta )\prec 1+log\left(\frac{1+\zeta }{1-\zeta }\right),\zeta \in \Omega ,& (2)\end{array}$

where

$\begin{array}{c}{\sigma }_0=\frac{log(4)}{log(3)}=1.26186,{\sigma }_1=\frac{log(4)}{log(1+log(3))}=1.8701,\\ {\sigma }_2=5.35044041019216.\end{array}$

Proof: Case 1.

Let k = 0. Then, by Equation 1, we get:

$\begin{array}{l}1+{\sigma }_0(\zeta {\phi }^{\prime }(\zeta ))\prec \frac{1+\zeta }{1-\zeta },\zeta \in \Omega .\end{array}$

Define a function Φ_σ0:Ω → ℂ as follows:

${\Phi }_{{\sigma }_0}(\zeta )=1-\frac{(2log({\sigma }_0-{\sigma }_0\zeta ))}{{\sigma }_0}+\frac{(2log({\sigma }_0))}{{\sigma }_0}.$

Clearly, Φ_σ0(ζ) is analytic in Ω such that Φ_σ0(0) = 1, and it is a solution of the first order differential equation

$\begin{array}{l}1+{\sigma }_0(\zeta {\Phi }_{{\sigma }_0}{(\zeta )}^{\prime })=\frac{1+\zeta }{1-\zeta },\zeta \in \Omega \end{array}$

Burt $\frac{1+\zeta }{1-\zeta }$ is starlike in Ω, and then according to Miller-Mocanu Lemma in Miller and Mocanu [4] -P132, the subordination

$1+{\sigma }_0(\zeta {\phi }^{\prime }(\zeta ))\prec 1+{\sigma }_0(\zeta {\Phi }_{{\sigma }_0}{(\zeta )}^{\prime })$

yields

$\phi (\zeta )\prec {\Phi }_{{\sigma }_0}(\zeta ),\zeta \in \Omega .$

Now, we aim to show that

${\Phi }_{{\sigma }_0}(\zeta )\prec 1+log\left(\frac{1+\zeta }{1-\zeta }\right),\zeta \in \Omega .$

Obviously, Φ_σ0(ζ) achieves the inequality

$1-\frac{2log(3/2)}{{\sigma }_0}={\Phi }_{{\sigma }_0}(\frac{-1}{2})\le {\Phi }_{{\sigma }_0}(\frac{1}{2})=1+\frac{2log(2)}{{\sigma }_0},{\sigma }_0>0.$

Since $1+log\left(\frac{1-\zeta }{1+\zeta }\right)$ satisfies the following inequality

$\begin{array}{l}-0.09861...=1-log(3)=\left(1+log\left(\frac{1+\zeta }{1-\zeta }\right)\right){|}_{\zeta =-1/2}\le \\ \left(1+log\left(\frac{1+\zeta }{1-\zeta }\right)\right){|}_{\zeta =1/2}=\\ 1+log(3)=2.0986...& (3)\end{array}$

this function has two branch points ζ = ±1, and then, we get

$\begin{array}{c}1-log(3)<1-\frac{2log(3/2)}{{\sigma }_0}={\Phi }_{{\sigma }_0}(\frac{-1}{2})\le {\Phi }_{{\sigma }_0}(\frac{1}{2})=\\ 1+\frac{2log(2)}{{\sigma }_0}\le 1+log(3),\end{array}$

where ${\sigma }_0=\frac{log(4)}{log(3)}=1.26186$ and $1-\frac{2log(3/2)}{{\sigma }_0}=0.3573.$

As a consequence, we obtain the inequality subordination

$\phi (\zeta )\prec {\Phi }_{{\sigma }_0}(\zeta )\prec 1+log\left(\frac{1+\zeta }{1-\zeta }\right),|\zeta |\le 1/2.$

Thus, inequality (Equation 2) is valid.

Case 2

Let k = 1. From Equation 1, we have:

$1+{\sigma }_1\left(\frac{\zeta {\phi }^{\prime }(\zeta )}{\phi (\zeta )}\right)\prec \frac{1+\zeta }{1-\zeta },\zeta \in \Omega .$

Define a function Φ_σ1: Ω → ℂ as follows:

${\Phi }_{{\sigma }_1}(\zeta )=\frac{{({\sigma }_1-{\sigma }_1\zeta )}^{\frac{-2}{{\sigma }_1}}}{{\sigma }_1^{-\frac{2}{{\sigma }_1}}}.$

Obviously, Φ_σ1(ζ) is analytic in Ω with Φ_σ1(0) = 1. Moreover, it is indicated a solution of the differential equation

$\begin{array}{l}1+{\sigma }_1\left(\frac{\zeta {\Phi }_{{\sigma }_1}{(\zeta )}^{\prime }}{{\Phi }_{{\sigma }_1}(\zeta )}\right)=\frac{1+\zeta }{1-\zeta },\zeta \in \Omega .\end{array}$

Then Miller-Mocanu Lemma implies that the subordination

$1+{\sigma }_1\left(\frac{\zeta {\phi }^{\prime }(\zeta )}{\phi (\zeta )}\right)\prec 1+{\sigma }_1\left(\frac{\zeta {\Phi }_{{\sigma }_1}{(\zeta )}^{\prime }}{{\Phi }_{{\sigma }_1}(\zeta )}\right)$

gives

$\phi (\zeta )\prec {\Phi }_{{\sigma }_1}(\zeta ),\zeta \in \Omega .$

A computation yields

${(\frac{2}{3})}^{\frac{2}{{\sigma }_1}}={\Phi }_{{\sigma }_1}(\frac{-1}{2})\le {\Phi }_{{\sigma }_1}(\frac{1}{2})=2^{\frac{2}{{\sigma }_1}},{\sigma }_1>0.$

By using Equation 3, we obtain the inequality:

$1-log(3)<{(\frac{2}{3})}^{\frac{2}{{\sigma }_1}}={\Phi }_{{\sigma }_1}(\frac{-1}{2})\le {\Phi }_{{\sigma }_1}(\frac{1}{2})=2^{\frac{2}{{\sigma }_1}}\le 1+log(3),$

where ${\sigma }_1=\frac{log(4)}{log(1+log(3))}=1.8701.$

As a consequence, we obtain the inequality subordination:

$\phi (\zeta )\prec {\Phi }_{{\sigma }_1}(\zeta )\prec 1+log\left(\frac{1+\zeta }{1-\zeta }\right),|\zeta |\le 1/2.$

Thus, inequality (Equation 2) is valid.

Case 3

Let k = 2. From Equation 1, we have:

$1+{\sigma }_2\left(\frac{\zeta {\phi }^{\prime }(\zeta )}{{\phi }^2(\zeta )}\right)\prec \frac{1+\zeta }{1-\zeta },\zeta \in \Omega .$

Define a function Φ_σ2: Ω → ℂ as follows:

${\Phi }_{{\sigma }_2}(\zeta )=1-\frac{{\sigma }_2}{{\sigma }_2-2\log ({\sigma }_2-{\sigma }_2\zeta ))}+\frac{{\sigma }_2}{{\sigma }_2-2\log ({\sigma }_2)}.$

Obviously, Φ_σ2(ζ) is analytic in Ω with Φ_σ2(0) = 1. Moreover, it is indicated as a solution of the differential equation:

$\begin{array}{l}1+{\sigma }_2\left(\frac{\zeta {\Phi }_{{\sigma }_2}{(\zeta )}^{\prime }}{{\Phi }_{{\sigma }_2}^2(\zeta )}\right)=\frac{1+\zeta }{1-\zeta },\zeta \in \Omega .\end{array}$

Then Miller-Mocanu Lemma implies that the subordination

$1+{\sigma }_2\left(\frac{\zeta {\phi }^{\prime }(\zeta )}{{\phi }^2(\zeta )}\right)\prec 1+{\sigma }_2\left(\frac{\zeta {\Phi }_{{\sigma }_2}{(\zeta )}^{\prime }}{{\Phi }_{{\sigma }_2}^2(\zeta )}\right)$

gives

$\phi (\zeta )\prec {\Phi }_{{\sigma }_2}(\zeta ),\zeta \in \Omega .$

A computation yields

${\Phi }_{{\sigma }_2}(\frac{-1}{2})=\frac{{\sigma }_2}{{\sigma }_2-2log({\sigma }_2)}+\frac{{\sigma }_2}{2log(\frac{3{\sigma }_2}{2})-{\sigma }_2}+1$

and

${\Phi }_{{\sigma }_2}(\frac{1}{2})=\frac{{\sigma }_2}{{\sigma }_2-2log({\sigma }_2)}+\frac{{\sigma }_2}{2log(\frac{{\sigma }_2}{2})-{\sigma }_2}+1,$

which means that

${\Phi }_{{\sigma }_2}(\frac{-1}{2})\le {\Phi }_{{\sigma }_2}(\frac{1}{2}),{\sigma }_2>0.$

By using Equation 3, the inequality

$1-log(3)<{\Phi }_{{\sigma }_1}(\frac{-1}{2})\le {\Phi }_{{\sigma }_1}(\frac{1}{2})\le 1+log(3),$

has a maximum solution when

${\sigma }_2=5.35044041019216...$

As a consequence, we obtain the inequality subordination:

$\phi (\zeta )\prec {\Phi }_{{\sigma }_2}(\zeta )\prec 1+log\left(\frac{1+\zeta }{1-\zeta }\right),|\zeta |\le 1/2.$

Thus, inequality (Equation 2) is valid.

Example 3.2. One of the important applications in this direction is the modified Libera–Livingston–Bernardi integral operator over Ω, which has the following structure:

$\begin{array}{l}F(f(\zeta ))=\frac{c+1}{{\zeta }^c}{\displaystyle {\int }_0^{\zeta }}{\tau }^{c-1}f(\tau )d\tau .\end{array}$

For $\frac{\zeta }{1-\zeta }=\zeta +...,$ the integral satisfies

$\begin{array}{l}F(f(\zeta ))=(c+1){\zeta }^{-c}{B}_{\zeta }\left[c+1,0\right]\\ =\zeta +\frac{((c+1){\zeta }^2)}{(c+2)}+\frac{((c+1){\zeta }^3)}{(c+3)}+\frac{((c+1){\zeta }^4)}{(c+4)}+\\ \frac{((c+1){\zeta }^5)}{(c+5)}+O({\zeta }^6)\end{array}$

where B_ζ[, ] indicates the Beta function. Moreover, for $\frac{\zeta }{{(1-\zeta )}^2}=\zeta +...,$ the integral satisfies

$\begin{array}{l}F(f(\zeta ))=(c+1){\zeta }^{-c}\left(-\frac{{\zeta }^{c+1}}{\zeta -1}-c{B}_{\zeta }\left[c+1,0\right]\right)\\ =\zeta +\frac{(2(c+1){\zeta }^2)}{(c+2)}+\frac{(3(c+1){\zeta }^3)}{(c+3)}+\frac{(4(c+1){\zeta }^4)}{(c+4)}+\\ \frac{(5(c+1){\zeta }^5)}{(c+5)}+O({\zeta }^6).\end{array}$

Hence, the integral is preserved the normalization f(0) = f′(0)−1 = 0. Let

$\begin{array}{l}\phi (\zeta )=F{(f(\zeta ))}^{\prime }=1+...,F(f(\zeta ))=\frac{c+1}{{\zeta }^c}{\displaystyle {\int }_0^{\zeta }}{\tau }^{c-1}f(\tau )d\tau ,\end{array}$

with ℜ(φ(ζ)) > 0. Then, a computation yields

$\begin{array}{l}1+{\sigma }_k\frac{\zeta \phi {(\zeta )}^{\prime }}{{\left[\phi (\zeta )\right]}^k}=1+{\sigma }_k\left(\frac{\zeta {\left[F{(f(\zeta ))}^{\prime }\right]}^{\prime }}{{\left[F{(f(\zeta ))}^{\prime }\right]}^k}\right).\end{array}$

We have the following result:

Proposition 3.3. Consider f(ζ) is a normalized analytic function in Ω such that f(0) = f′(0)−1 = 0 and for $\phi (\zeta )=F{(f(\zeta ))}^{\prime },F(f(\zeta ))=\frac{c+1}{{\zeta }^c}{\int }_0^{\zeta }{\tau }^{c-1}f(\tau )d\tau ,$ with ℜ(φ(ζ)) > 0. If

$\begin{array}{l}1+{\sigma }_k\left(\frac{\zeta {\left[F{(f(\zeta ))}^{\prime }\right]}^{\prime }}{{\left[F{(f(\zeta ))}^{\prime }\right]}^k}\right)\prec \frac{1+\zeta }{1-\zeta },k=0,1,2\end{array}$

then

$\begin{array}{l}F{(f(\zeta ))}^{\prime }\prec 1+log\left(\frac{1+\zeta }{1-\zeta }\right),\zeta \in \Omega ,\end{array}$

where

$\begin{array}{c}{\sigma }_0=\frac{log(4)}{log(3)}=1.26186,{\sigma }_1=\frac{log(4)}{log(1+log(3))}=1.8701,\\ {\sigma }_2=5.35044041019216.\end{array}$

Proposition 3.3 indicates that F(f(ζ)) is bounded turning function. A bounded turning function is a type of mathematical function made up of straight line segments connected linked at predetermined locations, each segment having a bounded slope (or derivative). It is sometimes referred to as a piecewise linear function or zigzag function. Numerous applications, including as robotics, computer graphics, and signal processing, frequently make advantage of these features. Moreover, bounded turning describes the restriction that the rate of change (slope or derivative) of the function is restricted within a given range. This indicates that the graph of the function shows moderate shifts in orientation within predetermined bounds rather than abrupt or unbounded alterations.

4 Conclusion and discussion

The above investigation concerned about a new definition of the Steiner symmetrization using a special function $(1+log(\frac{1+\zeta }{1-\zeta })).$ The main result was about using the suggested definition to optimize a class of analytic functions. This optimization showed the geometric symmetrization of the class. In our research, we utilized the differential subordination based on Miller–Mocanu Lemma. The effort is satellited in the open unit disk, where the symmetrization can be recognized. Moreover, our result yielded the type of analytic functions that the set ${\Omega }_{\phi }^{*}$ can be contained. This type was the Carathéodory function. Because it offers a quantitative assessment of how these functions behave closely to a certain point, the Carathèodory function is significant in the theory of univalent functions, like the function $\frac{1+\zeta }{1-\zeta },\zeta \in \Omega$. It is useful in gaining an understanding of conformal mappings and geometric function theory among other fields of complex analysis.

Moreover, among polygons, Steiner symmetrization is a potent approach for maximizing the Laplace operator's initial eigenvalue with Dirichlet boundary conditions. It can use the characteristics of symmetric domains to minimize the eigenvalue by reshaping the polygon into a more symmetrical form. Nevertheless, careful numerical implementation and consideration of the particular qualities of the initial polygonal domain are necessary for the actual application of the technique. Depending on the domain's geometry, such as its volume and eigenvalue index, Polya's theorem gives a lower bound on the Laplace operator's eigenvalues. This facilitates the comprehension of the relationship between the eigenvalues and the domain's size and form. According to Hirsch's theorem, a domain's initial eigenvalue does not rise when it is symmetric. This is helpful in optimization issues when the goal is to change the domain into a more symmetric shape in order to reduce the first eigenvalue.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

IA: Resources, Writing – review & editing. RI: Formal analysis, Methodology, Writing – original draft.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Smith W, Stanoyevitch A, Stegenga DA. Planar poincar domains: geometry and Steiner symmetrization. J Anal Mathm. (1995) 66:137–83. doi: 10.1007/BF02788821

Crossref Full Text | Google Scholar

2. Peretz R. Applications of Steiner symmetrization to some extremal problems in geometric function theory. arXiv preprint arXiv:1607.01674. (2016).

Google Scholar

3. Janowski W. Some extremal problems for certain families of analytic functions I. In: Annales Polonici Mathematici. (1973). p. 297–326. doi: 10.4064/ap-28-3-297-326

PubMed Abstract | Crossref Full Text | Google Scholar

4. Miller SS, Mocanu PT. Differential Subordinations: Theory and Applications. London: CRC Press. (2000). doi: 10.1201/9781482289817

Crossref Full Text | Google Scholar

5. Betsakos D, Solynin A, Vuorinen M. Conformal capacity of hedgehogs. Confor Geom Dyn Am Mathem Soc. (2023) 27:55–97. doi: 10.1090/ecgd/381

Crossref Full Text | Google Scholar