No idle flow shop scheduling models for optimization of machine rental costs with processing and separated setup times

Scheduling is one of the many skills required for advancement in today’s modern industry. The flow-shop scheduling problem is a well-known combinatorial optimization challenge. Scheduling issues for flow shops are NP-hard and challenging. The present research investigates a two-stage flow shop scheduling problem with decoupled processing and setup times, where a correlation exists between probabilities, job processing times, and setup times. This study proposes a novel heuristic algorithm that optimally sequences jobs to minimize the makespan and eliminates machine idle time, thereby reducing machine rental costs. The proposed algorithm’s efficacy is demonstrated through several computational examples implemented in MATLAB 2021a. The results are compared with the existing approaches such as those by Johnson, Palmer, NEH, and Nailwal to highlight the proposed algorithm’s superior performance.

1 Introduction

The process of scheduling constitutes a pivotal facet of resource allocation, involving the meticulous planning and execution of asset deployment to facilitate activity execution. Scheduling primarily aims to ascertain the most optimal solution, considering the imperative for optimal achievement of a specific purpose or outcome. Optimizing specific performance metrics while scheduling two or more jobs over two or more pre-defined machines is the crux of the flow shop scheduling problem (FSSP), a prominent scheduling challenge. In industrial flow shop environments, a critical constraint entails the minimization of idle time on machines, necessitating continuous operation once initiated. Consequently, machines are mandated to operate without downtime, posing a significant operational challenge. Extensive scholarly efforts spanning over the past 50 years have been dedicated to addressing scheduling predicaments. Notably, Johnson is recognized as the trailblazer in advancing a pioneering mathematical model (1). A notable triumph was achieved when this model—a substantial breakthrough across the field—reached the optimum solution. Johnson’s model has garnered considerable attention from scholars, sparking investigations into its efficacy. For problems consisting of an assortment of m machines and n jobs, Palmer (2) introduced heuristic techniques to mitigate the makespan particularly. The discoveries of scholars offer valuable insights into the optimization of job sequencing to enhance the performance of overall efficiency. By employing this heuristic approach, Nailwal et al. (3) sought to mitigate the challenges posed by limited storage capacity effectively and offer potential solutions for improving job sequencing in situations where intermediate storage is not readily available. From that juncture on, schedule problems have begun emphasizing heavily on the NEH technique. Optimization of job scheduling over numerous machines is the main focus of the NEH method in order to reduce overall processing time (4). Jackson (5), Ignall (6), Campbell et al. (7), and Gupta and Shashi (8) have contributed significantly through the development and initial exploration of their research inquiries.

Arguably the top common problematic factors in task scheduling involves set up times, which have long been recognized to present significant challenges. Separating time for setup from the time it takes to process was the sole focus of the preliminary investigations towards the flow shop scheduling problem, which was launched by Yoshida and Hitomi (9). An expansion was implemented, enabling a more thorough examination, in furtherance of Johnson’s rule. In an effort to assess and improve the scheduling processes in an inadequate machine job shop, the researcher’s (10) paradigm incorporates sequence-dependent setup times through computational simulation approaches. The simulation accurately represents the intricacies involved in setup and job sequencing processes. Through a meticulous analysis of the above factors, research aimed for significant perspectives on the intricacies of this dilemma and, conceivably, propose innovative resolutions or strategies for it (11).

The implementation of no-idle constraints is a component of no-idle flow shop scheduling. This entails the continuous operation of machinery, devoid of any breaks or idle periods. Researchers have explored different algorithms, mathematical formulations and optimization techniques to address the complexities associated with this scheduling problem. A flow shop with m machines underwent a pilot research into the no-idle constraint (12). Kaur et al. (13) devised a methodology that addresses job weighting considerations which aimed at reducing hiring expenses in no-idle flow shop scheduling. Within the framework of flow shop scheduling under no-idle constraint, Singla et al. (14) proposed an innovative approach aimed at constraining leasing costs for 2 machines. The investigators sought to enhance the optimization of resource allocation while concurrently minimizing the total expenditures associated with rentals by integrating transportation time and weighting components to the scheduling protocol. The biodiversity of the natural world provides a profound repository of insights, motivating creatures for developing adaptations to the multifaceted challenges they face. Moreover, researchers and professionals had adeptly leveraged this accrued information for confronting complex engineering predicaments, exemplified by the contributions of Singla et al. (15, 16) and Kumari (17, 18). The literature extensively scrutinizes and documents the statistical optimization strategies under consideration across various scholarly publications. Of particular note are the substantive contributions made by scholars such as Kumari et al. (19) and Malik et al. (20) to the prevailing body of knowledge in this specialized domain.

Moreover, this study relies on the Gupta and Singh (21) work by factoring in the job setup times. The focus of the current research revolves around recognizing the finest optimum sequencing of jobs to lessen expenses associated with renting high-cost machinery.

The application of metaheuristic algorithms in solving NP-hard problems has significantly increased efficiency. This is particularly relevant to the scheduling field, where the flow shop scheduling problem (FSSP) is a significant and representative benchmark. Researchers have developed several benchmarks to evaluate and compare the optimization capabilities of various approaches (22). One such study focused on flow shop scheduling in an energy-efficient fuzzy system. The researchers extended the non-dominated sorting genetic algorithm-II (NSGA-II) to simultaneously minimize both the total fuzzy energy consumption and the fuzzy make-span (23). Recently, a comprehensive review and study of a multi-objective hybrid FSSP have been conducted (24, 25). This research highlights the potential of metaheuristic algorithms in addressing complex scheduling problems with multiple objectives.

The minimisation of the makespan, or total length of time required to complete a set of operations, is a crucial aspect of resource scheduling, particularly in cloud computing. Efficient resource allocation is a critical concern in cloud computing, as it directly impacts resource utilisation, the ability to meet service level agreements (SLAs), and overall customer satisfaction. Various scheduling techniques have been proposed to address this problem, among which dynamic Johnson sequencing (DJS) has gained significant attention. DJS is a well-established scheduling technique, originally designed for parallel machine manufacturing. However, the algorithm has experienced extensive adoption in cloud resource scheduling, attributed to its inherent simplicity and the capability to yield outcomes that are computationally efficient, thereby approaching optimality in time utilization. The DJS algorithm operates by dynamically sequencing jobs based on their processing times, resulting in an efficient allocation of resources. However, the rapidly evolving world of cloud computing demands fresh resource scheduling strategies to address the challenges of heterogeneous resources, virtualisation techniques, and dynamic responses to changing workloads. To overcome these challenges, advanced scheduling algorithms with optimisation techniques, heuristic-based approaches, and real-time monitoring capabilities have to be developed. To meet the demands of modern cloud environments and ensure optimal resource utilization, these algorithms ought to be flexible enough to adjust to shifting workloads and the availability of resources.

Banerjee et al. (26) proposed the OptiDJS+ dynamic Johnson sequencing strategy, which utilises two servers, as an alternative to traditional scheduling techniques. The authors demonstrated that the proposed approach significantly enhances the reduction of the makespan and increases resource utilisation. The following section presents a practical scenario of the Flow Shop Scheduling Problem (FSSP) for modelling purposes.

2 Practical situation

Everyday involvement with industrial and production environments often presents a range of observed scenarios that are both exploratory and practical. These situations typically involve carrying out a variety of tasks that require the use of various types of commercial machinery. Construction companies often face varying project requirements, timelines, and budgets, making equipment rental an attractive option. For instance, throughout the project, the construction firm requires a diverse range of heavy machinery such as excavators, cranes, concrete mixers, and bulldozers. Renting benefits in terms of flexibility, cost-effectiveness, mitigate financial risks, and maintain operational agility in a competitive market environment.

2.1 Assumptions

• In the context of autonomous job processing within sequential machines H₁ and H₂, it is evident that no provision exists for inter-machine transfer.

• Under the existing conditions, it is deemed impractical for two machines to process just one job concurrently.

• Until the job is completed beyond human possibility, all modifications to the machines’ instructions are strictly forbidden.

• Calculations of usage fail to account for the time required for setup or equipment breakdown.

2.2 Rental policy

Our rental policy allows for machines to be utilized as required and returned when no more needed. To be more precise, the first machine used in the job processing process was acquired via the rental contract. As soon as the initially hired machine’s first job is finished, another machine is to be acquired through rent.

3 Problem formulation

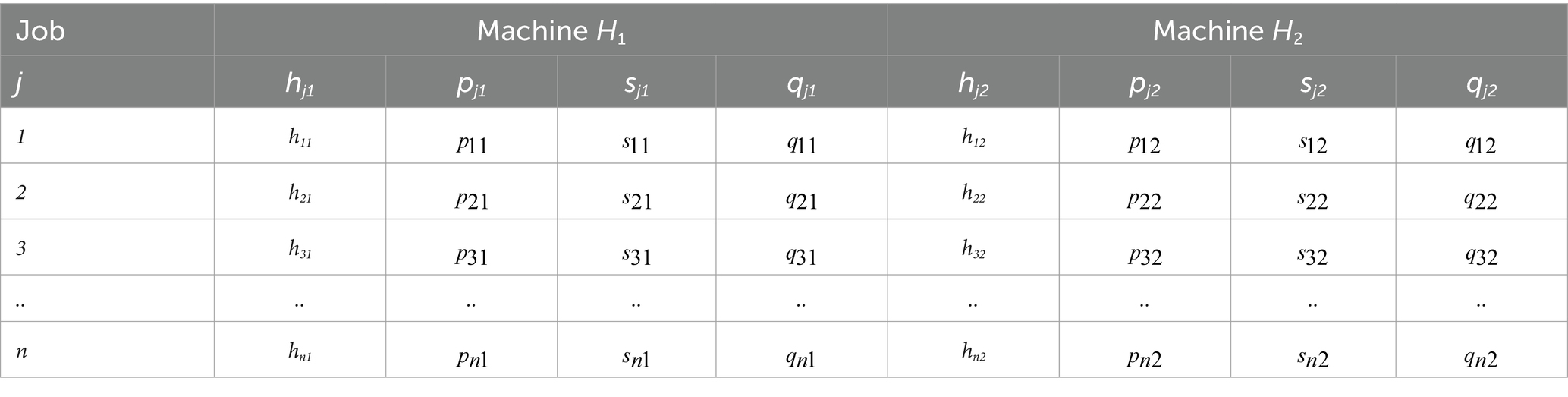
Consider the scheduling problem of job processing, where a set of jobs, denoted as j (with j ranging from 1 to n) are to be executed on two distinct machines, H₁ and H₂, with probabilistic processing times with setup times. Specifically, the processing time for job j on machines H₁ and H₂ are denoted by h_j1 and h_j2, respectively, and are associated with probabilities p_j1 and p_j2. Additionally, the setup times for job j on machines H₁ and H₂ are denoted by s_j1 and s_j2, respectively, and are associated with probabilities q_j1 and q_j2. To mathematically represent the model, we propose a matrix-based format which is expressed in Table 1. The objective is to determine the optimum sequence of jobs {s₁} to minimize capital expenditures for rented equipment.

Table 1

Table 1. Matrix formulation of the mathematical format.

4 Algorithm

Step 1: Calculate the processing times for machines $H_1\mathrm{and}{H}_2$ as follows:

$\begin{array}{ll}{H}_{j1}=h_{j1}\times p_{j1}-s_{j2}\times q_{j2}& (1)\end{array}$

$\begin{array}{ll}{H}_{j2}=h_{j2}\times p_{j2}-s_{j1}\times q_{j1}& (2)\end{array}$

where $H_{j1}\mathrm{and}{H}_{j2}$ are the processing times of job j for machines $H_1\mathrm{and}{H}_2$ .

Step 2: Implement Johnson’s method (1) to obtain the optimum sequence s₁ of jobs that minimizes the total elapsed time.

Step 3: Construct a flow in-out table for the optimum sequence s₁ to calculate the total elapsed time.

Step 4: Determine

$\begin{array}{ll}{l}_2=T_{j2}-{\displaystyle \sum }_{n=1}^{\infty }{H}_{j2}& (3)\end{array}$

Step 5: Use the starting point $l_2$ as the starting point for processing jobs on machine H₂ to construct a flow IN-OUT table.

Step 6: The utilization times, u₁ (s₁) and u₂ (s₁) for machines $H_1\mathrm{and}{H}_2$are determined by the following calculations:

$\begin{array}{ll}{u}_1\left(s_1\right)={\displaystyle \sum }_{n=1}^{\infty }{H}_{j1}& (4)\end{array}$

$\begin{array}{ll}{u}_2\left(s_1\right)=T_{j2}-l_2& (5)\end{array}$

Step 7: Finally, calculate.

$\begin{array}{ll}r\left(s_1\right)=u_1\left(s_1\right)\ast c_1+u_2\left(s_1\right)\ast c_2& (6)\end{array}$

5 Numerical illustration

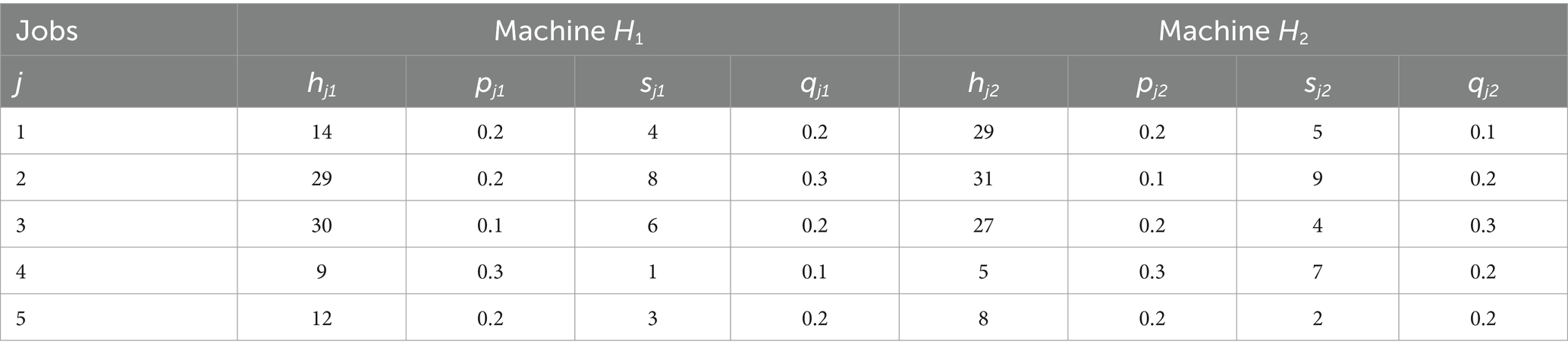
Consider the sequencing problem of five jobs (j = 1, 2, 3, 4, 5) to be two machines $H_1\mathrm{and}{H}_2\text{,}$where the processing times for each job on respective machines are specified in Table 2. The hiring cost of machines $H_1\mathrm{and}{H}_2$is four and six units of time, respectively. The objective is to determine optimum sequence of jobs to minimize the total cost of rented equipment.

Table 2

Table 2. Problem instance parameters for job sequencing problem.

5.1 Solution

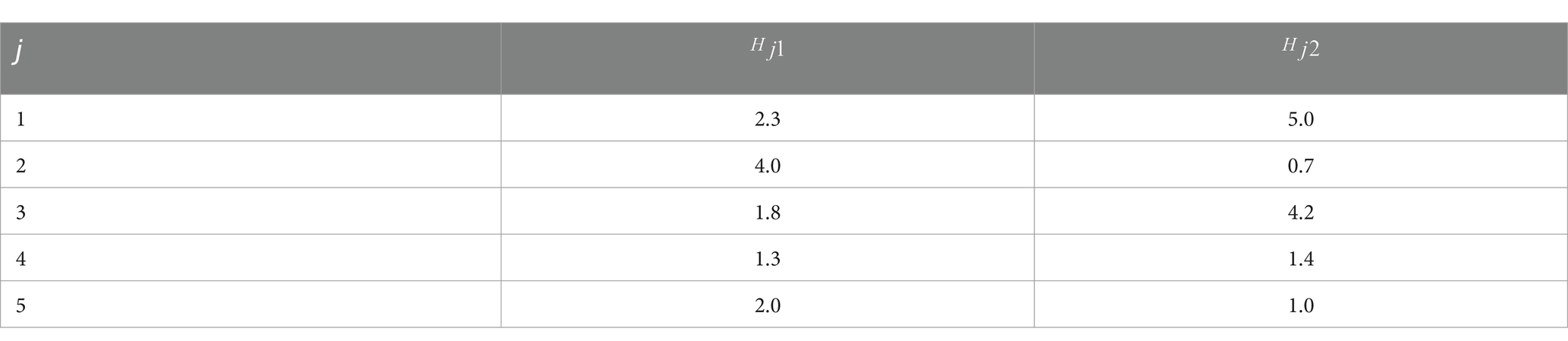
Step 1 outlines an analysis of the projected processing times on two machines $H_1\mathrm{and}{H}_2$ as per Equations (1) and (2). Table 3 displays the projected process times on two machines $H_1\mathrm{and}{H}_2\text{.}$ The table shows the anticipated processing times for jobs 1 through 5 on both machines, represented as $H_{i1}\mathrm{and}{H}_{i2}$ .

Table 3

Table 3. Anticipated processing time on machines H₁ and H₂.

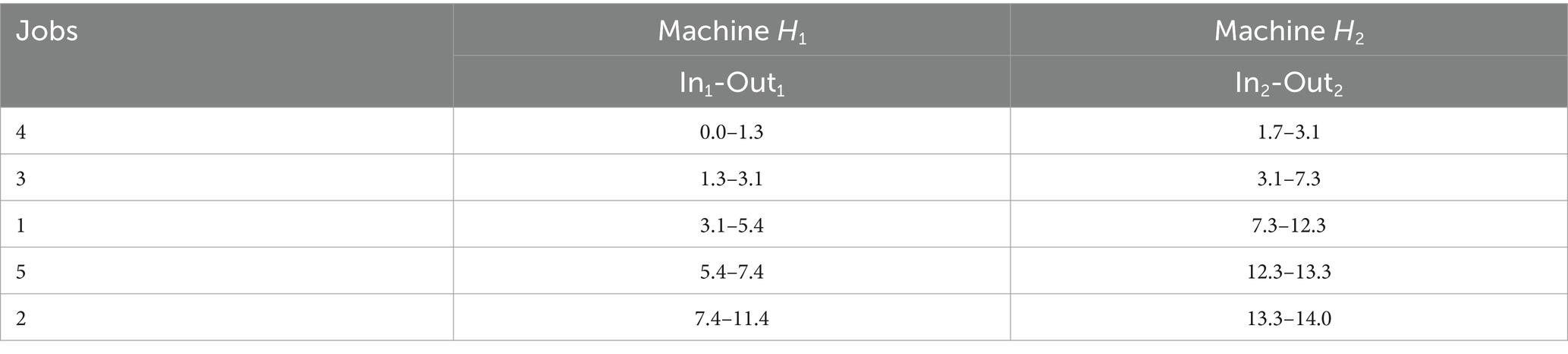
The optimal sequence $s_1$ , where $s_1=\left\{4,3,1,5,2\right\}$ , is determined in Step 2 of the research methodology to minimize the total elapsed time. To provide a comprehensive overview, Table 4 displays the cumulative inflow and outflow of jobs for each machine based on Step 3 based on the $s_1\text{.}$

Table 4

Table 4. Inflow and outflow table for schedule S₁.

Thus, total elapsed time C_max = 14.0

As per Step 5; by using Equation (3), $l_2$ = 14.0–12.3 = 1.7.

The IN-OUT table that incorporates the inflow and outflow of jobs is essential tool for solving the optimized scheduling problem as presented in Table 5. This table should be incorporated into the research methodology as outlined in Step 6.

Table 5

Table 5. In-out table for the optimized flow shop scheduling model.

As per Step-6; by using Equations (4, 5), we get u₁(s₁) = 11.4.

$u_2\left(s_1\right)=14.0–1.7=12.3\text{.}$

As per Step-7; by using Equation (6), i.e., r(s₁) = u₁(s₁) ∗ c₁ + u₂(s₁) ∗ c₂.

$={11.4}^{\ast }4+{12.3}^{\ast }6=119.4\mathrm{units}\text{.}$

The previously computed results are therefore recorded in Table 6 for machine route H₁ → H₂ of the optimized sequence s₁ = {4,3,1,5,2}. Thus, as Table 6 illustrates, the heuristic algorithm suggested for machine route H₁ → H₂ produces the lowest feasible utilization time and rental cost for the optimal solution s₁.

Table 6

Table 6. Comparative analysis of the outcomes.

6 Computational experiments

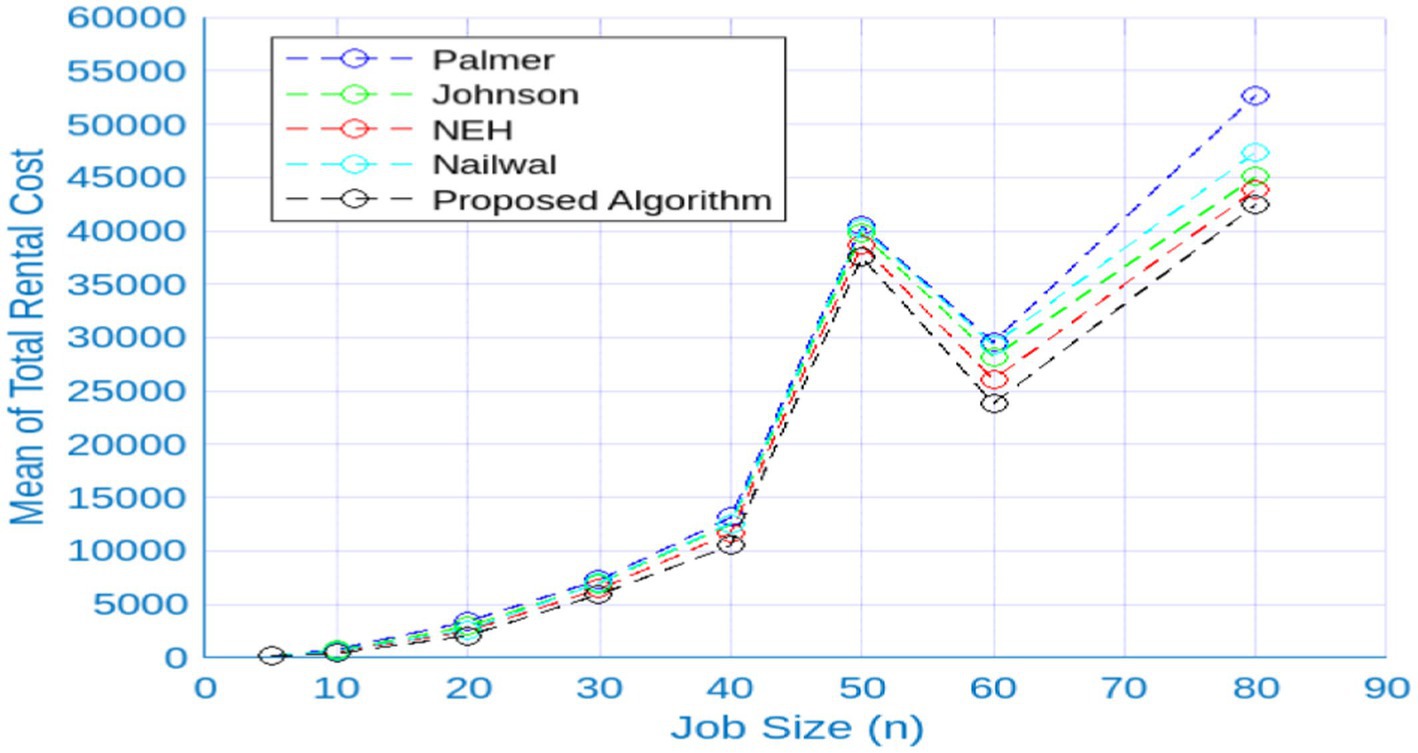
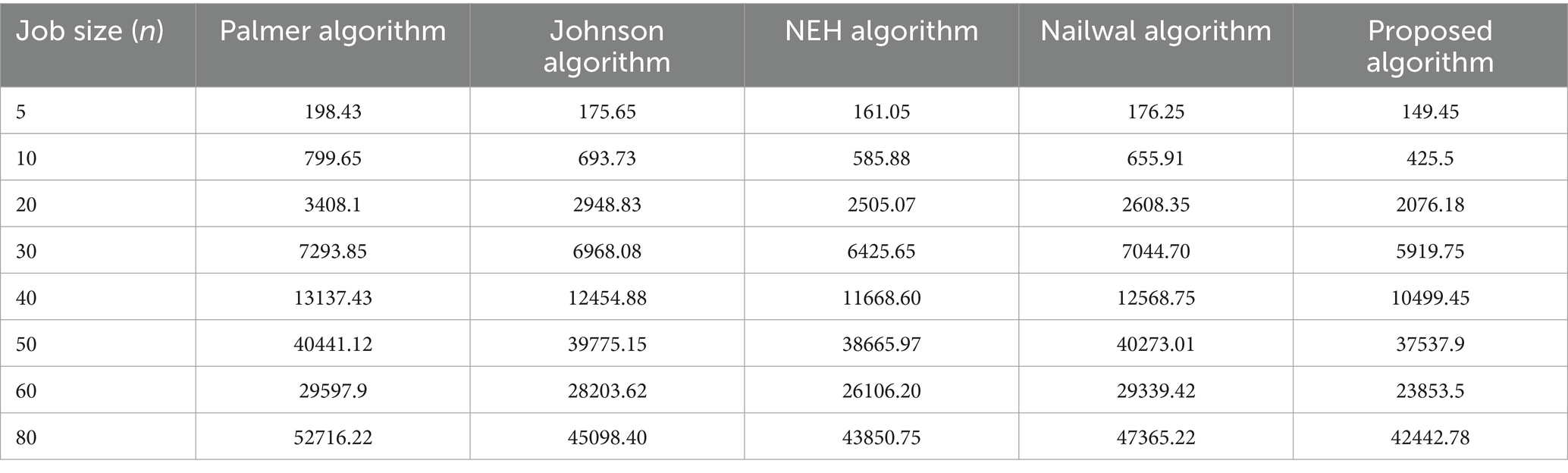
A multitude of samples have been selected for the purpose of examining the proposed algorithmic method, with each set comprising a random amount of jobs. Job sizes 5, 10, 20, 30, 40, 50, 60, and 80 are divided into eight distinct groups. Then, five unique trials that had been generated at random were applied to each group and observed. Palmer (2), Johnson (1), NEH (4), and Nailwal’s (3) existing make-span strategies have been compared to the proposed algorithm’s average entire rental cost. As seen in Figure 1, a graph has been created to depict the comparison, and the findings are reported in Table 7. These findings reveal that the path of the curve connected to the proposed method is quite a bit lower aside from of the rest of the curves. Of particular note lies the far greater elevation curve that Palmer’s algorithm exhibits in contrast with competing current methods. Furthermore, in comparing the curve of NEH (4) to other curves, it is observed that the curve of NEH (4) exhibits a closer proximity to the curve of the proposed algorithm.

Figure 1

Figure 1. Comparative analysis of computational outcomes.

Table 7

Table 7. Results of computational experiments.

Error percentage, serves as an evaluative measure for assessing the effectiveness and efficiency of the new algorithm in terms of rental cost optimization. The formula for computing the error percentage is given by:

$E_{rr}=\left[\left(R_{\delta }-R_{\theta }\right)/R_{\theta }\right]\times 100$

Where: $R_{\delta }$ =The sum of all rental costs calculated by the existing algorithms. $R_{\theta }=$ The total rental cost computed using the new algorithm.

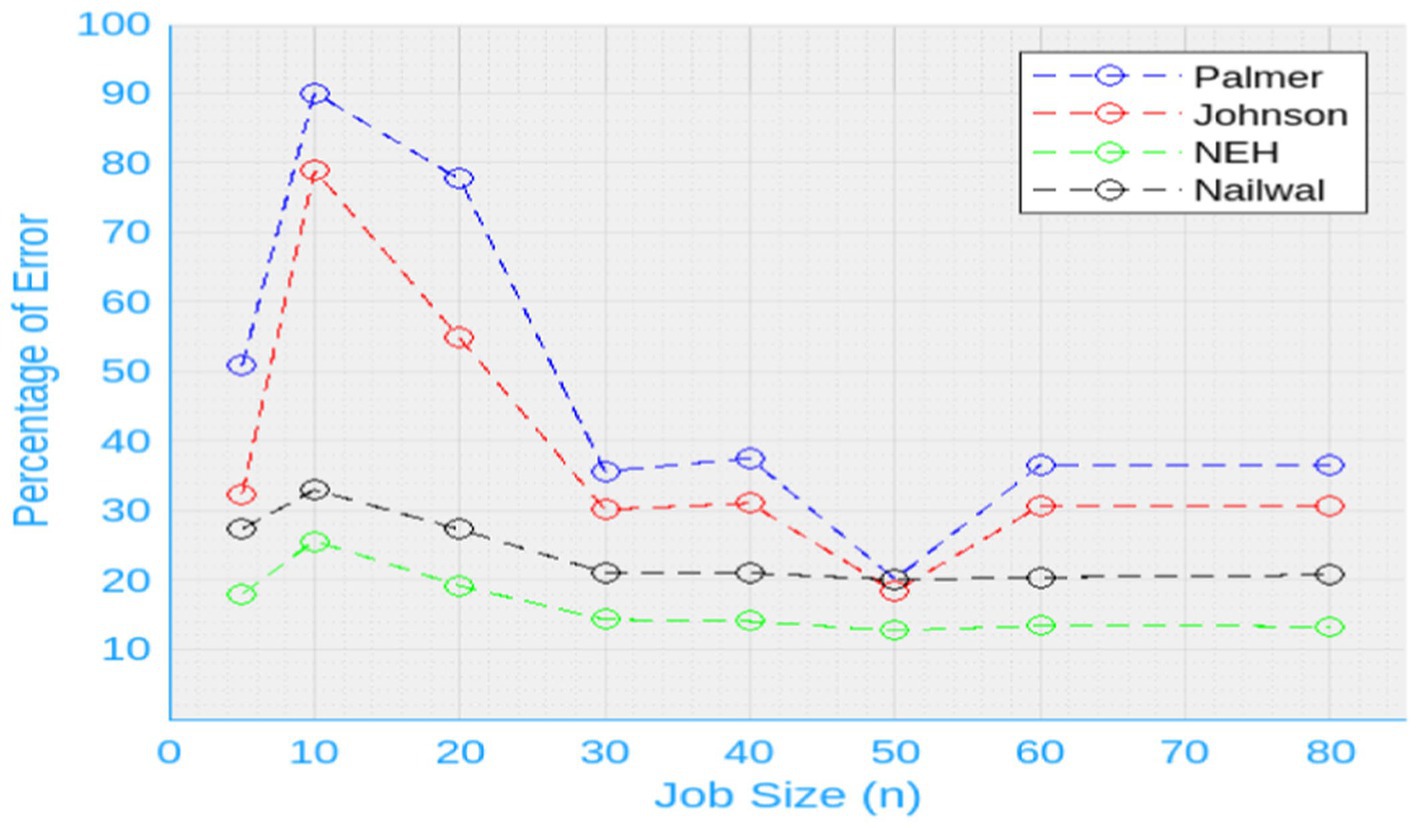
As seen in Figure 2, the outcomes are graphically represented in the subsequent figure.

Figure 2

Figure 2. Average error percentage.

In the analysis conducted, we investigate the performance of four different algorithms, namely NEH (4), Johnson (1), Palmer (2), and Nailwal (3), in terms of their ability to minimize rental costs. This observation is supported by the error curve, which demonstrates a consistent downward trend in rental costs when employing the NEH algorithm as shown in Figure 2. As the evidence by the data presented in Table 8 illustrates that the amount of jobs performed has no bearing on the detected error. Specifically, the mean percentage error for the group comprising 20 jobs in Johnson’s algorithm is 58.4 units. In this research study, we investigate the impact of job size on a specific data set of problems. Specifically, we examine the effect of increasing the job size to 40 units. Our computational experiments reveal that with this larger job size, the overall reduction in units achieved is 31.1. In the context of job size, an interesting observation can be made. The unit count climbs to 30.69 units when the job size increases to 60. However, the corresponding unit lowers once more to 18.37 units when the job size is 50. A noteworthy remark has been made as well regarding the NEH algorithm, where the mean error for various job categories does not fluctuate in a similar pattern as with the Palmer and Johnson algorithms.

Table 8

Table 8. Average error percentage.

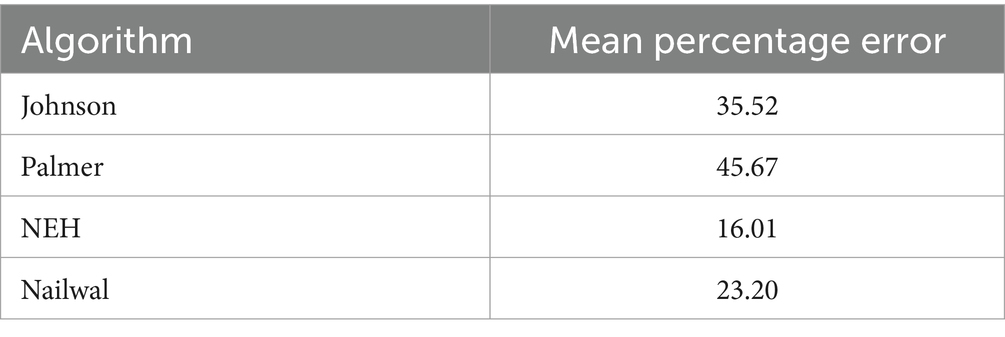
Moreover, the error generated by the Palmer (2) algorithm is considerably greater than that of the Johnson (1) algorithm, as shown in Table 9. NEH (4) approaches the precise and optimum solution to reduce the rental cost of machines.

Table 9

Table 9. Mean percentage error comparison.

7 Conclusion

This study presents the ideal outcome of reducing renting expenses using the suggested heuristic approach. A number of factors are weighed by the algorithm, such as separated setup times and processing times. Our main goal in this inquiry was to get the intended result for numerous job sizes. The scope of the variable “n” was confined to the interval of (1 ≤ n ≤ 5) in previous research because of the intricacy of the computation for small-scale jobs. However, we expanded to include jobs of a moderate size, where n is between 6 and 30.

In addition, we tried to achieve our objective for jobs of a significant magnitude, where n may have a value between 31 and 80. The present investigation encompassed a succession of effective computational evaluations. Palmer (2), Johnson (1), NEH (4), and Nailwal (3) all proposed heuristics that were surpassed by the devised heuristic algorithm, as demonstrated by the outcomes of these tests. Moreover, a number of factors, including the impact of weightage of job, fuzzy trapezoidal numbers, job block etc., might be included in this work to broaden it further. Additionally, the concept of Neutrosophic programming can be incorporated in future studies.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

SS: Supervision, Validation, Writing – review & editing, Conceptualization. HK: Conceptualization, Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft. DG: Supervision, Validation, Writing – review & editing. UM: Funding acquisition, Resources, Supervision, Validation, Writing – review & editing. JK: Investigation, Supervision, Validation, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The Editor in Chief along with the distinguished members of the editorial panel have been honored by the authors for the meticulous review of the paper as well as perceptive suggestions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Johnson, SM . Optimal two-and three-stage production schedules with setup times included. Nav Res Logist (NRL). (1954) 1:61–8. doi: 10.1002/nav.3800010110

Crossref Full Text | Google Scholar

2. Palmer, DS . Sequencing jobs through a multi stage process in the minimum total time-a quick method for obtaining a near optimum. Oper Res. (1985) 16:101–7. doi: 10.1057/jors.1965.8

Crossref Full Text | Google Scholar

3. Nailwal, KK, Gupta, D, and Jeet, K. Heuristics for no-wait flow shop scheduling problem. Int J Ind Eng Comput. (2016) 7:671–80. doi: 10.5267/j.ijiec.2016.2.005

Crossref Full Text | Google Scholar

4. Nawaz, M, Enscore, EE Jr, and Ham, I. A heuristic algorithm for the m-machine, n-job flow shop sequencing problem. Int J Manag Sci. (1983) 11:91–5. doi: 10.1016/0305-0483(83)90088-9

Crossref Full Text | Google Scholar

5. Jackson, JR . An extension of Johnson’s results on job IDT scheduling. Nav Res Logist Q. (1956) 3:201–3. doi: 10.1002/nav.3800030307

Crossref Full Text | Google Scholar

6. Ignall, E, and Schrage, L. Application of the branch and bound technique to some flow-shop scheduling problems. Oper Res. (1965) 13:400–12. doi: 10.1287/opre.13.3.400

Crossref Full Text | Google Scholar

7. Campbell, ML, Dudek, RA, and Smith, ML. A heuristic algorithm for the n job, m machine sequencing problem. Manag Sci. (1970) 16:B-630–7. doi: 10.1287/mnsc.16.10.B630

Crossref Full Text | Google Scholar

8. Gupta, D, Bala, S, and Sharma, S. To minimize the rental cost for 3- stage specially structured flow shop scheduling with job weightage. Int J Eng Res Appl. (2012) 2:912–6.

Google Scholar

9. Yoshida, T, and Hitomi, K. Optimal two-stage production scheduling with setup times separated. AIIE Trans. (1979) 11:261–3. doi: 10.1080/05695557908974469

Crossref Full Text | Google Scholar

10. Kim, SC, and Bobrowski, PM. Impact of sequence-dependent setup time on job shop scheduling performance. Int J Prod Res. (1994) 32:1503–20. doi: 10.1080/00207549408957019

Crossref Full Text | Google Scholar

11. Allahverdi, A, Gupta, JND, and Aldowaisan, T. A review of scheduling research involving setup considerations. Omega Int J Mgmt Sci. (1999) 27:219–39. doi: 10.1016/S0305-0483(98)00042-5

Crossref Full Text | Google Scholar

12. Adiri, I, and Pohoryles, D. Flow shop no-idle or no-wait scheduling to minimize the sum of completion times. Nav Res Logist. (1982) 29:495–504. doi: 10.1002/nav.3800290311

Crossref Full Text | Google Scholar

13. Gupta, D, Goel, R, and Kaur, H. Optimizing rental cost with no idle constraints in two machines with weightage. Mater Today Proc. (2021). doi: 10.1016/j.matpr.2021.01.090

Crossref Full Text | Google Scholar

14. Singla, S., Kaur, H., and Gupta, D., “Optimization of rental cost of machines in two stage no-idle scheduling with transportation time and weightage of jobs,” in 2023 10th International Conference on Computing for Sustainable Global Development (INDIACom) (2023), pp. 818–821. Available: https://ieeexplore.ieee.org/document/10112467 (Accessed August 05, 2023).

Google Scholar

15. Singla, S., Kaur, H., Gupta, D., and Kaur, J., “No idle constraint in flow shop scheduling with transportation time, weightage of jobs and job block criteria,” in 2023 IEEE 2nd International Conference on Industrial Electronics: Developments & Applications (ICIDeA), IEEE (2023), pp. 450–454. doi: 10.1109/ICIDeA59866.2023.10295180

Crossref Full Text | Google Scholar

16. Singla, S, Modibbo, UM, Mijinyawa, M, Malik, S, Verma, S, and Khurana, P. Mathematical model for analysing availability of threshing combine machine under reduced capacity. Yugoslav J Oper Res. (2022) 32:425–37. doi: 10.2298/YJOR220315019S

Crossref Full Text | Google Scholar

17. Kumari, S, Khurana, P, and Singla, S. RAP via constraint optimization genetic algorithm. Life Cycle Reliab Saf Eng. (2021) 10:341–5. doi: 10.1007/s41872-021-00173-0

Crossref Full Text | Google Scholar

18. Kumari, S, Khurana, P, and Singla, S. Behavior and profit analysis of a thresher plant under steady state. Int J Syst Assur Eng Manag. (2022) 13:166–71. doi: 10.1007/s13198-021-01183-y

Crossref Full Text | Google Scholar

19. Kumari, S, Khurana, P, Singla, S, and Kumar, A. Solution of constrained problems using particle swarm optimiziation. Int J Syst Assur Eng Manag. (2022) 13:1688–95. doi: 10.1007/s13198-021-01524-x

Crossref Full Text | Google Scholar

20. Malik, S, Verma, S, Gupta, A, Sharma, G, and Singla, S. Performability evaluation, validation and optimization for the steam generation system of a coal-fired thermal power plant. Methods X. (2022) 9:101852. doi: 10.1016/j.mex.2022.101852

PubMed Abstract | Crossref Full Text | Google Scholar

21. Gupta, D, and Singh, H. A heuristic approach to flow shop scheduling problem in which processing times are associated with their respective probabilities with no-idle constraint. ISRN Oper Res. (2013) 2013:1–9. doi: 10.1155/2013/948541

Crossref Full Text | Google Scholar

22. Liang, Z, Zhong, P, Liu, M, Zhang, C, and Zhang, Z. A computational efficient optimization of flow shop scheduling problems. Sci Rep. (2022) 12:845. doi: 10.1038/s41598-022-04887-8

PubMed Abstract | Crossref Full Text | Google Scholar

23. Wang, Y-J, Wang, G-G, Tian, F-M, Gong, D-W, and Pedrycz, W. Solving energy-efficient fuzzy hybrid flow-shop scheduling problem at a variable machine speed using an extended NSGA-II. Eng Appl Artif Intell. (2023) 121:105977. doi: 10.1016/j.engappai.2023.105977

Crossref Full Text | Google Scholar

24. Neufeld, JS, Schulz, S, and Buscher, U. A systematic review of multi-objective hybrid flow shop scheduling. Eur J Oper Res. (2023) 309:1–23. doi: 10.1016/j.ejor.2022.08.009

Crossref Full Text | Google Scholar

25. Zhou, B, and Liu, W. Energy-efficient multi-objective scheduling algorithm for hybrid flow shop with fuzzy processing time. Proc Inst Mech Eng Part I J Syst Control Eng. (2019) 233:1282–97. doi: 10.1177/0959651819827705

Crossref Full Text | Google Scholar

26. Banerjee, P, Roy, S, Modibbo, UM, Pandey, SK, Chaudhary, P, Sinha, A, et al. OptiDJS+: a next-generation enhanced dynamic Johnson sequencing algorithm for efficient resource scheduling in distributed overloading within cloud computing environment. Electronics (Basel). (2023) 12:4123. doi: 10.3390/electronics12194123

Crossref Full Text | Google Scholar

Glossary