Convergence analysis of particle swarm optimization algorithms for different constriction factors

Particle swarm optimization (PSO) algorithm is an optimization technique with remarkable performance for problem solving. The convergence analysis of the method is still in research. This article proposes a mechanism for controlling the velocity by applying a method involving constriction factor in standard swarm optimization algorithm, that is called CSPSO. In addition, the mathematical CSPSO model with the time step attractor is presented to study the convergence condition and the corresponding stability. As a result, constriction standard particle swarm optimization that we consider has a higher potential to balance exploration and exploitation. To avoid the PSO premature convergence, CSPSO modifies all terms of the PSO velocity equation. We test the effectiveness of the CSPSO algorithm based on constriction coefficient with some benchmark functions and compare it with other basic PSO variant algorithms. The theoretical convergence and experimental analyses results are also demonstrated in tables and graphically.

1 Introduction

The optimization techniques are fundamentally important in engineering and scientific computing. The PSO algorithm was first introduced by Kennedy and Eberhart [1] as a stochastic optimization technique of swarm particles (population). The motivation was primarily to model the social behavior of birds flocking. The meta-heuristic optimization algorithms (PSO) work effectively in many areas such as robotics, wireless networks, power systems, job-shop schedules, human healthcare, and classifying or training of ANN (artificial neural network) [2]. In PSO, the potential solutions, called particles, fly through the problem space (domain) by applying their intelligent collective behaviors.

The PSO algorithm is competitive in performance with the well-known huge numbers of variants such as SPSO and CPSO algorithms and is also an efficient optimization framework [3, 4].

Lately, researches on PSO mainly intended on algorithmic implementations, enhancements, and engineering applications with interesting findings derived under the system that assumes a fixed attractor [5]. Nevertheless, a comprehensive mathematical explanation for the general PSO is still quite limited. For instance, the works on stability and convergence analyses are two key problems of great significance that need to be investigated in depth because many of the works have given attention for standard PSO.

The PSO algorithm depends on three parameters (factors): the inertia, cognitive and social weight to guarantee the stability of PSO.

Stability analysis of PSO is mainly motivated by determining which combination of these parameters encourages convergence [6].

The working rule of PSO method is closely tied with the stability analysis, which investigates how the essential factors affect the swarms dynamics, and under what conditions particle swarm converges to some fixed value. For the first time, stability analysis of the particle dynamics was carried out by Clerc and Kennedy [7]. The study indicates that [8] particle trajectories could converge to a stable point. A more generalized stability analysis of the particle dynamics was conducted using the Lyapunov stability theorem [9]. Recently, based on a weak stagnation assumption, Liu [10] studied the order-2 stability of PSO, and a new definition of stability was proposed with an order-2 stable region. Dong and Zhang [11] analyzed order-3 recurrence relation of PSO kinematic equations based on two strategies to obtain the necessary and sufficient conditions of its convergence.

The convergence analysis determines whether a global optimum solution can be achieved when a particle swarm converges. Using stochastic process theory, Jiang et al. [12] presented a stochastic convergence analysis on the standard PSO. Combining with the finite element grid technique, Poli and Langdon [13] set up a discrete model of Markov chain of the bare-bones PSO. An absorbing Markov process model of PSO was developed in Cai et al. [14]. Cai et al. [14] suggested the main factor of convergence analysis is the attaining-state set and proposed an improved method of convergence in terms of the attaining-state set theorem of expansion. The basic PSO is neither a global nor a local search algorithm, based on the convergence criterion of the pure random search algorithm [15, 16]. To yield a lower bound for the time required to optimize any pseudo-Boolean functions with a unique optimum and to justify upper bounds, Dirk et al. [17] assigned an optimum-level argument that is deep-rooted for evolutionary algorithms of particle swarm optimization. The study in Sun et al. [18] discussed the convergence of the quantum-behaved particle swarm optimization (QBPSO) and proved that it is a global convergent algorithm.

As discussed in Per and Carsten [19], stagnation of the convergence properties for basic PSO may be disadvantageous to finding a sufficiently good solution within a logical time, and it may have infinite expected first hitting time on some functions.

Recently, the existing work on the convergence analyses of PSO including documents from 2013 was surveyed by Tarekegn et al. [6]. The stochastic approximation technique on the PSO algorithm was use to prove convergence of swarm in Yuan and Yin [20]. The global convergence of PSO [21] was investigated by introducing the transition probability of particles. Several properties related to the Markov chain were investigated, and it was found that the particle state space is not repeated and PSO is not globally convergent from the viewpoint of the transition probability [22]. Based on the different models of PSO examined [23], the Markov properties of the state sequences of a single particle and swarm one determine the transition probability of a particle. The transition probability of the optimal set is deduced by combining the law of total probability with the Markov properties [24], which proves that SPSO can reach the global optimum in probability. Although many methods in Poli and Langdon [13] have proposed PSO convergence analysis, most analyses are based on the assignment of stochastic systems of the Markov process, which strongly depends on the transition matrix and their eigenvalues. Therefore, when the population size is large, current PSO convergence analyses are very refined and investigate different PSO variants algorithms to obtain a solution that converges to global minimum.

Motivated by our recent study in Tarekegn et al. [6], this article proposes a PSO variant known as CSPSO, an algorithm for optimization problem solving.

A constriction factor integrated with an inertia weight are used for the construction. Fast convergent method to an optimal solution within the search space in a small time of iterations was obtained.

The rest of this study is organized as follows: Section 2 presents related works that include the basic PSO algorithm and its existing variants. In Section 3, the proposed CSPSO algorithm analysis is described in detail, while Section 4 presents comparison results on some variants of PSO such as SPSO and CPSO (implementing with test functions) and provides an in-depth discussion, with a conclusion in Section 5.

2 The PSO algorithm and some related studies

In the PSO with K particles in which each particle is treated as an individual in the D-dimensional space, the position and velocity vectors of the i-th particle at the t-th iteration are

$X_i^t=(X_{i1}^t,X_{i2}^t,\dots ,X_{iD}^t)$ and

$V_i^t=(V_{i1}^t,V_{i2}^t,\dots ,V_{iD}^t)$, respectively.

In SPSO algorithm [25], at iteration t, the d th dimension of particle i's velocity and position $P_i^t$ is local best position, $x_i^t$ is current position, and g^t is global best position. Both are updated as

$\begin{array}{ll}\begin{array}{l}{V}_i^{t+1}=\omega V_i^t+c_1{r}_1^t(P_i^t-X_i^t)+c_2{r}_2^t(g^t-X_i^t),\\ X_i^{t+1}=X_i^t+V_i^{t+1},\end{array}\hfill & (1)\end{array}$

for 1 ≤ i ≤ K; ω is an inertia weight; and c₁ and c₂ are called acceleration coefficients in real-space, R.

Vector $P_i^t=(P_{i1}^t,P_{i2}^t,\dots ,P_{iD}^t)$ is the best previous position of particle i called personal best (Pbest) position and vector $g^t=(g_1^t,g_2^t,\dots ,g_D^t)$ is the position of the best particle among all the particles in the population and called global best (gbest) position. The parameters $r_1^t$ and $r_2^t$ are sequences of two different random positive numbers in the uniform random distribution in (0, 1) i.e., U(0, 1).

Generally, the value of $V_{id}^t$ is restricted within the interval [−V_max, V_max], for each d ∈ {1, 2, …, D}. Without loss of generality, we consider the minimization problem:

Minimize f(X), such that

$\begin{array}{ll}X\in S\subset {ℝ}^D,& (2)\end{array}$

where f(X) is an objective function continuous almost everywhere and S is a feasible solution space. From (1), the non-homogeneous recurrence relation (NHRR) is obtained as follows: [8]

$\begin{array}{l}{X}_i^{t+1}=-\omega x_i^{t-1}+(1+\omega )x_i^t+\\ {\phi }_1^t(P_i^t-x_i^t)+{\phi }_2^t(g^t-x_i^t),& (3)\end{array}$

where ${\phi }_1^t=c_1{r}_1^t,{\phi }_2^t=c_2{r}_2^t$.

From NHRR, P^t and g^t, for 1 ≤ i ≤ K, are updated, respectively, as follows:

$\begin{array}{ll}{P}_i^{t+1}=\{\begin{array}{l}{x}_i^{t+1}:forf(x_i^{t+1})<f(P_i^t)\\ P_i^t:otherwise;\end{array}& (4)\end{array}$

$\begin{array}{l}\begin{array}{c}{g}^0={\displaystyle \underset{1\le i\le k}{argmin}}\left\{f(x_i^o)\right\},\\ g^{t+1}={\displaystyle \underset{1\le i\le k}{argmin}}\left\{f(x_i^{t+1}),f(g^t)\right\}.\end{array}\end{array}$

From (2), (3), the process of the particle's velocity and position change can be obtained, respectively, as follows. They are a second-order difference equations

$\begin{array}{ll}{V}_i^{t+2}+({\phi }^t-\omega -1)V_i^{t+1}+\omega V_i^t=0& (5)\end{array}$

$\begin{array}{l}{X}_i^{t+1}+({\phi }^t-\omega -1)x_i^t+\omega x_i^{t-1}={\phi }_1^t{P}_i^t+{\phi }_2^t{g}^t\\ ={\phi }^t{O}_i^t& (6)\end{array}$

where, ${\phi }^t={\phi }_1^t+{\phi }_2^t$

$\begin{array}{ll}{O}_i^t=\frac{{\phi }_1^t{p}_i^t+{\phi }_2^t{g}^t}{{\phi }^t}.& (7)\end{array}$

The terms $({\phi }^t-\omega -1)x_i^t$ and $\omega x_i^{t-1}$ on the left side of (6), both memorize the past values of position (i.e, the memory item of position). The value of the item ${\phi }^t{O}_i^t$ on the right side of (6) is obtained from the previous experience of particles (i.e, the learning item of position) and, in particular, $O_i^t$ is the attractor at the t th iteration in (7).

Now, let

$\begin{array}{ll}{Q}_x={\displaystyle \underset{x^t\in S_x\subset R}{max}}\mid x(t)\mid .& (8)\end{array}$

For $p^t,g^t\in S_x,$ $\left|p^t\right|\le Q_x$, and $\left|g^t\right|\le Q_x$. From (8), $O^t\in S_o$ means $\left|O^t\right|\le Q_o$ for all t.

Introducing a constriction coefficient in SPSO controls the balance between the cognitive component ($p_i^t-x_i^t$) and social component ($g^t-x_i^t$) in the velocity equation. The coefficient restricts the particle velocities within a certain range to prevent excessive exploration or exploitation.

$\begin{array}{l}{V}_i^{t+1}=\chi *\left(\omega V_i^t+{\phi }_1^t(P_i^t-x_i^t)+{\phi }_2^t(g^t-x_i^t)\right)\end{array}$

2.1 Convergence of some PSO variants

The importance of a hybrid method is to combine different optimization methods to take advantage of the virtues of each of the methods. In addition to standard PSO, several variants of the PSO in Kumar et al. [5] were constructed to improve the performance of PSO.

The SPSO

$\begin{array}{l}{X}_i^{t+1}=X_i^t+V_i^{t+1},\end{array}$

has a scalar function of position if $x_i^t=p_i^t=g_i^t$ for a particle, that is particle's update depends only on its previous velocity. This can make the algorithm to stop to flow on the swarm's global best position, even if that position is not a local optimum. For instance, based on (4), the guaranteed convergence PSO, GCPSO, overcomes this problem by using a modified position and velocity update equation for the global best particle, which forces that particle to search for a better position in a confined region around the global best position.

The GCPSO can be used with neighborhood topologies such as star, ring, and Von Neumann. Neighborhoods have a similar effect in the GCPSO [16, 19] as they do in the SPSO. Shi and Eberhart [25] introduced the concept of linearly decreasing inertia weight with generation number into PSO to improve the algorithmic performance.

Particles converge to a weighted average ($O_i^t$) between their personal and local best positions [8], referred to as a so-called theoretical attractor point (ATP). Kennedy [26] has proposed that the entire velocity update equation is replaced by a random number sampled from a Gaussian distribution (Gd) around the ATP, with a deviation of the magnitude of the distance between the personal and global best. The resultant algorithm is called the bare bones PSO (BBPSO). Kennedy also proposed an alternative bare bones PSO (aBBPSO) [26], where the particle sampled from the previous Gd is reunited with the particle's personal best position. The performance of PSO with a small and a larger nearby region might be better on multimodal and unimodal problems, respectively [27]. Changing dynamically the neighborhood structures has been proposed to avoid insufficiencies in fixed nearby regions [28].

The quantum-behaved particle swarm optimization was proposed to show many advantages to the traditional PSO. Fang et al. [24] proposed a quantum-behaved particle swarm optimization (QBPSO) algorithm and discuss the convergence of QBPSO within the framework of random algorithm's global convergence theorem. Inspired by natural speciation, some researchers have introduced evolution methods into PSO [29, 30]. The problem of premature convergence was studied on a perturbed particle swarm algorithm presented based on the new particle updating strategy [31]. To solve optimization problems, Tang et al. [32] developed a feedback-learning PSO algorithm with quadratic inertia weight, ω. Hybridized PSO with a local search technique for locating optimal solutions for multiple global and local solution in physical fitness of more than one global optimal solution for optimization problem using a memetic algorithm can be referred in Wang et al. [33]. An example-based learning PSO was proposed in Huang et al. [34] to overcome the failures of PSO by retaining a balance between swarm diversity and convergence speed. A variation of the global best PSO where the velocity update equation does not hold a cognitive component is called social PSO, expressed as

$\begin{array}{ll}{V}_i^{t+1}=\omega V_i^t+{\phi }_2(g_i^t-x_i^t),& (9)\end{array}$

The individuals are only supported by the global best position and their previous velocity. The particles are attracted toward the global best position, instead of a weighted average between global best and their personal best positions, leading to very fast convergence [19].

3 Relations of CSPSO and Markov chain

In this section, the global convergence of CSPSO is analyzed based on properties of Markov Chain and the transition probabilities of particle velocity and position are also computed.

$\begin{array}{ll}{V}_i^{t+1}=\{\begin{array}{l}\chi *(V_i^t+{\phi }_1^t(P_i^t-x_i^t)+\hfill \\ {\phi }_2^t(g^t-x_i^t)), for \omega =1\hfill \\ \chi *(\omega V_i^t+{\phi }_1^t(P_i^t-x_i^t)+\hfill \\ {\phi }_2^t(g^t-x_i^t)), otherwise\hfill \end{array}& (10)\end{array}$

In (10), the velocities of particles are updated using two main components: the cognitive component and the social component. The cognitive component guides a particle toward its personal-best position, while the social component directs a particle toward the best position found by the entire swarm.

We introduce some useful definitions, variables and propositions (based on single particle model) which may be important in this article [22, 23, 35, 36].

The following definitions provide a formal description of this property based on single particle model [22, 23, 35, 36].

Definition 1. (Stochastic process and Markov property). Assume all the variables are defined within the context of a common probability space or probability measure.

1. The random variables Y = (Y⁰, Y¹, …, Y^t) in a sequence are called a stochastic processes.

2. Let Y^t be a value in state space S, and the sequence ${\left\{Y^t\right\}}_{t\ge 0}$ is a discrete stochastic process.

For every t ≥ 0 and i^l ∈ S(l − 1 ≤ t).

3. The discrete stochastic process is a Markov Chain.

If the probability Pr{Y^t+1 = i^t+1 ∣ Y⁰ = i⁰, Y¹ = i¹, …, Y^t = i^t} = Pr{Y^t+1 = i^t+1 ∣ Y^t = i^t} > 0. and Pr{Y⁰ = i⁰, Y¹ = i¹, …, Y^t = i^t} > 0

Definition 2. (State of particle). The state of particle ${\kappa }_i^t=(x_i^{t-1},x_i^t,p_i^t,g^t)$ at the t-th iteration for particle i in (3).

The state of particle space is a set of all possible states of particle, denoted as S. ${\kappa }_i^t$, the update probability of the state of the particle can be calculated based on proposition-1.

Proposition 1. If the accelerating factors ${\phi }_1^t$ and ${\phi }_2^t$ in CSPSO satisfy ${\phi }_1^t,{\phi }_2^t\in U(0,c)$, then the probability for particle i changes from the position $x_i^t$ to the spherical region centered at $x_i^{t+1}$ with radius ϱ_t > 0. The event $A_i=\left\{{\kappa }_i^{t+1}\mid {\kappa }_i^t\right\}$, defining the state of particle i at the t-th iteration is updated to the state at the (t + 1)-th iteration, for each i ∈ {1, 2, …, K} can be computed as

$\begin{array}{ll}Pr(A_i)=\frac{{\varrho }_t^3}{\chi \omega \Vert x_i^t-X_i^{t-1}\Vert c\chi \Vert p_i^t-X_i^t\Vert c\chi \Vert g^t-X_i^t\Vert },& (11)\end{array}$

c is a constant within U(0, c) and δ → 0, where

$\begin{array}{ll}\varrho =c\chi *\{\begin{array}{c}\Vert p_i^t-X_i^t\Vert ,forf(x_i^t)-\delta \le f(P_i^t)\le f(x_i^t)+\delta \\ \Vert g^t-X_i^t\Vert ,forf(x_i^t)-\delta \le f(g^t)\le f(x_i^t)+\delta \end{array}& (12)\end{array}$

Proof. The 1-step transition probability of the i th state of particles, $P_i^{t+1}$ and g^t+1, are determined by $x_i^{t+1}$ for transferring ${\kappa }_i^t$ to ${\kappa }_i^{t+t}$ based on the following SPM-Single Particle Model [36]

$\begin{array}{l}{x}_i^{t+1}=x_i^t+\chi *(\omega (x^t-x_i^{t-1})+\\ {\phi }_1^t(P_i^t-x_i^t)+{\phi }_2^t(g^t-x_i^t)),& (13)\end{array}$

$x_i^{t+1}$ determined by χω, χφ₁, and χφ₂.

Three conditions in 1-step transition probability are:

1. $f(x_i^t)-\delta \le f(P_i^t),f(g^t)\le f(x_i^t)+\delta .$ $x_i^{t+1}=x_i^t+\chi \omega (x_i^t-x_i^{t-1})$ is determined uniquely by χω, where χω is unknown constant, having

$\begin{array}{ll}\begin{array}{c}P(x_i^{t+1}\mid {\kappa }_i^t)=\frac{{\int }_{x_i^{t+1}-\frac{1}{2}\varrho }^{x_i^{t+1}+\frac{1}{2}\varrho }dy}{{\int }_{x_i^t}^{x_i^t-\chi \omega (x_i^t-x_i^{t-1})}dy}\\ =\frac{\varrho }{\chi \omega \Vert x_i^t-x_i^{t-1}\Vert }\end{array}& (14)\end{array}$

2. $f(x_i^t)-\delta \le f(P_i^t),f(g^t)\le f(x_i^t)+\delta .$

Ordering implies $g^t\in \left\{p_i^t,g^t\right\}$

$\begin{array}{ll}\begin{array}{c}{x}_i^{t+1}=x_i^t+\chi \omega (x^t-x_i^{t-1})+\\ \chi {\phi }_2^t(g^t-x_i^t)\end{array}& (15)\end{array}$

Here, ${\phi }_2^t$ is random variable because $x_i^{t+1}$ is determined by $\chi \omega (x^t-x_i^{t-1})$ and $\chi {\phi }_2^t(g^t-x_i^t)$

$\begin{array}{ll}\begin{array}{c}P(x_i^{t+1}\mid {\kappa }_i^t)=\frac{{\int }_{x_i^{t+1}-\frac{1}{2}\varrho }^{x_i^{t+1}+\frac{1}{2}\varrho }dy}{{\int }_{x_i^t}^{x_i^t+\chi \omega (x_i^t-x_i^{t-1})}dy}*\frac{{\int }_{{\phi }_1^t-\frac{1}{2}\varrho }^{{\phi }_i^t+\frac{1}{2}\varrho }dy}{{\int }_{x_i^t}^{x_i^t+\chi c(g^t-x_i^{t-1})}dy}\\ =\frac{\varrho }{\chi \omega \Vert x_i^t-x_i^t\Vert }*\frac{\varrho }{\chi c\Vert g^t-x_i^t\Vert }\end{array}& (16)\end{array}$

3. $f(x_i^t)+\delta <f(P_i^t),f(g^t)<f(x_i^t)-\delta .$

$\begin{array}{ll}\begin{array}{c}{x}_i^{t+1}=x_i^t+\chi \omega (x^t-x_i^{t-1})+\chi {\phi }_1^t(P_i^t-x_i^t)\\ +\chi {\phi }_2^t(g^t-x_i^t))\hfill \end{array}& (17)\end{array}$

when $x_i^{t+1}\in ℝ,$ $x_i^{t+1}$ is determined by χ*(ω, φ₁, φ₂)

$\begin{array}{ll}\begin{array}{l}P(x_i^{t+1}\mid {\kappa }_i^t)=\frac{{\int }_{x_i^{t+1}-\frac{1}{2}\varrho }^{x_i^{t+1}+\frac{1}{2}\varrho }dy}{{\int }_{x_i^t}^{x_i^t+\chi \omega (x_i^t-x_i^{t-1})}dy}*\frac{{\int }_{{\phi }_1^t-\frac{1}{2}\varrho }^{{\phi }_1^t+\frac{1}{2}\varrho }dy}{{\int }_{x_i^t}^{x_i^t+\chi c(g^t-x_i^{t-1})}dy}*\\ \frac{{\int }_{{\phi }_2^t-\frac{1}{2}\varrho }^{{\phi }_2^t+\frac{1}{2}\varrho }dy}{{\int }_{x_i^t}^{x_i^t+\chi c(g^t-x_i^{t-1})}dy}\\ =\frac{\varrho }{\chi \omega \Vert x_i^t-x_i^{t-1}\Vert }*\\ \frac{\varrho }{\chi c\Vert P_i^t-x_i^t\Vert }*\\ \frac{\varrho }{\chi c\Vert g^t-x_i^t\Vert }\end{array}& (18)\end{array}$

From conditions in 1 − 3,

$\begin{array}{l}{\displaystyle \underset{P_i^t\to x_i^t}{lim}}\frac{\varrho }{\chi \omega \Vert P_i^t-x_i^t\Vert }=1\end{array}$

$\begin{array}{l}{\displaystyle \underset{g^t\to X_i^t}{lim}}\frac{\varrho }{\chi c\Vert g_i^t-x_i^t\Vert }=1.\end{array}$

$\begin{array}{ll}P(A_i)=\frac{{\varrho }^3}{\chi (\omega \Vert x_i^t-x_i^{t-1}\Vert c\Vert P_i^t-x_i^t\Vert sc\Vert g^t-x_i^t\Vert }& (19)\end{array}$

δ is a vector approaching to zero. When

  I. ϱ is the radius of $x_i^{t+1}$

 II. $f(x_i^t)-\delta \le f(P_i^t)\le f(x_i^t)+\delta ,$$\varrho =c\chi \Vert P_i^t-x_i^t\Vert$

III. $f(x_i^t)-\delta \le f(g^t)\le f(x_i^t)+\delta ,$$\varrho =c\chi \Vert g^t-x_i^t\Vert$

Definition 3. (State of swarm). The state of swarm in (3), at iteration t, denoted as η^t, is defined as ${\eta }^t=({\kappa }_1^t,{\kappa }_2^t,\dots ,{\kappa }_K^t).$

The state of swarm space is a set of all possible states of swarm, denoted as ϖ[22].

Proposition 2. (Markov chain). The set of collection of swarm state ${\left\{{\eta }^t\right\}}_{t\ge 1}$ is a Markov chain[23].

Proof. The proof follows by referring to equation of position that the state of swarm ${\eta }^{t+1}=({\kappa }_1^{t+1},{\kappa }_2^{t+1},\dots ,{\kappa }_m^{t+1})$ at iteration t + 1 depends on only the state of swarm ${\eta }^t=({\kappa }_1^t,{\kappa }_2^t,\dots ,{\kappa }_K^t).$ at iteration t. Therefore, ${\left\{{\eta }^t\right\}}_{t\ge 1}$ is a Markov chain.

Definition 4. Let ${\Gamma }_1^n$ denote the σ-field generated by particles state ${\kappa }_1^t,{\kappa }_2^t,\dots ,{\kappa }_n^t,(K\ge n)$ and define

$\begin{array}{l}\varphi (({\Gamma }_1^n, {\kappa }_{n+1}^t)=sup\{\mid Pr(B\backslash A)-Pr(B)\mid :\\ A\in {\Gamma }_1^n, B\in \sigma ({\kappa }_{n+1}^t)\},& (20)\end{array}$

$\begin{array}{ll}\varphi ={\displaystyle \underset{1\le n\le K-1}{sup}}\varphi ({\Gamma }_1^n,{\kappa }_{n+1}^t)& (21)\end{array}$

Due to the weak interdependent relationship among the particles, ϕ is approximately small.

Proposition 3. The transition probability from η^t to η^t+1 satisfies

$\begin{array}{ll}\mid Pr({\eta }^{t+1}\mid {\eta }^t)-{\displaystyle \prod _{i=1}^K}Pr({\kappa }_i^{t+1}\mid {\kappa }_i^t)\mid \le \mu & (22)\end{array}$

where μ can be made small enough, therefore, μ = (2^K−1 − 1)ϕ.

Proof. Based on the Definition 4, one has ∣Pr(B\A)−Pr(B)∣ ≤ ϕ.

The event $\left\{{\kappa }_i^{t+1}\mid {\kappa }_i^t\right\}$ denoted as A_i means that the state of particle i at the t-th iteration is changed to the state at the (t + 1)-th iteration, for each i ∈ {1, 2, …, K}.

$\begin{array}{ll}Pr({\displaystyle \prod _{i=1}^K}{A}_i)=Pr({\eta }^{t+1}\mid {\eta }^t)& (23)\end{array}$

is the transition probability from η^t to η^t+1.

Because g^t+1 depends on $x_i^t$ and $P_i^t$ for all 1 ≤ i ≤ K, A₁, A₂, …, A_K are not independent random events.

According to (6) and the conditional probability, one has the following cases:

$\begin{array}{l}\begin{array}{c}\text{Case 1: }Pr(A_1{A}_2)=Pr(A_1)Pr(A_2\mid A_1)\le Pr(A_1)\left[P(A_2)+\varphi \right]\\ \le Pr(A_1)Pr(A_2)+\varphi ,\end{array}\end{array}$

$\begin{array}{l}\begin{array}{l}\text{Case 2: }Pr(A_1)Pr(A_2)-\varphi \le Pr(A_1)\left[Pr(A_2)-\varphi \right]\\ \le Pr(A_1)Pr(A_2\mid A_1)=Pr(A_1{A}_2).\end{array}\end{array}$

This implies

$\begin{array}{ll}Pr(A_1)Pr(A_2)-\varphi \le Pr(A_1{A}_2)\le Pr(A_1)Pr(A_2)+\varphi & (24)\end{array}$

$\begin{array}{l}\begin{array}{l}\text{Case 3: }Pr(A_1{A}_2{A}_3)=Pr(A_1)Pr(A_2\mid A_1)Pr(A_3\mid A_1{A}_2)\\ \le Pr(A_1)\left[Pr(A_2)+\varphi \right]\left[Pr(A_3)+\varphi \right]\\ \le Pr(A_1)Pr(A_2)Pr(A_3)+3\varphi ,\end{array}\end{array}$

$\begin{array}{l}\begin{array}{l}\text{Case 4: }Pr(A_1)Pr(A_2)Pr(A_3)-3\varphi \le \\ Pr(A_1)\left[Pr(A_2)-\varphi \right]\left[Pr(A_3)-\varphi \right]\\ \le Pr(A_1)Pr(A_2\mid A_1)Pr(A_3\mid A_1{A}_2)\\ =Pr(A_1{A}_2{A}_3)\end{array}\end{array}$

Similarly, we can get

$\begin{array}{ll}\begin{array}{l}Pr(A_1)Pr(A_2)P(A_3)-3\varphi \le Pr(A_1{A}_2{A}_3)\le \\ Pr(A_1)Pr(A_2)Pr(A_3)+3\varphi \end{array}& (25)\end{array}$

Then,

$\begin{array}{ll}\begin{array}{l}{\displaystyle \prod _{i=1}^K}Pr(A_i)-(2^{K-1}-1)\varphi \le Pr({\displaystyle \prod _{i=1}^K}{A}_i)\le \\ {\displaystyle \prod _{i=1}^K}Pr(A_i)-(2^{K-1}-1)\varphi \end{array}& (26)\end{array}$

is the transition probability from η^t to η^t+1. Let μ = (2^K−1 − 1)ϕ. We have

$\begin{array}{ll}\mid Pr({\eta }^{t+1}\mid {\eta }^t)-{\displaystyle \prod _{i=1}^K}P({\kappa }_i^{t+1}\mid {\kappa }_i^t)\mid \le \mu & (27)\end{array}$

From (1), the interdependent relationship among the particles is weak, ϕ in (11) is sufficiently small so that the fact that K is finite implies that μ is a small enough positive number.

3.1 Probabilistic convergence analysis of CSPSO

In this subsection, we present the convergence analysis for the version of the standard PSO with constriction coefficient (CSPSO), by analogy of the method of analyzing convergence of the PSO convergence of the PSO in Kennedy and Mendes [27]. We also based on concepts of definitions and results in Section 3 above. Our analysis has the advantage of providing a much easier method to realize the convergence of the PSO with constriction coefficient (χ) in comparison to the original analysis [12]. To conduct the convergence analysis of the SPSO with constriction coefficient (CSPSO), we consider the time step value Δτ to describe the dynamics of the PSO, and rewrite the velocity and position update formulas in (1) as follows:

$\begin{array}{l}{V}_i^{t+1}=\chi \ast \{\omega V_i^t+{\phi }_1\frac{(P_i^t-x_i^t)}{\Delta \tau }+\\ {\phi }_2\frac{(g_i^t-x_i^t)}{\Delta \tau }\},& (28)\end{array}$

$\begin{array}{ll}{X}_i^{t+1}=X_i^t+V_i^{t+1}\Delta \tau ,& (29)\end{array}$

By replacing (28) into (29), we obtain the following probabilistic CSPSO:

$\begin{array}{l}{X}_i^1=X_i+\chi \ast \{\omega V_i+{\phi }_1\frac{(P_i-x_i)}{\Delta \tau }+\\ {\phi }_2\frac{(g_i-x_i)}{\Delta \tau }\}\Delta \tau ,& (30)\end{array}$

$\begin{array}{ll}\begin{array}{l}{X}_i^1=X_i+\chi \omega V_i\Delta \tau +\\ \chi \phi \left(\frac{\chi {\phi }_1{P}_i+\chi {\phi }_2{g}_i}{\chi \phi }-x_i\right)\end{array}& (31)\end{array}$

By rearranging the terms in (31), we obtain

$\begin{array}{ll}\begin{array}{c}{X}_i^1=(1-\chi \phi )X_i+\chi \omega \Delta \tau V_i+\\ \chi {\phi }_1{P}_i+\chi {\phi }_2{g}_i.\end{array}& (32)\end{array}$

In addition, by rearranging the terms in (29), we obtain

$\begin{array}{ll}\begin{array}{c}{V}_i^1=-\frac{\chi \phi }{\Delta \tau }{X}_i+\chi \omega V_i+\\ \chi {\phi }_1\frac{P_i}{\Delta \tau }+\chi {\phi }_2\frac{g_i}{\Delta \tau }.\end{array}& (33)\end{array}$

We combine the above two (32), (33) to have the following matrix form:

$\begin{array}{ll}\begin{array}{c}\left(\begin{array}{c}{X}_i^1\\ V_i^1\end{array}\right)=\left(\begin{array}{cc}1-\chi \phi & \chi \omega △\tau \\ -\frac{\chi \phi }{△\tau }& \chi \omega \end{array}\right)\left(\begin{array}{c}{X}_i\\ V_i\end{array}\right)+\\ \left(\begin{array}{cc}\chi {\phi }_1& \chi {\phi }_2\\ \frac{\chi {\phi }_1}{△\tau }& \frac{\chi {\phi }_2}{△\tau }\end{array}\right)\left(\begin{array}{c}{P}_i\\ g_i\end{array}\right)\end{array}& (34)\end{array}$

which can be thought of as a discrete dynamic system representation for the PSO in which (X V)^T is the state subject to an external input ${(P_i{g}_i)}^T$, and the two terms on the right side of the equation correspond to the dynamic and input matrices, respectively [37].

Supposing that no external excitation exists in the dynamic system, ${\left[P_i,g_i\right]}^T$ is constant, i.e., other particles cannot find better positions. Then, a convergent behavior could be maintained. If it converges as τ → ∞, ${(X_i^1{V}_i^1)}^T\to {(X_i{V}_i)}^T$. That is, the dynamic system becomes:

$\begin{array}{l}\begin{array}{c}\left(\begin{array}{c}0\\ 0\end{array}\right)=\left(\begin{array}{cc}1-\chi \phi & \chi \omega △\tau \\ -\frac{\chi \phi }{△\tau }& \chi \omega \end{array}\right)\left(\begin{array}{c}{X}_i\\ V_i\end{array}\right)+\\ \left(\begin{array}{cc}\chi {\phi }_1& \chi {\phi }_2\\ \frac{\chi {\phi }_1}{△\tau }& \frac{\chi {\phi }_2}{△\tau }\end{array}\right)\left(\begin{array}{c}{P}_i\\ g_i\end{array}\right)\end{array}\end{array}$

which holds only when V_i = 0 and X_i = P_i = g_i, where the convergent point is an equilibrium point if there is no external excitation, but better points are found by the optimization process with external excitation. For (34), Tarekegn et al. [6] has mentioned a sufficient strategies of improved convergence via theoretical analysis to get the relationship among χ, ω, and φ at the condition of convergence.

The derived probabilistic CSPSO can utilize any probabilistic form of prior information in the optimization process and, therefore, the benefits from prior information can lead probabilistic CSPSO to more probable search region and help optimize more quickly with hierarchical use of parameters [40].

By substituting (28) into (29), is transformed into (35)

$\begin{array}{ll}{V}_i^1=\chi \omega V_i+\frac{\chi \phi }{△\tau }\left[P(i)-x_i\right]& (35)\end{array}$

where $P(i)=\frac{{\phi }_1{P}_i+{\phi }_2{g}_i}{\phi }.$

Let y_i = P(i)−x_i, then (32), (35) can be transformed into (37), (38)

$\begin{array}{ll}{V}_i^1=\chi \omega V_i+\frac{\chi \phi }{△\tau }{y}_i& (36)\end{array}$

$\begin{array}{ll}{Y}_i^1=\chi \omega V_i+\left(1+\frac{\chi \phi }{△\tau }\right)y_i& (37)\end{array}$

Combining (36) an iterative equation in the form of vector is obtained as (38)

$\begin{array}{ll}\left(\begin{array}{c}{V}_i^1\\ Y_i^1\end{array}\right)=\left(\begin{array}{cc}\chi \omega & \frac{\chi \phi }{△\tau }\\ \chi \omega & 1+\frac{\chi \phi }{△\tau }\end{array}\right)\left(\begin{array}{c}{V}_i\\ y_i\end{array}\right)& (38)\end{array}$

which can be viewed as a general forecasting model of Markov chain as follows: ${\eta }^t=P{K}_i^t,$ where, $K_i^t$ is a vector as presented below

${({\eta }^t)}^T=\left[\begin{array}{c}{V}_i^1{Y}_i^1\end{array}\right]$

$P^T=\left[\begin{array}{cc}\chi \omega & \chi \omega \\ \frac{\chi \phi }{△\tau }& 1+\frac{\chi \phi }{△\tau }\end{array}\right],$

${(K_i^t)}^T=\left[\begin{array}{c}{V}_i{y}_i\end{array}\right]$

(38) is the model with no external excitation, which is useful in studying the evolution of certain systems over repeated trials as a probabilistic (stochastic) model [37].

Using the Markov chain method, the position (η^t)^T(t + 1) of the d th element of the i th particle at the (t + 1) th iteration in CSPSO can be computed using the following formula:

$\begin{array}{ll}{({\eta }^t)}^T(t+1)=\left[{(k_i^t)}^T(t)\right]X{P}^T& (39)\end{array}$

superscript T denotes the transposition.

Based on [20, 41] the CSPSO algorithm analysis in Markov chain theory, the algorithm satisfies the context of almost sure convergence as follows:

1. As the algorithm progresses and more iterations are performed, it will converge to an optimal solution with a probability of 1 and

2. Given sufficient time and iterations, it will find the globally optimal solution.

3.2 Stability analysis of CSPSO

We further get insight into the dynamic system in (39). First, we solve the characteristic equation of the dynamic system as follows:

${\lambda }^2-(1+\chi \omega +\frac{\chi \phi }{\Delta \tau })\lambda +\chi \omega =0.$

The eigenvalues are obtained as follows:

${\lambda }_{1,2}=\frac{(1+\chi \omega +\frac{\chi \phi }{\Delta \tau }\pm \gamma )}{2},$

$\gamma =\sqrt{{(1+\chi \omega +\frac{\chi \phi }{\Delta \tau })}^2-4\chi \omega }$

with λ₁ ≥ λ₂. The explicit form of the recurrence relation (29) is then given by

$Y_i^1(t)=r_1+r_2{\lambda }_1^t+r_3{\lambda }_2^t$

where r₁, r₂, and r₃ are constants determined by the initial conditions of the system. From updated velocity

$\begin{array}{ll}{V}_i^1(t+1)=\frac{Y_i^1(t+1)-Y_i(t)}{\Delta \tau }& (40)\end{array}$

result in

$\begin{array}{c}{V}_i^1(t+1)=\frac{r_2({\lambda }_1^{t+1}-{\lambda }_1^t)+r_3({\lambda }_2^{t+1}-{\lambda }_2^t)}{\Delta \tau }\end{array}$

$\begin{array}{c}{V}_i^1(t+1)=(r_2\frac{{\lambda }_1-1}{\Delta \tau }){\lambda }_1^t+(r_3\frac{{\lambda }_2-1}{\Delta \tau }){\lambda }_2^t\end{array}$

$k_1=\frac{r_1({\lambda }_1-1)}{\Delta \tau }$ and $k_2=\frac{r_2({\lambda }_2-1)}{\Delta \tau }$

$\begin{array}{c}{\displaystyle \underset{t\to \infty }{lim}}{V}_i^1(t+1)={\displaystyle \underset{t\to \infty }{lim}}{k}_1{\lambda }_1^t+{\displaystyle \underset{t\to \infty }{lim}}{k}_2{\lambda }_2^t\end{array}$

$\begin{array}{ll}{\displaystyle \underset{t\to \infty }{lim}}{X}_i^1(t+1)=\{\begin{array}{c}{\displaystyle \underset{t\to \infty }{lim}}{x}_i^1(t)ifmax(\Vert {\lambda }_1\Vert ,\Vert {\lambda }_2\Vert )<1,\\ (k_{1}or{k}_{2}or{k}_1+k_2)+{\displaystyle \underset{t\to \infty }{lim}}{x}_i^1(t)if\\ max(\Vert {\lambda }_1\Vert ,\Vert {\lambda }_2\Vert )=1\end{array}& (41)\end{array}$

(41) implies that if the CSPSO algorithm is convergent, then velocity of the particles will decrease to zero or stay unchanged until the end of the iteration.

3.3 Constriction factor and its impact

When the PSO algorithm is run without controlling the velocity, the system explodes after a few iterations. To control the convergence properties of a particle swarm system, an important model having constriction factor and ω together is shown below:

$\begin{array}{l}{V}_i^{t+1}=\chi \ast \{\omega V_i^t+{\phi }_1(P_i^t-x_i^t)+\\ {\phi }_2(g_i^t-x_i^t)\},& (42)\end{array}$

$2\kappa =\chi \mid 2-\phi -\sqrt{{\phi }^2-4\phi }\mid ,$

φ₁ + φ₂ = φ ≥ 4, 0 ≤ κ ≤ 1.

Under these assumption conditions, the particle's trajectory in the CSPSO system is stable [6].

$\begin{array}{ll}\begin{array}{l}{\omega }^{t+1}={\omega }_{max}-\left(\frac{{\omega }_{max}-{\omega }_{min}}{t_{max}}\right)t,\\ {\omega }_{max}>{\omega }_{min}\end{array}& (43)\end{array}$

where, ω_max and ω_min are the predefined initial and final values of the inertia weight, respectively, t_max is the maximum iteration number, and t is the current iteration number for a linearly decreasing inertia weight scheme.

3.4 Global convergence analysis of QBCSPSO

A sequence generated by the iterative PSO algorithm converges to a solution point. Several PSO variants were proposed to enhance convergence performance of PSO [5, 24], which combines quantum results with CSPSO, denoted as QBCSPSO. In this subsection, the global convergence of QBCSPSO is investigated.

From the Monte Carlo method, the current velocity for the position $x_i^{t+1}$ of the d th element of the i th particle at the (t + 1) th iteration in QBCSPSO can be obtained using the following formula:

$\begin{array}{ll}\begin{array}{l}{V}_i^{t+1}=Y_i^t\pm L_i^{t}ln(u_i^{-(t+1)}),\\ u_i^{t+1}~U(0,1)\end{array}& (44)\end{array}$

where $U_i^t\in (0,1).$ Referring to Sun et al. [18, 24], where δ the (wave) function

$\delta (Y_i^{t+1})=\frac{1}{\sqrt{L_i^t}}exp(-Y_i^{t+1}/L_i^t)$

with $Y_i^{t+1}=\mid x_i^{t+1}-P_i^t\mid ,$ and

the characteristic length $L_i^t$ is obtained by

$\begin{array}{ll}{L}_i^t=\gamma |x_i^t-C^t|& (45)\end{array}$

the term C^t used in (45) is $C^t=\frac{1}{K}\sum _{i=1}^K{P}_i^t.$ [24].

The contraction-expansion coefficient γ can be adjusted to balance the trade-off between global and local exploration ability of the particles during the optimization process for two main purposes [38]:

• a larger γ value enables particles to have a stronger exploration ability but a less exploitation ability.

• a smaller γ allows particles a more precise exploitation ability.

Notice that in this article, most of the (1)-(45) represent velocities or positions or both of them.

4 Results and discussions

To demonstrate the working of the CSPSO algorithm, two well-known test functions in a global optimization were widely used in evaluating performance of evolutionary methods, and have the global minimum at the origin or very close to the origin. We compare the performance of PSO, SPSO, CPSO, and CSPSO.

Example 1. Unimodal function

$\begin{array}{ll}\begin{array}{l}minf(x_i)={\displaystyle \sum _{i=1}^K}{x}_i^2\\ Subjectto-10\le x_i\le 10.\end{array}& (46)\end{array}$

Example 2. Multi modal function

$\begin{array}{ll}\begin{array}{l}minf(x)={\displaystyle \sum _{i=1}^K}-x_{i}sin(\sqrt{\mid x_i\mid })\\ Subjectto-10\le x_i\le 10.\end{array}& (47)\end{array}$

In the experiments, inertia weight decreases from 0.9 to 0.4 and the generation stops when $E_i=\mid F{g}^t(x_i)-F{p}^t(x_i)\mid \le tolerance$ satisfied. Here, Fp is the function value of the best personal in current iteration and Fg denotes the global optimum and c₁ = c₂ = 1.49 and c₁ = c₂ = 2 are used in PSO and CSPSO, respectively.

For all algorithms, results are averaged over 100 independent runs and iterations while the population size is 50.

Following the recommendations of the original references, the best function value settings of some compared algorithms are summarized in Table 1.

Table 1

Table 1. Comparison of algorithms on optimization test functions.

The mean velocity v^t+1 of (46) is shown using Table 1 and graphically (Figures 1–3) for the algorithms in Table 1. Figure 1 shows the convergence of PSO without controlling factor inertia weight exploded. One of the main limitations of PSO is that particles prematurely converge toward a local solution.

Figure 1

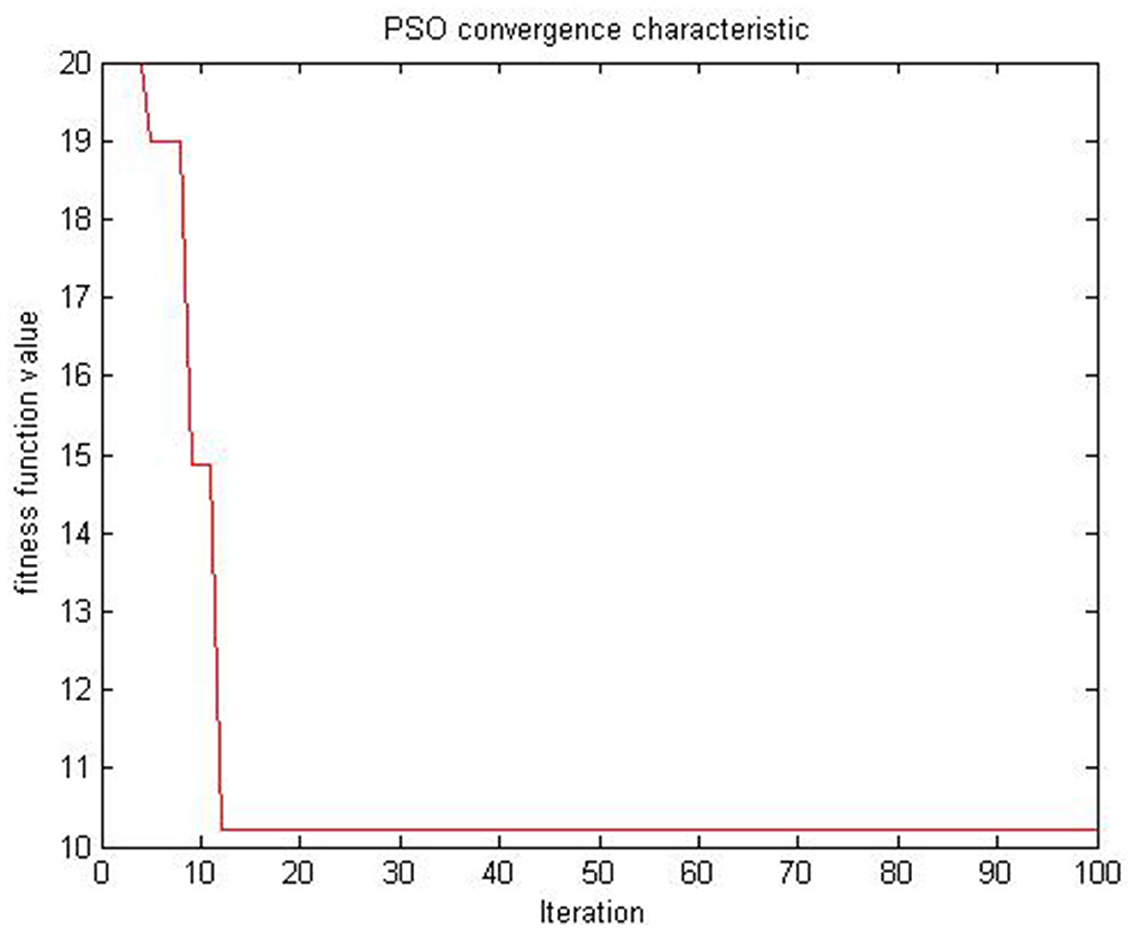
Figure 1. Basic PSO with no inertia weight for (46) on example 1.

The evaluation results of the compared algorithms are shown in Figures 2, 3 for decreasing and increasing inertia weight, respectively. Figure 2 shows the evolution of inertial weight of the compared algorithms over the running time. The main disadvantage is that once the inertia weight is decreased, the swarm loses its ability to search new areas [39]. Figure 3 shows the evolution of convergence characteristic for CSPSO based on inertial weight during the run. CSPSO can avoid premature convergence by performing efficient exploration that can help to find better solutions as the number of iterations increases and can avoid premature convergence by balancing exploration and exploitation. The algorithm CSPSO has shown fast convergence speed on unimodal functions.

Figure 2

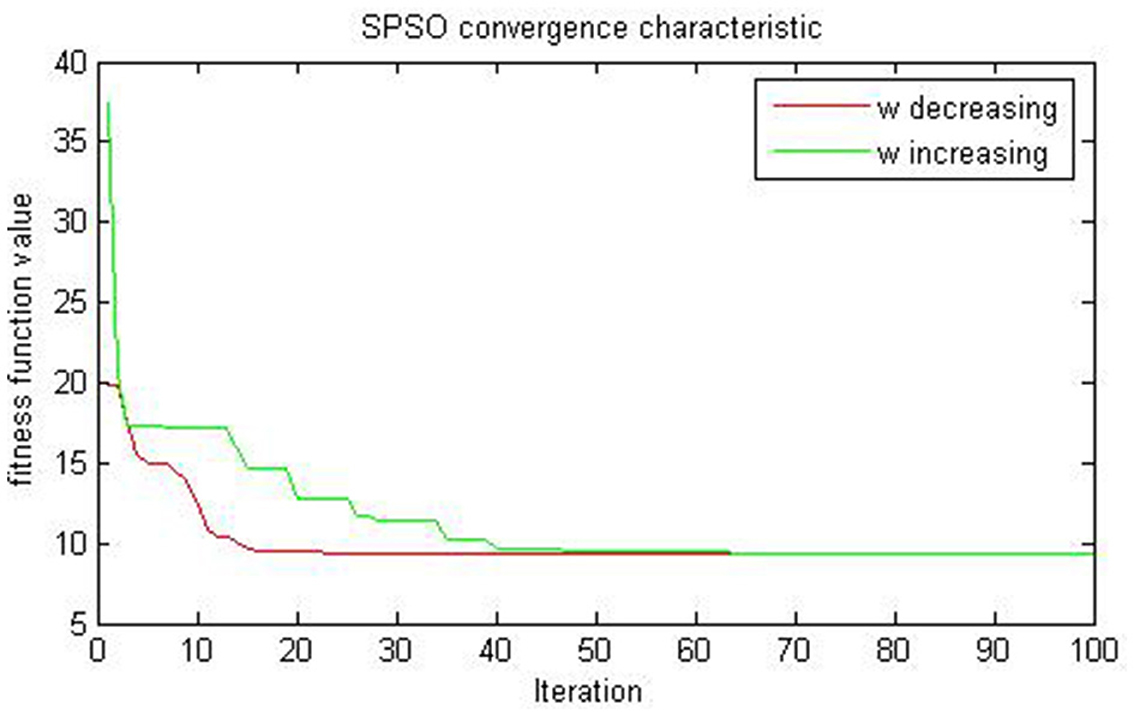
Figure 2. Evaluation of SPSO for (46) on example 1.

Figure 3

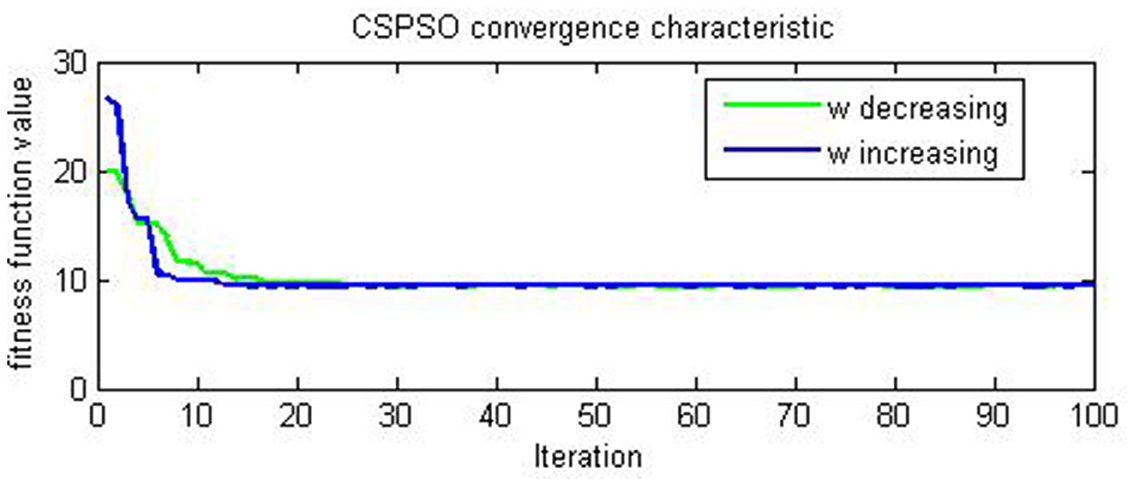
Figure 3. Evaluation of CSPSO for (46) on example 1.

In order to confirm the performance on multi-modal functions, we carry out a similar simulation by using (47).

The same set of parameters is assigned for all algorithms of Table 2 as in (46). Where in this function the number of local minima increases exponentially with the problem dimension. Its global optimum value is approximately −5.74, as we see from Table 2.

Table 2

Table 2. Comparison of algorithms on optimization test functions of multi-modal.

Figures 4, 5 are simulations obtained from Table 2 results, and all the figures meet the objective of the CSPSO algorithm for the optimization problem given in (47) and its evaluation in Figure 6.

Figure 4

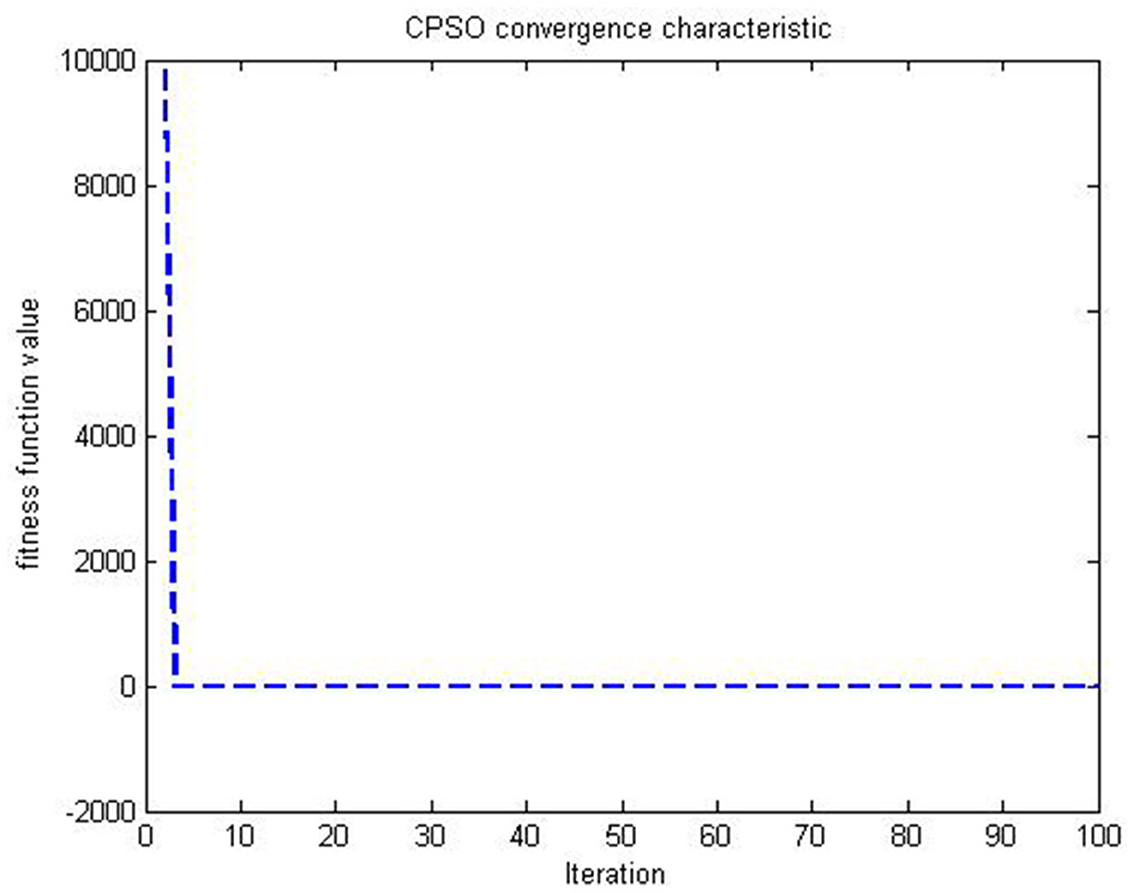
Figure 4. CPSO when ω = 1 for (47) on example 2.

Figure 5

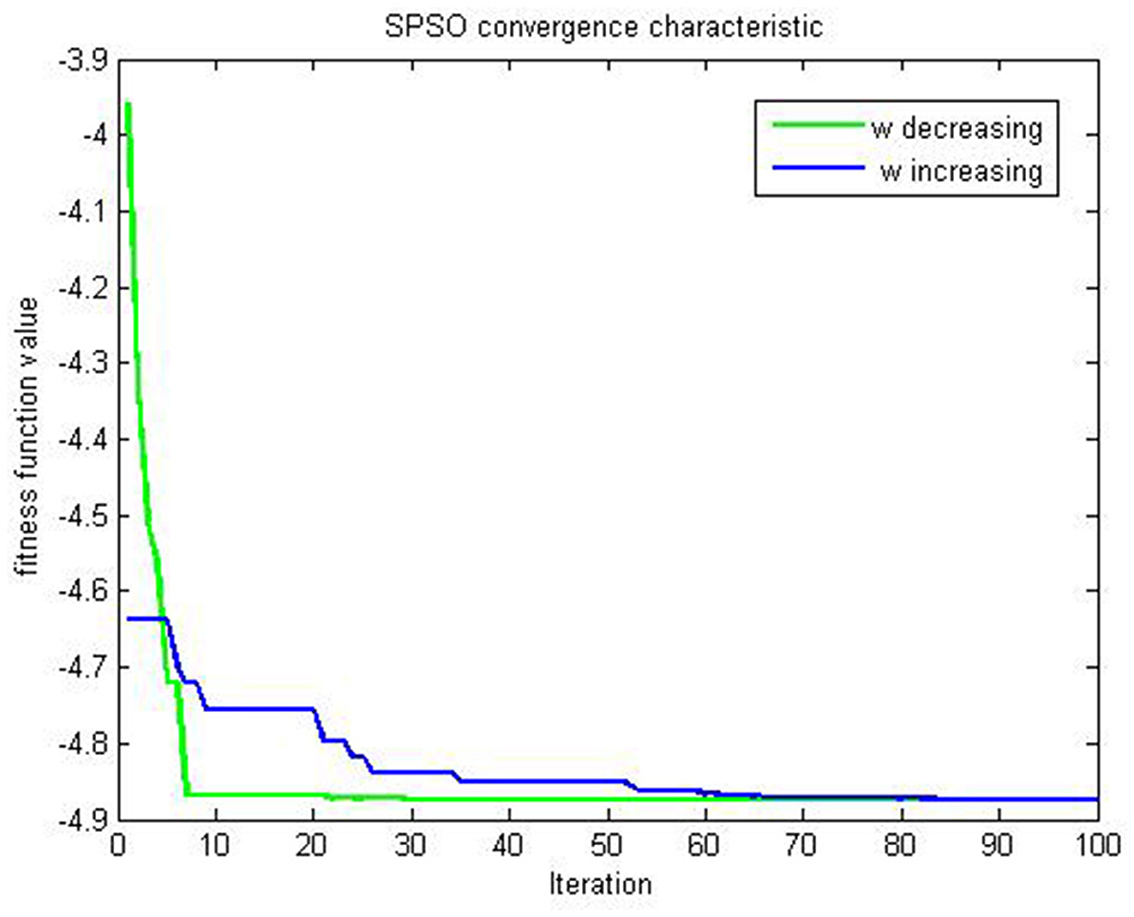
Figure 5. Evaluation of SPSO for (47) on example 2.

Figure 6

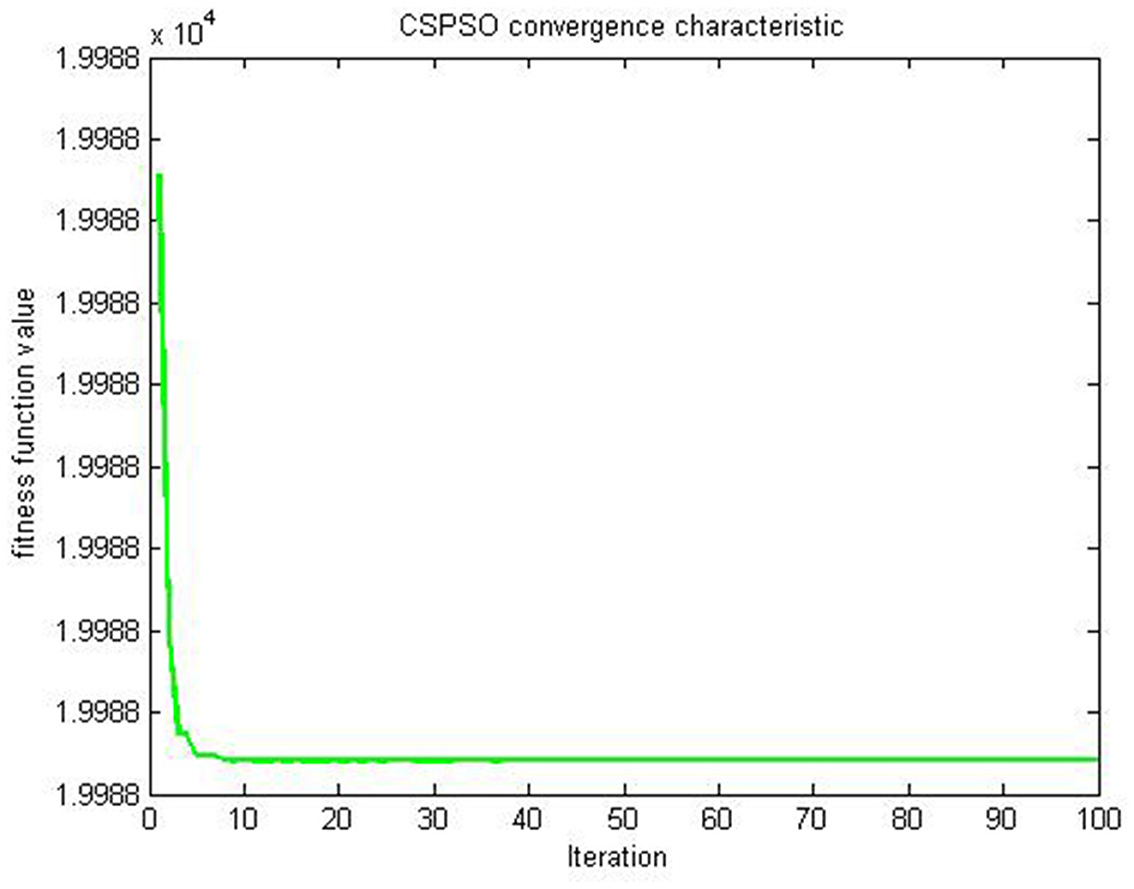
Figure 6. Evaluation of CSPSO for (47) on example 2.

5 Conclusion

This article mainly concerns the convergence and stability analysis of the CSPSO algorithm and its performance improvement for different constriction coefficients. We first investigated the convergence of the SPSO algorithm by relating it to the Markov chain in which the stochastic process and Markov properties employ quantum behaviors to improve the global convergence and prove Markov chain transition probability, showing that the CSPSO algorithm converges to the global optimum in probability. We also compared the proposed algorithm with basic PSO, SPSO, and CPSO algorithms evaluating the optimal value (fitness value) based on the range of ω. The proposed algorithm is fast and efficient, and the run plans of CSPSO for ω linearly decreasing from 0.9 to 0.4 are easy to implement. The CSPSO algorithm performs better because it regenerated those results to minimize the test functions. On the other hand, the proposed heuristic algorithm did not seek solutions that minimized the delay time or cost function, and the adjustment process would be stopped if no ω was identified as regular. The CSPSO algorithm is verified to be a global convergent algorithm. These promising results motivate other researchers to apply CSPSO to solve optimization problems. And in the future we will make further investigations on convergence and stability of PSO variants.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

DT: Formal analysis, Writing—original draft, Software, Investigation, Project administration. TG: Supervision, Methodology, Validation, Project administration, Writing—review & editing. SL: Conceptualization, Supervision.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

Authors are grateful to the referees and handling editor for their constructive comments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Kennedy J, Eberhart RC. Particle swarm optimization. In: Proceedings of the IEEE International Conference on Neural Networks, (1995). p. 1942–1948.

Google Scholar

2. Ahmed G. GadParticle swarm optimization algorithm and its applications: a systematic review. Arch Comput Methods Eng. (2022) 29:2531–61. doi: 10.1007/s11831-021-09694-4

Crossref Full Text | Google Scholar

3. Banks A, Vincent J, Anyakoha CA. A review of particle swarm optimization. Part I: background and development. Nat Comput. (2007) 6:467–84. doi: 10.1007/s11047-007-9049-5

Crossref Full Text | Google Scholar

4. AlRashidi MR, El-Hawary ME. A survey of particle swarm optimization applications in electric power systems. IEEE Trans Evol Comput. (2009) 14:913–8. doi: 10.1109/TEVC.2006.880326

Crossref Full Text | Google Scholar

5. Kumar A, Singh BK, Patro BD. Particle swarm optimization: a study of variants and their applications. Int J Comput Applic. (2016) 135:24–30. doi: 10.5120/ijca2016908406

Crossref Full Text | Google Scholar

6. Tarekegn D, Tilahun S, Gemechu T. A review on convergence analysis of particle swarm optimization. Int J Swarm Intell Res. (2023) 14:328092. doi: 10.4018/IJSIR.328092

Crossref Full Text | Google Scholar

7. Clerc M, Kennedy J. The particle swarm-explosion, stability and convergence in a multidimensional complex space. IEEE Trans Evol Comput. (2002) 6:58–73. doi: 10.1109/4235.985692

Crossref Full Text | Google Scholar

8. van den Bergh F, Engelbrecht AP. A study of particle swarm optimization particle trajectories. Inform Sci. (2006) 178:937–71. doi: 10.1016/j.ins.2005.02.003

Crossref Full Text | Google Scholar

9. Kadirkamanathan V, Selvarajah K, Fleming PJ. Stability analysis of the particle dynamics in particle swarm optimizer. IEEE Trans Evol Comput. (2006) 10:245–55. doi: 10.1109/TEVC.2005.857077

Crossref Full Text | Google Scholar

10. Liu QF. Order-2 stability analysis of particle swarm optimization. Evol Comput. (2015) 23:187–216. doi: 10.1162/EVCO_a_00129

PubMed Abstract | Crossref Full Text | Google Scholar

11. Dong WY, Zhang RR. Order-3 stability analysis of particle swarm optimization. Inf Sci. (2019) 503:508–20. doi: 10.1016/j.ins.2019.07.020

PubMed Abstract | Crossref Full Text | Google Scholar

12. Jiang M, Luo YP, Yang SY. Stochastic convergence analysis and parameter selection of the standard particle swarm optimization algorithm. Inform Process Lett. (2007) 102:8–16. doi: 10.1016/j.ipl.2006.10.005

Crossref Full Text | Google Scholar

13. Poli R, Langdon WB. Markov chain models of bare-bones particle swarm optimizers. In: Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation. (2007). p. 142–149. doi: 10.1145/1276958.1276978

Crossref Full Text | Google Scholar

14. Cai ZQ, Huang H, Zheng ZH, Luo W. Convergence improvement of particle swarm optimization based on the expanding attaining-state set. J Huazhong Univ Sci Technol. (2009) 37:44–7.

Google Scholar

15. Solis F, Wets R. Minimization by random search techniques. Math Oper Res. (1981) 6:19–30. doi: 10.1287/moor.6.1.19

Crossref Full Text | Google Scholar

16. van den Bergh F, Petrus Engelbrecht A. A convergence proof for the particle swarm. Optimiser Fund Inform. (2010) 105:341–74. doi: 10.3233/FI-2010-370

Crossref Full Text | Google Scholar

17. Dirk S, Carsten W. Runtime analysis of a binary particle swarm optimizer. Theor Comput Sci. (2010) 411:2084–100. doi: 10.1016/j.tcs.2010.03.002

Crossref Full Text | Google Scholar

18. Sun J, Wu X, Palade V, Fang W, Lai CH, Xu W. Convergence analysis and improvements of quantum-behaved particle swarm optimization. Inf Sci. (2012) 193:81–103. doi: 10.1016/j.ins.2012.01.005

Crossref Full Text | Google Scholar

19. Per KL, Carsten W. Finite first hitting time versus stochastic convergence in particle swarm optimization. Adv Metaheur. (2013) 53:1–20. doi: 10.1007/978-1-4614-6322-1_1

Crossref Full Text | Google Scholar

20. Yuan Q, Yin G. Analyzing convergence and rates of convergence of particle swarm optimization algorithms using stochastic approximation methods. IEEE T Automat Contr. (2015) 60:1760–73. doi: 10.1109/TAC.2014.2381454

Crossref Full Text | Google Scholar

21. Ren ZH, Wang J, Gao Y. The global convergence analysis of particle swarm optimization algorithm based on Markov chain. Control Theory Applic. (2011) 28:462–6.

Google Scholar

22. Xu G, Yu G. On convergence analysis of particle swarm optimization algorithm. J Comput Appl Math. (2017) 333:65–73. doi: 10.1016/j.cam.2017.10.026

Crossref Full Text | Google Scholar

23. Feng P, Xiao-Ting LI, Qian ZH, Wei-Xing LI Qi GA. Analysis of standard particle swarm optimization algorithm based on Markov Chain. Acta Autom Sinica. (2013) 39:381–9. doi: 10.1016/S1874-1029(13)60037-3

Crossref Full Text | Google Scholar

24. Sun J, Feng B, Xu WB. Particle swarm optimization with particles having quantum behavior. In: Proceedings of the 2004 Congress on Evolutionary Computation, CEC04, Portland, USA (2004). p. 326–331.

Google Scholar

25. Shi YH, Eberhart RC. Empirical study of particle swarm optimization. In: Proceedings of the Congress on Evolutionary Computation, (1999). p. 1945–1950.

Google Scholar

26. Kennedy J. Bare bones particle swarms. In: Proceedings of the 2003 IEEE Swarm Intelligence Symposium, IEEE (2003). p. 80–87.

Google Scholar

27. Kennedy J, Mendes R. Population structure and particle swarm performance. In: Proceedings of the Congress on Evolutionary Computation. (2002). p. 1671–6.

Google Scholar

28. Liang JJ, Suganthan PN. Dynamic multi-swarm particle swarm optimizer. In: Proceedings of the IEEE Swarm Intelligence Symposium. (2005). p. 124–129.

Google Scholar

29. Parrott D, Li X. Locating and tracking multiple dynamic optima by a particle swarm model using speciation. IEEE Trans Evol Comput. (2006) 10:440–58. doi: 10.1109/TEVC.2005.859468

Crossref Full Text | Google Scholar

30. Brits R, Engelbrecht AP, van den Bergh F. Locating multiple optima using particle swarm optimization. Appl Math Comput. (2007) 189:1859–83. doi: 10.1016/j.amc.2006.12.066

Crossref Full Text | Google Scholar

31. Zhao X. A perturbed particle swarm algorithm for numerical optimization. Appl Soft Comput. (2010) 10:119–24. doi: 10.1016/j.asoc.2009.06.010

Crossref Full Text | Google Scholar

32. Tang Y, Wang ZD, Fang JA. Feedback learning particle swarm optimization. Appl Soft Comput. (2011) 11:4713–25. doi: 10.1016/j.asoc.2011.07.012

Crossref Full Text | Google Scholar

33. Wang HF, Moon I, Yang SX, Wang DW. A memetic particle swarm optimization algorithm for multimodal optimization problems. Inform Sci. (2012) 197:38–52. doi: 10.1016/j.ins.2012.02.016

PubMed Abstract | Crossref Full Text | Google Scholar

34. Huang H, Qin H, Hao Z, Lim A. Example-based learning particle swarm optimization for continuous optimization. Inform Sci. (2012) 182:125–38. doi: 10.1016/j.ins.2010.10.018

Crossref Full Text | Google Scholar

35. Lawler GF. Introduction to Stochastic Processes, second edition. London: Chapman and Hall/CRC Press. (2006).

Google Scholar

36. Xiao XY, Yin HW. Moment convergence rates in the law of logarithm for moving average process under dependence. Stochastics. (2014) 86:1–15. doi: 10.1080/17442508.2012.748057

Crossref Full Text | Google Scholar

37. Hu D, Qiu X, Liu Y, Zhou X. Probabilistic convergence analysis of the stochastic particle swarm optimization model without the stagnation assumption. Inf Sci. (2021) 547:996–1007. doi: 10.1016/j.ins.2020.08.072

Crossref Full Text | Google Scholar

38. Chen J, Xin B, Peng Z, Dou L, Zhang J. Optimal contraction theorem for explorationexploitation tradeoff in search and optimization. IEEE Trans Syst Man Cybern Part A. (2009) 39:680–91. doi: 10.1109/TSMCA.2009.2012436

Crossref Full Text | Google Scholar

39. Ezugwu AE, Agushaka JO, Abualigah L, Mirjalili S, Gandomi AH. Prairie dog optimization algorithm. Neural Comput Applic. (2022) 34:20017–65. doi: 10.1007/s00521-022-07530-9

Crossref Full Text | Google Scholar

40. Lee J, Mukerji T. Probabilistic Particle Swarm Optimization (Pro]PSO) for Using Prior Information and Hierarchical Parameters. Department of Energy Resources Engineering, Stanford University (2014).

Google Scholar

41. Schmitt M, Wanka R. Particle swarm optimization almost surely finds local optima. Theor Comput Sci. (2014) 561:57–72. doi: 10.1016/j.tcs.2014.05.017

Crossref Full Text | Google Scholar

Appendix

Matlab codes

tic

clc

clear all

close all

rng default

LB=[0 0 0]; UB=[10 10 10];

m=3; n=50;

wmin=0.9; wmax=0.4; c1=2; c2=2;

maxite=100; maxrun=100;

for run=1:maxrun

run

for i=1:n

for j=1:m

x0(i,j)=round(LB(j) + (UB(j)-LB(j))*rand());

end

end

x=x0; v=0.1*x0; for i=1:n

f0(i,1)=ofun(x0(i,:));

end

pbest=x0;

[fmin0,index0]=min(f0);

gbest=x0(index0,:);

ite=1;

tolerance=1;

rho=0.9;

while ite <= maxite && tolerance > 10⁻¹²

w =wmax-(wmax-wmin)*ite/maxite; kappa=1; phi1=2.05; phi2=2.05;

phi=phi1+phi2;

chi = 2*kappa/abs(2−phi−sqrt(phi² − 4*phi));

a=1/w;

for i=1:n

for j=1:m

v(i,j)=chi*[w*v(i,j)+c1*rand()*(pbest(i,j)-x(i,j))+c2*rand()*(gbest(1,j)-x(i,j))];

end

end

for i=1:n

for j=1:m

x(i,j)=x(i,j)+v(i,j);

end

end

for i=1:n

for j=1:m

if x(i,j)<LB(j)

x(i,j)=LB(j);

elseif x(i,j)>UB(j)

x(i,j)=UB(j);

end

end

end

for i=1:n

f(i,1)=ofun(x(i,:));

end

for i=1:n

if f(i,1)<f0(i,1)

pbest(i,:)=x(i,:);

f0(i,1)=f(i,1);

end

end

[fmin,index]=min(f0);

ffmin(ite,run)=fmin;

ffite(run)=ite;

if fmin<fmin0

gbest=pbest(index,:);

fmin0=fmin;

end

if ite>100;

tolerance=abs(ffmin(ite-100,run)-fmin0);

end

if ite==1;

disp(sprintf('Iteration Best particle objective fun'));

end

disp(sprintf('

ite=ite+1;

end

gbest;

fvalue=-x(1)*sin(sqrt(abs(x(1))))-x(2)*sin(sqrt(abs(x(2))))-x(3)*sin(sqrt(abs(x(3))));

fff(run)=fvalue;

rgbest(run,:)=gbest;

disp(sprintf('——–'));

end

disp(sprintf(”));

disp(sprintf('************'));

disp(sprintf('Final Results——'));

[bestfun, bestrun] = min(fff)

best_variables = rgbest(bestrun, :)

disp(sprintf('**********'));

toc

plot(ffmin(1:ffite(bestrun),bestrun),'–b','linewidth',2);

xlabel('Iteration ');

ylabel('fitness function value');

title('CSPSO convergence characteristic')